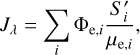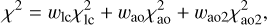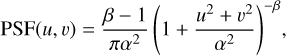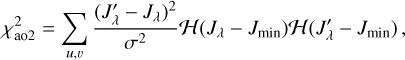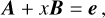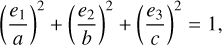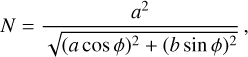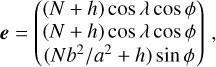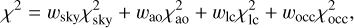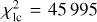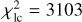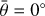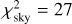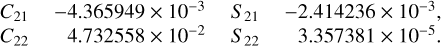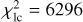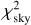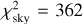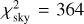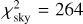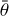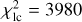| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202346326 | |
| Published online | 09 August 2023 | |
2021 occultations and transits of Linus orbiting (22) Kalliope
I. Polygonal and cliptracing algorithms
1
Charles University, Faculty of Mathematics and Physics, Institute of Astronomy,
V Holešovičkách 2,
18000
Prague,
Czech Republic
e-mail: mira@sirrah.troja.mff.cuni.cz
2
Arecibo Observatory, University of Central Florida, HC-3
Box 53995,
Arecibo, PR
00612,
USA
3
Korea Astronomy and Space Science Institute,
776 Daedeok-daero,
Yuseong-gu, Daejeon,
South Korea
4
Space sciences, Technologies and Astrophysics Research (STAR) Institute, University of Liège,
Allée du 6 Août 19,
4000
Liège,
Belgium
5
Department of Earth, Atmospheric and Planetary Sciences, MIT,
77 Massachusetts Avenue,
Cambridge, MA
02139,
USA
6
Academy of Sciences of the Czech Republic, Astronomical Institute,
Fričova 1,
25165
Ondřejov,
Czech Republic
7
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange,
France
Received:
4
March
2023
Accepted:
7
June
2023
Aims. The satellite Linus orbiting the main-belt asteroid (22) Kalliope exhibited mutual occultation and transit events in late 2021. A photometric campaign was organised and observations were undertaken by the TRAPPIST-South, SPECULOOS-Artemis, OWL-Net, and BOAO telescopes, with the goal to further constrain dynamical and photometric models of this sizeable asteroid-satellite system.
Methods. Our dynamical model is sufficiently complex, featuring multipoles (up to the order of ℓ = 2), internal tides, and external tides. The model was constrained by astrometry (spanning 2001–2021), occultations, adaptive-optics imaging, and calibrated photometry, as well as relative photometry. Our photometric model was substantially improved. A new precise (<0.1 mmag) light curve algorithm was implemented, based on polygon intersections, which are computed exactly by including partial eclipses and partial visibility of polygons. Moreover, we implemented a ‘cliptracing’ algorithm, again based on polygon intersections, in which partial contributions to individual pixels are computed exactly. Both synthetic light curves and synthetic images then become very smooth.
Results. Based on our combined solution, we confirmed the size of Linus, namely, (28 ± 1)km. However, this solution exhibits some tension among the light curves and the PISCO speckle-interferometry dataset, acquired simultaneously with the 2021 events. This indicates that improvements of the shape are still possible. In most solutions, Linus is darker than Kalliope, with the single-scattering albedos Aw = 0.40 vs. 0.44. This is confirmed on deconvolved images. A detailed revision of astrometric data has allowed us to revise also the J2 ≡ −C20 value of Kalliope. Most importantly, a homogeneous body is excluded. For a differentiated body, two solutions exist: low-oblateness (C20 ≃ −0.12), with a spherical iron core, and, alternatively, high-oblateness (C20 ≃ −0.22) with an elongated iron core. These values correspond, respectively, to the low- and high-energy collisions we studied via SPH simulations in our previous work.
Key words: minor planets, asteroids: individual: (22) Kalliope / planets and satellites: individual: Linus / celestial mechanics / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Mutual events between asteroids and their satellites are not rare occurrences (e.g., Pravec & Hahn 1997; Ragozzine & Brown 2009; Wong & Brown 2019; Scheirich & Pravec 2022) and the timings of occultations, transits, or eclipses can be used for various precise measurements. Such timings were recently used to measure the outcome of the DART experiment (Cheng et al. 2018; Statler et al. 2022; Thomas et al. 2023).
The (22) Kalliope and Linus binary system exhibited eclipse events back in 2007 (Descamps et al. 2008). With the shape of Kalliope derived from light curves, along with an assumed spherical shape for Linus, they obtained its size (28 ± 2) km, based on magnitude drops due to eclipses. This value is compatible with the shadow of Linus, which was observed during the stellar occultation event on 7 November 2006.
Here, we use more complex dynamical and photometric models of the (22) Kalliope and Linus system to interpret 2021 mutual occultation and transit events. At the same time, our preferred shape model was constrained by the VLT/SPHERE high-resolution AO imaging (Ferrais et al. 2022). Finally, a new context has been set up by the discovery of the first M-type Kalliope family (Brož et al. 2022a), which strongly suggests a differentiated interior.
The paper is organized as follows. In Sect. 2, new light curve data are presented, together with other data used to constrain the model. In Sect. 3, a new polygonal light curve algorithm is described. It is generally needed to achieve high precision (<0.1 mmag), whenever a moon is relatively small or the signal-to-noise ratio is relatively high. In Sect. 4, a ‘cliptracing’ procedure is described, used to compute synthetic images that are as smooth as possible. Additionally, in Sect. 5, we explain the stellar occultation algorithm. In Sect. 6, the results of our astrometric and photometric models are presented.
2 Observational data
2.1 New light curves
We obtained a calibrated photometry in the Rc band at the 0.6-m TRAPPIST-South telescope (Jehin et al. 2011) and in the custom ‘z cut’ filter at the 1-m Artemis telescope (Burdanov et al. 2022) of the SPECULOOS network (Delrez et al. 2018). The narrowband ‘z cut’ filter (transmittance >90% from 860 to 1100 nm) was used to avoid saturation of the CCD pixels and to suppress the effect of atmospheric water absorption. The relative precision of these data is about 3 mmag. Additional offsets are present between individual nights, which cannot be explained by the variable distance or the phase curve. Hence, the absolute precision is (at worst) 80 mmag.
Out of all the light curves, the first one includes a total occultation of Linus. The second is a total transit of Linus. The third is a partial transit of Linus, when only a dark part of (22) was hidden. The fourth is a partial occultation of Linus, when approximately half of Linus was hidden. The event times were prediced using the ephemeris from Ferrais et al. (2022).
We also obtained a relative photometry in the Rc band at the 1.6-m OWL-Net (Park et al. 2018) and 1.8-m BOAO (Sung et al. 2012) telescopes. The data from 2459557, 2459559 were removed because the signal-to-noise ratio (S/N) was worse due to weather conditions.
Additional dense light curves were taken from the DAMIT database (Ďurech et al. 2010), in particular, 2454175, 2455965. An additional reference light curve from 2459711 was obtained by the BlueEye600 telescope (Ďurech et al. 2018) to constrain the rotation phase.
Light curves from the previous series of events (Descamps et al. 2008) was also used, in particular, 2454167, 2454176, (denoted as ‘16’, ‘25’ by Descamps et al. 2008), together with the cited authors’ reference curves (‘14’, ‘27’). They included a total eclipse of Linus, and an annular eclipse of Kalliope. These data were precisely digitised from figures. All the data were consistently converted from the UTC to the TDB timescale. The summary of observational circumstances is presented in Table 1.
2.2 Calibrated photometry
Moreover, we used sparse calibrated photometry from Gaia (Gaia Collaboration 2018), namely 19 points, with a <1 mmag precision. They were transformed from G to V as follows (van Leeuwen et al. 2018):
where a = −0.02907, b = −0.02385, c = −0.22970, d = −0.001768, and B − V = 0.70 mag was taken from Lupishko et al. (1982). In order to interpret these high-precision data, access to a precise shape model of (22) is necessary; otherwise the phase curve could not be fitted at all. The data from 2457865.8993, 2457886.9754 were removed from the fit because they were too offset with respect to the neighbouring points.
In order to extend the phase coverage, from 2 up to 20°, we also included the calibrated UBV photometry from Gehrels & Owings (1962), Scaltriti et al. (1978), Surdej et al. (1986).
2.3 Astrometry
All astrometric data were summarised in Ferrais et al. (2022). In this work, SCAM, PHARO, IRCAL, NIRC2, NACO, NIRI, BTA, SOR, SPHERE, and PISCO datasets were used. Out of the Keck/NIRC2 dataset, four close-in-time measurements, 2452270, 2452270, 2452270, and 2452270, were removed from the fit because they exhibited a systematic photocentre offset. We checked the original images, which were fuzzy due to tracking problems (in fact, there were even two Linuses present in one image).
The astrometry of Descamps et al. (2008), inferred from the eclipse events, 2454167, 2454167, 2454176, and 2454176, was removed due to unrealistic uncertainties, which were certainly correlated with the shape. However, the shape was somewhat uncertain at that time (cf. their Fig. 2 and Ferrais et al. 2022).
The C2PU/PISCO dataset (Scardia et al. 2019), measured by speckle interferometry, is important because it is temporarily close to the 2021 events. The data from 2459580.6281 were removed due to a substantial offset with respect to the neighbouring points. Photocentre-to-centre-of-mass corrections were derived from our photometric model (Sect. 3) and applied consistently to all astrometric data.
2.4 AO imaging
The AO imaging by the VLT/SPHERE/ZIMPOL was already described in Ferrais et al. (2022). In this work, 35 deconvolved images were used to obtain observed silhouettes and to constrain the orientation of (22) or to prevent unwanted pole orientations. The uncertainty of silhouettes was nominally assumed 1 mas; the pixel scale is 3.6 mas pxl−1, so it corresponds to a sub-pixel precision. It is a very useful regularisation of our dynamical model because it is sensitive to the inclination of Linus’ orbit with respect to the equator of (22).
Moreover, some of the deconvolved images include Linus itself, in the limited field of view. This can be used to constrain the albedos of both bodies, in other words, to determine whether Linus is darker (or brighter) than (22) Kalliope.
2.5 Stellar occultations
The occultation of (22) Kalliope was already used to refine the shape model (Ferrais et al. 2022). Here, we use the most precise astrometric position inferred from the 7 November 2006 occultation, which included also Linus (Descamps et al. 2008). In this case, the astrometry is free from any photocentre offsets.
Another occultation on 2 March 2022 did not include Linus, unfortunately. For (22) Kalliope, only minor systematic differences at the limb were apparent, with respect to the nominal shape model.
2.6 Shape model
In this work, we use the ADAM shape model from our previous work (Ferrais et al. 2022). It was well-constrained by the AO imaging, light curves, and occultations. However, it could be revised if the pole inferred from dynamics is significantly different from the nominal pole (l = 195°, b = 4°). For a homogeneous body, the oblateness is J2 = −C20 = 0.1586.
This shape was derived with a regularisation of the centre of mass and the moment of inertia tensor, in order to enforce a rotation about the principal axis. The respective photometry is thus insensitive to any offsets of the centre of mass; it is similar to the case of re-centring.
However, there are possible offsets due to the inhomogeneous structure. Hydrodynamic simulations of collisions with a differentiated body, as described in Brož et al. (2022a), suggest mantle ejection, core deformation, gravitational reaccumulation, and asymmetric deposition (cf. 2 hills, elongated core). Consequently, centre-of-mass offsets will be eventually treated as free parameters.
Observational circumstances of photometric data.
2.7 Scattering law
Initially, we assumed the Hapke scattering law (Hapke 1981), with parameters similar to those of (216) Kleopatra, which is also also an M-type (Descamps et al. 2008). Namely, the opposition effect amplitude B0 = 1.276, the o. e. width h = 0.0470, the asymmetry factor g = −0.254, and the roughness 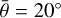 .
.
However, preliminary tests showed that the roughness must be 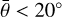 , otherwise the light curve is too curved. We thus preferred to use the roughness from Spjuth (2009), namely, their Table 6.3, for (2867) Šteins,
, otherwise the light curve is too curved. We thus preferred to use the roughness from Spjuth (2009), namely, their Table 6.3, for (2867) Šteins, 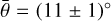 . For the phase-curve fitting, we also need the spectral slope γ = 0.45 between the V, Rc bands. This value was derived from the observed spectra of (22) Kalliope (DeMeo et al. 2009).
. For the phase-curve fitting, we also need the spectral slope γ = 0.45 between the V, Rc bands. This value was derived from the observed spectra of (22) Kalliope (DeMeo et al. 2009).
3 Polygonal light curve algorithm
First, we implemented a new polygonal light curve algorithm to compute light curves of asteroid-satellite systems as precisely as possible. Apart from a stand-alone Fortran module, it was included in our asteroid modelling tool Xi tau1, The algorithm is based on an analytical computation of polygon intersections (Vatti 1992) and the Clipper2 C++ library2. This is a similar approach as in the stellar modelling tool Phoebe2 (Prša et al. 2016), but complicated by the fact that we have to compute not only the visibility, but also non-convex shadowing, which is critical for asteroids.
In our model, everything is orbiting, rotating, or being affected by free parameters, including the Sun, Earth, (22) Kalliope, and Linus. At every time step, occultations, transits, or eclipses must be computed efficiently and exactly. This includes not only the total, but also the partial or annular events. Moreover, the algorithm should work even if polygons of the first body are several times smaller that those of the second body. Of course, uncertainties of the shape itself cannot be avoided (e.g., sphere versus icosahedron), but the discretisation errors due to the finite number of polygons should be minimised (to <1 mmag).
In order to obtain one light curve point, we proceed as follows. At the stellar surface, we first compute the monochromatic intensity:
the monochromatic flux:
the monochromatic power:
and the pass-band power:
where ∆eff denotes the effective passband.
At the asteroid surface, we compute the incoming monochromatic flux:
where d1 denotes the Sun-asteroid distance; the pass-band flux:
the reflectance for the given spectral slope γ:
and the Lambert law factor:
where Aw denotes the single-particle albedo (at 0,55 μm).
At the observer location, we evaluate the solid angle:
where d2 denotes the asteroid-observer distance; and the passband calibration flux:
Originally, the shape model is composed of triangular faces. A scaling of nodes, axis rotations, pole orientations, and relative positions of both (22) and Linus are subsequently computed.
A conversion to i sets of polygons si is then performed; this is important because a clipping of one triangle by another triangle is one or more polygons. Every set contains j polygons pij. Every polygon contains k points pi,j,k. Yet, each set, si, is always located in the same plane because we retain the original geometry.
The geometry is described by the normals 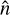 , the centres c, and the directional cosines μi, μe. The non-illuminated and non-visible polygons do not need to be computed (μi < 0 ∧ μe ≤ 0).
, the centres c, and the directional cosines μi, μe. The non-illuminated and non-visible polygons do not need to be computed (μi < 0 ∧ μe ≤ 0).
The first transformation is determined by the asteroid→Sun unit vector s, which determines the new basis:
and the respective coordinates:
To optimise the computation, we perform bounding-box tests. It is only if polygons are in the proximity, we then compute the two-dimensional (2D) shadowing (clipping) with the three-dimensional (3D) back-projection as:
where 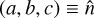 , and
, and 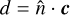 .
.
The second transformation is determined similarly by the asteroid→observer unit vector o, with the same Eq. (13). We then compute the visibility (clipping), and the back-projection, with the same Eq. (14). The surface area of the resulting polygons is computed as:
where a is the first of the polygon points рцх and b, с are the second, third, etc. pi,j,k, pi,j,k+1. The sign test is necessary for small polygons ≪ big polygons (or annular eclipses).
The incoming monochromatic flux (in W m−2 m−1) is then:
the monochromatic intensity (in W m−2 sr−1 m−1) is determined by the bi-directional scattering function:
depending on the cosines and the phase angle α. The outgoing monochromatic flux is:
Finally, the integration over the surface determines the monochromatic luminosity (in W sr−1 m−1):
the pass-band flux:
and the brightness (in mag):
A two-sphere test of the algorithm is demonstrated in Fig. 1 and the respective light curve for different discretisations in Fig. 2. A tiny-triangle test (Fig. 3) shows that annular eclipses are computed exactly, even for a coarse discretisation.
 |
Fig. 1 Two-sphere test of the polygon light curve algorithm. We can even use a very coarse discretisation of 42 nodes for each sphere, because we compute partial eclipses, partial occultations, or partial transits. Shades of gray show the monochromatic intensity Iλ (in W m−2 sr−1 m−1), green lines show the non-eclipsed and non-occulted polygons used to compute the surface areas. The orange arrow shows the direction towards the Sun and blue towards the observer. The test bodies are metre-sized, 1 au from the Sun and 1 au from the observer. See also Fig. 2. |
4 Cliptracing algorithm
Second, we implemented a new ‘cliptracing’ algorithm, which deals with the discretisation errors of synthetic images. Traditional raytracing algorithms perform an inside-triangle test and use parameters of the respective triangle. Hereinafter, we compute contributions of polygons to individual pixels exactly.
We defined one pixel as one polygon in the sky-plane coordinates (u, υ, w):
where u, υ correspond to the centre of pixel, ∆u, ∆υ to the size of pixel. In a cycle over all non-shadowed ∧ visible polygons, we ‘crop’ (intersect) each of them by p1, and sum individual contributions to one pixel, to get the monochromatic luminosity of one pixel:
where we used already projected surface area 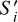 , because in our previous formalism (i.e. Eq. (20)), we multiply by the unprojected areas, Si. Everything is computed analytically, with no discretisation artefacts or edge artefacts, and the outcome is a smooth synthetic image (see Figs. 4 and 5).
, because in our previous formalism (i.e. Eq. (20)), we multiply by the unprojected areas, Si. Everything is computed analytically, with no discretisation artefacts or edge artefacts, and the outcome is a smooth synthetic image (see Figs. 4 and 5).
When we compare the synthetic image with the observed one, we have to re-center (with a sub-pixel precision). Let us denote c the photocentre of the observed AO image and c' as the photocentre of the synthetic AO image. The cliptracing is therefore computed with a centre shifted to −c + c'.
An optimisation is performed by using a number of bounding-box tests, namely: the observed bounding-box, the over-all-polygons bounding-box, the one-pixel bounding-box, and the individual bounding-boxes of polygons.
Another problem we have to deal with at this level of precision, is a correlation of ‘everything’ with the shape. Especially since the timings of events depend on details of the shape, henceforth, we created a new version of our modelling tool focused on the fitting of shape (‘Xi taushp’).
The parameters are radius vectors of the ‘control’ shape, which is processed by a sub-division algorithm (Kobbelt 2000; Viikinkoski et al. 2015), with between one and four levels. The input orbit is read from the previous output, for simplicity.
To constrain the shape, we use a modified χ2 metrics:
where the individual contributions (and weights) correspond to the light curves (LC), silhouettes (AO), and synthetic images (AO2). If not stated otherwise, we use unit weights. The computation of silhouettes was already described in Brož et al. (2021). Here, it was improved by a multi-point interpolation, which is smooth even for low resolution, even for deconvolution artefacts, which is occasionally present as a drop of signal at the edge (‘staircase’).
The synthetic image is convolved with the point-spread function (PSF). We use the Moffat PSF:
with free parameters α, β. Alternatively, an observed stellar PSF can be input; it is rather complex, with the Strehl ratio about 0.1, a diffraction pattern, a ring, a cross, remaining AO artefacts. However, for deconvolved images, we would need a ‘residual’ PSF instead.
The respective χ2 contribution for synthetics images is computed as a sum over pixels:
where Jλ(u, υ) denotes the observed monochromatic luminosity, 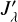 synthetic, ℋ(x) the Heaviside step function. The Poisson uncertainty is computed as
synthetic, ℋ(x) the Heaviside step function. The Poisson uncertainty is computed as 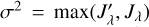 for each pixel, because sometimes we have to compare to darkness (Jλ = 0). The minimum luminosity is computed as Jmin = f max(Jλ) for all pixels, because background is rather extended and uneven; the factor f (threshold) often corresponds to the silhouettes.
for each pixel, because sometimes we have to compare to darkness (Jλ = 0). The minimum luminosity is computed as Jmin = f max(Jλ) for all pixels, because background is rather extended and uneven; the factor f (threshold) often corresponds to the silhouettes.
 |
Fig. 2 Light curves for a two-sphere test, computed for different discretisations: 42, 272, and 1123 nodes. The precision is of the order < 0.1 mmag, even for the coarse discretisation. Tiny changes of the derivative are related to subsequently eclipsing or occulting large triangles with different normals. The magnitude in V band is computed for the effective wavelength λeff = 545 nm and the effective passband ∆eff = 85 nm. |
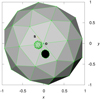 |
Fig. 3 Similar to Fig. 1. A tiny-triangle test, where one body is large and other body is small. It demonstrates that annular eclipses, as well as partial eclipses, partial occultations, and partial transits, are computed exactly. The polygon corresponding to the shadow (black) has a negative signed area. |
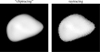 |
Fig. 4 1:1 comparison of the ‘cliptracing’ (left) and the raytracing (right) algorithms. In the former, polygons were clipped by individual pixels (analytically) and the synthetic image of (22) is very smooth. In the latter, a simple inside-polygon test was used for each ray, which creates discretisation artefacts and the synthetic image is then ‘noisy’. The Lambert scattering law was used in this test. |
 |
Fig. 5 Same as Fig. 4, but showing the corresponding shape composed of polygonal faces (gray) and a grid of either square pixels or points (green). |
5 Stellar occultation algorithm
Third, we implemented a new occultation algorithm in Xi tau. It is used to check the astrometric positions, timings of occultations, and precision of the ephemerides. At the start, we used a sphere-intersection test to speed-up the computation. We applied a standard TDB to UT1 conversion (IAU SOFA Center 2014), precession (Lieske et al. 1977) nutation (Wahr 1981; Wolf 1992), an equatorial-of-J2000 to equatorial-of-date transformation, a proper motion of the respective star (from the Gaia DR3), and an ellipsoid-intersection test:
specifically for the WGS-84 ellipsoid (a = b = 6.378173 × 106 m, c = 6.3567523142 × 106 m), where A denotes the Earth→asteroid vector, B star→asteroid (normalised), and e is the intersection point on the ellipsoid, while x is a nuisance parameter. The equation is quadratic in x. At the end, we applied UT1 to the GST conversion, the Earth’s rotation, and a transformation to the geodetic coordinates:
with an iterative procedure for the inverse.
An example for (22) Kalliope is shown in Fig. 6. The algorithm was verified against selected events from the Occult software (Herald et al. 2020), for instance, the astrometric position of (216) Kleopatra, on Mar 12, 2015 (see Fig. A.1).
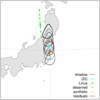 |
Fig. 6 7 November 2006 stellar occultation of (22) Kalliope and Linus, computed for the model with χ2 = 6695 (from Table 2). The trajectories of (22) and Linus are plotted (cyan, green), together with several shadows of (22) computed for the observed timings (black), observers’ locations (blue), synthetic locations of the nearest shadow points (yellow), and residuals (red). The timings were taken from the occultation database (Herald et al. 2019, 2020). Absolute time measurements were used to check the ephemeris accuracy. The gnomonic projection was used, showing Japan, Honshu. |
6 Occultation, transit, and eclipse events
Before we proceed with a description of the fitting, it is useful to summarise our dynamical model: it uses the Bulirsch-Stoer numerical integrator adaptive time step, which allows us to compute non-Keplerian orbits, multipoles up to the order ℓ = 2, internal tides, or external tides caused by the Sun (Brož 2017; Brož et al. 2021, 2022b). In the nominal model, we assume the tidal time lag ∆t1 ≃ 40 s inferred for (216) Kleopatra.
Modifications were described in detail in Sects. 3–5. Explanations for all the parameters is included in Table 2. In particular, we added a few free parameters, namely: С20,1, Aw1, Aw2, B0, h, g, and 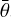 , which allowed us to fit the astrometry, light curves, and scattering parameters. Alternatively, we added offsets in
, which allowed us to fit the astrometry, light curves, and scattering parameters. Alternatively, we added offsets in 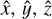 directions, to account for a possible rotation about different axis.
directions, to account for a possible rotation about different axis.
We used several types of observations to constrain the model:
where individual contributions correspond to astrometry (the so-called SKY dataset), silhouettes (AO), light curves (LC), or occultations (OCC); all of them with corresponding weights. Previously, we used wao = 0.003, so that AO contributes comparably as SKY. Of course, every model requires reasonable initial conditions; therefore we used the best fit from Ferrais et al. (2022), with the osculating elements adjusted to match a slightly simplified dynamics (ℓ = 2). We verified that omitting high-order terms does not substantially shift the values of low-order terms, in particular, of the oblateness, С20.
Parameters, along with their values and uncertainties for the nominal and high-oblateness models of the (22) Kalliope and Linus system.
6.1 Long-arc scattering model
First, we focused on the phase curve, which is controlled by six free parameters: Aw1, Aw2, B0, h, g, and 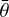 . We used the calibrated photometry from Gehrels & Owings (1962), Scaltriti et al. (1978), Surdej et al. (1986), as well as this work and Gaia DR3 data. The zero points were fixed, however, we expected calibration systematics up to 0.05 mag. A shape model of (22) Kalliope is necessary, because the lightcurve amplitude can reach 0.6 mag, depending on geometry. The simplex and subplex (i.e., simplex on subspaces; Rowan 1990) algorithms were used, with several restarts. The resulting phase curve is shown in Fig. 7.
. We used the calibrated photometry from Gehrels & Owings (1962), Scaltriti et al. (1978), Surdej et al. (1986), as well as this work and Gaia DR3 data. The zero points were fixed, however, we expected calibration systematics up to 0.05 mag. A shape model of (22) Kalliope is necessary, because the lightcurve amplitude can reach 0.6 mag, depending on geometry. The simplex and subplex (i.e., simplex on subspaces; Rowan 1990) algorithms were used, with several restarts. The resulting phase curve is shown in Fig. 7.
The model is sensitive mostly to Aw1, B0, and h scattering parameters. The unreduced 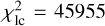 is too large compared to the number of observations, nlc = 1892, due to any remaining calibration systematics. If 0.05 mag uncertainties are used instead, the χ2 decreases down to n. Nevertheless, the best-fit values, Aw1 = 0.419, B0 = 1.733, h = 0.0295, seem to be reasonable. A correlation exists between g, Aw1, B0, because small g can be compensated by large Aw1, B0. Hence, the overall uncertainties are increased to 0.10, 0.1, 0.01, respectively. If g and
is too large compared to the number of observations, nlc = 1892, due to any remaining calibration systematics. If 0.05 mag uncertainties are used instead, the χ2 decreases down to n. Nevertheless, the best-fit values, Aw1 = 0.419, B0 = 1.733, h = 0.0295, seem to be reasonable. A correlation exists between g, Aw1, B0, because small g can be compensated by large Aw1, B0. Hence, the overall uncertainties are increased to 0.10, 0.1, 0.01, respectively. If g and 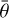 are also free, their values tend to converge towards
are also free, their values tend to converge towards 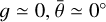 , which does not seem to be common (cf. Li et al. 2015). In order to fit both the phase curve and the light curve with the given shape of (22), we use these values until we modify the shape (Sect. 6.7). Their uncertainties are of the order of 0.10, and10°, respectively. The detailed light curve shape is also sensitive to g,
, which does not seem to be common (cf. Li et al. 2015). In order to fit both the phase curve and the light curve with the given shape of (22), we use these values until we modify the shape (Sect. 6.7). Their uncertainties are of the order of 0.10, and10°, respectively. The detailed light curve shape is also sensitive to g, 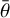 .
.
6.2 Short-arc scattering model
We fitted details on two light curves from SPECULOOS-Artemis (datasets 3 and 4) because we have to use calibrated photometry and avoid any zero-point offsets between datasets. We note again that the zero points were fixed. We computed a systematic grid for g, 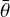 parameters, which were kept fixed, while the R1, R2, Prot1, Aw1, and Aw2 parameters were free. According to Fig. 8, the fit is still not perfect (
parameters, which were kept fixed, while the R1, R2, Prot1, Aw1, and Aw2 parameters were free. According to Fig. 8, the fit is still not perfect (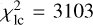 , nlc = 909) partly because everything is interrelated – albedo, scattering, shape, pole, Linus, orbit, occultations, transits, eclipses, and so on. It is possible to find solutions for g = −0.10 up to 0.05, and
, nlc = 909) partly because everything is interrelated – albedo, scattering, shape, pole, Linus, orbit, occultations, transits, eclipses, and so on. It is possible to find solutions for g = −0.10 up to 0.05, and 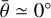 . Small values of g seem to be excluded, because the albedo Aw2 of Linus is pushed to unrealistic low values. Large values of
. Small values of g seem to be excluded, because the albedo Aw2 of Linus is pushed to unrealistic low values. Large values of 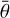 seem to be excluded, because the light curve amplitude is incorrect (at least for the given shape). Given the preference for negative g (Spjuth 2009), we prefer solutions close to g = −0.025,
seem to be excluded, because the light curve amplitude is incorrect (at least for the given shape). Given the preference for negative g (Spjuth 2009), we prefer solutions close to g = −0.025, 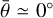 . Alternatively, albedo variegation, or roughness variegation may be present on the surface.
. Alternatively, albedo variegation, or roughness variegation may be present on the surface.
 |
Fig. 7 Phase curve of the (22) Kalliope and Linus system. The reduced brightness H0 versus the phase angle α is plotted. Calibrated photometry from Gehrels & Owings (1962), Scaltriti et al. (1978), Surdej et al. (1986), this work, and the Gaia DR3 was used. The observed curve (×) is plotted in colour (according to the Julian date) and the synthetic (+) is in yellow. The range of α is from 2 to 22°. There is an unreduced |
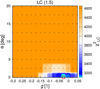 |
Fig. 8 Asymmetry factor g versus roughness |
 |
Fig. 9 Orbit of Linus in the (u, υ) plane, derived from the short-arc astrometric + photometric model. It fits the PISCO dataset around 2459579, namely, close to the mutual occultation events, when the orbit is seen from the edge. The synthetic orbit of Linus (i.e., body 2) is plotted in green, the observed astrometry in yellow, the residuals in red, the shape of (22) in black. The viewing geometry is changing in the course of time; otherwise the orbit is elliptical. The position at the reference epoch T0 is marked by the cross. The contribution χ2 is |
6.3 Short-arc astrometric + photometric model
As the next step, we fit four light curves from SPECULOOS-Artemis and TRAPPIST-South (dataseis 1, 2, 3, and 4), together with the PISCO astrometric dataset, which was acquired very close to the occultation and transit events. Also, the silhouettes were used to prevent incompatible pole orientations, which influence the events. Analytical zero points were computed, compensating for any remaining offsets between the respective light curves. The best-fit weighted and unreduced total is χ2 = 6462, with the individual contributions 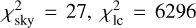 , and
, and 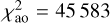 , where the respective numbers of observations are nsky = 36, nlc = 1829, nао = 12960. The fit exhibits no systematics in astrometry (see Fig. 9). Minor systematics are present in the light curves, (Fig. 10), nevertheless, the amplitude as well as the duration of the occultations and transit events are matched almost perfectly. An example of the geometry is shown in Fig. 11. We checked that a mirror solution (occultation ↔ transit) is not possible; the variable geometry allows us to distinguish between these solutions.
, where the respective numbers of observations are nsky = 36, nlc = 1829, nао = 12960. The fit exhibits no systematics in astrometry (see Fig. 9). Minor systematics are present in the light curves, (Fig. 10), nevertheless, the amplitude as well as the duration of the occultations and transit events are matched almost perfectly. An example of the geometry is shown in Fig. 11. We checked that a mirror solution (occultation ↔ transit) is not possible; the variable geometry allows us to distinguish between these solutions.
6.4 Long-arc astrometric model
In order to constrain the dynamical parameters, astrometric measurements from 2452151 to 2459580 were used, as well as the silhouettes to prevent incompatible pole orientations. In this case, the free parameters were: msum, P1, log e1, i1, Ω1, ϖ1, λ1, lроlel, bpolel, ϕ01, while the fixed parameters: q1, C20,1, ∆t1. Actually, we computed an extended grid for the latter two parameters, in the range between −0.22 and −0.08, 0 and 60 s, respectively. Apart from C20,1, we included other multipoles up to ℓ = 2, which were computed for a homogeneous structure:
A very important result is establishing that two solutions exists for the oblateness, C20,1, either ≃ − 0.20 or ≃ − 0.12 (see Fig. 12). A homogeneous body with С20,1 = −0.1586 was excluded. These two solutions correspond to one or three nodal precession cycles (see, e.g., Fig. 16). There is no other option (four or one cycles), because С20,1 would then be unrealistic (too high or too low). The best-fit value is 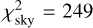 , or alternatively
, or alternatively 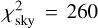 . It indicates no systematics and possibly overestimated uncertainties because the number of data points is nsky = 344 (both p, θ).
. It indicates no systematics and possibly overestimated uncertainties because the number of data points is nsky = 344 (both p, θ).
We also checked a range of log e1, i1 values (Fig. A.2). We tested mirror solutions, retrograde solutions, and shifted-by-180° solutions. There is no alternative solution for the eccentricity, nor the inclination. The uncertainties are up to 0.5 (in log-scale), that is: 0.5°.
 |
Fig. 10 Phased light curves for the short-arc, astrometric + photometric model (top). It shows the first occultation of Linus and the second transit of Linus, together with the reference light curves. The observed light curve is plotted as blue (with error bars), the synthetic as yellow, the residuals as red. The shades of blue correspond to the Julian date. The drop in brightness is up to 0.05 mag. Both the amplitude and duration of the events are in agreement. For comparison, we also plot the difference О − С (bottom). Remaining systematics occur on all light curves; so they must be related to the shape, not the occultations. The contribution to χ2 is |
 |
Fig. 11 Example of geometry for the mutual occultation of Linus by (22) Kalliope, namely, the event 2459546. The monochromatic intensity Iλ (in W m−2 sr−1 m−1) is shown as shades of gray. The ADAM shape model with 800 faces was used for (22), and a sphere with 80 faces for Linus. It is sufficient because partial occultations of faces were computed by the polygonal light curve algorithm. |
 |
Fig. 12 Quadrupole moment C20,1 vs. the tidal time lag ∆t1 of the central body. The corresponding |
6.5 Long-arc, astrometric + photometric model
In order to constrain the physical parameters, four light curves (datasets 1, 2, 3, and 4), all astrometric measurements, and all silhouettes were used. Apart from the dynamical parameters, the additional free parameters, R1, R2, Prot1, Aw2, can be now constrained by mutual occultation and transit events. We fixed the parameters: Aw1, B0, h, g, 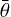 , otherwise the model would not match the calibrated photometry (Sect. 6.1). Again, a grid of С20,1, ∆t1 was computed (Fig. 13).
, otherwise the model would not match the calibrated photometry (Sect. 6.1). Again, a grid of С20,1, ∆t1 was computed (Fig. 13).
The best-fit χ2 = 7095, with the individual contributions 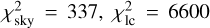 , and
, and 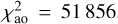 . All of them are slightly worse, most likely due to a combination of more observational datasets, but it is an acceptable compromise.
. All of them are slightly worse, most likely due to a combination of more observational datasets, but it is an acceptable compromise.
Regarding the oblateness, С20,1 ≃ −0.12 seems to be a bit more compatible with the light curves, but we still cannot exclude the −0.22 solution. The tidal time lag is not well constrained. The volume-equivalent diameters of (22), D1 = 151.0 km, is still compatible with the ADAM or MPCD shapes (Ferrais et al. 2022), with the uncertainty on the order of 1 km.
A specific grid was computed for R2, Aw2 of Linus (Fig. 14). It further improved the result, with χ2 = 6695. In this particular model, D2 = 28.8 km, with a similar uncertainty. It is compatible with the stellar occultation observed on 7 November 2006 (Descamps et al. 2008). All parameters of this model are presented in Table 2. The global uncertainties of parameters were estimated from a series of alternative admissible solutions (cf. models above; Figs. 12-14). In this order-of-magnitude estimate, we included also a contribution from systematic uncertainties. We verified these results by using all available light curves (from Table 1), which resulted in a statistically equivalent model (cf. Table A.1). The Markov chain Monte Carlo (MCMC) simulation is presented in Fig. A.3, which demonstrates typical local uncertainties and correlations in the surroundings of one local minimum (close to χ2 = 6695).
Linus’ orbit, together with available astrometric measurements, is shown in Fig. 15. It was checked by the stellar occultation computation (Fig. 6). The temporal evolution of osculating elements is demonstrated in Fig. 16.
In most solutions, Linus seems to be darker compared to (22), the single-scattering albedo is Aw2 = 0.400, Aw1 = 0.438, respectively, with the local uncertainties of the order of 0.02. They are naturally correlated. The darkness is also apparent on those deconvolved AO images, which capture both (22) and Linus at the same time. The appearance is only partly affected by a difference between a (more) flat versus a (more) curved surface.
Finally, we should not be misled by sparse local minima, which are relatively deep; they compensate for some systematics on the light curve which are, however, unrelated to the mutual occultation or transit events. Yet such solutions are in contradiction with the PISCO astrometric dataset (see Fig. 15). Thus, we prefer solutions where the of fit the orbit just prior and posterior to the events. Possibly, the shape of (22) Kalliope should be also adjusted.
 |
Fig. 13 Similar to Fig. 12 for three datasets SKY, AO, LC, and the total χ2. A subset of four light curves was used. The LC dataset allows the respective parameters (C20,1, ∆t1) to be constrained even better, because one occultation and one transit must have a specific geometry. The AO contribution is mostly blue, but it does not mean that this dataset is unimportant. Actually, it excludes a lot of models with incompatible poles. |
 |
Fig. 14 Similar to Fig. 12 for the three datasets of SKY, AO, and LC. The radius, R2, vs. the single-particle albedo, Aw2, of Linus is plotted. Models were converged for 121 combinations of the fixed parameters; all other parameters were free. The preferred solution has |
 |
Fig. 15 Same as Fig. 9, for the long-arc, astrometric + photometric model. It was constrained by the astrometry over the time span 2001–2022. The most important measurements are indicated by blue labels (Julian date – 2400 000). The contribution to χ2 is |
 |
Fig. 16 Evolution of osculating orbital elements of Linus for the model with χ2 = 6695 (from Table 2). From bottom to top: a1 semimajor axis, e1 eccentricity, i1 inclination, Ω1 longitude of the ascending node, and ϖ1 longitude of pericentre. The reference frame is related to the equator of (22) Kalliope; the epoch T0 = 2459546.692102 (TDB). The model includes multipoles (ℓ = 2), internal tides, and external tides. Over the time span of astrometric observations (2001–2021), it exhibits two nodal precession cycles. |
6.6 Possible centre-of-mass offset of (22)
The simplest adjustment is a centre-of-mass offset due to an asymmetric internal structure. This implies rotation about a different axis and different extent of the central body in different directions. Because the orbit of Linus is well constrained by astrometry, the timings of mutual occultations or transits offer an opportunity to measure the offset not directly (in space), but indirectly (in time).
Therefore, we added three more free parameters to our model, the offsets in 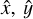 , or
, or 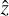 directions. After testing values up to 20 km, which did affect χ2 substantially, we conclude that it did not converge to a unique significant minimum. We thus have to look for a more complex solution.
directions. After testing values up to 20 km, which did affect χ2 substantially, we conclude that it did not converge to a unique significant minimum. We thus have to look for a more complex solution.
 |
Fig. 17 Residuals from the fitting of 35 deconvolved AO images of (22) Kalliope (taken from Ferrais et al. 2022), with contributions to χ2 of individual pixels plotted in colour. The projected shape changes due to rotation and viewing geometry. The pixel scale is 3.6 mas pxl−1. After the convergence of the shape parameters, with help of the polygonal algorithm and ‘cliptracing’, the total is |
6.7 Possible shape adjustment of (22)
In order to have a full control, we derived a new shape model of (22) Kalliope. We started with a low-resolution ellipsoid, (with the number of nodes n = 42), which serves as a ‘control’ shape. After three sub-divisions, we obtained a high-resolution shape (n = 1082), which was converged and constrained by AO silhouettes as well as light curves. We used no additional regularisation term in our χ2 metric. Nevertheless, we ascertained that χ2 is indeed sensitive to all shape parameters.
In order to capture the finer details, we used the medium-resolution (22)-like shape (n = 122), after the first subdivision. After two more sub-divisions, we again obtained a highresolution shape, which was constrained by AO images and light curves.
In particular, we converged the following free parameters: Rshp,i radii of control nodes, R1, Prot1, lpole1, bpole1, ϕ01, Aw1, g, and 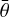 , with several restarts of simplex or subplex. The best-fit shape model is shown in Fig. 17.
, with several restarts of simplex or subplex. The best-fit shape model is shown in Fig. 17.
The total signal contained in all pixels in all images is ‘huge’, the unreduced 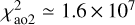 , while the number of points (pixels) taken into account is nao2 = 22 843. This is at least partly due to rotation, which changes the projected shape during an exposure in a non-trivial way, remaining deconvolution artefacts, present on images taken at 2458643, 2458661, 2458672, or a relatively low background level on the same set of images.
, while the number of points (pixels) taken into account is nao2 = 22 843. This is at least partly due to rotation, which changes the projected shape during an exposure in a non-trivial way, remaining deconvolution artefacts, present on images taken at 2458643, 2458661, 2458672, or a relatively low background level on the same set of images.
Overall, our new shape is still similar to the ADAM model (Fig. A.5) and it is even more so in the lines-of-sight projections. However, it is fine-tuned to the respective datasets, with the respective contributions, 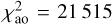 versus 35 209 and
versus 35 209 and 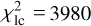 versus 6223, significantly improved. Systematics on the light curves related to the shape were at least partly eliminated (cf. Fig. A.4).
versus 6223, significantly improved. Systematics on the light curves related to the shape were at least partly eliminated (cf. Fig. A.4).
In principle, this shape ought to be re-used and the analysis started over again (from Sects. 6.1, 6.2, …). While it is not beyond the scope of this paper, we postpone such an in-depth study, including optimisations of ‘everything’ together with shape, to a future work.
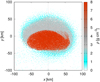 |
Fig. 18 One of the SPH simulations from Brož et al. (2022a), showing a medium-energy impact to a differentiated body, which created an elongated iron core. The time 10 000 s corresponds to the end of fragmentation phase. The density is indicated by the colour scale. The oblateness J2 = −C20 is higher (not lower) than for a homogeneous body. This could correspond to our long-arc, astrometric model with three precession cycles. |
7 Conclusions
In this work, the mutual occultation, transit, and eclipse events of Linus orbiting (22) Kalliope were used to constrain combined astrometric + photometric models of this binary system. Using innovative algorithms for photometric computations (see Sects. 3 and 4), we confirmed the size of Linus (28 ± 1)km, improved the shape of (22) Kalliope, and put strong constraints on its dynamical oblateness.
On one hand, we were not surprised by the low-oblateness (C20 ≃ −0.12) solution because (22) Kalliope is probably the best candidate for a differentiated body (Vernazza et al. 2021). At the same time, the iron core is usually considered to be (more or less) spherical because this is a standard outcome of differentiation.
On the other hand, we were surprised by the second solution, characterised by high oblateness (C20 ≃ −0.20). Surprisingly, it should correspond to an irregular (or highly ellipsoidal) iron core. In fact, (22) Kalliope suffered a major collision about 900 My ago, which gave birth to the Kalliope family (Brož et al. 2022a). Some of the SPH simulations of this event, we performed in our previous work, indicate that the iron core of the original body is deformed and may even be elongated, especially in medium- to high-energy collisions (with the projectile size > 45 km). One example is shown in Fig. 18.
In the future, it should be possible to distinguish these two solutions by new astrometric (imaging or speckle-interferometric) observations, obtained at a suitable phase(s) of the precession cycle (seen, e.g., Fig. 16).
Acknowledgements
This work has been supported by the Czech Science Foundation through grants 21-11058S (M. Brož), 23-04946S (J. Ďurech, J. Hanuš). In this work, measurements from the BlueEye600 telescope, supported by the Charles University, were used. The TRAPPIST is a project funded by the Belgian Fonds (National) de la Recherche Scientifique (F.R.S.-FNRS) under grant PDR T.0120.21. J.de.W. and MIT gratefully acknowledge financial support from the Heising-Simons Foundation, Dr. and Mrs. Colin Masson and Dr. Peter A. Gilman for Artemis, the first telescope of the SPECULOOS network situated in Tenerife, Spain. This paper was partially based on observations obtained at the Optical Wide-field patroL Network (OWL-Net) and the Bohyunsan Optical Astronomy Observatory (BOAO) which are operated by the Korea Astronomy and Space Science Institute (KASI). We also thank an anonymous referee for constructive comments.
Appendix A Supplementary figures
Stellar occultation algorithm verification for (216) Kleopatra is show in Fig. A.1. Additional models from Sect. 6.4 are shown in Fig. A.2. The corner plot discussed in Sect. 6.5 si shown in Fig. A.3. The adjusted shape model and the respective light curve fit discussed in Sec. 6.7 is shown in Figs. A.5, A.4. An additional best-fit model is presented in Table A.1.
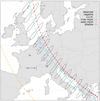 |
Fig. A.1 Verification of the stellar occultation algorithm for the occultation of the star HIP 54599 by asteroid (216) Kleopatra, on Mar 12, 2015. The shadow on the WGS-84 ellipsoid is plotted in black, the centre-of-mass location shown as a cyan line, the first moon in red, the second moon in orange, positive measurements as blue squares, negative measurements in gray. The gnomonic projection was used in this test. |
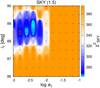 |
Fig. A.2 Similar to Fig. 12. The logarithm of eccentricity log e1 vs. the inclination i1 is plotted. Models were converged for 99 combinations of the fixed parameters; all other parameters were free. For each combination, 1000 iteration were computed, i.e., 99000 models in total. The overall best-fit result is |
 |
Fig. A.3 MCMC simulation for the model with χ2 = 6695 (from Table 2). Distributions of all parameters, corresponding to local uncertainties, and correlations of all pairs of parameters is plotted as a standard ‘corner’. The order of 22 parameters is as follows (↓, →): msum, q1, P1, log e1, i1, Ω1, ϖ1, λ1, R1, R2, Prot1, ∆t1, С20,1, lpole1, bpole1, ϕ01, Aw1, Aw2, B0, h, g, and |
 |
Fig. A.4 Same as Fig. 10, but referring the adjusted shape model of (22) Kalliope. Systematics on the light curves related to the shape were at least partly eliminated. The respective contribution has decreased to |
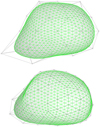 |
Fig. A.5 Comparison of the adjusted shape of (22) Kalliope (top) vs. the original ADAM shape (bottom). The control points (gray) and the high-resolution mesh (green) are indicated. Shades of gray correspond to the z coordinate. |
References
- Brož, M. 2017, ApJS, 230, 19 [Google Scholar]
- Brož, M., Marchis, F., Jorda, L., et al. 2021, A&A, 653, A56 [Google Scholar]
- Brož, M., Ferrais, M., Vernazza, P., Ševeček, P., & Jutzi, M. 2022a, A&A, 664, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brož, M., Ďurech, J., Carry, B., et al. 2022b, A&A, 657, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burdanov, A. Y., de Wit, J., Gillon, M., et al. 2022, PASP, 134, 105001 [CrossRef] [Google Scholar]
- Cheng, A. F., Rivkin, A. S., Michel, P., et al. 2018, Planet. Space Sci., 157, 104 [CrossRef] [Google Scholar]
- Delrez, L., Gillon, M., Queloz, D., et al. 2018, SPIE Conf. Ser., 10700, 107001I [Google Scholar]
- DeMeo, F. E., Binzel, R. P., Slivan, S. M., & Bus, S. J. 2009, Icarus, 202, 160 [Google Scholar]
- Descamps, P., Marchis, F., Pollock, J., et al. 2008, Icarus, 196, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Ďurech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 513, A46 [Google Scholar]
- Ďurech, J., Hanuš, J., Brož, M., et al. 2018, Icarus, 304, 101 [CrossRef] [Google Scholar]
- Ferrais, M., Jorda, L., Vernazza, P., et al. 2022, A&A, 662, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrels, T., & Owings, D. 1962, ApJ, 135, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuš, J., Ďurech, J., Oszkiewicz, D. A., et al. 2016, A&A, 586, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hapke, B. 1981, J. Geophys. Res., 86, 3039 [NASA ADS] [CrossRef] [Google Scholar]
- Herald, D., Frappa, E., Gault, D., et al. 2019, NASA Planetary Data System, 3 [Google Scholar]
- Herald, D., Gault, D., Anderson, R., et al. 2020, MNRAS, 499, 4570 [Google Scholar]
- IAU SOFA Center 2014, Astrophysics Source Code Library [record ascl:1403.026] [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Kobbelt, L. 2000, Proc. of the 27th Annual Conference on Computer graphics and interactive techniques, (ACM Press/Addison-Wesley Publishing Co.) 103 [Google Scholar]
- Li, J. Y., Helfenstein, P., Buratti, B., Takir, D., & Clark, B. E. 2015, in Asteroids IV (Tucson: University of Arizona Press), 129 [Google Scholar]
- Lieske, J. H., Lederle, T., Fricke, W., & Morando, B. 1977, A&A, 58, 1 [NASA ADS] [Google Scholar]
- Lupishko, D. F., Belskaia, I. N., Tupieva, F. A., & Chernova, G. P. 1982, Astronomicheskii Vestnik, 16, 101 [NASA ADS] [Google Scholar]
- Park, J.-H., Yim, H.-S., Choi, Y.-J., et al. 2018, Adv. Space Res., 62, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., & Hahn, G. 1997, Icarus, 127, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., Conroy, K. E., Horvat, M., et al. 2016, ApJS, 227, 29 [Google Scholar]
- Ragozzine, D., & Brown, M. E. 2009, AJ, 137, 4766 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan, N. 1990, Ph.D. thesis, University of Texas Austin, USA [Google Scholar]
- Scaltriti, F., Zappala, V., & Stanzel, R. 1978, Icarus, 34, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Scardia, M., Rivet, J.-P., Prieur, J.-L., et al. 2019, Astron. Nachr., 340, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Scheirich, P., & Pravec, P. 2022, Planet. Sci. J., 3, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Spjuth, S. 2009, Ph.D. thesis, Technical University of Braunschweig, Germany [Google Scholar]
- Statler, T. S., Raducan, S. D., Barnouin, O. S., et al. 2022, Planet. Sci. J., 3, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Sung, H.-I., Park, Y.-H., Lee, S.-M., et al. 2012, Pub. Korean Astron. Soc., 27, 95 [Google Scholar]
- Surdej, J., Pospieszalska-Surdej, A., Michalowski, T., & Schober, H. J. 1986, A&A, 170, 167 [NASA ADS] [Google Scholar]
- Thomas, C. A., Naidu, S. P., Scheirich, P., et al. 2023, Nature, 616, 448 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F., de Bruijne, J. H. J., Arenou, F., et al. 2018, Gaia DR2 doc- umentation, European Space Agency; Gaia Data Processing and Analysis Consortium [Google Scholar]
- Vatti, B. R. 1992, Comm. ACM, 35, 56 [CrossRef] [Google Scholar]
- Vernazza, P., Ferrais, M., Jorda, L., et al. 2021, A&A, 654, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viikinkoski, M., Kaasalainen, M., & Ďurech, J. 2015, A&A, 576, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahr, J. M. 1981, Geophys. J., 64, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, M. 1992, Astronomická příručka (San Francisco: Academia) [Google Scholar]
- Wong, I., & Brown, M. E. 2019, AJ, 157, 203 [CrossRef] [Google Scholar]
All Tables
Parameters, along with their values and uncertainties for the nominal and high-oblateness models of the (22) Kalliope and Linus system.
All Figures
 |
Fig. 1 Two-sphere test of the polygon light curve algorithm. We can even use a very coarse discretisation of 42 nodes for each sphere, because we compute partial eclipses, partial occultations, or partial transits. Shades of gray show the monochromatic intensity Iλ (in W m−2 sr−1 m−1), green lines show the non-eclipsed and non-occulted polygons used to compute the surface areas. The orange arrow shows the direction towards the Sun and blue towards the observer. The test bodies are metre-sized, 1 au from the Sun and 1 au from the observer. See also Fig. 2. |
| In the text | |
 |
Fig. 2 Light curves for a two-sphere test, computed for different discretisations: 42, 272, and 1123 nodes. The precision is of the order < 0.1 mmag, even for the coarse discretisation. Tiny changes of the derivative are related to subsequently eclipsing or occulting large triangles with different normals. The magnitude in V band is computed for the effective wavelength λeff = 545 nm and the effective passband ∆eff = 85 nm. |
| In the text | |
 |
Fig. 3 Similar to Fig. 1. A tiny-triangle test, where one body is large and other body is small. It demonstrates that annular eclipses, as well as partial eclipses, partial occultations, and partial transits, are computed exactly. The polygon corresponding to the shadow (black) has a negative signed area. |
| In the text | |
 |
Fig. 4 1:1 comparison of the ‘cliptracing’ (left) and the raytracing (right) algorithms. In the former, polygons were clipped by individual pixels (analytically) and the synthetic image of (22) is very smooth. In the latter, a simple inside-polygon test was used for each ray, which creates discretisation artefacts and the synthetic image is then ‘noisy’. The Lambert scattering law was used in this test. |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but showing the corresponding shape composed of polygonal faces (gray) and a grid of either square pixels or points (green). |
| In the text | |
 |
Fig. 6 7 November 2006 stellar occultation of (22) Kalliope and Linus, computed for the model with χ2 = 6695 (from Table 2). The trajectories of (22) and Linus are plotted (cyan, green), together with several shadows of (22) computed for the observed timings (black), observers’ locations (blue), synthetic locations of the nearest shadow points (yellow), and residuals (red). The timings were taken from the occultation database (Herald et al. 2019, 2020). Absolute time measurements were used to check the ephemeris accuracy. The gnomonic projection was used, showing Japan, Honshu. |
| In the text | |
 |
Fig. 7 Phase curve of the (22) Kalliope and Linus system. The reduced brightness H0 versus the phase angle α is plotted. Calibrated photometry from Gehrels & Owings (1962), Scaltriti et al. (1978), Surdej et al. (1986), this work, and the Gaia DR3 was used. The observed curve (×) is plotted in colour (according to the Julian date) and the synthetic (+) is in yellow. The range of α is from 2 to 22°. There is an unreduced |
| In the text | |
 |
Fig. 8 Asymmetry factor g versus roughness |
| In the text | |
 |
Fig. 9 Orbit of Linus in the (u, υ) plane, derived from the short-arc astrometric + photometric model. It fits the PISCO dataset around 2459579, namely, close to the mutual occultation events, when the orbit is seen from the edge. The synthetic orbit of Linus (i.e., body 2) is plotted in green, the observed astrometry in yellow, the residuals in red, the shape of (22) in black. The viewing geometry is changing in the course of time; otherwise the orbit is elliptical. The position at the reference epoch T0 is marked by the cross. The contribution χ2 is |
| In the text | |
 |
Fig. 10 Phased light curves for the short-arc, astrometric + photometric model (top). It shows the first occultation of Linus and the second transit of Linus, together with the reference light curves. The observed light curve is plotted as blue (with error bars), the synthetic as yellow, the residuals as red. The shades of blue correspond to the Julian date. The drop in brightness is up to 0.05 mag. Both the amplitude and duration of the events are in agreement. For comparison, we also plot the difference О − С (bottom). Remaining systematics occur on all light curves; so they must be related to the shape, not the occultations. The contribution to χ2 is |
| In the text | |
 |
Fig. 11 Example of geometry for the mutual occultation of Linus by (22) Kalliope, namely, the event 2459546. The monochromatic intensity Iλ (in W m−2 sr−1 m−1) is shown as shades of gray. The ADAM shape model with 800 faces was used for (22), and a sphere with 80 faces for Linus. It is sufficient because partial occultations of faces were computed by the polygonal light curve algorithm. |
| In the text | |
 |
Fig. 12 Quadrupole moment C20,1 vs. the tidal time lag ∆t1 of the central body. The corresponding |
| In the text | |
 |
Fig. 13 Similar to Fig. 12 for three datasets SKY, AO, LC, and the total χ2. A subset of four light curves was used. The LC dataset allows the respective parameters (C20,1, ∆t1) to be constrained even better, because one occultation and one transit must have a specific geometry. The AO contribution is mostly blue, but it does not mean that this dataset is unimportant. Actually, it excludes a lot of models with incompatible poles. |
| In the text | |
 |
Fig. 14 Similar to Fig. 12 for the three datasets of SKY, AO, and LC. The radius, R2, vs. the single-particle albedo, Aw2, of Linus is plotted. Models were converged for 121 combinations of the fixed parameters; all other parameters were free. The preferred solution has |
| In the text | |
 |
Fig. 15 Same as Fig. 9, for the long-arc, astrometric + photometric model. It was constrained by the astrometry over the time span 2001–2022. The most important measurements are indicated by blue labels (Julian date – 2400 000). The contribution to χ2 is |
| In the text | |
 |
Fig. 16 Evolution of osculating orbital elements of Linus for the model with χ2 = 6695 (from Table 2). From bottom to top: a1 semimajor axis, e1 eccentricity, i1 inclination, Ω1 longitude of the ascending node, and ϖ1 longitude of pericentre. The reference frame is related to the equator of (22) Kalliope; the epoch T0 = 2459546.692102 (TDB). The model includes multipoles (ℓ = 2), internal tides, and external tides. Over the time span of astrometric observations (2001–2021), it exhibits two nodal precession cycles. |
| In the text | |
 |
Fig. 17 Residuals from the fitting of 35 deconvolved AO images of (22) Kalliope (taken from Ferrais et al. 2022), with contributions to χ2 of individual pixels plotted in colour. The projected shape changes due to rotation and viewing geometry. The pixel scale is 3.6 mas pxl−1. After the convergence of the shape parameters, with help of the polygonal algorithm and ‘cliptracing’, the total is |
| In the text | |
 |
Fig. 18 One of the SPH simulations from Brož et al. (2022a), showing a medium-energy impact to a differentiated body, which created an elongated iron core. The time 10 000 s corresponds to the end of fragmentation phase. The density is indicated by the colour scale. The oblateness J2 = −C20 is higher (not lower) than for a homogeneous body. This could correspond to our long-arc, astrometric model with three precession cycles. |
| In the text | |
 |
Fig. A.1 Verification of the stellar occultation algorithm for the occultation of the star HIP 54599 by asteroid (216) Kleopatra, on Mar 12, 2015. The shadow on the WGS-84 ellipsoid is plotted in black, the centre-of-mass location shown as a cyan line, the first moon in red, the second moon in orange, positive measurements as blue squares, negative measurements in gray. The gnomonic projection was used in this test. |
| In the text | |
 |
Fig. A.2 Similar to Fig. 12. The logarithm of eccentricity log e1 vs. the inclination i1 is plotted. Models were converged for 99 combinations of the fixed parameters; all other parameters were free. For each combination, 1000 iteration were computed, i.e., 99000 models in total. The overall best-fit result is |
| In the text | |
 |
Fig. A.3 MCMC simulation for the model with χ2 = 6695 (from Table 2). Distributions of all parameters, corresponding to local uncertainties, and correlations of all pairs of parameters is plotted as a standard ‘corner’. The order of 22 parameters is as follows (↓, →): msum, q1, P1, log e1, i1, Ω1, ϖ1, λ1, R1, R2, Prot1, ∆t1, С20,1, lpole1, bpole1, ϕ01, Aw1, Aw2, B0, h, g, and |
| In the text | |
 |
Fig. A.4 Same as Fig. 10, but referring the adjusted shape model of (22) Kalliope. Systematics on the light curves related to the shape were at least partly eliminated. The respective contribution has decreased to |
| In the text | |
 |
Fig. A.5 Comparison of the adjusted shape of (22) Kalliope (top) vs. the original ADAM shape (bottom). The control points (gray) and the high-resolution mesh (green) are indicated. Shades of gray correspond to the z coordinate. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



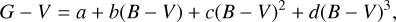
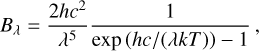
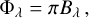
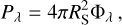
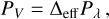
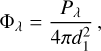
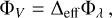
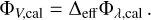
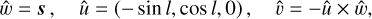
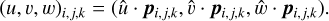
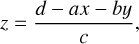
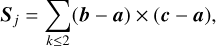
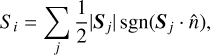
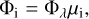
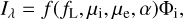
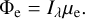
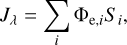
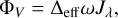
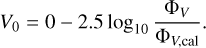
![$ {{\bf{p}}_1} = \left[ {\left( {u - {1 \over 2}{\rm{\Delta }}u,\upsilon - {1 \over 2}{\rm{\Delta }}\upsilon {\rm{,0}}} \right), \ldots ,\left( {u - {1 \over 2}{\rm{\Delta }}u,\upsilon + {1 \over 2}{\rm{\Delta }}\upsilon {\rm{,0}}} \right)} \right] $](/articles/aa/full_html/2023/08/aa46326-23/aa46326-23-eq29.png)