EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 676 (August 2023) A&A, 676 (2023) A125 Full HTML
Open Access
Issue
A&A
Volume 676, August 2023
Article Number A125
Number of page(s) 9
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202346181
Published online 22 August 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Only a few years after the theoretical prediction of the dynamic expansion of the solar corona into the heliosphere in the form of the solar wind by Parker (1958) was its existence confirmed by the first in situ measurements in the interplanetary space (Gringauz et al. 1960; Neugebauer & Snyder 1962). At the most basic level, the solar wind at 1 au is classified into fast (> 500 km s−1) quasi-steady and slow (< 500 km s−1) variable wind streams (e.g., McComas et al. 2000). Although it is now clear that fast winds originate from polar coronal holes, the origins of the slow streams are more elusive (see recent reviews Antiochos et al. 2012; Abbo et al. 2016; Cranmer et al. 2017; Viall & Borovsky 2020, and references therein). The difference in variability between fast and slow streams seems to indicate differences in the source region and/or release mechanism(s) behind these streams. Naturally, much research on slow wind focuses on how much it deviates from a steady release regime and what spatio-temporal scales and physical mechanisms are involved (e.g., Viall & Borovsky 2020). Recent observational studies by Antonucci et al. (2023), Baker et al. (2023), and Chitta et al. (2023) supplied evidence in favour of the S-web slow-solar wind model (Antiochos et al. 2011). This model postulates that the slow wind emanates from a network of narrow open-field corridors in the low corona that are connected to a web of separatrices and quasi-separatrix layers in the heliosphere.

The research is focused at the cradle of the solar wind, the solar corona. Coronagraphs and heliospheric imagers provide the main observational means for the study of the near-Sun solar wind. These instruments typically record the visible corona (K-corona) that results from the scattering of the photospheric radiation from the coronal free electrons. Because of the optically thin nature of this emission, the observed signals correspond to the line-of-sight (LoS) integral of the electron density. Therefore, the features seen in a coronagraph or a heliospheric image represent the overlap of density structures along the LoS.

The time series of images from the Large Angle and Spectroscopic Coronagraphs (LASCO; Brueckner et al. 1995) on board the Solar and Heliospheric Observatory mission (SOHO; Domingo et al. 1995) and from the Sun-Earth Connection Coronal and Heliospheric Investigation (SECCHI; Howard et al. 2008) instrument suite on board the twin spacecraft of the Solar TErrestrial RElations Observatory mission (STEREO; Kaiser et al. 2008) have been providing ample evidence of intermittent density outflows in and around streamers. Some of the larger outflows have the shape of a blob, hence they are called streamer blobs (Sheeley et al. 1997; Wang et al. 1998). Streamer blobs have been shown to be magnetic flux ropes resulting from intermittent magnetic reconnection between closed and open magnetic field lines (e.g., Wang et al. 1998; Sheeley et al. 2009; Antiochos et al. 2011; Higginson & Lynch 2018). About two to six streamer blobs per day are recorded during solar minimum and maximum conditions, respectively, with typical speeds of a few hundred km s−1 (e.g., Wang et al. 1998; Sheeley et al. 2009; Rouillard et al. 2010).

The blobs, and more generally transient slow solar wind density structures, exhibit quasi-periodic behaviour with periods ranging from ≈1 h to 19 h, and with radial sizes from ≈12 to 1 R⊙ or less (e.g., Viall et al. 2010; Viall & Vourlidas 2015; Sanchez-Diaz et al. 2017; Stansby & Horbury 2018). Magnetohydrodynamic (MHD) modelling suggests that tearing mode instability may be a candidate mechanism as it can give rise to periodic mass release in streamers with periods from ≈20 h to 1–2 h (Réville et al. 2020). On the other hand, it should be remembered that these statistics are based on 1 au measurements that suffer considerable projection effects that tend to smear structure and confuse its origins. Specialized campaigns of high-cadence (5 min) and deep exposure (36 s) SECCHI/COR2 observations have revealed higher spatio-temporal intermittency embedded in streamer flows (DeForest et al. 2018). However, the observing distance and long LoS limit the amount of information that can be extracted from 1 au imaging observations. Outflows in coronagraphic and heliospheric imaging data are often analysed with J-maps (Sheeley et al. 1997). These are maps of elongation versus time of the brightness along a given position angle; they offer an efficient method to assess coronal activity over long time periods.

The Parker Solar Probe (PSP; Fox et al. 2016) mission offers an unprecedented opportunity to break these constraints thanks to its unique design and payload. PSP’s orbit brings it ever deeper into the corona, starting at 35 R⊙ in 2018 and ending at 9.8 R⊙ in 2025, making it the first mission to measure and image the origins of the solar wind from within the corona. The imaging payload consists of the Wide-field Imager for Parker Solar Probe (WISPR; Vourlidas et al. 2016) whose two telescopes have a combined radial field of view (FoV) of 13.5°–108° elongation from the Sun centre. Its coronal vantage point within the corona removes much of the LoS confusion intrinsic to 1 au imagers and allows unprecedented observations of the fine-scale structures of coronal mass ejections and background streamer structures (Howard et al. 2019; Rouillard et al. 2020). On the other hand, the rapidly changing viewpoint introduces a set of novel challenges in the analysis of imaging data that do not pertain to the SOHO or STEREO observations from 1 au.

Nindos et al. (2021, hereafter Paper I) reported the first kinematic analysis of outflows in the WISPR images by developing a methodology to account for the rapidly varying viewpoint. They identified four to five quasi-linear tracks of outflowing features per day, during the fourth solar encounter of PSP (E4) from 23 January 00:44:26 to 3 February, 2020 23:04:26 UT. The measurements were taken over a one-degree wide wedge along the PSP orbit plane. The heliospheric neutral line marking the streamer belt, during this period, was within 10° of the solar equatorial plane (Fig. 1), and hence it was close to the PSP orbital plane (the PSP orbit is inclined by 3.4° relative to the equatorial plane). The detected outflows are therefore associated with streamers. Paper I, however, did not investigate the implications of these results.

thumbnail Fig. 1.

Synoptic map of the radial component of the heliospheric magnetic field (in nT) at 30 R⊙, on 29 January 2020, 12 UT, from a medium-resolution run of the MAS code (e.g., Mikić et al. 1999; Riley et al. 2012) corresponding to Carrington rotation 2226. The green line corresponds to the heliospheric neutral line. The simulation data are from http://www.predsci.com/.

The core goal of our paper is to supply constraints on various properties of transient slow solar wind density structures, such as their spatio-temporal periods and total number. This is achieved via Monte Carlo simulations of synthetic WISPR-I J-maps, spanning E4, and for different scenarios, encapsulating plausible properties of density structure release motivated by pertinent observations and modelling, which are then juxtaposed with the observed J-map in Paper I. Our paper has the following outline. We describe the simulations in Sect. 2 and the construction of the synthetic J-maps in Sect. 3. We present the results in Sect. 4 and discuss them in Sect. 5. We conclude in Sect. 6.

2. Simulations of transient solar wind density structures

2.1. The need for simulations

In J-maps, any outward propagating density structure will create a track with either an upward (accelerating) or a downward (decelerating) curve (see Fig. 2). The slope is a function of the feature’s own kinematics and of projection effects. In other words, a given feature’s kinematic profile cannot be taken at face value, but requires analysis and the use of various constraints, as has been described in numerous publications (e.g., Sheeley et al. 1997; Davies et al. 2009; Rouillard et al. 2011; Lugaz et al. 2009; Liu et al. 2010; Sheeley & Rouillard 2010). Depending on the particulars, the analysis results in speed, direction, and solar origin estimates.

thumbnail Fig. 2.

WISPR-I J-map during PSP E4. The purple crosses correspond to the automatically detected tracks. The figure is modified from Paper I.

Projection effects are always a concern in the analysis of coronal observations, but are especially important in the PSP case due to the rapidly varying heliocentric distance. A key property of Thomson scattering is that the location of maximum scattering efficiency lies on the so-called Thomson surface (TS; Vourlidas & Howard 2006), which is a sphere with a diameter equal to the Sun–observer distance. The TS dependence on the Sun–observer distance implies that the recorded intensity in inner heliospheric observations is more heavily weighted towards the near-spacecraft environment than a similar observation from 1 au. In the case of WISPR, this effect turns the instrument into a local imager (Vourlidas et al. 2016); however, it has a rapidly varying sensitivity due to the orbit. The temporal variation of both the LoS integration and the distance between observer and feature will affect the shape of the tracks in J-maps to various degrees, and therefore will influence the interpretation. In addition, the small size of transient outflows and the LoS effects discussed result in lower limits for the actual numbers of released density structures from the streamer belt. Therefore, we construct synthetic observations under a variety of scenarios to further explore the potential of WISPR-based analysis.

2.2. Constructing simulated J-maps

With our simple simulations we emulate transient releases of slow solar wind parcels. The simulations consist of idealized density structures released from the solar equatorial plane during the PSP fourth solar encounter (23 January to 3 February 2020, ≈11.9 days). We consider four scenarios to encapsulate a wide range of plausible properties of density structure release. The scenarios are motivated by the observations and modelling discussed in the Introduction, and are described below. The structures are released at a heliocentric distance of 5 R⊙ for all four scenarios (e.g., Sheeley et al. 1999). They propagate radially at a constant speed randomly drawn from the interval [100,400] km s−1, consistent with the observations of streamer blobs.

– Scenario 1, periodic release longitudes and release times and random speeds: In Scenario 1 ntheta density structures are released every dt minutes from equally spaced longitudes in the equatorial plane. Hence, a total of 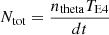structures are released during the duration TE4 of E4. We consider nine dt values, equally spaced logarithmically in the interval [1, 25.6] h, and six ntheta values, equally spaced logarithmically in the interval [4, 128]. This scenario corresponds to density structures released every ≈3–90 deg across the solar equatorial plane.

– Scenario 2, corotating release longitudes, periodic release times and random speeds: In Scenario 2 ntheta equatorial density structures are released every dt minutes during E4, from equally spaced Carrington (i.e., corotating) longitudes. This scenario corresponds to fixed release sites on a rotating Sun.

– Scenario 3, random release longitudes and speeds, periodic release times: In Scenario 3 ntheta density structures are released every dt minutes from randomly selected equatorial longitudes. We note that here the ntheta and dt grids and total number of released density structures are the same in Scenarios 1–3.

– Scenario 4, random release longitudes, release times, and speeds: In scenario 4 Ntot density structures are released at randomly distributed times and from randomly distributed equatorial longitudes. Ntot takes 13 values equally distributed logarithmically from the interval [20,81 920] and was chosen in order to encompass the corresponding intervals employed in Scenarios 1–3. As for Scenarios 1–3 a logarithmic grid was used.

The employed release times are consistent with observations and with the modelling of quasi-periodic mass release discussed in the Introduction, and they span the interval from 1 h to 20 h (e.g., Viall et al. 2010; Viall & Vourlidas 2015; Sanchez-Diaz et al. 2017; Stansby & Horbury 2018; Réville et al. 2020). Likewise, for the spatial scales of release (i.e., ntheta) synoptic maps of the coronal brightness in the outer corona using rotational tomography constructed by Morgan & Cook (2020) showed that in some cases streamers repeat themselves over several tens of degrees. Streamers, as discussed in the Introduction, represent potential sites of transient slow solar wind release. Moreover, the observations reported by Sanchez-Diaz et al. (2017) suggest a 15-degree separation of transient slow solar wind outflows, as captured by heliospheric imagers. Finally, for transient mass releases associated with coronal jets from the quiet Sun, the relevant spatial scale here (e.g., Raouafi et al. 2016, 2023) is the chromospheric network size, which corresponds to ≈2.5 deg.

As both the employed ntheta and dt studied intervals used in Scenarios 1–3 span an order of magnitude, and to save on computing time given the large number of simulated structures and generally the large number of iterations inherent to Monte Carlo methods, we populated these intervals with logarithmic grids. The same applies to the choice of a logarithmic grid for Ntot for Scenario 4. For this scenario the range of Ntot was chosen to be consistent with the Ntot range used in Scenarios 1–3. The number of points in each considered interval was chosen in order to cover the corresponding interval with a reasonable number of points.

Using finer grids of the input parameters dt and ntheta would lead to higher precision in the determination of the ranges of these parameters that are consistent with the observations. However, this is beyond the scope of the present study; we do not wish to fine-tune dt and ntheta to the observations, but rather to supply some estimates of the ranges of these parameters that are consistent with the observations.

For simplicity and computational efficiency (i.e., to avoid LoS integrations over a large number of discrete structures) (e.g., Patsourakos & Vial 1997; Liewer et al. 2019; Nisticò et al. 2020), we treated the density structures as zero-mass and point-like entities. Therefore, the implicit assumption in the construction of the synthetic J-maps is that the density structures are sufficiently massive to be detected by WISPR. We also did not take into account the 3° offset between the solar equatorial plane ecliptic and the PSP orbital plane because visible light structures are generally wider than 3°. Moreover, this small offset does not impact the calculation of elongations of structures released close to the PSP orbital plane (Liewer et al. 2020).

Next, we performed 1000 Monte Carlo simulations for each scenario resulting in a large number of simulations and J-maps. Namely, we obtained 48 000 synthetic J-maps for Scenarios 1–3 and 13 000 for Scenario 4. For each Monte Carlo simulation we drew randomly selected parameter(s) as needed for each scenario’s specifics.

3. Construction of synthetic J-maps

We constructed J-maps for every Monte Carlo simulation as follows. Using a 20 min cadence to emulate the WISRP-I synoptic programme cadence, we recorded a density structure if the following two conditions were met: (1) its elongation lies within the elongation range of the WISRP-I FoV (that is 13.5–50°); (2) the density structure lies inside the corresponding TS. We note here that the vantage point of each considered timestamp during E4 in our simulations followed the actual motion of the PSP spacecraft with respect to the Sun during that interval; in other words, each vantage point, and hence corresponding FoV, was determined from the corresponding PSP location.

Next, for each timestamp in our simulations, we counted the number of density structures satisfying the two detection criteria over an elongation grid with a bin size of 2 deg spanning the WISPR-I FoV, resulting essentially to a histogram of detections versus elongation. Time-stacking these histograms resulted into the simulated J-maps, which obviously do not record brightness, as the actual J-maps do. However, non-zero J-map values at any given time-elongation pair imply the presence of density structure(s), and therefore record the outflows. Large (small) J-map values correspond to a large (small) number of density structures for a given elongation-time pair. We applied a box-car filter to smooth local variations in the synthetic J-maps. J-map examples for Scenarios 1 and 4 are shown in Figs. 3 and 4, respectively. Similar maps were obtained for the other two scenarios, but are not presented here for the sake of brevity. The lack of tracks at the beginning of the synthetic J-maps is due to the finite start time and reflects the time it takes for the first density structures to enter the WISRP-I FoV. The synthetic J-maps exhibit quasi-linear tracks similar to those in the observed J-map of Fig. 2. In addition, the track duration in the simulated J-maps (i.e., the time it takes the associated density structure to traverse the WISPR-I FoV) is of the order of one day, similar to what was found for the observed J-map in Paper I. In addition, we can observe tracks in the simulated J-maps in Figs. 3 and 4, which become progressively vertical. This indicates outflows approaching PSP (Liewer et al. 2019). As expected, the track density follows the number of simulated structures (check the value of Ntot in the captions of Figs. 3 and 4).

thumbnail Fig. 3.

Example synthetic J-maps for Scenario 1. The colour-coding from black to green to white corresponds to increasing J-map values. The purple crosses indicate the detected tracks.

thumbnail Fig. 4.

Same as Fig. 3, but for Scenario 4.

Given the large number of our simulations, we employ a simple method to automatically detect tracks in the synthetic J-maps. The method searches for local maxima in J-map time series created by averaging the J-map over a 4° wide elongation bin centred at the middle of the WISRP-I FoV, which ensures the inclusion of transient outflows that traversed a significant part of the relevant FoV. The detected local maxima is consistent with the temporal width (i.e., the duration) of the tracks of the J-map in Paper I, which resulted from the calculation of the autocorrelation function of the J-map time series at the centre of WISPR-I FOV of the J-map in Paper I.

We validate the track-detection algorithm on the observed J-map in Paper I (see Fig. 2) and the sample simulated J-maps (Figs. 3 and 4). The purple crosses in Figs. 2–4 give the locations of the detected tracks, which are largely consistent with visual inspection.

4. Results

To derive constraints on the properties of the density outflows, we first examine the dependence of the number of detected tracks on the spatio-temporal periods of the released density structures. Figure 5 is a colour representation of the daily average (over the 1000 Monte Carlo simulations per scenario) of detected tracks per day (Ntracks) as a function of release longitude (ntheta) and time (dt) for Scenarios 1–3.

thumbnail Fig. 5.

Average daily number of detected tracks (Ntracks) in synthetic J-maps from 1000 Monte Carlo simulations for Scenarios 1 (top), 2 (middle), and 3 (bottom) as a function of the number of release longitudes (ntheta) and repeat time (dt) of the corresponding density structures.

In addition, the higher the number of released density structures, the larger the Ntracks. A large portion of the plots corresponds to Ntracks equal to or greater than six (corresponding to yellow). We come back to this later on. Periods of transient density structure release are given in Table 1. In Fig. 5 and Table 1 we note that the rather extended ranges of both the spatial (≈3°–45°) and temporal (≈1–25 h) release periods are consistent with the observations. The temporal periods of the density structures discussed above are consistent with observational (e.g., Viall et al. 2010; Viall & Vourlidas 2015; Sanchez-Diaz et al. 2017) or theoretical (e.g., Réville et al. 2020) studies of periodic mass release from streamers.

Table 1.

Spatio-temporal release periods of density structures for Scenarios 1–3 leading to four or five detected tracks in the synthetic J-maps per day, as resulting from the observed J-map.

Next, we examine the daily dependence of the number of detected tracks versus the number of released structures for all four scenarios (Fig. 6). We note that the x-axis values for Scenario 4 strictly correspond to the averaged daily number of released density structures. In Fig. 6 we display the daily 5, 50, and 95% percentiles of the number of detected tracks distributions for the corresponding 1000 Monte Carlo simulations as a function of the daily number of released structures. It should be noted in Fig. 6 that the abscissae of the corresponding panels, containing the daily number of detected tracks resulting from the synthetic J-maps, are not expressed in integer values; the same applies to Fig. 8. This choice is dictated by our main goal in building these figures. We decided to use the Ntot − Ntracks curves resulting from the simulations to infer Ntot, which is consistent with the results of Paper I. This is achieved by essentially finding the intersection between the Ntot − Ntracks curves and horizontal lines at Ntracks equal to 4 and 5, which is consistent with the observations in Paper I. Rounding the Ntracks values would obviously decrease the accuracy at which Ntot is calculated. All scenarios show a similar behaviour. The number of detected tracks rises slowly for small numbers (< 10) of released structures; it increases rapidly with increasing number of structures before reaching a plateau of six detections beyond about 100–200 released structures per day, depending on the scenario.

thumbnail Fig. 6.

Quartiles of the daily number of detected tracks for the 1000 Monte Carlo simulations (5% in orange, 50% in red line, and 95% in blue) for Scenarios 1 (top left), 2 (top right), 3 (bottom left), and 4 (bottom right). The two horizontal dashed lines correspond to four and five daily J-map tracks, consistent with the Paper I observations.

We can now estimate the range of released structures that are consistent with the observations. The horizontal dashed lines in Fig. 6 give the observed range of four or five tracks per day. The resulting numbers of released structures for each of the four scenarios are compiled in Table 2. The differences among the four scenarios are small. Scenarios 3 and 4, whose use is based on randomly drawn distributions for input parameters of the simulations besides their speed, result in the wider ranges.

Table 2.

Daily number of released structures in four simulated environments that are consistent with the number of detections in WISPR J-maps in Paper I.

Figures 5 and 6 indicate that the most important factor in determining the number of track detections is the number of released density structures. The dependence on the spatio-temporal release periods is much weaker since multiple periods across extended ranges correspond to the same number of detections.

A salient assumption in our analysis is that each track corresponds to a single density structure. This translates to a lower limit on the number of released density structures that are consistent with the observations. This conclusion is supported by the reasonable expectation that the properties of some structures (size or intensity), (see e.g., the simulations of Higginson & Lynch 2018) may drive them below WISPR’s detection thresholds in terms of spatial resolution, cadence, and/or sensitivity. We note, however, that a close comparison of the WISPR time series with the associated J-map shows that there is a one-to-one correspondence between density structures in the movie and the corresponding J-map tracks.

5. Discussion

The weak correspondence between the number of detected tracks and both the considered scenario and the spatio-temporal release periods is unsurprising. We use the number of tracks to compare the synthetic and observed J-maps, which is expected to depend primarily on the number of released density structures rather than on the specifics of their release. This is clearly seen in Fig. 6, which shows a clear dependence of the number of detected tracks on the number of released density structures.

However, at relatively high daily numbers of released density structures (> ≈200), the number of detected synthetic tracks becomes insensitive to that parameter. A factor influencing this could be the observing image cadence. In Fig. 7 we display two synthetic J-maps produced by Scenario 1 where we consider the same speed (200 km s−1) for all density structures. The only difference between the two J-maps is the cadence of 20 min (upper panel) and 1 min (lower panel). The total number of released structures is ≈220 for both simulations and therefore lies in the ‘saturated’ portion of the number of released structures (Nds)-number of detected tracks (Ntracks) curves in Fig. 6. Clearly, the high-cadence J-map recovers more structures, something to be investigated with higher-cadence observations.

thumbnail Fig. 7.

Synthetic J-maps resulting from Scenario 1 considering the same speed (200 km s−1) for all density structures. The only difference between the two J-maps is the cadence: 20 min (upper panel) and 1 min (lower panel).

Our automated track detection scheme is based on the inferred value of temporal width based on the observations of J-map tracks from Paper I. However, we wonder how sensitive our analysis is to the choice of this parameter. In Fig. 8 we display the 50% quartiles of the Ntracks distributions from the 1000 Monte Carlo simulations of Scenario 4 as a function of Nds, for four different choices of the J-map track duration: 60, 120, 240, and 480 min. We recall that in our analysis we used a J-map track duration of 120 min (green line in Fig. 8). As expected, the shorter the considered track duration, the larger the number of the detected tracks. For instance, the shorter considered track duration (blue line) gives rise to a maximum Ntracks equal to 7; conversely, the shorter considered track width (brown line) gives rise to maximum Ntracks below 4, which is outside the range of the observations in Paper I. However, the intersections of the horizontal dashed lines at Ntracks 4 and 5 with the blue and green lines are consistent with rather small differences of less than a factor of two in Nds. The same applies to when no smoothing is applied to the J-map and the same temporal width as in our original study is used (purple curve in Fig. 8). Taking all these together, this suggests the robustness of our approach. In retrospective, for periods with faster and smaller density structures (i.e., when solar activity is higher than at E4) our framework could also be applied. Finally, it is possible that the plateaus of the Ntot − Ntracks curves at large values of Ntot discussed above could also result from the line-of-sight overlap of multiple density structures.

thumbnail Fig. 8.

50% quartiles of the daily number of detected tracks for the 1000 Monte Carlo simulations for Scenario 4 for J-map track duration (i.e., the interval between detected tracks; see Sect. 3) of 60, 120, 240, and 480 min (blue, green, red, brown lines, respectively). The purple line corresponds to results to when no smoothing is applied to the J-maps and the same temporal width as in our original study is used. The two horizontal dashed lines correspond to four and five daily J-map tracks, consistent with the observed J-map in Paper I.

The derived number of released density structures from the solar equatorial plane is about 35–130, which is clearly above the estimates of Sanchez-Diaz et al. (2017). These authors used observations taken by HI-1/SECCHI on board the STEREO A spacecraft, corresponding to a period of highly inclined heliospheric neutral lines during solar maximum conditions, and therefore enabling a face-on view of the streamer belt. Using a combination of different maps, Sanchez-Diaz et al. (2017) found that patches of enhanced emission at 30 R⊙, which they attributed to plasma blobs, occurred every 19.5 h and were separated by 15 deg in latitude. These findings suggested the release of 24 density structures from the streamer belt. One reason for the difference in the number of released structures may be linked to the fact that a corotating interaction region (CIR) was observed during the Sanchez-Diaz et al. (2017) observations. However, a possibly much more important factor is that the Sanchez-Diaz et al. (2017) results are based on emission patches, which, as they also discuss, could be the amalgamation of several individual smaller density structures. The size of the density structures of the Sanchez-Diaz et al. (2017) study is ≈12 × 5 R⊙, whereas the density structures of our WISPR observations could be significantly smaller; for example, the density structure indicated with an arrow in panel b in Fig. 8 of Paper I is ≈8 deg in elongation and 4 degrees in latitude (which corresponds to ≈5.6 × 2.8 R⊙), as viewed from a PSP viewpoint of 40 R⊙.

We now consider the implications from our J-map simulations for PSP in situ measurements of large-scale density structures during E4. We assume that a simulated density structure would be detected in situ by PSP if its distance from PSP is comparable to the size of the density structure. Given that remote sensing observations are generally biased towards large-scale density structures, we considered density structure–PSP distances in the range of 2–8 R⊙, consistent with inferred spatial scales of density structures from the WISPR-I E4 observations, as discussed above. By counting the number of timestamps leading to detections, we were able to estimate the percentage of the E4 orbit that would contain in situ structure detections. We note here that there could be timestamps populated by multiple density structures.

Our estimates are shown in Fig. 9, where the percentage of the E4 orbit with in situ structure detections is plotted against the number of released density structures in the solar equatorial plane for Scenario 4. The coloured lines correspond to the 50% quartiles of the distributions resulting from the 1000 Monte Carlo simulations for in situ density structures–PSP distance (i.e., density structure size) of 2, 4, 6, and 8 R⊙. The horizontal dashed lines correspond to 1, 5, 10, and 20% of the E4 orbit. The inferred daily number of released density structures for Scenario 4 from the analysis of the J-maps in the previous section (i.e., 35–127; see Fig. 6 and Table 1) correspond to in situ detections for 1–20% of the E4 duration. This prediction requires further investigation via a detailed analysis of the PSP E4 in situ density observations in a manner similar to past studies (e.g., Viall et al. 2008; Stansby & Horbury 2018) for observations at 1 au and 0.3–0.5 au, respectively.

thumbnail Fig. 9.

50% quartiles of the percentage of the E4 duration consistent with in situ detection of density structures with radial sizes, 2 R⊙ (green line), 4 R⊙ (orange line), 6 R⊙ (red line), and 8 R⊙ (blue line) as a function of the daily number of released density structures from the equatorial plane for the 1000 Monte Carlo simulations for Scenario 4. The horizontal dashed lines (from bottom to top) correspond to 1, 5, 10, and 20% of the E4 duration.

6. Summary

Determining the global properties of transient slow solar wind density structures is a key goal in the study of the slow solar wind. To this end, we performed simple Monte Carlo simulations for different scenarios regarding the properties of the released density structures, and compared the resulting synthetic J-maps against an observed J-map during PSP’s fourth perihelion. Our findings can be summarized as follows:

  1. The synthetic J-maps exhibit quasi-linear tracks similar to the observed tracks.

  2. For scenarios employing periodic spatio-temporal density structure release, multiple spatio-temporal period pairs give rise to the same daily number of synthetic tracks as seen in the observations. The periods span extended intervals (i.e., 3°–45° and 1–25 h).

  3. The four considered scenarios are consistent with similar ranges 35–45 to 96–127 of released density structures per day from the solar equatorial plane (see Table 1) and result in the same number of daily detected tracks as the observations in Paper I. For relatively high release rates (> ≈200), the number of detected synthetic tracks becomes insensitive to the release rate, and hence the exact number of released density structures cannot be inferred from WISRP-I E4 observations.

  4. Our results predict that PSP in situ detections of density structures, with sizes in the range 2–8 R⊙, will occur over 1–20% of the E4 orbit.

The estimates of the global release rates of density structures of this paper represent the first step in assessing their potential contribution to the slow solar wind mass budget. This will be achieved by calculations of the mass content of the density structures observed by WISPR, which will be confronted with the corresponding in situ observations, and by further J-map calculations for other PSP as well as Solar Orbiter (Müller et al. 2013) perihelia, in the latter scenario using EUI Rochus et al. (2020), METIS (Antonucci et al. 2020), and SolO-HI (Howard et al. 2020) observations. Finally, it is important to compare PSP remote-sensing and in situ measurements of transient density structures to investigate whether the predictions of this work are correct.

Acknowledgments

The authors would like to thank the referee for useful comments and suggestions. AV is supported by WISPR Phase-E funding to APL. We acknowledge the work of the PSP operations team. Parker Solar Probe was designed, built, and is now operated by the Johns Hopkins Applied Physics Laboratory as part of NASA’s Living with a Star (LWS) program (contract NNN06AA01C). We also acknowledge the efforts of the WISPR team developing and operating the instrument. SP and AV would like to thank AV for the invitation and hospitality during their visit to APL when this work was initiated. SP and AN acknowledge support by the ERC Synergy Grant ‘Whole Sun’ (GAN: 810218).

References

  1. Abbo, L., Ofman, L., Antiochos, S. K., et al. 2016, Space Sci. Rev., 201, 55 [NASA ADS] [CrossRef] [Google Scholar]
  2. Antiochos, S. K., Mikić, Z., Titov, V. S., Lionello, R., & Linker, J. A. 2011, ApJ, 731, 112 [Google Scholar]
  3. Antiochos, S. K., Linker, J. A., Lionello, R., et al. 2012, Space Sci. Rev., 172, 169 [Google Scholar]
  4. Antonucci, E., Romoli, M., Andretta, V., et al. 2020, A&A, 642, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Antonucci, E., Downs, C., Capuano, G. E., et al. 2023, Phys. Plasmas, 30, 022905 [Google Scholar]
  6. Baker, D., Demoulin, P., Yardley, S. L., et al. 2023, ApJ, 950, 65 [CrossRef] [Google Scholar]
  7. Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chitta, L. P., Seaton, D. B., Downs, C., DeForest, C. E., & Higginson, A. K. 2023, Nat. Astron., 7, 133 [NASA ADS] [Google Scholar]
  9. Cranmer, S. R., Gibson, S. E., & Riley, P. 2017, Space Sci. Rev., 212, 1345 [Google Scholar]
  10. Davies, J. A., Harrison, R. A., Rouillard, A. P., et al. 2009, Geophys. Res. Lett., 36, L02102 [Google Scholar]
  11. DeForest, C. E., Howard, R. A., Velli, M., Viall, N., & Vourlidas, A. 2018, ApJ, 862, 18 [Google Scholar]
  12. Domingo, V., Fleck, B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [Google Scholar]
  13. Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
  14. Gringauz, K. I., Kurt, V. G., Moroz, V. I., & Shklovskii, I. S. 1960, AZh, 37, 716 [Google Scholar]
  15. Higginson, A. K., & Lynch, B. J. 2018, ApJ, 859, 6 [Google Scholar]
  16. Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
  17. Howard, R. A., Vourlidas, A., Bothmer, V., et al. 2019, Nature, 576, 232 [Google Scholar]
  18. Howard, R. A., Vourlidas, A., Colaninno, R. C., et al. 2020, A&A, 642, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Kaiser, M. L., Kucera, T. A., Davila, J. M., et al. 2008, Space Sci. Rev., 136, 5 [Google Scholar]
  20. Liewer, P., Vourlidas, A., Thernisien, A., et al. 2019, Sol. Phys., 294, 93 [Google Scholar]
  21. Liewer, P. C., Qiu, J., Penteado, P., et al. 2020, Sol. Phys., 295, 140 [Google Scholar]
  22. Liu, Y., Thernisien, A., Luhmann, J. G., et al. 2010, ApJ, 722, 1762 [Google Scholar]
  23. Lugaz, N., Vourlidas, A., & Roussev, I. I. 2009, Ann. Geophys., 27, 3479 [Google Scholar]
  24. McComas, D. J., Barraclough, B. L., Funsten, H. O., et al. 2000, J. Geophys. Res., 105, 10419 [Google Scholar]
  25. Mikić, Z., Linker, J. A., Schnack, D. D., Lionello, R., & Tarditi, A. 1999, Phys. Plasmas, 6, 2217 [Google Scholar]
  26. Morgan, H., & Cook, A. C. 2020, ApJ, 893, 57 [CrossRef] [Google Scholar]
  27. Müller, D., Marsden, R. G., St. Cyr, O. C., & Gilbert, H. R. 2013, Sol. Phys., 285, 25 [CrossRef] [Google Scholar]
  28. Neugebauer, M., & Snyder, C. W. 1962, Science, 138, 1095 [Google Scholar]
  29. Nindos, A., Patsourakos, S., Vourlidas, A., et al. 2021, A&A, 650, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Nisticò, G., Bothmer, V., Vourlidas, A., et al. 2020, Sol. Phys., 295, 63 [Google Scholar]
  31. Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
  32. Patsourakos, S., & Vial, J. C. 1997, AIP Conf. Ser., 385, 129 [NASA ADS] [CrossRef] [Google Scholar]
  33. Raouafi, N. E., Patsourakos, S., Pariat, E., et al. 2016, Space Sci. Rev., 201, 1 [Google Scholar]
  34. Raouafi, N. E., Stenborg, G., Seaton, D. B., et al. 2023, ApJ, 945, 28 [NASA ADS] [CrossRef] [Google Scholar]
  35. Réville, V., Velli, M., Rouillard, A. P., et al. 2020, ApJ, 895, L20 [Google Scholar]
  36. Riley, P., Linker, J. A., Lionello, R., & Mikic, Z. 2012, J. Atmos. Solar-Terrest. Phys., 83, 1 [NASA ADS] [CrossRef] [Google Scholar]
  37. Rochus, P., Auchère, F., Berghmans, D., et al. 2020, A&A, 642, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Rouillard, A. P., Davies, J. A., Lavraud, B., et al. 2010, J. Geophys. Res. (Space Phys.), 115, A04103 [NASA ADS] [Google Scholar]
  39. Rouillard, A. P., Sheeley, N. R., Jr, Cooper, T. J., et al. 2011, ApJ, 734, 7 [NASA ADS] [CrossRef] [Google Scholar]
  40. Rouillard, A. P., Poirier, N., Lavarra, M., et al. 2020, ApJS, 246, 72 [Google Scholar]
  41. Sanchez-Diaz, E., Rouillard, A. P., Davies, J. A., et al. 2017, ApJ, 851, 32 [Google Scholar]
  42. Sheeley, N. R., Jr, & Rouillard, A. P. 2010, ApJ, 715, 300 [NASA ADS] [CrossRef] [Google Scholar]
  43. Sheeley, N. R., Wang, Y. M., Hawley, S. H., et al. 1997, ApJ, 484, 472 [Google Scholar]
  44. Sheeley, N. R., Walters, J. H., Wang, Y. M., & Howard, R. A. 1999, J. Geophys. Res., 104, 24739 [Google Scholar]
  45. Sheeley, N. R., Jr, Lee, D. D. H., Casto, K. P., Wang, Y. M., & Rich, N. B. 2009, ApJ, 694, 1471 [Google Scholar]
  46. Stansby, D., & Horbury, T. S. 2018, A&A, 613, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Viall, N. M., & Borovsky, J. E. 2020, J. Geophys. Res. (Space Phys.), 125, e26005 [NASA ADS] [Google Scholar]
  48. Viall, N. M., & Vourlidas, A. 2015, ApJ, 807, 176 [Google Scholar]
  49. Viall, N. M., Kepko, L., & Spence, H. E. 2008, J. Geophys. Res. (Space Phys.), 113, A07101 [Google Scholar]
  50. Viall, N. M., Spence, H. E., Vourlidas, A., & Howard, R. 2010, Sol. Phys., 267, 175 [Google Scholar]
  51. Vourlidas, A., & Howard, R. A. 2006, ApJ, 642, 1216 [Google Scholar]
  52. Vourlidas, A., Howard, R. A., Plunkett, S. P., et al. 2016, Space Sci. Rev., 204, 83 [Google Scholar]
  53. Wang, Y. M., Sheeley, N. R., Jr, Walters, J. H., et al. 1998, ApJ, 498, L165 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Spatio-temporal release periods of density structures for Scenarios 1–3 leading to four or five detected tracks in the synthetic J-maps per day, as resulting from the observed J-map.

In the text
Table 2.

Daily number of released structures in four simulated environments that are consistent with the number of detections in WISPR J-maps in Paper I.

In the text

All Figures

thumbnail Fig. 1.

Synoptic map of the radial component of the heliospheric magnetic field (in nT) at 30 R⊙, on 29 January 2020, 12 UT, from a medium-resolution run of the MAS code (e.g., Mikić et al. 1999; Riley et al. 2012) corresponding to Carrington rotation 2226. The green line corresponds to the heliospheric neutral line. The simulation data are from http://www.predsci.com/.
In the text
thumbnail Fig. 2.

WISPR-I J-map during PSP E4. The purple crosses correspond to the automatically detected tracks. The figure is modified from Paper I.
In the text
thumbnail Fig. 3.

Example synthetic J-maps for Scenario 1. The colour-coding from black to green to white corresponds to increasing J-map values. The purple crosses indicate the detected tracks.
In the text
thumbnail Fig. 4.

Same as Fig. 3, but for Scenario 4.
In the text
thumbnail Fig. 5.

Average daily number of detected tracks (Ntracks) in synthetic J-maps from 1000 Monte Carlo simulations for Scenarios 1 (top), 2 (middle), and 3 (bottom) as a function of the number of release longitudes (ntheta) and repeat time (dt) of the corresponding density structures.
In the text
thumbnail Fig. 6.

Quartiles of the daily number of detected tracks for the 1000 Monte Carlo simulations (5% in orange, 50% in red line, and 95% in blue) for Scenarios 1 (top left), 2 (top right), 3 (bottom left), and 4 (bottom right). The two horizontal dashed lines correspond to four and five daily J-map tracks, consistent with the Paper I observations.
In the text
thumbnail Fig. 7.

Synthetic J-maps resulting from Scenario 1 considering the same speed (200 km s−1) for all density structures. The only difference between the two J-maps is the cadence: 20 min (upper panel) and 1 min (lower panel).
In the text
thumbnail Fig. 8.

50% quartiles of the daily number of detected tracks for the 1000 Monte Carlo simulations for Scenario 4 for J-map track duration (i.e., the interval between detected tracks; see Sect. 3) of 60, 120, 240, and 480 min (blue, green, red, brown lines, respectively). The purple line corresponds to results to when no smoothing is applied to the J-maps and the same temporal width as in our original study is used. The two horizontal dashed lines correspond to four and five daily J-map tracks, consistent with the observed J-map in Paper I.
In the text
thumbnail Fig. 9.

50% quartiles of the percentage of the E4 duration consistent with in situ detection of density structures with radial sizes, 2 R⊙ (green line), 4 R⊙ (orange line), 6 R⊙ (red line), and 8 R⊙ (blue line) as a function of the daily number of released density structures from the equatorial plane for the 1000 Monte Carlo simulations for Scenario 4. The horizontal dashed lines (from bottom to top) correspond to 1, 5, 10, and 20% of the E4 duration.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.