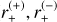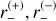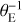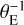| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 14 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202142429 | |
| Published online | 17 August 2023 | |
Interferometric visibility of single-lens models: The thin-arcs approximation
Institut d’Astrophysique de Paris, Sorbonne Université, CNRS, UMR 7095,
98 bis bd Arago,
75014
Paris, France
e-mail: arnaud.cassan@iap.fr
Received:
13
October
2021
Accepted:
26
June
2023
Long baseline interferometry of microlensing events can resolve the individual images of the source produced by the lens, which combined with the modelling of the microlensing light curve, leads to the exact lens mass and distance. Interferometric observations thus offer a unique opportunity to constrain the mass of exoplanets detected by microlensing, and to precisely measure the mass of distant isolated objects such as stars and brown dwarfs, and of stellar remnants such as white dwarfs, neutron stars, and stellar black holes. Having accurate models and reliable numerical methods is of particular importance as the number of targets is expected to increase significantly in the near future. In this work we discuss the different approaches to calculating the fringe complex visibility for the important case of a single lens. We propose a robust integration scheme to calculate the exact visibility, and introduce a novel approximation, which we call the ‘thin-arcs approximation’, which can be applied over a wide range of lens-source separations. We find that this approximation runs six to ten times faster than the exact calculation, depending of the characteristics of the event and the required accuracy. This approximation provides accurate results for microlensing events of medium to high magnification observed around the peak (i.e. a large fraction of potential observational targets).
Key words: gravitational lensing: micro / techniques: interferometric / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Measuring the mass of isolated objects in our Milky Way is a major challenge in astrophysics, whether it be the mass of stars, brown dwarfs, or stellar remnants such as white dwarfs, neutron stars, or stellar black holes. Few observational techniques allow such measurements to be made with high precision and/or independently of assumptions about the structure of the targeted objects. Gravitational microlensing (Paczynski 1986), based on the deflection of light rays by a lensing body transiting the line of sight of a distant star, provides the solution of choice for measuring the mass of such isolated lenses. The technique allows us to probe objects, intrinsically luminous or not, up to Galactic scales and independently of the light emitted by the lens itself.
Microlensing affects the shape and the number of images of the source star, which results in a global enhancement of the total flux received by the observer. As the individual images produced by the microlens cannot be separated by classical telescopes, what is usually measured is the increase (or magnification) in the flux of the source star as a function of time. Nevertheless, when for bright-enough microlensing events, the lensed images can in principle be resolved with long baseline interferometers (Delplancke et al. 2001; Dalal & Lane 2003; Rattenbury & Mao 2006; Cassan & Ranc 2016) since their typical separation is of the order of a milliarcsecond (i.e. within the reach of interferometers with baselines of ~40–100 metres. A first series of successful interferometric observations was recently made with the Very Large Telescope Interferometer (ESO/VLTI) on microlensing events TCP J05074264+2447555 ‘Kojima-1’ (Dong et al. 2019) and Gaia19bld (Cassan et al. 2022).
To measure the mass of the lens, two quantities must be derived from the observations. The first is πE, the microlensing parallax; the second is θE, the angular Einstein ring radius, which is the angular radius of the ring-like image of the source were it to be perfectly aligned with the lens. The mass follows from M = θE/κπE, where κ = 8.144 mas/M⊙ (Gould 2000). Ground-based observations can access πE for long-lasting microlensing events, for which the transverse motion of the Earth is significant enough to allow a good parallax measurement, while for shorter microlensing events space-based parallax is in general required to provide a different vantage point from Earth. Classically, θE can be estimated from the photometric light curve if the spatial extension of source reveals itself by producing noticeable deviations in the light curve and if the source star is well characterised; in the case of bright microlenses, high-resolution adaptive-optics imaging can also access θE typically 5–10 yr after the microlensing event is over, when the background star and the microlens can be resolved individually. As for long baseline interferometry, it provides a direct measurement of θE by resolving the split images of the source star and measuring their angular separations. An additional constraint on πE can be obtained when times series observations are performed as they allow the direction of the relative motion between the lens and the source to be measured (Cassan et al. 2022).
The modelling of interferometric data requires both robust and efficient numerical methods to compute the microlensing models, with a good control on numerical errors, in order to calculate the wide range of models typically required by Markov chain Monte Carlo (MCMC) algorithms. In this work we discuss in detail the case of single-lens models. In Sect. 2, we propose a new and more efficient approach for the exact calculation of the complex interferometric visibility than exists in the literature; we also establish a new approximation, called the thin-arcs approximation, which runs six to ten times faster than the exact calculation, and should apply to a large fraction of potential observational targets. In Sect. 3, we illustrate and discuss the domain of validity of the thin-arcs approximation by comparing it to the exact calculation, and also to the point-source approximation. We discuss the possible shortcomings of ill-defined parametrisations, and advocate for suitable sets of parameters that depend on the characteristics of the observed microlensing event. Finally, in Sect. 4 we summarise the main results and discuss the perspectives of optical/infrared long baseline inter-ferometric observations of microlensing events, in particular in the context of recent developments of the ESO VLTI/GRAVITY instrument.
2 Visibility of reference single-lens models
2.1 Key concepts and equations
The lens equation relates the angular position of the background source star to that of its multiple images. If we set up a Cartesian frame of reference (O, x, y) with axes fixed in the plane of the sky (e.g. north, east) and if we choose the lens to be at the centre of the coordinate system, the complex lens equation for an isolated massive body reads
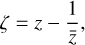 (1)
(1)
where ζ is the affix of the (point-like) centre of the source, z the affix of one of the individual point-like images, and 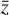 the complex conjugate of z. For the lens equation to be correct, the quantities ζ and z are further normalised by θE, the Einstein angular ring radius (Einstein 1936), which is a function of the lens mass M, the observer-lens distance DL, and the observer-source distance DS through
the complex conjugate of z. For the lens equation to be correct, the quantities ζ and z are further normalised by θE, the Einstein angular ring radius (Einstein 1936), which is a function of the lens mass M, the observer-lens distance DL, and the observer-source distance DS through
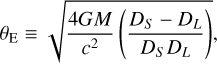 (2)
(2)
with c is the speed of light and G the gravitational constant. The typical separation of the images is of the order of θE; when the source, lens, and observer are perfectly aligned, the image is seen as a perfect ring-shaped image, called an Einstein ring. For a given position ζ = u1eiθ of the source centre 𝒮 (Fig. 1), the single lens Eq. (1) is easily solved by writing z = reiθ, with r solution of r2 − u1r − 1 = 0. This yields two solutions for the images, z(±) = r(±)eiθ, where
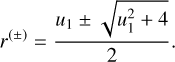 (3)
(3)
If we assume u1 > 0, the image with r(+) > 0 is the major image (𝔗(+) in Fig. 1) and that with r(−) < 0 is the minor image (𝔗(−) in the figure). As ζ, z(+), and z(−) have the same argument, 𝒮, 𝔗(+), and 𝔗(−) are aligned together with the lens, as shown in Fig. 1. If the lens is perfectly aligned with the lens (i.e. ζ = 0), then Eq. (1) yields |ζ| = 1 and the image is an Einstein ring of physical angular radius θE. To avoid any confusion in the units in the angular quantities we discuss here, in the following we assign a subscript ‘E’ to all angular coordinates expressed in θE units. Hence, we write ζ = ξE + iηE and z = xE + iyE, with
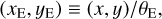 (4)
(4)
where (x, y) are expressed in radians and (xE, yE) in θE units.
The complex (fringe) visibility measured by the interferometer is the Fourier transform of the spatial distribution of light I(xE, yE) in the plane of the sky (more precisely here, the surface brightness of the images), or
![$ {\cal F}\left[ I \right]\left( {{u_{\rm{E}}},{\upsilon _E}} \right) \equiv \int\!\!\!\int_{{{\rm{R}}^2}} I \left( {{x_{\rm{E}}},{y_{\rm{E}}}} \right){e^{ - {\rm{i}}2\pi \left( {{u_{\rm{E}}}{x_{\rm{E}}} + {\upsilon _{\rm{E}}}{y_{\rm{E}}}} \right)}}{\rm{d}}{x_{\rm{E}}}{\rm{d}}{y_{\rm{E}}}, $](/articles/aa/full_html/2023/08/aa42429-21/aa42429-21-eq12.png) (5)
(5)
where (uE, υE) are the conjugate coordinates of (xE, yE). The latter are thus expressed as
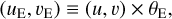 (6)
(6)
where (u, υ) are the usual spatial frequencies, related to the projected baselines Bu and Bυ (respectively in the (Ox) and (Oy) directions) by u = Bu/λ and υ = Bυ/λ, with λ the wavelength of observations; (u, υ) are expressed in radians and (uE, υE) in 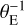 units (Cassan & Ranc 2016). Hereafter, we also call ‘visibility’ the quantity
units (Cassan & Ranc 2016). Hereafter, we also call ‘visibility’ the quantity
![$ {V_{\rm{E}}}\left( {{u_{\rm{E}}},{\upsilon _{\rm{E}}}} \right) \equiv {{{\cal F}\left[ I \right]\left( {{u_{\rm{E}}},{\upsilon _{\rm{E}}}} \right)} \over {{\cal F}\left[ I \right]\left( {0,0} \right)}}, $](/articles/aa/full_html/2023/08/aa42429-21/aa42429-21-eq15.png) (7)
(7)
which is a normalised version of Eq. (5), as the term in the denominator is the total flux. The squared visibility is the squared modulus of the visibility, |VE|2, and its phase is ϕ = arg VE.
We now consider a circular uniformly bright source of constant surface brightness I(xE, yE) = IS, lensed by an isolated massive body (limb-darkened sources are treated in Sect. 2.5). As IS cancels out in the expression of VE in Eq. (7), it is convenient to use the quantity Φ = ℱ[I]/IS (which we also call ‘visibility’ for simplicity); for the lensed images, we then have
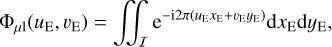 (8)
(8)
where the subscript ‘µl’ stands for microlensed. The integration is performed within the boundaries 𝔗 of the (multiple) lensed images. These images are elongated around the Einstein ring, as shown in Fig. 1 for the 𝒮2 and 𝒮3 sources.
In addition to the lensed images of the source, bright stars in the observing line of sight, although not magnified by the lens, may also be considered as contributing blend’ stars of total visibility ΦB. In particular, if the lens itself is bright enough, it may indeed contribute to a blend term ΦL. Other stars than the lens are unlikely to be involved, even in crowded fields in the Galactic bulge region, because most stars in the immediate vicinity of the lens are faint. We define the blending factor of individual blend star k as the ratio
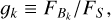 (9)
(9)
where 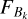 is the flux of blend star k and FS = IS S the flux of the source when it is not lensed, with S = πρ2 and ρ the radius of the source in θE units. We justify that IS is used to calculate the flux of both the source and its lensed images, as gravitational lensing has the important property of preserving surface brightness when forming the lensed images. For a given blend star k of surface Sk (in
is the flux of blend star k and FS = IS S the flux of the source when it is not lensed, with S = πρ2 and ρ the radius of the source in θE units. We justify that IS is used to calculate the flux of both the source and its lensed images, as gravitational lensing has the important property of preserving surface brightness when forming the lensed images. For a given blend star k of surface Sk (in 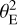 units), the star’s (constant) surface brightness reads
units), the star’s (constant) surface brightness reads 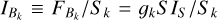 . As in general these stars are not resolved by the interferometer (including the lens; a typical solar-mass lens at 4 kpc has an angular diameter of about 2 µas), Sk can be considered infinitely small and we can write
. As in general these stars are not resolved by the interferometer (including the lens; a typical solar-mass lens at 4 kpc has an angular diameter of about 2 µas), Sk can be considered infinitely small and we can write 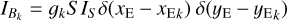 , with δ the Dirac distribution and
, with δ the Dirac distribution and 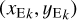 the coordinates of star k. Considering all blend stars, the surface brightness reads
the coordinates of star k. Considering all blend stars, the surface brightness reads
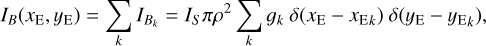 (10)
(10)
so that the blend visibility is given by
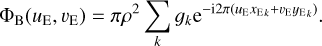 (11)
(11)
In particular, a bright lens (in the centre of the frame) would contribute to ΦL = gLπρ2, with gL = FL/FS the blend-to-source flux ratio. The overall visibility is expressed as
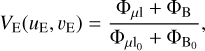 (12)
(12)
where 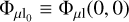 and
and 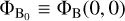 . When three or more baselines are involved, the bispectrum BE,1,2,3 and closure phase ϕE,T3 of each triangle of baselines are given by
. When three or more baselines are involved, the bispectrum BE,1,2,3 and closure phase ϕE,T3 of each triangle of baselines are given by
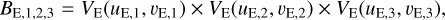 (13)
(13)
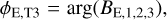 (14)
(14)
where (uE,3, υE,3) = −(uE,1, υE,1) − (uE,2, υE,2), (or an equivalent formula considering that 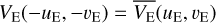 ).
).
For an interferometer observing in the H band (λ ≃ 1.65 µm) with projected baseline B = 100 m along the x-axis, and typical values of θE of 0.5, 1, 1.5, and 2 mas, the interferometer probes uE-values of 0.15, 0.30, 0.45, and 0.60 (in 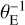 units). As the angular separation of the major and minor images is ~2 × θE (see Fig. 1), we expect the visibility to be modulated with a period of ~0.5 along uE, with a first minimum at uE ~ 0.25 (in
units). As the angular separation of the major and minor images is ~2 × θE (see Fig. 1), we expect the visibility to be modulated with a period of ~0.5 along uE, with a first minimum at uE ~ 0.25 (in 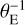 units). This means that provided the microlensing event is bright enough to be observed, the lensed images can be resolved in most cases, and the value of θE measured.
units). This means that provided the microlensing event is bright enough to be observed, the lensed images can be resolved in most cases, and the value of θE measured.
In the following sections, we derive suitable formulae to compute efficiently Eq. (8) for three reference single-lens models: the point-source approximation, the exact formula, and a novel thin-arcs approximation, for uniform and limb-darkened sources.
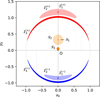 |
Fig. 1 Schematics of the three reference single-lens models detailed in the text. In all cases, the source centre lies on the yE-axis, and the source surface is uniformly bright. Both axes are in θE units. The microlens is the black dot at the centre of the frame, and the Einstein ring is indicated by the dotted circle of radius unity. In the point-source approximation, the source star 𝒮1 (in orange) is point-like and has two point-like images: the major image |
2.2 Point-source approximation
The visibility for a single lens in the point-source approximation was first studied by Delplancke et al. (2001). The resulting major and minor point-like images can then be modelled by Dirac distributions, respectively located at r(+) and r(−), from Eq. (3) and Fig. 1, and weighted by their individual magnification factor µ(+) and µ(−) given by
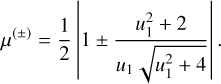 (15)
(15)
When there is no source of blend (Delplancke et al. 2001), the squared visibility reads
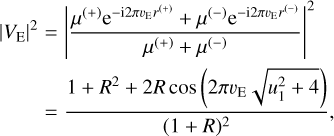 (16)
(16)
where R = µ(+)/µ(−) is the ratio of the magnification of the major image to that of the minor image. The quantity |VE|2 is a sinusoidal function along the (OyE) direction, and is invariant along the (OxE) direction. The modulation has a period of 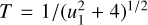 and the squared visibility oscillates between
and the squared visibility oscillates between 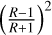 and 1. If u1 is not too large (i.e. u1 ⪅ 0.5), the periodicity is approximately constant and equal to T ≈ 0.5. The amplitude is largest when u1 is small, as µ(+) and µ(−) are both approximated by 1/2u1 so that R ≈ 1. However, we show in Sect. 3 that the point-source model provides in this case a poor approximation of the visibility as the lens strongly distorts the images.
and 1. If u1 is not too large (i.e. u1 ⪅ 0.5), the periodicity is approximately constant and equal to T ≈ 0.5. The amplitude is largest when u1 is small, as µ(+) and µ(−) are both approximated by 1/2u1 so that R ≈ 1. However, we show in Sect. 3 that the point-source model provides in this case a poor approximation of the visibility as the lens strongly distorts the images.
In the general case when one or several unrelated objects k contribute to the blending flux (Sect. 2.1), the resulting complex visibility reads
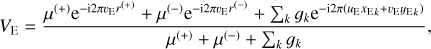 (17)
(17)
where (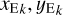 ) are the location of the blend sources on the plane on the sky in θE units, and gk their blending factors as defined by Eq. (9).
) are the location of the blend sources on the plane on the sky in θE units, and gk their blending factors as defined by Eq. (9).
Finally, we note that a single lens event will always lead to a strong interferometric signal, even for microlensing events with relatively low peak magnification or observed far from the peak of the light curve. From the definition of R in Eqs. (16) and (15), it is possible to compute the maximum amplitude of the oscillation of 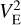 , which is equal to
, which is equal to 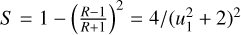 . Even for an unrealistic observation at very low magnification (e.g. 1.4; u1 = 0.9), we have S > 0.5, and for a more standard value of u1 < 0.2 (magnification >5), the contrast reaches values greater than S > 0.96.
. Even for an unrealistic observation at very low magnification (e.g. 1.4; u1 = 0.9), we have S > 0.5, and for a more standard value of u1 < 0.2 (magnification >5), the contrast reaches values greater than S > 0.96.
2.3 Exact formula for an extended source star
The visibility and closure phase for an extended-source single-lens model was first studied by Rattenbury & Mao (2006). As the images are elongated along the Einstein ring (Fig. 1) with analytically well-defined contours (Sect. 2.1), the authors proposed computing numerically the visibility defined in Eq. (5) by a line integral along the outer boundary of each of the major and minor images.
Here, however, we follow a different route and set up another approach to compute Eq. (5), motivated by different arguments. Firstly, our tests have shown that while the line integration scheme works well when the images are reasonably elongated (i.e. at low to medium magnifications), when the images take the form of thin arcs the parametrisation of the contours is far from optimal, as the individual points defining the images contours become strongly unevenly spaced. To achieve reasonable accuracy, the points on the contours need to be resampled, and in any case the number of contour points must be significantly increased. This operation is mandatory, as the line integral basically operates a subtraction between the wedge-shaped area subtended by the outer boundary and that subtended by the inner boundary, which are both of the order of φ/2 (as they are located at r ≃ 1), where φ is the opening angle defined in Fig. 2. In contrast, when ρ ≪ 1 the area enclosed in a given image is of the order of ρφ, and the fractional difference corresponding to the searched visibility is of the order of ρφ/(φ/2) = 2ρ ≪ 1. Hence, an accurate visibility requires a very high accuracy on the line integrals, in particular in the portions where the contours are not well sampled by the parametrisation. The approach we derive below is both robust and computationally much more efficient, and allows a precise control on the final accuracy. This can be achieved by calculating Eq. (5) as a two-dimensional integral in polar coordinates, as we detail below.
We again let u1 > 0 be the ordinate of the centre of the source 𝒮 along the yE-axis, and ρ the source radius (both in θE units), as shown in Fig. 3. We again assume that the source is uniformly bright (and also the images, since surface brightness is preserved). We let θ be the angle of the usual polar coordinates, and u+ and u− the radii where the radial black line in Fig. 3 intersects the upper and lower contours of the source. From geometrical considerations, these are given by
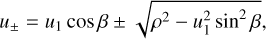 (18)
(18)
where β = θ − π/2. If ρ < u1, we restrict β to vary between – arcsin η1 and arcsin η1 (left panel of Fig. 3), where
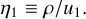 (19)
(19)
Otherwise, if 0 < u1 < ρ, we limit β to vary between −π/2 and π/2 (right panel). These choices are sufficient to parametrise the two arc-shaped images (or the ring) as we obtain two points above the horizontal axis for the major image 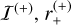 , and
, and 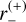 , and two points below for the minor image
, and two points below for the minor image 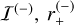 , and
, and 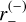 , given by
, given by
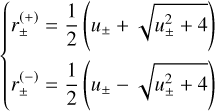 (20)
(20)
from Eq. (3). In all cases, 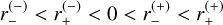 . If u1 = 0, the ring is perfectly symmetric (Einstein ring) as u± = ±ρ, so that
. If u1 = 0, the ring is perfectly symmetric (Einstein ring) as u± = ±ρ, so that 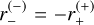 and
and 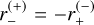 . To calculate the visibility, we further perform the integration of Eq. (8) in polar coordinates,
. To calculate the visibility, we further perform the integration of Eq. (8) in polar coordinates,
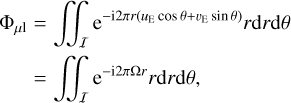 (21)
(21)
We also decompose the full integral into two separates integrals, one for the image above the horizontal axis (elongated image or half-ring), Φ(+), and one for the image below, Φ(−), with
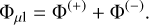 (23)
(23)
We first consider the case ρ < u1 (or 0 < η1 < 1). Since 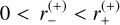 and π/2 – arcsin η1 ≤ θ ≤ π/2 + arcsin η1, we can write the integral Eq. (21) for the major image as
and π/2 – arcsin η1 ≤ θ ≤ π/2 + arcsin η1, we can write the integral Eq. (21) for the major image as
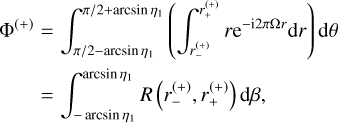 (24)
(24)
where we change to variable β in the second line,
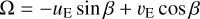 (25)
(25)
The first terms of the series expansion (with respect to Ω) of the expression inside the brackets are
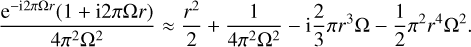 (27)
(27)
When Ω ≪ 1, the term 1/4π2Ω2 becomes large, possibly generating numerical issues, although theoretically this term cancels out in the difference Eq. (26). Hence, the formula 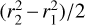 may be used for values of Ω below a threshold of typically Ω ~ 10−3 if we want the second term of the series (in Δr3) to contribute no more than ~10−3 times the term in Δr2.
may be used for values of Ω below a threshold of typically Ω ~ 10−3 if we want the second term of the series (in Δr3) to contribute no more than ~10−3 times the term in Δr2.
We proceed in a similar way for the minor image, but this time with 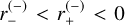 and −π/2 – arcsin η1 ≤ θ ≤ −π/2 + arcsin η1, so that the integral reads
and −π/2 – arcsin η1 ≤ θ ≤ −π/2 + arcsin η1, so that the integral reads
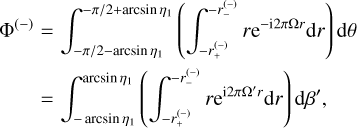 (28)
(28)
after changing the variable to β′ = θ + π/2, and introducing Ω′ = −uE sin β′ + υE cos β′ = − [uE cos(β′ − π/2) + υE sin(β′ − π/2)] = −Ω. As β′ is a dummy variable, we call it β and write
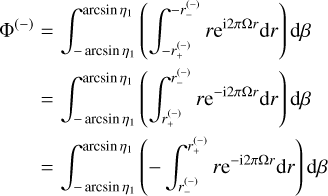 (29)
(29)
by changing variable r to −r and inverting the boundaries of the integral, so that
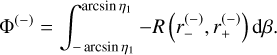 (30)
(30)
We now examine the case 0 < u1 < ρ (or η1 > 1). In this situation the lens lies inside the source, and there is a single ringlike image. The full ring can be drawn by varying θ from 0 to π, as 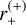 and
and 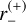 draw the half-ring above the horizontal axis and
draw the half-ring above the horizontal axis and 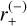 and
and 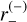 the half ring below it. Hence, the calculation is exactly the same as for ρ < u1 the only difference is that the integration is now performed between −π/2 ≤ β≤ π/2.
the half ring below it. Hence, the calculation is exactly the same as for ρ < u1 the only difference is that the integration is now performed between −π/2 ≤ β≤ π/2.
In summary, for all values of u1 > 0 and ρ > 0 (i.e. η1 > 0) we have
![$ {{\rm{\Phi }}_{\mu {\rm{l}}}} = \int_{ - {\beta _m}}^{{\beta _m}} {\left[ {R\left( {r_ - ^{\left( + \right)},r_ + ^{\left( + \right)}} \right) - R\left( {r_ - ^{\left( - \right)},r_ + ^{\left( - \right)}} \right)} \right]{\rm{d}}\beta } , $](/articles/aa/full_html/2023/08/aa42429-21/aa42429-21-eq70.png) (31)
(31)
When u1 = 0 (Einstein ring), this formula still holds with βm = π/2. In that case the visibility has no imaginary part, which is expected from the symmetry of the ring image.
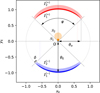 |
Fig. 2 Geometry of major (red) and minor (blue) images when the images are arc-shaped (i.e. for 0 < η1 < 1, where η1 = ρ/u1). The Einstein ring is shown as the black dotted circle, and both axes are in θE units. When the arcs are thin, the images thickness δ is not resolved by the interferometer and two sources 𝒮1 and 𝒮2 (in orange) of same ratio η1 produce arc-shaped images of equal angular elongation, φ = 2 arcsin η1. The projected extension of the arcs onto the xE-axis is θa = η1θE, is hence comparable to θE, and is thus resolved by the interferometer. When η1 > 1, the image of the source is a ring (and φ = π). |
 |
Fig. 3 Geometry and parameters used to calculate interferometric visibility of an extended source star lensed by a single lens. In both panels the Einstein ring is shown as the black dotted circle, and both axes are in θE units. u1 ≥ 0 is the position of the centre of the source along the yE-axis, u+ and u− are the intersections of the black line (polar angle θ) with the contour of the source, and ( |
2.4 The thin-arcs approximation
We consider a common case in practice where the source has a small radius ρ compared to θE (typically, ρ ⪅ 0.1) and passes the lens at small impact parameter, typically u1 ⪅ 0.2 (which corresponds to a point-source magnification at a peak of about 5). This situation is illustrated in Fig. 2 for two sources of radii 𝒮1 and 𝒮2. In the figure it is clear that if the major and minor images are resolved by the interferometer along the (OyE) axis (typical angular separation of 2 × θE, cf. Fig. 2), they have a good chance to be resolved along the (OxE) axis as well (typical angular separation of 2 × θa, where ‘a’ stands for arcs). Since the opening angle of the images is given by φ = 2 aresin η1 (with η1 = ρ/u1 < 1, and φ = π for a ring-like image), we have θa = η1θE (or θa = θE for a ring). Values of η1 > 0.5 are easily reached for the range of values of u1 we discussed above. Hence, we expect this situation to be common in observed microlensing events.
While the major and minor images are resolved in their individual elongations (~2θa) and mutual separation (~2θE), on the contrary their thickness (δ in Fig. 2) will most certainly never be resolved by current interferometric facilities: a value of δ of the order of ρ requires reaching, at best, typical angular resolutions of δ ≈ ρθE < 10 µas. Measuring the thickness of the arcs, however, is not in itself a requirement for measuring θE, as the thickness and the extension of the arcs are directly related by the model. It simply means that the source size ρ is not measured directly by interferometry, but it does not matter in practice as ρ is usually obtained from the modelling of the photometric light curve. It thus appears natural to investigate the possibility of an approximation formula for the visibility that does not directly depend on ρ. A second argument for it is that, as shown in Fig. 2, two sources of different radii but with same opening angle φ (i.e. the same value of η1) are difficult to distinguish from an interferometric point of view, as the displacement is again of the order of ρθE. Hence, a natural model parameter for the sought-after approximation is η1 (i.e. the ratio of ρ/u1 instead of the parameters ρ and u1 individually). Conversely, if ρ to u1 are used in the situation of arc-shaped images (using the exact formula given in Sect. 2.3), we expect these parameters to be strongly correlated (if not degenerate), which may alter the smooth running of the fitting process when modelling interferometric data.
To further illustrate this aspect, Fig. 4 shows the difference in squared visibility Δ|VE|2 between a model computed for parameters ρ = 0.05 and u1 = 8.3 × 10−2, and a reference model obtained with ρ = 0.001 and u1 = 1.7 × 10−3, so that both models have same parameter η1 = 0.6. It appears from the figure that while the source radius is multiplied by a factor of 50 between the two models, the squared visibility is not changed by more than 6 × 10−3 (for a maximum excursion between 0 and 1).
To establish a suitable approximation, which we call the thin-arcs approximation, we note that when both ρ and u1 are small (see Sect. 3.1), u± aie small as well so that we can expand 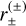 to first order in u±:
to first order in u±:
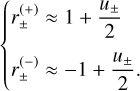 (33)
(33)
Calculating R in Eq. (26) for Ω ≥ 0 yields
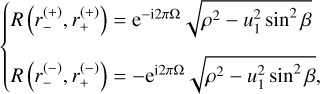 (34)
(34)
which allows us to write, in Eq. (31),
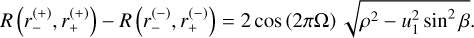 (35)
(35)
From Eq. (25), the real part of cos(2πΩ) is the product cos(2πuE sin β) × cos(2πυE cos β), while its imaginary part reads – sin(2πuE sin β) × sin(2πυE cos β). As we integrate from −βm to βm, the imaginary part cancels out while the real part is doubled. Finally, for u1 > 0 the visibility reads1
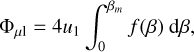 (36)
(36)
where again βm = aresin [min (η1, 1)] and
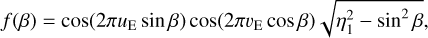 (37)
(37)
while for u1 = 0 (Einstein ring),
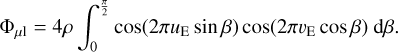 (38)
(38)
As expected, the integrand Eq. (37) does not depend on ρ and u1 individually, but on their ratio η1 (for the perfect Einstein ring, the integrand Eq. (38) does not depend of any of these parameters). In both cases (assuming no blend stars, or ΦB = 0), the factors 4u1 or 4ρ cancel out in Eq. (12), so that the visibility VE depends on η1 only for u1 > 0. It is noteworthy that in the thin-arcs approximation, ϕ = arg Φµ1 can take only two values, 0 and π. It means that the bispectrum BE,1,2,3 in Eq. (13) is also real, and the closure phases ϕE,T3 in Eq. (14) are 0 or π. As u1 increases, the exact value of ϕE,T3 starts to differ from these two values, and should be calculated with the exact formula derived in Sect. 2.3.
Our numerical simulations show that the thin-arcs approximation speeds up the computation by a factor of 6 to 10 (depending on the specific configuration of the images) compared to the exact formula, under a common implementation in Python using the scipy/romberg integration scheme and a given achieved accuracy (5 × 10−5) on both the real and imaginary parts of VE. As we further discuss in Sect. 3.1, the domain of validity of the thin-arcs approximation is wide. Considering |VE|2, for the usual values of ρ and typical excursions in the uEυE-plane, the point-source approximation can be linked with the thin-arcs approximation without having to use the exact formula at all.
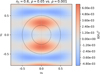 |
Fig. 4 Difference in squared visibility between two single-lens models with same parameter η1 = 0.6. Both axes are in |
2.5 Stellar limb darkening
The most convenient way to treat limb-darkening effects is to decompose the source (assumed to be a disk) into N concentric annuli of inner and outer radii ρk−1 < ρk (1 ≤ k ≤ N) of constant surface brightness Ik, with ρ0 = 0 and ρN = ρ. The visibility is then simply calculated as
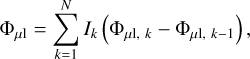 (39)
(39)
where Φµl, k is computed for a source of radius ρk (or equivalently for the thin-arcs approximation, η1, k, with η1, 0 = 0 and η1, N = η1). As limb-darkening affects the border of the disk of the source star, it will affect the ends of the arc-shaped images and will contribute as a correction only to the visibility.
In any case, a linear limb-darkening law will always provide a suitable description of the source’s limb darkening. Adopting the (microlensing) convention that the limb-darkening law is normalised to total unit flux yields 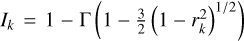 , where Γ is the linear limb-darkening coefficient (0 ≤ Γ ≤ 1), and where rk = ρk/ρ = η1, k/η1. The coefficient Γ is related to the more usual coefficient a by a = 3Γ/(2 + Γ). The choice of the particular set of values ρk (or η1, k) can be optimised to minimise N (e.g. with a linear sampling of Ik between its maximum and minimum values from centre to limb, respectively (1 + Γ/2) and (1 − Γ)).
, where Γ is the linear limb-darkening coefficient (0 ≤ Γ ≤ 1), and where rk = ρk/ρ = η1, k/η1. The coefficient Γ is related to the more usual coefficient a by a = 3Γ/(2 + Γ). The choice of the particular set of values ρk (or η1, k) can be optimised to minimise N (e.g. with a linear sampling of Ik between its maximum and minimum values from centre to limb, respectively (1 + Γ/2) and (1 − Γ)).
3 Application
3.1 Examples and discussion
Typical examples of visibilities (|VE|2 and ϕ = arg VE) are shown in Figs. A.1 to A.6. All the figures were calculated for the same value of ρ = 0.03, slightly above the typical values to challenge the approximations derived in the previous sections. From Figs. A.1 to A.5 the distance of the source to the lens is decreased from u1 = 0.6 to 0.032, and Fig. A.6 is a perfect Einstein ring (u1 = 0). For each figure the upper panels show, on the left, the positions and shapes of the source and the images with the lens in the centre and, on the right, a three-dimensional view of the squared visibility in the Einstein uEυE-plane. The middle panels show the squared visibility |VE|2 (left plot) and the phase ϕ (right plot). The bottom panels show the difference in squared visibility between either the point-source approximation (left) or the thin arcs approximation (right) and the exact calculation. For reference, the colour scale for these plots is set to saturate at Δ|VE|2 ± 0.1 (negative values in blue, positive in red) as they are typical minimum instrumental values of error bars on |VE|2.
For relatively large source-lens separations, such as u1 = 0.6 in Fig. A.1, the images are just slightly elongated, and the point source provides a good approximation to the visibility. The minimum squared visibility differs from 0 and the phase spans a range of values because the two images have different magnifications. The thin-arcs approximation does not provide a good approximation in that case. When u1 = 0.3 (Fig. A.2), the point-source approximation still holds for typical (uE, υE) values probed by the interferometer (data points expected at best between the two dashed circles), and the thin-arcs approximation starts to provide a fair approximation within the inner dashed circle.
When u1 ⪅ 0.2 (peak point-source magnification of about 5), the situation is reversed, as seen in Fig. A.3 for u1 = 0.1. The thin-arcs approximation now provides a very good approximation to the squared visibility (error ≤ 10−2) even outside the outer dashed circle. The point-source approximation is no longer a suitable model. In Fig. A.4 (u1 = 0.05) and Fig. A.5 (u1 = 0.032), the squared visibility progressively takes a circular shape, while the phase does not differ more than a few degrees from 0 or 180 deg. Finally, in Fig. A.6, the image is a perfect ring (u1 = 0) and the thin-arcs approximation is as accurate as the exact calculation. The phase takes only the two values 0 and 180 deg.
In the situation described here (ρ = 0.03), the transition from the point-source to the thin-arcs approximation appears smooth for |VE|2, and unless we have to model interferometric data with very small error bars, it appears unnecessary to perform the exact calculation. The closure phase, however, still requires using the exact calculation, but its value is not expected to deviate more than a few degrees from 0. Finally, for smaller values of ρ, the thin-arcs approximation gives even better results for |VE|2, which justifies its use for a wide range of single-lens parameters.
3.2 Practical modelling
In this section, we study possible strategies for fitting inter-ferometric data to single-lens models, and we discuss suitable choices of model parameters for single-epoch or time-series data. In the following, we assume that the limb-darkening coefficient Γ of the source can be estimated independently (e.g. from a colour-magnitude diagram). The main parameters we discuss below are shown in Fig. 5.
We first consider individual interferometric epochs. We first insist that the images are almost static during the time of an interferometric exposure (~10 min). To compute the visibility, the point-source approximation requires u1 as parameter, the exact formula (u1, ρ), and the thin-arcs approximation η1. To fit the interferometric data, in all cases we must add α1 as a parameter (orientation on the sky of the images) as well as θE (to convert Einstein units into radians). If the lens is luminous, an extra parameter must be added (Sect. 2.1): gL. In general, we expect gL to be at least partly constrained by the light curve, so this parameter may not necessarily be fitted.
In the case of time-series interferometric observations, unless we independently obtain a precise information on the exact trajectory of source relative to the lens, we can assume that the source-lens trajectory is well approximated by a straight line. This approximation holds as long as the different epochs of observation span a relatively short interval of time, typically less than two weeks. The model parameter θE is again used as it gives the overall angular scale of the problem. When using the exact formula, the source radius p must be added as a parameter. Using the lens as a blend star adds another parameter, gL. To describe the source-lens straight trajectory, we need to add the parameters a, the trajectory angle, and t0, a time origin (usually chosen to be the date at which the source is closest to the lens).
When using the exact formula or the point-source approximation, we also have to add in the list of parameters the Einstein timescale tE (i.e. the time it takes for the source to travel θE) as well as u0, the minimum impact parameter of the source-lens trajectory. However, when using the thin-arcs approximation, u0 is no longer a convenient parameter: if for every individual epoch only η1 = ρ/u1 can be measured, then (from Thales’ theorem) only η0 ≡ ρ/u0 can be used as a parameter of the model. Similarly, tE cannot be determined individually, as a trajectory with a higher value of u0 implies a slower moving source (i.e. a higher value of tE) for (almost) the same shape and location of the images; more precisely, the time Δt it takes for the source to travel between two epochs of observation is Δt ∝ u0tE, which means the product p = u0tE is constant. Hence, in principle p could be used as a model parameter, but in practice it appears more convenient to use the source radius crossing time, t* = ρtE, as it is the product of the two constant quantities η0 × u0tE, and a classical parameter in microlensing modelling.
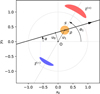 |
Fig. 5 Model parameters for a straight-line source-lens trajectory. The lens is the black dot in the centre, the source (unseen) is the orange disk 𝒮 of radius ρ, and the red and blue arcs 𝔗+ and 𝔗− are the major and minor lensed images, respectively. The line joining the centre of the two images makes an angle α1 with the xE-axis, with the convention that the source centre lies at a distance u1 > 0 from the lens, so that the major image is up for α1 ∈ [0, π] The trajectory of the source with respect to the lens is shown as the thick black arrow. It makes an angle a with the xE-axis, and u0 is its signed impact parameter. As the source moves relative to the lens along the black arrow, the images rotate around the lens. |
4 Summary and perspectives
In this work, we first reviewed the main concepts and general formulae of interferometric microlensing, and detailed the equations useful for treating the case of a single lens. We recalled the well-known visibility formula for a point source, and then treated the case of an extended source, for which we proposed a new approach for the calculation of the visibility, allowing a robust and numerically efficient calculation.
This formalism allowed us to establish a new approximation, which we called the thin-arcs approximation, and which applies to microlensing events of medium or higher magnification observed around the peak (i.e. a large fraction of potential observational targets). We demonstrated that the computation time using this approximation is 6–10 times faster than with the exact formula, and applies over a wide range of lens-source separations. It even turns out that a direct transition from the point-source to the thin-arcs approximations is possible in many situations, without having to calculate the visibility with the exact formula.
Accurate models and reliable numerical methods are of particular importance as the number of targets is expected to increase significantly in the near future. Based on a 4 yr of statistics of microlensing events alerted by the OGLE collaboration (2011–2014, about 7000 events), Cassan & Ranc (2016) found that the number of potential interferometric targets N scales as 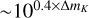 with the event’s peak magnitude mK (obtained from a linear regression of the event’s count, right panel of Fig. 3 in Cassan & Ranc 2016); in other words, a gain in ~2.4 magnitudes in the instrument sensitivity results in about ten times more potential microlensing targets. Pushing the limiting magnitude of current or new-generation interferometers will therefore have a huge impact on the field.
with the event’s peak magnitude mK (obtained from a linear regression of the event’s count, right panel of Fig. 3 in Cassan & Ranc 2016); in other words, a gain in ~2.4 magnitudes in the instrument sensitivity results in about ten times more potential microlensing targets. Pushing the limiting magnitude of current or new-generation interferometers will therefore have a huge impact on the field.
Until recently, interferometric facilities suffered from a lack of sensitivity, limiting the pool of observable microlensing targets to the very bright tip of the distribution. Observations like those obtained for Gaia19bld at the VLTI (peak magnitude of H = 6.2, just above the PIONIER instrument’s limiting magnitude of H = 7.5, see Ext. Data. Figure 1 in Cassan et al. 2022) hence remained exceptional. However, the latest improvements in interferometric instruments are going to be a ‘game-changer’, in particular for the ESO GRAVITY instrument at the VLTI. The new dual-field wide mode now available for GRAVITY, which uses a close and brighter star in the vicinity of the target to push the limiting magnitude up to K ~ 16, will significantly increase the number of potential microlensing targets in upcoming observing campaigns. The expectations are 10–30 targets per year (and perhaps more), instead of about 1 target per year with the previous set-up. In addition to pinpointing the masses of exoplanets discovered through microlensing, these observations will allow us, for the first time, to unambiguously find isolated stellar black holes, and measure their masses with an exquisite precision.
Appendix A Additional figures
 |
Fig. A.1 Plots for ρ = 0.03 and u1 = 0.6. Upper panels: Shown in the plot on the left are the lens (black dot in the centre), the (unseen) extended source (orange disk), and its two lensed images (red and blue arc-shaped images), displayed in (xE, yE) coordinates which are normalised by the angular Einstein ring radius θE. The plot on the right displays a three-dimensional view of the squared visibility |VE|2 in the Einstein uEυE-plane, normalised by |
 |
Fig. A.6 Same as Fig. A.1, but for u1 = 0. In this case the point-source approximation yields a circle instead of two point-like images and is not shown here. |
References
- Cassan, A., & Ranc, C. 2016, MNRAS, 458, 2074 [NASA ADS] [CrossRef] [Google Scholar]
- Cassan, A., Ranc, C., Absil, O., et al. 2022, Nat. Astron., 6, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Dalal, N., & Lane, B. F. 2003, ApJ, 589, 199 [CrossRef] [Google Scholar]
- Delplancke, F., Górski, K. M., & Richichi, A. 2001, A&A, 375, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dong, S., Mérand, A., Delplancke-Ströbele, F., et al. 2019, ApJ, 871, 70 [CrossRef] [Google Scholar]
- Einstein, A. 1936, Science, 84, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A. 2000, ApJ, 535, 928 [Google Scholar]
- Paczynski, B. 1986, ApJ, 304, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rattenbury, N. J., & Mao, S. 2006, MNRAS, 365, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Yoo, J., DePoy, D. L., Gal-Yam, A., et al. 2004, ApJ, 603, 139 [Google Scholar]
The denominator of VE in Eq. (12), 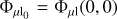 , can be written as
, can be written as 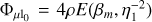 , where
, where 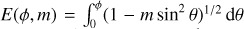 is the incomplete elliptic integral of the second kind. The total source flux magnification A being the ratio of the total area of the images
is the incomplete elliptic integral of the second kind. The total source flux magnification A being the ratio of the total area of the images 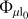 to the area of the source, πρ2, we obtain
to the area of the source, πρ2, we obtain 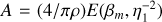 , which is the approximation derived by Yoo et al. (2004), though with a slightly different definition of E and z= 1/η1.
, which is the approximation derived by Yoo et al. (2004), though with a slightly different definition of E and z= 1/η1.
All Figures
 |
Fig. 1 Schematics of the three reference single-lens models detailed in the text. In all cases, the source centre lies on the yE-axis, and the source surface is uniformly bright. Both axes are in θE units. The microlens is the black dot at the centre of the frame, and the Einstein ring is indicated by the dotted circle of radius unity. In the point-source approximation, the source star 𝒮1 (in orange) is point-like and has two point-like images: the major image |
| In the text | |
 |
Fig. 2 Geometry of major (red) and minor (blue) images when the images are arc-shaped (i.e. for 0 < η1 < 1, where η1 = ρ/u1). The Einstein ring is shown as the black dotted circle, and both axes are in θE units. When the arcs are thin, the images thickness δ is not resolved by the interferometer and two sources 𝒮1 and 𝒮2 (in orange) of same ratio η1 produce arc-shaped images of equal angular elongation, φ = 2 arcsin η1. The projected extension of the arcs onto the xE-axis is θa = η1θE, is hence comparable to θE, and is thus resolved by the interferometer. When η1 > 1, the image of the source is a ring (and φ = π). |
| In the text | |
 |
Fig. 3 Geometry and parameters used to calculate interferometric visibility of an extended source star lensed by a single lens. In both panels the Einstein ring is shown as the black dotted circle, and both axes are in θE units. u1 ≥ 0 is the position of the centre of the source along the yE-axis, u+ and u− are the intersections of the black line (polar angle θ) with the contour of the source, and ( |
| In the text | |
 |
Fig. 4 Difference in squared visibility between two single-lens models with same parameter η1 = 0.6. Both axes are in |
| In the text | |
 |
Fig. 5 Model parameters for a straight-line source-lens trajectory. The lens is the black dot in the centre, the source (unseen) is the orange disk 𝒮 of radius ρ, and the red and blue arcs 𝔗+ and 𝔗− are the major and minor lensed images, respectively. The line joining the centre of the two images makes an angle α1 with the xE-axis, with the convention that the source centre lies at a distance u1 > 0 from the lens, so that the major image is up for α1 ∈ [0, π] The trajectory of the source with respect to the lens is shown as the thick black arrow. It makes an angle a with the xE-axis, and u0 is its signed impact parameter. As the source moves relative to the lens along the black arrow, the images rotate around the lens. |
| In the text | |
 |
Fig. A.1 Plots for ρ = 0.03 and u1 = 0.6. Upper panels: Shown in the plot on the left are the lens (black dot in the centre), the (unseen) extended source (orange disk), and its two lensed images (red and blue arc-shaped images), displayed in (xE, yE) coordinates which are normalised by the angular Einstein ring radius θE. The plot on the right displays a three-dimensional view of the squared visibility |VE|2 in the Einstein uEυE-plane, normalised by |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but for u1 = 0.3. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1, but for u1 = 0.1. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.1, but for u1 = 0.05. |
| In the text | |
 |
Fig. A.5 Same as Fig. A.1, but for u1 = 0.032. |
| In the text | |
 |
Fig. A.6 Same as Fig. A.1, but for u1 = 0. In this case the point-source approximation yields a circle instead of two point-like images and is not shown here. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



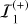
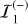
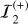
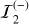
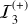
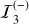
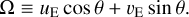
![$ \matrix{ {R\left( {{r_1},{r_2}} \right)} \hfill & { \equiv \int_{{r_1}}^{{r_2}} {r{e^{ - {\rm{i}}2\pi {\rm{\Omega }}r}}} {\rm{d}}r} \hfill \cr {} \hfill & {\left\{ {\matrix{ {{1 \over 2}\left( {r_2^2 - r_1^2} \right)} \hfill & {{\rm{if}}\,{\rm{\Omega }} = 0,} \hfill \cr {\left[ {{{{{\rm{e}}^{ - {\rm{i}}2\pi {\rm{\Omega }}r}}\left( {1 + {\rm{i}}2\pi {\rm{\Omega }}r} \right)} \over {4{\pi ^2}{{\rm{\Omega }}^2}}}} \right]_{{r_1}}^{{r_2}}} \hfill & {{\rm{otherwise}}{\rm{.}}} \hfill \cr } } \right.} \hfill \cr } $](/articles/aa/full_html/2023/08/aa42429-21/aa42429-21-eq59.png)
![$ {\beta _m} = {\rm{arcsin}}\left[ {\min \left( {{\eta _{\rm{l}}},1} \right)} \right]. $](/articles/aa/full_html/2023/08/aa42429-21/aa42429-21-eq71.png)