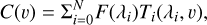| Issue |
A&A
Volume 674, June 2023
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202245539 | |
| Published online | 01 June 2023 | |
The PEPSI Exoplanet Transit Survey (PETS)
III. The detection of Fe I, Cr I, and Ti I in the atmosphere of MASCARA-1 b through high-resolution emission spectroscopy
1
INAF - Osservatorio Astrofisico di Catania,
Via S. Sofia 78,
95123
Catania, Italy
e-mail: gaetano.scandariato@inaf.it
2
INAF - Osservatorio Astronomico di Brera,
Via E. Bianchi, 46,
23807
Merate (LC), Italy
3
INAF - Osservatorio Astrofisico di Torino,
Strada Osservatorio 20,
10025
Pino Torinese, Italy
4
Department of Astronomy, The Ohio State University,
4055 McPherson Laboratory, 140 West 18th Ae.,
Columbus, OH
43210, USA
5
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg, Germany
6
Leibniz-Institute for Astrophysics Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam, Germany
7
INAF - Osservatorio Astronomico di Padova,
Vicolo dell'Osservatorio 5,
35122
Padova, Italy
8
Dipartimento di Fisica e Astronomia "Galileo Galilei", Universita degli Studi di Padova,
35122
Padova, Italy
9
Universitäts-Sternwarte, Ludwig-Maximilians-Universität München,
Scheinerstrasse 1,
81679
München, Germany
10
Exzellenzcluster Origins,
Boltzmannstraße 2,
85748
Garching, Germany
11
School of Earth and Space Exploration, Arizona State University,
660 S. Mill Ave.,
Tempe, AZ
85281, USA
12
INAF - Osservatorio Astrofisico di Arcetri,
Largo Enrico Fermi 5,
50125
Firenze, Italy
13
Institute of Physics & Astronomy, University of Potsdam,
Karl-Liebknecht-Str. 24/25,
14476
Potsdam, Germany
14
Steward Observatory, University of Arizona,
933 N. Cherry Ave.,
Tucson, AZ
85721, USA
15
Large Binocular Telescope Observatory,
933 N. Cherry Ave.,
Tucson, AZ
85721, USA
16
Department of Astronomy, University of Science and Technology of China,
Hefei
230026, PR China
17
Institute of Astrophysics, University of Göttingen,
Friedrich-Hund-Platz 1,
37077
Göttingen, Germany
Received:
23
November
2022
Accepted:
6
April
2023
Context. Hot giant planets such as MASCARA-1 b are expected to have thermally inverted atmospheres, which makes them perfect laboratories for atmospheric characterization through high-resolution spectroscopy. Nonetheless, previous attempts at detecting the atmosphere of MASCARA-1 b in transmission have led to negative results.
Aims. We aim to detect the optical emission spectrum of MASCARA-1 b.
Methods. We used the high-resolution spectrograph PEPSI to observe MASCARA-1 (spectral type A8) near the secondary eclipse of the planet. We cross-correlated the spectra with synthetic templates computed for several atomic and molecular species.
Results. We detect Fe I, Cr I, and Ti I in the atmosphere of MASCARA-1 b with a S/N ≈ 7, 4, and 5, respectively, and confirm the expected systemic velocity of ≈13 km s−1 and the radial velocity semi-amplitude of MASCARA-1 b of ≈200 km s−1. The detection of Ti is of particular importance in the context of the recently proposed phenomenon of Ti cold-trapping below a certain planetary equilibrium temperature.
Conclusions. We confirm the presence of an atmosphere around MASCARA-1 b through emission spectroscopy. We conclude that the atmospheric non-detection in transmission spectroscopy is due to the strong gravity of the planet and/or to the overlap between the planetary track and its Doppler shadow.
Key words: techniques: spectroscopic / planets and satellites: composition / planets and satellites: atmospheres / planets and satellites: individual: MASCARA-1 b
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Atmospheric studies of ultra-hot Jupiters (UHJs), short-period giant planets with equilibrium temperatures exceeding ~2000 K due to strong incident stellar flux, have increased significantly in recent years. High-resolution transmission spectroscopy of UHJs, which has been proven to be the most powerful technique for investigating their atmospheres, has revealed the presence of many atomic species in their atmospheres (e.g., Yan & Henning 2018; Hoeijmakers et al. 2019; Casasayas-Barris et al. 2020; Borsa et al. 2021a,b; Tabernero et al. 2021; Kesseli et al. 2022; Prinoth et al. 2022) and has been used to probe their dynamics (e.g., Ehrenreich et al. 2020; Seidel et al. 2021; Borsa et al. 2021b; Kesseli & Snellen 2021).
MASCARA-1 b (Talens et al. 2017) is one of the hottest known UHJs and orbits one of the brightest transiting exoplanet host stars (see Table 1 for details of the system parameters). Nevertheless, high-resolution transmission spectroscopy studies have failed to find any trace of its atmosphere (Stangret et al. 2022; Casasayas-Barris et al. 2022). This has been attributed to the possibility that the atmospheric scale height is too small for successful transmission spectroscopy mainly because of the large surface gravity (log gp = 3.6 (cgs); Casasayas-Barris et al. 2022). Moreover, due to the geometric configuration of the system, the planetary track, which depends on the planetary velocity in the stellar rest frame and the projected spin-orbit angle (Casasayas-Barris et al. 2022), almost completely overlaps with the Doppler shadow, which depends on the stellar rotation.
A complementary technique to transmission spectroscopy, which probes the terminator region of the planet, is phase-resolved emission spectroscopy, which searches for emission signals from the planetary dayside. This technique exploits the fact that, for UHJs, the atmospheric temperature-pressure profile is expected to be inverted (e.g., Lothringer & Barman 2019), causing atomic lines to be seen in emission on the dayside of the planet. Since with this technique we do not need to see through the atmosphere, the atmospheric density issue can be overcome. This technique has already been shown to be useful when using transmission spectroscopy as it gives clues about the atmospheres of UHJs (e.g., Pino et al. 2020; Nugroho et al. 2020; Borsa et al. 2022), and it is possibly the most appropriate for investigating the atmosphere of MASCARA-1 b (Casasayas-Barris et al. 2022).
This technique has already been shown to be complementary to transmission spectroscopy in probing the atmospheres (both the dayside and the terminator region) of UHJs (e.g., Pino et al. 2020; Nugroho et al. 2020; Borsa et al. 2022). Furthermore, emission spectroscopy is likely the most appropriate for investigating the atmosphere of MASCARA-1 b (Casasayas-Barris et al. 2022).
In this work, we analyze high-resolution spectra of MASCARA-1, in which Holmberg & Madhusudhan (2022) already detected H2O and CO in emission in the near-infrared. We used the Potsdam Echelle Polarimetric and Spectroscopic Instrument (PEPSI) spectrograph to observe MASCARA-1 b when it shows its dayside, looking for signals of the planetary atmosphere in the optical and near-infrared bands. In Sect. 2, we present the data we collected and their reduction. In Sect. 3, we describe how we extracted the planetary signal, and we conclude in Sect. 4 with final remarks.
Stellar and system parameters.
2 Observations and data reduction
The PEPSI Exoplanet Transit Survey (PETS) is a collaboration that aims to spectroscopically analyze exoplanetary transits and secondary eclipses as well as characterize their host stars (Keles et al. 2022; Johnson et al. 2022). The project takes advantage of the light collecting power of the Large Binocular Telescope (LBT) and the high-resolution spectroscopy of PEPSI (Strassmeier et al. 2015, 2018).
In the framework of the PETS programs, we observed the MASCARA-1 (HD 201585) system, which consists of a Jupiter-sized planet orbiting a fast-rotating (υ sin i* = 109 ± 4 km s−1) A8 type star every ~2.14 days (Talens et al. 2017). Given the architecture of the system, MASCARA-1 b is one of the most irradiated exoplanets known to date. Hooton et al. (2022) recently reanalyzed the system, confirming the orbital misalignment and estimating an extremely high dayside temperature of more than 3000 K. The stellar, planetary, and orbital parameters most relevant for our work are listed in Table 1.
While attempting to collect the emission spectrum of the planet, we collected the spectra of the system over two nights, to cover the orbital phases preceding and succeeding the planetary eclipse, when the planet-to-star flux ratio was most favorable for the planetary emission spectroscopy. The orbital phases preceding the secondary eclipse were covered on June 10, 2021 (N1 hereafter), while the post-eclipse phases were covered on the night of June 19, 2021 (N2 hereafter). For each night of observations, we used the LBT in binocular mode, using the cross-disperser (CD) of the PEPSI spectrograph CD3 in the blue arm (4800–5441 Å, R ~ 115 000) and CD6 in the red arm (7419–9067 Å, R ~ 115 000). The exposure time of each camera was 10 min, and, despite a negligible lag of a few seconds due to different duty cycles in the two arms, we can assume perfect simultaneity between the series of spectra of the blue and red arms. Where not specified, in the following we always refer to a single spectrum observed by LBT, covering both the CD3 and CD6 spectral ranges. After some preliminary analysis, we rejected the last four spectra taken on N1 that were obtained at twilight and one spectrum on N2 with S/N < 100. The log book of the remaining observations is reported in Table 2.
Data reduction was performed in the same way as presented in Keles et al. (2022). In summary, all science and calibration images after bias subtraction were first corrected for the master flat field image to eliminate pixel-to-pixel noise. The optimal extraction of each of the five slices of all spectral orders was done by fitting the smoothed spatial profile to the raw data. All extracted slices were then averaged with weights of their pixel variances to the wavelength grid of the middle slice. The continuum fit was performed with a constrained 2D polynomial to co-align the overlapping parts of the spectral orders after continuum normalization. Finally, the spectral orders were rectified into a single 1D spectrum with a weighted average of the overlapping parts of orders while keeping the wavelength scale of the preceding orders. The extracted 1D spectra from the two LBT mirrors were averaged with weights and subjected to a final continuum correction with a smoothing spline in clip-and-fit mode, which selects only the continuum wavelength pixels. The wavelength scales of the resulting spectra were then transformed into the Solar System barycenter by using the Jet Propulsion Laboratory ephemeris. In this work we performed our analysis on the 1D final spectra.
To correct the telluric absorption in the spectra, we computed the best telluric model, including both H2O and O2. To this purpose, we injected into MOLECFIT (Kausch et al. 2015; Smette et al. 2015) the spectral ranges least affected by the stellar absorption lines listed in Table 3. We then used the best-fit telluric model to correct the full spectra. An example of the telluric correction is shown in Fig. 1.
We then shifted the spectra to the stellar rest frame using the system parameters in Table 1 and resampled them to a common wavelength step of 0.01 Å for CD3 and 0.03 Å for CD6. We computed the median of the spectra, thus obtaining a high S/N representation of the stellar spectrum void of the contribution of the emission spectrum of the planet. As a matter of fact, the planetary emission lines are expected to shift due to the Doppler effect from one observation to the next one in the stellar rest frame, and get canceled out by the median computation (see Scandariato et al. 2021, for a detailed description).
We thus divided each spectrum by the average spectrum and analyzed the residuals of each spectrum with respect to the median spectrum. This analysis emphasized the presence of a few spikes, mainly due to cosmic rays hits, which we clipped out with a 5σ rejection criterion and substituted with the median flux. Secondly, we identified and masked out spectral regions where the telluric correction left residuals stronger than the spectral noise, typically in the case of strong or saturated telluric O2 lines in the red part of the spectra (7590–7700 Å, 8100–8370 Å, and >8900 Å). Finally, we refined the normalization of each spectrum by fitting the residuals with a low-order Savitzky-Golay filter, which preserves the spectral lines while correcting second-order inaccuracies in the reduction and normalization of the spectra.
Log book of the observations.
Wavelength ranges used to compute the telluric absorption model.
 |
Fig. 1 Example of the telluric correction performed using MOLECFIT, showing the case of the H2O (top panel) and O2 (bottom panel) telluric lines. In each panel, the telluric spectrum has been shifted upward for clarity. |
3 Method
We divided each spectrum in the N1 and N2 series by the corresponding median spectrum: this procedure removed the stellar absorption lines while preserving the planetary emission spectrum. These spectra represent a phase-resolved series of continuum-normalized planetary emission spectra.
To extract the planetary signal buried in the noise, we used the cross-correlation function (CCF) technique (Snellen et al. 2010), which has already been successfully applied in the analysis of emission spectroscopy (see, for example, Nugroho et al. 2020; Yan et al. 2020, 2022). Given a spectrum, F(λ), and a template, Τ(λ, υ), Doppler-shifted at the velocity υ, the CCF C(υ) is computed as
where the summation is extended over all the N spectral points in the observed spectrum. In principle, the contribution of the echelle orders can be weighted by their respective S/N. In practice, since the S/N does not change significantly along the orders, for the sake of simplicity we prefer not to weight by the S/N. This also preserves the relative contribution of the spectral lines in the templates.
We generated emission template spectra using petitRADTRANS (Mollière et al. 2019), assuming solar metallicity and equilibrium chemistry. We used the temperature-pressure profile presented in Lothringer & Barman (2019) for a planet with Teq = 2250 K orbiting an A0 host star with no TiO in the atmosphere (see their Fig. 3). The choice of using the profile with no TiO was motivated by the fact that so far it has been detected only in the atmosphere of WASP-189 b (Prinoth et al. 2022) and WASP-33 b (Nugroho et al. 2017; Cont et al. 2021), while its detection is at best controversial for other UHJs, despite predictions that it is in their atmospheres and is a possible cause of the thermal inversion (e.g., Hubeny et al. 2003; Fortney et al. 2008). The absence of TiO is also supported a posteriori by the fact that we do not detect it in the collected spectra (TiO was also modeled and searched for with the theoretical temperature-pressure profile assuming TiO in the atmosphere). To scale the templates to the same units as the reduced spectra, we added the stellar blackbody spectrum with Teff = 7490 K (Table 1) and continuum-normalized them.
We generated the templates for the species Fe I, Fe II, FeH, Ca I, CaH, Cr I, Si I, Ti I, V I, Y I, TiO, and VO, which have the largest number of lines in the wavelength range covered by our spectra (see, for example, Appendix A.1 in Kitzmann et al. 2021). We removed all the spectral lines in the templates that are weaker than 1% of the strongest line in the template, as they are prone to introduce noise into the CCF computation.
We used the templates to compute the CCF of each planetary emission spectrum. For each night and for each template, we thus derived a stack of CCFs. In a 2D representation, the planetary signal is expected to show up as an emission feature moving in the velocity space according to the planetary Keplerian motion in the stellar rest frame. This approach did not lead us to a detection because the expected signal, if present, is smaller than the noise of the CCFs (see, for example, Fig. 2).
To enhance the detectability of the planetary signal, it is common practice to realign and stack the CCFs into the planetary rest frame. To this purpose, we iteratively assumed a value for υsys in the range −5–30 km s−1 with a step of 0.5 km s−1 and a value for the planetary radial velocity semi-amplitude, Kp, in the range 50–300 km s−1 with a step of 1 km s−1. For each pair of υsys and Kp, we thus re-centered each CCF into the planetary rest frame, assuming the ephemeris in Table 1, and we computed the average planetary CCF at velocity υ = 0, where the peak of the planetary signal is expected. This procedure generated a 2D Kp–υsys map that is expected to show a peak at the (Kp,υsys) coordinates coinciding with the Kp and υsys derived for the planet and the system. Conversely, pixels far from the expected peak should be randomly distributed around zero depending on the noise of the spectra and how it interferes with the templates used for the cross-correlation. To estimate the S/N of the detection, we normalized the Kp–υsys maps by the mean absolute deviation of the pixels in the map. The computation is extended to the whole map and, by construction, is robust against outlier pixel values.
In Fig. 3, we show the Kp−υsys maps for Fe I, Cr I, and Ti I: while they ubiquitously show positive and negative artifacts, it is striking that they also show a strong positive signal close to where we expect the planetary emission signal (see Table 1). We thus claim clear detection with a S/N higher than 4 (Table 4). For the other templates, we do not find anything statistically significant, meaning that those species do not produce a CCF signal stronger than noise.
For each map, we extracted the horizontal slice that intersects the peak. To quantify the center of the detected emission feature and the corresponding uncertainty, we computed a Gaussian fit to estimate υsys. Similarly, we obtained a vertical slice through the map peak and fit a Gaussian function to estimate Kp (see the central and right columns in Fig. 3). In both cases, due to correlated noise introduced by the CCF technique, it is difficult to estimate the uncertainties on the centroids. For the sake of simplicity, we thus used the widths of the Gaussian fits as the uncertainties for the best-fit parameters. The υsys and Kp best estimates are listed together with their corresponding uncertainties in Table 4. We find that the measurements all agree, within the uncertainties, with one another and with the estimates listed in Table 1.
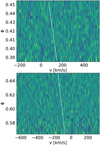 |
Fig. 2 CCFs of the planetary emission spectrum for nights N1 (top panel) and N2 (bottom panel) as a function of the planetary orbital phase. The CCFs shown in these plots were computed using the Fe I spectral template, for which we claim the strongest detection (see Table 4). In each panel, the dashed white line marks where the planetary emission signal is expected according to the system parameters in Table 1. The emission trace is not obvious in this 2D plot and is only detected significantly in the Kp–υsys map, as shown in Fig. 3. |
 |
Fig. 3 Atmospheric planetary signal obtained with the Fe I, Cr I, and Ti I templates (top, central, and bottom row, respectively). The left column shows the Kp-υsys bi-dimensional map, with the color bar encoding the significance of the detection. The cross in white dashes marks the position where the planetary signal is expected according to Table 1. The central (right) column shows the cut along the vertical (horizontal) direction on the map and corresponding to the peak detection, together with its Gaussian best fit (dashed blue line). |
Summary of the detected species in the Kp–υsys maps.
4 Conclusions
In this work we confirm the atmospheric signal for MASCARA-1 b, an UHJ. We observed its dayside at two epochs, before and after the secondary eclipse, respectively, using the PEPSI high-resolution spectrograph mounted at the LBT. By means of cross-correlation techniques, we detected Ti I, Cr I, and Fe I emission in the atmosphere of the planet for the first time. This detection confirms that the atmosphere of MASCARA-1 b can be detected through emission spectroscopy (Holmberg & Madhusudhan 2022) despite the fact that high-resolution transmission spectroscopy has so far been unsuccessful (Stangret et al. 2022; Casasayas-Barris et al. 2022).
The system of reference of all our detections is fully consistent with the expected systemic velocity and radial velocity amplitude of MASCARA-1 b, thus confirming their planetary nature (Table 4). The absence of a signal in transmission in previous publications is thus likely due to the strong gravity of the planet or to the overlap of the planetary track with the Doppler shadow, as discussed by Casasayas-Barris et al. (2022). Another interesting interpretation highlights the 3D nature of MASCARA-1 b's atmosphere, with atomic species more visible in the planetary dayside because of being dissociated due to the higher temperatures with respect to the terminator.
In a thermal radiation spectrum, the flux of the spectral lines originates from higher altitudes than the continuum (Yan et al. 2022). The detection of lines in emission from the planet thus indicates hotter temperatures at higher altitudes, and confirms for MASCARA-1 b the thermal inversion observed by Holmberg & Madhusudhan (2022) and observed in the atmosphere of other UHJs (e.g., Lothringer & Barman 2019; Pino et al. 2020; Nugroho et al. 2020; Yan et al. 2022; Borsa et al. 2022). For these planets, the thermal inversion is caused by the high UV flux received from the host star (which is an A type in most cases).
The detection of Ti in the atmosphere of MASCARA-1b is of particular relevance. Recently, by analyzing high-resolution emission spectroscopy of the UHJ WASP-121 b and not finding traces of Ti, Hoeijmakers et al. (2022) proposed the possibility of Ti cold-trapping. In particular, they propose a sharp transition above which Ti become detectable in exoplanetary atmospheres to be between the Teq of WASP-121 b (2358+52K) and WASP-189 b (2641+34K), (Prinoth et al. 2022). In this work, we find evidence of the presence of Ti in the atmosphere of MASCARA-1 b, with a Teq of 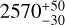 (Talens et al. 2017), which further reduces the transition temperature interval.
(Talens et al. 2017), which further reduces the transition temperature interval.
High-resolution emission spectroscopy is confirmed to be an excellent and complementary technique to transmission spectroscopy when investigating the atmospheres of UHJs. This is the first case where an absence of signal in transmission has been subsequently followed by a detection in emission, as was suggested for this planet by Casasayas-Barris et al. (2022).
Acknowledgements
The LBT is an international collaboration among institutions in the United States, Italy and Germany. LBT Corporation Members are: The University of Arizona on behalf of the Arizona Board of Regents; Istituto Nazionale di Astrofisica, Italy; LBT Beteiligungsgesellschaft, Germany, representing the Max-Planck Society, The Leibniz Institute for Astrophysics Potsdam, and Heidelberg University; The Ohio State University, representing OSU, University of Notre Dame, University of Minnesota and University of Virginia. G.Sc. acknowledges support from CHEOPS ASI-INAF agreement no. 2019-29-HH.0. G.Sc. is grateful to C.M.C.S. for the best funds coming in small packages (agreement Aug, 30 2019). We acknowledge the support by INAF/Frontiera through the "Progetti Premiali" funding scheme of the Italian Ministry of Education, University, and Research and from PRIN INAF 2019. This research was supported by the Excellence Cluster ORIGINS which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC-2094 – 390783311. K.P. acknowledges funding from the German Leibniz-Gemeinschaft under project number P67/2018.
References
- Borsa, F., Allart, R., Casasayas-Barris, N., et al. 2021a, A & A, 645, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borsa, F., Fossati, L., Koskinen, T., Young, M. E., & Shulyak, D. 2021b, Nat. Astron., 6, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Borsa, F., Giacobbe, P., Bonomo, A. S., et al. 2022, A & A, 663, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2020, A & A, 640, A6 [Google Scholar]
- Casasayas-Barris, N., Borsa, F., Palle, E., et al. 2022, A & A, 664, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cont, D., Yan, F., Reiners, A., et al. 2021, A & A, 651, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehrenreich, D., Lovis, C., Allart, R., et al. 2020, Nature, 580, 597 [Google Scholar]
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [CrossRef] [Google Scholar]
- Hoeijmakers, H. J., Ehrenreich, D., Kitzmann, D., et al. 2019, A & A, 627, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoeijmakers, H. J., Kitzmann, D., Morris, B. M., et al. 2022, A & A, [arXiv:2218.12847] [Google Scholar]
- Holmberg, M., & Madhusudhan, N. 2022, AJ, 164, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Hooton, M. J., Hoyer, S., Kitzmann, D., et al. 2022, A & A, 658, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubeny, I., Burrows, A., & Sudarsky, D. 2003, ApJ, 594, 1011 [Google Scholar]
- Johnson, M. C., Wang, J., Pai Asnodkar, A., et al. 2022, AJ, 165, 157 [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A & A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keles, E., Mallonn, M., Kitzmann, D., et al. 2022, MNRAS, 513, 1544 [NASA ADS] [CrossRef] [Google Scholar]
- Kesseli, A. Y., & Snellen, I. A. G. 2021, ApJ, 908, L17 [Google Scholar]
- Kesseli, A. Y., Snellen, I. A. G., Casasayas-Barris, N., Mollière, P., & Sanchez-Lopez, A. 2022, AJ, 163, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzmann, D., Hoeijmakers, J. H., Grimm, S. L., et al. 2021, A & A, 669, A113 [Google Scholar]
- Lothringer, J. D., & Barman, T. 2019, ApJ, 876, 69 [Google Scholar]
- Mollière, P., Wardenier, J. P., van Boekel, R., et al. 2019, A & A, 627, A67 [CrossRef] [EDP Sciences] [Google Scholar]
- Nugroho, S. K., Kawahara, H., Masuda, K., et al. 2017, AJ, 154, 221 [Google Scholar]
- Nugroho, S. K., Gibson, N. P., de Mooij, E. J. W., et al. 2020, ApJ, 898, L31 [Google Scholar]
- Pino, L., Désert, J.-M., Brogi, M., et al. 2020, ApJ, 894, L27 [Google Scholar]
- Prinoth, B., Hoeijmakers, H. J., Kitzmann, D., et al. 2022, Nat. Astron., 6, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Scandariato, G., Borsa, F., Sicilia, D., et al. 2021, A & A, 646, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seidel, J. V., Ehrenreich, D., Allart, R., et al. 2021, A & A, 653, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A & A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [Google Scholar]
- Stangret, M., Casasayas-Barris, N., Pallé, E., et al. 2022, A & A, 662, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Ilyin, I., Järvinen, A., et al. 2015, Astron. Nachr., 336, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Ilyin, I., & Weber, M. 2018, A & A, 612, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabernero, H. M., Zapatero Osorio, M. R., Allart, R., et al. 2021, A & A, 646, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talens, G. J. J., Albrecht, S., Spronck, J. F. P., et al. 2017, A & A, 606, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, F., & Henning, T. 2018, Nat. Astron., 2, 714 [Google Scholar]
- Yan, F., Pallé, E., Reiners, A., et al. 2020, A & A, 640, A5 [Google Scholar]
- Yan, F., Pallé, E., Reiners, A., et al. 2022, A & A, 661, A6 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Example of the telluric correction performed using MOLECFIT, showing the case of the H2O (top panel) and O2 (bottom panel) telluric lines. In each panel, the telluric spectrum has been shifted upward for clarity. |
| In the text | |
 |
Fig. 2 CCFs of the planetary emission spectrum for nights N1 (top panel) and N2 (bottom panel) as a function of the planetary orbital phase. The CCFs shown in these plots were computed using the Fe I spectral template, for which we claim the strongest detection (see Table 4). In each panel, the dashed white line marks where the planetary emission signal is expected according to the system parameters in Table 1. The emission trace is not obvious in this 2D plot and is only detected significantly in the Kp–υsys map, as shown in Fig. 3. |
| In the text | |
 |
Fig. 3 Atmospheric planetary signal obtained with the Fe I, Cr I, and Ti I templates (top, central, and bottom row, respectively). The left column shows the Kp-υsys bi-dimensional map, with the color bar encoding the significance of the detection. The cross in white dashes marks the position where the planetary signal is expected according to Table 1. The central (right) column shows the cut along the vertical (horizontal) direction on the map and corresponding to the peak detection, together with its Gaussian best fit (dashed blue line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.