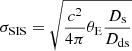EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) A20 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number A20
Number of page(s) 13
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/202245082
Published online 24 March 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The Hubble constant, H0, denotes the current expansion rate of our Universe. The value of H0, though first measured almost a century ago, is still a matter of debate. Utilizing cosmic microwave background (CMB) radiation, which is a relic from the early universe, the Planck collaboration has measured a Hubble parameter at the last scattering surface (z ∼ 1100) and then inferred a H0 value of 67.4 ± 0.5 km s−1 Mpc−1 (Planck Collaboration VI 2020) under the assumption of the standard cosmological model (cold dark matter with a cosmological constant, ΛCDM). However, using data from the local (or late) Universe and a cosmic distance ladder approach, where absolute magnitudes of type Ia supernovae in the Hubble flow have been calibrated by Cepheids and parallax distances, the SH0ES team has measured H0 = 73.04 ± 1.04 km s−1 Mpc−1 (Riess et al. 2022). Several other independent probes also bolster this discrepancy between the model-dependent extrapolation and direct measurement of H0 (e.g., Abbott et al. 2018; Aiola et al. 2020; Freedman et al. 2020; Pesce et al. 2020; Kourkchi et al. 2020; Blakeslee et al. 2021). This unambiguous discrepancy is currently known as the Hubble tension (Verde et al. 2019; Abdalla et al. 2022). If systematic uncertainties in the measurement processes cannot account for this discrepancy, modifying the standard cosmological model or introducing new physics would be necessary. In this picture, more independent probes are crucial to resolving this issue.

One independent way to measure H0 is to use the time-delay strong lensing method (Refsdal 1964). When a time variable source such as a quasar or a supernova is strongly lensed by a foreground galaxy (deflector), multiple images of the background source form and the lensed light from these images arrive at different times. These relative delays depend on the gravitational potential (mass distribution) of the deflector, the large-scale mass distribution along the line of sight, and a combination of angular diameter distances involving the source, deflector, and observer, called the time-delay distance (DΔt). By measuring high-precision time delays from multiple images and redshifts of the deflector and the source from spectroscopy, accurately modeling the mass distribution within the deflector, and estimating the extra-lensing deflection due to the large-scale mass distribution between the source and observer along the line of sight, one can infer DΔtand angular diameter distance to the deflector (Dd), and, hence constrain H0 as it is inversely proportional to the time-delay distance (e.g., Wong et al. 2020; Millon et al. 2020b; Birrer et al. 2020; Rusu et al. 2020; Shajib et al. 2020; Chen et al. 2019). Since the first robust measurement of the time delays in the J0957+561 system, and the associated determination of H0 (Kundić et al. 1997; Oscoz et al. 1997; Oscoz et al. 1996), considerable improvements in the data quality and analysis techniques in all the aspects of the time-delay strong lensing approach over the last two decades have transformed this method into an effective and reliable tool to measure H0. However, the well-known mass-sheet transform (MST; Falco et al. 1985; Schneider & Sluse 2013) can still introduce significant uncertainty in this method (e.g., Birrer et al. 2020). The MST is a mathematical degeneracy which implies that different mass distributions in the deflector can predict the same set of imaging observables (image position, flux ratios, etc.). As these different mass models lead to different time-delay distances, the precision of the measured value of H0 suffers considerably. Assuming a specific mass model such as the power-law mass profile can induce a potential systematic in the H0 because such an assumption artificially breaks the MST (e.g., Xu et al. 2016; Sonnenfeld 2018; Kochanek 2020; Kochanek 2021). However, this mathematical degeneracy is mitigated by introducing an independent tracer of mass, such as the stellar velocity dispersion of the deflector (Treu & Koopmans 2002; Koopmans et al. 2003; Suyu et al. 2014). Therefore, the stellar kinematics of the deflector is one of the crucial ingredients to accurately measure H0 using time-delay cosmography when the maximal degeneracy in H0 due to the MST of the mass model is allowed to be explored (Birrer et al. 2020; Birrer & Treu 2021). One can also impose tighter constraints on other cosmological parameters from joint inference of Dd and DΔt by combining the time-delay measurements and lens models with the stellar velocity dispersions of the deflectors (e.g., Jee et al. 2015, 2016; Birrer et al. 2016, 2019; Shajib et al. 2018).

Besides improving the robustness of the analysis methods, and checking for unknown systematics (Millon et al. 2020b; Gilman et al. 2020; Chen et al. 2021; Van de Vyvere et al. 2022; Shajib et al. 2022; Gomer et al. 2022), another ongoing effort of the Time-Delay COSMOgraphy (TDCOSMO) collaboration is to increase the sample size of lensed quasar systems with measured DΔt. By mitigating the uncertainties at the population level, this large sample of quasar-galaxy lens systems with their associated data, especially stellar velocity dispersion of the deflectors, can help to achieve a sub-percent measurement of H0 (Birrer & Treu 2021). This coordinated effort covers observations and analyses of important properties. For example, measuring time delays requires monitoring of the source images’ light curves with adequate sampling (e.g., Courbin et al. 2018; Millon et al. 2020a). High-resolution imaging from the Hubble Space Telescope (HST) or ground-based adaptive optics (AO) instruments is crucial for lens modeling (e.g., Wong et al. 2017; Shajib et al. 2019; Chen et al. 2019). High S/N spectroscopic observations provide redshifts of the source and the deflector along with stellar kinematics of the deflector (e.g., Suyu et al. 2017). Environmental studies of the lens systems to quantify the extra-lensing distortion also depend on photometric and spectroscopic observations (e.g., Rusu et al. 2017; Sluse et al. 2019). As a part of this effort, in this paper, we report newly measured redshifts and single aperture velocity dispersions of the deflectors from eight quasar-galaxy lens systems – J0147+4630, B0445+123, B0631+519, J0659+1629, J0818−2613, J0924+0219, J1433+6007, and J1817+2729.

Due to limitations associated with the ground-based observations, the 2D spectra of the quasar-galaxy lens systems are typically spatially blended, and it is a challenging task to extract clean and high S/N 1D spectra of the deflectors. To overcome this issue, we have implemented a forward modeling method to extract 1D spectra of the deflectors and, provided the S/N of the extracted spectra are sufficiently high, we have measured single aperture velocity dispersions and the redshifts. This paper is structured in the following way. In Sect. 2, a brief description of the target lens systems and related information is provided. Next, the observational setup, data reduction pipeline, and how the 1D spectra have been extracted using the forward modeling method are described in Sect. 3. In Sect. 4, the measurement process of the redshifts and the single aperture velocity dispersions of the deflectors are presented along with the results. Finally, Sects. 5 and 6 discuss the reported results and conclusions respectively. A flat ΛCDM cosmology with H0 = 70.0 km s−1 Mpc−1 and Ωm = 0.3 is adopted when necessary.

2. Targets

This section provides a brief description of the eight quasar-galaxy lens systems for which the deflector redshifts and velocity dispersions are measured. The images of these lens systems along with the slit positions are presented in Fig. 1.

2.1. J0147+4630

This quadruple lensed quasar system was coincidentally discovered (Berghea et al. 2017) in the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS1; Chambers et al. 2016) survey data. The spectroscopic redshift of the quasar is 2.341 ± 0.001 (Lee 2017). The redshift of the deflector is also measured, zd = 0.678 ± 0.001, along with the velocity dispersion, 313 ± 14 km s−1, by Goicoechea & Shalyapin (2019). In this paper, we provide an independent measurement of the velocity dispersion of the deflector using a larger wavelength range than the one used in the previous measurement. Lens modeling has been carried out by Shajib et al. (2019) using HST imaging of the system.

2.2. B0445+123

This radio-loud double-imaged AGN was discovered by Argo et al. (2003) in the Cosmic Lens All-Sky Survey (CLASS; Myers et al. 2003; Browne et al. 2003). Radio observations have measured the separation between the lensed images to be 1.32″. Although the AGN redshift is yet to be measured, spectroscopic observations have found that the deflector redshift is zd = 0.5583 ± 0.0003 (McKean et al. 2004).

2.3. B0631+519

This is another radio-loud double-imaged lens system discovered by CLASS (York et al. 2005). Observations at different radio wavelengths have revealed two compact lensed images separated by around 1.16″. HST imaging of the system has shown that there are two galaxies along the line of sight of the quasar. The main lensing galaxy is at redshift, zd = 0.6196 ± 0.0004 and the other one is at redshift 0.0896 ± 0.0001 (McKean et al. 2004). However, the quasar redshift is yet unknown.

2.4. J0659+1629

This quadruply-lensed quasar was first identified as a lens candidate by Delchambre et al. (2019) using Gaia data release 2 (Gaia Collaboration 2018). This detection was confirmed by Stern et al. (2021) with measured source redshift, zs = 3.083 and deflector redshift, zd = 0.766. The system was also independently discovered by Lemon et al. (2023). Lens modeling of the system is conducted by Schmidt et al.(2023) using HST imaging.

2.5. J0818−2613

Stern et al. (2021) first discovered this quadruply imaged quasar system using Gaia data release 2 and measured the quasar redshift, zs = 2.164, using Keck-LRIS spectroscopy. This lens system was also independently reported by Lemon et al. (2023) with a measured quasar redshift, zs = 2.155. Schmidt et al.(2023) performed lens modeling using HST images of the system. In this paper, we report the redshift and velocity dispersion of the deflector.

2.6. J0924+0219

This quadruply lensed quasar was discovered using Sloan Digital Sky Survey (SDSS; York et al. 2000) data. Inada et al. (2003) first reported this quad along with the measured source redshift zs = 1.524, while Ofek et al. (2006) and Eigenbrod et al. (2006) measured the lens redshift, zd = 0.393. Time-delay data between the two brightest images is available (Millon et al. 2020a). Lens modeling is presented by Eigenbrod et al. (2006) using HST imaging and recently by Chen et al. (2022) using AO-based imaging.

2.7. J1433+6007

This quad was detected in the SDSS data release 12 photometric catalog (Alam et al. 2015). The source and deflector redshift, and deflector velocity dispersion were first measured byAgnello et al. (2018). The reported redshifts of the source and the deflector are, zs = 2.737 ± 0.003 and zd = 0.407 ± 0.002, respectively. The measured velocity dispersion is 216 ± 55 km s−1using a 1″ aperture (Agnello et al. 2018). However, this measurement only used the Ca K line and the spectrum was significantly contaminated by quasar light. In this paper, we present a new velocity dispersion measurement on a larger wavelength range and higher S/N deflector spectrum.Shajib et al. (2019)and Schmidt et al.(2023) both performed lens modeling using HST imaging.

2.8. J1817+2729

This quad was first identified as a lens candidate by Delchambre et al. (2019) using Gaia data release 2 and then independently confirmed with measured source redshift, zs = 3.07, by Lemon et al. (2019), Stern et al. (2021). Detailed mass modeling has been conducted by Rusu & Lemon (2018) using SUBARU/FOCAS imaging and by Schmidt et al.(2023) using HST imaging. In this paper, we present the deflector’s redshift and velocity dispersion.

3. Observations and data reduction

In this section, we first describe the observations for our sample of eight lens systems, which include two different spectrographs and three different setups. Next, the data reduction pipelines are described. Finally, we present the forward modeling method and how the 1D spectra were extracted from the respective 2D spectra.

3.1. Observations

The spectroscopic observations for the target lens systems were carried out using the Low Resolution Imaging Spectrometer (LRIS; Oke et al. 1995) and the Echellette Spectrograph, and Imager (ESI; Sheinis et al. 2002) mounted on the 10m Keck telescopes. The observing nights were spread over three years, from 2018 to 2020, with typical seeing conditions (FWHM) ranging ∼0.7 ″–1.33 ″. The ESI spectra were taken in Echellette mode using the 1.0″ wide slit which provides a spectral resolution R ≈ 4000. This setup covers a wavelength range from 3900 Å to 10 900 Å with a constant dispersion in logarithmic space corresponding to 11.5 km s−1 in velocity, while the pixel scale in the spatial direction varies from 0.120″ in the bluest order to 0.168″ in the reddest order. The LRIS spectra were collected in the long-slit mode using both blue and red arms simultaneously. A dichroic was used to split the light beam at 5696 Å. The blue side was configured with a 600/4000 grism that provides a 0.63 Å/pixel dispersion and covers a wavelength range of 3040–5630 Å with a spectral resolution of R ≈ 1100 at central wavelength λ ≈ 4340 Å. On the red side, two different configurations were used. To observe the lens systems B0445+123 and B0631+519, a 600/7500 grating was used, which produces a dispersion of 0.8 Å/pixel while covering a wavelength range of 5600–9000 Å. For the lens system J0659+1629, the 1200/7500 grating was used, which covers a wavelength range of 5600–7250 Å with a dispersion of 0.4 Å/pixel. Both setups on the red side provide a spectral resolution of R ≈ 1400. The plate scales on the blue and the red side are 0.123″/pixel and 0.135″/pixel, respectively. The position angle (PA) of a slit was generally chosen in such a way that the brightest quasar image of the corresponding lens system fell within the slit along with the deflector and at least another quasar image. The total integration time for each system was divided typically into n × 2400 s or n × 1800 s or n × 1200 s exposures. A summary of the main observing information is provided in Table 1.

Table 1.

Summary of spectroscopic observation of the lens systems for which redshifts and stellar velocity dispersions of the deflectors have been reported in this paper.

3.2. Data reduction

The LRIS data for the lens system B0445+123 and B0631+519 were reduced using the PYPEIT (Prochaska et al. 2020) pipeline and for J0659+1629 using the LPIPE (Perley 2019) pipeline. These packages performed overscan subtraction, bias and dark current correction, and flat-fielding. Finally, the packages produced sky-subtracted 2D science spectra and the corresponding variance and wavelength data. PYPEIT provides 2D wavelength images while LPIPE generates 1D wavelength solutions. The pixels contaminated with cosmic rays were marked by comparing each frame to the respective median frame. A median frame for each system was created by combing all the 2D image frames from that system. After that, a rectification was applied to all reduced 2D data to account for any possible tilts present in the spectra, using a spline interpolation method. These rectified science, variance, and wavelength data were used to extract the 1D spectra, as described in the next section.

The ESI data were processed via a custom python-based data reduction package. The code automatically locates the ten individual spectral orders, performs a bias subtraction and flat field correction on the data, rectifies the orders, subtracts the sky emission, and performs a wavelength calibration. The cosmic-ray rejection for the ESI data was performed by running edge-detection algorithms that our tests have shown to be effective for this process. The output of the code includes the calibrated and background-subtracted data for each exposure and the corresponding variance spectra.

For B0445+123 and B0631+519, the 1D deflector spectra were extracted from each 2D science frame and then coadded using an inverse-variance weighting process to get the final 1D spectra. As the 2D wavelength solutions for these two systems varied from frame to frame, it was easier to handle the issue when the 1D spectra were extracted from each frame. For the remainder of the lens systems, first, the individual 2D spectra were coadded with a inverse variance weighting, and then the 1D deflector spectra were extracted from the coadded 2D spectra.

3.3. Forward modeling and 1D extraction

The angular separations between the quasar images and the deflector in a lens system are typically on the order of 1″. Hence, in seeing limited ground-based observations, the 2D spectra of the lens systems become spatially blended. This situation gets more complicated as the deflectors are generally orders of magnitude fainter than the bright quasar images. For example, in Fig. 1 the 2D spectra of J0147+4630, J0924+0219, and J1817+2729 do not show any distinct trace from the deflector. In this situation, it is challenging to extract uncontaminated and high S/N 1D spectra of the deflectors. Traditional optimal extraction codes based on the algorithm of Horne (1986) are not up to the task as they do not account for the blending or cross-contamination. To overcome this challenge, we have implemented a forward modeling method (e.g., Sluse et al. 2007; Shalyapin & Goicoechea 2017; Goicoechea & Shalyapin 2019). First, a global model is created that emulates the data in a 1D spatial profile of the 2D science spectrum. The 1D spatial profile is constructed by collapsing part of the 2D spectrum, typically containing a spectral width of 300–400 pixels, along the spectral axis. The model consists of several Moffat (Moffat 1969) profiles along with an additive polynomial function. Each component profile in the model represents either a quasar image or the deflector that is wholly or partially captured by the slit and therefore has a significant contribution to the total light distribution across the slit, while the polynomial models the background. The model is further refined by constraining the parameters of the profiles in the following way. The projected center to center distances of the objects along the slit are fixed based on the corresponding measured distances between the objects using archival HST images or AO-based images of the systems. We assume that the same point spread function (PSF) is applicable for all objects in the slit, and therefore they require that the profiles have the same shape parameters. This is a reasonable assumption for the galaxies given their point-like sizes in the images of the lens systems, especially when considering the effects of seeing. Figure 2 shows a refined global model for each lens system along with individual profile components. This figure also shows the residuals normalized to the uncertainties in the data of the corresponding 1D spatial profiles. Once the initial global description of the spatial profile has been determined, we take a multi-step approach to determine the component fluxes at each wavelength. The spatial profile in a single column of the detector, that is, at a specific wavelength, is typically too noisy to do a full model fit to that single profile. Therefore, we take the following steps to use binned data to determine the model parameter values in each individual column. (1) We divide the 2D spectrum into spectral bins of equal widths, typically around 20–25 spectral pixels, and construct a series of 1D spatial profiles by summing the 2D data within these spectral-bins. Then we fit the global model to these spatial profiles. From the fitted models, we get a set of values for each centroid and shape parameter in the global model. (2) We fit a low-order polynomial as a function of wavelength to each set of fitted centroid and shape parameters values to describe their wavelength-dependence. (3) We create an individual model similar to the global model for each wavelength using the above-mentioned fitted polynomials, where all the parameters except the amplitudes are kept fixed, and then we fit the amplitudes. (4) We obtain the total flux for each object (quasar or galaxy) at each wavelength by integrating the corresponding fitted Moffat profile along the spatial direction. We also calculate the associated variance on flux using the covariance matrix generated in the fitting process.

thumbnail Fig. 1.

Images of the lens systems, part of the collected 2D spectra, and the corresponding 1D spatial profiles. The 1D spatial profiles have been generated by collapsing the data in the 2D spectra along the spectral axis. The slit position (green) for each lens system is also shown. For the lens system, J0147+4630, J0659+1629, J0818−2613, J1433+6007, and J1817+2729, we have used archival HST images (PI: T. Treu) and for B04453+123, B0631+519 and J0924+0219, we have used ground based AO images (PI: C. D. Fassnacht).

thumbnail Fig. 2.

Illustration of model fitting to 1D spatial profiles. Left column: each row shows the 1D spatial profile (blue) with individual model components for a single lens system. The model components are Moffat profiles, which represent the deflector and lensed quasars, with an additive polynomial function representing the background. The profile component representing the deflector is marked black and other profile components generally representing the lensed quasar images are marked with yellow. Right column: the top panel in each row shows the 1D spatial profile (blue) with 1σ uncertainty (orange) and the corresponding model (green) that fits the data in that profile. The bottom panel shows the residual (red) between the data and the model normalised to the uncertainties in data. The uncertainties on the spatial profiles of B0445+123 and B0631+519 are higher compared to others because these 1D profiles were generated from single frames, while for other lens systems, the corresponding profiles were generated from coadded frames.

All the extracted 1D spectra have been response-corrected using a spectrophotometric standard stellar spectrum collected by the same spectrograph on the corresponding observing night and extracted following the procedure described above. In Figs. 3–5, the extracted and smoothed deflector spectra are presented with the absorption and telluric lines marked. The smoothing has been done using a boxcar filter of size around 2.5 Å.

thumbnail Fig. 3.

1D spectra and velocity dispersion fits for the deflectors from the lens system J0147+4630 and B0445+123. The plot for each system consists of three panels. Top panel: the extracted and smoothed 1D spectrum of the deflector is plotted over the observed wavelength where the smoothing has been done using a boxcar filter of size around 2.5 Å. Prominent stellar and telluric absorption lines are marked if present. And the measured redshift of the deflector is mentioned in the lower right corner of the plot. Middle panel: the pPXF generated model fit (red) to measure the velocity dispersion is plotted on top of the original unsmoothed spectrum (black). A smoothed version (yellow) of the original spectrum is also presented to show the goodness of the fit. The grey parts are the masked or excluded regions from the fit. Bottom panel: the green dots show the residuals between the unsmoothed flux and the model fit for each wavelength normalized to the respective model fits.

thumbnail Fig. 4.

1D spectra and velocity dispersion fits for the deflectors from the lens system B0631+519, J0659+1629 and J0818−2613. The description of the figure is same as Fig. 3.

thumbnail Fig. 5.

1D spectra and velocity dispersion fits for the deflectors from the lens system J0924+0219, J1433+6007 and J1817+2729. The description of the figure is same as Fig. 3.

4. Data analysis

In this section, we discuss the redshift and velocity dispersion measurements of the deflectors and their associated uncertainties. We also discuss how the S/N of the spectra were measured and describe a test to check the covariance of the velocity dispersion measurements.

4.1. Redshift measurement

Among the eight lensing galaxies presented in this paper, only the redshifts of the deflectors in J0818−2613 and J1817+2729 were not previously measured. The aforementioned forward modeling method enabled us to extract the deflector spectra for both of these systems with sufficient S/N where several absorption lines such as Ca II K and H and the G-band are clearly visible after smoothing (Figs. 4 and 5). The redshifts are presented in Table 2. The reported uncertainties are the standard deviations of the redshifts measured using several absorption lines such as CN, Ca II K and H, G band, Hβ, Hδ, and Mg b. Our measured redshifts for the remainder of the six deflectors are consistent with the previously known values.

Table 2.

Measured redshifts of the deflectors with associated uncertainties using the extracted 1D spectra.

4.2. Velocity dispersion measurement

To achieve reliable velocity dispersion measurements, high S/N spectra are necessary. The mean S/N per angstrom for all the extracted deflector spectra except J0659+1629 were calculated using rest-frame wavelength ranges 4150–4250 Å and 4630–4760 Å. These two wavelength ranges were chosen based on the lack of any prominent absorption or telluric lines and also because none of the spectra have any emission lines or other contamination present within these ranges. However, as these rest-frame wavelength ranges were not available for the extracted deflector spectrum of J0659+1629 system, a separate rest-frame wavelength range from 3990 Å to 4090 Å was used to calculate the S/N per angstrom. The estimated S/N of the deflector spectra are reported in Table 3.

Table 3.

Measured S/N per angstrom of the extracted deflector spectra and single aperture velocity dispersion with associated statistical and systematic uncertainties.

To measure the line-of-sight (LOS) stellar velocity dispersions of the lensing galaxies, we have used a penalized pixel fitting method implemented through an in-house analysis pipeline VELDIS1 which is a wrapper around the pPXF package (Cappellari & Emsellem 2004; Cappellari 2017). This method measures the velocity dispersion by fitting a model to the observed galaxy spectrum in pixel space. The models are created using a weighted linear combination of the broadened stellar templates to which a sum of orthogonal polynomials is added. The additive polynomials are used to adjust the continuum shape of the templates during the fit. As templates we have used the Indo-US stellar library (Valdes et al. 2004), which consists of 1273 stellar spectra covering a wavelength range of 3460–9464 Å with constant dispersion of 0.4 Å and FWHM resolution ∼1.35 Å (Beifiori et al. 2011). The FWHM resolutions of the instruments used to collect our spectra have been measured by fitting Gaussian profiles to several emission lines at varying wavelengths from the corresponding sky spectra. Though the measured FWHM resolutions depend on wavelength, the range of resolutions is not significant enough to affect the velocity dispersion measurement. Thus we have adopted a constant FWHM resolution and ignored its wavelength dependence. As prescribed in Cappellari (2017), we have shifted the galaxy wavelengths and FWHM resolutions of the galaxy spectrographs to the rest frame, as the redshifts of the observed deflectors are relatively high. In the observed frame, the FWHM of all our observations was higher than that of the templates. However, Gaussian smoothing was carried out on the template spectra only if the observed FWHM was higher than the templates’ after shifting to the rest frame. For all the galaxy spectra, we have masked the atmospheric A-band and B-band absorption lines, if present. Emission lines from the foreground galaxies and contaminated regions due to quasar light, if any, have also been excluded from the fit. Figures 3–5 show all the fits generated by pPXF. In these plots, the gray-colored spectra are the unsmoothed, logarithmically rebinned deflector spectra, the red-colored spectra are the best fit models, and the yellow-colored spectra are the smoothed versions of the original spectra. The vertical shaded regions mark the excluded part of the deflector spectra from the fitting. The green dots show the residuals between the unsmoothed flux and the model fit for each wavelength normalized to the respective model fits. Unlike the optimal extraction-based methods, the extraction technique presented in this paper and others (e.g., Goicoechea & Shalyapin 2019; Melo et al. 2021) doesn’t require defining an aperture along the spatial direction. Thus, the measured velocity dispersions correspond to the integrated velocity dispersions within a rectangular spectroscopic aperture of the respective slit-widths and slit-lengths centered on the deflectors (see Table 1). After obtaining the velocity dispersion measurements from the fits, we have estimated the statistical and systematic uncertainties associated with the corresponding measurements. To determine the statistical uncertainty, we have performed three hundred Monte-Carlo simulations by adding Gaussian noise to the smoothed deflector spectra. The noise at each wavelength has been generated using normal distributions with variances equal to the variances of the corresponding galaxy spectra while ignoring the pixel-to-pixel covariances, as they are negligible compared to the respective variances. The fits are carried out with the same setup used to measure the respective velocity dispersion reported here. We measured the systematic uncertainties by conducting roughly three hundred fits while varying the wavelength range of the observed galaxy spectrum that was used for the measurement, the subset of templates, and the degree of the additive polynomials. The measured velocity dispersions of the deflectors along with the associated statistical and systematic uncertainties are reported in Table 3.

While fitting for the velocity dispersion, we have attempted to include as many absorption lines as possible without compromising the respective S/N of the deflector spectra. However, the S/N levels of the extracted spectra affect the measured velocity dispersions significantly. From the reported uncertainties in Table 3, it is clear that both the statistical and systematic uncertainty increase noticeably as the S/N levels decrease. On the contrary, both of these uncertainties improve when the S/N levels of the extracted spectra are around 20 or above, as is the case for the deflectors in the B0631+519, J0924+0219, and J1433+6007 lens system. In any case, all the extracted spectra are mostly uncontaminated by the quasar light, and the absorption features are sufficiently strong enough to conduct a velocity dispersion measurement.

We have also checked whether the velocity dispersion measurements of the deflectors vary preferentially in the same direction given the same set-up, for example, the same rest-frame wavelength range and the same set of templates. The lens system J0659+1629 has been excluded from this analysis as the extracted deflector spectrum for this system only covers a small wavelength range and thus provides almost no scope to vary the wavelength. With the rest of the deflectors, we have performed around three hundred sets of fits under different set-ups while using the same set-up for each group of seven fits corresponding to seven deflectors. The set-ups were varied by changing the wavelength ranges, the templates used, and the degree of the additive polynomial. These measurements and how they co-vary for each pair of deflectors are shown as a corner plot in Fig. 6. The figure also presents the heat-map of the covariance matrix calculated from these velocity dispersion measurements, where the measurements were normalized to their respective mean. From this figure, one can see that except in a few cases, there is almost no correlation among the velocity dispersion measurements of the seven deflectors. However, in those cases the off-diagonal terms in the covariance matrix are essential and can not be ignored.

thumbnail Fig. 6.

Illustration showing relations among the velocity dispersion measurements of the deflectors. The scatter plots between each pair of deflectors show corresponding velocity dispersion measurements for three hundred setups where each marker shows the measurements from the same setup. The blue-shaded curves are the individual velocity dispersion distributions of the deflectors. The set-ups were varied by changing the wavelength ranges, set of the spectra of the templates, and degree of the additive polynomial. In general, the covariance terms are negligible except in a few cases, for which they should be taken into account. The lens system J0659+1629 has been excluded from this analysis as the extracted deflector spectrum for this system only covers a small wavelength range. The plot in the upper-right shows a heat-map of the covariance matrix calculated from these velocity dispersion measurements, where the measurements were normalized to their respective mean.

5. Discussion

5.1. Comparison to previous redshift and velocity dispersion measurements

The redshifts of the six deflectors, which were previously known, match our measurements to within 1σ. Among the eight lens systems, the deflector velocity dispersions of the J0147+4630, and J1433+6007 lens systems were previously measured. For the deflector in J0147+4630, the previous measurement is 313 ± 14 km s−1 using a 0.5″-width slit under subarcsecond seeing conditions (Goicoechea & Shalyapin 2019). This result is within the uncertainty of our measurement of 283 ± 30 ± 12 km s−1(see Table 3). However, using the same wavelength range (6000–7500 Å) as in the previous measurement, but with the setting used in this paper, we obtained a velocity dispersion value of 311 km s−1. Hence, the difference between the measurements in their means may arise from the difference in the used wavelength ranges, aperture sizes and seeing conditions, etc. For the deflector in J1433+6007, the previous measurement is 216 ± 55 km s−1 by fitting only to Ca K line (Agnello et al. 2018). The data for this measurement was collected using a 1″ wide spectroscopic aperture under ∼1″ seeing. Our measured velocity dispersion for this deflector is 261 ± 6 ± 7 km s−1(see Table 3), which is higher but still within the uncertainty of the previous measurement.

5.2. Comparison to predictions from SIS lens models

The strength of the absorption lines, especially Ca II K and H, presence of 4000 Å break and the lack of emission lines in the extracted spectra confirm that the deflectors of the lens systems reported in this paper are early-type galaxies. Thus as a sanity check, we have compared measured velocity dispersion values with theoretically derived ones by assuming a singular isothermal sphere (SIS) profile for the galaxies. This mass profile is the simplest choice to predict the velocity dispersion using only a single lens model parameter, that is the Einstein radius. Under this assumption, the single-aperture velocity dispersion of the system σSIScan be calculated as -

σ SIS = c 2 4 π θ E D s D ds $$ \begin{aligned} \sigma _{\rm SIS} = \sqrt{\frac{c^2}{4\pi }\theta _{\rm E} \frac{D_{\rm s}}{D_{\rm ds}}} \end{aligned} $$

where θE is the Einstein radius in arcseconds, Ds and Dds are the angular diameter distances between the observer and the source, and the deflector and the source, respectively, and c is the speed of light. For lens systems J0147+4630, J0659+1629, J0818−2613, J1433+6007, and J1817+2729, the mean value of Einstein radius obtained by lens modeling in Schmidt et al. (2023) was used, and for the system J0924+0219, the mean value of Einstein radius obtained by lens modeling in Chen et al.(2022) was used. However, as detailed lens modeling for B0445+123 and B0631+519 is not available, the Einstein radius was set to half of the quasar image separation measured from AO-based images. Also, the source and deflector redshifts of these lens systems are known, except for B0445+123 and B0631+519, for which the source redshifts are still not measured. Thus, we have assumed a possible range of source redshift for these two lens systems. Using a flat ΛCDM cosmology with H0 = 70.0 km s−1 Mpc−1, Ωm = 0.3, we have calculated the angular diameter distances and the corresponding SIS velocity dispersions of the deflectors. In our sample, all the measured velocity dispersions in their mean are lower than the corresponding SIS velocity dispersions. These offsets are due to the vast simplification of the mass distribution assumption and chosen arbitrary cosmology. The deviation of the measurements from the respective SIS predictions is within 3%–20%, except for B0445+123. The mean and scatter of the measured to SIS velocity dispersion ratios (σmeasured/σSIS) are 0.87 and 0.08. This systematic overestimation of the SIS predictions may not persist for a bigger sample size. We will explore this hypothesis in the future when such a sample is available. If this trend continues, it would be possible to estimate what modifications to the assumed galaxy mass model would minimize this trend. The Einstein radii, source and deflector redshifts, and SIS velocity dispersion values are noted in Table 3.

6. Conclusion

The redshifts and velocity dispersions of the lensing galaxies are crucial data for measuring the Hubble constant using the time-delay strong lensing method. However, collecting stellar kinematics data with a high S/N is challenging from seeing limited gound-based setups as the spectra of the lensing galaxies become spatially blended with those of the often much brighter lensed quasar images. In this paper we have :

  • Developed a forward modeling technique and used it to extract 1D spectra of eight lensing galaxies, even in the presence of much brighter lensed quasar images.

  • Used the extracted spectra to measure the deflector redshifts in all of our targets, including two that have never been measured before, in the J0818−2613 and J1817+2729 systems. For the remainder of the targets, our measured redshifts agree with those in the literature to within 1σ.

  • Made the first measurements of the stellar velocity dispersions for six of the eight lensing galaxies in our sample. The new velocity dispersion measurements were made for the deflectors in B0445+123, B0631+519, J0659+1629, J0818−2613, J0924+0219 and J1817+2729 systems.

  • Checked whether there exists significant covariance among the velocity dispersion measurements of the seven deflectors. In general, we found that covariances are negliglible except in a few cases, for which they should be taken into account.

  • Compared the measured velocity dispersions to those predicted by a SIS mass model as a sanity check. In our sample, all the measured velocity dispersions in their mean are lower than the corresponding SIS predictions, and the deviations of the measurements are within 3%–20% of the respective SIS velocity dispersions except B0445+123.

The Hubble tension is one of the major unanswered questions in current physics with immense consequences, and time-delay cosmography has proved its potential in resolving this issue. Though the mass-sheet transform (MST) poses significant uncertainty in the inferred H0 using this method, stellar kinematics such as single aperture velocity dispersion can help break this degeneracy (Birrer et al. 2020). However, to achieve percent-level precision, a sample of 40 or more time-delay lenses is required, for which we have measured integrated velocity dispersions of the deflectors to 5% or better. Even in this scenario, kinematic measurements from a sample of ∼200 nontime-delay lens systems are still necessary (Birrer & Treu 2021). The results in this paper will help to reach this percent-level precision by adding to the current sample.

Acknowledgments

We thank Simon Birrer and Dominique Sluse for useful discussions and comments that improved this manuscript. PM and CDF acknowledge support for this work from the National Science Foundation under Grant No. AST-1907396. TT acknowledges support by the National Science Foundation through grants 1906976 and 1836016, by the National Aeronautics and Space Administration through grants HST-GO-15652 and JWST-GO-1794, and by the Gordon and Betty Moore Foundation through grant 8548. CS is supported by an ‘Hintze Fellow’ at the Oxford Centre for Astrophysical Surveys, which is funded through generous support from the Hintze Family Charitable Foundation. For the spectral resampling SPECTRES (Carnall 2017) code was used. This research also made use of NUMPY (Oliphant 2015), SCIPY (Jones et al. 2001), ASTROPY (Astropy Collaboration 2013 2018), JUPYTER (Kluyver et al. 2016), MATPLOTLIB (Hunter 2007) and SEABORN (Waskom et al. 2014). The data presented herein were obtained at the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Maunakea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain.

References

  1. Abbott, T. M. C., Abdalla, F. B., Annis, J., et al. 2018, MNRAS, 480, 3879 [Google Scholar]
  2. Abdalla, E., Abellán, G. F., Aboubrahim, A., et al. 2022, J. High Energy Astrophys., 34, 49 [NASA ADS] [CrossRef] [Google Scholar]
  3. Agnello, A., Grillo, C., Jones, T., et al. 2018, MNRAS, 474, 3391 [CrossRef] [Google Scholar]
  4. Aiola, S., Calabrese, E., Maurin, L., et al. 2020, JCAP, 2020, 047 [Google Scholar]
  5. Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [Google Scholar]
  6. Argo, M. K., Jackson, N. J., Browne, I. W. A., et al. 2003, MNRAS, 338, 957 [NASA ADS] [CrossRef] [Google Scholar]
  7. Astropy Collaboration 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Astropy Collaboration 2018, AJ, 156, 123 [Google Scholar]
  9. Beifiori, A., Maraston, C., Thomas, D., & Johansson, J. 2011, A&A, 531, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Berghea, C. T., Nelson, G. J., Rusu, C. E., Keeton, C. R., & Dudik, R. P. 2017, ApJ, 844, 90 [NASA ADS] [CrossRef] [Google Scholar]
  11. Birrer, S., & Treu, T. 2021, A&A, 649, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Birrer, S., Amara, A., & Refregier, A. 2016, JCAP, 2016, 020 [CrossRef] [Google Scholar]
  13. Birrer, S., Treu, T., Rusu, C. E., et al. 2019, MNRAS, 484, 4726 [Google Scholar]
  14. Birrer, S., Shajib, A. J., Galan, A., et al. 2020, A&A, 643, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Blakeslee, J. P., Jensen, J. B., Ma, C.-P., Milne, P. A., & Greene, J. E. 2021, ApJ, 911, 65 [NASA ADS] [CrossRef] [Google Scholar]
  16. Browne, I. W. A., Wilkinson, P. N., Jackson, N. J. F., et al. 2003, MNRAS, 341, 13 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cappellari, M. 2017, MNRAS, 466, 798 [Google Scholar]
  18. Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [Google Scholar]
  19. Carnall, A. C. 2017, ArXiv e-prints [arXiv:1705.05165] [Google Scholar]
  20. Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
  21. Chen, G. C. F., Fassnacht, C. D., Suyu, S. H., et al. 2019, MNRAS, 490, 1743 [NASA ADS] [CrossRef] [Google Scholar]
  22. Chen, G. C. F., Fassnacht, C. D., Suyu, S. H., et al. 2021, A&A, 652, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Chen, G. C. F., Fassnacht, C. D., Suyu, S. H., et al. 2022, MNRAS, 513, 2349 [NASA ADS] [CrossRef] [Google Scholar]
  24. Courbin, F., Bonvin, V., Buckley-Geer, E., et al. 2018, A&A, 609, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Delchambre, L., Krone-Martins, A., Wertz, O., et al. 2019, A&A, 622, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Eigenbrod, A., Courbin, F., Dye, S., et al. 2006, A&A, 451, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Falco, E. E., Gorenstein, M. V., & Shapiro, I. I. 1985, ApJ, 289, L1 [Google Scholar]
  28. Freedman, W. L., Madore, B. F., Hoyt, T., et al. 2020, ApJ, 891, 57 [Google Scholar]
  29. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Gilman, D., Birrer, S., & Treu, T. 2020, A&A, 642, A194 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Goicoechea, L. J., & Shalyapin, V. N. 2019, ApJ, 887, 126 [NASA ADS] [CrossRef] [Google Scholar]
  32. Gomer, M. R., Sluse, D., van de Vyvere, L., Birrer, S., & Courbin, F. 2022, A&A, 667, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Horne, K. 1986, PASP, 98, 609 [Google Scholar]
  34. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  35. Inada, N., Becker, R. H., Burles, S., et al. 2003, AJ, 126, 666 [NASA ADS] [CrossRef] [Google Scholar]
  36. Jee, I., Komatsu, E., & Suyu, S. H. 2015, JCAP, 2015, 033 [Google Scholar]
  37. Jee, I., Komatsu, E., Suyu, S. H., & Huterer, D. 2016, JCAP, 2016, 031 [Google Scholar]
  38. Jones, E., Oliphant, T., & Peterson, P. 2001, SciPy:Open source scientific tools for Python [Google Scholar]
  39. Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, in Positioning and Power in Academic Publishing: Players, Agents and Agendas, eds. F. Loizides, & B. Schmidt, (Amsterdam, Netherlands: IOS Press BV), 87 [Google Scholar]
  40. Kochanek, C. S. 2020, MNRAS, 493, 1725 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kochanek, C. S. 2021, MNRAS, 501, 5021 [Google Scholar]
  42. Koopmans, L. V. E., Treu, T., Fassnacht, C. D., Blandford, R. D., & Surpi, G. 2003, ApJ, 599, 70 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kourkchi, E., Tully, R. B., Eftekharzadeh, S., et al. 2020, ApJ, 902, 145 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kundić, T., Turner, E. L., Colley, W. N., et al. 1997, ApJ, 482, 75 [Google Scholar]
  45. Lee, C. H. 2017, A&A, 605, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Lemon, C. A., Auger, M. W., & McMahon, R. G. 2019, MNRAS, 483, 4242 [NASA ADS] [CrossRef] [Google Scholar]
  47. Lemon, C., Anguita, T., Auger-Williams, M. W., et al. 2023, MNRAS, 520, 3305 [NASA ADS] [CrossRef] [Google Scholar]
  48. McKean, J. P., Koopmans, L. V. E., Browne, I. W. A., et al. 2004, MNRAS, 350, 167 [NASA ADS] [CrossRef] [Google Scholar]
  49. Melo, A., Motta, V., Godoy, N., et al. 2021, A&A, 656, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Millon, M., Galan, A., Courbin, F., et al. 2020a, A&A, 639, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Millon, M., Courbin, F., Bonvin, V., et al. 2020b, A&A, 640, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
  53. Myers, S. T., Jackson, N. J., Browne, I. W. A., et al. 2003, MNRAS, 341, 1 [Google Scholar]
  54. Ofek, E. O., Maoz, D., Rix, H.-W., Kochanek, C. S., & Falco, E. E. 2006, ApJ, 641, 70 [NASA ADS] [CrossRef] [Google Scholar]
  55. Oke, J. B., Cohen, J. G., Carr, M., et al. 1995, PASP, 107, 375 [Google Scholar]
  56. Oliphant, T. E. 2015, Guide to NumPy, 2nd edn. (USA: CreateSpace Independent Publishing Platform) [Google Scholar]
  57. Oscoz, A., Serra-Ricart, M., Goicoechea, L. J., Buitrago, J., & Mediavilla, E. 1996, ApJ, 470, L19 [NASA ADS] [CrossRef] [Google Scholar]
  58. Oscoz, A., Mediavilla, E., Goicoechea, L. J., Serra-Ricart, M., & Buitrago, J. 1997, ApJ, 479, L89 [NASA ADS] [CrossRef] [Google Scholar]
  59. Perley, D. A. 2019, PASP, 131, 084503 [Google Scholar]
  60. Pesce, D. W., Braatz, J. A., Reid, M. J., et al. 2020, ApJ, 891, L1 [Google Scholar]
  61. Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Prochaska, J., Hennawi, J., Westfall, K., et al. 2020, J. Open Sour. Software, 5, 2308 [NASA ADS] [CrossRef] [Google Scholar]
  63. Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS] [CrossRef] [Google Scholar]
  64. Riess, A. G., Yuan, W., Macri, L. M., et al. 2022, ApJ, 934, L7 [NASA ADS] [CrossRef] [Google Scholar]
  65. Rusu, C. E., & Lemon, C. A. 2018, Res. Notes Am. Astron. Soc., 2, 187 [NASA ADS] [Google Scholar]
  66. Rusu, C. E., Fassnacht, C. D., Sluse, D., et al. 2017, MNRAS, 467, 4220 [NASA ADS] [CrossRef] [Google Scholar]
  67. Rusu, C. E., Wong, K. C., Bonvin, V., et al. 2020, MNRAS, 498, 1440 [Google Scholar]
  68. Schmidt, T., Treu, T., Birrer, S., et al. 2023, MNRAS, 518, 1260 [Google Scholar]
  69. Schneider, P., & Sluse, D. 2013, A&A, 559, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Shajib, A. J., Treu, T., & Agnello, A. 2018, MNRAS, 473, 210 [Google Scholar]
  71. Shajib, A. J., Birrer, S., Treu, T., et al. 2019, MNRAS, 483, 5649 [Google Scholar]
  72. Shajib, A. J., Birrer, S., Treu, T., et al. 2020, MNRAS, 494, 6072 [Google Scholar]
  73. Shajib, A. J., Wong, K. C., Birrer, S., et al. 2022, A&A, 667, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Shalyapin, V. N., & Goicoechea, L. J. 2017, ApJ, 836, 14 [NASA ADS] [CrossRef] [Google Scholar]
  75. Sheinis, A. I., Bolte, M., Epps, H. W., et al. 2002, PASP, 114, 851 [Google Scholar]
  76. Sluse, D., Claeskens, J. F., Hutsemékers, D., & Surdej, J. 2007, A&A, 468, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Sluse, D., Rusu, C. E., Fassnacht, C. D., et al. 2019, MNRAS, 490, 613 [NASA ADS] [CrossRef] [Google Scholar]
  78. Sonnenfeld, A. 2018, MNRAS, 474, 4648 [Google Scholar]
  79. Stern, D., Djorgovski, S. G., Krone-Martins, A., et al. 2021, ApJ, 921, 42 [NASA ADS] [CrossRef] [Google Scholar]
  80. Suyu, S. H., Treu, T., Hilbert, S., et al. 2014, ApJ, 788, L35 [NASA ADS] [CrossRef] [Google Scholar]
  81. Suyu, S. H., Bonvin, V., Courbin, F., et al. 2017, MNRAS, 468, 2590 [Google Scholar]
  82. Treu, T., & Koopmans, L. V. E. 2002, MNRAS, 337, L6 [NASA ADS] [CrossRef] [Google Scholar]
  83. Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [Google Scholar]
  84. Van de Vyvere, L., Gomer, M. R., Sluse, D., et al. 2022, A&A, 659, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Verde, L., Treu, T., & Riess, A. G. 2019, Nat. Astron., 3, 891 [Google Scholar]
  86. Waskom, M., Botvinnik, O., Hobson, P., et al. 2014, seaborn: v0.5.0 (November 2014) [Google Scholar]
  87. Wong, K. C., Suyu, S. H., Auger, M. W., et al. 2017, MNRAS, 465, 4895 [NASA ADS] [CrossRef] [Google Scholar]
  88. Wong, K. C., Suyu, S. H., Chen, G. C. F., et al. 2020, MNRAS, 498, 1420 [Google Scholar]
  89. Xu, D., Sluse, D., Schneider, P., et al. 2016, MNRAS, 456, 739 [Google Scholar]
  90. York, D. G., Adelman, J., Anderson, John E. J., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] [Google Scholar]
  91. York, T., Jackson, N., Browne, I. W. A., et al. 2005, MNRAS, 361, 259 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Summary of spectroscopic observation of the lens systems for which redshifts and stellar velocity dispersions of the deflectors have been reported in this paper.

In the text
Table 2.

Measured redshifts of the deflectors with associated uncertainties using the extracted 1D spectra.

In the text
Table 3.

Measured S/N per angstrom of the extracted deflector spectra and single aperture velocity dispersion with associated statistical and systematic uncertainties.

In the text

All Figures

thumbnail Fig. 1.

Images of the lens systems, part of the collected 2D spectra, and the corresponding 1D spatial profiles. The 1D spatial profiles have been generated by collapsing the data in the 2D spectra along the spectral axis. The slit position (green) for each lens system is also shown. For the lens system, J0147+4630, J0659+1629, J0818−2613, J1433+6007, and J1817+2729, we have used archival HST images (PI: T. Treu) and for B04453+123, B0631+519 and J0924+0219, we have used ground based AO images (PI: C. D. Fassnacht).
In the text
thumbnail Fig. 2.

Illustration of model fitting to 1D spatial profiles. Left column: each row shows the 1D spatial profile (blue) with individual model components for a single lens system. The model components are Moffat profiles, which represent the deflector and lensed quasars, with an additive polynomial function representing the background. The profile component representing the deflector is marked black and other profile components generally representing the lensed quasar images are marked with yellow. Right column: the top panel in each row shows the 1D spatial profile (blue) with 1σ uncertainty (orange) and the corresponding model (green) that fits the data in that profile. The bottom panel shows the residual (red) between the data and the model normalised to the uncertainties in data. The uncertainties on the spatial profiles of B0445+123 and B0631+519 are higher compared to others because these 1D profiles were generated from single frames, while for other lens systems, the corresponding profiles were generated from coadded frames.
In the text
thumbnail Fig. 3.

1D spectra and velocity dispersion fits for the deflectors from the lens system J0147+4630 and B0445+123. The plot for each system consists of three panels. Top panel: the extracted and smoothed 1D spectrum of the deflector is plotted over the observed wavelength where the smoothing has been done using a boxcar filter of size around 2.5 Å. Prominent stellar and telluric absorption lines are marked if present. And the measured redshift of the deflector is mentioned in the lower right corner of the plot. Middle panel: the pPXF generated model fit (red) to measure the velocity dispersion is plotted on top of the original unsmoothed spectrum (black). A smoothed version (yellow) of the original spectrum is also presented to show the goodness of the fit. The grey parts are the masked or excluded regions from the fit. Bottom panel: the green dots show the residuals between the unsmoothed flux and the model fit for each wavelength normalized to the respective model fits.
In the text
thumbnail Fig. 4.

1D spectra and velocity dispersion fits for the deflectors from the lens system B0631+519, J0659+1629 and J0818−2613. The description of the figure is same as Fig. 3.
In the text
thumbnail Fig. 5.

1D spectra and velocity dispersion fits for the deflectors from the lens system J0924+0219, J1433+6007 and J1817+2729. The description of the figure is same as Fig. 3.
In the text
thumbnail Fig. 6.

Illustration showing relations among the velocity dispersion measurements of the deflectors. The scatter plots between each pair of deflectors show corresponding velocity dispersion measurements for three hundred setups where each marker shows the measurements from the same setup. The blue-shaded curves are the individual velocity dispersion distributions of the deflectors. The set-ups were varied by changing the wavelength ranges, set of the spectra of the templates, and degree of the additive polynomial. In general, the covariance terms are negligible except in a few cases, for which they should be taken into account. The lens system J0659+1629 has been excluded from this analysis as the extracted deflector spectrum for this system only covers a small wavelength range. The plot in the upper-right shows a heat-map of the covariance matrix calculated from these velocity dispersion measurements, where the measurements were normalized to their respective mean.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.