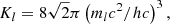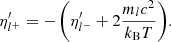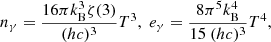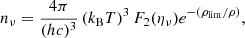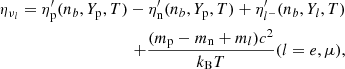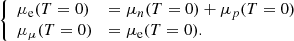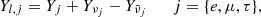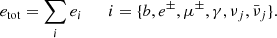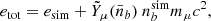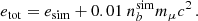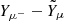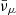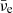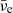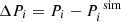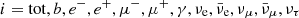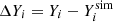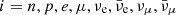| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 19 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202244927 | |
| Published online | 10 April 2023 | |
Muons in the aftermath of neutron star mergers and their impact on trapped neutrinos
1
Gran Sasso Science Institute, Viale Francesco Crispi 7, 67100 L’Aquila, Italy
e-mail: eleonora.loffredo@gssi.it
2
INFN – Laboratori Nazionali del Gran Sasso, Via G. Acitelli 22, 67100 Assergi L’Aquila, Italy
3
INAF – Osservatorio Astronomico d’Abruzzo, Via M. Maggini snc, 64100 Teramo, Italy
4
Dipartimento di Fisica, Universitá di Trento, Via Sommarive 14, 38123 Trento, Italy
5
INFN-TIFPA, Trento Institute for Fundamental Physics and Applications, Via Sommarive 14, 38123 Trento, Italy
6
Dipartimento di Fisica, Universitá di Pisa, Largo B. Pontecorvo, 3, 56127 Pisa, Italy
7
INFN, Sezione di Pisa, Largo B. Pontecorvo, 3, 56127 Pisa, Italy
Received:
8
September
2022
Accepted:
15
February
2023
Context. In the upcoming years, present and next-generation gravitational wave observatories will detect a larger number of binary neutron star (BNS) mergers with increasing accuracy. In this context, improving BNS merger numerical simulations is crucial to correctly interpret the data and constrain the equation of state (EOS) of neutron stars (NSs).
Aims. State-of-the-art simulations of BNS mergers do not include muons. However, muons are known to be relevant in the microphysics of cold NSs and are expected to have a significant role in mergers, where the typical thermodynamic conditions favour their production. Our work is aimed at investigating the impact of muons on the merger remnant.
Methods. We post-process the outcome of four numerical relativity simulations of BNS mergers performed with three different baryonic EOSs and two mass ratios considering the first 15 milliseconds after merger. We compute the abundance of muons in the remnant and analyse how muons affect the trapped neutrino component and the fluid pressure.
Results. We find that depending on the baryonic EOS, the net fraction of muons is between 30% and 70% the net fraction of electrons. Muons change the flavour hierarchy of trapped (anti-)neutrinos such that deep inside the remnant, muon anti-neutrinos are the most abundant, followed by electron anti-neutrinos. Finally, muons and trapped neutrinos modify the neutron-to-proton ratio, affecting the remnant pressure by up to 7% when compared with calculations neglecting them.
Conclusions. This work demonstrates that muons have a non-negligible effect on the outcome of BNS merger simulations, and they should be included to improve the accuracy of a simulation.
Key words: dense matter / equation of state / gravitational waves / neutrinos / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The detection of the gravitational wave (GW) event GW170817 from the inspiral phase of a binary neutron star (BNS) merger (Abbott et al. 2017a) opened a new window into the microphysics of microphysics of neutron stars (NSs). The measurement of the tidal deformability in addition to the constraint represented by the maximum measured NS mass has allowed researchers to put constraints on the equation of state (EOS) of cold NSs (Abbott et al. 2018; De et al. 2018). More stringent constraints have been obtained by combining information from the GW signal with the properties of the detected electromagnetic counterparts (Abbott et al. 2017b), specifically a short gamma-ray burst and a kilonova (e.g. Bauswein et al. 2017; Margalit & Metzger 2017; Radice et al. 2018b). The improved sensitivity planned in the next runs of observations by present GW detectors, such as the Laser Interferometer Gravitational-Wave Observatory (LIGO), the Virgo interferometer, and the Kamioka Gravitational Wave Detector (KAGRA) will increase the number of detected BNS mergers and the chance to observe their electromagnetic counterparts (Abbott et al. 2020; Patricelli et al. 2022; Colombo et al. 2022). The next generation of GW observatories, such as the Einstein Telescope (Punturo et al. 2010) and the Cosmic Explorer (Evans et al. 2021), are expected to significantly enlarge the horizon of detectable BNS mergers and to dramatically improve the estimate of the source parameters (Grimm & Harms 2020; Maggiore et al. 2020; Ronchini et al. 2022; Iacovelli et al. 2022). To date, post-merger GWs from BNS mergers have not been detected, but the Einstein Telescope and the Cosmic Explorer should reach the required sensitivity and largely increase the probability of detecting these signals. Such a discovery would strongly impact our knowledge of the nuclear EOS at high densities, even at a finite temperature (Sekiguchi et al. 2011b; Bauswein et al. 2012; Takami et al. 2014; Weih et al. 2020; Perego et al. 2022; Breschi et al. 2022), which is still quite uncertain. In this context, precise numerical simulations based on accurate modelling of the merger microphysics are mandatory. On the one hand, they are pivotal to interpret the collected data and to help constrain the nuclear EOS in both the zero and finite temperature regimes. On the other hand, they can provide reliable predictions of the properties of electromagnetic counterparts that can be used to optimise multi-messenger observational campaigns.
The EOS provides the relation between matter density, temperature, and the thermodynamical variables characterising a certain system. Building general-purpose EOSs for astrophysical simulations is extremely challenging because of the wide range of densities, temperatures, and charge fractions involved (Oertel et al. 2017). For this reason, it is important to assess the relevant degrees of freedom (d.o.f.) for a given astrophysical system. The thermodynamical conditions of BNS mergers are extreme, with temperatures reaching T ∼ 50 − 100 MeV and densities approaching nb ∼ 3 − 6 n0, where nb and n0 are the baryon density and the nuclear saturation density, respectively (Sekiguchi et al. 2011a; Bernuzzi et al. 2016; Radice et al. 2018a; Perego et al. 2019). The d.o.f. usually included in a BNS merger simulation are nucleons, nuclei, electrons, positrons, and photons. Some simulations take into account hyperons, quarks, and/or trapped neutrinos (Sekiguchi et al. 2011a; Foucart et al. 2016a; Most et al. 2019; Radice et al. 2022). However, state-of-the-art simulations do not include muons even though the typical merger temperatures and densities allow for their presence.
Muons are already known to play a relevant role in the thermodynamics of proto-neutron stars (Prakash et al. 1997) and have a non-negligible abundance inside cold NSs in neutrinoless β-equilibrium (Cohen et al. 1970; Cameron 1970; Glendenning 1997; Haensel et al. 2000, 2001; Steiner et al. 2005; Alford & Good 2010). Their potential role in the context of BNS mergers was investigated by Fore & Reddy (2020) and Alford et al. (2021). For example, it was found that weak reactions involving muons and negatively charged pions at nuclear densities nb ≲ n0 and temperatures T ∼ 30 MeV significantly reduce the mean free path of low energy muon (anti-)neutrinos. These processes are expected to modify the energy transport inside the merger remnant and to affect its stability (Fore & Reddy 2020). Moreover, muonic Urca processes and (anti-)neutrino scattering off muons produce a relevant contribution to the equilibration processes taking place in the post-merger remnant (Alford et al. 2021). Muons have already been included in some core-collapse supernova (CCSN) simulations (Bollig et al. 2017, 2020; Guo et al. 2020; Fischer et al. 2020). The appearance of a significant muonic fraction has been demonstrated after core bounce, and, albeit to a lesser extent, even prior to it (Fischer et al. 2020). In this context, muons induce a softening of the EOS, prompt a burst of muon neutrinos soon after the core bounce, and possibly facilitate the supernova explosion by enhancing the neutrino emission and changing the emitted neutrino spectra (Bollig et al. 2017; Guo et al. 2020; Fischer et al. 2020).
In addition to the nuclear EOS and the related d.o.f., other variables, such as thermal pressure, differential rotation, and rotation rate, influence the evolution of the merger remnant (Kaplan et al. 2014). In particular, thermal pressure affects the angular velocity threshold of mass shedding and the remnant evolution during the phase of secular instability, with non-trivial implications for the time of collapse (Kaplan et al. 2014). Another important contribution to the merger thermodynamics comes from trapped neutrinos, which are present deep inside the merger remnant. Indeed, they are relevant, especially for the implications on the stability of differentially rotating remnants. Their inclusion in BNS merger simulations is extremely challenging and requires a proper radiation transport scheme. To date, only a few BNS simulations have explicitly included them (e.g. Foucart et al. 2016a; Radice et al. 2022). These simulations showed electron anti-neutrinos are the dominant trapped neutrinos and their appearance results in an increase of the electron and proton fractions. These results are consistent with the outcome of Perego et al. (2019), where the relevance of the trapped neutrino component was quantified within a post-processing approach. By changing the proton-to-neutron content, trapped neutrinos induce a pressure decrease of approximately 5%−10% inside the remnant (Perego et al. 2019), so they may speed up the collapse of massive binaries to black holes. Nevertheless, muonic and tauonic (anti-)neutrinos have been treated at the same level as heavy-lepton (anti-)neutrinos in previous works because muons were not included in the microphysics modelling. To the best of our knowledge, there are no BNS merger simulations taking into account the coupling between neutrinos and muons.
In the present work, we develop a post-processing technique to quantify the fractions of muons and trapped neutrinos in the remnants of BNS mergers in order to assess their combined effect on fluid pressure. We apply our analysis to the outcome of four fully relativistic numerical simulations employing three different microphysical EOSs and two different mass ratios. We aim to show that the production of muons and the trapping of neutrinos modify the remnant pressure, which changes asymmetrically in space with respect to the case in which muons and neutrinos are neglected, depending on the assumed baryonic EOS and binary mass ratio.
This paper is structured as follows. In Sect. 2, we briefly discuss the mechanism of muon production and neutrino trapping in BNS mergers and estimate the typical timescales and energies involved. In Sect. 3, we introduce our method based on a post-processing approach. From Sect. 4 to Sect. 6, we present our results, analysing the abundance of muons in the remnant (Sect. 4), the trapping of neutrinos (Sect. 5), and how muons and trapped neutrinos affect the remnant pressure (Sect. 6). In Sect. 7, we discuss our results, comparing them to state-of-the-art simulations. Finally, we summarise our work and present our conclusions in Sect. 8.
2. Preliminary estimates
2.1. Muons in BNS mergers
The fraction of muons in a BNS remnant is determined both by the fraction of muons in the two cold NSs before merger and by the efficiency of (anti)muon production during and after merger. We consider as an example a fluid element taking part in a BNS merger. During the inspiral, muons are already present in the two cold NSs for sufficiently high densities when the electron chemical potential, μe, exceeds the muon rest mass, mμc2 ∼ 106 MeV (Cohen et al. 1970; Cameron 1970; Glendenning 1997; Haensel et al. 2000, 2001; Steiner et al. 2005; Alford & Good 2010). For relativistic degenerate electrons, the former can be estimated as:
where pF, e is the Fermi impulse of electrons, while Ye− = ne−/nb and ne− are the electron fraction and the electron number density, respectively. Clearly, for neutrinoless β-equilibrated nuclear matter, Ye− ∼ 0.05 − 0.1, muons are expected to be present as non-relativistic degenerate particles already close to saturation density. A simple estimate of their chemical potential, μμ−, is given by:
where pF, μ is the Fermi impulse of muons, while Yμ− = nμ−/nb and nμ− are the fraction of muons and the muon number density, respectively.
We next investigate whether the typical thermodynamical conditions in BNS mergers allow for the creation of muons. During the merger, nuclear matter is heated and the average photon energy, Eγ ≈ 2.7 kBT, overcomes the muon mass threshold when the temperature reaches kBT ≳ 40 MeV. Therefore, in this temperature regime, thermal processes such as
drive the creation of μ± pairs. Additionally, neutrino pairs of all flavours are produced via thermal processes (see e.g. Haft et al. 1994; Ruffert et al. 1996)
or nucleon-nucleon bremsstrahlung (see e.g. Hannestad & Raffelt 1998)
where ν denotes any flavour neutrino, while N is a nucleon. For example, in the case of e± annihilation, the average energy of the neutrino pairs is (Cooperstein 1988):
where ηe− = μe−/kBT is the (relativistic) electron degeneracy parameter and Fn(η) is the Fermi function of order n. For very degenerate electrons (ηe− ≫ 1) and accounting for Eq. (1)
Even when muonic (anti-)neutrinos thermalise, their average energy is
Thus, once high energy νμ and 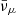 are formed, (anti)muons can be created via charged-current (CC) semi-leptonic reactions
are formed, (anti)muons can be created via charged-current (CC) semi-leptonic reactions
as in the case of CCSNe (Bollig et al. 2017; Guo et al. 2020; Fischer et al. 2020). In addition, neutron decay, 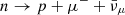 , plays a relevant role in the high density-low temperature regime (Alford et al. 2021) typical of the remnant core. Finally, purely CC leptonic processes, such as νμ + e− → νe + μ−, and inverse muon decay can enhance the abundance of muons at low average neutrino energies ≲50 MeV since the amount of electrons exceeds the amount of positrons (Guo et al. 2020; Fischer et al. 2020; Alford et al. 2021).
, plays a relevant role in the high density-low temperature regime (Alford et al. 2021) typical of the remnant core. Finally, purely CC leptonic processes, such as νμ + e− → νe + μ−, and inverse muon decay can enhance the abundance of muons at low average neutrino energies ≲50 MeV since the amount of electrons exceeds the amount of positrons (Guo et al. 2020; Fischer et al. 2020; Alford et al. 2021).
In general, matter in BNS mergers is not in weak and thermal equilibrium, and it is not obvious that weak reactions are fast enough to allow for muon creation at short enough timescales everywhere inside the remnant (see e.g. Hammond et al. 2022). We estimate the rate at which these reactions occur by considering the reaction νμ + n → p + μ− as a representative example. In the zero momentum transfer limit, neglecting the momentum transferred to nucleons and assuming |pN|≪mN, where pN and mN are the nucleon momentum and mass, respectively, the reaction rate of νμ + n → p + μ− is at leading order:
where G is the Fermi constant, gV and gA are the weak couplings, Q = mn − mp is the neutron-proton mass difference, fi(Ei) is the Fermi-Dirac distribution function of particle i with energy Ei, and ωnp is given by
where nN and  indicate the number density and the non-relativistic chemical potential of nucleons N = p, n, respectively. An order of magnitude estimate of the reaction rate can be easily obtained in the non-degenerate regime, ωnp → nn, by neglecting the neutron-proton mass difference1 and considering neutrino energies Eνμ ≃ μμ− ≳ mμc2 (see Eq. (2)). The inverse rate thus gives the muon production timescale:
indicate the number density and the non-relativistic chemical potential of nucleons N = p, n, respectively. An order of magnitude estimate of the reaction rate can be easily obtained in the non-degenerate regime, ωnp → nn, by neglecting the neutron-proton mass difference1 and considering neutrino energies Eνμ ≃ μμ− ≳ mμc2 (see Eq. (2)). The inverse rate thus gives the muon production timescale:
We note that  for high enough densities and neutrino energies where tdyn ∼ 10−4 s is the merger dynamical timescale (see e.g. Radice et al. 2020). Because of the high degeneracy of neutrons, CC semi-leptonic reactions are expected to favour the production of μ− over μ+. Accordingly, the opacity of νμ to CC semi-leptonic reactions exceeds that of
for high enough densities and neutrino energies where tdyn ∼ 10−4 s is the merger dynamical timescale (see e.g. Radice et al. 2020). Because of the high degeneracy of neutrons, CC semi-leptonic reactions are expected to favour the production of μ− over μ+. Accordingly, the opacity of νμ to CC semi-leptonic reactions exceeds that of  (at least in cases with high enough neutrino energy; see also the discussion in Guo et al. 2020; Fischer et al. 2020), and the net muon fraction becomes enhanced.
(at least in cases with high enough neutrino energy; see also the discussion in Guo et al. 2020; Fischer et al. 2020), and the net muon fraction becomes enhanced.
2.2. Neutrino trapping
In this section, we provide an estimate of the neutrino diffusion timescale from a BNS merger remnant to explore the conditions in which neutrinos can be considered trapped, that is, when their diffusion timescale, tdiff, exceeds the dynamical timescale, as well as the conditions in which trapped neutrinos are in thermal and weak equilibrium with matter. Since neutrino scattering off nucleons is among the largest sources of opacity for all neutrino flavours, we considered an approximate expression of its corresponding mean free path, λνN(Eν)∼1/(nbσνN(Eν)), where
gives the ν − N scattering cross section and σ0 ≈ 1.76 × 10−44 cm2 (Shapiro & Teukolsky 1983). Using random-walk arguments, we estimated tdiff as
where ℓ is the characteristic length scale of the diffusion process and τ is the optical depth, which we estimated as τ ∼ ℓ/λ. For example, in the case of thermal neutrinos diffusing from a remnant core of size RNS,
and RNS and TNS are the characteristic radius and temperature of the massive NS remnant, respectively (see e.g. Bernuzzi 2020). We can repeat the estimate for thermal neutrinos diffusing from the innermost part of the disc surrounding the massive central remnant:
where Hdisc and Tdisc are the characteristic disc height and temperature, respectively. We note that the average energy of thermal neutrinos at kBT ∼ 5 MeV is Eν ∼ 15 MeV, which corresponds to the typical energy of the neutrinos emitted at infinity by BNS merger remnants (e.g. Ruffert & Janka 1998; Rosswog & Liebendoerfer 2003; Sekiguchi et al. 2016; Foucart et al. 2016a,b; Cusinato et al. 2022). As implied by Eq. (12), the diffusion timescale of neutrinos with energy Eν ∼ 15 MeV from the disc becomes comparable to the dynamical timescale around nb ∼ 5 × 10−3 fm−3, corresponding to a rest mass density ρ = mamunb ∼ 1012 g cm−3, where mamu is the atomic mass unit. Other interactions involving neutrinos in addition to ν − N scattering provide further opacity. Thus, the above estimates can be understood as conservative upper limits for the trapping density.
Due to the presence of inelastic processes (such as absorption of neutrinos on free nucleons, inverse pair processes, and scattering off electrons and positrons), neutrinos are not only efficiently trapped, but they couple to matter and photons if the corresponding mean free path is short enough. The situation is however complicated by the fact that neutrinos have a spectral distribution and that cross sections have a non-trivial energy dependence. As a result, neutrinos of different flavours and energies decouple from matter at different locations. Rest mass density has been shown to be the most relevant matter property in determining the location of both the last scattering surface and the surfaces where weak and thermal equilibrium freezes out (Endrizzi et al. 2020). In particular, according to Endrizzi et al. (2020), we observe that for densities larger than 1012 g cm−3, almost all relevant neutrinos are within the last scattering surface (Fig. 8), while for densities larger than 1013 g cm−3, they are also in thermal and weak equilibrium (Fig. 10). In the case of νe and 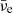 , these surfaces are even characterised by densities one order of magnitude smaller. Thus, we defined a limiting density ρlim such that neutrinos can be considered as a trapped gas if ρ ≳ ρlim. For electron (anti-)neutrinos, we considered ρlim, e = 1011 g cm−3, while for muonic and tauonic (anti-)neutrinos, we set ρlim, x = 1012 g cm−3. Moreover, at ρ ≳ 10 × ρlim neutrinos can be approximately modelled as a gas in equilibrium with other constituents of matter.
, these surfaces are even characterised by densities one order of magnitude smaller. Thus, we defined a limiting density ρlim such that neutrinos can be considered as a trapped gas if ρ ≳ ρlim. For electron (anti-)neutrinos, we considered ρlim, e = 1011 g cm−3, while for muonic and tauonic (anti-)neutrinos, we set ρlim, x = 1012 g cm−3. Moreover, at ρ ≳ 10 × ρlim neutrinos can be approximately modelled as a gas in equilibrium with other constituents of matter.
3. Method
We present our method to estimate the fraction of muons and their impact on the trapped neutrino component in BNS merger remnants by post-processing the outcome of a significant sample of numerical relativity simulations. First, we review the properties of the simulations considered in this work (Sect. 3.1). Next, we describe how we model the nuclear EOS, including muons and trapped neutrinos (Sect. 3.2). Finally, we explain our post-processing technique by arguing for the physical rationale and the limits of validity (Sect. 3.3).
3.1. The simulation sample
We considered the outcomes of four BNS merger simulations in numerical relativity targeted to GW170817 (see Table 1) published in Nedora et al. (2019, 2021), and Bernuzzi et al. (2020). The term MA, B refers to the gravitational mass of each of the two NSs at infinity such that the binary mass ratio is defined as q = MB/MA ≥ 1. More details about the simulations and their numerical setup can be found in the references listed in Table 1 and in Radice et al. (2018a). In the following paragraphs, we provide a summary of the simulation properties necessary to understand our post-processing procedure.
List of the BNS merger simulations considered in this work.
Our simulation sample contains three symmetric (q = 1) simulations. These simulations were performed with three different nuclear EOSs, namely, BLh (Bombaci & Logoteta 2018; Logoteta et al. 2021), HS (DD2; Typel et al. 2010; Hempel & Schaffner-Bielich 2010), and SFHo (Steiner et al. 2013). In the following sections, we refer to the second EOS simply as DD2. Details about these nuclear EOSs are provided in Sect. 3.2.1. These simulations predicted quite different merger outcomes. In particular, for SFHo the remnant collapsed into a black hole within a few milliseconds after the merger, while it survived for at least 90 ms in the other two cases. In addition, we considered a simulation of a significantly asymmetric BNS merger (q = 1.43) using the BLh EOS. Within this sample, we could explore how the presence of muons and trapped neutrinos correlates with the properties of the nuclear EOS and with the mass asymmetry degree of the binary. Additionally, half of the simulations included the effect of physical viscosity of magnetic origin (Radice et al. 2016). The simulation sample is however too small to address the impact of viscosity on our results, and we leave such an investigation to future studies. In the following sections, we refer to each simulation by specifying the nuclear EOS and q according to the notation: (EOS, q).
All simulations modelled NS matter as made of neutrons, protons (both free and bound in nuclei), photons, electrons, and positrons. No muons and trapped neutrinos were considered. All the simulations included the effect of neutrino radiation through a leakage plus M0 scheme, whose details can be found in Radice et al. (2016, 2018a). Electron neutrinos and anti-neutrinos were considered separately, while there was no distinction between muonic and tauonic (anti-)neutrinos, which were treated as a single species (heavy-lepton neutrinos). The leakage prescription was used to compute the net rate of change in the internal energy and in the lepton fraction for matter in optically thick conditions due to neutrino diffusion. Even though the particle and energy density of trapped neutrinos were estimated by the leakage algorithm in order to compute the neutrino diffusion rates, they were not dynamically evolved, and their contribution to the thermodynamical state of matter was not explicitly taken into account in the simulations. This also implies that the energy density and pressure of the neutrinos were not included in the stress-energy tensor of matter and radiation.
In our analysis, we considered snapshots of the computational domain from the post-merger phase in the time interval ∼5 − 15 ms post-merger where the merger time is defined by the maximum in the ℓ = m = 2 mode in the GW waveform. In this phase, the merger remnant is still in the GW-dominated phase (e.g. Bernuzzi et al. 2016; Zappa et al. 2018), but the initial, highly dynamical transients that characterise the very first milliseconds after the merger have disappeared and a disc around the central remnant has formed. From each snapshot, we extracted the full 3D profile of the local baryon number density  , net electron fraction
, net electron fraction 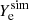 , and energy density esim, as directly obtained by the simulation. The net electron fraction was defined as Ye = (ne− − ne+)/nb, where ne−(ne+) is the electron (positron) number density. By using the same EOS used in the simulation, we could reconstruct the full thermodynamic states anywhere inside the computational domain, including the values of the temperature Tsim, chemical potentials
, and energy density esim, as directly obtained by the simulation. The net electron fraction was defined as Ye = (ne− − ne+)/nb, where ne−(ne+) is the electron (positron) number density. By using the same EOS used in the simulation, we could reconstruct the full thermodynamic states anywhere inside the computational domain, including the values of the temperature Tsim, chemical potentials  , particle fractions
, particle fractions 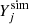 , partial pressures
, partial pressures 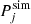 , and total pressure Psim, where the subscript j = {n, p, e±, γ} indicates neutrons, protons, electrons, positrons, and photons. In Fig. 1, we show as an example the rest mass density
, and total pressure Psim, where the subscript j = {n, p, e±, γ} indicates neutrons, protons, electrons, positrons, and photons. In Fig. 1, we show as an example the rest mass density 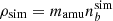 , the temperature, and the electron fraction from the outcome of the simulation (BLh, 1.00) at approximately 5 ms after merger. The dense and cold core of the remnant can be recognised, characterised by ρsim ≳ 1015 g cm−3, Tsim < 20 MeV, and
, the temperature, and the electron fraction from the outcome of the simulation (BLh, 1.00) at approximately 5 ms after merger. The dense and cold core of the remnant can be recognised, characterised by ρsim ≳ 1015 g cm−3, Tsim < 20 MeV, and 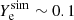 . The core is surrounded by warm matter in the density regime ρsim ∼ 1014 − 1015 g cm−3, with the temperature reaching up Tsim ∼ 50 MeV in correspondence to the hot spots and a slightly smaller electron fraction
. The core is surrounded by warm matter in the density regime ρsim ∼ 1014 − 1015 g cm−3, with the temperature reaching up Tsim ∼ 50 MeV in correspondence to the hot spots and a slightly smaller electron fraction 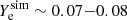 . At a lower density ρsim ≲ 1014 g cm−3, cold and warm matter streams alternate. In the following sections, we explain how these data are used to post-process the original simulations.
. At a lower density ρsim ≲ 1014 g cm−3, cold and warm matter streams alternate. In the following sections, we explain how these data are used to post-process the original simulations.
 |
Fig. 1. Outcome of the numerical simulation (BLh, 1.00) at 4.6 ms after merger. The left, central, and right panels show the rest mass density, the temperature, and the electron fraction on the equatorial plane, respectively. The black lines mark isodensity contours corresponding to 1012 g cm−3 (solid line), 1013 g cm−3 (dashed line), 1014 g cm−3 (dashed-dotted line), and 1015 g cm−3 (dotted line). |
3.2. EOS modelling
In our analysis, we considered baryons, massive leptons, photons, and neutrinos as the relevant d.o.f. to describe matter and radiation in BNS mergers. Baryons, massive leptons, and photons are assumed to be in thermal and nuclear statistical equilibrium everywhere inside the remnant. Nuclear statistical equilibrium is reached when strong and electromagnetic reactions are in equilibrium, and the nuclear composition is provided by the minimum of the free energy. For astrophysically relevant conditions, this is verified as long as kBT ≳ 0.6 MeV (e.g. Hix & Thielemann 1999). In astrophysical plasma, the negative net charge of massive leptons is balanced by the positive charge of protons. In the presence of more than one massive lepton, charge neutrality implies:
where Yp = np/nb is the proton fraction; np is the proton number density; Yl = (nl− − nl+)/nb is the net fraction of the massive lepton l; and e, μ, and τ stand for electron, muon, and tauon, respectively.
Every relevant species was characterised by its own EOS. These EOSs can be expressed in terms of any thermodynamical potential, such as the Helmholtz free energy F with the volume V, the number of particles N, and the temperature T, as independent variables. Neglecting the modifications of the thermodynamical potentials due to the interaction between different d.o.f., the total free energy was given by
where the subscript i = {b, l, γ, ν} indicates baryons, massive leptons, photons, and neutrinos, respectively. All the thermodynamic variables, such as the chemical potentials, μi, the energy densities, ei, and the pressures, Pi, were derived from Fi at fixed temperature T, number of particles Ni, and volume V according to the standard rules of the canonical ensemble. Hence, the total energy density and pressure were simply given by
In the following sections, we provide a detailed description of the EOSs used in this work for each species.
3.2.1. Baryons
Our knowledge of the baryonic matter EOS is still affected by large uncertainties. Therefore, to bracket possible uncertainties in this work, the baryonic contribution was taken into account via three different nuclear EOSs in tabulated form corresponding to the ones used in the simulations presented in Sect. 3.1: the BLh (Bombaci & Logoteta 2018; Logoteta et al. 2021), the DD2 (Typel et al. 2010; Hempel & Schaffner-Bielich 2010), and the SFHo (Steiner et al. 2013)2. We note that we did not consider the possible formation of hyperons (Oertel et al. 2012; Fortin et al. 2018) or a phase transition to quark matter (Weissenborn et al. 2011; Klähn et al. 2013; Chatterjee & Vidaña 2016; Bombaci et al. 2016; Logoteta et al. 2019; Logoteta 2021). The BLh EOS is a microscopic EOS constructed following the framework of the Brueckner-Bethe-Goldstone many-body theory extended at finite temperatures within the Brueckner-Hartree-Fock approximation. In contrast, the modelling of nuclear interactions in DD2 and SFHo is based on a relativistic mean field theory. For each nuclear EOS, the independent variables are (nb, T, Yp). The range of (nb, T, Yp) for each EOS table is reported in Table 2. The three EOSs are in reasonable agreement with the experimental constraints on the properties of nuclear matter at n0 and T = 0 (for experimental constraints, see Shlomo et al. 2006; Danielewicz & Lee 2014; Oertel et al. 2017; Drischler et al. 2019). Moreover, all three EOSs satisfy to a good extent present astrophysical constraints on the NS maximum mass Mmax > 2.01 M⊙ and NS radius (Antoniadis et al. 2013; Lattimer & Steiner 2014; Oertel et al. 2017; Riley 2019; Miller et al. 2019, 2021; Raaijmakers et al. 2021).3 In Table 2, we report for each EOS the values of the nuclear saturation density, the maximum mass Mmax of a cold non-rotating NS, the corresponding radius Rmax, the radius R1.4 of a 1.4 M⊙ NS, and the dimensionless tidal deformability 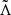 (e.g. Hinderer 2008; Damour et al. 2012; Favata 2014) for GW170817 targeted binaries. We note that SFHo supports a smaller maximum NS mass with a smaller radius. More generally, SFHo produces more compact NSs compared to the other two EOSs. In the case of BLh, it predicts slightly larger Mmax and Rmax, but the values are still close to the ones from SFHo. Conversely, DD2 exhibits significantly larger values for Mmax and Rmax and a smaller compactness. Despite the fact that the maximum NS properties of SFHo and BLh are relatively close, it is worth noting that for other properties at densities equal to several times n0, SFHo and DD2, regarding the symmetry energy, and DD2 and BLh, for incompressibility, are more similar. With this selection of baryonic EOSs, we could explore very different microphysical descriptions and a wide range of thermodynamical conditions and macroscopic properties of merging BNSs.
(e.g. Hinderer 2008; Damour et al. 2012; Favata 2014) for GW170817 targeted binaries. We note that SFHo supports a smaller maximum NS mass with a smaller radius. More generally, SFHo produces more compact NSs compared to the other two EOSs. In the case of BLh, it predicts slightly larger Mmax and Rmax, but the values are still close to the ones from SFHo. Conversely, DD2 exhibits significantly larger values for Mmax and Rmax and a smaller compactness. Despite the fact that the maximum NS properties of SFHo and BLh are relatively close, it is worth noting that for other properties at densities equal to several times n0, SFHo and DD2, regarding the symmetry energy, and DD2 and BLh, for incompressibility, are more similar. With this selection of baryonic EOSs, we could explore very different microphysical descriptions and a wide range of thermodynamical conditions and macroscopic properties of merging BNSs.
Properties of nuclear EOS tables used in this work and of cold, spherically symmetric NSs for each nuclear EOS.
3.2.2. Massive leptons and photons
We treated massive leptons as ideal Fermi gases in thermal equilibrium. In particular, we incorporated electrons and positrons e± as well as muons and anti-muons μ±, while we neglected tauons and anti-tauons τ± due to their large mass compared to the typical temperatures and Fermi energies in the system. The EOS of a non-interacting gas4 of fermions at a finite temperature is well known in the literature, and it provides the expressions for the number density nl±, the specific energy density el±, and the pressure Pl± (Bludman & van Riper 1977):
where ml is the lepton mass and Kl is a constant
θl and 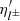 are the relativity and the non-relativistic degeneracy parameters, respectively,
are the relativity and the non-relativistic degeneracy parameters, respectively,
while  are the generalised Fermi functions of order k. At thermal equilibrium, the degeneracy parameter of anti-particles
are the generalised Fermi functions of order k. At thermal equilibrium, the degeneracy parameter of anti-particles 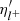 is related to that of particles
is related to that of particles 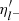 (Timmes & Arnett 1999):
(Timmes & Arnett 1999):
By inverting Eq. (16), the term 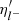 can be expressed as a function of (nb, Yl, T), as was suggested in Timmes & Arnett (1999).
can be expressed as a function of (nb, Yl, T), as was suggested in Timmes & Arnett (1999).
Photons form an ideal Bose gas in thermal equilibrium with matter and with zero chemical potential, μγ = 0. The resulting EOS of photons depends only on T:
and Pγ = eγ/3.
3.2.3. Trapped neutrinos
Based on the discussion in Sect. 2 and as typical neutrino energies inside the remnant are much larger than any neutrino mass, we modelled the trapped neutrino component as a massless Fermi gas in weak and thermal equilibrium with matter and radiation. Accordingly, the particle number density nν, the energy density eν, and the pressure Pν of any flavour neutrino ν were given by
where the exponential factor e−(ρlim/ρ) was introduced in order to model the fading of the trapped component at ρ ≲ ρlim (see also Kaplan et al. 2014 and Perego et al. 2019 for a similar choice). The degeneracy parameter of anti-neutrinos was fixed by 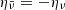 because of thermal equilibrium. Furthermore, ηντ = 0 since the fraction of tauons is negligible, while weak equilibrium defined the degeneracy parameters of electronic and muonic neutrinos:
because of thermal equilibrium. Furthermore, ηντ = 0 since the fraction of tauons is negligible, while weak equilibrium defined the degeneracy parameters of electronic and muonic neutrinos:
where 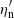 and
and 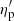 are the non-relativistic degeneracy parameters of neutrons and protons, respectively. Accordingly, the EOS of electron (muon) neutrinos depends on T, Yp, and Ye (Yμ), while the EOS of tauon neutrinos depends only on T and does not distinguish between ντ and
are the non-relativistic degeneracy parameters of neutrons and protons, respectively. Accordingly, the EOS of electron (muon) neutrinos depends on T, Yp, and Ye (Yμ), while the EOS of tauon neutrinos depends only on T and does not distinguish between ντ and  . The fraction of neutrinos and their mean energy were defined as Yν = nν/nb and Eν = eν/nν, respectively.
. The fraction of neutrinos and their mean energy were defined as Yν = nν/nb and Eν = eν/nν, respectively.
From the previous discussion, if all the species are assumed to be in thermal and reaction equilibrium, the set of variables needed to describe the complete EOS is given by (nb, T, Yp, Ye, Yμ). However, the charge neutrality of NS matter constrains the proton fraction Yp = Ye + Yμ, reducing the set of independent variables to (nb, T, Ye, Yμ).
3.3. The post-processing technique
Based on the simulation outcome discussed in Sect. 3.1, we estimated the amount and the impact of muons in post-processing as well as their influence on the trapped neutrino properties. In particular, we were interested in the implications for the remnant on a timescale Δt ∼ 5 − 15 ms after the merger and in the density region ρ ≳ 1013 g cm−3 where the approximation of weak and thermal equilibrium better applies. The absence of muons inside the original simulations posed a significant issue and required some modelling (shown in Sect. 3.3.1) before the post-processing technique could be applied (discussed in Sect. 3.3.2).
3.3.1. Modelling
We modelled the NS fluid elements before the merger as being composed of neutrons, protons, electrons, and muons in cold neutrinoless weak equilibrium:
In Fig. 2, we show the fractions of electrons, muons, and protons as a function of nb, obtained by solving Eq. (27). At nb ≈ 0.3fm−3 ∼ 2 n0, the muon fraction is approximately 40% of the electron fraction for all the considered EOSs, and it increases monotonically with nb. For comparison, we also show the electron fraction calculated by assuming β-equilibrium without muons (see dashed black line in Fig. 2), which corresponds to the initial conditions used in the simulations presented in Sect. 3.1. A common feature of all three models is that when muons are included, the electron fraction becomes smaller, while the proton fraction tends to increase, that is, Yp = Ye + Yμ. In particular, the system lowers the Fermi energy of electrons by converting electrons into muons up to the point where the chemical potentials of electrons and muons are equal, balancing the difference between the neutron and proton chemical potentials. Moreover, when muons are included, neutrons can turn into protons plus muons via Urca processes (Leinson 2002; Yakovlev & Pethick 2004; Potekhin et al. 2015). The three EOSs show pronounced differences in the density behaviour of the electron fraction. In particular, BLh predicts a higher Yp at large densities compared to DD2 and SFHo. Such differences are mainly due to the different density behaviours of the symmetry energy in the three models. Symmetry energy is indeed the principal source that determines matter composition at a given density and temperature. In the following paragraphs, we refer to the particle fractions of the cold NSs obtained by solving Eq. (27) as 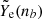 and
and  which are represented as solid lines in Fig. 2, and to the net electron fraction computed in cold weak equilibrium without muons (see dashed black line in Fig. 2) as
which are represented as solid lines in Fig. 2, and to the net electron fraction computed in cold weak equilibrium without muons (see dashed black line in Fig. 2) as 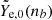 .
.
 |
Fig. 2. Particle fractions computed at T = 0 in neutrinoless β-equilibrium for three different EOS: BLh (left), DD2 (centre), and SFHo (right). Black lines show the electron fraction computed in two different cases: equilibrium with muons (solid lines) or without muons (dashed lines). The green line corresponds to the fraction of protons at equilibrium with muons, while the red line corresponds to the muon fraction. We note that when muons are not included, the proton fraction coincides with the electron one (dashed black line). |
During a merger, the density, temperature, and composition of the fluid elements change because of matter compression and decompression, and neutrinos are produced. If a fluid element is in good approximation within the last scattering neutrino surface (i.e. ρ ≳ ρlim), a trapped neutrino gas is formed in weak and thermal equilibrium with matter. In these conditions, it is convenient to introduce for each fluid element the electron, muon, and tauon lepton numbers
and the total fluid energy
The central part of the remnant, characterised by ρ ≳ 1014 g cm−3, is formed by the fusion of the two NSs cores, and it is characterised by fluid elements whose density is significantly in excess of the neutrino surface density during their evolution. Such fluid elements are not affected by shocks and significant neutrino emission. In particular, as discussed in Sect. 2, the neutrino diffusion timescale, tdiff, is in the order of seconds; thus tdiff ≫ Δt ∼ 5 − 15 ms (see Eq. (11)). So these fluid elements conserve their electron and muon lepton fractions over Δt, which are ultimately equal to the electron and muon lepton fractions set by the initial cold neutrinoless equilibrium, Eq. (27)5 A close inspection of the thermodynamic conditions experienced by matter in a BNS merger event and of their corresponding evolution (Perego et al. 2019) revealed that the conservation of the lepton numbers is well realised for matter originally inside the outer core of the two cold NSs, that is, at ρ ≳ 1014 g cm−3 also during the inspiral. In contrast, most of the matter at a lower density inside the merger remnant, ρ < 1014g cm−3, originates from the decompression of matter originally around ρ ∼ 1014 g cm−3 inside the two merging NSs. In this case, matter is significantly heated by shocks and compression such that the electron and muon lepton numbers of each fluid element become considerably altered. In this density domain, the electron fraction evolved through the numerical relativity simulations is a better proxy of Yl, e: 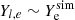 . The muon lepton fraction is instead approximately given by Yl, μ ∼ 0.01, which corresponds to the typical muon fraction in the original NSs at the edge of the outer core, that is, around and just below saturation density (see Fig. 2).
. The muon lepton fraction is instead approximately given by Yl, μ ∼ 0.01, which corresponds to the typical muon fraction in the original NSs at the edge of the outer core, that is, around and just below saturation density (see Fig. 2).
Concerning the relativistic internal energy, no significant energy leaks out in the form of neutrinos from the fluid elements until tdiff ≫ Δt in neutrino trapping conditions. Thus, the evolution of esim inside the simulation is also expected to reproduce in good approximation the evolution (i.e. the variation) of the total internal energy once muons and neutrinos are present. However, the presence of physical muons inside the two cold NSs alters the absolute value of the relativistic internal energy due to their rest mass contribution. Nevertheless, this contribution remains approximately constant in time as long as the bulk of the muons present in the remnant comes from the two cold NSs.
3.3.2. Algorithm
Based on the above considerations, we designed the following post-processing algorithm. We considered the time snapshots of the simulations listed in Table 1 in the time interval ∼5 − 15 ms. From each snapshot, we read the full 3D profile of the baryon number density 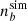 , the net electron fraction
, the net electron fraction 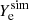 , and the internal energy density esim on a Cartesian grid (x, y, z) with −30 km ≤ x, y, z ≤ +30 km. Given
, and the internal energy density esim on a Cartesian grid (x, y, z) with −30 km ≤ x, y, z ≤ +30 km. Given  on the Cartesian grid and for each snapshot, we performed our analysis according to the following steps.
on the Cartesian grid and for each snapshot, we performed our analysis according to the following steps.
Given 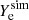 , we computed the baryon density
, we computed the baryon density 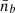 such that
such that  (See Sect. 3.3.1 and dashed black line in Fig. 2.) We note that
(See Sect. 3.3.1 and dashed black line in Fig. 2.) We note that 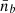 corresponds to the original density of the fluid element inside the NSs during the inspiral, and it is, in general, different from
corresponds to the original density of the fluid element inside the NSs during the inspiral, and it is, in general, different from 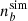 .
.
We computed the cold equilibrium electron and muon net fractions corresponding to 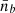 (i.e.
(i.e. 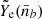 and
and 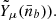 (See Sect. 3.3.1 and solid black and red lines in Fig. 2.)
(See Sect. 3.3.1 and solid black and red lines in Fig. 2.)
Given the simulation baryon number density 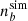 , we computed
, we computed 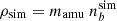 . If ρsim > 1014 g cm−3, then the lepton numbers were separately conserved (see discussion in Sect. 3.3.1). Therefore, we identified the electron and muon lepton fractions with
. If ρsim > 1014 g cm−3, then the lepton numbers were separately conserved (see discussion in Sect. 3.3.1). Therefore, we identified the electron and muon lepton fractions with
If instead ρsim < 1014 g cm−3, we imposed
In accordance with our assumptions, Yl, τ = 0 everywhere and at any time. We note that the proton fraction (which in the simulation is equal to 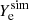 ) is now larger than
) is now larger than  since
since 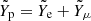 .
.
Given the simulation energy esim, if ρsim > 1014 g cm−3, we computed the total internal energy density of each fluid element as
while if ρsim < 1014 g cm−3, we computed
The terms proportional to 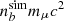 correspond to the rest mass energy density of the muons already present in the two cold NSs.
correspond to the rest mass energy density of the muons already present in the two cold NSs.
We imposed 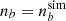 , and we solved the system
, and we solved the system
with respect to (T, Ye, Yμ), where 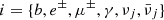 and j = {e, μ, τ}, to find the equilibrium configuration in the presence of (anti)muons and trapped neutrinos. The (anti-)neutrino fractions, Yν, and energies, eν, are defined in Sect. 3.2.3. We note that the condition on the tauon lepton number, Yl, τ = 0, is automatically satisfied in the absence of physical tauons and by the resulting ηντ = 0 assumption. Nevertheless, the contribution of tauon (anti-)neutrinos was taken into account in the calculation of the total energy and pressure.
and j = {e, μ, τ}, to find the equilibrium configuration in the presence of (anti)muons and trapped neutrinos. The (anti-)neutrino fractions, Yν, and energies, eν, are defined in Sect. 3.2.3. We note that the condition on the tauon lepton number, Yl, τ = 0, is automatically satisfied in the absence of physical tauons and by the resulting ηντ = 0 assumption. Nevertheless, the contribution of tauon (anti-)neutrinos was taken into account in the calculation of the total energy and pressure.
We computed all the other thermodynamic variables, such as fractions of trapped neutrinos, chemical potentials, and pressures as functions of (nb, T, Ye, Yμ), as prescribed in Sect. 3.2.
We note that in our procedure, we did not prescribe any time evolution. Rather, we post-processed each available time snapshot of the original simulation in the interval ∼5 − 15 ms after merger.
3.3.3. Limits of validity
Our post-processing analysis allowed us to compute, a posteriori, the thermodynamics of the merger aftermath taking into account the presence of muons and trapped neutrinos. We note that since there are no muons nor any explicit neutrinos in the original simulations, the definition of Yl, e, Yl, μ, and etot based on the simulation outcome cannot be done in a unique and fully consistent way. The choice described in the previous paragraph has the advantage of including the contribution given by the muons already present in the cold NSs. However, it relies on the assumption that the merger dynamics and esim, once corrected for the muons rest mass energy, are not significantly altered by them. To bracket the uncertainties due to this choice, in Appendix A, we discuss our results for a different choice of Yl, e, Yl, μ, and etot where the initial muon fraction from the cold NSs is neglected.
In our modelling of neutrinos, we assumed that above ρlim, e, there is a full Fermi-Dirac distribution of trapped neutrinos. However, neutrinos with energy smaller than 10 − 20 MeV were not expected to be in equilibrium with matter in this density regime. Moreover, from Eq. (12) it follows that the diffusion timescale of neutrinos with energy Eν ∼ 15 MeV becomes comparable to Δt ∼ 10 ms around ρ ∼ 1012 g cm−3. For this reason, even though we applied our post-processing procedure in the density domain ρ > ρlim, e, we restricted our analysis of the results to ρ > 1013 g cm−3, where the assumption of neutrino trapping and weak equilibrium is robust, being tdiff ≫ tdyn, and the post-processing approach is more reliable, being tdiff ≫ Δt. We also note that our modelling of the trapped neutrino component closely follows the one used by Perego et al. (2019). Recent numerical results obtained by including neutrino transport through a grey M1 moment scheme in BNS merger simulations (Zappa et al. 2023) are very consistent with the outcome of the post-processing analysis of Perego et al. (2019).
Finally, we highlight that in our procedure, the population of anti-muons is given by a Fermi-Dirac distribution in thermal equilibrium. Therefore, anti-muons arise as a thermal tail at a high enough temperature.
4. The fraction of muons in the remnant
We started our post-processing analysis from the simulation (BLh, 1.00). In Fig. 3, we show the fractions of μ±, νμ, and 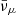 as well as the muon chemical potential approximately 5 ms after merger. The fraction of muons, Yμ−, is ∼0.01 − 0.07 in the high-density region characterised by ρ > 1014 g cm−3, while it decreases down to ∼10−3 − 10−2 at the lower density ρ ∼ 1013 − 1014 g cm−3. By computing the difference
as well as the muon chemical potential approximately 5 ms after merger. The fraction of muons, Yμ−, is ∼0.01 − 0.07 in the high-density region characterised by ρ > 1014 g cm−3, while it decreases down to ∼10−3 − 10−2 at the lower density ρ ∼ 1013 − 1014 g cm−3. By computing the difference 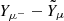 (upper-right panel of Fig. 3 ), we deduced that the bulk of muons comes from the two cold NSs. This result is consistent with the hypothesis of our post-processing procedure (see Sect. 3.3.1). However, a fraction of the muons was created during the merger, corresponding to ∼10−3 − 10−2. Muon creation became enhanced in correspondence to the hot spots where kBTsim ≳ 50 MeV (see the second panel of Fig. 1) and at high density, that is, above 1015 g cm−3. By inspecting the change in temperature and particle fractions
(upper-right panel of Fig. 3 ), we deduced that the bulk of muons comes from the two cold NSs. This result is consistent with the hypothesis of our post-processing procedure (see Sect. 3.3.1). However, a fraction of the muons was created during the merger, corresponding to ∼10−3 − 10−2. Muon creation became enhanced in correspondence to the hot spots where kBTsim ≳ 50 MeV (see the second panel of Fig. 1) and at high density, that is, above 1015 g cm−3. By inspecting the change in temperature and particle fractions
 |
Fig. 3. Particle fractions and chemical potential in the muon flavour sector computed by post-processing the simulation (BLh, 1.00) at 4.6 ms after merger. In the upper panels, we show the fraction of μ− (left), the fraction of μ+ (centre), and the difference between the muon fraction and the one inherited from the cold NSs, that is, |
where T and Yi result from post-processing calculations, while Tsim and 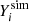 are read from the simulation, we could guess which were the processes more likely to be involved in muon creation. In the hot spots, both muons and anti-muons were produced, and the fraction of newly created muons Yμ− ∼ 10−2 exceeded the fraction of anti-muons Yμ+ ∼ 10−3 (see Fig. 3, upper-centre and right panels). At the same time, we observed ΔT < 0, ΔYn < 0 and ΔYe− > 0. We concluded that, on the one hand, thermal processes drive the creation of μ± pairs at the expense of the system’s internal energy, and on the other hand, the reduction in the degeneracy of muons due to the high temperature (see Fig. 3, lower-right panel) favours the conversion of n into p + μ−, further enhancing the production of μ−. In addition, we found an enhancement in the creation of e± pairs and e−, but the amount of newly created μ− systematically exceeded that of the newly created e−. In the core of the remnant, the density of fluid elements was enhanced by matter compression, and μ− as well as e− were created at the expense of the neutrons’ degeneracy (ΔYn < 0). Finally, at a lower density, ρ < 1014 g cm−3, the initial muon fraction from cold, decompressing NSs matter was almost entirely converted into muon neutrinos. We note that the values of Yμ− are stable in the time domain of our analysis.
are read from the simulation, we could guess which were the processes more likely to be involved in muon creation. In the hot spots, both muons and anti-muons were produced, and the fraction of newly created muons Yμ− ∼ 10−2 exceeded the fraction of anti-muons Yμ+ ∼ 10−3 (see Fig. 3, upper-centre and right panels). At the same time, we observed ΔT < 0, ΔYn < 0 and ΔYe− > 0. We concluded that, on the one hand, thermal processes drive the creation of μ± pairs at the expense of the system’s internal energy, and on the other hand, the reduction in the degeneracy of muons due to the high temperature (see Fig. 3, lower-right panel) favours the conversion of n into p + μ−, further enhancing the production of μ−. In addition, we found an enhancement in the creation of e± pairs and e−, but the amount of newly created μ− systematically exceeded that of the newly created e−. In the core of the remnant, the density of fluid elements was enhanced by matter compression, and μ− as well as e− were created at the expense of the neutrons’ degeneracy (ΔYn < 0). Finally, at a lower density, ρ < 1014 g cm−3, the initial muon fraction from cold, decompressing NSs matter was almost entirely converted into muon neutrinos. We note that the values of Yμ− are stable in the time domain of our analysis.
Next, we compare the results obtained from the simulation (BLh, 1.00) with the ones from (DD2, 1.00) and (SFHo, 1.00). In the latter cases, muons were also present in the full-density region, ρ > 1013 g cm−3. However, the muon fraction Yμ− ∼ 10−3 − 0.05 presented a slightly smaller maximum with respect to (BLh, 1.00). This is expected since, as discussed in Sect. 3.3.1, DD2 and SFHo predict a smaller muon fraction for cold nuclear matter in weak equilibrium (see also Fig. 2). The amount of muons created during the merger (i.e. 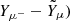 is comparable for the three simulations and correlates in the same way with ΔT and ΔYi, defined in Eq. (35). The amount of μ− and
is comparable for the three simulations and correlates in the same way with ΔT and ΔYi, defined in Eq. (35). The amount of μ− and 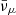 produced in the centre of the remnant, however, was smaller for (DD2, 1.00) and (SFHo, 1.00) with respect to (BLh, 1.00), with a difference that can reach one order of magnitude if we compare (DD2, 1.00) to (BLh, 1.00). As in the case of the cold, neutrinoless weak equilibrium conditions presented in Fig. 2, such a difference between the BLh EOS and the DD2 EOS is mostly due to the larger slope of the symmetry energy in the former case. Additionally, the fraction of μ− was on average slightly larger in (SFHo, 1.00) than in (DD2, 1.00) because the softer EOS SFHo exhibits larger temperatures and densities than the stiffer DD2 EOS (see e.g. Foucart et al. 2016a; Sekiguchi et al. 2016; Radice et al. 2018a; Perego et al. 2019).
produced in the centre of the remnant, however, was smaller for (DD2, 1.00) and (SFHo, 1.00) with respect to (BLh, 1.00), with a difference that can reach one order of magnitude if we compare (DD2, 1.00) to (BLh, 1.00). As in the case of the cold, neutrinoless weak equilibrium conditions presented in Fig. 2, such a difference between the BLh EOS and the DD2 EOS is mostly due to the larger slope of the symmetry energy in the former case. Additionally, the fraction of μ− was on average slightly larger in (SFHo, 1.00) than in (DD2, 1.00) because the softer EOS SFHo exhibits larger temperatures and densities than the stiffer DD2 EOS (see e.g. Foucart et al. 2016a; Sekiguchi et al. 2016; Radice et al. 2018a; Perego et al. 2019).
To assess the relevance of muons in the merger remnants, we compared the equilibrium net muon fraction obtained in our post-processing procedure with the equilibrium net electron fraction by analysing the ratio Yμ/Ye, as shown in Fig. 4. We note that for all the simulations, the net muon fraction was at least 30%−40% of the net electron fraction. The ratio Yμ/Ye was the largest for (BLh, 1.00), where it can reach a maximum of approximately 0.7, while it reached up to 0.6 and 0.5 for (SFHo, 1.00) and (DD2, 1.00), respectively. We stress, however, that due to the large mass difference between electrons and muons, the amount of both electrons and positrons was largely increased where the temperature was high such that Ye− ≳ Ye+ and Ye = Ye− − Ye+ ∼ 0.1, while Yμ− ≫ Yμ+ and Yμ ≈ Yμ−.
 |
Fig. 4. Ratio of the net muon fraction over the net electron fraction, Yμ/Ye, on the equatorial plane obtained by post-processing simulations (BLh, 1.00) (upper left), (BLh, 1.43) (upper right), (DD2, 1.00) (lower left), and (SFHo, 1.00) (lower right) at 5 − 6 ms after merger. As in Fig. 1, the black lines mark isodensity contours. |
Finally, we post-processed data from the simulation (BLh, 1.43), which had a significantly larger mass asymmetry. We did not observe notable differences while comparing the maximum value of Yμ/Ye in (BLh, 1.00) and (BLh, 1.43). However, (BLh, 1.43) exhibited a more extended spatial region where Yμ/Ye ∼ 0.5 − 0.6 (see Fig. 4). This region is characterised by a large temperature, ≳40 MeV, because it embeds the core of the secondary NS, which was broadened and strongly heated by compression and shocks during the merger.
5. Trapped neutrino properties
In Figs. 3 and 5, we show all flavour (anti-)neutrino abundances as well as the chemical potentials of baryons and massive leptons computed by post-processing the simulation (BLh, 1.00) at approximately 5 ms after merger. Trapped gases of (anti-)neutrinos were present in the full-density regime of our analysis, ρ > 1013 g cm−3, but the abundances and the species hierarchy varied according to the system density and temperature.
 |
Fig. 5. Fractions of νe, |
In the very-high-density regime, ρ ≳ 7 × 1014 g cm−3, νe and νμ were suppressed (Yνe, μ < 10−4), while  and
and 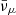 had typical fractions
had typical fractions 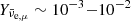 , with
, with  being slightly more abundant than
being slightly more abundant than 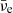 . We note that the excess of
. We note that the excess of 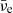 and
and 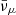 exactly compensates for the amount of newly created electrons and muons (see the discussion in the previous section). Among the remaining neutrino species, ντ and
exactly compensates for the amount of newly created electrons and muons (see the discussion in the previous section). Among the remaining neutrino species, ντ and 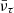 were the most abundant, with a fraction ∼10−4 − 10−3.
were the most abundant, with a fraction ∼10−4 − 10−3.
When ρ ∼ 2 − 6 × 1014 g cm−3, the fractions of neutrinos increased up to ∼10−3, but electron and muon anti-neutrinos still remained the most abundant neutrino species, with 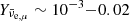 . All the (anti-)neutrino abundances peaked in the hot spots. However, muon production dominated in this density and temperature regime (see the discussion in the previous section) so that the
. All the (anti-)neutrino abundances peaked in the hot spots. However, muon production dominated in this density and temperature regime (see the discussion in the previous section) so that the 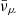 species was the most abundant, followed by
species was the most abundant, followed by 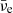 and then ντ, νe, and νμ, in that order.
and then ντ, νe, and νμ, in that order.
At the lower density, ρ ∼ 1013 − 1014 g cm−3, all neutrinos and anti-neutrinos were present in warm matter streams characterised by kBTsim ∼ 25 MeV, with order of magnitude fractions ∼10−2, and the 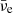 species dominated, followed in order by
species dominated, followed in order by 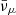 , ντ, νμ, and νe. On the contrary, in cold matter streams with kBTsim ∼ 10 − 15 MeV, anti-neutrinos were suppressed, and the νμ species dominated, with a maximum fraction of ∼0.01, followed by νe, with Yνe ≳ 10−3, and ντ, with Yντ ∼ 10−4.
, ντ, νμ, and νe. On the contrary, in cold matter streams with kBTsim ∼ 10 − 15 MeV, anti-neutrinos were suppressed, and the νμ species dominated, with a maximum fraction of ∼0.01, followed by νe, with Yνe ≳ 10−3, and ντ, with Yντ ∼ 10−4.
The different abundances and the hierarchy reflect the behaviour of the neutrino chemical potentials at equilibrium (see Eq. (26)), which ultimately depend on the EOS both directly, through the nuclear interaction, and indirectly, through the different thermodynamic conditions realised in the remnant. The regions where anti-neutrinos dominated over neutrinos were characterised by a higher density and a higher value of the neutron chemical potential μn, which exceeded μp + μl− with l = {e, μ}, as we deduced from Figs. 3 and 5. In such regions, the density was increased by matter compression, and the fraction of protons increased as well since the lepton number was fixed. This coincided with the enhancement of electrons and muon production at the expense of free neutrons (see discussion in Sect. 4), and the equilibrium condition Eq. (26) enforced the creation of the corresponding anti-neutrinos. In contrast, neutrinos dominated in relatively cold matter streams in the outer layers, where the proton chemical potential increased (see Fig. 5) so that μp + μl− > μn. The enhancement of μp is indeed correlated with the decrease of both density and temperature experienced by the expanding matter in such regions. This is illustrated in Fig. 6, where we plotted μp and μn in the ρ − T plane for Yp fixed to a relevant value for the analysis (i.e. Yp = 0.08). We note that μp started increasing when ρ ≲ 1014 g cm−3 and kBT ≲ 15 MeV, while μn decreased in the same ρ − T region. This is because when ρ ≲ 1014 g cm−3 and kBT ≲ 15 MeV, nucleons start clustering in nuclei so that the chemical potential of free protons is enhanced and the amount of free protons drops (see e.g. Fig. 8 of Hempel & Schaffner-Bielich 2010). At a fixed lepton fraction and at equilibrium, this results in a conversion of electrons and muons into the corresponding neutrinos.
 |
Fig. 6. Proton and neutron chemical potentials (rest mass subtracted) of BLh in the density-temperature plane at fixed Yp = 0.08. The proton fraction Yp = 0.08 is the equilibrium proton fraction at 4.6 ms after merger around the point x = 0.64 km, y = 12.76 km, z = 0 km, where ρ ∼ 5 × 1013 g cm−3, Tsim ∼ 10 MeV, and neutrinos dominate, while anti-neutrinos are suppressed (see also Figs. 1, 3 and 5). We notice that the colour bars are scaled differently. |
The properties of the neutrino gases are better characterised in terms of their degeneracy parameters. In Fig. 7, we show the degeneracy parameter of electron and muon neutrinos computed for three snapshots of (BLh, 1.00): ∼5 ms, ∼7 ms, and ∼12 ms after merger. The spatial distribution of ηνe and ηνμ clearly indicates the presence of trapped degenerate gases of the 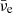 and
and 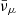 species in the remnant core and of the νe and νμ species in the outer layers. In this latter region, the trapped gas of electron neutrinos is characterised by a degeneracy parameter ηνe ranging between three and six, while in the remnant core degenerate electron antineutrinos have
species in the remnant core and of the νe and νμ species in the outer layers. In this latter region, the trapped gas of electron neutrinos is characterised by a degeneracy parameter ηνe ranging between three and six, while in the remnant core degenerate electron antineutrinos have 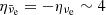 . The degenerate gases of muonic neutrinos (in the outer layers) and muonic antineutrinos (in the core) exhibited the same qualitative behaviour as the νe and
. The degenerate gases of muonic neutrinos (in the outer layers) and muonic antineutrinos (in the core) exhibited the same qualitative behaviour as the νe and  species, with a degeneracy parameter ηνμ ranging between -4 and 9 so that these muon (anti-)neutrino gases were slightly more degenerate than the electron ones.
species, with a degeneracy parameter ηνμ ranging between -4 and 9 so that these muon (anti-)neutrino gases were slightly more degenerate than the electron ones.
 |
Fig. 7. Degeneracy parameter of νe (first row) and νμ (lower row) on the equatorial plane obtained by post-processing the simulation (BLh, 1.00). Three different time slices are shown corresponding from left to right to 4.6 ms, 6.7 ms, and 11.8 ms after merger. As in Fig. 1, the black lines mark the isodensity contours as in Fig. 1. |
The spatial distribution of the abundances as well as the neutrino hierarchy in (DD2, 1.00) and (SFHo, 1.00) are fully analogous to the ones of (BLh, 1.00). Accordingly, we can analyse the differences among the three EOSs by inspecting the degeneracy parameters. Similarly to (BLh, 1.00),  and
and 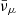 formed degenerate trapped gases in the remnant core, while νe and νμ formed degenerate trapped gases in the cold matter streams of the outer layers. The degeneracy parameter of electron neutrinos, ηνe, ranged between −2 and 6 for both (DD2, 1.00) and (SFHo, 1.00), while in the case of muonic neutrinos, we found ηνμ ranging between −2 and 11 for (DD2, 1.00) and between −2 and 12 for (SFHo, 1.00). In general, the gases of
formed degenerate trapped gases in the remnant core, while νe and νμ formed degenerate trapped gases in the cold matter streams of the outer layers. The degeneracy parameter of electron neutrinos, ηνe, ranged between −2 and 6 for both (DD2, 1.00) and (SFHo, 1.00), while in the case of muonic neutrinos, we found ηνμ ranging between −2 and 11 for (DD2, 1.00) and between −2 and 12 for (SFHo, 1.00). In general, the gases of  and
and 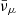 are more degenerate for (BLh, 1.00) than for (DD2, 1.00) and (SFHo, 1.00). The main cause of this resides in the differences among the neutron and the proton chemical potentials, which depend on the selected EOS and on the values of ρ, T, and Yp in the remnant core. In particular, the average values of
are more degenerate for (BLh, 1.00) than for (DD2, 1.00) and (SFHo, 1.00). The main cause of this resides in the differences among the neutron and the proton chemical potentials, which depend on the selected EOS and on the values of ρ, T, and Yp in the remnant core. In particular, the average values of 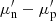 (rest masses subtracted) at a radius of approximately 3 km from the centre of the remnants correspond to ∼200 MeV for DD2, ∼245 MeV for SFHo, and ∼325 MeV for BLh. Hence, the degeneracy of the trapped anti-neutrinos is comparable for DD2 and SFHo but quite different for BLh (see Eq. (26)). In this sense, anti-neutrino trapping in the core of the remnant shows a significant and non-trivial dependence on the EOS through the nucleons’ chemical potentials. If the merger dynamics are significantly affected, this characteristic could become a probe for investigating matter properties in the high-density regime.
(rest masses subtracted) at a radius of approximately 3 km from the centre of the remnants correspond to ∼200 MeV for DD2, ∼245 MeV for SFHo, and ∼325 MeV for BLh. Hence, the degeneracy of the trapped anti-neutrinos is comparable for DD2 and SFHo but quite different for BLh (see Eq. (26)). In this sense, anti-neutrino trapping in the core of the remnant shows a significant and non-trivial dependence on the EOS through the nucleons’ chemical potentials. If the merger dynamics are significantly affected, this characteristic could become a probe for investigating matter properties in the high-density regime.
Finally, by post-processing the results of the simulation (BLh, 1.43), we observed that the degeneracy of the trapped component of anti-neutrinos was the same as in (BLh, 1.00). However, the trapped neutrino gases at ρ ∼ 1013 − 1014 g cm−3 were less degenerate for q = 1.43, displaying ηνe ∼ 4 and ηνμ ∼ 7. This feature depends mostly on the temperature in the density region 1013 − 1014 g cm−3, which is systematically larger in the case of q = 1.43 compared to q = 1.00.
To test the validity of the approximations used in Sect. 2 and to further characterise the properties of neutrinos trapped inside the remnant in the presence of muons for the first time, we computed the neutrino mean energies, Eν, in post-processing. In Fig. 8, we show the spatial distribution of Eν for the remnant of simulation (BLh, 1.00) at approximately 5 ms after merger. In the density region ρ > 1013 g cm−3, we found Eν > 30 MeV for all flavour neutrinos, unless a certain flavour was suppressed in a portion of space. Electron and muon anti-neutrinos were the most energetic, with 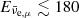 MeV. Then, for ντ we found Eντ ≲ 170 MeV, while νe and νμ were the least energetic, with Eνe, μ ≲ 160 MeV. In the case of (DD2, 1.00), the values of Eν closely followed the ones discussed for (BLh, 1.00). However, (SFHo, 1.00) exhibited larger energies for all flavour neutrinos, with Eνe, μ, τ ≲ 180 MeV and
MeV. Then, for ντ we found Eντ ≲ 170 MeV, while νe and νμ were the least energetic, with Eνe, μ ≲ 160 MeV. In the case of (DD2, 1.00), the values of Eν closely followed the ones discussed for (BLh, 1.00). However, (SFHo, 1.00) exhibited larger energies for all flavour neutrinos, with Eνe, μ, τ ≲ 180 MeV and  MeV, due to larger remnant temperatures.
MeV, due to larger remnant temperatures.
 |
Fig. 8. Mean energy Eν of trapped neutrinos on the equatorial plane computed by post-processing simulation (BLh, 1.00) at 4.6 ms after merger. As in Fig. 1., the black lines mark isodensity contours. |
6. Changes in the remnant pressure
In this section, we investigate how the result of the post-processing, which consistently included muons and trapped neutrinos, modifies the pressure of the remnant with respect to the values extracted from the original simulation. In Fig. 9, we show the ratio between the pressure computed in post-processing and the simulation pressure, P/Psim, for (BLh, 1.00), (DD2, 1.00), and (SFHo, 1.00). Similar to Sect. 4 and Sect. 5, we start our discussion with the (BLh, 1.00) simulation. In the time domain of our analysis, the equilibrium pressure computed in post-processing decreased by 6 − 7% in the region characterised by ρ ∼ 5 × 1014 g cm−3, while it increased by a maximum of 3% around 10 km from the centre at ρ ∼ 1014 g cm−3 compared to the pressure from the original simulation.
 |
Fig. 9. Pressure ratio P/Psim for (BLh, 1.00) (left), (DD2, 1.00) (centre), and (SFHo, 1.00) (right) where P is obtained in post-processing, while Psim is the simulation pressure. For (BLh, 1.00), we explicitly mark the maximum P/Psim ∼ 1.03 (white circle) and the minimum P/Psim ∼ 0.94 (white cross) at ρ > 1014 g cm−3. As in Fig. 1., the black lines mark isodensity contours. |
To understand which processes are responsible for the changes in pressure, we analysed the role of each particle species in detail. In Fig. 10, we have plotted the difference in pressures and particle fractions after muons and neutrinos were introduced
 |
Fig. 10. Change of particle pressure and fractions obtained in correspondence to the space-time coordinates explicitly marked in the left panel of Fig. 9 and corresponding to P/Psim = 0.94 (upper row) and P/Psim = 1.03 (lower row). The bar plots in blue (left) give the difference between the equilibrium pressure computed in post-processing and in the simulation, |
for all the particle species at two representative points inside the simulations, explicitly marked in Fig. 9 and corresponding to P/Psim ∼ 0.94 and P/Psim ∼ 1.03, respectively. The drop in pressure was localised inside a hot spot at kBTsim ∼ 55 MeV, and it was mainly due to a decrease of baryonic pressure. Once muons were included in the microphysics, the system reached a new equilibrium characterised by a smaller neutron fraction; larger proton, electron, and muon fractions; and a smaller temperature (see also discussion in Sect. 4). The decrease in both the neutron fraction and of the temperature lowered the baryonic pressure, and the pressure provided by muons and trapped anti-neutrinos was not large enough to compensate. Accordingly, the total pressure also decreased. This effect is strongly correlated with the enhancement in the production of massive leptons and (anti-)neutrinos at high temperatures. An increase of pressure occurred at a lower initial temperature, kBTsim ∼ 15 MeV, and it was correlated with the inclusion of muons from the cold NSs. As shown in Fig. 2, including muons in cold neutrinoless β-equilibrium implies lowering the initial electron and neutron fraction in favour of the muon and proton fractions. Therefore, the pressure of the system increased because some relativistic particles (electrons) were replaced with non-relativistic particles (muons). An additional contribution came from the increase of the baryon pressure 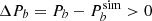 , where Pb is computed in post-processing while
, where Pb is computed in post-processing while 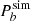 is read from the simulation outcome. In general, we would expect ΔPb < 0 since the neutron fraction was reduced. However, we observed a small increase of temperature ΔT = 1.3 MeV, which was large enough to result in ΔPb > 0, as shown in the colour-coded plot in the second row of Fig. 10. We note that the increase in temperature was expected because it is the only way the system could simultaneously reduce the number of neutrons and electrons, which are highly degenerate at kBTsim ∼ 15 MeV and at a fixed internal energy. Interestingly, adding new d.o.f. without supplementary repulsive forces did not simply result in a softening of the EOS, as we would have expected, because of the role played by the equilibrium temperature.
is read from the simulation outcome. In general, we would expect ΔPb < 0 since the neutron fraction was reduced. However, we observed a small increase of temperature ΔT = 1.3 MeV, which was large enough to result in ΔPb > 0, as shown in the colour-coded plot in the second row of Fig. 10. We note that the increase in temperature was expected because it is the only way the system could simultaneously reduce the number of neutrons and electrons, which are highly degenerate at kBTsim ∼ 15 MeV and at a fixed internal energy. Interestingly, adding new d.o.f. without supplementary repulsive forces did not simply result in a softening of the EOS, as we would have expected, because of the role played by the equilibrium temperature.
The causes of the changes in pressure in (DD2, 1.00) and (SFHo, 1.00) are the same as in (BLh, 1.00). From our analysis up to 15 ms after merger, we found that P/Psim ranges from 0.94 to 1.05 for (DD2, 1.00) and from 0.93 to 1.04 for (SFHo, 1.00). As shown in Fig. 9, (DD2, 1.00) was subjected mostly to a pressure increase, while (SFHo, 1.00) exhibited a pressure increase in the region closer to the core and a pressure decrease in the outer shells. The amount of pressure decrease is comparable to the one found in Perego et al. (2019), while the pressure increase is a new prediction.
Pressure modifications correlate in a complex way with other thermodynamical variables, such as density, electron and muon fractions, temperature, and chemical potentials. However, a more important role is played by temperature. A close inspection of the distribution of P/Psim in the  space revealed that for all the EOSs, the pressure decrease was more frequent at larger Tsim. This is because electrons and muons are less degenerate, so the of conversion neutrons into protons is favoured and the baryonic pressure reduces to a greater extent. Regarding the pressure increase, it was frequent at smaller kBTsim < 20 MeV because of the dominant role played by the muons coming from the NSs in colder temperature regimes. We concluded that the remnant formed in (DD2, 1.00) exhibits mostly a pressure increase because its temperature is, on average, smaller compared to (BLh, 1.00) and (SFHo, 1.00).
space revealed that for all the EOSs, the pressure decrease was more frequent at larger Tsim. This is because electrons and muons are less degenerate, so the of conversion neutrons into protons is favoured and the baryonic pressure reduces to a greater extent. Regarding the pressure increase, it was frequent at smaller kBTsim < 20 MeV because of the dominant role played by the muons coming from the NSs in colder temperature regimes. We concluded that the remnant formed in (DD2, 1.00) exhibits mostly a pressure increase because its temperature is, on average, smaller compared to (BLh, 1.00) and (SFHo, 1.00).
We conclude this section by analysing how the pressure is modified in the case of an asymmetric binary mass ratio. If q = 1.43, then the ratio P/Psim ranges in the interval 0.93 − 1.05, showing a pressure decrease compatible with the case where q = 1.00 but has a pressure increase that is significantly larger. This behaviour depends mostly on the difference between the electron fractions in the two simulations. In the case of q = 1.43, the regions with the highest P/Psim also have a larger  compared to q = 1.00 and as a consequence a larger
compared to q = 1.00 and as a consequence a larger 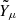 (see Fig. 2). Since the pressure increase is mainly driven by the muon fraction coming from the cold NSs, a larger
(see Fig. 2). Since the pressure increase is mainly driven by the muon fraction coming from the cold NSs, a larger  results in a larger P/Psim. In Fig. 11, we show the comparison between the pressure ratios for q = 1.00 and q = 1.43 at approximately 7 ms after merger. We found that the spatial distribution of P/Psim for q = 1.43 is quite asymmetric compared to q = 1.00 in the full-time domain of our analysis. In this case, the pressure decrease is localised in the core of the secondary NS, which is strongly heated by the shocks developing at the contact surface. The pressure increases in the cold external layers of the secondary NS, which are stripped away during the dynamical evolution without being significantly heated.
results in a larger P/Psim. In Fig. 11, we show the comparison between the pressure ratios for q = 1.00 and q = 1.43 at approximately 7 ms after merger. We found that the spatial distribution of P/Psim for q = 1.43 is quite asymmetric compared to q = 1.00 in the full-time domain of our analysis. In this case, the pressure decrease is localised in the core of the secondary NS, which is strongly heated by the shocks developing at the contact surface. The pressure increases in the cold external layers of the secondary NS, which are stripped away during the dynamical evolution without being significantly heated.
 |
Fig. 11. Pressure ratio P/Psim computed by post-processing (BLh, 1.00) (top) and (BLh, 1.43) (bottom) at 6.7 ms after merger. As in Fig. 1, the black lines mark the isodensity contours. |
7. Discussion
Based on our results, in this section we speculate about the possible consequences for the evolution of the remnant and the emitted neutrinos. The fraction of muons is enhanced at high temperatures. Therefore, muons are expected to play a more important role in BNS mergers characterised by larger masses and in the case of soft EOSs producing more compact NSs. Such high temperatures develop mostly at the contact interface between the two fusing cores during the first milliseconds after a merger. In addition, CC reactions involving μ±, νμ, and  provide a new source of opacity for muonic (anti-)neutrinos, as these reactions influence their diffusion. The neutrino surfaces of
provide a new source of opacity for muonic (anti-)neutrinos, as these reactions influence their diffusion. The neutrino surfaces of 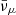 and νμ are expected to split in a manner similar to νe and
and νμ are expected to split in a manner similar to νe and  (Endrizzi et al. 2020), with the surface of
(Endrizzi et al. 2020), with the surface of 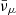 located at a larger rest mass density compared to νμ. Hence, the luminosity and the spectrum of the emitted
located at a larger rest mass density compared to νμ. Hence, the luminosity and the spectrum of the emitted 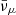 will deviate from that of νμ, with possible implications for the emitted spectrum and for the neutrino oscillations (see Fischer et al. 2020 for luminosity and spectra of νμ and
will deviate from that of νμ, with possible implications for the emitted spectrum and for the neutrino oscillations (see Fischer et al. 2020 for luminosity and spectra of νμ and 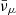 in CCSN). Furthermore, the formation of trapped degenerate gases of νe and νμ in the outer layers can favour the development of neutrino-bursts during the dynamical evolution, similar to the case of CCSN (Fischer et al. 2020), when dense, hot matter expands in the forming disc and becomes transparent. The change in pressure induced by muons and trapped neutrinos can change the time of the collapse of the remnant and affect the dynamical mass ejection. In particular, in (DD2, 1.00) and (SFHo, 1.00), we observed a diffuse pressure increase near the core (see discussion in Sect. 6), which can possibly postpone the collapse of the remnant. For (BLh, 1.00), the drop in pressure at high density induces a softening that could speed up the collapse of more massive binaries, while the larger pressure at smaller densities could affect the low-density dynamics, including the ejecta production, the disc formation, and the stability of the remnant produced in low mass BNS mergers. In Sect. 6, we established a correlation between P/Psim and Tsim, pointing out that P/Psim > 1 (P/Psim < 1) when kBTsim is below (above) ∼20 MeV. This feature could induce positive feedback that amplifies pressure variations once muons and trapped neutrinos are included at the dynamical stage of the simulation. When the pressure decreases, the temperature of the more compressed system will increase, possibly triggering processes that lower the pressure even more. Nevertheless, when the pressure increases, the temperature of the expanded system will decrease, possibly favouring further pressure enhancement. However, feedback effects can be assessed only by including muons and trapped neutrinos in the dynamical evolution of the system. Moreover, the effect of pressure variations is, in general, non-trivial to predict. Indeed, pressure is one of the source terms in the Einstein equations and its significant increase could result in a faster collapse.
in CCSN). Furthermore, the formation of trapped degenerate gases of νe and νμ in the outer layers can favour the development of neutrino-bursts during the dynamical evolution, similar to the case of CCSN (Fischer et al. 2020), when dense, hot matter expands in the forming disc and becomes transparent. The change in pressure induced by muons and trapped neutrinos can change the time of the collapse of the remnant and affect the dynamical mass ejection. In particular, in (DD2, 1.00) and (SFHo, 1.00), we observed a diffuse pressure increase near the core (see discussion in Sect. 6), which can possibly postpone the collapse of the remnant. For (BLh, 1.00), the drop in pressure at high density induces a softening that could speed up the collapse of more massive binaries, while the larger pressure at smaller densities could affect the low-density dynamics, including the ejecta production, the disc formation, and the stability of the remnant produced in low mass BNS mergers. In Sect. 6, we established a correlation between P/Psim and Tsim, pointing out that P/Psim > 1 (P/Psim < 1) when kBTsim is below (above) ∼20 MeV. This feature could induce positive feedback that amplifies pressure variations once muons and trapped neutrinos are included at the dynamical stage of the simulation. When the pressure decreases, the temperature of the more compressed system will increase, possibly triggering processes that lower the pressure even more. Nevertheless, when the pressure increases, the temperature of the expanded system will decrease, possibly favouring further pressure enhancement. However, feedback effects can be assessed only by including muons and trapped neutrinos in the dynamical evolution of the system. Moreover, the effect of pressure variations is, in general, non-trivial to predict. Indeed, pressure is one of the source terms in the Einstein equations and its significant increase could result in a faster collapse.
It is interesting to compare our results to the findings from CCSN simulations that include muons (Bollig et al. 2017; Fischer et al. 2020). Our estimate of Yμ exceeds the muon fraction in the proximity of the core bounce by one order of magnitude (Fischer et al. 2020), while it is compatible with Yμ in the late post-bounce phase (Bollig et al. 2017). This is because in CCSNe, matter density and temperature increase after the core bounce, while Ye decreases, thus approaching the regime of our analysis. Since temperatures are significantly larger in BNS mergers than in CCSNe, thermal processes could contribute more significantly to the creation of μ±, while they are negligible in CCSNe (Bollig et al. 2017; Guo et al. 2020; Fischer et al. 2020). However, the enhancement of the net muon fraction, Yμ, with the temperature is in agreement with the results of Bollig et al. (2017), Fischer et al. (2020).
We note that while the inclusion of muons always implies a softening of the EOS in the post-bounce phase in CCSNe (Bollig et al. 2017; Fischer et al. 2020), in our case, the pressure can either increase or decrease with respect to the case where muons are neglected from the beginning. This difference is expected since in BNS mergers, the pressure increase obtained in our analysis is driven by the muons already present in the two cold NSs (see Sect. 6). Notably, muons are not present in stellar iron cores before a collapse.
Next, we relate our results to state-of-the-art BNS merger simulations that include trapped neutrinos either in post-processing (Perego et al. 2019) or through an M1 scheme (e.g. Foucart et al. 2016a; Radice et al. 2022; Zappa et al. 2023). The neutrino hierarchy resulting from our analysis is in disagreement with these works. In these previous papers, matter is dominated by  and followed by heavy-lepton neutrinos and then νe, whereas we found that
and followed by heavy-lepton neutrinos and then νe, whereas we found that  are the most abundant, followed in order by
are the most abundant, followed in order by 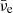 ,
, 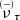 , νe, and νμ. According to Perego et al. (2019), the fluid pressure decreases after the inclusion of trapped neutrinos, but we show that it can also increase in some regions of the remnant. This is an indirect confirmation that the enhancement of pressure is mainly due to muons. Nonetheless, our estimate of the pressure decrease is compatible with the one computed in Perego et al. (2019).
, νe, and νμ. According to Perego et al. (2019), the fluid pressure decreases after the inclusion of trapped neutrinos, but we show that it can also increase in some regions of the remnant. This is an indirect confirmation that the enhancement of pressure is mainly due to muons. Nonetheless, our estimate of the pressure decrease is compatible with the one computed in Perego et al. (2019).
8. Conclusions
In this paper, we evaluated the contribution of muons in the post-merger remnant formed during BNS mergers as well as their impact on the trapped neutrino component during the first milliseconds after the merger. In particular, we considered a sample of numerical relativity simulations targeted at GW170817 that were performed using three different nuclear EOSs (BLh, DD2, and SFHo). Based on the remnant conditions, we estimated the abundances and the properties of muons and trapped neutrinos in post-processing, assuming weak and thermal equilibrium for rest mass densities in excess of 1013 g cm−3. We found that a non-negligible amount of muons is present in the remnant, and they significantly alter the neutrino hierarchy, favouring the production of muon anti-neutrinos. Moreover, the new equilibrium conditions modify the pressure inside the remnant in a non-trivial way with respect to the case in which muons and trapped neutrinos are neglected.
More specifically, we found that a significant amount of muons is present at baryon densities ρ > 1013 g cm−3 with a fraction Yμ− ∼ 10−3 − 0.07 for the BLh EOS and Yμ− ∼ 10−3 − 0.05 for the DD2 and SFHo EOSs. The net fraction of muons is between 30% and 50–70% of the net electron fraction, with a maximum depending on the nuclear EOS. The bulk of muons comes from the two cold NSs, while a fraction corresponding to 10−3 − 10−2 is created during the merger via conversion of neutrons into protons plus muons and thermal processes. Accordingly, muon production is enhanced in the high-density fusing cores and in the hot spots characterising the remnant structure during the first milliseconds after the merger.
The presence of muons modifies the flavour hierarchy of the trapped neutrino component. In the core, matter is dominated by anti-neutrinos, with 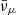 being the most abundant species. Immediately outside the core and in correspondence with the hot spots, gases of trapped neutrinos and anti-neutrinos coexist, but the
being the most abundant species. Immediately outside the core and in correspondence with the hot spots, gases of trapped neutrinos and anti-neutrinos coexist, but the 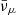 species still dominates, followed in order by
species still dominates, followed in order by 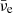 ,
, 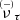 , νe, and νμ. In contrast, in the cold matter streams at ρ ∼ 1013 − 1014 g cm−3, anti-neutrinos are suppressed, while neutrinos dominate and the νμ species is the most abundant. Anti-neutrinos and neutrinos are degenerate in the core and in the cold matter streams, respectively. The level of degeneracy depends on the thermodynamical conditions of the remnant and on μn − μp. In particular, typical values of the degeneracy parameters of
, νe, and νμ. In contrast, in the cold matter streams at ρ ∼ 1013 − 1014 g cm−3, anti-neutrinos are suppressed, while neutrinos dominate and the νμ species is the most abundant. Anti-neutrinos and neutrinos are degenerate in the core and in the cold matter streams, respectively. The level of degeneracy depends on the thermodynamical conditions of the remnant and on μn − μp. In particular, typical values of the degeneracy parameters of 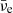 and
and 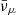 are
are 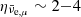 , with larger (smaller) values associated with larger (smaller) μn − μp. Therefore, the properties of trapped (anti-)neutrinos in BNS mergers have a non-trivial dependence on the properties of the EOS at densities well above n0.
, with larger (smaller) values associated with larger (smaller) μn − μp. Therefore, the properties of trapped (anti-)neutrinos in BNS mergers have a non-trivial dependence on the properties of the EOS at densities well above n0.
The presence of muons and trapped neutrinos affect the remnant pressure, whose value can decrease by 7% or increase by up to 5%, depending on the nuclear EOS, compared with the case in which they are neglected. The pressure drops mainly in the hot spots, where the processes driving muon production reduce the temperature and number of neutrons. The greater pressure mostly observed at low temperatures and high density is due to the muons coming from the cold NSs. This new result shows how adding a d.o.f. in the system microphysics does not always imply a decrease in pressure, as we could naively expect. Finally, we demonstrated that in asymmetric binaries, the pressure decrease is localised in the shocked core of the secondary NS, while the pressure increase is found in the cold outer layers of the secondary NS, which are stripped away by the primary NS.
Since the procedure to post-process the simulation data is not unique, in Appendix A we discuss the robustness of our results with respect to the arbitrary choices in our procedure. For example, we show that when neglecting muons inside the cold NSs before merger, the major results are the same as when the presence of muons in the inspiraling NSs is considered. The comparison with the first post-processing procedure emphasises that a significant muon contribution originates from the muons already present in the cold NSs.
Our work is nevertheless limited by the post-processing approach. To understand how muons really affect the merger and post-merger dynamics, it is necessary to implement a transport scheme that includes muons as an independent d.o.f.. Also, adding the rates of the reactions involved in muon production (see Sect. 2) would be important for estimating the effect of muons on the neutrino opacity and luminosity, as done in CCSN simulations (Guo et al. 2020; Fischer et al. 2020). Additionally, the role of pions coupling to muons and muonic (anti-)neutrinos should be considered while computing the mean free path of low energy νμ and  (Fore & Reddy 2020). We also highlight that in the description of NS matter, we have neglected the possible formation of hyperons (Oertel et al. 2012; Fortin et al. 2018) and/or that a deconfinement phase transition to quark matter may take place (Weissenborn et al. 2011; Klähn et al. 2013; Chatterjee & Vidaña 2016; Bombaci et al. 2016; Logoteta et al. 2019; Logoteta 2021). The inclusion of these additional d.o.f. will be the focus of future investigations.
(Fore & Reddy 2020). We also highlight that in the description of NS matter, we have neglected the possible formation of hyperons (Oertel et al. 2012; Fortin et al. 2018) and/or that a deconfinement phase transition to quark matter may take place (Weissenborn et al. 2011; Klähn et al. 2013; Chatterjee & Vidaña 2016; Bombaci et al. 2016; Logoteta et al. 2019; Logoteta 2021). The inclusion of these additional d.o.f. will be the focus of future investigations.
This work shows, for the first time, that muons have a discernible impact on the trapped neutrino component and possibly on the thermodynamics and dynamics of BNS mergers. Our results emphasise the need of including muons in future simulation modelling of the post-merger remnant of BNS mergers.
The corresponding EOS tables are publicly available from the CompOSE repository https://compose.obspm.fr/.
We note, however, that the dimensionless tidal deformability predicted by DD2 for GW170817-like events is > 800, which is in possible tension with constraints derived from GW170817 (e.g. Abbott et al. 2017a, 2019; Breschi et al. 2021).
We note that the electromagnetic interaction of negatively charged leptons with positively charged ions is however taken into account by applying a correction to the lepton chemical potential, as prescribed in Hempel & Schaffner-Bielich (2010).
At high density, neutrino oscillations are suppressed (see e.g. Richers et al. 2019) so that electron and muon lepton fractions are separately conserved.
Acknowledgments
The authors thank David Radice, Sebastiano Bernuzzi, Micaela Oertel, and Francesco Pederiva for useful discussions. They also thank the anonymous Referee for their valuable comments and suggestions. They acknowledge the INFN for the usage of computing and storage resources through the tullio cluster in Turin, and the Computational Relativity (CoRe) collaboration for providing access to the simulation data used in the work. MB and EL acknowledge financial support from MIUR (PRIN 2020 grant 2020KB33TP). MB acknowledges financial support from MIUR (PRIN 2017 grant 20179ZF5KS).
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017a, Phys. Rev. Lett., 119, 161101 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017b, ApJ, 848, L12 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2018, Phys. Rev. Lett., 121, 161101 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, Phys. Rev. X, 9, 011001 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2020, Liv. Rev. Relativ., 23, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M., Harutyunyan, A., & Sedrakian, A. 2021, Phys. Rev. D, 104, 103027 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M. G., & Good, G. 2010, Phys. Rev. C, 82, 055805 [NASA ADS] [CrossRef] [Google Scholar]
- Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 448 [Google Scholar]
- Bauswein, A., Janka, H. T., Hebeler, K., & Schwenk, A. 2012, Phys. Rev. D, 86, 063001 [Google Scholar]
- Bauswein, A., Just, O., Janka, H.-T., & Stergioulas, N. 2017, ApJ, 850, L34 [Google Scholar]
- Bernuzzi, S. 2020, General Relativ. Gravitation, 52, 108 [CrossRef] [Google Scholar]
- Bernuzzi, S., Radice, D., Ott, C. D., et al. 2016, Phys. Rev. D, 94, 024023 [Google Scholar]
- Bernuzzi, S., Breschi, M., Daszuta, B., et al. 2020, MNRAS, 497, 1488 [Google Scholar]
- Bludman, S. A., & van Riper, K. A. 1977, ApJ, 212, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Bollig, R., DeRocco, W., Graham, P. W., & Janka, H.-T. 2020, Phys. Rev. Lett., 125, 051104 [NASA ADS] [CrossRef] [Google Scholar]
- Bollig, R., Janka, H. T., Lohs, A., et al. 2017, Phys. Rev. Lett., 119, 242702 [NASA ADS] [CrossRef] [Google Scholar]
- Bombaci, I., & Logoteta, D. 2018, A&A, 609, A128 [EDP Sciences] [Google Scholar]
- Bombaci, I., Logoteta, D., Vidaña, I., & Providência, C. 2016, Eur. Phys. J. A, 52, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Breschi, M., Gamba, R., & Bernuzzi, S. 2021, Phys. Rev. D, 104, 042001 [NASA ADS] [CrossRef] [Google Scholar]
- Breschi, M., Bernuzzi, S., Godzieba, D., Perego, A., & Radice, D. 2022, Phys. Rev. Lett., 128, 161102 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. G. W. 1970, ARA&A, 8, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, D., & Vidaña, I. 2016, Eur. Phys. J. A, 52, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. M., Langer, W. D., Rosen, L. C., & Cameron, A. G. W. 1970, Ap&SS, 6, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, A., Salafia, O. S., Gabrielli, F., et al. 2022, ApJ, 937, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Cooperstein, J. 1988, Phys. Rept., 163, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Cusinato, M., Guercilena, F. M., Perego, A., et al. 2022, EPJA, 58, 99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damour, T., Nagar, A., & Villain, L. 2012, Phys. Rev. D, 85, 123007 [NASA ADS] [CrossRef] [Google Scholar]
- Danielewicz, P., & Lee, J. 2014, Nucl. Phys. A, 922, 1 [NASA ADS] [CrossRef] [Google Scholar]
- De, S., Finstad, D., Lattimer, J. M., et al. 2018, Phys. Rev. Lett., 121, 091102; Erratum: 121, 259902 [Google Scholar]
- Drischler, C., Hebeler, K., & Schwenk, A. 2019, Phys. Rev. Lett., 122, 042501 [Google Scholar]
- Endrizzi, A., Perego, A., Fabbri, F. M., et al. 2020, Eur. Phys. J. A, 56, 15 [EDP Sciences] [Google Scholar]
- Evans, M., Adhikari, R. X., Afle, C., et al. 2021, ApJ, submitted [arXiv:2109.09882] [Google Scholar]
- Favata, M. 2014, Phys. Rev. Lett., 112, 101101 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T., Guo, G., Martínez-Pinedo, G., Liebendörfer, M., & Mezzacappa, A. 2020, Phys. Rev. D, 102, 123001 [NASA ADS] [CrossRef] [Google Scholar]
- Fore, B., & Reddy, S. 2020, Phys. Rev. C, 101, 035809 [NASA ADS] [CrossRef] [Google Scholar]
- Fortin, M., Oertel, M., & Providência, C. 2018, PASA, 35, e044 [NASA ADS] [CrossRef] [Google Scholar]
- Foucart, F., Haas, R., Duez, M. D., et al. 2016a, Phys. Rev. D, 93, 044019 [NASA ADS] [CrossRef] [Google Scholar]
- Foucart, F., O’Connor, E., Roberts, L., et al. 2016b, Phys. Rev. D, 94, 123016 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. K. 1997, Compact stars. Nuclear Physics, Particle Physics, and General Relativity [Google Scholar]
- Grimm, S., & Harms, J. 2020, Phys. Rev. D, 102, 022007 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, G., Martínez-Pinedo, G., Lohs, A., & Fischer, T. 2020, Phys. Rev. D, 102, 023037 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., Levenfish, K. P., & Yakovlev, D. G. 2000, A&A, 357, 1157 [NASA ADS] [Google Scholar]
- Haensel, P., Levenfish, K. P., & Yakovlev, D. G. 2001, A&A, 372, 130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222; Erratum: 1995, 438, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Hammond, P., Hawke, I., & Andersson, N. 2022, ApJ, submitted [arXiv:2205.11377] [Google Scholar]
- Hannestad, S., & Raffelt, G. 1998, ApJ, 507, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Hempel, M., & Schaffner-Bielich, J. 2010, Nucl. Phys. A, 837, 210 [Google Scholar]
- Hinderer, T. 2008, ApJ, 677, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Hix, W. R., & Thielemann, F.-K. 1999, ApJ, 511, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Iacovelli, F., Mancarella, M., Foffa, S., & Maggiore, M. 2022, ApJ, 941, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, J. D., Ott, C. D., O’Connor, E. P., et al. 2014, ApJ, 790, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Klähn, T., Łastowiecki, R., & Blaschke, D. B. 2013, Phys. Rev. D, 88, 085001 [CrossRef] [Google Scholar]
- Lattimer, J. M., & Steiner, A. W. 2014, ApJ, 784, 123 [Google Scholar]
- Leinson, L. B. 2002, Nucl. Phys. A, 707, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Logoteta, D. 2021, Universe, 7, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Logoteta, D., Vidana, I., & Bombaci, I. 2019, Eur. Phys. J. A, 55, 207 [CrossRef] [Google Scholar]
- Logoteta, D., Perego, A., & Bombaci, I. 2021, A&A, 646, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maggiore, M., Van Den Broeck, C., Bartolo, N., et al. 2020, J. Cosmol. Astropart. Phys., 2020, 050 [CrossRef] [Google Scholar]
- Margalit, B., & Metzger, B. D. 2017, ApJ, 850, L19 [Google Scholar]
- Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2019, ApJ, 887, L24 [Google Scholar]
- Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2021, ApJ, 918, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Most, E. R., Papenfort, L. J., Dexheimer, V., et al. 2019, Phys. Rev. Lett., 122, 061101 [NASA ADS] [CrossRef] [Google Scholar]
- Nedora, V., Bernuzzi, S., Radice, D., et al. 2019, ApJ, 886, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Nedora, V., Bernuzzi, S., Radice, D., et al. 2021, ApJ, 906, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Oertel, M., Fantina, A. F., & Novak, J. 2012, Phys. Rev. C, 85, 055806 [NASA ADS] [CrossRef] [Google Scholar]
- Oertel, M., Hempel, M., Klähn, T., & Typel, S. 2017, Rev. Modern Phys., 89, 015007 [NASA ADS] [CrossRef] [Google Scholar]
- Patricelli, B., Bernardini, M. G., Mapelli, M., et al. 2022, MNRAS, 513, 4159 [NASA ADS] [CrossRef] [Google Scholar]
- Perego, A., Bernuzzi, S., & Radice, D. 2019, Eur. Phys. J. A, 55, 124 [EDP Sciences] [Google Scholar]
- Perego, A., Logoteta, D., Radice, D., et al. 2022, Phys. Rev. Lett., 129, 032701 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., Pons, J. A., & Page, D. 2015, Space Sci. Rev., 191, 239 [Google Scholar]
- Prakash, M., Bombaci, I., Prakash, M., et al. 1997, Phys. Rep., 280, 1 [Google Scholar]
- Punturo, M., Abernathy, M., Acernese, F., et al. 2010, CQG, 27, 194002 [NASA ADS] [CrossRef] [Google Scholar]
- Raaijmakers, G., Greif, S. K., Hebeler, K., et al. 2021, ApJ, 918, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Radice, D., Galeazzi, F., Lippuner, J., et al. 2016, MNRAS, 460, 3255 [NASA ADS] [CrossRef] [Google Scholar]
- Radice, D., Perego, A., Hotokezaka, K., et al. 2018a, ApJ, 869, 130 [Google Scholar]
- Radice, D., Perego, A., Zappa, F., & Bernuzzi, S. 2018b, ApJ, 852, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Radice, D., Bernuzzi, S., & Perego, A. 2020, Ann. Rev. Nucl. Part. Sci., 70, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Radice, D., Bernuzzi, S., Perego, A., & Haas, R. 2022, MNRAS, 512, 1499 [NASA ADS] [CrossRef] [Google Scholar]
- Richers, S. A., McLaughlin, G. C., Kneller, J. P., & Vlasenko, A. 2019, Phys. Rev. D, 99, 123014 [NASA ADS] [CrossRef] [Google Scholar]
- Riley, T. E., et al. 2019, ApJ, 887, L21 [CrossRef] [Google Scholar]
- Ronchini, S., Branchesi, M., Oganesyan, G., et al. 2022, A&A, 665, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosswog, S., & Liebendoerfer, M. 2003, MNRAS, 342, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffert, M., & Janka, H. T. 1998, A&A, 338, 535 [NASA ADS] [Google Scholar]
- Ruffert, M., Janka, H. T., & Schaefer, G. 1996, A&A, 311, 532 [NASA ADS] [Google Scholar]
- Sekiguchi, Y., Kiuchi, K., Kyutoku, K., & Shibata, M. 2011a, Phys. Rev. Lett., 107, 211101 [NASA ADS] [CrossRef] [Google Scholar]
- Sekiguchi, Y., Kiuchi, K., Kyutoku, K., & Shibata, M. 2011b, Phys. Rev. Lett., 107, 051102 [NASA ADS] [CrossRef] [Google Scholar]
- Sekiguchi, Y., Kiuchi, K., Kyutoku, K., Shibata, M., & Taniguchi, K. 2016, Phys. Rev. D, 93, 124046 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes, White Dwarfs, and Neutron Stars : the Physics of Compact Objects [Google Scholar]
- Shlomo, S., Kolomietz, V. M., & Colò, G. 2006, Eur. Phys. J. A, 30, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Prakash, M., Lattimer, J. M., & Ellis, P. J. 2005, Phys. Rep., 411, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Hempel, M., & Fischer, T. 2013, ApJ, 774, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Takami, K., Rezzolla, L., & Baiotti, L. 2014, Phys. Rev. Lett., 113, 091104 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Arnett, D. 1999, ApJS, 125, 277 [Google Scholar]
- Typel, S., Röpke, G., Klähn, T., Blaschke, D., & Wolter, H. H. 2010, Phys. Rev. C, 81, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- Weih, L. R., Hanauske, M., & Rezzolla, L. 2020, Phys. Rev. Lett., 124, 171103 [NASA ADS] [CrossRef] [Google Scholar]
- Weissenborn, S., Sagert, I., Pagliara, G., Hempel, M., & Schaffner-Bielich, J. 2011, ApJ, 740, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Zappa, F., Bernuzzi, S., Radice, D., Perego, A., & Dietrich, T. 2018, Phys. Rev. Lett., 120, 111101 [NASA ADS] [CrossRef] [Google Scholar]
- Zappa, F., Bernuzzi, S., Radice, D., & Perego, A. 2023, MNRAS, 520, 1481 [Google Scholar]
Appendix A: An alternative assumption on Yl, μ
As discussed in Sect. 3.3, there is not a unique way to assign Yl, μ, Yl, e, and etot appearing on the left-hand side of Eq. (34) given the outcome of the simulations presented in Sect. 3.1. Therefore, in this Appendix, we consider a limiting case opposite to the one discussed in Sect. 3.3 as a different possible choice. In particular, we assume that muons are negligible in the initial conditions, that is, in the two cold NSs, and we impose Yl, μ = 0. Then, we identify the simulation electron fraction, 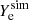 , and energy density, esim, with Yl, e and etot, respectively:
, and energy density, esim, with Yl, e and etot, respectively:
(see from Eq. (30) to Eq. (33)). This choice, despite being inconsistent with what we expect, has the advantage of being fully coherent with the simulation assumptions, and it provides an easier initialisation of our post-processing calculation. In the following paragraphs, we discuss the results obtained with this choice, and we compare them with the ones discussed in the previous sections. From this point on, we refer to this particular choice as Yl, μ = 0 and to the one discussed in Sect. 3.3 as 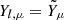 .
.
A.1. The fraction of muons
If Yl, μ = 0, all the muons in the final state are produced during the merger. For all the simulations in Table 1, the equilibrium muon fraction at density ρ > 1014 g cm−3 is Yμ− ∼ 10−3 − 3 × 10−2. At a lower density, ρ ∼ 1013 − 1014 g cm−3, the muon fraction is Yμ− ∼ 10−3 if Tsim ≳ 10 MeV; otherwise, muons are not present. We note that the amount of muons produced only during the merger is slightly smaller when 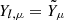 (see Sect. 4) because of the Pauli blocking coming from the muons already present in the cold NSs.
(see Sect. 4) because of the Pauli blocking coming from the muons already present in the cold NSs.
For all the simulations, Yμ/Ye ∼ 0.3 − 0.4, but the maximum Yμ/Ye is larger for DD2 and SFHo than for BLh because the latter exhibits a larger Ye (see also Fig. 2). The creation of muons is enhanced in correspondence to the hot spots for all the EOSs. In the case of (BLh, 1.00), muon production also increases in the density region ρ > 1015 g cm−3. This effect depends on the significantly larger electron fraction obtained with the BLh EOS since the more degenerate electrons block the conversion of neutrons into protons plus electrons, favouring instead the conversion into protons plus muons.
A.2. The trapping of neutrinos
The initial assumption on Yl, μ does not significantly affect the behaviour of electron (anti-)neutrinos, but it does imply discernible consequences on the muon neutrinos. If Yl, μ = 0, muon neutrinos appear only in correspondence to the hot spots and the warm matter streams, with a maximum fraction Yνμ ∼ 0.01. All νμ are produced together with 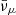 since there is not an initial muon fraction that can be converted into νμ. In contrast, the amount of
since there is not an initial muon fraction that can be converted into νμ. In contrast, the amount of 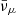 at equilibrium is strongly enhanced to guarantee the conservation of Yl, μ. Therefore,
at equilibrium is strongly enhanced to guarantee the conservation of Yl, μ. Therefore, 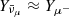 for all the simulations considered, and
for all the simulations considered, and 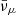 constitute the most abundant species amongst all flavour (anti-)neutrinos in the regions that are not dominated by thermal production.
constitute the most abundant species amongst all flavour (anti-)neutrinos in the regions that are not dominated by thermal production.
The differences in the equilibrium fractions of neutrinos depending on the chosen Yl, μ reflect the differences in the degeneracy parameters. For all the simulations ηνμ ≤ 0 and the production of νμ, only thermal and trapped degenerate νμ are suppressed. In addition, the gases of 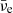 and
and 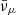 trapped in the remnant core are more degenerate when Yl, μ = 0 compared to when
trapped in the remnant core are more degenerate when Yl, μ = 0 compared to when 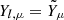 . This follows in part from the enhanced production of
. This follows in part from the enhanced production of 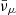 when Yl, μ = 0, but it also depends on the equilibrium temperature T, which is systematically larger when
when Yl, μ = 0, but it also depends on the equilibrium temperature T, which is systematically larger when  . Actually, in the latter case, the system lowers the fraction of electrons and neutrons to take into account the fraction of muons from the cold NSs, which practically means reducing the system degeneracy by increasing the temperature (see the discussions in Sect. 3.3 and Sect. 6).
. Actually, in the latter case, the system lowers the fraction of electrons and neutrons to take into account the fraction of muons from the cold NSs, which practically means reducing the system degeneracy by increasing the temperature (see the discussions in Sect. 3.3 and Sect. 6).
We stress that the presence of a trapped degenerate component of 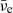 and
and 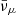 in the core and of νe in the outer layers of the remnant is a robust prediction independent of the initial assumption on Yl, μ. Instead, the presence of a degenerate gas of νμ in the cold matter streams depends on the initial choice of Yl, μ.
in the core and of νe in the outer layers of the remnant is a robust prediction independent of the initial assumption on Yl, μ. Instead, the presence of a degenerate gas of νμ in the cold matter streams depends on the initial choice of Yl, μ.
A.3. The changes in pressure
In conclusion, we analysed the ratio P/Psim where P is computed in post-processing under the assumption Yl, μ = 0. In this case, we did not observe a significant pressure increase after muons were introduced (i.e. P/Psim > 1) for any of the simulations in Table 1. This result is expected since, within this assumption, we neglected the muons from the cold NSs, which are indeed responsible for the pressure increase when  , as discussed in Sect. 6. In fact, the amount and the spatial distribution of the pressure decrease are common to all the simulations irrespective of the initial assumption on Yl, μ. In particular, the pressure decrease is still favoured in correspondence to the hot spots because, in these regions, the final equilibrium fractions of muons and (anti-)neutrinos are comparable for the two choices of Yl, μ.
, as discussed in Sect. 6. In fact, the amount and the spatial distribution of the pressure decrease are common to all the simulations irrespective of the initial assumption on Yl, μ. In particular, the pressure decrease is still favoured in correspondence to the hot spots because, in these regions, the final equilibrium fractions of muons and (anti-)neutrinos are comparable for the two choices of Yl, μ.
All Tables
Properties of nuclear EOS tables used in this work and of cold, spherically symmetric NSs for each nuclear EOS.
All Figures
 |
Fig. 1. Outcome of the numerical simulation (BLh, 1.00) at 4.6 ms after merger. The left, central, and right panels show the rest mass density, the temperature, and the electron fraction on the equatorial plane, respectively. The black lines mark isodensity contours corresponding to 1012 g cm−3 (solid line), 1013 g cm−3 (dashed line), 1014 g cm−3 (dashed-dotted line), and 1015 g cm−3 (dotted line). |
| In the text | |
 |
Fig. 2. Particle fractions computed at T = 0 in neutrinoless β-equilibrium for three different EOS: BLh (left), DD2 (centre), and SFHo (right). Black lines show the electron fraction computed in two different cases: equilibrium with muons (solid lines) or without muons (dashed lines). The green line corresponds to the fraction of protons at equilibrium with muons, while the red line corresponds to the muon fraction. We note that when muons are not included, the proton fraction coincides with the electron one (dashed black line). |
| In the text | |
 |
Fig. 3. Particle fractions and chemical potential in the muon flavour sector computed by post-processing the simulation (BLh, 1.00) at 4.6 ms after merger. In the upper panels, we show the fraction of μ− (left), the fraction of μ+ (centre), and the difference between the muon fraction and the one inherited from the cold NSs, that is, |
| In the text | |
 |
Fig. 4. Ratio of the net muon fraction over the net electron fraction, Yμ/Ye, on the equatorial plane obtained by post-processing simulations (BLh, 1.00) (upper left), (BLh, 1.43) (upper right), (DD2, 1.00) (lower left), and (SFHo, 1.00) (lower right) at 5 − 6 ms after merger. As in Fig. 1, the black lines mark isodensity contours. |
| In the text | |
 |
Fig. 5. Fractions of νe, |
| In the text | |
 |
Fig. 6. Proton and neutron chemical potentials (rest mass subtracted) of BLh in the density-temperature plane at fixed Yp = 0.08. The proton fraction Yp = 0.08 is the equilibrium proton fraction at 4.6 ms after merger around the point x = 0.64 km, y = 12.76 km, z = 0 km, where ρ ∼ 5 × 1013 g cm−3, Tsim ∼ 10 MeV, and neutrinos dominate, while anti-neutrinos are suppressed (see also Figs. 1, 3 and 5). We notice that the colour bars are scaled differently. |
| In the text | |
 |
Fig. 7. Degeneracy parameter of νe (first row) and νμ (lower row) on the equatorial plane obtained by post-processing the simulation (BLh, 1.00). Three different time slices are shown corresponding from left to right to 4.6 ms, 6.7 ms, and 11.8 ms after merger. As in Fig. 1, the black lines mark the isodensity contours as in Fig. 1. |
| In the text | |
 |
Fig. 8. Mean energy Eν of trapped neutrinos on the equatorial plane computed by post-processing simulation (BLh, 1.00) at 4.6 ms after merger. As in Fig. 1., the black lines mark isodensity contours. |
| In the text | |
 |
Fig. 9. Pressure ratio P/Psim for (BLh, 1.00) (left), (DD2, 1.00) (centre), and (SFHo, 1.00) (right) where P is obtained in post-processing, while Psim is the simulation pressure. For (BLh, 1.00), we explicitly mark the maximum P/Psim ∼ 1.03 (white circle) and the minimum P/Psim ∼ 0.94 (white cross) at ρ > 1014 g cm−3. As in Fig. 1., the black lines mark isodensity contours. |
| In the text | |
 |
Fig. 10. Change of particle pressure and fractions obtained in correspondence to the space-time coordinates explicitly marked in the left panel of Fig. 9 and corresponding to P/Psim = 0.94 (upper row) and P/Psim = 1.03 (lower row). The bar plots in blue (left) give the difference between the equilibrium pressure computed in post-processing and in the simulation, |
| In the text | |
 |
Fig. 11. Pressure ratio P/Psim computed by post-processing (BLh, 1.00) (top) and (BLh, 1.43) (bottom) at 6.7 ms after merger. As in Fig. 1, the black lines mark the isodensity contours. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



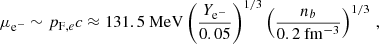
![$$ \begin{aligned} \mu _{\mu ^{-}} \sim m_{\mu }c^2 + \frac{p_{\mathrm{F},\mu }^2}{2 m_{\mu }} \approx \left[ 106 + 28 \left(\dfrac{Y_{\mu ^-}}{0.01}\right)^{2/3} \left( \dfrac{n_{b}}{0.2 \mathrm{~fm^{-3}}}\right)^{2/3} \right] \mathrm{MeV}, \end{aligned} $$](/articles/aa/full_html/2023/04/aa44927-22/aa44927-22-eq2.gif)

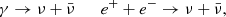

![$$ \begin{aligned} E_{\nu \bar{\nu }} = k_{\rm B} T \left[ \frac{F_4(\eta _{\mathrm{e}^-})}{F_3(\eta _{\mathrm{e}^-})} + \frac{F_4(- \eta _{\mathrm{e}^-})}{F_3(- \eta _{\mathrm{e}^-})} \right], \end{aligned} $$](/articles/aa/full_html/2023/04/aa44927-22/aa44927-22-eq6.gif)
![$$ \begin{aligned} E_{\nu \bar{\nu }} \sim k_{\rm B} T \left[ \frac{4}{5} \eta _{\mathrm{e}^-} + 4 \right] \gtrsim m_\mu c^{2}. \end{aligned} $$](/articles/aa/full_html/2023/04/aa44927-22/aa44927-22-eq7.gif)
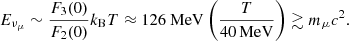

![$$ \begin{aligned} R_{\nu _\mu + n \rightarrow p + \mu ^{-}} = \dfrac{G^2 c}{\pi ~ (\hbar c)^4} \left(g_V^2 + 3 g_A^2\right) \omega _{np} \left[1 - f_\mu (E_{\nu _\mu } + Q)\right] \nonumber \\ \times \left(E_{\nu _\mu } + Q \right)^2 \left[1 - \dfrac{m_\mu ^2}{\left(E_{\nu _\mu } + Q \right)^2}\right]^{1/2}\!, \end{aligned} $$](/articles/aa/full_html/2023/04/aa44927-22/aa44927-22-eq12.gif)
![$$ \begin{aligned} \omega _{np} = \dfrac{n_{\rm p} - n_{\rm n}}{\exp \left[(\mu^\prime _{\rm p} - \mu^\prime _{\rm n})/k_{\rm B} T\right]-1}, \end{aligned} $$](/articles/aa/full_html/2023/04/aa44927-22/aa44927-22-eq13.gif)
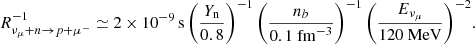
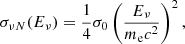
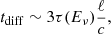
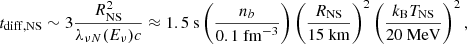
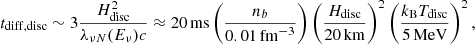
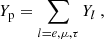
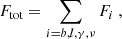
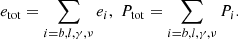
![$$ \begin{aligned} n_{l^\pm } = K_{l} \theta _{l}^{3/2} \left[ F_{1/2} (\eta^\prime _{l^\pm }, \theta _{l}) + \theta _{l} F_{3/2} (\eta^\prime _{l^\pm }, \theta _{l})\right] \end{aligned} $$](/articles/aa/full_html/2023/04/aa44927-22/aa44927-22-eq37.gif)
![$$ \begin{aligned} e_{l^\pm } = K_{l} m_{l} c^2 \theta _{l}^{5/2} \left[F_{3/2}(\eta^\prime _{l^\pm },\theta _{l}) + \theta _{l} F_{5/2} (\eta^\prime _{l^\pm },\theta _{l})\right] + m_l c^2 n_{l^{\pm }} \end{aligned} $$](/articles/aa/full_html/2023/04/aa44927-22/aa44927-22-eq38.gif)
![$$ \begin{aligned} P_{l^\pm } = \dfrac{K_{l} m_l c^2}{3} \theta _l^{5/2} \left[ 2 F_{3/2} (\eta^\prime _{l^\pm },\theta _{l}) + \theta _{l} F_{5/2} (\eta^\prime _{l^\pm },\theta _{l}) \right],\end{aligned} $$](/articles/aa/full_html/2023/04/aa44927-22/aa44927-22-eq39.gif)