| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202244412 | |
| Published online | 14 April 2023 | |
Forward modelling of brightness variations in Sun-like stars
II. Light curves and variability
1
Institut für Astrophysik und Geophysik, Georg-August-Universität Göttingen,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
e-mail: nina-elisabeth.nemec@uni-goettingen.de
2
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
3
Department of Computer Science, Turkish-German University,
Şahinkaya Cd. 94,
34820
Beykoz Istanbul,
Turkey
4
School of Space Research, Kyung Hee University,
Yongin, Gyeonggi,
446-701,
Korea
Received:
4
July
2022
Accepted:
3
March
2023
Context. The amplitude and morphology of light curves of Sun-like stars change substantially with increasing rotation rate: brightness variations are amplified and become more regular. This has not been explained so far.
Aims. We develop a modelling approach for calculating brightness variations of stars with various rotation rates and use it to explain the observed trends in stellar photometric variability.
Methods. We combined numerical simulations of magnetic flux emergence and transport with a model for stellar brightness variability to calculate synthetic light curves of stars as observed by the Kepler telescope. We computed the distribution of the magnetic flux on the stellar surface for various rotation rates and degrees of active-region nesting (i.e. the tendency of active regions to emerge in the vicinity of recently emerged regions). Using the resulting maps of the magnetic flux, we computed the rotational variability of our simulated stellar light curves as a function of rotation rate and nesting of magnetic features and compared our calculations to Kepler observations.
Results. We show that both the rotation rate and the degree of nesting have a strong impact on the amplitude and morphology of stellar light curves. In order to explain the variability of most of the Kepler targets with known rotation rates, we need to increase the degree of nesting to values that are much higher than the values on the Sun.
Conclusions. The suggested increase in nesting with the rotation rate can provide clues about the flux emergence process for high levels of stellar activity.
Key words: stars: activity / stars: general / stars: rotation / stars: magnetic field / stars: solar-type
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
Planet-hunting missions such as the Convection, Rotation and planetary Transits (CoRoT; Baglin et al. 2006; Bordé et al. 2003), Kepler (Borucki et al. 2010), and the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2014) allow studying stellar brightness variations caused by transits of magnetic features as stars rotate. These brightness variations were discovered for the Sun almost half a century ago (Willson et al. 1981; Willson & Hudson 1981). Since then, the models of solar brightness variations have matured and are now not only capable of accurately reproducing most of the available measurements (see Solanki et al. 2013; Ermolli et al. 2013, for reviews), but also provide a starting point for explaining a plethora of stellar photometric data (see e.g. Lagrange et al. 2010; Meunier & Lagrange 2013; Meunier et al. 2015; Borgniet et al. 2015; Nèmec et al. 2020b).
Recently, Nèmec et al. (2020b, hereafter N20b) have combined the spectral and total irradiance reconstruction model (SATIRE; Fligge et al. 2000; Krivova et al. 2003) with a surface flux transport model (SFTM; Cameron et al. 2010) to compute the power spectra of solar brightness variations as they would be measured at different inclinations, that is, the angle between the solar rotation axis and the direction to the observer. These calculations helped to remove a number of strong observational biases when solar variability is compared to the variability of other stars (Nèmec et al. 2020a; Reinhold et al. 2020). Notably, by employing the N20b model and using the approach developed by Witzke et al. (2018, 2020) to extend it to stars with non-solar metallicities, Reinhold et al. (2021) have found that rotation periods of a majority of G dwarfs with near-solar age remain undetected. These results explained the discrepancy between the predictions for the number of Sun-like rotators in the Kepler field and the actual number of detected rotators (see van Saders et al. 2019).
In this work, we additionally extend the solar paradigm for modelling the variability of stars that rotate faster than the Sun. Namely, we combine the solar variability model of N20b, which was extensively tested against solar irradiance measurements, with the modelling framework for computing the surface distribution of magnetic flux on stars with solar fundamental parameters, but various rotation rates developed by (Işık et al. 2018, hereafter Paper I). The flux emergence and transport (FEAT) model presented in Paper I involves physics-based calculations of the emergence latitudes and tilt angles of bipolar magnetic regions (BMRs) for given stellar rotation rates, and the subsequent modelling of the evolution of the radial magnetic flux at the photosphere via an SFTM. The FEAT model is self-consistently able to reproduce the observations of polar spots that appear on stars with rotation periods shorter than about 3 days (see e.g. Jeffers et al. 2002; Marsden et al. 2004; Järvinen et al. 2006; Waite et al. 2015). Recently, the FEAT model was successfully applied to the young solar analogue EK Dra (Ṣenavcı et al. 2021) to explain the Doppler images that indicated near-polar spots and extended spot patterns towards low latitudes. In the present work, we extend the model of Paper Paper I to calculate the brightness variations of stars for which a variety of rotation rates are observed at various inclination. We also allow for different degrees and modes of nesting of magnetic features on their surfaces (i.e. the tendency of active regions to emerge in the vicinity of recently emerged regions). We compare our results to the observational trends found by McQuillan et al. (2014) and Santos et al. (2021) from Kepler data and propose a possible explanation of these trends.
In Sect. 2 we briefly describe the FEAT model (see Işık et al. 2018, for a more detailed description) and explain how this model is extended for calculating stellar brightness variability. In Sect. 3 we discuss the resulting light curves (LCs). These LCs are then used to calculate the amplitude of the variability, which we compare to observations in Sect. 4. We discuss our findings within the frameworks of various other recent studies in Sect. 5 before we present our conclusions in Sect. 6.
2 Model
2.1 Flux emergence and transport
To simulate the magnetic flux emergence on other stars, we used the FEAT model Paper (I). In essence, the FEAT model extends the pattern of emergence and evolution of the magnetic fields observed on the surface of the Sun to stars rotating faster than the Sun (which are therefore more active than the Sun). This is done in five steps (see Paper I, Fig. B1).
- Step 1.
We adopted the synthetic record of solar active-region emergences during cycle 22 from Jiang et al. (2011). While this approach cannot be used to reconstruct the solar irradiance on a specific day, N20b have shown that the records of Jiang et al. (2011) allow reproducing the overall solar variability pattern. Cycle 22 was chosen because it represents a cycle of moderate to strong activity level, which makes it suitable for modelling the most active stars.
- Step 2.
We defined the time-dependent emergence rate of BMRs on a star as
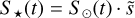 , where S★ and S⊙ are the stellar and solar emergence rates, respectively, and
, where S★ and S⊙ are the stellar and solar emergence rates, respectively, and 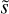 is a scaling factor. To reflect the observed rotation-activity relation, we followed Paper I and took
is a scaling factor. To reflect the observed rotation-activity relation, we followed Paper I and took 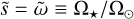 , where Ω★ is the rotation rate of a star, and Ω⊙ is the solar rotation rate.
, where Ω★ is the rotation rate of a star, and Ω⊙ is the solar rotation rate. - Step 3.
The resulting input record of emergences was mapped down to the base of the convection zone using thin flux-tube simulations (Schüssler et al. 1996; Işık et al. 2018) for the solar rotation rate Ω⊙.
- Step 4.
The record of emergences at the base of the convective zone was mapped back to the surface, but in contrast to step 3, using thin flux-tube simulations for a star with a given rotation rate Ω★. These simulations follow the rise of the flux tubes throughout the convection zone up to the surface of the star, where they emerge in the form of a loop with two foot-points of opposite polarity (i.e. BMRs). An important feature of these simulations is that they account for the Coriolis effect, which pushes rising flux tubes towards higher latitudes for higher rotation rates (Schüssler & Solanki 1992).
- Step 5.
Assuming that the size distribution of BMRs does not change with the rotation rate, we modified the emergence locations of flux loops to simulate different degrees and modes of active-region nesting (see the similar approach by Işık et al. 2020), motivated by the observed activity complexes on the Sun. The details of this step are described below in this section.
- Step 6.
In this last step, the calculated locations of emergence and the tilt angles of BMRs were fed into the surface flux transport model (SFTM). The SFTM describes the passive transport of magnetic fields of the BMRs on the surface of stars by taking both large-scale flows (meridional flow and differential rotation) and the diffusion of the fields into account (Cameron et al. 2010; Işık et al. 2018).
In the present work, we employed the steps outlined above to obtain the surface distribution for stars with 1, 2, 4, and 8Ω⊙. The emergence patterns of the BMRs (e.g. the input record) for 1Ω⊙ and 8Ω⊙ are shown in Fig. 1. The main purpose of this study is to model stellar variability on the rotational timescale. We followed the approach of Paper I and took the solar temporal profile of activity (even though it is unlikely to be observed on the faster-rotating and more active stars; we discuss this choice below), but we modelled the LCs only over the 4-yr window centred at the activity maximum (marked in Fig. 1). Our LCs (and the resulting variability amplitudes) correspond to a representative stellar activity level scaled from the solar maximum. They are therefore largely unaffected by the temporal profile of the underlying activity cycle.
In Fig. 2, we present snapshots of the magnetic field distribution on the surface of stars with 1 Ω⊙ (top row) and 8Ω⊙ (bottom row) for various inclinations. The figure nicely demonstrates the difference in the emergence frequency, as the 8Ω⊙ star is covered by more BMRs. The difference in the latitudinal distribution is also remarkable. This is a result of step 4 of the FEAT approach, which in turn leads to the formation of strong polar fields for the fast rotator depicted here. We also show snapshots of the magnetic field distribution of the surface of stars with Ω⊙ and 8Ω⊙ for various inclinations in Fig. 2.
Additionally, the emergence pattern of BMRs is altered when active-region nesting is introduced. This effect is observed on the Sun, but only to a small degree (see e.g. Pojoga & Cudnik 2002, who estimated that 40–50% of the solar active regions can be associated with nests), and it has recently been suggested that nesting can be substantially stronger on highly variable stars with almost solar rotation rates (Işık et al. 2020). Following Işık et al. (2020), we introduce two modes of nesting (Step 5): the active longitude (AL) and the free nesting (FN) modes. In both modes, we define a degree of nesting, p, that gives the probability of a given BMR to be part of a nest. In the AL mode, these nests are centred around two fixed longitudes with a separation of 180 degrees. If the BMR is drawn to belong to a nest, then it is shifted to one of the two ALs (with equal probability). Its new longitude is defined by a 1D normal distribution around the AL (with a standard deviation of 10°), whereas the latitude is kept unchanged. This ensures that the emergence latitudes still follow the general trends of the solar butterfly diagram. In the FN mode, nesting occurs around central latitudes and longitudes, which are randomly picked from the unaltered (i.e. non-nested) emergence record. If the BMR is drawn to belong to a nest, then its emergence location is moved to a random location drawn from a 2D normal distribution, with the mean at the nest centre having standard deviations of 2° in latitude and 3° in longitude. For more details on the nesting definition and choice of the parameters, we refer to Işık et al. (2018) for the FN employed here and Işık et al. (2020) for AL.
We compare the two nesting modes for 1Ω⊙ in Fig. 3. In order to distinguish more easily between the two modes, we show both time-latitude (left panels) and time-longitude diagrams, with the colour bar indicating the longitude and latitude. The AL nesting is easier to identify in the time-longitude diagrams, whereas the FN nesting is easier to observe in a time-latitude graph.
 |
Fig. 1 Butterfly diagrams of BMR emergence for 1Ω⊙ (left panel) and 8Ω⊙ (right panel). The colour bar gives the emergence longitudes, and the vertical dashed lines indicate the 4yr of the 11 yr cycle that were considered in our brightness variation calculations. No amount of nesting is included here. |
 |
Fig. 2 Snapshot of the magnetic field distribution for 1Ω⊙ (top row) and 8Ω⊙ (bottom row) as returned by the FEAT model at various inclination angles around maximum of the activity cycle. The first column shows i = 90°, the second column shows i = 57°, the third column shows i = 30°, and the forth column shows i = 0°. |
 |
Fig. 3 Butterfly diagrams of BMR emergence for 1Ω⊙, with p = 0.7 in the different nesting modes considered in this work. Top row: AL nesting. Bottom row: FN nesting. The left panels show time-latitude diagrams, with the colour bar indicating the longitudes. The right panels are time-longitude diagrams, with the colour bar indicating the latitude. |
2.2 Defining the area coverages
The output of the FEAT model consists of full stellar surface maps (360° by 180°) of the magnetic fields with a resolution of 1° × 1° per pixel. As our brightness calculations rely on the area coverages of spots and faculae, we first have to convert the magnetic field maps into the surface distributions of spots and faculae. N20b did this by following the evolution of sunspots after their emergence to calculate the coverage of the solar disc by spots. While this approach proved itself to be accurate for calculating solar variability (see also Dasi-Espuig et al. 2014), it did not account for spots that appeared by superposition of the magnetic flux from different active regions. In other words, the main assumption of this approach was that all spots on the stellar surface have emerged as spots within the corresponding active region. While this is a good assumption for our Sun, it prohibits the formation of polar spots, which are observed on young and rapidly rotating G stars (Jeffers et al. 2002; Marsden et al. 2004; Järvinen et al. 2008; Waite et al. 2015; Ṣenavcı et al. 2021). These polar spots most likely form via flux superposition. We therefore took a slightly different approach than in N20b. We acknowledge that in addition to the intrinsic mechanism in the FEAT model, it is theoretically also possible to form polar spots by overly increasing the rate of BMR emergence (Schrijver & Title 2001) or the meridional flow rate (Holzwarth et al. 2006), but leaving the emergence latitudes Sun-like.
To calculate the spot area coverage of a given pixel of the synthetic magnetogram returned by FEAT, we defined two thresholds: a lower cut-off, Bmin, and an upper saturation level, Bmax. The spot coverage of a given pixel is related to the field in the pixel following
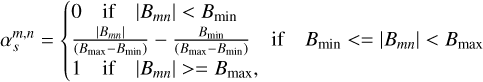 (1)
(1)
where 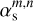 is the spot filling factor of a pixel with coordinates m and n of the magnetogram, and |Bmn| is the absolute value of the field in this pixel.
is the spot filling factor of a pixel with coordinates m and n of the magnetogram, and |Bmn| is the absolute value of the field in this pixel.
In order to calculate the facula area coverage in each pixel, we followed an approach similar to N20b by setting a saturation threshold Bsat (see also the papers describing SATIRE, e.g. Fligge et al. 2000; Krivova et al. 2003). When a pixel was already partially by spots, we disregarded this pixel for the facular masking. Wehn a given pixel was spot free, we calculated the facula area coverage following
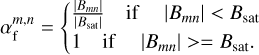 (2)
(2)
The parameter values were selected such that the current model returns the same rotational variability (see Sect. 2.4) for the solar case (i.e. Ω★ = Ω⊙) as the N20b model.
2.3 Calculating the brightness variations
Using Eqs. (1) and (2), we obtained maps of area coverages per pixel of the visible stellar disc. The part of the full surface (hence the disc) of a star that is visible depends on the inclination between the stellar rotation axis and the line of sight to the observer. The spectral irradiance, S (t, λ), (i.e. the spectral stellar flux, normalized to 1 AU), where t is the time and λ the wavelength, is then calculated by summing up the intensities weighted by the corresponding area coverages by magnetic features of a pixel as given by
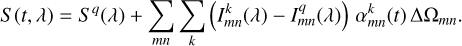 (3)
(3)
The summation was made over the pixels of the maps of the visible 2D stellar disc, and the m and n indices are the pixel coordinates (longitude and latitude, respectively), 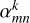 is the pixel (m, n) coverage by magnetic feature k (in our work, faculae, umbra, or penumbra), and ∆Ωmn is the solid angle of the area on the stellar disc corresponding to one pixel, as seen from the distance of 1 AU.
is the pixel (m, n) coverage by magnetic feature k (in our work, faculae, umbra, or penumbra), and ∆Ωmn is the solid angle of the area on the stellar disc corresponding to one pixel, as seen from the distance of 1 AU. 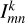 is the intensity spectrum of the magnetic feature k observed at the location corresponding to pixel (m, n). We used the values computed by Unruh et al. (1999) with the radiative transfer code ATLAS9 (Kurucz 1992; Castelli & Kurucz 1994).
is the intensity spectrum of the magnetic feature k observed at the location corresponding to pixel (m, n). We used the values computed by Unruh et al. (1999) with the radiative transfer code ATLAS9 (Kurucz 1992; Castelli & Kurucz 1994).
Sq is the quiet–star irradiance, defined as
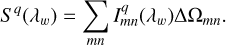 (4)
(4)
The solid angles of the pixels, as well as the corresponding intensity values, depend on the vantage point. Hence S (t, λ) is sensitive to the stellar inclination. The calculations we present were performed in the Kepler passband, following
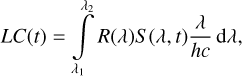 (5)
(5)
where λ1 and λ2 are the blue and red threshold wavelengths of the filter passband, R(λ) is the response function of the filter, S (λ, t) is the spectral irradiance at a given wavelength and time t, h is the Planck constant, and c is the speed of light.
2.4 Defining the model parameters
As mentioned previously, we fixed the model parameters introduced in Sect. 2.2 to return the same level of rotational variability, represented via Rvar, of the solar case as N20b. N20b showed that their model is able to reproduce the observed brightness variations of the Sun. The N20b model and the model we develop here are both based on the SFTM, with similar underlying statistical BMR emergence records. We therefore use the N20b model as our reference. To do this, we considered the 4-yr interval (indicated by vertical dashed black lines in Fig. 1) around the maximum of the synthetic cycle.
We then split the time series into 90-day segments, de-trended the new time series by their mean value, and calculated the difference between the extrema in each of the segments using the approach outlined above and that of N20b. We note that we directly considered the difference between the extrema instead of the differences between the 95th and 5th percentiles of sorted flux values, as is usually done in the literature with the more noisy Kepler measurements (see e.g. Basri et al. 2013).
We compare the Rvar values for the solar case as returned by N20b and our model in Fig. 4. The best- values for the parameters Bmin, Bmax, and Bsat were found to be 60, 700, and 250 G, respectively, and were chosen, as they resulted in a slope of the linear regression close to unity (1.029) and a high r2 value (0.957). The mean rotational variability in our model is comparable to that of the N20b model (1459.6 to 1457.71 ppm). However, we note that the threshold approach used in this model favours spots over faculae. While this is not necessarily accurate for the solar rotator in this work, it leads to the formation of polar spots and spot domination of the stellar variability for the faster-rotating stars. We present maps for different inclinations and nesting degrees of the spot and facula distributions (following the description in Sect. 2.2 and the choice of the parameters presented just above) for a star with 8Ω⊙ as returned by FEAT with various nesting degrees (see Sect. 2.1) in Figs. 5 and 6. The polar spots are clearly visible in Fig. 5.
 |
Fig. 4 Comparison of Rvar (in ppm) as returned by the N20b model and our model. All values are given in ppm. The solid black line gives the linear regression, and the dashed blue line is the one-to-one correspondence between the two models. |
 |
Fig. 5 Spot area coverage per pixel for different nesting realisations at different viewing angles for the 8Ω⊙ case. First column shows i = 90°, second column i = 57°, third column i = 30°, and forth column i = 0°. Top row is the non-nested case, middle row includes p = 0.7 in the free-nesting (FN) case, bottom row includes p = 0.7 in the active-longitude (AL) case. |
3 Light curves
Using the model described in Sect. 2.1, we generated a synthetic 11-yr-long cycle for each rotation rate considered in this work. We focused on the 4 yr around the activity maximum for two reasons. Firstly, we aim to explain the upper envelope of the variability distribution of stars as a function of the rotation period (McQuillan et al. 2014). Secondly, we modelled a single activity cycle, without overlapping cycles preceding and following it. Modelling cycle overlap is beyond the scope of this paper, and it would affect the activity level around cycle minima, which we therefore excluded from the analysis. We note that the LCs shown in this section are 180–day–long snippets of the full LCs and were simply chosen for demonstration.
Firstly, we considered the LCs of stars that are observed equator-on (i = 90°). Figure 7 displays the detrended LCs for the non-nested case (p = 0) for different rotation rates. The faster the star rotates, the higher its variability amplitude (mainly due to the shorter rotation periods: the lifetimes of the active regions change far less), which is a consequence of the activity-rotation scaling (see step 2 from Sect. 2.1). The small bumps in the LCs that are mostly seen for the Ω★ = 1Ω⊙ are a result of firstly having all BMRs emerge at their maximum size in the SFTM. Because the emergence rate is generally low and not many other BMRs are present, this affects the LCs more severely in this low-activity case. Secondly, and lastly, due to the nature of the threshold approach outlined in Sect. 2.2, flux superposition (in case of same-polarity encounters) and cancellation (in case of opposite-polarity encounters) leads to the possibility that flux rapidly switches from being associated with faculae to spots (or spots to faculae). Similar effects for the solar rotator will be visible in the following plots as well for the very same reason.
Figure 7 shows that not only the amplitude, but also the shape of the LCs strongly depends on the stellar rotation rate. For the case of the solar rotation (Ω★ = 1Ω⊙, top panel of Fig. 7), most of the individual dips in the LCs correspond to transits of different active regions (because active regions evolve on shorter timescales than solar rotation). As active regions emerge randomly in time, the LCs appear quite irregular. In contrast, the LCs of the more rapidly rotating stars show gradually more regular patterns in brightness variations (see the lower three panels in Fig. 7). This is because active regions on these stars can survive several rotation periods. Furthermore, the large number of BMR emergences over mid to high latitudes with large tilt angles leads to the formation of polar spots at about 4Ω⊙, with prominent polar spot caps being present for the 8Ω⊙ rotator (see Fig. 5). The formation of polar spots for stars with these rotation rates are consistent with Paper I and Doppler-imaging observations. We note that the polar spots in our simulations are non-axisymmetric unipolar caps. Their overall structure is rather stable because their decay is compensated for by the magnetic flux coming from the new emergences as long as the activity level and the BMR polarity orientations are sustained. As a next step, we considered models with active-region nesting.
We first considered the effect of the active-longitude nesting (see Sect. 2.1). Figure 8 shows LCs synthesised with AL nesting of 70% (i.e. p = 0.7). The overall shape of the LC for 1Ω⊙ is still rather irregular compared to the faster rotators because the emergence frequency is low. With increasing rotation rate, dips related to BMR transits not only occur at the separation of the rotation period, but also at half of the rotation period. In addition to a change in the morphology of the LCs, the variations are amplified with respect to the corresponding non-nested case at each rotation rate (solid black lines versus coloured lines).
Figure 9 gives the most extreme case of AL nesting, for which we assumed that all BMRs emerge in one of the two active longitudes (e.g. p =1). Clearly, both dips (at an interval of one and a half rotational period) occur in all of the cases, and the LC amplitudes are further augmented. The LCs in Fig. 9 additionally show that the two peaks have almost the same amplitude for the faster rotators. In case of the solar rotator and the low-emergence frequency, asymmetries between the two AL can temporarily arise in case of the emergence of a large BMR. However, with increasing emergence frequency, the two ALs become increasingly more symmetric, and hence the amplitude of the two dips due to the ALs as the star rotates are comparable to a large extent.
We now focus on the behaviour of the LCs in the FN mode. In Fig. 10 we present the LCs produced with p = 0.7. The variability amplitudes increase for all four rotation periods. The LCs also appear more regular than those calculated with p = 0. We increase the nesting even further to p = 0.99 in Fig. 11. The change in the LCs with respect to the non-nested case is remarkable. The amplitude of the LCs is enhanced for all cases, and the runs with p = 0.99 exhibit regular patterns, even in the solar case (top panel of Fig. 10). The LCs show not only dips with the separation of the rotation period, but also with half of the rotation period (e.g. most prominently seen in the 4Ω⊙ star). This is interesting because the dips at half the rotation period appear and disappear and are not constant, in contrast to the AL case. We discuss this further in Sect. 5.
Next, we considered the inclination effect on the LCs. For demonstration purposes, we limited ourselves to the non-nested cases with different rotation rates. In Fig. 12, we show the time span of 0–90 days from Fig. 7 for inclinations of 90°, 60°, and 30°. In the given time span, for 1Ω⊙, the amplitude of the variability decreases with decreasing inclination. The transit shapes also change. For 2 and 4Ω⊙, the LC amplitudes also decrease for the inclinations shown here. Interestingly, the situation changes for the 8Ω⊙ case. The amplitude increases from i = 90° to 60° and then decreases from i = 60° to i = 30°. The variability amplitude observed at i = 30° is also larger than that at i = 90°. These inclination dependencees can be explained with the help of the magnetic field maps in Fig. 5. For the case of 1Ω⊙, all regions emerge within ±30° around the equator. The Coriolis effect increases with increasing rotation rate, so that for the 8Ω⊙ star, the BMRs can emerge at latitudes up to ±70°, while a latitudinal belt free of active regions opens up around the equator between ±20° latitudes (see Sect. 5). For i = 90°, the high-latitude spots appear close to the limb, where their effect on the brightness is significantly reduced due to foreshortening. With decreasing inclination, most spots shift towards the centre of the visual disc and their effect on brightness increases, so that at intermediate inclinations, the variability is highest (see Figs. 13, panel a), before it again decreases, as the spots move towards the limb of the visible disc once more.
 |
Fig. 7 Synthetic LCs for stars with different rotation rates as they would be observed in the Kepler passband at an inclination of i = 90°. We show non-nested cases (p = 0) with rotation rate values of 1Ω⊙ (blue), 2Ω⊙ (orange), 4Ω⊙ (green), and 8Ω⊙ (red). |
 |
Fig. 8 Similar to Fig. 7, where the black curves represent the calculations with p = 0 for each rotation rate, and the coloured curves represent calculations to which AL-type nesting at p = 0.7 was added. |
 |
Fig. 12 Similar to Fig. 7 for different inclination shown in three columns for i = 90°, 60°, and i = 30°. |
4 Comparison to observations
In the following, we compare our model to observational records of Sun-like stars obtained by the Kepler telescope. Since our model builds on the solar paradigm, we selected stars with near solar effective temperatures between 5500–6000 K and surface gravity log g ≥ 4.2 using the updated fundamental parameters of Kepler stars from Berger et al. (2020). Next, we considered stars with known rotational periods using the data sets of McQuillan et al. (2014, hereafter McQ14) and Santos et al. (2021, hereafter S21). These constraints led to a sample of 6,228 stars for the McQ14 rotation periods and 11,493 stars for the S21 rotation periods.
We express the variability through the quantity Rvar, first introduced by Basri et al. (2010, 2011). We used a slightly modified version of the range Rvar: we computed the difference between the 95th and 5th percentile of the sorted differential intensities. Even for the latest Kepler data reduction (DR25), some quarters occasionally still include instrumental systematics that might influence the range. We then computed the median absolute deviation (MAD) of all Rvar values, and removed the quarters that deviated more than six times the MAD. Afterwards, the median was taken of all remaining quarters, which we call Rvar. Because the SFTM returns instantaneous values with 6-h cadences, we took every 12th data point (the Kepler long cadence is ≈30 min) and computed Rvar for this unbinned time series. All computations were based on the latest Kepler data release (DR25) using the PDC-MAP LCs. We also crosschecked our calculated variabilities represented through Rvar, with the metric Rper used by McQuillan et al. (2014) and found very good agreement.
Before computing Rvar of the models, we needed to add noise to the LCs. We followed the same strategy as described in detail in Reinhold et al. (2020). We multiplied the noise with a factor of 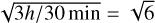 to account for the different time bins. For each inclination, 1000 noise realisations were considered, and the mean and standard deviations were computed. This was done only for the 1 Ω⊙ p = 0 case because we found that the noise level is significantly lower than the actual stellar variability in all other cases.
to account for the different time bins. For each inclination, 1000 noise realisations were considered, and the mean and standard deviations were computed. This was done only for the 1 Ω⊙ p = 0 case because we found that the noise level is significantly lower than the actual stellar variability in all other cases.
In Figs. 13 and 14, we show the comparison between the calculated Rvar values of our simulated stars for various degrees of nesting in the AL and the FN mode, respectively, and the two samples of Kepler stars shown as grey (McQ14) and black (S21) dots. Evidently, when no nesting is included (p = 0), our calculated variabilities underestimate the bulk of the observed variability amplitudes, especially for the faster rotators. With increasing nesting level (Figs. 13 and 14b–e), Rvar increases and the values move towards the upper edge of the distribution. Interestingly, p = 0.99 in the FN mode (Fig. 14e) overestimates the variability of the solar rotators, but leads to similar variability values as the upper envelope of the variability distributions of the faster-rotating stars. We note that, while the numbers of BMR emerging is the same for a given rotation rate between the nonnested and nested cases, the spot disc area coverage increases with higher nesting degrees because spots form by flux superposition. As a consequence, the spot area coverage is not preserved, in contrast to the approach presented in Işık et al. (2020), and the nesting has a stronger effect on variability in our model than in Işık et al. (2020). We elaborate on this point further in Sect. 5.
For a more detailed comparison between the simulations and the observations, we binned the distribution of the observed variabilities. Namely, we compared the variabilities returned by our model for a star rotating X times faster than the Sun, with variabilities of a sample of stars with periods in the range [23/X, 27/X] days from the Kepler samples. This comparison is shown in Fig. 15. The histograms in grey and black display the range of variabilities within each of the rotation period bins. We note that the number of stars within each rotation bins decreases from panels a to d. Similarly to Figs. 13 and 14, Fig. 15 shows that the calculations with p = 0 clearly underestimate the variability for the 2Ω⊙ and 4Ω⊙ sub-samples (while the small number of Kepler stars in the 8 Ω⊙ rotation bin makes an interpretation of panel d rather difficult).
For the stars with near-solar rotation periods (i.e the 1Ω⊙ case), there is a substantial difference between the stars in McQ14 and S21. The sample of S21 contains many more stars with variabilities lower than the solar variability at the maximum of cycle 22 (blue curve in the left panel of Fig. 15), while both samples roughly contain the same number of stars that are substantially more variable than the Sun (i.e. the high-variability tail). This result again raises the question of whether the Sun might also become as variable as these stars in the high-variability tail (Reinhold et al. 2020). Moreover, it agrees with the conclusions drawn in Reinhold et al. (2020, 2021) that the solar variability is not unexpectedly low, but that the rotation periods of many stars with similar variabilities have just been missed by previous rotation period surveys (e.g. McQ14).
At the same time, the p = 0.99 FN calculations in Fig. 15 lie towards the upper bound of the variability distribution of the faster rotators while highly overestimating the variability of stars with near-solar rotation periods. Different nesting modes can lead to similar values of median Rvar, especially when the inclination of the stellar rotation axis is not known. This degeneracy might be lifted if alternative metrics were used. We discuss further metrics of characterising stellar variability, including the morphology of the LCs, in Sect. 5.
 |
Fig. 13 Comparison of Rvar as a function of the rotation period between stars with effective temperatures with 5500–6000 K and log g > 4.2 with detection rotation periods from McQ14 (grey dots) and S21 (black dots) and the modelled stars. Each panel includes different nesting probabilities p in the form of AL nesting. The different colours indicate the inclination of the modelled stars. |
 |
Fig. 15 Dependence of Rvar on the inclination. Each panel represents different realisations of the BMR emergence for a given rotation rate. The grey histograms are drawn from the McQ14 stars and the black histograms from the S21 stars, with the limitations of [23/X, 27/X] days for a given rotation rate X in units of the solar rotation (i.e. for X=2, meaning stars with 2Ω⊙, the stars have rotation periods between [11.5,13.5] days). |
5 Discussion
The premise of this work was to extend the solar paradigm to model the distribution of magnetic features on stars rotating faster than the Sun so that these stars might be used to consecutively calculate the stellar LCs and the variability amplitude. Figure 15 shows that while our calculations with a rather high degree of nesting can reproduce most of the variabilities in the Kepler sample, they do not catch the maximum of the variability distribution. This might be because we have used the emergence frequency of BMRs for solar cycle 22 as reference cycle and scaled the emergence frequency as a function of the rotation period based on that cycle (i.e. a star rotating twice as fast as the Sun exhibits twice as many BMR emergences). First, solar cycle 22 does not represent the maximum level of activity the Sun is capable of (see e.g. Usoskin 2017). Second, the activity-rotation scaling itself is rather approximate (see Işık et al. 2018, for more details). We refer here to Işık et al. (2020), who considered the effect of an activity increase on the variability with a considerably simpler model limited to stars with near-solar rotation rates.
Empirical studies suggest that the activity cycles of faster-rotating stars are shorter than the cycle of the Sun at present (Böhm-Vitense 2007). In spite of this, as the main purpose of this study is to model stellar variability on the rotational timescale, we followed the approach of Paper I and assumed for simplicity that the solar temporal profile of activity remains unchanged for the faster rotators. However, we only considered the maximum level of activity (in a 4-yr window during activity maximum; see Fig. 1). Thus, our LCs (and the resulting peak-to-peak variability) correspond to the maximum of the stellar activity cycle and are largely unaffected by the temporal profile of the underlying activity cycle.
Another parameter space that we did not take into account in this study is the effect of stellar fundamental parameters (e.g. the effective temperature and the stellar metallicity). While we limited our sample of Kepler stars to a temperature range of 5500–6000 K, the sample contains stars with a rather broad range of metallicity values. Witzke et al. (2020) have shown that changing the metallicity for a star with a solar activity level enhances the possibility of recovering its rotation period because the star moves beyond the compensation regime between facular and spot contribution on the rotational timescale. It is less intuitively clear, however, how the change in metallicity will affect the calculations presented in this paper. According to our calculations, the rotational variability in the rapid rotators is primarily driven by spots, but the spot component is less affected by the change in metallicity than the facular component (see Witzke et al. 2018, for a more coherent discussion). However, metallicity might affect the activity of a star and the surface distribution of magnetic features (Amard & Matt 2020; Amard et al. 2020; See et al. 2021). This effect is beyond the scope of this study, however.
The emergence latitude calculated through flux-tube simulations (see Sect. 2 and Paper I) places a well-defined lower limit on the emergence latitude, which becomes more visible for fast rotators (see Fig. 1). This is a consequence of the inward-directed Coriolis force in the rotating frame, which consistently acts on rising flux tubes with a prograde azimuthal flow (i.e. they rotate faster than their locality). This leads to a well-defined minimum emergence latitude that corresponds to the minimum non-zero injection latitude near the equator at the base of the convection zone. Whether such a latitudinal gap around the equator occurs on rapid rotators is unknown (see Ṣenavcı et al. 2021, for a discussion), but we would expect that stochastic effects (e.g. convection) can induce scatter around the minimum emergence latitude. This additional scatter probably does not affect the photometric variability to a high degree, however.
A comparison of the different rows in Fig. 5 shows an interesting feature: the spot area coverage is larger for the free nesting mode than for the non-nested case and active longitude nesting. This is because the proximity of neighbouring magnetic flux elements leads to a high possibility of same-polarity encounters. Magnetic flux that accumulates in this way leads to the formation of spots. We note that the possibility of spontaneous spot formation via flux superposition has been detected in numerical simulations (Kitiashvili et al. 2010), but so far, a formation like this has not been observed on the Sun, probably due to its relatively low activity level and the low degree of nesting of solar magnetic features.
Figures 7–11 show that nesting affects not only the amplitude of the variability, but also the morphology of the LCs (see also the discussion in Sect. 3), in parallel with the computations by Işık et al. (2020). For example, in the case of AL nesting, dips in the LCs mainly occur each half of the stellar rotation period. Basri & Nguyen (2018) have introduced the so-called single/double ratio (SDR) metric, which provides information about the ratio of the time a star spends in single- or double-dip modes (i.e. its LC shows one or two peaks per period). The SDR was proposed to be an effective metric for characterising stellar LCs. The SDR as well as other metrics might be useful for testing the models and constraining the distribution of stellar magnetic features. Figure 15 shows that both AL- and FN-type modes of nesting can result in the same amplitude of variability, but at different nesting degrees. Any metric, such as Rvar, which we used here, does not take into account LC morphology because the metrics only measure the peak-to-peak variability. Using metrics that are sensitive to the morphology of the LCs will help to distinguish between various modes of nesting. This will be addressed in a forthcoming publication.
Finally, our calculations were based on the assumption that the size distribution of emerging spots is the same on Sun-like stars and on the Sun, that is, it does not depend on the rotation rate and stellar activity level. Specifically, the source term in Jiang et al. (2011) we used in this study (see step 1 in Sect. 2.1) is based on the sunspot size distribution during solar cycle 22. This neglects the possible dependence of the spot size distribution on the activity level (see e.g. Solanki & Unruh 2004; Krivova et al. 2021). We note that an increase in spot sizes in the source term of the SFTM model would simultaneously amplify the variability of a star and make its LC more regular. Thus, the change in the distribution of emerging spots might be another mechanism that might explain Kepler observations (together with the nesting we investigated). Since the lifetime of sunspots depends on their sizes, a change in the size distribution of spots would also lead to a change in their lifetimes, which would have a very direct effect on the variability amplitude and the LC statistics, with longer-living spots making the LC more regular. In this sense, extending the lifetime of a spot should have a similar effect as stronger nesting. This is an important parameter, whose influence will be studied in a future publication.
6 Conclusions
We coupled the model for the emergence and surface transport of magnetic flux in Sun-like stars (Işık et al. 2018, Paper I) with a model for calculating stellar brightness variations (partly based on the approach presented in Nèmec et al. 2020b). This allowed us to compute the LCs of stars with rotation rates between 1 and 8Ω⊙ as they would be observed by Kepler at different inclination angles. Following up on the findings of Işık et al. (2018) and Işık et al. (2020), we investigated the impact of active-region nesting on the LCs, and in particular, the variability amplitude.
We compared the output of our model to the observed variabilities of Kepler stars in the temperature range 5500–6000 K. In particular, we aimed at explaining the dependence of the variability amplitude on the rotation rate. Recently, Işık et al. (2020) showed that the model without nesting underestimates the variability of stars with known near-solar rotation periods (see also Reinhold et al. 2020). We found that the same is true for stars rotating faster than the Sun. Our runs without nesting dramatically underestimate the stellar variability at all rotation rates.
We showed that the observed dependence of Kepler variabilities on the rotation period for stars with detected rotation periods can be explained by an increase in the nesting degree with rotation rate, in parallel with an increasing activity level. As both modes of nesting we used in this work led to similar levels of variability for stars with different rotation rates, we plan to further investigate the use of metrics that consider LC morphologies (instead of the peak-to-peak variability) to retrieve more information regarding the surface magnetic activity of stars. Additionally, we plan to include the effects of different rotation-activity relations, cycle length, and stellar fundamental parameters (i.e. effective temperature and metallicities) on the variability. The applications of the FEAT model extend beyond stellar photometric variability, which is presented in this work. The model has been adapted to study the astrometric jitter introduced by stellar magnetic activity (Sowmya et al. 2021, 2022) and Doppler imaging (Ṣenavcı et al. 2021). It can also be used to study the magnetic contamination of high- and low-resolution transmission spectra (see e.g. Rackham et al. 2018, 2019, 2022; Dravins et al. 2021).
Acknowledgements
The research leading to this paper has received funding from the European Research Council under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 715947).
References
- Amard, L., & Matt, S. P. 2020, ApJ, 889, 108 [Google Scholar]
- Amard, L., Roquette, J., & Matt, S. P. 2020, MNRAS, 499, 3481 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, in COSPAR Meeting, 36, 3749 [NASA ADS] [Google Scholar]
- Basri, G., & Nguyen, H. T. 2018, ApJ, 863, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Basri, G., Walkowicz, L. M., Batalha, N., et al. 2010, ApJ, 713, L155 [Google Scholar]
- Basri, G., Walkowicz, L. M., Batalha, N., et al. 2011, AJ, 141, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Basri, G., Walkowicz, L. M., & Reiners, A. 2013, ApJ, 769, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. A., Huber, D., van Saders, J. L., et al. 2020, AJ, 159, 280 [Google Scholar]
- Böhm-Vitense, E. 2007, ApJ, 657, 486 [CrossRef] [Google Scholar]
- Bordé, P., Rouan, D., & Léger, A. 2003, A&A, 405, 1137 [Google Scholar]
- Borgniet, S., Meunier, N., & Lagrange, A. M. 2015, A&A, 581, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Cameron, R. H., Jiang, J., Schmitt, D., & Schüssler, M. 2010, ApJ, 719, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 1994, A&A, 281, 817 [NASA ADS] [Google Scholar]
- Dasi-Espuig, M., Jiang, J., Krivova, N. A., & Solanki, S. K. 2014, A&A, 570, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dravins, D., Ludwig, H.-G., & Freytag, B. 2021, A&A, 649, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ermolli, I., Matthes, K., Dudok de Wit, T., et al. 2013, Atmos. Chem. Phys., 13, 3945 [NASA ADS] [CrossRef] [Google Scholar]
- Fligge, M., Solanki, S. K., & Unruh, Y. C. 2000, A&A, 353, 380 [NASA ADS] [Google Scholar]
- Holzwarth, V., Mackay, D. H., & Jardine, M. 2006, MNRAS, 369, 1703 [NASA ADS] [CrossRef] [Google Scholar]
- Isik, E., Solanki, S. K., Krivova, N. A., & Shapiro, A. I. 2018, A&A, 620, A177 [CrossRef] [EDP Sciences] [Google Scholar]
- Isik, E., Shapiro, A. I., Solanki, S. K., & Krivova, N. A. 2020, ApJ, 901, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Järvinen, S. P., Berdyugina, S. V., Korhonen, H., Ilyin, I., & Tuominen, I. 2006, IAU Joint Discussion, 26, 48 [Google Scholar]
- Järvinen, S. P., Korhonen, H., Berdyugina, S. V., et al. 2008, A&A, 488, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffers, S. V., Barnes, J. R., & Collier Cameron, A. 2002, MNRAS, 331, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2011, A&A, 528, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitiashvili, I. N., Kosovichev, A. G., Wray, A. A., & Mansour, N. N. 2010, ApJ, 719, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Krivova, N. A., Solanki, S. K., Fligge, M., & Unruh, Y. C. 2003, A&A, 399, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivova, N. A., Solanki, S. K., Hofer, B., et al. 2021, A&A, 650, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 1992, Rev. Mex. Astron. Astrofis., 23, 23, 45 [Google Scholar]
- Lagrange, A. M., Desort, M., & Meunier, N. 2010, A&A, 512, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsden, S. C., Waite, I. A., Carter, B. D., & Donati, J. F. 2004, Astron. Nachr., 325, 246 [NASA ADS] [CrossRef] [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [Google Scholar]
- Meunier, N., & Lagrange, A. M. 2013, A&A, 551, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A. M., Borgniet, S., & Rieutord, M. 2015, A&A, 583, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nèmec, N. E., Isik, E., Shapiro, A. I., et al. 2020a, A&A, 638, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nèmec, N. E., Shapiro, A. I., Krivova, N. A., et al. 2020b, A&A, 636, A43 [Google Scholar]
- Pojoga, S., & Cudnik, B. 2002, Sol. Phys., 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Rackham, B. V., Apai, D., & Giampapa, M. S. 2018, ApJ, 853, 122 [Google Scholar]
- Rackham, B. V., Apai, D., & Giampapa, M. S. 2019, AJ, 157, 96 [Google Scholar]
- Rackham, B. V., Espinoza, N., Berdyugina, S. V., et al. 2022, ArXiv e-prints [arXiv:2201.09905] [Google Scholar]
- Reinhold, T., Shapiro, A. I., Solanki, S. K., et al. 2020, Science, 368, 518 [Google Scholar]
- Reinhold, T., Shapiro, A. I., Witzke, V., et al. 2021, ApJ, 908, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, Proc. SPIE, 9143, 914320 [Google Scholar]
- Santos, A. R. G., Breton, S. N., Mathur, S., & García, R. A. 2021, ApJS, 255, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Title, A. M. 2001, ApJ, 551, 1099 [Google Scholar]
- Schüssler, M., & Solanki, S. K. 1992, A&A, 264, L13 [NASA ADS] [Google Scholar]
- Schüssler, M., Caligari, P., Ferriz-Mas, A., Solanki, S. K., & Stix, M. 1996, A&A, 314, 503 [NASA ADS] [Google Scholar]
- See, V., Roquette, J., Amard, L., & Matt, S. P. 2021, ApJ, 912, 127 [Google Scholar]
- Senavci, H. V., Kilicoglu, T., Isik, E., et al. 2021, MNRAS, 502, 3343 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., & Unruh, Y. C. 2004, MNRAS, 348, 307 [Google Scholar]
- Solanki, S. K., Krivova, N. A., & Haigh, J. D. 2013, ARA&A, 51, 311 [Google Scholar]
- Sowmya, K., Nemec, N. E., Shapiro, A. I., et al. 2021, ApJ, 919, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Sowmya, K., Nemec, N. E., Shapiro, A. I., et al. 2022, ApJ, 934, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Unruh, Y. C., Solanki, S. K., & Fligge, M. 1999, A&A, 345, 635 [NASA ADS] [Google Scholar]
- Usoskin, I. G. 2017, Living Rev. Solar Phys., 14, 3 [NASA ADS] [CrossRef] [Google Scholar]
- van Saders, J. L., Pinsonneault, M. H., & Barbieri, M. 2019, ApJ, 872, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Waite, I. A., Marsden, S. C., Carter, B. D., et al. 2015, MNRAS, 449, 8 [CrossRef] [Google Scholar]
- Willson, R. C., & Hudson, H. S. 1981, ApJ, 244, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Witzke, V., Reinhold, T., Shapiro, A. I., Krivova, N. A., & Solanki, S. K. 2020, A&A, 634, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willson, R. C., Gulkis, S., Janssen, M., Hudson, H. S., & Chapman, G. A. 1981, Science, 211, 700 [CrossRef] [Google Scholar]
- Witzke, V., Shapiro, A. I., Solanki, S. K., Krivova, N. A., & Schmutz, W. 2018, A&A, 619, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Butterfly diagrams of BMR emergence for 1Ω⊙ (left panel) and 8Ω⊙ (right panel). The colour bar gives the emergence longitudes, and the vertical dashed lines indicate the 4yr of the 11 yr cycle that were considered in our brightness variation calculations. No amount of nesting is included here. |
| In the text | |
 |
Fig. 2 Snapshot of the magnetic field distribution for 1Ω⊙ (top row) and 8Ω⊙ (bottom row) as returned by the FEAT model at various inclination angles around maximum of the activity cycle. The first column shows i = 90°, the second column shows i = 57°, the third column shows i = 30°, and the forth column shows i = 0°. |
| In the text | |
 |
Fig. 3 Butterfly diagrams of BMR emergence for 1Ω⊙, with p = 0.7 in the different nesting modes considered in this work. Top row: AL nesting. Bottom row: FN nesting. The left panels show time-latitude diagrams, with the colour bar indicating the longitudes. The right panels are time-longitude diagrams, with the colour bar indicating the latitude. |
| In the text | |
 |
Fig. 4 Comparison of Rvar (in ppm) as returned by the N20b model and our model. All values are given in ppm. The solid black line gives the linear regression, and the dashed blue line is the one-to-one correspondence between the two models. |
| In the text | |
 |
Fig. 5 Spot area coverage per pixel for different nesting realisations at different viewing angles for the 8Ω⊙ case. First column shows i = 90°, second column i = 57°, third column i = 30°, and forth column i = 0°. Top row is the non-nested case, middle row includes p = 0.7 in the free-nesting (FN) case, bottom row includes p = 0.7 in the active-longitude (AL) case. |
| In the text | |
 |
Fig. 6 Similar to Fig. 5, but showing the facula area coverages. |
| In the text | |
 |
Fig. 7 Synthetic LCs for stars with different rotation rates as they would be observed in the Kepler passband at an inclination of i = 90°. We show non-nested cases (p = 0) with rotation rate values of 1Ω⊙ (blue), 2Ω⊙ (orange), 4Ω⊙ (green), and 8Ω⊙ (red). |
| In the text | |
 |
Fig. 8 Similar to Fig. 7, where the black curves represent the calculations with p = 0 for each rotation rate, and the coloured curves represent calculations to which AL-type nesting at p = 0.7 was added. |
| In the text | |
 |
Fig. 9 Similar to Fig. 8 with AL-type nesting and p = 1. |
| In the text | |
 |
Fig. 10 Similar to Fig. 8, with free nesting and p = 0.7. |
| In the text | |
 |
Fig. 11 Similar to Fig. 8, with free nesting and p = 0.99. |
| In the text | |
 |
Fig. 12 Similar to Fig. 7 for different inclination shown in three columns for i = 90°, 60°, and i = 30°. |
| In the text | |
 |
Fig. 13 Comparison of Rvar as a function of the rotation period between stars with effective temperatures with 5500–6000 K and log g > 4.2 with detection rotation periods from McQ14 (grey dots) and S21 (black dots) and the modelled stars. Each panel includes different nesting probabilities p in the form of AL nesting. The different colours indicate the inclination of the modelled stars. |
| In the text | |
 |
Fig. 14 Similar to Fig. 13, with different degrees of FN. |
| In the text | |
 |
Fig. 15 Dependence of Rvar on the inclination. Each panel represents different realisations of the BMR emergence for a given rotation rate. The grey histograms are drawn from the McQ14 stars and the black histograms from the S21 stars, with the limitations of [23/X, 27/X] days for a given rotation rate X in units of the solar rotation (i.e. for X=2, meaning stars with 2Ω⊙, the stars have rotation periods between [11.5,13.5] days). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


