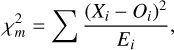| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 25 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202244189 | |
| Published online | 17 April 2023 | |
Barium stars as tracers of s-process nucleosynthesis in AGB stars
II. Using machine learning techniques on 169 stars
1
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences (CSFK), ELKH,
Konkoly Thege M. út 15–17,
1121
Budapest,
Hungary
e-mail: ayaguelopez@lanl.gov
2
CSFK, MTA Centre of Excellence,
Konkoly Thege Miklós út 15–17,
Budapest
1121,
Hungary
3
Computer, Computational and Statistical Sciences (CCS) Division, Center for Theoretical Astrophysics, Los Alamos National Laboratory,
Los Alamos,
NM 87545,
USA
4
MTA-ELTE Lendület “Momentum” Milky Way Research Group,
Hungary
5
E. A. Milne Centre for Astrophysics, University of Hull,
Hull,
7RX,
UK
6
ELTE Eötvös Loránd University, Institute of Physics,
Pázmány Péter sétány 1/A,
Budapest
1117,
Hungary
7
Observatório Nacional/MCTI,
Rua General José Cristino, 77,
20921-400,
Rio de Janeiro,
Brazil
8
Laboratory of Observational Astrophysics, Saint Petersburg State University,
Universitetski pr. 28,
198504,
Saint Petersburg,
Russia
9
Laboratório Nacional de Astrofísica/MCTI,
Rua dos Estados Unidos 154, Bairro das Nações,
37504-364,
Itajubá,
Brazil
10
School of Physics and Astronomy, Monash University,
VIC
3800,
Australia
11
Joint Institute for Nuclear Astrophysics – Center for the Evolution of the Elements,
640 S Shaw Lane,
East Lansing MI
48824,
USA
Received:
4
June
2022
Accepted:
28
November
2022
Context. Barium (Ba) stars are characterised by an abundance of heavy elements made by the slow neutron capture process (s-process). This peculiar observed signature is due to the mass transfer from a stellar companion, bound in a binary stellar system, to the Ba star observed today. The signature is created when the stellar companion is an asymptotic giant branch (AGB) star.
Aims. We aim to analyse the abundance pattern of 169 Ba stars using machine learning techniques and the AGB final surface abundances predicted by the FRUITY and Monash stellar models.
Methods. We developed machine learning algorithms that use the abundance pattern of Ba stars as input to classify the initial mass and metallicity of each Ba star’s companion star using stellar model predictions. We used two algorithms. The first exploits neural networks to recognise patterns, and the second is a nearest-neighbour algorithm that focuses on finding the AGB model that predicts the final surface abundances closest to the observed Ba star values. In the second algorithm, we included the error bars and observational uncertainties in order to find the best-fit model. The classification process was based on the abundances of Fe, Rb, Sr, Zr, Ru, Nd, Ce, Sm, and Eu. We selected these elements by systematically removing s-process elements from our AGB model abundance distributions and identifying the elements whose removal had the biggest positive effect on the classification. We excluded Nb, Y, Mo, and La. Our final classification combined the output of both algorithms to identify an initial mass and metallicity range for each Ba star companion.
Results. With our analysis tools, we identified the main properties for 166 of the 169 Ba stars in the stellar sample. The classifications based on both stellar sets of AGB final abundances show similar distributions, with an average initial mass of M = 2.23 M⊙ and 2.34 M⊙ and an average [Fe/H] = −0.21 and −0.11, respectively. We investigated why the removal of Nb, Y, Mo, and La improves our classification and identified 43 stars for which the exclusion had the biggest effect. We found that these stars have statistically significant and different abundances for these elements compared to the other Ba stars in our sample. We discuss the possible reasons for these differences in the abundance patterns.
Key words: stars: abundances / nuclear reactions, nucleosynthesis, abundances / stars: AGB and post-AGB / binaries: spectroscopic / stars: late-type / methods: statistical
NuGrid Collaboration, http://nugridstars.org
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Barium (Ba) stars are part of binary systems (McClure et al. 1980; McClure 1983), and their companions are white dwarfs that went through the asymptotic giant branch (AGB) phase (for reviews on AGB stars, see Herwig 2005; Straniero et al. 2006; Karakas & Lattanzio 2014). The spectra of Ba stars show enhanced abundances of slow neutron capture (s-process) elements that are heavier than Fe as compared to solar abundances (Bidelman & Keenan 1951). It is commonly accepted that the overabundance of these s-process elements is due to mass transfer from the (former AGB) companion star.
There are two neutron source reactions in AGB stars that can provide the neutrons for the s-process. The first is the 13C(α,n)16O reaction, which produces the neutrons in the 13C-rich region (13C-pocket) between the He- and H-burning shells in the AGB star. The second neutron source is 22Ne(α,n)25Mg, which produces only a small number of neutrons compared to the 13C-pocket and is activated in the thermal pulses, which are recurrent convective episodes of He-burning. The 22Ne neutron source produces higher neutron densities than the 13C neutron source, which allows for the activation of branching points along the s-process path (e.g. Bisterzo et al. 2015). The s-process abundances made in the He intershell are brought to the surface by the third dredge-up event (e.g. Gallino et al. 1998). The characterisation of the s-process signature in AGB stars is commonly obtained by comparing the s-process production at the first s-process peak (neutron magic number N = 50, including Sr, Y, and Zr) and at the second s-process peak (neutron magic number N = 82, including Ba, La, and Ce) and either deriving an average production or using individual elements from the two peaks (Busso et al. 2001; Cseh et al. 2018; Lugaro et al. 2020).
Homogeneous observations of Ba stars were limited until the study of de Castro et al. (2016) was published. In that work, the high-precision spectra of 182 Ba star candidates were presented as observed and analysed in a self-consistent manner. Error bars for the ratios of the first and second peak s-process elements were calculated by Cseh et al. (2018). Those authors also found that for each specific metallicity, a spread of about a factor of three is present in the ratios. This range needs to be explained by variations in the physical features, such as initial mass and internal mixing.
As the complete s-process pattern of stellar evolution models carries the signatures of those abovementioned features (for an extensive review, see Karakas & Lattanzio 2014), it should therefore be possible to infer the initial AGB mass and metallicity, as well as other physical features, by comparing the individual abundance patterns of Ba stars to single AGB models. However, the pattern cannot be directly compared with the s-process patterns of AGB models. The reason is that the material in the envelope of the Ba star is a mixture of its original envelope and the accreted material from the AGB star donor. To account for this mixture, we must modify the s-process patterns in the AGB final surface abundances by a dilution factor.
Cseh et al. (2022, henceforth Paper I) started the process of matching individual spectra with single models by applying a simplified method of matching the models to the determined [Ce/Fe] abundances. The authors investigated 28 of the Ba stars in the sample of de Castro et al. (2016) for which it was possible to more accurately determine the masses (Jorissen et al. 2019) using Gaia DR2 data (Gaia Collaboration 2018). Jorissen et al. (2019) estimated the masses of the Ba star companions, the white dwarfs, by using assumptions of the inclination of the binary system and the mass ratio of the two binary stars. Using an initial-final mass relation (El-Badry et al. 2018), it was then possible to estimate the initial mass of the companion stars and thus the initial mass of the AGB models. Of the 28 Ba stars, the authors of Paper I were able to find good matches with the models for 21 Ba stars and independently confirmed the initial AGB mass estimate for the stars from Jorissen et al. (2019). The authors of Paper I also reported some problems. For instance, for 16 of the 21 Ba stars, the observed abundances of Nb, Ru, Sm, Mo, and/or Nd were higher than predicted. Furthermore, three stars were matched to AGB models with a lower mass than those of Jorissen et al. (2019). Finally, four stars showed higher first s-process peak abundance values than in the AGB models.
Comparing all the Ba stars to all the AGB models of FRUITY and Monash one by one without any information on the initial AGB mass is a time consuming task and prone to human bias. Indeed, the full set of 169 Ba stars would have to be compared to the thousands of diluted AGB final surface abundances. The use of modern machine learning (ML) techniques allows us to not only automatise this classification process but perform it faster while also removing the risk of human bias. ML techniques are increasingly common, as data sets in astronomy keep increasing in size. A recent example of using ML techniques in astronomy is Karinkuzhi et al. (2021), who compare the use of ML techniques to manual analysis in the identification of s-process enrichment in Ba stars.
The aim of this paper is to identify the main features of the old AGB star companions of 169 Ba stars by comparing observations to theoretical AGB models. The structure of the paper is as follows: in Sect. 2, we describe our data sets of Ba star spectra and sets of AGB final surface abundances. In Sect. 3, we present our full pipeline of algorithms and the set of elements we include in our pipeline. In Sect. 4, we compare the results of our classification methods to those in Paper I. Then, in Sect. 5, we apply the classification process to the full set of 169 stars, draw statistics, and show the peculiar cases. In Sect. 6, we focus on understanding why the exclusion of certain elements leads to better classifications. We present our conclusions in Sect. 7.
2 Data sets
2.1 Abundances of Ba stars
For the verification and validation of our classification algorithms, we used the same set of 28 Ba stars from Paper I. These 28 stars are the overlap of the samples of de Castro et al. (2016); Roriz et al. (2021a,b) and Jorissen et al. (2019). As a result, we have for those stars a large set of self-consistently derived abundances and independent estimates of the initial mass of the AGB star and the mass of the Ba star observed today in the binary system. The mass estimates provided an extra constraint for the models and sped up the manual classification process in Paper I by reducing the pool of possible models. Because we did not have the mass estimates for all 169 Ba stars, we did not include them in our classification algorithms. Instead, the initial masses of the AGB stars are a result of our classification algorithms.
After verifying and validating the algorithms, we used them to classify the full set of Ba stars. All stars were observed with FEROS (Fiberfed Extended Range Optical Spectrograph, R = 48 000, Kaufer et al. 1999), which allowed us to derive a large set of elemental abundances around the s-process peaks as well as light elements (for discussion on these elements, see de Castro et al. 2016; Roriz et al. 2021a,b; Cseh et al. 2022). A total of 182 stars were analysed by de Castro et al. (2016), from which 169 stars were found to be Ba stars. These stars comprise our whole set, and for most of the stars, s-process elemental abundances are available for Rb, Sr, Y, Zr, Nb, Mo, Ru, La, Ce, Nd, Sm, and Eu.
For the elements whose abundances were derived using three or more lines, we included the observational error bars from the spectral measurements (for details, see Roriz et al. 2021b). For some elements, the abundances were derived using fewer than three spectral lines. In these cases, we adopted an artificial error bar of 0.5 dex to account for the fact that the measurement was uncertain. When Rb was not available, we added an artificial Rb abundance of 1 ± 1 dex.
We note that seven stars (HD 749, HD 5424, HD 12392, HD 116869, HD 123396, HD 210709, and HD 223938) have also been published by Allen & Barbuy (2006). Overall, we found our abundance values of these stars to be in agreement (mostly within the error bars, where available) with Allen & Barbuy (2006) and Allen & Porto de Mello (2007) data, which used the same ionisation states for the elements. The largest discrepancy, however, is between the Ru abundances for HD 12392, as Roriz et al. (2021b) reported 0.74 ± 0.26 dex, while Allen & Porto de Mello (2007) derived 1.41 dex for the same star.
2.2 AGB final surface abundances
The AGB final surface abundances included in our comparison are from two extensive sets of AGB stellar nucleosynthesis models: FRUITY1 (Cristallo et al. 2009b, 2011, 2015; Piersanti et al. 2013) and Monash (Lugaro et al. 2012; Fishlock et al. 2014; Karakas & Lugaro 2016; Karakas et al. 2018). We have included all initial stellar masses Mini (ranging from Mini 1.25 to 8 M⊙) and all initial metallicities Zini (ranging from 0.0028 to 0.03) of both sets of AGB final surface abundances. Furthermore, we included the slow rotating models with an initial rotational velocity at or below 60 km s−1, even though evidence may suggest that those models rotate too fast during the AGB phase (see den Hartogh et al. 2019). Finally, we note that Monash and FRUITY models use different methods and assumptions to inject protons in the He intershell to create the 13C-pocket. Monash inserts an artificial mixing profile, which is the same in each thermal pulse, while FRUITY allows for the creation of the profile by free parameters based on physical mixing processes.
The AGB final surface abundances cannot be directly compared to the abundances derived from the spectra of the Ba stars. As explained in the introduction of this paper, a dilution factor has to be included. The diluted abundances are given by
where [X/Fe]ini is the initial abundance of element X, [X/Fe]AGB is the final surface abundance of the AGB model, and δ is the effect of dilution, which we treat as a free parameter and relates to the dilution factor, dil, as δ = 1/dil. We limited δ to a maximum of 0.9, as done in Paper I, because higher values imply that the Ba star envelope is (almost) entirely composed of AGB material. We assumed the initial abundances follow a scaled solar distribution, which makes [X/Fe]ini = 0 in Eq. (1). We diluted each model within our sets of AGB final surface abundances with δ = [0, 0.9] in increments of 0.002, creating a grid of diluted AGB final surface abundances. We removed diluted abundance distributions from the analysis if they were identical within the first three decimals to other abundance distributions derived from the same AGB model. AGB final surface abundances where the maximum [X/Fe] value of all the included elements is below 0.2 were also excluded, as those are considered to be not enriched enough in s-process nucleosynthesis.
2.3 Correlations between elements
We performed an initial comparison of the correlation coefficients between the different elements within one data set, and we then performed this comparison for the Ba stars and the two sets of AGB final surface abundances. We included only Fe and elements heavier than Fe in the comparison, and we did not include the error bars when analysing the observed data. The resulting correlation matrices are shown in Fig. 1.
In all three data sets, [Fe/H] is negatively correlated with the other elements (red shaded boxes), and all the other elements are positively correlated with each other (blue shaded boxes). Strong positive correlations are found in all data sets, but the patterns are different. As we mentioned in Sect. 2.2, the profiles and subsequent 13C-pockets in the FRUITY models are less homogeneous than in the Monash models. Therefore, the s-process patterns in the AGB final surface abundances of FRUITY are also less homogeneous than the s-process patterns in the AGB final surface abundances of Monash.
In the AGB final surface abundances of FRUITY, we found strong positive correlations between all the first peak elements and again between all the second peak elements. The AGB final surface abundances of Monash (middle panel) show strong correlations (above 0.9) between all the first peak elements, all the second peak elements, and also between the two peaks. In contrast, the correlations between the observed abundances show weaker correlations, and only the second peak elements are strongly correlated with each other and with Zr. Thus, based on these initial results, there seems to be a difference between the Ba star observations and our theoretical understanding of the nucleosynthesis in the first s-process peak. However, we do not know if this difference is due to observational uncertainties or theoretical limitations.
3 Algorithms
We used two different classification algorithms: the first is an artificial neural network (ANN) ensemble (Sect. 3.2), while the second is a nearest-neighbour classification algorithm (Sect. 3.3). The motivation for using two algorithms was to supplement their respective shortcomings. The nearest-neighbour algorithm finds the closest fitting model without regard for any particular pattern, while the ANN ensemble is more sensitive to the pattern and therefore might fail to find a match for an observed set of abundances if the pattern in that set does not match the patterns within the AGB final surface abundances.
In the following sections, we first provide a visualisation of the classification problem. Then, we introduce the classification algorithms in Sects. 3.2 and 3.3. Next, we cover how we combined their results in Sect. 3.4. At the end of this section, we introduce the set of elements we used in our classification.
3.1 Visualisation of classification challenge
We visualise our classification problem in Fig. 2, where we show the set of AGB final surface abundances of Monash and the set of Ba star observations after reducing them into two dimensions. This was done using principal component analysis, which is a procedure that converts observations of correlated features into an often smaller set of linearly uncorrelated features. For one star, we also show the results of Monte Carlo sampling the error bars on the observed abundances, which we explain in detail in Sect. 3.3. From this figure, we can identify two potential issues: (1) several observed Ba stars fall outside the parameter space covered by the set of AGB final surface abundances, and (2) some of the diluted models become indistinguishable from each other. The same issues are present when using the set of AGB final surface abundances of FRUITY instead of the Monash set.
The first issue is probably due to the observed spectra showing abundance trends that the models cannot match. This may be caused by present limitations in the theoretical AGB nucleosynthesis models and/or by observational uncertainties. Our classification algorithms can thus identify abundance patterns of Ba stars that might be difficult to classify, which allows us to further specify the features that are present in the AGB final surface abundances but not in the Ba stars and vice versa. The second issue can be improved either by grouping similar AGB final surface abundances and giving the group one name or labelling at the start or at the end of the classification pipeline, or by using a technique to classify the observed spectra that does not require the AGB final surface abundances to be named.
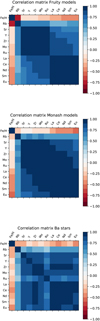 |
Fig. 1 Correlation matrix demonstrating linear relationship between pairs of elements in AGB final surface abundances of FRUITY (top panel), Monash (middle panel), and observed Ba star sample (bottom panel, excluding the error bars on the observations). The stronger the correlation, the darker the color of the boxes. Blue shaded boxes: positive correlation. Red shaded boxes: negative correlation). |
 |
Fig. 2 Visualisation of diluted AGB final surface abundances set of Monash (black circles, dilution increments of 0.01 instead of 0.002 to improve the visibility of the figure) and subset of 28 Ba stars (blue stars). Principal component analysis (see text for explanation) was used to reduce the dimensions of the AGB final surface abundances sets and derive abundances to only two linearly uncorrelated dimensions, x1 and x2, that do not have a physical meaning. For one star, BD −14°2678 (blue diamond), we plotted the results of Monte Carlo sampling of the error bars on the abundances (red circles, showing 500 samples), for details see Sect. 3.3. |
3.2 Artificial neural networks
We used Tensorflow (Abadi et al. 2016) to create our ANN ensembles, one for each set of AGB final surface abundances. The training, cross-validation, and testing sets were 56%, 24%, and 20% of either diluted set, respectively. Before using a certain set of AGB final surface abundances, the set was balanced and randomly shuffled. For the training of the networks, we grouped all the models with the same initial mass and metallicity in one short label. The reason for this was that the models with same mass and metallicity only differ in parameters such as 13C-pocket size and (low) rotational velocity, and these variations in the abundances are often already accounted for in the dilution process.
We trained our network with a randomly selected 56% of the diluted set of the AGB final surface abundances, as introduced in Sect. 2.2. Therefore, the values for the initial mass of the 28 stars (as presented in Jorissen et al. 2019) are not included in our algorithms.
The typical accuracy of a single ANN was around 95% for both the FRUITY and Monash ANN. For the input layer, we used a number of nodes equal to the number of elements we used to classify plus all the possible unique pairs of elements2. We also included a dropout rate of 30%, which represents the probability of training a node in a particular training iteration to reduce the chance of overriding. We did not use mass and metallicity as input variables. The number and size of hidden layers is different for each set of AGB final surface abundances. For the FRUITY set, we used a single hidden layer 100 times the size of the output layer, which has 65 nodes (one per FRUITY label). For the Monash set, we used two hidden layers ten times the size of the output layer, which has 69 nodes. Every hidden layer had a dropout rate of 30%. A FRUITY ANN was trained with four epochs and a learning rate of 0.001, while a Monash ANN was trained with two epochs and a learning rate of 0.0015. For both cases, we used the Tensorflow RMSprop optimisation algorithm.
Our ANN ensembles are a collection of 20 ANNs for each set of AGB final surface abundances. We saved the predictions from all the networks so that we would have more than one classification for each observation. This is not the standard method when including ensembles of neural networks. usually when ensembles are used, the ensemble output layer is calculated as the median of each individual ANN output layer node-wise. However, this procedure may hide relevant statistical information from the ensemble that could be useful when obtaining a range of masses and metallicities for our classification. Therefore, we instead took the classification of each ANN in the ensemble. When all ANNs agreed on the classification, there was only one match from the whole ensemble to compare to the outcome of the nearest-neighbour algorithm, leading to smaller ranges in the overlapping classification. When the ANNs did not agree, there were collections of matches from the ensemble to compare to the outcome of the nearest-neighbour algorithm, leading to larger ranges in the overlapping classification.
When classifying the observations with the ensembles, a value of 1 dex (with an error of 1 dex) was used for a missing abundance3. This was the case in seven of the 169 Ba stars. This approach is necessary due to the ANNs requiring all the inputs for the classification process. The arbitrary value and error bar did not pose a problem for the classification because of the dropout regularisation used during the training, as long as the substituted values were less than 30% of the total.
3.3 Nearest-neighbour and goodness of fit
The nearest-neighbour algorithm takes each set of AGB final surface abundances and calculates the goodness of fit (GoF) of all diluted AGB final surface abundances. The output of the algorithm is the set with the highest GoF and the corresponding dilution.
In the literature, one common way of calculating the GoF of AGB final surface abundances for a given observed Ba spectra is through the χ2-test. However, as stated by Abate et al. (2015a) and Stancliffe (2021), using χ2 for the GoF is ‘naive’ because the observed abundances of the different s-process elements cannot be correctly modelled as normal independent distributions. In addition, an observed value of zero indicates no detection in a traditional χ2 test, while in [X/Fe] notation it simply indicates that the abundance over iron scales like solar abundances.
To compensate for these two shortcomings, we decided to use a modified χ2-test. Thus, we first divided by the 1σ uncertainty value instead of the observed value,
where Xi and Oi are the predicted and observed abundances for element i and Ei is the observational uncertainty. The index i only represents the elements considered in the classification (see Sect. 3.5). By dividing by the observational uncertainty, the test weights by how accurate an observation is. The more the predicted and observed abundances agree, the smaller the 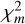 value is. The GoF was then calculated from a tail distribution of
value is. The GoF was then calculated from a tail distribution of 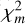 values (see Eq. (2)) calculated for random samples of the observed abundances (the creation of the tail distribution is explained in the next paragraph). The tail distribution is 1 − CDF, where CDF is the cumulative distribution function of all calculated
values (see Eq. (2)) calculated for random samples of the observed abundances (the creation of the tail distribution is explained in the next paragraph). The tail distribution is 1 − CDF, where CDF is the cumulative distribution function of all calculated 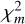 values. The GoF of an AGB model for a given star is the value of this observation-derived tail distribution at the point where
values. The GoF of an AGB model for a given star is the value of this observation-derived tail distribution at the point where 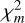 is equal to the given diluted AGB model. Thus, the smaller the value for
is equal to the given diluted AGB model. Thus, the smaller the value for 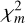 , the higher the value for the GoF.
, the higher the value for the GoF.
To create the tail distribution, we used a Monte Carlo method to generate 105 possible predictions Xi out of the observed values Oi. We took into account that the abundances depend on the atmospheric parameters by randomly sampling the atmospheric parameters from normal distributions and propagated these uncertainties into the Oi to generate Xi. We used the generated Xi in Eq. (2) to calculate the tail distribution that would be compared to our predicted models.
The dependency of the abundance determinations with the physical parameters was taken as an average of Tables 8–10 from de Castro et al. (2016) and Tables 2–4 from Roriz et al. (2021b). The final distributions for the abundances were normalised such that the median is equal to Oi and the standard deviation is equal to Ei. Finally, we rejected all classifications with a GoF below 50% and saved the five models with the highest GoF values.
3.4 Combining the classifications
With our algorithms, we classified our set of Ba stars. This led to a set of four files (two per set of AGB final surface abundances) with the results for all Ba stars. The four different classification sets were then combined into one classification for each star and for each set of predicted AGB abundances. This classification includes a mass range, a metallicity range, and the minimum of the GoF values from the shortest distance algorithm. In order to define the mass and metallicity ranges, we collected all the masses and metallicities from the two classifications of each set of AGB abundances. Then, we identified the overlapping values within the mass and metallicity ranges defined independently. We did this separately for the FRUITY and Monash sets, selecting the overlap between the classification from the nearest-neighbour algorithm and of the ANN ensemble for each star. Thus, if the nearest-neighbour classification using the Monash set resulted in a mass range of 2.0−3.0 M⊙ and the ANN ensemble using the Monash set resulted in a range of 2.5−3.0 M⊙, then the table of Monash classifications would list 2.5−3.0 M⊙ as the overlapping mass range.
For some stars, the overlapping range has only one value (e.g. 2.5 M⊙). This is because our sets of AGB final surface abundances are discrete and often have gaps of 0.5 M⊙ between consecutive masses. To correct for this, we broadened the final ranges slightly. We added (subtracted) 0.25 M⊙ to (from) the maximum (minimum) of our determined mass range and multiplied (divided) the maximum (minimum) of our determined metallicity range by 1.7. These factors are based on the values for the initial mass and metallicity that were present in our sets of AGB final surface abundances and were chosen to close the gaps between the initial values of the mass and metallicities present in the sets. After applying these factors, we had our final classifications. All algorithms as well as the four different sets of classifications can be found online4.
3.5 Elements used in classification
The abundances of 21 elements were measured from the spectra of the Ba star sample considered in our analysis. However, this paper focuses on the s-process classification, and we thus eliminated all elements lighter than Fe. That left us with 13 elements. Finally, we also excluded Nb since this element is often shown to have an observed abundance much higher than theoretical s-process predictions (Cseh et al. 2022).
As mentioned in Sects. 2.3 and 3.1, there might be trends in the observed data that are not present in the AGB final surface abundances and vice versa. We aimed to match all Ba stars with an s-process pattern, and we thus wanted to exclude the elements that decrease the GoF of our classifications. To determine which elements to exclude, we systematically removed elements from set A and kept those with the highest improvement on the accuracy of the networks when compared to the full set. The results indicated that Mo and then La and Y, in that order, are the elements with the highest impact on the nearest-neighbour algorithm accuracy for both FRUITY and Monash ensembles. Therefore, we defined a new set, set F (‘F’ for final), by removing Mo, La, and Y from set A. Removing more elements had marginal effects on the overall accuracy. set F is therefore defined by Fe, Rb, Sr, Zr, Ru, Nd, Ce, Sm, and Eu.
While there are difficulties when measuring Sr related to blending with CN molecules, we have included this element because Roriz et al. (2021b) carefully selected Sr lines free from contamination of the other elements/molecules. Furthermore, NLTE effects on Sr at solar metallicity lead to a correction of approximately ±0.1 dex (Bergemann et al. 2012), which is less than its typical ±0.3 dex error bar.
In Fig. 3, we show the distribution of GoF values for the classifications using the nearest-neighbour algorithm for each set of AGB final surface abundances. Differences between the distributions of set A and set F are clear: (1) the median values are higher when using set F instead of set A; (2) there are fewer identifications with a GoF below 50% in set F than in set A; and (3) the distribution peaks at a higher value in set F compared to set A.
Finally, we note that our method of selecting the elements exploits the fact that a decrease in the GoF when a specific element is included is an indication that either (1) this element does not have a pure s-process origin, (2) the observations have issues (Sect. 6.2), or (3) the models are missing relevant physics, affecting the abundance pattern (e.g. missing neutron fluxes; see discussion and models in Sect. 6.3). Our approach of changing the list of elements to maximise the GoF allows us to discover which of the observed elements do and do not display the patterns predicted by the models. We removed elements individually in order to avoid the effects of any previous bias (e.g. what is an s-process element and what is not and lines that are known to be problematic to measure).
 |
Fig. 3 Histograms of GoF distributions for set A (top panel) and set F (bottom panel). The results are shown for the output of the nearest-neighbour algorithm and for the AGB final surface abundances of FRUITY (yellow) and Monash (blue). The solid black line marks the 50% GoF, and the dashed lines are the median values of the two sets of AGB final surface abundances. |
4 Classification of the 28 Ba stars considered in Paper I
In this section, we discuss how we validated the ML algorithms by classifying the 28 stars previously analysed in Paper I. We first present our classification based on the ML algorithms, and we compare our results with Paper I. Finally, we discuss the seven Ba stars where we found a different initial mass for the AGB companion compared to the analysis of Jorissen et al. (2019; Groups 2 and 3 in Paper I).
4.1 Classification of the 28 stars with our algorithms
The final classifications of the subset of 28 stars are shown in Table 1. When comparing the results of Paper I with our final classifications, we found a different mass range for the AGB star companions of four stars: HD 18182, HD 84678, HD 107541, and HD 134698. We found a mass range different from Paper I for both sets of stellar AGB abundances. These four stars are listed among the seven reported by Paper I as being difficult to identify (we discuss these stars in more detail in Sect. 4.2). For the other 24 stars, there is least one final classification that agrees with Paper I. Therefore, we verified the capabilities of the ML algorithms implemented in the present analysis.
Another method to check our algorithms and their results involves comparing the metallicity ranges of the final classifications to the metallicity derived from observations. The calculated [Fe/H] should be within the error bar of the observed values. This is the case for 27 (26) of the 28 final classifications using Monash (FRUITY) predictions. The exceptions are HD 84678 and HD 18182, which are both amongst the four stars that are discussed in more detail in the following section. Thus, also from this comparison, we can conclude that our algorithms provide accurate classifications.
Final classification of the subset of 28 stars.
 |
Fig. 4 Comparison between observed abundanced and classifications plus the residuals of the classifications. Top panel: comparison between the observed abundances (star symbols where red/yellow symbols are elements that are included/excluded in our classification) and results (lines) of nearest-neighbour algorithm. Bottom panel: residuals of the classification (i.e. observed abundance minus predicted abundance for each element). This star is difficult to classify because the abundances in the first s-process peak are higher than predicted by the best-fit models. |
4.2 Four challenging classifications: HD 18182, HD 84678, HD 107541, and HD 134698
The mass and metallicity ranges found for HD 18182 in Paper I for both sets of AGB final surface abundances were similar to the observed values: a mass of 1.5−2 M⊙ and a metallicity of [Fe/H] = −0.24 or −0.15. However, the observation-derived values are 1.9 M⊙ and the metallicity is −0.17 ± 0.10. Our final classification using the Monash (FRUITY) set contains a mass range of 2.25 to 2.75 (2.5−3.5) M⊙ and a metallicity range of −0.23 to 0.23 (0.1−0.23). Thus, the Monash values fit the observed values better. The minimum GoF of the final classification using the Monash set is 78%, and using the FRUITY set, it is 68% (see Table 1 and Fig. 4). In the figure, we only show the classifications of the nearest-neighbour algorithm. As for the ANN, we grouped the predicted abundances with the same initial mass and metallicity into one label; thus this label does not correspond to a single set of abundances, and only a single set of abundances can be added to the figure. We generated short model names to make our figures more readable and to easily identify specific AGB models. Those names are summarised with the relevant model parameters in Tables C.1 and D.1. When comparing the models with observations, the observed [Mo/Fe] is not matched, which affects the overall fit of the observed abundance trend.
The second challenging star is HD 84678 (see Fig. 5). The main reason is that the focus in the manual classification was on models with an initial mass close to the mass derived from binary parameters (M = 3.8 M⊙). The conclusion in Paper I is that the initial mass should be below M = 2.5 M⊙, although there was only one match found in Paper I with M = 2.5 M⊙. Our final classifications using both sets of AGB final surface abundances agree on an initial mass of 1.75 M⊙ and an initial metallicity range of [Fe/H] = −0.23 to −0.07, which overlaps with the observed metallicity range of −0.13 ± 0.16. The minimum GoF is only 50% and 52% for the two sets of AGB final surface abundances, which is due to the high values of [Nd/Fe] and [Sm/Fe] in combination with the low value for [Eu/Fe]. The classification of the second s-process peak is thus still an issue.
The third star to discuss is HD 107541 (see Fig. 6). Paper I did not find a good agreement between models and the star because the masses derived from binary parameters point at an initial mass lower than M = 2 M⊙. Our algorithms, however, agreed on a final classification of M = 2.25 to 2.75 M⊙ and [Fe/H] = −0.54 to −0.47, with a GoF of at least 62%. Thus, the mass derived from binary parameters is likely too low.
The last star to discuss is HD 134698 (see Fig. 7). No classification was found for this star in Paper I. The mass derived from binary parameters is M = 1 .2 M⊙. However, current stellar models with such low initial masses do not develop third dredge-up events during the AGB phase, and their envelope does not become s-process rich. The final classification using the Monash (FRUITY) set has an initial mass range of M = 1.25 to 3.25 M⊙ (3.25−3.75 M⊙) and an initial metallicity range of [Fe/H] = −0.91 to −0.14 (−0.23 to −0.07). The mass and metallicity derived from binary parameters for this star are M = 1.2 M⊙ and [Fe/H] = −0.52 ± 0.12. These values are thus both matched by the final classification using the Monash AGB final surface abundances.
In summary, we can classify these four stars by using our ML tools. However, issues remain in fitting the element abundance patterns.
5 Classification of the full set of Ba stars
In this section, we present the classifications of the full set of Ba stars and the statistics of these classifications. We present the Ba stars for which we have final classifications, one for the Monash AGB models and/or one for the FRUITY AGB models, in Sect. 5.1. In Sect. 5.2, we discuss the stars for which we do not have a final classification constructed from the overlap in mass range and metallicity of the outcomes from the ANNs and the nearest-neighbour algorithm.
 |
Fig. 5 Same figure format as in Fig. 4. This star was difficult to classify manually because the binary-derived AGB mass is higher than the initial masses of the best-fit models (Group 3 stars in Paper I). We were able to classify this star with our algorithms, indeed with models with initial masses lower than the binary-derived value, but matching the observed values in the second s-process peak is still an issue. |
 |
Fig. 6 Same figure format as in Fig. 4. This Ba star was difficult to classify manually because the abundances in the first s-process peak are higher than predicted by the best-fit models (Group 2 stars in Paper I). We were able to classify it using models with slightly higher initial masses than their mass derived from binary parameters. |
 |
Fig. 7 Same figure format as in Fig. 4. This star is one of the four Ba stars that was difficult to classify manually because the abundances in the first s-process peak are higher than predicted by the best-fit models (Group 2 stars in Paper I). We found a final classification for this star with our algorithms. However, [Nb/Fe] is too high to be matched by our AGB final surface abundances. |
 |
Fig. 8 Distributions of final classifications for both sets of AGB final surface abundances. From top to bottom we show the distributions for the (1) metallicities, (2) masses, and (3) minimum GoFs of the classifications as listed in the tables in Appendix A. The left column shows the distribution for FRUITY and the right column shows those for Monash. |
5.1 Ba stars for which classifications overlap
Our final classifications of both sets of AGB final surface abundances are listed in Tables A.1 and B.1. Using both FRUITY and Monash AGB models, 85% of the [Fe/H] observed values are consistent with our results within 0.02 dex. Since we do not have initial mass estimates for the full set of 169 Ba stars to compare with, we cannot perform the comparison between masses.
The distributions of the mass and metallicity ranges of the final classifications are shown in Fig. 8. In particular, the final classifications of FRUITY and Monash are shown to peak in the same bin for both the same mass and metallicity. The mean and standard deviation for the mass of the final classifications using the FRUITY set are M = 2.23 and 0.44 M⊙, respectively, and for the metallicity, they are [Fe/H] = −0.21 and 0.18, respectively. For the final classifications using the Monash set, the mean and standard deviation for the mass are M = 2.34 and 0.52 M⊙, respectively, and for the metallicity, they are [Fe/H] = −0.11 and 0.19, respectively. The distributions are not the same (as expected from Sect. 2.3).
Figure 8 also shows the distributions for the minimum value of the GoFs for each star. The mean and standard deviation for the FRUITY classifications are 78% and 23%, respectively. For the MONASH classifications, we obtained 81% and 20%, respectively. In de Castro et al. (2016), Gaussian distributions were fitted to the data. The mean and standard deviation of those distributions are [Fe/H] = −0.12 ± 0.49 and MBa_star = 2.76 ± 0.84 M⊙, respectively. The average [Fe/H] conforms well with our results and is within the uncertainties. We could not directly compare our mass distribution derived for the former AGB star companions since de Castro et al. (2016) derived the current mass of the observed Ba stars after the mass transfer event.
 |
Fig. 9 Same figure format as in Fig. 4. For both stars in this figure, only one model was able to reach a GoF above 50%. The reason for this is due to the unusually high [Ru/Fe] combined with low [Rb/Fe] in both stars. |
5.2 Ba stars with no final classifications
In the following subsection, we discuss the four stars for which our algorithms were not able to find final classifications with the AGB final surface abundances from either FRUITY or Monash. These stars have either issues with the abundance pattern at the first or second peak, or have no classification with a GoF above 50.
5.2.1 Issue with first peak pattern: HD 123396, HD 219116
We found only one diluted AGB s-process distribution that matches the observed abundances with a GoF above 50% for the two stars HD 123396 and HD 219116 (see Fig. 9). Their GoFs are barely above the cutoff limit and sit below 55%. In both cases, the observed abundances in the second s-process peak are matched or almost matched by the model. The reason for the low GoFs is the first s-process peak. In HD 123396 the [Rb/Fe] and [Ru/Fe] are not reproduced, while in HD 219116 [Ru/Fe] is problematic. Furthermore, the trend of increasing abundance with increasing atomic number is missing in the stellar model predictions. In Sect. 6, we speculate that the low number of models with a GoF >50% and the peculiar abundance pattern at the first s-process peak may be a signature of a nucleosynthesis contribution different from the s-process.
5.2.2 Issue with the second peak: BD +09°2384
For BD +09°2384 (Fig. 10), we could not find final classifications. There are two reasons for this. First, [Sr/Fe] and [Ru/Fe] are unknown, and thus we are missing crucial information to properly match the first s-process peak. Furthermore, the abundances in the second s-process peak show an unusually high ratio of [Ce/Fe] over [Nd/Fe] in combination with small error bars. These abundances would be even more difficult to match if [La/Fe] was also included in the classification. These are all signs that there might be another nucleosynthetic process responsible for the enrichment pattern other than the s-process, which we discuss in Sect. 6.
5.2.3 No classifications with a GoF above 50%
For HD 62017 (Fig. 11), all GoFs were found to be between 23% and 34%, thus below our threshold of 50%. However, the ANNs agree with the classifications of the nearest-neighbour algorithm. The final classification based on the low GoFs and the ANNs using FRUITY models is M = 3.5 M⊙ with [Fe/H] ≃ −0.14 to 0. Using the Monash models, we found M = 2.5 M⊙ with [Fe/H] ≃ −0.14 to 0. The two sets of AGB final surface abundances thus do not agree on the mass, but they do agree on the metallicity range. The observed metallicity are [Fe/H] = −0.32 ± 0.14, thus lower than the classifications.
The reason for the low GoFs is clearly shown in Fig. 11. The models struggle to match both the high value of [Rb/Fe] and the low values for [Sr/Fe] and [Zr/Fe]. Furthermore, none of the models reach the high value for [Ru/Fe] or its error bar. Thus, we again reached the conclusion that there might be a nucleosynthetic process responsible for this enrichment pattern that is not the s-process.
 |
Fig. 10 Same figure format as in Fig. 4. For this star, no final classifications were found. This is likely due to the abundances in the second s-process peak, in particular Ce and Nd. |
 |
Fig. 11 Same figure format as in Fig. 4. There are no classifications with a GoF above 50% for this star due to the strong increase in the elemental abundances of the first s-process peak and the strong decrease in the elemental abundances of the second s-process peak. |
6 Discussion
In this section, we return to the elements that were excluded for the classifications and focus on understanding why the nearest-neighbour algorithm performs better, finding higher GoFs on average for the classifications (see Fig. 3), when the elements are excluded. We discuss whether there may be issues with the observations or specific reasons related to astrophysics causing the difficulties with the classifications.
6.1 Different GoFs when using SET A
To compare the average GoFs of the classification of stars using set A to the classifications using set F, we labelled all the stars for which the difference between the two GoFs is larger than ten percentage points, regardless of whether the GoFs belong to the same AGB final surface abundance in both classifications or not. We found that in 43 Ba stars, the difference between the average GoFs was larger than the threshold. We list these 43 stars in Table 2.
To better understand where this difference comes from, we show the residuals between the observational data and the set F nearest-neighbour classifications for the elements that were excluded in set F (Y, Mo, La, and Nb) in Figs. 12 and 13. We did not include the error bars on the observed values in these calculations. We grouped the 43 stars listed in Table 2 in red and the other stars in black. We performed one-sided t-tests to determine how likely it is that both groups could be samples of the same population. A t-test determines if there was a statistically significant difference between the mean of one group and the mean of another group. Our null hypothesis was thus μ43_stars = μrest, and we set the confidence interval to 5%. This means that if the probability, p, that the means are the same is smaller than 5%, then we reject the null hypothesis and conclude that the means are not the same.
Our results for the t-tests are shown in Table 3. In the FRUITY and Monash classifications, we were able to reject our null hypothesis for [Mo/Fe], [La/Fe], and [Nb/Fe] but not for [Y/Fe]. This result supports our exclusion of these elements in Sect. 3.5. The biggest improvement in the classifications occurs when [Mo/Fe] is excluded from the set and the null hypothesis of μ43_stars = μrest is rejected with the highest certainty (highest p-value) for [Mo/Fe]. For the 43 stars, the mean of the [Mo/Fe] residuals is a larger positive value than that of the other stars. A smaller improvement occurs when [La/Fe] is excluded, which still causes the null hypothesis to be rejected but with a smaller certainty than for [Mo/Fe]. For the 43 stars, the mean of the [La/Fe] residuals is a larger negative value than that of the other stars. Exclusion of [Y/Fe] caused the smallest improvement on the classification. In the case of [Nb/Fe], we rejected the null hypothesis using both AGB stellar sets, and the 43 stars have a larger positive mean than the other stars (see Table 3 and Fig. 13).
With the same statistical test, we also checked the other elemental abundances, and we found that the null hypothesis can be rejected for [Sm/Fe] and [Rb/Fe]. For [Sm/Fe], the 43 stars have a larger positive mean, while for [Rb/Fe], the 43 stars have a smaller negative mean residual than the other stars. However, for [Rb/Fe] we were only able to reject the null hypothesis for the FRUITY classifications.
In Paper I, high Nb values were often difficult to match by the models. For 12 of the 28 stars considered in that paper, Nb is the only element that is higher than what was predicted by the models. And in several other stars, a group of elements that includes Nb is also higher than the models when the error bars are included. Thus, we were interested in investigating whether the same issues with Nb in Paper I occurred in our classifications of the 169 Ba stars, but we could not do this with our classifications as shown in Tables A.1 and B.1, as Nb was not included in our algorithms. We thus performed another set of classifications that included Nb. We focused in this analysis on the Ba stars for which the GoF differs by more than ten percentage points when comparing the classifications found with set A with and without Nb, following a similar procedure as at the start of this section. We performed this test only with the AGB final surface abundances of Monash. We found that for 43 of the 169 stars, the difference is bigger than ten percentage points. These 43 stars overlap with those in Paper I that were flagged for a high [Nb/Fe] value. Of the 43 stars, however, only four are among the 43 shown in Table 2. We are thus dealing with a different subset of Ba stars. In conclusion, and as also mentioned in Paper I, there are still many open questions concerning the observed [Nb/Fe] values, and more work is needed before drawing any conclusions.
In summary, the 43 stars have elemental abundances that are different from the other Ba stars and show statistically significant higher [Mo/Fe], [Nb/Fe], and [Sm/Fe] and lower [La/Fe] values. The [Rb/Fe] was found to be higher as well, but this was only statistically significant in the FRUITY classifications.
 |
Fig. 12 Histograms of residuals between observational data and set F nearest-neighbour classifications using FRUITY (top panel) and Monash (bottom panel) stellar sets for three elements excluded from the classification: Y, Mo, and La. The residuals for the 43 stars listed in Table 2 are shown in red, and the other stars are in black. The means and standard deviations of the two groups are shown in the legend. |
Names of the 43 stars for which GoF of set A and set F differ by more than 10 percentage points.
Results of one-sided t-tests.
6.2 Possible observational problems
Except for Y, we did not identify any observational issues of the three elemental abundances discussed in Sect. 6.1. Ionised lines were used for the analysis of Y, while neutral lines were used for Sr and Zr, which are the other two elements in the first s-process peak. As noted by Allen & Barbuy (2006), the derivation of Sr and Zr abundances from neutral lines results in lower abundances than when using ionised lines. This difference makes Sr and Zr abundances lower than Y and can cause a discrepancy in the pattern of the first s-process peak when compared to the AGB stellar models. As discussed in Paper I, the differences between ionised and neutral lines are attributed to the departures from the local thermodynamic equilibrium (LTE) approximation, which was assumed to derive the abundances from our stellar sample (de Castro et al. 2016). Therefore, the first peak could be easier to classify with a high GoF value if Y is removed.
Overall, the error bars of the second peak elements are smaller than those of the first peak. This is related to the fact that more lines with lower standard deviation of the derived abundances were used in the analysis of the second peak elements. The fact that fewer lines were available for the determination of some elements (e.g. Sr) is reflected in the lack of error bars. This is because no error bars are available in the original studies of de Castro et al. (2016) and Roriz et al. (2021b) for elements with less than three lines used to derive the abundance.
As a result, the smaller number of reported error bars makes matching the observed [La/Fe] and [Се/Fe] more challenging. However, we note that [La/Fe] and [Се/Fe] were determined in separate studies. Roriz et al. (2021b) determined La together with Sr, Nb, Mo, Ru, Sm, and Eu, while de Castro et al. (2016) determined Ce together with Y, Zr, and Nd. This fact might introduce additional errors in the corresponding width measurements well beyond the reported errors.
Observational issues for Rb and Nb are also possibly relevant to our analysis. In some of the sample stars, [Rb/Fe] is negative, making such cases impossible to match with AGB models. Rb abundances used in this study were derived from only one Rb I line: the D2 resonance line at 7800.2 Å, assuming LTE approximation and taking into account the hyperfine structure of Rb. Recently, Korotin (2020) calculated non-LTE (NLTE) corrections in cool stars with metallicities in the range of our sample stars for the same Rb line. Korotin has shown that when neglecting the NLTE effects, the errors can be as high as 0.3 dex, depending on temperature, metallicity, log g, and the Rb abundance itself. However, this effect is weak, around 0.1 dex, in the case of our sample stars with the mean temperature of 4800 ± 260 K and log g of 2.3 ± 0.48 (see Figs. 4 and 5 in Korotin 2020). Nevertheless, Korotin (2020) also found that departures from NLTE strengthen the Rb resonance lines in the solar spectrum and determined NLTE absolute Rb abundance5 as A(Rb) = 2.35 ± 0.05. This finding is in agreement with the meteoritic value of A(Rb) = 2.36 ± 0.03 from Lodders (2019) and is much lower than the solar value used to derive the Rb abundances in this study, 2.60 ± 0.15 (Grevesse & Sauval 1998). In contrast, Takeda (2021) found a lower NLTE correction for the solar value of −0.05 dex. This difference could have a much larger impact on the observed [Rb/Fe] abundances, but a more detailed analysis is required. In any case, applying the lower value instead of the higher value would result in higher Rb values for our sample stars, and therefore, it would imply non-negative [Rb/Fe] abundances for all of our sample stars.
Due to blending with other lines, Nb abundances were calculated from a maximum of three lines using the spectral synthesis technique. We note that almost half of the sample stars have artificial error bars for Nb in this study since less than three lines were used for the abundance derivation. The consideration of the hyperfine splitting in the calculation of the Nb abundances avoids the overestimation of Nb that would occur if this factor were neglected. The fact that the Nb abundances in the 43 stars are higher than in the models could therefore indicate that a process different from the s-process is occurring in the polluter AGB stars and producing the high Nb values seen in about 25% of our Ba star sample.
6.3 Signatures of i-process nucleosynthesis in Ba star spectra
From our sample of 169 Ba stars, the ML algorithms adopted in this work identified 43 stars (25% of the total) showing anomalous abundance patterns, mainly at the first neutron magic peak above iron (N = 50). This could suggest that, along with the s-process, one or more unidentified nucleosynthesis components contributed to the production of heavy elements in the atomic mass region of the evolved AGB stellar companion.
Together with the classical s-process, an additional contribution from the intermediate neutron capture process (i-process; Cowan & Rose 1977) has been identified in a fraction of carbon-enhanced metal-poor (CEMP) stars carrying heavy element enrichment, the analogue of Ba stars at much lower metallicities (e.g. Dardelet et al. 2014; Abate et al. 2015b; Cristallo et al. 2016; Hampel et al. 2016, 2019; Choplin et al. 2021). Additionally, the i-process has been proposed as being responsible for some of the anomalous abundances observed in metal-poor post-AGB stars (e.g. Lugaro et al. 2015; Hampel et al. 2016). In the same metallicity range of the Ba stars discussed in this study, the post-AGB star Sakurai’s object was the first star with a clearly identified i-process nucleosynthesis signature (Herwig et al. 2011). Therefore, a reasonable hypothesis would be that the anomalies in the first s-process peak are indeed indicative of an i-process activation in about 25% of the evolved companions of the Ba stars observed by de Castro et al. (2016). In order to test this hypothesis, we compared the heavy element abundances of four of the 43 anomalous Ba stars with i-process abundances (see Fig. 14). These stars are HD 4048 and HD 107270, for which we only found one final classification; CPD −64°4333, for which we found two final classifications with low GoFs; and HD 107541, which was also problematic to classify in Paper I. The latter three stars are part of the 43-star stellar sample (see Table 2). In contrast, HD 4048 is not part of that sample.
For the calculations, we used a simplified i-process trajectory, as adopted by Bertolli et al. (2013) and Dardelet et al. (2014). By using a solar scaled initial composition beyond Fe, we assumed that there were no previous contributions from other processes. Nucleosynthesis calculations were performed using the NuGrid codes (e.g. Herwig et al. 2011). Starting from the Fe seeds in these conditions, it took about a couple of hours of i-process exposure at typical neutron densities of 1014–16 neutrons cm−3 to build the elements at the first peak. Despite the simplicity of the adopted simulation framework, the i-process seems to appropriately reproduce the pattern between Sr and Ru observed in the four stars (see Fig. 14). However, in all four stars considered in Fig. 14, the i-process seems to produce a higher amount of Rb (by at least a factor of three) compared to observations. It is unlikely that such a large discrepancy could be fully explained by the issue with the NLTE correction, as discussed in Sect. 6.2.
Nuclear uncertainties could affect the i-process production of Rb compared to other nearby elements where neutron capture rates of neutron-rich, radioactive nuclei along the i-process nucleosynthesis path are only theoretical (e.g. Denissenkov et al. 2018). Also worth consideration is the possibility that the calculated i-process trajectory is not correctly reproducing Rb because of the simplicity of the approach. One simplication is that we are ignoring the impact of the complex stellar environments hosting the i-process on the neutron capture nucleosynthesis itself. To be accurate, we should be following an H-ingestion event, as multi-dimensional hydrodynamic effects can shape the local stellar structure (e.g. Stancliffe et al. 2011; Herwig et al. 2014; Woodward et al. 2015). Another simplication is that, in our specific case, the same stellar hosts (i.e. the evolved companions of Ba stars) were also carrying the s-process component, and the i-process may therefore be activated in conjunction with the s-process. We do not consider either of these aspects in our calculations.
We also note that with the present approach, we cannot capture minor effects on elements heavier than Ru. The i-process may be able to produce minor effects on a previously enriched s-process abundance distribution, and this may account for the offset of La and Sm residuals in our 43 stars, shown in Fig. 13. Such effects could be captured by combined i-process and s-process stellar simulations and provide additional valuable constraints on the neutron exposure of the i-process events.
From a theoretical point of view, stellar models have been predicted to have a possibly significant H-ingestion event early on in the AGB phase at low metallicities (e.g. Iwamoto et al. 2004; Cristallo et al. 2009a; Choplin et al. 2021), creating the conditions for the i-process to happen. However, these events are not expected to take place during the AGB phase within the metallicity range typical of Ba stars.
Nonetheless, some post-AGB stars develop a late thermal pulse or a very late thermal pulse event before becoming white dwarfs (see, e.g. Bloecker 1995). During such events, some degree of H-ingestion, and possibly i-process, is occurring, as demonstrated by Sakurai’s object (see, e.g. Herwig et al. 2011). Because of this, about 20% of AGB stars become H-deficient white dwarfs (e.g. Werner & Herwig 2006). Therefore, a possibility could be that the anomalous Ba stars have been polluted with i-process-rich material during the final evolutionary stages of the evolved post-AGB companion. The feasibility of this scenario (or of other possible pathways within these binary systems) will need to be investigated in the future with the guidance of multi-dimensional hydrodynamic simulations (e.g. Denissenkov et al. 2019). From the observational point of view, it would be interesting to check if anomalous Ba stars are indeed preferentially associated to H-deficient white dwarf companions. This association would be consistent with the similar statistics between observations of anomalous Ba stars and post-AGB stars.
 |
Fig. 14 Comparison between abundance distribution of four stars and i-process calculations. Abundance distributions normalised to solar for four stars (HD 4084 at [Fe/H] = −0.42; HD 107270 at [Fe/H] = +0.05; CPD −64°4333 at [Fe/H] = −0.1; and HD 107541 at [Fe/H] = −0.63), carrying a composition in the mass region Rb–Ru (at the light neutron magic peak, N = 50) anomalous with respect to the s-process in AGB models. Observations are compared with the i-process calculations at time of exposure between 0.076 and 0.085 days (see text for details). The theoretical abundances are normalised to the observations at Sr. In the plots, the added vertical lines correspond to the atomic number of Sr, Ba and Eu. |
7 Conclusions
We developed two algorithms to classify the 169 Ba stars of de Castro et al. (2016) based on their abundance patterns. These algorithms make use of ML techniques in order to minimise human bias in the classification process and to speed up analysis. For our study, we used AGB final surface abundances of FRUITY and Monash stellar sets and only included the s-process elements heavier than Fe in the classification. In each algorithm, the dilution of the AGB surface abundances required to reproduce the s-process enrichment in Ba stars is a free parameter.
The first algorithm is an ANN ensemble classifier, and the second algorithm is a nearest-neighbour classifier. For the first algorithm, we used Tensorflow to train an ensemble of 20 networks. Neural networks need distinguishable labels, so we had to group the AGB final surface abundances. We grouped all AGB final surface abundances that resulted from the models with the same initial mass and metallicity. The final classification was done by taking the medians of all output nodes. For the nearest-neighbour algorithm, we calculated the modified χ2 value for a Monte Carlo sample set based on the observed values, taking into consideration the error bars on the abundances as well as dependencies in the atmospheric parameters. We then calculated the χ2 value of the diluted set of AGB final surface abundances, found the model with the highest GoF, and saved its name and the corresponding dilution. Our final classification concerned the range of mass and metallicity included in the classifications coming from the two algorithms using the same set of AGB final surface abundances. We extended these ranges to account for the discrete character of our two sets of AGB final surface abundances. To determine which elements to include in our classification, we systematically removed elements from the set of 12 s-process elements, and we recorded the impact of the removal on the GoF distribution of the classification with the nearest-neighbour algorithm. We found that the Fe, Rb, Sr, Zr, Ru, Nd, Ce, Sm, and Eu set of elements leads to the highest GoFs with our AGB final surface abundances. We thus excluded Y, Mo, La, and Nb and investigated their abundances in more detail.
After validating the ML tools with a smaller sample of 28 Ba stars, we used them to study the full stellar sample. We found one or two classifications using Monash and FRUITY AGB nucleosynthesis predictions for 166 of the 169 Ba stars. For 85% of the stars, we found [Fe/H] values consistent with observations. The average stellar mass and metallicity of the stellar sample was also consistent with previous studies.
For three of the 169 Ba stars, we were unable to find any classification. Two of these stars show an abundance pattern in the first s-process peak that is different from the typical AGB s-process abundances. The third star shows an unusual pattern in the second s-process peak.
We wanted to better understand why our nearest-neighbour algorithm performs better when we exclude Y, Mo, and La from our classification, and therefore we compared our classification results to the classifications we would get when we include the three elements. We found that for 43 stars, the average GoFs differ by more than ten percentage points. We performed statistical tests to find out if this group of 43 stars is different from the other stars and found that this is indeed the case for Nb, Mo, La, and Sm. The 43 stars have statistically significant higher [Nb/Fe], [Mo/Fe], [Sm/Fe], and lower [La/Fe] values.
Inspired by the CEMP stars in which i-process nucleosynthesis signatures are found, we suspected that at least some of these 43 stars might be enriched by an i-process component. We performed i-process nucleosynthesis calculations to test this hypothesis. The resulting nucleosynthesis pattern seems to reproduce the observed pattern between Sr and Ru of these four stars well. In a future work, we will study these 43 stars in more detail in order to determine whether an extra i-process component is indeed the reason why they are different from the other Ba stars.
By using ML tools, we may have found evidence that in the surface abundances of ~20% of the AGB stars that are in a binary system with Ba stars, another nucleosynthetic component could be present. These AGB stars are also part of Galactic chemical evolution (GCE), and they may have contributed to the radioactive signature of the early Solar System. We note that Trueman et al. (2022) found 107Pd was missing in GCE calculations, and it could be that the missing Pd and the overabundance seen in part of our sample are connected and that the radioactive signatures are the key in solving this puzzle of the missing nucleosynthetic component.
Acknowledgements
This work is supported by the ERC Consolidator Grant (Hungary) programme (RADIOSTAR, G.A. no. 724560). We thank the ChETEC COST Action (CA16117), supported by the European Cooperation in Science and Technology, and the ChETEC-INFRA project funded by the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 101008324. M.P. acknowledges the financial support of NuGrid/JINA-CEE (NSF Grant PHY-1430152) and STFC (through the University of Hull’s Consolidated Grant ST/R000840/1), and ongoing access to viper, the University of Hull High Performance Computing Facility. M.P. thanks the Joint Institute for Nuclear Astrophysics - Center for the Evolution of the Elements, USA and the US IReNA Accelnet network (Grant No. OISE-1927130). M.L. and M.P. acknowledge the support from the “Lendület-2014” Programme of the Hungarian Academy of Sciences (Hungary). The work of A.Y.L. was supported by the US Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of US Department of Energy (Contract no. 89233218CNA000001). The authors would like to thank A. Jorissen for providing data. B.Cs. and M.L. acknowledge the support of the Hungarian National Research, Development and Innovation Office (NKFI), grant KH_18 130405. B.V. is supported by the ÚNKP-21-1 New National Excellence Program of the Ministry for Innovation and Technology from the source of the National Research, Development and Innovation Fund. M.P.R. acknowledges financial support by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES). N.A.D. acknowledges financial support by Russian Foundation for Basic Research (RFBR) according to the research projects 18_02-00554 and 18-52-06004. Software: Numpy (Harris et al. 2020), matplotlib (Hunter 2007), and Tensorflow (Abadi et al. 2016).
Appendix A Table with complete classifications − FRUITY
Appendix B Table with complete classifications − Monash
Appendix C Table with parameter values associated with the labels - FRUITY
Appendix D Table with parameter values associated with the labels - Monash
References
- Abadi, M., Agarwal, A., Barham, P., et al. 2016, ArXiv e-prints [arXiv:1603.04467], software available from tensorflow.org [Google Scholar]
- Abate, C., Pols, O.R., Izzard, R.G., & Karakas, A.I. 2015a, A&A, 581, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abate, C., Pols, O.R., Stancliffe, R.J., et al. 2015b, A&A, 581, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, D.M., & Barbuy, B. 2006, A&A, 454, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, D.M., & Porto de Mello, G.F. 2007, A&A, 474, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Hansen, C.J., Bautista, M., & Ruchti, G. 2012, A&A, 546, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertolli, M.G., Herwig, F., Pignatari, M., & Kawano, T. 2013, ArXiv e-prints [arXiv:1310.4578] [Google Scholar]
- Bidelman, W.P., & Keenan, P.C. 1951, ApJ, 114, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S., Gallino, R., Käppeler, F., et al. 2015, MNRAS, 449, 506 [Google Scholar]
- Bloecker, T. 1995, A&A, 297, 727 [Google Scholar]
- Busso, M., Gallino, R., Lambert, D.L., Travaglio, C., & Smith, V.V. 2001, ApJ, 557, 802 [CrossRef] [Google Scholar]
- Choplin, A., Siess, L., & Goriely, S. 2021, A&A, 648, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowan, J.J., & Rose, W.K. 1977, ApJ, 212, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2009a, PASA, 26, 139 [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009b, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Piersanti, L., & Gobrecht, D. 2015, ApJS, 219, 40 [Google Scholar]
- Cristallo, S., Karinkuzhi, D., Goswami, A., Piersanti, L., & Gobrecht, D. 2016, ApJ, 833, 181 [Google Scholar]
- Cseh, B., Lugaro, M., D’Orazi, V., et al. 2018, A&A, 620, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cseh, B., Világos, B., Roriz, M.P., et al. 2022, A&A, 660, A128 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dardelet, L., Ritter, C., Prado, P., et al. 2014, in XIII Nuclei in the Cosmos (NIC XIII), 145 [Google Scholar]
- de Castro, D.B., Pereira, C.B., Roig, F., et al. 2016, MNRAS, 459, 4299 [NASA ADS] [CrossRef] [Google Scholar]
- den Hartogh, J.W., Hirschi, R., Lugaro, M., et al. 2019, A&A, 629, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denissenkov, P., Perdikakis, G., Herwig, F., et al. 2018, J. Phys. G Nuclear Phys., 45, 055203 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P.A., Herwig, F., Woodward, P., et al. 2019, MNRAS, 488, 4258 [NASA ADS] [CrossRef] [Google Scholar]
- El-Badry, K., Rix, H.-W., & Weisz, D.R. 2018, ApJ, 860, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Fishlock, C.K., Karakas, A.I., Lugaro, M., & Yong, D. 2014, ApJ, 797, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A.G.A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [Google Scholar]
- Grevesse, N., & Sauval, A.J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Hampel, M., Stancliffe, R.J., Lugaro, M., & Meyer, B.S. 2016, ApJ, 831, 171 [CrossRef] [Google Scholar]
- Hampel, M., Karakas, A.I., Stancliffe, R.J., Meyer, B.S., & Lugaro, M. 2019, ApJ, 887, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C.R., Millman, K.J., van der Walt, S.J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Pignatari, M., Woodward, P.R., et al. 2011, ApJ, 727, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Woodward, P.R., Lin, P.-H., Knox, M., & Fryer, C. 2014, ApJ, 792, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J.D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Iwamoto, N., Kajino, T., Mathews, G.J., Fujimoto, M.Y., & Aoki, W. 2004, ApJ, 602, 377 [CrossRef] [Google Scholar]
- Jorissen, A., Boffin, H.M.J., Karinkuzhi, D., et al. 2019, A&A, 626, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karakas, A.I., & Lattanzio, J.C. 2014, PASA, 31, e030 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A.I., & Lugaro, M. 2016, ApJ, 825, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A.I., Lugaro, M., Carlos, M., et al. 2018, MNRAS, 477, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Karinkuzhi, D., Van Eck, S., Jorissen, A., et al. 2021, A&A, 654, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
- Korotin, S.A. 2020, Astron. Lett., 46, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2019, ArXiv e-prints [arXiv:1912.00844] [Google Scholar]
- Lugaro, M., Karakas, A.I., Stancliffe, R.J., & Rijs, C. 2012, ApJ, 747, 2 [Google Scholar]
- Lugaro, M., Campbell, S.W., Van Winckel, H., et al. 2015, A&A, 583, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lugaro, M., Cseh, B., Világos, B., et al. 2020, ApJ, 898, 96 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, R.D. 1983, ApJ, 268, 264 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, R.D., Fletcher, J.M., & Nemec, J.M. 1980, ApJ, 238, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Cristallo, S., & Straniero, O. 2013, ApJ, 774, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Roriz, M.P., Lugaro, M., Pereira, C.B., et al. 2021a, MNRAS, 501, 5834 [NASA ADS] [CrossRef] [Google Scholar]
- Roriz, M.P., Lugaro, M., Pereira, C.B., et al. 2021b, MNRAS, 507, 1956 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R.J. 2021, MNRAS, 505, 5554 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R.J., Dearborn, D.S.P., Lattanzio, J.C., Heap, S.A., & Campbell, S.W. 2011, ApJ, 742, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Straniero, O., Gallino, R., & Cristallo, S. 2006, Nuclear Phys. A, 777, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y. 2021, Astron. Nachr., 342, 515 [Google Scholar]
- Trueman, T.C.L., Côté, B., Yagüe López, A., et al. 2022, ApJ, 924, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, K., & Herwig, F. 2006, PASP, 118, 183 [Google Scholar]
- Woodward, P.R., Herwig, F., & Lin, P.-H. 2015, ApJ, 798, 49 [Google Scholar]
All Tables
Names of the 43 stars for which GoF of set A and set F differ by more than 10 percentage points.
All Figures
 |
Fig. 1 Correlation matrix demonstrating linear relationship between pairs of elements in AGB final surface abundances of FRUITY (top panel), Monash (middle panel), and observed Ba star sample (bottom panel, excluding the error bars on the observations). The stronger the correlation, the darker the color of the boxes. Blue shaded boxes: positive correlation. Red shaded boxes: negative correlation). |
| In the text | |
 |
Fig. 2 Visualisation of diluted AGB final surface abundances set of Monash (black circles, dilution increments of 0.01 instead of 0.002 to improve the visibility of the figure) and subset of 28 Ba stars (blue stars). Principal component analysis (see text for explanation) was used to reduce the dimensions of the AGB final surface abundances sets and derive abundances to only two linearly uncorrelated dimensions, x1 and x2, that do not have a physical meaning. For one star, BD −14°2678 (blue diamond), we plotted the results of Monte Carlo sampling of the error bars on the abundances (red circles, showing 500 samples), for details see Sect. 3.3. |
| In the text | |
 |
Fig. 3 Histograms of GoF distributions for set A (top panel) and set F (bottom panel). The results are shown for the output of the nearest-neighbour algorithm and for the AGB final surface abundances of FRUITY (yellow) and Monash (blue). The solid black line marks the 50% GoF, and the dashed lines are the median values of the two sets of AGB final surface abundances. |
| In the text | |
 |
Fig. 4 Comparison between observed abundanced and classifications plus the residuals of the classifications. Top panel: comparison between the observed abundances (star symbols where red/yellow symbols are elements that are included/excluded in our classification) and results (lines) of nearest-neighbour algorithm. Bottom panel: residuals of the classification (i.e. observed abundance minus predicted abundance for each element). This star is difficult to classify because the abundances in the first s-process peak are higher than predicted by the best-fit models. |
| In the text | |
 |
Fig. 5 Same figure format as in Fig. 4. This star was difficult to classify manually because the binary-derived AGB mass is higher than the initial masses of the best-fit models (Group 3 stars in Paper I). We were able to classify this star with our algorithms, indeed with models with initial masses lower than the binary-derived value, but matching the observed values in the second s-process peak is still an issue. |
| In the text | |
 |
Fig. 6 Same figure format as in Fig. 4. This Ba star was difficult to classify manually because the abundances in the first s-process peak are higher than predicted by the best-fit models (Group 2 stars in Paper I). We were able to classify it using models with slightly higher initial masses than their mass derived from binary parameters. |
| In the text | |
 |
Fig. 7 Same figure format as in Fig. 4. This star is one of the four Ba stars that was difficult to classify manually because the abundances in the first s-process peak are higher than predicted by the best-fit models (Group 2 stars in Paper I). We found a final classification for this star with our algorithms. However, [Nb/Fe] is too high to be matched by our AGB final surface abundances. |
| In the text | |
 |
Fig. 8 Distributions of final classifications for both sets of AGB final surface abundances. From top to bottom we show the distributions for the (1) metallicities, (2) masses, and (3) minimum GoFs of the classifications as listed in the tables in Appendix A. The left column shows the distribution for FRUITY and the right column shows those for Monash. |
| In the text | |
 |
Fig. 9 Same figure format as in Fig. 4. For both stars in this figure, only one model was able to reach a GoF above 50%. The reason for this is due to the unusually high [Ru/Fe] combined with low [Rb/Fe] in both stars. |
| In the text | |
 |
Fig. 10 Same figure format as in Fig. 4. For this star, no final classifications were found. This is likely due to the abundances in the second s-process peak, in particular Ce and Nd. |
| In the text | |
 |
Fig. 11 Same figure format as in Fig. 4. There are no classifications with a GoF above 50% for this star due to the strong increase in the elemental abundances of the first s-process peak and the strong decrease in the elemental abundances of the second s-process peak. |
| In the text | |
 |
Fig. 12 Histograms of residuals between observational data and set F nearest-neighbour classifications using FRUITY (top panel) and Monash (bottom panel) stellar sets for three elements excluded from the classification: Y, Mo, and La. The residuals for the 43 stars listed in Table 2 are shown in red, and the other stars are in black. The means and standard deviations of the two groups are shown in the legend. |
| In the text | |
 |
Fig. 13 Same figure format as in Fig. 12. The elements shown here are Nb, Rb, and Sm. |
| In the text | |
 |
Fig. 14 Comparison between abundance distribution of four stars and i-process calculations. Abundance distributions normalised to solar for four stars (HD 4084 at [Fe/H] = −0.42; HD 107270 at [Fe/H] = +0.05; CPD −64°4333 at [Fe/H] = −0.1; and HD 107541 at [Fe/H] = −0.63), carrying a composition in the mass region Rb–Ru (at the light neutron magic peak, N = 50) anomalous with respect to the s-process in AGB models. Observations are compared with the i-process calculations at time of exposure between 0.076 and 0.085 days (see text for details). The theoretical abundances are normalised to the observations at Sr. In the plots, the added vertical lines correspond to the atomic number of Sr, Ba and Eu. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![${\left[ {{{\rm{X}} \over {{\rm{Fe}}}}} \right]_{{\rm{Ba}}}} = {\log _{10}}\left[ {\left( {1 - \delta } \right) \times {{10}^{{{\left[ {{{\rm{X}} \mathord{\left/ {\vphantom {{\rm{X}} {{\rm{Fe}}}}} \right. \kern-\nulldelimiterspace} {{\rm{Fe}}}}} \right]}_{{\rm{ini}}}}}} + \delta \times {{10}^{{{\left[ {{{\rm{X}} \mathord{\left/ {\vphantom {{\rm{X}} {{\rm{Fe}}}}} \right. \kern-\nulldelimiterspace} {{\rm{Fe}}}}} \right]}_{{\rm{AGB}}}}}}} \right],$](/articles/aa/full_html/2023/04/aa44189-22/aa44189-22-eq1.png)