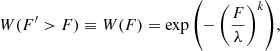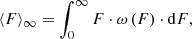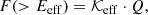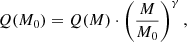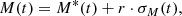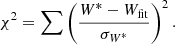EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 670 (February 2023) A&A, 670 (2023) L22 Full HTML
Open Access
Issue
A&A
Volume 670, February 2023
Article Number L22
Number of page(s) 9
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202245810
Published online 24 February 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The majority of charged relativistic particles in the vicinity of Earth, known as cosmic rays, are galactic cosmic rays (GCRs), which are always present and have a moderate solar-modulation variability (e.g., Potgieter 2013; Aguilar et al. 2021). However, the lower-energy (≲100 MeV) part of the cosmic-ray flux is dominated by solar energetic particles (SEPs), which are accelerated in solar eruptive processes such as flares and coronal mass ejections (e.g., Desai & Giacalone 2016; Vainio et al. 2009). Although the energy of SEPs is lower than that of GCRs, their fluxes are much stronger and are highly variable in time. SEPs determine the near-Earth radiation environment, which is crucial for modern technology (e.g., Dyer et al. 2004), and they pose hazards for spacecraft, aircraft, and even habitability (Thomas et al. 2013; Yamashiki et al. 2019). Moreover, SEPs form the only measurable index of solar eruptive events in the past and thus can expand the range of our knowledge on solar physics from tens to millions of years (Reedy 1999; Usoskin et al. 2006; Cliver et al. 2022).

Three independent ways are currently used to study SEP fluxes on different timescales. One way (see Sect. 2.1) is based on direct measurements of SEPs in space (e.g., Shea & Smart 2000; Reedy 2012; Vainio et al. 2013) by various spacecraft since the 1960s, but these estimates earlier suffered from large uncertainties related to the difficult intercalibration of various space-borne detectors. Primary SEP detectors on board the Geostationary Operational Environmental Satellite (GOES) family have recently been recalibrated (Raukunen et al. 2022), which reduced the uncertainties of the SEP flux measurements since 1984.

Another way (Sect. 2.2) to study past SEP fluxes is by cosmogenic isotopes (CIs) 14C, 10Be, and 36Cl produced by energetic particles in the Earth’s atmosphere, which are stored in natural stratified archives such as tree trunks or polar ice and are measured in modern laboratories (e.g., Usoskin et al. 2006; Beer et al. 2012; Usoskin 2017). Normally, CI production is dominated by GCR fluxes, and the SEP contribution cannot be resolved (Usoskin et al. 2020; Mekhaldi et al. 2021). However, as discovered recently (e.g., Miyake et al. 2012, 2013; Usoskin et al. 2013; Paleari et al. 2022; Brehm et al. 2022), our Sun can occasionally produce extreme solar particle events (ESPEs) that lead to an enhanced (several orders of magnitude greater than for SEP events that were directly measured during the space era) CI production notably exceeding that by GCRs on the annual scale. The average SEP flux estimated from the direct data alone does not contain ESPEs because they did not occur during the space era.

The third way (Sect. 2.3) to assess the average SEP flux on a very long timescale is related to CIs measured in lunar samples brought to Earth by the Apollo missions in 1969–1972 (e.g., Fink et al. 1998; Jull et al. 1998; Reedy 1999; Nishiizumi et al. 2009; Poluianov et al. 2018). Since the Moon is not protected from energetic particles by the atmosphere and magnetosphere, CIs in lunar rocks can serve as a rough cosmic-ray spectrometer (Miyake et al. 2019; Poluianov et al. 2018) over the isotope lifetime, which may reach several megayears. The GCR contribution to lunar CI production can be estimated using the data from deep layers of lunar soil cores (Rancitelli et al. 1975; Nishiizumi et al. 1984; Poluianov et al. 2018), which enables the quantitative estimation of the lower-energy (30–80 MeV) average SEP flux using the data of the shallower lunar soil layers. This method cannot resolve individual SEP events (including ESPEs) nor the time variability, but it provides a robust estimate of the long-term average SEP flux. All these three methods assess the average SEP flux on different timescales and in independent ways.

The current paradigm is that the megayear-averaged spectrum of SEPs is consistent with that over the past decades (e.g., Reedy 2012; Poluianov et al. 2018). In this Letter, we critically revise the existing paradigm and address the outstanding question of whether the SEP fluxes measured or derived by different methods on different timescales agree with each other and whether we can obtain a consistent view of the average flux of SEPs produced by the Sun in its current evolution state. This question is crucially important for studies in the fields of solar and stellar physics, terrestrial and planetary sciences, astrobiology, space weather, and modern technology.

2. Datasets

Solar energetic particles have traditionally been quantified via the integral particle flux F(> E) (in units of cm−2 s−1) above the given energy E. This flux definition differs from the standard definition, and should strictly speaking be called the omnidirectional intensity (see Chap. 1.6.3 in Grieder 2001), but it has been used in the field historically. Typical energies E for the measured integral flux of SEPs are 10, 30, 60, 100, and 200 MeV (Shea & Smart 2000; Raukunen et al. 2022), with the corresponding integral fluxes denoted henceforth as F10 through F200, respectively.

2.1. Direct measurements

We used the annually averaged SEP integral fluxes based on the GOES dataset (Raukunen et al. 2022) in the energy range from 30–200 MeV for 1987–2019 (solar cycles (SCs) 22–24), shown in Table 1. This dataset is an estimate of the regular SEP flux, including the occurrence of weak-to-strong SEP events, but excluding ESPEs.

Table 1.

SEP fluxes (cm−2 s−1) above 30, 60, 100, and 200 MeV, averaged over different timescales.

The period between the onset of the space era and the end of SC 23 in 2009 corresponds to the Modern Grand solar maximum (Usoskin et al. 2003; Solanki et al. 2004) of an unusually active Sun, with the cycle-averaged SEP flux in SC 22–23 about five times stronger than during the moderate SC 24 (Table 1). This is typical for the long-term solar activity (Usoskin 2017).

2.2. ESPEs in terrestrial CIs

Extreme solar particle events were discovered and are studied based on CIs that were recorded in terrestrial archives such as tree trunks or the polar ice (e.g., Usoskin et al. 2006, 2020; Cliver et al. 2022); see Appendix A. We reconstructed integral ESPE fluxes using the recently developed effective-energy method (Kovaltsov et al. 2014; Koldobskiy et al. 2022), which estimates the SEP fluxes F234, F236, and F60 based on the global production of 14C (Brehm et al. 2022) and based on the production and deposition of 10Be and 36Cl in the polar caps (Mekhaldi et al. 2015), respectively. A short description of the method is presented in Appendix B. For the ESPE dated 7176 before the common era (BCE), the SEP flux values were taken from Paleari et al. (2022). The obtained ESPE flux values are summarized in Table 2.

Table 2.

ESPE integral fluxes reconstructed from terrestrial CI data (Mekhaldi et al. 2015; Brehm et al. 2022; Paleari et al. 2022), in 103 cm−2 s−1.

Since the CI method detects only ESPEs but no regular SEP events (Usoskin et al. 2020; Mekhaldi et al. 2021), it cannot evaluate the total average SEP flux. Thus, this information is complementary to the regular SEP flux assessed from direct data (Sect. 2.1).

2.3. Megayear SEP flux estimates from lunar samples

In contrast to terrestrial proxies, lunar CI data lack a temporal resolution and thus cannot resolve individual ESPEs, but work as a simple particle spectrometer providing an integral cosmic-ray spectrum averaged over the CI lifetime (see Appendix A). The SEP flux averaged over long timescales in the energy range 30–80 MeV was recently estimated, as shown in Table 1, using data of cosmogenic 26Al (lifetime 1.03 Myr) measured in lunar rocks (Poluianov et al. 2018), without an a priori assumption on the spectral form (see the brief description in Appendix C). The lunar-CI-based SEP fluxes should include both the regular (Sect. 2.1) and ESPE components (Sect. 2.2) because their long-time averaging guarantees that rare ESPEs are covered, potentially even those with an occurrence rate < 10−4 year−1.

3. Methods

Terrestrial CI data have an annual time resolution at best. To compare the statistics of proxy-based and direct datasets, we averaged the directly measured data to annual fluxes. Thus, possible recurrent SEP events produced by the same solar active regions are not distinguished and are seen as one annual event. We used GOES data for 33 years (Sect. 2.1) and CI data for eight ESPEs during 12 000 years of the Holocene (Sect. 2.2) to calculate the complementary cumulative distribution function (CCDF), that is, the probability that the average flux for a randomly chosen year exceeds the given value. For each annual flux data point, we estimated (following the method of Usoskin & Kovaltsov 2012) the median value of the probability ⟨W⟩ and its 68% confidence interval (c.i.) σW. Since the number of ESPE flux reconstructions F30–F100 is limited to three events (Table 2), their occurrence probability was assessed using F200 data with a larger statistic. Figure 1 shows statistics of the annual SEP integral fluxes F30, F60, F100, and F200 in the CCDF form, where data of regular SEP events and ESPEs are depicted by circles and stars, respectively. Conservative upper limits for GOES and terrestrial CI data are shown by filled symbols. They are defined under the assumption that a flux that is twice as high as the highest observed flux has confidently not appeared during the given period (33 years of the space era, or 12 000 years of the Holocene).

thumbnail Fig. 1.

CCDF (see text for definition) for SEP flux F30, F60, F100, and F200 in panels a–d, respectively. The uncertainties are evaluated using the Poisson statistics (e.g., Usoskin & Kovaltsov 2012). Open circles correspond to direct measurements (Raukunen et al. 2022), and the black dots depict conservative upper limits (see text). The open and filled blue stars represent the annual flux estimates for ESPEs from terrestrial CI data (Table 2) and the conservative upper limits (Usoskin 2017), respectively. The green curves depict the Weibull distributions fit to the combined direct and terrestrial CI datasets (Sect. 3). All error bars and filled areas bound the 68% c.i. The vertical red bar in panel d indicates the sensitivity threshold of the terrestrial CI method to an ESPE on a 3σ level (Usoskin et al. 2020).

The CCDF of the SEP event occurrence is often described by the Weibull distribution (Weibull 1951; Gopalswamy 2018),

(1)

where W is the probability of the flux F′ (e.g., F200) for a randomly chosen year to exceed the given value F, k (dimensionless), and λ (in cm−2 s−1) are the distribution parameters.

We fit the experimental data (Fig. 1) with the Weibull distribution using the iterative Monte Carlo procedure. The procedure is described in Appendix D.

The best-fit parameters and their uncertainties are shown in Table 3. While the scaling parameter λ has large uncertainties and varies essentially with the SEP energy, the shape of the distribution (parameter k) is robustly defined and stable over all energies. This suggests that ESPEs are driven by physical processes that scale with the event strength (flux). The obtained parameters are interrelated, as discussed in Appendix D. The fit also included GOES-based data limited to the moderate cycle SC 24 as presented in the right-hand side (RHS) block, Cols. 4–5 of Table 3.

Table 3.

Best-fit Weibull parameters along with the 68% c.i.

To validate the fit, we also tried fitting the obtained CCDF (Fig. 1) with other distribution types. Neither purely exponential nor power-law distributions can formally fit the data. The Band function (Band et al. 1993) can provide a poor formal fit to the CCDF, but because it uses four free parameters compared to the two parameters in the Weibull distribution, it is rejected by the Akaike and Bayes information criteria (Chakrabarti & Ghosh 2011). Moreover, the large uncertainties of the Band-function fit prevent evaluations of ⟨F⟩∞ (see Sect. 4).

4. Results and discussion

The combined statistics of the direct and terrestrial-CI proxy data are nearly perfectly fit by the Weibull distribution (Fig. 1). Knowing (or estimating) the CCDF of the integral SEP flux, we can compute the full average flux (i.e., averaged over an infinite exposure time) as

(2)

where ω(F) is the differential Weibull distribution. However, if the dataset is limited so that the highest observed flux is ℱ, as is the case for the space era (Fig. 1), for example, the formal average flux ⟨F⟩ℱ (replacing ∞ with ℱ in Eq. (2)) might be significantly underestimated compared to the true value because the contribution from rare strong-flux events is missed.

The ratio ⟨F⟩ℱ/⟨F⟩∞ as a function of ℱ is shown in Fig. 2 for F60 using the Weibull distribution given in the RHS block of Table 3. Direct space-era observations are limited to weak–moderate SEP fluxes (as marked in Fig. 2) and represent only ≈40% of the total flux ⟨F⟩∞. For other energies, this fraction ranges from 20% to 55% (up to 71% for F30, caused by larger ESPE flux uncertainties in this energy range). However, the inclusion of the ESPEs data accounts for ⪆95% of ⟨F⟩∞. Thus, in contrast to the current paradigm, the directly measured SEP flux during the space era is not representative of the long-term flux because a great part of the ESPE contribution is missing.

thumbnail Fig. 2.

Ratio ⟨F60⟩ℱ/⟨F60⟩∞ as a function of maximum observed SEP flux ℱ (see Eq. (2)) for the Weibull distribution shown in the RHS block of Table 3. Shading represents the 68% c.i. The vertical dashed lines, black and blue, with the horizontal red arrows, indicate the upper limits of the SEP flux for the space era and Holocene, respectively, i.e., the black dot and blue star in Fig. 1b.

Next, we compare in Fig. 3 the ⟨F⟩∞ values estimated from the GOES and terrestrial CI data with the megayear-averaged SEP fluxes assessed independently from the lunar data (Poluianov et al. 2018) for the energy range 30–200 MeV. The average SEP fluxes that were directly measured during the space era are systematically lower than the megayear-averaged lunar data. This implies a significant discrepancy, particularly for the moderate SC 24, which represents the typical long-term solar activity (Usoskin et al. 2014, 2016). However, the average fluxes ⟨F⟩∞ based on the combined space-era and CI-proxy dataset are fairly consistent with the lunar-based data as the shaded areas overlap (see also Table 1). Since the average SEP flux was high during SCs 22–23 because of the Modern Grand maximum, we also calculated ⟨F*⟩∞, which is similar to ⟨F⟩∞, but based on direct observations during SC 24 alone. The agreement between ⟨F*⟩∞ and the SEP fluxes from lunar data is very good, implying that the combined statistic of SEPs during a moderate SC and rare ESPEs is fully consistent with the megayear-averaged SEP spectrum.

thumbnail Fig. 3.

Energy dependence of the average SEP flux evaluated using different sources: Megayear-averaged flux estimated from lunar data (gray) (Poluianov et al. 2018), ⟨F⟩∞ based on the combined direct and CI-proxy datasets (green; Fig. 1), similar to the green line, including CI-proxy data, but with the direct data for SC 24 alone ⟨F*⟩∞ (blue), directly measured average fluxes for SC 22–24 (green stars) (Raukunen et al. 2022), and the directly measured average fluxes for SC 24 (blue dots) (Raukunen et al. 2022). Uncertainties are for the full range for the lunar data and 68% c.i. for the other reconstructions. The plotted flux values are listed in Table 1.

5. Conclusions

In this Letter, we have analyzed average SEP fluxes in the energy range 30–200 MeV, estimated with different methods and datasets for different timescales: direct spacecraft measurements over the past few decades, ESPEs reconstructed from terrestrial CI-proxy data on the multi-millennial timescale, and lunar CI data over a megayear timescale. We conclude that direct data for the past decades are not representative of the long-term SEP flux. They contribute only 20–55% to it. Rare ESPEs, which were absent during the space era but were reconstructed with the terrestrial CI proxy over the Holocene, contribute 40–80% to the long-term SEP flux. This is a major contribution. The combined statistics of the direct and proxy-based SEP fluxes are fully consistent with the megayear-averaged SEP fluxes that were reconstructed independently from lunar samples.

Thus, we showed for the first time to our knowledge that two different components of the SEP flux, that is, the regular cycle variability and rare extreme events, contribute significantly to the long-term SEP flux, as shown by a good agreement with the lunar data. Neither of these datasets alone can represent the SEP flux variability, which is needed, for instance, to assess the radiation environment for planetary evolution and habitability and for the planning of long-lasting space missions.

Acknowledgments

This work was partly supported by the Academy of Finland (Projects ESPERA no. 321882, QUASARE no. 330064 and FORESAIL no. 336809), University of Oulu (Project SARPEDON). The ISSI Team #510 (Solar Extreme Events: Setting up a Paradigm, led by F. Miyake and I. Usoskin) is acknowledged for stimulating discussions.

References

  1. Aguilar, M., Cavasonza, L. A., Ambrosi, G., et al. 2021, Phys. Rev. Lett., 127, 271102 [NASA ADS] [CrossRef] [Google Scholar]
  2. Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [Google Scholar]
  3. Beer, J., McCracken, K., & von Steiger, R. 2012, Cosmogenic Radionuclides: Theory and Applications in the Terrestrial and Space Environments (Berlin: Springer) [Google Scholar]
  4. Brehm, N., Christl, M., Knowles, T. D. J., et al. 2022, Nat. Commun., 13, 1196 [NASA ADS] [CrossRef] [Google Scholar]
  5. Chakrabarti, A., & Ghosh, J. 2011, in Philosophy of Statistics, eds. P. Bandyopadhyay, & M. Forster (Amsterdam: North-Holland), Handbook of the Philosophy of Science, 7, 583 [CrossRef] [Google Scholar]
  6. Cliver, E. W., Schrijver, C. J., Shibata, K., & Usoskin, I. G. 2022, Liv. Rev. Sol. Phys., 19, 2 [NASA ADS] [CrossRef] [Google Scholar]
  7. Desai, M., & Giacalone, J. 2016, Liv. Rev. Sol. Phys., 13, 3 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dyer, C. S., Hunter, K., Clucas, S., & Campbell, A. 2004, IEEE Trans. Nucl. Sci., 51, 3388 [CrossRef] [Google Scholar]
  9. Fink, D., Klein, J., Middleton, R., et al. 1998, Geochim. Cosmochim. Acta, 62, 2389 [NASA ADS] [CrossRef] [Google Scholar]
  10. Gopalswamy, N. 2018, in Extrem. Events Geosp., ed. N. Buzulukova (Elsevier), 37 [CrossRef] [Google Scholar]
  11. Grieder, P. 2001, Cosmic Rays at Earth (Amsterdam: Elsevier Sci) [Google Scholar]
  12. Jull, A., Cloudt, S., Donahue, D., et al. 1998, Geochim. Cosmochim. Acta, 62, 3025 [NASA ADS] [CrossRef] [Google Scholar]
  13. Knudsen, M. F., Riisager, P., Donadini, F., et al. 2008, Earth Planet. Sci. Lett., 272, 319 [CrossRef] [Google Scholar]
  14. Koldobskiy, S., Raukunen, O., Vainio, R., Kovaltsov, G. A., & Usoskin, I. 2021, A&A, 647, A132 [CrossRef] [EDP Sciences] [Google Scholar]
  15. Koldobskiy, S., Usoskin, I., & Kovaltsov, G. A. 2022, J. Geophys. Res. Space Phys., 127, 1 [CrossRef] [Google Scholar]
  16. Kovaltsov, G. A., Usoskin, I. G., Cliver, E. W., Dietrich, W. F., & Tylka, A. J. 2014, Sol. Phys., 289, 4691 [Google Scholar]
  17. Mekhaldi, F., Muscheler, R., Adolphi, F., et al. 2015, Nat. Commun., 6, 8611 [Google Scholar]
  18. Mekhaldi, F., Adolphi, F., Herbst, K., & Muscheler, R. 2021, J. Geophys. Res. Space Phys., 126 [CrossRef] [Google Scholar]
  19. Miyake, F., Nagaya, K., Masuda, K., & Nakamura, T. 2012, Nature, 486, 240 [NASA ADS] [CrossRef] [Google Scholar]
  20. Miyake, F., Masuda, K., & Nakamura, T. 2013, Nat. Comm., 4, 1748 [NASA ADS] [CrossRef] [Google Scholar]
  21. Miyake, F., Usoskin, I., & Poluianov, S. 2019, Extreme Solar Particle Storms (IOP Publishing) [CrossRef] [Google Scholar]
  22. Nevalainen, J., Usoskin, I. G., & Mishev, A. 2013, AdSpR, 52, 22 [NASA ADS] [Google Scholar]
  23. Nishiizumi, K., Arnold, J. R., Klein, J., & Middleton, R. 1984, Earth Planet. Sci. Lett., 70, 164 [CrossRef] [Google Scholar]
  24. Nishiizumi, K., Arnold, J. R., Kohl, C. P., et al. 2009, Geochim. Cosmochim. Acta, 73, 2163 [NASA ADS] [CrossRef] [Google Scholar]
  25. Paleari, C. I., Mekhaldi, F., Adolphi, F., et al. 2022, Nat. Commun., 13, 214 [NASA ADS] [CrossRef] [Google Scholar]
  26. Panovska, S., Constable, C. G., & Korte, M. 2018, Geochem. Geophys. Geosyst., 19, 4757 [NASA ADS] [CrossRef] [Google Scholar]
  27. Poluianov, S., Kovaltsov, G. A., & Usoskin, I. G. 2018, A&A, 618, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Potgieter, M. 2013, Liv. Rev. Sol. Phys., 10, 3 [Google Scholar]
  29. Rancitelli, L. A., Fruchter, J. S., Felix, W. D., Perkins, R. W., & Wogman, N. A. 1975, Lunar Planet. Inst. Sci. Conf. Proc., 6, 1891 [Google Scholar]
  30. Raukunen, O., Usoskin, I., Koldobskiy, S., Kovaltsov, G., & Vainio, R. 2022, A&A, 665, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Reedy, R. C. 1999, Lunar Planet. Inst. Sci. Conf. Abstr., 30, 1643 [Google Scholar]
  32. Reedy, R. C. 2012, Lunar Planet. Inst. Sci. Conf. Abstr., 43, 1285 [Google Scholar]
  33. Shea, M. A., & Smart, D. F. 2000, Space Sci. Rev., 93, 229 [NASA ADS] [CrossRef] [Google Scholar]
  34. Solanki, S. K., Usoskin, I. G., Kromer, B., Schüssler, M., & Beer, J. 2004, Nature, 431, 1084 [Google Scholar]
  35. Thomas, B. C., Melott, A. L., Arkenberg, K. R., & Snyder, B. R. 2013, Geophys. Resl. Lett., 40, 1237 [NASA ADS] [CrossRef] [Google Scholar]
  36. Usoskin, I. G. 2017, Liv. Rev. Sol. Phys., 14, 3 [Google Scholar]
  37. Usoskin, I. G., & Kovaltsov, G. A. 2012, ApJ, 757, 92 [NASA ADS] [CrossRef] [Google Scholar]
  38. Usoskin, I. G., Solanki, S. K., Schüssler, M., Mursula, K., & Alanko, K. 2003, Phys. Rev. Lett., 91, 211101 [Google Scholar]
  39. Usoskin, I., Solanki, S., Kovaltsov, G., Beer, J., & Kromer, B. 2006, Geophys. Res. Lett., 33, L08107 [NASA ADS] [Google Scholar]
  40. Usoskin, I. G., Kromer, B., Ludlow, F., et al. 2013, A&A, 552, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Usoskin, I. G., Hulot, G., Gallet, Y., et al. 2014, A&A, 562, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Usoskin, I. G., Gallet, Y., Lopes, F., Kovaltsov, G. A., & Hulot, G. 2016, A&A, 587, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Usoskin, I., Koldobskiy, S., Kovaltsov, G., et al. 2020, J. Geophys. Res. (Space Phys.), 125 [Google Scholar]
  44. Vainio, R., Desorgher, L., Heynderickx, D., et al. 2009, Space Sci. Rev., 147, 187 [Google Scholar]
  45. Vainio, R., Valtonen, E., Heber, B., et al. 2013, J. Space Weather Space Clim., 3, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Weibull, W. 1951, J. Appl. Mech., 18, 293 [NASA ADS] [Google Scholar]
  47. Yamashiki, Y. A., Maehara, H., Airapetian, V., et al. 2019, ApJ, 881, 114 [Google Scholar]

Appendix A: Peculiarities of energetic particle measurements with terrestrial and lunar cosmogenic isotopes

Here, we provide an oversimplified illustration (Figure A.1) of the formation of cosmogenic-isotope records in terrestrial and lunar natural archives. More details can be found elsewhere (Beer et al. 2012; Usoskin 2017).

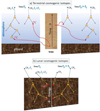thumbnail Fig. A.1.

Oversimplified sketch of the formation of cosmogenic-isotope records in terrestrial (panel a) and lunar (panel b) archives. Primary cosmic-ray particles CR1 and CR2 with energies E1 and E2 < E1 are denoted by blue dots, nuclear reactions by stars, secondaries by arrows, and produced cosmogenic isotopes by red dots. Two different moments of time t1 and t2 > t1 are shown on the left- and right-hand sides, respectively.

Fig. A.1a illustrates the formation of terrestrial isotopes exemplified in 14C in tree rings. We first consider, in the left-hand side of the plot, two cosmic-ray particles impinging on the Earth’s atmosphere at time t1: CR1 with energy E1 and CR2 with energy E2 < E1, as depicted by the blue dots. An energetic CR1 particle can initiate a fully developed nucleonic cascade in the atmosphere and produce 14C atoms near the ground. This cosmogenic 14C becomes absorbed by living trees and is used to build a tree ring, corresponding to time t1 (middle panel). Less energetic CR2 particle can induce only a partial cascade and produce 14C atoms in the middle stratosphere. These 14C atoms are transported by the atmospheric circulation and can also eventually be absorbed by trees in the same annual ring. We now consider a similar pair of cosmic-ray particles, but a pair that impinges on Earth at time t2 (as illustrated in the RHS of the plot), which is some years later. The 14C atoms produced by CR1 and CR2 particles are stored in a way similar to that shown on the left-hand side, in a tree ring corresponding to the time t2. Thus, terrestrial cosmogenic 14C provides a temporal resolution (different tree rings), but no spectrometry for CRs. If there were an enhanced flux of cosmic rays during a specific year, it would have been observed as a peak in the 14C concentration in the corresponding tree ring. This allows us to study ESPEs and the times of their occurrence using terrestrial cosmogenic-isotope proxies. The scheme is similar for other isotopes, for example, 10Be or 36Cl, which are measured in stratified and independently dateable polar ice cores. The use of multiproxy data enables a rough estimate of the spectra because different isotopes have different energy thresholds for their production.

A sketch of the formation of the lunar cosmogenic isotope record is shown in Figure A.1b. We consider the same pair of cosmic-ray particles, that is, CR1 and CR2, that impinges on the lunar surface at time t1 (left-hand side). The more energetic CR1 initiates a nucleonic cascade in the soil or rock, eventually producing an atom of 26Al at some depth in situ. After production, the 26Al atom remains exactly at the same depth at which it had been produced because there is no transport inside the rock. The less energetic CR2 produces a 26Al atom at a shallower depth, where it remains since then. Similarly, the CR1-CR2 pair arriving at the moment t2 (RHS) produces 26Al atoms at the same depths, depending only on the cosmic-ray energy, regardless of the arrival time. The measured concentration of 26Al is defined by the balance between production and decay rates. Depth in the soil or rock roughly represents the energy of the incoming particles, thus serving as an energy-integrating spectrometer. Thus, the lunar isotope provides an energy resolution, but no time resolution. Accordingly, we can robustly assess the long-term average spectrum of cosmic rays without resolving individual events.

Appendix B: Reconstructing the integral flux of ESPEs

To estimate the ESPE integral flux, we used the effective-energy method (also known as the bow-tie method) based on an assumption that there is an energy value, called effective energy Eeff, that causes the CI response Q (i.e., the global production of 14C or polar deposition of 10Be and 36Cl) for SEP events to be directly proportional to the integral flux of SEP particles with an energy that exceeds the effective energy,

(B.1)

for a reasonably broad range of spectral shapes and parameters. The effective-energy method was validated, and the values of Eeff and 𝒦eff were determined for different CIs by Koldobskiy et al. (2022). We used this approach, enriched with Monte Carlo modeling to assess the uncertainties as described below, and CI-proxy data Q from Mekhaldi et al. (2015) and Brehm et al. (2022) to calculate integral fluxes F60, F234, and F236, corresponding to 36Cl, 14C, and 10Be, respectively, for the ESPE events listed in Table 2 in the main text.

The values of Q need to be corrected for the changing geomagnetic field, which is typically represented by its virtual axial dipole moment, VADM (e.g., Nevalainen et al. 2013). To account for the realistic geomagnetic conditions corresponding to the exact time of the ESPE, we used the verified correction method (see Equation 5 in Koldobskiy et al. 2022) to reduce the value of Q to the standard present-day conditions,

(B.2)

where M0 = 7.75 ⋅ 1022 A⋅m2 is the present-day VADM, and the factor γ can be found in Table 2 of Koldobskiy et al. (2022). To account for notable uncertainties in the VADM reconstruction, we used the Monte Carlo modeling applied to two recent VADM series by Knudsen et al. (2008) and Panovska et al. (2018). For each iteration, we first randomly chose these VADM series. Then we randomly selected the exact value of VADM M(t), corresponding to the time t of the ESPE, within the reported uncertainties as

(B.3)

where M*(t) and σM(t) are the listed VADM values and their uncertainty for the time t, and r is a pseudo-random number with zero mean and unit dispersion. Then, the flux F was calculated using Equation B.1, where the value of 𝒦eff was randomly selected, similarly to Equation B.3, but for the values taken from Table 2 of Koldobskiy et al. (2022). The flux values calculated in this way were saved for each iteration. After 1000 iterations, we calculated the median ESPE integral flux values and their 68% confidence intervals.

Because 14C and 10Be have similar effective energies (234 and 236 MeV, respectively), the corresponding fluxes were averaged. The necessary data for both 36Cl and 10Be exist for only three ESPEs (Table 2), which enables us to estimate fluxes in different energies. The other five ESPEs have only 14C measurements, and only F234 can therefore be estimated for them.

The values of F200, F100, and F30 were inter- and extrapolated using the values of F234 and F60. By assuming that the ESPE integral flux has a spectral shape similar to strong regular SEP events (Usoskin et al. 2020; Paleari et al. 2022), we based our inter- and extrapolations on the recent reconstructions of integral fluxes for the 58 strongest recently observed SEP events (Koldobskiy et al. 2021). The corresponding ratios and their 1σ uncertainties are F200/F234 = 1.45 ± 0.10, F30/F60 = 3.41 ± 1.58, and F60/F100 = 2.66 ± 0.69.

Appendix C: Lunar cosmogenic-isotope data for reconstructing the SEP flux

The measured activity (concentration) of a cosmogenic isotope (CI) in a lunar rock or lunar soil has a distinct depth profile in which the isotope content continuously decreases over the depth. The example shown in Fig. C.1 is a compilation of the 26Al measurements in lunar rock 64455 and the deep soil core Apollo-15 (Rancitelli et al. 1975; Nishiizumi et al. 1984, 2009). The double-slope shape is caused by the sum of CIs produced by GCRs and SEPs. Because GCRs are more energetic and thus produce CI in deeper layers (see Appendix A), CI measured in deep soil cores at depths > 10 g/cm2 can be used to estimate the average GCR flux, which forms the background production of CI in shallower layers. The fraction of CI produced by SEP is calculated as the excess above the GCR-related CI background for each depth. This enables estimating the average energy spectrum of the SEP flux, as illustrated in Fig. C.1. The uppermost layers are corrected for surface erosion.

thumbnail Fig. C.1.

Depth profile of 26Al compiled from measurements (colored symbols as described in the legend) in lunar rock 64455 (N09) (Nishiizumi et al. 2009) and the deep lunar-soil core Apollo-15 (R75, N84) (Rancitelli et al. 1975; Nishiizumi et al. 1984). Areas denoted SEP and GCR approximately show the amount of 26Al produced by SEP and GCR, respectively.

Full details of how exactly GCR and SEP average fluxes are reconstructed from the CI measurements can be found in Poluianov et al. (2018). The reconstructed integral SEP spectrum is shown in Fig. 3 of the main text, along with the full-range uncertainties.

Appendix D: Fitting CCDF with the Weibull distribution

The CCDFs (Fig. 1 of the main text), which include both regular SEP and ESPE data points characterized by values of their annual integral flux F and occurrence probability W along with their 68% c.i.s σF and σW, respectively, were fit with the Weibull distribution using an iterative Monte Carlo procedure as described below. For each iteration, we first, randomly selected from the regular SEP dataset (sorted in ascending order) N points, where N is the number of data points available for the ESPE dataset (stars in Figure 1). These selected regular SEP points together with the ESPE data points formed a fitting subset, characterized by F*, σF*, W*, and σW*. This was done to equalize weights of the regular and ESPE events in the fitting procedure and to avoid a statistical bias toward points with low annual flux. Second, we randomly selected, using a pseudo-random number r, normally distributed with zero mean and unit variance, the values of 𝔉 for each point of the subset produced in step 1 as 𝔉 = F* + r ⋅ σF*. The combinations of 𝔉 and W* were resorted to ensure decreasing W* with an increase in 𝔉. Next, we found the best-fit parameters k* and λ* by minimizing χ2 between the data and fit probabilities Wfit,

(D.1)

The best fit was found by a scan over the grid space of parameters. The values of k* and λ* and the corresponding minimum χ2 were stored for each iteration.

After 10000 iterations, we analyzed the distribution of χ2 values. The set of parameters giving the minimum value 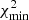was considered as the best-fit solution with the 68% c.i. of the parameters defined as χ2 ≤  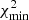+ 2.30. In Figure D.1 we show an example of the distributions of the Weibull parameters versus χ2 value and the parameter correlation plot for F30 obtained for GOES SC 24 and terrestrial CIs. The best-fit solution is denoted with the red stars, and blue dots denote solutions within the 68% c.i. The corresponding values of the parameters are listed in Table 3 (first line, RHS block) in the main text. As shown in Fig. D.1 (RHS block), the obtained parameters k and λ appear to be strongly correlated.

thumbnail Fig. D.1.

Distributions of Weibull parameters λ and k vs. χ2 and parameter correlation plot for F30 fit obtained using GOES SC 24 and terrestrial CI proxy data. Red stars correspond to the best-fit parameter values (), and blue dots have χ2 ≤  + 2.30, as shown with the dashed red line.

The results are qualitatively similar for other energies and are listed in Table 3 in the main text.

All Tables

Table 1.

SEP fluxes (cm−2 s−1) above 30, 60, 100, and 200 MeV, averaged over different timescales.

In the text
Table 2.

ESPE integral fluxes reconstructed from terrestrial CI data (Mekhaldi et al. 2015; Brehm et al. 2022; Paleari et al. 2022), in 103 cm−2 s−1.

In the text
Table 3.

Best-fit Weibull parameters along with the 68% c.i.

In the text

All Figures

thumbnail Fig. 1.

CCDF (see text for definition) for SEP flux F30, F60, F100, and F200 in panels a–d, respectively. The uncertainties are evaluated using the Poisson statistics (e.g., Usoskin & Kovaltsov 2012). Open circles correspond to direct measurements (Raukunen et al. 2022), and the black dots depict conservative upper limits (see text). The open and filled blue stars represent the annual flux estimates for ESPEs from terrestrial CI data (Table 2) and the conservative upper limits (Usoskin 2017), respectively. The green curves depict the Weibull distributions fit to the combined direct and terrestrial CI datasets (Sect. 3). All error bars and filled areas bound the 68% c.i. The vertical red bar in panel d indicates the sensitivity threshold of the terrestrial CI method to an ESPE on a 3σ level (Usoskin et al. 2020).
In the text
thumbnail Fig. 2.

Ratio ⟨F60⟩ℱ/⟨F60⟩∞ as a function of maximum observed SEP flux ℱ (see Eq. (2)) for the Weibull distribution shown in the RHS block of Table 3. Shading represents the 68% c.i. The vertical dashed lines, black and blue, with the horizontal red arrows, indicate the upper limits of the SEP flux for the space era and Holocene, respectively, i.e., the black dot and blue star in Fig. 1b.
In the text
thumbnail Fig. 3.

Energy dependence of the average SEP flux evaluated using different sources: Megayear-averaged flux estimated from lunar data (gray) (Poluianov et al. 2018), ⟨F⟩∞ based on the combined direct and CI-proxy datasets (green; Fig. 1), similar to the green line, including CI-proxy data, but with the direct data for SC 24 alone ⟨F*⟩∞ (blue), directly measured average fluxes for SC 22–24 (green stars) (Raukunen et al. 2022), and the directly measured average fluxes for SC 24 (blue dots) (Raukunen et al. 2022). Uncertainties are for the full range for the lunar data and 68% c.i. for the other reconstructions. The plotted flux values are listed in Table 1.
In the text
thumbnail Fig. A.1.

Oversimplified sketch of the formation of cosmogenic-isotope records in terrestrial (panel a) and lunar (panel b) archives. Primary cosmic-ray particles CR1 and CR2 with energies E1 and E2 < E1 are denoted by blue dots, nuclear reactions by stars, secondaries by arrows, and produced cosmogenic isotopes by red dots. Two different moments of time t1 and t2 > t1 are shown on the left- and right-hand sides, respectively.
In the text
thumbnail Fig. C.1.

Depth profile of 26Al compiled from measurements (colored symbols as described in the legend) in lunar rock 64455 (N09) (Nishiizumi et al. 2009) and the deep lunar-soil core Apollo-15 (R75, N84) (Rancitelli et al. 1975; Nishiizumi et al. 1984). Areas denoted SEP and GCR approximately show the amount of 26Al produced by SEP and GCR, respectively.
In the text
thumbnail Fig. D.1.

Distributions of Weibull parameters λ and k vs. χ2 and parameter correlation plot for F30 fit obtained using GOES SC 24 and terrestrial CI proxy data. Red stars correspond to the best-fit parameter values (), and blue dots have χ2 ≤  + 2.30, as shown with the dashed red line.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.