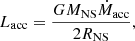EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 670 (February 2023) A&A, 670 (2023) A80 Full HTML
Open Access
Issue
A&A
Volume 670, February 2023
Article Number A80
Number of page(s) 8
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202245081
Published online 07 February 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1. Introduction

The growing number of observations of Galactic X-ray binaries (XRBs) provides tools that help us to constrain the formation of compact objects and related processes during which the kinematic properties of these binaries are expected to change. One interesting, yet unresolved issue, is the process under which natal kicks are imparted to the compact object, either a black hole (BH) or a neutron star (NS), during its formation, associated with supernova explosions. These natal kicks are believed to be responsible for the large transverse motions on the plane of the sky of NSs in binaries and isolated pulsars. Although there is no direct observation of such kicks, their existence can be inferred from the peculiar velocities measured in a variety of isolated NSs, and also from the high eccentricity observed in some XRBs containing NSs. Gathering observational information about the current state of XRBs, such as masses, orbital periods, and positions in the Hertzsprung–Russell (HR) diagram, can then be complemented with kinematic constraints to discern the complete evolutionary path and to provide a consistent picture of compact object formation scenarios and the crucial role played by natal kicks.

Of particular interest is GX 301–2, an XRB discovered by Ricker et al. (1973) that contains a compact object and an optical star, named Wray 977 (BR Cru, Vidal 1973; Bradt et al. 1977). Based on spectroscopic observations, Kaper et al. (1995) classified Wray 977 as a B1 Ia+ hypergiant, which makes it the only hypergiant star known to be within a binary system. In addition, the mass function derived from pulse-timing analyses indicates that the mass of Wray 977 is larger than 31 M⊙ (Sato et al. 1986), making it a member of the high-mass X-ray binary (HMXB) class. Coleiro & Chaty (2013) derived a distance to the binary of 3.10 ± 0.64 kpc using near-infrared magnitudes from the Two Micron All Sky Survey (2MASS) point-source catalogue. The source presents X-ray pulsations with a period of 11.6 min (White et al. 1976) and a history of rapid spin-up episodes (Koh et al. 1997). Studying the occurrence of X-ray flares, Watson et al. (1982) determined an orbital period of 41.5 days. Furthermore, GX 301–2 is one of the most eccentric systems among all the HMXBs known (Liu et al. 2006). In the period between 2018 and 2020, the binary experienced a new spin-up process (Ding et al. 2021). Observations during this period suggest a disc-accretion scenario favouring the efficient transfer of angular momentum (Liu et al. 2021), rather than a wind-accretion one. The spin orientation of the NS has been under discussion recently with some authors favouring a retrogradely spinning NS (Mönkkönen et al. 2020), while others tend to favour a prograde spin solution (Liu 2020). Given the highly unequal masses measured in the binary components, as well as their particular nature, GX 301–2 stands as a very rare and unique object, whose individual properties are particularly different from every other known XRB, which naturally makes its rate of occurrence quite low, as we subsequently address and discuss in this paper.

The combination of the individual masses (and the mass ratio) and orbital parameters in this binary make it an interesting source to try and understand how binary evolution leads to core collapse and, in addition, what the role being played by the natal kicks being imparted onto newly born compact objects is. In one of the first detailed calculations of its evolution, Brown et al. (1996) favoured a very massive NS progenitor, of ∼45 M⊙, originating from the initially most massive star in the binary system. Along the same lines, Ergma & van den Heuvel (1998) proposed a massive progenitor of ≳50 M⊙, by assuming a fully inefficient mass-transfer (MT) scenario. Perhaps the most detailed binary evolution study on the progenitor of GX 301–2 is presented in Wellstein & Langer (1999). In their work, the authors explore a channel that would arise from the smallest possible initial mass for the progenitor binary, with the aim being to find the lower limit in masses leading to a BH. For that reason, they restricted their search to almost equal initial masses in a close binary such that stars went through an efficient MT phase during the main sequence (MS) evolution, known as Case A of MT (Kippenhahn & Weigert 1967), while avoiding the inclusion of a kick onto the NS. They found that an initial primary mass of ∼26 M⊙ with a companion of similar characteristics in a circular orbit with a period of ∼3.5 days could match the observed properties of GX 301–2. More recently, Belczynski et al. (2012) studied a similar case to that in Wellstein & Langer (1999), but focussing on the future evolution of the binary. They predict that a MT phase should occur after the hypergiant companion swells enough and, given the unequal mass ratio, this MT phase will most likely be dynamically unstable, leading to a common-envelope (CE) phase (Ivanova et al. 2013), which even with the most optimistic assumptions will be unable to eject its envelope and survive this phase, thus finishing its evolution as a peculiar object in a CE merger (Thorne & Zytkow 1977; Fryer & Woosley 1998; Zhang & Fryer 2001).

In this paper we follow the study presented in Wellstein & Langer (1999) by using updated physical prescriptions for important stellar evolutionary phases. In addition, we address the role of supernova-induced kicks on the NS in light of the new measurements done by the Gaia satellite on the proper motion of the binary (Gaia Collaboration 2021) and its radial velocity (Kaper et al. 2006). The paper is organized as follows. Section 2 contains a brief description of the setup of our detailed binary evolution models. In Sect. 3 we start by presenting a representative evolution of a binary leading to conditions similar to current GX 301–2 properties. We then show the results from a grid of detailed binary simulations of stars until core collapse. We then present results on the impact of natal kicks in Sect. 4. Our concluding remarks are finally given in Sect. 6.

2. Methods: Stellar evolution

Interacting binaries are calculated using the detailed stellar-evolution code MESA (version 10398, Paxton et al. 2011, 2013, 2015, 2018, 2019). All computed stars are assumed to be non-rotating and to have an initial solar metallicity content, Z = Z⊙ = 0.017 (Grevesse & Sauval 1998). We used default nuclear reaction networks present in MESA: basic.net, co_burn.net, and approx21.net which were switched dynamically once later stages in the evolution were reached. Convective regions, which were obtained from the Ledoux criterion (Ledoux 1947), were modelled using the standard mixing-length theory (Böhm-Vitense 1958) with a mixing-length parameter αMLT = 2.0. Semi-convection was modelled following Langer et al. (1983) with an efficient parameter αSC = 1. We included an exponential overshooting beyond convective boundaries (Herwig 2000) with overshoot mixing parameters of f = 0.01 and f0 = 0.005. In order to avoid some numerical problems during the evolution of massive stars until the Wolf-Rayet (WR) stage, we used the MLT++ formalism as presented in Paxton et al. (2013) which reduces the super-adiabaticity in regions where the convective velocities approach the speed of sound. Additionally, the effect of thermohaline mixing follows Kippenhahn et al. (1980) with an efficiency parameter of αth = 1. The modelling of stellar winds follows that of Brott et al. (2011) as described in Marchant et al. (2017).

Binary systems are initially assumed to have circular orbits with both components being at their zero-age main sequence (ZAMS). Binary interaction was computed with the MESAbinary module of MESA. When one of the stars in the binary overflowed its Roche lobe, the MT rate was implicitly computed following the prescription of Kolb & Ritter (1990). Furthermore, we assume there is no mass lost during this phase, that is, a fully conservative case of MT throughout the entire evolution. As late stages in the evolution do not produce significant changes to the binary properties since the remaining time-to-core collapse is notably short, we assumed the occurrence of a supernova (SN) when one of the stars reached core Carbon depletion, leaving behind a compact remnant. The mass of the remnant was obtained from the delayed prescription from Fryer et al. (2012), which depends on the masses of the carbon-oxygen (CO) core and the envelope at core carbon depletion1.

3. Results

3.1. An example evolution

Before examining the wider parameter space explored, we describe here a representative case of binary evolution, which is followed by the majority of the binary systems modelled in this work. In Fig. 1 we show the evolutionary tracks in the HR diagram of a primary star of 27.60 M⊙ with a companion (secondary) star of 23.18 M⊙ (which corresponds to a mass ratio q = 0.84) in an initially circular orbit with an orbital period of Porb = 2 days. We consider that both stars are born in the ZAMS. During core Hydrogen (H) burning, the primary overflows its Roche lobe and a Case A of MT starts (Kippenhahn & Weigert 1967). This phase, which happens in a nuclear timescale, strips the primary of a fraction of its envelope mass and stops shortly before the primary depletes the H in its core. During this MT phase, the mass ratio is reversed and the secondary becomes the more massive of the pair. The secondary star, which is accreting all the mass that is transferred, becomes overluminous while keeping an almost constant effective temperature, Teff.

thumbnail Fig. 1.

Evolutionary tracks in the HR diagram of a close binary system with an initial primary mass of 27.60 M⊙ and a secondary mass of 23.18 M⊙. This binary is assumed to start its evolution in a circular orbit with Porb = 2 days, in a fully conservative MT scenario throughout its entire lifetime. The evolution of the primary (secondary) star is represented in solid blue (orange) line. Different MT phases are plotted on top of each star: in green (grey) we show Case A (early Case B) MT. The dotted grey lines represent constant radii for 1, 10, and 100 R⊙, while the dotted black line designates the evolution of the secondary star after the formation of the first compact object (GX 301–2) if the companion NS star was absent. The yellow star marks the location where the primary exploded as a SN. For comparison, the ZAMS corresponding to stars of the same composition is shown by the black dashed line.

While the primary is crossing the Hertzsprung gap (HG), it overflows its Roche lobe for a second time and an early Case B of MT phase starts (Kippenhahn & Weigert 1967). In this fast MT episode, most of the H-rich envelope of the primary is removed, until detachment is reached. Although a small fraction of envelope mass remains in the primary at the end of this second MT phase, strong winds from the WR phase help to remove it. By the end of its evolution, the primary star, which is almost completely depleted of H, explodes as a hot He-rich star, leaving behind a 2.2 M⊙ NS. The mass of the compact remnant was calculated following the prescription of Fryer et al. (2012), as we mention later in Sect. 3.2. On the other hand, the secondary, which was rejuvenated by the accreted H-rich material of the previous MT episodes, is still burning H in its core.

3.2. Grid of models

Given the large difference in masses between the components of GX 301–2, we can set some constraints for the exploration of the initial parameters: masses (M1, M2) and Porb. First, if we assume that the stars evolved as if they were isolated, that is, with no MT interaction between them, then the progenitor of the NS should have been more massive than current measurements for Wray 977, with an initial mass above 40 M⊙. However, masses as high as those are likely to contain a massive CO core, which would end up collapsing into a BH instead of a NS (Fryer et al. 2012; Sukhbold et al. 2016; Patton & Sukhbold 2020). Second, the total initial mass Mtot, i in the system must be larger than current estimated values, which imposes a lower limit in masses such that Mtot, i ≳ 40 M⊙. From this, we suggest that the system likely experienced an interaction phase in which the initially less massive star accreted a significant amount of mass from its companion. In order to maximize this stage of interaction so as to increase the mass of the accreting star, we initialized the stars close to each other ensuring that the MT phase started when H was being burned in their cores, as in Wellstein & Langer (1999). Furthermore, to avoid an unstable MT phase leading to a merger of the stars, the initial mass ratio q should be close to unity (Hjellming & Webbink 1987). Thus, for our binary models, we considered primary stars with masses between M1 = 22 − 30 M⊙, mass ratios in the q = 0.8 − 0.9 range, and Porb = 2 − 10 days. For the simulation grid, we used linear steps of 0.2 M⊙, 0.02 and 0.2 days, respectively. This grid was chosen after performing an initially wider search in all three mentioned parameters, aimed at obtaining masses consistent with GX 301–2, as listed in Table 1.

Table 1.

Binary parameters of GX 301–2 and stellar parameters of Wray 977 corresponding to the values listed in Kaper et al. (2006).

In Fig. 2 we show a grid of binary models explored for a fixed mass ratio of q = 0.80, where each rectangle is a detailed binary calculation. As shown in Fig. 2, there is a narrow range of primary masses in which we find binaries that end up with a star collapsing into a NS and a companion star with a mass within the values derived by Kaper et al. (2006), as presented in Table 1, while having an initial orbital period between 2 and 5 days. In the lower end of primary masses, we find that the allowed initial orbital periods become wider when increasing the initial masses. Between 24 and 26 M⊙, the range of allowed initial orbital periods is the longest, with compatible masses obtained for Porb = 2 − 5 days. Additionally, we find that for the higher initial masses, the range of initial orbital periods decreases to our lower limit of Porb = 2 days. Thus, in order to obtain the proper mass range, we needed a lower limit for the primary star mass of 23 M⊙ and an upper limit of 29 M⊙.

thumbnail Fig. 2.

Example of a grid of binary systems showing initial periods (in days) and initial primary masses for a fixed initial mass ratio of q = 0.8. Each rectangle represents a single detailed binary evolution model. Light blue is used for binaries with a primary collapsing into a NS while having a companion mass within the values derived by Kaper et al. (2006) (named ‘in range’). In a darker blue colour, we show binaries with primaries forming BHs or being outside the constraint imposed by the observed masses (named ‘out of range’). The hatched region represents a binary that ends its evolution without reaching a core-collapse stage. For the entire grid of models computed, we find that these non-collapsing models either merge during a CE phase between two non-degenerate stars, or stop due to numerical issues. Other initial mass ratios produce similar results.

We find progenitors with consistent masses only if the initial orbital period is below 5 days. This limiting value also depends on the initial primary mass: an increment in the mass requires a shorter initial period. Moreover, binaries with orbital periods of less than 2 days fail to reach the core-collapse stage. In all of these cases, and as a consequence of the complete conservative MT regime explored, both of the stars overflow their Roche lobe producing a contact system (Dewi et al. 2006; Almeida et al. 2015). These binaries will likely end up in a CE phase (Ivanova et al. 2013) which, given the range of obtained orbital periods, will unavoidably merge during the CE phase. Finally, this scenario is also found for binaries with orbital periods of more than 5 days, in which the MT leads to a contact system.

Binaries in which the primary star reaches the core carbon depletion are assumed to collapse and produce either a NS or a BH according to the conditions established by Fryer et al. (2012) in the delayed scenario. At this final stage, we find that those binaries with masses in range of GX 301–2 are constrained to have pre-collapse primary masses between 5 and 7 M⊙, companion stars of 34 to 39 M⊙, and orbital periods in the range of 16−22 days.

4. Natal kicks

During an SN explosion, both mass loss and a kick imparted onto the newly formed NS change the orbital binary parameters. In order to understand the impact that natal kicks have on the progenitor of GX 301–2, we selected the binary presented in Sect. 3.1, which presents components with masses at core collapse within the range derived for GX 301–2, and we randomly drew 2000 kicks from a Maxwellian distribution with a root mean square of σ = 265 km s−1 in the magnitude as constrained from pulsar observations (Hobbs et al. 2005). We further assumed an isotropic orientation for the drawn kicks and we reduced the kick strength by a factor of (1 − ffb), with ffb being the fraction of mass that falls back to the proto-NS at core collapse (Fryer et al. 2012)2. For all of these kicks, we calculated the post-SN orbital period Ppost-kick and eccentricity epost-kick following Kalogera (1996), assuming no interaction between the ejecta of the SN and the companion of the exploding star. We then evolved the binaries that remained bound after the imparted kick using MESA, including the additions described in García et al. (2021). Our goal is to find which combinations of kick strengths and orientations are able to reproduce, after following the evolution from formation of the NS onwards, current estimates for the binary parameters of GX 301–2. It is worth mentioning that among some of these additions, we included a treatment for a putative CE phase. Given the extreme masses in GX 301–2, if at any time the companion star overflows its Roche lobe, the development of a CE phase becomes unavoidable. Furthermore, given the high envelope binding energy, this CE phase finally leads to a merger of the NS with the core of the companion star (Belczynski et al. 2012).

Figure 3 shows the outcome of all of the detailed simulations in the period-eccentricity plane. Orbital parameters can only be found in a limited region derived from the different conservation laws (Kalogera 1996). We see a clear relation between binaries with numerical issues and those merging due to the orientation of the kick. This is experienced by binaries whose kicks lead to systems in which the donor star overflows its Roche lobe and starts transferring mass just after the kick.

thumbnail Fig. 3.

Post-kick binary systems in the period-eccentricity plane. Each point represents a detailed binary simulation between a non-degenerate donor star an a NS. The colours indicate the χ2 minimum found during the entire evolution of each binary, considering observational constraints on binary parameters (i.e. masses of the NS and its companion, orbital period, and eccentricity; see Table 1). Diamonds represent binaries with matching binary properties to the observed ones. With black squares we show binaries merging just after core collapse due to the kick orientation, while grey squares represent binaries for which numerical problems were encountered and the simulations were not completed. The location of the case of a symmetric kick in this plane is shown with an arrow.

In order to constrain the orbital parameters (and the kicks associated with them), we analysed the evolution of each individual binary to find the ones that best match the observed properties of GX 301–2. We quantified this by applying a minimum χ2 method to their evolving individual masses, periods, and eccentricities, so that for each timestep taken in MESA we could evaluate the corresponding χ2 value. In order to do this, we imposed an uncertainty (systematic) in the orbital period of 0.5 days and of 0.1 in the eccentricity for the values listed in Table 1. These values replace the actual observational (statistical) errors, since they are so small that they dominate the χ2 value. These best-matching binaries are shown as diamonds in Fig. 3. We find compatible post-kick periods ranging from 40 days (with a respective epost-kick ∼ 0.4) up to 4000 days (epost-kick ≳ 0.9). These large ranges of Ppost-kick and epost-kick have been obtained as a direct consequence of tides acting on the evolution of these binary parameters, which tend to asymptotically reach an equilibrium condition with the binary being circularized (Hut 1981; Repetto & Nelemans 2014).

Natal kicks for binaries that best match the orbital properties of GX 301–2 lie on a well-defined region for the kick velocity magnitude and inclination between the pre- and post-kick orbit, as seen in Fig. 4. Increasing the magnitude of the kick favours higher inclination values: for vkick ≳ 450 km s−1, we only obtain progenitors with a tilted post-SN orbit ≳π/2, suggesting that a retrograde NS might be reminiscent of the natal kick imposed during the explosion of the NS progenitor (Hills 1983; Brandt & Podsiadlowski 1995; Kalogera 2000). An ongoing debate on the orientation of the spin of the NS in GX 301–2 exists, with some authors favouring the scenario of a retrograde spinning NS based on data from the Fermi Gamma-Ray Burst Monitor (Mönkkönen et al. 2020) and others favouring a prograde spin of the NS (Liu 2020). In our simulations, we have determined that only when the strength of the kick is above 450 km s−1, does the binary contain a retrograde spinning NS. One important caveat concerning this analysis comes from the fact that we do not consider stellar rotation. This implies that the role that tides have in the evolution is not exhaustively taken into account. Tidal evolution tends to lead a binary to an equilibrium state of coplanarity, circularity, and corotation (Hut 1981), thus by assuming non-rotating stars we are forcing coplanarity to be reached instantly. Additionally, evolution until co-rotation can change the orbital angular momentum, impacting different orbital parameters such as Porb.

thumbnail Fig. 4.

Post-kick inclination of the orbital plane (with respect to the pre-kick plane) and binary systemic velocity, vsys, as a function of the natal kick magnitude vkick. In light blue we show binaries matching the orbital parameters of GX 301–2 in its HMXB phase, while grey points represent all the natal kicks explored in detail. In the top and on the right, we show the weighted histograms. Black solid lines show the contour of the 99% credible regions for the chosen kicks’ distributions.

We also find a clear trend for the systemic velocity (vsys) of the binary (see Fig. 4), in which higher vkick implies a higher post-kick vsys. A recent analysis of Gaia observations derived a value of vsys ∼ 56 km s−1 (Fortin et al. 2022), which in our simulations is matched for vkick ≳ 450 km s−1.

To illustrate the typical characteristics of the progenitors of GX 301–2, in Fig. 5 we show the evolution of the observational properties of one of the binaries, which has been selected as an example. We note that the range of donor masses matching current measures of Wray 977 is thought to be larger than 33 M⊙. In the top panel of the figure, we show the evolution of the orbital period after the formation of the NS. The orbital period initially increases due to strong winds from the companion star. After leaving the main sequence, the star swells up and begins a fast MT phase in which the period decreases. Given the high mass ratio, it is likely to result in an unstable MT phase followed by the development of a CE in which the NS would subsequently merge with the core of the companion. During the phase in which the orbital period increases, the eccentricity remains almost constant as there is no strong tidal circularization, as shown in the middle panel of Fig. 5. When the star overflows its Roche lobe, the eccentricity begins to reduce and the system tends to circularize (Verbunt & Phinney 1995).

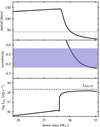thumbnail Fig. 5.

Evolution of orbital period, eccentricity, and released accretion energy of a selected binary model as a function of the mass of the optical companion. Time evolution proceeds from left to right. Light-blue regions represent observational constraints with increased error bars (see Sect. 4). The x-axis corresponds to possible matching values for Wray 977, which is thought to be above 33 M⊙ (Kaper et al. 2006).

We computed the luminosity released by accretion of matter (Lacc) as follows:

L acc = G M NS M ˙ acc 2 R NS , $$ \begin{aligned} L_{\rm acc} = \dfrac{GM_{\rm NS} \dot{M}_{\rm acc}}{2R_{\rm NS}}, \end{aligned} $$(1)

where G is the gravitational constant, Ṁacc is the accretion rate onto the NS that considers the contribution of wind accretion by the Bondi-Hoyle mechanism (Bondi & Hoyle 1944; Hurley et al. 2002), and RNS is the radius of the NS that we set to 10 km. As shown in Fig. 5, during the time leading up to the start of MT, Lacc which was released by wind accretion is around 1036 erg s−1. Considering that a fraction of this energy is radiated as X-rays, it can be detected by any current X-ray space telescope. After the MT starts, this luminosity reaches a maximum value of the Eddington luminosity (LEdd, NS) as a direct consequence of having limited accretion up to the Eddington limit of the NS.

Other important constraints are found in the behaviour of the companion star. As seen in Fig. 6, the radius of the star begins too low to match the radius estimation from Kaper et al. (2006) of R = 70 R⊙; also, just after the star leaves the MS and travels through the HG, it is able to match the values quoted in Kaper et al. (2006) of R = 70 R⊙. This is also true for the effective temperature, Teff, of the star: it needs to be cooler than those (within that mass range) found in the main sequence. On the other hand, the expected luminosity for the star is higher compared to the values derived from observations of log L/L⊙ = 5.67 (Kaper et al. 2006), which can be further studied by exploring the influence that different free parameters of physical conditions in the stellar interiors – such as convective overshooting, semi-convection efficiency, among others – have on the observable properties of a star (Kippenhahn et al. 2012; Kaiser et al. 2020; Klencki et al. 2020).

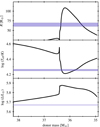thumbnail Fig. 6.

Evolution of the parameters of the donor star of the selected model. Time evolution proceeds from left to right. Light-blue regions represent observational constraints from Kaper et al. (2006). In the case of the radius R, we use the range given by Wellstein & Langer (1999) of 60 <  R <  70 R⊙. The x-axis range matches possible values for Wray 977, with a mass estimation of above 33 M⊙ (Kaper et al. 2006).

In order to compute the expected number of binaries with observational parameters measured for GX 301–2, we followed the method described in Mineo et al. (2012), which provides an estimation for the number of HMXBs at any time as a function of the birth rate of compact objects and the star formation rate (SFR). First, we derived the number of binaries with properties similar to those of GX 201–2 using the birth rate of the NS in the system from the range of initial masses we obtained, 23 − 29 M⊙, assuming an initial mass distribution as in Salpeter (1955). Also considering the constraints in the initial Porb and q and the natal kicks, we could then derive the fraction that become X-ray sources such as GX 301–2 and its duration. We obtain a rate of 2.89 × 10−3 per SFR. Additionally, assuming that the number of HMXBs with a luminosity L >  1035 erg s−1 is ≈135 per SFR (Mineo et al. 2012), we determined that the fraction of HMXBs with properties similar to GX 301–2 is 6.64 × 10−5, implying a low chance of finding a similar binary in the Milky Way. For consistency, we used a different approach to compute the fraction of HMXBs similar to GX 301–2, as presented in Oskinova et al. (2018), and again obtain a very low fraction of 10−4.

5. Discussion

In this work, we have studied the progenitor properties and formation channel of the NS XRB GX 301–2. This HMXB is of particular interest as it contains a NS accompanied by a very massive hypergiant star. In the standard picture of binary evolution, this system requires the progenitor of the NS to have transferred most of its envelope to the companion, now known as Wray 977, in a highly accretion-efficient scenario. We used the publicly available stellar-evolution code MESA to evolve a grid of initial massive binaries, starting from their position in the ZAMS until they reached the HMXB stage, including a natal kick distribution applied to the NS that formed after one of the stars in the binary core collapsed. With the exploration of different strengths in the natal kicks, we were able to find binary systems that match the particular and unique observational constraints associated with GX 301–2.

We found that only a very narrow range of initial masses have final masses compatible with GX 301–2. This narrow constraint in the initial conditions is also true for the orbital period, as binaries with periods above ∼5 days contain stars with masses outside the derived range, thus being unable to be compatible with GX 301–2. Given the highly uncertain nature of asymmetric natal kicks imparted when the NS is born, kicks are generally treated in a stochastic way by assuming certain distributions for their strengths and directions, which consequently lead to changes in important binary parameters such as eccentricity, separation, inclination between the spin of the components and the orbital angular momentum, among others. Values for the strength of the natal kicks can be further constrained if new observational data are considered: a value of vsys ∼ 56 km s−1 (Fortin et al. 2022) is only obtained for vkick ≳ 450 km s−1. A kick velocity of such a magnitude produces a post-SN orbit with a tilt angle ≳π/2, which could be related to a retrograde NS present in this particular binary, as suggested by Mönkkönen et al. (2020), although this proposal is still under debate (Liu 2020).

We caution that our range of preferred initial conditions is subject to several uncertainties due to the poorly constrained parameters associated with the interior evolution of stars and to binary interactions. For instance, considering that rotating stars can have a large impact on the range of values found, this means that it is likely that MT proceeds in a fully conservative way only until the accretor reaches its critical rotational velocity, at which point accretion might be prevented by, for instance, the development of a strong wind (Petrovic et al. 2005; Cantiello et al. 2007). Additionally, the effects of tides after the formation of the NS are expected to have an impact on how the angular momentum is redistributed within the binary, thus varying the spin of the companion star, the eccentricity, and the orbital period (Hut 1981; Repetto & Nelemans 2014). In this work we use a Maxwellian distribution with a velocity dispersion of 265 km s−1 that was inferred from the proper motion of pulsars (Hobbs et al. 2005). However, other works found more complex distributions such as a bimodal distribution with characteristic velocities of 90 km s−1 and 500 km s−1 from the velocities of isolated radio pulsars (Arzoumanian et al. 2002). There is also evidence of a low-kick population (30 km s−1) and a high-kick population (400 km s−1) based on observed binary NSs (Beniamini & Piran 2016). However, it is expected that changes in the distribution of the strength of natal kicks used would not alter the distribution of orbital parameters compatible with GX 301–2, but rather the probability of obtaining such configurations.

We also study the expected fraction of binaries with properties matching those measured for GX 301–2, using, as priors, standard distributions associated with the initial binary parameters and we found that the chances of producing such a binary are very low. However, these results are tightly connected to the chosen SFR and the distribution of initial parameters; nevertheless, given the small region of binary parameters leading to such a configuration, it is unlikely that changing these distributions would significantly increment the number of expected GX 301–2-like binaries.

6. Conclusions

The unusual combination of masses measured in GX 301–2 makes it an interesting binary in which to study stellar evolution scenarios involving highly efficient mass-accretion regimes between stars. To this end, we performed detailed binary evolution calculations in a wide grid of initial parameters, which allowed us to find models with properties matching the ones measured in GX 301–2. Below, we summarize the main results of this work:

  • Initial masses: Possible progenitors, defined as systems that are able to form a binary with a NS orbiting around a star with a mass consistent with Wray 977, are only found for M1 = 23 − 30 M⊙ with companions such that the initial mass ratio is q = 0.8 − 0.9. Masses outside of this range either produce a BH as a compact object after the first collapse, or they contain a companion with a mass outside of the range derived for Wray 977.

  • Orbital periods: Porb ≲ 5 days are favoured to produce such possible progenitors, thus leading to a Case A scenario of MT before the first SN event. Above this limit, the accretion is not sufficient enough to increase the mass of the companion to be inside the range derived for Wray 977. Additionally, Porb <  2 days are also disfavoured as the MT would end up producing a contact system.

  • Asymmetric natal kicks: Thanks to new astrometric observations, the natal kick strength is likely to have been vkick ≳ 450 km s−1, which is expected to produce a tilt angle of ≳π/2.

  • Estimated rates: Weighting of our results with commonly used distributions of initial binary parameters, we estimate that the chances of having HMXBs with properties similar to the ones found in GX 301–2 are very low, that is less than two out of 100 000 binaries. We thus do not expect to find another binary with similar properties in the Milky Way.

Given the constraints derived from new observations available on the kinematics of different eccentric HMXBs, thanks to the extremely precise astrometric measurements obtained with the Gaia satellite (Gaia Collaboration 2021) which allows for the systemic velocity of these systems to be inferred, incorporating more details as to binary evolutionary models can provide better constraints on the evolution of progenitors until their current observed states as HMXBs. For GX 301–2, new observations of the source in different electromagnetic bands will help to constrain the evolution even further, followed by its progenitor binary, its future prospects, and the role it has on the environment. For instance, detailed measurements of surface abundances on Wray 977 would help to unravel the role of a previous MT episode. It would be an interesting topic for a future work to incorporate the effects of rotation and tides to predict how initial binary parameters are mapped to the parameters just after the formation of the NS until nowadays how GX 301–2 is observed.

1

Input files with the chosen parameters that are necessary to reproduce our results are available on Zenodo: https://zenodo.org/record/7261481.

2

We repeated this study by applying the same natal kick distribution to another randomly drawn binary in the appropriate mass range in order to confirm the validity of these results.

Acknowledgments

A.S.B. is a fellow of CONICET. F.G. and J.A.C. are CONICET researchers. J.A.C. is a María Zambrano researcher fellow funded by the European Union – NextGenerationEU – (UJAR02MZ). F.G. and J.A.C. acknowledge support by PIP 0113 (CONICET). This work received financial support from PICT-2017-2865 (ANPCyT). J.A.C. was also supported by grant PID2019-105510GB-C32/AEI/10.13039/501100011033 from the Agencia Estatal de Investigación of the Spanish Ministerio de Ciencia, Innovación y Universidades, and by Consejería de Economía, Innovación, Ciencia y Empleo of Junta de Andalucía as research group FQM-322, as well as FEDER funds. S.C. acknowledges the CNES (Centre National d’Etudes Spatiales) for the funding of MINE (Multi-wavelength INTEGRAL Network). A.S.B., F.G. and S.C. are grateful to the LabEx UnivEarthS for the funding of Interface project I10 “From binary evolution towards merging of compact objects”. Software: MESA (http://mesa.sourceforge.net/), (Paxton et al. 2011, 2013, 2015; Paxton et al. 2018, 2019), ipython/jupyter (Kluyver et al. 2016), matplotlib (Hunter 2007), numpy (Harris et al. 2020), scipy (Virtanen et al. 2020).

References

  1. Almeida, L. A., Sana, H., de Mink, S. E., et al. 2015, ApJ, 812, 102 [Google Scholar]
  2. Arzoumanian, Z., Chernoff, D. F., & Cordes, J. M. 2002, ApJ, 568, 289 [NASA ADS] [CrossRef] [Google Scholar]
  3. Belczynski, K., Bulik, T., & Fryer, C. L. 2012, ArXiv e-prints [arXiv:1208.2422] [Google Scholar]
  4. Beniamini, P., & Piran, T. 2016, MNRAS, 456, 4089 [NASA ADS] [CrossRef] [Google Scholar]
  5. Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
  6. Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [Google Scholar]
  7. Bradt, H. V., Apparao, K. M. V., Clark, G. W., et al. 1977, Nature, 269, 21 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brandt, N., & Podsiadlowski, P. 1995, MNRAS, 274, 461 [NASA ADS] [CrossRef] [Google Scholar]
  9. Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Brown, G. E., Weingartner, J. C., & Wijers, R. A. M. J. 1996, ApJ, 463, 297 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cantiello, M., Yoon, S. C., Langer, N., & Livio, M. 2007, A&A, 465, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Coleiro, A., & Chaty, S. 2013, ApJ, 764, 185 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dewi, J. D. M., Podsiadlowski, P., & Sena, A. 2006, MNRAS, 368, 1742 [NASA ADS] [CrossRef] [Google Scholar]
  14. Ding, Y. Z., Wang, W., Epili, P. R., et al. 2021, MNRAS, 506, 2712 [NASA ADS] [CrossRef] [Google Scholar]
  15. Ergma, E., & van den Heuvel, E. P. J. 1998, A&A, 331, L29 [Google Scholar]
  16. Fortin, F., Garcia, F., Chaty, S., Chassande-Mottin, E., & Simaz Bunzel, A. 2022, A&A, 665, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Fryer, C. L., & Woosley, S. E. 1998, ApJ, 502, L9 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91 [Google Scholar]
  19. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. García, F., Simaz Bunzel, A., Chaty, S., Porter, E., & Chassande-Mottin, E. 2021, A&A, 649, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
  22. Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
  23. Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
  24. Hills, J. G. 1983, ApJ, 267, 322 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [Google Scholar]
  26. Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [Google Scholar]
  27. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [Google Scholar]
  29. Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
  30. Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
  31. Kaiser, E. A., Hirschi, R., Arnett, W. D., et al. 2020, MNRAS, 496, 1967 [Google Scholar]
  32. Kalogera, V. 1996, ApJ, 471, 352 [Google Scholar]
  33. Kalogera, V. 2000, ApJ, 541, 319 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kaper, L., Lamers, H. J. G. L. M., Ruymaekers, E., van den Heuvel, E. P. J., & Zuiderwijk, E. J. 1995, A&A, 300, 446 [NASA ADS] [Google Scholar]
  35. Kaper, L., van der Meer, A., & Najarro, F. 2006, A&A, 457, 595 [CrossRef] [EDP Sciences] [Google Scholar]
  36. Kippenhahn, R., & Weigert, A. 1967, ZAp, 65, 251 [Google Scholar]
  37. Kippenhahn, R., Ruschenplatt, G., & Thomas, H. C. 1980, A&A, 91, 175 [Google Scholar]
  38. Kippenhahn, R., Weigert, A., & Weiss, A. 2012, Stellar Structure and Evolution (Berlin, Heidelberg: Springer) [Google Scholar]
  39. Klencki, J., Nelemans, G., Istrate, A. G., & Pols, O. 2020, A&A, 638, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, in Positioning and Power in Academic Publishing: Players, Agents and Agendas, eds. F. Loizides, & B. Scmidt (IOS Press), 87 [Google Scholar]
  41. Koh, D. T., Bildsten, L., Chakrabarty, D., et al. 1997, ApJ, 479, 933 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kolb, U., & Ritter, H. 1990, A&A, 236, 385 [NASA ADS] [Google Scholar]
  43. Langer, N., Fricke, K. J., & Sugimoto, D. 1983, A&A, 126, 207 [NASA ADS] [Google Scholar]
  44. Ledoux, P. 1947, ApJ, 105, 305 [NASA ADS] [CrossRef] [Google Scholar]
  45. Liu, J. 2020, MNRAS, 496, 3991 [NASA ADS] [CrossRef] [Google Scholar]
  46. Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2006, A&A, 455, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Liu, J., Ji, L., Jenke, P. A., et al. 2021, MNRAS, 504, 2493 [NASA ADS] [CrossRef] [Google Scholar]
  48. Marchant, P., Langer, N., Podsiadlowski, P., et al. 2017, A&A, 604, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Mineo, S., Gilfanov, M., & Sunyaev, R. 2012, MNRAS, 419, 2095 [Google Scholar]
  50. Mönkkönen, J., Doroshenko, V., Tsygankov, S. S., et al. 2020, MNRAS, 494, 2178 [CrossRef] [Google Scholar]
  51. Oskinova, L. M., Bulik, T., & Gómez-Morán, A. N. 2018, A&A, 613, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Patton, R. A., & Sukhbold, T. 2020, MNRAS, 499, 2803 [NASA ADS] [CrossRef] [Google Scholar]
  53. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  54. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  55. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  56. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  57. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  58. Petrovic, J., Langer, N., & van der Hucht, K. A. 2005, A&A, 435, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Repetto, S., & Nelemans, G. 2014, MNRAS, 444, 542 [NASA ADS] [CrossRef] [Google Scholar]
  60. Ricker, G. R., McClintock, J. E., Gerassimenko, M., & Lewin, W. H. G. 1973, ApJ, 184, 237 [NASA ADS] [CrossRef] [Google Scholar]
  61. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  62. Sato, N., Nagase, F., Kawai, N., et al. 1986, ApJ, 304, 241 [NASA ADS] [CrossRef] [Google Scholar]
  63. Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H. T. 2016, ApJ, 821, 38 [NASA ADS] [CrossRef] [Google Scholar]
  64. Thorne, K. S., & Zytkow, A. N. 1977, ApJ, 212, 832 [Google Scholar]
  65. Verbunt, F., & Phinney, E. S. 1995, A&A, 296, 709 [NASA ADS] [Google Scholar]
  66. Vidal, N. V. 1973, ApJ, 186, L81 [NASA ADS] [CrossRef] [Google Scholar]
  67. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
  68. Watson, M. G., Warwick, R. S., & Corbet, R. H. D. 1982, MNRAS, 199, 915 [NASA ADS] [Google Scholar]
  69. Wellstein, S., & Langer, N. 1999, A&A, 350, 148 [NASA ADS] [Google Scholar]
  70. White, N. E., Mason, K. O., Huckle, H. E., Charles, P. A., & Sanford, P. W. 1976, ApJ, 209, L119 [NASA ADS] [CrossRef] [Google Scholar]
  71. Zhang, W., & Fryer, C. L. 2001, ApJ, 550, 357 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Binary parameters of GX 301–2 and stellar parameters of Wray 977 corresponding to the values listed in Kaper et al. (2006).

In the text

All Figures

thumbnail Fig. 1.

Evolutionary tracks in the HR diagram of a close binary system with an initial primary mass of 27.60 M⊙ and a secondary mass of 23.18 M⊙. This binary is assumed to start its evolution in a circular orbit with Porb = 2 days, in a fully conservative MT scenario throughout its entire lifetime. The evolution of the primary (secondary) star is represented in solid blue (orange) line. Different MT phases are plotted on top of each star: in green (grey) we show Case A (early Case B) MT. The dotted grey lines represent constant radii for 1, 10, and 100 R⊙, while the dotted black line designates the evolution of the secondary star after the formation of the first compact object (GX 301–2) if the companion NS star was absent. The yellow star marks the location where the primary exploded as a SN. For comparison, the ZAMS corresponding to stars of the same composition is shown by the black dashed line.
In the text
thumbnail Fig. 2.

Example of a grid of binary systems showing initial periods (in days) and initial primary masses for a fixed initial mass ratio of q = 0.8. Each rectangle represents a single detailed binary evolution model. Light blue is used for binaries with a primary collapsing into a NS while having a companion mass within the values derived by Kaper et al. (2006) (named ‘in range’). In a darker blue colour, we show binaries with primaries forming BHs or being outside the constraint imposed by the observed masses (named ‘out of range’). The hatched region represents a binary that ends its evolution without reaching a core-collapse stage. For the entire grid of models computed, we find that these non-collapsing models either merge during a CE phase between two non-degenerate stars, or stop due to numerical issues. Other initial mass ratios produce similar results.
In the text
thumbnail Fig. 3.

Post-kick binary systems in the period-eccentricity plane. Each point represents a detailed binary simulation between a non-degenerate donor star an a NS. The colours indicate the χ2 minimum found during the entire evolution of each binary, considering observational constraints on binary parameters (i.e. masses of the NS and its companion, orbital period, and eccentricity; see Table 1). Diamonds represent binaries with matching binary properties to the observed ones. With black squares we show binaries merging just after core collapse due to the kick orientation, while grey squares represent binaries for which numerical problems were encountered and the simulations were not completed. The location of the case of a symmetric kick in this plane is shown with an arrow.
In the text
thumbnail Fig. 4.

Post-kick inclination of the orbital plane (with respect to the pre-kick plane) and binary systemic velocity, vsys, as a function of the natal kick magnitude vkick. In light blue we show binaries matching the orbital parameters of GX 301–2 in its HMXB phase, while grey points represent all the natal kicks explored in detail. In the top and on the right, we show the weighted histograms. Black solid lines show the contour of the 99% credible regions for the chosen kicks’ distributions.
In the text
thumbnail Fig. 5.

Evolution of orbital period, eccentricity, and released accretion energy of a selected binary model as a function of the mass of the optical companion. Time evolution proceeds from left to right. Light-blue regions represent observational constraints with increased error bars (see Sect. 4). The x-axis corresponds to possible matching values for Wray 977, which is thought to be above 33 M⊙ (Kaper et al. 2006).
In the text
thumbnail Fig. 6.

Evolution of the parameters of the donor star of the selected model. Time evolution proceeds from left to right. Light-blue regions represent observational constraints from Kaper et al. (2006). In the case of the radius R, we use the range given by Wellstein & Langer (1999) of 60 <  R <  70 R⊙. The x-axis range matches possible values for Wray 977, with a mass estimation of above 33 M⊙ (Kaper et al. 2006).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.