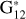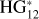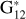| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202243479 | |
| Published online | 09 November 2022 | |
Absolute colors and phase coefficients of asteroids★
1
Instituto de Astrofísica de Andalucía, CSIC,
Apt 3004,
18080
Granada, Spain
e-mail: varobes@gmail.com
2
Instituto de Física Aplicada a las Ciencias y las Tecnologías, Universidad de Alicante,
San Vicent del Raspeig,
03080
Alicante, Spain
3
Observatório Nacional/MCTIC,
Rua General José Cristino 77,
Rio de Janeiro, RJ
20921-400, Brazil
4
Universidad Internacional de Valencia,
Valencia, Spain
5
Instituto de Astronomía Teórica y Experimental, CONICET-UNC,
Laprida 854,
Córdoba, Argentina
Received:
4
March
2022
Accepted:
21
September
2022
Context. We use the phase curves of small bodies to measure absolute magnitudes and, together with complementary theoretical and laboratory results, to understand the micro- and macroscopic properties of their surfaces. Although we can observe asteroids up to phase angles of about 30 deg, the range of phase angles covered by outer Solar System objects usually does not go further than 7−10 deg for centaurs and 2 deg for trans-Neptunian objects, and a linear relation between magnitude and phase angle may be assumed.
Aims. We aim to directly compare data taken for objects in the inner Solar System (inside the orbit of Jupiter) with data for centaurs and trans-Neptunian objects.
Methods. We use the SLOAN Moving Objects Catalog (MOC) data to construct phase curves restricted to phase angles of less than or equal to 7.5 deg, which is compatible with the angles observed for the trans-Neptunian and Centaur population. We assume a linear model for the photometric behavior to obtain absolute magnitudes and phase coefficients in the ugirz, V, and R filters.
Results. We obtain absolute magnitudes in seven filters for over 4000 objects. Our comparison with outer Solar System objects suggests the surfaces have a common property: intrinsically redder objects become blue with increasing phase angle, while the opposite happens for intrinsically bluer objects.
Key words: methods: data analysis / catalogs / minor planets, asteroids: general
Full Table 3 is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/667/A81
© A. Alvarez-Candal et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Small bodies show variations in their brightness. These variations are periodic and usually approximate a series of sines and cosines (see e.g., Harris & Lupishko 1989). Some of these variations are related to the rotation of a given body along its spin axis. Other brightness variations are related to the changing geometry of the system formed by the Sun, the small body, and the Earth. We are interested in this last kind of brightness variation.
Geometrically speaking, brightness variations happen because of the changing distances from the object to the Sun and to the Earth and the fraction of surface illuminated as seen from the Earth. If we disregard the rotational variations, we can correct the effect of the distances using the reduced magnitudes:
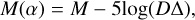 (1)
(1)
where M is the observed apparent magnitude, in any filter, D is the object-Sun distance, and Δ is the object-Earth distance (both in astronomical units). The phase angle α is the angular distance between the Earth and the Sun as seen from the small body. Once we remove the distance effects, we can study the brightness change due to the changing α using phase curves.
For the scope of this work, two previous studies are of particular interest, and we briefly introduce each of them. In Alvarez-Candal et al. (2019), we presented a catalog of phase curves in two filters, V and R, of 117 trans-Neptunian objects (TNOs) and centaurs. There, we studied the strong anti-correlation between absolute color and relative phase coefficients (we define both quantities in Sect. 3), indicating that redder objects have steeper phase curves in the R filter than in the V filter, or, in other words, redder objects tend to become bluer with increasing α. This work showed that phase curves in more than one wavelength are essential tools that are usually overlooked (to our knowledge the only exception being Mahlke et al. 2021). On the other hand, in Alvarez-Candal et al. (2022, hereafter AC22), we obtained multi-wavelength phase curves for asteroids using the data from the Moving Objects Catalog (MOC) of the SLOAN Digital Sky Survey for over 14 000 asteroids. We used the 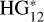 model as implemented by Penttilä et al. (2016), obtaining the probability distributions of the absolute magnitudes and phase coefficients for each filter.
model as implemented by Penttilä et al. (2016), obtaining the probability distributions of the absolute magnitudes and phase coefficients for each filter.
We used the same input data as in AC22 to test whether a similar anti-correlation between absolute color and relative phase coefficient exists for asteroids. We use the same selection criteria as in Alvarez-Candal et al. (2019): at least three data points and α ∈ [0, 7.5] deg; the range in α covers that spanned by centaurs (<7 or 8 deg) and TNOs < 2 deg. We assumed a simple linear model to make a fair comparison with Alvarez-Candal et al. (2019). We note that this range of α is slightly lower than that covered by their data. We stress that the region α ≤ 7.5 deg is within "opposition effect" regime due to a combination of shadow-hiding (Hapke 1963) and coherent back-scattering (Muinonen 1989). This effect is characterized by an apparent surge in brightness starting at about α = 5−10 deg and extending to its maximum at opposition, that is, α ≈ 0 deg. However, we note that in some TNOs, it may start as low as α ≈ 0.1 deg (Verbiscer et al. 2022). In Appendix A, we will tackle the validity of the linear approach for our work.
We organize this work as follows: in Sect. 2 we briefly present the dataset we used. In Sect. 3, we describe the procedure we applied, while in Sects. 4 and 5 the results are discussed and the conclusions of this work are summarized.
 |
Fig. 1 Observational circumstances of the data used in this work. Left panel: cumulative distribution of the number of observations per filter. Right panel: minimum α versus span in α. |
2 Dataset
We use the SLOAN MOC extended with the SVOMOC (see Ivezic et al. 2001; Juric et al. 2002; Carry et al. 2016); we refer to this as the MOC here for simplicity. Briefly, the database contains 277747 u′, g′, r′, i′, z′ magnitudes, and their errors1, for 141388 moving objects. In the remaining text, we use m to refer to the apparent magnitude in any of the SLOAN filters or the V or R filters, unless explicitly stating otherwise. We use italics when speaking about magnitudes and normal text when naming a filter. We chose objects according to the following selection criteria: (i) data with α ≤ 7.5 deg, (ii) at least three data points, and (iii) m : σm ≤ 1. These criteria produced a total of 5848 objects. Most of these have α ∈ (2.5, 5.5) deg. There are a few objects that cover the whole interval, but most objects have only three observations (Fig. 1).
3 Analysis
Phase curves are exciting and powerful tools for obtaining different information, especially absolute magnitudes (H) and phase coefficients. The absolute magnitude relates to the amount of light reflected by the object with its reflective area (illuminated) and how the light is reflected (albedo). On the other hand, the phase coefficients describe the shape of the curve and tell us about the scattering properties of the surface, although in no clear nor direct manner (see, e.g., Lumme & Bowell 1981; Hapke 2002). The phase coefficients and their physical interpretation depend on the adopted photometric model, which depends on the data quality and how well-sampled the phase curve is. The model adopted by the International Astronomical Union is the HG1G2 (Muinonen et al. 2010), with improvements made to work with low-quality measurements and sparsely covered curves in the 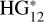 model (Penttilä et al. 2016). In our case, we use a simpler two-parameter model, assuming that the phase curves are linear:
model (Penttilä et al. 2016). In our case, we use a simpler two-parameter model, assuming that the phase curves are linear:
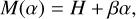 (2)
(2)
where M(α) is the reduced magnitude shown in Eq. (1), Η is the absolute magnitude, and β is the phase coefficient in units of mag deg−1. We use the linear model for all the filter sets considered in this work (see Appendix A).
We follow the method developed in AC22, using their probability distributions of possible rotational states P(Δm|HV) (see their Eq. (2)) for the objects in common while computing our own whenever necessary. We then perform a Monte Carlo simulation to estimate the absolute magnitudes. The nominal values are the median of the distributions, while the uncertainty interval is between the 16th and 84th percentile (see Fig. 2). The figure shows that the distributions in Hr and βr are broad, producing large uncertainties (seen as the black cross in the plot). In total, we have results for more than 4500 objects in all five filters of the MOC and also in the V and R filters (Table 1). These last two are obtained transforming the ugriz magnitudes into Johnson-Cousins magnitudes (see Table 1 in Jester et al. 2005, for stars witht R − I < 1.15)2.
 |
Fig. 2 Example of the density distribution obtained for asteroid 1034 T-1. The black cross shows the adopted Ητ and βτ before applying the prior in magnitudes, while the red cross shows the final values. |
Number of absolute magnitudes obtained.
3.1 Using the results for AC22 as prior
As hinted in Fig. 2, the uncertainties in H and β tend to be relatively large, especially when a low number of points cover the phase curve (see the impact in Appendix A of Alvarez-Candal et al. 2019). Nevertheless, it is possible to improve them, at least for a significant number of objects. In AC22, we obtained solutions of H for over 14000 objects in the form of probability distributions with a different photometric model. We use these probability distributions as priors to improve our results. We used the probabilities in HAC22, P(HAC22), in two steps:
Absolute magnitudes, in this case, the re-assignment of probabilities was performed directly in the absolute magnitudes space:
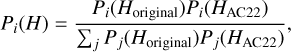 (3)
(3)
where P(Horiginal) is the probability distribution obtained in this work; see the right histogram in Fig. 2. We use a bin width of 0.02 mag in the interval from 8 to 24 for the probability distributions. We ran the process for 3206 objects.
Phase coefficients. In AC22, the phase coefficients were the 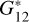 , which are not comparable to β. Therefore, their
, which are not comparable to β. Therefore, their 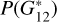 cannot be used as priors here. In this case, we use a similar approach to that in AC22 and use the P(β|Horiginal) as follows:
cannot be used as priors here. In this case, we use a similar approach to that in AC22 and use the P(β|Horiginal) as follows:
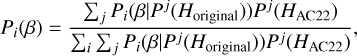 (4)
(4)
where P(β|Pj(Horiginal)) is binned between −3 and 3 mag deg−1 with a bin width of 0.005 mag deg−1. The application of the priors from AC22 led to smaller uncertainties and slightly different nominal values (see Figs. 2 and 3, and Table 2). From this point on, our database is composed of the updated magnitudes for the 3206 objects with priors available plus 2642 objects which did not, to keep the total of 5848 objects.
 |
Fig. 3 Distributions of uncertainties. The red dashed line indicates AC22. The continuous black line shows the uncertainties before applying the prior for AC22, and the blue dot-dashed line shows the final uncertainty distribution after applying the prior. The left panel shows the uncertainties in Hr, while the right panel shows them for the phase coefficient. We note that in the latter, the coefficients differ between AC22 and ours. |
Median uncertainties
 |
Fig. 4 Phase curves of asteroid 1034 T-1. Different panels show data in different filters (labeled in each inset). |
3.2 Colors and Δβ
An essential part of this work is the comparison of color and Δβ (also referred to as the relative phase coefficient in other parts of the text). Given two quantities represented by their probability distributions P1 and P2, the nominal value of the difference is the difference between the nominal values. On the other hand, the uncertainty range is not determined by the expected propagation of errors as it does not consider the complete information contained in the distributions. In this case, we opted to compute the probability distribution of the difference between two quantities X and Y as Ζ = X − Y:
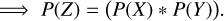 (5)
(5)
Therefore, in the case of a color Cij = Mi − Mj or Δβij = βi − βj, we obtain the probability distributions P(Cij) and Ρ(Δβij) where the uncertainty intervals are determined − as before − as the 16th and 84th percentiles.
The final results of Η and β are shown in Table 3. As noted above, these are values after applying AC22 priors. We also draw attention to the fact that the table shows median values of a probability distribution, which may not be the optimal solution (e.g., one obtained by applying a minimization algorithm). We show an example of the phase curves in Fig. 4 for asteroid 1034 T-13 The full table with the results is available at the CDS and upon request. The probability distributions and figures are available upon request.
4 Results and discussion
We show the distributions of Η and β in the two panels of Fig. 5. In the case of H, all filters show similar distributions, except for Hu, which peaks at fainter magnitudes than the rest − as discussed in AC22 − partly showing the solar u − g = 1.43. For β on the other hand, the distributions seem centered at similar values (median values fall within 0.068 and 0.071 mag deg−1) with standard deviations ranging from 0.13 mag deg−1 for βr, up to 0.21 mag deg−1 for βu. These figures are a proxy of the depth of the survey if we only considered objects observed with α ≤ 7.5 degrees.
The next step is to compute the absolute colors from Η and Δβ. Following the procedure outlined above (Sect. 3.2) to assign uncertainties, we created a series of plots shown in Fig. 6 for the MOC filters. The figure displays only colors within 2.5 mag of the median of the distribution and with a one-sided uncertainty of less than 1 mag. Following these criteria, the figures show 57% of the data in the u − g plot (69% in g − r, 74% in r − i, and 69% in i − z). We note that we did this for clarity only. The bulk of the data follows the main trends discussed below independently of the size of their uncertainties.
All panels in Fig. 6 show the same trend: a strong anti-correlation between absolute color and Δβ. We ran a Spearman test, obtaining a rejection of the null hypothesis (that the two variables do not correlate) with high confidence in all cases. The relation indicates that redder objects show steeper phase curves in any pair of filters in the redder filter. Physically, this means that objects with redder colors tend to become bluer with increasing phase angle, while bluer objects tend to get redder with increasing phase angle.
This phenomenon was already seen in TNOs by Alvarez-Candal et al. (2019) using V − R. To directly compare our results with those of these latter authors, we also computed the phase curves in V and R filters transforming from ugriz to UVBRI. The results are in Fig. 7 where the data from Alvarez-Candal et al. (2019) are overplotted in red asterisks. We proposed that this phenomenon may be related to large-sized particles on the surface of (perhaps) icy bodies and that it may show a predominance of single-scattering at a low phase angle rather than multiple scattering, but probably not related to the surface composition. In the case presented in this work, we are referring to smaller objects whose surfaces should be volatile-poor, strengthening our hypothesis that there is no relation with surface composition.
We also used the taxonomy classification presented by Colazo et al. (2022). Briefly, the authors used the H of AC22 and unsupervised machine learning algorithms to find four clusters in the Hg − Ht versus Ht − Hz space. Colazo et al. (2022) associate each cluster with the four major complexes: the S-complex, the C-complex, the X-complex, and the V-complex. We show the results in Fig. 8, where it is possible to see that all taxa follow the same trend of anti-correlation found for the complete sample. Nevertheless, it is possible to see that the taxa are not identically distributed. In particular the C- and S-complexes seem to follow parallel trends, with the C-complex slightly on the blue side. The V-complex appears very similar to the S-complexes, while the X-complex seems to fall between the C- and S-complex. These slight differences are related to the characteristic spectra of each complex: the C- and X-complexes are more linear with no strong absorption features, while the S- and V-complexes show absorption bands starting at about 750 nm and redder slopes before the onset of the band. These results confirm that the relation between absolute color and relative phase coefficient does not depend on any particular surface composition.
It is important to consider the possibility that the correlation is due to some systematic error that we are not considering. Beck et al. (2021) presented a thorough study of the phase curves of meteoritic material, targeting especially to low-albedo material. Their work also detected that objects initially red at a low-phase angle tend to become blue with increasing or. However, they reported that the relationship happened on normalized reflectance and that it happened because the shadow-hiding effect is (almost) an additive effect and therefore the blueing should not be a physical effect. We note that using colors is just a way of showing normalized reflectance. To compare our results to theirs, we proceed as follows: first, we matched our data with the AKARI database (Ali-Lagoa et al. 2018) and found 59 objects in common. Second, we computed colors relative to Ητ for all objects and removed the solar colors to compute relative reflectance using
![${S^r}\left( \alpha \right) = \left\{ {{S_j}} \right\} = \left\{ {{{10}^{ - 0.4\left[ {\left( {{C_{jr}}\left( \alpha \right) - {{\left( {j - r} \right)}_ \odot }} \right.} \right]}}} \right\},$](/articles/aa/full_html/2022/11/aa43479-22/aa43479-22-eq14.png) (6)
(6)
where ⊙ indicates solar colors and
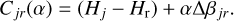 (7)
(7)
These values provide relative reflectance normalized to 1 at the effective wavelength of the r filter at a given α4. Third, we re-normalized the data to 1 at the effective wavelength of the V filter (540 nm), measured by a simple linear interpolation between g and r magnitudes, and scaled it by the corresponding AKARI albedo:
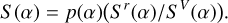 (8)
(8)
In Fig. 1 of Beck et al. (2021), it is clear that when using "absolute reflectance", the spectra at different phase angles are not normalized. To include this, we used their supplementary information to compute the average change in reflectance for α ∈ [0, 30] degrees (S′ = −0.00093 units of bidirectional reflectance deg−1) and applied in the scaling mentioned above via
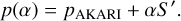 (9)
(9)
Finally, we computed the spectral slope for different phase angles using Eq. (8) and fitting a linear function and computed its change with α, Sα. We show the results as red asterisks in Fig. 9, where we have removed obvious outliers. The figure shows that objects with a blue slope (negative) at opposition (S (α = 0) < 0 nm−1) tend to get redder with increasing α (Sα > 0 nm−1 deg−1). Nevertheless, there are relatively few data points; in order to increase the statistics, we use the complete sample of objects and compute Sr(α) for all possible objects. Because most objects do not have a measurement for pAKARI we draw random values from the dataset and assume these to be the "real" values. The rest of the process was identical to that described before. We show the results as a two-dimensional histogram in Fig. 9, showing that the correlation holds and is clearer. Sanchez et al. (2012) measured the effect of phase reddening on near-Earth asteroids and found that spectra of ordinary chondrite meteorites observed in the laboratory change their slope very little below 30 deg; these authors report an initial slope in the range of 10−4 nm−1 with a span in the order of 0.4 × 10−4 nm−1 deg−1. Considering that our data include larger observational errors and different types of asteroids, the agreement in the order of magnitude with Sanchez et al. (2012) is compelling, while the anti-correlation found in color (and spectral slope) appears to be real.
Figure 9.12 of Grynko & Shkuratov (2008) shows numerical phase curves obtained for different density packing of a given material. The phase curve with a lower density is steeper than that with the higher packing density. How is this related to our work? Perhaps we see a variation in the packing density or the number of particles interacting with the light at different wavelengths. If shadow-hiding is the primary mechanism acting here, we are in the geometric optics domain and see particles that are larger than the incident wavelength. This means that the effect we detect, the anti-correlation, may be due to the size distribution of particles on the surfaces.
Sample of the results.
 |
Fig. 5 Distributions of Η (left panel) and β (right panel), u is shown in the blue line, g in green, r in red, i in purple, and z in black. |
 |
Fig. 6 Absolute color versus Δβ for pairs of filters. Top left: u − g; top right: g − r; bottom left: r − i; bottom right: i − z. |
 |
Fig. 7 Ηγ − HR versus Δβ. Our results are shown as black dots, while the results for TNOs from Alvarez-Candal et al. (2019) are shown as red asterisks. |
 |
Fig. 8 Hg − Hr versus Δβ. In all panels, the complete sample is shown as gray dots, while different colors mark the different complexes: S-complex in blue (upper left panel), C-complex in green (upper right panel), V-complex in red (bottom left panel), and X-complex in purple (bottom right panel). We do not show the error bars for clarity. |
 |
Fig. 9 Spectral slope at α = 0 deg versus rate of change of spectral slope with α. Red asterisks show objects with measured pAKARI while the 2D histogram shows the complete dataset with random values of albedo. We do not show the error bars for clarity. |
5 Conclusions
The main objective of this work is to decipher whether or not the phase curves of asteroids share the same anti-correlation found for TNOs using HV − HR and Δβ (Ayala-Loera et al. 2018; Alvarez-Candal et al. 2019) when using the same photometric model (linear) and range of phase angles. To improve the quality of our results, we applied the P(HAC22) as priors. We used the same approach as in AC22 to obtain over 4000 absolute magnitudes for objects observed with α < 7.5 deg. We see that using previous results as priors in our new processing improves the results significantly, causing the results obtained with a simple linear approach in low-α to resemble those obtained with a full 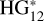 model and complete range of α (Fig. 6).
model and complete range of α (Fig. 6).
We obtained strong correlations in consecutive pairs of colors. These correlations are probably associated with the particle-size distribution present on the surface of the objects. The anti-correlations indicate that intrinsically redder objects become bluer with increasing phase angle, while the opposite happens for intrinsically bluer objects. We checked that the correlation is not due to a normalization issue. When including taxonomy information, we see that the absolute color versus Δβ space is covered slightly differently by the different main complexes, particularly the C and S-complex although the anti-correlation holds for all taxa. The slightly different space covered by the C and S complexes resembles the parallel sequences seen in Fig. 17 of AC22, keeping in mind that their phase coefficients were 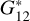 and not β. To conclude, we suggest that the term phase-reddening should be changed to the more generic phase-coloring because some objects tend to become bluer with increasing phase angle.
and not β. To conclude, we suggest that the term phase-reddening should be changed to the more generic phase-coloring because some objects tend to become bluer with increasing phase angle.
Acknowledgements
We thank the input provided by the referee who improved this manuscript. A.A.C. acknowledges support from the State Agency for Research of the Spanish MCIU through the "Center of Excellence Severe Ochoa" award to the Instituto de Astrofisica de Andalucia (SEV-2017-0709). Funding for the creation and distribution of the SDSS Archive has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the U.S. Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. The SDSS Web site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium (ARC) for the Participating Institutions. The Participating Institutions are The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, the Korean Scientist Group, Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. This work is partially based on data from the SVO MOC Data Access Service at CAB (CSIC-INTA). This work used https://www.python.org/, https://www.scipy.org/, and Matplotlib (Hunter 2007).
Appendix A The linear approximation of a nonlinear region
The phase curve of small bodies (up to α ≈ 30 degrees) can be roughly described as a linear behavior for α > 10 degrees, while for smaller angles, a nonlinear behavior could appear especially in moderate to high albedo objects (Belskaya & Shevchenko 2000). This nonlinear behavior was named the opposition effect (OE, Gehrels 1956). Therefore, if the phase curve is nonlinear at low-α, can we describe it adequately with a simple linear model?
To answer this question, we proceeded as follows: We assumed an object with Η = 17 (footnote 5) and used the 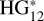 model to create three different phase curves using
model to create three different phase curves using 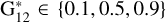 , keeping in mind that lower values of
, keeping in mind that lower values of 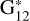 imply larger nonlinear behaviors. From the modeled phase curves we randomly extracted n pairs (αi;, mi), i from 1 to n, with n = 3, 6, 9, or 12. We used the same selection criterion described in the main text: at least three data points. In this case, we did not include the effect of observational errors because they may blur the results further than desired.
imply larger nonlinear behaviors. From the modeled phase curves we randomly extracted n pairs (αi;, mi), i from 1 to n, with n = 3, 6, 9, or 12. We used the same selection criterion described in the main text: at least three data points. In this case, we did not include the effect of observational errors because they may blur the results further than desired.
Using the data (αi;, mi) we computed linear fits to obtain Hlinear, and then computed the difference 17 − Hlinear. For each value of 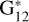 and n, we extracted 1000 different samples to create histograms and to avoid spurious results due to the random nature of our selection of samples. We show the results in Fig. A.1, where we labeled the four panels with the number of pairs used and each histogram with its respective value of phase coefficient.
and n, we extracted 1000 different samples to create histograms and to avoid spurious results due to the random nature of our selection of samples. We show the results in Fig. A.1, where we labeled the four panels with the number of pairs used and each histogram with its respective value of phase coefficient.
 |
Fig. A.1
|
We summarize our findings from this figure: As expected, the stronger nonlinear behavior shows larger discrepancies when using a linear model, with a maximum at about −0.4 mag, but with many results better than −0.2 mag. Curiously, with low n, the difference may decrease to about zero or be slightly positive; this does not mean that the linear model describes well the nonlinear behavior, but that with a sparse coverage, the estimated absolute magnitude does not differ significantly from the one using more complex photometric models. With large n, this is not the case (as seen in the bottom panels of the figure), although the median differences for a given 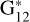 seems to be roughly independent of n (Table A.l) In conclusion, the linear model is not adequate to study OE, but it provides absolute magnitudes in a reasonable to good agreement with the
seems to be roughly independent of n (Table A.l) In conclusion, the linear model is not adequate to study OE, but it provides absolute magnitudes in a reasonable to good agreement with the 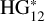 model.
model.
 |
Fig. A.2 Comparison between linear and |
To assess the impact of a simple linear model applied to our data, we compare our Η with those of AC22 (Fig. A.2). As already seen in Fig. A.1, the linear approach underestimates the absolute magnitudes, which is also the case for the actual data with a median difference of 0.10. Generally, the difference is less than 2−2.5%. The difference between the actual and modeled data is that the actual data account for observational errors and possible rotational states, and priors have also been applied, which made the final magnitudes closer to these obtained with the 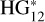 model. The results are similar in all filters. We verified that the median difference is roughly independent of the minimum α and the coverage of the phase curve. Considering all of the above, we confirm that assuming a linear behavior, although it underestimates H, fits the majority of objects satisfactorily.
model. The results are similar in all filters. We verified that the median difference is roughly independent of the minimum α and the coverage of the phase curve. Considering all of the above, we confirm that assuming a linear behavior, although it underestimates H, fits the majority of objects satisfactorily.
As a plus, we computed the same effect but considering TNOs, that is, maximum α = 2 degrees and no other constraint. The processing was the same as above, and we show the results in Fig. A.3. In this case, the linear approach works much better than in asteroids due to the restricted phase angle range, with a maximum difference of about -0.15 mag. The shape of the distribution for n = 3 is different from the other n because, with such a small phase angle coverage, three values of mi close together may account for a larger difference in the linear parameters than better-spaced values. The linear approximation works well in most cases, which justifies its use in ground-based data of TNOs.
 |
Fig. A.3
|
Nevertheless, we must keep in mind that a few TNOs and centaurs show a nonlinear behavior at low-phase angle: Bienor (Rabinowitz et al. 2007), Varuna (Hicks et al. 2005; Belskaya et al. 2006), Pluto, Charon, and Triton (Verbiscer et al. 2022). Except for Charon, all other objects have (or may have) associated phenomena that affect their photometric behavior: Varuna has a large-amplitude rotational light curve, Bienor shows an odd photometric behavior (Fernández-Valenzuela et al. 2017), and Pluto and Triton have atmospheres.
References
- Alí-Lagoa, V., Müller, T.G., Usui, F., & Hasegawa, S. 2018, A&A, 612, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez-Candal, A., Ayala-Loera, C., Gil-Hutton, R., et al. 2019, MNRAS, 488, 3035 [NASA ADS] [CrossRef] [Google Scholar]
- Alvarez-Candal, A., Benavidez, P. G., Campo Bagatin, A., & Santana-Ros, T. 2022, A&A, 657, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ayala-Loera, C., Alvarez-Candal, A., Ortiz, J. L., et al. 2018, MNRAS, 481, 1848 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P., Schmitt, B., Potin, S., Pommerol, A., & Brissaud, O. 2021, Icarus, 354, 114066 [NASA ADS] [CrossRef] [Google Scholar]
- Belskaya, I. N., & Shevchenko, V. G. 2000, Icarus, 147, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Belskaya, I. N., Ortiz, J. L., Rousselot, P., et al. 2006, Icarus, 184, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Carry, B., Solano, E., Eggl, S., & DeMeo, F. E. 2016, Icarus, 268, 340 [CrossRef] [Google Scholar]
- Colazo, M., Alvarez-Candal, A., & Duffard, R. 2022, A&A, 666, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fernández-Valenzuela, E., Ortiz, J. L., Duffard, R., Morales, N., & Santos-Sanz, P. 2017, MNRAS, 466, 4147 [NASA ADS] [Google Scholar]
- Gehrels, T. 1956, ApJ, 123, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Grynko, Y., & Shkuratov, Y. G. 2008, Light Scattering from Particulate Surfaces in Geometrical Optics Approximation, ed. A.A. Kokhanovsky (Berlin, Heidelberg: Springer), 329 [Google Scholar]
- Hapke, B. W. 1963, J. Geophys. Res., 68, 4571 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 2002, Icarus, 157, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., & Lupishko, D. F. 1989, in Asteroids II, eds. R.P. Binzel, T. Gehrels, & M.S. Matthews, 39 [Google Scholar]
- Hicks, M. D., Simonelli, D. P., & Buratti, B. J. 2005, Icarus, 176, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezic, Ž., Tabachnik, S., Rafikov, R., et al. 2001, AJ, 122, 2749 [NASA ADS] [CrossRef] [Google Scholar]
- Jester, S., Schneider, D. P., Richards, G. T., et al. 2005, AJ, 130, 873 [Google Scholar]
- Juric, M., Ivezic, Ž., Lupton, R. H., et al. 2002, AJ, 124, 1776 [CrossRef] [Google Scholar]
- Lumme, K., & Bowell, E. 1981, AJ, 86, 1705 [NASA ADS] [CrossRef] [Google Scholar]
- Mahlke, M., Carry, B., & Denneau, L. 2021, Icarus, 354, 114094 [Google Scholar]
- Muinonen, K. 1989, Appl. Opt., 28, 3044 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., Belskaya, I. N., Cellino, A., et al. 2010, Icarus, 209, 542 [Google Scholar]
- Penttilä, A., Shevchenko, V. G., Wilkman, O., & Muinonen, K. 2016, Planet. Space Sci., 123, 117 [Google Scholar]
- Rabinowitz, D. L., Schaefer, B. E., & Tourtellotte, S. W. 2007, AJ, 133, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez, J. A., Reddy, V., Nathues, A., et al. 2012, Icarus, 220, 36 [CrossRef] [Google Scholar]
- Verbiscer, A. J., Helfenstein, P., Porter, S. B., et al. 2022, Planet. Sci. J., 3, 95 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Observational circumstances of the data used in this work. Left panel: cumulative distribution of the number of observations per filter. Right panel: minimum α versus span in α. |
| In the text | |
 |
Fig. 2 Example of the density distribution obtained for asteroid 1034 T-1. The black cross shows the adopted Ητ and βτ before applying the prior in magnitudes, while the red cross shows the final values. |
| In the text | |
 |
Fig. 3 Distributions of uncertainties. The red dashed line indicates AC22. The continuous black line shows the uncertainties before applying the prior for AC22, and the blue dot-dashed line shows the final uncertainty distribution after applying the prior. The left panel shows the uncertainties in Hr, while the right panel shows them for the phase coefficient. We note that in the latter, the coefficients differ between AC22 and ours. |
| In the text | |
 |
Fig. 4 Phase curves of asteroid 1034 T-1. Different panels show data in different filters (labeled in each inset). |
| In the text | |
 |
Fig. 5 Distributions of Η (left panel) and β (right panel), u is shown in the blue line, g in green, r in red, i in purple, and z in black. |
| In the text | |
 |
Fig. 6 Absolute color versus Δβ for pairs of filters. Top left: u − g; top right: g − r; bottom left: r − i; bottom right: i − z. |
| In the text | |
 |
Fig. 7 Ηγ − HR versus Δβ. Our results are shown as black dots, while the results for TNOs from Alvarez-Candal et al. (2019) are shown as red asterisks. |
| In the text | |
 |
Fig. 8 Hg − Hr versus Δβ. In all panels, the complete sample is shown as gray dots, while different colors mark the different complexes: S-complex in blue (upper left panel), C-complex in green (upper right panel), V-complex in red (bottom left panel), and X-complex in purple (bottom right panel). We do not show the error bars for clarity. |
| In the text | |
 |
Fig. 9 Spectral slope at α = 0 deg versus rate of change of spectral slope with α. Red asterisks show objects with measured pAKARI while the 2D histogram shows the complete dataset with random values of albedo. We do not show the error bars for clarity. |
| In the text | |
 |
Fig. A.1
|
| In the text | |
 |
Fig. A.2 Comparison between linear and |
| In the text | |
 |
Fig. A.3
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.