EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 667 (November 2022) A&A, 667 (2022) A41 Full HTML
Open Access
Issue
A&A
Volume 667, November 2022
Article Number A41
Number of page(s) 10
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202243323
Published online 04 November 2022

© M. Wang et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1 Introduction

Unlike the Earth, which has a global dipole magnetic field, Mars only retains a weak crustal magnetic field (e.g., Acuna et al. 1999). The distribution of the Martian crustal magnetic field is complicated, and the intense crustal field regions are mainly located in the Terra Sirenum region of the southern hemisphere corresponding to the longitude range of 150° E to 240° E and latitude range from 30° S to 85° S (e.g., Connerney et al. 1999). In this area, the multipolar crustal magnetic fields display the features of “magnetic stripes”, which are roughly along the east-west direction, and the magnetic strength is about 220 nT at the Mars Global Surveyor (MGS) mapping altitude (~400 km) (Connerney et al. 2005).

Besides the crustal magnetic field, Mars also has an atmosphere that interacts directly with the solar wind (e.g., Nagy et al. 2004). Generally, owing to the planetary ion pickup and solar wind mass loading processes, which are driven by the solar wind convection electric field and the kinetic processes, the interplanetary magnetic field (IMF) can pile up on the dayside ionosphere (e.g., Szegö et al. 2000; Fang et al. 2018; Dubinin et al. 2019, and references therein). The compressed magnetic field balances the solar wind dynamic pressure and results in the formation of the Martian induced magnetosphere (Matsunaga et al. 2017; Holmberg et al. 2019). On the nightside, the magnetic field tends to have a quasi-radial orientation with respect to the Sun as the draped IMF produces an induced magnetotail (Crider et al. 2004).

Due to the complex magnetic topologies in the Martian ionosphere, reconnection between different magnetic fields can take place (Halekas et al. 2009), such as between the IMF on both sides, the IMF on one side and crustal field on the other, and the crustal fields on both sides (Harada et al. 2018). Among them, the magnetic reconnection on the dayside plays a fundamental role in the dynamics of the terrestrial magnetosphere (Dungey 1961), and it can affect the interaction of solar wind and the terrestrial magnetosphere in many ways. For instance, by changing magnetic field morphology, dayside magnetic reconnection at Mars can influence the planetary pickup ion acceleration (e.g., Fang et al. 2008; Halekas et al. 2017), the ion escape (e.g., Harada et al. 2018), the plasma sheet orientation, and the tail configuration(e.g., DiBraccio et al. 2018).

Although the impacts of dayside reconnection at Mars are significant, the direct measurements of in situ reconnection signatures, such as accelerated plasma flows and Hall magnetic fields within current sheets (e.g., Paschmann et al. 2013), are rarely reported. This is largely due to the fact that, before the Mars Atmosphere and Volatile EvolutioN (MAVEN) mission, both of the particle and field data could not be obtained simultaneously. MGS had no ion measurements, while the Mars Express (MEX) lacked a magnetometer. Nevertheless, the signature of the Hall magnetic field with a nonzero normal field still could be applied to identify the reconnection with the MGS data (e.g., Eastwood et al. 2008; Halekas et al. 2009). For example, by systematically searching the MGS data at 400 km altitude with this method, Halekas et al. (2009) identified 26 Hall field events and found only one case that was observed on the dayside (the solar zenith angles (SZA) < 70°).

After the MAVEN observations were available, Harada et al. (2018) reported the first comprehensive and definitive measurements of ion, electron, and magnetic field signatures of dayside magnetic reconnection over crustal magnetic fields at Mars. Specifically, this case was observed by MAVEN from 18:03:00 to 18:12:00 UTC on October 6, 2016, and the reconnection occured roughly at SZA ≈ 45° on the southern hemisphere of the X–Z plane in the MSO coordinates when the intense crustal field was on the dayside. However, the instantaneous upstream IMF direction corresponding to the case is difficult to estimate because the direction of draped IMF is variable within the magnetosheath and magnetic pileup region (Harada et al. 2018). The IMF condition for the Martian dayside magnetic reconnection remains inconclusive. Later, Harada et al. (2020) also conducted a global survey of ion jets within current sheets in the induced magnetosphere, which are a primary product of magnetic reconnection, and showed that the magnetic reconnection can take place in a wide range of SZAs, altitudes, and geographic locations within the Martian magnetosphere. Recently, based on the MAVEN observations, Wang et al. (2021b) reported a magnetic reconnection at the dayside ion composition boundary (ICB, referred to as the Martian induced magnetopause (IMP) in their paper, which is the boundary between the Martian induced magnetosphere and magnetosheath, and is characterized by the sudden changes of magnetic fields and ion compositions). They demonstrated that the newly arrived IMF and the anchored magnetic field in the induced magnetosphere could reconnect with each other at the ICB. Similarly, the details of the upstream solar wind condition are indeterminate, as well as their effects on the Martian dayside reconnection.

In this paper, using magnetohydrodynamic (MHD) simulations, we investigate the magnetic reconnection between the solar wind and the crustal field in the dayside ionosphere of Mars. The influences of the IMF orientation, the solar wind dynamic pressure, and the location of the intense crustal field, on the dayside magnetic reconnection are examined.

2 Simulation model

In this work, we employ the three-dimensional multispecies MHD model originally developed by Ma et al. (2004) to study the interaction between the solar wind and the Martian magnetosphere (Fang et al. 2010; Ma et al. 2014a,b; Fang et al. 2015, 2017). Recently, we have also used this model to construct a three-dimensional parametric Martian bow shock model (Wang et al. 2020b), and to study the solar wind density and velocity effect on the subsolar standoff distance of the Martian magnetic pileup boundary (MPB; Wang et al. 2021a). The effectiveness and reliability of this MHD model have been further demonstrated by these studies.

In the model of Ma et al. (2004), the input solar wind parameters include the components of solar wind velocity (VX, VY, VZ), the solar wind number density (n), the solar wind temperature (T), and the components of IMF (BX, BY, BZ) in the Mars-centered solar orbital (MSO) coordinate system. In the MSO coordinate system, the origin is located at the Mars center, the X-axis points to the Sun, the Z-axis is normal to the Martian orbital plane, and the Y-axis completes the right-handed system. The numerical model of Ma et al. (2004) is implemented within the Space Weather Modeling Framework (SWMF; Tóth et al. 2012).

The computational domain of a typical simulation is defined within −24 RM ≤ X ≤ 8RM, −16 RM ≤ Y, Z ≤ 16RM, where RM = 3396 km is the radius of Mars, and the inner boundary is taken to be 100 km above the Martian surface. This model applies a nonuniform, spherical grid near Mars, in which the resolution in longitude and latitude is uniform at 3°, while the radial resolution varies from 10 km at the lower boundary to 630 km at the outer boundary. In the radial direction, the grid size is < 0.01 RM within 1.20 RM ≤ r ≤ 1.40 RM, where the day-side region of the Martian magnetosheath is mainly located. The other details of the model are given in Ma et al. (2004).

A 60-order spherical harmonic model developed by Arkani-Hamed (2001) is employed to describe the crustal field and represents different orientations of Mars with respect to the solar wind direction. For most simulations analyzed in this work, following Wang et al. (2020b) and Wang et al. (2021a), the subsolar location is fixed to 180° west longitude and 0° north latitude, which represents the strongest Martian crustal magnetic field being located in the dayside region (e.g., Crider et al. 2002; Fang et al. 2017). Preliminary results for the other longitudes located at the Martian subsolar location are also discussed in Fig. 6.

As the solar extreme ultraviolet (EUV) radiation or the solar cycle condition can affect the background Martian atmosphere and/or ionosphere conditions (e.g., Kim et al. 1998; Bougher et al. 2000; Lundin et al. 2013), in this model the two fixed conditions of solar cycle maximum and minimum are adopted to describe the density profiles of the neutral species of the background Martian atmosphere, which are assumed to be spherically symmetric. Specifically, all the simulations are set under the solar maximum condition in this work, which is identical to Case 1 of Ma et al. (2004).

The other solar wind parameters are set as follows: the solar wind velocities VY and VZ are chosen to be 0, the upstream solar wind ion temperature T = 5 × 104 K, and the electron temperature Te = 3 × 105 K (for the single fluid approach, the total temperature is set to be 3.5 × 105 K). With these parameter sets, which are the observed normal solar wind conditions upstream of Mars (e.g., Halekas et al. 2017; Liu et al. 2021; Andreone et al. 2022), we simulate different conditions of IMF, solar wind dynamic pressure, and the location of the intense crustal field to study their effect on the dayside magnetic reconnection between the solar wind and the Martian crustal field.

thumbnail Fig. 1

Magnetic field topology in the southern hemisphere of the X–Z plane in the MSO coordinates for different IMF cone angles. Panels a–f stand for the IMF cone angle µ = 45°, 90°, 135°, 225°, 270°, and 315°, respectively. The solar wind conditions are Pd = 1 nPa and Bt = 3 nT (BY = 0 nT). The arrows indicate the upstream IMF direction, the black lines with arrows represent the magnetic field lines, the red lines describe the separatrix angles of the magnetic reconnection configurations, and the color bars show the solar wind thermal pressure.

3 Results

3.1 IMF orientation effect

As we mentioned above, the intense crustal field sources of Mars are mainly concentrated in the region of the southern hemisphere; for most simulations analyzed in this work, the subsolar location is fixed to 180° W and 0° N, which represents the strongest crustal magnetic field located on the dayside (Arkani-Hamed 2001; Ma et al. 2004). In this vein, the topology of the crustal field should show the multiple magnetic semi-loops in the southern hemisphere of the X–Z plane in the MSO coordinates. Also, according to the case reported by Harada et al. (2018), the possible reconnection site might be close to SZA ≈ 45° in the southern hemisphere of the X–Z plane in the MSO coordinates. Hence, to investigate the magnetic reconnection between the Martian crustal field and the IMF, we firstly set the simulation cases with different upstream IMF cone angles that vary by IMF BX and BZ, while BY = 0 nT, and the IMF cone angle is defined as the angle between the IMF direction and X-axis in the MSO coordinates, .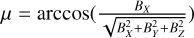

Figure 1 shows the magnetic field topologies under different IMF cone angles. Firstly, when the IMFs contain a northward or southward component, the magnetic field topologies are basically identical. That is, the magnetic field topologies of panels a–c are very similar for the IMF cone angle µ = 45°, 90°, and 135°; panels d–f also generally agree with each other as the IMFs have a southward component. Specifically, panels ac display that, for the IMF with a northward component, the crustal field and the IMF roughly point to the same direction at SZA ≈ 45°, where a local bulged “mini-magnetopause” appears in place of the magnetic pileup boundary and the magnetic field lines are piled up there (e.g., Mitchell et al. 2001; Harnett & Winglee 2003; Brain et al. 2005). Due to the “magnetic stripes” of the crustal field along the east-west direction, at the flanks of the “mini-magnetopause” (SZA ≈ 30° and 60°), the directions of the crustal field and the IMF are opposite there that causes the X-line structure of the magnetic field, indicating the occurrence of magnetic reconnections. Under a southward IMF component in panels d–f, at the same location of SZA ≈ 45°, the antiparallel orientations between the crustal field and IMF cause the X-line structure and the magnetic reconnection, which results in the erosion of the crustal field and a local “cusp” area. Meanwhile its flank regions (SZA ≈ 30° and 60°) experience the magnetic pileup. The separatrix angles of the magnetic reconnection configurations in panels d–f reach as large as ≈85°. As the presence of large separatrix angles is usually caused by a large normal magnetic field, which corresponds to the case with a highly nonuniform boundary and highly bent magnetic field lines, these large separatrix angles also indicate the steady state reconnection configurations in the simulations (e.g., Lee & Lee 2020). In addition, as the intense crustal field is strongest near the region of SZA ≈ 45° in this work, the scale of the X-line structure of magnetic reconnection at SZA ≈ 45° under the southward IMF is much larger than the scales at SZA ≈ 30° and 60° under the northward IMF. So, we mainly focus on the dayside magnetic reconnection on the large scale in this work, while the small scales are not taken into consideration. Hence, in the southern hemisphere, the “mini-magnetopause” dominates under the IMFs with a northward component, while the magnetic reconnection plays a prominent role under a southward component IMF.

By comparison with the observation result, the reconnection site from our simulation result is very close to the location reported by Harada et al. (2018). Harada et al. (2018) showed the dayside reconnection case by MAVEN observations from 18:03:00 to 18:12:00 on October 6, 2016; the reconnection occurred roughly at SZA ≈ 45° in the southern hemisphere when the intense crustal field was on the dayside, in a good agreement with our simulation results. Our simulation further indicates that this reconnection happens under the intense crustal field located on the dayside when the IMFs have a southward component. Moreover, the distance of the observation reconnection case from Mars center is about 1.17 RM when the satellite is moving across the outflow region, while our simulations further show that the center of X-line is ≈1.26, 1.23, and 1.24RM for panels d–f, respectively. Also, the shear angle in this observation case is 142°, while our simulation shows the separatrix angles of the magnetic reconnection configurations in panels d–f reach as large as 85°.

In addition, the differences in the magnetic field topology among panels a, b, and c are quite tiny, which represent the IMF conditions with a sunward, non-radial, and anti-sunward component, respectively. A similar result of the small differences can also be seen for panels d, e, and f. This indicates that, compared with the impact of the north-south component of the IMF on the magnetic field topology, the radial IMF component effect is barely measurable. However, on the X-Z plane of the Martian magnetosheath when the solar wind flows by, the radial IMF ought to partly convert to a portion of the north-south component, which should play the same role as the north-south IMFs. The reason for the different effects of the north-south and radial IMFs is not clear, and thus we further examine the magnetic field topology for the pure radial IMF conditions, as shown in Fig. 2.

Figure 2 shows the complex magnetic field topology on the X–Z plane in the MSO coordinates for the pure radial IMF conditions. In panel a, when the solar wind flows to the magnetosheath, the sunward IMFs partly convert to the southward component on the northern hemisphere and the northward component on the southern hemisphere, respectively. It is opposite in panel b, and a portion of the negative radial IMFs transform into the northward and southward components on the northern and southern hemispheres, respectively. On the northern hemisphere, due to the weak crustal field, the IMFs are generally flowing around the Martian induced magnetosphere with the solar wind for both positive and negative radial IMF conditions. In the southern hemisphere where the intense crustal field is located, although there are some regions of the opposite directions between the crustal field and the IMF (SZA ≈ 30° and 60° for the sunward IMF and SZA ≈ 45° for IMF cone angle equal to 180°), the distinct X-line structure is not observed, indicating the magnetic reconnection does not happen there.

The absence of the magnetic reconnection under the radial IMF might be due to the magnetic tension effect and the kinetic processes under this condition. Compared with the other IMF conditions, the radial IMF effects on the planetary magnetosphere are less well investigated and remain controversial. At the Earth, which has a global dipole magnetic field, it is suggested that under the radial IMF condition, the kinetic processes upstream of the bow shock can deflect solar wind flow, which results in the smaller strength and greater turbulence of the magnetic field in the magnetosheath, along with a weaker pressure imposed on the magnetopause (e.g., Engebretson et al. 1991; Lin et al. 1991; Samsonov et al. 2012). The locations of the magnetopause and bow shock, and the energy transfer across the magnetopause are also influenced by the radial IMFs (e.g., Dušík et al. 2010; Wang et al. 2020a; Lu et al. 2021). For Venus, which has no intrinsic magnetic field, but has an ionosphere and an induced magnetosphere, it is reported that by providing an additional driver, the magnetic tension pointing outward from Venus can force the magnetosheath plasma to flow faster in the azimuthal direction around Venus, while decelerating the upstream plasma in the X direction (e.g., Chang et al. 2020). Hence, the magnetic barrier becomes weak and the ionosphere of Venus can be demagnetized under a nearly flow-aligned IMF (e.g., Zhang et al. 2009; Rong et al. 2016). At Mars, we believe that the similar additional magnetic tension under the radial IMF condition can also provide an additional driver to resist the dynamic pressure outside the MPB, especially at the middle latitude region. In addition, under the radial IMF condition, the kinetic processes also contribute to the deceleration of solar wind (e.g., Tsurutani & Lakhina 1997; Szegö et al. 2000). As the pickup ions and the reflected particles can interact with the inflowing solar wind to generate a number of plasma instabilities, the subsequent wave-particle interaction will ensure the momentum and energy exchange, leading to a slight deceleration of the incident flow (e.g., Blanco-Cano et al. 2009, 2011; Omidi et al. 2013; Walsh 2017). While operating at a lower efficiency inside the magnetosheath, these kinetic processes nonetheless contribute to some deflection of the plasma flow (e.g., Halekas et al. 2017; Baraka et al. 2021). Hence, the X component of the solar wind velocity is decreased and the pressure in the magnetosheath cannot keep pushing the IMF to a lower altitude to reconnect with the crustal magnetic field, especially at the middle latitude region. As a result, the magnetic reconnection does not happen at the place under the radial IMF condition. Moreover, under the radial IMF condition, the locations of the planetary magnetopause and bow shock are different from those under the other IMF conditions (e.g., Dušík et al. 2010; Wang et al. 2020a). Recently, using a three-dimensional multispecies numerical model, Li et al. (2021) suggested that the subsolar distance and the terminator radius of the Martian bow shock, as well as the magnetotail radius, increase with the Parker spiral angle. Hence, we further study the effects of IMF cone angle on the location of the Martian MPB and bow shock.

Figure 3 displays the locations of the Martian MPB in the southern hemisphere of the X–Z plane in the MSO coordinates for different IMF cone angles. In general, there are three shape types of the Martian MPB for the different IMF cone angles. First, the MPB locations for the radial IMFs (the sunward in panel a and the anti-sunward in panel e) are basically the same. That is, the subsolar regions of the MPB are located closer to Mars for the radial IMFs than those for the other IMF conditions, and the difference is about 0.16 RM (from ~1.14 to ~1.30 RM) at the subsolar point. At the middle latitude region (30° < SZA < 60°), the MPB shapes for the radial IMF are more in accordance with those under a southward IMF component (panels f–h), although for the radial IMF conditions the magnetic reconnection does not happen there, while the high-latitude regions (60° < SZA < 90°) agree with those under a northward IMF component (panels b–d). Second, for the IMF with a northward component (panels b–d), at the middle-latitude region the Martian MPB expands from Mars compared with the other IMF conditions; this difference can reach ~0.2 RM (from ~1.20 to ~1.40 RM) at SZA ≈ 45°. Moreover, the MPB locations under the IMF with a radial component (IMF cone angle equal to 45° (panel b) and 135° (panel d)) are slightly closer to Mars than those under the pure northward IMF panel c), especially at the dayside region. Third, when the IMF has a southward component (panels f–h), due to the magnetic reconnection at the middle latitude region near SZA ≈ 45°, the MPB is located closer to Mars and appears here locally with a “cusp” shape, while the high-latitude regions flare larger than those for the other IMF conditions. In addition, under the IMF with a radial component (panels f and h) the MPB also moves closer to Mars slightly than those under the pure southward IMF (panel g), which is similar to the result under the northward IMF component of panels b–d. Compared with the empirical model result of Vignes et al. (2000), the shape of the Martian MPB does not seem as smooth as the empirical model suggested. Our simulation result shows that the magnetic field configuration at Mars, which is influenced by the IMF orientation, has a significant impact on the location of the MPB. This effect needs to be further investigated under the different solar wind conditions and taken into consideration in the MPB model in the future.

Next, we also examine the effect of the IMF cone angles on the locations of the Martian bow shock on the southern hemisphere of the X–Z plane in the MSO coordinates as shown in Fig. 4. Figure 4 shows that the influence of the IMF cone angles on the Martian bow shock is far less than that on the MPB, and the identified locations of the bow shock are very close to the model results of Vignes et al. (2000) for all those showing IMF conditions. Besides, the bow shocks are located slightly closer to Mars under the radial IMFs (panels a and e) than those under the other IMF conditions, and it is more obvious at the subsolar region. When the IMF has a southward component (panels f–h), the high-latitude regions of the bow shock move further away a bit from the model results of Vignes et al. (2000).

In comparison with the IMF cone angle effect on the location of the Martian MPB in the southern hemisphere of the X–Z plane in the MSO coordinates, its influence on the bow shock is relatively tiny. The shapes of the bow shock in our simulation results agree well with the model result of Vignes et al. (2000) under different IMF cone angles, while the shapes of the MPB vary with IMF cone angles and do not seem as smooth as the empirical model suggested. The location of the MPB is identified at the place where the pressure balance is reached ((Pth + Pd)/PB = 1.0) in this work; by changing the magnetic reconnection site, the IMF cone angle can alter the magnetic topology near the MPB that would affect the pressure conditions there. As a result, the IMF cone angle has a significant impact on the MPB location. As the bow shock is created because the solar wind encounters the obstacle of the MPB, the change in the MPB location should affect the location of the bow shock. However, our simulation shows that the bow shock locations do not change much under different IMF cone angles, except the slightly closer subsolar regions under the radial IMF condition. The reason for this difference is still unknown and needs to be further studied in the future.

thumbnail Fig. 2

Magnetic field topology on the X–Z plane in the MSO coordinates for the radial IMF conditions. Panels a and b stand for an IMF cone angle equal to 0° (BX = 3 nT) and 180° (BX = −3 nT). The solar wind dynamic pressure Pd = 1 nPa. The arrows indicate the upstream IMF direction, the black lines with arrows represent the magnetic field lines, and the color bars show the solar wind thermal pressure.
thumbnail Fig. 3

Martian MPB locations in the southern hemisphere of the X–Z plane in the MSO coordinates for different IMF cone angles. Panels a–h represent the MPB location for IMF cone angles equal to 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°, respectively. The solar wind conditions are Pd = 1 nPa and Bt = 3 nT (BY = 0 nT). The dots represent the MPB location identified by the pressure balance (Pth + Pd)/PB = 1.0, and the lines are the model results of Vignes et al. (2000).
thumbnail Fig. 4

Martian bow shock locations in the southern hemisphere of the X–Z plane in the MSO coordinates for different IMF cone angles (same format as Fig. 3). The bow shock location is determined at the place where the radially inward gradient of the thermal pressure is maximized according to Wang et al. (2020b), and the lines are the bow shock model results of Vignes et al. (2000).
thumbnail Fig. 5

Solar wind dynamic pressure effect on the magnetic field topology in the southern hemisphere of the X–Z plane in the MSO coordinates under the northward and southward IMFs. The left, middle, and right panels stand for Pd = 1, 3, and 5 nPa, respectively; the upper and bottom panels represent the IMF conditions of BZ = 3 and −3 nT. The arrows indicate the upstream IMF direction, the black lines with arrows represent the magnetic field lines, the red lines describe the separatrix angles of the magnetic reconnection configurations, and the color bars show the solar wind thermal pressure. The locations of the Martian MPB (the white dots) are identified by the same method of Fig. 3; the white lines are the MPB model results of Vignes et al. (2000).

3.2 Solar wind dynamic pressure effect

Besides the influence of IMF orientation, the solar wind dynamic pressure (Pd) effect on the magnetic field topology on the southern hemisphere of the X–Z plane in the MSO coordinates has also been studied. Figure 5 shows that with increasing Pd, the structure of the magnetic field does not change; the size of the crustal field region decreases and the draped fields correspondingly move to the lower altitudes at the place where the IMF and crustal field have the same direction, such as at the middle-latitude region near SZA ≈ 45° when IMF has a northward IMF component (panels a–c), or SZA ≈ 30° and 60° under a southward IMF component (panels d–f). When the IMF has a southward component and the magnetic reconnection occurs at SZA ≈ 45°, the reconnection site does not change much with increasing dynamic pressure (1.23, 1.26, and 1.26 RM for panels d, e, and f, respectively); the region of the closed topology of the crustal field and the draped IMF also do not change much. With increasing Pd, the separatrix angle of the magnetic reconnection at high latitude remains around 82°, while the low-latitude one decreases (85°, 75°, and 60° for Pd = 1, 3, and 5 nPa, respectively). The Martian MPB keeps moving closer to Mars when Pd increases for both northward and southward IMFs. In addition, the bow shock is also located closer to Mars with increasing Pd, which we do not show here.

Similar to the Earth’s magnetopause, the Martian MPB is located at the place where the inside pressure approximately equals the outside pressure (e.g., Lu et al. 2015). Although Mars is an unmagnetized planet, the inside pressure is also the magnetic pressure (e.g., Holmberg et al. 2019), and the importance of the thermal pressure cannot be ignored (Wang et al. 2021a). The outside pressure consists of the dynamic, thermal, and magnetic pressures (e.g., Brain et al. 2010). As a result, when the upstream Pd increases, it pushes the MPB closer to the surface of Mars. This also partly agrees with the observation result that, during the high solar wind pressure, the presence of closed topology across Mars should be decreased and draped fields at the day-side region also extend to lower altitudes (Weber et al. 2019). However, our simulation shows that under the higher dynamic pressure, these decreasing closed topology and the lower altitudes of the draped fields are only observed at the place where the IMF and crustal field have the same direction, such as at the middle-latitude region near SZA ≈ 45° when the IMF has a northward IMF component (panels a–c), or SZA ≈ 30° and 60° under a southward IMF component (panels d–f). While under the IMF with a southward component at SZA ≈ 45° where the magnetic reconnection occurs, the reconnection site, as well as the region of the closed topology of the crustal field and the draped IMFs, do not change much with the increasing dynamic pressure. The reason for this is suggested as follows: when the solar wind dynamic pressure is enhanced, at the crustal field regions near SZA ≈ 30° and 60° where the orientations of the IMF and crustal field are roughly the same (panels d–f), the closed topology of the crustal field and the draped fields move to lower altitudes. However, the height of the closed topology of the crustal field still exceeds the height of the reconnection site at SZA ≈ 45°, which can prevent the solar wind IMF from reconnecting with the crustal field at a lower altitude. Correspondingly, the separatrix angle of the magnetic reconnection at a low latitude still decreases with dynamic pressure. If the intense crustal filed regions at SZA ≈ 30° and 60° do not exist, the reconnection site at SZA ≈ 45° could also move to a lower altitude under a higher solar wind dynamic pressure. In addition, for an even larger solar wind dynamic pressure, such as an interplanetary coronal mass ejection event (e.g., Lentz et al. 2021), when the flank regions of the SZA ≈ 45° are impressed to an even lower altitude, the reconnection site might also move to a corresponding lower altitude.

thumbnail Fig. 6

Crustal field effect on the magnetic field topology in the southern hemisphere of the X–Z plane in the MSO coordinates under the southward IMF (BZ = −3 nT). In panels a–f, the subsolar location of Mars is fixed to the 0° north latitude when the west longitude is 0°, 45°, 90°, 120°, 150°, and 180°, respectively. The black lines with arrows represent the magnetic field lines, and the color bars show the solar wind thermal pressure. The locations of the Martian MPB (the red dots) are identified by the same method of Fig. 3; the red lines are the MPB model results of Vignes et al. (2000).

3.3 Intense crustal field location effect

Figure 6 displays the crustal field effect on the magnetic field topology in the southern hemisphere of the X–Z plane in the MSO coordinates under the southward IMF. As we mentioned above, the intense crustal sources of Mars are mainly concentrated in the Terra Sirenum region of the southern hemisphere, which is located in the longitude range of 150° E to 240° E and latitude range of 30° S to 85° S (e.g., Connerney et al. 1999). In this work, we investigate the effect of the longitude located at the Martian subsolar location on the magnetic field topology when the latitude is set to 0° N. Hence, longitude = 0° W represents the weak crustal field located on the dayside, longitude =180° W stands for the intense crustal field condition, and the other crustal field conditions are between them.

Figure 6 shows that under the weak crustal field condition (longitude = 0° W), no distinct X-line structure of the magnetic field is observed, indicating that the magnetic reconnection of the large scale does not easily occur under this condition. This is mainly due to the relatively weak crustal field on the day-side. However, the magnetic reconnection on a local small scale might also happen when the weak crustal field is on the day-side. Moreover, the shape of the MPB is smooth and very close to the model results of Vignes et al. (2000). While under the intense crustal field condition (longitude = 180° W), the same results as the previous figures are displayed, showing that the X-line structure and the magnetic reconnection at SZA ≈ 45° lead to the erosion of the crustal field and the “cusp” shape of the MPB there. The results for longitude = 45° W and = 90° W are very similar to that of longitude = 0° W in which the weak crustal field region are mainly located on the dayside. Under longitude = 120° W, due to a relative intense crustal field on the dayside that is weaker than that for longitude = 180° W, the crustal magnetic field topology and the MPB location are similar to those of longitude = 180° W, while the X-line structure is relatively smaller and the reconnection site moves to a lower altitude, as well as the closer location of the MPB. For panel (e) of longitude = 150° W it is a bit odd that its condition is not in accordance with panel f, as there is no distinct magnetic reconnection. On the one hand, this might be due to the irregular crustal field at longitude = 150° W where it is at the edge of the intense crustal field region. On the other hand, the crustal field model (Arkani-Hamed 2001) may also affect the result that can be improved by a more accurate model with the latest magnetic field data in the future (e.g., Morschhauser et al. 2014; Langlais et al. 2019; Gao et al. 2021). Besides the longitude effect, the latitude information is also important (e.g., Fang et al. 2017), as the change of the latitude at the subsolar point would definitely influence the location of the intense crustal field and the magnetic field topology in the north-south direction of the MSO coordinates. Along with the longitude, the effect of the latitude, as well as the IMF orientation, on the Martian magnetic field topology would become much more complicated and also needs to be further studied in the future.

4 Conclusions and discussions

In this paper, using a three-dimensional multispecies MHD model, we study the effects of the IMF orientation, solar wind dynamic pressure, and the intense crustal field location on the dayside magnetic reconnection between the solar wind and the Martian crustal field. Our main results are concluded as follows:

  • (1)

    Different IMF orientations result in the different magnetic field configurations and reconnection conditions on the Martian dayside. The dayside magnetic reconnection between the solar wind and the Martian crustal field tends to occur in the region with SZA ≈ 45° in the southern hemisphere when the intense crustal field is located on the dayside and the IMF has a southward component. The separatrix angles of the magnetic reconnection configurations can reach as large as ≈85°, which indicates the steady state of the magnetic reconnection in the simulation. This steady state and the large separatrix angle of the dayside magnetic reconnection are partly caused by the multipolar crustal magnetic fields at the place. In comparison with the observation result, the reconnection site of our simulation result is very close to the location of the observation case reported by Harada et al. (2018). When the IMF has a northward component and the intense crustal field is located on the dayside, the crustal field and the IMF roughly point to the same direction at SZA ≈ 45° in the southern hemisphere of the X–Z plane in the MSO coordinates where the Martian magnetic pileup boundary forms a local bulged “mini-magnetopause” and the magnetic field lines are piled up. Under the pure radial IMFs, although there are some regions where directions between the crustal field and IMF are observed as antiparallel, the magnetic reconnection is absent, which might be due to the presence of additional outward magnetic tension that reduces the upstream solar wind dynamic pressure (Chang et al. 2020), as well as strong changes in the interaction linked to kinetic effects not described by the present MHD model.

  • (2)

    The magnetic field configuration and the reconnection condition at Mars, which are influenced by the IMF orientation, can change the shape of the Martian MPB, while the bow shock location is weakly affected. When the intense crustal field is located on the dayside, under the radial IMF, the subsolar regions of the MPB are located closer to Mars than those for other IMF conditions, and the difference can reach about 0.16 RM at the subsolar point. When the IMF has a northward component, at the middle-latitude region, the Martian MPB expands from Mars compared with the other IMF conditions; this difference can reach ~0.2 RM at SZA ≈ 45°. When the IMF has a southward component, due to the magnetic reconnection at the middle-latitude region near SZA ≈ 45°, the MPB is located closer to Mars with a “cusp” shape. In comparison with the empirical model result of Vignes et al. (2000), the shape of the Martian MPB does not seem as smooth as the empirical model suggested, especially when the intense crustal field is located on the dayside. The influence of the IMF cone angles on the Martian bow shock is much less than that on the MPB, and the locations of the bow shock are very close to the model results of Vignes et al. (2000) for all these IMF conditions.

  • (3)

    With increasing solar wind dynamic pressure, the structure of the magnetic field does not change, while the size of the crustal field region decreases and the draped fields correspondingly move to lower altitudes at the place where the IMF and crustal field have the same direction, such as at the middle-latitude region near SZA ≈ 45° when the IMF has a northward IMF component, or SZA ≈ 30° and 60° under a southward IMF component. When the IMF has a southward IMF component and the magnetic reconnection occurs at SZA ≈ 45°, the reconnection site, the region of the closed topology of the crustal field, and the draped IMF do not change much with increasing dynamic pressure. We suggest the multipolar crustal magnetic fields can protect the Martian magnetic field from eroding to a lower altitude under the normal solar wind conditions. That is, the crustal field regions near SZA ≈ 30° and 60° where the orientations of the IMF and crustal field are roughly the same can prevent the solar wind IMF from further reconnecting with the crustal field to a lower altitude when the solar wind dynamic pressure is enhanced. Naturally, for a much larger solar wind dynamic pressure, such as an interplanetary coronal mass ejection event (e.g., Lentz et al. 2021), when the flank regions of the SZA ≈ 45° are impressed to an even lower altitude, the reconnection site might also move to a corresponding lower altitude.

  • (4)

    The dayside magnetic reconnection of the large scale is prone to happen when the intense crustal field is on the day-side. However, the effects of the crustal field location, including the longitude and latitude of the subsolar location, as well as the IMF orientation on the Martian magnetic field topology, are much more complicated and need to be further studied in the future.

As the IMF orientation, solar wind dynamic pressure, and the intense crustal field location can significantly influence the magnetic reconnection condition and the magnetic field configuration on the Martian dayside, these factors would also change the planetary pickup ion acceleration (e.g., Fang et al. 2008; Halekas et al. 2017), the plasma sheet orientation and the tail configuration (e.g., DiBraccio et al. 2018), and the ion escape (e.g., Harada et al. 2018). The details of these influences also need to be further investigated in the future.

Acknowledgments

The work is supported by the National Natural Science Foundation of China (grants 42074195, 42030203, 41974190, 42122061), the Science and Technology Development Fund (FDCT) of Macau (0002/2019/A1), Macau Foundation and the pre-research project on Civil Aerospace Technologies No. D020104, D020308 funded by China’s National Space Administration. This research is funded by Pandeng Program of National Space Science Center, Chinese Academy of Sciences. The work is also supported by Beijing Municipal Science and Technology Commission (Grant No. Z191100004319001), the Key Research Program of the Chinese Academy of Sciences (Grant NO. ZDBS-SSW-TLC00103), and MOST grant in Taiwan (Grant No. MOST 110-2111-M-002-017). We acknowledge the CSEM team in University of Michigan for the use of BATS-R-US code. The numerical calculations in this paper have been carried out on the super computing system in the Supercomputing Center of Nanjing University of Information Science & Technology. We especially acknowledge Yingjuan Ma at UCLA for the multi-species MHD model used in this work.

References

  1. Acuna, M. H., Connerney, J. E. P., Ness, N. F., et al. 1999, Science, 284, 790 [NASA ADS] [CrossRef] [Google Scholar]
  2. Andreone, G., Halekas, J. S., Mitchell, D. L., et al. 2022, J. Geophys. Res. (Space Phys.), 127, e29404 [NASA ADS] [Google Scholar]
  3. Arkani-Hamed, J. 2001, J. Geophys. Res., 106, 23197 [Google Scholar]
  4. Baraka, S. M., Le Contel, O., Ben-Jaffel, L., et al. 2021, J. Geophys. Res. (Space Phys.), 126, e29528 [NASA ADS] [Google Scholar]
  5. Blanco-Cano, X., Omidi, N., & Russell, C. T. 2009, J. Geophys. Res. (Space Phys.), 114, A01216 [Google Scholar]
  6. Blanco-Cano, X., Kajdic, P., Omidi, N., et al. 2011, J. Geophys. Res. (Space Phys.), 116, A09101 [Google Scholar]
  7. Bougher, S. W., Engel, S., Roble, R. G., et al. 2000, J. Geophys. Res., 105, 17669 [Google Scholar]
  8. Brain, D. A., Halekas, J. S., Lillis, R., et al. 2005, Geophys. Res. Lett., 32, L18203 [Google Scholar]
  9. Brain, D., Barabash, S., Boesswetter, A., et al. 2010, Icarus, 206, 139 [Google Scholar]
  10. Chang, Q., Xu, X., Xu, Q., et al. 2020, ApJ, 900, 63 [Google Scholar]
  11. Connerney, J. E. P., Acuna, M. H., Wasilewski, P. J., et al. 1999, Science, 284, 794 [NASA ADS] [CrossRef] [Google Scholar]
  12. Connerney, J. E. P., Acuña, M. H., Ness, N. F., et al. 2005, Proc. Natl. Acad. Sci. U.S.A., 102, 14970 [NASA ADS] [CrossRef] [Google Scholar]
  13. Crider, D. H., Acuña, M. H., Connerney, J. E. P., et al. 2002, Geophys. Res. Lett., 29, 1170 [Google Scholar]
  14. Crider, D. H., Brain, D. A., Acuña, M. H., et al. 2004, Space Sci. Rev., 111, 203 [NASA ADS] [CrossRef] [Google Scholar]
  15. DiBraccio, G. A., Luhmann, J. G., Curry, S. M., et al. 2018, Geophys. Res. Lett., 45, 4559 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dubinin, E., Modolo, R., Fraenz, M., et al. 2019, Geophys. Res. Lett., 46, 12722 [NASA ADS] [CrossRef] [Google Scholar]
  17. Dungey, J. W. 1961, Phys. Rev. Lett., 6, 47 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dušík, Š., Granko, G., Šafránková, J., et al. 2010, Geophys. Res. Lett., 37, L19103 [Google Scholar]
  19. Eastwood, J. P., Brain, D. A., Halekas, J. S., et al. 2008, Geophys. Res. Lett., 35, L02106 [NASA ADS] [CrossRef] [Google Scholar]
  20. Engebretson, M. J., Lin, N., Baumjohann, W., et al. 1991, J. Geophys. Res., 96, 3441 [NASA ADS] [CrossRef] [Google Scholar]
  21. Fang, X., Liemohn, M. W., Nagy, A. F., et al. 2008, J. Geophys. Res. (Space Phys.), 113, A02210 [NASA ADS] [Google Scholar]
  22. Fang, X., Liemohn, M. W., Nagy, A. F., et al. 2010, J. Geophys. Res. (Space Phys.), 115, A04308 [NASA ADS] [Google Scholar]
  23. Fang, X., Ma, Y., Brain, D., et al. 2015, J. Geophys. Res. (Space Phys.), 120, 10926 [Google Scholar]
  24. Fang, X., Ma, Y., Masunaga, K., et al. 2017, J. Geophys. Res. (Space Phys.), 122, 4117 [NASA ADS] [CrossRef] [Google Scholar]
  25. Fang, X., Ma, Y., Luhmann, J., et al. 2018, Geophys. Res. Lett., 45, 3356 [Google Scholar]
  26. Gao, J. W., Rong, Z. J., Klinger, L., et al. 2021, Earth Space Sci., 8, e01860 [NASA ADS] [CrossRef] [Google Scholar]
  27. Halekas, J. S., Eastwood, J. P., Brain, D. A., et al. 2009, J. Geophys. Res. (Space Phys.), 114, A11204 [NASA ADS] [CrossRef] [Google Scholar]
  28. Halekas, J. S., Ruhunusiri, S., Harada, Y., et al. 2017, J. Geophys. Res. (Space Phys.), 122, 547 [NASA ADS] [CrossRef] [Google Scholar]
  29. Harada, Y., Halekas, J. S., DiBraccio, G. A., et al. 2018, Geophys. Res. Lett., 45, 4550 [NASA ADS] [CrossRef] [Google Scholar]
  30. Harada, Y., Halekas, J. S., Xu, S., et al. 2020, J. Geophys. Res. (Space Phys.), 125, e28576 [NASA ADS] [Google Scholar]
  31. Harnett, E. M., & Winglee, R. M. 2003, Geophys. Res. Lett., 30, 2074 [NASA ADS] [CrossRef] [Google Scholar]
  32. Holmberg, M. K. G., André, N., Garnier, P., et al. 2019, J. Geophys. Res. (Space Phys.), 124, 8564 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kim, J., Nagy, A. F., Fox, J. L., et al. 1998, J. Geophys. Res., 103, 29339 [Google Scholar]
  34. Langlais, B., Thébault, E., Houliez, A., et al. 2019, J. Geophys. Res. (Planets), 124, 1542 [NASA ADS] [CrossRef] [Google Scholar]
  35. Lee, L. C., & Lee, K. H. 2020, Rev. Mod. Plasma Phys., 4, 9 [Google Scholar]
  36. Lentz, C. L., Baker, D. N., Andersson, L., et al. 2021, J. Geophys. Res. (Space Phys.), 126, e28105 [Google Scholar]
  37. Li, Y., Lu, H., Cao, J., et al. 2021, ApJ, 921, 139 [NASA ADS] [CrossRef] [Google Scholar]
  38. Lin, N., Engebretson, M. J., McPherron, R. L., et al. 1991, J. Geophys. Res., 96, 3455 [NASA ADS] [CrossRef] [Google Scholar]
  39. Liu, D., Rong, Z., Gao, J., et al. 2021, ApJ, 911, 113 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lu, J. Y., Wang, M., Kabin, K., et al. 2015, Planet. Space Sci., 106, 108 [Google Scholar]
  41. Lu, J. Y., Zhang, H. X., Wang, M., et al. 2021, ApJ, 920, 52 [NASA ADS] [CrossRef] [Google Scholar]
  42. Lundin, R., Barabash, S., Holmström, M., et al. 2013, Geophys. Res. Lett., 40, 6028 [Google Scholar]
  43. Ma, Y., Nagy, A. F., Sokolov, I. V., et al. 2004, J. Geophys. Res. (Space Phys.), 109, A07211 [NASA ADS] [CrossRef] [Google Scholar]
  44. Ma, Y. J., Fang, X., Nagy, A. F., et al. 2014a, J. Geophys. Res. (Space Phys.), 119, 1272 [NASA ADS] [CrossRef] [Google Scholar]
  45. Ma, Y., Fang, X., Russell, C. T., et al. 2014b, Geophys. Res. Lett., 41, 6563 [Google Scholar]
  46. Matsunaga, K., Seki, K., Brain, D. A., et al. 2017, J. Geophys. Res. (Space Phys.), 122, 9723 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mitchell, D. L., Lin, R. P., Mazelle, C., et al. 2001, J. Geophys. Res., 106, 23419 [NASA ADS] [CrossRef] [Google Scholar]
  48. Morschhauser, A., Lesur, V., & Grott, M. 2014, J. Geophys. Res. (Planets), 119, 1162 [CrossRef] [Google Scholar]
  49. Nagy, A. F., Winterhalter, D., Sauer, K., et al. 2004, Space Sci. Rev., 111, 33 [NASA ADS] [CrossRef] [Google Scholar]
  50. Omidi, N., Sibeck, D., Blanco-Cano, X., et al. 2013, J. Geophys. Res. (Space Physics), 118, 823 [NASA ADS] [CrossRef] [Google Scholar]
  51. Paschmann, G., Øieroset, M., & Phan, T. 2013, Space Sci. Rev., 178, 385 [Google Scholar]
  52. Rong, Z. J., Stenberg, G., Wei, Y., et al. 2016, J. Geophys. Res. (Space Phys.), 121, 10978 [Google Scholar]
  53. Samsonov, A. A., Němeček, Z., Šafránková, J., et al. 2012, J. Geophys. Res. (Space Phys.), 117, A05221 [Google Scholar]
  54. Szegö, K., Glassmeier, K.-H., Bingham, R., et al. 2000, Space Sci. Rev., 94, 429 [CrossRef] [Google Scholar]
  55. Tsurutani, B. T., & Lakhina, G. S. 1997, Rev. Geophys., 35, 491 [NASA ADS] [CrossRef] [Google Scholar]
  56. Tóth, G., van der Holst, B., Sokolov, I. V., et al. 2012, J. Comput. Phys., 231, 870 [Google Scholar]
  57. Vignes, D., Mazelle, C., Rème, H., et al. 2000, Geophys. Res. Lett., 27, 49 [NASA ADS] [CrossRef] [Google Scholar]
  58. Walsh, B. M. 2017, Dawn-Dusk Asymm. Planet. Plasma Environ., 230, 29 [NASA ADS] [Google Scholar]
  59. Wang, M., Lu, J. Y., Kabin, K., et al. 2020a, AJ, 159, 227 [NASA ADS] [CrossRef] [Google Scholar]
  60. Wang, M., Xie, L., Lee, L. C., et al. 2020b, ApJ, 903, 125 [Google Scholar]
  61. Wang, M., Lee, L. C., Xie, L., et al. 2021a, A&A, 651, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Wang, J., Yu, J., Xu, X., et al. 2021b, Geophys. Res. Lett., 48, e95426 [NASA ADS] [Google Scholar]
  63. Weber, T., Brain, D., Mitchell, D., et al. 2019, Geophys. Res. Lett., 46, 2347 [Google Scholar]
  64. Zhang, T. L., Du, J., Ma, Y. J., et al. 2009, Geophys. Res. Lett., 36, L20203 [Google Scholar]

All Figures

thumbnail Fig. 1

Magnetic field topology in the southern hemisphere of the X–Z plane in the MSO coordinates for different IMF cone angles. Panels a–f stand for the IMF cone angle µ = 45°, 90°, 135°, 225°, 270°, and 315°, respectively. The solar wind conditions are Pd = 1 nPa and Bt = 3 nT (BY = 0 nT). The arrows indicate the upstream IMF direction, the black lines with arrows represent the magnetic field lines, the red lines describe the separatrix angles of the magnetic reconnection configurations, and the color bars show the solar wind thermal pressure.
In the text
thumbnail Fig. 2

Magnetic field topology on the X–Z plane in the MSO coordinates for the radial IMF conditions. Panels a and b stand for an IMF cone angle equal to 0° (BX = 3 nT) and 180° (BX = −3 nT). The solar wind dynamic pressure Pd = 1 nPa. The arrows indicate the upstream IMF direction, the black lines with arrows represent the magnetic field lines, and the color bars show the solar wind thermal pressure.
In the text
thumbnail Fig. 3

Martian MPB locations in the southern hemisphere of the X–Z plane in the MSO coordinates for different IMF cone angles. Panels a–h represent the MPB location for IMF cone angles equal to 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°, respectively. The solar wind conditions are Pd = 1 nPa and Bt = 3 nT (BY = 0 nT). The dots represent the MPB location identified by the pressure balance (Pth + Pd)/PB = 1.0, and the lines are the model results of Vignes et al. (2000).
In the text
thumbnail Fig. 4

Martian bow shock locations in the southern hemisphere of the X–Z plane in the MSO coordinates for different IMF cone angles (same format as Fig. 3). The bow shock location is determined at the place where the radially inward gradient of the thermal pressure is maximized according to Wang et al. (2020b), and the lines are the bow shock model results of Vignes et al. (2000).
In the text
thumbnail Fig. 5

Solar wind dynamic pressure effect on the magnetic field topology in the southern hemisphere of the X–Z plane in the MSO coordinates under the northward and southward IMFs. The left, middle, and right panels stand for Pd = 1, 3, and 5 nPa, respectively; the upper and bottom panels represent the IMF conditions of BZ = 3 and −3 nT. The arrows indicate the upstream IMF direction, the black lines with arrows represent the magnetic field lines, the red lines describe the separatrix angles of the magnetic reconnection configurations, and the color bars show the solar wind thermal pressure. The locations of the Martian MPB (the white dots) are identified by the same method of Fig. 3; the white lines are the MPB model results of Vignes et al. (2000).
In the text
thumbnail Fig. 6

Crustal field effect on the magnetic field topology in the southern hemisphere of the X–Z plane in the MSO coordinates under the southward IMF (BZ = −3 nT). In panels a–f, the subsolar location of Mars is fixed to the 0° north latitude when the west longitude is 0°, 45°, 90°, 120°, 150°, and 180°, respectively. The black lines with arrows represent the magnetic field lines, and the color bars show the solar wind thermal pressure. The locations of the Martian MPB (the red dots) are identified by the same method of Fig. 3; the red lines are the MPB model results of Vignes et al. (2000).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.