| Issue |
A&A
Volume 666, October 2022
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202243905 | |
| Published online | 31 October 2022 | |
Asteroid spin-states of a 4 Gyr collisional family★,★★
1
Section of Astrophysics, Astronomy and Mechanics, Department of Physics, National and Kapodistrian University of Athens,
Zografos GR
15784,
Athens, Greece
2
Charles University, Faculty of Mathematics and Physics, Institute of Astronomy,
V Holešovičkách 2,
CZ-18000,
Prague, Czech Republic
e-mail: josef.hanus@mff.cuni.cz
3
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange,
Nice, France
4
BSA Osservatorio (K76),
Strada Collarelle 53,
12038
Savigliano, Cuneo, Italy
5
Bigmuskie Observatory (B88),
via Italo Aresca 12,
14047
Moberelli, Asti, Italy
6
NOAK Observatory (L02),
Stavraki Ioannina, Greece
7
Lowell Observatory,
1400 West Mars Hill Road,
Flagstaff,
AZ 86001, USA
8
Observatoire des Hauts Patys,
84410
Bédoin, France
9
Observatoire de Chinon,
Mairie de Chinon,
37500
Chinon, France
10
Geneva Observatory,
CH-1290
Sauverny, Switzerland
11
Observatoire des Engarouines,
1606 chemin de Rigoy,
84570
Malemort-du-Comtat, France
12
Via Capote Observatory,
Thousand Oaks, CA
91320, USA
13
AstroQueyras,
05530
Saint-Véran, France
14
Le Florian,
Villa 4, 880 chemin de Ribac-Estagnol,
06600
Antibes, France
15
Observatoire du Bois de Bardon,
16110
Taponnat, France
16
Observatorio Uraniborg,
41400
Écija, Sevilla, Spain
17
Hunters Hill Observatory,
7 Mawalan Street,
Ngunnawal
ACT 2913, Australia
18
The Observatories of the Carnegie Institution for Science,
813 Santa Barbara St.,
Pasadena, CA
91101, USA ; NHFP Einstein Fellow
19
Observatoire de Durtal,
49430 Durtal, France
20
Antelope Hills Observatory,
980 Antelope DR W,
Bennett, CO
80102 USA
21
Astronomical Observatory Institute, Faculty of Physics, A. Mickiewicz University,
Słoneczna 36,
60-286
Poznań, Poland
22
Institut d’Astrophysique de Paris, 98 bis boulevard Arago, UMR 7095 CNRS et Sorbonne Universités,
75014
Paris, France
23
Blue Mountains Observatory,
Leura, Australia
24
Charles University, Faculty of Mathematics and Physics, Institute of Theoretical Physics,
V Holešovičkách 2,
18000
Prague, Czech Republic
25
Observatoire de Blauvac,
293 chemin de St Guillaume,
84570
Blauvac, France
Received:
29
April
2022
Accepted:
30
June
2022
Context. Families of asteroids generated by the collisional fragmentation of a common parent body have been identified using clustering methods of asteroids in their proper orbital element space. However, there is growing evidence that some of the real families are larger than the corresponding cluster of objects in orbital elements, and there are families that escaped identification by clustering methods. An alternative method has been developed in order to identify collisional families from the correlation between the asteroid fragment sizes and their proper semi-major axis distance from the family centre (V-shape). This method has been shown to be effective in the cases of the very diffuse families that formed billions of years ago.
Aims. Here we use multiple techniques for observing asteroids to provide corroborating evidence that one of the groups of asteroids identified as a family from the correlation between size and proper semi-major axis of asteroids are real fragments of a common parent body, and thus form a collisional family.
Methods. We obtained photometric observations of asteroids in order to construct their rotational light curves; we combine them with the literature light curves and sparse-in-time photometry; we input these data in the light curve inversion methods, which allow us to determine a convex approximation to the 3D shape of the asteroids and their orientation in space, from which we extract the latitude (or obliquity) of the spin pole in order to assess whether an object is prograde or retrograde. We included in the analysis spin pole solutions already published in the literature aiming to increase the statistical significance of our results. The ultimate goal is to assess whether we find an excess of retrograde asteroids on the inward side of the V-shape of a 4 Gyr asteroid family identified via the V-shape method. This excess of retrograde rotators is predicted by the theory of asteroid family evolution.
Results. We obtained the latitude of the spin poles for 55 asteroids claimed to belong to a 4 Gyr collisional family of the inner main belt that consists of low-albedo asteroids. After re-evaluating the albedo and spectroscopic information, we found that nine of these asteroids are interlopers in the 4 Gyr family. Of the 46 remaining asteroids, 31 are found to be retrograde and 15 prograde. We also found that these retrograde rotators have a very low probability (1.29%) of being due to random sampling from an underlying uniform distribution of spin poles.
Conclusions. Our results constitute corroborating evidence that the asteroids identified as members of a 4 Gyr collisional family have a common origin, thus strengthening their family membership.
Key words: minor planets / asteroids: general / astronomical databases: miscellaneous
Table B.5 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/666/A116
© D. Athanasopoulos et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The study of asteroid families has been an active field of research since the discovery of the first groupings of asteroids in orbital element space (Hirayama 1918). As more asteroids were discovered, these initial groupings became more numerous, thus substantiating their significance. At the same time, more asteroid groupings (i.e. families) were discovered. Studies of the physical properties of asteroids highlighted that the families were also homogenous in colour, albedo, and spectral properties, in general (see Masiero et al. 2015, for a review). This corroborated the idea that these groups of asteroids in orbital element space were fragments of a common parent body. This the reason why they are also called collisional asteroid families (see Nesvorný et al. 2015, for a review on the subject).
The identification of the collisional families has been done using classical methods, such as the hierarchical clustering method (HCM; Zappala et al. 1990, 1995). Surveys of identification of asteroid collisional families have found that about one-third of the known asteroid population is associated with over 120 collisional families (see e.g. the Minor Planet Physical Properties Catalogue, MP3C)1. However, it is well known that the large majority of asteroid family identification surveys are conservative in order to clearly identify the core of the family and keep a good separation between the nearby families as well (Nesvorný et al. 2015).
A very important question is how many of the asteroids that are included in the background population (i.e. that do not belong to families) of the main belt are instead collisional members that have not been associated with known families. There is evidence that this number is very large, implying (i) that collisional families are larger than is reported in our current catalogues (Brož & Morbidelli 2013; Tsirvoulis et al. 2018; Dermott et al. 2021) and (ii) that there are still undiscovered families. This problem derives from the difficulty in linking the collisional members that currently reside far away in orbital elements to the family core (Milani et al. 2014). It has also been shown that there is an unexpected lack of asteroid families that formed more than 2 Gyr years ago from a parent body larger than about 100 km (Brož & Morbidelli 2013). Moreover, Tsirvoulis et al. (2018) attempted to identify families using an aggressive version of the HCM, such that it was very generous in linking large number of asteroids to their respective families. These authors found evidence of undetected family members in the investigated region of the main belt from the study of the size frequency distribution of the non-family members. These observations also corroborate hypotheses (i) and (ii).
As a collisional family ages, a non-gravitational force known as the Yarkovsky effect (see e.g. the review in Vokrouhlický et al. 2015) pushes asteroids away from the centre of the family with a drift rate da/dt that is proportional to the inverse diameter (1/D) where a is the asteroid orbital semi-major axis. Prograde rotating asteroids have da/dt >0 and move to a larger semi-major axis, while retrograde asteroids, with da/dt < 0, move to a smaller semi-major axis. This creates correlations of points in the (1/D) vs a) plane called V-shapes, because they resemble the letter V, whose slope (K) indicates the family age. As an asteroid family spreads in the orbital semi-major axis, family members cross orbital resonances with planets, which perturb their eccentricity and inclination. Hence, old families are less compact than younger ones in all three proper orbital element space. This makes old families (whose members have large orbital element spreading) more difficult to be identified by the HCM (e.g. Bolin et al. 2017), and cause families to overlap to each other.
Based on the V-shape characteristic, a method was developed to discover old and dispersed asteroid families (Bolin et al. 2017; Delbo et al. 2017). This V-shape identification method has already been used to discover five families of the inner main belt: the Eulalia and New Polana families (Walsh et al. 2013); a ‘primordial’ family with a nominal age of 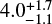 Gyr, but that could be as old as the Solar System; the Athor family,
Gyr, but that could be as old as the Solar System; the Athor family, 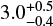 Gyr; and the Zita family,
Gyr; and the Zita family, 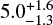 Gyr (Delbo et al. 2017, 2019).
Gyr (Delbo et al. 2017, 2019).
Although the V-shape family identification method is indeed a powerful tool, its efficiency decreases with increasing family age (Deienno et al. 2021) because the most dispersed family members can no longer be distinguished from the background, which might also consist of old and dispersed overlapping families. Given the current limitations of the detection methods, we are looking for independent ways to confirm family members and thus the borders of the families identified on the basis of their V-shapes. One of these independent methods is to check the spin state of the family members. According to the theory of the Yarkovsky effect, it is expected that most of the asteroids on the inward side (the left side of the V) of the family are retrograde, and prograde on the outward side (the right side of the V). This has been shown in notable HCM asteroid families (Hanuš et al. 2013a, 2018).
One of the most effective techniques to identify the spin state of asteroids is the inversion of their photometric light curves (Kaasalainen & Torppa 2001; Kaasalainen et al. 2001). This method requires the acquisition of large datasets of photometric measurements, where most of them are currently retrieved from all-sky surveys. However, these data are sparse in time by nature and often do not allow the unambiguous determination of asteroid rotational periods due to their low photometric accuracy of typically 0.1 magnitude. Often the addition of classical dense-in-time optical light curves to the sparse dataset leads to the removal of such ambiguity.
In this work we study the spin states of asteroids that belong to the innermost border of the inward side of a primordial family of the inner main belt that was reported by Delbo et al. (2017). This primordial family has orbital elements (a, e, i) roughly (2.26, 0.14, 5.75°) for the inward wing as only this has been identified and is suspected to contain low-albedo C-complex asteroids. For this, we ran our own observing programme (called Ancient Asteroids) and obtained dense-in-time light curves, which we combined with existing sparse-in-time photometric data.
In Sect. 2 we present the optical datasets used in this work and present our observing campaign. In Sects. 3 and 4 we describe the light curve inversion method used for the analysis of the optical data and for the determination of asteroidal physical properties. In Sect. 5 we present our results on the spin poles of our dataset indicating also the potential asteroid interlopers of the primordial family, while in Sect. 6 we discuss the results.
2 Datasets
In order to verify membership in the primordial family, we focus our analysis on the asteroids that are located between the inward border of the primordial family and the respective border of the Polana family (see Fig. 1). The latter, which is also called New Polana after its reassessment by Walsh et al. (2013), is another large but younger family in the inner main belt of similar carbonaceous composition and low albedo. We use the V-shapes of Walsh et al. (2013) and Delbo et al. (2017) to distinguish between the two families. This group of objects should belong either to the vast and extensive primordial family or to the unidentified background population. In order to study the spin poles of the primordial family we combined a great deal of data, including asteroid light curves that we collected from the databases, sparse photometric data obtained from different surveys, existing complete or incomplete shape models, and our own photometric observations.
2.1 Currently available asteroid models
The vast majority of asteroid shape models have been produced by the light curve inversion method (Kaasalainen & Torppa 2001; Kaasalainen et al. 2001). The Database of Asteroid Models from Inversion Techniques (DAMIT)2 contains ~6000 asteroid models for ~3460 asteroids (March 2022) that are publicly available (Durech et al. 2010). Shape models for 15 asteroids from our list are already included in DAMIT (see Table B.1). Furthermore, we also considered the partial models published in Durech et al. (2020). For these models only the sidereal rotation period, the ecliptic latitude of the spin axis, and its range are reported. This information is sufficient for our purposes, as it often allows us to securely decide whether the asteroid is a prograde or a retrograde rotator.
2.2 Archival photometric data
Photometric data of asteroids are scattered throughout various public databases or were provided to us directly by the observers. During the past two decades a large internal database of optical light curves maintained at the Institute of Astronomy of Charles University has been routinely used for shape modelling. A large amount of data was obtained from the Asteroid light curve Data Exchange Format (ALCDEF) database3 (Stephens & Warner 2018; 147 dense photometric light curves that exist for 19 of our asteroid targets). Additional dense light curves were downloaded from the Asteroid Photometric Catalogue (APC; Lagerkvist & Magnusson 2011) and the Courbes de rotation d’astéroïdes et de comètes database (CdR4) or were provided directly by the observers (see Table B.2).
The sparse-in-time data that come from various sky-surveys were obtained from corresponding databases and archives connected to the publications. We used data from the US Naval Observatory in Flagstaff (USNO-Flagstaff, IAU code 689), the Catalina Sky Survey (CSS, IAU code 703; Larson et al. 2003), Gaia Data Release 2 (GaiaDR2; Gaia Collaboration 2018), the All-Sky Automated Survey for Supernovae (ASAS-SN; Shappee et al. 2014; Kochanek et al. 2017; Hanuš et al. 2021), the Asteroid Terrestrial-impact Last Alert System (ATLAS; Tonry et al. 2018; Durech et al. 2020), the Zwicky Transient Facility (ZTF, IAU code I41; Bellm et al. 2019), the Palomar Transient Factory Survey (PTF; Chang et al. 2015; Waszczak et al. 2015), and TESS (Ricker et al. 2015; Pál et al. 2020). Tables B.3 and B.4 summarise the typical number of measurements from these surveys that were available for our targets. In general, data from USNO-Flagstaff, GaiaDR2, ZTF, TESS, and PTF are rather limited for our targets, while hundreds of individual measurements are available from the CSS, ASAS-SN, and ATLAS surveys. The CSS, USNO-Flagstaff, and ZTF data were obtained through the AstDys-2 database5.
 |
Fig. 1 Primordial family members presented in proper semi-major axis vs. inverse diameter plane, along with the low-albedo asteroids located in the innermost region of the main belt. Panel A: the yellow diamonds indicate members with known spin pole from the literature. The plus signs, crossed, and squares are members for which there are dense light curves only from literature, from this work, and from both sources, respectively (see details in Table B.2). Panel B: left side of the V-shape of the primordial family. The prograde asteroids are shown in red and the retrograde asteroids in blue. |
2.3 ASAS-SN g-band data
As discussed in Sect. 2.2, we use V-band sparse data from the ASAS-SN survey through the catalogue of Hanuš et al. (2021). However, since 2018 ASAS-SN has used the SLOAN g filter and significantly expanded to more telescope units and sites; we utilised these data in our work as well. We accessed and processed the g-band data following the same procedure as in Hanuš et al. (2021). The time coverage is already more than three years. Moreover, the g-band limiting magnitude is larger by about one magnitude than that of the V-band. Therefore, the g-band dataset is often comparable in terms of the number of measurements to the V-band dataset for brighter objects, and outperforms the V-band dataset for fainter objects. Both filters are treated independently in the shape modelling.
2.4 Ancient Asteroids: An international observing campaign
In order to enlarge our input dataset used for the shape modelling, which would potentially lead to new and improved shape solutions, we performed additional ground-based photometric observations. An international observing campaign has been initiated in the framework of our international initiative called Ancient Asteroids6 in order to collect dense photometric data for asteroids that belong to the oldest asteroid families (Athanasopoulos et al. 2021). Ancient Asteroids establishes anetwork of astronomers, currently from four countries, who follow a common observing plan. In the following we present the observing facilities and their corresponding equipment that participated in this work and provided data for 35 asteroids in our dataset.
Bonamico Star Adventure Astronomical Observatory The Bonamico Star Adventure (BSA) is an amateur observatory located in Savigliano, Italy. For this study BSA used a robotic 0.3 m (f/8) Ritchey-Chretien telescope and an open-filter SBIG ST-9 XME CCD detector.
Lowell Observatory Lowell is located in Arizona, United States, and for this project it operated two robotic telescopes: the Titan Monitor Telescope (TiMo), a 20″ PlaneWave CDK20 telescope equipped with a Moravian instruments G3-6300 CCD detector, and the 1 m PlaneWave (PW1) telescope equipped with a Finger Lakes Instruments ML-16803 CCD imager. TiMo is located on Lowell’s main Mars Hill campus (IAU Code 690), whereas the PW1 is on Lowell’s Anderson Mesa campus (IAU Code 688). All the observations were performed in the Sloan r’ filter.
Bigmuskie Observatory Bigmuskie is an amateur observatory located in Mombercelli-Asti, Italy. Bigmuskie utilises a 40 cm (f/8.25) Ritchey-Chrétien telescope. The observations were performed unfiltered by using a Moravian G3-1000 CCD detector.
Observatoire de la Côte d’Azur The observations were performed at two stations, which belong to the Observatoire de la Côte d’Azur (OCA) in France. The first station is the C2PU facilityin Calern, at an altitude of a 1300 m. C2PU operated the 1.04 m Cassegrain telescope (known as Omicron@C2PU) with an f/3.2 parabolic, prime focus and with a three-lens Wynne coma corrector using an unfiltered QHY600 CMOS camera (Bendjoya et al. 2012). The second station is located on Mont Gros, the historical site of the OCA, on the east-side hills of the town of Nice, France. Mont Gros station operated the 0.4 m (f/5) diameter telescope (called Schaumasse) equipped with with a QSI 583ws CCD camera.
University of Athens Observatory The University of Athens Observatory (UOAO) belongs to the National and Kapodistrian University of Athens in Greece, which utilises a robotic 0.4 m (f/8) Cassegrain telescope equipped with an SBIG ST-10 XME CCD detector (Gazeas 2016). All the observations were performed unfiltered.
Helmos Observatory Helmos observatory is operated by the National Observatory of Athens and is located on Mount Helmos (Aroania) in Greece, at an altitude of 2340 m. It utilises a robotic 2.3 m (f/8) Ritchey-Chrétien telescope (called Aristarchos; Goudis et al. 2010). All the observations were performed unfiltered by using the Princeton Instruments VersArray 2048B LN CCD camera.
NOAK Observatory The NOAK observatory is located in the city of Ioannina, Greece. It utilises a 0.25 m (f/4.7) robotic Newtonian telescope. All the observations were performed unfiltered by using an ATIK 460EXM CCD camera.
BlueEye 600 Observatory The BlueEye 600 robotic observatory (BE600) is operated by the Astronomical Institute of the Charles University and is located in Ondrejov, Czech Republic. It utilises a 60 cm Ritchey-Chrétien telescope (Officina Stellare). All the observations were performed by Martin Lehký7 utilising the standard Johnson R filter and the E2V42–40 CCD camera (Durech et al. 2018b).
Pic de Château-Renard Observatory The Pic de Château-Renard Observatory (ChR) is located at an altitude of 2936 m in Saint-Véran in the French Alps. The facility is operated by the Paris-Meudon Observatory and AstroQueyras, an amateur association. Observations were performed unfiltered by using a 0.5 m (f/8) Ritchey- Chrétien telescope equipped with a SBIG STX 16803 camera.
Observatoire du Bois de Bardon The Observatoire du Bois de Bardon (OBdB) is an amateur observatory located in Taponnat, France. OBdB used a 0.28 m (f/3) Schmidt-Cassegrain telescope equipped with a SBIG ST-402 ME CCD camera. Observations were performed with an r′ (Sloan) filter.
Blue Mountains Observatory The Blue Mountains Observatory is located at an altitude of 900 m in Leura, Australia. The photometric observations were done with a classical Celestron Schmidt Cassegrain telescope, 0.35 m in diameter operating at f/5. All images were taken unfiltered using a SBIG CCD camera ST8-XME at bin 1 × 1.
3 Photometric reduction
The photometric datasets used in this work include both dense photometric data from ground-based facilities (retrieved from the literature or from our observing campaign), as well as sparse data from several sky surveys and space missions, as described above. These two different datasets require different analysis techniques.
3.1 Observations in the Ancient Asteroids programme
Our observations were performed mainly in clear filter in order to increase the signal-to-noise ratio in our light curves, while keeping the exposure time as short as possible and increasing the sampling frequency. The exposure time varied between 30 s and 240 s, depending on the brightness of the target, telescope aperture, and observing conditions.
The collected data from all the observatories were reduced, following the standard image processing procedure of calibration and aperture photometry (e.g. Massey 1997; Gallaway 2020). The calibration was performed for all light frames in three steps: bias subtraction, dark subtraction, and flat-field correction. Aperture photometry is a quite simple technique and most applicable to stellar fields that are relatively sparse. This procedure was compiled by utilising AIP4Win software(Berry & Burnell 2005) for the fields observed by the C2PU, UOAO, Helmos, and NOAK observatories; IRIS software8 for the images performed by the OBdB and ChR observatories; and MPO Canopus software (Warner 2015) for the remaining images (see Table B.5).
The differential photometry was performed either with five bright field stars or by estimating an artificial comparison star, following the methodology presented by Broeg et al. (2005). The resulting measurements were provided in differential magnitudes with a photometric accuracy of 0.02−0.1 mag. In the case of OBdB and ChR, the differential photometric data were performed by estimating an artificial comparison star following the methodology described by Fauvaud & Fauvaud (2013, 2014).
We used the sigma-clipping method (see Gallaway 2020) to remove the prominent outliers in our measurements, which were usually caused by cosmic rays or satellites passing through the field. In the case where an asteroid was passing near a field star within a range of an aperture size (typically of the order of 57 arcseconds) we trimmed the light curve and we kept only the ‘clear’ parts.
We used the Pogson equation (m = −2.5 log(F) + c) to transform the differential magnitude (m) to relative flux (F). The relative flux values were normalised by defining the average flux of each light curve as one. For all the epochs of the observed light curves we performed the light travel time correction (from the asteroid to the observer) and computed the ecliptic Cartesian coordinates (x, y, z) of the Sun and of the Earth, with the asteroid as the reference point, in [au] via the Miriade service (Berthier et al. 2009). This format is required by the convex inversion (CI) method that we used for the shape modelling, as described in Sect. 4.
3.2 Adopted data
The dense photometric data from databases such as the Asteroid Lightcurve Data Exchange Format database (ALCDEF) or APC are in magnitude values, so we converted them to relative fluxes by following the procedure described in Sect. 3.1.
In addition to the dense photometric data, we included sparse-in-time photometric measurements from various sources as they proved to be useful in constraining the asteroid models, despite their usually low photometric accuracy of ~0.1 mag (Ďurech et al. 2009, 2016; Hanuš et al. 2011, 2013b). In order to use the sparse data for the shape modelling by the CI method, we processed them following the procedure of Hanuš et al. (2011). For more details, we refer to the most recent description of the procedure applied to ASAS-SN data by Hanuš et al. (2021). All individual measurements within each sparse dataset (i.e. specific survey and photometric filter) are internally calibrated; therefore, we process each dataset separately. First, the sparse data are usually available in magnitude values, which we transform into fluxes utilising the Pogson equation and, for convenience, setting the zero magnitude to 15. We then apply the light travel time correction to each epoch. Next we normalise the fluxes to a referenced one astronomical unit distance of the asteroid to the Earth and the Sun. The final steps were sigma-clipping to reject the outliers and estimating the relative weights of each sparse dataset with respect to the dense data (see Hanuš et al. 2021).
4 Determination of the spin poles
We used the CI method developed by Kaasalainen & Torppa (2001); Kaasalainen et al. (2001). This gradient-based inversion technique is based on shape model parametrisation by a set of facets and their normal vectors and their optimisation such that they fit to the observed light curves. Assuming a convex shape representation of the asteroid shape, the inversion problem is unique. However, adding the rotation state (i.e. sidereal rotation period and spin axis orientation) as additional free parameters, we lose the uniqueness of the solution, and the parameter space becomes full of local minima. We have to search the parameter space on a grid of input parameters and find the local minimum that corresponds to the global minimum, and thus the correct set of searched parameters. The production of the model light curve, that is compared by the method to the observed light curves, is performed by using an empirical light-scattering model, which is a combination of single Lommel-Seeliger and multiple Lambert scattering models (Kaasalainen et al. 2002). To date, the CI has been used to derive asteroid models for more than 3460 asteroids that are stored in the DAMIT database.
We assume that the shape effects in the light curves are independent of the photometric filters used while covering the reflected-dominated spectral range. Therefore, we can treat all dense light curves as relative (i.e. normalised to unity). Although each sparse dataset is, in principle, internally calibrated in a different photometric system, we also use the sparse data as normalised to unity. The only caveat is that we assume that the phase function is the same in each photometric system. This is not fully correct; for example, Ďurech et al. (2020) found statistically significant differences in the ATLAS data taken in the c and o filters, in accordance with the phase reddening effect (Millis et al. 1976; Lumme & Bowell 1981). However, for our purposes it is sufficient to have a single phase function for all sparse datasets.
We combined all the available datasets and applied CI to them. We weighted individual light curves and sparse datasets based on their accuracy (expected rms). The individual weights wi were normalised such that Σ(wi) = N, where N is the number of dense light curves plus the number of sparse datasets. The process that we followed is described in Hanuš et al. (in prep.).
4.1 Rotation period
For asteroids with previously known rotation periods we searched for the best-fit model with the period parameter varying between boundaries defined by 5, 10, and 20% of the previously reported period in the LightCurve DataBase (LCDB; Warner et al. 2009), depending on the reliability flag provided for each period estimate 3 and 3−, 2+, 2. Rotation periods for asteroids with other reliability flags were considered unknown.
Fourier-based algorithms are unable to efficiently estimate the rotation period of asteroids in cases of only sparse photometric data availability or extreme slow rotators, where their rotation period far exceeds the night duration. In these cases we performed a dense scanning in the rotation period parameter space from 2 h, which has been observed as an approximate lower limit of asteroids (>150 m in size) by Pravec et al. (2002), up to 5 000 h, which was motivated by the recent discovery of superslow rotating asteroids by Erasmus et al. (2021).
It should be noted that the period search is actually a full shape and rotation state optimisation by the CI. However, this procedure was performed on a grid of pole orientations limited to only ten values evenly distributed on a sphere and rather rough shape model resolution. We only recorded the rotation period and the best-fit rms (and χ2) value within the grid of pole directions. We considered the best-fitting period searched for on a selected period interval as unique if its 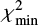 is the only solution below the threshold defined as
is the only solution below the threshold defined as
where v corresponds to the number of degrees of freedom (number of observations minus the number of free parameters).
Interestingly, the difference between two local minima in the period parameter space ΔP is dependent only on the time span of the data T and the sidereal rotation period P itself
and thus, for instance, independent of the shape resolution. We sample the period with a step of 0.5ΔP that we recompute every step. We note that ~1/20 of ΔP is a reliable uncertainty for the derived rotation period as it corresponds to a rotation phase offset of about 10°, which is a typical uncertainty on the pole direction.
4.2 Spin pole and shape
After the determination of the rotation period, we applied the CI method on a much denser grid of initial spin directions (ecliptic longitude λ and latitude β) and a higher shape resolution9. The best-fitting shape and spin pole solution is considered unique if it fulfils the condition of Eq. (1). Most of the cases presented two symmetrical solutions with respect to ecliptic longitude (λ± 180°), the so-called pole ambiguity (Kaasalainen & Lamberg 2006).
If photometric data are rich enough in observing geometries and have reasonable accuracy relative to the amplitude of the asteroid light curve, the unique solution can be often derived. Sometimes, however, the photometric data are insufficient to derive a unique solution, but they allow us to derive a unique period and three or four pole solutions that have similar values of the ecliptic latitude β. These so-called partial models are still useful, especially for our study, as it is possible to decide whether the asteroid is a prograde or a retrograde rotator. Therefore, we made an effort to identify such cases here together with the unique solutions.
5 Results
5.1 New period estimates
We derived improved values of the sidereal rotation period for 29 asteroids, as presented in Tables B.3 and B.4 (see also Fig. A.1 for an example of typical periodograms). All these period values are consistent with the synodic periods reported in the LCDB database10. The revised asteroid models have almost the same period as the previous solutions. Moreover, we measured rotation periods for seven asteroids for the first time. These periods were derived using sparse photometric data. Of these asteroids one is a super-slow rotator with P = 3253.5 h and one a slow rotator with P = 152.62 h, which are (2776) Baikal and (8315) Bajin, respectively. All the others, namely (12722) Petrarca, (13066) 1991 PM13, (23495) 1991 UQ1, (49863) 1999 XK 104, and (70184) 1999 RU3, are rather fast rotators, with periods between 3 and 10 h.
5.2 Spin pole directions
By combining new and literature data, we successfully determined the shapes and spin states for 55 asteroids that belong to the nominal population of the primitive primordial family of the inner main belt (Delbo et al. 2017). This corresponds to 51% of the population in the sliver between the left-wing border of the Polana family and the primordial family (see Fig. 1). In particular, we calculated 25 new complete asteroid models, 20 revised and 4 new partial models (see Tables B.3 and B.4). Specifically, 34 asteroids have retrograde rotation, while 21 are prograde. The case of (2575) Bulgaria is presented as an example of model fits to the dense and sparse photometric data in Figs. A.2 and A.3, respectively. Figure A.4 shows an example of four shape models derived from our analysis.
5.3 Identification of interlopers
In order to proceed and study the spin states of the inner main belt primordial family, we need to eliminate any potential interlopers beforehand. These are defined as objects that may reside inside the V-shape of a family and/or that are grabbed by the HCM methods in the same cluster, but their physical properties, such as the geometric visible albedo pV and spectral class, are totally different from the bulk composition of the family (Nesvorný et al. 2015). These asteroids that are clearly non-family members, may belong to the background population or to other nearby families.
In our case seven asteroids have reported spectral (visible or near-infrared) or spectrophotometric (e.g. SDSS, ECAS, and MOVIS) data that do not match the primordial family composition, which is composed primarily of dark albedo and featureless spectra. Specifically, asteroids (1806) Derice, (2171) Kiev, (2575) Bulgaria, and (6125) Singto are classified as S-complex asteroids; (2768) Gorky as an A-type; and (5524) Lecacheux and (15415) Rika as V-types in any of the main classification schemes of Tholen (Tholen 1989), Bus (Bus & Binzel 2002), and Bus&DeMeo (DeMeo et al. 2009). Of these, asteroids (1806), (2171), (2575), and (2768) had been already assigned to the nearby bright family of Flora that consists of S-complex asteroid members, which leaves no doubts that they are interlopers of the low-albedo primordial family of Delbo et al. (2017). Although asteroids (2536) Kozyrev and (2705) Wu have no spectral or spectrophotometric information, their pV values are moderate and beyond the 12% that is generally defined as the separation between the S and C spectroscopic complexes (Delbo et al. 2017). In the studied sample there are seven asteroids (220, 428, 917, 1244, 1544, 1700, 3633) whose pv is in agreement with the primordial family but are classified as members of the X-complex. Using only the visible part of the spectrum (or spectrophotometric data) is not always sufficient to distinguish the slope between the X- and C-complex asteroids, the latter being the main components of the primordial family. So, although these seven asteroids could indeed be interlopers, at this stage we cannot definitely exclude them from the family.
On the other hand, in the population that is studied in this work there are asteroids that had been previously assigned using the clustering methods to the other nearby families of Flora and Vesta (Nesvorný et al. 2015), such as the asteroids (428) Monachia, (4524) Barklajdetolli, (2839) Annette, and (3633) Mira. However, their low (<10%) pV values and their featureless spectrophotometric data are in contrast to this assignment, and therefore remain in the primordial family.
The above analysis indicated nine interlopers in the sample of 55 studied objects. From these 46 confirmed asteroid members of the primordial family, 31 asteroid models (67%) have retrograde rotation and 15 prograde, including the partial solutions. Excluding the seven X-complex asteroids the abundance of retrograde asteroids reaches 72%. The distribution of the sense of rotation (i.e. prograde or retrograde) within the family is presented in Fig. 1 (Panel B). Additionally, Fig. 2 illustrates the distribution of spin axis directions. Table B.6 presents all the objects studied in this work, indicating their prograde or retrograde spin along with their physical properties. Diameters (D) and geometric albedos (pV) were calculated as the weighted averages of all the available measurements in the literature and were retrieved from the Minor Planet Physical Properties Catalogue. All uncertainty-weighted averages use 1/σ2 as weights, where σ is the error of each measurement.
6 Discussion
6.1 The cases of (2171) Kiev, (7132) Casuli and (2705) Wu
Most of the asteroids studied in our sample are found to be single objects with no evidence of any close companion body or satellite. However, two asteroids in our sample host a satellite, while another is probably a non-principal-axis (NPA) rotator.
The first two cases are (2171) Kiev and (7132) Casuli, which have been reported as binaries by Loera-González et al. (2020) and Franco et al. (2020a), respectively. Our dense photometric data confirm that (2171) Kiev and (7132) Casuli are indeed binary asteroids; however, the observed light curves are not enough to further constrain the orbits of secondaries. In each case the eclipsing part of the light curve was removed and the CI method was applied to the rotational light curves of the primary body. Thus, the results presented in Tables B.6 and B.3 are only for the primary bodies. Although the derived parameters do not deviate from the rest of the sample, care should be taken given that the companion body can alter the spin axis and rotational characteristics of the primary body.
The third case, (2705) Wu, is a slow retrograde rotator, as our analysis and that of Ďurech et al. (2020) have shown by using sparse photometric data. Previous dense-in-time observations have shown that it is possibly a NPA rotator (i.e. tumbler, Oey 2010). As has been noted, some deviations from the single periodicity are clearly seen, but not at a conclusive level, while more photometric data are needed to resolve the second period. In this study no further dense-in-time observations were obtained. The characteristic timescale of damping of the excited NPA rotation can be estimated as ![${\tau _d} = {{P_{\left[ h \right]}^3} \mathord{\left/ {\vphantom {{P_{\left[ h \right]}^3} {\left( {{C^3} \cdot D_{\left[ {km} \right]}^2} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{C^3} \cdot D_{\left[ {km} \right]}^2} \right)}}$](/articles/aa/full_html/2022/10/aa43905-22/aa43905-22-eq7.png) [Gyr] by Harris (1994), where C = 17 ± 2.5 Gyr · km2/h3. For this asteroid, the damping timescale is estimated to be 12 ± 5 Gyr, which is greater than the age of our Solar System. This is statistically common for NPAs, which have a diameter larger than ~0.4 km (Pravec et al. 2005). So, if (2705) Wu is a tumbler, the spin solution of our study related to the sense of rotation can be trusted.
[Gyr] by Harris (1994), where C = 17 ± 2.5 Gyr · km2/h3. For this asteroid, the damping timescale is estimated to be 12 ± 5 Gyr, which is greater than the age of our Solar System. This is statistically common for NPAs, which have a diameter larger than ~0.4 km (Pravec et al. 2005). So, if (2705) Wu is a tumbler, the spin solution of our study related to the sense of rotation can be trusted.
 |
Fig. 2 Distribution of the complete spin pole solutions for the primordial family members. The main plot is a sinusoidal equal-area cartographic representation, where the vertical grey lines define the longitude (λ) and the horizontal curves define the latitude (β). The right histogram represents the latitude (β) of prograde (red) and retrograde (blue) rotators. The bottom histogram represents the longitude (λ) of prograde (red) and retrograde (blue) rotators. The specific values for each asteroid are shown in Tables B.3 and B.4. |
6.2 Distribution of the spin poles
All asteroid models with retrograde solutions, except the solutions for (933) Susi and (49863) 1999 XK104, have large ecliptic pole latitude values ∣β∣ ≥ 30° with a large predominance towards the YORP end state values approaching β 90°. The latitude distribution for prograde rotators differs slightly from the retrograde rotators by having more values with ∣β∣ ≤ 60°. This is likely due to various resonances acting only on prograde rotators. Similar behavior is also observed in other asteroid families (Hanuš et al. 2013a).
The distribution of ecliptic pole longitudes is bi-modal for prograde rotators (with two peaks, at ~45° and ~225°) and irregular for retrograde asteroids (with two peaks, at ~75° and ~ 255°). Previous studies have estimated that the longitude distribution for main belt asteroids is uniform with no statistically significant features (Kryszczyńska et al. 2007; Hanuš et al. 2011). On the contrary, more recent studies present an anisotropic longitude distribution with two symmetrical maxima around ~ 50° and ~230° and minima around ~140° and ~320° (Bowell et al. 2014; Cibulková et al. 2016).
Retrograde and prograde asteroids also have different period distributions. As Fig. 3 shows, the majority of slow rotators are retrograde. Moreover, the periods of retrograde asteroids have a non-Maxwellian distribution with excesses at the fast and the slow rotations. This bimodal distribution is in agreement with that of main belt asteroids <40 km, as a result of the YORP effect (Pravec & Harris 2000; Pravec et al. 2002). The period distribution of prograde asteroids is irregular, with small peaks for slow, moderate, and fast rotations. Thus, prograde and retrograde seem to have different spin rate distributions. A simple model by Pravec et al. (2008) estimated that a uniform distribution for < 40 km main belt asteroids could happen on large timescales. Moreover, the different spin rate distributions could signify a different YORP evolution (Pravec & Harris 2000; Pravec et al. 2002, 2008, and references therein).
 |
Fig. 3 Histogram of spin rate for members of the primordial asteroid family. The prograde rotators are in red and the retrograde in blue. The light grey bars represent the primordial family members whose rotational period is known either from this study or the literature. |
6.3 Statistical predominance of the retrograde spin poles
It is possible to test whether the observed predominance of the retrograde spin poles could be due to chance, created by random sampling of an equal-probability population of prograde and retrograde asteroids. In particular, we test the probability of obtaining 15 or fewer prograde rotators from 46 observed asteroids, drawing from a population having an equal probability (0.5) of being retrograde or prograde:
An evaluation of Eq. (3) gives p(≤ 15, 46) = 1.29%. This shows that our observations rule out the null hypothesis (i.e. there is no statistical predominance of the retrograde spin poles) at 98.71% probability.
6.4 The YORP reorientation timescale for the primordial family members
Although a predominance of retrograde spinning asteroids is expected in the inward wing of the V-shape of a collisional family, it is also likely to find prograde rotators. During the family lifespan of a few billion years, there are a number of processes that can re-orient the spin vector on an asteroid, such as non-catastrophic collisions, activity, or topographic changes, for example due to mass wasting and/or movement (see e.g. Paolicchi & Knežević 2016; Bottke et al. 2015, for a discussion). Torques on asteroids due to the unbalanced emitted and reflected radiation (which cause the YORP effect Rubincam 2000) are very sensitive to topographic features, and so are the strength and sign of the YORP effect (which can be reversed; Statler 2009). Statler (2009) theoretically showed that YORP is sensitive to small surface features, and hence even a small impact or mass movement could alter the shape sufficiently and change the sense of pole-period evolution. Moreover, as the YORP effect drives some of the family members towards the critical threshold for fast rotation, topographic instability might easily occur, leading to new YORP coefficients, which can drive the spin-pole in the opposite direction. The older a family is, the higher the cumulative probability is that some family members may had undergone shape changes or received non-catastrophic impacts, hence the higher the probability of detecting prograde rotators in the wing of the V-shape with a predominance of retrograde rotators.
Given the above, we used the model of Vokrouhlický et al. (2006) to estimate the evolution of the spin vectors of the family member asteroids. The model of Vokrouhlický et al. (2006) takes into account the change in orbital semi-major axis due to the Yarkovsky effect and the changes in the rotation rate 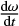 and spin axis obliquity11
and spin axis obliquity11 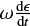 of the spin axis due to the YORP torques. In particular, the values of
of the spin axis due to the YORP torques. In particular, the values of 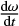 and
and 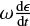 are multiplied by a constant named CYORP, which Bottke et al. (2015) have proposed to be between 0.5 and 0.7. However, Vokrouhlický et al. (2006) found that values of CYORP ~ 1 could produce model asteroid families that well represent the real ones. Hence, for simplicity, we assumed here that CYORP = 1. The values of
are multiplied by a constant named CYORP, which Bottke et al. (2015) have proposed to be between 0.5 and 0.7. However, Vokrouhlický et al. (2006) found that values of CYORP ~ 1 could produce model asteroid families that well represent the real ones. Hence, for simplicity, we assumed here that CYORP = 1. The values of 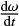 and
and 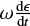 are functions of the orbital and physical parameters of asteroids, as described by Vokrouhlický et al. (2006), which we follow hereafter.
are functions of the orbital and physical parameters of asteroids, as described by Vokrouhlický et al. (2006), which we follow hereafter.
Following Vokrouhlický et al. (2006), we modelled the evolution of the 46 family members for which we have a pole solution. We assumed they all started with an initial retrograde spin direction, which we randomly assigned uniformly between 90° and 180° obliquity. We initialised model asteroids with the known diameters and current spin periods. We evolved the model with a time step of 10 Myr for 4 Gyr. At each time step the values of a, ω, and ϵ were updated by summing their respective time derivatives multiplied by the step in time. At each time step we also evaluated the probability that an asteroid could suffer a non-catastrophic collision capable of changing its spin axis. This probability is given by the 10 Myr time step divided by the re-orientation timescale, τreor, which is estimated as
Then, for each asteroid (at each time step), we extracted a random number, uniformly distributed between 0 and 1, and we re-oriented the spin state of the asteroid when the random number was smaller than said probability. The spin axis reorientation is performed by picking a new random direction of the obliquity uniformly distributed between 0° and 180°.
After the model was completed, we counted how many of the initially retrograde asteroids became prograde rotators due to spin evolution. We ran the model 10 000 times and we found that the probability of having 15 or fewer prograde rotators of the initial 46 retrograde objects is 13.5%; on average, we found 11.4 prograde asteroids.
However, Delbo et al. (2017) showed that D ≥ 35 km asteroids could be primordial objects that accreted as planetesimals from the dust of our protoplanetary disk. It is therefore possible that some of them are within the inward wing of the V-shape of the primordial family. Hence, we also considered the above model only for D < 35 asteroids, of which 14 are prograde rotators and 29 retrograde rotators. In this case we found a 20% probability of having 14 or fewer prograde rotators of the initial 43 retrograde objects is 20%.
We can conclude that it is possible to observe the current mix of retrograde and prograde rotators within the inward wing of the 4 Gyr collisional family.
7 Conclusions
We carried out a campaign of photometric observations of those asteroids that have been classified as members of one of the oldest collisional (primordial) families in the Solar System (Delbo et al. 2017). We constructed photometric time series, the light curves, for 49 asteroids. This corresponds to 46% of the members of the primordial family. We combined our light curves with those from the literature, and with sparse-in-time photometry in order to create multi-epoch photometric datasets to be used as inputs for the convex inversion method. We obtained 49 new and revised shape models and their spin vector solutions. We combined this with the literature spin vectors (for six objects).
We reassessed the albedo values for the observed asteroids and studied their literature spectra. This allowed us to find nine interlopers among the initial list of family members of Delbo et al. (2017). After removing these interlopers, we find that 31 and 15 out of the remaining 46 asteroids are retrograde and prograde, respectively. We show that this predominance of retrograde compared to prograde asteroids is very unlikely (1.29% probability) to be due to sampling a distribution of objects with equal probability of being prograde and retrograde. This corroborates the hypothesis that the statistical predominance of the retrograde spin poles is due to a physical process, as was claimed by Delbo et al. (2017), namely formation as collisional fragments of a common parent body, a subsequent dynamical evolution driven by the Yarkovsky effect.
Acknowledgements
M.D. and C.A. acknowledge support from ANR “ORIGINS” (ANR-18-CE31-0014). This work is based on data provided by the Minor Planet Physical Properties Catalogue (MP3C) of the Observatoire de la Côte d’Azur. The research of JH has been supported by the Czech Science Foundation through grant 20-08218S. The work of OP has been supported by INTER-EXCELLENCE grant LTAUSA18093 from the Ministry of Education, Youth, and Sports. Support for T.W.-S.H. was provided by NASA through the NASA Hubble Fellowship grant HST-HF2-51458.001-A awarded by the Space Telescope Science Institute (STScI), which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. We thank the Las Cumbres Observatory and their staff for its continuing support of the ASAS-SN project. ASAS-SN is supported by the Gordon and Betty Moore Foundation through grant GBMF5490 to the Ohio State University, and funded in part by the Alfred P. Sloan Foundation grant G-2021-14192 and NSF grant AST-1908570. Development of ASAS-SN has been supported by NSF grant AST-0908816, the Mt. Cuba Astronomical Foundation, the Center for Cosmology and AstroParticle Physics at the Ohio State University, the Chinese Academy of Sciences South America Center for Astronomy (CAS-SACA), the Villum Foundation, and George Skestos.
Appendix A Supplementary figures
 |
Fig. A.1 Typical periodograms of six different asteroids and their new shape model determinations. Each dot represents one trial run that samples all the local minima at a fixed rotation period (Eq. 2) within the searched interval. The vertical lines indicate the best-fit values. The horizontal line represents the χ2 threshold defined by Eq. 1. |
 |
Fig. A.2 Example of fits to the dense light curves for asteroid (2575) Bulgaria. All five light curves were obtained in the framework of this study (observed by Andrea Ferrero). |
 |
Fig. A.3 Example of fits to the sparse datasets for asteroid (2575) Bulgaria. The function f(α) is our fit of a semi-empirical phase function (Kaasalainen et al. 2002). The datasets (from top to bottom) are ASAS-SN V-band, ASAS-SN g-band, ATLAS c-band, and ATLAS o-band. |
 |
Fig. A.4 Examples of several shape models. The first panel (top) is the equatorial view with a 90° rotation offset; the third panel is north pole-on view. The shape models correspond to the first pole solution (λ1,β1) for each asteroid. The asteroids (from top to bottom) are (1159) Granada, (1700) Zvezdara, (2575) Bulgaria, and (2792) Ponomarev. |
Appendix B Tables
Asteroids whose spin poles are known from the literature.
Photometric observations of targets in the frame of the Ancient Asteroids campaign.
Rotation state properties and summary of the optical dataset for asteroids for which we derived a new shape solution or estimated the sense of rotation.
Updated shape models.
Physical properties of asteroids of the inner main belt primordial family presented in this study.
References
- Alvarez-Candal, A., Duffard, R., Lazzaro, D., & Michtchenko, T. 2006, A&A, 459, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Athanasopoulos, D., Bonamico, R., Van Belle, G., et al. 2021, Eur. Planet. Sci. Cong., 15, 335 [Google Scholar]
- Bellm, E.C., Kulkarni, S.R., Graham, M.J., et al. 2019, PASP, 131, 018002 [NASA ADS] [CrossRef] [Google Scholar]
- Bendjoya, P., Abe, L., Rivet, J.P., et al. 2012, in SF2A-2012: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. S. Boissier, P. de Laverny, N. Nardetto, R. Samadi, D. Valls-Gabaud, & H. Wozniak, 643 [Google Scholar]
- Berry, R., & Burnell, J. 2005, The Handbook of Astronomical Image Processing (USA: Willmann-Bell), 2 [Google Scholar]
- Berthier, J., Hestroffer, D., Carry, B., et al. 2009, Eur. Planet. Sci. Cong., 2009, 676 [Google Scholar]
- Bolin, B.T., Delbo, M., Morbidelli, A., & Walsh, K.J. 2017, Icarus, 282, 290 [CrossRef] [Google Scholar]
- Bonamico, R., & van Belle, G. 2021, Minor Planet Bulletin, 48, 210 [NASA ADS] [Google Scholar]
- Bottke, W.F., Vokrouhlickÿ, D., Walsh, K.J., et al. 2015, Icarus, 247, 191 [CrossRef] [Google Scholar]
- Bowell, E., Oszkiewicz, D.A., Wasserman, L.H., et al. 2014, Meteorit. Planet. Sci., 49, 95 [CrossRef] [Google Scholar]
- Broeg, C., Fernandez, M., & Neuhäuser, R. 2005, Astron. Nachr., 326, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Brož, M., & Morbidelli, A. 2013, Icarus, 223, 844 [CrossRef] [Google Scholar]
- Bus, S.J., & Binzel, R.P. 2002, Icarus, 158, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Carvano, J.M., Hasselmann, P.H., Lazzaro, D., & Mothé-Diniz, T. 2010, A&A, 510, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chang, C.-K., Ip, W.-H., Lin, H.-W., et al. 2015, ApJS, 219, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Cibulkova, H., Durech, J., Vokrouhlickÿ, D., Kaasalainen, M., & Oszkiewicz, D.A. 2016, A&A, 596, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cooney, W., Benishek, V., Pravec, P., et al. 2017, Central Bureau Electronic Telegrams, 4401, 1 [NASA ADS] [Google Scholar]
- Deienno, R., Walsh, K.J., & Delbo, M. 2021, Icarus, 357, 114218 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., Walsh, K., Bolin, B., Avdellidou, C., & Morbidelli, A. 2017, Science, 357, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., Avdellidou, C., & Morbidelli, A. 2019, A&A, 624, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DeMeo, F.E., Binzel, R.P., Slivan, S.M., & Bus, S.J. 2009, Icarus, 202, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Dermott, S.F., Li, D., Christou, A.A., et al. 2021, MNRAS, 505, 1917 [NASA ADS] [CrossRef] [Google Scholar]
- Durech, J., Kaasalainen, M., Warner, B.D., et al. 2009, A&A, 493, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 513, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durech, J., Hanuš, J., Oszkiewicz, D., & Vanco, R. 2016, A&A, 587, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durech, J., Hanuš, J., & Ah-Lagoa, V. 2018a, A&A, 617, A57s/ [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durech, J., Hanuš, J., Brož, M., et al. 2018b, Icarus, 304, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Durech, J., Hanuš, J., & Vanco, R. 2019, A&A, 631, A2 [Google Scholar]
- Durech, J., Tonry, J., Erasmus, N., et al. 2020, A&A, 643, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erasmus, N., Navarro-Meza, S., McNeill, A., et al. 2020, ApJS, 247, 13 [CrossRef] [Google Scholar]
- Erasmus, N., Kramer, D., McNeill, A., et al. 2021, MNRAS, 506, 3872 [NASA ADS] [CrossRef] [Google Scholar]
- Fauvaud, S., & Fauvaud, M. 2013, Minor Planet Bull., 40, 224 [NASA ADS] [Google Scholar]
- Fauvaud, S., & Fauvaud, M. 2014, Minor Planet Bull., 41, 143 [NASA ADS] [Google Scholar]
- Ferrero, A. 2021, Minor Planet Bull., 48, 215 [NASA ADS] [Google Scholar]
- Franco, L., Marchini, A., Bonnoli, G., et al. 2020a, ATel, 13590, 1 [NASA ADS] [Google Scholar]
- Franco, L., Marchini, A., Saya, L.-F., et al. 2020b, Minor Planet Bull., 47, 242 [NASA ADS] [Google Scholar]
- Gaia Collaboration, (Spoto, F., et al.) 2018, A&A, 616, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallaway, M. 2020, in An Introduction to Observational Astrophysics (Berlin: Springer), 169 [CrossRef] [Google Scholar]
- Gazeas, K. 2016, Rev. Mex. Astron. Astrofis. Conf. Ser., 48, 22 [NASA ADS] [Google Scholar]
- Goudis, C., Hantzios, P., Boumis, P., et al. 2010, ASP Conf. Ser., 424, 422 [NASA ADS] [Google Scholar]
- Hanuš, J., Durech, J., Brož, M., et al. 2011, A&A, 530, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Brož, M., Durech, J., et al. 2013a, A&A, 559, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Durech, J., Brož, M., et al. 2013b, A&A, 551, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Durech, J., Oszkiewicz, D.A., et al. 2016, A&A, 586, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Delbo, M., Ali-Lagoa, V., et al. 2018, Icarus, 299, 84 [CrossRef] [Google Scholar]
- Hanuš, J., Pejcha, O., Shappee, B.J., et al. 2021, A&A, 654, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A.W. 1994, Icarus, 107, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Hirayama, K. 1918, AJ, 31, 185 [Google Scholar]
- Kaasalainen, M., & Lamberg, L. 2006, Inv. Prob., 22, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., & Torppa, J. 2001, Icarus, 153, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Mottola, S., & Fulchignoni, M. 2002, in Asteroids III (Tucson: University of Arizona press), 139 [Google Scholar]
- Kochanek, C.S., Shappee, B.J., Stanek, K.Z., et al. 2017, PASP, 129, 104502 [NASA ADS] [CrossRef] [Google Scholar]
- Kryszczynska, A., La Spina, A., Paolicchi, P., et al. 2007, Icarus, 192, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerkvist, C.I., & Magnusson, P. 2011, NASA Planetary Data System, EAR [Google Scholar]
- Larson, S., Beshore, E., Hill, R., et al. 2003, BAAS, 35, 982 [NASA ADS] [Google Scholar]
- Lazzaro, D., Angeli, C.A., Carvano, J.M., et al. 2004, Icarus, 172, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Loera-Gonzalez, P., Olguin, L., Saucedo-Morales, J., & Nunez-Lopez, R. 2020, Minor Planet Bull., 47, 348 [NASA ADS] [Google Scholar]
- Lumme, K., & Bowell, E. 1981, AJ, 86, 1705 [NASA ADS] [CrossRef] [Google Scholar]
- Mahlke, M., Carry, B., & Denneau, L. 2021, Icarus, 354, 114094 [Google Scholar]
- Masiero, J.R., Carruba, V., Mainzer, A., Bauer, J.M., & Nugent, C. 2015, ApJ, 809, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P. 1997, National Optical Astronomy Observatory (Tucson: University of Arizona Press) [Google Scholar]
- Milani, A., Cellino, A., Kneževic, Z., et al. 2014, Icarus, 239, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Millis, R.L., Bowell, E., & Thompson, D.T. 1976, Icarus, 28, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Morate, D., de Leon, J., De Pra, M., et al. 2019, A&A, 630, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nesvornÿ, D., Brož, M., & Carruba, V. 2015, Asteroids IV, Identification and Dynamical Properties of Asteroid Families, eds. P. Michel, F.E. DeMeo, & W.F. Bottke (Tucson: University of Arizona Press), 297 [Google Scholar]
- Oey, J. 2010, Minor Planet Bull., 37, 53 [NASA ADS] [Google Scholar]
- Pal, A., Szakats, R., Kiss, C., et al. 2020, ApJS, 247, 26 [CrossRef] [Google Scholar]
- Paolicchi, P., & Kneževic, Z. 2016, Icarus, 274, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Polakis, T. 2021, Minor Planet Bull., 48, 158 [NASA ADS] [Google Scholar]
- Popescu, M., Licandro, J., Carvano, J.M., et al. 2018, A&A, 617, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pravec, P., & Harris, A.W. 2000, Icarus, 148, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A.W., & Michalowski, T. 2002, in Asteroids III (Tucson: University of Arizona Press), 113 [CrossRef] [Google Scholar]
- Pravec, P., Harris, A.W., Scheirich, P., et al. 2005, Icarus, 173, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A.W., Vokrouhlickÿ, D., et al. 2008, Icarus, 197, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G.R., Winn, J.N., Vanderspek, R., et al. 2015, J. Astron. Teles. Instrum. Syst., 1, 014003 [Google Scholar]
- Rubincam, D.P. 2000, Icarus, 148, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B.J., Prieto, J.L., Grupe, D., et al. 2014, ApJ, 788, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Statler, T.S. 2009, Icarus, 202, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, R.D. 2011, Minor Planet Bull., 38, 23 [NASA ADS] [Google Scholar]
- Stephens, R., & Warner, B.D. 2018, AAS/Div. Planet. Sci. Meeting Abs., 50, 417.03 [Google Scholar]
- Stephens, R.D., & Warner, B.D. 2019, Minor Planet Bull., 46, 449 [NASA ADS] [Google Scholar]
- Stephens, R.D., & Warner, B.D. 2020, Minor Planet Bull., 47, 224 [NASA ADS] [Google Scholar]
- Tholen, D.J. 1989, in Asteroids II, eds. R.P. Binzel, T. Gehrels, & M.S. Matthews (University of Arizona Press), 1139 [Google Scholar]
- Tonry, J.L., Denneau, L., Heinze, A.N., et al. 2018, PASP, 130, 064505 [NASA ADS] [CrossRef] [Google Scholar]
- Tsirvoulis, G., Morbidelli, A., Delbo, M., & Tsiganis, K. 2018, Icarus, 304, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlickÿ, D., Brož, M., Bottke, W.F., Nesvornÿ, D., & Morbidelli, A. 2006, Icarus, 182, 118 [CrossRef] [Google Scholar]
- Vokrouhlickÿ, D., Bottke, W.F., Chesley, S.R., Scheeres, D.J., & Statler, T.S. 2015, in Asteroids IV, eds. P. Michel, F.E. DeMeo, & W.F. Bottke (The University of Arizona Press), 509 [Google Scholar]
- Walsh, K.J., Delbo, M., Bottke, W.F., Vokrouhlickÿ, D., & Lauretta, D.S. 2013, Icarus, 225, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B.D. 2015, MPO Canopus software [Google Scholar]
- Warner, B.D., Harris, A.W., & Pravec, P. 2009, Icarus, 202, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Waszczak, A., Chang, C.-K., Ofek, E.O., et al. 2015, AJ, 150, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Zappala, V., Cellino, A., Farinella, P., & Knezevic, Z. 1990, AJ, 100, 2030 [CrossRef] [Google Scholar]
- Zappala, V., Bendjoya, P., Cellino, A., Farinella, P., & Froeschlé, C. 1995, Icarus, 116, 291 [CrossRef] [Google Scholar]
- Zellner, B., Tholen, D.J., & Tedesco, E.F. 1985, Icarus, 61, 355 [NASA ADS] [CrossRef] [Google Scholar]
For the search for the rotation period we fit 72 coefficients of the spherical harmonic expansion and start with ten different pole directions uniformly distributed on the sphere. The denser grid utilises 92 coefficients of the expansion and 48 input pole directions. The typical polyhedron representing the final shape solution contains about 1000 vertices and 2000 facets.
The only exception is asteroid (1159) Granada with the reported LCDB period of 77.28 h. However, this period adopted from the CdR database is preliminary and inconsistent with the period reported, for example, by Waszczak et al. (2015), which is similar to the value we derived.
All Tables
Photometric observations of targets in the frame of the Ancient Asteroids campaign.
Rotation state properties and summary of the optical dataset for asteroids for which we derived a new shape solution or estimated the sense of rotation.
Physical properties of asteroids of the inner main belt primordial family presented in this study.
All Figures
 |
Fig. 1 Primordial family members presented in proper semi-major axis vs. inverse diameter plane, along with the low-albedo asteroids located in the innermost region of the main belt. Panel A: the yellow diamonds indicate members with known spin pole from the literature. The plus signs, crossed, and squares are members for which there are dense light curves only from literature, from this work, and from both sources, respectively (see details in Table B.2). Panel B: left side of the V-shape of the primordial family. The prograde asteroids are shown in red and the retrograde asteroids in blue. |
| In the text | |
 |
Fig. 2 Distribution of the complete spin pole solutions for the primordial family members. The main plot is a sinusoidal equal-area cartographic representation, where the vertical grey lines define the longitude (λ) and the horizontal curves define the latitude (β). The right histogram represents the latitude (β) of prograde (red) and retrograde (blue) rotators. The bottom histogram represents the longitude (λ) of prograde (red) and retrograde (blue) rotators. The specific values for each asteroid are shown in Tables B.3 and B.4. |
| In the text | |
 |
Fig. 3 Histogram of spin rate for members of the primordial asteroid family. The prograde rotators are in red and the retrograde in blue. The light grey bars represent the primordial family members whose rotational period is known either from this study or the literature. |
| In the text | |
 |
Fig. A.1 Typical periodograms of six different asteroids and their new shape model determinations. Each dot represents one trial run that samples all the local minima at a fixed rotation period (Eq. 2) within the searched interval. The vertical lines indicate the best-fit values. The horizontal line represents the χ2 threshold defined by Eq. 1. |
| In the text | |
 |
Fig. A.2 Example of fits to the dense light curves for asteroid (2575) Bulgaria. All five light curves were obtained in the framework of this study (observed by Andrea Ferrero). |
| In the text | |
 |
Fig. A.3 Example of fits to the sparse datasets for asteroid (2575) Bulgaria. The function f(α) is our fit of a semi-empirical phase function (Kaasalainen et al. 2002). The datasets (from top to bottom) are ASAS-SN V-band, ASAS-SN g-band, ATLAS c-band, and ATLAS o-band. |
| In the text | |
 |
Fig. A.4 Examples of several shape models. The first panel (top) is the equatorial view with a 90° rotation offset; the third panel is north pole-on view. The shape models correspond to the first pole solution (λ1,β1) for each asteroid. The asteroids (from top to bottom) are (1159) Granada, (1700) Zvezdara, (2575) Bulgaria, and (2792) Ponomarev. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



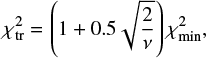
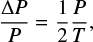
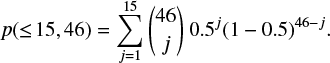
![$ {\tau _{{\rm{reor}}}} = 0.845{\left( {{5 \over {{P_{\left[ h \right]}}}}} \right)^{{5 \mathord{\left/ {\vphantom {5 6}} \right. \kern-\nulldelimiterspace} 6}}}{\left( {{{{D_{\left[ {{\rm{km}}} \right]}}} \over 2}} \right)^{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-\nulldelimiterspace} 3}}}\left[ {{\rm{Gyr}}} \right]. $](/articles/aa/full_html/2022/10/aa43905-22/aa43905-22-eq15.png)