| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 24 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202142835 | |
| Published online | 19 August 2022 | |
A proposed network of gamma-ray burst detectors on the global navigation satellite system Galileo G2★
1
Max-Planck Institute for extraterrestrial Physics,
Giessenbachstr. 1,
85748
Garching, Germany
e-mail: jcg@mpe.mpg.de
2
Technical University of Munich, Institute for Astronomical and Physical Geodesy,
Arcisstr. 21,
80333
Munich, Germany
3
Ioffe Institute,
Polytechnikheskaya 26,
St. Petersburg
194021,
Russia
Received:
5
December
2021
Accepted:
17
May
2022
The accurate localization of gamma-ray bursts (GRBs) remains a crucial task. Historically, improved localizations have led to the discovery of afterglow emission and the realization of their cosmological distribution via redshift measurements; however, a more recent requirement comes with the potential of studying the kilonovae of neutron star mergers. Gravitational wave detectors are expected to provide locations to not better than 10 square degrees over the next decade. With their increasing horizon for merger detections the intensity of the gamma-ray and kilonova emission also drops, making their identification in large error boxes a challenge. Thus, a localization via the gamma-ray emission seems to be the best chance to mitigate this problem. Here we propose to equip some of the second-generation Galileo satellites with dedicated GRB detectors. This saves costs for launches and satellites for a dedicated GRB network, the large orbital radius is beneficial for triangulation, and perfect positional and timing accuracy come for free. We present simulations of the triangulation accuracy, demonstrating that short GRBs as faint as GRB 170817A can be localized to 1 degree radius (1σ).
Key words: gamma-ray burst: general / gravitational waves / instrumentation: detectors / space vehicles: instruments
© J. Greiner et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
The coincident detection of gravitational waves (GWs) from a binary neutron star merger with aLIGO/Virgo and shortlived gamma-ray (GR) emission with Fermi-GBM (called GW 170817) in August 2017 is a milestone for the establishment of multi-messenger astronomy (Abbott et al. 2017), which is the measurement of electromagnetic radiation, gravitational waves, and/or particles or neutrinos from the same astrophysical source. Merging neutron stars (NSs) represent the standard scenario (Eichler et al. 1989) for short-duration (<2 s) gamma-ray bursts (sGRBs) which are produced in a collimated relativistically expanding jet with an opening angle of a few degrees and a bulk Lorentz factor Γ of 300-1000. While the aLIGO detection is consistent with predictions, the measured faint gamma-ray emission from GW 170817A is about 1000x less luminous than known short-duration GRBs. Hence, the presence of this sGRB in the local Universe is either a very rare event or points to a dramatic misunderstanding of the emission properties of sGRBs outside their narrow jets. By now we know that the jet in this GRB had an opening angle of <5°, but we observed it from ~20–30° off-axis (Mooley et al. 2018). In all previous models, no emission was predicted to occur outside the opening angle.
Thus, the previous estimates of the volume density of NS-NS mergers were also wrong, and need to be corrected (Burgess et al. 2020). This has important implications for our understanding of the chemical evolution of our Galaxy and the Universe, as NS-NS mergers are believed to be the main source of heavy elements (Kasen et al. 2017), known as r-process elements (like gold and platinum). This material is expelled both during the tidal disruption of the NSs and through winds during the subsequent disk accretion onto the compact core. Further progress in our understanding of NS-NS mergers will depend on measurements in the electromagnetic regime, and these in turn will only be possible if the localizations of these events can be reduced to a few square degrees on the sky. While there are several large-field-of-view optical sky surveys, covering up to several thousand square degrees, the challenge is to find the kilonova among the many other transient sources. Future NS-NS mergers will likely all be at a greater distance than GW 170817, and thus their kilonova much fainter. Already the four NS-NS merger events from 2019–2020 were three times more distant than GW 170817. None of these was detected in gamma rays, and their expected optical emission would have peaked at 23rd mag (if at the same luminosity as GW 170817). Except for one particularly poor localization, the error regions of the other three events encompass 2300–14 700 square degrees each (Abbott et al. 2022). At the expected optical brightness, there will be about 3-60 transient alerts per square degree down to 21 mag (Masci et al. 2019), or estimated 5x more at 23rd mag, against which the kilonova will have to be identified. Thus, a prerequisite to identify the kilonova is the fast and precise localization of the GW/GR event.
Expectations for the fourth observing run O4 are 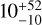 BNS mergers, with a median
BNS mergers, with a median 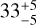 square degrees localization. Although it is not likely to occur before 2026 (Abbott et al. 2020), the GW detector network of LIGO, Virgo, and KAGRA is looking forward to including LIGO-India, which promises a reduction of the GW error regions to < 10 square degrees. Further
square degrees localization. Although it is not likely to occur before 2026 (Abbott et al. 2020), the GW detector network of LIGO, Virgo, and KAGRA is looking forward to including LIGO-India, which promises a reduction of the GW error regions to < 10 square degrees. Further
reduction of the localization error is foreseen with the Einstein Telescope in Europe, or the Cosmic Explorer in the USA, both not earlier than the mid-2030s.
Thus, accurate localization of the GW events should be sought elsewhere. Gamma rays provide an interesting alternative, at least for those NS-NS mergers whose jets would be broadly pointed toward us. With γ-ray emission at large off-axis angles as in GRB 170817A, up to 30% of mergers will be simultaneously detectable in γ rays (Howell et al. 2019; Burgess et al. 2020). Obviously, accurate measurements of many GRBs will be beneficial for other science questions beyond kilonova physics, such as (1) the structure of jets in GRBs (e.g., Janka et al. 2006) and the origin of the off-axis emission, which is distinctly different to on-axis emission (Begue et al. 2017), or (2) the potential emission of high-energy neutrinos as measured by IceCube (Aartsen et al. 2013), promising a potential triple messenger (i.e., electromagnetic radiation, gravitational waves, and particles). Kimura et al. (2017) estimated that GRB 170817A could have been detectable by IceCube if the jet had been viewed on-axis instead of ~30° off-axis.
Here, we propose adding a GRB detector on some of the next two dozen second-generation Galileo satellites (G2) in order to improve the localization capability for short GRBs to the one-degree level, reducing the error region by a factor of 100-1000.
Comparison of different γ-localization methods in the 200–2000 keV band.
2 Prospects of Accurate GRB Localization
2.1 Challenges of Short GRBs
Short-duration GRBs (sGRB) have three properties which make their localization in large numbers more difficult than that of long-duration GRBs: (1) their short duration, on the order of 0.01–2 s, implies that their observable fluence is on the order of 5–50× smaller than in long-duration GRBs; (2) their peak fluxes during their maximum spike are typically a factor of 2 smaller than long-duration GRBs (though at very short timescales they are similar), making the discrepancy from (1) even larger; (3) sGRBs are also harder, with their spectral peak at higher energies. This implies that the flux at soft gamma rays (20–100 keV) is smaller than that in long-duration GRBs even if the energy-integrated flux is equal.
These factors together imply detection and localization disadvantages in various detector types. In coded-mask imagers like Swift/BAT or INTEGRAL/IBIS, the mask elements become increasingly transparent at higher energy, leading to shadows that are less “sharp”, and thus detection sensitivity. Thus, the ratio of long to short GRBs in Swift/BAT is about 10:1, while it is 10:2.5 in Fermi/GBM. In counting experiments like Fermi/GBM, short spikes can more easily be mistaken for noise spikes. Moreover, at the higher photon energies, the cosine dependence of the effective area is much less pronounced in detectors with slab-like scintillators, due to the larger absorption probability at inclined incidence angles.
2.2 Localization Methods
Independent of the different γ-ray detection technology (gas detectors, scintillation detectors, or solid-state detectors) are the methods with which gamma rays can be localized. The four main methods with their advantages and disadvantages are described below (Table 1). The summarizing statement is that large field-of-view (FOV) instruments with high GRB detection rates operate at softer energies, not appropriate for short-duration GRBs, while detectors at higher energies suffer from either bad localization capabilities or low detection rates. Over the last 20 years, all techniques except triangulation have been used in space applications with the maximum possible capability.
Triangulation
One of the first methods of localizing sources in gamma-ray astronomy was triangulation, measuring the time difference of a signal arriving at different detectors. This was the method used by the Vela satellites in the 1960s to verify the Nuclear Arms Treaty between the USA and Russia, which then led to the discovery of GRBs. This method requires four detectors or satellites, and accurate knowledge of the time and the relative position of the detectors; it allows the whole sky to be covered, and provides localizations in the arcsec-arcmin range for widely spaced satellites (Hurley et al. 2017). However, since GRB detectors on interplanetary spacecraft are auxiliary instruments, and thus small, triangulation offers substantial improvements.
Orientation-dependent Rate Measurements
Measuring relative rates of orientation-dependent γ-ray detectors, typically scintillation crystals, was used for GRB localizations with the BATSE instrument on the Compton Observatory, and is currently being used with the GRB Monitor (GBM) on Fermi. This method requires from four to six detectors with different orientations on the sky, and the localization accuracy is on the degree-scale at best (Berlato et al. 2019).
Coded-mask Imaging
Coded-mask imaging also allows a 2D reconstruction on the sky, and has frequently been used over the last 30 yr (e.g., as Granat, Swift, and INTEGRAL). It also requires large detector sizes (m3 scale) and has a restricted field of view, but allows localizations in the arcmin range.
Photon-by-photon Imaging
Photon-by-photon imaging provides proper imaging (2D reconstruction) of individual photons on the sky. This method was used by the COMPTEL telescope in the 1990s. Improved versions require electron tracking, and thus will be appropriate for large and heavy telescopes. However, the localizations (degrees) and fields of view (up to 70° radius) are advantageous.
2.3 Missions with GRB Capabilities
Except for planned missions beyond 2027, the near future can be summarized by the following three strategies: (i) new large(r) missions just represent a replication of existing missions, such as GECAM (replicating Fermi/GBM) and SVOM (replicating Swift); (ii) new small(er) missions are mainly driven by enhancing the sky coverage, not improving localizations; (iii) a euphoric engagement in CubeSat swarms using triangulation, which will not provide accurate (degree) localizations, due to their size and low-Earth orbit (LEO). All of these strategies will not change the lack of well-localized short-duration GRBs. The operational and planned (to our knowledge) missions are briefly sketched out below.
The dedicated GRB mission Swift (USA) uses a coded-mask imager called the Burst Alert Telescope (BAT) in the 15–150 keV range for GRB localization, to an accuracy of 3 arcmin radius (Barthelmy et al. 2005). It has a 1.4 steradian field of view (half-coded), and detects about 100 GRBs yr−1, predominantly as rate triggers (excess counts in the total rate of a detector module). Due to the soft energy band and the combined noise of the 32768 CdZnTe detector cells, the detection rate of short-duration GRBs is only ~10% (10 sGRBs yr−1).
The Fermi gamma-ray observatory (USA) features a Gamma-ray Burst Monitor (Fermi/GBM) aimed at localizing GRBs outside of the zenith-facing field of view of the prime instrument, the Large Area Telescope (LAT; 100 MeV–10 GeV). The GBM consists of two subsystems: a collection of 12 Nal scintillation detectors for the energy range 8–500 keV, and two thick BGO scintillation detectors for the high-energy range up to 40 MeV (Meegan et al. 2009). It is currently the most prolific GRB detector, with the detection and localization of about 240 GRBs yr−1, among those about 40 short-duration GRBs (von Kienlin et al. 2020). The localization method used during the lasts 30 years (based on orientation-dependent rates in different detectors) came with large systematic errors (Connaughton et al. 2015). The cause of these systematics have recently been understood (Burgess et al. 2018), but even after correction the typical error regions have 5°–10° radius (Berlato et al. 2019), with the 17° error radius for GRB 170817A completely dominated by the statistical error.
The Interplanetary Network (IPN) is the logistic combination of different spacecrafts equipped with GRB detectors. The locations of GRBs are determined by the comparison of the arrival times of the event at the locations of the GRB detectors. The precision is proportional to the distance of spacecraft separations, so that the localization accuracy of a network with baselines of thousands of light-seconds can be equal or superior to that of any other technique (Hurley et al. 2017). A major disadvantage of the IPN method is the one to two day delay in the downlink of the GRB data from the spacecraft. At present, the main IPN contributors are Konus-WIND, Mars Odyssey, INTEGRAL, RHESSI, Swift, AGILE, BepiColombo, and Fermi/GBM.
The European gamma-ray satellite INTEGRAL can detect GRBs with three of its instruments: in the field of view of ISGRI (a 15–300 keV coded-mask imager with a few arcmin localization accuracy) or SPI (a 200–8000 keV coded-mask imager with degree localization accuracy but very high-energy resolution), and the SPI anti-coincidence system ACS (working at >80 keV). Due to the small field of view of ISGRI and SPI, their combined GRB detection rate is only ~10 GRBs yr−1 (Bosnjak et al. 2014). The ACS detects about 150 GRBs yr−1, but has no localization capability (Savchenko et al. 2012).
CALET (Japan), Insight-HXMT (China), and AstroSat/CZTI (India) are operational satellite experiments with the capability of detecting GRBs in their particle detectors or shields, without localizations. Due to their low-Earth orbit, they do not provide useful triangulation constraints, and thus are not (or very rarely) used in the IPN.
GECAM (China)
The Gravitational Wave Electromagnetic Counterpart All-sky Monitor (GECAM) is a twin spacecraft mission to monitor GRBs coincident with GW events (Zheng & Xiong 2019). With a dome-shaped distribution of multiple scintillators it reaches an effective area (and energy range) similar to that of Fermi/GBM. The planned main advantage was the ≈ 100% sky coverage due to the 180 deg phasing of the two spacecrafts in their orbit. Launched on 2020 December 9, only one of the spacecrafts returns data.
GRBAlpha (Hungary/Czech/Slovakia/Japan)
GRBAlpha, launchedon2021 March 22, is a1UCubeSatdemonstrationmission (Pal et al. 2020) for a future CubeSat constellation (Werner et al. 2018). The detector consists of a 75 × 75 × 5 mm3 CsI scintillator read out by a SiPMarray, covering the energy range 50–1000 keV.
BurstCube (USA) is a planned 6U CubeSat to be released into low-Earth orbit from the ISS to detect GRBs. The instrument is composed of four CsI scintillator plates, each 9 cm in diameter, read out by arrays of silicon photo-multipliers (Smith et al. 2019). It reaches an effective area of 70% of Fermi/GBM at 15° incidence, but the localization accuracy is substantially worse, with 7° radius at best for the brightest GRBs (launch 2022).
SVOM (China/France)
The Space-based multi-band astronomical Variable Objects Monitor (SVOM) is a Swift- and Fermi-like mission with both, a wide-field-of-view γ-ray detector for GRB localization and a separate GRB detector for 15–5000 keV spectroscopy, and an X-ray and an optical telescope for rapid follow-up of the GRB afterglow (Yu et al. 2020). A total of 60 GRBs yr−1 will be localized to 10′ accuracy with a coded-mask telescope with a 89° × 89° field of view, working in the 4–250 keV band. Due to this soft energy coverage the focus is on high-redshift GRBs (launch late 2023).
HERMES (Italy) is an Italian-led project to launch 100 Cube-Sats with X-ray/γ-ray detectors to localize GRBs, and to derive limits on quantum gravity (Fuschino et al. 2019). Presently, six 3U CubeSats are funded for a two-year pathfinder mission, with ~56 cm2 effective area per CubeSat in the 3–1000 keV band (launch 2022). The anticipated localization accuracy for transients with millisecond (ms) variability is 3° for the pathfinder and 10 arcsec for the full fleet in LEO (Fuschino et al. 2019; Burderi et al. 2020, 2021), though this seems very optimistic given the detection of 0.05 ph/s even for the brightest bursts per CubeSat.
Glowbug (NASA) is a funded small (30 × 30 × 40 cm3) satellite to detect GRBs and other transients in the 30 keV–2 MeV band (Grove et al. 2020). With an effective area about 2.5× that of Fermi/GBM, about 70 short GRBs are expected per year. The localization accuracy is expected to be slightly better than GBM, in the 5° (1σ radius) range. The nominal lifetime is 1 yr (launch 2023).
POLAR-2 (China/Switzerland; launch 2024) is a dedicated GRB polarimeter to be flown on board China’s space station. With a field of view of half the sky, the position determination will be a few degrees only. Detailed polarization measurements are expected for 50 GRBs yr1, though more GRBs are expected to be detected (Kole 2019).
COSI (USA)
The Compton Spectrometer and Imager is an approved NASA/SMEX mission, working in the 0.2–5 MeV band, and scheduled for launch in 2025. Its wide field of view of 3 sr will allow the detection of 7–10 short GRBs per year, at subdegree localization (Tomsick et al. 2021).
eXTP (China/ESA)
The enhanced X-ray Timing and Polarimetry mission (eXTP) will study the X-ray sky with four different instruments, covering the 0.5–50 keV band. It will likely be the first to simultaneously measure the spectral-timing-polarimetry properties of cosmic sources (launch 2027). Relevant for GRB detection is the Wide-field monitor (WFM): with a field of view of 1 sr (fully coded) the detection of 16 GRBs/day is predicted (Zhang et al. 2017), the brighter ones with 1 arcmin localization accuracy. While this GRB rate is far above the predicted total number of GRBs in the Universe (~5×), the soft energy response of the WFM implies a small fraction of short GRBs (5%–10%).
HSP (USA)
The proposed High Resolution Energetic X-ray Imager SmallSat Pathfinder (HSP) is a wide-field hard X-ray (3–200 keV) coded aperture telescope with 1024 cm2 CdZnTe detectors and a Tungsten mask (Grindlay 2020). With 4′.7 resolution covering 36° × 36° (full width at half maximum, FWHM), HSP localizes transients and GRBs within <30″ in less than 10 min. (launch >2025).
In summary, there is a need to more accurately localize short-duration GRBs. We propose that GRB triangulation with the Galileo satellite network provides such an opportunity.
3 The Galileo System as a Perfect Host for Triangulation
The Galileo Global Navigation Satellite System (GNSS) has five parameters which makes it a nearly ideal satellite constellation for triangulation: (i) all satellites are synchronized with a very accurate atomic clock, ensuring time-stamps for the GRB signal at the 10−9 s level; (ii) the satellites are distributed over three orbital planes, perpendicular to each other, making triangulation positions close to round; (iii) the position knowledge of all satellites is accurate to submeter levels, and thus does not contribute to the error budget in realistic GRB measurements, similar to the timing; (iv) the knowledge of the orientation of each satellite is known to better than 1°, removing any ambiguity in the relative rate measurements for GRBs; (v) the orbital radius is large enough that one can realistically expect subdegree localizations, but small enough that light travel time distances are short and communication (data transfer) is quick. This differentiates it from the canonical IPN, where the baseline is much longer, and thus allows arcmin-scale localizations, but the triangulation can only be done 1–2 days after the GRB.
The first satellites of the present Galileo constellation were launched on 2011, October 21. Today, 26 satellites are in orbit, two of which are unusable (one with technical problems, one declared as spare due to issues with clocks) and two on non-nominal orbits due to launch failure of the third rocket stage but otherwise fully operational and usable. In December 2016, the Initial Service Declaration was announced. Currently
12 satellites, known as the Batch 3 satellites, are under production; deployment started in 2021. As the design lifetime of Galileo satellites is 12 yr, the constellation has to be replenished in the coming years. The first satellites of this second generation will then follow starting in 2024.
The Galileo constellation is a Walker constellation (Walker 1984). This constellation type is characterized by the three numbers 24, 3, and 1:
-
n1
Total number of satellites (i.e., eventually 24 satellites), equally distributed over the orbital planes;
-
n2
Number of equally spaced orbital planes (i.e., 3), with eight satellites each;
-
n3
Relative spacing between satellites in adjacent planes. The difference in argument of latitude (in degrees) for equivalent satellites in neighboring planes is equal to n3 * 360/n1.
The revolution period corresponds to 17 revolutions in 10 sidereal days (i.e., 14h04m). With a semimajor axis of 29.600 km, the orbital inclination is 56°. For current Galileo satellites the eccentricity is below 0.0007 except for the two satellites on non-nominal orbits that have an eccentricity of 0.166. Figure 1 shows the histogram of pair-wise distances between Galileo satellites in a Walker 24/3/1 constellation. The maximum distance is 59 000 km (i.e., the orbit diameter), while the mean distance is 42000 km. The peaks in the figure indicate the constant distances between satellites in the same orbital plane.
Orbits and clock corrections for Galileo satellites are available with high precision in real time. While precise orbits at a level of a few centimeters and clock corrections at below the nanosecond level are available in postprocessing, submeterorbits and clock corrections of a few nanoseconds are available through the broadcast messages that are updated every 10 minutes. While the eccentric satellites show slightly larger broadcast orbit errors, mainly along-track, the rms of broadcast orbit errors for the other satellites is at a level of 32 cm (12.5 cm radial, 25 cm along-track, 15 cm cross-track).
In contrast, the broadcast clock quality of eccentric Galileo satellites is comparable to the other satellites. The rms of the difference is 0.50 ns. For GRB triangulation it can thus be assumed that perfect positions and time tagging are known in real time at any given time.
The attitude of the Galileo satellites is a nominal yaw steering in order to point the navigation antenna (body-fixed z-axis) to the center of the Earth, and the solar panel axis (y-axis) is perpendicular to the direction of the Sun. The Sun is thus always located in the body-fixed x – z plane. While the positive x-surface is always illuminated by the Sun, the negative x-surface constantly points to dark sky. The nominal attitude is controlled by Earth and Sun sensors to below 0° 1, except for non-nominal noon and midnight yaw maneuvers, if the Sun is closer to the orbital plane than about 2° for the 4 in-orbit verification satellites (2011/2012) and about 4° for the other satellites (since 2014), and the nominal yaw rate would exceed the maximum hardware rate of 0°2 s−1. The negative z-axis is always pointing in zenith direction with a precision below 0° 1.
 |
Fig. 1 Histogram of pair-wise distances between Galileo satellites. The peaks indicate constant distances between satellites in the same orbital plane. |
4 Triangulation: Methods and Prospects
The triangulation method uses measurements of differences of arrival times of the same signal (GRB) at different clocks (each on a different satellite). In general, time differences between three independent satellite pairs are needed to derive a unique position on the sky, and not all these satellites will be in the same plane.
The relation cos θ = c·t/d holds for the time difference of a signal between two satellites. Under the simplifying assumption of perfect satellite clocks and perfectly known satellite positions, the width of the annulus ∆θ is obtained as the derivative of the above equation; this means that it is just determined by the error ∆t with which the time delay t between the two signals (light curves) can be measured:
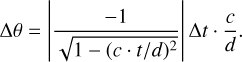 (1)
(1)
There are two possible approaches to triangulation. In the first, one can compare two light curves to find the time lag (i.e., a simple cross-correlation of background subtracted time series) (Hurley et al. 2013; Pal’shin et al. 2013). Each satellite pair results in one time lag, and a corresponding triangulation ring. Combining multiple (>3) pairs then provides a unique sky position as the overlap of these triangulation rings. Cross-correlation is computationally fast, but suffers from several drawbacks (Burgess et al. 2021): (i) they only work for binned light curves, at fixed binning; (ii) no mathematical method exists to estimate the proper error of the cross-correlation; (iii) the approximation of χ2 rarely holds, in particular when small bin sizes are chosen in order to increase the temporal accuracy; (iv) the subtraction of two Poisson rates results in Skellam rather than Poisson distributed data, often leading to over-confidence; (v) it cannot take into account light curves taken at different energies. In the second approach, one can forward-fold an identical model through the (different) response of each detector and fit each observed light curve (Burgess et al. 2021). This technique is computationally expensive, but offers the major advantage that it produces a complete posterior probability distribution allowing for a very precise estimate of the uncertainty formally in ∆θ, but due to the forward-folding directly in sky coordinates ∆RA, ∆Dec. This nazgul code (Burgess et al. 2021) has been made publicly available1.
5 Simulation Setup
In order to test each of the localization methods and verify their performance for different satellite configurations, we developed a simulation framework utilizing the Python package PyIPN2. This package allows for the generation of synthetic GRB light curves as seen by detectors distributed within the solar systems. We added a procedure to this framework to generate realistic light curve shapes and detector configurations that mimic the orbit of the Galileo constellation. Below we detail the setup and procedure for the generation of mock data sets which allow us to test our methods.
5.1 Simulating GRB Light Curves
The simulation of the triangulation capability of a network of GRB detectors requires creating mock GRB light curves, which then hit differently oriented detectors. These mock light curves cover a peak flux range as bright as those seen with previous experiments (CGRO/BATSE, Swift/BAT, Fermi/GBM), and down to our proposed sensitivity limit of 1 × 10−7 erg cm−2 s−1 in the 25–150 keV band. We pick the 256 ms timescale for the peak flux as a compromise between being short enough to cover spikes in short-duration GRBs and being general enough also for long-duration GRBs.
Gamma-ray burst light curves are generally very complex, and unique for each GRB. In many cases the variability timescale is significantly shorter than the overall burst duration. Only in a minority of GRB light curves there is only one peak, with no substructure. The most straightforward way is to assemble GRB light curves by the superposition of different pulses. We assume that candidate pulses can be modeled with the Norris et al. (1996, 2005) empirical functional pulse form
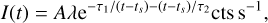 (2)
(2)
where t is time since trigger, A is the pulse amplitude, ts is the pulse start time, τ1 and τ2 are characteristics of the pulse rise and pulse decay, and the constant 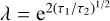 . The pulse peak occurs at time
. The pulse peak occurs at time 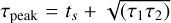 . Typically, the rise times in individual GRBs are very short (steep rise), and the decay times are substantially longer in most times. Thus, for single-pulse GRBs, the decay time τ2 scales with the T90 duration of a GRB.
. Typically, the rise times in individual GRBs are very short (steep rise), and the decay times are substantially longer in most times. Thus, for single-pulse GRBs, the decay time τ2 scales with the T90 duration of a GRB.
In order to implement the stochastic nature of the light emission process, and to incorporate unavoidable background at the measurement process, individual photon events are sampled according to an inhomogeneous Poisson distribution following the intrinsic pulse shape specified. The photon arrival times are sampled via an inverse cumulative distribution function rejection sampling scheme (Rubinstein & Kroese 2016). As the rate for the signal evolves with time, a further rejection sampling step is implemented that thins the arrival times according to the evolving light curve. This is done by first sampling a waiting time t and computing the light curve intensity I(t). Another draw from p ∈ {0, 1} is made and the sample is accepted if p ≲ I(t) (Burgess et al. 2021).
The cross-correlation of two light curves depends crucially on the intensity of the GRB above background, and the structure of the light curves. We therefore need a sample of different light curves. In order to create a realistic sample, we need to make sure that we reproduce a rough −3/2 logN-logS intensity distribution between the brightest GRBs seen so far (2 × 10−4 erg cm−2 s−1) and our aimed-at limit of 1 × 10−7 erg cm−2 s−1. For a canonical GRB spectrum below Epeak, meaning a power-law spectrum with a slope in the range −0.9 to −1.1 (long/soft) and 0.0 to −0.2 (short/hard), the following conversion holds for the 25–150 keV band with a detector size of 3600 cm2 (see below):
1 × 10−7 erg cm−2 s−1 = 0.65 ± 0.10 ph cm−2 s−1. Thus, we substitute the sampling over the 2 × 10−4–1 × 10−7 erg cm−2 s−1 range by that over 1300–0.65 ph cm−2 s−1. We also need to reproduce the observed T90 duration distribution of GRBs (Kouveliotou et al. 1993) and some realistic distributions between single- and multi-pulse light curve structures. We can assemble multi-pulse light curves by overlapping multiple single pulses, each with the shape used by Norris et al. (1996), but with different parameters and properly delayed with respect to each other.
For the last we implemented a pulse avalanche, a linear Markov process, as proposed by Stern & Svensson (1996) and described in detail in Appendix A. Example light curves with this simulation setup are shown in Fig. 2.
Energy-dependent effects in GRB light curves are ignored. Conceptually, we treat our proposed energy band of 25–150 keV as a mono-energetic band.
 |
Fig. 2 Example mock light curves of the long-duration class created with the pulse avalanche description of Norris-like pulses. |
5.1.1 Light Curve Detectability by Different Detectors
The steps given above provide theoretical light curves of GRBs (as emitted) that are representative in intensity distribution, duration distribution, and pulse structure of the GRBs as measured over the last 30 yr. These light curves are now being measured by identical detectors on a number of Galileo satellites. While the details of the Galileo satellite network is described later, three effects combine to establish the measured light curves. First, since the detectors are oriented in different directions, each will detect photons according to the cosine between the scintillator normal (we adopt thin but large-area scintillator plates as the baseline) and the GRB; second, the detector will measure quasi-isotropic γ-ray background, which has the effect of washing out low-intensity features; and third, in the case of multiple detector plates per satellite, the sensitivity can be improved by co-adding the data. However, this helps only for a certain incidence angle range since the GRB signal varies with the incidence angle, but the isotropic background does not.
An example of such a set of measured light curves for a given GRB and differently-oriented detectors is given in Fig. 3. These are the final measured light curves (in counts s−1) over a certain duration in the 25–150 keV band, which are then used for triangulation.
5.1.2 Implementation of the Discrete Correlation Function
A modified version of the discrete correlation function method (Edelson & Krolik 1988) was implemented in PyIPN with the
following three parts. First, the model is initialized by setting a GRB position and defining all detectors. The actual simulation creates the GRB signal (light curve) and computes the arrival times at the detectors as detailed above.
The final step performs the cross-correlation and computes the center point and opening angle of the circle for a specified pair of detectors. Rather than relying on mathematical covariance matrix estimations of uncertainty, cross-correlation methods heuristically derive uncertainties in one of two ways. First, the discretized time bins of the light curve yield discrete estimates of the time lag between each pair of light curves. For each value a pseudo-χ2 statistic3 is derived for a grid of values which yield a rough parabolic shape. The minimum of these values is taken as the true time lag (best fit). The 1, 2, and 3σ uncertainty regions are recovered by moving up the grid of statistics at the appropriate levels and reading off the implied time lags. This has several drawbacks. First, the best-fit time lag can never be below the timing resolution of the light curve. Additionally, the uncertainties are locked to the resolution of the grid and can thus easily be over- or underestimated. To get around this, another heuristic can be introduced. One can fit this grid of uncertainties with a parabolic shape to effectively interpolate to finer timing resolution. While this alleviates the issues with discretization in the previous method, it introduces the problem that the interpolation has an associated uncertainty that is not accounted for. Moreover, the chosen shape of this parabolic fit cannot incorporate asymmetries in the grid and thus can easily over- or underestimate the true uncertainty. However, given the lack of a mathematically strict method, we use this procedure, but keep the problems in mind.
 |
Fig. 3 Light curves of the same GRB as seen with a flat detector plate from different incidence angles. The labels in each plot give the angle under which the GRB impinges on the detector plane. With increasing angle, the effective area shrinks with the cosine of the angle, while the background remains the same. The “mother” light curve of this GRB was generated with a pulse avalanche scheme (see Sect. 5.1.1). |
5.2 Gamma-ray Background in the Galileo Orbit
The background that a γ-ray detector (whether scintillation detector or other type) experiences in space is composed of several different components (e.g., Weidenspointner et al. 2003, 2005; Wunderer et al. 2006; Cumani et al. 2019). In the 10–250 keV band, the most important components are the extra-galactic diffuse γ-ray background, Earth albedo photons (for
LEO), Galactic cosmic-ray protons, and radioactive decay of activated detector and spacecraft material due to cosmic-ray bombardment. For a satellite in MEO, the diffuse γ-ray background dominates below 100 keV, while at ~200 keV the rising proton contribution has reached the level of the diffuse γ-ray background. We therefore just incorporate the extragalactic diffuse γ-ray background in our simulations.
We adopt the following smoothly broken power law for the diffuse background spectrum (Ajello et al. 2008)
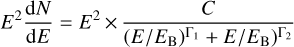 (3)
(3)
with the following constants: C = 0.102 ± 0.008 ph cm−2 s−1 sr−1keV−1, Γ1 = −1.32 ± 0.02, Γ2 = −2.88 ± 0.02, and a break at EB = 30.0 ± 1.1 keV. Integrating over the 25–150 keV energy range and the 2π sky coverage is consistent with both the Konus-Wind (Aptekar et al. 1995) and the Fermi/GBM (Burgess et al. 2018) measurements, and leads to ≈4 cts cm−2 s−1. This background rate is then added to the scaled light curve generated with the pulse avalanche method (see previous subsection).
 |
Fig. 4 Half-width error Δθ (1σ) of the triangulation annulus for a GRB arriving at a pair of satellites 42 000 km apart (corresponding to the mean of Fig. 1). Indicated are the different delay times (bottom x-axis) and angles relative to the line connecting the two satellites (top x-axis) for different accuracies Δt of 1, 3, 10 and 50 ms with which the time delay can be measured. |
5.3 Required Detector Timing
With a dedicated GRB detector on the Galileo satellites, we can dramatically improve the localization accuracy. Using the formal triangulation error (see Eq. (1)), it is easy to compute the required temporal resolution, usually the bin size in the classical scheme, for a perfect system with satellites at known distances. Figure 4 shows that sub-ms accuracy in the determination of the time delay is required to reach subdegree localization accuracy with two satellites at a distance of 42 000 km (which corresponds to the mean for Galileo’s Walker constellation; see Fig. 1). For comparison, the Anti-Coincidence system of the INTEGRAL spectrometer (SPI-ACS; top curve) has a time resolution of 50 ms, and the shortest binning of Fermi-GBM is 64 ms, with individual events time-tagged at 2 µs.
Figure 4 only applies to a perfect system. As discussed below, the classical triangulation method with its use of a cross-correlation of binned data sets does not provide a mathematically self-consistent error handling. In contrast, the alternative method by Burgess et al. (2020) does, but lacks the beauty of a simple equation. We therefore show below via simulations how close this new method comes to the estimate of Eq. (1).
5.4 Required Detector Sensitivity
Good timing resolution provides a necessary but not yet sufficient condition. The detector needs to be large enough to detect a significant signal at these short timescales, to measure a significant signal independent on the arrival direction, and to provide this high time resolution data for analysis, either on board or on the ground, rather than binning it up to save telemetry bandwidth.
A simple estimate of the minimum detector size can be made by recognizing that short-duration GRBs have structure, and have durations substantially longer than the 3 ms timescale that Fig. 4 implies as a requirement for subdegree localization accuracy. Assuming a canonical shape of a short GRB prompt emission light curve, and knowing that for GRB 170817A a single Fermi/GBM detector measured 20-30 cts/0.1 s in the 20–500 keV band at peak against ~30 cts rms from background fluctuations, we estimate to need 2000 cts per short-duration (2 s) GRB or 10 cts/1 ms at peak, so ~30× the effective area of a single GBM detector of 125 cm2, or 3500–4000 cm2. Incorporating the correspondingly higher background rate at the Galileo orbit with respect to the LEO of Fermi will modify this estimate, but for the simulations presented here we consider a detector of 60 cm × 60 cm geometrical area.
5.5 Detector Geometry
As we show, the generally preferred and assumed zenith-facing detector is not a good choice. Since the best localization accuracy is reached at the largest satellite separation and facing perpendicular to the satellite-connecting line (see Eq. (1) and Fig. 4), detectors sensitive sideward (i.e., 90° of zenith) are preferred.
Since the anticipated detector size has a ≈60 cm side length, adding a cube of that size to the zenith-facing side of the Galileo satellite might be challenging in terms of satellite momentum balance or station keeping, thus we also consider configurations where 1D detector plates are mounted on different sides of the Galileo satellite (Fig. 5). Any such 3D detector has several advantages. First, multiple detector units provide independent measurements to be used in the cross-correlation. For the same reason, a coincidence veto against particle hits can be implemented, reducing the rate of false triggers. Finally, since 3D detectors cover a field-of-view of more than 2π of the sky, detectors on some “behind-the-Earth” Galileo satellites will be able to detect the GRB, thus increasing not only the number of measuring detectors, but more crucially extending the baseline (maximum distance between detectors) for the time delay measurement.
We consider nine different detector geometries (Fig. 5): a single detector facing zenith (called detector 01), a hollow cube detector with 30 cm height on the zenith-facing side (detector 02), four sideways-facing detector plates (detector 03), two neighboring sideways-facing plates (+X, +Y; detector 04), four sideways-facing plus a zenith-facing detector (detector 05), two oppositely sideways-facing and one zenith-facing (+X, −X; detector 06), one sideways-facing only (+X; detector 07), one
sideways-facing plus one zenith-facing (+X; detector 08), and two oppositely sideways-facing detectors (+X, −X; detector 09).
All the sideways-facing plates are 60 cm × 60 cm in size and 1 cm thick. These configurations obviously change the zenith-angle-dependent variation of the effective area (see Fig. 6); the green area corresponds to two equal-size detectors on two neighboring sides (Fig. 5). Two-dimensional versions of theses dependences (including azimuthal variation) are shown in Sect. 6.1.1.
 |
Fig. 5 Different detector geometries simulated: detectors 1-3 (top row), 4-6 (middle row), and 7-9 (bottom row). |
 |
Fig. 6 Off-axis dependence of the different detector geometries. The blue shaded range corresponds to the minimum-maximum range according to azimuth angle for the cube detector. Beyond 90° the cube detector offers continued effective area, but shadowing by the satellite bus leads to a rapid drop. The green shaded area corresponds to equal-size detectors on two neighboring sides, with the top boundary corresponding to 45° view onto both, and the lower to 90° on only one of the two detectors. |
5.6 Setup of GNSS Configuration
Since we use an existing satellite network, only one more configuration choice needs to be considered in the simulations, namely the number of satellites per orbital plane equipped with GRB detectors to allow a 4π coverage of the sky. We use the notation of [1] or [0] if a GRB detector is placed on a given satellite or not, respectively. With eight satellites per orbital plane, and dealing
with these planes consecutively, a configuration of every second satellite equipped with a GRB detector would read [10101010 10101010 10101010]. The set of simulated configurations is given in Table 2.
We compute two maps: one “instantaneous” snapshot and one averaged over one orbital period. Simulations are done in steps of 5°, which provides 72 subsequent snapshots for a full 14h04m orbital revolution of the Galileo satellite network, meaning that the averaged map is the average of these 72 snapshots. GRBs are distributed on the sky on a 2° grid, thus providing a full sky map for each snapshot.
In order to allow any arbitrary combination of Galileo satellites to be chosen, a simulation tool has been set up (Rott 2020) that allows the user to switch on or off single Galileo satellites or detectors. This is implemented as a MATLAB function galileo_skyCoverage.m, which computes the sky coverage of any Galileo constellation and one or more given off-axis detector response(s) (Fig. 7).
An example is shown in Fig. 8 for a flat GRB detector on two Galileo satellites in separate orbital planes, for one single snapshot of the constellation. Dark blue shows the sky area not covered, light blue the sky covered by both detectors. Summing over one 14h04m period (i.e., 72 snapshots with 5° rotation steps) results in Fig. 9, showing the mean sky coverage by two satellites.
We note that the distribution of detectors over the satellites in a given orbital plane, or also between orbital planes, has a substantial impact on the results. As a demonstration of the effect, Fig. 10 shows two different constellations with the same number of satellites (with a GRB detector) per orbital plane, but grossly different distributions: (1) one with equal distribution (i.e., every second satellite has a GRB detector) and (2) all four
satellites (with GRB detector) per orbital plane are centered over one pole of the Earth at the start configuration (first epoch of the 72 epochs). The top panel shows the total coverage after 14h04m, which is equal for both options as it depends only on the number of satellites. The other two panels show the mean variance of the coverage at any sky position. In the equal distribution, there is no point on the sky that is covered by fewer than five or more than six satellites, while in the one-sphere constellation large regions of the sky are covered only with one or two satellites at a given time, with the consequence that triangulation would not be possible with this total number of satellites.
Since the Earth is not infinitely small, there is a 5% chance that one Galileo satellite is Earth-occulted at any given time. This is included in our computations.
Simulated detector configurations.
 |
Fig. 7 Structure of the skycov tensor, i.e., sky maps for the combinations of constellations and off-axis angle response. For this example a step size (time step) of 5° is assumed, resulting in 360/5 = 72 sky maps. |
 |
Fig. 8 Example of interactive plot for the sky coverage achieved with two Galileo satellites in separate planes, equipped with a flat GRB detector. The slide bar moves through the 72 epochs at 5° steps. |
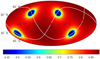 |
Fig. 9 Mean sky coverage, i.e., the sum of 72 epochs (as in Fig. 8). Only 50% coverage is achieved at the two poles of each of the two orbital planes in which the detectors move. |
6 Simulations
The simulations involve multiple steps. They are as follows:
Define the different detector geometries (Sect. 5.5);
Define the number of satellites and which satellites per orbital plane are equipped (Sect. 5.6);
Compute the effective area per detector configuration (Sect. 6.1.1);
Compute the accuracy of the localization via classical cross-correlation, depending on the effective areas of the detectors on separate satellites (Sect. 6.1.2);
Simulate the sky coverage and the GRB localization accuracy (Sect. 6.1.3).
In order to cover the range of GRB peak intensities (amplitude A in Eq. (2)) four intensity intervals are created such that faint intensity levels can be differentiated (see Table 3).
We fix the detector temporal resolution at 3 ms. Finally, we use the present 24/3/1 walker configuration of the GNSS system, and assume that satellites in all three orbital planes are indeed equipped with a detector.
These simulations return sky maps that are used to verify the extent to which 4π coverage is possible with a homogeneous localization accuracy over the sky, to verify the extent to which 4π coverage is possible with a homogeneous flux sensitivity level, to show the differences in sky coverage and localization accuracy as a function of the different number of satellites to be equipped with a detector and the detector geometry, and to provide absolute values of the GRB localization accuracy (distribution) for both single snapshots and time-averaged over the GNSS orbital period of 14h04m.
Given the CPU-intensive forward-folding triangulation technique, the full range of parameter testing in the simulation is done by using the classical cross-correlation. Only one individual setup is computed with the forward-folding triangulation technique in order to obtain proper error estimates and compare the absolute values of GRB location accuracy (distribution). We note that in this case steps (3) and (4) above are not necessary since this is part of the model forward-folding.
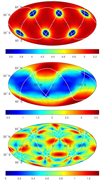 |
Fig. 10 Extreme example of the influence of the distribution of GRB detectors over the orbital plane top: identical mean sky coverage, ranging between 3.5 and ~5.3; middle: all 12 detectors distributed over one pole; and bottom: all 12 detectors equally distributed. The lower two panels show the standard deviation for each point on the sky. |
Four GRB intensity intervals.
6.1 Classical Scheme using Cross-correlation
6.1.1 Lookup Table for Direction-dependent Effective Area
Depending on the placement of single-plate detectors on different sides of a Galileo satellite, the 3D distribution of the effective area is grossly different. We illustrate these distributions in Fig. 11. The left panels show the effective area as a function of azimuth and zenith angle between 0° (figure center) to 180° (border of figure) of an illuminating source (GRB). The right panels show the corresponding area of the detectors that are illuminated (i.e., the area relevant for the noise). This is different from the left column figures, since the measured GRB counts per detector scale with the cosine of the incidence angle, while the background (noise) is isotropic.
The corresponding 360 × 180 degree matrices are used as detector lookup tables to identify the effective area for a given illumination direction. The effective areas obtained in this way from the two detectors of a baseline are used to access the lookup table of the accuracy matrix (see next subsection). Using both together, the different Galileo detector-equipment constellations are computed.
6.1.2 Accuracy Matrix
For the computation of the effects of the relative orientations of different detectors on different Galileo satellites according to the given satellite equipment scheme, we need to map the effect of detector-related parameters on the localization accuracy in a way that they can be efficiently used. Since this localization quality depends on at least two angles (the relative orientation of the detector normals of two detectors relative to the GRB direction) and the total intensity, this is a matrix rather than a factor. It is straightforward to realize that the cosine off-axis dependence of the detector sensitivity is a geometrical effect similar to different detector geometries. Thus, instead of computing effective area matrices per angle pair, we can incorporate the detector geometry (in terms of total effective area per direction) and compute the error of a delay measurement per angle pair. Such an accuracy matrix was computed via both methods (Fig. 12), and then serves as input to the Galileo satellite mapping simulation.
6.1.3 Results with Different Detectors
In this section we present, for all different detector configurations considered, the sky coverage (both, for one given moment and
the average over one Galileo orbital period), and the mean localization accuracy, separately for different intervals of the GRB intensity.
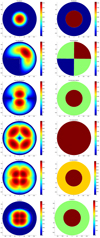 |
Fig. 11 Two-dimensional variation of the effective area (left column) and the illuminated area (right) for our proposed geometries (each detector is 60 cm × 60 cm). Top row: flat detector, zenith-facing. Second row: two detectors on two neighboring satellite surfaces. Third row: two detectors on opposite sides and zenith. Fourth row: four detectors on each side of the satellite, none toward zenith; Earth’s shadow is included. Fifth row: five detectors, one on each side and one zenith-facing. Bottom row: Zenith-facing cube with 30 cm height; shadow included. |
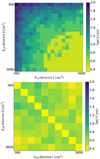 |
Fig. 12 Distribution of the error of the time-delay (color-coded) for different angles of two detectors (x- and y-axis) at the same position (=satellite). This means the nominal time delay should be zero. The matrices shown are the median of all simulated GRBs in the bright fluence bin (#4 in Table 3), separately computed for the classical cross-correlation method (top) and the forward-folding nazgul method (bottom), and separate matrices for the other intensity bins. For identical effective areas, i.e., the diagonal, nazgul recovers the nominal time delay of zero, so it was set to 0.3 to avoid division by zero in the follow-up steps. The placement on the same satellite also mimics (along the diagonal) the net effect on the accuracy of two identical detectors on different satellites facing exactly toward the same sky location. Each pixel is the median of the time-delay of many different GRB light curves. The time resolution of the detector is assumed to be 3 ms. The effective area distribution mimics a 1D detector with 3600 cm2 seen at different off-axis angles. |
Detector 1: Zenith-facing
We start with a single detector plate, facing at zenith, with each of the 24 Galileo satellites, and also every second satellite, equipped with one such detector. We use this constellation to show the different aspects of the simulated data; for the other detector geometries we primarily show example distributions and summarize the results in a table.
Figure 13 shows the sky coverage for an instantaneous moment (left) and averaged over the orbit (right) for the 24- and 12-satellite options, and Figs. 14 and 15 show the localization accuracy for two different GRB flux intervals.
For the simple 1D detector plate facing toward the zenith, the geometry of the satellite kinematics leads to a relation between the distance of the Galileo satellites and the difference of their zenith-pointing direction, as shown in the left panel of Fig. 16. The larger the angle, the lower the area in the sky that the GRB detectors on the two satellites jointly observe. More importantly, since the sensitivity of triangulation is best for GRBs occurring perpendicular to the connecting line of two satellites, zenith-facing flat detectors will not make use of the maximum baseline of the Galileo satellite system, but use at most 2/3 of it (<1.3 orbital radii). Our simulations over a full orbital cycle now return the frequency of occurrence of these distances between pairs of Galileo satellites for an isotropic distribution of GRBs. This shows that for the maximum GRB detector equipment rate on the GNSS (i.e., a GRB detector on each of the 24 Galileo satellites) about half of the detector pairs occur at satellite separations of <1.2 orbital radii (middle panel of Fig. 16). When reducing the satellite equipment rate, this rate gets even worse (right panel of Fig. 16). Thus, a single zenith-facing detector per satellite is far from optimal.
Overview of all Detector Geometries
Before elucidating the details of the other detector configurations, we start with comparing the nine different GRB detector geometries by using the maximum equipment rate in Fig. 17 (all 24 Galileo satellites carrying a GRB detector): the sky coverage for any given moment (left column), the average of the sky coverage over one Galileo orbital period (middle), and the mean localization accuracy of the faintest GRB intensity bin (where our goal is to obtain a subdegree localization).
The green filled circles in Fig. 17 make an interesting pattern on the brown sky background in the left column for detectors 03, 05, 06, and 09. These detectors all cover the whole sky (ignoring the cosine dependence of the effective area; see right column of Fig. 11). The green circles reduce the coverage by one, due to the shadowing of the Earth in nadir-direction, with a 12° radius. Due to the three orbital planes being perpendicular to each other, there are six positions on the sky where two satellites from two orbital planes get close to each other, and their 12° radii overlap to form a small region where the coverage is reduced by two satellites (blue regions).
Another aspect is symmetry. While a single detector facing toward zenith on all 24 satellites produces a homogeneous sky coverage, this is not true for a single sideward-facing detector (#07, #08) or an asymmetrical detector (#04); given the Sun-pointing constraints of the Galileo system, their sky coverage is very asymmetrical.
In the following subsections we describe most of these configurations in more detail.
Detector 2
As a consequence of the average short baselines for a flat zenith-facing detector (Fig. 16), we next test a cube detector on the zenith-facing side of the Galileo satellites. These detectors have the same area as detector 01 toward zenith, and half of this (due to the height of only 30 cm) toward all four sides. With more satellites at large baselines and the large effective area available for large parts of the sky, this substantially improves the localization accuracy of the zenith-facing flat detector (see Figs. 18 and 19).
Figure 20 illustrates why the cube detector is so much better in performance. The distribution of the mean baselines, which are realized for given pairs of detectors, and their projected effective areas as determined by their viewing direction relative to a GRB clearly shows that the long baselines for higher effective areas dominate. Thus, we reach subdegree localization accuracy for the brightest GRB intensity bin (though for the faintest it is still on the order of 10°).
Detector 3
Because the zenith-facing detectors are not optimal, we now look at an arrangement where all four sides of a
Galileo satellite are equipped with a 60 cm × 60 cm detector, with the nadir- and zenith-facing sides without GRB detector. The localization accuracy is very good (see Fig. 22) even for this faintest GRB intensity level. The averaged sky coverage shows an identical sky pattern, independent of whether we equip 6, 9, or 12 satellites with a GRB detector (see Fig. 21), but we note the different color-coding normalization. When more satellites are equipped with a detector, then there is a larger number of satellites seeing a given GRB.
In Fig. 23 we show the effect of the “merged” configuration, which is the temporal re-binning to 6 ms whenever the 3 ms sampling combined with the small baselines performs worse. This happens for a certain intensity range where the increased S/N overcompensates the reduced temporal resolution of the
detector. This is best shown with a single time slice, not the orbit-averaged accuracy plot. The re-binning improves the bad localization accuracy regions (red in the left panel of Fig. 23) by about 20% (from 1°1 to about 0°9). For even fainter intensity intervals the same happens for 9 ms, and so on. This holds for any number of satellites equipped with a GRB detector.
 |
Fig. 13 Sky coverage for a zenith-facing detector each on 24 satellites (top) and 12 satellites (bottom; every second along each orbital plane) for an instantaneous moment (left) and averaged over one orbit (right). The color-coding (with different scales) gives the number of satellites that see a GRB depending on where the GRB happens on the sky. |
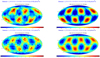 |
Fig. 14 Localization accuracy for a zenith-facing detector on each of the 24 satellites for an instantaneous moment (left) and averaged over one orbit (right), for GRBs in the brightest peak flux bin of 6–100 ph cm−2 s−1 (top row) and the faintest peak flux bin of 1.5–2 h cm−2 s−1 (bottom row). |
 |
Fig. 16 Geometrical properties of the Galileo network. Left: relation between distance between Galileo satellites and zenith pointing difference. Middle: frequency of occurrence of satellite distances, averaged over one orbital cycle for an isotropic GRB distribution, if all Galileo satellites are equipped with a GRB detector. Right: same, but for every second Galileo satellite equipped with a GRB detector. |
Detector 4
With the intention to minimize the number of detector plates on a given Galileo satellite, we included this geometry with only two instead of four sides equipped with a 60 cm × 60 cm detector plate. The simulations show that the sky coverage is substantially worse (Fig. 24), which is a consequence of the “eyes” problem, meaning that the detector on the y-side (together with a solar panel boom) will never look toward the Sun. In addition, as a consequence of the yaw-steering attitude, the detector mounted on the +X surface always looks into the hemisphere containing the Sun, meaning that the direction toward the anti-Sun is not covered by any detector on any satellite. The sky coverage and the localization precision thus dramatically degrade toward this direction.
Detector 5
This is a kind of maximum detector concept per satellite, and unsurprisingly the performance is very good (Fig. 25). However, we see that it performs slightly worse than the four-lateral-only detector geometry for fainter GRB intensity levels (Table B.1). This is likely due to the fact that using detectors at large inclination angles toward the GRB does not help in improving the S/N since co-adding the background noise of the second (or third) plate dominates over the gain in signal. Figure 27 shows the effect for a single plate, and the sum of two and three perpendicular-oriented plates: at large inclination angles (i.e., small effective area due to the cosine effect) the S/N after combining detectors does not improve. This calls for an optimization of the co-adding of signals from multiple detector plates: it should not be performed on the satellite, but on the ground, as it depends on the actual noise level for each satellite
(which we expect to vary along the orbit). Then, cutoff angles can be applied, above which no co-addition is done. Also for this detector we find eyes in the spatial distribution of localization precision caused by the fact that a maximum of two (instead of three) of the detector plates for any satellite can cover the Sun and anti-Sun directions.
 |
Fig. 17 Sky coverage for a single time slice (left) averaged over one Galileo orbit (middle) and the averaged localization accuracy for the faintest GRB intensity bin (right) for detector geometries 1-9 (from top to bottom, as labeled in blue for each map). |
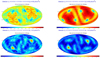 |
Fig. 18 Localization accuracy for a zenith-facing cube detector each on 24 satellites for an instantaneous moment (left) and averaged over one orbit (right), for GRBs in the brightest peak flux bin of 6–100 ph cm−2 s−1 (top row) and the faintest peak flux bin of 1.5–2 ph cm−2 s−1 (bottom row). |
Detector 6
This three-element option, which leaves the sides with the solar panels free, eliminates the bad localization performance in the Sun and anti-Sun directions (eyes above). However, the Sun-equator is less well covered (Fig. 26). Otherwise, it provides a very uniform localization capability over the sky, at substantially improved accuracy as compared to the case of two neighboring detectors.
Detector 7–9
Detectors 07, 08, and 09 were included for completeness and verification purposes, and the results are given in the overview plot of Fig. 17.
 |
Fig. 20 Distribution of mean baseline lengths for combinations of effective areas for pairs of detectors seeing a GRB for the geometries of detector 01 (left), 02 (middle), and 03 (right). |
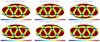 |
Fig. 21 Sky coverage for four-side detectors on 6 (top), 9 (left and middle of bottom row), and 12 (lower right) satellites averaged over one orbit (right). The satellites are distributed differently along each orbital plane, with three different options for the 6 satellites, and two options for 9 satellites. The color-coding provides the number of satellites that see a given GRB at a given time, averaged over one orbital period. |
 |
Fig. 22 Localization accuracy for a four-side detector each on 6 (top row), 9 (lower left and middle), and 12 satellites (lower right) for the faintest intensity interval. The 6- and 9-satellite options are shown for two different configurations along the orbital plane. |
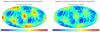 |
Fig. 23 Localization accuracy for a four-side detector on each of 12 satellites for the first time slice, and for the second highest intensity interval for unbinned (left) and binned (right) accuracy matrix, i.e., when the 6 ms binned matrix performs better than the 3 ms matrix. |
 |
Fig. 24 Sky coverage (left) and localization accuracy (right; for the second-brightest GRB intensity interval) of 12 satellites equipped with two detector plates on neighboring sides. The sky coverage is substantially worse than any previous detector geometry. |
Summary of Detector Geometries
Table B.1 summarizes the different detector geometries and satellite constellations considered, providing the all-sky averaged accuracy for each of the four GRB intensity intervals in Table 3. Thus, it is clear that the localization accuracy improves with the number of satellites equipped since among the detectors seeing a GRB there is a larger likelihood of having satellite pairs with a large distance (baseline); these are the ones that improve the localization accuracy.
The placement of detectors on satellites positioned opposite to each other in the orbital plane causes moving patterns on the sky with reduced localization accuracy, and thus should be avoided; this applies primarily for low equipment rates (e.g., the versions with six and nine satellites).
An interesting feature is seen in the case with six satellites. When the GRB detectors are distributed isotropically (i.e., two per orbit at antipodal positions), there is a pattern on the sky at which the localization is substantially worse (top left panel in Fig. 22). This can be avoided by placing detectors not in antipodal positions (top middle panel in Fig. 22).
One special effect to comment on are the two eyes in Fig. 22 (bottom row). These are due to the position of the Sun in the simulation (α = 90°, δ = 23°) and the anti-Sun direction, and in practice would move over the sky over the course of a year. These are caused by the yaw-steering motion of the satellite guaranteeing pointing of the navigation antenna continuously to the Earth and the solar panels to the Sun. As a consequence of this attitude mode the +Y and −Y surfaces of the satellite where the solar panel booms are mounted never look toward the Sun. The Sun and anti-Sun directions are thus covered only by one detector plate per satellite with varying orientation toward the Sun. The result is a reduced localization precision in these directions. For the GRB/GW application this is acceptable since optical follow-up of the GRB or neutron star merger close to the Sun is not possible from the ground.
To obtaining the localization accuracy in Table B.1, we averaged over the full sky. However the various figures clearly show that there are certain small regions on the sky (a few to 10% of the sky) that are worse than the majority of the sky. We therefore provide a more accurate accounting of the localization accuracy for our best options in Table B.2. This provides the worst accuracy for the best 50 and 90% of the sky (i.e., the accuracy is better than the specified value for that percentage of the sky), as well as the best and the worst single GRB accuracy of the sky. For the selected best detector and satellite configurations, we also provide a graphical representation in Fig. 28 which provides the accuracy for any fraction of sky coverage.
6.2 Bayesian Scheme using Nazgul
Due to the massive computation time requirements, a simulation with nazgul was only done for one particular satellite constellation (nine satellites, three in each orbital plane, equally distributed) with one detector (#03, facing toward four sides). We used the same setup as the one to reconstruct the time with the cross-correlation algorithm. Instead of 1000 different GRB light
curves, we used only one light curve shape, with five different flux normalizations. In addition, the triangulation was only computed at 134 sky positions, instead of 10 000. From each fit we obtained a distribution of the time delay, which was used to compute both the best-fit value (the median in this case) and the 68% probability uncertainties through the highest posterior density interval (i.e., the shortest possible interval) necessary to accumulate the chosen probability level. While the source position distribution reconstructed by nazgul is not in general an annulus, for the sake of a straightforward comparison with the classical correlation method we computed an equivalent annulus from the fitted time delay. The central ring of the annulus was computed from the median of the time delay distribution, while the width is given by the uncertainties in an analogous way to that done for the correlation method (see, e.g., Pal’shin et al. 2013). This methodology, although to some extent simplistic, allows us to compare the characteristic widths of the positional distributions fitted by nazgul and the correlation algorithm. The corresponding map is shown in Fig. 29 for the faintest intensity interval, together with the corresponding map from the cross-correlation method. This shows that the two methods are nicely compatible with each other.
A more quantitative comparison of the localization accuracy is given in Fig. 30, showing the histogram of the 1σ localization errors of nazgul versus the cross-correlation method. This shows that the nazgul distribution is a factor of ~2 narrower (FWHM of about 4° vs. 8°), and has much less GRB reconstruction in the long tail. Thus, the nazgul method leads to overall improvements, but is particularly superior at the faint end of the intensity distribution.
 |
Fig. 25 Localization accuracy of 12 (left) and 9 (right) satellites equipped with four lateral detectors and a zenith-facing detector, for the second-brightest GRB intensity interval). |
 |
Fig. 26 Sky coverage (left) and localization accuracy (right; for the second-brightest GRB intensity interval) of 12 satellites equipped with two opposite detectors plus one zenith-facing detector. |
 |
Fig. 27 Accuracy of different detector configurations. As one adds perpendicular-oriented detector plates, and since the background radiation is isotropic and does not scale with the cosine of the incidence angle, the S/N depends on the relative inclination angles of the detector plates. It is best for a single plate (green), and gets worse for two plates inclined by 90 degrees (blue), and even worse for three plates inclined by 90 degrees (red; corresponding to the five-detector case for any given GRB). |
6.3 Comparison to Previous Simulations
Recently, Hurley (2020) has combined a new localization method with the simulation of a near-Earth network of GRB
detectors. The basic concept of this method is similar to ours, namely avoiding cross-correlation and instead testing positions on the sky via a likelihood method. While this method is a substantial improvement over the classical cross-correlation, it still suffers from drawbacks (iii) and (iv) in Sect. 4, which is accounted for in our nazgul scheme (Burgess et al. 2021). In his simulations, Hurley (2020) uses individual detectors of 100 cm2 effective area on a fleet of nine satellites, and derives localization accuracies for three different GRB peak intensities. His faintest and middle intensity intervals fall in our brightest interval. In terms of sky coverage, Hurley (2020) reaches only 40%, so a single-plate detector on each of nine satellites is by far too little to reach all-time, all-sky coverage. While we did not simulate such a constellation, this result is consistent with our picture (i.e., the need to look at multiple sides at this small satellite number). The 1σ average localization for his faintest fluence GRB (16 ph cm−2 s−1) is an ellipse with a dimension of 4°.5 × 17.°.0, corresponding to an effective radius (circle of same area) of 4°.5 (1σ). Our closest constellation is a one-side, zenith-facing detector on 12 satellites, where our simulation for our brightest intensity interval (6–100 ph cm−2s−1) gives 2°.9. The difference between these two simulations is in effective area (100 vs. 3600cm2), orbit radius (7000 vs. 29 000 km), and timing accuracy (0.1 vs. 3 ms). Assuming the typical square-root dependence on effective area, the combination of these three factors suggests that our error should be  = 1.2 × that of the Hurley (2020) simulation, quite close to what we obtain (given that our intensity bin is very wide).
= 1.2 × that of the Hurley (2020) simulation, quite close to what we obtain (given that our intensity bin is very wide).
 |
Fig. 28 Accuracy of different detector and satellite configurations per sky fraction. Each curve shows the percentage of the sky for which the accuracy is better than the corresponding y-axis in degrees. Top: Faintest intensity bin for the 24-satellite equipment rate; bottom: Each color represents one configuration from Table B.2 for detector 3, with solid lines for the brightest GRB interval and dotted lines for the faintest. |
6.4 Potential for Improvements
Given the comparison in the previous subsection, we asked ourselves whether reducing the time resolution in our simulations (fixed at 3 ms) would substantially improve our localization accuracy. The answer is in theory yes, in practice likely not. The simple reason is that the variability timescale in GRBs is at the level of a few milliseconds (MacLachlan et al. 2013) and not submilliseconds (Walker et al. 2000). Thus, it is necessary to cross-correlate the rising edge of a pulse to better then the rise time. This is complicated even more because the slopes of the rise are energy dependent; this means that detectors like the scintillator plates preferred here will see different slopes from the same GRB as soon as the incidence angles on two detectors are not exactly the same. This is the reason why for instance co-adding light curves of different GBM detectors is not useful.
For configurations with more than one detector plate per satellite, we co-added multiple single-plate detectors per satellite. As described earlier, this does not automatically provide better S/N since the background radiation is added in full, not diminished with the cosine law as the source counts. Therefore, some optimization for adding two or three detector plates could be implemented. This affects mostly the faint end of the GRB intensity distribution, and the optimization is expected to improve the localization accuracy. On a practical note, the data from different detector plates should thus not be combined on board, but sent down to Earth separately. As a side effect, the onboard triggering algorithm can make use of the separate light curve measurements to filter out particle hits, thus dramatically reducing false triggers.
There is yet another way to improve the accuracy distribution, computed via the classical cross-correlation analysis, namely systematically using a re-binning procedure (in a frequentist approach, and the corresponding χ2 analysis). In practice, when moving from bright to fainter GRBs, there is a transition region where re-binning from the original 3 ms time resolution of the detector, for example toward 6 ms, provides a gain over the noise fluctuations and leads to an improved localization, as we show with our merged map for one case (Fig. 23). However, moving down in intensity, the same happens for further re-binning to 9 or 12 ms, and so on. The effect of this re-binning is to optimize between noise in the light curve versus the best accuracy in the time delay measurement. Obviously, it does not improve on the best accuracy side, but improves the bad end by approximately 15–20%. This does not apply to our forward-folding nazgul localization since this is Bayesian, and the information in the low S/N bins is properly accounted for.
6.5 Inclusion of Satellites Beyond GNSS
The inclusion of any satellite farther out in space than the Galileo satellites would help reduce the localization accuracy, which shrinks linearly with the increase in the baseline. Potential options are a GRB detector on the Gateway4, a multi-purpose
space station in a highly elliptical (3000 km × 70000 km) seven-day near-rectilinear halo orbit around the Moon, assembly planned for 2024–2028, or on the Moon LCS (Lunar navigation and communication system), a network of 3–4 satellites that would provide communications and navigation services to support human and robotic exploration on the Moon. A GRB detector in Lunar orbit would reduce the localization error by a factor of -6 if the GRB detector has the same size as discussed here for the GNSS. Of course, this improvement would only apply in one dimension of the error box, for GRBs coming from a direction perpendicular to the Earth-Moon line.
 |
Fig. 29 Localization accuracy for detector 03 (four sides) and nine satellites for the first of 72 snapshot per orbital phase and the faintest GRB intensity bin, computed with cross-correlation (left) and nazgul (right). The Sun is not included in the nazgul simulation, and thus the eyes are missing. |
 |
Fig. 30 Distribution of the absolute value of the difference between simulated and reconstructed time delays for nazgul (blue) and the cross-correlation method (green), again for detector 03 (four sides) and nine satellites. |
7 GNSS System Requirements
7.1 Communication Speed
The GRB afterglow brightness fades by a factor of three during the first 10 min after the burst, another factor of three during the next 50 min, and another factor of three during the next 23 h. The kilonova emission of short GRBs decays even faster. Moreover, clarifying the most important open astrophysics questions of merging neutron stars such as distinguishing the physical source of energy input (e.g., from the central remnant or via radioactivity) or associated processes (e.g., internal shock-reheating or heating of the outer ejecta by free neutrons) requires ground-based optical-near-infrared spectroscopy during the first 12 h (Metzger 2020). Thus, rapid communication on a timescale of minutes is required in order to support the identification of the kilonova.
Gamma-ray bursts occur at unpredictable times and sky positions. For the GRB position to be determined via triangulation, we need the measured data of each of the four (multiple) detectors per satellite on one computer. In order to be scientifically useful, the data should be downlinked within a few minutes. Thus, we require that at any time every Galileo satellite should be able to send off its measured data, either directly or via another satellite to a ground-station. Since only six Telemetry, Tracking and Control (TT&C) stations around the world are responsible for collecting and sending the telemetry data that was generated by the Galileo satellites, relaying data between different Galileo satellites to the one (or more) that do have ground contact is a viable solution. This should be done dynamically, without the need of commanding; in other words, each satellite (computer) should know at any time its acting relay satellite.
We distinguish two data transmission rates: (i) full rate to be downlinked to Earth within minutes; for a typical GRB this implies sending 0.5–1 MB over a time period of a few minutes (e.g., 4–8 kB s−1 over 2 min per satellite); (ii) reduced rate for quick-look localization; as described above, this would reduce the data amount by a factor of 100–1000.
The inter-satellite data transmission rate is likely slower than a satellite-ground contact rate. Assuming four Galileo satellites without ground-contact that send data to one other satellite with ground-contact leads to a required transfer rate of 4 MB on a timescale of minutes. In an ideal case, this can be done in parallel. If not, the above 4–8 kB s−1 are a minimum requirement.
Rapid uplink capability is not needed since the GRB detectors should be self-triggering.
7.2 Ground Segment
The light curve data as measured by the multiple Galileo satellites should be collected at one place on Earth, where the triangulation (and thus GRB localization) can be computed. We suggest that the final localization be made publicly available immediately; the GRB community has been using the Gamma-ray Burst Coordinate Network (GCN) for this for decades. This system would guarantee distribution to every interested user in the world. This would typically happen automatically, but oversight through one or more GRB astronomers is certainly not a bad idea. This could be organized via a small group of interested scientists, similar to groups that collaborate in the follow-up observations of GRBs at optical or radio observatories. In parallel, the raw data should also be made publicly available at the shortest possible delay time, to allow other groups with potential access to other long-baseline GRB data to use the data. The high-energy mission archive at ESA would be a logical place, but other satellite data centers in Europe might be alternative options.
8 Conclusions
The GNSS provides a nearly perfect satellite system for the localization of GRBs via triangulation. It provides a very promising compromise between satellite baselines (not too long to undergo data transmission restrictions), number of satellites, and required size of GRB detectors to reach subdegree localizations. It is the combination of detector geometry (in how many of the six directions of the Galileo surfaces are the detectors facing) and the number of satellites to be equipped that provides a scientifically useful GRB triangulation network.
Sideways-facing detectors are a crucial ingredient. We suggest equipping at least 12 satellites, four per orbital plane, with a four-side facing (excluding nadir and zenith) detector, each side with 3600 cm2 and 1 cm thickness. This will provide subdegree localization of GRBs, in particular faint short-duration GRBs such as GRB 170817A, as expected from binary neutron star mergers to be routinely measured at a rate of dozens per year in the upcoming runs of the worldwide gravitational wave detectors. Instead, a flat zenith-facing detector provides only 10-20° localizations. Equipping only 9 Galileo satellites with such a GRB detector leads to a 30% loss in localization accuracy, while the 24-satellite solution improves it by a factor of 2.
This configuration should be feasible to implement given the moderate requirements of mass (<20 kg) and power (~20 W) of a single detector plate (i.e., <80 kg and ~80 W for the four-side detector) compared to the overall budget of a Galileo satellite, noting that this corresponds to about 10% of the satellite mass. The realization of such a large-format GRB detector plate is also technologically feasible: scintillators of the proposed type have been flown for 40 years (TRL 9), and the Si detectors for read-out have also seen their first space applications.
Equipping second-generation Galileo satellites with GRB detectors would turn the navigation constellation into an observatory supporting the research on fundamental astrophysical and cosmological problems.
Acknowledgements
J.M.B. acknowledges support from the Alexander von Humboldt foundation. We are grateful to Dr Javier Ventura-Traveset, Dr Erik Kuulkers, Dr Luis Mendes and Dr Francisco Amarillo for their excellent scientific and technical support, as part of the European Space Agency supervision in the execution of this research activity. We acknowledge valuable suggestions from D. Svinkin. The work reported in this paper has been partly funded by the EU under a contract of the European Space Agency in the frame of the EU Horizon 2020 Framework Programme for Research and Innovation in Satellite Navigation. The view expressed herein can in no way be taken to reflect the official opinion of the European Union and/or the European Space Agency. Neither the European Union nor the European Space Agency shall be responsible for any use that may be made of the information it contains.
Appendix A Implementation of Simulated Light Curves
For a realistic distribution of single-pulse versus multi-pulse light curves, we implemented a pulse avalanche, a linear Markov process, as proposed by Stern & Svensson (1996). Here each pulse acts as a “parent” pulse giving rise to a number of “baby” pulses µb, sampled from a Poisson distribution p2(µb) = µ−1exp(−µb/µ), with the average number being µ. A baby pulse is assumed to be delayed by a time ∆t with respect to the parent pulse. The probability distribution for the Poisson delay is parameterized as p3(∆t) = (ατ)−1exp(−∆t/ατ), where τ is the time constant of the baby pulse and a is the delay parameter. From observed GRBs, the time constant τ of baby pulses is of the same order of magnitude, but shorter than the time constant τ1 of the parent pulse. This allows the process to converge since the pulse avalanche eventually reaches an arbitrarily short timescale, where a natural frequency cutoff should exist. The corresponding probability distribution is considered to be uniform in log(τ/τ1), and parameterized as p4[log(τ/τ1)] = |δ2 − δ1|−1 in the range [δ1, δ2] with δ1 < 0, δ2 ≳ 0, and |δ1| > |δ2|. The number of spontaneous pulses µs is sampled from a Poisson distribution p5(µs) = µ−1exp(−µs/µo), with µs the average number of spontaneous pulses per GRB. Finally, the probability distribution of the time constants τ0 of spontaneous pulses is taken as p(τ0) ∝ 1/τ0, corresponding to a 1/f flicker noise spectrum. Observations imply a maximum τmax for τ0. We then sample logτ0 uniformly between and τmax (i.e., p6(logτ0) = (logτmαx − logτmin)−1), where τmin should be smaller than the time resolution. Varying τmax rescales all average avalanche properties in time. Since more than one parent pulse is allowed per GRB, these spontaneous primary pulses are all assumed to be delayed with different time intervals t with respect to a common invisible trigger event. We parameterize the probability distribution for the Poisson delay t of a given spontaneous pulse as p7(t) = (ατ0)−1exp(−t/ατ0), where α is the constant delay parameter used for all pulses and τ0 is the time constant of the spontaneous pulse. Each spontaneous pulse gives rise to a pulse avalanche, and it is the overlap of µs pulse avalanches that form a GRB. From the analysis of about 600 CGRO/BATSE GRBs, Stern & Svensson (1996) suggest the following parameters: µ = 1.2, α = 4, δ1 = −0.5, δ2 = 0, µ0 = 1, τmax = 26 s. Differently from Stern & Svensson (1996), we pick τmin = 0.2 s to allow for a better time resolution for the Galileo detector. We simulate short and long GRBs separately to better tune some of the τi parameters (see the example light curves in Fig. 2).
Appendix B Location accuracy
Average localization accuracy for different detector geometries on a differing number of satellites.
References
- Aartsen, M. G., Abbasi, R., Abdou, Y., et al. 2013, PRL, 111, 021103 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, ApJ, 848, L13 [CrossRef] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D. et al. 2020, Liv. Rev. Relativ., 23, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, R., Abbott, B.P., Acernese, F., et al. 2022, ArXiv eprints [arXiv:2111.03606] [Google Scholar]
- Ajello, M., Greiner, J., Sato, G., et al. 2008, ApJ, 689, 666 [Google Scholar]
- Aptekar, R. L., Frederiks, D. D., Golenetskii, S. V., et al. 1995, Space Sci. Rev., 71, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D. L. 2003, ApJ, 588, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [Google Scholar]
- Begue, D., Burgess, J. M., & Greiner, J. 2017, ApJ, 851, 19 [Google Scholar]
- Berlato, F., Greiner, J., & Burgess, J. M. 2019, ApJ, 873, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Bošnjak, Ž., Götz, D., Bouchet, L., Schanne, S., & Cordier, B. 2014, A&A, 561, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Burderi, L., Salvo, T., Riggio, A., et al. 2020, Proc. SPIE, 11444, 114444Y [NASA ADS] [Google Scholar]
- Burderi, L., Sanna, A., Di Salvo, T., et al. 2021, Exp. Astron., 51, 1255 [CrossRef] [Google Scholar]
- Burgess, J. M., & Greiner, J. 2020, Front. Astron. Space Sci., 7, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, J. M., Yu, H.-F., Greiner, J., & Mortlock, D. 2018, MNRAS, 476, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, J. M., Cameron, E., Svinkin, D., & Greiner, J. 2021, A&A, 654, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Connaughton, V., Briggs, M. S., Goldstein, A., et al. 2015, ApJS, 216, 32 [Google Scholar]
- Cumani, P., Hernanz, M., Kiener, J., et al. 2019, Exp. Astron., 47, 273 [CrossRef] [Google Scholar]
- Edelson, R. H., & Krolik, J. H. 1988, ApJ 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Fuschino, F., Campana, R., Labanti, C., et al. 2019, NIMA, 936, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Grindlay, J. 2020, https://www.nasa.gov/sites/default/files/atoms/files/hsp.pdf [Google Scholar]
- Grindlay, J., Allen, B., Hong, J., et al. 2020, BAAS, 52, 1 [Google Scholar]
- Grove, J. E., Cheung, C. C., Kerr, M., et al. 2020, in Proc. Yamada Conf. LXXI: “GRBs in the Gravitational Wave Era” 2019, Yokohama [arXiv: 2009.11959] [Google Scholar]
- Howell, E. J., Ackley, K., Rowlinson, A., & Coward, D. 2019, MN, 485, 1435 [NASA ADS] [Google Scholar]
- Hurley, K. 2020, ApJ, 905, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley K., Pal’shin, V. D., Aptekar, R.L., et al. 2013, ApJS, 207, 39 [Google Scholar]
- Hurley, K., Aptekar, R. L., Golenetskii, S. V., et al. 2017, ApJS, 229, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Janka, H.-T., Aloy, M.-A., Mazzali, P.A., & Pian, E. 2006, ApJ, 645, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Metzger, B., Barnes, J., et al. 2017, Nature, 551, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, S. S., Murase, K., Mészáros, P., & Kiuchi, K., 2017, ApJ, 848, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Kole, M. 2019, 36th Int. Cosmic-Ray Conf., Madison, PoS(ICRC2019)572, https://pos.sissa.it/358/572/pdf [Google Scholar]
- Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, 413, L101 [NASA ADS] [CrossRef] [Google Scholar]
- MacLachlan, G. A., Shenoy, A., Sonbas, E., et al. 2013, MN, 432, 857 [NASA ADS] [Google Scholar]
- Masci, F. J., Laher, R. R., Rusholme, B., et al. 2019, PASP, 131, 018003 [Google Scholar]
- Meegan, C., Lichti, G., Bhat, P.N., et al. 2009, ApJ, 702, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D. 2020, Liv. Rev. Relativ., 23, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Mooley, K. P., Deller, A. T., Gottlieb, O., et al. 2018, Nature, 561, 355 [Google Scholar]
- Norris, J. P., Nemiroff, R. J., Bonnell, J. T., et al. 1996, ApJ, 459, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. P., Bonnell, J. T., Kazanas, D., et al. 2005, ApJ, 627, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Pal, A., Ohne, M., Meszaros, L., et al. 2020, Proc. SPIE, 11444, 114444V [NASA ADS] [Google Scholar]
- Pal’shin, V. D., Hurley K., Svinkin D.S., et al. 2013, ApJS, 207, 38 [CrossRef] [Google Scholar]
- Rott, M. 2020, Bsc thesis, TU Munich, Germany [Google Scholar]
- Rubinstein, R. Y., & Kroese, D. P. 2016, in Simulation and the Monte Carlo Method, 3rd edn. (Hoboken: Wiley Publication) [Google Scholar]
- Savchenko, V., Neronov, A., & Courvoisier, T. J.-L. 2012, A&A, 541, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, J. R., Briggs, M. S., Bruno, A., et al. 2019, 36th ICRC, Madison, PoS(ICRC2019)604, https://pos.sissa.it/358/604/pdf [Google Scholar]
- Stern, B. E., & Svensson, R. 1996, ApJ, 469, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Tomsick, J. A., Boggs, S. E., Zoglauer, A., et al. 2021, ArXiv eprints [arXiv:2109.10403] [Google Scholar]
- von Kienlin, A., Meegan, C. A., Paciesas, W. S., et al. 2020, ApJ, 893, 46 [Google Scholar]
- Walker, J. G. 1984, J. British Interplanet. Soc., 37, 559 [NASA ADS] [Google Scholar]
- Walker, K. C., Schaefer, B. E., Fenimore, E. E., et al. 2000, ApJ, 537, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenspointner, G., Kiener, J., Gros, M., et al. 2003, A&A, 411, L113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenspointner, G., Harris, M. J., Sturner, S., et al. 2005, ApJS, 156, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, N., Ripa, J., Pal, A., et al. 2018, Proc. SPIE, 10699, 106992P [NASA ADS] [Google Scholar]
- Wunderer, C. B., Kippen, R. M., Bloser, P. F., et al. 2006, New Astron. Rev., 50, 608 [CrossRef] [Google Scholar]
- Yu, S.-J., Gonzalez, F., Wei, J.-Y., Zhang, S.-N., & Cordier, B. 2020, Chin. Astron. & Astrophys., 44, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S. N., Santangelo, A., Feroci, M., et al. 2017, Sci. Chin. Phys., Mech. & Astron., 62, 29502 [Google Scholar]
- Zheng, S., & Xiong, S. 2019, https://doi.org/10.5281/zenodo.3478126 [Google Scholar]
All Tables
Average localization accuracy for different detector geometries on a differing number of satellites.
All Figures
 |
Fig. 1 Histogram of pair-wise distances between Galileo satellites. The peaks indicate constant distances between satellites in the same orbital plane. |
| In the text | |
 |
Fig. 2 Example mock light curves of the long-duration class created with the pulse avalanche description of Norris-like pulses. |
| In the text | |
 |
Fig. 3 Light curves of the same GRB as seen with a flat detector plate from different incidence angles. The labels in each plot give the angle under which the GRB impinges on the detector plane. With increasing angle, the effective area shrinks with the cosine of the angle, while the background remains the same. The “mother” light curve of this GRB was generated with a pulse avalanche scheme (see Sect. 5.1.1). |
| In the text | |
 |
Fig. 4 Half-width error Δθ (1σ) of the triangulation annulus for a GRB arriving at a pair of satellites 42 000 km apart (corresponding to the mean of Fig. 1). Indicated are the different delay times (bottom x-axis) and angles relative to the line connecting the two satellites (top x-axis) for different accuracies Δt of 1, 3, 10 and 50 ms with which the time delay can be measured. |
| In the text | |
 |
Fig. 5 Different detector geometries simulated: detectors 1-3 (top row), 4-6 (middle row), and 7-9 (bottom row). |
| In the text | |
 |
Fig. 6 Off-axis dependence of the different detector geometries. The blue shaded range corresponds to the minimum-maximum range according to azimuth angle for the cube detector. Beyond 90° the cube detector offers continued effective area, but shadowing by the satellite bus leads to a rapid drop. The green shaded area corresponds to equal-size detectors on two neighboring sides, with the top boundary corresponding to 45° view onto both, and the lower to 90° on only one of the two detectors. |
| In the text | |
 |
Fig. 7 Structure of the skycov tensor, i.e., sky maps for the combinations of constellations and off-axis angle response. For this example a step size (time step) of 5° is assumed, resulting in 360/5 = 72 sky maps. |
| In the text | |
 |
Fig. 8 Example of interactive plot for the sky coverage achieved with two Galileo satellites in separate planes, equipped with a flat GRB detector. The slide bar moves through the 72 epochs at 5° steps. |
| In the text | |
 |
Fig. 9 Mean sky coverage, i.e., the sum of 72 epochs (as in Fig. 8). Only 50% coverage is achieved at the two poles of each of the two orbital planes in which the detectors move. |
| In the text | |
 |
Fig. 10 Extreme example of the influence of the distribution of GRB detectors over the orbital plane top: identical mean sky coverage, ranging between 3.5 and ~5.3; middle: all 12 detectors distributed over one pole; and bottom: all 12 detectors equally distributed. The lower two panels show the standard deviation for each point on the sky. |
| In the text | |
 |
Fig. 11 Two-dimensional variation of the effective area (left column) and the illuminated area (right) for our proposed geometries (each detector is 60 cm × 60 cm). Top row: flat detector, zenith-facing. Second row: two detectors on two neighboring satellite surfaces. Third row: two detectors on opposite sides and zenith. Fourth row: four detectors on each side of the satellite, none toward zenith; Earth’s shadow is included. Fifth row: five detectors, one on each side and one zenith-facing. Bottom row: Zenith-facing cube with 30 cm height; shadow included. |
| In the text | |
 |
Fig. 12 Distribution of the error of the time-delay (color-coded) for different angles of two detectors (x- and y-axis) at the same position (=satellite). This means the nominal time delay should be zero. The matrices shown are the median of all simulated GRBs in the bright fluence bin (#4 in Table 3), separately computed for the classical cross-correlation method (top) and the forward-folding nazgul method (bottom), and separate matrices for the other intensity bins. For identical effective areas, i.e., the diagonal, nazgul recovers the nominal time delay of zero, so it was set to 0.3 to avoid division by zero in the follow-up steps. The placement on the same satellite also mimics (along the diagonal) the net effect on the accuracy of two identical detectors on different satellites facing exactly toward the same sky location. Each pixel is the median of the time-delay of many different GRB light curves. The time resolution of the detector is assumed to be 3 ms. The effective area distribution mimics a 1D detector with 3600 cm2 seen at different off-axis angles. |
| In the text | |
 |
Fig. 13 Sky coverage for a zenith-facing detector each on 24 satellites (top) and 12 satellites (bottom; every second along each orbital plane) for an instantaneous moment (left) and averaged over one orbit (right). The color-coding (with different scales) gives the number of satellites that see a GRB depending on where the GRB happens on the sky. |
| In the text | |
 |
Fig. 14 Localization accuracy for a zenith-facing detector on each of the 24 satellites for an instantaneous moment (left) and averaged over one orbit (right), for GRBs in the brightest peak flux bin of 6–100 ph cm−2 s−1 (top row) and the faintest peak flux bin of 1.5–2 h cm−2 s−1 (bottom row). |
| In the text | |
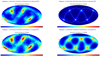 |
Fig. 15 Same as Fig. 14 but for 12 satellites (every second along each orbital plane). |
| In the text | |
 |
Fig. 16 Geometrical properties of the Galileo network. Left: relation between distance between Galileo satellites and zenith pointing difference. Middle: frequency of occurrence of satellite distances, averaged over one orbital cycle for an isotropic GRB distribution, if all Galileo satellites are equipped with a GRB detector. Right: same, but for every second Galileo satellite equipped with a GRB detector. |
| In the text | |
 |
Fig. 17 Sky coverage for a single time slice (left) averaged over one Galileo orbit (middle) and the averaged localization accuracy for the faintest GRB intensity bin (right) for detector geometries 1-9 (from top to bottom, as labeled in blue for each map). |
| In the text | |
 |
Fig. 18 Localization accuracy for a zenith-facing cube detector each on 24 satellites for an instantaneous moment (left) and averaged over one orbit (right), for GRBs in the brightest peak flux bin of 6–100 ph cm−2 s−1 (top row) and the faintest peak flux bin of 1.5–2 ph cm−2 s−1 (bottom row). |
| In the text | |
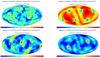 |
Fig. 19 Same as Fig. 18, but for 12 satellites (every second satellite along each orbital plane). |
| In the text | |
 |
Fig. 20 Distribution of mean baseline lengths for combinations of effective areas for pairs of detectors seeing a GRB for the geometries of detector 01 (left), 02 (middle), and 03 (right). |
| In the text | |
 |
Fig. 21 Sky coverage for four-side detectors on 6 (top), 9 (left and middle of bottom row), and 12 (lower right) satellites averaged over one orbit (right). The satellites are distributed differently along each orbital plane, with three different options for the 6 satellites, and two options for 9 satellites. The color-coding provides the number of satellites that see a given GRB at a given time, averaged over one orbital period. |
| In the text | |
 |
Fig. 22 Localization accuracy for a four-side detector each on 6 (top row), 9 (lower left and middle), and 12 satellites (lower right) for the faintest intensity interval. The 6- and 9-satellite options are shown for two different configurations along the orbital plane. |
| In the text | |
 |
Fig. 23 Localization accuracy for a four-side detector on each of 12 satellites for the first time slice, and for the second highest intensity interval for unbinned (left) and binned (right) accuracy matrix, i.e., when the 6 ms binned matrix performs better than the 3 ms matrix. |
| In the text | |
 |
Fig. 24 Sky coverage (left) and localization accuracy (right; for the second-brightest GRB intensity interval) of 12 satellites equipped with two detector plates on neighboring sides. The sky coverage is substantially worse than any previous detector geometry. |
| In the text | |
 |
Fig. 25 Localization accuracy of 12 (left) and 9 (right) satellites equipped with four lateral detectors and a zenith-facing detector, for the second-brightest GRB intensity interval). |
| In the text | |
 |
Fig. 26 Sky coverage (left) and localization accuracy (right; for the second-brightest GRB intensity interval) of 12 satellites equipped with two opposite detectors plus one zenith-facing detector. |
| In the text | |
 |
Fig. 27 Accuracy of different detector configurations. As one adds perpendicular-oriented detector plates, and since the background radiation is isotropic and does not scale with the cosine of the incidence angle, the S/N depends on the relative inclination angles of the detector plates. It is best for a single plate (green), and gets worse for two plates inclined by 90 degrees (blue), and even worse for three plates inclined by 90 degrees (red; corresponding to the five-detector case for any given GRB). |
| In the text | |
 |
Fig. 28 Accuracy of different detector and satellite configurations per sky fraction. Each curve shows the percentage of the sky for which the accuracy is better than the corresponding y-axis in degrees. Top: Faintest intensity bin for the 24-satellite equipment rate; bottom: Each color represents one configuration from Table B.2 for detector 3, with solid lines for the brightest GRB interval and dotted lines for the faintest. |
| In the text | |
 |
Fig. 29 Localization accuracy for detector 03 (four sides) and nine satellites for the first of 72 snapshot per orbital phase and the faintest GRB intensity bin, computed with cross-correlation (left) and nazgul (right). The Sun is not included in the nazgul simulation, and thus the eyes are missing. |
| In the text | |
 |
Fig. 30 Distribution of the absolute value of the difference between simulated and reconstructed time delays for nazgul (blue) and the cross-correlation method (green), again for detector 03 (four sides) and nine satellites. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


