EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 663 (July 2022) A&A, 663 (2022) A57 Full HTML
Open Access
Issue
A&A
Volume 663, July 2022
Article Number A57
Number of page(s) 16
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202243485
Published online 13 July 2022

© R. Tazaki and C. Dominik 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1 Introduction

The collisional growth of dust aggregates is the first step in planet formation. The properties of the constituent particles (monomers) of an aggregate are important as they directly affect the impact strength of the aggregate, which is closely linked to the maximum aggregate radius that is to be reached by collisional growth (Birnstiel et al. 2012; Okuzumi et al. 2016; Pinilla et al. 2017; Okuzumi & Tazaki 2019). In particular, the monomer size and surface materials coating each monomer are of crucial relevance for the impact strength. For example, larger monomers or less sticky materials make aggregates more fragile (Chokshi et al. 1993; Dominik & Tielens 1997; Wada et al. 2009). Although the material dependence of the impact strength has been extensively studied by laboratory experiments in recent decades (e.g., Poppe et al. 2000; Gundlach & Blum 2015; Musiolik et al. 2016a,b), the monomer size remains uncertain.

Previous studies of dust coagulation commonly assume sub-micron-sized monomers (Weidenschilling 1984, 1997; Dullemond & Dominik 2005; Ormel et al. 2007; Okuzumi et al. 2012; Kataoka et al. 2013; Krijt et al. 2016; Kobayashi & Tanaka 2021). This monomer size has been motivated by previous studies on the subunit sizes of interplanetary dust particles (Brownlee 1985; Rietmeijer 1993; Wozniakiewicz et al. 2013) or the largest interstellar grains (Mathis et al. 1977; Draine & Lee 1984; Jones et al. 2013). Recent in situ measurements of dust aggregates of the comet 67P/Churyumov–Gerasimenko (C-G) also suggest the presence of sub-micron-sized subunits (Bentley et al. 2016; Mannel et al. 2016, 2019). In this way, the current estimates of the monomer radius have relied on studies focused on the Solar System or the interstellar medium.

Despite its essential importance in collisional growth, the monomer radius has not yet been meaningfully constrained by observations of planet-forming disks. (Graham et al. 2007) found that optical scattered light from the debris disk around AU Mic is highly polarized, hinting at the presence of porous aggregates of sub-micron monomers; however, the authors mainly focused on the porosity of the aggregates rather than the size of the monomers. In contrast, recent observations of younger disks start to question the presence of sub-micron-sized monomers. The detections of millimeter-wave scattering polarization seem to imply that collisional growth stalls at a small aggregate size (~100 μm) (Kataoka et al. 2016; Stephens et al. 2017), which may be attributed to fragile nature of aggregates, such as due to micron-sized (or even larger) monomers or less sticky materials (Okuzumi & Tazaki 2019; Arakawa & Krijt 2021).

Observations of polarized scattered light from planet-forming disks would be crucial in attempting to gain clarity on the monomer size. The scattering polarization properties of large porous aggregates have been suggested to strongly reflect the properties of the monomer, as reported in numerical simulations (West 1991; Kozasa et al. 1993; Lumme et al. 1997; Petrova et al. 2000, 2004; Kimura 2001; Kimura et al. 2006; Bertini et al. 2007; Kolokolova & Kimura 2010; Tazaki et al. 2016; Min et al. 2016; Halder et al. 2018) and laboratory experiments (Zerull et al. 1993; Gustafson & Kolokolova 1999; Volten et al. 2007). In contrast, (Shen et al. 2009) pointed out that the effect of monomer size on polarization is negligible for aggregates with a porosity of ~60%. However, they only investigated small monomer sizes, and hence, it is unclear whether their conclusions remain valid for larger monomers. In the Solar System, optical polarimetry of comets has successfully revealed the presence of sub-micron-sized monomers in cometary aggregates (Gustafson & Kolokolova 1999; Kimura et al. 2003, 2006).

This study aims to investigate the monomer size from a new vantage point, that is, Polarimetrie observations of planet-forming disks from optical to near-infrared (IR) wavelengths. To our knowledge, this is the first attempt at deriving the monomer radius from disk observations. As shown later in this paper, optical and near-IR wavelengths are the optimal wavelengths for distinguishing sub-micron- and micron-sized monomers.

Figure 1 compiles the maximum values of the observed polarization fractions 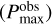for several planet-forming disks, where the polarization fraction means the degree of linear polarization of the observed polarization signals from the disk. Except for an edge-on debris disk (AU Mic), we generally have access to light reflected off the disk with a scattering angle of 90 degrees at which the degree of linear polarization of aggregates is often maximized (e.g., Kimura et al. 2006; Volten et al. 2007; Min et al. 2016). Thus, the observed maximum polarization fraction should be correlated with the maximum degree of polarization of light scattered by each aggregate (Pmax) in those disks. We can also say that the maximum degree of polarization of aggregates must be higher than the observed maximum polarization fractions 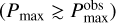because disk-scattered light usually suffers from a depolarizing effect due to multiple scattering (for an optically thick disk), line-of-sight integration (for an optically thin edge-on disk, such as AU Mic), or limited spatial resolution. Considering the presence of such depolarization effects, we can rule out the aggregate models that yield .

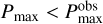As the number of disks with quantitative polarimetry data is currently limited, we shall adopt a working hypothesis that the monomer size and composition are the same among those disks, but the aggregate size and porosity may vary from one disk to another. With the hypothesis, aggregates with a successful monomer model should be capable of producing the degree of polarization of ≳24−40% and ≳35−66% at optical and near-IR wavelengths, respectively, as well as a reddish polarization color, namely, .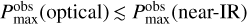

The main goal of this paper is to clarify what kind of aggregates and monomers can meet these criteria. To this end, we calculate Pmax values of various kinds of aggregates by performing exact light scattering simulations. In comparing the obtained Pmax values with 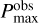, we demonstrate that aggregates are likely consisting of monomers less than or comparable to 0.4 μm in radius, while a larger monomer model fails to explain the observations.

The paper is organized as follows. Section 2 summarizes our aggregate models and a method for solving light scattering. The outcomes of the light scattering simulations are presented in Sect. 3. In Sect. 4, we apply the simulation results to recent quantitative Polarimetrie observations of the disk around HD 142527. In Sect. 5, we discuss the results. Finally, in Sect. 6, we summarize our findings.

thumbnail Fig. 1

Observed maximum polarization fractions of several planet-forming disks. References: HD 142527 (Hunziker et al. 2021), HD 169142 (Tschudi & Schmid 2021), HD 34700 A (Monnier et al. 2019), GG Tau (Silber et al. 2000), AB Aur (Perrin et al. 2009), UX Tau A (Tanii et al. 2012), TW Hya (Poteet et al. 2018), HL Tau nebula region (Murakawa et al. 2008), and AU Mic (Graham et al. 2007).

2 Models and methods

Dust coagulation in a planet-forming disk starts with hit-and-stick collisions, which have often been modeled by ballistic cluster cluster aggregation (BCCA) or ballistic particle cluster aggregation (BPCA). These aggregation models tend to produce fluffy aggregates whose porosity is higher than ~85%. As they grow, the aggregates may experience bouncing collision (Zsom et al. 2010; Lorek et al. 2018), although it is still a matter of debate whether fluffy aggregates are eligible for bouncing collision (Wada et al. 2011; Seizinger & Kley 2013). If bounce collisions occur, the aggregates suffer gradual compaction after each collision, and then the porosity will decrease to ~64% (Weidling et al. 2009).

With these in mind, we adopt three types of aggregates built from mono-disperse spherical monomers1. The first aggregation model is BPCA, where a single monomer particle is shot one-by-one to the target aggregate. Typically, BPCA clusters have a fractal dimension of ~3 and a porosity of 85−87% at N ≥ 32, where N is the number of monomers. Since the degrees of polarization of BCCA and BPCA clusters are more or less similar (Kolokolova et al. 2006; Kimura et al. 2006), we focus only on BPCA as a representative of hit-and-stick agglomerates. To investigate aggregates with lower porosity, we also consider aggregation models called BAM1 and BAM2 (Shen et al. 2008), which are a modified version of BPCA. The first contact point between an arriving monomer and the target aggregate was found similarly to BPCA, but BAM1 and BAM2 allow the newly attached monomer to roll over the aggregate surface to find the second and third contact points, respectively. In this way, the resultant aggregates become less porous than BPCA clusters, namely, a porosity of ~69−78% for BAM1 and ~47−68% for BAM2 at N ≥ 32. The BAM2 clusters have a similar porosity to compressed aggregates with multiple bouncing collisions (Weidling et al. 2009). The aggregate shapes are shown in Fig. 2.

To measure the size of an aggregate, we use the volume-equivalent radius RV = R0N1/3, where R0 is the monomer radius. For example, if two aggregates have the same RV value, they have the same material volume. As the volume-equivalent radius usually does not represent an apparent size of an aggregate, we also calculate the characteristic radius 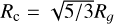as a measure of its apparent size, where Rg is the radius of gyration (Kozasa et al. 1992; Mukai et al. 1992). Hence, RV and Rc specify the mass and apparent size of an aggregate, respectively. The size parameters of the monomer and the aggregate are defined by x0 = 2πR0/λ and xc = 2πRc/λ, respectively, where λ is a wavelength. Also, to measure the porosity of an aggregate, we adopt a commonly used definition: ℘ = 1 − (RV/Rc)3.

This study adopts three different monomer radii: R0 = 0.1, 0.2, and 0.4 μm. The number of monomers is set as N = 2i, where i runs from 3 to imax with an increment of one, and imax = 12, 9, 6 for R0 = 0.1, 0.2, and 0.4 μm, respectively. Thus, the largest aggregates we studied have RV = 1.6 μm, corresponding to Rc = 2.3, 2.6, and 3.1 μm for BAM2, BAM1, and BPCA clusters with R0 = 0.1 μm, respectively. These sizes are large enough to study aggregates at the disk surfaces probed by optical and near-IR observations, as larger aggregates tend to settle down below the disk scattering surfaces.

As a monomer composition, we considered a mixture of pyroxene silicate (Mg0.7Fe0.3SiO3) (Dorschner et al. 1995), water ice (Warren & Brandt 2008), carbonaceous material (either organics or amorphous carbon), and troilite (Henning & Stognienko 1996) with the mass fractions provided by (Birnstiel et al. 2018). The mass abundance of water ice adopted in (Birnstiel et al. 2018) was reduced from its base models (Pollack et al. 1994; D’Alessio et al. 2001). Such a reduced water-ice abundance is in line with recent modelings of water-ice features arising from the surface regions of the disks (Tazaki et al. 2021; Betti et al. 2022). Since the actual form of carbonaceous material is rather uncertain, we also consider two carbonaceous materials: one is organics (Henning & Stognienko 1996), and the other one is amorphous carbon (Zubko et al. 1996).

We derived an effective refractive index for a mixture of the four materials using the Bruggeman mixing rule. The resultant optical constants are summarized in Table 1. The monomers comprising organics have refractive indices lower than those comprising amorphous carbon. We refer to each model as the org model and amc model. To specify the monomer size and composition, we use a model name formulated as COMP-SIZE, where COMP and SIZE specify the monomer composition (org or amc) and radius in unit of nm (100, 200, or 400), respectively. For example, amc-200 indicates a monomer with an amc composition and a radius of 200 nm. We also tested the effect of ice-mantled monomers on the polarization characteristics of aggregates and found no significant differences between ice-mantled and fully mixed cases. Thus, in the following, we assume homogeneous monomers for simplicity.

To solve light scattering by dust aggregates, we used an exact numerical technique known as the cluster T-matrix method (Mackowski & Mishchenko 1996, and references therein). We used a publicly available code for the cluster T-matrix method MSTM v3.0 (Mackowski & Mishchenko 2011). The great advantage of the T-matrix approach is its analyticity with respect to the mathematical formulation, which allows for analytical orientation averaging. We adopted analytical orientation averaging for all cluster T-matrix simulations presented in this paper. The results are also averaged over four realizations for each aggregate model. We found that the degree of linear polarization does not vary significantly between realizations, and therefore increasing the number of realizations furthermore would not change our conclusions.

Table 1

Real (n) and imaginary (k) parts of the refractive index of each monomer made of a mixture of silicate, water ice, carbonaceous (organics or amorphous carbon), and troilite.

3 Results

We present the results of cluster T-matrix simulations. First of all, we study the effect of monomer size on the degree of linear polarization of light scattered by aggregates in Sect. 3.1. In Sect. 3.2, we summarize the results of our comprehensive parameter survey on the polarization properties, which will then be compared with the observed polarization fractions in Sect. 3.3 to derive the monomer radius in planet-forming disks.

3.1 Effect of monomer size on scattering polarization

To derive the monomer radius from polarized disk scattered light, it is important to clarify the effect of the monomer radius on the polarization characteristics. Here we investigate to what extent the monomer radius affects the degree of linear polarization if the size, porosity, and composition (refractive index) of large aggregates (xc > 1) are the same. To this end, we consider BPCA clusters with the org composition and Rc = 3.1 μm, as shown in Fig. 2 (upper panel).

To assess the effect of monomer radius on scattering polarization, we need to fix the parameters of aggregates other than the monomer radius, such as the porosity and characteristic radius. Since BPCA clusters have a fractal dimension of 3, the characteristic radius scales as N1/3. To fix Rc, the number of monomers should be decreased by a factor of 8 if the monomer radius is increased by a factor of 2. Therefore, we consider three aggregates having the following sets of parameters (N, R0) = (4096, 100 nm), (512, 200 nm), and (64, 400 nm). All of them have nearly the same characteristic radii and porosities (Rc, ℘) = (3.14 μm, 86.8%), (3.12 μm, 86.4%), and (3.12 μm, 86.5%) for R0 = 100, 200, and 400 nm, respectively. Furthermore, the three aggregates have the same material volume, as they have RV = R0N1/3 = 1.6 μm.

Figure 3 shows the degree of linear polarization of scattered light for unpolarized incoming light (−S12/S11) for the three aggregates, where Sij represents a scattering matrix element (Bohren & Huffman 1983). Since we have fixed the parameters other than the monomer radius, the difference in the polarization can be attributed to a monomer-size effect.

In Fig. 3, the upper panel shows the angular dependence of polarization at λ = 1.04 μm. At this wavelength, the size parameters of the three aggregates are xc ≃ 19, and the size parameters of the monomers are x0 = 0.6, 1.2, and 2.4 for R0 = 100, 200, and 400 nm, respectively. For x0 = 0.6 (R0 = 100 nm), the polarization curve appears to be very similar to that of Rayleigh scattering despite the large aggregate size (xc ≫ 1). In contrast, for x0 > 1 (R0 = 200 and 400 nm), the degree of polarization drops rapidly and eventually oscillates around zero. In this way, the monomer radius has a significant impact on the degree of polarization of aggregates. The lower panel shows the wavelength dependence of the maximum degree of polarization Pmax, which is defined as the maximum value of −S12/S11 for all scattering angles. For the upper panel, the values of Pmax are 89, 73, and 9.7% for R0 = 100, 200, and 400 nm, respectively. The maximum polarization is found to be almost monotonically decreasing with decreasing λ for all cases. At λ = 3.78 μm, the size parameters of the three monomers are all lie in x0 < 0.67. In this case, the difference in Pmax between different monomer sizes is less than 5% points, and thus, changing the monomer radius does not result in changing the maximum polarization significantly. The polarization for R0 = 400 nm starts to decrease at λ = 2.18 μm, which corresponds to x0 ≃ 1.2. The difference in Pmах between different monomer sizes now reaches ~10% points, and becomes more prominent for a shorter wavelength. Therefore, the effect of monomer size seems to appear only when the monomer is sufficiently large, namely, x0 ≳ 1.

Overall, Fig. 3 suggests that the aggregates consisting of 400-nm monomers fail to explain a high observed polarization fraction at λ ≲ 1.25 μm for several disks. Although a more detailed parameter study and the comparison with observations will be presented later (see Sects. 3.2 and 3.3), this result already hints at the presence of relatively small monomers in disks.

Shen et al. (2009) claimed that the monomer size has negligible effect on polarization for moderately porous aggregates (℘ ≈ 60%), although they only considered relatively small monomers (x0 ≲ 1.6). To compare our results with theirs, we selected two aggregates with a porosity of ~60% as follows. The first selected aggregate is BAM2 clusters with 128 monomers with a radius of 200 nm. The other aggregate is BAMl clusters with 16 monomers with a radius of 400 nm. The two aggregates have the same material volume (RV = R0N1/3 ≃ 1.01 μm). Their characteristic radii and porosities are also very similar: (Rc, ℘) = (1.35 μm, 58.4%) and (1.37 μm, 60.1%). Althoug there is still a subtle difference in porosity, we think that such a tiny difference does not significantly alter our conclusions.

Figure 4 shows the degree of polarization for the two low-porosity aggregates (~59%). We found that the wavelength dependence of Pmax is surprisingly similar between the two when λ ≳ 1.63 μm, which corresponds to x0 ≲ 1.54. Thus, it appears to reaffirm the conclusion made by Shen et al. (2009). However, we also found a significant difference in -Pmax at λ ≲ 1.25 μm, which corresponds to x0 ≳ 2.01. Therefore, a manifestation of the monomer size effect needs a slightly larger x0 value for low-porosity aggregates, that is, x0 ≳ 2. In other words, the absence of the monomer size effect in Shen et al. (2009) is likely due to its limited range of size parameters (x0 ≲ 1.6).

To summarize, even if we fix the aggregate size, porosity, and composition, the degree of polarization depends sensitively on the monomer size unless x0 ≲ 1−2. This tendency has been confirmed for a wide range of aggregate porosity (59−87%). Conversely, if aggregates consist of small monomers such that x0 ≲ 1, the polarization is insensitive to the monomer radius and is determined by the porosity, size, and composition of aggregates (Fig. 4, see also Shen et al. 2009). This is in agreement with the findings from laboratory experiments (Zerull et al. 1993; Gustaf son & Kolokolova 1999). Our results suggest that, if we try to distinguish between sub-micron- and micron-sized monomers, the optical and near-IR wavelengths are the optimal wavelengths, because the monomer size parameter is close to or larger than unity at these wavelengths.

thumbnail Fig. 2

BPCA (upper), BAMl (middle), and BAM2 (lower) clusters with the volume-equivalent radius of RV = 1.6 μm. From left to right, the number of monomers and the monomer radius (N, R0) are (64, 400 nm), (512, 200 nm), and (4096, 100 nm), respectively.
thumbnail Fig. 3

Effect of monomer size for aggregates with a porosity of ~87%. Upper panel: degree of linear polarization of light scattered by aggregates with the org composition at λ = 1.04 μm. The blue, orange, and green lines are the results for R0 = 100, 200, 400 nm, respectively. Lower panel: wavelength dependence of the maximum polarization. The observed maximum polarization fractions are plotted as lower limits, since the amount of depolarization that the observed polarized light suffered is unknown.
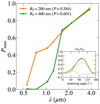thumbnail Fig. 4

Effect of monomer size for the aggregates with a porosity of ~59%. The orange and green lines are the results for R0 = 200 nm (BAM2 clusters of 128 monomers) and 400 nm (BAM1 clusters of 16 monomers), respectively. The porosity of each aggregate is indicated in the legend. The inset panel shows the angular dependence of the degree of polarization (−S12/S11) at two wavelengths (solid lines: λ = 1.63 μm, dotted lines: λ = 1.04 μm).

3.2 Maximum polarization for various aggregates

We showed that the monomer size is important for the polarization characteristics of aggregates. Next, we study how the maximum polarization Pmax depends on aggregate radius, porosity, composition, and monomer radius.

Figure 5 shows the effect of aggregate radius on the maximum polarization for the case of BPCA. A similar plot for BAM1 and BAM2 is available in Appendix A. Apart from the porosity effect on the maximum polarization, the overall dependencies for BAM1 and BAM2 are similar to the case of BPCA. Figure 6 shows the effect of porosity on the maximum polarization. In these figures, we also plot the observed maximum polarization as a lower limit because the amount of depolarization that the observed polarized light suffered is unknown. To estimate the Pmax values from 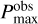, we need a more detailed modeling, namely, radiative transfer calculations for each disk, which is beyond the scope of this paper. The key dependencies seen in Figs. 5 and 6 are summarized below.

3.2.1 Dependence on aggregate radius

Each panel of Fig. 5 shows the wavelength dependence of Pmax for various aggregate radii. For comparison, we also plot the wavelength dependence for the single monomer (gray solid line). For org-100, each monomer obeys Rayleigh scattering, and the maximum polarization is nearly 100% at all wavelengths. As with a single monomer, the maximum polarization of aggregates remains high at all wavelengths even if RV increases to 1.6 μm (the characteristic radius of 3.1 μm). In contrast, for org-200 and -400, as Pmax of the monomer drops, Pmax of the aggregate does as well. The above results nicely illustrate the fact that the polarization for aggregates tends to reflect the polarization characteristics of the monomers, as known since the early 1990s (West 1991; Kozasa et al. 1993).

The resemblance in the polarization among aggregates and monomers is physically reasonable as multiple scattering is often subdominant (not negligible though) for highly porous aggregates (xc > 1 and x0 ≪ 1) (Berry & Percival 1986; Botet et al. 1997; Tazaki et al. 2016; Tazaki & Tanaka 2018). In the single scattering limit, every nonzero scattering matrix element is equally affected due to the constructive and destructive interference of light waves from aggregates. Consequently, each scattering matrix element does depend on the aggregate structure, but the ratio of them, that is, the degree of linear polarization, is independent of the aggregate structure and size and is solely determined by the properties of monomers (see Eq. (9) in Tazaki etal. 2016).

The deviation of Pmax of the aggregates from that of the monomer is due to multiple scattering within each aggregate. Larger aggregates provide a higher probability of multiple scattering, resulting in lower Pmax values. However, the dependence on the aggregate radius is generally weak compared to that of the monomer radius. For example, even if we increase RV by more than an order of magnitude (from 0.1 to 1.6 μm), the reduction of Pmax is less than a factor of two, whereas increasing the monomer radius only by a factor of two considerably affects the maximum polarization (Fig. 3). Such weak aggregate size dependencies have also been seen in previous numerical simulations (Kozasa et al. 1993; Kimura 2001; Kimura et al. 2003, 2006; Petrova et al. 2004; Bertini et al. 2007) and micro-wave analog experiments (Zerull et al. 1993; Gustafson & Kolokolova 1999).

3.2.2 Dependence on monomer composition

The top and bottom panels of Fig. 5 show the maximum polarization for aggregates made of the org and amc composition, respectively. In general, the monomer composition has a strong impact on the maximum polarization.

For all monomer radii, the maximum polarizations of the amc model are lower and higher than those of the org model at near-IR and optical wavelengths, respectively. Higher n values or lower k values tend to decrease the maximum polarization of aggregates (Petrova et al. 2004; Kimura et al. 2006; Lumme & Penttilä 2011), because such a change in refractive index tends to induce more multiple scattering within each aggregate. As shown in Table 1, the amc model has a higher refractive index in both the real and imaginary parts than the org model. Because of the higher real part, Pmax is smaller at near-infrared wavelengths, and because of the higher imaginary part, Pmax is larger at optical wavelengths. As a result, the wavelength dependence of the maximum polarization of the amc model is shallower than that of the org model.

For R0 = 400 nm, the wavelength dependence is complex. For both compositions, the maximum polarization drops rapidly at λ ~ 1−2 μm. This drop in polarization is triggered by a rapid reduction in the degree of polarization of the monomer itself (see gray line), not by multiple scattering within the aggregate. We initially suspected that such a sharp drop is an artifact arising from the assumption of perfectly spherical monomers in our aggregate models and might be mitigated by considering more realistic, nonspherical monomers. However, comparing the degree of polarization of spherical and nonspherical particles, we found that a similar sharp drop can occur for nonspherical particles as well (see Appendix B for more detailed discussion). Thus, we suppose that the sharp drop is a realistic property, although a more detailed study on the polarization of aggregates of nonspherical monomers is desirable.

thumbnail Fig. 5

Wavelength dependence of Pmax for BPCA with the org (upper panels) and amc (lower panels) compositions. From left to right: monomer radius of the aggregates is R0 = 100, 200, and 400 nm, respectively. The gray solid line in each panel represents Pmax for a single spherical monomer.

3.2.3 Dependence on aggregate porosity

Figure 6 shows the effect of porosity on the maximum polarization. To isolate the effect of porosity, we fixed the characteristic radius of aggregates to Rc = 2.0 μm by interpolating the simulation data.

For the org case, the maximum polarization monotonically decreases with decreasing λ for all porosities. Decreasing the porosity also results in decreasing the maximum polarization, because a denser aggregate results in more multiple scattering (Kolokolova & Kimura 2010). For the amc case, lower porosity aggregates (BAMl and BAM2) exhibit an inverted wavelength dependence of the polarization: increasing Pmax with decreasing λ. Shen et al. (2009) also found a similar inverted trend for BAM2. Because of this inverted trend, the maximum polarization of BAM2 will be similar to or even slightly higher than that of BPCA at optical wavelengths.

We interpret this inverted behavior as follows. The wavelength at which the inversion sets in found to be the wavelength at which the radiation field in the aggregate begins to be nonuniform. The non-uniform radiation field is due to attenuation of the incoming radiation at the surface of the aggregate. With decreasing wavelength from this, the successive orders of scattering get fewer (less multiple scattering), which results in increasing Pmax. The above interpretation is further augmented by the following points. We confirmed that the radiation field for org aggregates is almost uniform for all porosities and wavelengths we investigated, and therefore they are not eligible for inversion. Although BPCA clusters with amc composition exhibit a non-uniform radiation field, they are less efficient multiple scatterers in the first place and, hence, the inversion effect does not appear clearly.

Another intriguing feature seen in Fig. 6 is that the porosity dependence diminishes for shorter wavelengths for org aggregates. This effect is reminiscent of the neighborhood effect (Kimura & Mann 2004; Kolokolova & Kimura 2010); the degree of polarization is characterized by a local structure of a length scale of ~λ/2π or so within an aggregate. Once the size parameter of the monomers exceeds around unity, the electromagnetic interactions between neighboring monomers, rather than the overall aggregate structure, characterize the degree of polarization. In our cases, the porosity dependence diminishes in the case of λ ≤ 0.735 μm for R0 = 200 nm and ≤ 1.25 μm for R0 = 400 nm, which translate to x0 ≥ 171 and 2.01, respectively. In other words, the diminished porosity dependence occurs when the size parameter of monomers x0 ≳ 1.71−2.01 for the org composition.

Kolokolova & Kimura (2010) point out that the neighborhood effect appears easily for more absorbing aggregates. We confirmed that the converging behavior already starts to appear for amc-100 at optical wavelengths. However, the convergent behavior is missing for amc-200 and -400. We speculate that this is perhaps due to (i) artifacts arising from ripple patterns in polarization curves or (ii) different coordination number of monomers, although further clarification seems difficult within the limit of our simulation data. As discussed in Appendix B, strong ripple patterns were confirmed in the polarization curves for amc-200 and -400 at an optical wavelength, while it is absent for org-200 and -400. Such a ripple pattern would not be present for realistic monomers, as the monomers must not be mono-disperse and perfectly spherical particles and, hence, their poly-dispersity and non-sphericity will smear them out. More detailed light scattering simulations taking into account aggregates of nonspherical monomers is necessary to clarify this point.

thumbnail Fig. 6

Effect of porosity on the maximum polarization for the aggregates with Rc = 2.0 μm with the org (upper panels) and amc (lower panels) compositions. From left to right: monomer radius of the aggregates is R0 = 100, 200, and 400 nm, respectively. The yellow, brown, and cyan lines represent the results for BPCA, BAM1, and BAM2. The porosity of each aggregate model, ℘, is indicated in each legend.

3.3 How large are the monomers in planet-forming disks?

In Sects. 3.1 and 3.2, we investigated the wavelength dependence of the maximum polarization for various aggregates and clarified the impact of the monomer size on the polarization. In particular, as we discussed in Sect. 3.1, the optical and near-IR wavelengths are the optimal wavelengths for distinguishing submicron- and micron-sized monomers because the size parameter of the monomers becomes close to or larger than unity at these wavelengths. Comparing the simulation results with the observed maximum polarization fraction, namely, Fig. 1, we can assess the monomer radius of aggregates in planet-forming disks for the first time.

Currently available disk measurements favor the presence of relatively small monomers. As shown in Figs. 5 and 6, the aggregates with monomers of R0 = 400 nm fail to reproduce the combination of a high polarization fraction and a reddish polarization color at optical and near-IR wavelengths – regardless of the aggregate size, composition, and porosity. For the nebula scattered light around HL Tau, the observed maximum polarization fractions may be marginally explained by aggregates with amc-400 unless the observed signals are depolarized by multiple scattering. This is in harmony with the findings of Murakawa et al. (2008). Using a one-dimensional (1D) single scattering model with the Mie theory, Murakawa et al. (2008) modeled polarized scattered light from the HL Tau nebulosity and then estimated the maximum grain radius to be 0.4 μm. Since we have shown that the degree of polarization of aggregates reflects the monomer property, the maximum grain radius they derived may be interpreted as the monomer radius rather than the aggregate size.

Monomers larger than R0 = 400 nm would be unfavorable because their polarization will be even lower or bluish at an optical wavelength. As a result, we arrive at the conclusion that the monomers of aggregates in planet-forming disks are likely no greater than 400 nm (= 0.4 μm). The inferred monomer size is similar to the one seen in cometary dust aggregates and the maximum size of interstellar grains (see Sect. 5.1).

Although a monomer radius of 100 or 200 nm is consistent with the observations, we cannot exclude the presence of monomers much smaller than 100 nm. This point will be clarified by studying the presence/absence of the variation in 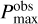at optical wavelengths across various disks. In Fig. 6, we showed that the maximum polarization is insensitive to aggregate porosity when x0 ≳ 1.71−2.01 at least for the org composition. This may imply that if aggregate porosity is diverse from one disk to another, the near-IR maximum polarization fractions should vary accordingly, but such a variation is suppressed for optical wavelengths when R0 > 100 nm. Conversely, if the variation at the optical wavelength is similar to the near-IR counterpart, the monomer radius is likely less than 100 nm. This strategy of deriving the monomer radius has been employed in the cometary field (Gustafson & Kolokolova 1999; Kimura et al. 2003, 2006).

Figure 1 shows that the variation in optical and near-IR polarizations are around ~16% points and ~30% points, hinting at less variation for shorter wavelengths, and this may indicate the presence of monomers larger than 100 nm. However, the number of current observational data points is rather limited, and therefore the time is not yet ripe to draw a robust conclusion about the lower size limit. A future survey on optical polarization will be crucial in strengthening this argument.

Figure 1 also points to a red polarization color. Within the limits of our composition models, dust aggregates in disks are unlikely to be dark and dense aggregates, namely, BAM2 with amc composition, because such aggregates tend to exhibit an inverted, or blueish, wavelength dependence. In other words, such an inverted trend is smoking gun evidence of dark and dense aggregates (or can be dark monolithic grains). However, it is worth keeping in mind that the wavelength dependence could be affected by the assumption of a refractive index. If one allows more conducting materials (i.e., amorphous carbon or metals) or less dielectric materials (i.e., water ice), |m| and d|m|/dλ will be larger than our amc model. In this case, the inverted trend might be alleviated, although it is unclear whether such a composition model is reasonable for protoplanetary dust. In any case, the wavelength dependence of polarization is useful for diagnosing not only the monomer radius but also the monomer composition.

4 Application to the HD 142527 disk

Our argument so far has been based on the premise of the working hypothesis, that is, the monomer radius and its composition are the same for various disks. However, this may not be always true, and hence, each aggregate model does not necessarily satisfy all lower limits shown in Figs. 5 and 6. Therefore, multiwavelength quantitative polarimetry for a specific planet-forming disk is crucial for a monomer size study. Here, as a case study, we focus on the disk around HD 142527, because polarization measurements have been made with the widest wavelength coverage among the disks shown in Fig. 1.

HD 142527 is a binary star surrounded by a large circumbinary disk, whose optical/near-IR scattered light has been extensively investigated (Fukagawa et al. 2006; Rameau et al. 2012; Avenhaus et al. 2014, 2017; Rodigas et al. 2014; Hunziker et al. 2021). Hunziker et al. (2021) found that a high polarization fraction toward this disk, hinting at aggregate nature of dust particles. Tazaki et al. (2021) found that the observed reddish disk color is consistent with dust particles of a radius of ~3 μm. Also, the reddish scattered light is more likely explained by compact aggregates2 rather than fractal aggregates (Min et al. 2016; Tazaki et al. 2019). From these results, compact dust aggregates of ~3 μm in radius are thought to be responsible for the scattered light of the disk. Such aggregates are quite similar to those presented in Fig. 2, and therefore we may apply our simulation results to interpret the observations.

Hunziker et al. (2021) conducted a quantitative polarimetric measurement of the disk around HD 142527 at optical (the VBB) and near-IR (the H-band) wavelengths. They accurately derived disk polarization fractions at the far side: 28.0 ± 0.9% at the VBB and 35.1 ± 2.1% at the H-band. They also argued that the maximum polarization fraction may be as high as 30 ± 5% for the VBB and 40 ± 10% for the H-band. In this study, we adopt 28.0 ± 0.9% and 35.1 ± 2.1% for the maximum polarization fractions at optical and near-IR wavelengths for this disk because the disk far side is close to a scattering angle of 90 degrees at which the degree of polarization is often maximized (see Fig. 3) and better accuracy of the data.

Since the observed polarization fractions suffer a depolarization effect due to multiple scattering at the disk surface, we converted the observed maximum polarization fraction to Pmax by using a simple plane-parallel model developed by Ma & Schmid (2022). The depolarization effect depends on the single scattering albedo of dust aggregates. The single scattering albedo of our aggregates with RV = 1.6 μm ranges from 0.5−0.95. Within this range, the plane-parallel model predicts that Pmax ~ 42−86% for the VBB and ~52−100% for the H-band. The estimated range agrees with the Pmax values estimated in Hunziker et al. (2021), where they derived Pmax = 50 % and 70% at VBB and the H-band, respectively.

Figure 7 summarizes Pmax values at the VBB and the H-band for various aggregate porosities, monomer radii, and compositions. We assumed the aggregate radius of RV = 1.6 μm, and then characteristic radii are around 2.3−3.1 μm, which approximately agree with the sizes inferred from a previous modeling (Tazaki et al. 2021). The inferred observational range of Pmax is shown with the gray-hatched square in the plot. The inferred range falls onto the region wheret R0 = 100−200 nm, while aggregates with R0 = 400 nm produce either too small optical or near-IR polarization fraction. One may wonder if an intermediate composition between amc and org yields a closer fit to the observations. However, we found that even if we consider an intermediate composition, the large monomer still fails to reproduce the estimated maximum polarization (Appendix C).

Therefore, the wavelength dependence of the maximum polarization fractions of the HD 142527 disk is consistent with large aggregates (~3 μm) with relatively small monomers (R0 = 100−200 nm). In particular, the Pmax values estimated by Hunziker et al. (2021) are similar to the model of BPCA clusters with amc–200 monomers or BAM2 clusters with org–100 monomers (Fig. 8). To distinguish between the two possibilities, a further detailed study is necessary, which is left for our future tasks.

thumbnail Fig. 7

Maximum polarization of dust aggregates at the VBB (optical) and the H-band (near-IR) with RV = 1.6 μm. Different line styles correspond to different aggregate models (BPCA: solid, BAM1: dashed, BAM2: dotted lines), and different symbols correspond to different composition models (circles: org, squares: amc). The number beside each point denotes the monomer radius in unit of μm. The dark gray hatched area is the maximum polarization estimated by Hunziker et al. (2021), while the light gray hatched area is the estimated Pmax values for an assumed range of the single scattering albedo of 0.5−0.95.

5 Discussion

5.1 Comparison with previous estimates on the monomer radius

In this work, we demonstrate that the monomer radius is likely less than or comparable to 400 nm to explain the observed polarization fractions. We are aware, however, that our results may be biased toward aggregates with smaller monomers because aggregates with larger monomers, if present, may sink below the disk scattering surface probed by optical and near-IR observations. This issue is inevitable as the younger disks are generally optically thick at shorter wavelengths.

One possibility to overcome this issue is to observe debris disks, which are optically thin. Graham et al. (2007) showed that scattered light around AU Mic may be explained by fluffy, presumably primordial, aggregates. At a wavelength of λ = 0.590 μm, the observed polarization fraction is as high as 0.4, and the authors estimated the maximum polarization of each aggregate to be Pmax > 0.5. Although a high polarization at an optical wavelength could be explained by large and dark compact aggregates (see Fig. 6 lower, right panel), these aggregates tend to make the disk color reddish (Min et al. 2016), while the fluffy aggregates makes it gray or blueish (Tazaki et al. 2019). Given bluish scattered light around AU Mic (Fitzgerald et al. 2007), the assumption of fluffy aggregates with sub-micron monomers seems favorable. A similarity of the monomer size between optically thick younger disks and a debris disk lends further credibility to that sub-micron-sized monomers are an apt representative of a dominant building block of aggregates.

It is worth mentioning that there are some debris disks that show qualitatively different scattering polarization properties from the AU Mic disk, such as HR 4796 A. For HR 4796 A, the total intensity phase function exhibits enhanced back scattering (Milli et al. 2017), and the degree of polarization peaks at a scattering angle of 40−50 degrees (Perrin et al. 2015; Arriaga et al. 2020). None of our simulation results satisfy these properties. However, very large (≳100 μm), densely packed aggregates of sub-micron- and micron-sized monomers may explain such observations (Markkanen et al. 2018). Thus, light scattering simulations for very large aggregates would be crucial in constraining the monomer sizes for such disks.

The monomer sizes inferred in this study are smaller than those needed to explain the disk observations of millimeter-wave scattering polarization (R0 ≳ μm) (Okuzumi & Tazaki 2019; Arakawa & Krijt 2021). On the other hand, the inferred sizes are reminiscent of the maximum sizes of interstellar grains or typical subunits sizes seen in solar system dust aggregates. For the interstellar grain model, the maximum grain radius of 250 nm has been often employed (Mathis et al. 1977; Draine & Lee 1984). A more recent model also adopts a grain size distribution peaked at ~200 nm (Jones et al. 2013).

In the solar system, the chondritic porous interplanetary dust particle (CP IDP) typically exhibits a cluster-of-grapes morphology with an average subunit size of 300 nm in diameter (Brownlee 1985). Rietmeijer (1993) measured the subunit-size distribution of one CP IDP and found that the subunit size spans from 64 to 7580 nm with a mean of 585 nm in diameter and follows a log-normal distribution. One of the major constituents of CP IDP is GEMS (glass with embedded metal and sulfide). Wozniakiewicz et al. (2013) measured the size distribution of GEMS in four CP IDPs. The geometric mean subunit sizes are ranging from 76−138 nm in radius for the four CP IDPs. Despite its similarity to the interstellar grain sizes, GEMS has been considered to be the condensates at the early solar nebula rather than the one directly inherited from the interstellar medium (Keller & Messenger 2011).

Recent in situ measurements of dust aggregates of the comet 67P/C-G by the Rosetta/MIDAS instrument have also revealed the presence of sub-micron-sized subunits. Bentley et al. (2016) identified seven subunits in particle D (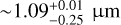 in size), using a 80-nm-scan resolution, which range from 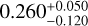to 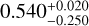in diameter. Mannel et al. 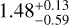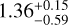(2016) also derived a subunit distribution of larger particles E and F and obtained the mean subunit diameter of and , respectively, although the scan resolutions of particles E and F are 210 nm and 195 nm, respectively and, thereby, they are worse than those used to analyze particle D. Mannel et al. (2019) analyzed the subunits of particle G with a high-resolution scan (8 nm resolution) and derived the arithmetic mean subunit diameter of 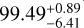. They also hypothesized that particles D, E, and F, which were analyzed with a lower scan resolution in earlier studies, also consist of ~100 nm subunits in diameter.

The tensile strength of the comet 67P/C-G provides another way to study the cometary monomer size. Based on a formula derived from numerical simulations, Tatsuuma et al. (2019) estimated a monomer radius to be 3.3−220 μm to explain the tensile strengths. Kimura et al. (2020b) claims, however, that sub-micron sized monomers can still explain the observation if the volume effect in tensile strengths plays a role. In this way, the monomer radius derived from the tensile strength of the comet 67P/C-G seems still inconclusive and further study is necessary.

Although our results do not allow us to distinguish the origin of monomers, such as interstellar origin and condensation at the disk forming epoch, the common statement that the planet formation begins with coagulation of sub-micron monomers has been confirmed from the vantage of disk observations for the first time.

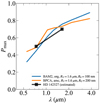thumbnail Fig. 8

Wavelength dependence of the maximum polarization toward the disk around HD 142527. The orange and blue lines show BPCA clusters with amc-200 monomers and BAM2 clusters with org-100 monomers, respectively. Both aggregate models have RV = 1.6 μm.

5.2 On the stickiness of icy aggregates in planet-forming disks

Recent detections of millimeter-wave scattering polarization provide new insight into the aggregate sizes in planet-forming disks (Kataoka et al. 2016; Stephens et al. 2017; Hull et al. 2018; Ohashi et al. 2018,2020; Ohashi & Kataoka 2019; Bacciotti et al. 2018; Dent et al. 2019; Mori & Kataoka 2021). To reproduce the millimeter-wave polarization of the HL Tau disk, Okuzumi & Tazaki (2019) argued that the critical fragmentation velocity should be as low as 0.1−1 m s−1. However, the origin of such a low critical fragmentation velocity is still unknown.

The critical fragmentation velocity is known to scale as (Dominik & Tielens 1997) 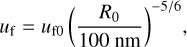(1)

where uf0 is the fragmentation velocity of aggregates consist of 0.1-μm-sized monomers. In general, uf0 depends on surface materials coating each monomer and aggregate structure. To explain the suggested low uf value, two possibilities exist (i) larger monomer radii (R0 ≳ μm) and/or (ii) lower adhesion forces (a low uf0 value). As we found that the monomer radius in the HL Tau nebula may be around 0.4 μm (Sect. 3.3), the second possibility appears to be more likely. When R0 = 400 nm, we require the following: uf0 ≲ 3 m s−1.

For H2O-ice aggregates, by performing numerical collisional simulations, Wada et al. (2009) derived uf0 = 50 m s−1 for collisions between equal-sized aggregates. The velocity may vary from uf0 ~ 25−80 m s−1 depending on the mass ratio of colliding aggregates (Wada et al. 2013; Hasegawa et al. 2021). Laboratory experiments have also supported this highly sticky properties of H2O ice (Gundlach & Blum 2015). Although recent experiments suggest a weaker stickiness of H2O ice at a lower temperature (Musiolik & Wurm 2019; Gundlach et al. 2018), the interpretation of temperature dependence is still a matter of discussion (Kimura et al. 2020a,b). If H2O ice is as sticky as previously thought, the values of uf0 are an order of magnitude higher than our necessary value, uf0 ≲ 3 m s−1. Therefore, H2O ice would not be the primary surface composition of monomers, at least not in the outer disk regions that we can observe.

One possible explanation is the presence of CO2 ice on the monomer surface. Laboratory experiments have shown that CO2 ice is much less sticky than H2O ice (Musiolik et al. 2016a,b; Fritscher & Teiser 2021), namely, uf0 ~ 5 m s−1 (Okuzumi & Tazaki 2019). Arakawa & Krijt (2021) attributed the higher stickiness of H2O ice than CO2 to viscoelastic dissipation upon collisions. Due to its poor stickiness, the presence of CO2 ice has significant impact on dust coagulation outside the CO2 snowline (Pinilla et al. 2017; Okuzumi & Tazaki 2019). Although the value (uf0 ~ 5 m s−1) is still higher than the required values, it has a similar order of magnitude. Thus, we speculate that monomers at the outer disk regions are covered by non-sticky ice, such as CO2, and then efficient collisional fragmentation gives rise to relatively small aggregate sizes, as inferred from observations.

5.3 Implications for streaming instability

One scenario for planetesimal formation is the streaming instability (Youdin & Goodman 2005) followed by a strong dust clumping (Johansen et al. 2007, 2009; Bai & Stone 2010a,b; Sekiya & Onishi 2018; Carrera et al. 2021). In the absence of external turbulence, dust settling will set the maximum dust-to-gas ratio, which is proportional to the metallicity. The threshold metallicity required to trigger the strong clumping rapidly increases with decreasing the particle Stokes number (Carrera et al. 2015; Yang et al. 2017; Li & Youdin 2021). One key question is whether collisional growth results in a Stokes number large enough to trigger such a strong clumping (Drazkowska & Dullemond 2014; Lorek et al. 2018).

If dust coagulation in the disks is limited by collisional fragmentation, the Stokes number of the maximum grain radius will be given by (Birnstiel et al. 201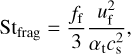2): (2)

where αt is the turbulence parameter, cs is the sound speed, and ff = 0.37 is a numerical factor. It is important to notice the fact that Stfrag no longer depends on the gas surface density and the material density. By substituting Eq. (1) into Eq. (2), we obtain 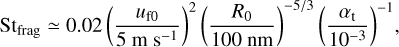(3)

where we have used cs = 3.8 × 104 cm s−1.

We estimate the metallicity, Z, needed to trigger strong clumping by using a model by Li & Youdin (2021). Assuming a typical pressure gradient parameter Π = 0.05, we obtain Z ≥ 0.1 for α = 10−3 and Stfrag = 0.02, and Z ≥ 0.008 for α = 10−4 and Stfrag = 0.2. Thus, in the moderate turbulence case (αt = 10−3), we need a metallicity that is ten times lager than a nominal value of 0.01 to trigger the strong clumping due to the streaming instability.

Therefore, even in the outer region of the disk, efficient particle accumulation seems necessary for triggering strong clumping unless the turbulence is extremely low. In the above estimate, the role of turbulence is to just determine the thickness of the dust disk layer. However, a role for turbulence would not be that simple. Johansen et al. (2007) found that turbulence driven by magneto-rotational instability may create a temporary overdense region, which promotes the subsequent clumping by the streaming instability. In this way, on the one hand, external turbulence renders clumping challenging. On the other hand, it promotes clumping. Therefore, clarifying the interplay between external turbulence and the streaming instability would be essential to draw conclusions regarding the question of whether it works out in a turbulent disk.

6 Summary

We studied the effect of monomer size and composition on scattering polarization of dust aggregates by using an exact light scattering technique. Applying the simulation results to disk observations, we have estimated the monomer radius of aggregates in planet-forming disks for the first time. The main findings of this paper are as follows. – The maximum degree of polarization of aggregates sensitively depends on the monomer size when the monomer size parameter x0 ≳ 1−2. Contrary to the previous study, we showed that the effect of monomer size appears not only for highly porous aggregates (℘ ~ 87%) but also for less porous aggregates (℘ ~ 59%), although less porous aggregates need a slightly larger monomer size for this effect to appear (Sect. 3.1).

  • In contrast, the maximum degree of polarization of aggregates becomes insensitive to monomer size when x0 ≲ 1. In this case, the maximum polarization depends mainly on aggregate size, porosity, and composition. In general, aggregates with a larger size, lower porosity, or a higher real part of the refractive index tend to yield a lower maximum polarization fraction at near-IR wavelengths (Sects. 3.1 and 3.2).

  • Since the effect of monomer size is noticeable when x0 ≳ 1−2, the optical or near-IR wavelengths are the optimal wavelengths to distinguish between sub-micron-sized and micron-sized monomers because the monomer size parameter becomes close to or larger than unity at these wavelengths (Sect. 3.1).

  • By comparing our results with the observations, we found that the monomer radius appears to be no greater than 0.4 μm for several planet-forming disks (Sect. 3.3). We also found that a monomer radius of 0.1−0.2 μm seems favorable to explain the recent polarimetric observations of the disk around HD 142527 (Sect. 4).

  • It may be possible that the monomers are much smaller than 0.1 μm. In this case, our results predict that the variation in the maximum polarization fractions of various disks at optical wavelengths will be similar to that at near-IR wavelengths. In contrast, the variation in optical polarization would be small compared to the near-IR variation when the monomer are larger than 0.1 μm. A large optical polarization survey of planet-forming disks is therefore useful to test the monomer size (Sect. 3.3).

  • Within the limit of our composition model, we can rule out dark densely-packed aggregates at the disk surfaces, as they exhibit a bluish color of the maximum degree of polarization at optical and near-IR wavelengths, which is inconsistent with the observed reddish colors (Sect. 3.3).

Optical and near-IR quantitative polarimetry will provide the observational grounds on the initial conditions required for dust coagulation, and thereby, planetesimal formation in disks.

Acknowledgements

R.T. acknowledges the JSPS overseas research fellowship. We thank Daniel Mackowski and Maxim A. Yurkin for making the MSTM and ADDA codes publicly available, respectively. We also thank Bruce Draine for the availability of particle data of BA, BAM1, and BAM2. We thank J. Ma and H. M. Schmid for a fruitful discussion.

Appendix A Maximum polarization of BAM1 and BAM2 clusters

Fig. A.1 shows the maximum polarization for BAM1 and BAM2 clusters.

thumbnail Fig. A.1

Wavelength dependence of Pmax for BAM1 (upper panels) and for BAM2 (lower panels) with the org (upper rows) and amc (lower rows) compositions. From left to right: Monomer radius of the aggregates is R0 = 100, 200, and 400 nm, respectively. The gray solid line in each panel represents Рщах for a single spherical monomer.

Appendix B Effect of particle shapes on the maximum polarization

This study assumes spherical monomers. One of the artifacts arising from the assumption of spherical monomers is appearance of oscillatory patterns, sometimes referred to as ripples, in polarization curves when x0 > 1 (Bohren & Huffman 1983). Irregular particle shape usually results in smoother polarization curves, particularly for absorbing materials (Yanamandra-Fisher & Hanner 1999; Muinonen & Pieniluoma 2011). Although the presence of touching spherical monomers in an aggregate tends to suppress the oscillation (Xing & Hanner 1997), it is still possible that the perfect sphere assumption might introduce some artifact in wavelength dependence of polarization, particularly when the monomer size parameter exceeds unity.

Previous studies have shown that the maximum polarization of aggregates of nonspherical monomers tends to be similar or slightly lowered to those of spherical monomers. Xing & Hanner (1997) compared optical properties of aggregates of spheres and tetrahedral monomers with m = 1.88 + 0.71i. Although the scattering polarization by a single sphere and tetrahedron differs significantly, once the monomers are aggregated and touched each other, the resultant maximum polarizations from aggregates of ten spheres and ten tetrahedrons are surprisingly similar to each other (see, e.g., Fig. 9ab in Xing & Hanner 1997). Meanwhile, Moreno et al. (2007) investigated aggregates of 256-spheres and -cubes with an absorbing composition and found that Pmax of aggregates of cubic monomers show a lower polarization degree by about 20% points. In their comparison, the side length of the cube and sphere diameter were taken to be the same. However, as pointed out by Kimura et al. (2016), their comparison allows cubic monomers to be larger than spherical monomers in terms of volume, and thus it is unclear to what extent the difference in Pmax can be purely attributed to the shape effect of the monomers. Lumme & Penttilä (2011) performed simulations using discrete dipole approximation (DDA) for aggregates consisting of Gaussian random sphere (GRS) particles with a less absorbing composition (k = 0.01). Although the maximum polarization degree is lowered for aggregates of nonspherical monomers, the effect is found to be non-significant.

To assess the effect of monomer shape on the degree of polarization, we compared the scattering polarization of a single sphere and a nonspherical particle. For the nonspherical particle, we generated GRS particles (Muinonen et al. 1996). As a Legendre expansion coefficient for the autocorrelation function, we adopt a power law function cl; ∝ l−v (l ≥ 2) (Nousiainen et al. 2003). We adopt v = 3.4 and the relative standard deviation of radius σ = 0.2. With these parameters, we can aptly mimic the irregularity of solid particles in nature, for instance, saharan dust particles (Muñoz et al. 2007). We generated ten realizations of GRS particles. One realization of GRS particles is shown in Fig. B.1. We adopt a DDA technique to solve the light scattering by GRS particles, using a publicly available code ADDA (Yurkin & Hoekstra 2011). Since the impact of non-sphericity on the degree of polarization appears mainly for x0 ≳ 1, we consider particles with 200 nm and 400 nm in volume-equivalent radius.

The results are shown in Fig. B.2. At near-IR wavelengths, the maximum degree of polarization of the GRS particles is almost identical to that of spherical particles for all cases. On the other hand, at optical wavelengths, the maximum polarization of the GRS particles deviates significantly from that of the spherical particles for the amc composition. This is mainly because the nonspherical particles smear out ripple patterns in the polarization curves (Fig. B.1).

Because such a strong ripple can be similarly suppressed by the presence of touching spherical monomers (see the polarization curve of the BPCA clusters in Fig. B.1), the differences in the maximum polarization between aggregates made of GRS and spherical particles would be less noticeable than those seen in Fig. B.2 (Xing & Hanner 1997). However, some difference may possibly remain. Therefore, the assumption of spherical monomers would be robust at least around near-IR wavelengths, but might introduce some artifacts at optical wavelengths, particularly for amc-200 and -400.

thumbnail Fig. B.1

Effect of non-sphericity on polarization curves. Scattered light of a single sphere (dashed line) and GRS particles (solid line) with amc-400 at λ = 0.554 μm. The volume-equivalent size parameter is 4.54. The results for GRS particles are averaged over ten realizations. A realization of GRS particles and a sphere are also shown. For comparison, the polarization curve for aggregates with 64-spherical monomers with amc-400 is shown as well.
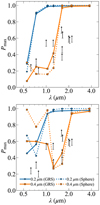thumbnail Fig. B.2

Effect of particle shape on the degree of polarization for the org (upper panel) and amc (lower panel) compositions. The blue and orange lines represent the results for RV = 0.2 μm and 0.4 μm, respectively. The solid and dashed lines represent the results for GRS particles and spherical particles, respectively.

Appendix C Effect of an intermediate composition on the maximum polarization

In Sect. 4, we argued that the observed maximum polarization fractions are inconsistent with aggregates with R0 = 400 nm. However, it is unclear to what extent this conclusion remains true if we relax the assumption of refractive indices. In particular, it follows from Fig. 7 that an intermediate composition between org and amc copmosition may yield a closer fit to the observations.

To test this possibility, we performed additional T-matrix simulations for BPCA clusters with an intermediate dust composition. We thus considered a mixture of organics and amorphous carbon as a carbonaceous component so that each monomer is made of five different materials: silicate, water ice, organics, amorphous carbon, and troilite. By changing the mass ratio of organics to total carbon (organics + amorphous carbon), we calculated the maximum degree of polarization.

The results are shown in Fig. C.1. It is found that even if we consider an intermediate composition, the results are still located outside the observationally inferred region. Although models with forg = 0.4−0.6 may be close to the observation, these models predict a significantly low polarization fraction at the J-band (Fig. C.1, left). The presence or absence of such a dip in the polarization fraction can be testable by future observations.

thumbnail Fig. C.1

Effect of an intermediate composition on the maximum polarization. Left panel: BPCA clusters with RV = 1.6 μm and R0 = 400 nm with five-composite materials (silicate, water ice, amorphous carbon, organics, and troilite); forg represents a mass fraction of organics with respect to total carbonaceous materials (organics + amorphous); forg = 0.0 and 1.0 mean the carbonaceous component is pure amorphous carbon and organics, respectively. Right panel: Same as Fig. 7, but for BPCA clusters with RV = 1.6 μm and R0 = 400 nm with five-composite materials.

References

  1. Arakawa, S., & Krijt, S. 2021, ApJ, 910, 130 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arriaga, P., Fitzgerald, M.P., Duchêne, G., et al. 2020, AJ, 160, 79 [NASA ADS] [CrossRef] [Google Scholar]
  3. Avenhaus, H., Quanz, S.P., Schmid, H.M., et al. 2014, ApJ, 781, 87 [NASA ADS] [CrossRef] [Google Scholar]
  4. Avenhaus, H., Quanz, S.P., Schmid, H.M., et al. 2017, AJ, 154, 33 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bacciotti, F., Girart, J.M., Padovani, M., et al. 2018, ApJ, 865, L12 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bai, X.-N., & Stone, J.M. 2010a, ApJ, 722, 1437 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bai, X.-N., & Stone, J.M. 2010b, ApJ, 722, L220 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bentley, M.S., Schmied, R., Mannel, T., et al. 2016, Nature, 537, 73 [NASA ADS] [CrossRef] [Google Scholar]
  9. Berry, M.V., & Percival, I.C. 1986, Optica Acta, 33, 577 [CrossRef] [Google Scholar]
  10. Bertini, I., Thomas, N., & Barbieri, C. 2007, A&A, 461, 351 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Betti, S.K., Follette, K., Jorquera, S., et al. 2022, AJ, 163, 145 [NASA ADS] [CrossRef] [Google Scholar]
  12. Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Birnstiel, T., Dullemond, C.P., Zhu, Z., et al. 2018, ApJ, 869, L45 [CrossRef] [Google Scholar]
  14. Bohren, C.F., & Huffman, D.R. 1983, Absorption and Scattering of Light by Small Particles (Hoboken: Wiley) [Google Scholar]
  15. Botet, R., Rannou, P., & Cabane, M. 1997, Appl. Opt., 36, 8791 [NASA ADS] [CrossRef] [Google Scholar]
  16. Brownlee, D.E. 1985, Ann. Rev. Earth Planet. Sci., 13, 147 [CrossRef] [Google Scholar]
  17. Carrera, D., Johansen, A., & Davies, M.B. 2015, A&A, 579, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Carrera, D., Simon, J.B., Li, R., Kretke, K.A., & Klahr, H. 2021, AJ, 161, 96 [NASA ADS] [CrossRef] [Google Scholar]
  19. Chokshi, A., Tielens, A.G.G.M., & Hollenbach, D. 1993, ApJ, 407, 806 [NASA ADS] [CrossRef] [Google Scholar]
  20. D'Alessio, P., Calvet, N., & Hartmann, L. 2001, ApJ, 553, 321 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dent, W.R.F., Pinte, C., Cortes, P.C., et al. 2019, MNRAS, 482, L29 [NASA ADS] [CrossRef] [Google Scholar]
  22. Dominik, C., & Tielens, A.G.G.M. 1997, ApJ, 480, 647 [NASA ADS] [CrossRef] [Google Scholar]
  23. Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [Google Scholar]
  24. Draine, B.T., & Lee, H.M. 1984, ApJ, 285, 89 [NASA ADS] [CrossRef] [Google Scholar]
  25. Drazkowska, J., & Dullemond, C.P. 2014, A&A, 572, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Dullemond, C.P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Fitzgerald, M.P., Kalas, P.G., Duchêne, G., Pinte, C., & Graham, J.R. 2007, ApJ, 670, 536 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fritscher, M., & Teiser, J. 2021, ApJ, 923, 134 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fukagawa, M., Tamura, M., Itoh, Y., et al. 2006, ApJ, 636, L153 [Google Scholar]
  30. Graham, J.R., Kalas, P.G., & Matthews, B.C. 2007, ApJ, 654, 595 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gundlach, B., & Blum, J. 2015, ApJ, 798, 34 [Google Scholar]
  32. Gundlach, B., Schmidt, K.P., Kreuzig, C., et al. 2018, MNRAS, 479, 1273 [NASA ADS] [CrossRef] [Google Scholar]
  33. Gustafson, B.Â.S., & Kolokolova, L. 1999, J. Geophys. Res., 104, 31711 [NASA ADS] [CrossRef] [Google Scholar]
  34. Halder, P., Deb Roy, P., & Das, H.S. 2018, Icarus, 312, 45 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hasegawa, Y., Suzuki, T.K., Tanaka, H., Kobayashi, H., & Wada, K. 2021, ApJ, 915, 22 [NASA ADS] [CrossRef] [Google Scholar]
  36. Henning, T., & Stognienko, R. 1996, A&A, 311, 291 [NASA ADS] [Google Scholar]
  37. Hull, C.L.H., Yang, H., Li, Z.-Y., et al. 2018, ApJ, 860, 82 [NASA ADS] [CrossRef] [Google Scholar]
  38. Hunziker, S., Schmid, H.M., Ma, J., et al. 2021, A&A, 648, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Johansen, A., Oishi, J.S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [NASA ADS] [CrossRef] [Google Scholar]
  40. Johansen, A., Youdin, A., & Mac Low, M.-M. 2009, ApJ, 704, L75 [NASA ADS] [CrossRef] [Google Scholar]
  41. Jones, A.P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Kataoka, A., Tanaka, H., Okuzumi, S., & Wada, K. 2013, A&A, 557, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Kataoka, A., Tsukagoshi, T., Momose, M., et al. 2016, ApJ, 831, L12 [Google Scholar]
  44. Keller, L.P., & Messenger, S. 2011, Geochim. Cosmochim. Acta, 75, 5336 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kimura, H. 2001, J. Quant. Spectr. Rad. Transf., 70, 581 [NASA ADS] [CrossRef] [Google Scholar]
  46. Kimura, H., & Mann, I. 2004, J. Quant. Spectr. Rad. Tranf., 89, 155 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kimura, H., Kolokolova, L., & Mann, I. 2003, A&A, 407, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Kimura, H., Kolokolova, L., & Mann, I. 2006, A&A, 449, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Kimura, H., Kolokolova, L., Li, A., & Lebreton, J. 2016, ArXiv e-prints [arXiv:1683.83123] [Google Scholar]
  50. Kimura, H., Wada, K., Kobayashi, H., et al. 2020a, MNRAS, 498, 1801 [Google Scholar]
  51. Kimura, H., Wada, K., Yoshida, F., et al. 2020b, MNRAS, 496, 1667 [NASA ADS] [CrossRef] [Google Scholar]
  52. Kobayashi, H., & Tanaka, H. 2021, ApJ, 922, 16 [NASA ADS] [CrossRef] [Google Scholar]
  53. Kolokolova, L., & Kimura, H. 2010, A&A, 513, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Kolokolova, L., Kimura, H., Ziegler, K., & Mann, I. 2006, J. Quant. Spectr. Rad. Transf., 100, 199 [NASA ADS] [CrossRef] [Google Scholar]
  55. Kozasa, T., Blum, J., & Mukai, T. 1992, A&A, 263, 423 [NASA ADS] [Google Scholar]
  56. Kozasa, T., Blum, J., Okamoto, H., & Mukai, T. 1993, A&A, 276, 278 [NASA ADS] [Google Scholar]
  57. Krijt, S., Ormel, C.W., Dominik, C., & Tielens, A.G.G.M. 2016, A&A, 586, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Li, R., & Youdin, A.N. 2021, ApJ, 919, 107 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lorek, S., Lacerda, P., & Blum, J. 2018, A&A, 611, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Lumme, K., & Penttilä, A. 2011, J. Quant. Spectr. Rad. Transf., 112, 1658 [NASA ADS] [CrossRef] [Google Scholar]
  61. Lumme, K., Rahola, J., & Hovenier, J.W. 1997, Icarus, 126, 455 [NASA ADS] [CrossRef] [Google Scholar]
  62. Ma, J., & Schmid, H.M. 2022, A&A, in press https://doi.org/10.1051/0004-6361/202142954 [Google Scholar]
  63. Mackowski, D.W., & Mishchenko, M.I. 1996, J. Opt. Soc. Am. A, 13, 2266 [NASA ADS] [CrossRef] [Google Scholar]
  64. Mackowski, D.W., & Mishchenko, M.I. 2011, J. Quant. Spectr. Rad. Transf., 112, 2182 [NASA ADS] [CrossRef] [Google Scholar]
  65. Mannel, T., Bentley, M.S., Schmied, R., et al. 2016, MNRAS, 462, S304 [NASA ADS] [CrossRef] [Google Scholar]
  66. Mannel, T., Bentley, M.S., Boakes, P.D., et al. 2019, A&A, 630, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Markkanen, J., Agarwal, J., Väisänen, T., Penttilä, A., & Muinonen, K. 2018, ApJ, 868, L16 [NASA ADS] [CrossRef] [Google Scholar]
  68. Mathis, J.S., Rumpl, W., & Nordsieck, K.H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
  69. Milli, J., Vigan, A., Mouillet, D., et al. 2017, A&A, 599, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Min, M., Rab, C., Woitke, P., Dominik, C., & Ménard, F. 2016, A&A, 585, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Monnier, J.D., Harries, T.J., Bae, J., et al. 2019, ApJ, 872, 122 [NASA ADS] [CrossRef] [Google Scholar]
  72. Moreno, F., Muñoz, O., Guirado, D., & Vilaplana, R. 2007, J. Quant. Spectr. Rad. Transf., 106, 348 [NASA ADS] [CrossRef] [Google Scholar]
  73. Mori, T., & Kataoka, A. 2021, ApJ, 908, 153 [NASA ADS] [CrossRef] [Google Scholar]
  74. Muinonen, K., & Pieniluoma, T. 2011, J. Quant. Spec. Radiat. Transf., 112, 1747 [NASA ADS] [CrossRef] [Google Scholar]
  75. Muinonen, K., Nousiainen, T., Fast, P., Lumme, K., & Peltoneimi, J. 1996, J. Quant. Spectr. Rad. Transf., 55, 577 [NASA ADS] [CrossRef] [Google Scholar]
  76. Mukai, T., Ishimoto, H., Kozasa, T., Blum, J., & Greenberg, J.M. 1992, A&A, 262, 315 [Google Scholar]
  77. Muñoz, O., Volten, H., Hovenier, J.W., et al. 2007, J. Geophys. Res. Atmos., 112, D13215 [Google Scholar]
  78. Murakawa, K., Oya, S., Pyo, T.S., & Ishii, M. 2008, A&A, 492, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Musiolik, G., & Wurm, G. 2019, ApJ, 873, 58 [NASA ADS] [CrossRef] [Google Scholar]
  80. Musiolik, G., Teiser, J., Jankowski, T., & Wurm, G. 2016a, ApJ, 818, 16 [Google Scholar]
  81. Musiolik, G., Teiser, J., Jankowski, T., & Wurm, G. 2016b, ApJ, 827, 63 [NASA ADS] [CrossRef] [Google Scholar]
  82. Nousiainen, T., Muinonen, K., & RäIsäNen, P. 2003, J. Geophys. Res. Atmos., 108, 4025 [NASA ADS] [CrossRef] [Google Scholar]
  83. Ohashi, S., & Kataoka, A. 2019, ApJ, 886, 103 [Google Scholar]
  84. Ohashi, S., Kataoka, A., Nagai, H., et al. 2018, ApJ, 864, 81 [NASA ADS] [CrossRef] [Google Scholar]
  85. Ohashi, S., Kataoka, A., van der Marel, N., et al. 2020, ApJ, 900, 81 [Google Scholar]
  86. Okuzumi, S., & Tazaki, R. 2019, ApJ, 878, 132 [Google Scholar]
  87. Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
  88. Okuzumi, S., Momose, M., Sirono, S.-I., Kobayashi, H., & Tanaka, H. 2016, ApJ, 821, 82 [NASA ADS] [CrossRef] [Google Scholar]
  89. Ormel, C.W., Spaans, M., & Tielens, A.G.G.M. 2007, A&A, 461, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Perrin, M.D., Schneider, G., Duchene, G., et al. 2009, ApJ, 707, L132 [NASA ADS] [CrossRef] [Google Scholar]
  91. Perrin, M.D., Duchene, G., Millar-Blanchaer, M., et al. 2015, ApJ, 799, 182 [NASA ADS] [CrossRef] [Google Scholar]
  92. Petrova, E.V., Jockers, K., & Kiselev, N.N. 2000, Icarus, 148, 526 [NASA ADS] [CrossRef] [Google Scholar]
  93. Petrova, E.V., Tishkovets, V.P., & Jockers, K. 2004, Sol. Syst. Res., 38, 309 [NASA ADS] [CrossRef] [Google Scholar]
  94. Pinilla, P., Pohl, A., Stammler, S.M., & Birnstiel, T. 2017, ApJ, 845, 68 [NASA ADS] [CrossRef] [Google Scholar]
  95. Pollack, J.B., Hollenbach, D., Beckwith, S., et al. 1994, ApJ, 421, 615 [NASA ADS] [CrossRef] [Google Scholar]
  96. Poppe, T., Blum, J., & Henning, T. 2000, ApJ, 533, 454 [NASA ADS] [CrossRef] [Google Scholar]
  97. Poteet, C.A., Chen, C.H., Hines, D.C., et al. 2018, ApJ, 860, 115 [NASA ADS] [CrossRef] [Google Scholar]
  98. Rameau, J., Chauvin, G., Lagrange, A.M., et al. 2012, A&A, 546, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Rietmeijer, F.J.M. 1993, Earth Planet. Sci. Lett., 117, 609 [CrossRef] [Google Scholar]
  100. Rodigas, T.J., Follette, K.B., Weinberger, A., Close, L., & Hines, D.C. 2014, ApJ, 791, L37 [NASA ADS] [CrossRef] [Google Scholar]
  101. Seizinger, A., & Kley, W. 2013, A&A, 551, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Sekiya, M., & Onishi, I.K. 2018, ApJ, 860, 140 [NASA ADS] [CrossRef] [Google Scholar]
  103. Shen, Y., Draine, B.T., & Johnson, E.T. 2008, ApJ, 689, 260 [NASA ADS] [CrossRef] [Google Scholar]
  104. Shen, Y., Draine, B.T., & Johnson, E.T. 2009, ApJ, 696, 2126 [NASA ADS] [CrossRef] [Google Scholar]
  105. Silber, J., Gledhill, T., Duchêne, G., & Ménard, F. 2000, ApJ, 536, L89 [Google Scholar]
  106. Stephens, I.W., Yang, H., Li, Z.-Y., et al. 2017, ApJ, 851, 55 [NASA ADS] [CrossRef] [Google Scholar]
  107. Tanii, R., Itoh, Y., Kudo, T., et al. 2012, PASJ, 64, 124 [NASA ADS] [Google Scholar]
  108. Tatsuuma, M., Kataoka, A., & Tanaka, H. 2019, ApJ, 874, 159 [Google Scholar]
  109. Tazaki, R., & Tanaka, H. 2018, ApJ, 860, 79 [NASA ADS] [CrossRef] [Google Scholar]
  110. Tazaki, R., Tanaka, H., Okuzumi, S., Kataoka, A., & Nomura, H. 2016, ApJ, 823, 70 [NASA ADS] [CrossRef] [Google Scholar]
  111. Tazaki, R., Tanaka, H., Muto, T., Kataoka, A., & Okuzumi, S. 2019, MNRAS, 485, 4951 [NASA ADS] [CrossRef] [Google Scholar]
  112. Tazaki, R., Murakawa, K., Muto, T., Honda, M., & Inoue, A.K. 2021, ApJ, 921, 173 [NASA ADS] [CrossRef] [Google Scholar]
  113. Tschudi, C., & Schmid, H.M. 2021, A&A, 655, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Volten, H., Muñoz, O., Hovenier, J.W., et al. 2007, A&A, 470, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2009, ApJ, 702, 1490 [Google Scholar]
  116. Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2011, ApJ, 737, 36 [CrossRef] [Google Scholar]
  117. Wada, K., Tanaka, H., Okuzumi, S., et al. 2013, A&A, 559, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Warren, S.G., & Brandt, R.E. 2008, J. Geophys. Res. Atmos., 113, D14220 [NASA ADS] [CrossRef] [Google Scholar]
  119. Weidenschilling, S.J. 1984, Icarus, 60, 553 [NASA ADS] [CrossRef] [Google Scholar]
  120. Weidenschilling, S.J. 1997, Icarus, 127, 290 [NASA ADS] [CrossRef] [Google Scholar]
  121. Weidling, R., Güttler, C., Blum, J., & Brauer, F. 2009, ApJ, 696, 2036 [NASA ADS] [CrossRef] [Google Scholar]
  122. West, R.A. 1991, Appl. Opt., 30, 5316 [NASA ADS] [CrossRef] [Google Scholar]
  123. Wozniakiewicz, P.J., Bradley, J.P., Ishii, H.A., Price, M.C., & Brownlee, D.E. 2013, ApJ, 779, 164 [NASA ADS] [CrossRef] [Google Scholar]
  124. Xing, Z., & Hanner, M.S. 1997, A&A, 324, 805 [NASA ADS] [Google Scholar]
  125. Yanamandra-Fisher, P.A., & Hanner, M.S. 1999, Icarus, 138, 107 [NASA ADS] [CrossRef] [Google Scholar]
  126. Yang, C.-C., Johansen, A., & Carrera, D. 2017, A&A, 606, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Youdin, A.N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
  128. Yurkin, M.A., & Hoekstra, A.G. 2011, J. Quant. Spectr. Rad. Transf., 112, 2234 [NASA ADS] [CrossRef] [Google Scholar]
  129. Zerull, R.H., Gustafson, B.A.S., Schulz, K., & Thiele-Corbach, E. 1993, Appl. Opt., 32, 4088 [NASA ADS] [CrossRef] [Google Scholar]
  130. Zsom, A., Ormel, C.W., Güttler, C., Blum, J., & Dullemond, C.P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  131. Zubko, V.G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
1

The particle position data is available from B. T. Draine’s Web site https://www.astro.princeton.edu/~draine/agglom.html

2

The usage of “compact aggregates” refers those with a higher fractal dimension (see Fig. 10 in Tazaki et al. 2019). Thus, this statement does not necessarily mean low porosity aggregates. For example, BPCA clusters have a fractal dimension of 3 and are thought to be eligible for producing a reddish color, but their porosity of ~85% is still a class of highly porous.

All Tables

Table 1

Real (n) and imaginary (k) parts of the refractive index of each monomer made of a mixture of silicate, water ice, carbonaceous (organics or amorphous carbon), and troilite.

In the text

All Figures

thumbnail Fig. 1

Observed maximum polarization fractions of several planet-forming disks. References: HD 142527 (Hunziker et al. 2021), HD 169142 (Tschudi & Schmid 2021), HD 34700 A (Monnier et al. 2019), GG Tau (Silber et al. 2000), AB Aur (Perrin et al. 2009), UX Tau A (Tanii et al. 2012), TW Hya (Poteet et al. 2018), HL Tau nebula region (Murakawa et al. 2008), and AU Mic (Graham et al. 2007).
In the text
thumbnail Fig. 2

BPCA (upper), BAMl (middle), and BAM2 (lower) clusters with the volume-equivalent radius of RV = 1.6 μm. From left to right, the number of monomers and the monomer radius (N, R0) are (64, 400 nm), (512, 200 nm), and (4096, 100 nm), respectively.
In the text
thumbnail Fig. 3

Effect of monomer size for aggregates with a porosity of ~87%. Upper panel: degree of linear polarization of light scattered by aggregates with the org composition at λ = 1.04 μm. The blue, orange, and green lines are the results for R0 = 100, 200, 400 nm, respectively. Lower panel: wavelength dependence of the maximum polarization. The observed maximum polarization fractions are plotted as lower limits, since the amount of depolarization that the observed polarized light suffered is unknown.
In the text
thumbnail Fig. 4

Effect of monomer size for the aggregates with a porosity of ~59%. The orange and green lines are the results for R0 = 200 nm (BAM2 clusters of 128 monomers) and 400 nm (BAM1 clusters of 16 monomers), respectively. The porosity of each aggregate is indicated in the legend. The inset panel shows the angular dependence of the degree of polarization (−S12/S11) at two wavelengths (solid lines: λ = 1.63 μm, dotted lines: λ = 1.04 μm).
In the text
thumbnail Fig. 5

Wavelength dependence of Pmax for BPCA with the org (upper panels) and amc (lower panels) compositions. From left to right: monomer radius of the aggregates is R0 = 100, 200, and 400 nm, respectively. The gray solid line in each panel represents Pmax for a single spherical monomer.
In the text
thumbnail Fig. 6

Effect of porosity on the maximum polarization for the aggregates with Rc = 2.0 μm with the org (upper panels) and amc (lower panels) compositions. From left to right: monomer radius of the aggregates is R0 = 100, 200, and 400 nm, respectively. The yellow, brown, and cyan lines represent the results for BPCA, BAM1, and BAM2. The porosity of each aggregate model, ℘, is indicated in each legend.
In the text
thumbnail Fig. 7

Maximum polarization of dust aggregates at the VBB (optical) and the H-band (near-IR) with RV = 1.6 μm. Different line styles correspond to different aggregate models (BPCA: solid, BAM1: dashed, BAM2: dotted lines), and different symbols correspond to different composition models (circles: org, squares: amc). The number beside each point denotes the monomer radius in unit of μm. The dark gray hatched area is the maximum polarization estimated by Hunziker et al. (2021), while the light gray hatched area is the estimated Pmax values for an assumed range of the single scattering albedo of 0.5−0.95.
In the text
thumbnail Fig. 8

Wavelength dependence of the maximum polarization toward the disk around HD 142527. The orange and blue lines show BPCA clusters with amc-200 monomers and BAM2 clusters with org-100 monomers, respectively. Both aggregate models have RV = 1.6 μm.
In the text
thumbnail Fig. A.1

Wavelength dependence of Pmax for BAM1 (upper panels) and for BAM2 (lower panels) with the org (upper rows) and amc (lower rows) compositions. From left to right: Monomer radius of the aggregates is R0 = 100, 200, and 400 nm, respectively. The gray solid line in each panel represents Рщах for a single spherical monomer.
In the text
thumbnail Fig. B.1

Effect of non-sphericity on polarization curves. Scattered light of a single sphere (dashed line) and GRS particles (solid line) with amc-400 at λ = 0.554 μm. The volume-equivalent size parameter is 4.54. The results for GRS particles are averaged over ten realizations. A realization of GRS particles and a sphere are also shown. For comparison, the polarization curve for aggregates with 64-spherical monomers with amc-400 is shown as well.
In the text
thumbnail Fig. B.2

Effect of particle shape on the degree of polarization for the org (upper panel) and amc (lower panel) compositions. The blue and orange lines represent the results for RV = 0.2 μm and 0.4 μm, respectively. The solid and dashed lines represent the results for GRS particles and spherical particles, respectively.
In the text
thumbnail Fig. C.1

Effect of an intermediate composition on the maximum polarization. Left panel: BPCA clusters with RV = 1.6 μm and R0 = 400 nm with five-composite materials (silicate, water ice, amorphous carbon, organics, and troilite); forg represents a mass fraction of organics with respect to total carbonaceous materials (organics + amorphous); forg = 0.0 and 1.0 mean the carbonaceous component is pure amorphous carbon and organics, respectively. Right panel: Same as Fig. 7, but for BPCA clusters with RV = 1.6 μm and R0 = 400 nm with five-composite materials.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.