| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 11 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202243366 | |
| Published online | 12 July 2022 | |
Hydrogen abstraction reactions in formic and thioformic acid isomers by hydrogen and deuterium atoms
1
Institute for Theoretical Chemistry, University of Stuttgart,
Stuttgart, Germany
e-mail: molpeceres@theochem.uni-stuttgart.de
2
Centro de Astrobiología (CSIC-INTA),
Ctra. de Ajalvir Km. 4, Torrejón de Ardoz,
28850
Madrid, Spain
e-mail: ijimenez@cab.inta-csic.es
3
Institute of Low Temperature Science, Hokkaido University,
Sapporo, Hokkaido, Japan
e-mail: oba@lowtem.hokudai.ac.jp
4
Insituto de Estructura de la Materia (IEM-CSIC), IEM-CSIC,
Calle Serrano 121,
28006
Madrid, Spain
5
Chemistry Institute, Federal University of Rio de Janeiro,
Rio de Janeiro, Brazil
Received:
18
February
2022
Accepted:
6
April
2022
Context. The isomerism of molecules in the interstellar medium and the mechanisms behind it are essential questions in the chemistry of organic molecules in space. In the particular case of simple formic and thioformic acids, the low temperatures found in molecular clouds indicate that cis-trans isomerization in the gas-phase must be impeded. Reactions taking place on top of interstellar dust grains may explain the isomer interconversion at low temperatures.
Aims. We studied the isomerization processes of formic and thioformic acid that are likely to take place on the surface of interstellar dust grains after being initiated by H abstraction reactions. Similarly, deuterium enrichment of the acids can occur by the same mechanism. Our objective is to shed light on both topics to expand our understanding of the key precursors of organic molecules in space.
Methods. We determined the rate constants for the H abstraction reactions as well as the binding energies for the acids on water ice using ab initio calculations and the instanton method for calculating the rate constants, including quantum tunneling. In addition, we tested the viability of the deuteration of formic acid with tailored experiments and looked for it on the L1544 source.
Results. For formic acid, there is a clear dependence of the H abstraction reactions on the isomer of the reactant, with rate constants at ~50 K that differ by five orders of magnitude. Correspondingly, we did not observe the trans-cis reaction in our experiments. In the case of thioformic acid, a very similar cis-trans reactivity is found for abstraction reactions at the thiol (-SH) group in contrast to a preferential reactivity that is found when abstractions take place at the -CH moiety. We found comparable binding energies for both isomers with average binding energies of around −6200 and −3100 K for formic and thioformic acid, respectively. Our binding energy calculations show that the reactions are precluded for specific orientations, affecting the overall isomerization rate. For H abstractions initiated by deuterium atoms, we found very similar trends, with kinetic isotope effects varying in most cases between 13 and 20.
Conclusions. Our results support the cis-trans interconversion of cis-formic acid on dust grains, suggesting that such an acid should not withstand the conditions found on these objects. On the other hand, the trans isomer is very resilient. Both isomers of thioformic acid are much more reactive. A non-trivial chemistry is behind the apparent excess of its trans isomer that is found in cold molecular clouds and star-forming regions due to a subtle combination of preferential reactivity and binding with the surface. In light of our results, all the deuterated counterparts of thioformic acid are viable molecules to be present on the ISM. In contrast, only the trans isomer of deuterated formic acid is expected, for which we provide upper bounds of detection. Given the mechanisms presented in this paper, other mechanisms must be at play to explain the tiny fraction of cis-formic acid observed in interstellar cold environments, as well as the current trans-DCOOH and trans-HCOOD abundances in hot-corinos.
Key words: ISM: molecules / molecular data / astrochemistry / methods: numerical / methods: observational / methods: laboratory: molecular
© G. Molpeceres et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Recent detections of molecules toward different sources show that under the harsh conditions characterizing the interstellar medium (ISM), many molecules present a different isomerism than they do on Earth. As an example, formic acid (FA, HC(O)OH) is mostly found (>99.9%) in its trans isomer under laboratory conditions (Maçôas et al. 2003). In space, cis-formic acid (c-FA) is much more abundant, between 33% measured in photodissociation regions (PDR) (Cuadrado et al. 2016) to around 6% measured in cold cores (Taquet et al. 2017; Agúndez et al. 2019). In the core of the origin of isomerism in space, there is a rich interplay between different chemical and physical processes. Among those we can find: specific formation routes both in the gas phase and on grains (Vazart et al. 2015; Loomis et al. 2015; Quan et al. 2016; Melli et al. 2018; Bizzocchi et al. 2020; Molpeceres et al. 2021), quantum-tunneling mediated isomerization (García de la Concepción et al. 2021, 2022), photoisomerization (Cuadrado et al. 2016), or chemical conversion after formation on grains (Shingledecker et al. 2020).
The previously mentioned, FA is a well-known molecule in interstellar chemistry that has been detected in pre-stellar cores, protostars, and protoplanetary discs (Zuckerman et al. 1971; Cernicharo et al. 2012; Vastel et al. 2014; Cuadrado et al. 2016; Favre et al. 2018; Agúndez et al. 2019; Rodríguez-Almeida et al. 2021). Similarly, thioformic acid (TFA, HC(O)SH) was recently detected toward the giant molecular cloud G+0.693-0.027 (Rodríguez-Almeida et al. 2021) and tentatively in the hot molecular core G31 (García de la Concepción et al. 2022). Observations indicate that the trans-thioformic acid (t-TFA) is more abundant than its cis form (Rodríguez-Almeida et al. 2021; García de la Concepción et al. 2022). These acids are fundamental as a gateway for complex organic molecules (COM) (Hollis et al. 2000; Modica & Palumbo 2010; Vastel et al. 2014; Jiménez-Serra et al. 2016; Öberg 2016). Similarly, TFA is an essential precursor in prebiotic and primordial Earth processes (Chandru et al. 2016; Foden et al. 2020).
At the low temperatures of cold, molecular cores, molecules with the size of FA and TFA are depleted on the surface of ice-coated interstellar dust grains. In the early stages of a molecular cloud, the ice composition of the ice mantle is amorphous solid water (ASW) (Boogert et al. 2015). Although it is estimated that around 1% of the total mass of molecular clouds is locked on grains, a rich chemistry takes place on their surfaces. Reactions with atomic hydrogen are a viable source of chemical richness on the surface of dust grains. An important type of reaction of adsorbates that significantly alters the isomeric excess is H abstraction reactions. Following a cycle of H abstraction and subsequent addition, a particular isomer can be interconverted into the other. In addition to H abstraction reactions, H addition reactions can also alter the isomeric excess.
In this work, we put the focus on H abstraction reactions from FA and TFA acids on grains, continuing our recent efforts to understand their chemistry and isomerism. In addition to the formation routes of TFA (Nguyen et al. 2021; Molpeceres et al. 2021) we very recently tackled the tunneling-mediated isomerization in the gas phase of both FA and TFA to find that, according to this mechanism, t-FA ought to be the only observable isomer (García de la Concepción et al. 2022). At the same time, the situation is more complex in the case of TFA, where the isomerization is indeed possible in the interstellar medium. The reactivity of H with FA has been studied on the surface of dust grains (Bisschop et al. 2007; Chaabouni et al. 2020) and in rare-gas matrix experiments (Cao et al. 2014). In the latter case, addition reactions are dominant. On grains, where several processes are competitive (H2 recombination, H diffusion), seemingly contradictory results were found: one indicates that FA must be relatively inert to hydrogenation (Bisschop et al. 2007) while the other supports the destruction of FA to form, for instance, CO2 and H2O. In this context, H abstraction reactions have not been considered and may take place in the event of an overall low reactivity. The H abstraction reactions from t-FA were studied by some of us (Markmeyer et al. 2019) in the context of the HOCO radical formation, finding an overall slow reaction. No information on c-FA is available. The reactivity of TFA with H is much less studied, although intramolecular isomerization has been studied (Kaur & Vikas 2014; García de la Concepción et al. 2022). In addition to isomerization, exchange reactions also favor deuterium enrichment (Aikawa et al. 2012). The deuterium fractionation of molecules is a good estimator of the chemical maturity of interstellar objects (Bacmann et al. 2003; Aikawa et al. 2012; Ceccarelli et al. 2014) and dedicated data is required to fine-tune our understanding of isotopic fractionation processes. We have also contributed to that goal in the present paper, extending our study to HD abstraction reactions.
We employed theoretical methods with an accurate treatment of quantum tunneling (Meisner et al. 2017; Lamberts & Kästner 2017; Oba et al. 2018; Álvarez-Barcia et al. 2018; Molpeceres & Kästner 2021; Miksch et al. 2021; Molpeceres et al. 2021) to investigate H abstraction reactions from FA and TFA, both by H and D atoms. Moreover, the effect of the binding of the acids with the surface in the context of their chemistry was elucidated. Supporting experiments were used to constrain the viability of the slow hydrogenation and deuteration of t-FA and observations of deuterated isotopologues of FA are also included to expand our conclusions on some of the reactions that we present. After a description of the theoretical methods used in our work, we study the chemistry of the acids, providing activation energies, reaction energies, binding energies, and reaction rate constants for all the adsorbates. All the reaction rate constants are fitted to commonly used analytic expressions to ease the implementation into astrochemical models. In addition, we provide kinetic isotopic effects (KIE) for H abstraction reactions promoted by D atoms.
2 Methodology
2.1 Computational details
2.1.1 Reaction rate constants
We probed the reactivity of both isomers of FA and TFA by performing two series of independent calculations. In the first place, we studied the kinetics of the following H abstraction reactions employing an implicit surface approach (Meisner et al. 2017):
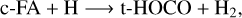 (1)
(1)
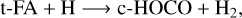 (2)
(2)
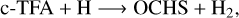 (3)
(3)
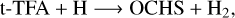 (4)
(4)
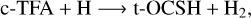 (5)
(5)
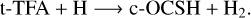 (6)
(6)
In the above reactions, c- and t-preceding the reactants indicate the cis (c) and trans (t) isomers of the reactant. In Fig. 1 we portray the structures of all reactants considered in this work. For TFA, we considered abstraction reactions both in the S-H and in the C-H moiety. Abstractions at the OH moiety are discarded on the basis of endothermicity (see below). To isomerize, the radicals formed on the surface can undergo subsequent hydrogenation:
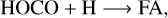 (7)
(7)
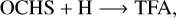 (8)
(8)
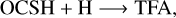 (9)
(9)
where the isomer form of the products is deliberately left ambiguous. In this second step, the parent molecule can be formed again as different isomer, depending on the orientation of the radical with the surface (Molpeceres et al. 2021).
For FA, preliminary explorations showed that the c,t-FA + H → t,c-OCHO reaction, e.g. abstraction of a H atom from the -OH moiety leading to the formation of the formate radical is endothermic irrespective of the parent FA isomer under consideration. For all the reactions (see Sect. 3), we also investigated the HD abstraction reactions. The protocol that we followed to study the reactions is as follows. First, we optimized the classical transition states from reasonable guesses of potential energy surface (PES) obtained from relaxed scan calculations. Second, we run intrinsic reaction coordinate (IRC) calculations starting from the transition state structure to obtain a guess for each reaction’s unimolecular reactant complex. The endpoints toward reactants of the IRC are later further optimized and used as reactant states for the rate constant calculations. Rate constants are then computed by means of semi-classical instanton theory (Langer 1967; Miller 1975; Coleman 1977; Rommel et al. 2011; Rommel & Kästner 2011) in the range from Tc to 50 K, with Tc being the crossover temperature for each reaction defined as the temperature where tunneling starts to dominate the rate constant value (see the formulation from Gillan 1987):
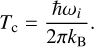 (10)
(10)
For reaction (2), we must stop at 65 K due to the difficulties of converging the instanton path below that temperature, as also found in a recent work (Markmeyer et al. 2019). These rate constants include a multidimensional treatment of quantum tunneling, which is a necessary trait for H abstraction reactions. The effect of a surface was simulated with the implicit surface approach (Meisner et al. 2017), as mentioned above, which allows for affordable treatment of surface effects. For computing the instanton rate constants, we optimized an initial instanton path close to the crossover temperature of each reaction. From that, we computed the rate constant at lower temperatures until the final temperature of 50 K (or 65 K in the case of t-FA, see above). There are no differences in the protocol between reactions involving H2 and HD. For all electronic structure calculations, we used the Gaussian16 (Frisch et al. 2016) suite of programs interfaced with DL-Find/ChemShell (Sherwood et al. 2003; Kästner et al. 2009; Metz et al. 2014). The level of theory employed throughout the rate constant calculations is MPWB1K/def2-TZVP (Zhao & Truhlar 2005; Weigend & Ahlrichs 2005), which rendered activation energies in excellent agreement (<1 kcal mol−1) with more expensive UCCSD(T)-F12a/cc-pVTZ calculations that we considered as our reference calculations. This level of theory was also ranked among the best ones in a previous study (Markmeyer et al. 2019). This functional behaves slightly worse for thermochemistry and the prediction of reaction energies, but such a magnitude does not interfere with the values of the rate constants. We nonetheless report also CCSD(T)-F12a/cc-pVTZ for this magnitude.
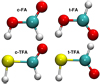 |
Fig. 1 Molecular structure of the FA and TFA isomers. |
2.1.2 Binding site estimation
We estimated the binding orientations for both isomers of FA and TFA from computational simulations explicitly accounting for the interaction between adsorbate and surface, in contrast to what is described in Sect. 2.1.1. The adsorbate orientation on a surface is fundamental to understanding reactivity. Some directions may promote or inhibit the reactions in specific places within the molecule. As a matter of fact, we recently found orientation effects during the formation of TFA from OCS due to the formation of hydrogen bonds of the OCSH radical with the surface (Molpeceres et al. 2021).
To determine the binding sites of the different adsorbates, we followed a sequential scheme following our previous works (Molpeceres & Kästner 2021). First, from a randomly generated water cluster containing 46 H2O molecules, we performed one molecular dynamics heating cycle at 300 K for 50 ps to amorphize the structure. From this simulation, we extracted five frames (one every 10 ps) and cooled them down to 10 K each for 10 ps. Each one of these structures is then further relaxed at the GFN2-xTB level of theory (Grimme et al. 2017; Bannwarth et al. 2019). This method allows for a fast and reliable exploration of adsorption geometries of closed-shell molecules, such as those covered in this study (Germain et al. 2021). In addition, we refined the electronic energies of the optimized structures with density functional theory (DFT) energies coming from the PW6B95-D3BJ/def2-TZVP method (Zhao & Truhlar 2005; Weigend & Ahlrichs 2005; Grimme et al. 2010, 2011). The choice of this functional is motivated by the improved thermochemistry associated with it (Zhao & Truhlar 2005). With the structural models for the ice in place, we set the molecules of interest, c/t-FA, and c/t-TFA, on the cluster, with the molecules’ centers of mass on equispaced points of an ellipsoid spanning a Fibonacci lattice. The initial distance between the molecules’ center of mass and the cluster is approximately 3 Å. We placed 12 adsorbates per structural model following this procedure, making a total of 12 × 5(structural models) × 4(adsorbates) = 240 initial structures. We finally relaxed the adsorbate+cluster structure for all of them. To ease the convergence of the structures, we fixed the atoms that were not at a minimum distance of 9 Å to any adsorbate atom at the beginning of the calculation. With all the necessary ingredients, the binding energies ΔEbin can be computed as:
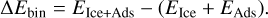 (11)
(11)
In the above equation, EIce+Ads corresponds to the potential energy of the adsorbate and ice complex at a short distance, EIce, to the potential energy of the water cluster and, EAds, to the potential energy of the adsorbate under consideration. We note that in a real ice, a greater variety of adsorption sites would be possible due to the codeposition of other molecules, for instance, CO on the ice. In this work, we are interested in the reactivity of FA and TFA with H/D and the possible orientation effects that stem from the interaction of the adsorbates with the surface leaving a particular molecular face available or forbidden for reaction. We have analyzed this effect in two steps. First, from the histogram of binding energies we took the structures corresponding to the high binding situations (e.g., higher than the average, 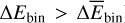 ) that are most likely to be populated under ISM conditions. Second, we measured the distance of any of the atoms susceptible to forming a hydrogen bond (all hydrogens and the carboxylic oxygen) with the closest water molecule for each one of these configurations. A value lower than ~2.2 Å indicates the formation of a localized hydrogen bond, locking that particular bond, and thus the orientation for the reaction. The formation of a hydrogen bond precludes the formation of an activated complex, due to the additional required energy to break the hydrogen bond between surface and adsorbate. The criterion that we apply is that each immobilized H atom from the adsorbate cannot react.
) that are most likely to be populated under ISM conditions. Second, we measured the distance of any of the atoms susceptible to forming a hydrogen bond (all hydrogens and the carboxylic oxygen) with the closest water molecule for each one of these configurations. A value lower than ~2.2 Å indicates the formation of a localized hydrogen bond, locking that particular bond, and thus the orientation for the reaction. The formation of a hydrogen bond precludes the formation of an activated complex, due to the additional required energy to break the hydrogen bond between surface and adsorbate. The criterion that we apply is that each immobilized H atom from the adsorbate cannot react.
2.2 Experimental setup
As shown in Sect. 3.1, for reaction (2), we found a low rate constant of around 1×10−1 s−1, as well as very similar behavior for HD abstraction. To experimentally check the viability of the reaction, experiments were performed using an Apparatus for Surface Reactions in Astrophysics (ASURA) at Hokkaido University. The ASURA mainly consists of a stainless-steel reaction chamber, an atomic source chamber, a quadrupole mass spectrometer, a Fourier-transform infrared spectrometer (FTIR), and an Al reaction substrate courted with amorphous silicates (Mg2SiO4) layers. More details can be found in Nguyen et al. (2020). The substrate temperature can be controlled between 5 and 300 K. Gaseous FA and D atoms were continuously co-deposited onto the pre-deposited porous amorphous solid water with the thickness of ~20 monolayers (MLs: 1 ML = 1 × 1015 molecules cm−2) at 10 K. The deposition rate of FA was 7.8 × 1011 molecules cm−2 s−1 and the D-atom flux was 4.6 × 1014 atoms cm−2 s−1, where the FA/D ratio was 1.7 × 10−3. D atoms were produced through the dissociation of D2 in a microwave-induced plasma in the atomic chamber and cooled to 100 K before landing on the substrate. Reaction products were monitored in situ by the FTIR.
2.3 Observations
We used the high-sensitivity observations carried out by Jiménez-Serra et al. (2016) toward the position of the dust peak in the L1544 pre-stellar core. This core is on the verge of gravitational collapse and it has experienced a strong depletion of CO, which induces deuterium fractionation as measured from deuterated species such as N2D+. Therefore, we have selected the position of the dust peak of L1544 because of the large D/H ratio measured toward this position (of ~25%; see Redaelli et al. 2019). The observations toward L1544 were carried out in the 3 mm band using the Institute de Radioastronomía Milimétrica (IRAM) 30 m telescope. The achieved rms noise level was 1.6–2.8 mK for the dust peak position in L1544. The details of these observations can be found in Jiménez-Serra et al. (2016). We note, however, that they did not cover the full 3 mm band.
In order to cover the frequency gaps of the high-sensitivity 3 mm survey of Jiménez-Serra et al. (2016), we also used the L1544 spectroscopic survey obtained within the ASAI (Astro-chemical Surveys At IRAM) Large Program (see Lefloch et al. 2017). The typical rms noise level achieved in the 3 mm band survey was 4–7 mK. The details of the observations can be found in Lefloch et al. (2017).
3 Results
3.1 H abstraction rate constants
In Table 1, we present all the energetic parameters of reactions (1)–(6). A detailed description for each reaction follows in the next subsections.
Reaction energies (including ZPE, ΔUr in kJ mol−1) at the MPWBlK7def2-TZVP level and at UCCSD(T)-F12/cc-pVTZ-F12 for the electronic energies (in parenthesis), activation energies (including ZPE, ΔUa) at the same level and crossover temperatures (Tc in K) for reactions (1) to (6).
 |
Fig. 2 Intrinsic reaction coordinate calculations for reactions 1 and 2 as described in the main text. Displayed energies are not corrected with zero point energy contributions. |
3.1.1 Formic acid (theoretical results)
The activation energies including ZPE contributions (ΔUa) for reactions (1) and (2) are 27.0 kJ mol−1 (30.3 kJ mol−1 at the UCCSD(T)-F12/cc-pVTZ-F12 level) and 40.2 (43.2) kJ mol−1. The activation energies in parenthesis refer always to UCCSD(T)-F12/cc-pVTZ-F12. Both activation energies are sufficiently separated to justify a preferential reactivity on the c-FA, which will be further developed in light of the orientation effects presented in the next section. The energy along the intrinsic reaction coordinate of both reactions is presented in Fig. 2. From the plot, we also observe that the H abstraction reaction is exothermic for both reactions with unimolecular reaction energies obtained from the optimization of the IRC endpoints of −19.2 (−27.3) kJ mol−1, in contrast to the values of c-FA, −37.8 (−44.1) kJ mol−1. This last result correlates with the value of the barrier and confirms preferential chemistry for the eis isomer. The different reactivity is, of course, also reflected in the different rate constants for the system, presented in Fig. 3. Our results agree with the values for the only available reaction (reaction (2)) (Markmeyer et al. 2019). As mentioned during Sect. 2.1.1, we could not converge instanten paths below 65 K for t-FA. From Fig. 3 we observe, however, that the reaction rate constants reasonably converge to the tunneling asymptotic limit.
The ~13 kJ mol−1 gap in the activation energies between the eis and trans isomer translates to more than five orders of magnitude in difference among the reaction rate constants. This renders the kinetics for the reaction radically different, favoring the destruction of c-FA over t-FA through H abstraction reactions. The shape of the barrier depicted in Fig. 2 also show that the barrier for reaction (2) is notably wider, which has a consequential effect in the rate constants as well.
 |
Fig. 3 Instanton reaction rate constants below Tc for reactions 1 and 2. |
3.1.2 Formic acid: Experiments
Another question that may arise regards whether reaction (2) really takes place or if it is not competitive with H diffusion or addition reactions (Bisschop et al. 2007; Chaabouni et al. 2020). A rate coefficient of 10−1 s−1 for the reaction is below the hopping rates for H diffusion found for average binding sites on amorphous solid water, as presented by Hama et al. (2012). Therefore, determining the viability of the reaction against diffusion is not trivial with respect to static quantum chemical calculations. We performed experiments with deuterium at low temperatures to check whether the reaction proceeds profiting from the small KIE of reaction (2) (see Sect. 4.2). The appearance of the C-D band at 2000–2200 cm−1 (typical wavenumbers for the C-D stretching band) will indicate that reaction (2) has taken place, followed by the addition of a D atom to the formed HOCO radical yielding DCOOH. Considering that FA is deposited in the UHV chamber at room temperature, it is safe to think that all FA is t-FA, taking into account an equilibrium constant (trans/cis) of 103 at 300 K (García de la Conceptión et al. 2022). In Sect. 4, we also present that H abstraction by deuterium in t-FA has very similar kinetics to H abstraction by hydrogen atoms; such a reaction will serve as an adequate proxy of reaction (2) in our experiments.
The results of the experiment, after a 3h co-deposition of FA and D atoms, are presented in Fig. 4. We do not clearly observe a C-D stretching band at 2000–2200 cm−1, and thus we consider reaction (2) non-viable under interstellar conditions. On the contrary, the abstraction of c-FA (Eq. (1)) cannot be directly observed under laboratory conditions owing to the large trans or eis equilibrium constant of FA, but experiments using the same setup show that rate constants in the order of fe(50) ~104s−1 are observable, as in the case of the hydrogénation of OCS (Molpeceres et al. 2021; Nguyen et al. 2021).
 |
Fig. 4 FTIR spectra obtained after (a) codeposition of FA and D atoms and (b) FA for 3 h at 10 K, along with (c) the difference spectrum between spectra (a) and (b). |
 |
Fig. 5 Intrinsic reaction coordinate calculations for reactions (3) to (6) as described in the main text. Displayed energies are not corrected with zero point energy contributions. |
3.1.3 Thioformic acid
In contrast to FA, hydrogen can be abstracted from TFA from two different positions of its structure, namely, in the thiol group (SH) and in the group (CH moiety). This is due to both hydrogen abstractions being exothermic, in contrast to the endothermic pathways found for the H abstraction in the OH group of formic acid, which serves as an analogy of what happens in H abstraction reactions on H2O and H2S.
In c-TFA, the H abstraction in the thiol group presents an activation barrier of 10.6 (9.9) kl mol−1 and the abstraction on the thiol group of t-TFA has a barrier of 10.3 (9.8) kJ mol−1, two very similar values. This is in contrast to the abstraction reactions on the CH moiety. Reaction (5) has an activation barrier of 12.9 (14.8) kJ mol−1, whereas reaction (6) presents a higher activation energy of 18.6 (20.3) kJ mol−1. The IRC for both abstractions is depicted in Fig. 5. We observe an identical reaction profile for the abstractions in the SH moiety in c/t-TFA. This is also in agreement with the very similar reaction energies of −57.8 (−63.9) and −54.5 (−61.3) kJ mol−1 for the eis and trans isomer, obtained from the IRC structures, as mentioned above. Both abstractions at the SH moiety present lower activation energies than their counterparts at the CH one. This trend is also coherent for the reaction energies, whose values are of −72.2 (−77.9) kl mol−1 for c-TFA and −60.1 (−66.7) kJ mol−1 for t-TFA using the same protocol, for the H abstraction at the CH moiety.
We portray the reaction rate constants for each reaction in Fig. 6. The results confirm the trend that we found for the activation energies. Although the abstraction in the thiol group does not show any particular trend, there is preferential destruction of c-TFA through reaction (5) to reaction (6). The specific importance of this reaction in the enrichment of t-TFA on dust requires information on the particular binding of c/t-TFA with the surface that we cover in the next section.
All the reactions on TFA present reaction timescales that should be observable in experiments. However, we have been unable to acquire pure TFA to conduct direct hydrogenation or deuteration experiments, and the conclusion must be made on the basis of on our theoretical results.
 |
Fig. 6 Instanton reaction rate constants below Tc for reactions (3)–(6). |
3.1.4 Fit to analytic expression
To ease the incorporation of the rate constants presented here into astrochemical models, we have fitted the results of the previous section to a modified Arrhenius–Kooij equation suited to account for the asymptotic profile of rate constants including quantum tunneling (Zheng & Truhlar 2010):
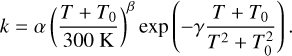 (12)
(12)
We fit the parameters: α (s−1), T0 (K), β and γ (K) for reactions (1)–(6) and the results are gathered in Table 2. Our fits deteriorate at low temperatures when a lot of points are included toward high temperatues, due to an over-representation of these points. Therefore (and also since we are interested in rate constants at low temperatures), we restricted the values of the fit to the rate constants below 250 K.
Fitted parameters of the modified Arrhenius-Kooij equation for reactions (1)–(6).
 |
Fig. 7 Binding energies of cis/trans-Formic acid. Dashed line -Gaussian fit of the binding energies. µcis = −6227 K, σcis = 1692 K. µtrans = −6170 K, σtrans = 1826 K. |
3.2 Binding energy estimation: Orientation effects
3.2.1 Formic acid
In addition to the reaction rate constants, orientation effects also drive the reactivity on ASW, especially considering that both FA and TFA are polar molecules. We determined the most favorable binding sites based on a distance criterion after computing the binding energies as described in Sect. 2.1.2. For FA, we present these binding energies in Fig. 7 with average binding energies µ and standard deviation σ. We observe hardly any difference in the binding energy distribution for both isomers. The average value for the binding energy, of around −6200 K, and the distributions are in very much concordance with the values already reported in the literature for pure DFT computations (Ferrero et al. 2020). A closer analysis on the possibility of hydrogen bonding revealing orientation effects is summarized in Table 3. The results show that the binding in formic acid is considerably localized, with the hydroxyl group permanently binding with the surface. Furthermore, in the case of t-FA, the C=O moiety is also always forming a bond with the surface (see Fig. 8).
3.2.2 Thioformic acid
The distribution of binding energies for the different isomers of TFA is presented in Fig. 9. The binding energies are, with average values of –3105 K for c-TFA and –3005 K for t-TFA, lower than in the case of FA and are very similar to the values of the OCSH radical (Molpeceres et al. 2021). Again the difference of binding energies between isomers is within the standard deviation values, and there is no significant change in the affinity of the molecules with the surface. As in the case of FA, we estimated the preferential binding mode for the binding sites with higher-than-average binding energies. The results are summarized in Table 4. Contrary to the situation found for FA, for TFA, not all the high binding situations are dominated by the interaction of the SH moiety with a water molecule, and some configurations leave room for reaction in the SH moiety. We found a similar behavior for the binding situations through the CO moiety. Another difference regarding FA appears when we determine the possibility of bonding through the CH group, which leads to a small, yet noticeable amount of binding situations (~7%). Finally, we found that c-TFA forms a hydrogen bond with ASW through the -SH moeity in a 88% of the high binding situations, in contrast to t-TFA where this quantity goes down to 63%, indicating that reactions in the thiol group are a 25% more likely in t-TFA (see Table 4, Col. (3)). A closer inspection of the structures reveals that the automated criterion is valid for a qualitative estimation of orientation effects.
Fraction of different localized binding for the high binding energy adsorption sites in the c/t-FA/H2O system.
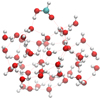 |
Fig. 8 Examplary binding orientation of t-FA on ASW. In the figure, we depict the clear localization in the binding orientation of the molecule forming two hydrogen bonds with different atoms of the surface. |
Fraction of different localized binding for the high binding energy adsorption sites in the c/t-TFA/H2O system.
 |
Fig. 9 Binding energies of cis/trans-Thioformic acid. Dashed line – Gaussian fit of the binding energies. Here, µcis = −3105 K, σcis = 1384 K. μtrans = −3005 K, σtrans = 1418 K. |
4 Discussion
4.1 Hydrogen abstraction of FA and TFA
The susceptibility of both FA and TFA to H abstraction reactions was found with kinetic (rate constants) and thermodynamic (binding sites) arguments. As explained during Sect. 2.1.1, the values of Table 3 and 4 refer to the fraction of orientations that prevent or enable a particular reactivity. In the case of reaction in the CH moiety, the attack site is available when no CH bonds are partaking in weak bindings with the surface. Similarly, when the SH moiety is involved, such an orientation is precluded when the SH bond is directly interacting with the surface. To facilitate the discussion, in Fig. 10 we present all the rate constants discussed in Sect. 3.1.
From the rate constants, we can extract several points for the isomerization of acids on the surface of interstellar grains in interstellar clouds. We confirmed a preferential reactivity based on isomerism by studying their interaction with hydrogen atoms. This preference emanates from two different factors, kinetic effects, and orientation effects. The short-range activation barriers for the reactions are different between isomers, a trend that was already observed for some reactions in a previous study (Shingledecker et al. 2020). This factor is usually the most important one, given the exponential dependence of the reaction rate constants on the magnitude of the activation energies and such is the case of H abstractions occurring on FA. However, we observe that the preferential binding has a significant effect on the reactivity of TFA isomers through reactions (3) and (4) (abstraction from the SH group). These two reactions, in turn, are the fastest from the present work. Reaction (3) occurs rarely, due to the SH group partaking in binding with the surface (0.88 of the molecules are locked, see Table 4). On the other hand, the localization fraction of t-TFA, of 0.63, suggests preferential t-TFA destruction. This finding contrasts with the chemical behavior found when comparing reactions (5) and (6). In this case, the rate constants vary by ~2 orders of magnitude with a negligible effect of the orientation effects (both isomers form hardly any localized bond with the surface, see Table 4, Col. 4), suggesting preferential c-TFA destruction. Therefore, it is tough for us to gauge the specific importance of the two factors for TFA, and we indicate that tailored kinetic simulations are required to shed light on this topic. Moreover, all the reactions with TFA are very fast and competitive with H diffusion on the grains (Hama et al. 2012).
The abstraction of H from any of the TFA isomers and positions combinations produces radicals that can further react with a specific stereochemistry (Molpeceres et al. 2021). Reactions (5) and (6) form either c/t-OCSH. While c/t-OCSH react with H to produce t/c-TFA (and sometimes H2S and CO (Nguyen et al. 2021; Molpeceres et al. 2021)), we found in our previous work that OCHS (produced from reaction (3) or reaction (4)) reacting with H produces either t-TFA or c-TFA with an estimated branching ratio of 0.67/0.33. A destruction of TFA through either reaction (3) or reaction (4) will eventually produce an enrichment on t-TFA. Nonetheless, one of the conclusions of our previous work was that OCS hydrogenation will produce hardly any c-TFA. With these new results we show, that even though it will still remain a small fraction, hydrogenation reactions on the grain can explain a small abundance of c-TFA, suggested by the recent tentative detection by us (García de la Conception et al. 2022).
The case of FA is more straightforward. The reactivity of FA with H in our considered reactions is so different between isomers that, according to our results, no c-FA should be present on the surface of interstellar dust grains. In addition, we did not find any evidence of localization effects of the CH moiety on FA. The presence of c-FA in cold regions (found in a fraction of ~1:20 to t-FA (Taquet et al. 2017; Agúndez et al. 2019; García de la Concepción et al. 2022) still remains a mystery. Indeed, García de la Concepción et al. (2022) recently found that the isomerization from c-FA to t-FA should dominate and, therefore, no c-FA is expected to be present in the gas phase of cold clouds. Similarly, in this work, we have found the same behavior, this time on grains. In summary, our results show that c-FA should not withstand the conditions of the cold ISM – and yet it does. Therefore, we have continued investigating the presence of c-FA in the ISM under various hypotheses, such as preferential gas-phase reactivity and photochemistry in the gas phase summed to the influence of nonthermal effects on the surface of the dust grains.
Parallel to H abstraction reactions, H additions might occur, affecting the overall balance of eis and trans isomers of both acids. In the case of FA, Chaabouni et al. (2020) reports that CO2 and H2O are the main products of the addition reactions on ASW. Reactions on other substrates (pyrolitic graphite) also lead to other organics, e.g., H2CO and H3COH but their presence is minor on ASW. As was mentioned in the introduction, the same reaction was not observed in other experiments (Bisschop et al. 2007), nor in the present study. Independent of whether the reaction is viable or not, a destruction channel forming CO2 and H2O (or CO2 and SH2 in the case of TFA) is irreversible and does not contribute to the isomerization processes that are the focus of the present work. In light of our results, t-FA, c-TFA, and t-TFA could be found on dust grains.
 |
Fig. 10 Rate constants for all the H abstraction reactions considered in the present work. |
4.2 Deuterium fractionation of FA and TFA
In addition to providing insights into the isomerism of both FA and TFA, the reactivity of the different species involved in this study with deuterium is important to elucidate fractionation effects. Two possibilities are at play. First, and after formation of H2, deuterium addition can proceed. Second, we can have HD formation where an incoming deuterium atom is the one reacting with the molecules.
For the D addition reactions, the same discussion as above for isomerism holds] and, therefore, we hypothesize that for TFA, all single deuterated species (t-HCOSD, c-HCOSD, t-DCOSH, c-DCOSH) are plausible. Similarly, double deuterated species are likely to be present. The computational cost of computing the instanton rate constants for all possible reaction and site combinations is very high. Therefore, we estimate that based on the high rate constants for HD abstraction (see below), the equivalent reactions from monodeuterated TFA are equally fast. For FA, only t-DCOOH is expected, owing to the endothermicity of the H abstraction from the OH group and the slow kinetics of reaction (2). Interestingly (and following this reasoning), the presence of t-DCOOH may imply a conversion on grains, indicating that at least some c-FA should deplete on top of them, where it is converted in t-FA. In Sect. 5, we explore whether t-DCOOH is detected under the coldest conditions of the interstellar medium as those found in pre-stellar cores.
Finally, we also estimated the rate constants for H abstractions with deuterium with the deuterated counterpart reactions of reactions (1)–(6). All of them, except for reaction (2), proceed fast enough, holding a very similar discussion as for the H abstraction reactions and showing KIE values of around ~ 10–20. In the case of reaction (2) and due to the smaller importance of tunneling at low temperatures, the reaction presents an inverse KIE of ~0.5. This occurs due to the reduced magnitude of the zero-point energy in the vibrational adiabatic barrier, rendering an overall lower barrier (by 4 kJ mol−1) that surpasses the effect of quantum tunneling at low temperatures. Whether there is a real inverse KIE or a null one will require computational methods capable of reaching spectroscopic accuracy. However, as we showed before, the reaction is not competitive to hydrogen (or deuterium) diffusion, and therefore, such an effect is uninteresting from an astrochemical point of view. The specific KIE for each reaction are summarized in Table 5 and the rate constants and corresponding fits are depicted in Fig. 11 and Table 6. We have not observed a significant preference for the reactions’ isomerism when using D atoms. Hence, all the trends discussed for H abstraction reactions hold for those of HD here.
To summarize, the reactivity of FA is clearly defined with preferential destruction of c-FA. The abstraction of H from c-FA forms t-HOCO that, after a subsequent H addition, reforms FA, with unknown isomerism. However, since t-FA does not experience such an abstraction, eventually all c-FA would be converted to t-FA, implying an excess of t-FA on grains by H abstraction reactions. This also holds for deuterations. In contrast, TFA is very reactive in all H-bearing positions, with some reactions showing preferential destruction thanks to either fast overall reaction or specific binding with the surface. It is clear that a very complex interplay of H2/HD abstractions and H/D additions exists and it requires a careful inspection by tailored kinetic models.
Kinetic isotope effects (KIE) at the lowest temperature (T in K) for the H abstraction reactions and their HD counterparts.
 |
Fig. 11 Rate constants for all the HD abstraction reactions considered in the present work. |
Fitted parameters of the modified Arrhenius-Kooij equation for the reactions (1)–(6) initiated by a D atom.
5 Comparison with observations of deuterated formic acid
As reported in Sect. 4.2, our kinetic calculations of the deuterium abstraction reactions for FA reveal that only trans-DCOOH is expected to be detected in the interstellar medium due to the endothermicity of the H abstraction reactions from the OH group. For hot sources such as hot corinos or hot cores, the formation efficiency of trans-DCOOH and trans-HCOOD on dust grains increases with increasing temperature (see Fig. 11) and therefore, we would expect to have higher chances of detection for this form of deuterated formic acid.
Consistently with our results, Jørgensen et al. (2018) reported the detection of trans-DCOOH toward the hot corino in IRAS 16293-2422 B. However, they also presented the discovery of trans-HCOOD toward the same source with a similar abundance. These results do not necessarily contradict our findings because FA could also form in the gas phase (Skouteris et al. 2018). It is however unknown whether deuterated formic acid can form efficiently in the gas phase, although we note that this formation route has been found to be efficient for more complex organics such as formamide (Skouteris et al. 2017).
For cold sources such as starless or pre-stellar cores, Fig. 11 reveals that trans-DCOOH should again be the most abundant form of deuterated formic acid in these sources, if produced on dust grains. To our knowledge, there are no observations of deuterated formic acid previously reported toward this type of sources; thus, we searched for it toward the L1544 pre-stellar core using the IRAM 30m high-sensitivity observations of Jiménez-Serra et al. (2016) and the ASAI Large Program data of Lefloch et al. (2017). Spectroscopic information for both the eis and trans isomers of DCOOH and HCOOD is available from the let Propulsion Laboratory (JPL) molecular line catalogue (see Pickett et al. 1998).
To search for these species, we used the SLIM (Spectral Line Identification and Modelling) tool within the MADCUBA package1 (Martín et al. 2019). SLIM generates the synthetic spectra of a molecular species assuming Local Thermodynamic Equilibrium (LTE) and derives the best fit of the observed spectra by using the Levenberg-Marquardt algorithm using the AUT-OFIT tool. The fit provides the physical parameters column density (Nobs), excitation temperature (Tex), velocity (Vlsr), and linewidth (Δυ)
The L1544 datasets do not reveal any emission detected from either c/t-DCOOH or c/t-HCOOD. In Table 7, we report the rms noise level and the upper limits of the column density and molecular abundance derived for all isomers of deuterated formic acid. The rms noise level has been calculated by considering the spectra within a velocity range of 5 km s−1 around each of the lines shown in Table 7. The upper limits to the column density and abundance of all forms of deuterated formic acid have been calculated assuming a radial velocity of VLSR = 7.2 km s−1 and a linewidth of Δυ = 0.4 km s−1. The derived column densities range from ≤2.9 × 1010 to ≤1.5 × 1011 cm−2, while the measured abundances range from ≤8.4 × 10−13 to ≤4.2 × 10−12.
Our results from Sect. 4.2 indicate that trans-DCOOH could be present in the ISM since it is expected to form efficiently on the surface of dust grains. Although we did not detect trans-DCOOH toward L1544, this non-detection does not allow us to rule out its grain surface formation because the derived abundance upper limit (of ≤2.0 × 10−12) is not stringent enough. Indeed, if we consider the abundance of t-HCOOH measured toward the position of L1544’s dust peak (of 8.9 × 10−12; Jiménez-Serra et al. 2021), and the D/H ratio determined for this source (of 25%; Redaelli et al. 2019), the expected trans-DCOOH abundance is ~2.2 × 10−12, namely, it is on the same order as the upper limit obtained for this molecule and source. Therefore, higher-sensitivity observations will be needed to establish whether trans-DCOOH is present in the cold gas of starless and pre-stellar cores.
Upper limits of the column density of trans/cis-DCOOH and trans/cis-HCOOD measured toward the dust peak of L1544.
6 Conclusions
In this work, we study the hydrogen abstraction reactions of characteristic small acids, formic acid, and thioformic acid under interstellar conditions, finding an overall high reactivity of these archetypes. This suggests that the reactions should be relevant for the chemistry of the ISM under cold conditions. The main conclusions of the present work are:
Hydrogen abstraction reactions on formic acid occur on its cis isomer faster by almost five orders of magnitude than the same reactions on the trans isomer. This finding, added to the general lack of reactivity of trans-formic acid, was also confirmed by our experiments. It heavily implies that no trans-cis interconversion may happen on the surface of ice-coated dust grains. Cis-trans interconversion can, in principle, proceed in the absence of competitive addition reactions.
In contrast to formic acid, H atoms are abstracted from thioformic acid very quickly. Abstractions at the thiol group are the fastest reactions found in this work and proceed at a similar rate for both isomers. Abstractions on the CH group are slower but present a marked dependence on the isomerism of the parent acid.
We calculated the binding energies on amorphous solid water for all isomers of the acids considered here. Their values are about −6000 K in the case of the formic acid and −3100 K for thioformic acid. Both isomers (cis and trans) have almost the same binding energies.
The binding of the acids with ASW is highly localized owing to hydrogen bonds between the acid and the surface. We analyzed the extent to which these orientations inhibit reactivity, finding that they do not have any effect in the case of formic acid. However, they are important to predict the chemistry of thioformic acid, especially concerning the hydrogen abstractions at the thiol group. From our statistical sampling of binding sites, 88% of cis-thioformic acid ones form a hydrogen bond with the surface, in contrast to the 63% of trans-thioformic acid.
We repeated our study for abstraction reactions by D atoms, finding equivalent conclusions as for H and kinetic isotopic effects of around 10–20, except for trans-formic acid where the lower relevance of quantum tunneling yields an inverse KIE.
Our recent tentative detection of cis-thioformic acid is supported by our calculations. The chemistry of thioformic acid on grains is very complicated, and our understanding of cis and trans ratios in the interstellar medium would benefit from extensive and specific modeling.
The mechanisms considered here cannot explain the presence of a small amount of cis-formic acid in cold cores. This is in agreement with theoretical gas-phase calculations but in contrast to the observations. Therefore, additional mechanisms must be at play to explain the presence of cis-formic acid in regions with a low density of photons such as molecular clouds.
Both t-DCOOH and t-HCOOD has been reported toward the hot gas of the IRAS16293-2422B hot corino with similar abundances. This would seem to contradict our results, however, it is possible that deuterated formic acid also forms efficiently in the gas phase. Future kinetic calculations will be needed to establish this route as a viable formation mechanism. At the cold temperatures of the L1544 pre-stellar core, neither c/t-DCOOH nor c/t-HCOOD are detected, although their derived upper limits are not stringent enough to disentangle whether they are formed on grain surfaces or in the gas phase.
The results presented here are complemented with the data found in the literature for addition reactions (Cao et al. 2014; Chaabouni et al. 2020). Similar calculations on the addition reactions to TFA are a viable continuation of the present work in pursuing an integral understanding of the chemistry of simple acids on top of interstellar dust grains.
Acknowledgements
Computer time was granted by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no. INST 40/467-1FUGG is greatly acknowledged. G.M. thanks the Alexander von Humboldt Foundation for a post-doctoral research grant. We thank the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for supporting this work by funding EXC 2075 - 390740016 under Germany’s Excellence Strategy. We acknowledge the support by the Stuttgart Center for Simulation Science (SimTech). I.J.-S. and J.G.d.l.C. have received partial support from the Spanish State Research Agency (AEI) through project numbers PID2019-105552RB-C41 and MDM-2017-0737 Unidad de Excelencia “María de Maeztu” - Centro de Astrobiología (CSIC-INTA). We also acknowledge support from the Spanish National Research Council (CSIC) through the i-Link project number LINKA20353. This work is also supported by JSPS KAKENHI grant Nos. JP21F21319, JP21H04501, JP21H05414, JP21K18639, and JP17H06087 This work also made use of ASAI “Astrochemical Surveys At IRAM” (Lefloch et al. 2017).
References
- Agúndez, M., Marcelino, N., Cernicharo, J., Roueff, E., & Tafalla, M. 2019, A&A, 625, A147 [Google Scholar]
- Aikawa, Y., Wakelam, V., Hersant, F., Garrod, R. T., & Herbst, E. 2012, ApJ, 760, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Álvarez-Barcia, S., Russ, P., Kästner, J., & Lamberts, T. 2018, MNRAS, 479, 2007 [Google Scholar]
- Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2003, ApJ, 585, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Bannwarth, C., Ehlert, S., & Grimme, S. 2019, J. Chem. Theory Comp., 15, 1652 [CrossRef] [Google Scholar]
- Bisschop, S. E., Fuchs, G. W., van Dishoeck, E. F., & Linnartz, H. 2007, A&A, 474, 1061 [CrossRef] [EDP Sciences] [Google Scholar]
- Bizzocchi, L., Prudenzano, D., Rivilla, V. M., et al. 2020, A&A, 640, A98 [EDP Sciences] [Google Scholar]
- Boogert, A. C., Gerakines, P. A., & Whittet, D. C. 2015, ARA&A, 53, 541 [Google Scholar]
- Cao, Q., Berski, S., Latajka, Z., Räsänen, M., & Khriachtchev, L. 2014, Phys. Chem. Chem. Phys., 16, 5993 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C., Caselli, P., Bockelée-Morvan, D., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 859 [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Chaabouni, H., Baouche, S., Diana, S., & Minissale, M. 2020, A&A, 636, A4 [Google Scholar]
- Chandru, K., Gilbert, A., Butch, C., Aono, M., & Cleaves, H. J. 2016, Sci. Rep., 6, 29883 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, S. 1977, Phys. Rev. D, 15, 2929 [NASA ADS] [CrossRef] [Google Scholar]
- Cuadrado, S., Goicoechea, J. R., Roncero, O., et al. 2016, A&A, 596, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Favre, C., Fedele, D., Semenov, D., et al. 2018, ApJ, 862, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrero, S., Zamirri, L., Ceccarelli, C., et al. 2020, ApJ, 904, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Foden, C. S., Islam, S., Fernández-García, C., et al. 2020, Science, 370, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16 Revision C.01 (Wallingford CT: Gaussian Inc.) [Google Scholar]
- García de la Concepción, J., Jiménez-Serra, I., Corchado, J. C., Rivilla, V. M., & Martín-Pintado, J. 2021, ApJ, 912, L6 [CrossRef] [Google Scholar]
- García de la Concepción, J., Colzi, L., Jiménez-Serra, I., et al. 2022, A&A, 658, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Germain, A., Corno, M., & Ugliengo, P. 2021, in Lecture Notes in Computer Science, including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics, eds. O. Gervasi, B. Murgante, S. Misra, et al. (Berlin: Springer International Publishing), 12953, 632 [Google Scholar]
- Gillan, M. J. 1987, J. Phys. C Solid State Phys., 20, 3621 [NASA ADS] [CrossRef] [Google Scholar]
- Grimme, S., Antony, J., Ehrlich, S., & Krieg, H. 2010, J. Chem. Phys., 132, 154104 [Google Scholar]
- Grimme, S., Ehrlich, S., & Goerigk, L. 2011, J. Comp. Chem., 32, 1456 [CrossRef] [Google Scholar]
- Grimme, S., Bannwarth, C., & Shushkov, P. 2017, J. Chem. Theory Comp., 13, 1989 [CrossRef] [Google Scholar]
- Hama, T., Kuwahata, K., Watanabe, N., et al. 2012, ApJ, 757, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Hollis, J. M., Lovas, F. J., & Jewell, P. R. 2000, ApJ, 540, L107 [Google Scholar]
- Jiménez-Serra, I., Vasyunin, A. I., Caselli, P., et al. 2016, ApJ., 830, L6 [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Vasyunin, A. I., Spezzano, S., et al. 2021, ApJ, 917, 44 [CrossRef] [Google Scholar]
- Jørgensen, J. K., Müller, H. S. P., Calcutt, H., et al. 2018, A&A, 620, A170 [Google Scholar]
- Kästner, J., Carr, J. M., Keal, T. W., et al. 2009, J. Phys. Chem. A, 113, 11856 [CrossRef] [Google Scholar]
- Kaur, G., & Vikas. 2014, Phys. Chem. Chem. Phys., 16, 24401 [NASA ADS] [CrossRef] [Google Scholar]
- Lamberts, T., & Kästner, J. 2017, J. Phys. Chem. A, 121, 9736 [Google Scholar]
- Langer, J. S. 1967, Ann. Phys., 41, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Lefloch, B., Ceccarelli, C., Codella, C., et al. 2017, MNRAS, 469, L73 [Google Scholar]
- Loomis, R. A., McGuire, B. A., Shingledecker, C., et al. 2015, ApJ, 799, 34 [Google Scholar]
- Maçôas, E. M., Lundell, J., Pettersson, M., et al. 2003, J. Mol. Spectr., 219, 70 [CrossRef] [Google Scholar]
- Markmeyer, M. N., Lamberts, T., Meisner, J., & Kästner, J. 2019, MNRAS, 482, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Martín, S., Martín-Pintado, J., Blanco-Sánchez, C., et al. 2019, A&A, 631, A159 [Google Scholar]
- Meisner, J., Lamberts, T., & Kästner, J. 2017, ACS Earth Space Chem., 1, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Melli, A., Melosso, M., Tasinato, N., et al. 2018, ApJ, 855, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Metz, S., Kästner, J., Sokol, A. A., Keal, T. W., & Sherwood, P. 2014, Interdiscip. Rev. Comput. Mol. Sci., 4, 101 [CrossRef] [Google Scholar]
- Miksch, A. M., Riffelt, A., Oliveira, R., Kästner, J., & Molpeceres, G. 2021, MNRAS, 505, 3157 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, W. H. 1975, J. Chem. Phys., 62, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Modica, P., & Palumbo, M. E. 2010, A&A, 519, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molpeceres, G., & Kästner, J. 2021, ApJ, 910, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Molpeceres, G., de la Concepción, J., & Serra, I. J. 2021, ApJ, 923, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, T., Oba, Y., Shimonishi, T., Kouchi, A., & Watanabe, N. 2020, ApJ, 898, L52 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, T., Oba, Y., Sameera, W. M. C., Kouchi, A., & Watanabe, N. 2021, ApJ, 922, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Oba, Y., Tomaru, T., Lamberts, T., Kouchi, A., & Watanabe, N. 2018, Nat. Astron., 2, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I. 2016, Chem. Rev., 116, 9631 [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [Google Scholar]
- Quan, D., Herbst, E., Corby, J. F., Durr, A., & Hassel, G. 2016, ApJ, 824, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Redaelli, E., Bizzocchi, L., Caselli, P., et al. 2019, A&A, 629, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-Almeida, L. F., Jiménez-Serra, I., Rivilla, V. M., et al. 2021, ApJ, 912, L11 [Google Scholar]
- Rommel, J. B., & Kästner, J. 2011, J. Chem. Phys., 134, 184107 [NASA ADS] [CrossRef] [Google Scholar]
- Rommel, J. B., Goumans, T. P., & Kästner, J. 2011, J. Chem. Theory Comp., 7, 690 [CrossRef] [Google Scholar]
- Sherwood, P., De Vries, A. H., Guest, M. F., et al. 2003, J. Mol. Struct., 632, 1 [Google Scholar]
- Shingledecker, C., Molpeceres, G., Rivilla, V., Majumdar, L., & Kästner, J. 2020, ApJ, 897, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Skouteris, D., Vazart, F., Ceccarelli, C., et al. 2017, MNRAS, 468, L1 [NASA ADS] [Google Scholar]
- Skouteris, D., Balucani, N., Ceccarelli, C., et al. 2018, ApJ, 854, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Taquet, V., Wirström, E. S., Charnley, S. B., et al. 2017, A&A, 607, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2014, ApJ, 795, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Vazart, F., Latouche, C., Skouteris, D., Balucani, N., & Barone, V. 2015, ApJ, 810, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Weigend, F., & Ahlrichs, R. 2005, Phys. Chem. Chem. Phys., 7, 3297 [Google Scholar]
- Zhao, Y., & Truhlar, D. G. 2005, J. Phys. Chem. A, 109, 5656 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, J., & Truhlar, D. G. 2010, Phys. Chem. Chem. Phys., 12, 7782 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Ball, J. A., & Gottlieb, C. A. 1971, ApJ, 163, L41 [NASA ADS] [CrossRef] [Google Scholar]
Madrid Data Cube Analysis on ImageJ is a software developed at the Center of Astrobiology (CAB) in Madrid; https://cab.inta-csic.es/madcuba/
All Tables
Reaction energies (including ZPE, ΔUr in kJ mol−1) at the MPWBlK7def2-TZVP level and at UCCSD(T)-F12/cc-pVTZ-F12 for the electronic energies (in parenthesis), activation energies (including ZPE, ΔUa) at the same level and crossover temperatures (Tc in K) for reactions (1) to (6).
Fitted parameters of the modified Arrhenius-Kooij equation for reactions (1)–(6).
Fraction of different localized binding for the high binding energy adsorption sites in the c/t-FA/H2O system.
Fraction of different localized binding for the high binding energy adsorption sites in the c/t-TFA/H2O system.
Kinetic isotope effects (KIE) at the lowest temperature (T in K) for the H abstraction reactions and their HD counterparts.
Fitted parameters of the modified Arrhenius-Kooij equation for the reactions (1)–(6) initiated by a D atom.
Upper limits of the column density of trans/cis-DCOOH and trans/cis-HCOOD measured toward the dust peak of L1544.
All Figures
 |
Fig. 1 Molecular structure of the FA and TFA isomers. |
| In the text | |
 |
Fig. 2 Intrinsic reaction coordinate calculations for reactions 1 and 2 as described in the main text. Displayed energies are not corrected with zero point energy contributions. |
| In the text | |
 |
Fig. 3 Instanton reaction rate constants below Tc for reactions 1 and 2. |
| In the text | |
 |
Fig. 4 FTIR spectra obtained after (a) codeposition of FA and D atoms and (b) FA for 3 h at 10 K, along with (c) the difference spectrum between spectra (a) and (b). |
| In the text | |
 |
Fig. 5 Intrinsic reaction coordinate calculations for reactions (3) to (6) as described in the main text. Displayed energies are not corrected with zero point energy contributions. |
| In the text | |
 |
Fig. 6 Instanton reaction rate constants below Tc for reactions (3)–(6). |
| In the text | |
 |
Fig. 7 Binding energies of cis/trans-Formic acid. Dashed line -Gaussian fit of the binding energies. µcis = −6227 K, σcis = 1692 K. µtrans = −6170 K, σtrans = 1826 K. |
| In the text | |
 |
Fig. 8 Examplary binding orientation of t-FA on ASW. In the figure, we depict the clear localization in the binding orientation of the molecule forming two hydrogen bonds with different atoms of the surface. |
| In the text | |
 |
Fig. 9 Binding energies of cis/trans-Thioformic acid. Dashed line – Gaussian fit of the binding energies. Here, µcis = −3105 K, σcis = 1384 K. μtrans = −3005 K, σtrans = 1418 K. |
| In the text | |
 |
Fig. 10 Rate constants for all the H abstraction reactions considered in the present work. |
| In the text | |
 |
Fig. 11 Rate constants for all the HD abstraction reactions considered in the present work. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


