EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 665 (September 2022) A&A, 665 (2022) A27 Full HTML
Open Access
Issue
A&A
Volume 665, September 2022
Article Number A27
Number of page(s) 10
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202243892
Published online 06 September 2022

© G. Molpeceres and V. M. Rivilla 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1 Introduction

The definition of interstellar complex organic molecules (COMs) encompasses all carbon-bearing molecules containing six atoms or more in their molecular backbone (Herbst & Van Dishoeck 2009). Many of the recently detected molecules in the interstellar medium (ISM) fall under this broad definition. In recent years, the rate of detections has greatly increased (McGuire 2022). Under the cold conditions of molecular clouds and prestellar cores, where the recent surge of molecular detections has taken place, chemistry is significantly hindered. For example, all reactions that proceed through endothermic pathways or present prohibitively large activation barriers are precluded, conditioning the chemistry both in the gas phase (see Puzzarini 2022 for a recent review) and on top of ice coated dust grains (Hama & Watanabe 2013; Cuppen et al. 2017). Yet, even with these restraints, more and more COMs are known to be present in the ISM. Ethyl- and vinyl-bearing molecules, that is to say molecules whose carbon skeleton backbone can be identified as proceeding from either the vinyl (C2H3) or ethyl (C2H5) radicals, have been particularly relevant, due to their prevalence:

C2H5OH (Zuckerman et al. 1975), C2H3OH (Agúndez et al. 2021), C2H5CN (Johnson et al. 1977), C2H3CN (Gardner & Winnewisser 1975), C2H5OCHO (Belloche et al. 2009), C2H5OCH3 (Tercero et al. 2018), C2H5CHO and C2H3CHO (Hollis et al. 2004), C2H5SH (Rodríguez-Almeida et al. 2021a), C2H5NCO (Rodrfguez-Almeida et al. 2021b), C2H3NH2 (Zeng et al. 2021), C2H3CCCH (Cernicharo et al. 2021), C2H3C3N (Kelvin Lee et al. 2021), NH2C2H4OH (Rivilla et al. 2021), or HOC2H2OH (Rivilla et al. 2022). We emphasize from this list of molecules that many of them have been detected in the last four years.

The chemistry occurring on top of icy dust grains display a particular idiosyncrasy, with weakly bound adsorbates landing on the grain, diffusing, reacting, and eventually returning to the gas phase, where they are detected by radio telescopes. All these motions favor hydrogen atoms as main chemistry initiators on grains, owing to a fast diffusion (Hama et al. 2012; Senevirathne et al. 2017; Ásgeirsson et al. 2017; Nyman 2021) and the possibility of a tunnel through potential energy barriers (Hama & Watanabe 2013). However, and thanks to nondiffusive mechanisms that appear as a consequence of an excess of energy inoculated into a particle (i.e., after photodissociation, chemical reaction, or cosmic-ray interaction Jin & Garrod 2020; Garrod et al. 2022), other radicals (OH, NH2, CH3) may play an important role in the chemical evolution of the ISM (Fedoseev et al. 2017; Chuang et al. 2020, 2021; Ioppolo et al. 2021; Tsuge & Watanabe 2021; Ishibashi et al. 2021).

In this work, we merge the knowledge attained through observations and experiments seeking for a mechanism able to explain the prevalence of ethyl- and vinyl-bearing molecules in cold environments. The mechanism that we propose, which does not exclude other possible gas phase and surface scenarios, relies on the processing of the closed-shell hydrocarbons acetylene (C2H2), ethylene (C2H4), and ethane (C2H6) by reactive radicals through addition and H abstraction reactions. Both of these reactions form reactive radicals that are prone to continue reacting with other incoming particles and form stable COMs. In particular, in this work we consider addition and abstraction reactions of the abovementioned molecules with the following radicals: H, OH, NH2, and CH3. We employed a theoretical approach in our work, and as we emphasize throughout the paper, our predictions will significantly benefit from experimental validation.

The paper is divided as follows: in Sect. 2 we discuss the particularities of the computational framework to study the wide range of reactions under consideration; in Sect. 3 we present our results, divided by a parent closed-shell molecule; and finally in Sect. 4, we gather all the trends obtained from the reactions, discuss the implications of our findings, and postulate new chemical species susceptible to detection following the mechanism that we propose.

2 Methodology

The computational setting for this work follows similar protocols as some of our previous works (e.g. Miksch et al. 2021 and references therein). Briefly, we have determined the activation energies (ΔUa, including zero-point energy contributions) and reaction energies (ΔUe) for a set of reactions of significance for the formation of ethyl- and vinyl-bearing radicals starting from (a) acetylene (C2H2), (b) ethylene (C2H4), and (c) ethane (C2H6). The reactions that we have considered for (a) are: (1) (2)

with X = H, OH, CH3, and NH2. Therefore, for (a) and (b) we have studied both addition reactions and abstraction ones. However, for (c), we have studied only H abstraction reactions: 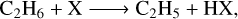(3)

because additions to (b) present a very high activation barrier, as a consequence of ethane being completely hydrogen saturated. All the reactions were studied in the context of surface science aiming for an implementation of our values into astrochemical gas-grain surface models. Because of the weak binding of (a) and (b) with amorphous solid water (ASW), and presumably with other interstellar relevant surfaces (Wakelam et al. 2017b), all the reactions studied here account for the effect of a surface via the implicit surface approach (Meisner et al. 2017), such as the rotational partition function of the transition state, and the reactant is kept fixed in subsequent rate constant calculations (see below). This approach effectively considers that the reactions are hardly affected by the interaction with the surface, and that the surface plays a role in increasing the concentration of reactants, as well as in dissipating the reaction energy for very exothermic reactions. Under this approach, the surface composition does not play any role, and therefore this approximation should not be assumed for other surfaces where the adsorbate–surface interaction is stronger. We tested the validity of the implicit surface approach for three reactions of our whole set of reactions in Appendix A. We considered unimolecular reactions in the context of a Langmuir-Hinshelwood mechanism, which is characteristic of surface reactions with a barrier.

We studied the reactions using density functional theory (DFT) calculations. In this work, we use the MN15-D3BJ/def2-TZVP (Weigend & Ahlrichs 2005; Grimme et al. 2011; Yu et al. 2016) exchange and correlation functional1. We chose this level of theory according to its performance in generally predicting activation barriers (Yu et al. 2016) when comparing with refined energies at the coupled-cluster level (UCCSD(T)-F12/cc-pVTZ-F12//MN15-D3BJ/def2-TZVP) values, considered as reference. All the energetic quantities presented in this work are given at the pure DFT level and with energies corrected using the explicitly correlated coupled-cluster theory mentioned above (Knizia et al. 2009), which are denoted in square brackets throughout the paper. For some specific reactions of our study, coupled-cluster theories are known to underperform against the values in the literature (Senosiain et al. 2005, 2006). These cases are explicitly indicated where relevant. All the calculations employ Gaus-sian16 (Frisch et al. 2016) interfaced with DL-Find/Chemshell (Metz et al. 2014; Kästner et al. 2009; Quan et al. 2016).

Once the stationary points in the potential energy surface (PES) are determined (reactant, transition states and products), we calculate the corresponding rate constants of reaction in their classical transition state formulation and incorporate quantum effects by means of semiclassical instanton theory (Langer 1967; Miller 1975; Coleman 1977; Rommel et al. 2011; Rommel & Kästner 2011). Quantum effects are determined below the crossover temperature using conventional instanton theory and reduced instanton theory (McConnell & Kästner 2017) above it. Crossover temperatures (Tc) are defined as the temperatures below which quantum effects dominate over thermal effects, and they are defined as in our previous works (Miksch et al. 2021; Molpeceres & Kästner 2021; Molpeceres et al. 2021), following the formulation of Gillan (1987): 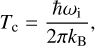(4)

where ωi is the absolute value of the imaginary frequency for the activated complex, and kB is the Boltzmann constant. Symmetry numbers (σ) are not included as prefactors in our calculated rate constants because there is not a univocal symmetry number for a reaction on a surface due to the total or partial break of symmetry in such reactions.

The anharmonicity of the instanton structures in C2H6 – CH3 and C2H6 – NH2 activated complexes precludes the calculation of reliable instanton rate constants at this stage of research, and this is discussed later in the paper. Similarly, in C2H4 + OH → C2H4OH, we could not converge instanton paths below 50 K. For all these exceptions, we calculated tunneling contributions stemming from a symmetric Eckart barrier to the rate constants. The latter are less exact than instanton calculations and should serve as an approximation of the real values.

Reaction energies are provided, with reactant energies coming from the prereactive complex identified in intrinsic reaction coordinate calculations. The energies of the product are always computed for the separated products. We have created a Zenodo repository to store all the structures gathered in this article (Molpeceres & Rivilla 2022)2. The naming convention for the reactions will be AD/AB X.Y with AD = addition, AB = abstraction; X= 1 (C2H2), 2 (C2H4) and 3 (C2H6); Y= 1 (H), 2 (OH), 3 (NH2) and 4 (CH3).

Table 1

Reaction energies (ΔUr in kJ mol−1) and activation energies (ΔUa in kJ mol−1) for the addition and abstraction reactions starting from C2H2 at the MN15-D3BJ/def2-TZVP level.

3 Results

3.1 Radicals reacting with acetylene

Reaction energies and activation barriers for the radical addition and H abstraction are presented in Table 1. A visual inspection of the table reveals that DFT values at the MN15-D3BJ/def2-TZVP yield reliable results for the activation energies, with all ΔUr below or very close to the chemical accuracy of (~4 kJ mol−1)3. All ΔUr are positive for H abstraction reactions, meaning that all reactions are endothermic and proceed with very high activation barriers (ΔUa). Therefore, abstraction reactions in ethylene are deemed impossible under astrochemical conditions. In fact, the Kinetic Database for Astrochemistry4, reports a rate constant of zero for AB1.2 in the gas phase in the ~ 10−150 K range. The ethynyl radical (C2H) is well known for its reactivity both in the gas phase (Herbst & Woon 1997; Chastaing et al. 1998; Sun et al. 2015; Fortenberry 2021), and on ices (Perrero et al. 2022). The transient nature of this radical in comparison with the parent closed-shell molecule (C2H2) serves as a viable explanation for the elevated endothermicities. In summary, forming the C2H radical is, in all cases, a nonfavored process. On the contrary, the addition reactions are, in all cases, exothermic, with activation barriers that vary between 10.1 kJ mol−1 (for OH addition) to 40.7 kJ mol−1 (for CH3 addition). Similarly, the match of our results for AD1.2 is in very good agreement with the literature (Senosiain et al. 2005), with small deviations of 2 kJ mol−1 for ΔUa in our DFT results. However, a difference between our MN15-D3BJ/def2-TZVP and UCCSD(T)-F12/cc-pVTZ-F12//MN15-D3BJ/def2-TZVP values is also apparent. It is key to note that Senosiain et al. (2005) reported that the coupled-cluster method was subpar for this particular reaction (and the OH addition to C2H4, see next section), and so our DFT values may be a better reference in this case.

The reaction rate constants for the addition channels are collated in Table 2. Instantons were converged to the unimolecular asymptotic µmit in most cases, as presented in Fig. 1 for the associated rate constants. From the rate constants, we observe that reactions for CH3 and NH2 are very slow, deeming the reactions nonviable under astrophysical conditions. On the contrary, the rate constants for H addition are competitive with H diffusion on ice (Hama et al. 2012; Senevirathne et al. 2017; Ásgeirsson et al. 2017; Nyman 2021). For example, residence times (Ásgeirsson et al. 2017) span a range that is mostly covered by log10kd = (−10)−(−3), with our values at ~−4.50 (i.e., in the upper bound of such a range). Our results for AD1.2 match very well the previous results presented in Kobayashi et al. (2017), with rate constants within the order of magnitude. We find the reaction with OH between both extreme values. Reaction AD1.2 presents a rate constant of k(40 K) = 7.3 × 101 s−1, which is normally considered a low value when compared with timescales of H diffusion. However, since OH is less mobile, this reaction may compete with OH diffusion. Recent studies have highlighted the importance of the OH radical in surface astrochemistry (Tsuge & Watanabe 2021; Ishibashi et al. 2021), and AD1.2 is a good candidate for studying these new avenues for reactivity on interstellar ices, thanks to the small activation barrier. Figure 1 shows the importance of quantum tunneling at low temperatures, rendering the reaction rate constants with H at low temperature orders of magnitude higher than the same reactions with heavier radicals. This is also nicely reflected by the magnitude of the crossover temperatures presented in Table 1, because reactions with H present higher transition frequencies, a key magnitude for tunneling.

Table 2

Crossover temperatures (Tc in K) and reaction rate-constants k (Tmin, in s−1) at the lowest temperature achieved in our calculations (Tmin in K), for the exothermic reactions starting from C2H2.

thumbnail Fig. 1

Instanton reaction rate constants in the [500, Tmin] range, with Tmin being the lowest temperature achieved in our calculation for each particular reaction starting from C2H2. The vertical line represents the crossover temperature, Tc.
Table 3

Reaction energies (ΔUr in kJ mol−1) and activation energies (ΔUa in kJ mol−1) for the addition and abstraction reactions starting from C2H2 at the MN15-D3BJ/def2-TZVP level.

3.2 Radicals reacting with ethylene

The next molecule for which we investigated abstraction and addition reactions is ethylene (C2H4). As in the case of C2H2, we studied radical additions and H abstraction reactions, with the main descriptors of the reaction gathered in Table 3. A quick visual analysis of the results on the table evinces that, once again, abstraction reactions are mostly endothermic, with the exception of H abstraction by OH radicals, which is exothermic and has a moderately low activation barrier. This route can form C2H3 radicals, such as reaction AD1.1. All the other abstraction reactions are, as mentioned, endothermic, but less than in the previous section. The vinyl radical (C2H3) is less reactive than the C2H radical, and thus the reactions to form it are less impeded. However, all the endothermic reactions are still nonviable in astrophysical environments.

Addition reactions, on the contrary, are again always exothermic and exhibit activation barriers in the same order as the addition reactions presented in the previous section. Once again, for the available comparisons, our values are in good agreement with the available values for H addition (AD2.1), for example within the order of magnitude for the rate constants (Kobayashi et al. 2017) and around ~2 kj mol−1 for the value of ΔUa in AD2.2 (Senosiain et al. 2006). Again, the agreement between coupled-cluster and DFT values is slightly worse in the case of reactions involving the OH radical, which is crucial due to the small barriers taking place in reactions with this radical. In Senosiain et al. (2006), internal tests showed that the coupled-cluster method underperformed with respect their employed method (UQCISD), which is in much better agreement with our DFT values, increasing the confidence of our subsequent rate constant calculations. For the other heavy radicals CH3 and NH2, the barriers are of the same order as for the reactions with C2H2, only slightly lower. There is a trend in ΔUa, which decreases with the hybridization of the carbon (see Sect. 4).

All the rate constants for exothermic reactions are gathered in Table 4 and Fig. 2 for the addition reactions, and Fig. 3 for the abstraction of H by OH. The rate constants confirm the points hinted at by ΔUa. AD2.1 is a fast reaction, also confirmed in Kobayashi et al. (2017), and is a source of C2H5 radicals that can react with another radical in a radical-radical recombination. For AD2.2 we were unable to obtain instanton paths below Tc, and therefore we substituted the instanton rate constants for Eckart corrected rate constants that, we recall, serve as an approximation of the real rate constants. The excellent agreement between the reduced instanton rate constants and Eckart in Fig. 2 stems from the value of Tc, which is small, indicating a lesser influence of quantum effects on this reaction. The Eckart corrected rate constant for AD2.2 is kEckart(30 K)= 1.2 × 104 s−1, corresponding to a fast reaction, especially considering the lower mobility of the OH radical on amorphous solid water in comparison with OH. Moreover, and as was introduced before, the OH radical is prone to nonthermally diffuse on the surface of the ice, indicating that the addition of OH to C2H4 is a viable reaction under interstellar conditions.

The abstraction of a H atom from C2H4 is possible mediated by an OH radical in the AB2.2 reaction. At 40 K, the reaction rate constant is 5.6 × 101 s−1, and it remains constant at lower temperatures due to its asymptotic behavior, arising from tunneling effects coming purely from the vibrational ground state. On the contrary, the rate constants for the addition reaction do not show an asymptotic behavior in this temperature range, which poses an interesting conundrum. For temperatures close to or above 30 K, addition must dominate, represented by the two orders of magnitude of difference (see the faded black line in Fig. 3). However, it is unclear, what the behavior at lower temperatures will be, in addition to the error associated with the addition rate constants using an Eckart correction for tunneling. Since both reactions are relatively fast reactions considering the low mobility of OH on water ice, we hypothesize that at temperatures T > 30 K, which better represent the nonthermal regime, addition reactions must dominate.

Table 4

Crossover temperatures (Tc in K) and reaction rate-constants k(Tmin, in s−1) at the lowest temperature achieved in our calculations (Tmin in K), for the exothermic reactions starting from C2H4.

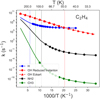thumbnail Fig. 2

Instanton reaction rate constants (and Eckart corrected rate constants in the case of C2H4 + OH → C2H4OH) in the [500, Tmin] range, with Tmin being the lowest temperature achieved in our calculations for each particular addition reaction starting from C2H4. The vertical line represents the crossover temperature, Tc.
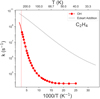thumbnail Fig. 3

Instanton reaction rate constants in the [500, Tmin] range, with Tmin being the lowest temperature achieved in our calculation for the C2H4 + OH → C2H3 + H2O, Tc. The reaction rate constants for the C2H4 + OH → C2H4O Hare in faded black.

3.3 Radicals reacting with ethane

To conclude with the ternary of closed-shell C2Hn molecules, we have H abstraction reactions from ethane. These abstractions, as opposed to those presented in the previous sections, are always exothermic and have activation barriers that are lower than for C2H2 and C2H4 (see Table 5). Logically, addition reactions are precluded in a saturated hydrocarbon such as C2H6.

The trend in activation energies and reaction energies for this case confirms OH as the most reactive agent, with ΔUa tens of kJ mol−1 lower than in all the other cases (AB3.2). Similar observations can be done on the basis of ΔUr. For C2H6, all reactions present very high Tc, and therefore reaction rate constants are significantly affected by quantum tunneling due to the high transition state frequencies associated with the H-X (X = H, OH, NH2, CH3) vibrations. The reaction rate constants for this reaction are presented in Table 6. As mentioned in Sect. 2, it is important to note that instanton calculations were particularly difficult for NH2 and CH3, and it was impossible to extract reliable rate constants from them. Hence, we present Eckart corrected rate constants as a compromise. For abstractions with OH and NH2, reaction rate constants are k(25 K) = 1.5 × 103 s−1 and k(20 K) = 6.3 × 100 s−1, respectively, which are sufficiently high to be viable. However, we note that rate constants for AB3.3 are approximated and the presented results must be adopted with caution. The reliability of the values for C2H6 + OH → C2H5 + H2O is much higher and they can be incorporated into astro-chemical models. For reactions initiated from CH3 and H, the rate constants are either very low (CH3) or competitive with diffusion, which casts doubts on the viability of these particular routes. A summary of the reaction rate constants is presented in Fig. 4. All things considered, the formation of the C2H5 radical is more favorable to proceed from addition reactions in C2H4 than from the abstraction reactions of this section.

Table 5

Reaction energies (ΔUr in kJ mol−1) and activation energies (ΔUa in kJ mol−1) at the MN15-D3BJ/def2-TZVP level for the abstraction reactions from C2H6.

Table 6

Crossover temperatures (Tc in K) and reaction rate-constants k(Tmin, in s−1) at the lowest temperature achieved in our calculations (Tmin in K), for the exothermic reactions starting from C2H6.

4 Discussion

We have provided an extensive catalog of reactions that can help in rationalizing the recent surge of two carbon-bearing COMs. Before discussing the astrophysical implications of our work, we would like to highlight the trends that we found, arising from the closed-shell molecules under consideration (C2H2, C2H4, and C2H6) and the reacting radicals (OH, H, NH2, and CH3). The average reaction energies and activation energies found across the sequences H/OH/NH2/CH3 and C2H2/C2H4/C2H6 are presented in Fig. 5.

The most significant trends that we can observe are summarized as follows. Reaction energies and activation energies mostly decrease following the sequence ΔUr,a(C2H2) < ΔUr,a(C2H4) < ΔUr,a(C2H6) for abstractions, without a clear trend for additions. It should be noted that addition reactions to C2H6 are forbidden. Following this trend, abstraction reactions start to be exothermic with C2H4, with all abstraction reactions in C2H6 fulfilling this condition. The change in activation energies correlates with the higher exothermicity, with barriers to abstract H from C2H6 being the lowest of all the abstraction reactions. The reason for the presence of these trends has been indicated before, and it has probably to do with the higher energy of the products. For instance, the ethynil radical (C2H) is among the most reactive radicals, and the formation of this radical is thermodynamically unfavored from C2H2.

We can also extract the trends that appear as a function of the radical partaking in the reaction. From the top panels of Fig. 6, we observe that the OH radical is the most reactive one by a large margin, presenting the lowest activation barriers of the whole sequence. For these reactions, we also observe that the reaction parameters for NH2 and H are similar, which is also coherent with what was observed in Markmeyer et al. (2019) for H abstraction energies in HC(O)OH (formic acid). Finally, we observe that CH3 is the most unreactive radical of those considered in this work, with all reactions yielding nonviable conversions in all cases.

From the trends that we observed and the specific values of the rate constants, we can infer some important conclusions for the chemistry of COMs in cold environments. The key concept arising from this study is that closed-shell molecules “activate” via addition and abstraction reactions with (mostly) H and OH. By “activate” in this context, we mean the generation of reactive radicals such as C2H3, C2H5, or C2H4OH, which are prone to further react with other radicals through barrierless radical–radical couplings. It is important to note that radical–radical reactions are not guaranteed to proceed without a barrier (see e.g., Enrique-Romero et al. 2019), but are likely to do so in different binding sites. Furthermore, for radical-radical reactions, bimolecular reactions (e.g., proceeding through the Eley-Rideal mechanism) are enabled (Ruaud et al. 2015), partially solving the necessary condition of effective surface diffusion imposed by the Langmuir-Hinshelwood mechanism. In this work, we did a systematic search of the possible reactions liable to occur on top of interstellar dust grains that would produce the previously mentioned radicals. Specifically, the formation of C2H3 and C2H5 is favored via H addition to C2H2 and C2H4, but abstraction reactions from H are not relevant for this mechanism. Heavier radicals such as CH3 and, to a lesser extent NH2, are not significantly reactive either for addition or for abstraction. Since tunneling is much less relevant in these cases, moderate barriers (>15 kJ mol−1 or 1800 K) are prohibitive for addition reactions of these radicals. The importance of tunneling is regained again for the reaction AB3.3, and that has a consequential effect on the rate constants for this reaction, probably the only one really viable involving NH2 from this study. Nonetheless, the reaction is slow.

From an astrochemical perspective, the most important finding of the present work is the viability of considering the OH radical an initiator of chemistry on the surface of interstellar dust grains. Reactions on surfaces involving H atoms are usually the most relevant reactions on the surface of dust grains (Hama & Watanabe 2013). However, very recently it has been demonstrated that methyl formate can be efficiently formed via the photolysis of H2O/CH3OH ices (Ishibashi et al. 2021). This reaction depends strongly on the photo-dissociation yield of the water ice, indicating that nonthermal OH radicals produced in the photolysis are taking part in the reaction. We can establish a parallelism with our results in this study. In water-rich environments, where the photolysis of H2O proceeds thanks to the secondary UV field (Prasad & Tarafdar 1983), OH radicals are formed, with an energy excess that can be used to effectively scan the ice surface (Jin & Garrod 2020), meeting reaction partners and employing part of this budget to overcome small reaction barriers. Given the small barriers found in this work, we suggest that the OH radicals are susceptible of reacting with unsaturated hydrocarbons (C2H2 and C2H4) to form the new species presented above, such as C2H3, C2Hs, C2H3OH, or C2H4OH. Even if the excess energy is only employed in nonthermal diffusion, the small barriers for the addition of OH to C2H2 and C2H4 provide rate constants that could be overcome5. The role of the water surface on the whole reaction remains to be established. A caveat of our simulations is that the effect of a surface is taken into account implicitly. However, calculations performed in similar systems with an explicit account of water molecules (H2 + OH → H2O + H, Meisner et al. 2017) show that the influence of the water surface in the reaction is small. On a similar note, the OH radical is also effective in generating C2H5 radicals, via reaction AB3.2, also affecting the budget of C2H5 radicals present on the surface of dust grains available for subsequent reaction to form COMs. For AB2.2, the situation is more complex, owing the competition with the AD2.2 reaction (see Sect. 3.2). Experiments are pivotal to understanding what is the leading reaction at 10 K.

To illustrate the importance of this mechanism in the formation of currently positively-, tentatively-, or not-yet-detected molecules in the ISM, we present a schematic portrait of our suggested mechanism in Fig. 6. In it, we present several more radicals (i.e., -SH, -NCO, -HCO or -CN) beyond the ones explicitly considered in Sect. 3, considering that the second radical addition proceeds via radical-radical barrierless reactions (see above). From our results, we can confidently say that the radicals C2H3, C2H5, C2H2OH, and C2H4OH can be formed via reactions AD1.1, AB2.2, AD2.1, AB3.2 AD1.2, and AD2.2. These radicals will stay on the surface waiting for an additional radical to react.

In this work we suggest a possible mechanism for the formation of these molecules, in addition to other possibilities such as gas-phase formation, that can serve to predict new molecules that are susceptible to detection. Some of these routes were already postulated, as in the case of C2H5 + NCO → C2H5NCO (Rodriguez-Almeida et al. 2021b). In addition to the extensive list of molecules presented in Sect. 1, there are still other non-detections our mechanism may hint at, such as C2H3NCO or C2H3SH, or tentative detections such as C2H5NH2 (Zeng et al. 2021). Similarly, we encourage laboratory studies of molecules falling under this definition, to obtain their rotational spectra (e.g. HOC2H2CN) and many other molecules arising from the combination of the radicals discussed above.

Another interesting discussion from this work concerns the prevalence of OH over other reactive radicals (in this work represented by NH2 and CH3), which may be an explanation for the segregation of O-bearing and N-bearing COMs in cold cores. Very briefly, and taking as an example the L1498 prestellar core, N-bearing molecules (such as CH3CN or CH2CHCN) were located in the outer shell of the core, while O-bearing molecules were not and are expected toward the more accreted center of the core. N-bearing molecules may be efficiently formed in the gas phase, thanks to the great reactivity of, for example, the CN radical (Balucani et al. 1999; Vazart et al. 2015; Sleiman et al. 2018; Puzzarini et al. 2020), while the formation of O-bearing molecules (such as CH3CHO and CH3OCH3) is favored at later stages, with the depletion of molecules onto interstellar ice surfaces. This hypothesis, in combination with further characterization of hydroxylation reactions atop ices is required to continue deepening into the intricacies of COM formation in interstellar environments.

thumbnail Fig. 4

Instanton reaction rate constants (and Eckart corrected rate constants in the case of C2H6 + NH2/CH3 → C2H5 + NH3/CH4) in the [500, Tmin] range, with being the lowest temperature achieved in our calculations for each particular addition reaction starting from C2H6. The vertical line represents the crossover temperature, Tc.
thumbnail Fig. 5

Activation energies (ΔUa in kJ mol−1, left panels) and reaction energies (ΔUa in kJ mol−1, right panels) as a function of the radical under consideration (upper panels) and the reacting hydrocarbon (lower panels).

5 Conclusion

In this work, we determined a series of possible routes to form ethyl and vinyl radicals and their derivatives, to explain the recent detections of COMs containing at least two carbon atoms. Using quantum chemical calculations, we found that the radicals C2H3, C2H5, C2H2OH, and C2H4OH are efficiently formed on the surface of grains starting from closed-shell molecules and H and OH radicals. The implication of other radicals such as NH2 and CH3 in the studied reactivity was found to be minor. The presented reactions act as onsets for additional radical-radical reactions, forming COMs. We reiterate the importance of the OH radical in surface processes. The low mobility of the OH radical on interstellar dust grains can be overcome by nonthermal effects, as recently studied in the literature (Ishibashi et al. 2021).

The main caveat of our simulations is that, due to the large amount of reactions under consideration, not all of them are tractable with a homogeneous methodology due to, for example, soft vibrational modes interfering in the convergence of the instantons. Most of the troublesome reactions are not significant for the conclusions our work, but one of them in particular, C2H4 + OH → C2H4OH, is important in order to understand the competition between OH addition and H abstraction in ethylene. We suggest that dedicated experiments or calculations (e.g. ring polymer molecular dynamics) are necessary to complete the picture.

We suggest that the mechanism proposed in this work may be behind the recent detection of COMs, and may also be partially responsible for the segregation of N- and O-bearing COMs in prestellar cores. We would like to encourage further experimental measurements on the viability of further hydroxylation reactions on dust grains, to complement our hypotheses in this work, as well as observations of COMs liable to be formed by this mechanism in prestellar and protostellar cores, and in hot corinos.

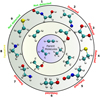thumbnail Fig. 6

Schematic diagram showing some of the possible chemical pathways starting from C2H2, C2H4, and C2H6 (inner circle) in the formation of COMs via activation of the closed-shell molecules by OH and H radicals, which forms the four radicals shown in the intermediate circle. It should be noted that not all of the possible reaction paths are indicated in the diagram. The COMs shown in the outer circle are: (1) CHOHCHNCO; (2) vinyl cyanide, C2H3CN; (3) 1,2-ethenediol, (CHOH)2; (4) ethyl mercaptan, C2H5SH; (5) ethyl isocyanate C2H5NCO; (6) ethanol, C2H5OH; (7) ethanolamine, NH2CH2CH2OH; (8) ethylamine, C2H5NH2; and (9) vinyl mercaptan C2H3SH.

Acknowledgements

We thank Prof. Dr. Johannes Kästner for estimulating discussions. Computer time was granted by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no. INST 40/467-1FUGG is greatly acknowledged. G.M. thanks the Alexander von Humboldt Foundation for a post-doctoral research grant. We thank the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for supporting this work by funding EXC 2075 – 390740016 under Germany’s Excellence Strategy. We acknowledge the support by the Stuttgart Center for Simulation Science (SimTech). V.M.R. has received funding from the Comunidad de Madrid through the Atracción de Talento Investigador (Doctores con experiencia) Grant (COOL: Cosmic Origins Of Life; 2019-T1/TIC-15379), and from the Agencia Estatal de Investigatión (AEI) through the Ramón y Cajal programme (grant RYC2020-029387-I).

Appendix A Test of implicit surface approach

Our calculations use an implicit surface approach to account for surface effects in the simulations. In such an approach, which was validated for weak and intermediate binding situations (Meisner et al. 2017; Lamberts et al. 2016; Molpeceres et al. 2021), the rotational contributions to the partition function are constant and consequentially their effects on the rate constants are canceled out. This vanishes the effect of the rotational thermal energy and entropy in the rate constant calculations. We have updated the consistency tests for the application of this approximation in this article. In particular, we have compared the bimolecular activation energies including zero point energy (AUa) with, for example, the energy of the reactants calculated separately (it should be noted that in the main text, we describe unimolecular activation energies) for a gas-phase model and the single water molecule depicted in Wakelam et al. (2017a) for C2H2, C2H4, and C2H6 (reoptimized at the MN15-D3BJ/def2-TZVP level of theory). We tested the validity of the approach for reactions AD1.1, AD2.1, and AB3.1 from the main text. In Figure A.1 we show a graphical example of how both models look. The results for the validation calculations are gathered in Table A.1. All the differences are below 1 kJ mol−1, indicating a tiny influence of the water molecule in the reaction activation energy.

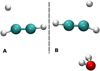thumbnail Fig. A.1

Models for the test of the implicit (A) vs explicit surface approach (B). The depicted figures correspond to reaction AD1.1
Table A.1

Comparison between the activation energies including ZPE for the implicit surface approach (ΔUa,imp) vs a model explicitly including one water molecule (ΔUa,exp).

References

  1. Agúndez, M., Marcelino, N., Tercero, B., et al. 2021, A&A, 649, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Ásgeirsson, V., Jónsson, H., & Wikfeldt, K. T. 2017, J. Phys. Chem. C, 121, 1648 [Google Scholar]
  3. Balucani, N., Asvany, O., Chang, A. H., et al. 1999, J. Chem. Phys., 111, 7457 [NASA ADS] [CrossRef] [Google Scholar]
  4. Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2009, A&A, 499, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021, Astronomy, 647 [Google Scholar]
  6. Chastaing, D., James, P. L., Sims, I. R., & Smith, I. W. 1998, Faraday Discuss., 109, 165 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chuang, K. J., Fedoseev, G., Qasim, D., et al. 2020, A&A, 635, A199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Chuang, K. J., Fedoseev, G., Scirè, C., et al. 2021, A&A, 650, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Coleman, S. 1977, Phys. Rev. D, 15, 2929 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cuppen, H. M., Walsh, C., Lamberts, T., et al. 2017, Space Sci. Rev., 212, 1 [Google Scholar]
  11. Enrique-Romero, J., Rimola, A., Ceccarelli, C., et al. 2019, ACS Earth Sp. Chem., 3, 2158 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fedoseev, G., Chuang, K.-J., Ioppolo, S., et al. 2017, ApJ, 842, 52 [NASA ADS] [CrossRef] [Google Scholar]
  13. Fortenberry, R. C. 2021, ApJ, 921, 132 [NASA ADS] [CrossRef] [Google Scholar]
  14. Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16 Revision C.01 (Wallingford, CT: Gaussian Inc.) [Google Scholar]
  15. Gardner, F. F., & Winnewisser, G. 1975, ApJ, 195, L127 [NASA ADS] [CrossRef] [Google Scholar]
  16. Garrod, R. T., Jin, M., Matis, K. A., et al. 2022, ApJS, 259, 1 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gillan, M. J. 1987, J. Phys. C: Solid State Phys., 20, 3621 [NASA ADS] [CrossRef] [Google Scholar]
  18. Goerigk, L., Hansen, A., Bauer, C., et al. 2017, Phys. Chem. Chem. Phys., 19, 32184 [CrossRef] [Google Scholar]
  19. Grimme, S., Ehrlich, S., & Goerigk, L. 2011, J. Comp. Chem., 32, 1456 [CrossRef] [Google Scholar]
  20. Hama, T., & Watanabe, N. 2013, Chem. Rev., 113, 8783 [Google Scholar]
  21. Hama, T., Kuwahata, K., Watanabe, N., et al. 2012, ApJ, 757, 185 [NASA ADS] [CrossRef] [Google Scholar]
  22. Herbst, E., & Van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
  23. Herbst, E., & Woon, D. E. 1997, ApJ, 489, 109 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hollis, J. M., Jewell, P. R., Lovas, F. J., Remijan, A., & Møllendal, H. 2004, ApJ, 610, L21 [Google Scholar]
  25. Ioppolo, S., Fedoseev, G., Chuang, K. J., et al. 2021, Nat. Astron., 5, 197 [NASA ADS] [CrossRef] [Google Scholar]
  26. Ishibashi, A., Hidaka, H., Oba, Y., Kouchi, A., & Watanabe, N. 2021, ApJ, 921, L13 [NASA ADS] [CrossRef] [Google Scholar]
  27. Jin, M., & Garrod, R. T. 2020, ApJS, 249, 26 [Google Scholar]
  28. Johnson, D. R., Lovas, F. J., Gottlieb, C. A., et al. 1977, ApJ, 218, 370 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kästner, J., Carr, J. M., Keal, T. W., et al. 2009, J. Phys. Chem. A, 113, 11856 [CrossRef] [Google Scholar]
  30. Kelvin Lee, K. L., Loomis, R. A., Burkhardt, A. M., et al. 2021, ApJ, 908, L11 [CrossRef] [Google Scholar]
  31. Knizia, G., Adler, T. B., & Werner, H.-J. 2009, J. Chem. Phys., 130, 054104 [Google Scholar]
  32. Kobayashi, H., Hidaka, H., Lamberts, T., et al. 2017, ApJ, 837, 155 [Google Scholar]
  33. Lamberts, T., Samanta, P. K., Köhn, A., & Kästner, J. 2016, Phys. Chem. Chem. Phys., 18, 33021 [NASA ADS] [CrossRef] [Google Scholar]
  34. Langer, J. S. 1967, Ann. Phys. (N.Y.), 41, 108 [NASA ADS] [CrossRef] [Google Scholar]
  35. Markmeyer, M. N., Lamberts, T., Meisner, J., & Kästner, J. 2019, MNRAS, 482, 293 [NASA ADS] [CrossRef] [Google Scholar]
  36. McConnell, S., & Kästner, J. 2017, J. Comp. Chem., 38, 2570 [CrossRef] [Google Scholar]
  37. McGuire, B. A. 2022, ApJS, 259, 30 [NASA ADS] [CrossRef] [Google Scholar]
  38. Meisner, J., Lamberts, T., & Kästner, J. 2017, ACS Earth Space Chem., 1, 399 [NASA ADS] [CrossRef] [Google Scholar]
  39. Metz, S., Kästner, J., Sokol, A. A., Keal, T. W., & Sherwood, P. 2014, Wiley Interdiscip. Rev. Comput. Mol. Sci., 4, 101 [Google Scholar]
  40. Miksch, A. M., Riffelt, A., Oliveira, R., Kästner, J., & Molpeceres, G. 2021, MNRAS, 505, 3157 [NASA ADS] [CrossRef] [Google Scholar]
  41. Miller, W. H. 1975, J. Chem. Phys., 62, 1899 [NASA ADS] [CrossRef] [Google Scholar]
  42. Molpeceres, G., & Kästner, J. 2021, ApJ, 910, 55 [NASA ADS] [CrossRef] [Google Scholar]
  43. Molpeceres, G., & Rivilla, V. 2022, https://doi.org/10.5281/zenodo.6581077 [Google Scholar]
  44. Molpeceres, G., de la Concepción, J. G., & Serra, I. J. 2021, ApJ, 923, 159 [NASA ADS] [CrossRef] [Google Scholar]
  45. Nyman, G. 2021, Front. Astron. Space Sci., 8 [CrossRef] [Google Scholar]
  46. Perrero, J., Enrique-Romero, J., Martínez-Bachs, B., et al. 2022, ACS Earth Space Chem., 6, 496 [NASA ADS] [CrossRef] [Google Scholar]
  47. Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [Google Scholar]
  48. Puzzarini, C. 2022, Front. Astron. Sp. Sci., 8 [Google Scholar]
  49. Puzzarini, C., Salta, Z., Tasinato, N., et al. 2020, MNRAS, 496, 4298 [CrossRef] [Google Scholar]
  50. Quan, D., Herbst, E., Corby, J. F., Durr, A., & Hassel, G. 2016, ApJ, 824, 129 [NASA ADS] [CrossRef] [Google Scholar]
  51. Rivilla, V. M., Jiménez-Serra, I., Martín-Pintado, J., et al. 2021, Proc. Natl. Acad. Sci. U.S.A., 118, e2101314118 [CrossRef] [Google Scholar]
  52. Rivilla, V. M., Colzi, L., Jiménez-Serra, I., et al. 2022, ApJ, 929, L11 [NASA ADS] [CrossRef] [Google Scholar]
  53. Rodríguez-Almeida, L. F., Jiménez-Serra, I., Rivilla, V. M., et al. 2021a, ApJ, 912, L11 [Google Scholar]
  54. Rodríguez-Almeida, L. F., Rivilla, V. M., Jiménez-Serra, I., et al. 2021b, A&A, 654, A1 [Google Scholar]
  55. Rommel, J. B., & Kästner, J. 2011, J. Chem. Phys., 134, 184107 [NASA ADS] [CrossRef] [Google Scholar]
  56. Rommel, J. B., Goumans, T. P., & Kästner, J. 2011, J. Chem. Theory Comp., 7, 690 [CrossRef] [Google Scholar]
  57. Ruaud, M., Loison, J. C., Hickson, K. M., et al. 2015, MNRAS, 447, 4004 [Google Scholar]
  58. Senevirathne, B., Andersson, S., Dulieu, F., & Nyman, G. 2017, Mol. Astrophys., 6, 59 [CrossRef] [Google Scholar]
  59. Senosiain, J. P., Klippenstein, S. J., & Miller, J. A. 2005, J. Phys. Chem. A, 109, 6045 [Google Scholar]
  60. Senosiain, J. P., Klippenstein, S. J., & Miller, J. A. 2006, J. Phys. Chem. A, 110, 6960 [NASA ADS] [CrossRef] [Google Scholar]
  61. Sleiman, C., El Dib, G., Rosi, M., et al. 2018, Phys. Chem. Chem. Phys., 20, 5478 [NASA ADS] [CrossRef] [Google Scholar]
  62. Sun, Y. L., Huang, W. J., & Lee, S. H. 2015, J. Phys. Chem. Lett., 6, 4117 [CrossRef] [Google Scholar]
  63. Tercero, B., Cuadrado, S., López, A., et al. 2018, A&A, 620, A6 [Google Scholar]
  64. Tsuge, M., & Watanabe, N. 2021, Acc. Chem. Res., 54, 471 [CrossRef] [Google Scholar]
  65. Vazart, F., Latouche, C., Skouteris, D., Balucani, N., & Barone, V. 2015, ApJ, 810, 111 [NASA ADS] [CrossRef] [Google Scholar]
  66. Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [Google Scholar]
  67. Wakelam, V., Bron, E., Cazaux, S., et al. 2017a, Mol. Astrophys., 9, 1 [Google Scholar]
  68. Wakelam, V., Loison, J. C., Mereau, R., & Ruaud, M. 2017b, Mol. Astrophy., 6, 22 [CrossRef] [Google Scholar]
  69. Weigend, F., & Ahlrichs, R. 2005, Phys. Chem. Chem. Phys., 7, 3297 [Google Scholar]
  70. Yu, H. S., He, X., Li, S. L., & Truhlar, D. G. 2016, Chem. Sci., 7, 5032 [CrossRef] [Google Scholar]
  71. Zeng, S., Jiménez-Serra, I., Rivilla, V. M., et al. 2021, ApJ, 920, L27 [NASA ADS] [CrossRef] [Google Scholar]
  72. Zuckerman, B., Turner, B. E., Johnson, D. R., et al. 1975, ApJ, 196, L99 [NASA ADS] [CrossRef] [Google Scholar]
1

The parameters for the dispersion correction term are the recommended parameters extracted from Goerigk et al. (2017), Supplementary Information, Table S.3. s6 = 1.0, a1 = 2.0971, s8 = 0.7862, and a2 = 7.5923.

3

1 kJ mol−1 = 120.27K

5

It should be noted that in this study we report thermal rate constants, and that these just serve as an indication of the timescales for nonthermal events.

All Tables

Table 1

Reaction energies (ΔUr in kJ mol−1) and activation energies (ΔUa in kJ mol−1) for the addition and abstraction reactions starting from C2H2 at the MN15-D3BJ/def2-TZVP level.

In the text
Table 2

Crossover temperatures (Tc in K) and reaction rate-constants k (Tmin, in s−1) at the lowest temperature achieved in our calculations (Tmin in K), for the exothermic reactions starting from C2H2.

In the text
Table 3

Reaction energies (ΔUr in kJ mol−1) and activation energies (ΔUa in kJ mol−1) for the addition and abstraction reactions starting from C2H2 at the MN15-D3BJ/def2-TZVP level.

In the text
Table 4

Crossover temperatures (Tc in K) and reaction rate-constants k(Tmin, in s−1) at the lowest temperature achieved in our calculations (Tmin in K), for the exothermic reactions starting from C2H4.

In the text
Table 5

Reaction energies (ΔUr in kJ mol−1) and activation energies (ΔUa in kJ mol−1) at the MN15-D3BJ/def2-TZVP level for the abstraction reactions from C2H6.

In the text
Table 6

Crossover temperatures (Tc in K) and reaction rate-constants k(Tmin, in s−1) at the lowest temperature achieved in our calculations (Tmin in K), for the exothermic reactions starting from C2H6.

In the text
Table A.1

Comparison between the activation energies including ZPE for the implicit surface approach (ΔUa,imp) vs a model explicitly including one water molecule (ΔUa,exp).

In the text

All Figures

thumbnail Fig. 1

Instanton reaction rate constants in the [500, Tmin] range, with Tmin being the lowest temperature achieved in our calculation for each particular reaction starting from C2H2. The vertical line represents the crossover temperature, Tc.
In the text
thumbnail Fig. 2

Instanton reaction rate constants (and Eckart corrected rate constants in the case of C2H4 + OH → C2H4OH) in the [500, Tmin] range, with Tmin being the lowest temperature achieved in our calculations for each particular addition reaction starting from C2H4. The vertical line represents the crossover temperature, Tc.
In the text
thumbnail Fig. 3

Instanton reaction rate constants in the [500, Tmin] range, with Tmin being the lowest temperature achieved in our calculation for the C2H4 + OH → C2H3 + H2O, Tc. The reaction rate constants for the C2H4 + OH → C2H4O Hare in faded black.
In the text
thumbnail Fig. 4

Instanton reaction rate constants (and Eckart corrected rate constants in the case of C2H6 + NH2/CH3 → C2H5 + NH3/CH4) in the [500, Tmin] range, with being the lowest temperature achieved in our calculations for each particular addition reaction starting from C2H6. The vertical line represents the crossover temperature, Tc.
In the text
thumbnail Fig. 5

Activation energies (ΔUa in kJ mol−1, left panels) and reaction energies (ΔUa in kJ mol−1, right panels) as a function of the radical under consideration (upper panels) and the reacting hydrocarbon (lower panels).
In the text
thumbnail Fig. 6

Schematic diagram showing some of the possible chemical pathways starting from C2H2, C2H4, and C2H6 (inner circle) in the formation of COMs via activation of the closed-shell molecules by OH and H radicals, which forms the four radicals shown in the intermediate circle. It should be noted that not all of the possible reaction paths are indicated in the diagram. The COMs shown in the outer circle are: (1) CHOHCHNCO; (2) vinyl cyanide, C2H3CN; (3) 1,2-ethenediol, (CHOH)2; (4) ethyl mercaptan, C2H5SH; (5) ethyl isocyanate C2H5NCO; (6) ethanol, C2H5OH; (7) ethanolamine, NH2CH2CH2OH; (8) ethylamine, C2H5NH2; and (9) vinyl mercaptan C2H3SH.
In the text
thumbnail Fig. A.1

Models for the test of the implicit (A) vs explicit surface approach (B). The depicted figures correspond to reaction AD1.1
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.