EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A39 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A39
Number of page(s) 12
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202347097
Published online 01 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

In the cold molecular clouds of the interstellar medium (ISM), a significant fraction of molecules are contained in a solid phase in the form of ice. Most of the molecules present in the ISM have been detected as being in a gas phase using radio telescopes and through their rotational transitions; however, direct observation of ices requires studying their vibrational transitions, which are commonly affected by telluric contamination. In this context, space telescopes, such as Spitzer or, more recently, JWST, are essential. Ice observations (Öberg et al. 2011; Boogert et al. 2015; McClure et al. 2023) reveal the presence of several components such as H2O, CO, CH3OH, and CO2, the object of this study. The abundance of these species, as well as their speciation in the ice or their presence in specific regions of the ISM, can only be explained by considering their formation routes and the chemical conditions necessary for their appearance.

The different components of interstellar ice may be formed in situ on the surface of refractory material. Such is the case of H2O, which is formed from the hydrogenation of atomic oxygen (Ioppolo et al. 2008; Dulieu et al. 2010; Lamberts et al. 2014, 2013; Meisner et al. 2017; Molpeceres et al. 2019), and of CH3 OH, which is formed from the hydrogenation of CO (Watanabe & Kouchi 2002; Fuchs et al. 2009; Rimola et al. 2014). Other significant components, such as CO, are primarily synthesized in the gas and accrete under extremely cold and dense conditions on the grain. Interstellar carbon dioxide, CO2, is thought to form via reactions on the surface (see, e.g., Garrod & Pauly 2011; Pauly & Garrod 2018). The postulated reactions contributing to CO2 formation are: CO + OH→CO2+H${\rm{CO}}\,{\rm{ + }}\,{\rm{OH}} \to {\rm{C}}{{\rm{O}}_2} + {\rm{H}}$(1) HCO + O→CO2+H${\rm{HCO}}\,{\rm{ + }}\,{\rm{O}} \to {\rm{C}}{{\rm{O}}_2} + {\rm{H}}$(2) CO + O→CO2.${\rm{CO}}\,{\rm{ + }}\,{\rm{O}} \to {\rm{C}}{{\rm{O}}_2}.$(3)

From this ternary of reactions, reaction (3) has a barrier energy when atomic oxygen is in its ground state, (3P)O (Minissale et al. 2013). reaction (2) is barrierless, and reaction (1), the reaction which we study in this paper, is assumed to have a minimal activation energy (~100 K; Garrod & Pauly 2011).

The assumption that the CO + OH → CO2 + H reaction requires a tiny amount of activation energy is supported by a plethora of experiments dealing with surface chemistry (Ioppolo et al. 2011; Noble et al. 2011; Oba et al. 2010a,b; Qasim et al. 2019; Gutiérrez-Quintanilla et al. 2021; Terwisscha van Scheltinga et al. 2022). Experiments differ in OH radical formation routes, including O2 hydrogenation (Ioppolo et al. 2011; Noble et al. 2011; Qasim et al. 2019), H2O molecule dissociation before ice deposition (Oba et al. 2010a,b), or direct H2O ice photodissociation (Terwisscha van Scheltinga et al. 2022). Substrate variations include amorphous silicates (Noble et al. 2011), CO (Qasim et al. 2019), matrix isolation Gutiérrez-Quintanilla et al. (2021), or H2O (Ioppolo et al. 2011; Oba et al. 2010a,b; Terwisscha van Scheltinga et al. 2022). On the modelling side, Garrod & Pauly (2011) built on the experimental knowledge and coarse-grained the title reaction in a combination of a direct formation route, CO + OH → CO2 + H operating at T ≥ 12 K and coinciding with the onset of CO diffusion on H2O, and an indirect three-body route on CO ices that relies on the formation of a kinetically excited OH radical O + H → OH* that subsequently partakes in the CO + OH* reaction. The latter route on CO ices allows for explanation of the CO2 bands in a nonpolar media observed in infrared observations of ices (Öberg et al. 2011; Boogert et al. 2015; McClure et al. 2023). In summary, there is ample evidence for reaction (1) to be efficient on dust grains. However, the same reaction in the gas phase is relatively slow, with rate constants as low as ~ 2 × 10−13 molecules cm−3 s−1 at 300 K (Frost et al. 1991). The title reaction in the gas phase has also been a source of extensive theoretical attention. It has been simulated using both semi-classical and quantum dynamics on highly accurate potential energy surfaces (PES; Ma et al. 2012; Caracciolo et al. 2018; Li et al. 2014). It was also studied in the presence of other CO2 molecules Masunov et al. (2018). The theoretical works find rate constants even lower than the values reported in Frost et al. (1991).

The different reactivity on surfaces and in the gas phase is puzzling and counterintuitive. In both phases, the reaction is acknowledged to proceed through the highly stable HOCO radical. The evolution from this radical is the primary source of uncertainty because of the high activation energies to form the bimolecular CO2 + H products. In the gas, where a third body to stabilize HOCO is unavailable, the reaction is more likely to occur, owing to the energy redistribution into the few vibrational degrees of freedom and ultimately leading to an irreversible reaction. On the surface, the ice molecules dissipate a significant fraction of this energy, ideally leading to the thermalization of HOCO, hence slowing or impeding the formation of CO2. This was proved by Arasa et al. (2013), initiating the conundrum we tackle in this work and that has also been debated from different prisms (Bredehöft 2020; Upadhyay et al. 2021; Tachikawa 2021). If the reaction is slow in the gas, it should not proceed on the ice, where little energy is left for the reaction after dissipation into the ice. Hence, it is unclear as to how the mismatch between the gas and solid phase experiments is possible. In this article, we aim to shed light on this particular issue. The two main possibilities to explain the disagreement include the following: In the first place is the operation of external energy input, either from the O2 + H or O + H reactions required to form the OH radical (i.e. chemical) or the excess energy used to photodis-sociate H2O. Secondly, free H atoms from the experiment may promote H-abstraction reactions, HOCO + H → CO2 + H2. While these two possibilities are often assumed when interpreting the experimental results, it is fundamental to distinguish which is dominant, if any, to establish under which conditions the laboratory measurements apply to the ISM. Determining the factors contributing to the reaction yield in the experiments is complicated because the detection techniques are suited for identifying only the final products. Quantum chemical calculations are instrumental and provide an atomistic perspective of the different elementary processes relevant to the reaction.

In this work, we simulate the title reaction on two different model ices, H2O and CO, and perform kinetic simulations using a microcanonical formalism to determine the importance of non-thermal effects in the reaction, including dissipation over different numbers of molecules, and thus we complete the picture left by the different experimental studies. The paper is structured as follows. In Sect. 2, we describe the employed computational methodology. In Sect. 3, we present the structural models for the ices (Sect. 3.1), the PES for the reactions in each of the surfaces (Sects. 3.2 and 3.2.2), and the associated kinetic analysis (Sect. 3.3). Sect. 4 is dedicated to interpreting our results from an astrophysical point of view, contextualising the preceding experiments. Finally, we summarize our main findings in Sect. 5.

2 Methodology

2.1 Quantum chemical calculations

The stationary points in the PES were characterized using density functional theory (DFT) calculations on model clusters mimicking H2O and CO ices. Because this work aims to determine the impact of energy redistribution in the formation of CO2 on ice, we needed to use sufficiently large structural models to allow for (ergodic) energy equipartition. In a preceding calculation, Rimola et al. (2018) used a cluster containing 33 H2O water molecules and discussed the suitability of a model of this size, indicating that energy dissipation should be well described with such a model. This was later confirmed with dedicated studies using ab-initio molecular dynamics simulations (Pantaleone et al. 2021, 2020; Ferrero et al. 2023; Molpeceres et al. 2023b). Therefore, in this study, we used the same 33 H2O cluster to simulate the H2O ice (Rimola et al. 2018), and we constructed a 33 CO cluster to simulate the CO ice. To construct this cluster, we used PACKMOL (Martinez et al. 2009) in an 8 Å radius sphere, ensuring that every molecule was at a minimum initial distance of 3 Å from each other. This initial cluster is later refined at the level of the theory described below.

The geometries of the initial clusters were optimized at the MN15-D3BJ/6-31+G(d,p) level of theory (Yu et al. 2016; Grimme et al. 2010, 2011; Hehre et al. 1972; Hariharan & Pople 1973; Ditchfield et al. 1971; Clark et al. 1983), with parameters for the D3BJ dispersion correction taken from Goerigk et al. (2017). The DFT and optimizations utilize the GAUSSIAN16 (rev.C.01) suite of programs (Frisch et al. 2016). We later placed the CO and OH admolecules on the clusters sequentially: first occupying a binding site for the CO molecule and later for OH. Once the two admolecules were located on the clusters, we followed the gas-phase reaction mechanism presented in Ma et al. (2012) for both clusters, except for an alternative exit path on CO ice (Sect. 3.2.2). Additional differences between the gasphase and surface-like profiles are highlighted in Sect. 3.2. After locating every stationary point, we confirmed them as either true minima or first-order saddle points, or transition states (TS), in the PES by computing the molecular Hessian of the system. The electronic energies of the stationary points on the PES were further refined using the domain-based local pair-natural orbital coupled cluster theory including singles and doubles with a perturbative treatment of triple excitations, DLPNO-CCSD(T) (Riplinger et al. 2016; Guo et al. 2018), by using a two-point complete basis set (CBS) extrapolation to the basis set limit using the cc-pVDZ and cc-pVTZ basis sets (Woon & Dunning 1993; Helgaker et al. 1997; Neese & Valeev 2011; Zhong et al. 2008; Neese et al. 2020). The internal options for the PNO localization scheme were set to normal, and resolution of the identity (RI) techniques were used to evaluate exchange and Coulomb integrals (RIJK) using a cc-PVTZ/JK auxiliary basis set. We applied the frozen core approximation in the correlated calculations. The ORCA (v.5.0.4) code was used for the DLPNO-CCSD(T)/CBS calculations (Neese 2012; Neese et al. 2020; Neese 2022).

In addition to cluster calculations, we also carried out gasphase calculations at the same level of theory for comparative purposes, which are indicated throughout the paper in square brackets. Finally, we assessed the quality of our theoretical method of choice, comparing our gas phase results to those of Ma et al. (2012), finding excellent agreement for all the relevant parts of the PES. These results are presented in the Appendix A. We find it worth noting here that our theoretical method does not predict the correct energetics for the high energy intermediate HCO2. This intermediate is not relevant to the kinetics of the system because its formation requires surmounting an emerged barrier of ~8–9 kcal mol−1 from the bimolecular OH + CO asymptote (38–39 kcal mol−1 from the HOCO potential well; Ma et al. 2012; Masunov et al. 2018). Moreover, we could not find this intermediate in the simulations on the H2O cluster. We therefore skipped the search for this intermediate in all cluster calculations. Nonetheless, we discuss the origin of this disagreement in Appendix A.

2.2 Kinetic analysis

We employed the microcanonical flavour of the transition state theory called Rice–Ramsperger–Kassel–Marcus (RRKM) to compute the energy-dependent rate constants k(E) for the transitions between reaction wells given by 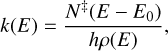k(E)=N‡(E−E0)hρ(E),$k\left( E \right) = {{{N^\ddag }\left( {E - {E_0}} \right)} \over {h\rho \left( E \right)}},$(4)

where h is the Planck’s constant, N‡(E – E0) is the sum of states of the transition state evaluated at energy E to the energy of the transition state, E0, and ρ(E) is the density of states of the reactant at energy E. In addition, the sum of states contains tunnelling corrections for which the non-symmetric Eckart potential model was employed (Eckart 1930; Johnston & Heicklen 1962). We did not include rotational symmetry factors in our calculations due to the symmetry breaking induced by the amorphous surface. The rigid-rotor harmonic oscillator model was used throughout the kinetic calculations. The application of RRKM to interstellar reactions is discussed in Rimola et al. (2018) and used or implied in several other works (Enrique-Romero et al. 2021; Perrero et al. 2022; Baiano et al. 2022)

As is explained later in this work (Sect. 3.3), the title reaction occurs strictly non-thermally at 10 K. Hence, we made our analysis based on k(E) for the entrance CO + OH → t − HOCO/c−HOCO and the exit channels c−HOCO → CO2 + H (and alternatively c−HOCO/t−HOCO + CO → CO2 + HCO, Sect. 3.2.2). We provide k(E) considering several energy dissipation scenarios. Each of them has a different number of molecules, n, over which instantaneous energy dissipation is allowed. We studied n = 16, 10, 5, and 0 (CO/H2O) molecules. In the case where n = 0, the energy redistribution occurs only within the CO + OH system. We carried out this study by projecting out the molecular Hessian matrix elements for the m molecules (where m = 33 − n) farther from the t−HOCO minima as the global minima of our study. The microcanonical rate constants obtained in this study were calculated with the MESS code (Georgievskii et al. 2013). We note that the sizes of the clusters (see Fig. 1) and the highest number of dissipating water molecules are sufficient according to previous studies (e.g. Pantaleone et al. 2020, 2021). Although no specific studies have addressed this issue for CO ice, we have made a reasonable assumption that the same holds true. We find it is worth highlighting again that we considered different dissipating CO ice molecules.

Table 1

Binding energies of the CO, OH, t-HOCO, and c-HOCO admolecules at the reaction site considered in this work on the H2O and CO clusters.

3 Results

3.1 Cluster model

The fully optimized H2O and CO clusters mimicking ice surfaces are presented in Fig. 1. While the CO ice model has a more spherical and compact shape with dimensions ~ 10 × 12 × 13 Å, the water model is slightly more elongated, ~15 × 9 × 10.5 Å. The latter also hosts a cavity where the CO + OH → CO2 + H reaction is simulated. In contrast, the more compact CO cluster does not have any clear deeper binding site. Hence the reaction site was randomly chosen.

The binding energies of the reactants and reaction intermediates on the surfaces are presented in Table 1. These were calculated as the energy difference between the complexes containing the surface and the admolecule and the sum of the isolated fragments, including ZPVE. In the H2O cluster cavity, we found a binding energy for CO of 4.64 kcal mol−1, which is higher than the values reported by Ferrero et al. (2020) (≤3.71 kcal mol−1). This indicates that our cavity is a really deep binding site with a maximized number of neighbour water molecules. For the OH radical, the cavity binding site yields lower than average binding energies (6.45 kcal mol−1) than other reported values, for instance, 10.33 kcal mol−1 (Duflot et al. 2021) and 10.6 kcal mol−1 (Enrique-Romero et al. 2022). The observed differences arise from the specific structure of our cavity, where the number of dangling H-bonds is saturated, and the binding mode of OH, whose acceptor and donor H-bonds are about 0.1 Å shorter than in the cavity case reported by Enrique-Romero et al. (2022). On the CO cluster, the CO/CO binding energy corresponds to the lower bound of the values presented in Ferrari et al. (2023), while the values of OH/CO are unreported. We note that the dual-level error introduced by our calculations is relevant for determining binding energies for CO/CO due to the mismatch of geometries arising from the weak CO-CO interaction in the ice (Ferrari et al. 2023). In the subsequent reactivity studies, the relative magnitude of this error is diminished because energy differences between reaction steps are much higher than the CO-CO interaction energy.

For the reactivity studies, we kept the CO binding site as determined above, while the OH radical was placed on a different binding site. We justify this choice based on two arguments. First, when both adsorbates are thermalized, the higher interstellar abundance of CO makes it more likely to be located in deep binding sites, such as the cavity formed in the H2O cluster. Second, in Sect. 3.3, we investigate the effect of a translationally excited OH radical colliding with a pre-adsorbed CO.

thumbnail Fig. 1

Views of the clusters employed to simulate the CO + OH → CO2 + H reaction. Top left: side view of the H2O ice cluster. Top right: top view of the H2O ice cluster. Bottom left: side view of the CO ice cluster. Bottom right: top view of the CO ice cluster. Colour code: White-Hydrogen, Red-Oxygen, Teal-Carbon. The size of a cluster was determined approximately by measuring its endpoints.

3.2 Potential energy surface construction

All the energy diagrams have been referenced from the asymptotes (i.e. from the sum of energies of the surface, reacting CO, and the reacting OH radical). We refer to this as the bimolecular system, and for the sake of simplicity we denote it as CO + OH regardless of the ice surface. This was also done for the sake of clarity, as the influence of the substrate in stabilizing the reactants and its catalytic effect on the barriers are much clearer.

3.2.1 H2O ice

We included two pre-reactant complexes following the literature (Ma et al. 2012; Masunov et al. 2018). The first is a pre-reactant complex with large dihedral ∠HOCO angles (PRC) that leads to the formation of the t-HOCO intermediate. Second is a near 0° dihedral angle pre-reactant complex (PRC’) that forms the c-HOCO intermediate (which was not found on CO ice, as discussed in Sect. 3.2.2). The transition states that connect the two pre-reactant complexes with the reaction wells are named TS1 and TS1’, respectively, and the transition state connecting these two wells is TS2. Finally, the transition state leading to CO2 + H from c-HOCO is named TS4. The reason for not naming it TS3 is that the TS3 label (specifically TS3’) is reserved for the exit transition state from t-HOCO, a stationary point we do not find on water ice.

The stationary points on the reaction profile are gathered in Fig. 2. The reaction profile has, for the most part, the same profile as in the gas phase but with two notable exceptions. The first concerns the absence of the HCO2 intermediate, as we already discussed in Sect. 2.1. The second is the inversion in energy between PRC and PRC’. This inversion appears following the formation of a HO––H2O hydrogen bond that locks the PRC’ geometry in the binding site contiguous to the CO binding site. The snapshots of the stationary points are collated in Fig. 3, where this effect can be observed. The higher stabilization of PRC’ also results in higher activation energy to c-HOCO through TS1’.

The binding energies of t-HOCO and c-HOCO on the cavity are 15.51 kcal mol−1 (7805 K) and 12.30 kcal mol−1 (6190 K), respectively. These binding energies are significantly higher than the ones for CO and OH presented in Table 1, and they are closer to the average values reported for the related molecule of formic acid, HC(O)OH (i.e., ~12.30 kcal mol−1 Molpeceres et al. 2022, 10.7–21.0 kcal mol−1 Ferrero et al. 2020). The t-HOCO and c-HOCO wells are significantly stabilized on the surface, evinced by the 13–16 kcal mol−1 difference in energy with the same intermediates in the gas phase. As a consequence, the activation energy of TS4 is higher on water. When breaking the O–H bond in c-HOCO, the energy corresponding to the OH moiety must be overcome (i.e. a significant fraction of the binding energy). The binding energy of the CO2 + H system on H2O was found to be 7.30 kcal mol−1 (3673 K).

Finally, from Fig. 2, it is evident that the reaction, if viable, must proceed through quantum tunnelling. The c−HOCO → CO2 + H barrier is 32.1 kcal mol−1, which is extremely high for ISM conditions. However, contrary to what happens in the gas phase, TS4 is submerged with respect to the reactant asymptote due to the stabilization promoted by the H2O surface. The product of the reaction, CO2 + H, is higher in energy than both radicals, and the reaction is significantly less exothermic because of the break of hydrogen bonds. Nonetheless, once CO2 + H is formed, H is susceptible to diffusing or evaporating, thus concluding the reaction.

thumbnail Fig. 2

Reaction profile for the CO + OH → CO2 + H reaction on the ASW cluster. Energies are referred to as the sum of the isolated components (e.g. CO, OH, (H2O)33). In square brackets are the energies for the gas-phase reaction. All energies have been ZPVE corrected.
thumbnail Fig. 3

Stationary points on the CO + OH → CO2 + H reaction profile for the reaction on top of the (H2O)33 cluster. For all the intermediates and transition states, we indicate the value of the dihedral angle ∠HOCO governing the isomerism of the t-HOCO and c-HOCO wells. Colour code: White-Hydrogen, Red-Oxygen, Teal-Carbon.
thumbnail Fig. 4

Reaction profile for the CO + OH → CO2 + H reaction on the amorphous CO cluster. The energies are referred to as the sum of the isolated components (e.g. CO, OH, (CO)33). In square brackets are the energies for the gas-phase reaction. All energies have been ZPVE corrected.

3.2.2 CO ice

The reaction profile on CO ice is shown in Fig. 4 and the stationary points in Fig. 5. With respect to the gas-phase process, as previously discussed, the profile lacks the HCO2 intermediate. When comparing with the results for the water cluster presented above, the main difference is the lack of PRC’, so the reaction must go through the t−HOCO intermediate to reach CO2. While PRC’ exists on the CO ice, we found it to be a first-order saddle point. Unlike in water, where PRC’ is stabilized because of the interaction of the OH radical with a dangling bond of H2O, this interaction is unavailable on CO, and the weak OH-CO interaction promotes the rotation to PRC. There is still the possibility that the lack of PRC’ is an effect of the random selection of the binding site; however, a full binding site sampling is beyond our computational resources. To reach the t−HOCO intermediate, the TS 1 must be crossed at the same energy level as the asymptote. Hence, significant energy dissipation would suppress the whole reaction unless enough energy input is provided via non-thermal mechanisms.

Additionally, the much reduced intermolecular interaction of the admolecules with the surface due to the lack of electrostatic and H-bonding interactions of CO ices affects the energetics of the stationary points. The most prominent examples are the lower stabilisation of intermediates and the barrier in TS4, which sits above the energy of the asymptote. In general, the energetics on CO ice are closer to the gas phase case, with small differences (e.g. the isomerisation barrier for the t−HOCO → cis−HOCO reaction on CO is about 1 kcal mol−1 lower and about 2 kcal mol−1 lower for the reverse reaction).

The fact that there are more CO molecules surrounding the reaction site opens a new possibility not available on water ice or the gas phase involving the reactivity of the t−HOCO and cis−HOCO intermediates with a neighbouring CO, leading to CO2 + HCO, see Fig. 6. Notably, these reactions possess lower activation energy barriers than TS4, see Fig. 7, and in the case of the cis−HOCO + CO → CO2 + HCO reaction, the barrier sits below the asymptote.

thumbnail Fig. 5

Stationary points on the CO + OH → CO2 + H reaction profile for the reaction on top of the (CO)33 cluster. For all the intermediates and transition states, we indicate the value of the dihedral angle ∠HOCO governing the isomerism of the t-HOCO and c-HOCO wells. Colour code: white – hydrogen, red – oxygen, teal – carbon.
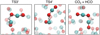thumbnail Fig. 6

Additional stationary points complementing those presented in Fig. 5 for the alternative reaction channel 2 CO + OH → CO2 + HCO. Colour code: white – hydrogen, red – oxygen, teal – carbon.

3.3 Microcanonical rate constants

We estimated the microcanonical rate constants for the PES entrance and exit channels described in the previous sections. The entrance channels start with the pre-reactant complexes and finish with t/c-HOCO, whereas the exit channels start with t/c-HOCO and finish with CO2 + H, and additionally CO2 + HCO for CO. These channels present the relevant rate constants for the kinetics of the reaction because the t−HOCO → c−HOCO is much faster, even when energy redistribution is at play. We note that due to the barriers (TS1 and TSF’), if the stationary points of the PES were populated according to a thermal distribution, the formation of the HOCO intermediates would be slow, and the formation of products would likely not happen at all. To simulate non-thermal reactions, an initial amount of energy is given to the system (see the next paragraph). Experiments of Oba et al. (2010b) show the formation of HOCO with an apparent small barrier or null barrier. We note that for the exit channel (c/t) −HOCO → CO2 + H/HCO, the starting potential well is very deep, and thermalization is more likely (Arasa et al. 2013). Nevertheless, as we show, under a microcanonical formalism, the formation of CO2 + H is found to be slow. Finally, different energy dissipation is allowed by changing the number of ice molecules considered in the microcanonical calculations, n.

Our PESs indicate that the adsorption energy (formation of PRC or PRC’) may not be completely dissipated and that it may be employed in forming HOCO. The energy reference is again the energy of the asymptotes. One could consider that this is not the best choice since the initial energy lies above the energy of the PRC and PRC, and it would actually mean that the initial state is actually higher in energy than a fully thermalized reactant set. However, we note that (i) if a reference state is an upper bound of the real one, and even in this case the reaction is not plausible, then starting from a more stable reference will not change the qualitative picture; and (ii) in cases where an incomplete energy dissipation is promoted by certain exothermic processes, like diffusion into deeper binding sites and possible Eley–Rideal mechanisms1 would actually involve higher initial energies than PRC and PRC’. This effect is irrelevant when the activation energy of a reaction is much higher than the exothermicity caused by the mentioned processes, but for CO + OH → HOCO, the activation energy of the reaction falls below the adsorption energy, and it is of small magnitude. The correct energy reference would lie somewhere in between that of the asymptote and the PRC and PRC’.

The microcanonical rate constants for the entrance step are shown in Figs. 8 and 9 for H2O and CO ice. In these figures, we show the reaction rate constants as a function of the energy, where k(E = 0) corresponds to the separated no-adsorption asymptote (CO + OH in Figs. 2 and 4). Energies above zero indicate extra energy from non-thermal excitation mechanisms. In this work, to compare our theoretical predictions with experimental observations, we considered the presence of extra energy from either (i) a prior О + H → OH reaction (∆U = 102.1 kcal mol−1) or (ii) half the energy deposited by a single Ly-α photon, assuming equal energy partition into the products of the H2O → OH + H, (∆U = 118.7 kcal mol−1). We note that the amount of extra energy used to promote the title reaction through the non-thermal mechanisms is unknown. Hence, we represent fractions of that energy, 0.10, 0.25, 0.50, as vertical dashed lines in Figs. 8 and 9 to serve as a guide to evaluate how the rate constants would increase under these assumed scenarios. As we introduced in Sect. 2, we evaluated the behaviour of the reaction assuming dissipation into a set of n molecules. The four different cases where n equals 0, 5, 10, and 16 are illustrated in Figs. 10 and 11.

The rate constants for the entrance step on H2O ice are, for all n dissipating molecules, fast for the PRC → t−HOCO step, indicating that external energy input is unnecessary for this reaction, as determined experimentally by Oba et al. (2010b) and computationally by Arasa et al. (2013). However, for the alternative PRC’ → c-HOCO reaction, we observed k(E = 0) ≤ 108 s−1 for the models with 10 and 16 H2O dissipating molecules. This means that if the timescale for thermalization is shorter than tens of nanoseconds, the adsorption energy alone is insufficient to overcome the entrance barrier. This constraint is lifted by considering extra energy. The reason for the difference between rate constants for the reactions starting from PRC and PRC stems from the significantly higher activation energy in the latter case.

For the CO model, we observed systematically lower values of k(0) than in water, due to the lower stabilization of the PRC complex on CO than on H2O leading to higher energy barriers than in the best case for H2O. This in turn yielded k(E = 0) ≤ 108 s−1 for all of our models. Because k(E) is a very steep function around E = 0, the reaction is viable with a small input of energy that can come from reactions, for example, O2 + H (Qasim et al. 2019). This finding reinforces the scenario presented in Garrod & Pauly (2011) for the three body formations of CO2 on CO ice, as we discuss in Sect. 4. An important comment for each of these rate constants is that we implicitly assumed an infinitely fast energy partition into n molecules, which may not be a good representation of this reaction on CO. At this research stage, we warn that extracting strong conclusions for a limit case such as the one found for PRC → t−HOCO on CO ice is difficult, and more sophisticated approaches are necessary. We are currently working on a molecular dynamics study of this reaction to illuminate this issue.

Similar to the entrance rate constants, the exit c−HOCO → CO2 + H rate constants on H2O ice and c/t−HOCO → CO2 + H/HCO rate constants on CO ice are plotted in Figs. 12 and 13 for the different dissipation scenarios. We find it important to remember that while the entrance channels are unaffected by quantum tunnelling, all the exit channels involve the migration of an H atom, turning quantum tunnelling into an important driver for the reaction, as already evinced by nuclear quantum dynamics calculations (Ma et al. 2012). Still, even with the influence of quantum tunnelling, the reactions are, in all cases, significantly slower than in the entrance step. The importance of the energy dissipation scheme is major for these reactions. There is a clear gap in the exit rate constant values between the (ideal) n = 0 dissipation model and the 5-, 10-, and 16-molecule dissipation models that, in all the cases, yield rate constants k(E = 0) ≤ 0 s−1. We highlight that these values must be verified against the thermalization timescale (i.e. if thermalization is faster, the reaction will not proceed). A rate constant of k(E = 0) ≤ 0 s−1 means a reaction time on the order of seconds, and we found it difficult to believe that thermalization would not happen on those timescales, as it would preclude all the c/t−HOCO → CO2 + H/HCO reactions in all the conditions and substrates considered in this work. We then concluded that without the input of any external energy other than the adsorption energy of the reactants, the reaction can proceed neither microcanonically nor from thermalized HOCO.

When including a degree of external energy from the mechanisms explained above (chemical and H2O photodissociation), the exit reaction becomes faster, as expected. However, only the n = 0 dissipation model yielded rate constants that are sufficiently high ≥ 108 s−1 to compete with thermalization. The upper bound of the timescale for (almost) complete thermalization of HOCO has been estimated to be similar to that of CO2 formed from the CO + (1D)O → CO2 reaction, that is, a few nanoseconds (Upadhyay et al. 2021). While the energy dissipation in RRKM is instantaneous and an incomplete energy dissipation may increase the values of the rate constants, our assumption for the external energy input is also rather ideal. Thus, we concluded that even in the presence of external energy input, we find it hard to justify the formation of CO2 and H/HCO from the title reaction. This suggests that the formation of CO2 relies on the subsequent reaction described as follows: 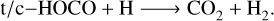t/c−HOCO + H→CO2 + H2.${{\rm{t}} \mathord{\left/ {\vphantom {{\rm{t}} {{\rm{c}} - {\rm{HOCO}}\,{\rm{ + }}\,{\rm{H}}}}} \right. \kern-\nulldelimiterspace} {{\rm{c}} - {\rm{HOCO}}\,{\rm{ + }}\,{\rm{H}}}} \to {\rm{C}}{{\rm{O}}_2}{\rm{ + }}{{\rm{H}}_2}.$(5)

Reaction (5) involves two radicals, and even though an activation barrier may be present on ice (Enrique-Romero et al. 2022), quantum tunnelling should play a major role, as it has been found to be the case for H-abstraction reactions (Molpeceres et al. 2022; Molpeceres et al. 2023a). Thus, reaction (5) must be viable. The inclusion of reaction (5) in the CO2 reaction network was already in place for the non-energetic formation of CO2, for example, in Qasim et al. (2019). Still, this article shows that it also applies to the energetic formation of CO2. We put our results in a laboratory, simulation and astrophysical context in Sect. 4.

Finally, despite the fact that it does not affect the outcome of the reactions studied in this work (e.g. the t/c−HOCO(+CO) → CO2 + H/HCO reactions remain nonviable under ISM conditions), it is interesting from a purely chemical perspective to comment on the effect observed for the two competing reactions c−HOCO → CO2 + H and t/c−HOCO + CO → CO2 + HCO. The competition between these two processes is energy dependent. For example, at low values of E, t/c−HOCO + CO → CO2 + HCO is favoured, whereas c−HOCO → CO2 + H is the preferred exit channel at higher energies between 10–120 kcal mol−1, depending on the number of dissipating molecules. The dependence on the energy and number of dissipating molecules clearly reveals that the dominion of the c−HOCO → CO2 + H route at high energies is an entropic effect. For both routes, the count of states at the TS energy (the numerator of Eq. (4)) depends on the height of the barrier and the number of low-frequency vibrational modes. In contrast with H, because HCO has two molecular vibrations, H–C and C = O, at 2800 and 1900 cm−1, the count of states will be smaller at high energies. The lower frequency H-CO vibrations in the t/c−HOCO → CO2 + H reaction on CO and their contribution to the sum of states overwhelm the purely kinetic effect arising from the lower barrier in the t/c−HOCO + CO → CO2 + HCO reaction on CO.

thumbnail Fig. 7

Reaction profile for the CO + OH → CO2 + H and 2 CO + OH → CO2 + HCO alternative reaction on the amorphous CO cluster. The energies are referred to as the sum of the isolated components (e.g. CO, OH, (CO)33). We note that we have omitted the separated reactants asymptote and pre-reactant complex energies already presented in Fig. 4. All energies have been ZPVE corrected.
thumbnail Fig. 8

Microcanonical (energy-dependent) rate constants for the CO + OH → t−HOCO (top) and CO + OH → c−HOCO (bottom) reaction step on H2O ice. The different solid lines represent different ergodic energy dissipation scenarios with n molecules accepting the reaction energy. The vertical dashed lines indicate fractions (0.1 and 0.25) of the О + H reaction (red) and of half the energy of a Lymann alpha photon (blue); see text. The zero of energy is defined as the PES asymptote (i.e. no adsorption).
thumbnail Fig. 9

Microcanonical (energy-dependent) rate constants for the CO + OH → t−HOCO reaction step on CO ice. The different solid lines represent different ergodic energy dissipation scenarios with n molecules accepting the reaction energy. The vertical dashed lines indicate fractions (0.1 and 0.25) of the О + H reaction (red) and of half the energy of a Lymann alpha photon (blue); see text. The zero of energy is defined as the PES asymptote (i.e. no adsorption).
thumbnail Fig. 10

Graphic representation of the different layers admitting energy dissipation through RRKM equipartition in the H2O model ice. The t-HOCO molecule (zero dissipating molecules) is represented with red, teal, and white spheres. The five H2O model includes the t-HOCO molecule, and the H2O molecules are shown in blue. The 10- and 16-molecule models are represented with gold and black molecules, respectively. Finally, the rest of the molecules are represented as transparent liquorices.
thumbnail Fig. 11

Graphic representation of the different layers admitting energy dissipation through RRKM equipartition in the CO model ice. The t-HOCO molecule (zero dissipating molecules) is represented with red, teal, and white spheres. The five CO model includes the t-HOCO molecule, and the CO molecules are shown in blue. The 10- and 16-molecule model are represented with gold and black molecules, respectively. Finally, the rest of the molecules are represented as transparent liquorices.
thumbnail Fig. 12

Microcanonical (energy-dependent) rate constants for the c−HOCO → CO2 + H reaction step on H2O ice. The different solid lines represent different ergodic energy dissipation scenarios with n molecules accepting the reaction energy. The vertical dashed lines indicate fractions (0.1, 0.25, and 0.5) of the О + H reaction (red) and of half the energy of a Lymann alpha photon (blue); see text. The zero of energy is defined as the PES asymptote (i.e. no adsorption).
thumbnail Fig. 13

Microcanonical (energy-dependent) rate constants for the c−HOCO → CO2 + H (top) and c−HOCO + CO → CO2 + HCO (bottom) reaction step on CO ice. The different solid lines represent different ergodic energy dissipation scenarios with n molecules accepting the reaction energy. The vertical dashed lines indicate fractions (0.1, 0.25, and 0.5) of the O + H reaction (red) and of half the energy of a Lymann alpha photon (blue); see text. The zero of energy is defined as the PES asymptote (i.e. no adsorption).

4 Discussion

4.1 The CO + OH → CO2 + H reaction in the laboratory

The experiments carried out in the CO + OH → CO2 + H reaction were reviewed in Sect. 1. For most of them, the biggest experimental conundrum was the generation of the OH radical, which is very unstable under laboratory conditions and needs to be generated in situ. The experimental methods for forming the OH radical in these experiments are, in most cases, different. However, all the possible formation pathways involve the co-deposition or co-generation of H atoms (e.g. formation with O2 + H, fragmentation of H2O in a microwave discharge, or H2O photodissociation). In general, it is impossible to experimentally discern whether the CO + OH reaction proceeds directly to CO2 + H or stops at t-HOCO, which is converted to CO2 via reaction (5).

A rigorous study of the reaction using molecular dynamics (Arasa et al. 2013) showed the probability of direct formation of CO2 on H2O ice as being lower than 1%. It is important to remark that in Arasa et al. (2013), the OH was generated with excess energy coming from photodissociation of H2O. Our results support the latter scenario and discard the direct reaction. Compared with our results, the small fraction observed for the direct formation of CO2 + H in Arasa et al. (2013) may come from the slower and more realistic non-ergodic energy dissipation present in the molecular dynamics study.

On CO ice, the reaction proceeds in a manner similar to H2O ice, both in our calculations and in the experiments of Qasim et al. (2019), as HOCO is explicitly included as the intermediate for the reaction. Qasim et al. (2019) discuss the competition with formic acid (HC(O)OH) through the reaction: HOCO + H→HC(O)OH${\rm{HOCO}}\,{\rm{ + }}\,{\rm{H}} \to {\rm{HC}}\left( {\rm{O}} \right){\rm{OH}}$(6)

with reaction (5). Our results complement these experiments as well, showing that in addition to what was already known, the formation of the HOCO complex has to surmount an activation energy of 2.2 kcal mol−1 with a mere adsorption energy of 2.5 kcal mol−1. This contrasts with H2O ice, where the higher stabilization of the PRC complex increases the energetic budget for the formation of HOCO. The consequence of this effect in the overall reaction scheme is that the formation of HOCO cannot be taken forgranted on CO ice undera non-energetic regime. In Qasim et al. (2019), such energy input is given by a preceding chemical reaction. The more impeded formation of the HOCO radical on CO is the main difference with H2O ice and is illustrated by the rate constants in Fig. 8 (top panel) and Fig. 9. This different reactivity on different substrates may explain the recent JWST observations of a higher degree of mixing of CO2 with H2O than with CO (McClure et al. 2023). However, and as we indicated in Sect. 3.3, further studies are being undertaken to understand the precise behaviour of the CO + OH → t−HOCO association step on CO ices.

Gutiérrez-Quintanilla et al. (2021) used matrix isolation, electron paramagnetic resonance, and FT-IR techniques, making it possible to observe several radicals, among which included HOCO and CO2. The HC(O)OH molecule was also detected, although its formation seems to be due to HCO + OH rather than a reaction (6). In this experiment, methanol molecules embedded in an Argon matrix were photolysed at 14 K. The resulting photo-products could relax, as the matrix acted as a third body. Later the sample was warmed to 35 K, and the Ar matrix was removed, allowing light species to diffuse. The peak of CO2 production occurred in this last stage. According to our results and interpretation, if CO2 is formed via reaction (1), there is either some extra energy input, as not all the energy from the photolysis step was completely dissipated, or H-abstraction reactions are present. In the latter case, this can be triggered by other radicals rather than reaction (5), which is something we did not consider in this work, but it would require either diffusion at warmer temperatures or the presence of a nearby radical species. In addition, an efficient H-abstraction radical-radical channel should be present in such a case and would certainly depend on the relative orientation of the two radicals (Enrique-Romero et al. 2022). We note that no ice surface is present in this experiment. Instead, there is the bare copper plate on top of which the matrix and reactant mixture was prepared. Finally, we would like to encourage more experiments on CO2 formation starting from thermalized reactants, especially on CO surfaces.

4.2 The CO + OH → CO2 + H reaction in the interstellar medium

The comparison between the experiments and our calculations presented in the last section motivated us to contextualize our results in the expected conditions of the ISM. We concluded that the sole CO + OH reaction is insufficient for the formation of CO2 on ices and that reaction (5) is the most promising candidate for the follow-up reaction. With this in mind, we questioned whether it is justified to consider a small activation energy for the OH + CO → CO2 + H reaction in astrochemical models of molecular clouds and pre-stellar cores. In light of our simulations, we considered that there are at least four different cases: 1) high coverage of H2O ice and high abundance of H atoms, 2) high coverage of H2O ice and low abundance of H atoms, 3) high coverage of CO ice and high abundance of H atoms, and 4) high coverage of CO ice and low abundance of H atoms.

On H2O ice (Cases 1 and 2), the formation of the HOCO complex is facile and does not require any energy input, with a fast reaction occurring thanks to the adsorption energy (or a fraction of it) on water ice. Moreover, the dominance of H2O in the early stages of a molecular cloud’s life, during the translucent cloud phase (Snow & McCall 2006), ensure mild temperature conditions (15–50 K) that allow for diffusion of CO molecules and relatively low extinction (Aυ ~ 1–2 mag). Under these conditions, Case 1 is the most likely, with H atoms produced from photodissociation of H2O and other hydrogenated molecules both in the gas and on the grain. Other mechanisms, such as cosmic ray ionization, also contribute to these fragmentation processes. Under these conditions, we determined that considering a null or low activation barrier for reaction (1) in astrochemical models is justified because the H atom will ensure prompt conversion of HOCO to CO2 through reaction (5). However, we warn that HC(O)OH abundance could be underestimated following this approach. At higher extinctions, but without enough CO surface coverage (Case 2, molecular cloud stage), the abundance of H atoms on grain surfaces will be reduced, and the HOCO complex will survive longer on the grain. Under these conditions, we recommend differentiating reaction (1) and 5.

The next two cases (Cases 3 and 4) can be treated conjointly. Our simulations show that forming the HOCO radical from CO + OH is not straightforward on CO ice and requires initial energy input. While the energy required to initiate the reaction is not very high, the very low temperatures where Cases 3 and 4 would dominate (dense pre-stellar cores with T = 10 K) discard the thermal energy as the initiator of the reaction. This energy input can come from a neighbouring chemical reaction because H2O photodissociation should be a small factor in CO ices. Therefore, we consider that the approach presented in Garrod & Pauly (2011) of modelling the CO2 formation as a three-body reaction (i.e. H + O + CO) is a good compromise to model the reaction on CO ice. Whether the three-body reaction can be coarse-grained to yield CO2 + H directly or HOCO (and later proceed through reaction (5)) is likely to depend on the H atom abundance. For example, an important factor should be the local cosmic ray ionization rate (ζ) determining the dissociation of H2 into 2 H and thus the ratio of HOCO radicals to H atoms. We must emphasize that coarse-graining the formation of CO2 through the title reaction to study CO2 formation and evolution may be acceptable only when H atom abundance overwhelms HOCO abundance. However, in doing so, the abundance of other HOCO-derived molecules, such as HC(O)OH, will be underestimated. Precaution is advised when the target of the models involves these molecules.

Finally, we discuss other possible scenarios. One possibility is that the excited formation of OH leads to non-thermal diffusion out of the reaction site or its desorption (we note that the latter would be more plausible on CO ices due to the lower binding energy), but in these cases the reaction would not take place. Another possible scenario regards the energy dissipation after HOCO is formed. Because of the high exothermicity of the CO + OH → HOCO reaction and the low binding energies of these radicals on CO ice, there is the possibility that HOCO chemically desorbs or triggers the desorption of a nearby ice CO molecule. In addition, if these reactions would have to take place in the inner layers of the ice, one must take into account that energy dissipation would be even more efficient due to the larger number of intermolecular interactions and the higher number of surrounding molecules, rendering each reaction step less and less efficient.

5 Conclusions

Using accurate quantum chemical calculations and microcanonical kinetic modelling, we found that the CO + OH → CO2 + H reaction, which has been considered as the most important producer of interstellar CO2, is rather inefficient, and its occurrence cannot be taken for granted. The reaction proceeds through a rather stable intermediate, HOCO, and more specifically through its two structural isomers, t-HOCO and c-HOCO. On H2O ice, the formation of HOCO is feasible, but its evolution to CO2 requires a further reaction step that most likely involves H-abstraction through reaction (5). On CO ice, we found, for the first time, that the formation of HOCO is not as efficient as currently assumed, due to the lower adsorption energy of OH and CO molecules on CO ice. We indicate that non-thermal effects are necessary to form HOCO and thus CO2 on CO ice. This limitation may be behind the recent ice observations showing a higher fraction of CO2 in water-dominated environments (Boogert et al. 2015; McClure et al. 2023), when compared with apolar (CO-dominated) ices.

Because our calculations assume an ideal energy redistribution in an infinitely short time after the reactions, our results represent a lower bound for the production of HOCO and CO2 from the CO + OH reaction. We aim to improve the description of energy dissipation in forthcoming works to resolve ambiguous cases. We encourage further experimental work on the topic, especially on CO ices following Qasim et al. (2019). Nonetheless, with our results, we are able to provide atomistic insight into the formation of CO2, one of the most important interstellar ice constituents, and indicate the cases where coarse-graining of the CO + OH reaction in astrochemical models is, to a first approximation, acceptable and where it is not.

Acknowledgements

G.M. thanks the Japan Society for the Promotion of Science (JSPS International Fellow P22013, and Grant-in-aid 22F22013) for its support. The authors acknowledge support by the Research Center for Computational Science in Okazaki, Japan (Projects: 22-IMS-C301, 23-IMS-C128), the state of Baden-Württemberg through the bwHPC consortium and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster) (Project: 22-IMS-C301). Y.A. acknowledges support by Grant-in-Aid for Transformative Research Areas (A) grant nos. 20H05847.

Appendix A Gas-phase comparison with Ma et al. (2012)

We compare our energetics of the CO + OH → CO2 + H gasphase reaction profile at the DLPNO-CCSD(T)/CBS//MN15-D3BJ/6-31+G(d,p) level with the high quality CCSD(T)/AVTZ results presented in Table A.1 of Ma et al. (2012). We note that the energies presented here are not ZPVE corrected, unlike in the main manuscript. We observed excellent deviations (between 0.0–1.3 kcal mol−1) between methods (e.g. chemical accuracy) for all structures except HCO2. As we introduced in the methods section, this intermediate and the associated entrance and exit transition states, TS5 and TS6, are irrelevant to the reaction kinetics or dynamics (Ma et al. 2012; Masunov et al. 2018). Hence, a wrong prediction of the energetics of this intermediate does not affect ourresults, and we do not include it in ourkinetic simulations. Yet, it is interesting to mention the reason for the discrepancy.

In Ma et al. (2012), the authors show that the HCO2 intermediate belongs to the C2υ symmetry point group at the CCSD(T)/AVTZ level of theory. However, the geometries at the MN15-D3BJ/6-31+G(d,p) level converge to a Cs intermediate. The T1 diagnostic at the DLPNO-CCSD(T)/cc-pVTZ level of theory for the HCO2 intermediate hints at a strong multi-reference character (T1 = 0.068), so it is not clear if the CCSD(T) or the MN15-D3BJ calculations are better at predicting the correct HCO2 geometry. However, it is clear that a dual-level approach, such as DLPNO-CCSD(T)/CBS//MN15-D3BJ/6-31+G(d,p), will fail due to the mismatch of geometries. Despite the discrepancy found for HCO2, the excellent agreement for all the relevant parts of the PES indicates that the studies on the H2O and CO clusters will yield the correct energetics for the system.

Table A.1

Comparison of the potential energy reaction profile (e.g. no zero-point energy corrected) between our computational method and high accuracy results presented in the literature.

References

  1. Arasa, C., Van Hemert, M. C., Van Dishoeck, E. F., & Kroes, G. J. 2013, J. Phys. Chem. A, 117, 7064 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baiano, C., Lupi, J., Barone, V., & Tasinato, N. 2022, J. Chem. Theory Comput., 18, 3111 [CrossRef] [Google Scholar]
  3. Boogert, A. C., Gerakines, P. A., & Whittet, D. C. 2015, ARA&A, 53, 541 [Google Scholar]
  4. Bredehöft, J. H. 2020, Front. Astron. Space Sci., 7, 33 [CrossRef] [Google Scholar]
  5. Caracciolo, A., Lu, D., Balucani, N., et al. 2018, J. Phys. Chem. Lett., 9, 1229 [CrossRef] [Google Scholar]
  6. Clark, T., Chandrasekhar, J., Spitznagel, G. W., & Schleyer, P. V. R. 1983, J. Comput. Chem., 4, 294 [CrossRef] [Google Scholar]
  7. Ditchfield, R., Hehre, W. J., & Pople, J. A. 1971, J. Chem. Phys., 54, 724 [NASA ADS] [CrossRef] [Google Scholar]
  8. Duflot, D., Toubin, C., & Monnerville, M. 2021, Front. Astron. Space Sci., 8, 24 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dulieu, F., Amiaud, L., Congiu, E., et al. 2010, A&A, 512, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Eckart, C. 1930, Phys. Rev., 35, 1303 [Google Scholar]
  11. Enrique-Romero, J., Ceccarelli, C., Rimola, A., et al. 2021, A&A, 655, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Enrique-Romero, J., Rimola, A., Ceccarelli, C., et al. 2022, ApJS, 259, 39 [NASA ADS] [CrossRef] [Google Scholar]
  13. Ferrari, B., Molpeceres, G., Kästner, J., et al. 2023, ACS Earth Space Chem., 7, 1423 [NASA ADS] [CrossRef] [Google Scholar]
  14. Ferrero, S., Zamirri, L., Ceccarelli, C., et al. 2020, ApJ, 904, 11 [NASA ADS] [CrossRef] [Google Scholar]
  15. Ferrero, S., Pantaleone, S., Ceccarelli, C., et al. 2023, ApJ, 944, 142 [NASA ADS] [CrossRef] [Google Scholar]
  16. Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian16 Revision C.01, pages: Gaussian 16, Revision C.01 (Wallin: Gaussian, Inc.) [Google Scholar]
  17. Frost, M. J., Sharkey, P., & Smith, I. W. 1991, Faraday Discuss. Chem. Soc., 91, 305 [CrossRef] [Google Scholar]
  18. Fuchs, G. W., Cuppen, H. M., Ioppolo, S., et al. 2009, A&A, 505, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Garrod, R. T., & Pauly, T. 2011, ApJ, 735, 15 [Google Scholar]
  20. Georgievskii, Y., Miller, J. A., Burke, M. P., & Klippenstein, S. J. 2013, J. Phys. Chem. A, 117, 12146 [NASA ADS] [CrossRef] [Google Scholar]
  21. Goerigk, L., Hansen, A., Bauer, C., et al. 2017, Phys. Chem. Chem. Phys., 19, 32184 [CrossRef] [Google Scholar]
  22. Grimme, S., Antony, J., Ehrlich, S., & Krieg, H. 2010, J. Chem. Phys., 132, 154104 [Google Scholar]
  23. Grimme, S., Ehrlich, S., & Goerigk, L. 2011, J. Comput. Chem., 32, 1456 [Google Scholar]
  24. Guo, Y., Riplinger, C., Becker, U., et al. 2018, J. Chem. Phys., 148, 011101 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gutiérrez-Quintanilla, A., Layssac, Y., Butscher, T., et al. 2021, MNRAS, 506, 3734 [CrossRef] [Google Scholar]
  26. Hariharan, P. C., & Pople, J. A. 1973, Theor. Chim. Acta, 28, 213 [CrossRef] [Google Scholar]
  27. Hehre, W. J., Ditchfield, R., & Pople, J. A. 1972, J. Chem. Phys., 56, 2257 [NASA ADS] [CrossRef] [Google Scholar]
  28. Helgaker, T., Klopper, W., Koch, H., & Noga, J. 1997, J. Chem. Phys., 106, 9639 [NASA ADS] [CrossRef] [Google Scholar]
  29. Ioppolo, S., Cuppen, H. M., Romanzin, C., Van Dishoeck, E. F., & Linnartz, H. 2008, ApJ, 686, 1474 [NASA ADS] [CrossRef] [Google Scholar]
  30. Ioppolo, S., van Boheemen, Y., Cuppen, H. M., van Dishoeck, E. F., & Linnartz, H. 2011, MNRAS, 413, 2281 [NASA ADS] [CrossRef] [Google Scholar]
  31. Johnston, H. S., & Heicklen, J. 1962, J. Phys. Chem., 66, 532 [CrossRef] [Google Scholar]
  32. Lamberts, T., Cuppen, H. M., Ioppolo, S., & Linnartz, H. 2013, Phys. Chem. Chem. Phys., 15, 8287 [NASA ADS] [CrossRef] [Google Scholar]
  33. Lamberts, T., Cuppen, H. M., Fedoseev, G., et al. 2014, A&A, 570, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Li, J., Chen, J., Zhang, D. H., & Guo, H. 2014, J. Chem. Phys., 140, 044327 [NASA ADS] [CrossRef] [Google Scholar]
  35. Ma, J., Li, J., & Guo, H. 2012, J. Phys. Chem. Lett., 3, 2482 [CrossRef] [Google Scholar]
  36. Martinez, L., Andrade, R., Birgin, E. G., & Martínez, J. M. 2009, J. Comput. Chem., 30, 2157 [CrossRef] [Google Scholar]
  37. Masunov, A. E., Wait, E. E., & Vasu, S. S. 2018, J. Phys. Chem. A, 122, 6355 [NASA ADS] [CrossRef] [Google Scholar]
  38. McClure, M. K., Rocha, W. R. M., Pontoppidan, K. M., et al. 2023, Nat. Astron., 7, 431 [NASA ADS] [CrossRef] [Google Scholar]
  39. Meisner, J., Lamberts, T., & Kästner, J. 2017, ACS Earth Space Chem., 1, 399 [NASA ADS] [CrossRef] [Google Scholar]
  40. Minissale, M., Congiu, E., Manicò, G., Pirronello, V., & Dulieu, F. 2013, A&A, 559, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Molpeceres, G., Rimola, A., Ceccarelli, C., et al. 2019, MNRAS, 482, 5389 [NASA ADS] [CrossRef] [Google Scholar]
  42. Molpeceres, G., Jiménez-Serra, I., Oba, Y., et al. 2022, A&A, 663, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Molpeceres, G., Rivilla, V. M., Furuya, K., et al. 2023a, MNRAS, 521, 6061 [NASA ADS] [CrossRef] [Google Scholar]
  44. Molpeceres, G., Zaverkin, V., Furuya, K., Aikawa, Y., & Kästner, J. 2023b, A&A, 673, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Neese, F. 2012, WIREs Comput. Mol. Sci., 2, 73 [CrossRef] [Google Scholar]
  46. Neese, F. 2022, WIREs Comput. Mol. Sci., 12 [Google Scholar]
  47. Neese, F., & Valeev, E. F. 2011, J. Chem. Theory Comput., 7, 33 [CrossRef] [Google Scholar]
  48. Neese, F., Wennmohs, F., Becker, U., & Riplinger, C. 2020, J. Chem. Phys., 152, 224108 [NASA ADS] [CrossRef] [Google Scholar]
  49. Noble, J. A., Dulieu, F., Congiu, E., & Fraser, H. J. 2011, ApJ, 735, 121 [NASA ADS] [CrossRef] [Google Scholar]
  50. Oba, Y., Watanabe, N., Kouchi, A., Hama, T., & Pirronello, V. 2010a, ApJ, 712, L174 [NASA ADS] [CrossRef] [Google Scholar]
  51. Oba, Y., Watanabe, N., Kouchi, A., Hama, T., & Pirronello, V. 2010b, ApJ, 722, 1598 [CrossRef] [Google Scholar]
  52. Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [Google Scholar]
  53. Pantaleone, S., Enrique-Romero, J., Ceccarelli, C., et al. 2020, ApJ, 897, 56 [NASA ADS] [CrossRef] [Google Scholar]
  54. Pantaleone, S., Enrique-Romero, J., Ceccarelli, C., et al. 2021, ApJ, 917, 49 [CrossRef] [Google Scholar]
  55. Pauly, T., & Garrod, R. T. 2018, ApJ, 854, 13 [NASA ADS] [CrossRef] [Google Scholar]
  56. Perrero, J., Enrique-Romero, J., Martínez-Bachs, B., et al. 2022, ACS Earth Space Chem., 6, 496 [NASA ADS] [CrossRef] [Google Scholar]
  57. Qasim, D., Lamberts, T., He, J., et al. 2019, A&A, 626, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Rimola, A., Taquet, V., Ugliengo, P., Balucani, N., & Ceccarelli, C. 2014, A&A, 572 [Google Scholar]
  59. Rimola, A., Skouteris, D., Balucani, N., et al. 2018, ACS Earth Space Chem., 2, 720 [Google Scholar]
  60. Riplinger, C., Pinski, P., Becker, U., Valeev, E. F., & Neese, F. 2016, J. Chem. Phys., 144, 024109 [NASA ADS] [CrossRef] [Google Scholar]
  61. Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
  62. Tachikawa, H. 2021, ACS Omega, 6, 16688 [CrossRef] [Google Scholar]
  63. Terwisscha van Scheltinga, J., Ligterink, N. F. W., Bosman, A. D., Hogerheijde, M. R., & Linnartz, H. 2022, A&A, 666, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Upadhyay, M., Pezzella, M., & Meuwly, M. 2021, J. Phys. Chem. Lett., 12, 6781 [CrossRef] [Google Scholar]
  65. Watanabe, N., & Kouchi, A. 2002, ApJ, 571, L173 [Google Scholar]
  66. Woon, D. E., & Dunning, T. H. 1993, J. Chem. Phys., 98, 1358 [NASA ADS] [CrossRef] [Google Scholar]
  67. Yu, H. S., He, X., Li, S. L., & Truhlar, D. G. 2016, Chem. Sci., 7, 5032 [CrossRef] [Google Scholar]
  68. Zhong, S., Barnes, E. C., & Petersson, G. A. 2008, J. Chem. Phys., 129, 184116 [NASA ADS] [CrossRef] [Google Scholar]
1

Eley–Rideal mechanism may be of relevance for CO molecules given their abundance on ISM ices.

All Tables

Table 1

Binding energies of the CO, OH, t-HOCO, and c-HOCO admolecules at the reaction site considered in this work on the H2O and CO clusters.

In the text
Table A.1

Comparison of the potential energy reaction profile (e.g. no zero-point energy corrected) between our computational method and high accuracy results presented in the literature.

In the text

All Figures

thumbnail Fig. 1

Views of the clusters employed to simulate the CO + OH → CO2 + H reaction. Top left: side view of the H2O ice cluster. Top right: top view of the H2O ice cluster. Bottom left: side view of the CO ice cluster. Bottom right: top view of the CO ice cluster. Colour code: White-Hydrogen, Red-Oxygen, Teal-Carbon. The size of a cluster was determined approximately by measuring its endpoints.
In the text
thumbnail Fig. 2

Reaction profile for the CO + OH → CO2 + H reaction on the ASW cluster. Energies are referred to as the sum of the isolated components (e.g. CO, OH, (H2O)33). In square brackets are the energies for the gas-phase reaction. All energies have been ZPVE corrected.
In the text
thumbnail Fig. 3

Stationary points on the CO + OH → CO2 + H reaction profile for the reaction on top of the (H2O)33 cluster. For all the intermediates and transition states, we indicate the value of the dihedral angle ∠HOCO governing the isomerism of the t-HOCO and c-HOCO wells. Colour code: White-Hydrogen, Red-Oxygen, Teal-Carbon.
In the text
thumbnail Fig. 4

Reaction profile for the CO + OH → CO2 + H reaction on the amorphous CO cluster. The energies are referred to as the sum of the isolated components (e.g. CO, OH, (CO)33). In square brackets are the energies for the gas-phase reaction. All energies have been ZPVE corrected.
In the text
thumbnail Fig. 5

Stationary points on the CO + OH → CO2 + H reaction profile for the reaction on top of the (CO)33 cluster. For all the intermediates and transition states, we indicate the value of the dihedral angle ∠HOCO governing the isomerism of the t-HOCO and c-HOCO wells. Colour code: white – hydrogen, red – oxygen, teal – carbon.
In the text
thumbnail Fig. 6

Additional stationary points complementing those presented in Fig. 5 for the alternative reaction channel 2 CO + OH → CO2 + HCO. Colour code: white – hydrogen, red – oxygen, teal – carbon.
In the text
thumbnail Fig. 7

Reaction profile for the CO + OH → CO2 + H and 2 CO + OH → CO2 + HCO alternative reaction on the amorphous CO cluster. The energies are referred to as the sum of the isolated components (e.g. CO, OH, (CO)33). We note that we have omitted the separated reactants asymptote and pre-reactant complex energies already presented in Fig. 4. All energies have been ZPVE corrected.
In the text
thumbnail Fig. 8

Microcanonical (energy-dependent) rate constants for the CO + OH → t−HOCO (top) and CO + OH → c−HOCO (bottom) reaction step on H2O ice. The different solid lines represent different ergodic energy dissipation scenarios with n molecules accepting the reaction energy. The vertical dashed lines indicate fractions (0.1 and 0.25) of the О + H reaction (red) and of half the energy of a Lymann alpha photon (blue); see text. The zero of energy is defined as the PES asymptote (i.e. no adsorption).
In the text
thumbnail Fig. 9

Microcanonical (energy-dependent) rate constants for the CO + OH → t−HOCO reaction step on CO ice. The different solid lines represent different ergodic energy dissipation scenarios with n molecules accepting the reaction energy. The vertical dashed lines indicate fractions (0.1 and 0.25) of the О + H reaction (red) and of half the energy of a Lymann alpha photon (blue); see text. The zero of energy is defined as the PES asymptote (i.e. no adsorption).
In the text
thumbnail Fig. 10

Graphic representation of the different layers admitting energy dissipation through RRKM equipartition in the H2O model ice. The t-HOCO molecule (zero dissipating molecules) is represented with red, teal, and white spheres. The five H2O model includes the t-HOCO molecule, and the H2O molecules are shown in blue. The 10- and 16-molecule models are represented with gold and black molecules, respectively. Finally, the rest of the molecules are represented as transparent liquorices.
In the text
thumbnail Fig. 11

Graphic representation of the different layers admitting energy dissipation through RRKM equipartition in the CO model ice. The t-HOCO molecule (zero dissipating molecules) is represented with red, teal, and white spheres. The five CO model includes the t-HOCO molecule, and the CO molecules are shown in blue. The 10- and 16-molecule model are represented with gold and black molecules, respectively. Finally, the rest of the molecules are represented as transparent liquorices.
In the text
thumbnail Fig. 12

Microcanonical (energy-dependent) rate constants for the c−HOCO → CO2 + H reaction step on H2O ice. The different solid lines represent different ergodic energy dissipation scenarios with n molecules accepting the reaction energy. The vertical dashed lines indicate fractions (0.1, 0.25, and 0.5) of the О + H reaction (red) and of half the energy of a Lymann alpha photon (blue); see text. The zero of energy is defined as the PES asymptote (i.e. no adsorption).
In the text
thumbnail Fig. 13

Microcanonical (energy-dependent) rate constants for the c−HOCO → CO2 + H (top) and c−HOCO + CO → CO2 + HCO (bottom) reaction step on CO ice. The different solid lines represent different ergodic energy dissipation scenarios with n molecules accepting the reaction energy. The vertical dashed lines indicate fractions (0.1, 0.25, and 0.5) of the O + H reaction (red) and of half the energy of a Lymann alpha photon (blue); see text. The zero of energy is defined as the PES asymptote (i.e. no adsorption).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.