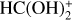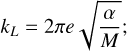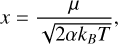| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202243966 | |
| Published online | 07 July 2023 | |
A sequential acid-base mechanism in the interstellar medium: The emergence of cis-formic acid in dark molecular clouds
1
Centro de Astrobiología (CSIC-INTA),
Ctra. de Ajalvir Km. 4, Torrejón de Ardoz,
28850
Madrid, Spain
2
Department of Organic and Inorganic Chemistry, Faculty of Sciences, and IACYS-Green Chemistry and Sustainable Development Unit, University of Extremadura,
06006
Badajoz, Spain
e-mail: jugarco@unex.es
3
Departamento de Ingeniería Química y Química Física, Facultad de Ciencias, and ICCAEx, Universidad Extremadura,
Badajoz, Spain
4
Institute for Theoretical Chemistry, University of Stuttgart,
Pfaffenwaldring 55,
70569
Stuttgart, Germany
Received:
6
May
2022
Accepted:
23
March
2023
Context. The different abundance ratios between isomers of an organic molecule observed in the interstellar medium (ISM) provide valuable information about the chemistry and physics of the gas and the history of molecular clouds. In this context, the origin of an abundance of cis-formic acid (c-HCOOH) of only 6% the trans isomer (t-HCOOH) abundance in cold cores remains unknown.
Aims. In this work, we aim to explain the presence of c-HCOOH in dark molecular clouds through the destruction and back formation of c-HCOOH and t-HCOOH in a cyclic process that involves HCOOH and highly abundant molecules such as HCO+ and NH3.
Methods. We used high-level ab initio methods to compute the potential energy profiles for the cyclic destruction and formation routes of c-HCOOH and t-HCOOH. Accurate global rate constants and branching ratios are calculated based on the transition state theory and the master equation formalism under the typical conditions of the ISM.
Results. The destruction of HCOOH by reaction with HCO+ in the gas phase leads to three isomers of the cation HC(OH)2+. The most abundant cation can react in a second step with other abundant molecules of the ISM such as NH3 to form back c-HCOOH and t-HCOOH. This mechanism explains the formation of c-HCOOH in dark molecular clouds. Considering this mechanism, the fraction of c-HCOOH with respect t-HCOOH is 25.7%. To explain the 6% reported by the observations, we propose that further destruction mechanisms of the cations of HCOOH by collisions with abundant molecules or interconversion reactions on dust grains should be taken into account.
Conclusions. The sequential acid-base (SAB) mechanism proposed in this work involves fast processes with very abundant molecules in the ISM. Thus, HCOOH very likely suffers our proposed transformations in the conditions of dark molecular clouds such as B5 and L483. This is a new approach in the framework of the isomerism of organic molecules in the ISM, which has the potential to explain the ratio between isomers of organic molecules detected in the ISM.
Key words: astrochemistry / ISM: abundances / ISM: molecules
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The reaction mechanisms associated with the isomerism of organic molecules in the interstellar medium (ISM) are gaining the attention of the astrophysical community. Understanding the chemical processes that control the ratios found for isomers in the ISM gives valuable information for the chemistry and physical processes taking place in molecular clouds. To explain the isomer ratios observed in the ISM of some organic molecules, several processes have been invoked such as isomer-ization processes (García de la Concepción et al. 2021, 2022; Molpeceres et al. 2021), different formation routes for both isomers (Balucani et al. 2018; Baiano et al. 2020; Lupi et al. 2020; Molpeceres et al. 2021), or higher destruction rates for one of the isomers (Loomis et al. 2015; Shingledecker et al. 2019, 2020). Recent quantum chemical studies have revealed that the E/Z and cis/trans ratios of the imines and some acids found in the ISM are likely due to intramolecular iso-merization reactions (García de la Concepción et al. 2021, 2022).
For some molecules with isomeric forms, direct isomer-ization cannot account for the observed abundances, at least at certain temperatures. For instance, direct isomerization processes enable the chemical equilibrium between the cis and trans isomers of formic acid in the ISM for a temperature range of Tkin ~ 200–400 K (García de la Concepción et al. 2022). However, at low temperatures this process cannot explain why the cis isomer of formic acid (c-HCOOH) is found to be ~6% of the trans isomer (t-HCOOH) in cold and dense molecular clouds such as Barnard 5 (B5 hereafter; Taquet et al. 2017) and L483 (Agúndez et al. 2019), where the gas kinetic temperature is very low (Tkin ~ 5–15 K; García de la Concepción et al. 2022). The current study therefore seeks to explore additional chemical pathways to form t-HCOOH and c-HCOOH at low temperatures to account for their observed abundances in cold molecular clouds.
Formic acid presents two isomers, trans (t-HCOOH) and cis (c-HCOOH), depending on the position of the hydrogen of the OH bond (Fig. 1). The trans isomer (t-HCOOH) is the most stable one by 4.04 kcal mol−1 (2033 K) (García de la Concepción et al. 2022). According to the equilibrium constant (Keq = K1/K−1) found between the two isomers at very low temperatures (Tkin ~ 5–15 K; García de la Concepción et al. 2022), the equilibrium should be completely displaced toward t-HCOOH (Keq(10 K) = 2.09 × 1088), indicating that the temperature is too low to enable intramolecular isomerizations (García de la Concepción et al. 2022).
This is likely the reason why t-HCOOH has been widely detected in the ISM (see García de la Concepción et al. 2022 and references therein). In contrast, c-HCOOH has only been detected in the photon-dominated region (PDR) of the Orion Bar (Cuadrado et al. 2016) and in the cold dark clouds L483 (Agúndez et al. 2019) and B5 (Taquet et al. 2017). The abundance of c-HCOOH with respect to t-HCOOH in the Orion Bar PDR is ~33%. In this case, the presence of c-HCOOH in the gas phase has been explained by photo-switching mechanisms because of the higher prevalence of UV photons (Cuadrado et al. 2016).
The presence of the c-HCOOH in the gas phase of cold sources such as B5 and L1483 in an amount that is 6% that of t-HCOOH, remains a mystery. Most of the chemistry in these cold sources is dominated by gas-phase chemistry. However, the formation of HCOOH (Ioppolo et al. 2010; Taquet et al. 2017) and its sulphur derivative (HCOSH; Nguyen et al. 2021; Molpeceres et al. 2021) occurs efficiently on dust grains. To date, it has not been possible to experimentally determine the isomeric ratio of HCOOH when formed on grain surfaces. However, it should be noted that, as was recently demonstrated by Molpeceres et al. (2022), c-HCOOH is destroyed on grain surfaces after reacting with hydrogen atoms. Thus, there should be a significant enrichment of the t-HCOOH isomer on dust grains. This finding indicates that the relative abundance between c-HCOOH and t-HCOOH observed in cold clouds cannot be explained through these grain surface destruction mechanisms. In fact, c-HCOOH should not withstand the conditions found on dust grains (Molpeceres et al. 2022). Therefore, it is not yet understood how c-HCOOH is present in the gas phase in these very cold objects.
In addition, it has been suggested that a plausible route of gas phase formation of HCOOH in dark molecular clouds is through the dissociative recombination of the OH-protonated formic acid (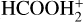 ; Vigren et al. 2010). However, the latter study does not discriminate between the isomers. Furthermore, the dissociative recombination of
; Vigren et al. 2010). However, the latter study does not discriminate between the isomers. Furthermore, the dissociative recombination of 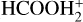 gives HCOOH + H as a minor product (Vigren et al. 2010). This means that, independently of the formation route of HCOOH, the initial cis/trans ratio of HCOOH remains uncertain.
gives HCOOH + H as a minor product (Vigren et al. 2010). This means that, independently of the formation route of HCOOH, the initial cis/trans ratio of HCOOH remains uncertain.
In this work, we report a new gas-phase mechanism of destruction and post-formation of HCOOH that can explain the presence of c-HCOOH in the gas phase of cold dark clouds. According to this mechanism, we characterized protonation of HCOOH via abundant HCO+ that yields multiple 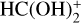 isomers and complexes with no intervening barriers. After this, we considered the reactions between the multiple
isomers and complexes with no intervening barriers. After this, we considered the reactions between the multiple 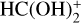 isomers and complexes with abundant NH3, which reform c-HCOOH and t-HCOOH acids in an isomeric ratio different from the one observed at the beginning of the chemical process. We note that
isomers and complexes with abundant NH3, which reform c-HCOOH and t-HCOOH acids in an isomeric ratio different from the one observed at the beginning of the chemical process. We note that 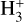 is also an important source of protons. However, its reaction with HCOOH has been shown to be completely dissociative (Mackay et al. 1978; Sekiguchi et al. 2004), and, therefore, it has not been explored in this work.
is also an important source of protons. However, its reaction with HCOOH has been shown to be completely dissociative (Mackay et al. 1978; Sekiguchi et al. 2004), and, therefore, it has not been explored in this work.
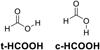 |
Fig. 1 Chemical structures of c-HCOOH and t-HCOOH. |
2 Computational details
2.1 Electronic structure calculations
All the geometries were optimized without constraints at the double-hybrid rev-DSD-PBEP86 functional (Kozuch & Martin 2011; Santra & Martin 2019) with the dispersion-corrected D3(BJ) (Grimme et al. 2010, 2011) method in combination with the augmented Dunning’s triple-zeta correlation-consistent basis set aug-cc-pVTZ (Dunning Jr. 1989; Kendall et al. 1992). All the calculations carried out in this work involve cation-neutral interactions; thus, the choice of the method (rev-DSD-PBEP86-D3(BJ)) is based on its good ability to describe non-covalent interactions of the cation-neutral pair (Spicher et al. 2021) as well as for kinetics and thermodynamics (Goerigk et al. 2017). All the stationary points were characterized by frequency calculations at the same level of theory, showing none and one imaginary frequencies for energy minima and transition structures, respectively. We checked that each transition structure belonged to the correct reaction path by the corresponding intrinsic reaction coordinate analysis (IRC). Electronic energies (E) were refined by computing single points with the CCSD(T)-F12 method (Adler et al. 2007; Knizia et al. 2009) on the rev-DSD-PBEP86-D3(BJ)/aug-cc-pVTZ geometries in combination with the auxiliary and special orbital basis set cc-pVTZ-F12-CABS and cc-pVTZ-F12, respectively. Finally, anharmonic ZPE (ZPEAnh) corrections were evaluated at the rev-DSD-PBEP86-D3(BJ)/aug-cc-pVTZ level within vibrational perturbative theory to second-order VPT2 (Barone 2004).
All the calculations with the double-hybrid and with the coupled cluster method were carried out with the Gaussian 16 (Frisch et al. 2016) and ORCA (Neese 2012; Neese et al. 2020) software packages, respectively. The images of the structures were done with the Cylview software (Legault 2009).
2.2 Downhill MEP calculations
For all barrierless processes, we computed the minimum energy path (MEP) downhill calculations. Starting from the equilibrium geometries of both fragments at a distance between 10 and 12 Å, we searched all the possible MEPs by rotating the equilibrium geometries of both fragments and then searching the MEP for all the input geometries. The initial geometries were generated by randomly sampling the Euler angles of the HCO+ fragment with respect to the acid molecule frame, with a distance between the center of masses randomly located in the 10–12 Å interval.
For each association, we ran 100 MEPs in order to cover all the possible orientations between the two fragments. For these calculations, we used the rev-DSD-PBEP86-D3(BJ) method in combination with the cc-pVDZ basis set. The results show that all the potentials converge to the same path below 8 angstrom. That is, the reorientation of the fragments until they acquire a position similar to that of the minimum energy geometry is achieved in about 3–4 Å. The increase in the basis functions changes neither the shape of the potentials nor the ratio found between competitive MEPs.
It should be noted that this methodology cannot not be compared with a rigorous dynamics study. Instead, our aim in this work is to sift through all possible barrierless association reactions that appear in this whole process.
2.3 Kinetics calculations
2.3.1 Barrierless association reactions
The rate constants for all barrierless bimolecular association reactions were computed within the phase space theory (PST) (Pechukas & Light 1965; Chesnavich 1986). The attractive potentials between both fragments is described by a 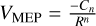 functional form. The Cn constant is the long-range coefficient and is obtained from a fit of the rev-DSD-PBEP86-D3(BJ)/cc-pVDZ energies. The energies used to carry out the fitting were those obtained from any of the 100 MEPs for each association starting at distances of about 8.5 Å. The variable R corresponds to the nuclear positions of the two atoms that are closer to each other along the MEP. We checked which functional form fits better to the potentials computed at rev-DSD-PBEP86-D3(BJ)/cc-pVDZ varying n from 2 to 6. The best fittings were obtained for n = 3. Thus, the functional form that better describes the interaction is
functional form. The Cn constant is the long-range coefficient and is obtained from a fit of the rev-DSD-PBEP86-D3(BJ)/cc-pVDZ energies. The energies used to carry out the fitting were those obtained from any of the 100 MEPs for each association starting at distances of about 8.5 Å. The variable R corresponds to the nuclear positions of the two atoms that are closer to each other along the MEP. We checked which functional form fits better to the potentials computed at rev-DSD-PBEP86-D3(BJ)/cc-pVDZ varying n from 2 to 6. The best fittings were obtained for n = 3. Thus, the functional form that better describes the interaction is 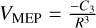 . Considering that the rate-determining step for the viable reactions found here are the initial barrier-less association reactions, we compared our global rate constants with those obtained from the Su-Chesnavich formula in order to validate our PST calculations. The comparison between the two kinetic treatments yields consistent results, as reported in Appendix A.
. Considering that the rate-determining step for the viable reactions found here are the initial barrier-less association reactions, we compared our global rate constants with those obtained from the Su-Chesnavich formula in order to validate our PST calculations. The comparison between the two kinetic treatments yields consistent results, as reported in Appendix A.
2.3.2 Global rate constants
For elementary steps associated with well-characterized transition structures, unimolecular rate constants were computed using Rice–Ramsperger–Kassel–Marcus (RRKM) theory within the rigid-rotor harmonic-oscillator (RRHO) approximation (Weston 1972). For each step, one-dimensional tunnelling corrections were computed using the Eckart model (Eckart 1930). The comparison of the rate constants without considering quantum tunnelling leads to identical results since this effect is negligible for submerged barriers in the low pressure limit. The imaginary frequencies of the transition structures showing energy barriers above the reactants are indeed low, which generates wide potentials that make the tunnelling ineffective.
Pressure and temperature-dependent rate constants were calculated by resolving the one-dimensional master equation using the MESS software (Georgievskii et al. 2013). The global rate constants were computed in the 15–400 K temperature range and at a pressure of 1 × 10−7 atm. Although herein we are interested in the low temperate range typical of the molecular clouds B5 and L483, we also computed rate constants up to 400 K with the aim of giving general and valuable kinetic information for the wide range of conditions of the ISM.
To describe the temperature dependence of the global rate constants and to give valuable kinetic data for astrochemical codes, we used the Arrhenius–Kooij formula (Kooij 1893):
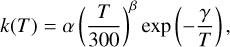 (1)
(1)
where α, β, and γ are fitting parameters determined using the computed rate coefficients at different temperatures.
 |
Fig. 2 Protonation of t-HCOOH and c-HCOOH with HCO+ to give the cations cat1, cat2, cat3, cat4, and CO−H3O+ (+ CO). |
3 Results
3.1 Reaction of c-HCOOH and t-HCOOH with HCO+
3.1.1 Reaction mechanism
As an initial approach, either c-HCOOH and/or t-HCOOH could react with HCO+, yielding four isomers of the cation 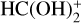 (Fig. 2). The four isomers of
(Fig. 2). The four isomers of  differ in the positions of the hydrogens held by the oxygen atoms: one of the isomers shows the hydrogen atoms in syn position (cat4); a second one has the hydrogen atoms in anti position (cat3); and the third and fourth isomers have one hydrogen in syn and the other one in anti configuration (cat2 and cat1; see Fig. 2). The reaction mechanism shows that there are five exit channels distributed in the formation of cat1, cat2, and cat3, cat4, and the complex CO−H3O+ (+ CO; see Fig. 3).
differ in the positions of the hydrogens held by the oxygen atoms: one of the isomers shows the hydrogen atoms in syn position (cat4); a second one has the hydrogen atoms in anti position (cat3); and the third and fourth isomers have one hydrogen in syn and the other one in anti configuration (cat2 and cat1; see Fig. 2). The reaction mechanism shows that there are five exit channels distributed in the formation of cat1, cat2, and cat3, cat4, and the complex CO−H3O+ (+ CO; see Fig. 3).
Considering that HCO+ is a strong Bronsted acid with an electrophilic point in the carbon atom, and that HCOOH has four lone pairs located in the oxygen atoms (two in the oxygen of the carbonyl group and two additional in the oxygen-holding hydrogen), six possible association reactions are possible for each isomer of HCOOH. 77 out of the 100 MEPs computed for the barrierless assotiation between HCO+ and c-HCOOH lead to a hydrogen donnation to the oxygen of the carbonyl group forming the cat3 complex with a hydrogen bonding to CO (c-Int2, see Fig. 3). In 22 out of the 100 MEPs, the same occurs but forming a cat1 complex (c-Int3). The last MEP found is a nucleophilic attack of the carbonyl group to the carbon of HCO+ (c-Int1).
For t-HCOOH, we found four barrierless association reactions. 93 out of 100 MEPs lead to t-Int2, 3 to t-Int1, 2 to t-Int3 and 2 to t-Int4. From the intermediates t-Int2, t-Int3, c-In2, and c-Int3, we obtain four out of the five final exit channels through barrierless dissociation reactions. The intermediates formed after the proton donation of HCO+ are the most stable with respect to c-HCOOH, being −50.82, −52.25, −48.84, and −50.18 kcal mol−1 for t-Int2, t-Int3, c-Int2, and c-Int3, respectively. The intermediates formed after the electrophilic attack of HCO+ are less stable than the previous ones, with energies of −15.15, −37.51, and −36.08 kcal mol−1 for t-Int4, t-Int1, and c-Int1, respectively.
The reaction mechanism studied for this reaction shows five additional intermediates formed from the pre-reactive complexes (t-Int6, 2CO−H3O+, t-Int5, c-Int4, and c-Int5). All of them are interconnected with each other through isomerization reactions (there are fifteen transition structures, see Fig. 3). t-Int5 is linked to c-Int1, c-Int3, t-Int5 and t-Int2 through the transition structures ct-TS1, c-TS4, t-TS3 and t-TS1. c-TS4 shows a high energy barrier that is 9.09 kcal mol−1 above the reactants, resulting in a non-viable isomerization in the conditions of the ISM. ct-TS1, t-TS3, and t-TS1 show submerged barriers (−21.94, −26.45, and −27.81 kcal mol−1, respectively). The only transition structure connecting t-Int4 with other intermediate is t-TS4 (−14.24 kcal mol−1), for which there is a proton transfer yielding t-Int3. t-Int2 is also connected to t-Int3 through the transition structure c-TS3, which is just 3.71 kcal mol−1 below the reac-tants. t-Int2 also leads to t-Int5 through t-TS2 and to c-Int2 through ct-TS2 (−35.71 kcal mol−1), which corresponds to a torsion of the O–C–O–H. Both c-Int2 and t-Int2 lead to the products cat3 and cat1, which are 38.43 and 40.08 kcal mol−1 below the reactants.
The intermediate t-Int3 yields the complex 2CO−H3O+ through t-TS5. The latter intermediate loses one molecule of CO to give the complex CO−H3O+ + CO. These products are 37.70 kcal mol−1 below the reactants. It should be noted that the majority of the energy in this process is likely dissipated by the increase in the translational energy of the products. In this way, the complex CO−H3O+ is likely a long-lived intermediate in the ISM since the complete dissociation into H3O+ and CO is 14.18 kcal mol−1 above the bimolecular exit channel (for the unimolecular transformations, see Fig. 4).
The rotation of the O–C–O–H bond of t-Int3 leads to c-Int5 through ct-TS6 (−28.45 kcal mol−1). Both intermediates, t-Int3 and c-Int5 yield the products cat4 and CO (−21.13 kcal mol−1). cat4 is a strong complex between H2O and HCO+ that could continue evolving into H2O and HCO+ and/or H3O+ and CO (Fig. 4). The evolution of cat4 was previously explored from the theoretical point of view (Sekiguchi et al. 2004). Our new and more accurate results (Fig. 4) show that the unimolecular isomerization of cat4 into cat1 shows a transition structure with a very high energy barrier (9.00 kcal mol−1 above the reactants) that cannot be overcome in the conditions of the ISM. cat 4 could also yield the complex CO−H3O+ through an energy barrier that is 20.24 kcal mol−1 below the reactants. This process could occur in the conditions considered here if the products (cat4 + CO) are not completely stabilized (the barrier is just 0.89 kcal mol−1 from cat4: see Fig. 4). To verify that this last process is possible, high-level quantum dynamics calculations are required, which is out of the scope of this work.
Finally, moving to the intermediates formed from c-HCOOH, c-Int1 leads both to c-Int3 through c-TS1 (−27.20 kcal mol−1) and to c-Int4 through ct-TS4 (−26.29 kcal mol−1). As for t-Int2, the dissociation of c-Int3 leads to cat1. c-Int3 can also isomerize to c-Int4 through c-TS2. The latter could go back to c-Int1 or yield the intermediate t-Int5.
We note that all stationary points are connected to each other and thus, the isomerization from c-HCOOH to t-HCOOH can proceed with the latter behaving as the exit channel. The inverse isomerization is not possible under the conditions of the ISM since it is an endothermic process (4.02 kcal mol−1).
 |
Fig. 3 E+ZPEAnh energy profiles (in kcal mol−1) for the reactions of c-HCOOH and t-HCOOH with HCO+. The meaning of the circles and arrows are indicated in the legend at the top of the figure. |
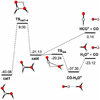 |
Fig. 4 E+ZPEAnh energy profiles (in kcal mol−1) for the unimolecu-lar decomposition of cat1. Relative energies are given with respect to c-HCOOH and HCO+. |
3.1.2 Kinetics
Figure 5 shows the global rate constants for the destruction of c-HCOOH (blue curves) and t-HCOOH (orange curves). Figure 5a shows the destruction of c-HCOOH and t-HCOOH to give cat1 and CO. Both reactions show a non-Arrhenius behavior in the whole range of temperatures, which is the typical trend for a barrierless association between a cation and a neutral species. Both reactions are very fast processes, on the order of 5.2−6.2 × 10−9 cm3 molecule−1 s−1 at 15 K. The destruction of c-HCOOH is slightly faster than that of the t-HCOOH in the whole range of temperatures. Considering all possible pathways investigated here, the formation of cat1 from c-HCOOH and t-HCOOH are the fastest routes of the reaction mechanism HCOOH + HCO+ (see below).
In contrast to the formation of cat1, the formation of cat2 from c-HCOOH (Fig. 5b) shows a non-Arrhenius behavior only up to ~260 K. This is because the rate of the reactions at very low temperatures is limited by the capture rate constants. Above ~260 K, the energy barriers increase their height and the temperature-dependent rate constants adopt an Arrhenius behavior. This kinetic behavior is also observed for the formation of cat2 from t-HCOOH (Fig. 5f), but the transition between the non-Arrhenius to Arrhenius behavior is reached at ~170 K. In this case, the formation of the product (cat2) is also faster from c-HCOOH than from t-HCOOH, showing a global rate constant of 4.57 × 10−11 and 1.13 × 10−13 cm3 molecule−1 s−1 at 15 K, respectively.
The same temperature-dependence is observed for the formation of cat3 from t-HCOOH (Fig. 5g), which is a faster process than the formation of cat2 from the same reactants, that is t-HCOOH + HCO+. On the other hand, the formation of the same product from c-HCOOH shows a non-Arrhenius behavior (Fig. 5c) for the whole range of temperatures since the rate is limited by the centrifugal barrier at the entrance channel, is the third fastest process of the whole mechanism, and has a global rate constant of 2.72 × 10−9 cm3 molecule−1 s−1 at 15 K.
Plot d in Fig. 5 reports the rate coefficients for the formation of cat4 + CO (solid blue line) and CO−H3O+ + CO (dotted blue line). These reactions are the slowest of the whole process since the system has to reach t-Int3 from c-HCOOH + HCO+. In these pathways, the system should pass through the transition state c-TS3, which shows the highest submerged barrier of the whole mechanism (−3.73 kcal mol−1). The rate of these reactions quickly decreases up to ~60 K since a slight increase in the temperature makes the energy barrier to increase, approaching to the energy of the reactants. After this inflection point, the rate constants show an Arrhenius behavior because the system starts to have thermal energy to overcome the energy barrier. On the other hand, the rate of the formation of these products from t-HCOOH + HCO+ is fast (see Fig. 5h) since, although the system should also pass throughout t-Int3, the formation of the latter intermediate comes from a barrierless process. Then, the global rate coefficients are limited by the capture rate constants. The formation of cat4, albeit less stable than CO−H3O+ by 16.57 kcal mol−1, is faster because there are two exit channels, one of which is a barrierless process. In contrast, for the formation of CO−H3O+ it is mandatory to pass through a transition state (t-TS5).
As commented in the previous section, all intermediates are directly or indirectly connected in this reaction, so the formation of t-HCOOH + HCO+ starting from c-HCOOH + HCO+ could occur in the conditions of the ISM. However, it is one of the slowest processes for this reaction. The reverse process is not viable in the ISM since it is endothermic.
In summary, the formation of cat1 is the most favored pathway starting from both c-HCOOH and t-HCOOH, showing the highest product branching ratio for the whole range of temperatures (15–400 K; see Appendix B). On the contrary, the formation of cat2 and cat3 covers the remainder of the product branching ratio when the reactant is c-HCOOH. Indeed, the formation of cat4 and the complex CO−H3O+ is negligible. When the reactant is t-HCOOH, however, there is no formation pathway of cat2, but the product branching fractions for cat4 and the complex CO-H3O+ are noticeable. From all this, it is likely that HCOOH is converted completely to its cations in molecular dark clouds as a consequence of the high rate for the formation of cat1, cat2, and cat3 and the high abundance of HCO+ in B5 and L483.
3.2 Reaction of 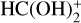 (cat1) with NH3
(cat1) with NH3
3.2.1 Reaction mechanism
Ammonia (NH3) is a very abundant species in B5 and L483, with a relative abundance with respect to H2 as high as the electron abundance (Agúndez & Wakelam 2013). Considering that most HCOOH should be converted to catl in molecular dark clouds (see Sect. 3.1), in this section we study the destruction of the latter cation with NH3.
The structure of catl presents two acidic hydrogens that are nearly equivalent. The capture of the proton in the eis position of catl by ÑH3 would lead back to t-HCOOH, whereas the capture of the proton in the trans position would lead to c-HCOOH.
Continuing with the methodology mentioned in Sect. 2.2, we calculate the MEPs for 100 different orientations of catl and NH3 in order to explore all possible entrance channels. We found three barrierless association reactions that are summarized in Fig. 6. 65 out of 100 MEPs lead to Int-H3, which is a hydrogen-bonding complex between t-HCOOH and ammonium ion ( ). 26% of the MEPs yield the same complex, but with c-HCOOH (Int-H2). Finally, 9% of MEPs lead to the intermediate Int-H1. For the latter, there is a non-covalent interaction between the lone pair of ammonia and the hydrogen held by the carbon atom of catl. The formation of this complex does not involve any breaking or forming bond. It is important to highlight that as soon as Int-H1 is formed, it isomerises to Int-H3 by overcoming a very low barrier (see below). Therefore, 74% of the MEPs end up in Int-H3.
). 26% of the MEPs yield the same complex, but with c-HCOOH (Int-H2). Finally, 9% of MEPs lead to the intermediate Int-H1. For the latter, there is a non-covalent interaction between the lone pair of ammonia and the hydrogen held by the carbon atom of catl. The formation of this complex does not involve any breaking or forming bond. It is important to highlight that as soon as Int-H1 is formed, it isomerises to Int-H3 by overcoming a very low barrier (see below). Therefore, 74% of the MEPs end up in Int-H3.
Figure 7 shows the full E+ZPEAnh energy profiles for the destruction of catl by reaction with NH3 leading back to c-HCOOH and t-HCOOH and ammonium ion ( ); N-protonated formamide (form) and H2O; and the complex
); N-protonated formamide (form) and H2O; and the complex 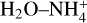 and CO. The blue profile of Fig. 7 shows the direct formation and post dissociation of the complex Int-H3 leading to t-HCOOH and
and CO. The blue profile of Fig. 7 shows the direct formation and post dissociation of the complex Int-H3 leading to t-HCOOH and 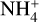 . The orange profile shows the same but for the formation of the intermediate Int-H2 and the post dissociation to c-HCOOH and
. The orange profile shows the same but for the formation of the intermediate Int-H2 and the post dissociation to c-HCOOH and 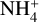 . The pink profile corresponds to the formation of the Van der Waals complex Int-H1, which is 29.77 kcal mol−1 and 31.09 kcal mol−1 above Int-H2 and Int-H3, respectively. The latter intermediates present an energy difference of just 1.32 kcal mol−1, the trans intermediate (Int-H3) being the most stable. The unstable complex Int-H1 could dissociate back to the reactants or isomerize rapidly to Int-H3 through the transition structure TSH1–H3, which is just 0.27 kcal mol−1 above Int-H1.
. The pink profile corresponds to the formation of the Van der Waals complex Int-H1, which is 29.77 kcal mol−1 and 31.09 kcal mol−1 above Int-H2 and Int-H3, respectively. The latter intermediates present an energy difference of just 1.32 kcal mol−1, the trans intermediate (Int-H3) being the most stable. The unstable complex Int-H1 could dissociate back to the reactants or isomerize rapidly to Int-H3 through the transition structure TSH1–H3, which is just 0.27 kcal mol−1 above Int-H1.
As in the mechanism depicted in Fig. 3, the stationary points of the mechanism shown in Fig. 7 are connected through isomer-ization reactions between the intermediates Int-H3 and Int-H2. We found two isomerization mechanisms; TSH2–H3 correspond with the torsion of the H–O–C–O diedral angle of the formic acid moiety of the complexes Int-H3 and Int-H2, which have energy barriers of 12.87 kcal mol−1 from Int-H3 and 11.55 kcal mol−1 from Int-H2. The other isomerization is a stepwise mechanism where the  moiety of Int-H3 gives a proton to the oxygen of the carbonyl group whilst a new N–C bond is formed in a concerted manner. This transition structure (TSNC−H3), which shows an energy barrier of 37.71 from Int-H3, leads to the intermediate Int-NC. The evolution of Int-NC into Int-H2 through TSH2−NC Is similar to the previous (TSNC−H3) but it involves the proton which is in the trans position, being 3.26 kcal mol−1 above the latter.
moiety of Int-H3 gives a proton to the oxygen of the carbonyl group whilst a new N–C bond is formed in a concerted manner. This transition structure (TSNC−H3), which shows an energy barrier of 37.71 from Int-H3, leads to the intermediate Int-NC. The evolution of Int-NC into Int-H2 through TSH2−NC Is similar to the previous (TSNC−H3) but it involves the proton which is in the trans position, being 3.26 kcal mol−1 above the latter.
Once Int-H2 is formed, either from the reactants through a barrierless association reaction or from Int-H3 through isomerization reactions, it could evolve through the exit channel that leads to c-HCOOH and  or isomerize into Cform through the transition structure TSH2−Cform. The latter is 3.72 kcal mol−1 above the reactants, making it an unfeasible process under ISM conditions. In this transition structure there is a transfer of a proton from the
or isomerize into Cform through the transition structure TSH2−Cform. The latter is 3.72 kcal mol−1 above the reactants, making it an unfeasible process under ISM conditions. In this transition structure there is a transfer of a proton from the  to the oxygen of the OH, while the substitution reaction of NH3 by OH forms the N-protonated formamide interacting with a water molecule (Cform) concertedly. The breaking of the hydrogen bond of the latter complex forms N-protonated formamide (
to the oxygen of the OH, while the substitution reaction of NH3 by OH forms the N-protonated formamide interacting with a water molecule (Cform) concertedly. The breaking of the hydrogen bond of the latter complex forms N-protonated formamide (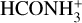 , called “form” herein) and H2O.
, called “form” herein) and H2O.
On the other hand, the trans intermediate Int-H3 suffers other type of rearrangements where there is a hydrogen transfer from the OH to the oxygen of the carbonyl group in the formic acid moiety though the transition structure TSH3−H3*, which shows a high energy barrier from Int-H3 but still submerged with respect to the reactants (40.05 kcal mol−1). This reaction pathway leads to H3* in which the  forms a hydrogen bonding with the OH group of t-HCOOH. This intermediate could evolve through three different reaction pathways. The first transition structure leads again to Cform through the transition structure TSH3*−Cform, whose geometry is similar to that of TSH2−Cform· The difference between both transition structures is the orientation of the hydrogen of the OH group. The energy of TSH3*−Cform is also 2.08 kcal mol−1 above the reactants, and thus it is unlikely that it leads to N-protonated form in the ISM.
forms a hydrogen bonding with the OH group of t-HCOOH. This intermediate could evolve through three different reaction pathways. The first transition structure leads again to Cform through the transition structure TSH3*−Cform, whose geometry is similar to that of TSH2−Cform· The difference between both transition structures is the orientation of the hydrogen of the OH group. The energy of TSH3*−Cform is also 2.08 kcal mol−1 above the reactants, and thus it is unlikely that it leads to N-protonated form in the ISM.
Int-H3 could also isomerize into the complexes C1 and C2. Both complexes are two conformations of the same molecules. In CI, the 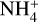 acts as a two-hydrogen-bonding donor of CO and H2O, whereas in C2 H2O acts as hydrogen donor with CO and a hydrogen-bond acceptor with
acts as a two-hydrogen-bonding donor of CO and H2O, whereas in C2 H2O acts as hydrogen donor with CO and a hydrogen-bond acceptor with 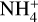 . The most energetically favoured situation is CI (5.61 kcal mol−1 below C2). In both complexes, the weakest hydrogen bond is that formed with CO, and thus they dissociate into the complex
. The most energetically favoured situation is CI (5.61 kcal mol−1 below C2). In both complexes, the weakest hydrogen bond is that formed with CO, and thus they dissociate into the complex 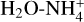 and CO. The formation of C2 from H3* shows a transition structure (TSH3*−C2) that is 2.27 kcal mol−1 above the reactants, whereas the formation of CI from H3* passes through TSH3*−C1 which is just 0.26 kcal mol−1 below the reactants. This situation makes this process viable at OK. However, a small increase in the temperature consequently increases the height of the energy barrier, making it a non-viable process even at 15 K. This computational study shows that the only viable processes in the destruction of catl with NH3 is the back formation of c-HCOOH and t-HCOOH (see below).
and CO. The formation of C2 from H3* shows a transition structure (TSH3*−C2) that is 2.27 kcal mol−1 above the reactants, whereas the formation of CI from H3* passes through TSH3*−C1 which is just 0.26 kcal mol−1 below the reactants. This situation makes this process viable at OK. However, a small increase in the temperature consequently increases the height of the energy barrier, making it a non-viable process even at 15 K. This computational study shows that the only viable processes in the destruction of catl with NH3 is the back formation of c-HCOOH and t-HCOOH (see below).
 |
Fig. 5 Global rate coefficients (logarithmic scale) for the destruction of c-HCOOH and t-HCOOH, with HCO+ in the 15–400 K range. |
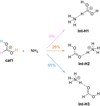 |
Fig. 6 Branching ratios of 100 MEPs computed for the barrierless association of catl with NH3. |
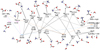 |
Fig. 7 E+ZPEAnh energy profiles (in kcal mol−1) for reaction of catl ( |
3.2.2 Kinetics
Figure 8 shows the plots of the rate constants for the destruction of catl described in Sect. 3.2.1. Figure 8a corresponds to the rate coefficient for the formation of c-HCOOH and  (blue line) and t-HCOOH and
(blue line) and t-HCOOH and  (orange line). Both reactions present a non-Arrhenius behavior since there is no energy barrier in the reaction pathways and the rate-determining step of the whole process is the first barrierless association reaction. This kinetic behavior was also observed in the formation of catl (Fig. 5a). The rate of formation of t-HCOOH is higher than that of c-HCOOH, varying by approximately a factor 3 in the whole temperature range.
(orange line). Both reactions present a non-Arrhenius behavior since there is no energy barrier in the reaction pathways and the rate-determining step of the whole process is the first barrierless association reaction. This kinetic behavior was also observed in the formation of catl (Fig. 5a). The rate of formation of t-HCOOH is higher than that of c-HCOOH, varying by approximately a factor 3 in the whole temperature range.
The dotted lines of the Fig. 8b reports the rate coefficients for the formation of N-protonated formamide. This process shows a typical Arrhenius temperature dependence with very low rate constant values in the 15–100 K temperature range. This reaction is unlikely to occur in the ISM since its formation requires overcoming energy barriers that are above the energy of the reactants. Likewise, the formation of 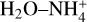 and CO is a non-viable process since the lowest energy barrier yielding the products is just 0.26 kcal mol−1 below the reactants at 0 K. Thus, an increase in the temperature places the energy barrier above the reactants, and it becomes a nonviable reaction under ISM conditions. This is the reason why the rate constant weakly increases at very low temperatures (see the black line in Fig. 8b).
and CO is a non-viable process since the lowest energy barrier yielding the products is just 0.26 kcal mol−1 below the reactants at 0 K. Thus, an increase in the temperature places the energy barrier above the reactants, and it becomes a nonviable reaction under ISM conditions. This is the reason why the rate constant weakly increases at very low temperatures (see the black line in Fig. 8b).
This kinetic study demonstrates that the destruction of catl by collisions with NH3 leads exclusively to c-HCOOH and t-HCOOH. The branching cis/trans ratio found between the rate coefficients for the formation of HCOOH is thus 25.7% at 15 K.
 |
Fig. 8 Global rate coefficients (in logarithmic scale) for the destruction of catl ( |
Fitting parameters for the destruction of c-HCOOH and t-HCOOH by a reaction with HCO+ for the temperature range indicated in parentheses.
4 Discussion
4.1 Destruction of HCOOH with HCO+
4.1.1 Product branching ratios
Our new high-level ab initio results show that the destruction of c-HCOOH, if present initially, and of t-HCOOH by reaction with HCO+ is a very fast process (see Table 1 for the Arrhenius-Kooij parameters). These destruction mechanisms lead exclusively to the formation of the HCOOH cations cat1, cat2, and cat3 (see Table 2 for the product branching ratios). The other cation of HCOOH, cat4, has previously been considered in astrochemical studies (Vigren et al. 2010). However, our kinetic study shows that cat4 should be formed through other chemical routes different from the one studied here since its destruction is likely to occur after its formation.
The branching ratios obtained with our kinetic study indicate that most c-HCOOH and t-HCOOH are transformed into the cation cat1. As mentioned in Sect. 1, c-HCOOH may not be present initially since it is destroyed very fast on grains by a reaction with hydrogen atoms (Molpeceres et al. 2022) and in the gas phase by isomerization reactions (García de la Concepción et al. 2022). Even so, c-HCOOH is detected in cold, molecular, dark clouds. Considering that HCO+ is a very abundant molecule in these sources, c-HCOOH could be transformed in the gas phase after reacting with it. This reaction yields mainly to the formation of cat1 (~69% of the total product branching ratio), cat3 (~30.6%), and to a lesser extent, cat2 (~0.5%; see Table B.1). On the other hand, t-HCOOH, much more abundant than c-HCOOH, leads to cat1 and cat3 with a ratio of 71.9% and 0.36% at 15 K, respectively. The rest is distributed in the formation of cat4 (9.76%) and CO−H3O+ (17.98%; see Table B.2). It should be noted that the formation of cat4 + CO is an exothermic process (−21.13 kcal mol−1) in which most of the energy goes into increasing the velocity of the fragments. However, cat4 could evolve into CO−H3O+ through a transition structure that is just 0.89 kcal mol−1 above the cation (cat4). Considering that the fragments could retain some internal energy, the lifetime of cat4 should be low, and it is completely transformed into 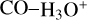 . This process has been demonstrated experimentally for the reaction of HCOOH with
. This process has been demonstrated experimentally for the reaction of HCOOH with 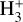 (see Sect. 4.1.2.).
(see Sect. 4.1.2.).
Product branching ratios (%) for the destruction of cat1 by reaction with NH3.
4.1.2 Comparison of the reactions HCOOH + HCO+ and 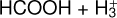
It has been shown that the reaction of HCOOH with 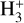 is a completely dissociative process that yields either H3O+ + CO or HCO+ + H2O under low-pressure conditions (Mackay et al. 1978; Sekiguchi et al. 2004). The first step of the reaction should be the formation of the cation cat1 and molecular hydrogen as well as for the reaction with HCO+ is cat1–cat4 and carbon monoxide (CO). In the reaction with
is a completely dissociative process that yields either H3O+ + CO or HCO+ + H2O under low-pressure conditions (Mackay et al. 1978; Sekiguchi et al. 2004). The first step of the reaction should be the formation of the cation cat1 and molecular hydrogen as well as for the reaction with HCO+ is cat1–cat4 and carbon monoxide (CO). In the reaction with 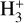 the total energy dissipation of the system through the increase of the translational energy of the fragments is not enough to thermalize the products (cat1 + CO). This is due to the reaction
the total energy dissipation of the system through the increase of the translational energy of the fragments is not enough to thermalize the products (cat1 + CO). This is due to the reaction 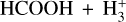 being highly exothermic, and thus the remaining internal energy in the fragments allows cat1 to isomerize into H3O+ + CO and HCO+ + H2O (Mackay et al. 1978). This process is, however, not observed for the reaction HCOOH + HCO+ because the formation of cat1 + CO is not exothermic enough to keep the fragments excited enough to isomerize to cat4; this is due to it being a reaction without detectable dissociation (Mackay et al. 1978). The energy of the transition structure that connects cat1 to cat4 is 9.00 kcal mol−1 above the reactants (c-HCOOH + HCO+), which makes it a non-viable process under the conditions considered here (see Fig. 4). Therefore, this indicates that cat1 should form in dark molecular clouds.
being highly exothermic, and thus the remaining internal energy in the fragments allows cat1 to isomerize into H3O+ + CO and HCO+ + H2O (Mackay et al. 1978). This process is, however, not observed for the reaction HCOOH + HCO+ because the formation of cat1 + CO is not exothermic enough to keep the fragments excited enough to isomerize to cat4; this is due to it being a reaction without detectable dissociation (Mackay et al. 1978). The energy of the transition structure that connects cat1 to cat4 is 9.00 kcal mol−1 above the reactants (c-HCOOH + HCO+), which makes it a non-viable process under the conditions considered here (see Fig. 4). Therefore, this indicates that cat1 should form in dark molecular clouds.
4.2 Destruction of 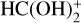 (cat1) with NH3: the origin of c-HCOOH in dark molecular clouds
(cat1) with NH3: the origin of c-HCOOH in dark molecular clouds
It has been proposed that the formation of HCOOH must occur in dust grains by hydrogenation of the HOCO radical (Ioppolo et al. 2010; Taquet et al. 2017). Recently, Molpeceres et al. (2022) demonstrated that whatever the cis/trans ratio of HCOOH is, c-HCOOH should not withstand the conditions on the surface of dust grains since its destruction by H atoms is a very fast process. In the gas phase, isomerization transformations should yield predominantly t-HCOOH, which does not explain the presence of c-HCOOH of 5% with respect to t-HCOOH in the gas phase of cold dark clouds (García de la Concepción et al. 2022).
In this work, we have shown that t-HCOOH and c-HCOOH can react by collisions with HCO+ forming cat1, cat2 and cat3 efficiently and being cat1 the most abundant product. This highly reactive species can be destroyed back to c-HCOOH and t-HCOOH by reaction with NH3 (see Sect. 3.2). To study the destruction of cat1, we selected NH3 since it is one of the most abundant molecules in molecular dark clouds such as B5 or L483. Our kinetic results demonstrate that the formation of c-HCOOH and t-HCOOH are the only products. Indeed, N-protonated formamide 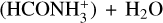 and the complex
and the complex 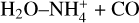 are not formed through this chemical process.
are not formed through this chemical process.
Tables 2 and 3 report, respectively, the branching ratios and the Arrhenius-Kooij parameters for the destruction of cat1, which are practically constant throughout the whole temperature range. At Tkin of ~15 K the ratio of c-HCOOH with respect t-HCOOH is 25.7%. It should be noted that this process is cyclic; that is, HCOOH is destroyed by HCO+ and then HCOOH is again formed by the destruction of cat1, giving rise to a constant cis/trans ratio over time.
Although not in the observed amount with respect to t-HCOOH, our study provides an origin for the presence of c-HCOOH under the cold temperatures of molecular dark clouds. The expected ratio is 25.7%, far from the one reported by observations (6%). This difference could be due the destruction of both cat2 and cat3, which should also be considered. In addition, we note that there could be other mechanisms for the destruction of the cations with abundant species acting as bases such as CO, OH, and H2O, among others.
The most intuitive way of justifying the destruction of a cation in the ISM is to invoke dissociative recombination reactions. However, dissociative recombinations of relatively large molecules typically produce fragments due to bond breaking between heavy atoms and to a much lesser extent, X–H breaks, with X being any atom heavier than deuterium. This effect has been demonstrated for several abundant molecules such as methanol. The dissociative recombination of protonated methanol was found to yield many products, of which only 3% is methanol. In the same way, the theoretical study of the dissociative recombination of protonated formamide (Ayouz et al. 2019) (NH2CHOH+) shows that this process only generates 15% of for-mamide (NH2CHO) + H, whilst the remaining 85% generates HCO + NH2 + H. Similar results were obtained in the experimental study of the dissociative recombination of cat1 and/or cat2 and cat3 (Vigren et al. 2010; we note that they do not distinguish between isomers). In this case, only 13% of the products lead to X–H bond breaking, while the remaining 87% of the products undergo bond breaking between heavy atoms. We note that 13% of the H–X breaking bonds involve up to seven exit channels, where only one of them lead to HCOOH + H.
Herbst (1985) proposed that the main route for the formation of cat1 (and/or cat2 and cat3) comes from the radiative association of HCO+ and H2O. However, we investigated the MEP for the association of both fragments, and the barrierless reaction led to the formation of the complex CO−H3O+. In this process, the fragment HCO+ donates a proton to H2O through an exothermic process that yields the dissociation of the complex giving CO and H3O+. This fast association-dissociation between a H+ -donor and a neutral partner should show similar rate coefficients to those calculated herein for the formation of cat1 from HCO+ and HCOOH (Fig. 3). These discrepancies led us to revisit the formation of cat1 (and/or cat2 and cat3; Herbst 1985) and, consequently, the chemical models that include that reaction (Vigren et al. 2010).
All these results point to the idea that the dissociative recombination of cat1 is not the main route for the formation of c-HCOOH and t-HCOOH. Instead, a fragmentation into smaller fragments is expected. Therefore, the most probable way of enhancing t-HCOOH with respect to c-HCOOH in dark clouds is the destruction of cat1, cat2, and cat3 after reacting with abundant molecules acting as a base such as NH3.
Is important to highlight that our new (SAB) mechanism proposed here is not only applicable to HCOOH, but to any organic molecule present in the ISM. Therefore, this mechanism could be behind the formation of high-energy isomers whose provenance is yet unknown.
Fitting parameters for the destruction of cat1 by reaction with NH3 for the temperature range indicated in parentheses.
5 Conclusions
In this work, we propose a novel cyclic reaction mechanism for destruction and backward formation (baptized the sequential acid-base mechanism) to explain the occurrence of c-HCOOH in dark molecular clouds. Our high-level ab initio quantum chemical and kinetic calculations show that the destruction of both isomers of HCOOH by reaction with HCO+ to give the cations (cat1, cat2, and cat3) is a very efficient process. Following these reactions, the most abundant cation (cat1) reacts with NH3, yielding c-HCOOH and t-HCOOH back with a cis/trans ratio of 25.7%. This result explains the presence of c-HCOOH in dark molecular clouds, although this ratio is far from the 6% ratio reported by observations. It may be that for reaching a ratio of 6% of c-HCOOH with respect to t-HCOOH, the destruction of cat2 and cat3 should also be considered. In addition, further destruction mechanisms of the three cations with other abundant chemical species acting as bases could be considered. The detection of the cation cat1 in the ISM would reinforce our proposal and would provide valuable information for the chemistry of molecular dark clouds.
This work brings a new approach in the destruction and formation of isomers in the ISM, which involves two abundant interstellar species, HCO+ and NH3. This mechanistic approach can be applied to any molecule present in the gas phase of molecular clouds, and it promises to be a key process for understanding the observed ratio of the isomers of organic molecules measured in the ISM.
Acknowledgements
J.G.d.l.C. acknowledges the Spanish State Research Agency (AEI) through project number MDM-2017-0737 Unidad de Excelencia “María de Maeztu”–Centro de Astrobiología (CSIC-INTA). J.G.d.l.C., I.J.-S., J.M.-P. and L.C. acknowledge support from grant no. PID2019-105552RB-C41 by the Spanish Ministry of Science and Innovation/State Agency of Research MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”. J.C.C. acknowledges the Junta de Extremadura and European Regional Development Fund, Spain, Project No. GR21032. G.M. acknowledges the support of the Alexander von Humboldt Foundation through a postdoctoral research grant. V.M.R. has received support from the project RYC2020-029387-I funded by MCIN/AEI /10.13039/501100011033, and from the Comunidad de Madrid through the Atracción de Talento Investigador Modalidad 1 (Doctores con experiencia) Grant (COOL: Cosmic Origins Of Life; 2019-T1/TIC-5379). Computational assistance was provided by the Supercomputer facilities of LUSITANIA founded by Cénits and Computaex Foundation.
Appendix A Calculation of rate constants for astrochemical models
The methodology we propose here is employed to provide a set of phenomenological rate constants to be introduced in astro-chemical models. In the case of gas phase reactions, these rate constants can be obtained from experiments, calculations, or from approximated theories. In the particular case of ion-molecule reactions, the Su-Chesnavich approach to compute the rate constant is employed (Su & Chesnavich 1981). Under this theory, the (global) rate constant for an ion-molecule reaction depends solely on the isotropic polarizability of the neutral molecule α and its dipole moment µ. The Su-Chesnavich rate constant thus reads as follows:
![${k_d} = \left\{ {\matrix{ {{k_L}\left[ {{{{{\left( {x + 0.5090} \right)}^2}} \over {10.526}} + 0.9754} \right]} \hfill & {x > 2} \hfill \cr {{k_L}\left( {0.4767x + 0.6200} \right)} \hfill & {x \ge 2} \hfill \cr } } \right.;$](/articles/aa/full_html/2023/07/aa43966-22/aa43966-22-eq48.png) (A.1)
(A.1)
with M being the reduced mass of the reacting fragments, e the charge of the electron, kB the Boltzmann constant, and T the gas temperature. The Su-Chesnavich relation has been applied to expand astrochemical networks significantly (Woon & Herbst 2009; Wakelam et al. 2010) or in the evaluation of individual rate constants (Shingledecker et al. 2020). While the rate constants obtained for this method are approximated, they serve to shed light on destruction routes of interstellar molecules in the absence of more sophisticated theories or experiments.
To put into context the rate constants derived in this work compared with the ones obtained from the Su-Chesnavich approach, we calculated the Su-Chesnavich rate constants using the magnitudes obtained at our level of theory DSD-revPBEP86-D3(BJ)/aug-cc-pVTZ. The derived magnitudes for the neutral reactions of our study are collated in Table A.1. The rate constant (and associated reduced mass) is considered for reactions c-HCOOH + HCO+ → products, t-HCOOH + HCO+ → products, and cat1 + NH3 → products. We indicate products in this notation because Su-Chesnavich rate constants are phenomenological rate constants that are independent of the obtained products.
Dipole moments (µ in Debye, D) and diagonal elements of the polarizability tensor (αii in Å3) for the neutral species considered in this work at the DSD-PBEP86-D3(BJ)/aug-cc-pVTZ level of theory.
In Figure A.1, we present the comparison between the rate constants obtained in Sect. 3 with those calculated using the Su-Chesnavich method. In light of these results, we conclude that the Su-Chesnavich formula in some cases underestimates and overestimates the reaction rate constants, but provides a qualitative picture that confirms the trends obtained using more sophisticated methods. Moreover, it gives a physical explanation for the increased reactivity of c-HCOOH over t-HCOOH, finding its origin in the different dipole moment of both isomers (α is very similar between isomers).
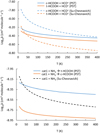 |
Fig. A.1 Comparison between global rate constants having employed PST and those obtained with the Su-Chesnavich formula. |
Appendix B Product branching ratios
Product branching ratios (%) for the destruction of c-HCOOH by reaction with HCO+.
Product branching ratios (%) for the destruction of t-HCOOH by reaction with HCO+.
References
- Adler, T. B., Knizia, G., & Werner, H.-J. 2007, J. Chem. Phys., 127, 221106 [Google Scholar]
- Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]
- Agúndez, M., Marcelino, N., Cernicharo, J., Roueff, E., & Tafalla, M. 2019, A&A, 625, A147 [Google Scholar]
- Ayouz, M. A., Yuen, C. H., Balucani, N., et al. 2019, MNRAS, 490, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Baiano, C., Lupi, J., Tasinato, N., Puzzarini, C., & Barone, V. 2020, Molecules, 25, 2873 [CrossRef] [Google Scholar]
- Balucani, N., Skouteris, D., Ceccarelli, C., et al. 2018, Mol. Astrophys., 13, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Barone, V. 2004, J. Chem. Phys., 120, 3059 [NASA ADS] [CrossRef] [Google Scholar]
- Chesnavich, W. J. 1986, J. Chem. Phys., 84, 2615 [NASA ADS] [CrossRef] [Google Scholar]
- Cuadrado, S., Goicoechea, J. R., Roncero, O., et al. 2016, A&A, 596, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunning T. H. Jr., 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Eckart, C. 1930, Phys. Rev., 35, 1303 [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16, Revision A.03 [Google Scholar]
- García de la Concepción, J., Jiménez-Serra, I., Carlos Corchado, J., Rivilla, V. M., & Martín-Pintado, J. 2021, ApJ, 912, L6 [CrossRef] [Google Scholar]
- García de la Concepción, J., Colzi, L., Jiménez-Serra, I., et al. 2022, A&A, 658, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgievskii, Y., Miller, J. A., Burke, M. P., & Klippenstein, S. J. 2013, J. Phys. Chem. A, 117, 12146 [NASA ADS] [CrossRef] [Google Scholar]
- Goerigk, L., Hansen, A., Bauer, C., et al. 2017, Phys. Chem. Chem. Phys., 19, 32184 [CrossRef] [Google Scholar]
- Grimme, S., Antony, J., Ehrlich, S., & Krieg, H. 2010, J. Chem. Phys., 132, 154104 [Google Scholar]
- Grimme, S., Ehrlich, S., & Goerigk, L. 2011, J. Comput. Chem., 32, 1456 [Google Scholar]
- Herbst, E. 1985, ApJ, 291, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Ioppolo, S., Cuppen, H. M., van Dishoeck, E. F., & Linnartz, H. 2010, MNRAS, 410, 1089 [Google Scholar]
- Kendall, R. A., Dunning T. H., Jr., & Harrison, R. J. 1992, J. Chem. Phys., 96, 6796 [NASA ADS] [CrossRef] [Google Scholar]
- Knizia, G., Adler, T. B., & Werner, H.-J. 2009, J. Chem. Phys., 130, 054104 [Google Scholar]
- Kooij, D. M. 1893, ZPhCh, 12, 155 [Google Scholar]
- Kozuch, S., & Martin, J. M. L. 2011, Phys. Chem. Chem. Phys., 13, 20104 [NASA ADS] [CrossRef] [Google Scholar]
- Legault, C. Y. 2009, http://www.cylview.org [Google Scholar]
- Loomis, R. A., McGuire, B. A., Shingledecker, C., et al. 2015, ApJ, 799, 34 [Google Scholar]
- Lupi, J., Puzzarini, C., & Barone, V. 2020, ApJ, 903, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, G. I., Hopkinson, A. C., & Bohme, D. K. 1978, J. Am. Chem. Soc., 100, 7460 [CrossRef] [Google Scholar]
- Molpeceres, G., de la Concepción, J. G., & Jiménez-Serra, I. 2021, ApJ, 923, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Molpeceres, G., Jiménez-Serra, I., Oba, Y., et al. 2022, A&A, 663, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neese, F. 2012, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2, 73 [CrossRef] [Google Scholar]
- Neese, F., Wennmohs, F., & Becker, U. Riplinger, C. 2020, J. Chem. Phys., 152, 224108 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, T., Oba, Y., Sameera, W. M. C., Kouchi, A., & Watanabe, N. 2021, ApJ, 922, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Pechukas, P., & Light, J. C. 1965, J. Chem. Phys., 42, 3281 [NASA ADS] [CrossRef] [Google Scholar]
- Santra, G., Sylvetsky, N., & Martin, J. M. L. 2019, J. Phys. Chem. A, 123, 5129 [NASA ADS] [CrossRef] [Google Scholar]
- Sekiguchi, O., Bakken, V., & Uggerud, E. 2004, J. Am. Soc. Mass Spectrom., 15, 982 [CrossRef] [Google Scholar]
- Shingledecker, C. N., Álvarez-Barcia, S., Korn, V. H., & Kästner, J. 2019, ApJ, 878, 80 [Google Scholar]
- Shingledecker, C. N., Molpeceres, G., Rivilla, V. M., Majumdar, L., & Kästner, J. 2020, ApJ, 897, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Spicher, S., Caldeweyher, E., Hansen, A., & Grimme, S. 2021, Phys. Chem. Chem. Phys., 23, 11635 [NASA ADS] [CrossRef] [Google Scholar]
- Su, T., & Chesnavich, W. J. 1981, J. Chem. Phys., 76, 5183 [Google Scholar]
- Taquet, V., Wirström, E. S., Charnley, A., et al. 2017, A&A, 607, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vigren, E., Hamberg, M., Zhaunerchyk, V., et al. 2010, ApJ, 709, 1429 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Smith, I. W., Herbst, E., et al. 2010, Space Sci. Rev., 156, 13 [CrossRef] [Google Scholar]
- Weston, R. E., & Schwartz, H. E., eds. 1972, Chemical Kinetics (Englewood Cliffs, NJ: Prentice-Hall Inc.) [Google Scholar]
- Woon, D. E., & Herbst, E. 2009, ApJS, 185, 273 [Google Scholar]
All Tables
Fitting parameters for the destruction of c-HCOOH and t-HCOOH by a reaction with HCO+ for the temperature range indicated in parentheses.
Fitting parameters for the destruction of cat1 by reaction with NH3 for the temperature range indicated in parentheses.
Dipole moments (µ in Debye, D) and diagonal elements of the polarizability tensor (αii in Å3) for the neutral species considered in this work at the DSD-PBEP86-D3(BJ)/aug-cc-pVTZ level of theory.
Product branching ratios (%) for the destruction of c-HCOOH by reaction with HCO+.
Product branching ratios (%) for the destruction of t-HCOOH by reaction with HCO+.
All Figures
 |
Fig. 1 Chemical structures of c-HCOOH and t-HCOOH. |
| In the text | |
 |
Fig. 2 Protonation of t-HCOOH and c-HCOOH with HCO+ to give the cations cat1, cat2, cat3, cat4, and CO−H3O+ (+ CO). |
| In the text | |
 |
Fig. 3 E+ZPEAnh energy profiles (in kcal mol−1) for the reactions of c-HCOOH and t-HCOOH with HCO+. The meaning of the circles and arrows are indicated in the legend at the top of the figure. |
| In the text | |
 |
Fig. 4 E+ZPEAnh energy profiles (in kcal mol−1) for the unimolecu-lar decomposition of cat1. Relative energies are given with respect to c-HCOOH and HCO+. |
| In the text | |
 |
Fig. 5 Global rate coefficients (logarithmic scale) for the destruction of c-HCOOH and t-HCOOH, with HCO+ in the 15–400 K range. |
| In the text | |
 |
Fig. 6 Branching ratios of 100 MEPs computed for the barrierless association of catl with NH3. |
| In the text | |
 |
Fig. 7 E+ZPEAnh energy profiles (in kcal mol−1) for reaction of catl ( |
| In the text | |
 |
Fig. 8 Global rate coefficients (in logarithmic scale) for the destruction of catl ( |
| In the text | |
 |
Fig. A.1 Comparison between global rate constants having employed PST and those obtained with the Su-Chesnavich formula. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.