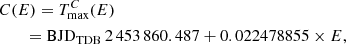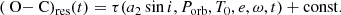| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202243293 | |
| Published online | 12 July 2022 | |
HD 133729: A blue large-amplitude pulsator in orbit around a main-sequence B-type star
Instytut Astronomiczny, Wydział Fizyki i Astronomii, Uniwersytet Wrocławski, Kopernika 11, 51-622 Wrocław, Poland
e-mail: Andrzej.Pigulski@uwr.edu.pl
Received:
9
February
2022
Accepted:
21
March
2022
Blue large-amplitude pulsators (BLAPs) form a small group of hot objects pulsating in a fundamental radial mode with periods of the order of 30 min. Proposed evolutionary scenarios explain them as evolved low-mass stars: ∼0.3 M⊙ shell-hydrogen-burning objects with a degenerated helium core, more massive (0.5–0.8) M⊙ core-helium-burning stars, or ∼0.7 M⊙ surviving companions of type Ia supernovae. Therefore, their origin remains to be established. Using data from Transiting Exoplanet Survey Satellite, we discovered that HD 133729 is a binary consisting of a late B-type main-sequence star and a BLAP. The BLAP pulsates with a period of 32.37 min decreasing at a rate of ( − 7.11 ± 0.33) × 10−11. The light curve is typical for BLAPs, but it shows an unusual 40-s drop at the descending branch. Due to light dilution by a brighter companion, the observed amplitude of pulsation is much smaller than in other BLAPs. From available photometry, we derived times of maximum light, which revealed the binary nature of the star via an O−C diagram. The diagram shows variations with a period of 23.08433 d that we attribute to the light-travel-time effect in the system. The analysis of these variations allowed us to derive the spectroscopic parameters of the BLAP’s orbit around the binary’s centre of mass. The presence of a hot companion in the system was confirmed by the analysis of its spectral energy distribution, which was also used to place the components in the Hertzsprung-Russell diagram. The obtained position of the BLAP fully agrees with the location of the other members of the class. With the estimated V ≈ 11 mag and the Gaia distance of less than 0.5 kpc, the BLAP is the brightest and the nearest of all known BLAPs. It may become a key object in the verification of the evolutionary scenarios for this class of variables. We argue that low-mass progenitors of the BLAP are excluded if the components are coeval and no mass transfer between the components took place.
Key words: stars: oscillations / binaries: spectroscopic / stars: fundamental parameters / stars: individual: HD 133729
© ESO 2022
1. Introduction
Large photometric ground-based surveys provided the astronomical community with a huge number of photometric measurements of millions of stars. Space missions were another source of a large quantity of photometric data, some with an unprecedented quality and time coverage. Although the surveys and the missions were primarily aimed at detecting microlensing events and transiting exoplanets, the data happened to be extremely useful in the characterisation of the different types of pulsating stars over the entire Hertzsprung-Russell (H-R) diagram. It is no wonder some exotic and very rare types of variable stars were found. An example is the discovery of a small group of short-period hot pulsators known as blue large-amplitude pulsators; hereafter, BLAPs (Pietrukowicz et al. 2017).
The first BLAP was discovered serendipitously by Pietrukowicz et al. (2013) in the Optical Gravitational Lensing Experiment (OGLE) data while searching for pulsating stars in the OGLE-III Galactic disc fields in the direction tangent to the Centaurus Arm. The star, OGLE-GD-DSCT-0058, showed a large peak-to-peak amplitude (ΔI = 0.24 mag) and light curve resembling fundamental-mode pulsators related to δ Scuti stars, that is, high-amplitude δ Scuti (HADS) stars and SX Phoenicis stars. The star was therefore tentatively classified as a δ Scuti variable. It differed from the members of these groups, however, by its exceptionally short period (28.26 min). The follow-up spectroscopic study (Pietrukowicz et al. 2015) showed that it cannot be a δ Scuti star because it is too hot – its effective temperature amounted to about 33 000 K. Searching for the other members of this group in the Galactic bulge OGLE data, Pietrukowicz et al. (2017) found 13 BLAPs. This allowed the characterisation of this new class of pulsating stars. BLAPs pulsate with periods between 22 and 40 min and have non-sinusoidal (a steep increase followed by a slow decrease of brightness) light curves with the peak-to-peak amplitudes of 0.2–0.4 mag in the V band. Amplitudes in the I band are on average about 20% lower than in the V band, which is typical for radially pulsating stars. In the H-R diagram, BLAPs are located between hot massive main-sequence stars and hot subdwarfs. Their luminosities (log(L/L⊙)=2.2–2.6) are, however, about an order of magnitude higher than the luminosities of hot subdwarfs, while surface gravities (log(g/(cm s−2)) = 4.5–4.8) are much lower than the surface gravities of hot subdwarfs. No BLAP was discovered in the Magellanic Clouds (Pietrukowicz et al. 2018), but these objects were at the limits of detection in the OGLE data.
The existence of a separate group of pulsating stars in a poorly populated region of the H-R diagram raises a question about their origin. Pietrukowicz et al. (2017) showed that two models reproduce pulsational characteristics of BLAPs. In the first model, a BLAP has a helium-burning core with a mass of about 1 M⊙ and can be a descendant of a main-sequence ∼5 M⊙ star. This model was supported by the calculations of Wu & Li (2018). In the other model, a BLAP has a degenerated helium core with a mass of ∼0.3 M⊙ burning hydrogen in a shell. Such a configuration is typical for an evolved main-sequence star with a mass of about 1 M⊙ prior to a helium flash. The low-mass model was supported by Romero et al. (2018) and Córsico et al. (2018), who proposed that BLAPs are hot counterparts of pre-extremely low-mass white dwarfs (WDs) with masses of 0.27–0.37 M⊙. This model was also favoured by Byrne & Jeffery (2020). They showed that the members of the short-period class of pre-WD pulsators discovered by Kupfer et al. (2019) can have a similar structure to BLAPs and therefore can be deemed ‘high-gravity BLAPs’. Both models proposed for BLAPs require a significant part of the initial stellar mass to be stripped off during pre-BLAP evolution. This is possible in binaries (e.g. Byrne et al. 2021), but no BLAP was known to reside in a binary. In this context, the solution proposed by Meng et al. (2020) seemed to solve the problem. These authors showed that BLAPs can be explained as the surviving companions of type Ia supernovae, which begin their evolution as ∼3 M⊙ stars, transfer a large part of their masses to WD companions, and end up as stars with masses of (0.76 ± 0.1) M⊙ at the time of supernova explosion. Either way, the origins of BLAPs remain unexplained.
We show in the present paper, based primarily on a detailed analysis of the Transiting Exoplanet Survey Satellite (TESS) photometry of HD 133729, that this star is a binary consisting of a late-B spectral type main-sequence primary and a BLAP secondary. This makes the secondary the first known BLAP in a binary and a key target for further studies of the properties of BLAPs and evolutionary channels leading to their origin. It is also the nearest and the brightest known star of this type.
2. HD 133729 and its known variability
HD 133729 is a bright (V= 9.1 mag) star of B6/7 V spectral type (Houk 1982). It was included in the blind search for variability among B-, A-, and F-type stars carried out by Holdsworth et al. (2014). They used data obtained within the Wide Angle Search for Planets (WASP) project (Pollacco et al. 2006). The search was focused on a discovery of short-period variability, mainly in rapidly-oscillating Ap (roAp) stars, pulsating Am stars, δ Scuti stars with high frequencies, and pre-main-sequence δ Scuti stars. The result of this search was the discovery of 375 stars showing variability with periods shorter than 30 min. The follow-up spectroscopy of 37 (about 10%) of these high-frequency WASP pulsators, combined with the detailed analysis of their photometry, allowed Holdsworth et al. (2014) to announce the discovery of ten new roAp stars, 13 pulsating Am stars, and δ Sct stars with frequencies higher than 100 d−1.
For HD 133729, Holdsworth et al. (2014) reported three nearly equidistant frequencies, 88.93, 88.97, and 89.02 d−1, with amplitudes equal to 6, 2, and 2 mmag, respectively. Variability with such high frequencies is not known in B-type main-sequence stars. The star was not included by these authors in the spectroscopic follow-up programme, and therefore its WASP photometry was not studied in detail. Hence, the nature of its variability remained unknown. The star was proposed for 2-min and 20-s cadence observations with the TESS satellite, however.
The present study shows that the dominating term found by Holdsworth et al. (2014) has a frequency equal to the lowest harmonic of the real pulsation frequency. The pulsation frequency of 44.49 d−1 was not detected by these authors because the lower limit of their frequency search was set to 50 d−1. The other two frequencies are orbital sidelobes caused by the light-travel-time effect in the system with the orbital period of about 23 days (Sect. 3.3).
Oelkers et al. (2018) gave an upper limit for non-variability of HD 133729 in the Kilodegree Extremely Little Telescope (KELT) data, but this study was based on integrated 30-min data, comparable with the variability period of the BLAP (Sect. 3.1). Given its low amplitude, the variability was averaged in this statistics. Some recent comments on the variability of HD 133729 were already based on the TESS data. Barceló Forteza et al. (2020) analysed a sample of nearly 2400 δ Sct candidates in their study aimed at finding scaling relations for δ Sct stars. HD 133729 did not seem interesting with regard to their goals, so they included it in the sub-sample of stars showing ‘other kind of variation’.
3. Analysis of photometry
3.1. TESS photometry
HD 133729 (TIC 75934024) was observed by the TESS satellite in Sector 11 with a 2-min cadence and in Sector 38 during the TESS Extended Mission with both 2-min and 20-s cadences. The Sector 11 data were secured between 2019 April 26 and May 20, covering nearly 24 days with a 4.5-day gap in the middle of the run. The Sector 38 data were obtained between 2021 April 29 and May 26, with a short one-day gap. All TESS data were downloaded from the Barbara A. Mikulski Archive for Space Telescopes (MAST) Portal1. The data consist of 13 887 and 18 248 data points with 2-min cadence in Sector 11 and 38, respectively. In addition, there are 109 581 data points with 20-s cadence in Sector 38. In our analysis, we used PDCSAP fluxes, removing only some short parts at the beginning and at the end of the Sector 11 time series.
The TESS data from both sectors were analysed separately. Frequency spectra of the data from both sectors are fully consistent. Figure 1 shows the frequency spectrum of Sector 38 2-min cadence data. The spectrum is dominated by the frequency at fP = 44.486 d−1 and its harmonics. In addition, small-amplitude signal can be seen at low (∼2.2 d−1) frequencies (Sect. 3.4). The presence of the harmonics of fP means that the light curve is non-sinusoidal, which can be seen in the top panel of Fig. 1. A subtraction of fP and its harmonics did not entirely remove the signal in the vicinity of these frequencies and some residual signal was left (Fig. 1, bottom panel inset). The pattern was dominated by ±0.043 d−1 sidelobes. As we show in Sect. 3.3, the sidelobes originate from phase changes caused by the orbital motion in a binary system.
 |
Fig. 1. Light curve and frequency spectrum of the TESS data of HD 133729. Top: half-day 2-min cadence TESS Sector 38 light curve of HD 133729. Fn stands for the relative flux Fi/⟨F⟩−1, where Fi is the TESS flux for the ith data point and ⟨F⟩ is average flux from all TESS observations in Sector 38. Bottom: frequency spectrum of the TESS Sector 38 data. In order to illustrate the occurrence of the ±0.043 d−1 orbital sidelobes, the inset shows a 2 d−1-wide frequency spectrum of the residuals in the vicinity of fP = 44.487 d−1, after subtracting fP and its harmonics. |
The shape of the light curve of HD 133729 and its period equal to 32.37 min fits the characteristics of BLAPs perfectly. The only problem is a small peak-to-peak amplitude in the TESS band equal to about 32 parts per thousand (ppt). This can be explained, however, by a dilution of BLAP’s light by the brighter companion, the late-B main-sequence star (Sect. 4). Therefore, we refer to fP as the pulsation frequency of the BLAP.
3.2. Archival photometry and the changes in the pulsation period
Since BLAPs show significant period changes (Pietrukowicz et al. 2017; Wu & Li 2018; Córsico et al. 2018), we checked if this is also the case for HD 133729. This can be done because archival photometry from HIPPARCOS space mission and two ground-based surveys, All-Sky Automated Survey (ASAS, Pojmański 1997, 2000, 2009), and WASP (Pollacco et al. 2006), is available for this star.
The archival photometry of HD 133729 from the HIPPARCOS mission, the ASAS survey, and the WASP survey, was first cleaned of outliers and some lower quality data. Since we were interested in the light curve of the BLAP, we also removed some obvious trends in photometry by filtering out low frequencies. In order to account for phase changes due to the orbital motion, the archival time-series photometry m(t) was fitted with the following variability model:
Parameters derived in this model are amplitudes An, An−, and An+, phases ϕn, ϕn−, and ϕn+, frequencies fP and forb, and mean magnitude m0. The value of N depended on the number of harmonics of fP detected in a given data set. We adopted N = 2 for the HIPPARCOS and the ASAS data, and N = 4 for the WASP data. For the TESS data, we had to proceed in a different way, because the data are short and each sector covers only about one orbital period. Therefore, we first derived the parameters of the orbit (Sect. 3.3) and then corrected times of observations according to the formula given by Irwin (1952) accounting for the light-travel-time delay, and only then did we fit a simplified model consisting of only fP and its harmonics up to N = 12, that is, without the last two terms in Eq. (1). The values of fP derived from the fits are listed in Table 1 and plotted in Fig. 2. Light curves from all surveys phased with the pulsation period are presented in Fig. 3.
 |
Fig. 2. Pulsation frequencies of BLAP in HD 133729 system derived from the HIPPARCOS, ASAS, WASP, and TESS data. Dashed line corresponds to the derived constant rate of frequency change, dfP/dt = (1.41 ± 0.07) × 10−7 d−2. |
 |
Fig. 3. Light curves of HD 133729 phased with pulsation period. (a)–(c): HIPPARCOS (a), ASAS (b), and WASP (c) light curves. (d) Phase-averaged TESS light curves in Sector 11 (green dots), Sector 38, 2-min cadence (red dots), and Sector 38, 20-s cadence (blue dots). For clarity, 5 ppt offsets were applied between the light curves. The 2-min cadence data are averaged in 0.005 phase intervals, and the 20-s cadence data are averaged in 0.002 phase intervals. Phase 0.0 corresponds to the time of maximum light. |
HIPPARCOS photometry of HD 133729 (HIP 73969) is very scarce (Fig. 3), meaning detection of fP is marginal, but it is very important when monitoring the changes in the pulsation period, because the data extend the time span of photometric data to ∼30 years. The star was deemed constant in the HIPPARCOS catalogue (ESA 1997).
The ASAS V-filter data of the star (ASAS 150658-3138.7) were downloaded from the ASAS web page2. They cover almost nine years between December 2000 and September 2009. Therefore, we split the ASAS data into two equal parts, which resulted in two points in Fig. 2.
The WASP data of HD 133729 were downloaded from the public database3. Over 11 000 original data points were available for the star, designated as 1SWASP J150658.93-313838.9. The data span three seasons, between 2006 and 2008. For the purpose of determining fP, each season was analysed separately, which resulted in three points in Fig. 2.
Figure 2 shows the resulting changes in the pulsation frequency, which at first approximation can be assumed linear. The derived rate of frequency change, dfP/dt = (1.41 ± 0.07) × 10−7 d−2, translates into the rate of period change dPP/dt ≡ ṖP = (−7.11 ± 0.33) × 10−11 or r ≡ ṖP/PP = (−11.5 ± 0.6) × 10−7 (yr)−1, where 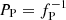 is the pulsation period. This is the largest negative value of the rate of the period change of all known BLAPs if the uncertain value of ṖP for OGLE-BLAP-002 derived by Wu & Li (2018) is not taken into account.
is the pulsation period. This is the largest negative value of the rate of the period change of all known BLAPs if the uncertain value of ṖP for OGLE-BLAP-002 derived by Wu & Li (2018) is not taken into account.
3.3. Light-travel-time effect
A periodic photometric signal sent by a component of a binary can serve as a clock and be used to derive the same orbital parameters that are derived for a single-lined spectroscopic binary. The involved effect is usually called light-travel-time effect (hereafter LTTE) and results in the occurrence of orbital sidelobes in frequency spectra at a separation equal to an orbital frequency, forb. For HD 133729, a separation of orbital sidelobes equal to about 0.043 d−1 (Fig. 1) implies an orbital period of 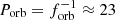 days.
days.
In order to analyse LTTE, we used times of maximum light of the pulsation of the BLAP (Fig. 3). Since data used to derive a single time of maximum light have to cover a reasonably small part of the orbital period, the only data suitable for this kind of analysis are the TESS and the WASP data. The TESS data were split into ∼1-day subsets. This resulted in 45 subsets: 20 for Sector 11 and 25 for Sector 38 observations. Then, a smoothed light curve was obtained by phasing the Sector 38 2-min cadence TESS light curve (Fig. 3). Next, the smoothed light curve was fitted to each subset separately by means of the least-squares method. In effect, a single time of maximum light was obtained for each subset. It was the closest to the midtime of observations in a given subset. A similar procedure was applied to the WASP data, but in this case we chose subsets corresponding to individual nights. Nights with fewer than 20 data points were excluded. In this way, 117 times of maximum light for the WASP data were obtained. The times of observations in the WASP data are given in Heliocentric Julian Days (HJD), while for the TESS data, they are given in Barycentric Julian Days in the standard of Barycentric Dynamical Time, TDB (BJDTDB). In order to make them consistent, we converted the WASP times of maximum light to BJDTDB using the online tool4 provided by J. Eastman (Eastman et al. 2010). All times of maximum light, Tmax, are given in Table A.1.
Figure 3 shows the superb quality of the TESS data. It can be also seen that the average light curves for 2-min cadence Sector 11 and Sector 38 data match perfectly. Since 2-min cadence TESS data are sufficient for the O−C analysis, we did not use 20-s cadence data for this purpose. However, these data were analysed in the same way as 2-min cadence data and, for completeness, the phase-averaged light curve for these data is shown in Fig. 3d. In general, the 20-s cadence data are consistent with the 2-min cadence data. The only difference is an unusual tiny drop of flux lasting only about 40 s at phase 0.05, which can be seen in the light curve of the 20-s cadence data. The feature is averaged in 2-min cadence data. It may have the same origin as the small drops following the epoch of maximum light that can be seen in the light curves of OGLE-BLAP-009 (Pietrukowicz et al. 2017; McWhirter et al. 2020) and ZGP-BLAP-05, -06, and -07 (McWhirter & Lam 2022).
Having obtained times of maximum light, Tmax, we used them to obtain the O−C diagram shown in Fig. 4, upper panel. The values of O−C were calculated with respect to the following ephemeris:
 |
Fig. 4. O−C diagrams for the pulsation period of HD 133729. Top: O−C diagram for WASP (green dots) and TESS (red dots) times of maximum light obtained using Eq. (2) as a reference. Dashed line shows fit with the assumed period change dPP/dt = −7.11 × 10−11 derived in Sect. 3.2. Dotted lines show fits of parabolae with the same dPP/dt separately to WASP and TESS data. Ordinate ranges one pulsation period. The two insets show zoomed-in images of TESS data, while the abscissa ticks are separated by 5 d. Bottom: residuals from the fits shown in the upper panel are phased with the orbital period of 23.08433 d. Red and green dots correspond to TESS and WASP data, respectively. Solid black line is a fit of Eq. (3) to the residual O−C data. Parameters of the fit are given in Table 2. Phase 0.0 corresponds to T0. |
where E is the number of pulsation periods elapsed from the initial epoch. The values of 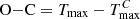 , where Tmax and
, where Tmax and 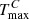 stand for the observed and calculated times of maximum light, respectively. They are given in Table A.1. The O−C diagram shows periodic variation with the period of about 23 d superimposed on changes covering a much longer timescale. As expected, the changes covering a long timescale reflect, to some extent, the decrease of pulsation period suggested in Sect. 3.2. However, it is also obvious that a constant rate of period change, represented by the dashed-line parabola, does not fit the observations well. The real changes in the pulsation period are more complicated. Unfortunately, they cannot be traced by the available photometry because of the gaps in the data. Since we are interested in the periodic variation in the O−C diagram, we subtracted the long term seen in Fig. 4, upper panel, separately for the WASP and the TESS data, by fitting ‘locally’ and subtracting parabolae with a quadratic term corresponding to Ṗ = −7.11 × 10−11 (Sect. 3.2). These parabolae are shown with the dotted lines in Fig. 4.
stand for the observed and calculated times of maximum light, respectively. They are given in Table A.1. The O−C diagram shows periodic variation with the period of about 23 d superimposed on changes covering a much longer timescale. As expected, the changes covering a long timescale reflect, to some extent, the decrease of pulsation period suggested in Sect. 3.2. However, it is also obvious that a constant rate of period change, represented by the dashed-line parabola, does not fit the observations well. The real changes in the pulsation period are more complicated. Unfortunately, they cannot be traced by the available photometry because of the gaps in the data. Since we are interested in the periodic variation in the O−C diagram, we subtracted the long term seen in Fig. 4, upper panel, separately for the WASP and the TESS data, by fitting ‘locally’ and subtracting parabolae with a quadratic term corresponding to Ṗ = −7.11 × 10−11 (Sect. 3.2). These parabolae are shown with the dotted lines in Fig. 4.
In order to derive parameters of the orbit of the BLAP, the residual O−C values, (O−C)res, were fitted with the following equation:
The values of (O−C)res are also given in Table A.1. In Eq. (3), the light-travel time τ is defined by Eq. (3) of Irwin (1952). Derived parameters are listed in Table 2. The residual O−C values phased with the derived orbital period are shown in the bottom panel of Fig. 4. The orbit is marginally eccentric. Although the WASP data resulted in much less precise times of maximum light than the TESS data, they are important for constraining Porb, because they increase the span of data to about 240 orbital cycles. High precision of K2 and mass function f(M1)5 is the result of the precise determination of the amplitude of LTTE, a consequence of the high precision of the times of maximum light derived from the TESS data. The standard deviation of residuals from the fit shown in Fig. 4 amounts to 16.0 s for the WASP data and only 0.7 s for the TESS data.
Parameters of the orbit of BLAP derived from fitting the O−C diagram.
3.4. Low frequencies
In addition to the variability caused by the pulsations of the BLAP, a weak signal at frequencies close to 2.2 d−1 was detected in the TESS data. The signal can be seen even in Fig. 1. We have combined data from both TESS sectors subtracting first the BLAP pulsations. The frequency spectrum of these data is shown in Fig. 5. The strongest signal can be well represented by four periodic terms with frequencies of 2.3266, 2.2431, 2.2104, and 2.2876 d−1 and semi-amplitudes of 0.76, 0.41, 0.15, and 0.11 ppt, respectively. Due to the large gap between both sectors, the frequencies are subject to strong aliasing. We do not know which component is responsible for this variability. Given the primary is a late B-type star, a suitable explanation is that this component is a slowly pulsating B-type (SPB) star, but in general, we cannot exclude the possibility that the low-frequency variability originates in the BLAP.
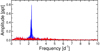 |
Fig. 5. Frequency spectrum of the combined sectors of the TESS data after subtracting BLAP pulsations (blue), and after pre-whitening four periodic terms that were detected (red). More details are given in the text. |
4. SED fitting and the parameters of the components
In order to verify if multi-band photometry of HD 133729 is consistent with a system consisting of a late B-type star and a BLAP, we performed spectral energy distribution (SED) analysis using the VOSA6 online tool (Bayo et al. 2008). In the optical part of the spectrum, we used TychoBT and VT (Høg et al. 2000) and GaiaG, Gbp, and Grp (Gaia Collaboration 2018) photometry. In the infrared (IR) domain, we chose photometry in 2MASS JHKs (Cutri et al. 2003), and WISE W1, W2, and W3 (Cutri et al. 2012) bands. Assuming that contribution of BLAP in the optical and IR domains is small compared to the contribution of the B-type primary, we obtained a best-fitting model with effective temperature Teff, 1 = 11 500 K and surface gravity log(g1/(cm s−2)) = 4.0 dex. We assumed total absorption in Johnson V band AV = 0.386 mag. This value was taken from the Gaia-2MASS three-dimensional map of absorption presented by Lallement et al. (2019) using their online tool7. During standard least-squares fitting procedure, we used Castelli-Kurucz ODFNEW/NOVER synthetic spectra (Castelli et al. 1997) and assumed solar metallicity. The fit is shown in Fig. 6a, and the residuals are shown in Fig. 6b. The plots also show another source of photometric data, that is, ultraviolet (UV) fluxes collected by Thor-Delta 1A (TD-1) satellite in four bands, 156.5, 196.5, 236.5, and 274.0 nm (Thompson et al. 1978, 1995). They were not used in the fit because contribution of the BLAP in the UV is significant. The star is barely detected in the three longest wavelength TD-1 bands (the errors are larger than the measured fluxes), but in the 156.5-nm band the flux amounts to (5.25 ± 0.49) × 10−14 W m−2 (nm)−1. A comparison of the ratios of TD-1 fluxes to those of the fitted SED model shows (Fig. 6b) that the observed flux in the 156.5-nm band is roughly three times higher than expected from a late B-type star. This can be explained only by the presence of a hot secondary, the BLAP. We therefore took a spectrum with parameters representing known BLAPs, Teff, 2 = 29 000 K and log(g2/(cm s−2)) = 4.5 dex, and scaled it to obtain a best fit of the combined spectrum to the TD-1 observations. The result is shown in Fig. 6a with a black line. It can be seen that by adding a hot companion to the fit, we obtained a satisfactory agreement in the whole range of the available bands.
 |
Fig. 6. Results of fitting SED to the photometric data of HD 133729. (a) Colour-coded points with error bars stand for observed fluxes de-reddened by the VOSA tool. The spectrum fitted to the optical and IR data is shown with solid red curve. The shaded area marks the effect of ±1000 K uncertainty in Teff, 1. The adopted spectrum of the BLAP scaled to account for the UV data is marked with blue line. (b) Residuals from fitting SED to the visual and IR photometry of HD 133729 in the terms of flux ratio. |
The fitted Teff, 1 corresponds to spectral type B8 or even B9, which is slightly later than B6/7 V derived by Houk (1982). Since the secondary’s contribution to the total flux in the blue region of the spectrum exceeds 20%, we speculate that its lines could have affected this classification.
The SEDs of both components allowed us to estimate a relative contribution of the components in different bands. In particular, the BLAP contribution to the total flux of the system amounts to about 19% in Johnson V and 16% in the TESS band. The latter value allows us to estimate the intrinsic amplitude of the BLAP. The observed peak-to-peak amplitude of the BLAP in the TESS band amounts to 31.6 ppt, which translates to the intrinsic amplitude of 0.21 mag, in full agreement with the I-filter amplitudes of BLAPs derived by Pietrukowicz et al. (2017).
In order to locate the components of the system in the H-R diagram, we used the results of the SED fitting. The measured Gaia Early Data Release 3 parallax of HD 133729 amounts to 2.136 ± 0.029 mas, which translates to the distance of D = 463 ± 7 pc (Bailer-Jones et al. 2021). We calculated V magnitude of the system translating TychoBT and VT magnitudes by means of Eq. (1) of Oja & Evans (1998). It is equal to 9.174 mag. In consequence, we obtained V1 ≈ 9.37 mag and V2 ≈ 11.0 mag by adopting the relative contributions of the components estimated from the SED fitting. This resulted in the absolute magnitude of the primary equal to MV, 1 = +0.66 mag. Adopting bolometric correction (BC)V, 1 = −0.596 mag, calculated from the equation provided by Pedersen et al. (2020) for Johnson V band, assuming Teff, 1 = 11 500 K and Mbol, ⊙ = 4.74 mag, we obtained the bolometric magnitude of the primary Mbol, 1 = +0.06 mag and its luminosity log(L1/L⊙)=1.87 ± 0.12. In these calculations, an uncertainty of ±1000 K for Teff, 1 was adopted. As can be seen in Fig. 6a, this value encompasses all photometric data and small differences in the visual and IR domains between the spectrum of the primary and the combined spectrum. Uncertainty of log(L1/L⊙) depends on the uncertainties of four parameters: distance, V1, AV, and (BC)V, 1. Adopting σ(AV)=0.1 mag, σ(V1)=0.15 mag, and σ((BC)V, 1)=0.25 mag, we obtained the uncertainty of log(L1/L⊙) equal to 0.12 dex. A comparison of the location of the primary with the evolutionary models (Fig. 7) places the star in the main-sequence phase of evolution, as expected from its luminosity class. The inferred mass of the primary amounts to (2.85 ± 0.25) M⊙.
 |
Fig. 7. Positions of HD 133729 components in the H-R diagram. The B-type primary is marked with the red dot, and the BLAP is marked with the blue dot. The light blue rectangle marks the position of BLAPs as defined by Pietrukowicz et al. (2017). Evolutionary tracks (labelled with mass in M⊙) and zero-age main-sequence line were taken from non-rotating models of Ekström et al. (2012). |
The SED fitting allowed us to estimate relative luminosities of the components by integrating the SEDs of both components. A relative luminosity, L2/L1 ≈ 1.9, combined with the luminosity of the primary derived above gives log(L2/L⊙)=2.15 ± 0.15. Along with the secondary’s effective temperature adopted for SED fitting (Teff, 2 = 29 000 K), this allows us to plot the position of the secondary in the H-R diagram. As can be seen in Fig. 7, it fits within the errors the ‘instability strip’ of BLAPs, as defined by Pietrukowicz et al. (2017). The location and size of the strip is still rather uncertain. It may extend towards lower luminosities, especially if BLAPs and high-gravity BLAPs form a homogeneous group. The location of the secondary in the H-R diagram is another argument in favour of recognising the star as a BLAP.
5. Discussion and conclusions
Blue large-amplitude pulsators are very rare objects. Only 14 were discovered during the extensive survey of the OGLE data by Pietrukowicz et al. (2017) and Pietrukowicz et al. (2018). Recently, McWhirter & Lam (2022) announced the discovery of a sample of 16 (candidate) BLAPs and six high-gravity BLAP candidates using the Zwicky Transient Facility (Bellm et al. 2019) DR3 time-series photometry. Adding four high-gravity BLAPs found by Kupfer et al. (2019) and one candidate with the period of 18.9 min found recently by Lin et al. (2022), the secondary of HD 133729 is a star belonging to the class that presently counts fewer than 30 members. This star is unusual for several reasons. First, it is the only known BLAP that resides in a binary. The binary is wide enough to make use of the light-travel-time effect for the determination of precise spectroscopic elements of its orbit (Sect. 3.3). Next, it is the nearest and the brightest star of this type. With an estimated V magnitude of about 11.0 (Sect. 4), it is almost 5 mag brighter than the next brightest BLAP, OGLE-BLAP-009 (V ≈ 15.7 mag). Finally, the unusual short-lived feature in the descending branch of the light curve (Fig. 3) is exceptional among radially pulsating stars. It was only detected thanks to a very good time resolution in the Sector 38 20-s cadence TESS data.
The discovery of a BLAP in a bright binary system prompts a detailed follow-up spectroscopic study, which we are going to carry out. First of all, this should provide the mass ratio of the components. Given the relatively tight constraint on the primary’s mass (Sect. 4), with the relative error of the order of 10%, this should allow us to constrain M2 with a comparable precision. For this purpose, we need to measure K1, the half-range of the primary’s radial-velocity variation, with relatively high precision. In this context, the domination of the primary in the optical part of the spectrum of the system might be a favourable circumstance. We already know K2 with a 0.1% precision from the O−C analysis (Sect. 3.3). Such a precision of K2 would be difficult to achieve from the analysis of optical spectra, as the secondary contributes only 15–20% to the optical spectrum and its spectral lines would be affected by the presence of the short-period large-amplitude pulsations. A precise value of the mass ratio, allowing us to also constrain the mass of the secondary, should allow us to conclude on the evolutionary status of this BLAP and to at least choose between scenarios leading to a shell-burning star with a mass of 0.3–0.4 M⊙ and those that predict a core-helium-burning star with a higher mass of 0.5–1.0 M⊙.
If a coevality of both components is assumed and no mass transfer onto the primary took place, the progenitor of the BLAP in the HD 133729 system must have started its evolution with an initial mass larger than ∼3 M⊙. This would exclude evolutionary scenarios that lead to low-mass BLAPs, because they start with ∼1 M⊙ progenitors. A detailed discussion of the possible evolutionary scenarios of the BLAP in HD 133729 system is, however, beyond the scope of this paper and is postponed to the spectroscopic study.
Acknowledgments
This work used the SIMBAD and Vizier services operated by Centre des Données astronomiques de Strasbourg (France), and bibliographic references from the Astrophysics Data System maintained by SAO/NASA. This paper makes use of data from the DR1 of the WASP data (Butters et al. 2010) as provided by the WASP consortium, and the computing and storage facilities at the CERIT Scientific Cloud, reg. no. CZ.1.05/3.2.00/08.0144 which is operated by Masaryk University, Czech Republic. This publication makes use of VOSA, developed under the Spanish Virtual Observatory project supported from the Spanish MICINN through grant AyA2008-02156. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC) (https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. A.P., K.K., and P.K.S. were supported by the National Science Centre (NCN) grants no. 2016/21/B/ST9/01126, 2019/33/N/ST9/01818, and 2019/35/N/ST9/03805, respectively.
References
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Barceló Forteza, S., Moya, A., Barrado, D., et al. 2020, A&A, 638, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002 [Google Scholar]
- Butters, O. W., West, R. G., Anderson, D. R., et al. 2010, A&A, 520, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Byrne, C. M., & Jeffery, C. S. 2020, MNRAS, 492, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Byrne, C. M., Stanway, E. R., & Eldridge, J. J. 2021, MNRAS, 507, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
- Córsico, A. H., Romero, A. D., Althaus, L. G., Pelisoli, I., & Kepler, S. O. 2018, ArXiv e-prints [arXiv:1809.07451] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2012, VizieR Online Data Catalog: II/311 [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
- ESA 1997, The Hipparcos and Tycho catalogues. Astrometric and photometric star catalogues derived from the ESA Hipparcos Space Astrometry Mission (Noordwijk, Netherlands: ESA Publications Division), ESA SP Ser., 1200 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
- Holdsworth, D. L., Smalley, B., Gillon, M., et al. 2014, MNRAS, 439, 2078 [NASA ADS] [CrossRef] [Google Scholar]
- Houk, N. 1982, Michigan Catalogue of Two-dimensional Spectral Types for the HD stars. Volume 3. Declinations -40 to -26 (University of Michigan) [Google Scholar]
- Irwin, J. B. 1952, ApJ, 116, 211 [Google Scholar]
- Kupfer, T., Bauer, E. B., Burdge, K. B., et al. 2019, ApJ, 878, L35 [Google Scholar]
- Lallement, R., Babusiaux, C., Vergely, J. L., et al. 2019, A&A, 625, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, J., Wang, X., Mo, J., et al. 2022, MNRAS, 509, 2362 [NASA ADS] [Google Scholar]
- McWhirter, P. R., & Lam, M. C. 2022, MNRAS, 511, 4971 [NASA ADS] [CrossRef] [Google Scholar]
- McWhirter, P. R., Lam, M. C., & Steele, I. A. 2020, MNRAS, 496, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X.-C., Han, Z.-W., Podsiadlowski, P., & Li, J. 2020, ApJ, 903, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Oelkers, R. J., Rodriguez, J. E., Stassun, K. G., et al. 2018, AJ, 155, 39 [Google Scholar]
- Oja, T., & Evans, D. W. 1998, A&A, 333, 673 [NASA ADS] [Google Scholar]
- Pedersen, M. G., Escorza, A., Pápics, P. I., & Aerts, C. 2020, MNRAS, 495, 2738 [Google Scholar]
- Pietrukowicz, P. 2018, in The RR Lyrae 2017 Conference. Revival of the Classical Pulsators: from Galactic Structure to Stellar Interior Diagnostics, eds. R. Smolec, K. Kinemuchi, & R. I. Anderson, 6, 258 [Google Scholar]
- Pietrukowicz, P., Dziembowski, W. A., Mróz, P., et al. 2013, Acta Astron., 63, 379 [Google Scholar]
- Pietrukowicz, P., Latour, M., Angeloni, R., et al. 2015, Acta Astron., 65, 63 [Google Scholar]
- Pietrukowicz, P., Dziembowski, W. A., Latour, M., et al. 2017, Nat. Astron., 1, 0166 [Google Scholar]
- Pojmański, G. 1997, Acta Astron., 47, 467 [NASA ADS] [Google Scholar]
- Pojmański, G. 2000, Acta Astron., 50, 177 [Google Scholar]
- Pojmański, G. 2009, in The Variable Universe: A Celebration of Bohdan Paczynski, ed. K. Z. Stanek, ASP Conf. Ser., 403, 52 [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, A. D., Córsico, A. H., Althaus, L. G., Pelisoli, I., & Kepler, S. O. 2018, MNRAS, 477, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, G. I., Nandy, K., Jamar, C., et al. 1978, Catalogue of stellar ultraviolet fluxes: a compilation of absolute stellar fluxes measured by the Sky Survey Telescope (S2/68) aboard the ESRO satellite TD-1 (UK: The Science Research Council) [Google Scholar]
- Thompson, G.I., Nandy, K., Jamar, C., et al. 1995, VizieR Online Data Catalog: II/59B [Google Scholar]
- Wu, T., & Li, Y. 2018, MNRAS, 478, 3871 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Table with values of Tmax
Times of maximum light obtained using the WASP data and the TESS 2-min cadence data. All times are given as BJDTDB− 2 450 000.0. The values of E, (O−C) and (O−C)res are explained in Sect. 3.3.
All Tables
Times of maximum light obtained using the WASP data and the TESS 2-min cadence data. All times are given as BJDTDB− 2 450 000.0. The values of E, (O−C) and (O−C)res are explained in Sect. 3.3.
All Figures
 |
Fig. 1. Light curve and frequency spectrum of the TESS data of HD 133729. Top: half-day 2-min cadence TESS Sector 38 light curve of HD 133729. Fn stands for the relative flux Fi/⟨F⟩−1, where Fi is the TESS flux for the ith data point and ⟨F⟩ is average flux from all TESS observations in Sector 38. Bottom: frequency spectrum of the TESS Sector 38 data. In order to illustrate the occurrence of the ±0.043 d−1 orbital sidelobes, the inset shows a 2 d−1-wide frequency spectrum of the residuals in the vicinity of fP = 44.487 d−1, after subtracting fP and its harmonics. |
| In the text | |
 |
Fig. 2. Pulsation frequencies of BLAP in HD 133729 system derived from the HIPPARCOS, ASAS, WASP, and TESS data. Dashed line corresponds to the derived constant rate of frequency change, dfP/dt = (1.41 ± 0.07) × 10−7 d−2. |
| In the text | |
 |
Fig. 3. Light curves of HD 133729 phased with pulsation period. (a)–(c): HIPPARCOS (a), ASAS (b), and WASP (c) light curves. (d) Phase-averaged TESS light curves in Sector 11 (green dots), Sector 38, 2-min cadence (red dots), and Sector 38, 20-s cadence (blue dots). For clarity, 5 ppt offsets were applied between the light curves. The 2-min cadence data are averaged in 0.005 phase intervals, and the 20-s cadence data are averaged in 0.002 phase intervals. Phase 0.0 corresponds to the time of maximum light. |
| In the text | |
 |
Fig. 4. O−C diagrams for the pulsation period of HD 133729. Top: O−C diagram for WASP (green dots) and TESS (red dots) times of maximum light obtained using Eq. (2) as a reference. Dashed line shows fit with the assumed period change dPP/dt = −7.11 × 10−11 derived in Sect. 3.2. Dotted lines show fits of parabolae with the same dPP/dt separately to WASP and TESS data. Ordinate ranges one pulsation period. The two insets show zoomed-in images of TESS data, while the abscissa ticks are separated by 5 d. Bottom: residuals from the fits shown in the upper panel are phased with the orbital period of 23.08433 d. Red and green dots correspond to TESS and WASP data, respectively. Solid black line is a fit of Eq. (3) to the residual O−C data. Parameters of the fit are given in Table 2. Phase 0.0 corresponds to T0. |
| In the text | |
 |
Fig. 5. Frequency spectrum of the combined sectors of the TESS data after subtracting BLAP pulsations (blue), and after pre-whitening four periodic terms that were detected (red). More details are given in the text. |
| In the text | |
 |
Fig. 6. Results of fitting SED to the photometric data of HD 133729. (a) Colour-coded points with error bars stand for observed fluxes de-reddened by the VOSA tool. The spectrum fitted to the optical and IR data is shown with solid red curve. The shaded area marks the effect of ±1000 K uncertainty in Teff, 1. The adopted spectrum of the BLAP scaled to account for the UV data is marked with blue line. (b) Residuals from fitting SED to the visual and IR photometry of HD 133729 in the terms of flux ratio. |
| In the text | |
 |
Fig. 7. Positions of HD 133729 components in the H-R diagram. The B-type primary is marked with the red dot, and the BLAP is marked with the blue dot. The light blue rectangle marks the position of BLAPs as defined by Pietrukowicz et al. (2017). Evolutionary tracks (labelled with mass in M⊙) and zero-age main-sequence line were taken from non-rotating models of Ekström et al. (2012). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} m(t)&= m_0 + \sum \limits _{n=1}^{N}\{A_n\sin (2\pi nf_{\rm P}t+\phi _n)\nonumber \\&\,\,\, + A_{n-}\sin [2\pi (nf_{\rm P}-f_{\rm orb})t + \phi _{n-}]\nonumber \\&\,\,\, + A_{n+}\sin [2\pi (nf_{\rm P}+f_{\rm orb})t + \phi _{n+}]\}. \end{aligned} $$](/articles/aa/full_html/2022/07/aa43293-22/aa43293-22-eq1.gif)