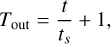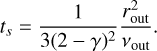| Issue |
A&A
Volume 661, May 2022
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202142391 | |
| Published online | 17 May 2022 | |
A low accretion efficiency of planetesimals formed at planetary gap edges
1
Lund Observatory, Department of Astronomy and Theoretical Physics, Lund University,
Box 43,
221 00
Lund,
Sweden
e-mail: linn@astro.lu.se
2
Center for Star and Planet Formation, GLOBE Institute, University of Copenhagen,
Øster Voldgade 5–7,
1350
Copenhagen,
Denmark
3
Institute for Computational Science, University of Zurich,
Winterthurerstr. 190,
8057
Zurich,
Switzerland
Received:
8
October
2021
Accepted:
24
February
2022
Observations and models of giant planets indicate that such objects are enriched in heavy elements compared to solar abundances. The prevailing view is that giant planets accreted multiple Earth masses of heavy elements after the end of core formation. Such late solid enrichment is commonly explained by the accretion of planetesimals. Planetesimals are expected to form at the edges of planetary gaps, and here we address the question of whether these planetesimals can be accreted in large enough amounts to explain the inferred high heavy element contents of giant planets. We performed a series of N-body simulations of the dynamics of planetesimals and planets during the planetary growth phase, taking gas drag into account as well as the enhanced collision cross section caused by the extended envelopes. We considered the growth of Jupiter and Saturn via gas accretion after reaching the pebble isolation mass and we included their migration in an evolving disk. We find that the accretion efficiency of planetesimals formed at planetary gap edges is very low: less than 10% of the formed planetesimals are accreted even in the most favorable cases, which in our model corresponds to a few Earth masses. When planetesimals are assumed to form beyond the feeding zone of the planets, extending to a few Hill radii from a planet, accretion becomes negligible. Furthermore, we find that the accretion efficiency increases when the planetary migration distance is increased and that the efficiency does not increase when the planetesimal radii are decreased. Based on these results, we conclude that it is difficult to explain the large heavy element content of giant planets with planetesimal accretion during the gas accretion phase. Alternative processes most likely are required, such as accretion of vapor deposited by drifting pebbles.
Key words: planets and satellites: formation / protoplanetary disks / planet-disk interactions
© ESO 2022
1 Introduction
Matching interior structure models of Jupiter and Saturn to their measured gravity fields requires that the planets have a minimum heavy-element content of ~20 M⊕, with upper bounds that are much higher and depend heavily on what model assumptions are used (e.g., Helled & Guillot 2013; Wahl et al. 2017; Helled 2018). Similarly, results from structure models of transiting planets show that extrasolar giants typically are enhanced in heavy elements, with estimated heavy element masses ranging from ~10–100 M⊕ (Guillot et al. 2006; Miller & Fortney 2011; Thorngren et al. 2016). Such large masses suggest that there are significant amounts of heavy elements in the H/He envelopes, indicating that giant planets typically have enriched atmospheres. Provided that envelope enrichment does not occur via erosion of the initial core alone (Stevenson 1982), this implies that multiple Earth masses of heavy elements must have been accreted after the end of core formation.
Late heavy-element enrichment is often explained by the accretion of planetesimals (e.g., Alibert et al. 2018). In order to match the estimated heavy-element contents of giant planets, a massive wide-stretched disk of planetesimals typically has to be assumed for studies of this process (e.g., Venturini & Helled 2020; Shibata et al. 2020). However, simulations of planetesimal formation via the streaming instability (SI), which is one of the favored mechanisms for forming planetesimals (Nesvorný et al. 2019), suggests that planetesimals form in regions with locally enhanced solid-to-gas ratios (Youdin & Goodman 2005; Johansen et al. 2009; Lyra et al. 2009; Bai & Stone 2010; Carrera et al. 2015; Yang et al. 2017). One such naturally occurring region is in the pressure bump generated at the edges of planetary gaps, where inward drifting pebbles are trapped (Stammler et al. 2019; Eriksson et al. 2020; Carrera et al. 2021).
In Eriksson et al. (2021), we studied the dynamical evolution of planetesimals formed at planetary gap edges, keeping the planet masses and locations fixed. We found that planetesimals are strongly scattered and that they leave their birthplace shortly after formation. In this study, we determine the amount of planetesimals that eventually collide with a planet, considering both planet migration and growth, and we investigate whether the delivered mass is high enough to explain the large heavy element masses in giant planets. We therefore performed a suite of N-body simulations, including the effect of gas drag on the planetesimals and the enhanced collision cross section caused by the extended planetary envelope. We focus on the formation of the Solar System’s two gas-giant planets, Jupiter and Saturn, as both are massive enough to open up deep gaps in the disk, and thus they likely had planetesimals forming at their gap edges. We consider two different formation pathways for the planets, where one leads to a large-scale planetary migration, while the second one leads to a migration over a few au only. We continuously formed planetesimals at the gap edges from the moment gas accretion initiated, that is to say when the pebble isolation mass was reached (Miso, Lambrechts et al. 2014; Bitsch et al. 2018), until the time of disk dissipation. By further varying the planetesimal size and the formation location of the planetesimals relative to the planet, we explored the sensitivity of the accretion efficiency to these parameters.
In Sect. 2, we present our models for disk evolution and planet formation, as well as the setup of our simulations. We present the results of our simulations in Sect. 3, where we show that the accretion efficiency of planetesimals formed at planetary gap edges is low, leading to the accretion of only a few Earth masses of planetesimals in the most favorable cases. In Sect. 4 we compare our results to the estimated heavy-element content of giant planets, and we reach the conclusion that alternative processes most likely are required in order to explain the high heavy element masses inferred from observations. The key findings of the paper are summarized in Sect. 5. Further information about our model and some additional figures can be found in Appendices A–C.
2 Model
In this section we describe the ingredients and parameters of our simulations. We start by introducing our model for the structure and evolution of the protoplanetary disk. Planetesimals that move through the disk experience a drag force, which we account for following the method outlined in Eriksson et al. (2021). Our model for planetary evolution contains planet migration, gas accretion, and gap opening. Collisions between planets and planetesimals are detected using a direct search method, which requires the capture radius of the planet being known. We used the approximation from Valletta & Helled (2021) for planets that have attained a gaseous envelope (planets with masses above the pebble isolation mass), and assumed that the capture radius is equal to the core radius for lower planetary masses. Finally we describe the numerical setup and initialization of our N-body simulations.
2.1 Disk model
The evolution of the unperturbed surface density Σunp was modeled using a standard alpha-disk model, which is dependent on the disk accretion rate 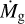 and the scaling radius rout (Lynden-Bell & Pringle 1974). The kinematic viscosity was approximated as
and the scaling radius rout (Lynden-Bell & Pringle 1974). The kinematic viscosity was approximated as
 (1)
(1)
where α is the viscosity parameter, Ω is the Keplerian angular velocity, and H is the scale height of the gaseous disk (Shakura & Sunyaev 1973). We considered the scale height to be H = cs/Ω, where cs is the sound speed. The disk’s midplane temperature was approximated using a fixed power-law structure for a passively irradiated disk (Chiang & Goldreich 1997). The disk accretion rate is given by the standard viscous accretion rate minus the rate at which gas was removed by photoevaporation 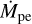 , which we considered to be a constant in time (see Appendix A for details on our disk model).
, which we considered to be a constant in time (see Appendix A for details on our disk model).
Massive planets perturb their birth disks by pushing material away from the vicinity of their orbits, leading to gap opening. We used a simple approach with Gaussian gap profiles to model these gaps. The height of the Gaussian was determined by the depth of the gap (see Sect. 2.4), and the width was considered to be one gas scale height at the planet location. Finally, in order to obtain the gas density at some height, z, over the midplane, we assumed vertical hydrostatic equilibrium for the gas in the disk.
2.2 Migration
For the migration of planets we followed Kanagawa et al. (2018), who found that embedded planets experience a torque which is equal to the classical type-I torque multiplied by the relative gap height, resulting in the following migration rate:
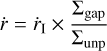 (2)
(2)
(see Eqs. (3)–(4) in Johansen et al. 2019 for the classical type-I migration rate). This results in little or no migration before the planet reaches a few Earth masses, fast migration during the last stages of pebble accretion and the first stages of gas accretion, and slow migration during runaway gas accretion when the gap has become deep. For the implementation of migration into the N-body code we followed Cresswell & Nelson (2008), who provide the timescales for radial migration as well as the associated eccentricity and inclination damping. The corresponding accelerations were then directly applied to the planets at fixed time intervals.
2.3 Gas accretion
Protoplanets can accrete gaseous envelopes already during the early phases of core formation. During this stage the heating of the envelope from the flux of pebbles prevents it from contracting onto the planet. At a later stage, when the protoplanet reaches the pebble isolation mass and the flux of pebbles stops, the envelope contracts. This is the first stage of significant gas accretion; however, even before this stage, some small amounts of highly polluted gas can become bound to the protoplanet inside its Hill sphere (Bitsch et al. 2015). We followed the assumption of Bitsch et al. (2015) that 10% of the material accreted by the planet prior to the pebble isolation mass is in gas, so that the final mass of the core is 0.9 × Miso. We note that this is a simplification, and in reality the gas fraction is expected to increase as the core grows more massive (Valletta & Helled 2020).
The gas accretion rate of a protoplanet during the contraction phase (also known as the attached phase) is highly uncertain and there are several prescriptions to describe this stage, many of which are vastly different. In this work we use the following two different prescriptions: scheme 1 results in a short contraction phase, while scheme 2 leads to a relatively long contraction timescale. In scheme 1 we followed the gas accretion model outlined in Johansen et al. (2019) (Eqs. (38)–(40)). The envelope’s contraction occurs on the Kelvin-Helmholtz timescale, which depends on the planetary mass Mp and the envelope’s opacity κ (Ikoma et al. 2000). For large planetary masses, this accretion rate becomes higher than what the disk can supply. At this point the planet enters the runaway gas accretion phase (also known as the detached phase), and the growth becomes limited by the rate at which gas can enter the Hill sphere (Tanigawa & Tanaka 2016). As an additional constraint, the planet cannot accrete at a rate which is higher than the global disk accretion rate 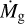 . Furthermore, Lubow & D’Angelo (2006) found that even high mass planets cannot block all gas from passing the gaps, and that the protoplanets do not accrete at a rate higher than 75–90% of the disk’s accretion rate. Therefore, we limited the maximum gas accretion rate to 80% of the disk’s accretion rate. The gas accretion rate onto the planet in scheme 1 was then considered to be the minimum of the three aforementioned rates.
. Furthermore, Lubow & D’Angelo (2006) found that even high mass planets cannot block all gas from passing the gaps, and that the protoplanets do not accrete at a rate higher than 75–90% of the disk’s accretion rate. Therefore, we limited the maximum gas accretion rate to 80% of the disk’s accretion rate. The gas accretion rate onto the planet in scheme 1 was then considered to be the minimum of the three aforementioned rates.
In scheme 2 we roughly followed the gas accretion model which was used in Bitsch et al. (2015). During the contraction phase, which is defined as Menv < Mcore here, the envelope contracts on a long timescale while accreting some gas. The accretion rate during this phase depends on the envelope opacity, the core density ρcore, the mass of the core and envelope, and the disk temperature (see Eq. (17) in Bitsch et al. 2015, originally derived in Piso & Youdin 2014). Runaway gas accretion initiates when Menv > Mcore, and for this phase we used the gas accretion rate from Tanigawa & Tanaka (2016), which is the same as in scheme 1. Furthermore, we also limited gas accretion to 80% of the disk accretion rate throughout the entire process. The dependence of all of the aforementioned gas accretion rates on the planetary mass is plotted in Fig. B.1.
2.4 Gap depth
For the relative depth of the planetary gaps, we followed Johansen et al. (2019), who show that the gap depth scales with the pebble isolation mass as follows:
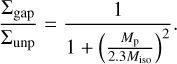 (3)
(3)
We used the fit from Bitsch et al. (2018) to calculate the pebble isolation mass, which depends on the turbulent viscosity αt and the unperturbed radial pressure gradient of the disk ∂ ln P/∂ ln r. We used an unperturbed surface density gradient of −15/14, which results in a radial pressure gradient of −2.7857.
2.5 Numerical setup and initialization
Table 1 lists the parameter values used in our simulations. The simulations were performed with the N-body code REBOUND and executed using the hybrid symplectic integrator MERCURIUS (Rein & Liu 2012; Rein et al. 2019). The WHFAST time step was set to be one twentieth of Jupiter’s current dynamical timescale, and we only performed disk evolution, migration, and gas accretion on this time step. The planets and the central star were added as active particles, and the planetesimals were added as test particles. We used a central star of solar mass and solar luminosity. Collisions were detected using a direct search algorithm and resulted in perfect merging. Particles that left the simulation domain, which is centered on the sun and stretches 100 au in the x and y direction and 20 au in the z direction, were recorded and removed from the simulation.
The protoplanetary disk was modeled using a linear grid with 1000 grid cells, stretching from 0.1 to 100 au. We used standard values of 75 au for the scaling radius and 10−2 for the viscosity parameter. The initial disk accretion rate was set to 10−7 M⊙ yr−1, and we chose the photoevaporation rate such that the disk obtained a lifetime of 3 Myr. We continued the orbital integration for an additional 7 Myr after disk dispersal.
We modeled Jupiter’s formation starting at the pebble isolation mass, and for Saturn we also included a prescription for the growth of the core. The reason is that in our model, Jupiter reaches the pebble isolation mass and begins to form planetesimals at the gap edge earlier than Saturn, and while we assume that there is no planetesimal formation at Saturn’s gap edge during core formation, the formation of its core could still dynamically effect the planetesimals formed at Jupiter’s gap edge. The initial semimajor axis and formation time of the planets are determined in Sect. 3.1. The initial orbital eccentricity and inclination were set to 10−3, and we used a constant opacity of 5 × 10−2 m2 kg−1 for the gaseous envelope.
Each simulation contained a total of 10 000 planetesimals, which were injected at the gap edges ten at a time from the beginning of the simulation until disk dissipation. Given the formation times provided in Table 2, this means that we injected ten planetesimals into the simulation roughly every 1000 yr. The planetesimal radii were varied in between the simulations and set to either 300 m, 10 km, or 100 km (Bottke et al. 2005; Morbidelli et al. 2009; Johansen et al. 2015). The exact formation location of planetesimals at gap edges is unknown (Carrera et al. 2021). Here we tried two different formation locations: in the first setup, we initiated the planetesimals uniformly between 2 and 3 Hill radii from the planets (thus interior of the single planet feeding zone at 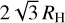 ); and in the second setup, we did so between 4 and 5 Hill radii from the planets (thus exterior of the feeding zone). The feeding zone is defined as the region where the Jacobi energy of the planetesimals is positive (Shiraishi & Ida 2008). Finally, in order to provide better statistics, we performed three simulations per parameter set.
); and in the second setup, we did so between 4 and 5 Hill radii from the planets (thus exterior of the feeding zone). The feeding zone is defined as the region where the Jacobi energy of the planetesimals is positive (Shiraishi & Ida 2008). Finally, in order to provide better statistics, we performed three simulations per parameter set.
Parameters used throughout the simulations.
3 Result
3.1 Planet growth tracks
Given our models for migration and gas accretion (introduced in Sects. 2.2 and 2.3), we searched for growth tracks that resulted in Jupiter and Saturn having their current mass and semimajor axis at the time of disk dissipation. The resulting time and semimajor axis at which the planets began to migrate and accrete gas, as well as the corresponding pebble isolation mass, can be found in Table 2. According to these results, Saturn reaches the pebble isolation mass much later than Jupiter. We began our simulations at the time when Jupiter reached the pebble isolation mass, and although we assumed that planetesimals do not form at Saturn’s gap edge during core formation, the formation of Saturn’s core could still dynamically affect the planetesimals that formed at Jupiter’s gap edge. Therefore we also included the growth and migration of Saturn’s core in our simulations.
Rather than calculating the actual pebble accretion rate at each iteration, we used a simple approach for Saturn’s core growth. We initiated the core at 0.1 M⊕ at the beginning of the simulation, and grew it up to Miso following a reasonable growth rate, which we chose to be Mcore ∝ t2. This growth rate is slightly shallower than the growth rate suggested by pebble accretion (Mcore ∝ t3 in the 3D regime, see e.g., Morbidelli et al. 2015); however, the effect on the simulation’s outcome should be negligible (as is shown in Sect. 3, accretion onto Jupiter happens before the planetesimals have any chance to dynamically interact with Saturn’s core). We note that during this phase, 10% of the accretion is assumed to be in the form of gas, so that the actual core mass is 90% of the above mass (see Sect. 2.3). Finally we also considered the migration of the core, which was performed using our normal migration prescription. The semimajor axis where the core needs to be initiated in order for Saturn to reach the pebble isolation mass at the right location is listed in the last column of Table 2.
The resulting growth tracks are presented in the left panel of Fig. 1, where 1 and 2 denote gas accretion scheme 1 and gas accretion scheme 2, respectively. In scheme 1 the envelope’s contraction occurs on a relatively short timescale, leading to quick gap opening and little migration. In scheme 2 the contraction phase is significantly longer, and as a result the planet migrates much farther before runaway gas accretion is initiated. Gravitational perturbations from Jupiter cause some variations in the growth track of Saturn’s core, but these are too small to have any impact on the simulation’s outcome. The corresponding time evolution of the capture radius for these growth tracks is presented in the right panel of Fig. 1. The capture radius during gas accretion was calculated using the approximation from Valletta & Helled (2021), which has two regimes depending on whether the planet is in the attached phase (Menv < Mcore) or the detached phase (Menv > Mcore). For the detached phase, we used the fit obtained at 107 yr. During the attached phase the envelope is enhanced, resulting in a large capture radius. This phase ends once runaway gas accretion initiates, and the capture radius decreases to about 1.5 times the current Jupiter radius.
 |
Fig. 1 Planetary growth tracks and evolution of the capture radii. Left: planet mass versus semimajor axis evolution for Jupiter (J) and Saturn (S) in gas accretion scheme 1 and 2. Large dots indicate a time of 2 and 3 Myr, and small dots are separated by 0.2 Myr. We started the simulation at the time when Jupiter reached the pebble isolation mass (tiso), and further included the growth and migration of Saturn’s core. In scheme 1 the contraction of the envelope occurs on a short timescale, resulting in fast gap opening and little migration. In scheme 2 this phase is significantly longer, and thus the planets migrate a further distance before coming to a halt due to gap opening. Right: capture radius versus time for the growth tracks presented in the left panel, calculated using a planetesimal radius of 100 km. The approximation for the capture radius has three regimes: before gas accretion is initiated, the capture radius is equal to the core radius; during the first phase of gas accretion, the envelope is enhanced, resulting in a large capture radius; and after the onset of runaway gas accretion, the capture radius decreases by roughly two orders of magnitude, and it takes on a value of about 1.5 times the current Jupiter radius. |
Parameters for the planet growth tracks.
3.2 Dynamical evolution of planetesimals
Planetesimals were continuously injected into the simulation until the time of disk dissipation, following the procedure outlined in Sect. 2.5. We make two important assumptions regarding planetesimal formation: (1) there is no planetesimal formation at the gap edges before the pebble isolation mass has been reached; and (2) all pebbles that reach the gap edges are trapped and immediately converted into planetesimals. Taken together, this means that when Saturn reaches the pebble isolation mass, the drift of pebbles toward Jupiter is terminated. The time it takes for the remaining pebbles to reach Jupiter’s gap edge after this is relatively short, only 103–104 yr, and therefore we assume that planetesimals cease to form at Jupiter’s gap edge when Saturn reaches the pebble isolation mass. Figure 2 shows the time evolution of the eccentricities and semimajor axes of the planetesimal orbits, and how they vary with the following: (1) the initial formation location relative to the planet; (2) the planetesimal size; and (3) the different gas accretion schemes. Lines of equal Tisserand parameter for coplanar orbits are included in the figure and can be used to understand the planet scattering.
The effect of varying the initial formation location of the planetesimals is shown in row 1 and 3 of Fig. 2. Initiating the planetesimals inside the feeding zone of the planet results in faster and stronger scattering compared to the case when they are initiated outside of the feeding zone. The number of planetesimals scattered into the inner Solar System is also significantly higher in the former case (see also Fig. C.2). The amount of planetesimals which are scattered beyond the simulation domain does, however, not vary with the formation location, which can be seen in Fig. 3. Regardless of the formation location, most planetesimals that remain in the system past disk dispersal are located in a disk beyond Saturn.
In row 2 and 4 of Fig. 2, we show how the dynamical evolution changes when we decreased the planetesimal size. Smaller planetesimals are more affected by gas drag than larger planetesimals, and therefore their eccentricities are more damped. Interior of Jupiter the gas density is high enough to circularize small planetesimals, resulting in a stable population of planetesimals that remain until the end of the simulation. This population has low eccentricities in the case of 300 m-sized planetesimals; it has eccentricities up to around 0.4 in the case of 10 km-sized planetesimals; and it does not exist at all in the case of 100 km-sized planetesimals. Furthermore, there is a small population of planetesimals located around the outer 3:2 resonance with Jupiter, which appears early on and remains until 10 Myr. As expected, the number of planetesimals that are left in the system at the end of the simulation increases with decreasing planetesimal size, which is because of the stronger gas drag (see Fig. 3).
Finally, the effect of changing the gas accretion scheme can be seen by comparing the two upper rows with the two lower rows in Fig. 2. Since the planets migrate larger distances in scheme 2, planetesimals form in a wider region of the disk. A significant amount of the planetesimals formed at Saturn’s gap edge become detached from the scattering region due to planet migration (recognized by being located beyond and below the equal Tisserand parameter lines), resulting in a broader planetesimal disk in scheme 2. Toward the end of the simulation, there are more planetesimals remaining in the system with gas accretion scheme 2 (see Fig. 3).
 |
Fig. 2 Eccentricity and semimajor axis evolution for the planetesimals in some selected simulations. Each simulation has a total of 10 000 planetesimals being injected continuously until the time of disk dissipation. The black dots indicate the current mass and location of Jupiter and Saturn. The black lines are lines of equal Tisserand parameter going through the planet location (solid line) and the planet location offset by 5 Hill radii (dashed line). Planetesimals initiated inside the feeding zone of the planet (labeled 2–3 RH) suffer from stronger and faster scattering than those initiated outside the feeding zone (labeled 4–5 RH). Decreasing the planetesimal size leads to more gas drag and lower eccentricities, and it results in a population of circularized planetesimals interior of Jupiter. |
 |
Fig. 3 Histogram showing the total planetesimal mass that has either been accreted onto the planets, that remains in the system at the end of the simulation, or that has been scattered beyond the simulation domain for all simulations in gas accretion scheme 1 (left) and gas accretion scheme 2 (right). Small planetesimals experience more efficient gas drag than large planetesimals, and they are retained in the system at a higher rate. |
3.3 Planetesimal accretion
In order to calculate the mass represented by each super-particle, we assumed that the pebbles follow the viscous evolution of the disk (Johansen et al. 2019), and that all pebbles which reach the gap edge are converted into planetesimals. The planetesimal formation rate is then simply 1% of the disk accretion rate (photo-evaporation is not considered in this calculation as it only affects the gas component of the disk), and the total planetesimal mass that forms in the simulation was calculated by integrating 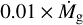 from tiso,jup to tevap. With these assumptions, we formed 23.8 M⊕ of planetesimals in scheme 1 and 32.3 M⊕ in scheme 2. The total planetesimal mass that formed at each individual gap edge is 14.1 M⊕ for Jupiter in scheme 1, 9.7 M⊕ for Saturn in scheme 1, 16.2 M⊕ for Jupiter in scheme 2, and 16.1 M⊕ for Saturn in scheme 2. Since the disk accretion rate decreases with time, the super-particles that formed in the beginning of the simulation are much more massive than those that formed toward the end. Given the assumed solid-to-gas ratio, disk model, and formation time of Jupiter, the above masses represent an upper limit on the formed planetesimal mass.
from tiso,jup to tevap. With these assumptions, we formed 23.8 M⊕ of planetesimals in scheme 1 and 32.3 M⊕ in scheme 2. The total planetesimal mass that formed at each individual gap edge is 14.1 M⊕ for Jupiter in scheme 1, 9.7 M⊕ for Saturn in scheme 1, 16.2 M⊕ for Jupiter in scheme 2, and 16.1 M⊕ for Saturn in scheme 2. Since the disk accretion rate decreases with time, the super-particles that formed in the beginning of the simulation are much more massive than those that formed toward the end. Given the assumed solid-to-gas ratio, disk model, and formation time of Jupiter, the above masses represent an upper limit on the formed planetesimal mass.
In Fig. 3 we show, for each simulation, how much of the total planetesimal mass that has either been accreted onto the planets, remains in the system, or has been scattered beyond the simulation domain at the end of the simulation. Figure 4 shows how much of the planetesimal mass has been accreted onto Jupiter and Saturn, along with the corresponding accretion efficiency. The first thing to be noticed is that the maximum accretion efficiency in any simulation and for any planet is <10%, and the highest amount of solid material accreted onto Jupiter and Saturn is 3.2 M⊕ and 2.3 M⊕, respectively. This shows that planetesimal accretion during the gas accretion phase of giant planet formation is a very inefficient process.
A comparison of the simulation results shows that initializing the planetesimals inside the feeding zone of the planet results in a lot more collisions than placing them outside of the feeding zone. This is partly because a fraction of the planetesimals that formed within the feeding zone were captured immediately after formation due to the enhanced envelope (see Figs. 1 and C.3). The planetesimals that formed beyond the feeding zone are too far away from the planet to be affected by the enhanced envelope, and they only suffer from strongly unfocused collisions later on during the evolution.
As mentioned above, decreasing the planetesimal size results in more gas drag. Furthermore, it also results in an increased capture radius of the planets during the enhanced envelope phase (Valletta & Helled 2021), as smaller planetesimals can be captured further up in the atmosphere. The combined effect on the accretion efficiency of planetesimals, however, turns out to be small. In the case of Jupiter, we found that 300 m-sized planetesimals are accreted at a 30% lower rate than 10 and 100 km-sized planetesimals when formed inside the feeding zone. This is because if the planetesimals are not accreted immediately, they are scattered and eccentricity damping through gas drag quickly puts them out of the feeding zone, resulting in fewer planetesimals crossing Jupiter’s orbit. In the case of Saturn, we found no difference between using small and large planetesimals. Some authors have suggested that using small planetesimals might solve the problem of the low planetesimal accretion efficiency (e.g., Alibert et al. 2018), but our results show that this is not the case for planetesimal accretion during the gas accretion phase.
When comparing the accretion efficiencies in scheme 1 and 2, we found that it is generally higher in scheme 2. This is because the enhanced envelope phase lasts longer in scheme 2, allowing for more planetesimals to be captured just after formation (see Fig. 1). Finally, in most of our simulations, Jupiter accreted a higher planetesimal mass than Saturn. In Fig. C.1 we show how the cumulative accreted planetesimal mass evolves with time.
 |
Fig. 4 Total accreted planetesimal mass onto Jupiter and Saturn, and the corresponding accretion efficiency for all simulations in gas accretion scheme 1 (left) and gas accretion scheme 2 (right). The accretion efficiency is much higher for planetesimals that formed inside the feeding zone, and it does not change significantly with planetesimal size. The maximum accretion efficiency obtained for any planet is < 10%, which corresponds to a mass of ~3 M⊕. |
4 Discussion
4.1 The fate of removed planetesimals
When a planetesimal is scattered beyond the simulation domain, it is removed from the simulation. In order to get an idea of how the planetesimal would have evolved given a larger simulation domain, we studied how the planetesimal orbits looked just before they were removed. The perihelion and aphelion for 1000 planetesimal orbits at the last time step before removal is showed in Fig. 5. Since most planetesimals have aphelion around 50 au and perihelion located ~1 au exterior of the planets, this indicates that they still belong to the planetary scattered disks at the time of removal. In other words, they do not suffer from strong planetary encounters and should not have been ejected from the system. It is therefore likely that these planetesimals would have also remained in or around the scattered disk at 10 Myr had the simulation domain been larger. If this is the case, then the amount of planetesimal mass deposited in the region exterior of Saturn is at least 10–20 M⊕.
 |
Fig. 5 Plot showing the perihelion and aphelion of 1000 planetesimal orbits at the last time step before they were scattered beyond the simulation domain and thus removed from the simulation, for one of the simulations in gas accretion scheme 1. The time evolution of the planet semimajor axes is included on the plot. The majority of the scattered planetesimals have an aphelion of ~50 au and a perihelion located ~1 au exterior of the planets, suggesting that they are not strongly scattered but rather are part of a scattered disk where eccentricities and aphelia increase gently with time. |
4.2 Implications for Solar System formation
The estimated total heavy element mass in Jupiter and Saturn is ≳20 M⊕, with upper bounds that are much higher (e.g., Helled & Guillot 2013; Wahl et al. 2017; Helled 2018). When initiating the planetesimals inside the feeding zone of the planets, we reached a total heavy element mass of 14.8 and 25.1 M⊕ for Jupiter in scheme 1 and 2, respectively. The same numbers for Saturn were 19.0 and 24.4 M⊕; however, we note that most of the solid mass comes from pebble accretion (the contribution from planetesimal accretion to these numbers was very small, maximally 12%). Considering scheme 2, we nearly reached the lower end of the predicted heavy element mass; however, we note that this is under the assumption that all planetesimals formed within the feeding zone of the planet, and that the entire pebble flux was converted into planetesimals. When the planetesimals were initiated beyond the feeding zone of the planets, the amount of planetesimal accretion became negligible and the total heavy element mass was almost identical to the pebble isolation mass.
Based on the above discussion, it is difficult to explain the large heavy-element contents of Jupiter and Saturn with planetesimal accretion during the gas accretion phase. In the following we discuss potential ways to increase the accreted planetesimal mass compared to our model.
If the protoplanetary disk mass was increased, more solids would be available, assuming the same solid-to-gas ratio. However, migration and gas accretion are accelerated in massive disks, meaning that the planets need to form later during disk evolution. As a consequence, planetesimal formation at the gap edges initiates later, and the total mass of planetesimals formed at gap edges would not necessarily be larger than in the case with a lower disk mass.
Increasing the solid-to-gas ratio above the standard 1% would result in a more available planetesimal mass. However, in our models, we end up with more than 10 M⊕ of planetesimals in a disk beyond Saturn (see Sect. 4.1). When the smallest planetesimal sizes were considered, we also injected 3–9 M⊕ of planetesimals into the inner Solar System (see Fig. C.2, we note that this is not the case for 100 km-sized planetesimals). If the formed planetesimal mass is increased by a factor of 10, for example, this means that we would en up with several hundred M⊕ of planetesimals beyond Saturn, which might not be consistent with constraints on the masses of the Solar System’s scattered disk and the Oort cloud (Brasser 2008). We nevertheless caution that inferring the original planetesimal mass from the current Oort cloud population is challenging and requires a number of assumptions to be made about the size distribution of the small comets that enter the inner Solar System (see Brasser 2008 for a discussion).
Planetesimals formed at planetary gap edges represent a later generation of planetesimals, which did not contribute to the formation of the giant planet cores. Some of the planetesimals which must have formed earlier during disk evolution, as well as planetesimals forming at other locations in the disk, could also exist in the system. Our results show that planetesimal accretion is very inefficient when the planetesimals form beyond the feeding zone of the planet; however, in Shibata et al. (2020, 2022), and Shibata & Helled (2022), they show that accretion can be significant if the planets are migrating far and shepherding the planetesimals in front of them. Taking into account the formation of planetesimals via other mechanisms interior of the planets might thus result in more accretion, although additional effects such as ablation need to be considered when icy planetesimals enter the inner Solar System (Eriksson et al. 2021).
The accretion of solids onto the planetary envelope could have an effect on the timescale for gas accretion, which would result in the planetary growth tracks changing compared to our model. If the rate of solid accretion during the attached phase is high, then runaway gas accretion can be delayed, resulting in a longer enhanced envelope phase and more planetesimal accretion (Alibert et al. 2018; Valletta & Helled 2020). The dependence of gas accretion on enrichment is discussed in Sect. 4.5.2.
If the planetary cores formed much earlier than in our model, regardless of whether this occurred via pebble accretion or via some other scenario (e.g., Kobayashi & Tanaka 2021), more solids would remain in the disk and thus the total mass of planetesimals forming at the gap edges would be larger. Our models for gas accretion and migration do not manage to produce Jupiter and Saturn in this scenario, as the planets would become far too massive. The accreted planetesimal mass would likely increase if the cores formed earlier.
4.3 Implications for exoplanets
The estimated heavy element mass for hot Jupiters ranges from ~ 10–100 M⊕, with many planets containing more than 50 M⊕ (Guillot et al. 2006; Miller & Fortney 2011; Thorngren et al. 2016). Although our work focuses on the formation of the cold Solar System giants, it is clear from our results that such large heavy element masses are difficult to explain by the accretion of planetesimals. Despite the fact that all planetesimals were initiated inside the feeding zone of the planet, and that we used a 100% pebble-to-planetesimal conversion efficiency at the gap edges, the maximum accretion efficiency obtained in our simulations was <10%. In order to accrete ~50 M⊕ of planetesimals, there would thus need to be more than 500 M⊕ of planetesimals forming at the gap edges.
Based on the discussion in Sect. 4.2, the most promising way of increasing the planetesimal accretion efficiency is to have a prolonged attached phase. One way to achieve this is if the bombardment of planetesimals onto the planetary envelope is high enough to delay runaway gas accretion itself (Alibert et al. 2018; Venturini & Helled 2020). Having a longer attached phase also implies a longer migration distance, such that the planet would start accreting gas further out in the disk. This is in line with the results by Shibata et al. (2020), who found that a Jupiter mass planet can accrete enough planetesimals to explain the observed metallicities, provided that the planet starts migrating at a few tens of au in a massive planetesimal disk (~100 M⊕). Efficient planetesimal accretion might thus not be impossible, but it requires extreme conditions. In other cases, alternative processes are required to explain the high metal content of extrasolar giants (see Sect. 4.4).
4.4 Alternative models for envelope enrichment
There are multiple alternative processes that can lead to envelope enrichment, such as accretion of enriched gas, erosion of the initial core, or giant impacts. The accretion of enriched gas is a natural outcome of planet formation models, where drifting pebbles sublimate at snow lines and subsequently enrich the gas that is closer to the star (Booth et al. 2017; Schneider & Bitsch 2021a,b). Giant planets forming within the snow lines accrete this metal-rich gas and automatically obtain enriched envelopes. In Schneider & Bitsch (2021a,b), they show that this process can result in heavy element contents that match the ones predicted by Thorngren et al. (2016) for hot Jupiter systems, provided that the solid-to-gas ratio in the disk is ~2%.
Erosion of the initially compact core and subsequent mixing of the heavy elements within the envelope would also result in an enhanced envelope metallicity (e.g., Madhusudhan et al. 2017). However, the efficiency of this mechanism is uncertain (Guillot et al. 2004) and it depends both on material properties and the mixing efficiency within the envelope (Wilson & Militzer 2012; Soubiran & Militzer 2016). Furthermore, in order to match the estimated heavy element content of exogiants, the initial core mass would have to be very large. On the positive side, if feasible, the resulting interior profile of the planet could be one with an extended diluted core, which is typically favored by internal structure models (e.g., Wahl et al. 2017).
Finally, studies by Li et al. (2010), and Liu et al. (2019) show that energetic head-on collisions between proto-Jupiter and large planetary embryos (several M⊕) could result in shattering and erosion of Jupiter’s core. The subsequent mixing of heavy elements into the proto-envelope lead to an enhanced envelope metallicity, and this could produce a diluted core profile. However, the question remains whether the frequency of giant impacts is high enough.
4.5 Shortcomings of the model
4.5.1 The effect of gas accretion on disk evolution
In our model for gas accretion, we did not consider the effect of gas accretion on disk evolution, other than the opening of a gap. This is a common simplification in planet formation studies; however, in reality the gas which is accreted onto the planet should be removed from the disk accretion rate onto the star. Consequently, if the disk contains multiple planets that are accreting gas simultaneously, then the amount of gas which is available to the inner planet depends on how much gas has been accreted by the outer one. In our model, gas accretion onto Jupiter and Saturn are treated independently, which could in practice result in the sum of the gas accretion rates onto both planets being larger than the disk accretion rate.
Taking the above effects into consideration would result in less gas drag on the planetesimals that are scattered interior of the planetary orbits. This could, for example, effect the population of circularized planetesimals interior of Jupiter that can be seen in panels 2 and 4 of Fig. 2. In the case of Jupiter’s formation, when Saturn reaches runaway gas accretion, the mass available for Jupiter to accrete would decrease compared to the current model. Therefore, Jupiter would have to reach the pebble isolation mass earlier during disk evolution. This would not result in a prolonged enhanced envelope phase (gas accretion is independent of the disk mass during the attached phase); however, given that the pebble flux is larger early on during disk evolution, the accreted planetesimal mass would likely increase a bit.
4.5.2 The dependence of gas accretion on enrichment
The accretion of solids onto the planetary envelope affects the efficiency of gas accretion in mainly two ways: (1) the envelope obtains thermal support from the dissipation of kinetic energy from infalling solids, which counteracts the gravity of the core and thus slows down envelope contraction (Alibert et al. 2018); and (2) the enriched envelope obtains a higher molecular weight, which has been shown to result in faster gas accretion and shorter formation timescales (e.g., Stevenson 1982; Venturini et al. 2016; Valletta & Helled 2020). If the first effect dominates, the onset of runaway gas accretion is delayed, resulting in a longer migration distance as well as a longer enhanced envelope phase. This would likely lead to a higher accretion efficiency of planetesimals. In Alibert et al. (2018), they find that a constant accretion rate of at least 10−6 M⊙ yr−1 is required in order to stall runaway gas accretion for 2 Myr. In principle, the solutions we find with a high planetesimal accretion rate could delay runaway gas accretion and be more consistent with these results.
If the second effect dominates, gas accretion occurs on a shorter timescale, meaning that the planets in our model would need to reach the pebble isolation mass later during disk evolution. This would likely result in a smaller accreted planetesimal mass. The question of how gas accretion is affected by solid enrichment is an important problem, which should be solved in a more self-consistent manner, with detailed calculations and a proper handling of thermal dynamics.
5 Conclusion
In this work, we study collisions between gap-opening planets and planetesimals forming at their gap edges, with the aim to determine whether the delivered mass is high enough to explain the large heavy element contents of giant planets. To this end, we used a suite of N-body simulations. We considered the formation of Jupiter and Saturn, taking into account the enhanced collision cross section caused by their extended envelopes. Two formation pathways were examined, where one leads to large-scale planet migration, and the other to migration over a few au only. We further varied the formation location of the planetesimals relative to the planets, and the planetesimal sizes. We find that:
The close proximity to the gap-opening planets causes the planetesimals to leave their birth location soon after formation. Most planetesimals that do not experience ejection or accretion eventually become members of Saturn’s scattered disk. In the case of small planetesimal radii, there is also a population of circularized planetesimals in the innermost disk region.
Planetesimal accretion during the gas accretion phase of giant planet formation is a very inefficient process. The maximum obtained accretion efficiency onto Jupiter or Saturn is less than 10%, corresponding to a mass of ~3 M⊕ and ~2 M⊕, respectively. Since these numbers were obtained assuming that all planetesimals form within the feeding zone of the planets, and that all pebbles reaching the gap-edges are turned into planetesimals, they represent an upper limit on the accreted planetesimal mass.
When planetesimal formation occurs beyond the feeding zone of the planets, accretion becomes negligible. This is a good indication that planetesimal accretion during the gas-accretion phase is inefficient also if the planetesimals form via other processes and in other regions of the disk.
Decreasing the planetesimal radii does not lead to more efficient accretion. In the literature it is often mentioned that having smaller planetesimals leads to more accretion (e.g., Alibert et al. 2018), but our results demonstrate that this is not the case for planetesimal accretion during the gas accretion stage.
The accretion efficiency is higher when we considered the formation pathway with a long migration distance. This is in line with the results by Shibata et al. (2020), who found that efficient accretion can occur if a massive planet starts migrating at a few tens of au in a massive planetesimal disk (~100 M⊕).
Based on our results, we conclude that it is difficult to explain the large heavy element contents of giant planets with planetesimal accretion during the gas accretion phase, provided they do not migrate very far in a very massive planetesimal disk (Shibata et al. 2020). Hence, alternative processes of envelope enrichment are most likely required in order to explain the high heavy element content inferred for Jupiter and Saturn, as well as that of transiting planets. The accretion of vapor deposited by drifting pebbles is one such promising mechanism (Schneider & Bitsch 2021a,b).
Acknowledgements
L.E. and A.J. are supported by the Swedish Research Council (Project Grant 2018–04867). T.R. and A.J. are supported by the Knut and Alice Wallenberg Foundation (Wallenberg Academy Fellow Grant 2017.0287). A.J. further thanks the European Research Council (ERC Consolidator Grant 724 687-PLANETESYS), the Göran Gustafsson Foundation for Research in Natural Sciences and Medicine, and the Wallenberg Foundation (Wallenberg Scholar KAW 2019.0442) for research support. R.H. and C.V. acknowledge support from the Swiss National Science Foundation (SNSF) under grant 200020_188460. Simulations in this paper made use of the REBOUND code which is freely available at http://github.com/hannorein/rebound. The computations were performed on resources funded by the Royal Physiographic Society of Lund.
Appendix A Details of the disk model
We used the analytic solution for the surface density evolution of an unperturbed thin accretion disk from Lynden-Bell & Pringle (1974):
![${\Sigma_{{\rm{unp}}}}\left(t \right) = {{{{\dot M}_{\rm{g}}}\left(t \right)} \over {3\pi {v_{{\rm{out}}}}{{\left({r{\rm{/}}{r_{{\rm{out}}}}} \right)}^\gamma}}}\exp \left[{- {{{{\left({r{\rm{/}}{r_{{\rm{out}}}}} \right)}^{\left({2 - \gamma} \right)}}} \over {{T_{{\rm{out}}}}}}} \right],$](/articles/aa/full_html/2022/05/aa42391-21/aa42391-21-eq11.png) (A.1)
(A.1)
In the equations above, 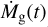 is the disk accretion rate at time t, r is the semimajor axis, rout is the scaling radius, vout = v(rout) where v is the kinematic viscosity, and γ is the radial gradient of v. The evolution of the disk accretion rate is given by
is the disk accretion rate at time t, r is the semimajor axis, rout is the scaling radius, vout = v(rout) where v is the kinematic viscosity, and γ is the radial gradient of v. The evolution of the disk accretion rate is given by
![${\dot M_{\rm{g}}}\left(t \right) = {\dot M_{\rm{g}}}\left({t = 0} \right){\left[{{t \over {{t_s}}} + 1} \right]^{- \left({{5 \over 2} - \gamma} \right)/\left({2 - \gamma} \right)}} - {\dot M_{{\rm{pe}}}},$](/articles/aa/full_html/2022/05/aa42391-21/aa42391-21-eq15.png) (A.4)
(A.4)
where 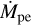 is the rate at which material is removed by photoevaporation, which we consider to be constant in time.
is the rate at which material is removed by photoevaporation, which we consider to be constant in time.
The sound speed in the disk was calculated as
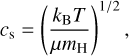 (A.5)
(A.5)
where kB is the Bolzmann constant, T is the temperature, µ is the mean molecular weight, and mH is the mass of the hydrogen atom. We used a value of 2.34 for the mean molecular weight (Hayashi 1981). The midplane temperature of the disk was approximated using a fixed power-law structure:
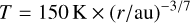 (A.6)
(A.6)
We used Gaussian gap profiles to model the planetary gaps, where the Gaussian is described by the equation
![$G\left(r \right) = \left({1 - {{{\Sigma_{{\rm{gap}}}}} \over {{\Sigma_{{\rm{unp}}}}}}} \right)\exp \left[{- {{{{\left({r - a} \right)}^2}} \over {2H_a^2}}} \right],$](/articles/aa/full_html/2022/05/aa42391-21/aa42391-21-eq19.png) (A.7)
(A.7)
where a is the semimajor axis of the planetary orbit and Ha is the corresponding gas scale height. The perturbed surface density profile could then be obtained by using the following expression:
 (A.8)
(A.8)
where each planet contributes their own Gaussian. Finally, the gas density at some height, z, away from the midplane was obtained by using the equation
![$\rho \left(z \right) = {\Sigma \over {\sqrt {2\pi} H}}\exp \left[{{{- {z^2}} \over {2{H^2}}}} \right],$](/articles/aa/full_html/2022/05/aa42391-21/aa42391-21-eq21.png) (A.9)
(A.9)
where we assumed vertical hydrostatic equilibrium for the gas in the disk.
Appendix B Gas accretion rate
In Fig. B.1 we have plotted the dependence on planetary mass for all the different gas accretion rates which were used in our models. The rates were calculated using a semimajor axis of 10 au and a disk time of 2 Myr. In scheme 1 the gas accretion rate during envelop contraction increases with increasing planetary mass, and runaway gas accretion initiates when this rate becomes higher than what the disk can supply. In scheme 2 the gas accretion rate during envelop contraction instead decreases with increasing planetary mass, and runaway gas accretion initiates when the core mass equals the envelope mass. At the chosen time and semimajor axis, gas accretion is limited by disk accretion for most of the runaway phase.
 |
Fig. B.1 Gas accretion rate as a function of planetary mass for a planet located at 10 au in a 2 Myr old protoplanetary disk. The labels Sc1 and Sc2 indicate in which gas accretion scheme the current model is being used. |
Appendix C Additional plots
In Fig. C.1 we show the amount of planetesimal mass that has been accreted onto Jupiter and Saturn as a function of time for all simulations, along with the corresponding accretion efficiency. This is the same data that are presented in Fig. 4. The “knee” on the accretion curves for planetesimals that formed within the feeding zone coincides with the location where Menv = Mcore, which is when runaway gas accretion initiates and the approximation for the capture radius becomes significantly smaller (see right panel of Fig. 1 for a plot of the capture radius versus time). Up until this point, a fraction of the planetesimals were captured immediately after formation due to the enhanced envelope. This trend is not seen in the accretion curves for planetesimals that formed beyond the feeding zone, since they were initiated too far away from the planet to be affected by the enhanced envelope.
In Fig. C.2 the total planetesimal mass residing in the inner Solar System is shown as a function of time (we consider a planetesimal to be in the inner Solar System if its aphelion is less than 4 au). In the case of 100 km-sized planetesimals, the amount of mass injection into the inner Solar System is negligible. Considering 10 km-sized planetesimals, we injected between 0.3 – 2 M⊕ of the planetesimals into the inner Solar System, which also remains after the dispersal of the gas disk. When using planetesimals of 300 m in size, we scattered and subsequently trapped 3 – 9 M⊕ of the planetesimals in the inner Solar System. We find that planetesimals forming inside the feeding zone of the planet have a higher chance of making it into the inner Solar System, which is because of the more efficient planetary scattering. If the amount of planetesimal formation at the gap edges were to drastically increase, the amount of mass entering the inner Solar System would do so as well.
 |
Fig. C.1 Cumulative accreted planetesimal mass as a function of time for all simulations in scheme 1 (left) and in scheme 2 (right). The corresponding accretion efficiency was calculated by dividing with the total planetesimal mass that formed in the system at the time of disk dissipation. Each scatter point in the plot is one collision event; however, since we performed three simulations per parameter set and show the combined results, the number of collisions in one simulation should be three times smaller than in this plot. The maximum obtained accretion efficiency onto any planet in scheme 1 is 5%, which corresponds to ~1 M⊕. The accretion efficiency is much higher for planetesimals that formed inside the feeding zone, and it does not change significantly with planetesimal size. The maximum accretion efficiency obtained for any planet in scheme 2 is 10%, which corresponds to a mass of ~3 M⊕. |
 |
Fig. C.2 Total planetesimal mass residing in the inner Solar System (planetesimals with aphelion less than 4 au) plotted as a function of time for all simulations in scheme 1 (left) and in scheme 2 (right). The chance of making it into the inner Solar System increases with decreasing planetesimal size and decreasing formation distance relative to the planet. |
In Fig. C.3 the median time before collision is presented as a function of the initial separation relative to the planet. Planetesimals that are initiated between 2 – 2.4 RH typically collide within 20 orbital periods. This suggests that a significant fraction of the accretion efficiency comes from immediate accretion (a lifetime of ten orbital periods corresponds to roughly two to three close encounters). We do not know whether or not it is realistic for planetesimals to form in regions with immediate accretion, and to our knowledge this has not been studied.
 |
Fig. C.3 Median time before collision versus the initial separation for all simulations with planetesimals initiated inside the feeding zone of the planets. The time is given in units of the orbital period of the planets at the time the planetesimals were formed. Planetesimals initiated between 2 – 2.4 RH typically collide within 20 orbital periods. |
References
- Alibert, Y., Venturini, J., Helled, R., et al. 2018, Nat. Astron., 2, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2010, ApJ, 722, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Morbidelli, A., Johansen, A., et al. 2018, A&A, 612, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Booth, R. A., Clarke, C. J., Madhusudhan, N., & Ilee, J. D. 2017, MNRAS, 469, 3994 [Google Scholar]
- Bottke, W. F., Durda, D. D., Nesvorný, D., et al. 2005, Icarus, 179, 63 [Google Scholar]
- Brasser, R. 2008, A&A, 492, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrera, D., Johansen, A., & Davies, M. B. 2015, A&A, 579, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrera, D., Simon, J. B., Li, R., Kretke, K. A., & Klahr, H. 2021, AJ, 161, 96 [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2008, A&A, 482, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eriksson, L. E. J., Johansen, A., & Liu, B. 2020, A&A, 635, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eriksson, L. E. J., Ronnet, T., & Johansen, A. 2021, A&A, 648, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., Stevenson, D. J., Hubbard, W. B., & Saumon, D. 2004, The Interior of Jupiter, eds. F. Bagenal, T. E. Dowling, & W. B. McKinnon (USA: Cornell University), 1, 35 [NASA ADS] [Google Scholar]
- Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [CrossRef] [EDP Sciences] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [Google Scholar]
- Helled, R. 2018, The Interiors of Jupiter and Saturn (Oxford: Oxford University Press), 175 [Google Scholar]
- Helled, R., & Guillot, T. 2013, ApJ, 767, 113 [CrossRef] [Google Scholar]
- Ikoma, M., Nakazawa, K., & Emori, H. 2000, ApJ, 537, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Youdin, A., & Mac Low, M.-M. 2009, ApJ, 704, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Mac Low, M.-M., Lacerda, P., & Bizzarro, M. 2015, Sci. Adv., 1, 1500109 [CrossRef] [Google Scholar]
- Johansen, A., Ida, S., & Brasser, R. 2019, A&A, 622, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanagawa, K. D., Tanaka, H., & Szuszkiewicz, E. 2018, ApJ, 861, 140 [Google Scholar]
- Kobayashi, H., & Tanaka, H. 2021, ApJ, 922, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, S. L., Agnor, C. B., & Lin, D. N. C. 2010, ApJ, 720, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S.-F., Hori, Y., Müller, S., et al. 2019, Nature, 572, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., & D’Angelo, G. 2006, ApJ, 641, 526 [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2009, A&A, 493, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madhusudhan, N., Bitsch, B., Johansen, A., & Eriksson, L. 2017, MNRAS, 469, 4102 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, N., & Fortney, J. J. 2011, ApJ, 736, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Bottke, W. F., Nesvorný, D., & Levison, H. F. 2009, Icarus, 204, 558 [Google Scholar]
- Morbidelli, A., Lambrechts, M., Jacobson, S., & Bitsch, B. 2015, Icarus, 258, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Li, R., Youdin, A. N., Simon, J. B., & Grundy, W. M. 2019, Nat. Astron., 364 [Google Scholar]
- Piso, A.-M.A., & Youdin, A. N. 2014, ApJ, 786, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., & Liu, S. F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., Hernandez, D. M., Tamayo, D., et al. 2019, MNRAS, 485, 5490 [Google Scholar]
- Schneider, A. D., & Bitsch, B. 2021a, A&A, 654, A71 [Google Scholar]
- Schneider, A. D., & Bitsch, B. 2021b, A&A, 654, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]
- Shibata, S., & Helled, R. 2022, ApJ, 926, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, S., Helled, R., & Ikoma, M. 2020, A&A, 633, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shibata, S., Helled, R., & Ikoma, M. 2022, A&A, 659, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shiraishi, M., & Ida, S. 2008, ApJ, 684, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, F., & Militzer, B. 2016, ApJ, 829, 14 [CrossRef] [Google Scholar]
- Stammler, S. M., Drażkowska, J., Birnstiel, T., et al. 2019, ApJ, 884, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, D. J. 1982, Planet. Space Sci., 30, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Tanigawa, T., & Tanaka, H. 2016, ApJ, 823, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Thorngren, D. P., Fortney, J. J., Murray-Clay, R. A., & Lopez, E. D. 2016, ApJ, 831, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Valletta, C., & Helled, R. 2020, ApJ, 900, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Valletta, C., & Helled, R. 2021, MNRAS, 507, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Venturini, J., & Helled, R. 2020, A&A, 634, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturini, J., Alibert, Y., & Benz, W. 2016, A&A, 596, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahl, S. M., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [CrossRef] [Google Scholar]
- Wilson, H. F., & Militzer, B. 2012, ApJ, 745, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C. C., Johansen, A., & Carrera, D. 2017, A&A, 606, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Planetary growth tracks and evolution of the capture radii. Left: planet mass versus semimajor axis evolution for Jupiter (J) and Saturn (S) in gas accretion scheme 1 and 2. Large dots indicate a time of 2 and 3 Myr, and small dots are separated by 0.2 Myr. We started the simulation at the time when Jupiter reached the pebble isolation mass (tiso), and further included the growth and migration of Saturn’s core. In scheme 1 the contraction of the envelope occurs on a short timescale, resulting in fast gap opening and little migration. In scheme 2 this phase is significantly longer, and thus the planets migrate a further distance before coming to a halt due to gap opening. Right: capture radius versus time for the growth tracks presented in the left panel, calculated using a planetesimal radius of 100 km. The approximation for the capture radius has three regimes: before gas accretion is initiated, the capture radius is equal to the core radius; during the first phase of gas accretion, the envelope is enhanced, resulting in a large capture radius; and after the onset of runaway gas accretion, the capture radius decreases by roughly two orders of magnitude, and it takes on a value of about 1.5 times the current Jupiter radius. |
| In the text | |
 |
Fig. 2 Eccentricity and semimajor axis evolution for the planetesimals in some selected simulations. Each simulation has a total of 10 000 planetesimals being injected continuously until the time of disk dissipation. The black dots indicate the current mass and location of Jupiter and Saturn. The black lines are lines of equal Tisserand parameter going through the planet location (solid line) and the planet location offset by 5 Hill radii (dashed line). Planetesimals initiated inside the feeding zone of the planet (labeled 2–3 RH) suffer from stronger and faster scattering than those initiated outside the feeding zone (labeled 4–5 RH). Decreasing the planetesimal size leads to more gas drag and lower eccentricities, and it results in a population of circularized planetesimals interior of Jupiter. |
| In the text | |
 |
Fig. 3 Histogram showing the total planetesimal mass that has either been accreted onto the planets, that remains in the system at the end of the simulation, or that has been scattered beyond the simulation domain for all simulations in gas accretion scheme 1 (left) and gas accretion scheme 2 (right). Small planetesimals experience more efficient gas drag than large planetesimals, and they are retained in the system at a higher rate. |
| In the text | |
 |
Fig. 4 Total accreted planetesimal mass onto Jupiter and Saturn, and the corresponding accretion efficiency for all simulations in gas accretion scheme 1 (left) and gas accretion scheme 2 (right). The accretion efficiency is much higher for planetesimals that formed inside the feeding zone, and it does not change significantly with planetesimal size. The maximum accretion efficiency obtained for any planet is < 10%, which corresponds to a mass of ~3 M⊕. |
| In the text | |
 |
Fig. 5 Plot showing the perihelion and aphelion of 1000 planetesimal orbits at the last time step before they were scattered beyond the simulation domain and thus removed from the simulation, for one of the simulations in gas accretion scheme 1. The time evolution of the planet semimajor axes is included on the plot. The majority of the scattered planetesimals have an aphelion of ~50 au and a perihelion located ~1 au exterior of the planets, suggesting that they are not strongly scattered but rather are part of a scattered disk where eccentricities and aphelia increase gently with time. |
| In the text | |
 |
Fig. B.1 Gas accretion rate as a function of planetary mass for a planet located at 10 au in a 2 Myr old protoplanetary disk. The labels Sc1 and Sc2 indicate in which gas accretion scheme the current model is being used. |
| In the text | |
 |
Fig. C.1 Cumulative accreted planetesimal mass as a function of time for all simulations in scheme 1 (left) and in scheme 2 (right). The corresponding accretion efficiency was calculated by dividing with the total planetesimal mass that formed in the system at the time of disk dissipation. Each scatter point in the plot is one collision event; however, since we performed three simulations per parameter set and show the combined results, the number of collisions in one simulation should be three times smaller than in this plot. The maximum obtained accretion efficiency onto any planet in scheme 1 is 5%, which corresponds to ~1 M⊕. The accretion efficiency is much higher for planetesimals that formed inside the feeding zone, and it does not change significantly with planetesimal size. The maximum accretion efficiency obtained for any planet in scheme 2 is 10%, which corresponds to a mass of ~3 M⊕. |
| In the text | |
 |
Fig. C.2 Total planetesimal mass residing in the inner Solar System (planetesimals with aphelion less than 4 au) plotted as a function of time for all simulations in scheme 1 (left) and in scheme 2 (right). The chance of making it into the inner Solar System increases with decreasing planetesimal size and decreasing formation distance relative to the planet. |
| In the text | |
 |
Fig. C.3 Median time before collision versus the initial separation for all simulations with planetesimals initiated inside the feeding zone of the planets. The time is given in units of the orbital period of the planets at the time the planetesimals were formed. Planetesimals initiated between 2 – 2.4 RH typically collide within 20 orbital periods. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.