| Issue |
A&A
Volume 657, January 2022
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 10 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202142188 | |
| Published online | 21 December 2021 | |
Laboratory observation and astronomical search of 1-cyano propargyl radical, HCCCHCN★,★★
1
Grupo de Astrofísica Molecular, Instituto de Física Fundamental (IFF-CSIC),
C/ Serrano 121,
28006
Madrid, Spain
e-mail: carlos.cabezas@csic.es
2
Department of Basic Science, Graduate School of Arts & Sciences, The University of Tokyo,
Komaba 3-8-1,
Meguro-ku,
Tokyo
153-8902, Japan
3
Department of Applied Chemistry, Science Building II, National Yang Ming Chiao Tung University,
1001 Ta-Hsueh Rd.,
Hsinchu
300098, Taiwan
Received:
9
September
2021
Accepted:
17
October
2021
Context. The reaction between carbon atoms and vinyl cyanide, CH2CHCN, is a formation route to interstellar 3-cyano propargyl radical, CH2C3N, a species that has recently been discovered in space. The 1-cyano propargyl radical (HC3HCN), an isomer of CH2C3N, is predicted to be produced in the same reaction at least twice more efficiently than CH2C3N. Hence, HC3HCN is a plausible candidate to be observed in space as well.
Aims. We aim to generate the HC3HCN radical in the gas phase in order to investigate its rotational spectrum. The derived spectroscopic parameters for this species will be used to obtain reliable frequency predictions to support its detection in space.
Methods. The HC3HCN radical was produced by an electric discharge, and its rotational spectrum was characterized using a Balle-Flygare narrowband-type Fourier-transform microwave spectrometer operating in the frequency region of 4–40 GHz. The spectral analysis was supported by high-level ab initio calculations.
Results. A total of 193 hyperfine components that originated from 12 rotational transitions, a- and b-type, were measured for the HC3HCN radical. The analysis allowed us to accurately determine 22 molecular constants, including rotational and centrifugal distortion constants as well as the fine and hyperfine constants. Transition frequency predictions were used to search for the HC3HCN radical in TMC-1 using the QUIJOTE survey between 30 and 50 GHz. We do not detect HC3HCN in TMC-1 and derive a 3σ upper limit to its column density of 6.0 × 1011 cm−2.
Key words: astrochemistry / ISM: molecules / ISM: individual objects: TMC-1 / methods: laboratory: molecular / molecular processes
Tables A.2 and A.3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/657/A24
© ESO 2021
1 Introduction
The radioastronomical discovery of new molecules in space is highly dependent on the availability of precise rotational spectroscopic laboratory data. Only a few molecular species have been detected in space prior to their characterization in the laboratory. Some examples of this type are HCO+ (Buhl & Snyder 1970), C4H (Gúelin et al. 1978), HCS+ (Thaddeus et al. 1981), C5H (Cernicharo et al. 1986), C6H (Suzuki et al. 1986), and C3H+ (Pety et al. 2012). All of them were confirmed later on in the laboratory. Other cases such as C5N− (Cernicharo et al. 2008), MgC3N and MgC4H (Cernicharo et al. 2019), HC5NH+ (Marcelino et al. 2020), MgC5N and MgC6H (Pardo et al. 2021), and H2NC (Cabezas et al. 2021a) have not been yet observed in the laboratory. Although most of these molecules are open-shell species, they display almost trivial spectral patterns, except for H2NC. These patterns allowed their identifications in the line surveys only supported by dedicated ab initio calculations. However, other interstellar molecules and potential candidates have much more complex rotational spectra due to the presence of two or three nuclei with nonzero nuclear spins, which causes complicated line splitting by interactions of different types of angular momenta. In these cases, ab initio calculations are not enough to identify their spectral features in the line surveys, and the laboratory experiments are invaluable tools (Cabezas et al. 2021c).
An example of this type of open-shell species is the 3-cyano propargyl radical, CH2C3N, which was recently discovered in space (Cabezas et al. 2021b). Its astronomical identification was possible through high-resolution laboratory experiments (Chen et al. 1998; Tang et al. 2001), which provided frequency predictions with an accuracy better than 10 kHz in the 30–50 GHz region. The hyperfine components for seven rotational transitions of CH2C3N were detected in the cold dark cloud TMC-1 using the Yebes 40 m telescope. The matching of these precise frequencies to interstellar features was then aided by the sharpness of the radio emission features in TMC-1, around 40 kHz at 40 GHz.
One of the routes to form CH2C3N in space is the reaction C + CH2CHCN → CH2C3N + H. This reaction has been studied using crossed molecular beam experiments and theoretical calculations (Su et al. 2005; Guo et al. 2006). These studies indicate that the reaction is barrierless and occurs through H atom elimination, yielding as main products the radicals 3-cyano propargyl (CH2C3N) and its isomer 1-cyano propargyl (HC3HCN). The latter is inferred to be produced at least twice more efficiently than the former (Guo et al. 2006), and thus, it is a good candidate for detection in TMC-1 as well.
As far as we could ascertain from the literature, no spectroscopic work on 1-cyano propargyl radical (HC3HCN) has been published so far. The only information about this species is that mentioned previously about crossed molecular beam experiments and theoretical calculations (Su et al. 2005; Guo et al. 2006). In the present work, we report the first rotational study of HC3HCN using Fourier transform microwave (FTMW) spectroscopy supported by ab initio calculations. In addition, we carried out an astronomical search of HC3HCN in TMC-1 using accurate frequency predictions derived from our spectroscopic study.
2 Experiment
The rotational spectrum of the HC3HCN radical was observed using a Balle-Flygare narrowband-type FTMW spectrometer operating in the frequency region of 4–40 GHz (Endo et al. 1994; Cabezas et al. 2016). The short-lived species HC3HCN was produced in a supersonic expansion by a pulsed electric discharge of a gas mixture of CH2CHCN (0.2%) and C2H2 (0.4%) diluted in Ar. This gas mixture was flowed through a pulsed-solenoid valve that is accommodated in the backside of one of the cavity mirrors and aligned parallel to the optical axis of the resonator. A pulse voltage of 900 V with a duration of 450 μs was applied between stainless-steel electrodes attached to the exit of the pulsed discharge nozzle (PDN), resulting in an electric discharge synchronized with the gas expansion. The resulting products generated in the discharge were supersonically expanded, rapidly cooled to a rotational temperature of ~2.5 K between the two mirrors of the Fabry-Pérot resonator, and then probed by FTMW spectroscopy. For measurements of the paramagnetic lines, the Earth’s magnetic field was cancelled by using three sets of Helmholtz coils placed perpendicularly to one another. Since the PDN is arranged parallel to the cavity of the spectrometer, it is possible to suppress the Doppler broadening of the spectral lines, which allows resolving small hyperfine splittings. The spectral resolution is 5 kHz, and the frequency measurements have an estimated accuracy better than 3 kHz.
3 Ab initio calculations
The geometry optimization calculation of HC3HCN was carried out using the spin-restricted coupled cluster method with single, double, and perturbative triple excitations (RCCSD(T); Raghavachari et al. 1989) with all electrons (valence and core) correlated and the Dunning correlation-consistent basis sets with polarized core-valence correlation quadruple-ζ (cc-pCVQZ;Woon & Dunning 1995). At the optimized geometry, electric dipole moment components along the a- and b-inertial axes were calculated at the same level of theory as that for the geometrical optimization. The calculations were performed using the MOLPRO 2020.2 program (Werner et al. 2020). The fine and hyperfine coupling constants of the HC3HCN radical were estimated at the second-order Møller-Plesset perturbation (MP2; Møller & Plesset 1934) and the quadratic configuration interaction with single- and double-excitation (QCISD; Pople et al. 1987) levels of calculations, with the cc-pVTZ basis set (Woon & Dunning 1995). Harmonic frequencies were computed at the MP2/cc-pVTZ level of theory to estimate the centrifugal distortion constants. These calculations were performed using the Gaussian16 (Frisch et al. 2016) program package. The calculated geometry of HC3HCN in the 2A″ ground electronic state is depicted in Fig. 1 together with that for the CH2C3N isomer. The calculated molecular parameters and the dipole moment components are summarized in Table 1.
In addition, we carried out optimization calculations for the CH2C3N isomer in order to ascertain the relative energies of this species and HC3HCN. The RCCSD(T)/cc-pCVQZ energies with the zeropoint energy corrections at RCCSD/cc-VQZ level of theory indicate that the CH2C3N isomer is slightly more stable than HC3HCN by 1.75 kJ mol−1. Su et al. (2005) carried out quantum chemical calculations for HC3HCN and CH2C3N isomers at the B3LYP/6-311G(d,p)//CCSD(T)/6-311G(d,p) level of theory. They found that CH2C3N is more stable by 14.9 kJ mol−1 when B3LYP/6-311G(d,p) energies are taken into account. However, HC3HCN is 2.1 kJ mol−1 more stable than CH2C3N if the CCSD(T)/6-311G(d,p) energies are considered. Given the small energy differences, which are of the order of the error of the calculations, we can consider that the two isomers CH2C3N and HC3HCN are nearly isoenergetic.
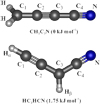 |
Fig. 1 Molecular structures and relative energies of the CH2C3N and HC3HCN radicals. |
4 Rotational spectrum analysis
The predicted a-type dipole moment for the HC3HCN radical is 3.70 D, and thus, the a-type rotational transitions are expected to be fairly strong. Hence, we first tried to observe this type of transition. In particular, we searched for the 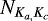 = 20,2–10,1 transition, which is predicted around 10.8 GHz. A group of more than 20 paramagnetic lines were observed in the 10.7 GHz region. The 30,3 –20,2, 40,4 –30,3, and 50,5 –40,4 transitions were then searched around 16.1, 21.5, and 26.8 GHz. Three groups of paramagnetic lines with a similar spectral pattern to that observed in the 10.7 GHz region were found around these frequencies. Figure 2 shows the recorded spectra for the a-type Ka = 0 rotational transitions. The HC3HCN radical was readily confirmed as the spectral carrier based on the following arguments. (i) The observed transition frequencies agree well with the calculated frequencies, (ii) each transition has a hyperfine spectral structure similar to that expected for an open-shell species with three coupling nuclei, and (iii) the lines exhibit the paramagnetic behavior.
= 20,2–10,1 transition, which is predicted around 10.8 GHz. A group of more than 20 paramagnetic lines were observed in the 10.7 GHz region. The 30,3 –20,2, 40,4 –30,3, and 50,5 –40,4 transitions were then searched around 16.1, 21.5, and 26.8 GHz. Three groups of paramagnetic lines with a similar spectral pattern to that observed in the 10.7 GHz region were found around these frequencies. Figure 2 shows the recorded spectra for the a-type Ka = 0 rotational transitions. The HC3HCN radical was readily confirmed as the spectral carrier based on the following arguments. (i) The observed transition frequencies agree well with the calculated frequencies, (ii) each transition has a hyperfine spectral structure similar to that expected for an open-shell species with three coupling nuclei, and (iii) the lines exhibit the paramagnetic behavior.
The hyperfine components for these four transitions were analyzed using an appropriate Hamiltonian for an asymmetric top molecule with a doublet electronic state (2 A″) and the centrifugal distortion expressed in Watson’s A-reduced form (Watson 1967). The employed Hamiltonian has the following form:
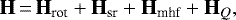 (1)
(1)
where Hrot contains rotational and centrifugal distortion parameters, Hsr is the spin-rotation term, Hmhf represents the magnetic hyperfine coupling interaction term due to the hydrogen and nitrogen nuclei, and HQ represents the nuclear electric quadrupole interaction due to the nitrogen nucleus. A complete description of these terms can be found in Hirota (1985). The coupling scheme used is J = N + S, F1 = J + I1, F2 = F1 + I2, and F = F2 + I3, where I1 = I(Hβ), I2 = I(Hα) and I3 = I(N).
An initial fit to the Ka = 0 transition frequencies provided a first set of experimental constants for HC3HCN, which was later on refined. The following assignment was performed in a classical bootstrap manner, where assigned transitions were used to improve the frequency predictions and to search for new ones. In this manner, we measured six Ka = 1 a-type transitions with N = 2, 3, and 4 and two b-type Q-branch transitions, 11,0 –10,1 and 21,1 –20,2. The final dataset consists of 193 hyperfine components that originated from 12 rotational transitions. Table A.1 contains theexperimental and calculated frequencies for all the observed hyperfine components as well as their relative intensities within a particular rotational transition, normalized to the degeneracy of the lower level. Twenty-two molecular constants were determined by the least-squares analysis for all the observed transition frequencies. The standard deviation of the fit is 2.0 kHz, which is slightly smaller than the experimental accuracy of the measurements, indicating that the complicated hyperfine structures caused by the three nuclei are well described by the employed Hamiltonian. The determined molecular constants are summarized in Table 1 along with those predicted by ab initio calculations.
Spectroscopic parameters of HC3HCN (all in MHz).
5 Discussion
As mentioned before, a total of 22 molecular constants were determined from the fit. For 2 of them, εab and 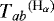 , only the relative signs could be determined. In addition to these 22 parameters, we included in the fit 3 parameters,
, only the relative signs could be determined. In addition to these 22 parameters, we included in the fit 3 parameters, 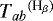 ,
, 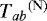 , and
, and 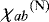 , fixed to the theoretical values. This resulted in an improvement of the standard deviation of the fit from 2.4 kHz to the final deviation of 2.0 kHz. In general, Table 1 shows that the experimentally determined values agreewell with the ab initio ones, which implies that the calculated molecular structure is reasonable. The B and C calculated constants show relative errors from the experimental values of 0.7 and 0.9%, respectively. In contrast, the relative error for the A constant is fairly large, around 4.3%. We tried to reproduce the experimental value of the A constant by increasing the level of calculation, but no better results were found. We also considered that this discrepancy could be due to the vibrational contribution. However, our vibration-rotation calculations showed that this contribution is not that large, it is smaller than 0.5%.
, fixed to the theoretical values. This resulted in an improvement of the standard deviation of the fit from 2.4 kHz to the final deviation of 2.0 kHz. In general, Table 1 shows that the experimentally determined values agreewell with the ab initio ones, which implies that the calculated molecular structure is reasonable. The B and C calculated constants show relative errors from the experimental values of 0.7 and 0.9%, respectively. In contrast, the relative error for the A constant is fairly large, around 4.3%. We tried to reproduce the experimental value of the A constant by increasing the level of calculation, but no better results were found. We also considered that this discrepancy could be due to the vibrational contribution. However, our vibration-rotation calculations showed that this contribution is not that large, it is smaller than 0.5%.
If scaled by the rotational constants, the spin-rotation interaction constants determined for HC3HCN are similar to those for the CH2C3N isomer, as shown in Table 2. The A, B, and C constants for CH2C3N are 288 000, 2195.08395, and 2177.77590 MHz, respectively (Tang et al. 2001). This implies that the two radicals have a nearly equal-energy excited states, 2B2 in the case of CH2C3N and 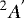 for HC3HCN, which contribute mainly to the spin-rotation interaction constants in the ground state through the spin-orbit coupling. The Fermi coupling constants give direct information of the unpaired electron density on the nuclei. The
for HC3HCN, which contribute mainly to the spin-rotation interaction constants in the ground state through the spin-orbit coupling. The Fermi coupling constants give direct information of the unpaired electron density on the nuclei. The 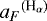 and
and 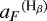 have negative values due to the spin-polarization in the C-H bonds. The difference in the absolute values between
have negative values due to the spin-polarization in the C-H bonds. The difference in the absolute values between 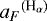 and
and 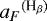 indicate that the unpaired electron density in C1 is lower than that in C3. This is consistent with the predictions of the molecular structure and the unpaired electron orbital depicted in Fig. 3.
indicate that the unpaired electron density in C1 is lower than that in C3. This is consistent with the predictions of the molecular structure and the unpaired electron orbital depicted in Fig. 3.
As shown in Table 2, the 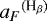 value is very similar to that found for the hydrogen nuclei of CH2C3N. Hence, it can be inferred that the unpaired electron density in C1 of CH2C3N is very muchlike that in C3 of HC3HCN, which is illustrated in Fig. 3. As for the nitrogen nucleus, the aF constant is almost similar in HC3HCN and CH2C3N. On the other hand, the determined Taa and Tbb constants for the nitrogen nucleus in HC3HCN are very similar and roughly satisfy the relation Tcc = −2Taa = −2Tbb. This indicates that the orientation of the unpaired electron is along the c-axis and occupies a pπ molecular orbital extending perpendicular to the molecular plane. This is shown in Fig. 3. The values for Taa and Tbb in both HC3HCN and CH2C3N radicals are comparable, which indicates that the unpaired electron density around the nitrogen nucleus in both radicals is almost the same. All these facts reveal similarities between the ground states of both radicals.
value is very similar to that found for the hydrogen nuclei of CH2C3N. Hence, it can be inferred that the unpaired electron density in C1 of CH2C3N is very muchlike that in C3 of HC3HCN, which is illustrated in Fig. 3. As for the nitrogen nucleus, the aF constant is almost similar in HC3HCN and CH2C3N. On the other hand, the determined Taa and Tbb constants for the nitrogen nucleus in HC3HCN are very similar and roughly satisfy the relation Tcc = −2Taa = −2Tbb. This indicates that the orientation of the unpaired electron is along the c-axis and occupies a pπ molecular orbital extending perpendicular to the molecular plane. This is shown in Fig. 3. The values for Taa and Tbb in both HC3HCN and CH2C3N radicals are comparable, which indicates that the unpaired electron density around the nitrogen nucleus in both radicals is almost the same. All these facts reveal similarities between the ground states of both radicals.
Three canonical forms can be used to describe the HC3HCN radical: H–C ≡C– H–C ≡N, H–
H–C ≡N, H– = C = CH–C ≡N, and H–C ≡C–CH = C =
= C = CH–C ≡N, and H–C ≡C–CH = C = 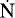 . The calculated bond lengths for HC3HCN are 1.217 Å, 1.385 Å, 1.407 Å, and 1.164 Åfor C1 –C2, C2 –C3, C3 –C4, and C4–N, respectively. The bond distances C1 –C2 and C4–N are almost identical to those found in the molecule HC3N (Botschwina et al. 1993), 1.206 Åand 1.161 Åfor C–C and C–N triple bonds, respectively. The C2 –C3 and C3 –C4 lengths are slightly larger than the C–C single-bond distance in HC3N. Although the three Lewis structures are contributing to the electronic structure for the 2 A″ ground state, the ab initio geometry indicates that the H–C ≡C–
. The calculated bond lengths for HC3HCN are 1.217 Å, 1.385 Å, 1.407 Å, and 1.164 Åfor C1 –C2, C2 –C3, C3 –C4, and C4–N, respectively. The bond distances C1 –C2 and C4–N are almost identical to those found in the molecule HC3N (Botschwina et al. 1993), 1.206 Åand 1.161 Åfor C–C and C–N triple bonds, respectively. The C2 –C3 and C3 –C4 lengths are slightly larger than the C–C single-bond distance in HC3N. Although the three Lewis structures are contributing to the electronic structure for the 2 A″ ground state, the ab initio geometry indicates that the H–C ≡C– H–C ≡N form contributes slightly more than the other two. This agrees with the molecular orbital of the unpaired electron for HC3HCN shown in Fig. 3 and the values determined for the Fermi constants.
H–C ≡N form contributes slightly more than the other two. This agrees with the molecular orbital of the unpaired electron for HC3HCN shown in Fig. 3 and the values determined for the Fermi constants.
 |
Fig. 2 Four Ka = 0 a-type rotational transitions for the HC3HCN radical. For the 20,2–10,1, 30,3 –20,2, and 40,4 –30,3 transitions, additional hyperfine components, which are not shown in this figure, were also observed. The abscissa corresponds to the frequency of the lines in MHz. The spectra were achieved by 100 shots of accumulation and a step scan of 0.5 MHz with a repetition rate of 10 Hz. The coaxial arrangement of the adiabatic expansion and the resonator axis produces an instrumental Doppler doubling. The resonance frequencies are calculated as the average of the two Doppler components. |
Spin-rotation interaction, Fermi coupling, and dipole-dipole constants for HC3HCN and CH2C3N (all in MHz).
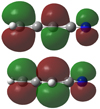 |
Fig. 3 Molecular orbital for the unpaired electron in CH2C3N (top) and HC3HCN (bottom). |
Rotational partition function for HC3HCN at different temperatures.
6 Astronomical search
From the spectroscopic parameters presented in Table 1, we generated reliable frequency predictions to guide the astronomical search for HC3HCN. The predictions have an accuracy better than 10 kHz in the Q band (30–50 GHz) and ~10–20 kHz in the W band (72–116 GHz). The rotational partition functions we used in these predictions are listed in Table 3. They were calculated considering a maximum value of N = 40. The frequency predictions for HC3HCN up to 300 GHz calculated at T = 10 and 300 K are available at the CDS, Tables A.2 and A.3 respectively.
We searched for the HC3HCN radical toward the cold dark molecular cloud TMC-1, where the CH2C3N isomer has been detected (Cabezas et al. 2021b). The spectral data employed in this work are part of the QUIJOTE1 line survey (Cernicharo et al. 2021a), performed toward TMC-1 (αJ2000 = 4h41m41.9s and δJ2000 = + 25°41′27.0″) in the Q band using the Yebes 40 m radiotelescope. The observations were performed in three different observing runs during November 2019 and April 2021. The first observing run allowed the detection of the C3N− and C5N− anions (Cernicharo et al. 2020a) and the discoveries of HC4NC (Cernicharo et al. 2020b), HC3O+ (Cernicharoet al. 2020c), and HC5NH+ (Marcelino et al. 2020). Sensitivity improvements from additional observations performed in October 2020 resulted in the detection of HDCCN (Cabezas et al. 2021c), HC3S+ (Cernicharoet al. 2021b), and CH3CO+ (Cernicharoet al. 2021b) and three isomers with the formula C4H3N (Marcelino et al. 2021). The last observing run performed between December 2020 and April 2021 resulted in new discoveries, including hydrocarbon species such as the CH2CCH radical (Agúndez et al. 2021a), CH2CHCCH and CH2CCHCCH (Cernicharo et al. 2021d,e), l-H2C5 (Cabezas et al. 2021d), c-C3HCCH, c-C5H6, and c-C9H8 (Cernicharo et al. 2021f); sulphur-bearing species such as NCS, HCCS, H2CCS, H2CCCS, C4S, HCSCN, and HCSCCH (Cernicharo et al. 2021g,h); O-bearing complex organic molecules such as C2H3CHO, C2H3OH, HCOOCH3, and CH3OCH3 (Agúndez et al. 2021b), and deuterated isotopologs such as CH2DC3N (Cabezas et al. 2021e).
All observations were carried out using the frequency-switching technique, with a frequency throw of 10 MHz during the first two observing runs and a throw of 8 MHz in the later ones. The intensity scale, the antenna temperature 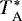 , was calibrated using two absorbers at different temperatures and the atmospheric transmission model (ATM; Cernicharo 1985; Pardo et al. 2001). Different frequency coverages were observed, 31.08–49.52 GHz and 31.98–50.42 GHz, which permit verifying that no spurious ghosts are produced in the down-conversion chain in which the signal coming from the receiver is downconverted to 1–19.5 GHz and then split into eight bands with a coverage of 2.5 GHz, each of which are analyzed by the FFTs. Calibration uncertainties were adopted to be 10% based on the observed repeatability of the line intensities between different observing runs. All data were analyzed using the GILDAS package2.
, was calibrated using two absorbers at different temperatures and the atmospheric transmission model (ATM; Cernicharo 1985; Pardo et al. 2001). Different frequency coverages were observed, 31.08–49.52 GHz and 31.98–50.42 GHz, which permit verifying that no spurious ghosts are produced in the down-conversion chain in which the signal coming from the receiver is downconverted to 1–19.5 GHz and then split into eight bands with a coverage of 2.5 GHz, each of which are analyzed by the FFTs. Calibration uncertainties were adopted to be 10% based on the observed repeatability of the line intensities between different observing runs. All data were analyzed using the GILDAS package2.
The frequency predictions were implemented in the MADEX code (Cernicharo 2012) to compute synthetic spectra assuming local thermodynamic equilibrium. We used the dipole moment components from Table 1 and assumed a rotational temperature of 7 K (Cabezas et al. 2021b) and a νLSR = 5.83 km s−1 (Cernicharo et al. 2020a). Figure 4 shows the spectrum of TMC-1 at the frequencies of selected transitions of HC3HCN, together with the synthetic spectra calculated with MADEX. Lines of HC3HCN are not clearly seen in our TMC-1 data. The sensitivity of the QUIJOTE line survey varies between 0.17 and 0.3 mK in the 31–50 GHz domain. Adopting the observed 3σ limits to the intensity of strongest components of HC3HCN, we derive a 3σ upper limit to the column density of this species in TMC-1 of 6.0 × 1011 cm−2.
Given the column density of CH2C3N in TMC-1, 1.6 × 1011 cm−2 (Cabezas et al. 2021b), the column density ratio between the two isomers HC3HCN/CH2C3N is <3.8. This means that even if HC3HCN is not detected, it could still be more abundant than CH2C3N. The nonobservation of the HC3HCN radical can be explained by the large partition function for HC3HCN compared to that for CH2C3N. For example, the partition function at 10 K for HC3HCN is 9462, while that for ortho-CH2C3N is 1718. Hence, the expected intensity of the lines of HC3HCN, assuming the same column density as for CH2C3N, will be much lower, which makes its detection more difficult. The chemistry of CH2C3N in TMC-1 has been discussed by Cabezas et al. (2021b). The main formation reactions are C + CH2CHCN, C2 + CH3CN, CN + CH2CCH, and CH3C3NH+ + e−. The best-studied of these reactions is C + CH2CHCN (Su et al. 2005; Guo et al. 2006). Theoretical calculations predict that in this reaction HC3HCN is formed five times faster than CH2C3N (Su et al. 2005), while crossed-beam experiments also favor HC3HCN as the main product, at least twice more than CH2C3N (Guo et al. 2006). It is still necessary to study the other potential routes to these radicals mentioned above. However, if the reaction C + CH2CHCN is one of the dominant routes to CH2C3N in TMC-1, as suggested by the chemical model presented by Cabezas et al. (2021b), and if this reaction produces HC3HCN with an even higher branching ratio than CH2C3N, it is likely that a deeper integration will lead to the detection of the HC3HCN radical in TMC-1. This will also allow us to better constrain the formation routes to these radicals and their role as intermediates in the buildup of large organic molecules in cold dark clouds.
 |
Fig. 4 Observed data of TMC-1 from the QUIJOTE line survey (black histogram) and synthetic spectra calculated adopting as column density the upper limit given in the text (red curve). For each rotational transition, the most intense hyperfine components are shown. The abscissa corresponds to the rest frequency assuming a local standard of rest velocity of 5.83 km s−1. The ordinate is the antenna temperature in millikelvin. |
7 Conclusion
We report the investigation of the rotational spectrum of 1-cyano propargyl radical, HC3HCN. This transient species was generated in the gas phase using an electric discharges technique and was then characterized by Fourier transform microwave spectroscopy. A total of 193 hyperfine components that originated from 12 rotational transitions were observed and analyzed with a 2A″ Hamiltonian. Accurate values for 22 molecular constants were derived from the analysis, indicating that the complicated hyperfine structures caused by the three nuclei with nonzero nuclear spin are well described by the employed Hamiltonian. The values of the hyperfine constants for the hydrogen and nitrogen nuclei were compared to those found for the CH2C3N isomer, and it seems that both radicals share some electronic similarities. Reliable frequency predictions were obtained from the molecular parameters derived from the spectroscopic analysis. These predictions were used to search for HC3HCN in TMC-1 using the QUIJOTE line survey. We cannot confirm the presence of HC3HCN in TMC-1, but we obtained a 3σ upper limit to its column density of 6.0 × 1011 cm−2.
Acknowledgements
The Spanish authors thank ERC for funding through grant ERC-2013-Syg-610256-NANOCOSMOS and Ministerio de Ciencia e Innovación for funding support through projects PID2019-106235GB-I00 and PID2019-107115GB-C21 / AEI / 10.13039/501100011033. M.A. thanks Ministerio de Ciencia e Innovación for grant RyC-2014-16277. Y.E. thanks Ministry of Science and Technology of Taiwan through grant MOST108-2113-M-009-25.
Appendix A Laboratory observed transition frequencies for HC3HCN
Observed transition frequencies for HC3HCN.
References
- Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]
- Agúndez, M., Marcelino, N., & Cernicharo, J., et al. 2018, ApJ, 861, L22 [Google Scholar]
- Agúndez, M., Cabezas, C., Tercero, B., et al. 2021a, A&A, 647, L10 [EDP Sciences] [Google Scholar]
- Agúndez, M., Marcelino, N., Tercero, B., et al. 2021b, A&A, 649, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botschwina, P., Horn, M., Seeger, S., & Flügge, J. 1993. Mol. Phys., 78, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Buhl, D., & Snyder, L. E. 1970, Nature, 228, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Cabezas, C., Guillemin, J.-C., & Endo, Y. 2016, J. Chem. Phys., 145, 184304 [Google Scholar]
- Cabezas, C., Agúndez, M., Marcelino, N., et al. 2021a, A&A, 654, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabezas, C., Agúndez, M., Marcelino, N., et al. 2021b, A&A, 654, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabezas, C., Endo, Y., Roueff, E., et al. 2021c, A&A, 646, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabezas, C., Tercero, B., Agúndez, M., et al. 2021d, A&A, 650, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabezas, C., Roueff, E., Tercero, B., et al. 2021e, A&A, 650, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, W., McCarthy, M. C., Travers, M. J., et al. 1998, ApJ, 492, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J. 1985, Internal IRAM Report (Granada: IRAM) [Google Scholar]
- Cernicharo, J. 2012, EAS Pub. Ser., 58, 251 [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Kahane, C., Gómez-González, J., & Guélin, M. 1986, A&A, 167, L5 [NASA ADS] [Google Scholar]
- Cernicharo, J., Guélin, M., Agúndez, M., et al. 2008, ApJ, 688, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Cabezas, C., Pardo, J. R., et al. 2019, A&A, 630, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Marcelino, N., Pardo, J. R., et al. 2020a, A&A, 641, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Marcelino, N., Agúndez, M., et al. 2020b, A&A, 642, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Marcelino, N., Agúndez, M., et al. 2020c, A&A, 642, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Agúndez, M., Kaiser, R., et al. 2021a, A&A, 652, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Cabezas, C., Endo, Y., et al. 2021b, A&A, 646, L3 [EDP Sciences] [Google Scholar]
- Cernicharo, J., Cabezas, C., Bailleux, S., et al. 2021c, A&A, 646, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021d, A&A, 647, L2 [EDP Sciences] [Google Scholar]
- Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021e, A&A, 647, L3 [EDP Sciences] [Google Scholar]
- Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021f, A&A, 649, L15 [EDP Sciences] [Google Scholar]
- Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021g, A&A, 648, L3 [EDP Sciences] [Google Scholar]
- Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021h, A&A, 650, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endo, Y., Kohguchi, H., & Ohshima, Y. 1994, Faraday Discuss., 97, 341 [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16 Revision A.03 [Google Scholar]
- Guélin, M., Green, S., & Thaddeus, P. 1978, ApJ, 224, L27 [CrossRef] [Google Scholar]
- Guo, Y., Gu, X., Zhang, F., et al. 2006, PCCP, 8, 5454 [CrossRef] [Google Scholar]
- Hirota, E. 1985, High-Resolution Spectroscopy of Transient Molecules (Berlin: Springer-Verlag) [CrossRef] [Google Scholar]
- Marcelino, N., Agúndez, M., Tercero, B., et al. 2020, A&A, 643, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcelino, N., Tercero, B., Agúndez, M., & Cernicharo, J. 2021, A&A, 646, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGuire, B. A. 2018, ApJS, 239, 17 [Google Scholar]
- McGuire, B. A., Burkhardt, A. M., Kalenskii, S., et al. 2018, Science, 359, 202 [Google Scholar]
- Møller, C., & Plesset, M. S. 1934, Phys. Rev., 46, 618 [Google Scholar]
- Pardo, J. R., Cernicharo, J., Serabyn, E. 2001, IEEE Trans. Antennas and Propagation, 49, 12 [Google Scholar]
- Pardo, J. R., Bermúdez, C., Cabezas, C. et al., 2020 A&A, 640, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pardo, J. R., Cabezas, C., Fonfría, J. P., et al. 2021, A&A, 652, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Gratier, P., Guzmán, V., et al. 2012, A&A, 548, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pople, J. A., Head-Gordon, M., & Raghavachari, K. 1987, J. Chem. Phys., 87, 5968 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [Google Scholar]
- Su, H.-F., Kaiser, R. I., & Chang, A. H. H. 2005, J. Chem. Phys., 122, 074320 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, H., Ohishi, M., Kaifu, N., et al. 1986, PASJ, 38, 911 [NASA ADS] [Google Scholar]
- Tang, J., Sumiyoshi, Y., & Endo, Y. 2001, ApJ, 492, 552, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Thaddeus, P., Guélin, M., & Linke, R. A. 1981, ApJ, 246, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, J. K. G. 1967, J. Chem. Phys. 46, 1935 [CrossRef] [Google Scholar]
- Werner, H.-J., Knowles, P. J., Knizia, G., et al. 2020, MOLPRO, version 2020.2 [Google Scholar]
- Woon, D. E., & Dunning, T. H. 1995, J. Chem. Phys., 103, 4572 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spin-rotation interaction, Fermi coupling, and dipole-dipole constants for HC3HCN and CH2C3N (all in MHz).
All Figures
 |
Fig. 1 Molecular structures and relative energies of the CH2C3N and HC3HCN radicals. |
| In the text | |
 |
Fig. 2 Four Ka = 0 a-type rotational transitions for the HC3HCN radical. For the 20,2–10,1, 30,3 –20,2, and 40,4 –30,3 transitions, additional hyperfine components, which are not shown in this figure, were also observed. The abscissa corresponds to the frequency of the lines in MHz. The spectra were achieved by 100 shots of accumulation and a step scan of 0.5 MHz with a repetition rate of 10 Hz. The coaxial arrangement of the adiabatic expansion and the resonator axis produces an instrumental Doppler doubling. The resonance frequencies are calculated as the average of the two Doppler components. |
| In the text | |
 |
Fig. 3 Molecular orbital for the unpaired electron in CH2C3N (top) and HC3HCN (bottom). |
| In the text | |
 |
Fig. 4 Observed data of TMC-1 from the QUIJOTE line survey (black histogram) and synthetic spectra calculated adopting as column density the upper limit given in the text (red curve). For each rotational transition, the most intense hyperfine components are shown. The abscissa corresponds to the rest frequency assuming a local standard of rest velocity of 5.83 km s−1. The ordinate is the antenna temperature in millikelvin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


