| Issue |
A&A
Volume 657, January 2022
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202141033 | |
| Published online | 14 January 2022 | |
Phase curves of small bodies from the SLOAN Moving Objects Catalog★
1
Instituto de Física Aplicada a las Ciencias y las Tecnologías, Universidad de Alicante,
San Vicent del Raspeig,
03080
Alicante,
Spain
e-mail: varobes@gmail.com
2
Instituto de Astrofísica de Andalucía, CSIC,
Apt 3004,
18080
Granada,
Spain
3
Observatório Nacional / MCTIC,
Rua General José Cristino 77,
Rio de Janeiro
20921-400,
Brazil
4
Departamento de Física Ingeniería de Sistemas y Teoría de la Señal, Universidad de Alicante,
San Vicent del Raspeig,
03080
Alicante,
Spain
5
Institut de Ciències del Cosmos (ICCUB), Universitat de Barcelona (IEEC-UB),
Martí Franquès 1,
08028
Barcelona,
Spain
Received:
9
April
2021
Accepted:
11
October
2021
Context. Extensive photometric surveys continue to produce enormous stores of data on small bodies. These data are typically sparsely obtained at arbitrary (or unknown) rotational phases. Therefore, new methods for processing such data need to be developed to make the most of these vast catalogs.
Aims. We aim to produce a method of recreating the phase curves of small bodies by considering the uncertainties introduced by the nominal errors in the magnitudes and the effect introduced by rotational variations. We use the SLOAN Moving Objects Catalog data as a benchmark to construct phase curves of all small bodies in u′, g′, r′, i′, and z′ filters. From the phase curves, we obtain the absolute magnitudes and we use them to set up the absolute colors, which are the colors of the asteroids that are not affected by changes in the phase angle.
Methods. We selected objects with ≥3 observations taken in at least one filter and spanning over a minimum of 5 degrees in the phase angle. We developed a method that combines Monte Carlo simulations and Bayesian inference to estimate the absolute magnitudes using the HG12* photometric system.
Results. We obtained almost 15 000 phase curves, with about 12 000 of these including all five filters. The absolute magnitudes and absolute colors are compatible with previously published data that support our method.
Conclusions. The method we developed is fully automatic and well suited for a run based on large amounts of data. Moreover, it includes the nominal uncertainties in the magnitudes and the whole distribution of possible rotational states of the objects producing what are possibly less precise values, that is, larger uncertainties, but more accurate, namely, closer to the actual value. To our knowledge, this work is the first to include the effect of rotational variations in such a manner.
Key words: methods: data analysis / catalogs / minor planets, asteroids: general
Full Table 2 (catalog) is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/657/A80
© ESO 2022
1 Introduction
The field of modern planetary sciences is experiencing a revolution thanks to: (1) space missions aimed at targets of interest and (2) massive databases produced as a result of extensive observational surveys. As far as point (1) is concerned, we only remark that even though they are extremely useful, space missions provide detailed information about a handful of objects. However, these data are used to impose constraints on whole populations. The two examples are: first, 67P, which was visited by ESA’s Rosetta mission (Barucci & Fulchignoni 2017, and references therein)1; and second, JAXA’s Hayabusa visit to Itokawa (Fujiwara et al. 2006, and references therein)2. Nevertheless, this approach is akin to admiring a painting at a very close range. On the other hand, extensive observational surveys produce large amounts of data, which allow us to study whole populations, their distribution in the observational parameters space, and relations. At the same time, it is more difficult to obtain detailed information about individual objects with such studies, usually because most of them have only been observed once or twice, which is much like admiring a painting from a distance, recognizing its patterns but not the details of the strokes. We present a method aimed at making the most of data provided by large observational surveys in this work.
Among the future and ongoing surveys, some of them will produce multi-wavelength photometric catalogs. Two examples include: the future Legacy Survey of Space and Time (LSST) to be carried out by the Vera C. Rubin Observatory, which will observe high numbers of small bodies (Jones et al. 2009), as well as the already published MOVIS catalog that gathers near-infrared magnitudes of small bodies from the VISTA-VHS survey (Popescu et al. 2016). In particular, for the scope of the present work, we are interested in two specific surveys: Javalambre Physics of the Accelerating Universe (J-PAS3, Benitez et al. 2014) that will observe 8000 sq degrees of the northern sky in 56 different filters (54 narrowband and two broadband), using a 2.5-m telescope, as well as the Javalambre Photometric Local Universe Survey (J-PLUS4, Cenarro et al. 2019) that is observing the same footprint as J-PAS but with 12 filters (5 of those broadband) using a 0.8-m telescope. The power of these surveys relies not only on the large footprint but also on the number of filters to be used for the observations, which provides unprecedented spectral coverage for spectro-photometry (Morate et al. 2021). Unfortunately, the data are sparse due to the observational strategy, so different filters may be observed at different epochs. Therefore, new methods must be developed to make these data useful in reference to small bodies.
With the aim of providing such a tool, we developed a combination of Monte Carlo simulations and Bayesian inference to include the effect of rotational variation between different epochs. As a test, and based on its importance in the study of small bodies, we concentrate on data produced by the SLOAN Digital Survey (York et al. 2000), whose photometric survey produced detection of several thousand moving objects, many of them linked to real objects in the survey’s Moving Objects Catalog (MOC, Ivezić et al. 2001; Jurić et al. 2002). The MOC data have been widely used to characterize diverse populations of asteroids, comets, and trans-Neptunian objects (TNOs). Some applications have also touched on the taxonomical classification of small bodies and the study of the mass distribution in the main asteroid belt (e.g., Roig & Gil-Hutton 2006; Roig et al. 2008; Gil-Hutton & Brunini 2008; Assandri & Gil-Hutton 2008; Gil-Hutton & Licandro 2010; Carvano et al. 2010; Solontoi et al. 2010, 2012; Ofek 2012; Alvarez-Candal 2013; DeMeo & Carry 2013, 2014; Hasselmann et al. 2015; Carry et al. 2016, and others). In particular, we concentrate on those objects that appear multiple times in the MOC (>15 000 with at least three different observations) in any of the five filters of the SLOAN photometric system. We aim to construct their phase curves in all filters used by the survey, providing a catalog of zero-phase magnitudes or absolute magnitudes. This work does not aim to perform an in-depth analysis of the results but to provide the community with a valuable set of data for further study.
The absolute magnitude, H, of an airless, small body is defined as the object’s apparent magnitude if illuminated by the Sun at 1 AU, while being observed from a distance of 1 AU at opposition. The importance of H comes from its well-known relation with the size of the object and its albedo (Bowell & Lumme 1979); thus, H is computedusing phase curves (PCs) that relate the change of the apparent magnitudes with the phase angle (α, which is the angular distance between the Sun and the Earth as seen from the object). Due to the characteristics of the PCs, it is necessary to (i) have observations at several different α, and (ii) to take into account the effect of the rotational variability. Therefore, a PC usually cannot be constructed with data of only one observational run (spanning just a few nights), except for near-Earth objects (NEOs) because there may not be enough coverage in α. We note that possible changes in brightness due to different apparitions (related to aspect angles) should also be included. Nevertheless, this issue is not tackled in this work.
Two different approaches can be used to create PCs. On the one hand, targeted observations of selected objects, with dedicated telescope (or telescopes) time (Carbognani et al. 2019, among others). This approach has obvious advantages: target selection, enough time to remove rotational variation (more on this in Sect. 3), and control over the overall observational setup (i.e., filter selection, range of α, etc.) On the downside, these observations can demand many telescope hours and careful planning to have maximum efficiency. On the other hand, it is possible to use the large amount of data produced by several extensive observational surveys (both ongoing and future). Key references in this regard are the almost half a million absolute magnitudes from the Minor Planets Center compiled by Oszkiewicz et al. (2011), the 250 000 Pan-STARRS absolute magnitudes (Vereš et al. 2015), the analysis of almost 100 000 asteroids from the ATLAS survey (Mahlke et al. 2021), as well as the almost 15 000 PCs from Gaia Data Release 2 (DR2) observations (Colazo et al. 2021). This second approach exerts no control over the observational setup or target selection and all work should be executed on the basis of serendipitous observations. The advantage relies on massive numbers that are several orders of magnitude larger than anything that can be done with targeted studies.
We aim in this work at constructing all possible PCs from the MOC for objects with at least three observations (different α and with a minimum spread of 5 degrees) in any of the filters. We obtain absolute magnitudes of several thousand objects that allow constructing colors at α = 0 degrees, that is, not affected by phase coloring, which could serve as templates for studying these effects. Therefore, in this work, we use data from MOC (described in Sect. 2) to create multi-wavelength phase curves (to the best of our knowledge, the only other similar approach was performed by Mahlke et al. 2021 using the cyan and orange filters of ATLAS). In order to do so, we devised a method to account for rotational variation using concepts of Bayesian statistics, shown in Sect. 3. The results are presented and discussed in Sect. 4. Finally, we draw our conclusions in Sect. 5.
2 Dataset
We use the fourth release of the MOC5 that contains 471 569 moving objects, with 220 101 linked to 104 449 small bodies. This release (the last one of the MOC, dated from 2007) includes data obtained under non-photometric conditions. We increased this database with the updated SVOMOC version (Carry et al. 2016), adding 57 646 new observations linked to 36 939 previously unidentified objects6. For simplicity, we keep the name of MOC for the input database.
The MOC contains the magnitudes u′, g′, r′, i′, and z′ 7 and their respective errors, σm (in the remainder of the text, we use m to refer to the apparent magnitude in any of the five SLOAN filters or the V filter, unless explicitly stated. We use italics when speaking about magnitudes and regular text when naming a filter). The catalog also provides the heliocentric (R) and the topocentric (Δ) distances as well as the α at the time of observation. We do not apply any cut in the database, except for the removal of any m: σm ≥ 1. We used only this quality-cut because the method is intended to be run automatically and provide, even in cases with poor coverage of the PCs or poor quality data, with a useful distribution of solutions that can later be used as priors once the databases are updated. To analyze the dataset, we devised a Python algorithm, based on our earlier work (e.g., Alvarez-Candal et al. 2016, 2019), which selects objects with at least three different α and with a minimum span of Δα ≥ 5.0 degrees (i.e., the distance between the maximum and the minimum α). We chose this value using a trial-and-error approach as a good balance between the number of objects and the quality of the results. In order to assess the reliability of our results, we compare them with four different sets of H, the first one from data compiled from the Minor Planets Center (Oszkiewicz et al. 2011), the second one from Pan-STARRS (Vereš et al. 2015), the third one from Gaia data (Colazo et al. 2021), and the last one from the ATLAS survey (Mahlke et al. 2021).
3 Analysis
To obtain the PCs, we first select a photometric model to fit the observational data. Among the several available in the literature (e.g., see Carbognani et al. 2019 for a comparison of three of them), we use the HG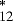 model, as described in Penttilä et al. (2016) because most objects have a sparse coverage of the PCs. The HG
model, as described in Penttilä et al. (2016) because most objects have a sparse coverage of the PCs. The HG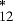 model is adapted from the HG1 G2 (Muinonen et al. 2010) and should not be confused with the HG12.
model is adapted from the HG1 G2 (Muinonen et al. 2010) and should not be confused with the HG12.
We stress that the observations in the MOC correspond to serendipitous observations of small bodies while they were crossing the field of view of the survey. Several thousand objects were observed more than once at different α, which permitted us to construct PCs in the filter system. Although observations in one run (one set of m) are taken almost simultaneously, and rotational variations could be disregarded, this is not the case for observations at different α, that were taken at an arbitrary rotational phase of the object. This is a crucial effect to be considered when creating PCs by joining data of different epochs (among other possible effects that will be mentioned below and in Sect. 4.7). In the following subsections, we discuss the computation of the PCs first and how we include the effect of the unknown amplitude of the rotational light curve (Δm).
3.1 Computation of the phase curve
The adopted form of the phase curves is:
![\begin{equation*}M(\alpha)\,{=}\,H-2.5\log{[G_1\Phi_1(\alpha)+G_2\Phi_2(\alpha)+(1-G_1-G_2)\Phi_3(\alpha)]},\end{equation*}](/articles/aa/full_html/2022/01/aa41033-21/aa41033-21-eq4.png) (1)
(1)
where M(α) = m − 5log(RΔ) is the reduced magnitude, H is the absolute magnitude, Φi are known functions of α (see Penttilä et al. 2016 for the tables), and Gi are the phase coefficients that provide the shape of the curve. In the HG model, G1 and G2 are parametrized by
model, G1 and G2 are parametrized by 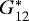 according to
according to 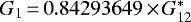 and
and 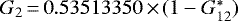 . From now on, we call
. From now on, we call 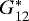 as G for simplicity unless explicitly stated otherwise, and we will not use sub-indexes to differentiate among filters unless necessary. We use the script written in Python made public by Penttilä et al. (2016)8 to compute the parameters H and G, given the values of M(α) and corresponding errors. The code returns the nominal values and an estimate of their errors based on a Monte Carlo simulation. However, we do not use their error estimates but instead compute them from our own Monte Carlo simulations because ours consider the nominal errors of the magnitudes and the possible rotational state of the objects (as described in the following sections).
as G for simplicity unless explicitly stated otherwise, and we will not use sub-indexes to differentiate among filters unless necessary. We use the script written in Python made public by Penttilä et al. (2016)8 to compute the parameters H and G, given the values of M(α) and corresponding errors. The code returns the nominal values and an estimate of their errors based on a Monte Carlo simulation. However, we do not use their error estimates but instead compute them from our own Monte Carlo simulations because ours consider the nominal errors of the magnitudes and the possible rotational state of the objects (as described in the following sections).
3.2 First test
We computed H and G for each object and filter using Eq. (1). We generated 10 000 different solutions of the PCs for each run by varying each magnitude within their errors following m * = m + randi, where randi is a random number extracted from a normal distribution with σ = σm. This is based on the method developed and tested in Alvarez-Candal et al. (2016, 2019) and Ayala-Loera et al. (2018) for TNOs. We note that it may happen that some of the 10 000 runs resulted in non-valid solutions. This means that the obtained H and G values result in PCs with no physical meaning, although being mathematically valid, for example, objects with abrupt drops (more than a couple of magnitudes) in brightness close to opposition, or objects with G outside its interval of formal validity [0, 1] (see Penttilä et al. 2016, for details). Therefore the final number of solutions is N ≤ 10 000. The outcome of a run for our test subject, 1034 T-19, in the r filter can be seen in Fig. 1 in the blue dashed line, labeled as σ only. In this case, Hr is very precisely estimated (see Table 1). Nevertheless, the quoted uncertainty (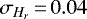 mag) does not reflect any possible effect of rotational variations in the magnitude, which will probably be larger than 0.04 based on its approximated diameter (between 3 and 6 km depending on its albedo), unless all observations were performed when the object was on a pole-on configuration. Nevertheless, we do not know this a priori, and it is unlikely that all observations were carried out based on such a configuration.
mag) does not reflect any possible effect of rotational variations in the magnitude, which will probably be larger than 0.04 based on its approximated diameter (between 3 and 6 km depending on its albedo), unless all observations were performed when the object was on a pole-on configuration. Nevertheless, we do not know this a priori, and it is unlikely that all observations were carried out based on such a configuration.
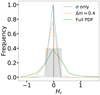 |
Fig. 1 Comparison between three different Probability Distribution Functions for the Hr of 1034 T-1. All distributions are centered at the median value of the magnitude obtained with the Full PDF. The blue dashed line considers only the errors in the magnitude, the orange dot-dashed line considers a single Δm = 0.4, and the continuous green line considers all possible values of Δm and the photometric errors (see text). The black vertical line represents the zero (i.e., the median of the Full PDF), while the shaded area covers the interval where the 68% of the solutions lie in the green curve. |
3.3 Second test
The previous test did not include the effect of any possible rotational variation between different observations. This effect can be quite dramatic. According to the light-curve database (Warner et al. 2019), there are objects with Δm = 3.0 mag, which may radically change the PCs if the effect is not taken into account. To test its effects, we ran a second test similar to the first, but in this case, instead of selecting randi from a normal distribution, we selected it from a uniform distribution ∈ [−Δmmed∕2, Δmmed∕2], where Δmmed = 0.4 is the median Δm from the whole small body population. The outcome of this test is also displayed in Fig. 1 but in orange dot-dashed line, labeled as Δm = 0.4. In this case, the distribution of Hr (called posterior distribution) is broader than in the previous test, 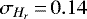 mag, which may appear as more realistic, but in this case, we are only considering one possible rotational state of the object, which mightnot be the correct one.
mag, which may appear as more realistic, but in this case, we are only considering one possible rotational state of the object, which mightnot be the correct one.
Absolute magnitude estimates for asteroid 1034 T-1.
3.4 Including Δm and σm
From the two previous tests, it is possible to see that including only the errors in the magnitudes (σm) provides a very precise value of H (see also Table 1), but it does not represent the real spread of the data (noting that we are dealing with sparse data taken at unknown rotational phases). If we only include the effect of Δm, the spread of the posterior distribution H increases, offering a lower level of precision but possibly greater overall accuracy, without significantly changing the mean (nor the median) values of H (Table 1). Nevertheless, even if we chose a similar method as in Alvarez-Candal et al. (2019), where Δm was chosen according to an estimate of H, this does not reflect the whole space of possible values that Δm could take for an object with a given H. This is because different objects with similar H may have different values of Δm. Therefore, we have adopted a new approach that includes the effect of the individual uncertainties in the magnitudes and also the whole space of possible values of Δm, that is, it includes the values of Δm for all objects with HV that are similar to the object of interest.
The method we devised includes the following steps (per object and per filter): (1) using Eq. (1), we ran 10 000 different solutions following Test 1, that is, using only σm, and applying it only to g and r; therefore, we computed Hg and Hr. Using the transformations in Table 1 of Jester et al. (2005) for all stars with R − I < 1.1510 we computed HV, obtaining its posterior distribution. We normalized this distribution to obtain a probability distribution function (PDF) in 30 bins, that is, P(HV) = {Pj(HV)}, and j is an integer ∈ [1, 30]. (2) From the distribution of Δm vs HV (Warner et al. 2019), we extracted all values Δm in each bin j in P(HV) and finally we summed them using the values of P(HV) as weights:
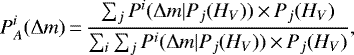 (2)
(2)
where 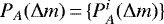 is the PDF of Δm for object A in 150 bins of width 0.02 mag, meant to cover the whole range of reported Δm ∈ [0.0, 3.0]. The denominator is a normalization factor. With this procedure, we created a PDF of possible values of Δm that the object could have (see example in Fig. 2, left panel). (3) To create the final PDF used to estimate the final range of possible solutions of H in all filters, we must also include the uncertainty in the measurement of m. In this case, we construct for each object and measurement the distribution, PA (m), as a normal distribution with σ = σm centered at m. The final PDF is the convolution of PA(m) and Eq. (2):
is the PDF of Δm for object A in 150 bins of width 0.02 mag, meant to cover the whole range of reported Δm ∈ [0.0, 3.0]. The denominator is a normalization factor. With this procedure, we created a PDF of possible values of Δm that the object could have (see example in Fig. 2, left panel). (3) To create the final PDF used to estimate the final range of possible solutions of H in all filters, we must also include the uncertainty in the measurement of m. In this case, we construct for each object and measurement the distribution, PA (m), as a normal distribution with σ = σm centered at m. The final PDF is the convolution of PA(m) and Eq. (2):
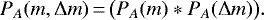 (3)
(3)
We note that in order to include realistic values of Δm in PA(m), the distribution in Fig. 2 (left) was mirrored along the y-axis and scaled by a factor 0.5 in the x-axis. This is done since an object with a givenΔm takes values of m in the domain [m − Δm∕2, m + Δm∕2] (see the final distribution in Fig. 2, right panel). Extracting 10 000 values randomly from PA(m, Δm) we ran the HG model obtaining the final values of H. The obvious consequence of our procedure is that the distribution of H is very wide(see Fig. 1 in the continuous green line, labeled as a “full PDF”, and also see the values in Table 1). We note that this is not related to the precision of H but its accuracy.
model obtaining the final values of H. The obvious consequence of our procedure is that the distribution of H is very wide(see Fig. 1 in the continuous green line, labeled as a “full PDF”, and also see the values in Table 1). We note that this is not related to the precision of H but its accuracy.
Our final results are H and G distributions for each object and filter (stored in a compressed ASCII file). The files are available upon request. An example for the Hr for the asteroid 1034 T-1 is shown in Fig. 1. We chose our representative value11 (see Table 2) as the median of the distribution and the uncertainties as to the values that enclose 68% of the solutions (seen in a continuous line and shaded region in the same figure).
 |
Fig. 2 Probability distribution functions (PDFs) used in this work. Left: example of PA (Δm), cut at 1.5 inthe x-axis for clarity, for asteroid 1034 T-1. Right: construction of the final PDF. |
4 Results and discussion
We computed H in all filters available in the MOC (see numbers in Table 3) following the procedure outlined above. In addition, we computed HV again using V obtained from g and r for each α when both magnitudes were available. Using V and the corresponding α, we processed the data the same way as all the rest. These computations have a multi-fold objective: the first is to compare our procedure with previously published works; in particular with Oszkiewicz et al. (2011, O11), Vereš et al. (2015, V15), and Colazo et al. (2021, C21). The second is to check the validity of using the HG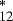 model, which is developed to obtain absolute magnitudes in the V filter. The third is aimed at future studies that will include albedos in order to estimate diameters12. We also include a comparison with Mahlke et al. (2021, M21) as other works that include multi-wavelength PCs.
model, which is developed to obtain absolute magnitudes in the V filter. The third is aimed at future studies that will include albedos in order to estimate diameters12. We also include a comparison with Mahlke et al. (2021, M21) as other works that include multi-wavelength PCs.
In Fig. 3, we show an example of the PCs for asteroid 1034 T-1 in the five filters of the SLOAN system and also in the transformed V filter. The curves represent the data satisfactorily, giving us confidence in the procedure we followed (see also Sect. 4.7 below). From the sample point of view, most objects have only three observations, although there are some with more than ten (Fig. 4, left panel), while the majority of objects are observed with αmin ~ 5 degrees. Wenote that there are objects observed from near opposition up to α ~25 degrees (Fig. 4, right panel), most of them main belt asteroids. The distributions of absolute magnitudes in all filters are displayed in Fig. 5. From the figure, it is clear that the Hu distribution is fainter than the others by about two magnitudes, which is compatible but still slightly larger, with the solar (u − g) = 1.43. Overall, a systematic decrease in brightness towards u filter indicates mostly positive spectral slopes in the Hu − Hm colors. The solar colors could explain part of this systematic, but not in full.
Sample of the catalog.
Number of absolute magnitudes obtained.
 |
Fig. 3 Phase curves in all filters for asteroid 1034 T-1. The phase function correspond to the representative values. |
 |
Fig. 4 Observational circumstances of the data used in this work. Left panel: cumulative distribution of number observations per filter for the objects in this work. Right panel: minimum α vs. span in α covered by the objects in this work. |
 |
Fig. 5 Frequency distribution of Hj obtained in this work. |
4.1 HG1G2 versus HG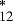
As described in Penttilä et al. (2016), the HG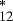 model is well suited for PCs with sparse coverage, which is the case of our work, with some limitations for some taxonomical classes (see Sect. 4.7). Nevertheless, M21 recently showed that H values obtained from the HG
model is well suited for PCs with sparse coverage, which is the case of our work, with some limitations for some taxonomical classes (see Sect. 4.7). Nevertheless, M21 recently showed that H values obtained from the HG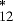 model are systematically offset from H obtained using the full HG1G2 model. Their results were obtained using ATLAS data on about 100 000 asteroids in two filters.
model are systematically offset from H obtained using the full HG1G2 model. Their results were obtained using ATLAS data on about 100 000 asteroids in two filters.
To check whether our H values are trustworthy, we ran the whole code using the full HG1G2 model and compared the absolute magnitudes obtained. The results for g are shown in Fig. 6; in all other filters, the results are qualitatively and quantitatively similar (see Table 4). We chose a percent representation of the data in the histograms to remove the impact of the actual value of H in the comparisons, for instance, a 0.5 mag difference at H = 10 implies a 5% difference, while at H = 20 it implies a 2.5%. For an object with Hg = 16, the median value in Table 4 indicates a median difference of 0.05 magnitude, which is below our median uncertainties. Therefore, we conclude that H, as computed with the HG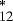 model, is well suited for our purposes. This does not preclude the possibility that in the future (if the data more aptly cover the PCs) we may adopt the HG1G2 model.
model, is well suited for our purposes. This does not preclude the possibility that in the future (if the data more aptly cover the PCs) we may adopt the HG1G2 model.
In M21,it is argued that the HG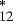 was not precise enough because of a systematic difference in the absolute magnitudes obtained and also because the
was not precise enough because of a systematic difference in the absolute magnitudes obtained and also because the 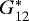 parameters they obtain tend to cluster towards 0 or 1 (see their Figs. 4 and 5). Nevertheless, we do not see the same trend in our study. Our G-values have the shape of a wide bell. We refer, as an example, to the comparison of Gcyan, Gorange, and our GV in Fig. 7.
parameters they obtain tend to cluster towards 0 or 1 (see their Figs. 4 and 5). Nevertheless, we do not see the same trend in our study. Our G-values have the shape of a wide bell. We refer, as an example, to the comparison of Gcyan, Gorange, and our GV in Fig. 7.
Comparison of absolute magnitudes.
 |
Fig. 6 Comparison between the HG1G2 and the HG |
4.2 Opposition effect impact on our estimations of H
As seen in Fig. 4 (right panel), many of the objects analyzed in this work have αmin > 5 degrees; therefore, their data do not cover the highly non-linear region of the opposition effect (OE). That may account for systematic differences between H obtained using PCs with data in the OE region with respect to data that do not. To test whether this could affect our results, we ran the code, using the HG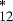 model but removing all data below 5 degrees. In this way, we can compare directly the same objects and check the impact of not covering theOE region. A comparison can be seen in Fig. 8. Numerical relevant values are shown in Table 4. We note that we restrict the comparison to the objects that had data removed; if they did not have any data below 5 degrees initially, they were left unchanged.
model but removing all data below 5 degrees. In this way, we can compare directly the same objects and check the impact of not covering theOE region. A comparison can be seen in Fig. 8. Numerical relevant values are shown in Table 4. We note that we restrict the comparison to the objects that had data removed; if they did not have any data below 5 degrees initially, they were left unchanged.
The median values are close to zero. For instance, for an object with Hg = 16, the median impact will account for a difference of 0.03 mag, well within our median uncertainties. Nevertheless, it is possible to see some substantial discrepancies, especially as some objects that come out as brighter when the low-phase angle data is removed. These Hs correspond to objects with a low number of observations, as shown in Fig. 9. In the figure, the x-axis corresponds to the number of observations in the g filter before removal. The large differences seem to be related to significant uncertainties that arise when removing one or two points at low-phase angles from original data with four to ten input points. We do not detect any other strong systematic in our results. Therefore, removing the OE region affects the uncertainty in the results when the original PC has few data points. However, we strongly underline that this does not happen for all objects. Therefore, we regard our results as trustworthy.
 |
Fig. 7 Comparison between G values, in different filters, obtained in M21 for the ATLAS survey (cyan and orange histograms) and GV in the blue histogram. |
 |
Fig. 8 Comparison between the data with and without OE. Left panel: Hg obtained by us (labeled H) against the magnitude obtained eliminating all data with α < 5 degrees. The red line indicates the 1:1 relation. Right panel: distribution of the percentage change between the obtained H. The x-axis is cut for clarity. |
 |
Fig. 9 Number of observations per percentile difference. The continuous lines enclose the region where 90% of the solutions lie. |
4.3 Comparison with other works
We compare our results with the four works mentioned above: O11, V15, C21, and M21. The first work presents over 400 000 PCs of objects using data compiled from the Minor Planets Center. As they were initially very heterogeneous in terms of observatories, instruments,and filters, these data were carefully calibrated to a V filter magnitude to be analyzed. In V15, almost a quarter of a million HV are given from the Pan-STARRS Data Release 1 (DR1). The magnitudes were computed using Monte Carlo techniques to include effects of rotational variations and taxonomy heterogeneity. The data comprised magnitudes obtained in SLOAN-like filters that were transformed to V. With this comparison, we sought to check the quality of our results with a well-tested sample. In the case of C21, they used data from the Gaia DR2. In particular, we will compare with the sample of objects observed only with the Gaia G filter (≳ 14 000 objects), without transforming it to V. Due to the scanning law used by Gaia, these data were taken with α > 10 degrees. This comparison is aimed to finding how our data compare to one of the largest databases of small bodies photometric measurements. Finally, M21 presented 127 012 PCs for 94 777 asteroids in a two-filter system: cyan and orange. The absolute magnitudes and phase coefficients were obtained using Bayesian inference and a Monte Carlo approach and reported as the mean values of the posterior distributions and the 95% high-density interval, namely, the interval where 95% of the solutions lie.
The first three works used the HG12 system as presented in Muinonen et al. (2010) and not the HG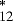 version presented in Penttilä et al. (2016), we note that O11 and V15 came out before it was published, while M21 did use the HG
version presented in Penttilä et al. (2016), we note that O11 and V15 came out before it was published, while M21 did use the HG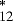 . Keep in mind that G12 and
. Keep in mind that G12 and 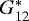 are not the same quantities. Due to this heterogeneity, we focus our comparison on the absolute magnitudes and not the phase coefficients, however, as shown below, we can draw useful information from the distribution of uncertainties of the different catalogs.
are not the same quantities. Due to this heterogeneity, we focus our comparison on the absolute magnitudes and not the phase coefficients, however, as shown below, we can draw useful information from the distribution of uncertainties of the different catalogs.
Figures 10–14 show the comparison of the H values from all researches (HV from this work, O11, and V15, HG in C21, and Hcyan/orange in M21). We can see that C21 reached a brighter population than the other four works (see the numerical comparison in Table 5). The difference cannot be explained only by the difference in the filters used: for an object with the color of the Sun (V − R) = 0.352 (from Ramírez et al. 2012) and using the transformations from Gaia system to Johnson-Cousins13, we obtain (G − V) = − 0.13. Interestingly, this result explains half the difference between our H and C21’s (see Table 5). The M21 magnitudes are also brighter than our HV, and those of O11 and V15, although not as much as C21. On the other hand, our distribution of HV is very similar (although slightly brighter, but still within one standard deviation of the distributions of ≳ 1 mag) to those of O11 and V15.
We also compared the uncertainties in the five works. We note that we defined the uncertainties as going up to the interval edges where 68% of the solutions lie. This gives asymmetric quantities when referred to the median of the distribution. In order to compare our uncertainties, we chose as the metric the uncertainty defined as ![$\{[(\sigma_{H_V}^+){}^2+(\sigma_{H_V}^-){}^2]\,{\times}\,0.5\}^{0.5}$](/articles/aa/full_html/2022/01/aa41033-21/aa41033-21-eq27.png) . The uncertainties in O11 were treated similarly. In M21, there are no reported uncertainties, but instead, magnitudes corresponding to the limits of the 95% high-density interval. We consider this interval as the formal uncertainty. It is clear from Fig. 10 that M21 and O11 have very precise values of H, with uncertainties lower than the other three14. Most of theM21 uncertainties, in both filters, lie within the first bin in the figure that is the reason for the abrupt behavior of the curve. Meanwhile, C21 has a long tail of high-uncertainty H and G. Our data seem to have greater uncertainties than O11, V15, and M21. However, they do not have the considerable uncertainties that appear for C21, especially inG. The long tail of highly uncertain values seen in C21 is possibly related to the fact that their data do not reach α <10 degrees (seealso Table 5). The authors complemented their PCs with ground-based V magnitudes (previously transforming Gaia G magnitude to V) to cover α < 10 degrees. Unfortunately, there are only six objects in common with our results, therefore precluding any reliable comparison.
. The uncertainties in O11 were treated similarly. In M21, there are no reported uncertainties, but instead, magnitudes corresponding to the limits of the 95% high-density interval. We consider this interval as the formal uncertainty. It is clear from Fig. 10 that M21 and O11 have very precise values of H, with uncertainties lower than the other three14. Most of theM21 uncertainties, in both filters, lie within the first bin in the figure that is the reason for the abrupt behavior of the curve. Meanwhile, C21 has a long tail of high-uncertainty H and G. Our data seem to have greater uncertainties than O11, V15, and M21. However, they do not have the considerable uncertainties that appear for C21, especially inG. The long tail of highly uncertain values seen in C21 is possibly related to the fact that their data do not reach α <10 degrees (seealso Table 5). The authors complemented their PCs with ground-based V magnitudes (previously transforming Gaia G magnitude to V) to cover α < 10 degrees. Unfortunately, there are only six objects in common with our results, therefore precluding any reliable comparison.
So far, we have compared all the valid datasets (noting that, e.g., in V15’s online catalog, there are lines with negative uncertainties that we do not consider valid). Then we compared the objects that are in common. We started by comparing our results with O11, then with V15 and C21, and finally with M21 (significant numbers are already displayed in Table 5). As mentioned above, it is not possible to compare the values of G because they were obtained using different definitions. Nevertheless, we can compare the absolute magnitudes obtained.
Our first comparison is with O11’s HV (Fig. 11). The red line over-plotted corresponds to a 1:1 correlation. The comparison is made over 3879 objects in common HV ∈ (10, 18). The agreement is good between both estimates of the absolute magnitudes, ours being fainter than that of O11 with a median difference of 0.23 mag, while most objects have a difference in HV between 0 and 0.5 mag. We consider the agreement to be quite good. Fig. 12 (left panel) shows the comparison between HV from this work and those published in V15. The figure shows that there is a very good agreement between both sets (8050 objects in common), given our magnitudes are slightly brighter than those of V15 (median difference −0.13 mag), while most of the objects lie between a range of 1 mag centered in 0 (right panel of Fig. 12). Next, we made a comparison with a less dense database than the others, but one that includes data that will probably become a benchmark for PC studies. In Fig. 13, we show our comparison with the Gaia DR2 data as presented by C21. There are only 521 objects in common (some of them with non-valid results). We emphasize that these authors’ results were obtained using the G filter of Gaia, which is very broad when compared with the V filter. Overall, the data seem to follow the same trend, with the C21 magnitudes shown to be brighter than ours (median difference 0.26 mag), which makes sense considering the broader nature of the Gaia G filter. In this case, it is possible to see more spread in the difference of magnitudes, while most of the objects lie between HC21 − Hours ∈ (−0.5, 1.0). Finally, we show the comparison with the ATLAS database (Mahlke et al. 2021). These data were obtained in two filters: cyan and orange, which are broader than the V filter. We have 1316 objects in common with the cyan magnitudes and 2743 with the orange magnitudes (Fig. 14). The comparison is quite good in both cases, especially with the cyan magnitudes (median difference 0.06), while our HV tends to be fainter than M21’s (median difference about 0.40). This may be because the cyan filter covers most of the V filter, while the orange filter only covers the reddest part of the V filter transmission curve.
Comparison between this work, O11, V15, C21, and M21.
 |
Fig. 10 Comparison of the frequency distributions of the uncertainties in H (left panel) and G (right panel) between this work (black continuous line), O11 (green dotted line), V15 (red dashed line), HG of C21 (blue dot-dashed), Hcyan (cyan dashed curve with big dots), and Horange (orange continuous line with big dots), the last two from M21. The x-axes were arbitrarily cut at 1 to exclude large values. |
 |
Fig. 11 Comparison between this work and O11. Left panel: comparison of HV. The red line indicates the 1:1 relation. Right panel: distribution of the differences between the obtained H. |
 |
Fig. 12 Comparison between this work and V15. Left panel: comparison of HV. The red line indicates the 1:1 relation. Right panel: distribution of the differences between the obtained H. |
 |
Fig. 13 Comparison between this work and C21. Left panel: comparison of HV and HG. The red line indicates the 1:1 relation. Right panel: distribution of the differences between the obtained H. |
 |
Fig. 14 Comparison between this work and M21. Left panel: comparison of HV and HM12. The red line indicates the 1:1 relation. The comparison with the cyan magnitudes were shifted by 3 in the y-axis for clarity. Right panel: distribution of the differences between the obtained H. |
4.4 Zero phase angle colors
Following Ayala-Loera et al. (2018) we define the absolute colors as the difference in the absolute magnitudes in different filters. We highlight that these colors are not affected by phase coloring and therefore represent a template to study these effects. The colors are shown as heat diagrams in Fig. 15. A quick comparison with Fig. 8 in Ivezić et al. (2001) shows that the space covered is similar (but reasonably lower in numbers).
In this work, we do not attempt to study the possible taxonomical distribution of our objects (as done in Oszkiewicz et al. 2012), nor its distributions. These issues will be addressed in a future work. Nevertheless, it is clear, especially when considering the right panel of Fig. 15, that we do recover the large bimodal distribution of colors, historically representingthe C and S type asteroids (see, e.g., Hasselmann et al. 2015) while also seeing a tail of object going down to (Hg− Hr) ≈ 0.7 and (Hi − Hz) < 0, associated with V-type asteroids.
 |
Fig. 15 Absolute color-color diagrams. The axes were cut to exclude a few remaining outliers. |
 |
Fig. 16 Absolute colors versus average colors: top left, u − g; top right, g − r; bottom left, r − i; bottom right, i − z. |
4.5 Absolute colors versus average colors
One of our motivations is to produce a series of data that are not affected by phase coloring and that may therefore be used with confidence to study, for example, the taxonomical distribution of objects in the main belt of asteroids. In Fig. 16, we show the weighted average of the colors per object compared with their respective absolute colors. These weighted colors were computed as the weighted average of the same data used to create the PCs. The weights are 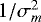 . The weighted standard deviation gives the error in each average color. Both sets of colors correlate (in all cases, the Spearman test produced rs ≳ 0.5 and
. The weighted standard deviation gives the error in each average color. Both sets of colors correlate (in all cases, the Spearman test produced rs ≳ 0.5 and 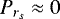 ), but it is clear that there is no one-to-one relation, reinforcing the idea that the average colors, although useful, do not necessarily represent the actual colors of the object and should be interpreted with great care.
), but it is clear that there is no one-to-one relation, reinforcing the idea that the average colors, although useful, do not necessarily represent the actual colors of the object and should be interpreted with great care.
 |
Fig. 17 Absolute colors versus the difference G for pairs of filters:top left, u − g; top right, g − r; bottom left, r − i; bottom right, i − z. |
Results from the Spearman rank-order correlation test.
4.6 Absolute colors and ΔG
We looked at the possible relationship between the absolute colors and the G values we obtained. In Fig. 17, we show the absolute colors versus the difference in G. There seem to be weak anticorrelations (see Table 6) between these quantities, possibly analogous to these found for TNOs (Ayala-Loera et al. 2018; Alvarez-Candal et al. 2019). In the latter work, we proposed it was related to a predominance of single-scattering at a low-phase angle, but the same cannot be said here; this is because, first, G is not the same as the phase coefficient β obtained from a simple linear model, and second, the PCs in this work are mostly of asteroids obtained at a wide range of phase angles (see the right panel of Fig. 4). Interestingly, in the g − r space, there seem to be two parallel sequences. We do not have a clear explanation yet, but these overall behaviors could be due to some unexplored phenomenon happening at a low-phase angle.
4.7 Warnings and caveats
We explained in Sect. 3 that we used the HG
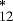 model presented by Penttilä et al. (2016). The
model presented by Penttilä et al. (2016). The 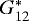 parameter is not well suited for asteroids classed as E and D-type. Nevertheless, we decided to stick to our method because we do not know the taxonomical classification of our objects a priori. In addition, the results shown in Figs. 12 and 15 and Sects. 4.1 and 4.2 give us confidence about our overall results. However, a revision will be done once we tackle the taxonomical classification of our objects.
parameter is not well suited for asteroids classed as E and D-type. Nevertheless, we decided to stick to our method because we do not know the taxonomical classification of our objects a priori. In addition, the results shown in Figs. 12 and 15 and Sects. 4.1 and 4.2 give us confidence about our overall results. However, a revision will be done once we tackle the taxonomical classification of our objects.The values we defined as representative of our quantities and the uncertainty interval work well in most cases. Nevertheless, we identified a few cases where they were not the best representatives. In these cases, probably the mean, or mode, could work better. We stress that the method presented here is fully automatic and, due to the number of objects analyzed, it is impossible to perform checks for all objects. Readers have full access, upon request, to the distributions per object and filter of H and G for performing their own analyses. We note that there are solutions that do not have physical meaning in these distributions, for instance, values of G < 0.
Our method intrinsically assumes that the variations in the brightness in all filters are due to rotational variation and that PA(Δm) is the same in all filters (i.e., due to form rather than different surface properties). We believe this is a reasonable trade-off between massive computation (and large numbers for statistics) and individual targeted studies when using integrated light from point sources, although detailed space missions observations show heterogeneity (e.g., DellaGiustina et al. 2020).
We did not apply any correction due to observations taken in different apparitions (changing aspect angle), which may be reflected in the PCs (see Fig. 10 in Mahlke et al. 2021 for an example). In the cases where this could have a significant effect, we expect it to be embedded in the posterior distributions of H and G. We stress that we did not search for cases like this.
We still do not know the possible rotational phase at which each datum was obtained. This effect may be taken into account by multiplying each value of Δm in Pi(Δm|Pj(HV)) by a random cosϕ, where ϕ is the rotational phase that takes values in [0, 2π). Preliminary tests show that this approach needs better coverage of the PCs than that provided by the MOC to improve the results.
Figure 7 shows that our values of G are distributed following bell-shape, centered more or less at values associated to C-type asteroids, see Fig. 2 in Penttilä et al. (2016), while it is expected that there should be many values at locations associated to S-type asteroids (G ≲ 0.2). This is because our G values are taken as the median of the posterior distributions determined in step 3 in Sect. 3.1.3. The median value is good for statistical analysis of large samples, but it may not be the best option when studying individual objects, as some distributions may appear flat, or bi- (or even multi-) modal.
5 Conclusions
In this work, we develop a method that combines Monte Carlo simulations and Bayesian inference to include the nominal errors in the magnitudes and the effects of rotational variations in the computation of phase curves with sparse data obtained by large photometricsurveys. We applied the method to the SLOAN MOC and computed the phase curves of almost 15 000 objects obtaining H and G in the five filter system of the SLOAN survey. We also converted from g and r to V to obtain HV and GV.
We compared our results, especially HV and our uncertainties, with published catalogs to evaluate the performance of our method with respect to others. These tests proved satisfactory, granting us confidence in the process we chose. Although the method presented was developed with J-PAS and J-PLUSsurveys in mind, it is flexible enough to be used with input magnitudes from other surveys, for instance, with data from the LSST, which will carry out observations in a similar photometric system as the MOC and will add a filter in the near-infrared, namely, the y filter (Ivezić et al. 2019). Therefore, we expect to have the capacity to apply the method to other catalogs, either multi-wavelength or otherwise. Its effectiveness in near-infrared magnitudes, or other wavelengths, is yet to be tested.
Useful information can be extracted from the absolute magnitudes when translating them to reflectance values to construct photo-spectra, while the values of G must be interpreted with care and should not be directly associated with taxonomical information. Finally, we would like to remark that the posterior distributions in H and G can be used when future data becomes available and other surveys for the same objects can be used as priors to refine the computations and improve uncertainties.
The next steps, in no particular order, of this work, include:
carrying out a cross-match with taxonomic information using the absolute colors.
using the zero-phase colors to study color variations with α.
improving our algorithm, including possible effects of changing aspect angle using the shape models derived from Gaia DR3 photometry using inversion methods (Cellino et al. 2019).
Acknowledgements
We thank the input provided by the referee who improved this manuscript. We thank M. Mahlke for useful discussions. A.A.C. acknowledges support from the Universidad de Alicante under contract UATALENTO18-02, and from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709). T.S.R. acknowledges support through grant APOSTD/2019/046 by Generalitat Valenciana (Spain). Funding for the creation and distribution of the SDSS Archive has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the U.S. Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. The SDSS Web site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium (ARC) for the Participating Institutions. The Participating Institutions are The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, the Korean Scientist Group, Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. This work is partially based on data from the SVO MOC Data Access Service at CAB (CSIC-INTA). This work used https://www.python.org/, https://www.scipy.org/, and Matplotlib (Hunter 2007).
References
- Alvarez-Candal, A. 2013, A&A, 549, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez-Candal, A., Pinilla-Alonso, N., Ortiz, J. L., et al. 2016, A&A, 586, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez-Candal, A., Ayala-Loera, C., Gil-Hutton, R., et al. 2019, MNRAS, 488, 3035 [NASA ADS] [CrossRef] [Google Scholar]
- Assandri, M. C., & Gil-Hutton, R. 2008, A&A, 488, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ayala-Loera, C., Alvarez-Candal, A., Ortiz, J. L., et al. 2018, MNRAS, 481, 1848 [NASA ADS] [CrossRef] [Google Scholar]
- Barucci, M. A., & Fulchignoni, M. 2017, A&ARv, 25, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Benitez, N., Dupke, R., Moles, M., et al. 2014, ArXiv e-prints [arXiv:1403.5237] [Google Scholar]
- Bowell, E., & Lumme, K. 1979, Colorimetry and Magnitudes of Asteroids, eds. T. Gehrels, & M. S. (Tucson: University of Arizona Press) Matthews, 132 [Google Scholar]
- Carbognani, A., Cellino, A., & Caminiti, S. 2019, Planet. Space Sci., 169, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Carry, B., Solano, E., Eggl, S., & DeMeo, F. E. 2016, Icarus, 268, 340 [CrossRef] [Google Scholar]
- Carvano, J. M., Hasselmann, P. H., Lazzaro, D., & Mothé-Diniz, T. 2010, A&A, 510, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cellino, A., Hestroffer, D., Lu, X. P., Muinonen, K., & Tanga, P. 2019, A&A, 631, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cenarro, A. J., Moles, M., Cristóbal-Hornillos, D., et al. 2019, A&A, 622, A176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colazo, M., Duffard, R., & Weidmann, W. 2021, MNRAS, 504, 761 [NASA ADS] [CrossRef] [Google Scholar]
- DellaGiustina,D. N., Burke, K. N., Walsh, K. J., et al. 2020, Science, 370, eabc3660 [NASA ADS] [CrossRef] [Google Scholar]
- DeMeo, F. E.,& Carry, B. 2013, Icarus, 226, 723 [NASA ADS] [CrossRef] [Google Scholar]
- DeMeo, F. E.,& Carry, B. 2014, Nature, 505, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Fujiwara, A., Kawaguchi, J., Yeomans, D. K., et al. 2006, Science, 312, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Gil-Hutton, R., & Brunini, A. 2008, Icarus, 193, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Gil-Hutton, R., & Licandro, J. 2010, Icarus, 206, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Hasselmann, P. H., Fulchignoni, M., Carvano, J. M., Lazzaro, D., & Barucci, M. A. 2015, A&A, 577, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Tabachnik, S., Rafikov, R., et al. 2001, AJ, 122, 2749 [Google Scholar]
- Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [Google Scholar]
- Jester, S., Schneider, D. P., Richards, G. T., et al. 2005, AJ, 130, 873 [Google Scholar]
- Jones, R. L., Chesley, S. R., Connolly, A. J., et al. 2009, Earth Moon Planets, 105, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Jurić, M., Ivezić, Ž., Lupton, R. H., et al. 2002, AJ, 124, 1776 [CrossRef] [Google Scholar]
- Mahlke, M., Carry, B., & Denneau, L. 2021, Icarus, 354, 114094 [Google Scholar]
- Morate, D., Carvano, J. M., Alvarez-Candal, A., et al. 2021, A&A, 655, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muinonen, K., Belskaya, I. N., Cellino, A., et al. 2010, Icarus, 209, 542 [Google Scholar]
- Ofek, E. O. 2012, ApJ, 749, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Oszkiewicz, D., Muinonen, K., Bowell, E., et al. 2011, J. Quant. Spectr. Rad. Transf., 112, 1919 [Google Scholar]
- Oszkiewicz, D. A., Bowell, E., Wasserman, L. H., et al. 2012, Icarus, 219, 283 [CrossRef] [Google Scholar]
- Penttilä, A., Shevchenko, V. G., Wilkman, O., & Muinonen, K. 2016, Planet. Space Sci., 123, 117 [Google Scholar]
- Popescu, M., Licandro, J., Morate, D., et al. 2016, A&A, 591, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Michel, R., Sefako, R., et al. 2012, ApJ, 752, 5 [CrossRef] [Google Scholar]
- Roig, F., & Gil-Hutton, R. 2006, Icarus, 183, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Roig, F., Ribeiro, A. O., & Gil-Hutton, R. 2008, A&A, 483, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solontoi, M., Ivezić, Ž., West, A. A., et al. 2010, Icarus, 205, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Solontoi, M., Ivezić, Ž., Jurić, M., et al. 2012, Icarus, 218, 571 [CrossRef] [Google Scholar]
- Vereš, P., Jedicke, R., Fitzsimmons, A., et al. 2015, Icarus, 261, 34 [CrossRef] [Google Scholar]
- Warner, B., Pravec, P., & Harris, A. P. 2019, Asteroid Lightcurve Data Base (LCDB) V3.0 urn:nasa:pds:ast-lightcurve-database::3.0. NASA Planetary Data System, available at https://sbn.psi.edu/pds/resource/lc.html [Google Scholar]
- York, D. G., Adelman, J., Anderson, John E., J., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Comparison between three different Probability Distribution Functions for the Hr of 1034 T-1. All distributions are centered at the median value of the magnitude obtained with the Full PDF. The blue dashed line considers only the errors in the magnitude, the orange dot-dashed line considers a single Δm = 0.4, and the continuous green line considers all possible values of Δm and the photometric errors (see text). The black vertical line represents the zero (i.e., the median of the Full PDF), while the shaded area covers the interval where the 68% of the solutions lie in the green curve. |
| In the text | |
 |
Fig. 2 Probability distribution functions (PDFs) used in this work. Left: example of PA (Δm), cut at 1.5 inthe x-axis for clarity, for asteroid 1034 T-1. Right: construction of the final PDF. |
| In the text | |
 |
Fig. 3 Phase curves in all filters for asteroid 1034 T-1. The phase function correspond to the representative values. |
| In the text | |
 |
Fig. 4 Observational circumstances of the data used in this work. Left panel: cumulative distribution of number observations per filter for the objects in this work. Right panel: minimum α vs. span in α covered by the objects in this work. |
| In the text | |
 |
Fig. 5 Frequency distribution of Hj obtained in this work. |
| In the text | |
 |
Fig. 6 Comparison between the HG1G2 and the HG |
| In the text | |
 |
Fig. 7 Comparison between G values, in different filters, obtained in M21 for the ATLAS survey (cyan and orange histograms) and GV in the blue histogram. |
| In the text | |
 |
Fig. 8 Comparison between the data with and without OE. Left panel: Hg obtained by us (labeled H) against the magnitude obtained eliminating all data with α < 5 degrees. The red line indicates the 1:1 relation. Right panel: distribution of the percentage change between the obtained H. The x-axis is cut for clarity. |
| In the text | |
 |
Fig. 9 Number of observations per percentile difference. The continuous lines enclose the region where 90% of the solutions lie. |
| In the text | |
 |
Fig. 10 Comparison of the frequency distributions of the uncertainties in H (left panel) and G (right panel) between this work (black continuous line), O11 (green dotted line), V15 (red dashed line), HG of C21 (blue dot-dashed), Hcyan (cyan dashed curve with big dots), and Horange (orange continuous line with big dots), the last two from M21. The x-axes were arbitrarily cut at 1 to exclude large values. |
| In the text | |
 |
Fig. 11 Comparison between this work and O11. Left panel: comparison of HV. The red line indicates the 1:1 relation. Right panel: distribution of the differences between the obtained H. |
| In the text | |
 |
Fig. 12 Comparison between this work and V15. Left panel: comparison of HV. The red line indicates the 1:1 relation. Right panel: distribution of the differences between the obtained H. |
| In the text | |
 |
Fig. 13 Comparison between this work and C21. Left panel: comparison of HV and HG. The red line indicates the 1:1 relation. Right panel: distribution of the differences between the obtained H. |
| In the text | |
 |
Fig. 14 Comparison between this work and M21. Left panel: comparison of HV and HM12. The red line indicates the 1:1 relation. The comparison with the cyan magnitudes were shifted by 3 in the y-axis for clarity. Right panel: distribution of the differences between the obtained H. |
| In the text | |
 |
Fig. 15 Absolute color-color diagrams. The axes were cut to exclude a few remaining outliers. |
| In the text | |
 |
Fig. 16 Absolute colors versus average colors: top left, u − g; top right, g − r; bottom left, r − i; bottom right, i − z. |
| In the text | |
 |
Fig. 17 Absolute colors versus the difference G for pairs of filters:top left, u − g; top right, g − r; bottom left, r − i; bottom right, i − z. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.