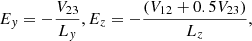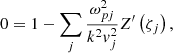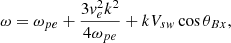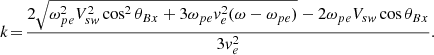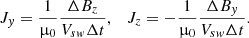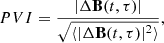| Issue |
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 13 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202140943 | |
| Published online | 14 December 2021 | |
Kinetic electrostatic waves and their association with current structures in the solar wind
1
Swedish Institute of Space Physics (IRF), Uppsala 75121, Sweden
e-mail: dgraham@irfu.se
2
Division of Space and Plasma Physics, School of Electrical Engineering and Computer Science, KTH Royal Institute of Technology, Stockholm 11428, Sweden
3
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
4
Institute of Atmospheric Physics of the Czech Academy of Sciences, Prague, Czech Republic
5
Space Sciences Laboratory, University of California, Berkeley, CA, USA
6
Physics Department, University of California, Berkeley, CA, USA
7
LPP, CNRS, Ecole Polytechnique, Sorbonne Université, Observatoire de Paris, Université Paris-Saclay, Palaiseau, Paris, France
8
LPC2E, CNRS, 3A avenue de la Recherche Scientifique, Orléans, France
9
Université d’Orléans, Orléans, France
10
CNES, 18 avenue Edouard Belin, 31400 Toulouse, France
11
Technische Universität Dresden, Helmholtz Str. 10, 01187 Dresden, Germany
12
Space Research Institute, Austrian Academy of Sciences, Graz, Austria
13
Astronomical Institute of the Czech Academy of Sciences, Prague, Czech Republic
14
Radboud Radio Lab, Department of Astrophysics, Radboud University, Nijmegen, The Netherlands
15
Imperial College London, South Kensington Campus, London SW7 2AZ, UK
Received:
30
March
2021
Accepted:
11
May
2021
Context. A variety of kinetic electrostatic and electromagnetic waves develop in the solar wind and the relationship between these waves and larger scale structures, such as current sheets and ongoing turbulence, remain a topic of investigation. Similarly, the instabilities producing ion-acoustic waves in the solar wind are still an open question.
Aims. The goals of this paper are to investigate electrostatic Langmuir and ion-acoustic waves in the solar wind at 0.5 AU and determine whether current sheets and associated streaming instabilities can produce the observed waves. The relationship between these waves and currents observed in the solar wind is investigated statistically.
Methods. Solar Orbiter’s Radio and Plasma Waves instrument suite provides high-resolution snapshots of the fluctuating electric field. The Low Frequency Receiver resolves the waveforms of ion-acoustic waves and the Time Domain Sampler resolves the waveforms of both ion-acoustic and Langmuir waves. Using these waveform data, we determine when these waves are observed in relation to current structures in the solar wind, estimated from the background magnetic field.
Results. Langmuir and ion-acoustic waves are frequently observed in the solar wind. Ion-acoustic waves are observed about 1% of the time at 0.5 AU. The waves are more likely to be observed in regions of enhanced currents. However, the waves typically do not occur at current structures themselves. The observed currents in the solar wind are too small to drive instability by the relative drift between single ion and electron populations. When multi-component ion or electron distributions are present, the observed currents may be sufficient for instabilities to occur. Ion beams are the most plausible source of ion-acoustic waves in the solar wind. The spacecraft potential is confirmed to be a reliable probe of the background electron density when comparing the peak frequencies of Langmuir waves with the plasma frequency calculated from the spacecraft potential.
Key words: solar wind / waves / turbulence
© ESO 2021
1. Introduction
The solar wind is weakly collisional and, thereby, non-Maxwellian, thus complex electron and ion distributions can develop (e.g., Marsch 2006). Such distributions may generate kinetic plasma waves in the solar wind. In the solar wind, many different types of electrostatic and electromagnetic plasma waves have been observed. These include Langmuir waves, ion-acoustic waves, electrostatic solitary waves (ESWs), whistler waves, lower hybrid waves, and Alfvén waves (e.g., Schwartz 1980).
Early wave observations in the solar wind found electrostatic oscillations measured at a few kHz (Gurnett & Anderson 1977). These oscillations have been interpreted as ion-acoustic waves Doppler-shifted to higher frequencies by the solar wind flow (Gurnett & Anderson 1977; Gurnett & Frank 1978; Gurnett et al. 1979). Additionally, nonlinear electrostatic structures such as ESWs have been observed in the solar wind (Mangeney et al. 1999; Malaspina et al. 2013). Various streaming instabilities have been proposed to generate ion-acoustic waves and ESWs. These include the electron-ion streaming instability (Bernstein & Kulsrud 1960), the ion-ion-acoustic instability (Lemons et al. 1979; Gary & Omidi 1987), and electron-electron-ion streaming instability (Lapuerta & Ahedo 2002; Norgren et al. 2015). Additionally, temperature gradients are also a possible source of ion-acoustic waves (Allan & Sanderson 1974).
In the solar wind, Langmuir waves are typically observed in the source regions of type II and type III solar radio bursts (Pulupa & Bale 2008; Graham & Cairns 2013, 2015), as well as in planetary electron foreshock regions (e.g., Filbert & Kellogg 1979). In these regions, Langmuir waves can readily reach large amplitudes (≳10 mV m−1 in the solar wind at 1 AU) (Graham & Cairns 2014, 2015). These waves are generated by the bump-on-tail instability, and undergo linear or nonlinear processes to generate radio waves at the local electron plasma frequency and the second harmonic (Ginzburg & Zhelezniakov 1958; Melrose 1980; Kellogg 1980). However, Langmuir waves have also been observed in the solar wind, which is not associated with type II and III source regions. For example, they have been observed in relation to magnetic holes (Lin et al. 1996; Briand et al. 2010). Similarly, Langmuir waves have been reported in association with solar wind current sheets (Lin et al. 1996) and magnetic reconnection (Huttunen et al. 2007).
The goal of this paper is to investigate the relation between kinetic ion-acoustic and Langmuir waves and currents observed in the solar wind. Our results show that the current densities estimated in the solar wind are too small to generate ion-acoustic waves by an electron-ion streaming instability that consists of single electron and ion distributions. Instead multi-component electron or ion distributions are required for establishing the instability. Statistically, we find that the ion-acoustic waves are weakly correlated with current structures in the solar wind. Additionally, we compare the observed frequency of Langmuir waves to the electron plasma frequency estimated from the spacecraft potential to confirm the reliability of the spacecraft potential as a probe of the background electron number density (Khotyaintsev et al. 2021).
The outline of this paper is as follows. In Sect. 2, we introduce the instruments and data used in this study. Section 3 provides a brief overview of the streaming instabilities that can generate ion-acoustic-like waves. In Sect. 4, we present observations of ion-acoustic and Langmuir waves. In Sect. 4.2, we also compare the Langmuir wave frequencies with the electron plasma frequency calculated from the spacecraft potential to confirm the reliability of the spacecraft potential as a density probe. In Sect. 5, we investigate the relationship between electrostatic waves and currents observed in the solar wind. In Sect. 6, we state our conclusions.
2. Instruments and data
In this work, we use field data from the Solar Orbiter spacecraft. We use electric field and potential data from the Low Frequency Receiver (LFR) and electric field data from the Time Domain Sampler (TDS) receiver of the Radio and Plasma Waves (RPW) instrument suite (Maksimovic et al. 2020) and magnetic field data from the Solar Orbiter Magnetometer (Horbury et al. 2020). The Magnetometer data are nominally sampled at 8 Hz. The LFR receiver provides continuous data, as well as high-frequency waveform snapshots captured at regular intervals. The LFR data come from the LF preamplifiers of the electric antennas, which have been conditioned by the BIAS unit (Maksimovic et al. 2020). The time between snapshots varies over the mission. For June 2020, snapshots were taken every 22 s, 100 s, and 300 s, with 300 s being the nominal setting. Snapshots are recorded at three different sampling rates: 256 Hz, 4 kHz, and 25 kHz. Only the 25 kHz can reliably resolve ion-acoustic waves, which typically have frequencies ranging from a few hundred Hz to several kHz, so this is the only sampling rate used in this paper. These 25 kHz snapshots have a duration of 83 ms. With these snapshots the maximum resolvable frequency is ≈10 kHz. We note that the frequency of ion-acoustic waves can exceed 10 kHz in some rare cases. The TDS receiver provides very high-resolution electric field snapshots, which are triggered by wave activity in the solar wind. The TDS data are routed directly from the HF preamplifiers (Maksimovic et al. 2020). These snapshots resolve ion-acoustic waves and Langmuir waves at the local electron plasma frequency fpe. The TDS snapshots are sampled at either 262 kHz and 524 kHz, corresponding to snapshot durations of 63 ms and 31 ms, respectively. All vector data are presented in the Spacecraft Reference Frame (SRF) coordinates, where x is Sunward, y is close to anti-aligned with the tangential direction, and z is close to the normal direction, unless otherwise stated. The probe-to-spacecraft potential Vpsp and potential differences between the probes are calculated using the three 6.5 m monopole electric antennas. By combining the measurements from the three antennas we calculate the two-dimensional electric field in the SRF y- and z-directions. The electric field E is calculated using
where V23 and V12 are the potential differences between probes 2 and 3 and 1 and 2, respectively, and Ly = 6.99 m and Lz = 6.97 m are the effective lengths in the y- and z-directions used in this paper. These effective lengths are based on the geometric lengths of the antennas and are in good agreement with estimates of the effective lengths based on deHoffman-Teller analysis using the DC electric and magnetic fields and comparing with the solar wind velocity (Steinvall et al. 2021), along with a comparison of the electric and magnetic fields associated with whistler waves (Kretzschmar et al. 2021). We apply this same calibration to both LFR and TDS potential data. We note that the TDS receiver channels were configured in three different ways to telemeter different combinations of probe potentials or potential differences between probe pairs over June 2020. The three different configurations are: (1) V1, V2, and V3, (2) V13, V21, and V32, and (3) V13, V21, and V2. In each case, the computed E agrees well with the E computed from LFR.
As an example of the calculation of E, Fig. 1 shows an ion-acoustic wave observed when LFR and TDS snapshots were recorded simultaneously. In Fig. 1 we plot the original potential data and the calculated E. Figure 1a shows the potentials V12, V13, and V23 from LFR. LFR measures V12, V23, and V1, while V13, V2, and V3 are computed on the ground during calibration. Figure 1b shows the potentials V13, V21, and V2 from TDS. We note that the measured TDS potentials differ from LFR and consist of dipole and monopole components. The y- and z-components of E from LFR and TDS are shown in Fig. 1c and d, respectively. The electric field from LFR and TDS are almost identical, as expected. Similarly, the power spectra of E, shown in Fig. 1e, from LFR and TDS are almost identical. Small differences between the signals may result from the differences between the LF and HF preamplifiers. Similar results are found for other events where LFR and TDS capture snapshots simultaneously (not shown).
 |
Fig. 1. Ion-acoustic wave simultaneously observed by the LFR and TDS receivers: (a) Potentials V12 (black), V13 (red), and V23 (blue) from LFR; (b) Potentials V13 (black), V21 (red), and V2 (blue) from TDS; (c) Ey computed from the LFR (black) and TDS receivers (red); (d) Ez computed from the LFR (black) and TDS receivers (red); (e) Power spectra of E from LFR (black) and TDS (red). The blue vertical line indicates the ion plasma frequency fpi calculated from ne, SC. |
We also use Vpsp from LFR to calculate the local solar wind electron density ne, SC, which is calibrated by comparing Vpsp with the plasma line identified from quasi-thermal noise. The details of the calibration can be found in Khotyaintsev et al. (2021). In brief, ne, SC is calculated by comparing Vpsp with ne derived from the plasma line due to quasi-thermal noise. This calibration changes for every change of the bias settings. In Sect. 4.2, we compare ne calculated with the frequencies of Langmuir waves ne, pk observed by TDS to assess the reliability of ne, SC.
In this paper, we investigate ion-acoustic and Langmuir waves observed over June 2020, when Solar Orbiter was close to its first perihelion. At this time, Solar Orbiter was located at a distance of ∼0.5 AU from the Sun.
3. Theory
In this section, we consider the theory of electrostatic kinetic instabilities, which can generate ion-acoustic waves in the solar wind. To model the instability, we use the kinetic unmagnetized electrostatic dispersion equation:
where ωp is the angular plasma frequency, k is the wave number, 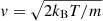 is thermal speed, ζ = (ω − kVj)/kvj, V is the bulk speed aligned with k, kB is Boltzmann’s constant, T is the temperature, m is the particle mass, Z′= − 2[1 + ζZ(ζ)] is the derivative of the plasma dispersion function Z (Fried & Conte 1961), and the subscripts j refer to the different particle species. Equation (2) assumes the distributions are Maxwellian. We consider the following three cases: (1) one electron and one ion component; (2) two electron components and one ion component; and (3) one electron component and two ion components. In each case the relative drift between difference components is the cause of instability.
is thermal speed, ζ = (ω − kVj)/kvj, V is the bulk speed aligned with k, kB is Boltzmann’s constant, T is the temperature, m is the particle mass, Z′= − 2[1 + ζZ(ζ)] is the derivative of the plasma dispersion function Z (Fried & Conte 1961), and the subscripts j refer to the different particle species. Equation (2) assumes the distributions are Maxwellian. We consider the following three cases: (1) one electron and one ion component; (2) two electron components and one ion component; and (3) one electron component and two ion components. In each case the relative drift between difference components is the cause of instability.
Figure 2 shows an example of each of these instabilities. We have chosen drift parameters marginally larger than the threshold required for growth to assess the current densities associated with each instability. In each case, the total number density is 30 cm−3, which is the median density measured over June 2020. Figure 2a shows the electron and ion distributions with a relative drift (case 1) and the associated unstable mode (Fig. 2b). The unstable mode, real frequency ω and growth rate γ, are shown, as well as the Doppler shifted dispersion relation (black dashed line) when k and the solar wind velocity Vsw are aligned for Vsw = 350 km s−1. We have used Te = 15 eV, Ti = 3 eV, and use an electron drift speed of 0.25ve. Without Doppler shift the dispersion relation has frequencies ranging from 0 at kλD = 0 to ∼ωpi at kλD = 1, where ωpi is the ion plasma frequency and λD is the Debye length. For the Doppler shifted dispersion relation we find that the frequency is substantially larger than ω in the rest frame, thus the linear dispersion relation becomes ω ≈ kVsw, i.e., the frequency increases approximately linearly with k. This is perhaps unsurprising, since the ion-acoustic speed is predicted to be CS ≈ 50 km s−1 for the conditions used in the model, and thus CS ≪ Vsw. Therefore, the observed wave frequency will typically be substantially larger than the wave frequency in the plasma rest frame, except when B and Vsw are close to perpendicular.
 |
Fig. 2. Parallel streaming instabilities and the dispersion relations of ion-acoustic waves. (a) The electron and ion distribution functions of the electron-ion streaming instability. For the electron distribution we use ne = 30 cm−3, Te = 15 eV, and Ve = 0.25ve and for the ion distribution we use ni = 30 cm−3, Ti = 3 eV. (c) The distribution for the electron-electron-ion streaming instability, consisting of core electrons and ions, and an electron beam. For core electrons we use ne = 28 cm−3 and Te = 15 eV, for core ions ni = 30 cm−3 and Ti = 3 eV, and beam electrons nb = 2 cm−3, Tb = 2 eV, and Vb = vb, where Vb and vb are the bulk and thermal speeds of the electron beam. (e) The distribution for the ion beam-driven instability, consisting of core electrons and ions and an ion beam. For core electrons we use ne = 30 cm−3, Te = 15 eV, for core ions ni = 25 cm−3 and Ti = 2 eV, and beam ions nb = 5 cm−3, Tb = 2 eV, and Vb = 4vb. Panels a, c, and e: the vertical dashed line indicates the phase speed of the unstable mode where the growth rate peaks. Panels b, d, and f: dispersion relations calculated from the distributions in panels a, c, and e, respectively. The solid black lines show the dispersion relations in the plasma rest frame or θBx = 90°, while the dashed black lines show the dispersion relations Doppler shifted due to the solar wind flow past the spacecraft for θBx = 0° and Vsw = 350 km s−1. The red curves show the growth rate γ. In panel f the higher-frequency dispersion relation is stable γ < 0 for all k, while the lower-frequency mode is unstable. |
In Fig. 2c, we show a distribution consisting of a single ion population, a core electron population, and a dense electron beam that is 6.7% of the total electron density (case 2). This relative density is consistent with the relative density of the strahl measured near 0.5 AU (Maksimovic et al. 2005). This distribution is unstable due to the electron-electron-ion instability. For these conditions the source of instability is the interaction between the electron beam and the stationary ion population. The resulting dispersion relation is almost the same as in Fig. 2b. As the beam speed is increased, the beam electrons will interact with the core electrons instead of the ions, generating beam-mode waves or electron-acoustic waves, with significantly higher phase speeds and frequencies. Thus, distributions of this form can be unstable to ion-acoustic waves or higher-frequency electrostatic waves.
In Fig. 2e, we consider the case of two ion populations (case 3), a core ion population and an ion beam, and a single electron population. For these conditions two modes in the ion plasma frequency range are found (Fig. 2f). The higher frequency mode is the ion-acoustic wave. This mode is stable for the conditions used in Fig. 2e (see caption). The lower-frequency mode is the ion-ion-acoustic mode (also called the ion beam-driven mode), which is unstable due to the interaction between the ion beam and core ion population. The dispersion relation is very similar to previous examples.
To provide an indication of the current density J required for instability, we compute J associated with the distributions in Fig. 2, using J = ∑jejnjVj, where ej is the charge of each particle species. The current densities are J = 2.8 × 103 nA m−2, 2.7 × 102 nA m−2, and 60 nA m−2 for the distributions in panels (a), (c), and (e), respectively. The value of J required for instability due to the relative drift between ions and electrons in Fig. 2a is extremely large compared with other streaming instabilities, and unlikely to occur at solar wind current sheets. When multiple electron and ion distributions are present, J required for instability can be substantially reduced from the values required when single electron and ion distributions are present. We also note that for either multi-component electron and ion distributions it is possible for instability to occur for J = 0, for example when the core and beam electrons have opposite bulk speeds relative to the ions for the electron-electron-ion instability, and vice versa for the ion-beam driven case. However, it is unclear how these distributions may form in the solar wind and might be very rare.
In summary, we propose three streaming instabilities as possible sources of ion-acoustic waves. These three instabilities produce nearly identical dispersion relations, so they cannot be distinguished from each other based on wave observations alone. Of these, the relative drift between a single ion and electron distribution is the most unlikely as this requires extremely large currents, which are unlikely to be observed in the solar wind. By allowing more complex distributions consisting of either multiple electron or ion components, the currents required for instability can be substantially reduced by over an order of magnitude, and can theoretically occur for J = 0. This makes these instabilities more plausible as sources of ion-acoustic waves in the solar wind.
4. Kinetic waves
4.1. Ion-acoustic waves
In this section we present the observation of ion-acoustic waves and show some example waveforms seen by LFR. For the purposes of this paper we include all electrostatic waves at ∼fpi and above, with frequencies f > 200 Hz. This includes nonlinear structures, such as electrostatic solitary waves. Figure 3 shows four examples of the types of waves observed by LFR. For each case we plot the time series of Ey and Ez, the time series of E∥ and E⊥, and the power spectra of E∥ and E⊥. Since we only have two components of E, we define E∥ as the component aligned with the projection of B onto the y–z plane, while E⊥ is perpendicular to B. We note that E⊥ is always perpendicular to B, while E∥ contains both parallel and perpendicular components of E, depending on the angle θBx between B and the SRF x-direction. In the case that the wave electric field is aligned with B, we expect E∥ ≫ E⊥ with E∥ underestimating the true value by sin−1θBx. In all four cases we find that E∥ ≫ E⊥, consistent with E being aligned with B. This is generally found for ion-acoustic waves seen in the LFR and TDS data. The statistical properties of ion-acoustic waves are investigated by Píša et al. (2021).
 |
Fig. 3. Four examples of ion-acoustic-like waves seen by LFR, shown in panels a–c, d–f, g–i, and j–l, respectively. For each event we plot Ey and Ez in panels a, d, g, and j, E∥ and E⊥ in b, e, h, and k, and the power spectra of E∥ and E⊥ in panels c, f, i, and l. Panels c, f, i, and l: the vertical blue line indicates the local ion plasma frequency fpi calculated from ne, SC. |
The first example, Figs. 3a–c, shows a waveform with relatively sinusoidal fluctuations in E∥ and has frequencies just above the local ion plasma frequency fpi. Compared with the other examples, the power occurs over a relatively small range of frequencies, which results in periodic fluctuations. The second example, Figs. 3d–f, shows a more complex waveform. The waveform is no longer clearly periodic, but rather the fluctuations are more complex. The power spectrum (Fig. 3f) is much broader than in the first example, and has two spectral peaks near fpi ∼ 1 kHz and ∼3 kHz. The third example, Figs. 3g–i, shows a non-sinusoidal waveform, with a broad spectral peak centered around fpi. The non-sinusoidal nature of the waves might suggest that nonlinear processes are occurring, such as the formation of solitary structures. The final example, Figs. 3j–l, shows a waveform corresponding to a series of electrostatic solitary waves (ESWs). The ESWs are characterized by bipolar fluctuations in E∥, and typically correspond to electron phase-space holes, which can evolve nonlinearly from ion-acoustic-like waves (Kakad et al. 2014; Zhou & Hutchinson 2018; Mozer et al. 2021). The ESWs are regularly spaced. For all ESWs, there is a positive E∥ followed by a negative E∥, which suggests that the ESWs all propagate in the same direction. The power spectrum (Fig. 3l) exhibits a broad range of frequencies near fpi and has a similar shape to the spectrum of the third example. In each case we find that wave power extends well above fpi and the spectral peaks typically occur above fpi. This is due to Doppler shift in the solar wind, as illustrated in Fig. 2.
We search all LFR and TDS data for ion-acoustic waves in June 2020. For the TDS data we use the following criteria: (1) The maximum electric field satisfies Emax > 0.05 mV m−1, and (2) the waves have frequencies f greater than 200 Hz. For the purposes of this search we considered all waveforms exemplified in Fig. 3, including sinusoidal waves, non-sinusoidal fluctuations, and ESWs. From TDS we identify 2553 waveform snapshots of ion-acoustic waves, corresponding to 60% of the TDS snapshots captured in June 2020. Since the TDS snapshots are triggered by wave activity ion-acoustic waves are far more likely to be observed by TDS than LFR. For LFR snapshot data we use the same search criteria, except Emax > 0.08 mV m−1, due to the higher background noise level on LFR. From the data in June 2020 we identify 423 waveform snapshots of ion-acoustic waves, which corresponds to 1.3% of all recorded snapshots. Since the LFR snapshots are taken regularly, rather than triggered by wave activity, this percentage provides an indication of how common ion-acoustic waves are in the solar wind at 0.5 AU.
4.2. Langmuir waves
Langmuir waves are electrostatic waves observed near the electron plasma frequency fpe. The waves are typically generated by electron beams. In this section, we look at the properties of Langmuir waves in the solar wind and compare the observed Langmuir wave frequencies to fpe, SC, where fpe, SC is the electron plasma frequency calculated from ne, SC.
Figure 4 shows two examples of Langmuir waves seen by TDS. In Fig. 4, we plot the potentials measured by TDS, V1, V2, and V3, the electric field in field-aligned coordinates, and power spectra of E∥ and E⊥. For both examples we find that E∥ ≫ E⊥. This is typically found for Langmuir waves seen in the solar wind by Solar Orbiter (not associated with type II or III source regions). The first example, Figs. 4a–c, shows a relatively broad spectral peak centered around fpe. This broad spectral peak may correspond to beam-mode waves rather than Langmuir waves. We note that beam-mode waves can have frequencies both below and above fpe (Fuselier et al. 1985; Soucek et al. 2019). The waveform shows that the wave is bursty, with a series of localized wave packets. The second example, Figs. 4d–f, shows a Langmuir wave with a very narrow spectral peak, just above fpe, SC. In this case, the waveform is quite localized and is characterized by E∥ ≫ E⊥. These characteristics are typical of Langmuir waves observed in the solar wind. From the peak in power we can estimate the local fpe, and hence ne, by assuming that the frequency of peak Langmuir wave power fpk corresponds to fpe. The frequencies fpe, SC and fpk are shown in Figs. 4c and f. For the first example we find that fpe, SC ≈ fpk, while for the second example fpk exceeds fpe, SC by 2.5 kHz, which could suggest that fpe, SC is underestimated at this time.
 |
Fig. 4. Two examples of Langmuir waves observed by TDS on 13 June 2020. Panels a–c: Langmuir or beam-mode wave with a relatively broad spectral peak, while panels d–f: typical example of Langmuir waves with a narrow spectral peak. Panels a,d: waveforms of the three potentials from TDS. For these cases TDS provides three monopole potentials V1 − 3 from each antenna. Panels b,e: waveforms of E∥ and E⊥. Panels c,f: power spectra of E∥ and E⊥. The blue and green vertical lines indicate fpe calculated from ne, SC and the frequency at which the power peaks fpk. |
We now investigate statistically the agreement between ne calculated from the spacecraft potential ne, SC and fpk of Langmuir waves. We search for Langmuir waves when both TDS data and spacecraft potential data are available over 2020. To search for and identify Langmuir waves we use the following criteria: (1) the frequency of peak Langmuir wave power fpk lies within 0.5fpe, SC < fpk < 1.5fpe, SC (we have checked that this range is sufficient to capture the observed Langmuir waves), where fpe, SC is the electron plasma frequency estimated from the spacecraft potential; (2) the peak wave power is two orders of magnitude above the background power in the frequency range surrounding the Langmuir waves. We inspected each of the snapshots to remove false positives due to artificial spectral peaks from spacecraft interferences. In particular, artificial spectral lines occur at ∼120 kHz due to the spacecraft power supply, and around 40 − 50 kHz, which is sometimes seen and varies with bias settings. The source of the latter spectral line is not currently known. Over 2020 we identify 961 Langmuir wave events, with 216 waveforms identified in June 2020. The statistical results are shown in Fig. 5. In Fig. 5a, we plot fpk/fpe, SC calculated from the spacecraft potential as a function of ne, SC. Each point corresponds to a TDS snapshot where we identify Langmuir waves. Overall, we find that most of the points are clustered at fpk/fpe, SC ≈ 1, with a median value of 1.05. Throughout 2020 the bias currents to the probes were changed multiple times, meaning different calibrations are required to calculate ne, SC. The points are color coded by the times when different calibrations were used (the times are given in the legend of Fig. 5a). In general, the results are similar for each calibration interval, with median values of 0.98, 1.03, 1.02, 0.98, 1.06, and 1.13 for the six time intervals (ordered sequentially in time). For the December interval fpk/fpe, SC typically exceeds 1 and has the highest median value. We note that some of the clumps of points with fpk/fpe, SC < 1 were observed in July 2020 (red crosses), when the bias currents to the probes was non-ideal resulting in a more uncertain ne, SC. In July 2020 the probes tended to saturate and some cases here may correspond to partial saturation. Figure 5b shows the density estimated from the Langmuir wave frequency ne, pk versus ne, SC. We find that there is good agreement between ne, pk and ne, SC, confirming that the spacecraft potential is reliable as a density probe. The only exception is at low ne, SC where ne, SC appears to be underestimated. These intervals were primarily observed in December when Solar Orbiter was approximately 1 AU from the Sun. This underestimation of ne, SC is likely due to the uncertainty in the calibration of ne, SC due to the difficulty of identifying the quasi-thermal noise spectral peak at low frequencies. However, from Fig. 5c where we plot ne, pk − ne, SC versus ne, SC, we see that the absolute difference between between ne, pk and ne, SC is small at low densities, and tends to increase with increasing ne, SC.
 |
Fig. 5. Comparison of Langmuir wave frequency fpk with the electron plasma frequency fpe, SC calculated from the spacecraft potential: (a) Scatterplot of fpk/fpe, SC versus ne, SC, where each point corresponds to a single TDS snapshot where Langmuir waves are observed; (b) Number density ne, pk calculated from Langmuir wave frequency versus ne, SC. (c) ne, pk − ne, SC versus ne, SC; (d) fpk/fpe, SC versus θBx. The different colored symbols correspond to the different time intervals indicated in the legend in panel a. |
We now investigate whether the observed scatter in fpk/fpe, SC can be attributed to fpk differing from the local electron plasma frequency or is due to the uncertainty in ne, SC. The linear dispersion relation of Langmuir waves in the spacecraft frame is:
where 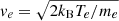 is the electron thermal speed and θBx is the angle between the solar wind flow and the wave vector k. The final term in Eq. (3) is the Doppler shift due to the plasma flow past the spacecraft. There are two effects that can cause fpk to differ from fpe, namely, the increase in frequency due to the thermal correction, and Doppler shift. We note that the Doppler shift can be both positive and negative. These effects are illustrated in Fig. 6, where we plot the dispersion relation of Langmuir waves driven by a weak electron beam. For simplicity, we use a single Maxwellian for the background electron distribution, neglecting the halo and Strahl contributions. Figure 6a shows an electron distribution consisting of a core population (ne = 30 cm−3 and Te = 15 eV) and a weak beam (nb = 3 × 10−3 cm−3, Tb = 15 eV and Vb = 7.1ve), which is unstable to Langmuir waves. Figure 6b shows the resulting dispersion relation (solid black line) for θBx = 90° (equivalent to the dispersion relation in the plasma rest frame). The fluctuation in ω around kλD = 0.1 is due to the electron beam. The red line indicates the growth and damping rate γ. For these parameters γ > 0 peaks for kλ just above 0.1 (the predicted wave number is kλD = ωpeλD/vb = 0.1 to simplest approximation). The upper and lower black dashed lines show the Doppler-shifted dispersion relations for outwardly directed k and inwardly directed k, respectively, where Vsw = 350 km s−1 is used. Figure 6b shows that there can be a significant change in the Langmuir wave frequency from fpe, if kλD becomes large enough. We note that it is possible for fpk to be slightly less than fpe if k is directed Sunward. At lower kλD, the deviation in wave frequency from fpe is primarily due to Doppler shift, while at larger kλD the thermal correction becomes more prominent. This is because the Doppler shift increases linearly with k, while the thermal correction is quadratic in k.
is the electron thermal speed and θBx is the angle between the solar wind flow and the wave vector k. The final term in Eq. (3) is the Doppler shift due to the plasma flow past the spacecraft. There are two effects that can cause fpk to differ from fpe, namely, the increase in frequency due to the thermal correction, and Doppler shift. We note that the Doppler shift can be both positive and negative. These effects are illustrated in Fig. 6, where we plot the dispersion relation of Langmuir waves driven by a weak electron beam. For simplicity, we use a single Maxwellian for the background electron distribution, neglecting the halo and Strahl contributions. Figure 6a shows an electron distribution consisting of a core population (ne = 30 cm−3 and Te = 15 eV) and a weak beam (nb = 3 × 10−3 cm−3, Tb = 15 eV and Vb = 7.1ve), which is unstable to Langmuir waves. Figure 6b shows the resulting dispersion relation (solid black line) for θBx = 90° (equivalent to the dispersion relation in the plasma rest frame). The fluctuation in ω around kλD = 0.1 is due to the electron beam. The red line indicates the growth and damping rate γ. For these parameters γ > 0 peaks for kλ just above 0.1 (the predicted wave number is kλD = ωpeλD/vb = 0.1 to simplest approximation). The upper and lower black dashed lines show the Doppler-shifted dispersion relations for outwardly directed k and inwardly directed k, respectively, where Vsw = 350 km s−1 is used. Figure 6b shows that there can be a significant change in the Langmuir wave frequency from fpe, if kλD becomes large enough. We note that it is possible for fpk to be slightly less than fpe if k is directed Sunward. At lower kλD, the deviation in wave frequency from fpe is primarily due to Doppler shift, while at larger kλD the thermal correction becomes more prominent. This is because the Doppler shift increases linearly with k, while the thermal correction is quadratic in k.
 |
Fig. 6. Example of the dispersion relation of Langmuir waves driven by the bump-on-tail instability using Eq. (2). (a) The distribution function used to calculate the dispersion relation (black line). The vertical dashed black line shows the vph of the wave correspond to maximum growth. (b) Dispersion relation of Langmuir waves (black line) and associated growth rate (red line) shifted up in frequency by ωpe. The upper and lower dashed lines show the Doppler-shifted dispersion dispersion relation for k aligned and anti-aligned with s solar wind flow of 350 km s−1. The blue shaded region shows the expected range of k and frequencies for Langmuir waves. |
We can provide a rough estimate of the wave numbers of Langmuir waves that are likely to be seen in the solar wind. From the observations, we find that the majority of Langmuir waves are approximately field-aligned E∥ ≫ E⊥. From previous observations of type III source regions, E∥ ≫ E⊥ was observed for vb/c ≲ 0.08, whereas for vb/c ≳ 0.08, Langmuir waves with strong perpendicular electric fields would also develop (Malaspina et al. 2011; Graham & Cairns 2013, 2014). This suggests that for most cases in the solar wind, vb/c ≲ 0.08, corresponding to kλD ≳ 0.07. From Fig. 6b, we find that Landau damping starts to become significant for kλD ≳ 0.25. Similarly, to excite Langmuir waves, electron beams are expected to satisfy Vb ≳ 3ve, corresponding to kλD ≲ 0.24. This also suggests that the largest probable wave number is kλD ∼ 0.25. This interval and the associated frequency range due to Doppler shift is indicated by the blue shaded region in Fig. 6b. Based on this range of kλD we find that the observed range of frequencies is 0.98 ≲ ω/ωpe ≲ 1.16, although this frequency range will increase as Vsw increases. We find that the overall median fpk/fpe is near the center of this predicted frequency range, and that ∼60% of the events in Fig. 5 lie within this frequency range.
From Fig. 6b, we see that the Doppler shifted dispersion relations have a wider range of frequencies as a function of k compared with dispersion relation without Doppler shift or θBx = 90°. Therefore, if the scatter in fpk/fpe, SC is due to the variability of the observed Langmuir wave frequency (hence, k), rather than the uncertainty in fpe, SC (estimated from the spacecraft potential), we expect to see more variability in fpk/fpe, SC as θBx decreases. In Fig. 5d, we plot fpk/fpe, SC versus θBx. We find little dependence on the scatter in fpk/fpe, SC as a function, θBx. This suggests that the uncertainty in ne, SC is too large to accurately resolve the difference in fpk and fpe. This is perhaps unsurprising since very precise estimates of ne, SC are required, and the statistical data incorporate multiple bias changes as the distance of Solar Orbiter from the Sun changes over its first orbit. However, we propose one situation below where it might be possible to quantify the difference between the Langmuir wave frequency and fpe and, hence, provide an estimate of k.
The TDS receiver is triggered by wave activity, so in some cases, a series of Langmuir wave snapshots can be captured in rapid succession, where the solar wind conditions are approximately constant. Figure 7 shows a solar wind interval observed on 2020 June 07, where we see a series of Langmuir wave snapshots. Figures 7a and b show B and ne, SC over a 90 second interval. The red crosses in Fig. 7b shows the times of the Langmuir wave snapshots and ne, pk calculated from the peak Langmuir frequency. In this interval, we find 15 Langmuir wave snapshots over a 40 second interval. The Langmuir waves are observed just prior to a narrow low-shear current sheet. When the waves are observed, the solar wind conditions are approximately constant, meaning that changes in θBx and fpe are negligible. In contrast, ne, pk and fpk change significantly, which suggests that k is changing, based on Eq. (3). In particular ne, pk varies from 45 cm−3 to 55 cm−3 (corresponding to 61 kHz ≲ fpk ≲ 67 kHz), while ne, SC remains relatively constant at 43 − 44 cm−3.
 |
Fig. 7. Langmuir waves observed near a solar wind current sheet on 2020 June 07. A series of Langmuir waves are observed with variable frequencies above the electron plasma frequency predicted from ne, SC. (a) B. (b) ne, SC. The red crosses indicate the TDS snapshots with Langmuir waves and the number density estimated from fpk. The three red shaded regions correspond to the three Langmuir wave examples in panels c–h. Panels c,e, and g: three Langmuir waveforms in field-aligned coordinates E∥ (black) and E⊥ (red). Panels d, f, and g: power spectra of E∥ (black) and E⊥ (red) associated with the Langmuir waveforms in panels c, e, and g, respectively. |
In Figs. 7c–h, we show the waveforms of three Langmuir wave snapshots and their associated power spectra, corresponding to the three red-shaded intervals in Figs. 7a and b. In all three cases, the Langmuir waves are quite localized and E∥ ≫ E⊥, similar to the event in Figs. 4d–f. In each case, the spectral peaks are quite narrow, indicating Langmuir waves rather than beam-mode waves, and fpk occurs above fpe, SC. However, we find that fpk differs in each case, while fpe, SC and θBx remain constant. This suggests that the k is changing significantly between snapshots. If we assume a constant ne = 43.5 cm−3 based on the average ne, SC we can estimate k of the Langmuir waves. From Eq. (3), we obtain
In Eq. (4), we assume k is directed outward from the Sun. We expect this to generally be the case, as electron beams exciting the Langmuir waves should originate Sunward of the spacecraft. Although there may be some cases where k is directed Sunward, such as backscattered Langmuir waves produced by three-wave electrostatic decay (e.g., Cairns 1987). Over the time interval in Fig. 7, we do not have any particle data, so we use the nominal Te = 15 eV and Vsw = 350 km s−1. Using these parameters and Eq. (4), we calculate kλD = 0.15, 0.24, and 0.20 for the Langmuir waves in Figs. 7c and d, Figs. 7e and f, and Figs. 7g and h, respectively. These values all lie within the range of expected kλD shown in Fig. 6b, which supports this method of estimating k being reasonable and ne, SC being reliable. For the Langmuir waves in this interval, we estimate the range of k to be 0.11 ≲ kλD ≲ 0.27. These values are reasonable and lie within the range of k where E∥ ≫ E⊥ is expected (Graham & Cairns 2014), which is consistent with the observations. The changes in k could result from either changes in electron beam speeds or low-amplitude density fluctuations (Smith & Sime 1979; Robinson 1992; Voshchepynets et al. 2015). Particle data is required for accurate estimations of Vsw and ve and more reliable estimations of k. However, these results show that the variability of fpk with respect to fpe, SC can in part result from the variability of k of Langmuir waves.
In summary, we find Langmuir waves throughout the first orbit of Solar Orbiter in the solar wind, which are not associated with type II or type III source regions. We compared the Langmuir wave frequencies with the electron plasma frequency calculated from the spacecraft potential. The results show that the spacecraft potential is a reliable probe of the background electron plasma density. The variability of the Langmuir wave frequency with respect to the estimated electron plasma frequency can in part be explained by the variability of the wave number of Langmuir waves.
5. Solar wind currents and waves
In this section, we estimate the currents in the solar wind and compare the occurrence of strong currents with ion-acoustic and Langmuir waves. We use two methods to identify strong currents and current structures in the solar wind, as follows.
In the first, we estimate current densities from the changes in B by assuming the current structures are frozen in to the solar wind flow. If we assume the current structures are moving with the solar wind flow we can estimate the current densities in the y–z plane using
Since the particle data is only intermittently available throughout June 2020, we simply assume Vsw = −350 km s−1 in the x-direction, which is close to the median value calculated when ion moments are available. We note that this estimate of J is most reliable when the normal to the current structure is in the x-direction, as this method assumes Jx = 0. In cases where the normal is highly oblique to the x-direction we expect J to be underestimated.
In the second, we use the Partial Variance of Increments (PVI) method to identify strong discontinuities in the solar wind. For single spacecraft measurements the PVI value is given by (Greco et al. 2008)
where ΔB(t, τ) = B(t + τ)−B(t), τ is the separation in time, and ⟨...⟩ indicates the average. Here, we calculate PVI over the entire June 2020 interval. The PVI value is increased by both changes in the magnitude of B and rotational changes (Greco et al. 2018).
To provide an overview of the currents observed over June 2020 we plot the histograms of J and PVI values over the entire month in Fig. 8. Figure 8a shows the histograms of J∥ and J⊥ (where we have used the same coordinate transformation as for E). As expected we find that the distributions peak at J = 0 and are non-Gaussian. We find that the maximum values of J∥ are ∼50 nA m−2. If we compare with the threshold currents required for instability based on Fig. 2, we find that only the ion beam driven case has a threshold J comparable to the maximum observed J∥. For the simple electron-ion streaming instability we find that the maximum observed J∥ is almost two orders of magnitude smaller than the threshold J required for instability. We note that J can be underestimated, for example, when the solar wind is slow or when current sheet normals are approximately perpendicular to the solar wind flow. However, it is highly implausible that J∥ is statistically underestimated by such a degree to make the electron-ion streaming instability possible. We conclude that the simple electron-ion streaming instability is unlikely to account for any of the observed ion-acoustic waves. For the electron-electron-ion streaming instability we find that the observed J∥ is well below the threshold based on Fig. 2. However, this instability does not have a definite threshold J because of the number of free parameters associated with the core electrons and electron beam. Additionally, it is possible that the instability can occur for J = 0, when the core and beam electrons have bulk velocities in opposite directions with respect to the ion population. Therefore, the electron-electron-ion instability remains a possible source of ion-acoustic waves.
 |
Fig. 8. Statistics of J and PVI over June 2020. (a) Histogram of J∥ (blue) and J⊥ (red). (b) Histogram of PVI using τ = 1 s (blue), 10 s (red), 60 s (gold). |
In Fig. 8b we plot the histograms of the PVI values for τ = 1 s, τ = 10 s, and τ = 60 s. For reference, for the median solar wind conditions the ion inertial length is di ≈ 40 km, which translates to a timescale of ∼0.1 s in the spacecraft frame. We use τ = 1 s to identify ion-scale current structures, while τ = 10 s and τ = 60 s will identify larger magnetohydrodynamic (MHD) scale current structures. The histograms for τ = 1 s and τ = 10 s exhibit similar features, with largest values of PVI being ≈20. For τ = 60 s the histogram is similar at low values, while the PVI values peaks around 10. Below we consider the current structures to be strong when the PVI value exceeds 5. For each τ, we find that ≈0.4% of points exceed 5. However, the number of points with PVI > 5 associated with a single structure increases as τ increases. As a result the number of distinct current structures for τ = 1 s is over an order of magnitude higher than the number identified for τ = 60 s.
To further investigate where the ion-acoustic waves and Langmuir waves are observed in relation to current structures, we show some specific solar wind intervals. In Fig. 9, we plot a 50 min solar wind interval on 2020 June 29. We plot B, ne, SC, PVI values, and J, and mark the times TDS observed ion-acoustic waves (blue-shaded regions) and Langmuir waves (red-shaded regions). Figure 9a shows that the interval is quite turbulent. While |B| remains relatively constant, current sheets are observed, in addition to fluctuations in B. The fluctuations in B and current sheets are primarily observed from 11:10 to 11:40 UT. We observe enhanced fluctuations in ne, SC in association with the fluctuations in B.
 |
Fig. 9. A turbulent solar wind interval with a clear magnetic hole observed by Solar Orbiter on 2020 June 29. (a) B. (b) ne, SC. The red crosses are ne, pk estimated from Langmuir waves. (c) PVI values for τ = 1 s (blue), 10 s (red), and 60 s (gold). (d) and (e) J in SRF and field-aligned coordinates, respectively. The blue-shaded and red-shaded regions indicate times when ion-acoustic and Langmuir wave snapshots are observed by TDS, respectively. |
Throughout this interval, we identify 18 ion-acoustic wave snapshots and 9 Langmuir wave snapshots from TDS. Most of the ion-acoustic waves are observed during the first half of the interval when the turbulent fluctuations are larger. By comparing the times of the ion-acoustic wave snapshots with when we see the largest PVI values and J, we see that the ion-acoustic waves occur when fluctuations in J are observed. However, the snapshots do not tend to occur when the PVI values or J peaks. This might suggest that the ion-acoustic waves are occurring in turbulent solar wind regions rather than being generated at the current sheets themselves. In Fig. 9, we observe all the Langmuir wave snapshots within the magnetic hole seen at 11:56 UT. The magnetic hole is observed over an approximately 40 second period. We find other magnetic holes with simultaneous Langmuir wave observations in the June 2020 period (not shown). The tendency of solar wind Langmuir waves to occur within magnetic holes was observed at 1 AU by Briand et al. (2010), and this tendency is also present closer to the Sun at 0.5 AU. Figure 9b also shows ne, pk associated with the Langmuir waves. As in the event displayed in Fig. 6, we find that ne, pk varies, indicating that fpk changes between snapshots. However, in this case the density varies across the magnetic hole to maintain pressure balance, so it is more difficult to determine if k is changing for the Langmuir waves.
As a second example of when ion-acoustic waves are observed, Fig. 10 shows a 3 hour solar wind interval from 2020 June 14. The interval in Fig. 10 is quieter than in Fig. 9. However, between 08:10 and 08:20 UT we observed very strong currents, which are amongst the strongest seen over June 2020 with a peak J close to 100 nA m−2. These currents are primarily aligned with B, although perpendicular currents are also present. The currents are associated with rapid rotations in B. At these structures |B| also increases, which is responsible for J⊥. When |B| increases there are sharp decreases in ne, SC, meaning strong density and pressure gradients are also present. At this time the largest PVI values are found, which peak at ≈20 for τ = 1 s. For τ = 10 s and 60 s we find significantly smaller PVI values, indicating that the current structures have ion spatial scales.
 |
Fig. 10. A solar wind interval by Solar Orbiter on 2020 June 14. (a) B. (b) ne, SC. (c) PVI values for τ = 1 s (blue), 10 s (red), and 60 s (gold). (d) and (e) J in SRF and field-aligned coordinates, respectively. The blue-shaded regions indicate times when ion-acoustic wave snapshots are observed by TDS. |
We find that most of ion-acoustic wave snapshots occur within this region of strong currents. We identify 19 ion-acoustic wave snapshots over the entire interval, with 11 of the snapshots being found in the region of strong currents. The remaining snapshots were observed when J was substantially smaller and spread out over the entire interval. In some cases, these waves are observed around smaller enhancements in J, while at other times ion-acoustic waves were observed when J was negligible.
From Figs. 9 and 10, we see that in some instances, there is a strong correlation of ion-acoustic waves and enhanced currents, which might suggest that large J is crucial to the generation of ion-acoustic waves. At other times we see that the detection of waves occurs in regions of strong solar wind turbulence but the ion-acoustic waves are not strongly correlated with specific current structures. Finally, we sometimes see ion-acoustic waves in quiet regions of the solar wind, which do not appear to be associated with any currents. We now consider a more statistics-based investigation of the relation between ion-acoustic wave observations and solar wind current structures.
We first consider the time between ion-acoustic wave observations and the nearest strong current structure, defined as having a maximum PVI value that exceeds 5. We calculate the time Δt between the snapshot and the nearest strong current structure. We do this for all LFR and TDS snapshots over June 2020, for both snapshots where ion-acoustic waves are observed and snapshots where we did not observe ion-acoustic waves. The results are shown in Fig. 11, where we plot the histograms of Δt for τ = 1 s, 10 s, and 60 s. The counts at the smallest 10−1 s correspond to snapshots observed at or within strong current structures. In Figs. 11a and b, we plot the histograms of Δt for LFR snapshots with ion-acoustic waves and LFR snapshots without ion-acoustic waves, respectively. Since the LFR snapshots are taken at regular times, the histograms in Fig. 11b provide distributions of the probable Δt regardless of whether ion-acoustic waves are observed or not (note that about 1% of all LFR snapshots contained ion-acoustic waves). In both Figs. 11a and b, we see that Δt increases as τ increases. This simply corresponds to smaller-scale current structures occurring more regularly than larger scale structures. This can be seen in Figs. 9 and 10. We find that when ion-acoustic waves are present the distribution of Δt is shifted to smaller values. However, only a small fraction of the ion-acoustic waves are observed at the strong current structures themselves. Most ion-acoustic waves are observed several minutes from the nearest ion-scale current structures (τ = 1 s). For ion-acoustic wave snapshots the median Δt are 3 min, 11 min, and 2 hr for τ = 1 s, 10 s, and 60 s, respectively. At times when no ion-acoustic waves are observed in the LFR snapshots, corresponding to regularly sampled times in the solar wind, the median Δt are 11 min, 40 min, and 6 hr for τ = 1 s, 10 s, and 60 s, respectively. Therefore, Δt are reduced when ion-acoustic waves are present.
 |
Fig. 11. Histograms of the time between observations of ion-acoustic waves Δt from LFR and TDS and the nearest strong current structure identified by PVI values greater than 5 for τ = 1 s (blue), 10 s (red), and 60 s (gold). (a) Histograms of Δt for ion-acoustic waves observed by LFR. (b) Histograms of Δt for LFR snapshots where we do not identify ion-acoustic waves. (c) Histograms of Δt for ion-acoustic waves observed by TDS. (d) Histograms of Δt for TDS snapshots where we do not identify ion-acoustic waves. The points at Δt = 10−1 s are snapshots at or within current structures. |
In Figs. 11c and d, we plot the histograms of Δt for TDS snapshots with and without ion-acoustic waves. In contrast to LFR, comparable numbers of snapshots with and without ion-acoustic waves are recorded. In Fig. 11c we find that the histograms of Δt are similar to those from LFR, and like the results in Fig. 11a we find that very few ion-acoustic waves were observed at the current structures themselves. We find that the median Δt are 2 min, 11 min, and 2 hr for τ = 1 s, 10 s, and 60 s, respectively, which agrees with the LFR results. When no ion-acoustic waves are observed by TDS we find significantly larger Δt, with median values of 15 min, 50 min, and 12 hrs for τ = 1 s, 10 s, and 60 s, respectively. Overall, we find that ion-acoustic waves are more likely to be observed closer to strong current structures compared to solar wind times without ion-acoustic waves. However, only a small fraction of the observed ion-acoustic waves occur at the strong current structures themselves. This suggests that the waves are either generated at the current structures and propagate away before they are observed or that the waves tend not to be generated at the most intense current structures. If we assume a weak damping rate of γ = −10−3ωpi the e-folding time is t ≈ 0.15 s. We expect the phase and group speeds to be comparable to the ion-acoustic speed Cs ∼ 50 km s−1, so the distance travelled by the waves before dissipating is only a few tens of kilometers if the waves propagate directly away from the current structure. This corresponds to Δt ≪ 1 s, which is well below the typical Δt in Fig. 11 and only accounts for a small fraction of the observed ion-acoustic waves. Therefore, it is unlikely that ion-acoustic waves being generated at the most intense current structures then propagate away from the structure can account for the observed distributions of Δt.
Finally, we consider statistically the local currents associated with ion-acoustic waves and compare them to the typical solar wind conditions to see if ion-acoustic waves are correlated with enhanced currents. To quantify the currents around the observed ion-acoustic waves we calculate the root-mean-square current Jrms over a 10 s interval, with the snapshot in the middle of the interval. We calculate these Jrms for ion-acoustic wave snapshots observed by TDS, and TDS snapshots without ion-acoustic waves. We also calculate Jrms over the entire month for comparison. Figures 12a–c show the histograms of Jrms, J‖,rms, and J⊥,rms, respectively, for all solar wind data (black), TDS snapshots with no ion-acoustic waves (blue), TDS snapshots with ion-acoustic waves (red), and LFR snapshots with ion acoustic waves (green). In each panel, we see that when ion-acoustic waves are observed, the distributions are shifted to larger Jrms, indicating that ion-acoustic waves tend to occur in regions of enhanced current. We find that J‖,rms, and J⊥,rms are both statistically larger when ion-acoustic waves are present. Over June 2020, we find a median Jrms of 1.5 nA m−2, while when ion-acoustic waves are observed by LFR and TDS the median Jrms are 2.2 nA m−2 and 2.7 nA m−2, respectively. This suggests that ion-acoustic waves are more likely to be seen in the more turbulent solar wind where the typical fluctuations in ion-scale currents are larger.
 |
Fig. 12. Histograms of the root-mean-square currents Jrms at the times when ion-acoustic and Langmuir waves are observed. Jrms are computed over 10 s intervals with the snapshot time centered in the middle. (a)–(c) Jrms, J‖,rms, and J⊥,rms for ion-acoustic wave intervals. The black curves are Jrms of all June 2020, the blue curves are TDS intervals with no ion-acoustic waves, the red curves are TDS intervals with ion-acoustic waves, and the green curves are LFR intervals with ion-acoustic waves. (d)–(f) Jrms, J‖,rms, and J⊥,rms for Langmuir wave intervals. The black curves are Jrms of all June 2020, the blue curves are TDS intervals with no Langmuir waves, the red curves are TDS intervals with Langmuir waves. |
In Figs. 12c–e, we perform the same analyses for Langmuir wave snapshots observed by TDS. We find that Langmuir waves in the solar wind are associated enhanced currents, similar to ion-acoustic waves. When Langmuir waves are present, we find a median Jrms of 2.4 nA m−2, which is comparable to the values obtained for ion-acoustic waves.
In summary, we have compared the observation of ion-acoustic and Langmuir waves with the local plasma conditions, focusing on the current density and current structures. We find that the largest observed currents are well below the threshold required for the electron-ion streaming instability. More complex streaming instabilities such as ion-beam-driven instability or electron-electron-ion streaming instabilities can occur because the threshold currents are much smaller, and they can occur for J = 0. Based on the observed currents, the ion-beam-driven instability is the most plausible source of ion-acoustic waves. This result is consistent with the recent observations of Mozer et al. (2020), who concluded that the ion-ion-acoustic instability was the most likely source of ion-acoustic waves. Statistically, we find that only rarely do the waves occur at or within regions characterized by a strong current. However, the waves more frequently occur in turbulent regions of the solar wind where strong current structures are more common. We conclude that the observed waves are likely the result of ongoing turbulence in the solar wind, which can modify the ion or electron distribution functions to generate ion-acoustic waves. Simulations have shown that ion beams can form during solar wind turbulence, which subsequently excite ion-acoustic-like waves (Valentini et al. 2008, 2011). These electrostatic waves may then play a role in energy conversion associated with ongoing turbulence in the solar wind.
6. Conclusions
In this paper, we presented observations of ion-acoustic and Langmuir waves observed by Solar Orbiter. We investigated the association of these waves with currents and current structures in the solar wind around 0.5 AU. The key results are:
-
Both the LFR and TDS receivers that are part of the RPW instrument on board Solar Orbiter frequently observe ion-acoustic waves in the solar wind at 0.5 AU. When both the LFR and TDS receivers capture waveform snapshots simultaneously, the electric field computed from the probe potentials are nearly identical, which indicates that the onboard processing is reliable for the two receivers.
-
We compared the frequency of Langmuir waves with the electron plasma frequency calculated from the spacecraft potential. We find that the peak Langmuir wave frequencies typically occur just above the calculated electron plasma frequency. This deviation from the plasma frequency is consistent with the increased frequency above the electron plasma frequency due to thermal corrections to the Langmuir dispersion relation and Doppler shift. In some cases, it may be possible to estimate the Langmuir wave number based on this frequency difference. We have provided one example to illustrate this, where multiple Langmuir waves at different frequencies are observed in uniform solar wind conditions. The estimated wave numbers of the observed Langmuir waves are in agreement with the expectations.
-
Based on the observed currents in the solar wind, we find that ion-acoustic waves cannot be driven by a simple electron-ion streaming instability. Rather, complex electron and ion distributions with multiple components are required to generate ion-acoustic waves. The electron-electron-ion streaming instability and the ion-beam-driven instability remain possible candidates for generating the ion-acoustic waves, with the ion-beam-driven instability being the most plausible.
-
We find that ion-acoustic waves are observed in the solar wind about 1% of the time at 0.5 AU. We find that Langmuir and ion-acoustic wave occurrences are associated with solar regions where currents are enhanced. However, the waves typically do not occur at current structures. It is rather the case that the waves are typically embedded in extended regions of elevated levels of current occurrences. We propose that the waves are associated with ongoing solar wind turbulence, rather than specific current structures.
Acknowledgments
We thank the Solar Orbiter team and instrument PIs for data access and support. Solar Orbiter data are available at http://soar.esac.esa.int/soar/#home. This work is supported by the Swedish National Space Agency, Grant 128/17. Solar Orbiter magnetometer operations are funded by the UK Space Agency (grant ST/T001062/1). Tim Horbury is supported by STFC grant ST/S000364/1. Solar Orbiter is a mission of international cooperation between ESA and NASA, operated by ESA. The RPW instrument has been designed and funded by CNES, CNRS, the Paris Observatory, The Swedish National Space Agency, ESA-PRODEX and all the participating institutes.
References
- Allan, W., & Sanderson, J. 1974, J. Plasma Phys., 16, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, I. B., & Kulsrud, R. M. 1960, Phys. Fluids, 3, 937 [CrossRef] [Google Scholar]
- Briand, C., Soucek, J., Henri, P., & Mangeney, A. 2010, J. Geophys. Res.: Space Phys., 115 [Google Scholar]
- Cairns, I. H. 1987, J. Plasma Phys., 38, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Filbert, P. C., & Kellogg, P. J. 1979, J. Geophys. Res.: Space Phys., 84, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Fried, B. D., & Conte, S. D. 1961, The Plasma Dispersion Function (New York: Academic Press) [Google Scholar]
- Fuselier, S. A., Gurnett, D. A., & Fitzenreiter, R. J. 1985, J. Geophys. Res., 90, 3935 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P., & Omidi, N. 1987, J. Plasma Phys., 37, 45 [CrossRef] [Google Scholar]
- Ginzburg, V. L., & Zhelezniakov, V. V. 1958, Sov. Astron., 2, 653 [Google Scholar]
- Graham, D. B., & Cairns, I. H. 2013, J. Geophys. Res., 118, 3968 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, D. B., & Cairns, I. H. 2014, J. Geophys. Res., 119, 2430 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, D. B., & Cairns, I. H. 2015, J. Geophys. Res.: Space Phys., 120, 4126 [NASA ADS] [CrossRef] [Google Scholar]
- Greco, A., Chuychai, P., Matthaeus, W. H., Servidio, S., & Dmitruk, P. 2008, Geophys. Res. Lett., 35, L19111 [Google Scholar]
- Greco, A., Matthaeus, W. H., Perri, S., et al. 2018, Space Sci. Rev., 214, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., & Anderson, R. R. 1977, J. Geophys. Res., 82, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., & Frank, L. A. 1978, J. Geophys. Res., 83, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., Marsch, E., Pilipp, W., Schwenn, R., & Rosenbauer, H. 1979, J. Geophys. Res., 84, 2029 [NASA ADS] [CrossRef] [Google Scholar]
- Horbury, T. S., OBrien, H., Carrasco Blazquez, I., et al. 2020, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huttunen, K. E. J., Bale, S. D., Phan, T. D., Davis, M., & Gosling, J. T. 2007, J. Geophys. Res., 112, A01102 [NASA ADS] [Google Scholar]
- Kakad, B., Kakad, A., & Omura, Y. 2014, J. Geophys. Res.: Space Phys., 119, 5589 [NASA ADS] [CrossRef] [Google Scholar]
- Kellogg, P. J. 1980, ApJ, 236, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Khotyaintsev, Yu. V., Graham, D. B., Vaivads, A., et al. 2021, A&A, 656, A19 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kretzschmar, M., Chust, T., Krasnoselskikh, V., et al. 2021, A&A, 656, A24 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lapuerta, V., & Ahedo, E. 2002, Phys. Plasmas, 9, 3236 [NASA ADS] [CrossRef] [Google Scholar]
- Lemons, D. S., Asbridge, J. R., Bame, S. J., et al. 1979, J. Geophys. Res.: Space Phys., 84, 2135 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, N., Kellogg, P. J., MacDowall, R. J., Tsurutani, B. T., & Ho, C. M. 1996, A&A, 316, 425 [Google Scholar]
- Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., et al. 2005, J. Geophys. Res.: Space Phys., 110 [CrossRef] [Google Scholar]
- Maksimovic, M., Bale, S. D., Chust, T., et al. 2020, A&A, 642, A12 [EDP Sciences] [Google Scholar]
- Malaspina, D. M., Cairns, I. H., & Ergun, R. E. 2011, Geophys. Res. Lett., 38, L13101 [Google Scholar]
- Malaspina, D. M., Newman, D. L., Willson, L. B., III, et al. 2013, J. Geophys. Res., 118, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Mangeney, A., Salem, C., Lacombe, C., et al. 1999, Ann. Geophys., 17, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E. 2006, Liv. Rev. Sol. Phys., 3, 1 [Google Scholar]
- Melrose, D. B. 1980, Space Sci. Rev., 26, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Mozer, F. S., Bonnell, J. W., Bowen, T. A., Schumm, G., & Vasko, I. Y. 2020, ApJ, 901, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Mozer, F. S., Bonnell, J. W., Hanson, E. L. M., Gasque, L. C., & Vasko, I. Y. 2021, ApJ, 911, 89 [CrossRef] [Google Scholar]
- Norgren, C., Andre, M., Graham, D. B., Khotyaintsev, Y. V., & Vaivads, A. 2015, Geophys. Res. Lett., 42, 7264 [NASA ADS] [CrossRef] [Google Scholar]
- Píša, D., Souček, J., Santolík, O., et al. 2021, A&A, 656, A14 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pulupa, M., & Bale, S. D. 2008, ApJ, 676, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, P. A. 1992, Sol. Phys., 139, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Schwartz, S. J. 1980, Rev. Geophys., 18, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. F., & Sime, D. 1979, ApJ, 233, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Soucek, J., Píša, D., & Santolik, O. 2019, J. Geophys. Res.: Space Phys., 124, 2380 [NASA ADS] [Google Scholar]
- Steinvall, K., Khotyaintsev, Yu. V., Cozzani, G., et al. 2021, A&A, 656, A9 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valentini, F., Veltri, P., Califano, F., & Mangeney, A. 2008, Phys. Rev. Lett., 101, 025006 [NASA ADS] [CrossRef] [Google Scholar]
- Valentini, F., Perrone, D., & Veltri, P. 2011, ApJ, 739, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Voshchepynets, A., Krasnoselskikh, V., Artemyev, A., & Volokitin, A. 2015, ApJ, 807, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, C., & Hutchinson, I. H. 2018, Phys. Plasmas, 25, 082303 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Ion-acoustic wave simultaneously observed by the LFR and TDS receivers: (a) Potentials V12 (black), V13 (red), and V23 (blue) from LFR; (b) Potentials V13 (black), V21 (red), and V2 (blue) from TDS; (c) Ey computed from the LFR (black) and TDS receivers (red); (d) Ez computed from the LFR (black) and TDS receivers (red); (e) Power spectra of E from LFR (black) and TDS (red). The blue vertical line indicates the ion plasma frequency fpi calculated from ne, SC. |
| In the text | |
 |
Fig. 2. Parallel streaming instabilities and the dispersion relations of ion-acoustic waves. (a) The electron and ion distribution functions of the electron-ion streaming instability. For the electron distribution we use ne = 30 cm−3, Te = 15 eV, and Ve = 0.25ve and for the ion distribution we use ni = 30 cm−3, Ti = 3 eV. (c) The distribution for the electron-electron-ion streaming instability, consisting of core electrons and ions, and an electron beam. For core electrons we use ne = 28 cm−3 and Te = 15 eV, for core ions ni = 30 cm−3 and Ti = 3 eV, and beam electrons nb = 2 cm−3, Tb = 2 eV, and Vb = vb, where Vb and vb are the bulk and thermal speeds of the electron beam. (e) The distribution for the ion beam-driven instability, consisting of core electrons and ions and an ion beam. For core electrons we use ne = 30 cm−3, Te = 15 eV, for core ions ni = 25 cm−3 and Ti = 2 eV, and beam ions nb = 5 cm−3, Tb = 2 eV, and Vb = 4vb. Panels a, c, and e: the vertical dashed line indicates the phase speed of the unstable mode where the growth rate peaks. Panels b, d, and f: dispersion relations calculated from the distributions in panels a, c, and e, respectively. The solid black lines show the dispersion relations in the plasma rest frame or θBx = 90°, while the dashed black lines show the dispersion relations Doppler shifted due to the solar wind flow past the spacecraft for θBx = 0° and Vsw = 350 km s−1. The red curves show the growth rate γ. In panel f the higher-frequency dispersion relation is stable γ < 0 for all k, while the lower-frequency mode is unstable. |
| In the text | |
 |
Fig. 3. Four examples of ion-acoustic-like waves seen by LFR, shown in panels a–c, d–f, g–i, and j–l, respectively. For each event we plot Ey and Ez in panels a, d, g, and j, E∥ and E⊥ in b, e, h, and k, and the power spectra of E∥ and E⊥ in panels c, f, i, and l. Panels c, f, i, and l: the vertical blue line indicates the local ion plasma frequency fpi calculated from ne, SC. |
| In the text | |
 |
Fig. 4. Two examples of Langmuir waves observed by TDS on 13 June 2020. Panels a–c: Langmuir or beam-mode wave with a relatively broad spectral peak, while panels d–f: typical example of Langmuir waves with a narrow spectral peak. Panels a,d: waveforms of the three potentials from TDS. For these cases TDS provides three monopole potentials V1 − 3 from each antenna. Panels b,e: waveforms of E∥ and E⊥. Panels c,f: power spectra of E∥ and E⊥. The blue and green vertical lines indicate fpe calculated from ne, SC and the frequency at which the power peaks fpk. |
| In the text | |
 |
Fig. 5. Comparison of Langmuir wave frequency fpk with the electron plasma frequency fpe, SC calculated from the spacecraft potential: (a) Scatterplot of fpk/fpe, SC versus ne, SC, where each point corresponds to a single TDS snapshot where Langmuir waves are observed; (b) Number density ne, pk calculated from Langmuir wave frequency versus ne, SC. (c) ne, pk − ne, SC versus ne, SC; (d) fpk/fpe, SC versus θBx. The different colored symbols correspond to the different time intervals indicated in the legend in panel a. |
| In the text | |
 |
Fig. 6. Example of the dispersion relation of Langmuir waves driven by the bump-on-tail instability using Eq. (2). (a) The distribution function used to calculate the dispersion relation (black line). The vertical dashed black line shows the vph of the wave correspond to maximum growth. (b) Dispersion relation of Langmuir waves (black line) and associated growth rate (red line) shifted up in frequency by ωpe. The upper and lower dashed lines show the Doppler-shifted dispersion dispersion relation for k aligned and anti-aligned with s solar wind flow of 350 km s−1. The blue shaded region shows the expected range of k and frequencies for Langmuir waves. |
| In the text | |
 |
Fig. 7. Langmuir waves observed near a solar wind current sheet on 2020 June 07. A series of Langmuir waves are observed with variable frequencies above the electron plasma frequency predicted from ne, SC. (a) B. (b) ne, SC. The red crosses indicate the TDS snapshots with Langmuir waves and the number density estimated from fpk. The three red shaded regions correspond to the three Langmuir wave examples in panels c–h. Panels c,e, and g: three Langmuir waveforms in field-aligned coordinates E∥ (black) and E⊥ (red). Panels d, f, and g: power spectra of E∥ (black) and E⊥ (red) associated with the Langmuir waveforms in panels c, e, and g, respectively. |
| In the text | |
 |
Fig. 8. Statistics of J and PVI over June 2020. (a) Histogram of J∥ (blue) and J⊥ (red). (b) Histogram of PVI using τ = 1 s (blue), 10 s (red), 60 s (gold). |
| In the text | |
 |
Fig. 9. A turbulent solar wind interval with a clear magnetic hole observed by Solar Orbiter on 2020 June 29. (a) B. (b) ne, SC. The red crosses are ne, pk estimated from Langmuir waves. (c) PVI values for τ = 1 s (blue), 10 s (red), and 60 s (gold). (d) and (e) J in SRF and field-aligned coordinates, respectively. The blue-shaded and red-shaded regions indicate times when ion-acoustic and Langmuir wave snapshots are observed by TDS, respectively. |
| In the text | |
 |
Fig. 10. A solar wind interval by Solar Orbiter on 2020 June 14. (a) B. (b) ne, SC. (c) PVI values for τ = 1 s (blue), 10 s (red), and 60 s (gold). (d) and (e) J in SRF and field-aligned coordinates, respectively. The blue-shaded regions indicate times when ion-acoustic wave snapshots are observed by TDS. |
| In the text | |
 |
Fig. 11. Histograms of the time between observations of ion-acoustic waves Δt from LFR and TDS and the nearest strong current structure identified by PVI values greater than 5 for τ = 1 s (blue), 10 s (red), and 60 s (gold). (a) Histograms of Δt for ion-acoustic waves observed by LFR. (b) Histograms of Δt for LFR snapshots where we do not identify ion-acoustic waves. (c) Histograms of Δt for ion-acoustic waves observed by TDS. (d) Histograms of Δt for TDS snapshots where we do not identify ion-acoustic waves. The points at Δt = 10−1 s are snapshots at or within current structures. |
| In the text | |
 |
Fig. 12. Histograms of the root-mean-square currents Jrms at the times when ion-acoustic and Langmuir waves are observed. Jrms are computed over 10 s intervals with the snapshot time centered in the middle. (a)–(c) Jrms, J‖,rms, and J⊥,rms for ion-acoustic wave intervals. The black curves are Jrms of all June 2020, the blue curves are TDS intervals with no ion-acoustic waves, the red curves are TDS intervals with ion-acoustic waves, and the green curves are LFR intervals with ion-acoustic waves. (d)–(f) Jrms, J‖,rms, and J⊥,rms for Langmuir wave intervals. The black curves are Jrms of all June 2020, the blue curves are TDS intervals with no Langmuir waves, the red curves are TDS intervals with Langmuir waves. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.