| Issue |
A&A
Volume 655, November 2021
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 20 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202141469 | |
| Published online | 24 November 2021 | |
Constraining the radius and atmospheric properties of directly imaged exoplanets through multi-phase observations
1
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin,
Hardenbergstraße 36,
10623
Berlin,
Germany
e-mail: o.carriongonzalez@astro.physik.tu-berlin.de; oscar.carrion.gonzalez@gmail.com
2
AIM, CEA, CNRS, Université Paris-Saclay, Université de Paris,
91191
Gif-sur-Yvette,
France
3
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas,
4150-762
Porto,
Portugal
4
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre,
4169-007
Porto,
Portugal
5
Deutsches Zentrum für Luft- und Raumfahrt,
Rutherfordstraße 2,
12489
Berlin,
Germany
6
Institute of Geological Sciences, Freie Universität Berlin,
Malteserstraße 74-100,
12249
Berlin,
Germany
Received:
4
June
2021
Accepted:
23
August
2021
Context. The theory of remote sensing shows that observing a planet at multiple phase angles (α) is a powerful strategy to characterize its atmosphere. Here, we study this observing strategy as applied to future disc-integrated direct imaging of exoplanets in reflected starlight.
Aims. We analyse how the information contained in reflected-starlight spectra of exoplanets depends on the phase angle and the potential of multi-phase measurements to better constrain the atmospheric properties and the planet radius (Rp).
Methods. We simulate spectra (500−900 nm) at α = 37°, 85°, and 123° with a spectral resolution of R ~ 125−225 and signal-to-noise ratio (S∕N) = 10, consistent with the expected capabilities of future direct-imaging space telescopes. Assuming a H2-He atmosphere, we use a seven-parameter model that includes the atmospheric methane abundance (fCH4), the optical properties of a cloud layer and Rp. All these parameters are assumed to be unknown a priori and are explored with a Markov chain Monte Carlo retrieval method.
Results. No single-phase observation can robustly identify whether the atmosphere has clouds or not. A single-phase observation at α = 123° and S∕N = 10 can constrain Rp with a maximum error of 35%, regardless of the cloud coverage. We find that combining small (37°) and large (123°) phase angles is a generally effective strategy to break multiple parameter degeneracies. This enables us to determine the presence or absence of a cloud and its main properties, fCH4 and Rp, with higher confidence in all the explored scenarios. Other strategies, such as doubling S∕N to 20 for a single-phase observation or combining small (37°) and moderate (85°) phase angles, fail to achieve this. We show that the improvements in multi-phase retrievals are associated with the shape of the scattering phase function of the cloud aerosols and that the improvement is more modest for isotropically scattering aerosols. We finally discuss that misidentifying the background gas in the retrievals of super-Earth observations leads to systematic underestimation of the absorbing gas abundance.
Conclusions. Exoplanets with wide ranges of observable phase angles should be prioritized for atmospheric characterization in reflected starlight.
Key words: planets and satellites: atmospheres / planets and satellites: gaseous planets / radiative transfer
© ESO 2021
1 Introduction
Directly imaging exoplanets in reflected starlight will become possible in this decade with the launch of the Nancy Grace Roman Space Telescope (hereafter, the Roman Telescope; Spergel et al. 2013). This technique will enable the atmospheric characterization of a population of cold and temperate long-period planets that cannot be studied in transit. A thorough understanding of the physical parameters of a planet that affect the reflected-starlight spectra will be required to correctly interpret such measurements. In addition, such understanding will help to define optimal observing strategies in order to better characterize exoplanets.
Several authors have studied the information content of reflected-starlight spectra through so-called retrieval studies that aim to infer the properties of a planet and its atmosphere from a measurement (e.g. Lupu et al. 2016; Nayak et al. 2017; Feng et al. 2018; Damiano & Hu 2020; Lacy et al. 2019; Carrión-González et al. 2020; Damiano et al. 2020). Given the lack of direct-imaging observations of exoplanets in reflected starlight, these retrievals use simulated measurements. For this, a synthetic spectrum is computed by solving the radiative-transfer equation for an idealized atmospheric model and some noise is added to it.
Different approaches have been explored regarding the a priori knowledge of the atmosphere in the retrieval models. For instance, some works assume the cloud composition to be known by fixing the aerosol properties to those of a particular Solar System analogue (e.g. water clouds in Feng et al. 2018). In other cases, the cloud compositionis computed following some microphysical prescriptions for a specified atmospheric temperature–pressure (T-P) profile and information on the condensation levels of the gaseous species in the model (e.g. Damiano & Hu 2020; Damiano et al. 2020). In such cases, the T-P profile can either be a reasonable guess or the result of self-consistent computation. The latter is the approach followed by Hu (2019) for example, and requires several planetary properties as input, such as the gravity, metallicity, and both the irradiation and intrinsic temperatures. The drawback of such self-consistent computations is that several of the inputs, such as the gravity, metallicity, and intrinsic temperature, will be a priori unknown for directly imaged exoplanets and must therefore be estimated somehow. For instance, we note that the main component of the Venus clouds (H2SO4-H2O) is not a major constituent of its atmosphere but the result of ongoing photochemical processes. Predicting the occurrence of such clouds from first principles remains a considerable challenge.
Other works have followed a different approach, including the optical properties of the cloud as free parameters in the retrievals (e.g. Lupu et al. 2016; Nayak et al. 2017; Carrión-González et al. 2020), thus omitting any prior knowledge of the clouds that could be potentially gained from micro-physical considerations. These studies have revealed important correlations between model parameters that hinder the accurate characterization of an atmosphere. Cloud properties such as optical thickness (τc), vertical position in the atmosphere, or the single-scattering albedo of the aerosols (ω0) show strong degeneracies with for example the abundance of gaseous absorbing species. Nayak et al. (2017) discussed the correlations between an unknown planet radius (Rp) and an unknown star–planet–observer phase angle (α) in the retrievals. Carrión-González et al. (2020) analysed the correlations between an unknown Rp and the atmospheric properties of the planet by comparing retrievals in which Rp was assumed to be known to retrievals in which Rp was assumed to be unknown. That work showed that, if the planet radius is unknown, the correlations triggered between Rp and cloud properties such as τc degrade the quantitative findings from the atmospheric retrievals. These correlations worsen the constraints on the absorbing gases and prevent us from distinguishing between cloudy and cloud-free atmospheres. This shows that the conclusions of the retrievals are strongly dependent on some very basic assumptions of the models such as the treatment of the clouds. Most of these retrieval exercises have analysed reflected-starlight spectra at a single phase angle (Lupu et al. 2016; Feng et al. 2018; Damiano & Hu 2020; Carrión-González et al. 2020).
Nevertheless, observations of the Solar System planets have revealed the relevance of optical phase curves – which sample a range of phase angles – in constraining their atmospheric properties. The added value of phase curves over single-phase disc-integrated reflected-starlight measurements has been explored for both gas giants (e.g. Sudarsky et al. 2005; Dyudina et al. 2016; Mayorga et al. 2016) and terrestrial planets (e.g. Mallama 2009; Robinson et al. 2011; García Muñoz et al. 2014, 2017; Mayorga et al. 2020; Lee et al. 2020, 2021). These studies revealed the occurrence of different atmospheric phenomena such as glories, specular reflection by liquid surfaces and differential atmospheric rotation, and waves.
Our goal in this work is to determine how simultaneous retrievals of multi-phase spectra affect the atmospheric characterization of an exoplanet if neither its radius nor its cloud properties are known a priori. This is a follow-up of Carrión-González et al. (2020), where the models and results for full-phase (α = 0°) spectra are described in detail. The main conclusion of that work was that if Rp is unknown, as will generally happen for directly imaged exoplanets, retrievals at α = 0° cannot be used to determine the presence or absence of clouds. This result was obtained for a measurement with complete coverage between λ = 500−900 nm, spectral resolution R ~ 125–225, and signal-to-noise ratio (S∕N) = 10. Such measurements are beyond the capabilities of the Roman Telescope but are expected to be feasible with next-generation missions such as the Habitable Exoplanet Observatory (HabEx) (Mennesson et al. 2016; Gaudi et al. 2020) or the Large UV/Optical/IR Surveyor (LUVOIR) (Bolcar et al. 2016; The LUVOIR Team 2018).
We aim to understand how the observed degeneracies between model parameters (particularly, Rp, the cloud optical thickness, and the methane abundance) can be broken. To this end, we first analyse the information content of spectra at different phase angles by means of single-phase retrievals at α = 37°, 85°, and 123° with S∕N = 10. We then perform simultaneous retrievals combining the observation at α = 37° with others at larger phase angles (85° and 123°). We also explore how the single-phase retrievals at α = 37° improve if the S∕N is doubled to S∕N = 20.
The paper is structured as follows. In Sect. 2 we compare our approach to previous approaches described in the literature and indicate our new contributions. In Sect. 3 we describe the atmospheric model and the retrieval method that we use. The results are presented in Sect. 4 and several hypotheses explaining these results are tested in Sect. 5. The final summary and conclusions are given in Sect. 6.
2 Our work in the context of precedent studies
In preparation for future phase curves of directly imaged exoplanets in reflected starlight, Nayak et al. (2017) and Damiano et al. (2020) conducted atmospheric retrievals at several phase angles. Below we describe their methods and main results, highlighting the differences from and contributions of our analysis.
Nayak et al. (2017) carried out atmospheric retrievals at seven phase angles between α = 0° and 120°, with S/N of 5, 10, and 20. Building upon the work by Lupu et al. (2016), Nayak et al. assumed a two-cloud model without prior knowledge of the optical properties of the cloud aerosols. Out of the total of 11 model parameters considered in their retrievals, they focused on a subset of six parameters and studied how their retrieval results vary at several values of α. These parameters are the planet’s surface gravity, its radius, the observed phase angle, the atmospheric methane abundance, and the pressure levels both at the top of the upper cloud and at the top of the lower cloud. The authors concluded that Rp is better determined at large (crescent) phases (α > 90°) and that, for the rest of parameters, knowing the phase angle at the time of the observation would not remarkably improve the atmospheric retrievals. A preliminary investigation was presented on the potential gains from multi-phase observations by applying an intersection criterion between the retrieval results of single-phase observations. This criterion was applied to the marginalized posterior probability distributions of each individual parameter, such that the resulting solution when combining two observations is the subset of values that are common to both single-phase retrievals. Nayak et al. (2017) suggested that observations with low S/N especially benefit from the combination of phases and noted that performing simultaneous retrievals of spectra at different α would be needed to confirm their tentative findings.
Damiano et al. (2020) simulated observations for a Roman-like telescope equipped with a starshade (only three wavelength bands available: 0.45−0.55, 0.61−0.75, and 0.82−1.0 μm, and spectral resolution R = 50). These authors also considered a future mission like HabEx, with broad spectral coverage of 0.45−1 μm and R = 140. They carried out the retrievals at α = 60° and 90° using the methods developed in Hu (2019) and Damiano & Hu (2020). The cloud optical thickness and aerosol properties were therefore dictated through microphysical prescriptions and were not included as free parameters in the retrievals. To account for the unknown planet radius, Damiano et al. assumed the planet mass to be known and included the planetary gravity as a free parameter in the retrievals. They found that a single observation at α = 60° in the green band of the Roman Telescope (0.61−0.75 μm) with S∕N ~ 18 (~3.5 h of integration) is insufficient to accurately constrain the atmospheric properties because of parameter degeneracies. Three different strategies were found to break these degeneracies with comparable efficiency. The first is to combine the observation at α = 60° and S∕N ~ 18 with another one at α = 90° and S∕N = 11.5 and performing simultaneous retrievals. In a second, the wavelength coverage is expanded to the red filter (0.82−1.0 μm), with a reduced S∕N ~ 2. The third strategy is to double the integration time of the green band observation at α = 60°, achieving a S∕N ~ 25. For HabEx-like observations, with higher spectral resolution and wider wavelength coverage, Damiano et al. concluded that an observation at α = 60° is sufficient to constrain the main atmospheric properties. In this case, their retrievals would not improvesignificantly if the integration time were doubled or if an additional measurement at α = 90° were performed.
Our study differs from that of Nayak et al. (2017) in that we perform simultaneous retrievals of spectra at multiple phase angles. As shown below, the findings using our approach differ significantly from those where single-phase retrievals are combined. We also analyse the optical properties of the cloud and how the retrieved values for these parameters vary with α. We repeat our study for several cloud scenarios in order to derive general conclusions. This work also differs from that of Damiano et al. (2020) in that we do not assume any prior knowledge about the planet mass or the cloud properties. Hence, we include as free parameters in our retrievals the cloud optical properties and the planet radius. Furthermore, we also investigate the physical basis of the improvement in the simultaneous multi-phase retrievals. Similarly to both works, we assume a H2 -He-dominated atmosphere.
The focus of our work is thus mainly theoretical. Nevertheless, we note that our selected values of α ~ 40°−120° may be accessible for several exoplanets in an optimistic configuration of the Roman Telescope coronagraph (Carrión-González et al. 2021). These α will be well within the operational range of HabEx- and LUVOIR-like telescopes.
3 Atmospheric model and retrieval
In this section we summarize the fundamental details of our atmospheric model and retrieval method, which are thoroughly described in Carrión-González et al. (2020). We also describe how our retrieval method is adapted to perform simultaneous retrievals of observations at multiple phase angles.
3.1 Forward model
The model used here assumes an optically thick atmosphere composed of H2 -He with methane as the only absorbing gas and a cloud layer whose optical properties are independent of wavelength. This configuration is generally consistent with the properties of the giant and icy planets in the Solar System. The gas density is assumed to decrease exponentially with height and the methane abundance relative to the background gas (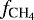 ) is assumed constant at all heights. The cloud is parameterized by its optical thickness (τc) and its geometrical vertical extension (Δc). The altitudeat which the top of the cloud is located is given by the optical thickness of the gas from the top of the atmosphere (TOA) to the top of the cloud (τc→TOA) at a reference wavelength λ = 800 nm. The aerosol particles are described by their single-scattering albedo (ω0) and the effective radius (reff). Finally, the planet radius (Rp) is also included as a model parameter. Table 1 summarizes our model parameters and the ranges of values defining the parameter space explored in our retrievals.
) is assumed constant at all heights. The cloud is parameterized by its optical thickness (τc) and its geometrical vertical extension (Δc). The altitudeat which the top of the cloud is located is given by the optical thickness of the gas from the top of the atmosphere (TOA) to the top of the cloud (τc→TOA) at a reference wavelength λ = 800 nm. The aerosol particles are described by their single-scattering albedo (ω0) and the effective radius (reff). Finally, the planet radius (Rp) is also included as a model parameter. Table 1 summarizes our model parameters and the ranges of values defining the parameter space explored in our retrievals.
The adopted set of free parameters for the retrieval represents a fine balance between describing a realistic atmosphere and maintaining an adequate level of model complexity with which to interpret the retrieval results. This balance in the choice of model parameters has long been discussed in the literature for reflected-starlight observations of Solar System objects (e.g. Smith & Tomasko 1984; Stephens & Heidinger 2000; Heidinger & Stephens 2000; Schmid et al. 2011) and we founded our choices on these works.
We recall that in the exponential background atmosphere adopted here, the scale height of the gas Hg does not appear explicitly in the radiative transfer equations (see Sect. 2.3 in Carrión-González et al. 2020). In our formulation, each of the slabs in which we discretize the atmosphere is described in terms of optical thickness. There is therefore no need to invoke a scale height that would only be required to explicitly convert between optical thickness and altitude. For example, two exponential atmospheres such as those used here with the same vertically integrated properties but different scale heights will result in the same reflected-starlight spectrum regardless of the actual value of Hg. Other radiative transfer codes such as DISORT (Stamnes et al. 1988) also operate through the specification of optical thicknesses rather than altitudes. For these reasons, neither Hg nor the planet’s gravity play a role in our calculated reflected-starlight spectra. Indeed, although the value of Δc is given in units of Hg (Table 1), this refers to the number of slabs in which the cloud aerosols are present (Fig. 1 in Carrión-González et al. 2020).
For a particular atmospheric configuration, we compute the planet-to-star contrast as
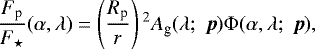 (1)
(1)
where r is the planet-to-star distance. For convenience, in our retrievals we use the planet radius normalized to that of Neptune (Rp ∕RN). The geometrical albedo (Ag) and the normalized scattering function (Φ) depend on the atmospheric properties, which are condensed in the vector of parameters 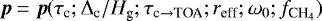 (see Table 1). We focus on mature long-period exoplanets and hence assume no thermal-emission component at these wavelengths.
(see Table 1). We focus on mature long-period exoplanets and hence assume no thermal-emission component at these wavelengths.
We specify our theoretical study to Barnard’s Star b (Ribas et al. 2018). This planet candidate orbits near the snowline of its host star (0.4 AU). Its minimum mass of 3.23 M⊕ places it in the super-Earth to mini-Neptune mass regime for which a H2 -He atmosphere is a physically plausible scenario (see Sect. 2.2 in Carrión-González et al. 2020). In addition, this system is located at only 1.8 pc from the Sun (Giampapa et al. 1996) which makes it a promising candidate for direct-imaging observations. Carrión-González et al. (2021) found that an optimistic configuration of Roman’s coronagraph could achieve a phase coverage of α∈ [35 ,120
,120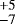 ] for this planet. The faint magnitude of Barnard’s Star (V = 9.5 mag) will likely impede an observation with Roman, but it is within the operating range of next-generation direct-imaging telescopes, which will also cover a broader range of observable phase angles. We also note that the existence of this planet was recently disputed by Lubin et al. (2021). In the present theoretical study, we nevertheless keep this target as an example of a typical cool planet around a nearby star. This also ensures a more straightforward comparison with Carrión-González et al. (2020).
] for this planet. The faint magnitude of Barnard’s Star (V = 9.5 mag) will likely impede an observation with Roman, but it is within the operating range of next-generation direct-imaging telescopes, which will also cover a broader range of observable phase angles. We also note that the existence of this planet was recently disputed by Lubin et al. (2021). In the present theoretical study, we nevertheless keep this target as an example of a typical cool planet around a nearby star. This also ensures a more straightforward comparison with Carrión-González et al. (2020).
In order to carry out a retrieval exercise, a certain atmospheric configuration has to be assumed for the observed planet. We refer to this as the true atmospheric configuration and in this work we analyse three possible scenarios which only differ in the cloud’s optical thickness. These are the same true atmospheric configurations as in Carrión-González et al. (2020) in order to make the results comparable. With values of τc = 0.05, 1.0, and 20.0, we refer to these configurations as no-, thin-, and thick-cloud scenarios, respectively.The rest of the model parameters are kept the same in all three scenarios: Δc /Hg = 2, τc →TOA = 9.1 × 10−3, reff = 0.50 μm, ω0 = 0.90, and 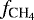 = 5 × 10−3. We assume a planet radius of Rp∕RN = 0.6 with a circular orbit with r = 0.4 AU. We alsoassume that the atmosphere does not change throughout the orbit. Cloud properties play a key role in the parameter correlations (e.g. τc − Rp,
= 5 × 10−3. We assume a planet radius of Rp∕RN = 0.6 with a circular orbit with r = 0.4 AU. We alsoassume that the atmosphere does not change throughout the orbit. Cloud properties play a key role in the parameter correlations (e.g. τc − Rp, 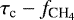 ), which hinders an accurate atmospheric characterization with reflected-starlight spectra (e.g. Lupu et al. 2016; Nayak et al. 2017; Carrión-González et al. 2020). By exploring different cloud scenarios, we aim to study the effects of aerosols in multi-phase retrievals more generally.
), which hinders an accurate atmospheric characterization with reflected-starlight spectra (e.g. Lupu et al. 2016; Nayak et al. 2017; Carrión-González et al. 2020). By exploring different cloud scenarios, we aim to study the effects of aerosols in multi-phase retrievals more generally.
Figure 1 shows (left column) the synthetic Fp ∕F⋆ for the no-, thin-, and thick-cloud configurations at phase angles of 37° (solid lines), 85° (dashed lines), and 123° (dotted lines). These spectra are computed with a backward Monte Carlo radiative transfer model (García Muñoz & Mills 2015) that ensures the accuracy of multiple-scattering for all phase angles. The most significant trend is the reduction of the planet-to-star contrast as α increases and thus the apparent illuminated surface of the planet decreases. Figure 1 also shows (right column) the spectra normalized to the value of Fp∕F⋆ at λ = 500 nm so that the relative changes in the shape of the spectra at different phase angles become evident. We find that the normalized spectra at α = 37° and 85° are practically identical and that the relative changes in their shape are only significant at larger phases (α = 123°).
In our model, reff determines the scattering phase function p(θ) of the aerosols, which is computed by means of Mie theory. For the range of reff values considered in this work, Fig. 2 shows the dependence of p(θ) on scattering angle (θ). In the single-scattering limit, θ and α are supplementary angles. The forward scattering component (θ ~ 0°, α ~ 180°) becomes stronger for larger reff. Correspondingly, p(θ) tends to become isotropic for smaller aerosols. The dependence of p(θ) on θ and reff suggests that the spectra obtained at different phases contain different information and that the specific information will also depend on the macroscopic properties of the aerosols. This consideration motivates the study of multi-phase retrievals as a strategy to constrain the atmospheric properties of the planet.
Model parameters used to compute the synthetic reflected-starlight spectra.
3.2 Simultaneous retrievals at multiple phases
To carry out the atmospheric retrieval from an individual observation we follow the same approach as in Carrión-González et al. (2020). We first simulate a measured spectrum by adding noise to the synthetic spectrum computed for the true atmospheric configuration. We assume a simplified, wavelength-independent noise model that is described by a normal distribution of mean value zero and standard deviation σm:
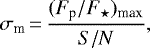 (2)
(2)
where S∕N is given as an input and 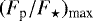 is the maximum value of the contrast reached in the noiseless synthetic spectrum. This simplified noise model was used in Carrión-González et al. (2020) and allows us to focus on the specifics of radiative transfer rather than on the details of instrument-specific noise sources.
is the maximum value of the contrast reached in the noiseless synthetic spectrum. This simplified noise model was used in Carrión-González et al. (2020) and allows us to focus on the specifics of radiative transfer rather than on the details of instrument-specific noise sources.
Once the measured spectrum is simulated, we use the Markov chain Monte Carlo (MCMC) sampler emcee (Foreman-Mackey et al. 2013)to explore the 7D parameter space. This 7D space comprises the six atmospheric parameters in the vector p and the planet radius. The samplertests atmospheric configurations and obtains the corresponding synthetic spectrum by interpolating from a pre-computed grid of ~300 000 atmospheric configurations at each specified phase angle (see Carrión-González et al. 2020). Each test spectrum is compared to the simulated measurement with the figure of merit χ2 (Bevington & Robinson 2003), computed from Eqs. (1) and (2) as:
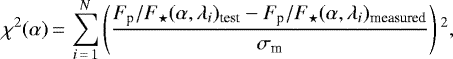 (3)
(3)
where N is the number of data points in the spectrum. Similarly, to perform simultaneous retrieval of n observations at phase angles α1,... αn we also start by simulating the corresponding planet-to-star contrasts of the measurements (Fp ∕F⋆(α1),... Fp∕F⋆(αn)). To this end, we add noise to each of the synthetic spectra with the desired S∕N, obtaining  . At each test atmospheric configuration, the sampler obtains the synthetic spectrum of the planet at each phase angle (
. At each test atmospheric configuration, the sampler obtains the synthetic spectrum of the planet at each phase angle (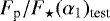 ,
, 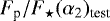 ) by interpolation. For this work, we recalculated the pre-computed grid of ~ 300 000 atmospheric configurations by solving the radiative-transfer equation for each configuration at α = 37°, 85°, and 123°. This results in a grid of ~ 300 000 × 3 spectra. For a total of n combined observations, each of them with an individual
) by interpolation. For this work, we recalculated the pre-computed grid of ~ 300 000 atmospheric configurations by solving the radiative-transfer equation for each configuration at α = 37°, 85°, and 123°. This results in a grid of ~ 300 000 × 3 spectra. For a total of n combined observations, each of them with an individual 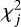 , the combined χ2 is computedas:
, the combined χ2 is computedas:
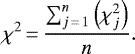 (4)
(4)
Unless stated otherwise, we assume S∕N = 10 at all phaseangles. We note that the integration time needed to achieve a certain S∕N will increase with α because the apparent brightness of the planet will decrease. Whether this will be feasible for future direct-imaging space telescopes needs to be addressed with noise models specific to the corresponding facilities. In the present work, we omit such considerations on integration times to focus on the theoretical opportunities of multi-phase observations.
 |
Fig. 1 Noiseless synthetic spectra (left column) for the no-cloud (top row and light blue), thin-cloud (middle row and darker blue), and thick-cloud (bottom row and purple) configurations. Solid lines in each subplot correspond to the spectrum at phase angle α = 37°, dashed lines at α = 85°, and dotted lines at α = 123°. The error bars indicated with vertical lines correspond to the noise at S∕N = 10 injected to create the noisy spectrum at each phase angle. Right column: same synthetic spectra but normalised with respect to the value of Fp∕F⋆(λ = 500 nm), revealing the shape changes in the spectra at different phases. |
 |
Fig. 2 Dependence of the aerosol scattering phase function p(θ) on the photon scattering angle θ for the considered values of reff. For clarity, the plot shows log10(p(θ)), where θ = 0° corresponds to forward scattering and θ = 180° to backwardscattering. |
4 Results
Below, we analyse the retrieval results and the potential gain from multi-phase measurements. To this end, we first study the retrievals of single-phase observations at phase angles α = 37°, 85°, and 123° separately (Sect. 4.1). We then explore several combinations of phase angles (Sect. 4.2).
The phase angle α = 85° is representative of orbital positions near quadrature, where the maximum planet–star angular separation is reached. This phase is expected to be accessible for several known exoplanets with different possible configurations of the Roman Telescope coronagraph (Carrión-González et al. 2021). Correspondingly, α = 37° and 123° are realistic lower and upper limits of the phase angles that will be observable with future direct-imaging space telescopes. This range of phases may only be accessible to the Roman Telescope coronagraph for a small number of exoplanets and in the best-case scenario of IWA, OWA, and Cmin considered in Carrión-González et al. (2021).
Retrieval results for different phase angles and their combinations, for all three cloud scenarios.
4.1 Retrievals for single-phase measurements
For each of the three cloud scenarios, we carried out single-phase retrievals for observations at α = 37°, 85°, and 123° with S∕N = 10 in all cases. Figures A.1−A.3 show the posterior probability distributions of the model parameters for each cloud scenario. Contour lines display the 1σ confidence level and the 1D histograms show the marginalized probability distribution for each parameter1 (also displayed in Fig. 3). For comparison, green lines indicate the true value given as input. The median values of these marginalized distributions, as well as their upper and lower uncertainties corresponding to the 84 and 16% quantiles (or, equivalently, to 1σ for Gaussian errors), are listed in Table 2.
As a general result we find that none of the single-phase retrievals can confirm the presence or absence of clouds regardless of the actual cloudcoverage of the planet. Indeed, the retrieval results for the cloud optical thickness are indistinguishable in the no- and thin-cloud scenarios (Fig. 3) and thus it is challenging to favour one scenario over the other. Moreover, high values of τc cannot be completely ruled out from the retrieval results in these two scenarios. As for the thick-cloud scenario, the posterior probability distribution of τc (Fig. 3, bottom) is flat. In case of a real observation, such a retrieval result would be compatible with both cloud-free and cloudy atmospheres. This extends the findings for α = 0° in Carrión-González et al. (2020) – regarding the correlations between model parameters that are triggered if Rp is unknown – to non-zero values of α.
To understand the fundamentals of these correlations and how they change with α depending on the cloud coverage, it is useful to analyse the retrieval results in each of the cloud scenarios. This provides insights that are valuable for real observations, where prior information on the true cloud coverage will be unavailable.
In the single-phase analyses, the aerosol properties (reff, ω0) and the cloud geometrical extension (Δc, normalized to Hg) remain largely unconstrained for all cloud scenarios. The vertical location of the cloud (τc →TOA) is reasonably well constrained in the thin-cloud scenario (Fig. 3). This estimate is somewhat less accurate in the thick-cloud scenario due to stronger parameter correlations which tend to place the cloud higher up in the atmosphere than the true value.
The correlations between the planet radius and the cloud properties propagate to other parameters affecting in particular the methane abundance. Indeed, the most accurate estimates of 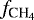 are retrieved in the no-cloud scenario while
are retrieved in the no-cloud scenario while 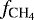 is severely underestimated in the thick-cloud scenario at all phases (Fig. 3). This was also found in Carrión-González et al. (2020) for a single-phase observation at α = 0°.
is severely underestimated in the thick-cloud scenario at all phases (Fig. 3). This was also found in Carrión-González et al. (2020) for a single-phase observation at α = 0°.
Remarkably, we find that it is possible to constrain the planet radius with an uncertainty smaller than a factor of two in all the scenarios and phase angles explored, similar to the findings by Carrión-González et al. (2020) for α = 0°. However, in the present work we also find that the retrievals of Rp improve as the phase angle increases. For our analysis at α = 123°, we estimate values of Rp∕RN of 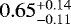 for the no-cloud scenario,
for the no-cloud scenario, 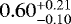 for the thin-cloud one and
for the thin-cloud one and 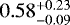 for the thick-cloud one. This means that, at this large phase angle, the maximum deviation from the true value (Rp ∕RN = 0.6) is of only 35%, regardless of the cloud coverage of the planet. In Sect. 5 we discuss the possible physical reasons. Constraining Rp to within a certain level of uncertainty also provides more restricted priors of this parameter for subsequent retrievals. As shown in Carrión-González et al. (2020), this can partially break some of the parameter correlations, which results in more accurate retrievals.
for the thick-cloud one. This means that, at this large phase angle, the maximum deviation from the true value (Rp ∕RN = 0.6) is of only 35%, regardless of the cloud coverage of the planet. In Sect. 5 we discuss the possible physical reasons. Constraining Rp to within a certain level of uncertainty also provides more restricted priors of this parameter for subsequent retrievals. As shown in Carrión-González et al. (2020), this can partially break some of the parameter correlations, which results in more accurate retrievals.
Overall, we find that the retrieval results change with α more dramatically in the thick-cloud scenario. This supports the idea that the information content in a spectrum depends on the phase angle α at which it was obtained and that this connection occurs through the scattering properties of the atmosphere.These ideas are further explored in Sect. 5. We also conclude that if Rp and the cloud properties are a priori unknown, a single-phase observation at S∕N = 10 cannot be used to break the degeneracies between model parameters and accurately constrain the atmospheric properties of an exoplanet. This holds true for a broad range of phase angles representative of the capabilities of future direct-imaging space telescopes.
 |
Fig. 3 Marginalized posterior probability distributions of each model parameter for single-phase observations in the no-, thin-, and thick-cloud scenarios (top, middle, and bottom rows, respectively). The single-phase observations are obtained at phase angles 37° (cyan lines), 85° (magenta lines), and 123° (yellow lines). In all cases, S∕N = 10. Green lines mark the true values of the model parameters (see Sect. 3.1) for this scenario. The 2D posterior probability distributions for these retrievals can be found in Figs. A.1−A.3. |
 |
Fig. 4 Marginalized posterior probability distributions of each model parameter for several combinations of observations in the no-, thin- and thick-cloud scenarios (top, middle, and bottom row, respectively). Blue lines mark the combination (37°+85°); red lines, (37°+123°) and black lines, (37°+85°+123°). For reference, cyan lines indicate the results of a single-phase observation at α = 37° but doubling the S/N to 20. Green lines mark the true values of the model parameters (see Sect. 3.1) for this observation. The 2D posterior probability distributions for these retrievals can be found in Figs. B.1−B.3. |
4.2 Retrievals for multi-phase combinations of measurements
Building upon the analysis of single-phase retrievals, we next proceed to the analysis of simultaneous multi-phase retrievals. Following a similar approach to that in Damiano et al. (2020), we assumed an observation at a small phase angle (in our case, α = 37° with S∕N = 10) and tested the improvement in the retrievals produced by different observing strategies. As a comparison, we also doubled the S∕N to 20 for a single-phase measurement at α = 37° to test whether or not such an observing strategy yields similar results to the combination of multiple phases.
We first explored the combination of small and moderate phase angles (37°+85°), and subsequently the effect of adding phases larger than quadrature with the combinations (37°+123°) and (37°+85°+123°). Figures B.1−B.3 show the corresponding posterior probability distributions for the three cloud scenarios. The results of the marginalized probability distribution for each parameter are displayed in Fig. 4 and summarized in Table 2.
We find that the best strategy to discern the presence or absence of clouds is to combine observations at small phase angles with others at phases larger than quadrature. In all cloud scenarios, the combinations (37°+123°) (red lines in Fig. 4) and (37°+85°+123°) (black lines) yield the most accurate estimates of τc. Both combinations allow us to more robustly distinguish between cloudy and cloud-free atmospheres and, furthermore, to more accurately estimate the true value of the optical thickness of the cloud (Table 2). Regarding the other strategies explored, in the no- and thin-cloud scenarios we find only minor differences between a combination (37°+85°) and a single-phase observation at α = 37° with S∕N = 20 (see Table 2 and Fig. 4). In the thick-cloud scenario, where the correlations between Rp and the cloud are stronger, combining (37°+85°) produces a better retrieval for τc than a single observation at α = 37° with S∕N = 20. This suggests that the complementary information content from multiple phases helps improve the retrievals more effectively than increasing the S∕N of a single-phase observation.
In the scenarios with a cloud layer (either thin or thick), combining small and large phases helps constrain the aerosol optical properties reff and ω0 (Fig. 4). The results are similar for the (37°+123°) and (37°+85°+123°) combinations, which are both slightly more accurate than either a combination of (37°+85°) or a single-phase observation at 37° with S∕N = 20. As expected, the improvements in the retrievals of reff and ω0 are more noticeable in the thick-cloud scenario, as the aerosol properties have a larger impact on the spectra. The retrievals of the cloud’s vertical location also improve when combining (37°+123°) or (37°+85°+123°), especially in the thick-cloud scenario. The geometrical extension of the cloud Δc remains unconstrained in all cases.
The retrieved methane abundances depend significantly on the cloud scenario, as expected from the impact of the 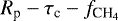 degeneracies in each case. For the no- and thin-cloud scenarios, a single-phase observation at α = 37° with S∕N = 20 appears to be the best strategy to reduce the uncertainties in the retrieved
degeneracies in each case. For the no- and thin-cloud scenarios, a single-phase observation at α = 37° with S∕N = 20 appears to be the best strategy to reduce the uncertainties in the retrieved 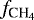 . However, this strategy cannot be generalized. For instance, in the case of α = 37° and S∕N = 20, the above parameter degeneracies in the thick-cloud scenario result in a
. However, this strategy cannot be generalized. For instance, in the case of α = 37° and S∕N = 20, the above parameter degeneracies in the thick-cloud scenario result in a 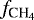 estimate that deviates significantly from the true value. On the other hand, in all cloud scenarios, the combinations (37°+123°) and (37°+85°+123°) yield estimates of
estimate that deviates significantly from the true value. On the other hand, in all cloud scenarios, the combinations (37°+123°) and (37°+85°+123°) yield estimates of 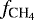 which are on the same order of magnitude as the true value.
which are on the same order of magnitude as the true value.
For the retrieved value of Rp, combining small and large phase angles is again the only strategy that works for all cloud scenarios. For the no- and thin-cloud scenarios, the resulting estimates are similarly accurate (with maximum deviations of about 60%) for all the cases explored here: the single-phase observation at α = 37° with S∕N = 20 and the combinations (37°+85°), (37°+123°), and (37°+85°+123°). However, in the thick-cloud scenario there is a significant underestimation of Rp both for the (37°+85°) combination and for α = 37° with S∕N = 20 (Fig. 4). In this case, only adding the observation at α = 123° breaks the degeneracies and recovers an estimate with a maximum deviation from the true value of about 50% (Table 2).
By comparing our single-phase retrievals (Fig. 3) with our multi-phase retrievals (Fig. 4) we find a general improvement in the latter that cannot be anticipated from the single-phase results. This indicates that combining the marginalized posterior probability distributions of single-phase retrievals is not equivalent to a simultaneous multi-phase retrieval. Hence our multi-phase results cannot be reproduced by applying the intersection criterion used by Nayak et al. (2017). Because this intersection approach works on the individual posterior probability distributions for each parameter, it likely misses the subtleties of fitting several spectra simultaneously in the multi-dimensional parameter space.
In summary, combining small and large phase angles proves to be the best general strategy with which to break some of the parameter correlations in all cloud scenarios. Both (37°+123°) and (37°+85°+123°) combinations can constrain the planet radius, the optical properties of the cloud, and the abundance of the absorbing gas reasonably well in all cloud scenarios. This indicates that the improvements are indeed caused by adding the information at α = 123° (see Sect. 5). Other strategies such as increasing S∕N to 20 can narrow the uncertainties in the retrieved 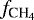 significantly but only if the cloud thickness is small or null.
significantly but only if the cloud thickness is small or null.
 |
Fig. 5 Atmospheric layers probed by the photons in our radiative-transfer computations. Layer 28 is the top of the atmosphere and layer 0 is the bottom (see Carrión-González et al. 2020 for details). Each row corresponds to a cloudscenario. Upper row: no-cloud; middle: thin-cloud; bottom: thick-cloud. Left column: phase angle of 37°; middle: α = 85°,right: α = 123°. The maximum photon contribution at each wavelength is normalized to 1. However, not all wavelengths have comparable absolute contributions to the spectra, as shown in Fig. 1. The right-hand panels of each subplot show the vertical profiles of these normalized photon contributions for a selection of wavelengths: 500 nm (purple lines), 600 nm (blue lines), 724 nm (yellow lines), and 884 nm (red lines). |
5 Discussion on the physical reasons for the improvement in multi-phase retrievals
From the above, we conclude that the information contained in reflected-starlight spectra depends on the phase angle of the observation, which results in improved values of the retrieved atmospheric properties and Rp by combining observations at multiple phases. In the following, we test several hypotheses to determine the physical reasons for this improvement in multi-phase retrievals.
We first analyse whether observations at different phases probe different altitudes of the atmosphere. We then analyse how the shape of the aerosol scattering phase function affects the multi-phase retrievals. Finally, we analyse how the retrieval results change if the cloud optical properties are assumed known a priori.
5.1 Atmospheric altitudes probed at each phase
We study which atmospheric layers are predominantly probed at each wavelength and whether that depends significantly on α. The aim of the exercise is to reveal whether the different information from each single-phase observation comes from a different range of altitudes probed in each case. In our multiple-scattering radiative transfer code (García Muñoz & Mills 2015), it is possible to trace the trajectory of each simulated photon and the atmospheric layer where it undergoes scattering collisions with the atmosphericmedium. It is also possible to compute how much each collision contributes to the overall brightness (e.g. García Muñoz et al. 2017).
Figure 5 shows, for each cloud scenario and assumed α, how the different atmospheric layers contribute to the spectrum. The photon interactions in the no-cloud scenario come either from Rayleigh scattering with the background gas or from methane absorption. In contrast, in both the thin and thick cloud scenarios, the majority of the scattering events contributing to the spectrum take place at the cloud layer. This holds true at the three phase angles considered and at all wavelengths except for the methane absorption band at ~884 nm. At this wavelength, CH4 absorption is very efficient and the photons are extinguished at higher atmospheric levels before reaching the cloud. In summary, we find that the simulated photons in the thin- and thick-cloud scenarios mostly probe the atmospheric layers at which the cloud is located, while in the no-cloud scenario a much broader range of altitudes can be probed.
For the wavelengths of 500, 600, 724, and 884 nm, we computed how many collisions the photons undergo on average at each phase angle and their relative contributions to the brightness (Fig. 6). These wavelengths are representative of spectral regions significantly affected by Rayleigh scattering (500 and 600 nm) and moderate and strong CH4 absorption (724 and 884 nm, respectively). We find that the number of effective scattering events is lower at α = 123° than at 37° or 85°. This trend is more noticeable in the thick-cloud scenario. For all scenarios and phases, photons at λ = 884 nm (the strongest absorption band) generally undergo only one scattering event before being completely absorbed. At λ = 724 nm (a weaker absorption band), the number of collisions increases as the cloud optical thickness increases. This happens because the aerosols are quite reflective (ω0 = 0.90) and increasethe number of scattering events, preventing the photons from reaching deeper atmospheric layers where they would be absorbedby methane.
In summary, the information contained in the reflected-starlight spectra of a cloudy atmosphere comes mainly fromthe atmospheric layers where the cloud is located. Hence, the improvement from multi-phase retrievals (Sect. 4.2) cannot be due to probing different atmospheric depths at each α. We also find that the number of photon collisions drops at α = 123°, especially inthe thick-cloud scenario, making large-phase observations closer to the single-scattering limit. Plausibly, this tendency towards the single-scattering limit reduces the possible trajectories of the photons within the atmosphere and, in turn, the degeneracies in the inverse exercise of retrieval. This is consistent with the more accurate Rp retrievals at α = 123° (Sect. 4.1) and the enhancement in multi-phase retrievals that combine small and large phases (Sect. 4.2).
 |
Fig. 6 Contribution to the overall spectral brightness of the successive scattering events that the simulated photons undergo in the atmosphere at λ = 500 nm (purple lines), 600 nm (blue lines), 724 nm (yellow lines), and 884 nm (red lines). At each wavelength, the maximum photon contribution to the overall brightness of the spectrum is normalized to 1. Each column corresponds to a phase angle: 37° (left), α = 85° (middle), and α = 123° (right). Each row corresponds to a cloud scenario, as indicated in the labels. Also included are the thick-cloud-scenario retrievals forvalues of reff = 0.10 and 2.0 μm (see Sect. 5.2). |
5.2 The impact of the aerosol’s scattering phase function
The findings above suggest that the improvements in multi-phase retrievals are due to the optical properties of the cloud because it is the primary layer being sampled. Next we aim to determine whether such an improvement is caused by the scattering phase function p(θ) of the aerosols. As shown in Fig. 2, p(θ) varies strongly with the scattering angle. We expect that at small phase angles backscattering (θ → 180°) will be particularly effective, whereas at large phase angles forward scattering (θ → 0°) will be particularly significant.
To test if the dependence of p(θ) on θ drives the improvement in multi-phase retrievals, we repeated the thick-cloud-scenario retrieval but assuming two values of the true reff different from the reff = 0.50 μm used in the rest of the present work. First, we adopt reff = 0.10 μm, which is the smallest value explored here and corresponds to a nearly isotropic scattering phase function (Fig. 2). We then adopt reff = 2.0 μm as representative of a large particle size with a strong dependence of p(θ) on θ and a high forward-scattering component. If the dependence of p(θ) on θ is indeed a cause of the improvement in multi-phase retrievals, this improvement should become more modest as p(θ) tends to an isotropic function. For context, the aerosol sizes reported in the literature for the upper cloud layers in the atmospheres of the Solar System gas giants are between reff = 0.40 and 0.75 μm (e.g. Morozhenko & Yanovitskij 1973; Mishchenko 1989; Pérez-Hoyos et al. 2012).
The retrievals for single-phase observations (α = 37°, 85° or 123°) are very similar for a thick-cloud scenario with either reff = 0.10, 0.50, or 2.0 μm (Fig. 7). Interestingly, multi-phase retrievals for reff = 0.10 μm yield somewhat less accurate estimates than for reff = 0.50 or 2.0 μm (Fig. 8). This is particularly noticeable for τc, 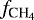 , and ω0 when small and large phases are combined, either (37°+123°) or (37°+85°+123°). Indeed, Fig. 8 shows that these combinations of small and large phases result in more accurate constraints of
, and ω0 when small and large phases are combined, either (37°+123°) or (37°+85°+123°). Indeed, Fig. 8 shows that these combinations of small and large phases result in more accurate constraints of 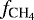 and ω0 and a sharp lower limit of τc for aerosols with non-isotropic scattering phase functions (reff = 0.50 or 2.0 μm). In contrast, the estimates of these model parameters are less accurate in the case of a nearly isotropic p(θ) (reff = 0.10 μm). Nevertheless, even in this least favourable scenario with reff = 0.10 μm, combining observations at α = 37° and 123° still strongly suggests the presence of a cloud layer but fails to constrain its properties. For both the reff = 0.10 μm and 2.0 μm scenarios, we observe in Fig. 6 a decreasing number of scattering events at α = 123° with respect to smaller phases, similar to the trend found for reff = 0.50 μm.
and ω0 and a sharp lower limit of τc for aerosols with non-isotropic scattering phase functions (reff = 0.50 or 2.0 μm). In contrast, the estimates of these model parameters are less accurate in the case of a nearly isotropic p(θ) (reff = 0.10 μm). Nevertheless, even in this least favourable scenario with reff = 0.10 μm, combining observations at α = 37° and 123° still strongly suggests the presence of a cloud layer but fails to constrain its properties. For both the reff = 0.10 μm and 2.0 μm scenarios, we observe in Fig. 6 a decreasing number of scattering events at α = 123° with respect to smaller phases, similar to the trend found for reff = 0.50 μm.
We conclude that the shape of the aerosol scattering phase function affects the constraining capability of multi-phase retrievals. This is consistent with our findings in Sect. 4.2 that these improvements are more evident for scenarios with optically thicker clouds and are only marginal in the no-cloud scenario.
 |
Fig. 7 Marginalized posterior probability distributions of each model parameter for single-phase observations in the thick-cloud scenario at phase angles 37° (cyan), 85° (magenta), and 123° (yellow). Top row: assuming a true value of reff = 0.10 μm for the cloud aerosols. Middle row: assuming a true value of reff = 0.50 μm for the cloud aerosols, as in Sect. 4. Bottom row: assuming a true value of reff = 2.0 μm for the cloud aerosols. Vertical green lines mark the true values of the model parameters (see Sect. 3.1). |
 |
Fig. 8 Marginalized posterior probability distributions of each model parameter for several combinations of observations in the thick-cloud atmospheric configuration, as described in Sect. 3.2. Blue lines mark the combination (37°+85°), red lines mark (37°+123°), and black lines mark (37°+85°+123°). Top row: assuming a true value of reff = 0.10 μm for the cloud aerosols. Middle row: assuming a true value of reff = 0.50 μm for the cloud aerosols, as in Sect. 4. Bottom row: assuming a true value of reff = 2.0 μm for the cloud aerosols. Vertical green lines mark the true values of the model parameters (see Sect. 3.1). |
 |
Fig. 9 Retrieval results for an exercise in which the aerosol properties of the thick-cloud scenario (τc, reff and ω0) are assumed known and are therefore not explored by the MCMC retrieval sampler. Left panel: single-phase retrievals as in Fig. A.3. Right panel: multi-phase retrievals as in Fig. B.3. |
5.3 The impact of a priori assumptions in the retrievals
Here we repeat our retrievals for a thick-cloud scenario but without including the cloud optical properties (τc, reff, ω0) as free parameters in the retrievals. By comparing these new calculations to our previous results in Sect. 4, we aim to understand how the model parameterization and the corresponding assumptions may affect the conclusions of the retrieval exercises. We therefore aim to draw general conclusions about the impact of having or assuming some prior knowledge of the cloud properties on the main retrieval findings. Such conclusions are relevant to place our work in the context of recent publications, some of which incorporate such prior knowledge of the cloud properties (e.g. Feng et al. 2018; Damiano et al. 2020).
In this case we find that several of the degeneracies between parameters described in Sect. 4 no longer occur. We find that any single-phase observation can constrain the planet radius and the methane abundance reasonably well (Fig. 9). The retrieved cloud-top location τc →TOA places the cloud somewhat higher than the true position. We find no significant differences between the retrievals of single-phase observations at α = 37° with S∕N = 10 and those with S∕N = 20, or combinedwith measurements at larger phase angles. Despite the different modelling approaches, these results agree with the findings of Damiano et al. (2020) for HabEx-like observations (which are comparable to the spectra used in our work in terms of wavelength coverage and spectral resolution).
If the cloud optical properties are assumed known a priori, we conclude that the prospects for atmospheric characterization (Fig. 9) are much more optimistic than if they are considered unknown (Figs. A.3, B.3). In the latter case, we show (Sects. 5.1 and 5.2) that the cloud is a main source of the information contained in the spectrum and that its optical properties affect the uncertainties in the retrieval results. The prior knowledge of the cloud optical properties also changes the conclusions as to which observing strategy would be best to improve the atmospheric retrievals.
We note that additional assumptions in the model might affect the conclusions of the retrievals. For instance, we assume an atmosphere dominated by H2 and He. This is consistent with the established knowledge of giant planets both in the Solar System and in extrasolar planetary systems. This is also consistent with the population of exoplanets that the Roman Telescope will be able to directly image. However, this assumption might not be correct for certain planets in the super-Earth regime that will be observed with the next generation of space telescopes such as HabEx or LUVOIR.
Super-Earths might have atmospheres dominated by N2, O2, CO2, H2O or other heavy molecules (Grenfell et al. 2020). The indeterminate nature of the background gas may introduce a systematic uncertainty in the volume mixing ratios of the absorbing gas (CH4 here) that is independent of the S/N in the observations. If the retrievals are carried out assuming (erroneously) H2 as background gas, the retrieval will underestimate the volume mixing ratio of CH4 by a certain factor depending on the actual background gas (Table 3). This will happen in particular when the effect of clouds and/or hazes on the total optical thickness is negligible (because their opacity is small overall, or because of the wavelengths of the observations) and therefore the atmosphere is effectively clear. This factor arises from the ratio of Rayleigh cross-sections σ(True gas)/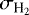 which dictates the actual optical thickness of the background gas. The approximate value of this factor is given in Table 3 for several possible background gases. Because the photons only react to optical thickness, misidentifying the background gas will translate to an erroneous estimate of the ratio between the absorbing (e.g. CH4) and the scattering (e.g. H2/He or N2) gases. This degeneracy is not present in transit observations because the absorption depths scale with the scale height, which will be very different for H2 and heavier-element atmospheres.
which dictates the actual optical thickness of the background gas. The approximate value of this factor is given in Table 3 for several possible background gases. Because the photons only react to optical thickness, misidentifying the background gas will translate to an erroneous estimate of the ratio between the absorbing (e.g. CH4) and the scattering (e.g. H2/He or N2) gases. This degeneracy is not present in transit observations because the absorption depths scale with the scale height, which will be very different for H2 and heavier-element atmospheres.
Values of Rayleigh cross-sections at λ ~ 5 μm (in units of 10−27 cm2) for several possible background gasses.
6 Conclusions
Atmospheric retrievals from simulated observations are needed to understand the scientific outcome of future direct-imaging telescopes. These exercises help us to understand which model parameters have a greater impact on the spectrum of a planet and reveal correlations among parameters that affect the interpretation of a measurement. Carrión-González et al. (2020) showed that including the planet radius as a free parameter in the retrievals triggers degeneracies between model parameters, which prevent an accurate atmospheric characterization. In this work, we performed retrievals at multiple phase angles (37°, 85°, and 123°) assuming no prior information on Rp or on the cloud properties. We extended the study to three cloud scenarios (no-, thin-, and thick-cloud) for generality. With this, we aimed to determine which observing strategy would be most effective in breaking the parameter degeneracies and constraining the atmospheric properties and Rp.
If Rp and the cloud properties of the exoplanet are a priori unknown, we find that no single-phase observation with S∕N = 10 can distinguish between cloudy and cloud-free atmospheres. This finding, reported in Carrión-González et al. (2020) for α = 0°, is here generalized for a broad range of phase angles. The retrieval results and thus the information content of the spectra vary with the phase angle (Sect. 4.1). In all cloud scenarios, a single-phase observation at α = 123° is found to constrain Rp remarkably better than at smaller phase angles, with a maximum deviation of 35% with respect to the true value.
We performed simultaneous multi-phase retrievals and find that the combination of small (37°) and large (123°) phases is the only strategy that can break some of the correlations between Rp, 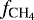 and the cloud properties in all cloud scenarios. We find that this is the most effective general observing strategy with which to identify the presence or absence of clouds and constrain atmospheric properties such as the methane abundance and the cloud optical properties. We tested other strategies, such as increasing S∕N to 20 for a single-phase observation at α = 37° or combining small (37°) and moderate (85°) phases. However, these failed in breaking the parameter correlations in the scenarios with thicker clouds.
and the cloud properties in all cloud scenarios. We find that this is the most effective general observing strategy with which to identify the presence or absence of clouds and constrain atmospheric properties such as the methane abundance and the cloud optical properties. We tested other strategies, such as increasing S∕N to 20 for a single-phase observation at α = 37° or combining small (37°) and moderate (85°) phases. However, these failed in breaking the parameter correlations in the scenarios with thicker clouds.
We found that the combination of small and large phases produces an improvement in the retrievals that is more noticeable for the thick-cloud scenario (Table 2). Furthermore, we verified that this improvement is more modest if the cloud aerosols have a nearly isotropic scattering phase function (Sect. 5.2). We therefore conclude that the optical properties of the cloud, and in particular the scattering phase function of the aerosols, have a significant impact on the information content of the spectra at each phase and on multi-phase retrievals. The idea that the shape of the phase curve is sensitive to the optical properties of the cloud aerosols is not new, as discussed above for Solar System observations. This idea has previously been proposed for the characterization of transiting exoplanets (e.g. García Muñoz & Cabrera 2018). Here we investigated its application for future direct-imaging efforts. We also ruled out that the changes in the information content of the spectra were caused by probing different altitudes of the atmosphere at each phase (Sect. 5.1). Indeed, for cloudy atmospheres we find that, at all phase angles, the photons contributing to the spectrum mainly probe the atmospheric layers where the cloud is located.
We identify a degeneracy in the retrieval of the absorbing gas abundance (CH4 here, but could be other molecule) that will affect the interpretation of reflected-starlight spectra of super-Earths. This degeneracy arises from the different Rayleigh cross-sections of plausible background gases (e.g. H2 or heavier elements) and may introduce a systematic uncertainty in the retrieved absorbing gas abundance. This will likely not affect the range ofplanets observed by the Roman Telescope, which will mainly be giants. However, it will play a role in future observations of planets in the super-Earth to mini-Neptune regime, whose atmospheres might not be H2 -dominated but might instead resemble those of the Earth, Venus, or Titan.
Our single-phase retrievals at different phase angles are consistent with the results of Nayak et al. (2017). However, our multi-phase retrievals differ from the combinations of measurements in Nayak et al. (2017) based on their intersection criterion. We conclude that simultaneous retrievals are needed to accurately model the effects of combining multiple measurements. Furthermore, we tested in Sect. 5.3 how our conclusions change if we do not include the cloud optical properties as free parameters in the retrievals. This is consistent to some extent with the assumptions in Feng et al. (2018) or Damiano et al. (2020), although the modelling approaches are somewhat different. We confirm that, in this case, the retrieval results are significantly more optimistic than if no prior knowledge is assumed on the cloud properties. As prior knowledge of the cloud properties will generally not be available, we conclude that additional correlations between model parameters will occur, reducing the accuracy of the retrievals as shown in Sect. 4.
Our findings are useful for the development of retrieval methods to be applied on future reflected-starlight observations and to establish the model parameters to be included. They also help in target prioritization for direct-imaging missions. For instance, the possibility of constraining the radius of a non-transiting exoplanet with an error of less than 35% underlines the importance of observing exoplanets at phase angles larger than quadrature. Furthermore, we conclude that exoplanets with broad intervals of observable phase angles should be considered prime targets for atmospheric characterization through optical phase-curve measurements.
Acknowledgements
The authors acknowledge the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets (GA 2557/1-1)”. N.C.S. acknowledges the support by FCT - Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 – Programa Operacional Competitividade e Internacionalização by these grants: UID/FIS/04434/2019; UIDB/04434/2020; UIDP/04434/2020; PTDC/FIS-AST/32113/2017 and POCI-01-0145-FEDER-032113; PTDC/FIS-AST/28953/2017 and POCI-01-0145-FEDER-028953.
Appendix A Posterior probability distributions of single-phase observations
A.1 No-cloud scenario, single-phase observations
 |
Fig. A.1 Posterior probability distributions of the model parameters for single-phase observations in the no-cloud atmospheric configuration at phase angles 37° (cyan), 85° (magenta), and 123° (yellow). In all cases, S∕N = 10. Green lines mark the true values of the model parameters (see Sect. 3.1) for this scenario. Two-dimensional subplots show the correlations between pairs of parameters. Contour lines correspond to the 1 σ confidence levels. A detailed description of the parameter correlations with additional σ levels in the 2D subplots can be found in Carrión-González et al. (2020) for measurements at α = 0°. |
A.2 Thin-cloud scenario, single-phase observations
A.3 Thick-cloud scenario, single-phase observations
Appendix B Posterior probability distributions of combined multi-phase observations
B.1 No-cloud scenario, combination of multi-phase observations
 |
Fig. B.1 Posterior probability distributions of the model parameters for several combinations of observations of the no-cloud atmospheric configuration, as described in Sect. 3.2. Blue lines indicate the combination (37°+85°), red lines, (37°+123°), and black lines, (37°+85°+123°). For reference, cyan lines indicate the results of a single-phase observation at α = 37° but doublingthe S∕N to 20). Green lines mark the true values of the model parameters (see Sect. 3.1) for this observation. Two-dimensional subplots show the correlations between pairs of parameters. Contour lines correspond to the 1 σ confidence levels. |
B.2 Thin-cloud scenario, combination of multi-phase observations
B.3 Thick-cloud scenario, combination of multi-phase observations
References
- Bevington, P. R., & Robinson, D. K. 2003, Data reduction and error analysis for the physical sciences (Boston, USA: McGraw-Hill) [Google Scholar]
- Bolcar, M. R., Feinberg, L., France, K., Rauscher, B. J., et al. 2016, Proc. SPIE, 9904, 99040J [CrossRef] [Google Scholar]
- Carrión-González, Ó., García Muñoz, A., Cabrera, J., et al. 2020, A&A, 640, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrión-González, Ó., García Muñoz, A., Santos, N. C., et al. 2021, A&A, 651, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damiano, M., & Hu, R. 2020, AJ, 159, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Damiano, M., Hu, R., & Hildebrandt, S. R. 2020, AJ, 160, 206 [Google Scholar]
- Dyudina, U., Zhang, X., Li, L., Kopparla, P., et al. 2016, ApJ, 822, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, Y. K., Robinson, T. D., Fortney, J. J., Lupu, R. E., et al. 2018 AJ, 155, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- García Munõz, A., & Cabrera, J. 2018, MNRAS, 473, 1801 [CrossRef] [Google Scholar]
- García Muñoz, A., & Mills, F. P. 2015, A&A, 573, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García Muñoz, A., Pérez-Hoyos, S., & Sánchez-Lavega, A. 2014, A&A, 566, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García Muñoz, A., Lavvas, P., & West, R. A. 2017, Nat. Astron., 1, 0114 [CrossRef] [Google Scholar]
- Gaudi, B. S., Seager, S., Mennesson, B., et al. 2020, ArXiv e-prints [arxiv:2001.06683] [Google Scholar]
- Giampapa, M. S., Rosner, R., Kashyap, V., et al. 1996, ApJ, 463, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Grenfell, J. L., Leconte, J., Forget, F., et al. 2020, Space Sci. Rev., 216, 98 [CrossRef] [Google Scholar]
- Heindinger, A. K., & Stephens, G. L. 2000, JAS, 57, 1615 [Google Scholar]
- Hu, R. 2019, ApJ, 887, 166 [Google Scholar]
- Lacy, B., Shlivko, D., & Burrows, A. 2019, AJ, 157, 132 [Google Scholar]
- Lee, Y. J., García Muñoz, A., Imamura, T., et al. 2020, Nat. Commun., 11, 5720 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. J., García Muñoz, A., Yamazaki, A., et al. 2021, Geophys. Res. Lett., 48, e90577 [NASA ADS] [Google Scholar]
- Lubin, J., Robertson, P., Stefansson, G., et al. 2021, AJ, 162, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Lupu, R. E., Marley, M. S., Lewis, N., et al. 2016, AJ, 152, 217 [Google Scholar]
- The LUVOIR Team 2018, ArXiv e-prints [arxiv:1809.09668] [Google Scholar]
- Mallama, A. 2009, Icarus, 204, 11 [CrossRef] [Google Scholar]
- Mayorga, L. C., Jackiewicz, J., West, R. A., et al. 2016, AJ, 152, 209 [Google Scholar]
- Mayorga, L. C., Charbonneau, D., & Thorngren, D. P. 2020, AJ, 160, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Mennesson, B., Gaudi, S., Seager, S., et al. 2016, Proc. SPIE, 9904, 990469 [NASA ADS] [CrossRef] [Google Scholar]
- Mishchenko, M. I. 1989, Icarus, 84, 296 [Google Scholar]
- Morozhenko, A. V., & Yanovitskij, E. G. 1973, Icarus, 18, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Nayak, M., Lupu, R., Marley, M. S., et al. 2017, PASP, 129, 973 [Google Scholar]
- Pérez-Hoyos, S., Sanz-Requena, J. F., Barrado-Izaguirre, N., et al. 2012, Icarus, 217, 256 [CrossRef] [Google Scholar]
- Ribas, I., Tuomi, M., Reiners, A., et al. 2018, Nature, 563, 365 [Google Scholar]
- Robinson, T. D., Meadows, V. S., Crisp, D., et al. 2011, Astrobiology, 11, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid, H. M., Buenzli, F. J. E., & Gisler, D. 2011, Icarus, 212, 701 [CrossRef] [Google Scholar]
- Shardanand, & Rao, A. D. P. 1977, NASA Technical Note D-8442 [Google Scholar]
- Smith, P. H., & Tomasko, M. G. 1984, Icarus, 58, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D., Gehrels, N., Breckinridge, J. 2013, ArXiv e-prints [arxiv:1305.5422] [Google Scholar]
- Stamnes, K., Tsay, S.-Chee; Jayaweera, K., & Wiscombe, W. 1988, Appl. Opt., 27, 2502 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, G. L., & Heindinger, A. K. 2000, JAS, 57, 1599 [Google Scholar]
- Sudarsky, D., Burrows, A., Hubeny, I., & Li, A. 2005, ApJ, 627, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, J. A., & Driscoll, J. F. 2004, Opt. Lett., 29, 2620 [NASA ADS] [CrossRef] [Google Scholar]
In order to compare retrievals with different numbers of samples, instead of plotting the total count of samples we plot at each histogram bin the corresponding number of counts divided by the total count and by the bin width. This way, the integral under the histogram is equal to 1 in all retrievals.
All Tables
Retrieval results for different phase angles and their combinations, for all three cloud scenarios.
Values of Rayleigh cross-sections at λ ~ 5 μm (in units of 10−27 cm2) for several possible background gasses.
All Figures
 |
Fig. 1 Noiseless synthetic spectra (left column) for the no-cloud (top row and light blue), thin-cloud (middle row and darker blue), and thick-cloud (bottom row and purple) configurations. Solid lines in each subplot correspond to the spectrum at phase angle α = 37°, dashed lines at α = 85°, and dotted lines at α = 123°. The error bars indicated with vertical lines correspond to the noise at S∕N = 10 injected to create the noisy spectrum at each phase angle. Right column: same synthetic spectra but normalised with respect to the value of Fp∕F⋆(λ = 500 nm), revealing the shape changes in the spectra at different phases. |
| In the text | |
 |
Fig. 2 Dependence of the aerosol scattering phase function p(θ) on the photon scattering angle θ for the considered values of reff. For clarity, the plot shows log10(p(θ)), where θ = 0° corresponds to forward scattering and θ = 180° to backwardscattering. |
| In the text | |
 |
Fig. 3 Marginalized posterior probability distributions of each model parameter for single-phase observations in the no-, thin-, and thick-cloud scenarios (top, middle, and bottom rows, respectively). The single-phase observations are obtained at phase angles 37° (cyan lines), 85° (magenta lines), and 123° (yellow lines). In all cases, S∕N = 10. Green lines mark the true values of the model parameters (see Sect. 3.1) for this scenario. The 2D posterior probability distributions for these retrievals can be found in Figs. A.1−A.3. |
| In the text | |
 |
Fig. 4 Marginalized posterior probability distributions of each model parameter for several combinations of observations in the no-, thin- and thick-cloud scenarios (top, middle, and bottom row, respectively). Blue lines mark the combination (37°+85°); red lines, (37°+123°) and black lines, (37°+85°+123°). For reference, cyan lines indicate the results of a single-phase observation at α = 37° but doubling the S/N to 20. Green lines mark the true values of the model parameters (see Sect. 3.1) for this observation. The 2D posterior probability distributions for these retrievals can be found in Figs. B.1−B.3. |
| In the text | |
 |
Fig. 5 Atmospheric layers probed by the photons in our radiative-transfer computations. Layer 28 is the top of the atmosphere and layer 0 is the bottom (see Carrión-González et al. 2020 for details). Each row corresponds to a cloudscenario. Upper row: no-cloud; middle: thin-cloud; bottom: thick-cloud. Left column: phase angle of 37°; middle: α = 85°,right: α = 123°. The maximum photon contribution at each wavelength is normalized to 1. However, not all wavelengths have comparable absolute contributions to the spectra, as shown in Fig. 1. The right-hand panels of each subplot show the vertical profiles of these normalized photon contributions for a selection of wavelengths: 500 nm (purple lines), 600 nm (blue lines), 724 nm (yellow lines), and 884 nm (red lines). |
| In the text | |
 |
Fig. 6 Contribution to the overall spectral brightness of the successive scattering events that the simulated photons undergo in the atmosphere at λ = 500 nm (purple lines), 600 nm (blue lines), 724 nm (yellow lines), and 884 nm (red lines). At each wavelength, the maximum photon contribution to the overall brightness of the spectrum is normalized to 1. Each column corresponds to a phase angle: 37° (left), α = 85° (middle), and α = 123° (right). Each row corresponds to a cloud scenario, as indicated in the labels. Also included are the thick-cloud-scenario retrievals forvalues of reff = 0.10 and 2.0 μm (see Sect. 5.2). |
| In the text | |
 |
Fig. 7 Marginalized posterior probability distributions of each model parameter for single-phase observations in the thick-cloud scenario at phase angles 37° (cyan), 85° (magenta), and 123° (yellow). Top row: assuming a true value of reff = 0.10 μm for the cloud aerosols. Middle row: assuming a true value of reff = 0.50 μm for the cloud aerosols, as in Sect. 4. Bottom row: assuming a true value of reff = 2.0 μm for the cloud aerosols. Vertical green lines mark the true values of the model parameters (see Sect. 3.1). |
| In the text | |
 |
Fig. 8 Marginalized posterior probability distributions of each model parameter for several combinations of observations in the thick-cloud atmospheric configuration, as described in Sect. 3.2. Blue lines mark the combination (37°+85°), red lines mark (37°+123°), and black lines mark (37°+85°+123°). Top row: assuming a true value of reff = 0.10 μm for the cloud aerosols. Middle row: assuming a true value of reff = 0.50 μm for the cloud aerosols, as in Sect. 4. Bottom row: assuming a true value of reff = 2.0 μm for the cloud aerosols. Vertical green lines mark the true values of the model parameters (see Sect. 3.1). |
| In the text | |
 |
Fig. 9 Retrieval results for an exercise in which the aerosol properties of the thick-cloud scenario (τc, reff and ω0) are assumed known and are therefore not explored by the MCMC retrieval sampler. Left panel: single-phase retrievals as in Fig. A.3. Right panel: multi-phase retrievals as in Fig. B.3. |
| In the text | |
 |
Fig. A.1 Posterior probability distributions of the model parameters for single-phase observations in the no-cloud atmospheric configuration at phase angles 37° (cyan), 85° (magenta), and 123° (yellow). In all cases, S∕N = 10. Green lines mark the true values of the model parameters (see Sect. 3.1) for this scenario. Two-dimensional subplots show the correlations between pairs of parameters. Contour lines correspond to the 1 σ confidence levels. A detailed description of the parameter correlations with additional σ levels in the 2D subplots can be found in Carrión-González et al. (2020) for measurements at α = 0°. |
| In the text | |
 |
Fig. A.2 As Fig. A.1, but for the thin-cloud scenario. |
| In the text | |
 |
Fig. A.3 As Fig. A.1, but for the thick-cloud scenario. |
| In the text | |
 |
Fig. B.1 Posterior probability distributions of the model parameters for several combinations of observations of the no-cloud atmospheric configuration, as described in Sect. 3.2. Blue lines indicate the combination (37°+85°), red lines, (37°+123°), and black lines, (37°+85°+123°). For reference, cyan lines indicate the results of a single-phase observation at α = 37° but doublingthe S∕N to 20). Green lines mark the true values of the model parameters (see Sect. 3.1) for this observation. Two-dimensional subplots show the correlations between pairs of parameters. Contour lines correspond to the 1 σ confidence levels. |
| In the text | |
 |
Fig. B.2 As Fig. B.1, but for the thin-cloud scenario. |
| In the text | |
 |
Fig. B.3 As Fig. B.1, but for the thick-cloud scenario. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


