EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A60 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A60
Number of page(s) 12
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202141714
Published online 11 October 2021

© ESO 2021

1 Introduction

The field of extrasolar planet detection through the radial velocity (RV) technique has evolved very quickly during the past decades. This evolution has been driven by technical developments, especially in wavelength calibration sources (e.g., Cersullo et al. 2019; Coffinet et al. 2019) and instrumental stability (e.g., Mayor et al. 2003). First the iodine cell, then the ThAr, and now the Fabry-Perot and laser frequency comb technologies are helping us to reach a precision of a few tens of cm s−1 in RV. The final precision of the instrument is also determined by the stability of the ambient conditions. Great efforts were made in this regard in the past, using vacuum chambers to isolate the instrument from external environmental changes (e.g., HARPS, Mayor et al. 2003; CARMENES, Quirrenbach et al. 2010; or HIRES, Vogt et al. 1994). The state of the art of this evolution is the ESPRESSO instrument (Pepe et al. 2021) at the Paranal Observatory. This instrument collects the light from any (or all) the Unit Telescopes from the Very Large Telescope (VLT) through the coudé trains (Cabral et al. 2010), which feed the instrument together with simultaneous wavelength calibration sources. The instrument is located in a three-layer isolation room where the ambient conditions (pressure, temperature, and humidity) are kept stable (Álvarez et al. 2018). This allows ESPRESSO to reach a RV precision of 10 cm s−1 on the sky (see Pepe et al. 2021).

The instrument has been available to the community since ESO period P104 (October 2018). Since then, by using the guaranteed time observations (GTOs), the ESPRESSO Consortium has shown the capability of the instrument to characterize the atmosphere of hot and warm Jupiters (e.g., Ehrenreich et al. 2020; Allart et al. 2020; Borsa et al. 2021; Santos et al. 2020; Tabernero et al. 2021b; Casasayas-Barris et al. 2021), determine the precise masses of transitingplanetary systems (e.g., Toledo-Padrón et al. 2020; Sozzetti et al. 2021; Mortier et al. 2020), and deeply investigate the complex architecture of planetary systems like TOI-178 (Leleu et al. 2019, 2021), π Mensae (Damasso et al. 2020), and Proxima Centauri (Suárez Mascareño et al. 2020). The community has also made use of this instrument for these purposes, with special mention to the largest RV dataset taken so far with ESPRESSO, 113 spectra of LHS 1140 that allowed the estimation of the water mass fraction of its habitable zone planet (Lillo-Box et al. 2020).

In this paper we report the first discovery and characterization of a planet made by this instrument in the context of the GTO observations. In Sect. 2 we present the observations used. In Sect. 3 we describe the stellar and planet characterization methods, and the results are presented in Sect. 4. We conclude in Sect. 5.

thumbnail Fig. 1

ESPRESSO radial velocity time series for HD 22496. Upper panel: complete series with the three datasets corresponding to the three ESPRESSO windows (ESPR18, ESPR19, and ESPR21). The median GP model is shown in blue and the median GP+Keplerian model is shown in red, with 95% confidence intervals shown as red shaded regions. Lower panel: close view of the ESPR19 (left) and ESPR21 (right) datasets after removing the median GP model.

2 Observations and general properties

We observed HD 22496 with ESPRESSO (Pepe et al. 2021) within the context of the GTOs granted to the ESPRESSO Consortium.The selection of this and other GTO targets surveyed in the context of a blind search for planets is described in Hojjatpanah et al. (2019). A total of 41 spectra with the HR21 mode and an exposure time of 900 s each were obtained from Paranal observatory (ESO, Chile), with a mean signal-to-noise ratio (S/N) of 270 at 550 nm and simultaneously illuminating the second fiber with the Fabry-Pérot interferometer. The observations span 895 days between 24 October 2018 and 06 April 2021 and with a typical cadence of one spectrum every 1–3 days for each campaign. We note that observations suffered from the long gap betweenMarch and December 2020 due to the pandemic situation of COVID-19. The first four data points were obtained prior to the ESPRESSO fiberlink exchange in June 2019 that improved the efficiency of the instrument by more than 50%, as described in Pepe et al. (2021). This intervention introduced an RV offset that leads to treating this dataset separately (denoted ESPR18 in this paper). In addition, during the ramp-up after the pandemic closure of the observatory, a calibration lamp exchange on 17 December 2020 introduced an additional offset in the RV measurements. Hence we consider the 16 spectra between June 2019 and December 2020 (denoted ESPR19 throughout this paper) and the 21 observations obtained afterwards (ESPR21) as independent datasets. We assume that these three datasets come from different instruments to allow for possible RV offsets and different levels of RV jitter.

The data were reduced with the instrument Data Reduction Software (DRS) pipeline version 2.2.81 (Pepe et al. 2021). The pipeline also extracts the RV by using the cross-correlation technique (Baranne et al. 1996) against a K5 mask, which was selected in this case. It also computes different activity indicators for each epoch, as described in Pepe et al. (2021). A summary of the derived RV, FWHM and BIS is shown in Table B.2. The median RV uncertainty of this dataset corresponds to 18 cm s−1 (and a mode of 15 cm s−1) and we found a scatter in the dataset corresponding to 2.7 m s−1 (more than one order of magnitude larger than the median uncertainty), a first indication of an additional source of variability. The ESPRESSO RV time series of HD 22496 is shown in Fig. 1.

HD 22496 was also observed by HARPS (Mayor et al. 2003) in the past, on lower-precision RV campaigns aiming at a multitude of objectives (program IDs 072.C-0488 – PI: M. Mayor–, 085.C-0019 – PI: G. Lo Curto–, and 183.C-0972 – PI: S. Udry). In total, 43 HARPS spectra are publicly available from the ESO archive. The radial velocities and activity indicators were computed by the instrument DRS v3.5. Given the relatively short exposure times (ranging from 90 to 900 s with a median of 120 s), the median uncertainty of this dataset corresponds to 2.2 m s−1 and a standard deviation of 4.9 m s−1 (see in Table B.2).

TESS (Ricker et al. 2014) observed HD 22496 during sectors 3, 4, 30, and 31. We retrieved the light curves from these sectors through the MAST archive2 and used the detrended Pre-search Data Conditioned Simple Aperture Photometry (PDCSAP) flux provided by the TESS SPOC pipeline (Jenkins et al. 2016). ESPRESSO18 observations were obtained during TESS Sector 4, ESPRESSO19 around seven months before Sector 30, and ESPRESSO 21 observations started around three months after Sector 31. Additional description of the light curve extraction and analysis is provided in Appendix A.

3 Analysis

3.1 Stellar properties

HD 22496 (also known as LHS 1563, GJ 146, or HIP 16711) is a bright (V =8.9 mag) late-type K-dwarf star in the solar vicinity. The Gaia (Gaia Collaboration 2016) EDR3 data release (Gaia Collaboration 2021) provides a precise parallax of π = 73.520 ± 0.016 mas (Lindegren et al. 2021), corresponding to a distance of d = 13.602 ± 0.003 pc (see Table B.1). According to the Gaia proper motions and the relations from Bensby et al. (2003), this star likely belongs to the Galactic thin disk (with a probability 67 times higher than belonging to the thick disk). The photometric information from the second data release (DR2, Gaia Collaboration 2018) also provides an effective temperature of 4250 K and log g = 4.5 dex, corresponding to a K5-K7 main-sequence star. Mann & von Braun (2015) derived a mass and radius of M⋆ = 0.684 M⊙ and R⋆ =0.45 R⊙ through spectroscopic characterization. Based on the comparison between Gaia and HIPPARCOS proper motion differences, Kervella et al. (2019) put constraints on potential companions to this star, and set a sensitivity of 0.45 ± 0.25 MJup at 1 au.

We combined all ESPRESSO observations of HD 22496 into a single high S/N spectrum to estimate the stellar atmospheric parameters (namely effective temperature Teff, surface gravity logg, and metallicity [Fe/H]). We used the spectral synthesis method by means of the steparsyn code (Tabernero et al. 2018, 2021a). We employed a grid of synthetic spectra computed with the Turbospectrum (Plez 2012) code alongside MARCS stellar atmospheric models (Gustafsson et al. 2008) and atomic and molecular data of the Gaia-ESO line list (Heiter et al. 2021). We employed a selection of Fe I lines following the line list given by Tabernero et al. (2019) for metal-rich dwarf stars. STEPARSYN allowed us to compute the following stellar atmospheric parameters: Teff = 4385 ± 21 K, log g = 4.69 ± 0.05 dex, [Fe/H] = −0.08 ± 0.02 dex.

The values reported in the TESS Input Catalog (TIC v8.0.1, Stassun et al. 2019, Teff ~ 4102 K, and log g ~ 4.52 dex) are not consistent with those derived in our spectroscopic analysis. However, our spectroscopic analysis is based on a very high-resolution, and high S/N ESPRESSO spectrum, compared to the photometric characterization in the TIC catalog. Moreover, using Gaia EDR3 paralaxes and photometry we obtain a trigonometric surface gravity of 4.73 ± 0.02 dex, consistent with the value derived by our spectrosocopic analysis.

We used the TESS light curve to explore the level of stellar variability and estimate a stellar rotation period. In Appendix A we provide a detailed description of the analysis performed. However, this in-depth study is still inconclusive, although it points to a stellar rotation period in the range 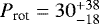days.

3.2 Radial velocity analysis

The generalized Lomb-Scargle periodogram of the ESPRESSO RV time series is shown in Fig. 2 (upper panel). It shows a “forest” of periodicities of around 30 days, similar to the expected rotation period from the 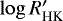relations from Suárez Mascareño et al. (2015) (35 days) and the same parameter space derived form the TESS light curve (see Appendix A). The periodogram of the different activity indicators (bisector span BIS, full width at half maximum FWHM of the CCF, the CCF contrast, and the 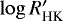) also show significant peaks at 35 days and its potential one-day aliases of 15.9 days and 70 days (see panels 3–6 in Fig. 2). The correlation of the CCF-FWHM with the RV time series yields a Pearson’s coefficient of 0.71, hence suggesting that part of the RV variations are due to stellar activity. The periodogram also reveals a clear signal at 5.09 days and its one-day alias at 1.2 days. The power of both signals is clearly enhanced by performing a simple weighted linear detrending with the CCF-FWHM indicator (see second panel of Fig. 2).

Based on this preliminary analysis, we analyzed the ESPRESSO RV data by assuming different possible scenarios with different number of planets and orbital configurations. In particular, we tested four models, including no planets (0p, null hypothesis), one planet in circular orbit (1p1c), one planet in eccentric orbit (1p), and two planets in circular orbits (2p1c2c). We account for stellar activity by using a Gaussian process (GP) approach where the CCF-FWHM activity indicator is used as a proxy3 (Suárez Mascareño et al. 2020). The Keplerian signals are modeled by a period (Pi), time of inferior conjunction (T0,i), and semi-amplitude (Ki) for each of the planets tested, and the eccentricity (ei) and argument of the periastron (ωi) for non-circular models. Additionally, we use a RV offset (δRV,j) and a jitter term (σRV,j) for each instrument considered (four in total, taking into account HARPS and the three ESPRESSOepochs). Since we are using the CCF-FWHM as a proxy, we also add an offset (δFWHM,j) and jitter (σFWHM,j) per instrument and epoch for these data. We use a quasi-periodic kernel (Ambikasaran et al. 2015; Faria et al. 2016) for both the RV and the FWHM, both sharing the rotation period (η3), timescale of the variation (η2), and the scaling factor (η4), while each has its own amplitude (η1,RV and η1,FWHM).

We use a broad Gaussian prior for the inner planet centered at approximately five days and with a one-day width, while for the outer component in the two-planet model we assume a uniform prior between 5 and 200 days. Nevertheless, we note that broad uninformative priors were also tested for the inner component (uniform between 1.1 and 20 days) and for the GP hyper-parameter associated with the stellar rotation period, η3 (log-uniform between 8 and 100 days). The exploratory results on these two parameters show strong evidence for the 5.09-day Keplerian signal against the null hypothesis and against the ~1.25-day alias, and for the η3 ~ 35 days against other possible periodicities also present in the periodogram of the activity indicators (see Fig. 2 and discussion above).

We use the emcee Markov chain Monte Carlo (MCMC) affine invariant ensamble sampler (Foreman-Mackey et al. 2013) to populate the posterior distribution of the different parameters involved. For each model, we use a first burn-in phase of 100 000 steps and four times as many walkers as number of parameters. A second phase (the production phase) contains 50 000 steps instead. This is enough to ensure the convergence of the chains. This is checked by estimating the autocorrelation time and the corresponding chain length, with the latest being at least 20 times longer than the autocorrelation time to consider convergence. We then use 15% of the final flattened chain (typically composed of 105 − 106 elements) to estimate the Bayesian evidence of each model (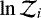) and its corresponding uncertainty through the perrakis implementation4 (Díaz et al. 2016).

This procedure is first performed on the ESPRESSO dataset (labeled E) and subsequently on the whole ESPRESSO and HARPS dataset (labeled H+E).

thumbnail Fig. 2

Periodogram of ESPRESSO time series. From top to bottom: ESPRESSO RV, ESPRESSO RVs after a simple weighted linear detrending with the BIS-SPAN activity indicator (green), and after removing a Keplerian signal with P = 5.09 days (red), FWHM of the CCF, CONTRAST of the CCF, log(RHK), BIS-SPAN, and the window function. The dashed red vertical lines give the location of the confirmed planet HD 22496 b, the stellar rotation period found by the GP, and its alias. In the two upper panels the dotted horizontal lines give the 0.1 and 1% false alarm probability levels. In the second panel the vertical dotted lines indicate the first ten alias periods of the HD 22496 b signal.

4 Results

The distribution of the Bayesian evidence values from the MCMC chains for the most relevant scenarios (those showing the largest values) is shown in Fig. 3 relative to the null hypothesis (i.e., the model with no planets). In this figure we include the results for both the ESPRESSO and ESPRESSO+HARPS datasets. As shown, the one-planet model assuming circular orbit (labeled 1p1c) is strongly preferred against the null hypothesis (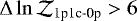, Jeffreys 1998) and against other more complex models. We note that the odds ratio between the 1p1c model and the null hypothesis surpasses the statistical significance standard threshold in the ESPRESSO (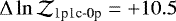) and the ESPRESSO+HARPS (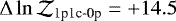) datasets. We thus conclude that the one-planet circular orbit model is the one best supported by our datasets. The ESPRESSO stand-alone dataset is enough to confirm this signal with statistical significance against the null hypothesis, and it was the one that originally allowed us to detect the planet signal. The addition of the HARPS data increases the significance of the detection, providing additional confidence that the planetary signal is present in the system by using an independent dataset. Consequently, we use the HARPS+ESPRESSO dataset for the subsequent discussion. The phase-folded median model for this scenario is presented inFig. 4 and the credible intervals for the different parameters involved are shown in Table B.3.

The largest evidence model (the one-planet in circular orbit scenario with the ESPRESSO+HARPS dataset) indicates that HD 22496 is orbited by a planetary-mass object with a minimum mass of 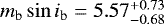M⊕. Only an orbital inclination below i < 0.8° (i.e., almost a fully face-on orbit) would place this companion above the planet-mass regime. Consequently, the probability of this being a planet signal (assuming random distribution for the orbital inclination) is 99.1%. We can thus safely consider this companion to be of planetary nature. Additionally, we find that for orbital inclinations above i > 20° the planet would have an absolute mass below the Neptune mass. On the other hand, based on the stellar rotation period and the upper limit of the projected stellar velocity provided in Hojjatpanah et al. (2019) (v sin i < 2 km s−1), we can infer a lower limit for the inclination of the stellar spin of i⋆ > 20°. Hence, in the case of spin-orbit alignment5, the absolute mass of the planet will be in the range mb = 5.6−16 M⊕. This places the planet at the boundary between the super-Earth (rocky) and sub-Neptune (mostly gaseous) regimes.

The planet revolves around its star every 5.09 days and receives an insolation flux 22.8 times that of the Earth’s. We tested the eccentric scenario and we found clear evidence in favor of the circular model, with an odds ratio of 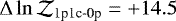, as stated above. Instead, we can set upper limits to the eccentricity of this planet up to eb < 0.15 at the 95% confidence level. The GP catches the expected rotation period of the star, providing 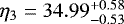days, compatible with the expected value (see Sect. 3.2).

Additionally, we tested the detectability limits of planets inside the habitable zone of this star. To this end, we follow an injection-recovery analysis similar to that from Lillo-Box et al. (2020). We simulate Keplerian signals at different periods (from 39 to 200 days, within the habitable zone) and with different minimum masses (from 0.1 to 16 M⊕), assuming circular orbits. We add these signals to the ESPRESSO+HARPS dataset and explore their detectability by modelingthe data in the same manner as explained in Sect. 3 (i.e., including the GPs and the activity indicators as proxies for their hyper-parameters). Figure 5 shows the resulting detectability matrix. In general terms, we can discard the presence of planets with minimum masses smaller than 5 M⊕ in the inner edge of the habitable zone (PHZ, out ~ 40 days) and 7 M⊕ in the outer boundary (PHZ, out ~ 200 days).

Based on the above RV-driven analysis we searched for transits of the 5.09-day period planet (and any other potential signal) in the TESS light curve. We used wotan (Hippke et al. 2019) to perform a smoothing of the photometrictime series to remove long-term variations (using the flatten routine with a window length of 0.5 days) potentially due to either stellar activity or instrumental effects (especially apparent in sector 4). Then we searched for transit-like dimmings using the tls software (Heller et al. 2019) on the detrended light curve. We found no significant peaks in thetls periodogram, suggesting that no transits are present in the data. We further phase-folded the TESS light curve by using the periodicity detected with the RV data (see Sect. 3.2). No apparent transit is detectable above 50 parts per million depth. This implies a minimum orbital inclination for HD 22496 b of i < 87.6° or otherwise a maximum size of 0.34 R⊕.

thumbnail Fig. 3

Distribution of the log-Bayesian evidence for the different models tested using the Gaussian process approach to accountfor the stellar activity (see Sect. 3). The shaded distributions correspond to the HARPS+ESPRESSO dataset (upper panel), while open distributions correspond to the ESPRESSO stand-alone dataset (lower panel). The median from the null hypothesis model for each dataset (labeled 0p) has been subtracted. In the upper panel the two-planet model (2p1c2c) has a very low odds ratio, hence lying outside of the plot limits.
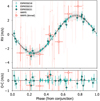thumbnail Fig. 4

Radial velocities from HARPS (red) and ESPRESSO (green) phase-folded with the period from planet HD 22496 b. The red open symbols represent binned values from HARPS measurements corresponding to 10% of the orbital phase. The median GP model has been subtracted. The bottom panel shows the residuals of the mean model.
thumbnail Fig. 5

Detectability matrix for the HARPS and ESPRESSO dataset within the habitable zone of HD 22496 performed through injection-recovery. The color-coding represents the significance in the posterior of the RV semi-amplitude parameter in units of its standard deviation, with ratios above 3 (signal detected) in blue. The dashed lines correspond to one and three times the standard deviation of the residuals from the one-planet circular model (i.e., 28 cm s−1).

5 Conclusions

We presented the first stand-alone detection and confirmation of an extrasolar planet with the ESPRESSO instrument. With only 41 900 s exposures, we reached a Bayesian evidence > 105 times larger than the null model hypothesis (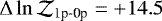), reaching a precision in the minimum mass of the planet of 13%, below the typically required precision for atmospheric studies (Batalha et al. 2019). HD 22496 b is likely a planet in the transition between super-Earth and sub-Neptunian planets ( 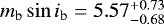M⊕) orbiting around a late K-type star. These stellar hosts are receiving increasing interest from the astrobiology community (see, e.g., the KOBE experiment6) as they represent friendly environments for life, with little stellar activity and a low flare rate (< 1%, Günther et al. 2020), and are found in a habitable zone sufficiently far from the star where the planets are less likely to be tidally locked (Barnes 2017), but sufficiently close to have a relatively high probability of transit andto be easy to detect through RV techniques. The case of HD 22496, however, only allows atmospheric studies through non-transiting techniques (e.g., phase curves with ARIEL, Tinetti et al. 2018) as the planet does not transit its host.

With one close-in planet detected, HD 22496 enters the group of late K dwarfs with known planets. Planet occurrence rates from the Kepler mission show that these K dwarfs have three to four planets per star (Kunimoto & Matthews 2020) and a high occurrence rate of 0.65 planets per star within the habitable zone, half of them being in the rocky regime. Hence, additional follow-up efforts should continue for this system to reveal the potential additional planets.

Acknowledgements

The authors acknowledge the ESPRESSO project team for its effort and dedication in building the ESPRESSO instrument. We also thank the referee for the thorough revision of this manuscript. J.L-B. acknowledges financial support received from “la Caixa” Foundation (ID 100010434) and from the European Union’s Horizon 2020 research and innovation programme under the Marie Skņodowska-Curie grant agreement No 847648, with fellowship code LCF/BQ/PI20/11760023. This research has also been partly funded by the Spanish State Research Agency (AEI) Projects No.ESP2017-87676-C5-1-R and No. MDM-2017-0737 Unidad de Excelencia “María de Maeztu”- Centro de Astrobiología (INTA-CSIC). J.P.F. is supported in the form of a work contract funded by national funds through FCT with reference DL57/2016/CP1364/CT0005. O.D.S.D. is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by national funds through Fundação para a Ciência e Tecnologia (FCT). A.M.S acknowledges support from the Fundação para a Ciência e a Tecnologia (FCT) through the Fellowship 2020.05387.BD. and POCH/FSE (EC). A.S.M., C.A.P., J.I.G.H., and R.R.L. acknowledge financial support from the Spanish Ministry of Science and Innovation (MICINN) project AYA2017-86389-P. This work was supported by FCT – Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 – Programa Operacional Competitividade e Internacionalização by these grants: UID/FIS/04434/2019; UIDB/04434/2020; UIDP/04434/2020; PTDC/FIS-AST/32113/2017 and POCI-01-0145-FEDER-032113; PTDC/FIS-AST/28953/2017 and POCI-01-0145-FEDER-028953; PTDC/FIS-AST/28987/2017 and POCI-01-0145-FEDER-028987. F.P.E. and C.L.O. would like to acknowledge the Swiss National Science Foundation (SNSF) for supporting research with ESPRESSO through the SNSF grants nr. 140649, 152721, 166227 and 184618. The ESPRESSO Instrument Project was partially funded through SNSF’s FLARE Programme for large infrastructures. The INAF authors acknowledge financial support of the Italian Ministry of Education, University, and Research with PRIN 201278X4FL and the “Progetti Premiali” funding scheme. N.J.N. acknowledges support form the following projects UIDB/04434/2020 and UIDP/04434/2020, CERN/FIS-PAR/0037/2019, PTDC/FIS-OUT/29048/2017, COMPETE2020: POCI-01-0145-FEDER-028987, and FCT: PTDC/FIS-AST/28987/2017.

Appendix A TESS light curve analysis

TESS observations from sectors 3, 4, 30, and 31 were retrieved from the MAST archive, and the PDCSAP detrended photometry was obtained. We used tpfplotter7 (Aller et al. 2020) to first check for possible contamination within the TESS aperture and found only one source inside the aperture with contrast ΔG = 7.4 mag in the Gaia passband (see Fig. A.1). This large contrast ensures a negligible contamination.

We excluded all exposures whose quality flags displays the bits 1, 2, 3, 4, 5, 6, 8, 10, and 12, as suggested by the TESS team. Based on the release notes of the TESS data8, we also excluded all measurements of sector 4 taken before 1413.26 TJD because of an incorrect pointing due to a erroneous guiding star table uploaded at the beginning of the sector. An interruption of communication between the instrument and the spacecraft also occurred towards the end of the first half of sector 4. The data collected after this interruptionand before the interruption at mid-sector for data downlink shows variations far greater than any other portions of LC in the SAP LC. The PDCSAP LC shows much smaller variations during this period, although it still displays clear variations correlated with the signal observed in the SAP LC, which have shorter timescales than the rest of the LC. We thus excluded data taken between 1421 and 1423 TJD. Even so, in sector 4 we observed clear box-shape signals before the last three momentum dumps of the reaction wheels. The correlation between the momentum dumps and these events associated with the fact that such signals are not observed in the rest of the LC indicates that these signals are not of astrophysical origin. Consequently, we excluded all data taken between 1430 and 1430.5883 TJD, between 1432.5 and 1433.5883 and after 1435.5 TJD in sector 4. During sector 3, we observed in the PDCSAP LC an exponential decrease in the flux at the beginning of the sector and an increasing ramp-like signal after the data downlink interruption that are absent from the SAP LC. We suspect that these signals are due to an overcorrection, and we removed all measurements taken before 1386.113 TJD in sector 3 andbetween 1396.50 and 1397.50 TJD. The resulting light curve is shown in Fig. A.2.

We then inspected the normalized TESS LC for signs of stellar activity-induced modulation. We used the start and the end of each sector and the time of each momentum dump of the reaction wheels to divide the LC into 24 chunks. Momentum dumps can produce jumps that could bias our analysis. We then fitted a model composed of a mean shift for each chunk and a GP with a quasi-periodic kernel implemented using the celerite Python package (Foreman-Mackey et al. 2017; Foreman-Mackey 2018). The functional form of the GP kernel is (A.1)

where Prot is an estimator of the stellar rotation period, L is the correlation timescale, B is a positive amplitude term, and C is a positivefactor (Foreman-Mackey et al. 2017, eq. 56). We optimized the fit using pre-optimization with a Nelder-Mead simplex algorithm (Nelder & Mead 1965) using the Python package scipy.optimize followed by a MCMC exploration maximizing posterior probability of the model using emcee. We used a multi-dimensional Gaussian distribution for the likelihood. For the priors, we used log-uniform priors: between 0.1 ppm and 1 for B, between 1 and 104 days for L, between 1 and 100 days for Prot, and between exp(−5) and exp(5) for C. The emcee used 64 walkers and a first exploration of 5 000 iterations per walker followed by a second exploration of 10 000 iterations starting from the last position of the previous exploration. The result provides a broad and asymmetric posterior distribution for the rotation period of 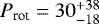days. This result is then still inconclusive about the actual rotation period of the star, but certainly points to values in this regime.

thumbnail Fig. A.1

Target pixel file plot (using tpfplotter Aller et al. 2020) of HD 22496 in Sector 3. The TESS pipeline aperture is highlighted with red shaded squares. The location of the target is given by a white cross, and all additional sources identified byGaia DR2 with red circles (with sizes inversely proportional to their magnitude).

Finally, to further investigate the periodicities present in the LC, we computed its generalized Lomb-Scargle periodogram (GLSP). However, to mitigate the impact of jumps between the different chunks of the LC, we first corrected the mean level of each chunk using the mean shift obtained by the previous fit. The resulting periodogram is shown in Fig. A.3. Given the large difference in the amplitude of the LC variability between TESS cycle 1 (sectors 3 and 4) and TESS cycle 3 (sectors 30 and 31), we also include in this figure the individual GLSP of each cycle. While cycle 1 shows clear long-term variability, cycle 3 shows a clear decrease in the amplitude of the variations. We interpret this as different instances of the stellar magnetic cycle. However, we have no additional data to test this hypothesis. Interestingly, the full GLSP (driven by variations from cycle 1) displays strong peaks at the different harmonics of the fundamental frequency corresponding to the expected (from empirical relations by Suárez Mascareño et al. 2015) and measured (from our RV analysis in Sect. 3) rotation period of around 35 days. However, the GLSP does not show any significant power at this fundamental frequency, while it displays a maximum power in the fourth harmonic (corresponding to a period of around nine days). An in-depth explanation of this is beyond the scope of this paper.

thumbnail Fig. A.2

TESS light curve from sectors 3, 4, 30, and 31 (from top to bottom). One-hour photometric bins are shown with black symbols. ESPRESSO observations of this target start on the date indicated by the red vertical line (Sector 5) and end two months after Sector 31.
thumbnail Fig. A.3

TESS light curve generalized Lomb-Scargle periodogram. Upper panel: GLSP using the full TESS dataset. Middle panel: GLSP using TESS data from Cycle 1, including sectors 3 and 4. Lower panel: GLSP using TESS data from Cycle 3, including sectors 30 and 31. In all panels are highlighted the first eight harmonics of the fundamental frequency corresponding to the expected rotation period of the star according to our RV analysis (see Sect. 3) and corresponding to the expected value from the empirical relations by Suárez Mascareño et al. (2015).

Appendix B Tables

Table B.1

General properties of HD 22496.

Table B.2

Radial velocities from HARPS and ESPRESSO used in this paper. The full table is accessible through CDS.

Table B.3

Inferred and derived parameters for the one-planet model.

References

  1. Allart, R., Pino, L., Lovis, C., et al. 2020, A&A, 644, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Aller, A., Lillo-Box, J., Jones, D., Miranda, L. F., & Barceló Forteza, S. 2020, A&A, 635, A128 [CrossRef] [EDP Sciences] [Google Scholar]
  3. Álvarez, D., Lizon, J.-L., Hughes, I., et al. 2018, SPIE Conf. Ser., 10702, 107026W [Google Scholar]
  4. Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2015, IEEE Trans. Pattern Anal. Mach. Intell., 38, 252 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Barnes, R. 2017, Celest. Mech. Dyn. Astron., 129, 509 [Google Scholar]
  7. Batalha, N. E., Lewis, T., Fortney, J. J., et al. 2019, ApJ, 885, L25 [Google Scholar]
  8. Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Borsa, F., Allart, R., Casasayas-Barris, N., et al. 2021, A&A, 645, A24 [EDP Sciences] [Google Scholar]
  10. Cabral, A., Moitinho, A., Coelho, J., et al. 2010, SPIE, 7739, 1383 [Google Scholar]
  11. Casasayas-Barris, N., Palle, E., Stangret, M., et al. 2021, A&A, 647, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Cersullo, F., Coffinet, A., Chazelas, B., Lovis, C., & Pepe, F. 2019, A&A, 624, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Coffinet, A., Lovis, C., Dumusque, X., & Pepe, F. 2019, A&A, 629, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Damasso, M., Sozzetti, A., Lovis, C., et al. 2020, A&A 642, A31 [CrossRef] [EDP Sciences] [Google Scholar]
  15. Díaz, R. F., Ségransan, D., Udry, S., et al. 2016, A&A, 585, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Ehrenreich, D., Lovis, C., Allart, R., et al. 2020, Nature, 580, 597 [Google Scholar]
  17. Faria, J. P., Haywood, R. D., Brewer, B. J., et al. 2016, A&A, 588, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Foreman-Mackey, D. 2018, Res. Notes Am. Astron. Soc., 2, 31 [CrossRef] [Google Scholar]
  19. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  20. Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, AJ, 154, 220 [Google Scholar]
  21. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Günther, M. N., Zhan, Z., Seager, S., et al. 2020, AJ, 159, 60 [CrossRef] [Google Scholar]
  25. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Heiter, U., Lind, K., Bergemann, M., et al. 2021, A&A, 645, A106 [EDP Sciences] [Google Scholar]
  27. Heller, R., Rodenbeck, K., & Hippke, M. 2019, A&A, 625, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Hippke, M., David, T. J., Mulders, G. D., & Heller, R. 2019, AJ, 158, 143 [Google Scholar]
  29. Hojjatpanah, S., Figueira, P., Santos, N. C., et al. 2019, A&A, 629, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Huber, D., Carter, J. A., Barbieri, M., et al. 2013, Science, 342, 331 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  31. Jeffreys, H. 1998, The Theory of Probability, Oxford Classic Texts in the Physical Sciences (Oxford: OUP Oxford) [Google Scholar]
  32. Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, SPIE Conf. Ser., 9913, 99133E [Google Scholar]
  33. Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019, A&A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Kunimoto, M., & Matthews, J. M. 2020, AJ, 159, 248 [NASA ADS] [CrossRef] [Google Scholar]
  35. Leleu, A., Lillo-Box, J., Sestovic, M., et al. 2019, A&A, 624, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Leleu, A., Alibert, Y., Hara, N. C., et al. 2021, A&A, 649, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Lillo-Box, J., Figueira, P., Leleu, A., et al. 2020, A&A, 642, A121 [CrossRef] [EDP Sciences] [Google Scholar]
  38. Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
  39. Mann, A. W.,& von Braun, K. 2015, PASP, 127, 102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  41. Mortier, A., Zapatero Osorio, M. R., Malavolta, L., et al. 2020, MNRAS, 499, 5004 [Google Scholar]
  42. Nelder, J. A., & Mead, R. 1965, Comput. J., 7, 308 [CrossRef] [Google Scholar]
  43. Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [CrossRef] [EDP Sciences] [Google Scholar]
  44. Perrakis, K., Ntzoufras, I., & Tsionas, E. G. 2014, Comput. Stat. Data Anal., 77, 54 [CrossRef] [Google Scholar]
  45. Plez, B. 2012, Astrophysics Source Code Library [record ascl:1205.004] [Google Scholar]
  46. Quirrenbach, A., Amado, P. J., Mandel, H., et al. 2010, ASP Conf. Ser., 430, 521 [NASA ADS] [Google Scholar]
  47. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, SPIE Conf. Ser., 9143, 20 [Google Scholar]
  48. Santos, N. C., Cristo, E., Demangeon, O., et al. 2020, A&A, 644, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Sozzetti, A., Damasso, M., Bonomo, A. S., et al. 2021, A&A, 648, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
  51. Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [NASA ADS] [CrossRef] [Google Scholar]
  52. Suárez Mascareño, A., Faria, J. P., Figueira, P., et al. 2020, A&A, 639, A77 [CrossRef] [EDP Sciences] [Google Scholar]
  53. Tabernero, H. M., Dorda, R., Negueruela, I., & González-Fernández, C. 2018, MNRAS, 476, 3106 [NASA ADS] [CrossRef] [Google Scholar]
  54. Tabernero, H. M., Marfil, E., Montes, D., & González Hernández, J. I. 2019, A&A, 628, A131 [CrossRef] [EDP Sciences] [Google Scholar]
  55. Tabernero, H. M., Dorda, R., Negueruela, I., & Marfil, E. 2021a, A&A, 646, A98 [EDP Sciences] [Google Scholar]
  56. Tabernero, H. M., Zapatero Osorio,M. R., Allart, R., et al. 2021b, A&A, 646, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Tinetti, G., Drossart, P., Eccleston, P., et al. 2018, Exp. Astron., 46, 135 [NASA ADS] [CrossRef] [Google Scholar]
  58. Toledo-Padrón, B., Lovis, C., Suárez Mascareño, A., et al. 2020, A&A 641, A92 [CrossRef] [EDP Sciences] [Google Scholar]
  59. Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, SPIE Conf. Ser., 2198, 362 [NASA ADS] [Google Scholar]
1

The ESPRESSO DRS is publicly available at https://www.eso.org/sci/software/pipelines/index.html

3

We also tried the bisector span measured on the CCF as an activity proxy with similar results.

4

https://github.com/exord/bayev. A python implementation by R. Díaz of the formalism explained in Perrakis et al. (2014).

5

This does not necessarily have to be the case, as demonstrated in many misaligned planetary systems with close-in components (e.g., Huber et al. 2013).

6

K-dwarfs Orbited By habitable Exoplanets (KOBE), PI: J. Lillo-Box, https://kobe.caha.es/

8

The release notes of all TESS sector including sectors 3, 4, 30, and 31 are available at https://archive.stsci.edu/tess/tess_drn.html.

All Tables

Table B.1

General properties of HD 22496.

In the text
Table B.2

Radial velocities from HARPS and ESPRESSO used in this paper. The full table is accessible through CDS.

In the text
Table B.3

Inferred and derived parameters for the one-planet model.

In the text

All Figures

thumbnail Fig. 1

ESPRESSO radial velocity time series for HD 22496. Upper panel: complete series with the three datasets corresponding to the three ESPRESSO windows (ESPR18, ESPR19, and ESPR21). The median GP model is shown in blue and the median GP+Keplerian model is shown in red, with 95% confidence intervals shown as red shaded regions. Lower panel: close view of the ESPR19 (left) and ESPR21 (right) datasets after removing the median GP model.
In the text
thumbnail Fig. 2

Periodogram of ESPRESSO time series. From top to bottom: ESPRESSO RV, ESPRESSO RVs after a simple weighted linear detrending with the BIS-SPAN activity indicator (green), and after removing a Keplerian signal with P = 5.09 days (red), FWHM of the CCF, CONTRAST of the CCF, log(RHK), BIS-SPAN, and the window function. The dashed red vertical lines give the location of the confirmed planet HD 22496 b, the stellar rotation period found by the GP, and its alias. In the two upper panels the dotted horizontal lines give the 0.1 and 1% false alarm probability levels. In the second panel the vertical dotted lines indicate the first ten alias periods of the HD 22496 b signal.
In the text
thumbnail Fig. 3

Distribution of the log-Bayesian evidence for the different models tested using the Gaussian process approach to accountfor the stellar activity (see Sect. 3). The shaded distributions correspond to the HARPS+ESPRESSO dataset (upper panel), while open distributions correspond to the ESPRESSO stand-alone dataset (lower panel). The median from the null hypothesis model for each dataset (labeled 0p) has been subtracted. In the upper panel the two-planet model (2p1c2c) has a very low odds ratio, hence lying outside of the plot limits.
In the text
thumbnail Fig. 4

Radial velocities from HARPS (red) and ESPRESSO (green) phase-folded with the period from planet HD 22496 b. The red open symbols represent binned values from HARPS measurements corresponding to 10% of the orbital phase. The median GP model has been subtracted. The bottom panel shows the residuals of the mean model.
In the text
thumbnail Fig. 5

Detectability matrix for the HARPS and ESPRESSO dataset within the habitable zone of HD 22496 performed through injection-recovery. The color-coding represents the significance in the posterior of the RV semi-amplitude parameter in units of its standard deviation, with ratios above 3 (signal detected) in blue. The dashed lines correspond to one and three times the standard deviation of the residuals from the one-planet circular model (i.e., 28 cm s−1).
In the text
thumbnail Fig. A.1

Target pixel file plot (using tpfplotter Aller et al. 2020) of HD 22496 in Sector 3. The TESS pipeline aperture is highlighted with red shaded squares. The location of the target is given by a white cross, and all additional sources identified byGaia DR2 with red circles (with sizes inversely proportional to their magnitude).
In the text
thumbnail Fig. A.2

TESS light curve from sectors 3, 4, 30, and 31 (from top to bottom). One-hour photometric bins are shown with black symbols. ESPRESSO observations of this target start on the date indicated by the red vertical line (Sector 5) and end two months after Sector 31.
In the text
thumbnail Fig. A.3

TESS light curve generalized Lomb-Scargle periodogram. Upper panel: GLSP using the full TESS dataset. Middle panel: GLSP using TESS data from Cycle 1, including sectors 3 and 4. Lower panel: GLSP using TESS data from Cycle 3, including sectors 30 and 31. In all panels are highlighted the first eight harmonics of the fundamental frequency corresponding to the expected rotation period of the star according to our RV analysis (see Sect. 3) and corresponding to the expected value from the empirical relations by Suárez Mascareño et al. (2015).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.