EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A64 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A64
Number of page(s) 15
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202141695
Published online 11 October 2021

© ESO 2021

1. Introduction

Shock waves associated with solar eruptive phenomena such as coronal mass ejections (CMEs; e.g. Cane et al. 1981; Nelson & Melrose 1985; Reiner et al. 1998; Bale et al. 1999; Vršnak & Cliver 2008; Magdalenić et al. 2014; Jebaraj et al. 2020) and flares (Magdalenić et al. 2010) have the ability to accelerate particles (e.g. Vlahos 1989). Solar eruptions and the associated phenomena can be observed in different wavelengths such as extreme ultraviolet (EUV), white light (WL) coronagraphic observations, and radio (Aschwanden 2019, for more details).

Solar radio bursts associated with shock waves (i.e. so-called type II radio bursts) are the oldest known signatures of shocks (Wild & McCready 1950; Pikel’Ner & Gintsburg 1964; Melrose 1980; Robinson & Cairns 2000; Claßen & Aurass 2002; Cairns et al. 2003). They are mostly used to map the propagation of the shocks through the corona and the interplanetary (IP) space (e.g. Cane et al. 1981; Aurass et al. 1994; Cane & Erickson 2005; Aguilar-Rodriguez et al. 2005; Magdalenić et al. 2012). Shock-associated radio emission is produced when non-thermal electrons undergo non-linear wave-particle interactions and emit electromagnetic radiation close to the fundamental (fpe) and the harmonic (2fpe) local plasma frequency (see Melrose 2017, for a review).

Type II bursts are observed in the dynamic spectra as slowly drifting and often intermittent radio emission in the narrow band (Kundu 1965; Zlotnik et al. 1998; Claßen & Aurass 2002). The morphological characteristics of the type II burst are dependent on the shock wave properties and the upstream plasma conditions. The drift rates of type II radio bursts can be related to the speed of the propagating disturbance by assuming a radial electron density model (e.g. Newkirk 1961; Saito 1970; Leblanc et al. 1998; Mann et al. 1999).

Over the past few decades, a large number of studies have been dedicated to establish the association between eruptive events and shock waves observed at different wavelengths, while also addressing the conditions necessary for shock wave formation and evolution (Zaitsev 1969; Vršnak & Cliver 2008; Warmuth 2015). A necessary condition for shock wave formation is for the speed of the pressure wave to exceed the local characteristic speed of the medium (the fast-magnetosonic speed) through which it propagates (Priest 2014). Theoretically, any large-amplitude, compressive magnetohydrodynamic (MHD) wave can steepen to a shock wave as it propagates away from its source region (Uchida et al. 1973; Uchida 1974; Bougeret 1985; Vršnak & Lulić 2000a,b).

The observations that are presently available have shown that the morphology of decametric and hectometric type II radio bursts is similar, although they differ in some respect to that of metric type II bursts. The bright, narrow, drifting bands, which have been referred to as the ‘backbone’ (Roberts 1959; Pikel’Ner & Gintsburg 1964; Cairns 1986; Benz & Thejappa 1988; Aurass 1997) can be observed in the majority of type II bursts. However, unlike metric and some decametric type II bursts, the hectometric type II bursts do not generally exhibit the structured emission known as ‘herringbones’ (Zlobec et al. 1993; Cairns & Robinson 1987, and references therein). The absence of these features may possibly be a result of the low spatial and spectral resolution of space-based radio observations.

Type II radio bursts provide evidence of shock wave formation and its properties. Therefore, it is useful to identify the locations of the source regions of type II radio emission and compare them with the observed shock wave. Determining the spatial and temporal relationship between shock waves and type II radio bursts is a long-standing problem. The complexity of this problem arises not only from the difficulty in estimating the source positions of radio emission but also from the chain of processes leading to radio emission itself (e.g. Gary et al. 1984; Klein et al. 1999; Maia et al. 2000; Cane & Erickson 2005; Magdalenić et al. 2008, 2010; Nindos et al. 2011; Zimovets et al. 2012; Jebaraj et al. 2020).

The processes leading to the generation of the shock associated radio emission are very complex because they depend on both macroscopic parameters such as shock wave properties and kinetic scales such as the distribution of the electrons and their properties (see e.g. Knock et al. 2003a). Cairns et al. (2003) showed that for a localised source with properties that vary over time, the resultant type II burst are seen to be intermittent and patchy. Conversely, Knock & Cairns (2005) showed that in the case of a large radio source with pre-accelerated electrons in the upstream region of the shock, the type II emission will be complex, more broadband, and characterised by multiple lanes. Observations have indeed shown cases of metric to decametric type II bursts with a number of complex bands (see e.g. Magdalenić et al. 2020). Additionally, the local maximum of the Alfvén speed (Warmuth et al. 2004; Gopalswamy et al. 2009), expected at the heights of the decametric wavelengths, may be one reason for the lack of strong or continuous type II radio emission in this range (e.g. Cane & Erickson 2005). Slow and weak shock waves can also produce intense radio emission if the particular geometry is provided in the interaction with nearby coronal structures or when the ambient plasma conditions are favourable for the generation of radio emission, such as the existence of pre-accelerated electrons (Gopalswamy et al. 2001, 2005).

We present a study of the CME-driven shock wave with a focus on understanding the conditions necessary for the production of type II radio emission at decametric to kilometric wavelengths1. We employ methods presented in Kouloumvakos et al. (2019, 2021) for shock wave modelling and results of the radio triangulation study by Jebaraj et al. (2020) to obtain the source positions of the type II radio burst. Our study compares the characteristics of the observed radio emission, the global evolution of the shock wave, and the shock wave conditions necessary for the generation of type II emission at the localized regions of the shock.

The paper is structured as follows. We introduce the observational data in Sect. 2 and the event overview in Sect. 3. We provide a summary of the radio triangulation results (Jebaraj et al. 2020) and present ways that it could be improved in Sect. 4. An introduction of the shock modelling technique is provided in Sect. 5 and its results in Sect. 5.1. We then examine the temporal evolution of different parameters globally in Sect. 5.2.1, localized to the high frequency type II (Sect. 5.2.2) and low frequency type II radio burst (Sect. 5.2.3). In Sect. 6, we present a novel technique used to study the relationship between the shock wave and the type II radio emission before discussing our results and conclusions in Sect. 7.1. Finally, we present the inconsistencies of the models used in this study in Sect. 7.2.

2. Observations

In this study, we used ground-based radio observations from the Culgoora solar radio spectrograph (Labrum 1972). We also used space-based observations from the two identical SWAVES instruments on-board Solar TErrestrial RElations Observatory Ahead and Behind (STEREO A and STEREO B; Bougeret et al. 2008) and the WAVES experiment on-board the Wind spacecraft (Bougeret et al. 1995). All three instruments provide dynamic radio spectra and goniopolarimetric measurements at a number of discrete frequencies in the range 100−1046 kHz. The STEREO/WAVES observations provide dynamic spectra in the range of 10−16 000 kHz, and Wind/WAVES in the range of 4−13 825 kHz (three antennas cover the range of 4−256 kHz, 20−1040 kHz and 1075−13 825 kHz). Goniopolarimetric observations at selected frequencies are provided in the similar frequency range for all three spacecraft (100−1040 kHz), but number of discrete frequencies is larger for STEREO spacecraft.

In order to obtain general information about the eruptive event associated with radio bursts, we employed the following observations:

– Soft X-ray (SXR) observations from the Geostationary Operational Environmental Satellite (GOES 15; Garcia 1994).

– White-light (WL) coronagraphic observations from the Large Angle and Spectroscopic Coronagraph (LASCO; Brueckner et al. 1995) on board the Solar and Heliospheric Observatory (SOHO; Domingo et al. 1995) (SOHO/LASCO C2 and C3) as well as the Solar TErrestrial RElations Observatory Ahead and Behind (STEREO A and STEREO B; Kaiser et al. 2008) (STEREO/COR1 and COR2).

– Extreme ultraviolet (EUV) observations from the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) on-board the Solar Dynamics Observatory (SDO; Pesnell et al. 2012) and the EUV Imagers (EUVI; Howard et al. 2008) on-board STEREO (STEREO/EUVI).

3. Event overview

The event on 27 September 2012 was associated with a GOES C3.7 flare, which peaked at 23:45 UT (cf. Veronig et al. 2019, for details on flare and filament eruptions), full-halo CME, EUV wave, and a shock wave (cf. Jebaraj et al. 2020, for observational details). The CME originated from the NOAA active region 11577 (located at N09W31) and had a projected speed (in the plane of the sky) of 1490 km s−1 (measured along the position angle of 65°). Jebaraj et al. (2020) employed the EUHFORIA model (EUropean Heliospheric FORecasting Information Asset; Pomoell & Poedts 2018) and found that the CME2 propagated in the north-west quadrant with a 3D speed of about 1200 km s−1.

3.1. Radio event

The complex radio event associated with the eruption on 27 September 2012 was observed by both ground and space-based instruments. A dynamic radio spectrum (presented in Fig. 1) was recorded by Culgoora Solar Radio Spectrograph. The spectrum shows a complex emission of fundamental and harmonic bands of type II burst. The intermittent radio emission started at about 23:43 UT, approximately at 28 MHz for the fundamental band and 56 MHz for the harmonic band.

thumbnail Fig. 1.

Dynamic radio spectra recorded by the Culgoora Solar Radio Spectrograph during the flare/CME event on September 27, 2012. The fundamental (F) and harmonic (H) bands of the high frequency type II burst are indicated by F and H.

The hectometric counterpart of the radio event was observed by WAVES instruments on board the STEREO and Wind spacecraft (Fig. 2). The continuation of the metric type II burst at hectometric wavelengths (Fig. 1) was best observed by the Wind/WAVES RAD2 instrument. Type II started at about 23:51 UT, and stopped at around 00:19 UT at frequency of approximately 4 MHz. The top panel of Fig. 2 shows the same type II burst observed by STEREO A/WAVES located at the time of event at about 120° west of Wind spacecraft. STEREO A observations of the type II burst show very intermittent emission of about one order of magnitude less intense than in Wind observations. The type II emission was occulted for STEREO B, located ∼120° east of the Wind spacecraft. If we take into account the intensity-directivity relationship (first discussed in this context by Magdalenić et al. 2014), which suggests that the radio emission is strongest in the direction of its propagation, we can constrain the source-region of the HF-type II to the south-western quadrant (for more detailed explanation, see Jebaraj et al. 2020).

thumbnail Fig. 2.

Dynamic radio spectra recorded by STEREO A/WAVES (top), STEREO B/WAVES (middle), and Wind/WAVES (bottom) showing the radio event associated with the flare/CME observed on September 27, 2012. The recorded radio flux is in normalized solar flux units (sfu). The black arrows mark the fundamental and harmonic bands of the high frequency type II burst. The white arrows mark the fundamental and harmonic bands of the low frequency type II burst and the red arrows mark examples of type III radio bursts associated with the event.

The second type II radio burst started at a much lower frequency than the first, namely, at about 2 MHz, and it was observed by all three spacecraft over the time interval of about 25 min (Fig. 2). Additionally, both the fundamental and harmonic bands of the type II burst were observed by the Wind/WAVES instruments. The fundamental band also seems to exhibit split-band features and was observed by all three spacecraft. In order to distinguish between these two different type II radio bursts associated with the same radio event, we named them the high frequency (HF-) and low frequency (LF-) type II burst. Both STEREO spacecraft observed only the fundamental band of the LF-type II burst. The intensity of LF-type II was strongest as observed by Wind, a bit less strong in STEREO B observations, and faint in STEREO A observations. This suggests that the source of the radio emission was located between Wind and STEREO B. Employing a classical method that combines the drift rate of type II burst and 1D coronal electron density model (3.5-fold Saito electron density model, Saito 1970), it was found that the radio sources of the HF-type II burst propagated at a speed of 1500 km s−1 (Jebaraj et al. 2020). Similarly, employing the one-fold Leblanc coronal electron density model (Leblanc et al. 1998), it was found that the source of the LF-type II propagated at a speed of 1100 km s−1 (Jebaraj et al. 2020). This analysis provides results that should be considered only as a first-order approximation because the 1D radial electron density models (Saito 1970; Leblanc et al. 1998) do not capture the non-radial propagation of the radio sources and can therefore be a source of error.

Figure 2 shows few groups of type III radio bursts associated with the same eruptive event. Depending on the time of their appearance, we distinguished type IIIs associated with the flare impulsive phase (FI-type IIIs) and one associated with the flare decay phase (FD-type IIIs). The relatively large number of type III bursts suggests existence of open magnetic field topology at the time of eruption.

4. Radio triangulation of LF-type II burst

The positions of radio sources in the 3D space can be only obtained by employing a so-called radio triangulation technique and direction-finding observations (e.g. Fainberg et al. 1972; Gurnett et al. 1978; Reiner & Stone 1988; Hoang et al. 1998; Reiner et al. 1998; Martínez Oliveros et al. 2012; Martínez-Oliveros et al. 2015; Krupar et al. 2014, 2016, 2018, 2019, 2020; Magdalenić et al. 2014; Mäkelä et al. 2016, 2018; Jebaraj et al. 2020). In employing radio triangulation, Jebaraj et al. (2020) studied the 3D source positions of the LF-type II radio burst using observations by Wind/WAVES and STEREO/WAVES instruments. Figure 3 shows results on the propagation of LF-type II sources as seen from three different vantage points. The source regions obtained for selected frequency pairs are marked by different coloured spheres and their sizes correspond to the full distance between the two wave vectors (see Sect. 7 of Jebaraj et al. 2020, for more details). The source regions are first observed in the South-East quadrant of the Sun and then sources moved towards the ecliptic near the central meridian (as seen from Earth). The non-radial propagation of the type II sources has been addressed in a number of studies (e.g. Kundu 1965; Kai 1969; Bougeret 1985; Claßen & Aurass 2002; Zucca et al. 2018; Jebaraj et al. 2020). The non-radial propagation of LF-type II sources suggests that they were produced in the regions where the shock wave encountered significantly denser plasma. Jebaraj et al. (2020) showed that the triangulated source heights of the LF-type II correspond to the enhanced coronal electron density, significantly higher as also predicted earlier by Claßen & Aurass (2002); in such a way, this provided additional evidence for interaction of the shock and denser regions of the streamer. Jebaraj et al. (2020) showed that the radio triangulation results can help us to localize these denser regions with respect to the shock wave and therefore investigate the radio emission mechanisms in IP space.

thumbnail Fig. 3.

Source regions of the LF-type II radio burst obtained from radio triangulation presented as observed from different viewpoints namely: STEREO B (left panel), Earth/Wind (center panel), and A (right panel), respectively. The different colored spheres correspond to the respective frequency pairs (in kHz), while their diameters are defined by the distance between the two wave vectors (source region). The plot is in sun-centred x, y, z 3D Cartesian coordinates with R⊙ units.

5. Shock wave modelling

In order to study the association of the shock wave characteristics and generation of the type II radio burst we modelled the shock wave. Details of the applied model are presented in Rouillard et al. (2016) and Kouloumvakos et al. (2019). An example of the model application with the aim to explain the generation of the low coronal shock signatures (i.e. metric wavelength type II) was presented in Zucca et al. (2018) and Kouloumvakos et al. (2021).

The model of the shock wave used in this study combines 3D shock reconstruction employing white light observations with the static MHD simulations, allowing us to calculate the shock kinematics and the shock parameters in the 3D space. We start with the 3D reconstruction of the observed pressure wave. The wave reconstruction is performed using the multi-viewpoint EUV and white-light observations of STEREO (EUVI at 195 Å, COR1, and COR2), SOHO (LASCO C2 and C3), and the 193 Å channel of SDO/AIA. An example of the reconstructed wave surface is presented in Fig. 4. This reconstruction allows us to model the wave in 3D space and calculate the speed along the entire wave front and along different propagation directions. The wave modelling was done with a temporal resolution of one minute.

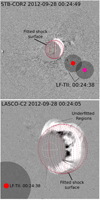thumbnail Fig. 4.

Shock wave fitting was done using multi-viewpoint observations from STEREO B/COR2 (top panel) and SOHO/LASCO C2 (bottom panel) at 00:24 UT. This is the time of observation of the highest triangulated frequency pair of the LF-type II burst. The red spherical mesh represents the fit to the white light shock. The regions indicated as under-fitted are the regions that are not accounted for in the shock wave modelling. The red and the fuchsia points are the centroids of the highest frequency LF-type II sources and the dark-shaded region is the full source region obtained from radio triangulation.

We note that in the case of geometric reconstruction of the pressure wave, the assumed self-similar expansion in the lateral directions will limit the accuracy of the modelled wave. The modelling errors will be considerable for events where the shock wave is strongly asymmetric. Our reconstruction was rather conservative in some directions, resulting in some under-fitting in the lateral regions (e.g. the regions labelled in Fig. 4). Nevertheless, we expect that in the regions of interest, the wave fitting was rather accurate. We estimate that the uncertainty in the reconstructions based on white light can be about 1 R⊙, at heights above 5 R⊙.

Once the pressure wave was reconstructed, we used the magnetic field and plasma properties of the solar corona provided by the Magneto-Hydrodynamic Around a Sphere Thermodynamic (MAST) model (Lionello et al. 2009; Riley et al. 2011) to determine the properties of the expanding wave. The shock parameters such as Mach number (MA), compression ratio, and shock geometry (θBN) were then computed on the surface of the modelled pressure wave.

This technique provides the properties of the pressure wave from the onset of the eruption in the low corona until the time when the observation of the LF-type II radio burst is halted. We investigated the conditions on the surface of the pressure wave and its association with both the HF and LF-type II radio bursts. The source positions of HF-type II burst were approximated using intensity-directivity relationship and the LF-type II burst source positions were estimated employing the radio triangulation technique (Jebaraj et al. 2020).

5.1. Shock wave parameters in 3D

First, we analyzed the 3D evolution of the modelled pressure wave, starting at about 23:45 UT, when the wave was in the low corona and when the first shock wave signatures were observed in dynamic spectrum (Fig. 1). In Fig. 5, we show a series of snapshots of the modelled pressure wave. The colours represent different shock parameters computed on the surface of the expanding pressure wave using the upstream MHD variables obtained from the MAST model. The combination of the three parameters plotted in Fig. 5 (arranged in columns) enables us to locate the regions where the shock wave was most likely to be formed and it gives a good indication on the generation of the type II radio emission. Panels a to d in Fig. 5 show snapshots of the modelled pressure wave at four different times selected for a detailed analysis. The times are selected in such a way to correspond with the different phases of the wave propagation and subsequent production of type II radio bursts.

thumbnail Fig. 5.

Snapshots of the modelled shock wave parameters at different times (a–d) and with different parameters estimated at the reconstructed pressure wave front surface (1–3). The yellow sphere represents the Sun and the colour coded ellipse represents the modelled pressure wave. The arrows indicate the propagation direction of the different triangulated radio bursts, while the black arrow indicates the Sun-Earth line. The coloured meridians visible on the surface of the Sun represent the solar central meridian as viewed from STEREO A (red), STEREO B (blue), and Earth (black). The presented times are: the start of the HF-type II (panel a), middle of HF-type II (panel b), start of LF-type II (panel c), and the end of LF-type II (panel d). The different parameters plotted in the rows are, (1) the Alfvén Mach number (MA), (2) the density compression ratio, and (3) the angle between the shock normal and the upstream magnetic field (θBN).

Figure 5 row a shows the modelled wave at 23:45 UT which corresponds to the onset of the HF-type II radio burst (23:43 UT). The F-component of the HF-type II was observed at 28 MHz which is approximately 1.9 R⊙ from the solar surface (when considering 3.5-fold Saito density model Saito 1970). The starting frequency of the HF-type II radio burst indicates that radio emission was formed higher up in the solar corona opposed to the metric type II radio bursts associated with low-coronal shock wave. The modelled pressure wave at this time was at a height of ∼2.1 R⊙ as it steepened to a shock only in some regions as seen in Figs. 5a1 and a2. In other regions (coloured black and dark blue) the compression ratio was less than one, indicating that a wave has not steepened into a shock. The shock wave was strong along narrow regions on the flanks where both the density compression and shock geometry had considerably high values of ∼3.5 and ∼60° respectively. Shock regions located near the apex of the CME are characterised by the high Alfvén mach number (MA ≫ 6) and density compression (∼3.5). However, in this region the shock geometry was predominantly quasi-parallel (θBN ≪ 30°), suggesting that in this regions the shock drift acceleration will not be very efficient.

Row b of Fig. 5 shows the wave at 00:00 UT which corresponds to the time of the middle of the HF-type II radio burst. The shock was formed near the apex of the CME, along its main direction of propagation. Additionally, at a few locations along the flanks we found a median value of ∼2.5 for the Alfvén Mach number MA indicating that the pressure wave also steepened into a shock. We note that these regions are located close to a coronal streamer where the Alfvén speed is low due to the weak magnetic field and the plasma density higher than the ambient density. The shock wave strength is enhanced when propagating through such a regions and, consequently, the shock is thus more efficient in electron acceleration. The density compression ratio shows similar behaviour to the Alfvén Mach number (e.g. Fig. 5b1). The highest values are found in the more extended region stretching from flank regions (near the streamer) and across the apex region. Panel b3 of Fig. 5 shows that the shock geometry was mostly quasi-parallel at the apex and was quasi-perpendicular towards the flanks.

At 00:30 UT (Fig. 5 row c), approximately after the onset of the LF-type II radio burst, the apex of the modelled wave was at a distance of 7.5 R⊙. The shock wave continued to strengthen at the apex region and a region along the eastern flanks. The propagation direction of the LF-type II (Sect. 5.2.3) is marked by the red arrow (Fig. 5c1). This region was also located in close proximity to the heliospheric current sheet (HCS) which is marked in panel c3 of Fig. 5 with the black strips on the shock bubble. The evolution of the shock wave parameters with respect to the regions where the LF-type II radio burst was produced is discussed in more details in Sect. 5.2.3.

The shock wave continued to evolve but less rapidly than in the previous snapshots (Fig. 5d). At approximately 00:50 UT the ending of the LF-type II burst was also observed. The regions close to the eastern-flank where the sources of the LF-type II are situated, we found that the shock wave geometry has now become oblique and somewhat quasi-parallel while still remaining a strong shock (MA ≫ 2). Furthermore, the shock compression in the lower regions of the flank are below unity suggesting that the shock wave may have already passed from a piston-driven phase into mostly a blast wave propagation and therefore subject to weakening.

5.2. Temporal evolution of the shock wave parameters

We examined the temporal evolution of the wave parameters in two steps. First, we studied the wave parameters along the entire wave front and then we inspected the selected regions is which we expect the type II radio emission to be produced. For each of the shock parameters, we computed the temporal evolution of the distribution characteristics (mean and median, along with the first and third quartile and decile values). We considered only the regions where a shock wave was formed (X > 1). The locations of the HF-type II were approximated by taking into account the intensity-directivity relationship and for the LF-type II burst the source positions are obtained by radio triangulation method (see Sect. 4).

5.2.1. Characteristics of the pressure wave

The temporal evolution of the pressure wave parameters over the entire surface of the wave is presented in Fig. 6. We discuss the parameters that are most important for a wave to be considered a shock, namely, the Alfvén Mach number, MA, which is often considered as indicator of the shock strength, along with the MFM compression ratio, and θBN as the angle between the shock normal and the upstream magnetic field.

thumbnail Fig. 6.

Global evolution of the wave parameters computed on the surface of the pressure wave. Panel a: evolution of the Alfvén Mach number (MA), panel b: fast magnetosonic Mach number, panel c: angle between the shock normal and the upstream magnetic field (θBN), and panel d: density compression ratio. The statistical distribution of the values are represented by the black line (median), blue line (mean), pink shade (quartiles), and the gray shade (decile) values.

Figure 6 shows that shock wave conditions were achieved soon after the modelling start time, but only at isolated regions of pressure wave bubble. The shock conditions were achieved a few minutes after the first appearance of the CME in SOHO/LASCO C2 field of view. From Figs. 5 and 6, we can conclude that the regions with the highest MA, namely, shock strength, are found mainly at the apex of the wave bubble and at some parts of the flanks. The median values of the Alfvén Mach number and compression ratio are greater than unity but the shock wave was sub-critical (MA ≤ 2.0) for most of the time. According to the quartile and decile values, the shock was super-critical only for a limited time of about one hour (until approximately 00:30 UT). The median values show θBN ∼ 60° indicating that the shock geometry is close to quasi-perpendicular. Since the shock wave started to form already low in the corona, the magnetic field lines connected to the shock surface are expected to be dominated by closed field regions. This favours a quasi-perpendicular shock geometry, especially on the flanks of the expanding wave, with θBN ≫ 45°.

The global wave strength at the onset of the HF-type II was larger than one, but still bellow the critical value of MA ∼ 2.0. This is expected as, at the time when it was form, the shock was still in the vicinity of the active region where the characteristic speed of the medium exceeds the speed of the disturbance. However, the wave parameter distributions in the upper quartile and decile suggest that there were regions where the shock wave was strong enough to accelerate particles. Figure 6a shows that the shock wave strength was increasing and at roughly 00:00 UT it reached an average value of MA ∼ 2.0. At the same time the shock geometry was θBN ∼ 50°, with an increasing density compression ratio of about 2.3. At 00:30 UT, a few minutes after the onset of the LF-type II, the wave is on average super-critical (MA ≥ 2.0; Fig. 5c). As it was expanding, the shock wave was getting stronger (increasing MA), and it reached a plateau median value of MA ∼ 3. The density compression also reached a plateau value of about 2.9. The wave geometry changed into oblique with θBN ∼ 45°. This is to be expected as the shock wave propagated away from the Sun, where the magnetic connections to the shock surface is dominated by mostly radial and open field lines. After 00:30 UT, the shock strength and the compression ratio remained nearly constant until the end of the modelling interval at 02:00 UT. On the other hand the shock geometry had changed to quasi-parallel about 1 h after the onset of the wave (Fig. 5c).

5.2.2. Characteristics of the wave associated with the HF-type II burst

In this section, we discuss the evolution of shock wave parameters in selected regions limited to the source regions of the HF-type II radio burst, situated at the south-western CME flank Jebaraj et al. (2020). These are dense regions that correspond to the slowest speeds of the EUV wave.

Figure 7 shows the shock strength on the western flank of the pressure wave surface at 23:50 UT. This time roughly corresponds to the onset of the HF-type II burst in Wind/WAVES observations. In Sect. 5.2.1, we discuss the fact that at 23:50 UT, the shock wave had already formed but the average strength of the shock wave, over the whole wave bubble was sub-critical (i.e. MA ≤ 2.0). The upper quartile and decile values were suggesting that some regions are super critical. Figure 7a shows that these are narrow regions in the flanks and slightly northward and southward of the wave apex. The shock geometry strongly varies for regions located closer to the apex (θBN ≪ 45°) and near the flanks (θBN ≫ 45°). The flanks regions are close to the nearby streamers (e.g. Magdalenić et al. 2014; Jebaraj et al. 2020), in which the characteristic speeds of the medium are lower than the speed of the shock wave (e.g. Kouloumvakos et al. 2021).

thumbnail Fig. 7.

HF-type II source regions on the pressure wave bubble. Panel a: modelled wave with the values of MA plotted on the wave’s surface roughly around the start of HF-type II radio burst. Circles titled L1–L4 represent the regions where the source of HF-type II could be located. Panel b: temporal evolution of the Alfvén mach number (MA) in the selected regions which are represented by the colored median lines. The quartiles and decile values are given only for L2. The temporal evolution of the geometry in these regions is presented in panel c.

We marked four regions (L1, L2, L3, and L4) of the pressure wave bubble where the shock strength was higher than MA ∼ 2.0. Regions L1 and L4 are situated close to the apex while regions L2 and L3 are located more on the flank. The temporal evolution of the shock strength (MA) and the shock geometry (θBN) are presented in panels b and c of Fig. 7. The evolution curve starts with the start of the wave modelling, at 23:30 UT. Although all these regions appear as situated rather close to each other, the wave properties can be very different. This is illustrated in the L3 and L4 region (panels b and c in Fig. 7). L1 and L4 which are located closer to the wave apex both started with a quasi-parallel geometry (θBN ∼ 33°). However, we note that L4 also started out as super-critical (MA ∼ 2.0) at the time of eruption and grew substantially in strength as time progressed. The other three regions show very different behaviour at the start of the modelling, and they reach MA > 2 condition just a few minutes apart from each other, namely, at about 23:42 to 23:45 UT. The sub-critical regime (MA ∼ 2.0) persisted for a few minutes. L2 and L3, which are located in the flank regions, started with a highly quasi-perpendicular (θBN ∼ 82°) regime that deteriorated towards an oblique geometry already at 00:10 UT.

A good correspondence was found between the region L3, where the shock strength and shock wave geometry favours generation of the radio emission, and the estimated position of the HF-type II burst. The shock wave in this region was super-critical (MA ≥ 2.0) at around 23:40 UT and the geometry was quasi-perpendicular (θBN ∼ 85°). The shock wave parameters remain favourable for generation of the radio emission also at 23:50 UT when then HF-type II was first recorded in Wind/WAVES observations. At that moment the shock strength, MA, was 5.0 and it continued to increase until 00:00 UT when it reached the value MA ∼ 6.0. A short dip to oblique regime of the wave geometry was observed at 23:50 UT, wave became quasi-perpendicular again at 00:00 UT. From about 00:00 UT, both the strength of the wave and quasi-perpendicular regime started to decrease simultaneously with the weakening of the radio emission, namely, the HF-type II burst. The radio emission stops at 00:17 UT, when the shock wave geometry is oblique (θBN ∼ 45°) and the shock strength reached a plateau at MA ∼ 2.

Another region of interest is region L2, where the shock strength and geometry started similarly as in region L3. However, the median values of MA remained significantly lower in comparison to L3, while the upper quartile and decile values were as high as for region L2. The wave geometry was also similar to the one for L3 in the time interval of interest (during the HF-type II), although slightly higher on average. As the wave parameters were similar for the regions L2 and L3, both regions could have contributed to the HF-type II emission. However, the lower median values for region L2 suggest that the shock wave strength (i.e. MA) was high only in isolated parts of this region. Since the area of emission contributes to the bandwidth of the resultant type II burst (Benz & Thejappa 1988), the radio emission from these small isolated sub-regions may not be well observed.

To summarise, the results of the analysis focused on specific regions on the pressure wave bubble suggest that the HF-type II radio burst was most likely generated in region L3. We note that at any given moment in the wave evolution, a particular combination of wave properties is necessary for generation of the radio emission. We showed that the wave geometry played an important role in the production of the HF-type II radio burst. In particular, although the strength of wave in region L4 was greater than for region L3, the region L4 could not be the source of radio emission due to the highly quasi-parallel shock geometry (which became even more quasi-parallel as the shock wave evolved).

5.2.3. Characteristics of the wave associated with the LF-type II radio burst

In this section, we discuss the parameters of the pressure wave in the region near the source location of the LF-type II radio burst obtained in radio triangulation analysis (Sect. 4). The propagation direction of the radio sources is represented with a red ray in Fig. 5. We focus on four regions (R1, R2, R3, and R4) situated around the red ray in Fig. 5. The radial heights of the LF-type II radio burst obtained in radio triangulation study are possibly overestimated. One of the reasons for this is the character of the triangulation technique itself. However, as we also do expect the increasingly larger sources at decreasing frequencies, it is difficult to disentangle the specific contribution of these two effects on the source shift. Since the direction of the wave propagation does not seem to be significantly affected by this problem, we decided to project the radio sources backwards, along the propagation line, on the pressure wave surface.

The four projected regions, represented with the differently coloured ellipsoids, are plotted on the pressure wave surface in Fig. 8a. Different diameters of the radio sources are due to the increasingly larger source sizes at decreasing observing frequency obtained from triangulation.

thumbnail Fig. 8.

Shock wave association with the LF-type II radio burst. Panel a: modelled pressure wave with the values of MA plotted on its surface around the start time of LF-type II radio burst. The colour-coded source regions named R1−R4 represent the LF-type II source regions observed in the time interval between 00:25 and 00:50 UT. The varying diameters of the source regions account for the large source sizes obtained from the radio triangulation results. Panel b: temporal evolution of the Alfvén mach number (MA) in the selected regions which are represented by the colored median lines. The quartiles and decile values are shown only for R4. The temporal evolution of the θBN in all regions is presented in panel c.

Figure 5 shows that the LF-type II radio sources seem to be located in a region close to the HCS. Modelling results indicate that the shock wave propagated along the HCS and crossed it on several occasions, which resulted in the enhanced wave strength (e.g. see Fig. 5). Figure 8a shows a snapshot of the modelled pressure wave at 00:30 UT, which is close to the time when the LF-type II was first observed by Wind/WAVES. The values of Alfvén Mach number, MA, are plotted on the surface of the pressure wave. The results of the temporal evolution of MA and θBN values are presented in Figs. 8b and c, respectively. The full statistics, namely, the first and third quartile and decile values, is shown only for the largest region R4, which encloses all other regions within itself. Accordingly, as the results are similar for all four considered regions, for regions R1, R2, and R3, we show only the median values. We also note that the analysis of the MFM and the compression ratio yield similar results to MA and are not shown here, as the fast mode speed in the interplanetary space becomes comparable to the Alfvén speed.

The LF-type II was first observed at 00:21 UT. At that time, the apex of the modelled pressure wave was at the height of about 5.7 R⊙. The Alfvén Mach number, namely, the shock strength at region R4 was moderate (MA ∼ 1.5). The shock strength at the center of the R4 region, which is also the part of the region R1, is lower in comparison to regions R2−R4. However, the third quartile and ninth decile values suggest that there are parts of the region R4 in which are the shock wave strength is greater. The wave geometry in all four regions is similar (θBN ∼ 45°), however, there is a small increase in the upper decile values around the same time where the values reach θBN ∼ 55°. The small increase in θBN could be due to the wave crossing the HCS. This is more visible in Fig. 5b3, where the location of the HCS is close to the red arrow.

The shock strength increases as the shock wave propagates away from the Sun. The stable rise in the shock strength is due to the continuous decrease in the characteristic speed of the medium. From 00:30 UT till the ending of the LF-type II burst, the shock geometry remains oblique (θBN ∼ 55°) and the shock strength continues to increase with the upper quartile and decile values reaching MA ∼ 3.5.

6. Synthetic radio spectra

To explore the importance of different variables and their role in the generation of radio emission, we assumed the shock drift acceleration mechanism (SDA; Toptygin 1980; Holman & Pesses 1983; Armstrong et al. 1985; Street et al. 1994; Ball & Melrose 2001; Mann & Klassen 2005; Mann et al. 2018, and references therein). For SDA, a pre-existing supply of non-thermal electrons is required since the acceleration of lower energy thermal electrons is not very efficient in low β plasma (solar corona). Nevertheless, this can be offset if the tail of the upstream thermal electron distribution can be accelerated to high-enough energies by a nearly-perpendicular (θBN ∼ 90°) shock wave geometry. For radio waves to be produced, high frequency electrostatic Langmuir waves need to be generated efficiently. Langmuir waves are generated by an unstable distribution of streaming electrons where the faster non-thermal electrons outrun the slower thermal electrons (Melrose 1980; Robinson & Cairns 2000; Mann et al. 2018).

Once they have been excited, the Langmuir waves may undergo wave-particle and wave-wave nonlinear interactions to produce radio emission in the fundamental and harmonic of the local plasma frequencies. The intensity of the emission at both bands is highly dependent on several factors such as the upstream electron and ion temperatures. Once the radio waves are emitted, the ambient density inhomogeneities may also suppress the waves produced close to the local plasma frequency (Melrose 2017). Therefore, the chain of events leading up to the production of radio emission are dependent on macroscopic details, such as shock wave and upstream properties, as well as kinetic factors, such as the distribution of the electrons and their properties (Knock et al. 2003a).

To quantify the relationship between the wave parameters (e.g. MA and θBN) in specific regions of the wave with the possibly associated radio emission, we used a novel approach introduced in Kouloumvakos et al. (2021). We produced 2D histogram maps, which is a spectrum like presentation of the wave parameters as a function of time (hereafter: synthetic spectra). The synthetic spectra was produced at close to the plasma frequency which allows comparison with the fundamental components of the radio emission observed in the dynamic spectra. Since the radio emission process depends on the Langmuir waves, we also used the model described in Mann & Klassen (2005) and Mann et al. (2018) to estimate the efficiency of the Langmuir waves production. The efficiency of this process can be examined using the cross-shock potential obtained from the Rankine-Hugoniot jump conditions (see Appendix A.1 of Mann & Klassen 2005; Mann et al. 2018, for more details). Mann et al. (2018) adopted the model described in Holman & Pesses (1983) for analysing the cross-shock potential of nearly perpendicular shock wave geometries as this determines the distribution of the unstable electron beams. Therefore, the efficiency at which Langmuir waves are produced and subsequently converted into electromagnetic radiation can be used to map the regions that are most favourable for the generation of type II radio emission (also see Kouloumvakos et al. 2021).

Columns 1 and 2 in Fig. 9 show a complex spectral evolution of the pressure wave’s strength and geometry (MA and θBN). The synthetic spectra presented in panels a1 and a2 show that there are several regions where the pressure wave is super-critical and quasi-perpendicular, namely, where shock wave characteristics are present. In these regions, Langmuir waves can be efficiently produced and subsequently converted into electromagnetic radiation (see panel a3). This indicates that the shock associated radio emission can be, in principle, generated co-temporally at more than one location but with strongly different efficiency. The panel a3 of Fig. 9 shows one dominant high intensity region, starting around 16 MHz (at 00:00 UT) and after a gap (region of low efficiency for production of Langmuir oscillations) continuing about 30 min later at about 2 MHz. The patchy signatures are again enhanced at 01:00 UT and continue till the end of the modelling time. For the high frequency region we find a moderate shock strength and highly quasi-perpendicular geometry, and for the low-frequency region, we find a high shock strength and an oblique geometry (Figs. 9a1 and a2).

thumbnail Fig. 9.

Histogram maps of different shock wave parameters plotted in a form of dynamic spectra. The four rows of 2D-histogram maps were produced in different areas of the wave. The histogram maps were constructed considering: (a) the full shock surface, (b) only L3 region of HF-type II, (c) region L2 of HF-type II (Sect. 5.2.2), and (d) region R4 of LF-type (Sect. 5.2.3). The three columns show different wave parameters: (1) the Alfen Mach number (MA), (2) the Shock wave geometry (θBN), and (3) the Langmuir wave conversion ratio (LWC > 1).

The panels in row b and c of Fig. 9 present the spectra of the wave parameters in the specific regions L2 and L3 (see Sect. 5.2.2). Those two regions are possible source regions of the HF-type II radio emission. The two regions have similar θBN values, while the MA is more enhanced for region L3 (see also Fig. 7). Further, also the bandwidth of the MA and θBN in the region L3 is broader in comparison to L2. Comparing the Langmuir wave conversion (Figs. 9c2 and c3) for both regions, it is clear that the L3 region is more likely to be the source of radio emission than the region L2. This result indicates that even small difference in the shock wave strength, MA, can be essential for the generation of the radio emission. We note that although the major contribution to the HF-type II radio emission is probably from region L3, a small contribution from the L2 region cannot be completely excluded (Fig. 9c3).

Row d of Fig. 9 shows the synthetic spectra of two main wave parameters and Langmuir wave conversion rate for the region R4. The location of region R4 was obtained in the radio triangulation study of LF-type II radio burst (Jebaraj et al. 2020). The synthetic spectrum for MA shows only a narrow region with the high shock strength in the range between 2 MHz and 1 MHz. The synthetic spectrum of θBN shows that the wave geometry was most of the time oblique. The quasi-perpendicular regime was found only in the frequency range 3−1 MHz and in the very limited time interval (00:20−00:50 UT). The synthetic spectrum of Langmuir wave conversion rate (Fig. 9d3) shows that the Langmuir waves can be efficiently produced in a very narrow, patchy and intermittent region starting at ∼00:40 UT at 2 MHz. This result does not fully coincide with the observations (Fig. 1), as the observed radio emission starts at about 00:20 UT at 1 MHz for the fundamental component that is modelled here. In Sect. 5.2.3, we show that the emission could be originating also from the upper quartile and decile regions of the localized area. Therefore, median histograms may not be completely representative of the real situation, inducing discrepancy between observation and modelled shock wave characteristics. Furthermore, our model considers a spherical surface for the wave, which is a somewhat idealised picture. We further discuss this aspect in Sect. 7.2.

7. Conclusions and discussion

This work is focussed on an analysis of the pressure wave parameters and their role in the generation of type II radio emission at decametric and hectometric wavelengths. It builds on studies carried out by Jebaraj et al. (2020) and Kouloumvakos et al. (2021), applying the conclusions of these two studies to constrain and improve our understanding of shock waves and their radio signatures, namely, type II radio bursts.

7.1. Conclusions

The CME-flare event observed on 27 September 2012 was associated with a shock wave and a complex radio event. In this work, we discuss the origin and generation of two subsequent (but morphologically very different) type II radio bursts: the high frequency (HF) and low frequency (LF) type II radio burst. The position of the type II radio bursts (see Jebaraj et al. 2020) was compared with the modelled pressure wave obtained from combined multi-viewpoint observations in EUV and WL, and MAST model (Rouillard et al. 2016; Kouloumvakos et al. 2019).

The first part of the study was focussed to the south-west region of the pressure wave bubble, most probably associated with the decametric HF-type II radio burst. We found two regions, namely, L2 and L3 (Fig. 7), where the wave geometry exceeded θBN ∼ 70° and the strength was as high as MA ∼ 5. Therefore, out of these two regions, region L3 appears to be most probable type II source region.

In the second part of the study, we found that the shock geometry at the time of the LF-type II radio burst was mostly oblique, between 55° at the start and 45° at the end of the observed LF-type II burst. The type II source regions, obtained from radio triangulation, were located close to the streamer and the HCS. It is quite probable that due to this position, the particular geometry provided was favourable to the enhancement of the shock strength (MA ∼ 3.5) and, consequently, the generation of the radio emission as well.

The most important results of the study are summarised below. Each point is also discussed in the framework of earlier studies.

  • The comparison of radio observations and modelled pressure wave associated with an eruptive event shows that the wave may steepen to a shock, however, if it remains sub-critical, it will not produce type II radio emission. We find that radio emission is generated only when the shock wave is super critical, which is in accordance to the shock drift acceleration model that we employed to make the histogram maps.

In this study, both the HF- and LF- type II radio bursts were formed when the shock wave was super-critical (MA ≥ 2.0). Comparing the modelling and radio observations, we found that the regions where the Alfvén Mach number was greater than unity, but sub-critical (MA ≤ 2.0), did not provide any contribution to the observed type II radio emission. This finding is also in accordance to Gopalswamy et al. (2010), who found that sub-critical shock waves are often radio quiet.

  • Our analysis shows that a specific combination of shock geometry, shock strength, shock speed, and the presence of energetic electrons is essential for generation of radio emission. We found that a quasi perpendicular geometry was crucial for the generation of the herein studied type II bursts. We also found that the generation of the radio emission depends less on the shock wave strength in the case of high values for fMA ≥ 3.0. This is more pronounced at larger heights where the shock strength and compression ratio show little variation.

The studies of the importance of shock wave geometry in the generation of radio emission by Krauss-Varban & Wu (1989) and Krauss-Varban et al. (1989) also showed that electrons are most efficiently energised in the quasi-perpendicular regime. We found that the decametric HF-type II was formed in regions where the shock geometry was θBN ≥ 70°; this finding is similar to those from Kouloumvakos et al. (2021) for metric type II radio bursts. For the LF-type II, the results were somewhat different. The type II was formed when the shock geometry, obtained from modelling, was more oblique than in the case of the HF-type II. We found small regions with the quasi-perpendicular regime and it is probable that the patchy LF-type burst was generated in these small regions. According to Kuncic et al. (2002) for a quasi-perpendicular shock wave geometry, the spatially varying cross shock potential only shows small changes when MA ≥ 3.0. Given that the strength of the shock wave in the interplanetary space is, on average, MA ≫ 2.0, the LF-type II radio emission may largely depend on the shock wave geometry and the upstream electron distribution.

  • We showed that intermittency of the radio emission, in particular of the HF-type II radio burst, was probably due to localised source regions with rapidly changing geometry. We also confirmed that the source of the HF-type II is located close to the western CME flank, as suggested by Jebaraj et al. (2020). This result also confirms that for the studied event, the intensity of the radio emission was highest towards the direction of the emission.

The generally observed intermittent type II radio emission was also studied by Cairns et al. (2003), Schmidt & Cairns (2016) who, similar to this study, showed that such a structuring of radio emission results from a localised source with time-varying properties. The particular morphology of the studied type II radio burst is a consequence of the changes in shock wave geometry, namely, an only intermittently present quasi-perpendicular regime, despite the rather strong shock wave: MA ≥ 2.0. Mann et al. (2018) showed that the intermittent generation of radio emission can be strongly pronounced during the early stage of the wave evolution when the geometry of the wave can change rapidly.

  • The synthetic spectra show that the shock associated radio emission can have contributions from more than one source on the shock wave. However, in considering the morphology of the type II emission (only one dominant drift rate) we can speculate that only one of the sources is dominant and that the radio emission originating from the additional sources is very weak.

In this study, we found that the region where the source of the HF-type II is located had other smaller regions, which switched on and off to Langmuir wave activity (and therefore radio emission). The emission from these regions may be recorded as extremely intermittent and could appear co-temporal and co-spatial with the primary source of the type II burst.

  • The LF-type II sources were found to be situated in a region close to the HCS, but also close to the nearby streamer as suggested by Jebaraj et al. (2020). This work shows that the shock wave characteristics, in particular, the strength and the geometry, nearby HCS and streamer regions are indeed favourable with regard to efficient electron acceleration.

While modelling showed that the shock wave during the LF-type II was mostly quasi-parallel, we found a region where the shock wave was quasi-perpendicular, namely: the region of the shock crossing the HCS. Similarly, Reiner et al. (1998) found that IP type II radio bursts can be efficiently produced when shock waves cross the HCS or stream interaction regions (SIRs) where a large number of moderately energetic electrons is present. Another possibility discussed by Pulupa & Bale (2008) assumes that the shock wave distortions in the form of ‘cavities’ can form naturally near the HCS. When β > 1 (e.g. Robinson & Cairns 2000; Vandas & Karlický 2000, 2011; Knock et al. 2003b; Cairns et al. 2003), the shock front distortion can be naturally formed. The self-consistent modelling of the evolution of such shocks with distortions (e.g. ripples or wavy features) is challenging and was done in 3D (Schwadron et al. 2015) only seldom. Kuncic et al. (2002) modelled simple ripples on the planetary bow shock and this was applied by Knock & Cairns (2005) in an interplanetary shock-wave model. The aim of the study by Knock & Cairns (2005) was to reproduce the in situ characteristics of the shock wave (observed by Bale et al. 1999) and the spectral morphology of the observed type II radio burst.

In the following sections, we discuss some of the most important results of the present study. This allows us to evaluate the uncertainties of the employed models and the considered assumptions influence the obtained results.

7.2. Discussion on the employed assumptions and model uncertainties

One of the goals of this study was to validate the accuracy of the shock wave model and the radio triangulation technique, while comparing results obtained by these two methods. We discuss the limitations of each of the method, in order to understand how the cumulative errors may have affected our results.

Our results show that the source regions of the type II radio emission are positioned further from the Sun than the modelled shock wave. We believe that this discrepancy results from both the shock wave model and radio triangulation method. We will first discuss the radio triangulation method. In order to obtain the position of the LF-type II radio burst source regions we used the radio triangulation technique. Two main effects that are intrinsic to the method are the rather larges source regions of the radio emission and the uncertainty on the radial distance of the source regions. The rather large source regions of the radio bursts are partially resulting from the intrinsic geometric errors of the technique (see Sect. 4 in Jebaraj et al. 2020, for more details). However, we note that as the radio source sizes are naturally increasing with the frequency, mostly due to propagation effects (Saint-Hilaire et al. 2013), large sources at the considered frequencies are also expected.

The uncertainty with regard to the radial distance of the source regions arises from the intrinsic geometric nature of the direction finding technique itself (Krupar et al. 2012, 2014). Additionally, some other effects such as radio wave propagation, namely, scattering processes (Thejappa et al. 2012; Krupar et al. 2014, 2018) can be also present. However, the study by Jebaraj et al. (2020) shows that even if the positions of the radio sources are estimated to be somewhat further from the Sun than their real positions, the propagation direction of the type II radio sources remains relatively well defined. In this study, we expanded the work by Jebaraj et al. (2020), providing evidence that the source of the LF-type II radio emission propagated in a non-radial manner using the shock wave model.

The estimation of the propagation direction of the radio bursts employing the intensity-directivity relationship, which was used to approximately estimate the HF-type II source positions, can also be affected by radio wave propagation effects (Melrose 1980; Robinson & Cairns 2000; Thejappa et al. 2007; Kontar et al. 2019). The fundamental emission which is close to the local plasma frequency is more prone to be scattered and absorbed by local density inhomogenities, while the harmonic emission is not as strongly affected by these processes, as the fundamental one. In the case of the HF-type II, radio emission was observed as strongest at both the fundamental and harmonic frequencies by ground (Culgoora) and space-based (Wind/WAVES) observatories at the Earth vantage point. The same HF-type II burst was considerably weaker when observed by STEREO A. The STEREO A observes the HF-type II burst at significantly lower intensities for both the fundamental and harmonic emission bands. Since both the fundamental and harmonic band are more intense for the observer at Earth, it is highly probable that radio sources were Earth-directed or, otherwise, heading in a direction close to Earth.

7.2.1. Shock wave model

The shock wave modelling employed in this study combines two different techniques that we discuss individually in the following.

Reconstruction of the wave: the modelled wave is based on EUV observations and also on WL observations from multiple view points. The reconstruction of the wave done using multi-viewpoint observations strongly reduces errors in comparison to 2D observations. However, depending on the complexity of the event, certain level of inaccuracy in the wave reconstruction is intrinsic to the method. For this event, the employed fitting covered major part of what we believe is a WL wave structure. However, as the observed wave is not having ideally symmetric and regular shape, some regions of the wave stayed out of the fitting frame (Fig. 4). This imperfect fitting can induce the error of about ∼1 R⊙ or more, in radial distance at the heights at which the HF and LF type II are observed. The discrepancy between the model results and observations may increase as the wave propagates through the solar wind plasma of different characteristics. It is generally accepted that the wave structure, as well as the structure of its driver CME, can strongly deform on the propagation from the Sun to Earth (e.g. Manchester et al. 2017, and references therein).

MAST: the pressure wave was propagated in a 3D MHD medium simulated by the state-of-the-art MAST model. While it has been used to study large scale eruptions (e.g. Schwadron et al. 2015; Török et al. 2018), this model may not be capable of reproducing (with a high level of accuracy) the magnetic topology of the solar corona.

Synthetic spectra: the synthetic spectra presented in Sect. 6 can highlight the wave model inaccuracy and inconsistency with observations. Additionally, the process of constructing synthetic spectra can itself increase the potential of inconsistency with regard to the observations (Sect. 6). We believe that in this study, the small regions with quasi-perpendicular regime were not reproduced well by the wave model and that they were therefore also lost in the process of constructing synthetic spectra; namely, when constructing the synthetic spectra, we used median values, whereas the small regions are generally seen only in decile values. The synthetic spectra showed a very good temporal and spectral fit with the observed HF-type II burst (Figs. 9b3 and c3). This indicates that the shock wave model performed sufficiently well in capturing the propagation of the wave close to the Sun. On the other hand, the synthetic spectra showed both temporal and spectral discrepancies with the observed LF-type II. This result is influenced by the wave model inaccuracy, the inaccuracy in estimating the plasma parameters by the MAST model, and the process of constructing synthetic spectra itself. Therefore, in the synthetic spectra, the effects of possible cumulative errors are well observed.

In this study, for the first time, the modelled shock wave properties at the possible type II source regions are addressed, already having been identified from radio observations (intensity-directivity and radio triangulation method). We demonstrate that the CME-driven shock wave goes on to produce radio emission where appropriate shock wave characteristics for electron acceleration are met. These conditions can be unique to different parts of the shock wave and they are a time-varying phenomenon. This study presents a promising method for unveiling the complex relationship between the shock waves and associated radio emission. However, more studies on the topic are needed to draw general conclusions about the association between these shocks and type II radio bursts.

1

The metric range is at 300−30 MHz, the decametric at 30−10 MHz, the hectometric at 10−0.3 MHz, and kilometric at 0.3−0.02 MHz.

2

In EUHFORIA CMEs are inserted at the inner boundary of the model at 21 R⊙.

Acknowledgments

EIT and LASCO data have been used courtesy of the SOHO/EIT and SOHO/LASCO consortium, respectively. The STEREO SECCHI data are produced by a consortium of RAL (UK), NRL (USA), LMSAL (USA), GSFC (USA), MPS (Germany), CSL (Belgium), IOTA (France), and IAS (France). The Wind/Waves instrument was designed and built as a joint effort of the Paris-Meudon Observatory, the University of Minnesota, and the Goddard Space Flight Center, and the data are available at the instrument website. We thank the radio monitoring service at LESIA (Observatoire de Paris) for providing value-added data that have been used for this study. We are grateful to the staff of the Bruny Island Radio Spectrometer for their open data policy. The authors would also like to thank the referee, Dr. Pietro Zucca for his suggestions to improve the paper. I. C. J. was supported by a PhD grant awarded by the Royal Observatory of Belgium. J. M. acknowledges funding by the BRAIN-be (Belgian Research Action through Interdisciplinary Networks) project CCSOM (Constraining CMEs and Shocks by Observations and Modelling throughout the inner heliosphere), and BRAIN-be project SWiM (Solar Wind Modelling with EUHFORIA for the new heliospheric missions). S. P. has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 870405, and the projects C14/19/089 (C1 project Internal Funds KU Leuven), G.0D07.19N (FWO-Vlaanderen), SIDC Data Exploitation (ESA Prodex-12). The IRAP team acknowledges support from the French space agency (Centre National des Etudes Spatiales; CNES; https://cnes.fr/fr) that funds activity in plasma physics data center (Centre de Données de la Physique des Plasmas; CDPP; http://cdpp.eu/) and the Multi Experiment Data & Operation Center (MEDOC; https://idoc.ias.u-psud.fr/MEDOC), and the space weather team in Toulouse (Solar-Terrestrial Observations and Modelling Service; STORMS; http://stormsweb.irap.omp.eu/). This includes funding for the data mining tools AMDA (http://amda.cdpp.eu/), CLWEB (clweb.cesr.fr/) and the propagation tool (http://propagationtool.cdpp.eu). A. K. acknowledges financial support from the ANR COROSHOCK project (ANR-17-CE31-0006-01). V. K. acknowledges the support by NASA under grants 18-2HSWO218-2-0010 and 19-HSR-19-2-0143.

References

  1. Aguilar-Rodriguez, E., Gopalswamy, N., MacDowall, R., Yashiro, S., & Kaiser, M. L. 2005, J. Geophys. Res.: Space Phys., 110, A12S08 [Google Scholar]
  2. Armstrong, T. P., Pesses, M. E., & Decker, R. B. 1985, Washington DC American Geophysical Union Geophysical Monograph Series, 35, 271 [NASA ADS] [Google Scholar]
  3. Aschwanden, M. J. 2019, New Millennium Solar Physics (Switzerland, AG: Springer Nature), 458 [Google Scholar]
  4. Aurass, H. 1997, Coronal Mass Ejections and Type II Radio Bursts (Berlin: Springer-Verlag), 483, 135 [NASA ADS] [Google Scholar]
  5. Aurass, H., Klein, K. L., & Mann, G. 1994, in Solar Dynamic Phenomena and Solar Wind Consequences, the Third SOHO Workshop, ed. J. J. Hunt, ESA Spec. Publ., 373, 95 [Google Scholar]
  6. Bale, S. D., Reiner, M. J., Bougeret, J. L., et al. 1999, Geophys. Res. Lett., 26, 1573 [Google Scholar]
  7. Ball, L., & Melrose, D. B. 2001, PASA, 18, 361 [NASA ADS] [CrossRef] [Google Scholar]
  8. Benz, A. O., & Thejappa, G. 1988, A&A, 202, 267 [NASA ADS] [Google Scholar]
  9. Bougeret, J. L. 1985, Washington DC American Geophysical Union Geophysical Monograph Series, 35, 13 [NASA ADS] [Google Scholar]
  10. Bougeret, J.-L., Kaiser, M. L., Kellogg, P. J., et al. 1995, Space Sci. Rev., 71, 231 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bougeret, J. L., Goetz, K., Kaiser, M. L., et al. 2008, Space Sci. Rev., 136, 487 [NASA ADS] [CrossRef] [Google Scholar]
  12. Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cairns, I. H. 1986, Proc. Astron. Soc. Aust., 6, 444 [NASA ADS] [Google Scholar]
  14. Cairns, I. H., & Robinson, R. D. 1987, Sol. Phys., 111, 365 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cairns, I. H., Knock, S. A., Robinson, P. A., & Kuncic, Z. 2003, Space Sci. Rev., 107, 27 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cane, H. V., & Erickson, W. C. 2005, ApJ, 623, 1180 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cane, H. V., Stone, R. G., Fainberg, J., et al. 1981, Geophys. Res. Lett., 8, 1285 [CrossRef] [Google Scholar]
  18. Claßen, H. T., & Aurass, H. 2002, A&A, 384, 1098 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Domingo, V., Fleck, B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fainberg, J., Evans, L. G., & Stone, R. G. 1972, Science, 178, 743 [NASA ADS] [CrossRef] [Google Scholar]
  21. Garcia, H. A. 1994, Sol. Phys., 154, 275 [NASA ADS] [CrossRef] [Google Scholar]
  22. Gary, D. E., Dulk, G. A., House, L., et al. 1984, A&A, 134, 222 [NASA ADS] [Google Scholar]
  23. Gopalswamy, N., Yashiro, S., Kaiser, M. L., Howard, R. A., & Bougeret, J.-L. 2001, ApJ, 548, L91 [Google Scholar]
  24. Gopalswamy, N., Aguilar-Rodriguez, E., Yashiro, S., et al. 2005, J. Geophys. Res.: Space Phys., 110, 12 [NASA ADS] [Google Scholar]
  25. Gopalswamy, N., Thompson, W. T., Davila, J. M., et al. 2009, Sol. Phys., 259, 227 [NASA ADS] [CrossRef] [Google Scholar]
  26. Gopalswamy, N., Xie, H., Mäkelä, P., et al. 2010, ApJ, 710, 1111 [CrossRef] [Google Scholar]
  27. Gurnett, D. A., Baumback, M. M., & Rosenbauer, H. 1978, J. Geophys. Res., 83, 616 [CrossRef] [Google Scholar]
  28. Hoang, S., Maksimovic, M., Bougeret, J.-L., Reiner, M. J., & Kaiser, M. L. 1998, Geophys. Res. Lett., 25, 2497 [NASA ADS] [CrossRef] [Google Scholar]
  29. Holman, G. D., & Pesses, M. E. 1983, ApJ, 267, 837 [NASA ADS] [CrossRef] [Google Scholar]
  30. Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
  31. Jebaraj, I. C., Magdalenic, J., Podladchikova, T., et al. 2020, A&A, 639, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Kai, K. 1969, Sol. Phys., 10, 460 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kaiser, M. L., Kucera, T. A., Davila, J. M., et al. 2008, Space Sci. Rev., 136, 5 [NASA ADS] [CrossRef] [Google Scholar]
  34. Klein, K.-L., Khan, J. I., Vilmer, N., Delouis, J.-M., & Aurass, H. 1999, A&A, 346, L53 [Google Scholar]
  35. Knock, S. A., & Cairns, I. H. 2005, J. Geophys. Res.: Space Phys., 110, A01101 [NASA ADS] [CrossRef] [Google Scholar]
  36. Knock, S. A., Cairns, I. H., Robinson, P. A., & Kuncic, Z. 2003a, J. Geophys. Res.: Space Phys., 108, 1126 [NASA ADS] [CrossRef] [Google Scholar]
  37. Knock, S. A., Cairns, I. H., & Robinson, P. A. 2003b, J. Geophys. Res.: Space Phys., 108, 1361 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kontar, E. P., Chen, X., Chrysaphi, N., et al. 2019, ApJ, 884, 122 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kouloumvakos, A., Rouillard, A. P., Wu, Y., et al. 2019, ApJ, 876, 80 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kouloumvakos, A., Rouillard, A., Warmuth, A., et al. 2021, ApJ, 913, 99 [NASA ADS] [CrossRef] [Google Scholar]
  41. Krauss-Varban, D., & Wu, C. S. 1989, J. Geophys. Res., 94, 15367 [NASA ADS] [CrossRef] [Google Scholar]
  42. Krauss-Varban, D., Burgess, D., & Wu, C. S. 1989, J. Geophys. Res., 94, 15089 [NASA ADS] [CrossRef] [Google Scholar]
  43. Krupar, V., Santolik, O., Cecconi, B., et al. 2012, J. Geophys. Res.: Space Phys., 117, 6101 [Google Scholar]
  44. Krupar, V., Maksimovic, M., Santolik, O., et al. 2014, Sol. Phys., 289, 3121 [NASA ADS] [CrossRef] [Google Scholar]
  45. Krupar, V., Eastwood, J. P., Kruparova, O., et al. 2016, ApJ, 823, L5 [CrossRef] [Google Scholar]
  46. Krupar, V., Maksimovic, M., Kontar, E. P., et al. 2018, ApJ, 857, 82 [NASA ADS] [CrossRef] [Google Scholar]
  47. Krupar, V., Magdalenić, J., Eastwood, J. P., et al. 2019, ApJ, 882, 92 [CrossRef] [Google Scholar]
  48. Krupar, V., Szabo, A., Maksimovic, M., et al. 2020, ApJS, 246, 57 [Google Scholar]
  49. Kuncic, Z., Cairns, I. H., Knock, S., & Robinson, P. A. 2002, Geophys. Res. Lett., 29, 1161 [Google Scholar]
  50. Kundu, M. R. 1965, Solar Radio Astronomy (New York: Interscience Publication) [Google Scholar]
  51. Labrum, N. R. 1972, Sol. Phys., 27, 496 [NASA ADS] [CrossRef] [Google Scholar]
  52. Leblanc, Y., Dulk, G. A., & Bougeret, J.-L. 1998, Sol. Phys., 183, 165 [NASA ADS] [CrossRef] [Google Scholar]
  53. Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
  54. Lionello, R., Linker, J. A., & Mikić, Z. 2009, ApJ, 690, 902 [CrossRef] [Google Scholar]
  55. Magdalenić, J., Vršnak, B., Pohjolainen, S., et al. 2008, Sol. Phys., 253, 305 [NASA ADS] [CrossRef] [Google Scholar]
  56. Magdalenić, J., Marqué, C., Zhukov, A. N., Vršnak, B., & Žic, T. 2010, ApJ, 718, 266 [NASA ADS] [CrossRef] [Google Scholar]
  57. Magdalenić, J., Marqué, C., Zhukov, A. N., Vršnak, B., & Veronig, A. 2012, ApJ, 746, 152 [NASA ADS] [CrossRef] [Google Scholar]
  58. Magdalenić, J., Marqué, C., Krupar, V., et al. 2014, ApJ, 791, 115 [NASA ADS] [CrossRef] [Google Scholar]
  59. Magdalenić, J., Marqué, C., Fallows, R. A., et al. 2020, ApJ, 897, L15 [CrossRef] [Google Scholar]
  60. Maia, D., Pick, M., Vourlidas, A., & Howard, R. 2000, ApJ, 528, L49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  61. Mäkelä, P., Gopalswamy, N., Reiner, M. J., Akiyama, S., & Krupar, V. 2016, ApJ, 827, 141 [CrossRef] [Google Scholar]
  62. Mäkelä, P., Gopalswamy, N., & Akiyama, S. 2018, ApJ, 867, 40 [CrossRef] [Google Scholar]
  63. Manchester, W., Kilpua, E. K. J., Liu, Y. D., et al. 2017, Space Sci. Rev., 212, 1159 [Google Scholar]
  64. Mann, G., & Klassen, A. 2005, A&A, 441, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Mann, G., Jansen, F., MacDowall, R. J., Kaiser, M. L., & Stone, R. G. 1999, A&A, 348, 614 [NASA ADS] [Google Scholar]
  66. Mann, G., Melnik, V. N., Rucker, H. O., Konovalenko, A. A., & Brazhenko, A. I. 2018, A&A, 609, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Martínez Oliveros, J. C., Raftery, C. L., Bain, H. M., et al. 2012, ApJ, 748, 66 [NASA ADS] [CrossRef] [Google Scholar]
  68. Martínez-Oliveros, J. C., Raftery, C., Bain, H., et al. 2015, Sol. Phys., 290, 891 [CrossRef] [Google Scholar]
  69. Melrose, D. B. 1980, Space Sci. Rev., 26, 3 [NASA ADS] [CrossRef] [Google Scholar]
  70. Melrose, D. B. 2017, Rev. Mod. Plasma Phys., 1, 5 [CrossRef] [Google Scholar]
  71. Nelson, G. J., & Melrose, D. B. 1985, in Type II Bursts. Solar Radiophysics: Studies of Emission from the Sun at Metre Wavelengths, eds. D. J. McLean, & N. R. Labrum (Cambridge: Cambridge University Press), 333 [Google Scholar]
  72. Newkirk, G. J. 1961, ApJ, 133, 983 [NASA ADS] [CrossRef] [Google Scholar]
  73. Nindos, A., Alissandrakis, C. E., Hillaris, A., & Preka-Papadema, P. 2011, A&A, 531, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
  75. Pikel’Ner, S. B., & Gintsburg, M. A. 1964, Sov. Astron., 7, 639 [Google Scholar]
  76. Pomoell, J., & Poedts, S. 2018, J. Space Weather Space Clim., 8, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Priest, E. 2014, Magnetohydrodynamics of the Sun (Cambridge: Cambridge University Press) [Google Scholar]
  78. Pulupa, M., & Bale, S. D. 2008, ApJ, 676, 1330 [NASA ADS] [CrossRef] [Google Scholar]
  79. Reiner, M. J., & Stone, R. G. 1988, A&A, 206, 316 [Google Scholar]
  80. Reiner, M. J., Fainberg, J., Kaiser, M. L., & Stone, R. G. 1998, J. Geophys. Res., 103, 1923 [NASA ADS] [CrossRef] [Google Scholar]
  81. Riley, P., Lionello, R., Linker, J. A., et al. 2011, Sol. Phys., 274, 361 [NASA ADS] [CrossRef] [Google Scholar]
  82. Roberts, J. A. 1959, Aust. J. Phys., 12, 327 [NASA ADS] [CrossRef] [Google Scholar]
  83. Robinson, P. A., & Cairns, I. H. 2000, Washington DC American Geophysical Union Geophysical Monograph Series, 119, 37 [NASA ADS] [Google Scholar]
  84. Rouillard, A. P., Plotnikov, I., Pinto, R. F., et al. 2016, ApJ, 833, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Saint-Hilaire, P., Vilmer, N., & Kerdraon, A. 2013, ApJ, 762, 60 [NASA ADS] [CrossRef] [Google Scholar]
  86. Saito, K. 1970, Ann. Tokyo Astron. Obs., 12, 51 [Google Scholar]
  87. Schmidt, J. M., & Cairns, I. H. 2016, Geophys. Res. Lett., 43, 50 [CrossRef] [Google Scholar]
  88. Schwadron, N. A., Lee, M. A., Gorby, M., et al. 2015, ApJ, 810, 97 [Google Scholar]
  89. Street, A. G., Ball, L., & Melrose, D. B. 1994, Proc. Astron. Soc. Aust., 11, 21 [NASA ADS] [CrossRef] [Google Scholar]
  90. Thejappa, G., MacDowall, R. J., & Kaiser, M. L. 2007, ApJ, 671, 894 [NASA ADS] [CrossRef] [Google Scholar]
  91. Thejappa, G., MacDowall, R. J., & Bergamo, M. 2012, ApJ, 745, 187 [NASA ADS] [CrossRef] [Google Scholar]
  92. Toptygin, I. N. 1980, Space Sci. Rev., 26, 157 [NASA ADS] [CrossRef] [Google Scholar]
  93. Török, T., Downs, C., Linker, J. A., et al. 2018, ApJ, 856, 75 [Google Scholar]
  94. Uchida, Y. 1974, Sol. Phys., 39, 431 [Google Scholar]
  95. Uchida, Y., Altschuler, M. D., & Newkirk, G., Jr. 1973, Sol. Phys., 28, 495 [NASA ADS] [CrossRef] [Google Scholar]
  96. Vandas, M., & Karlický, M. 2000, Sol. Phys., 197, 85 [NASA ADS] [CrossRef] [Google Scholar]
  97. Vandas, M., & Karlický, M. 2011, A&A, 531, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Veronig, A. M., Gömöry, P., Dissauer, K., Temmer, M., & Vanninathan, K. 2019, ApJ, 879, 85 [NASA ADS] [CrossRef] [Google Scholar]
  99. Vlahos, L. 1989, Sol. Phys., 121, 431 [NASA ADS] [CrossRef] [Google Scholar]
  100. Vršnak, B., & Cliver, E. W. 2008, Sol. Phys., 253, 215 [NASA ADS] [CrossRef] [Google Scholar]
  101. Vršnak, B., & Lulić, S. 2000a, Sol. Phys., 196, 157 [Google Scholar]
  102. Vršnak, B., & Lulić, S. 2000b, Sol. Phys., 196, 181 [NASA ADS] [CrossRef] [Google Scholar]
  103. Warmuth, A. 2015, Liv. Rev. Sol. Phys., 12, 3 [Google Scholar]
  104. Warmuth, A., Vršnak, B., Magdalenić, J., Hanslmeier, A., & Otruba, W. 2004, A&A, 418, 1101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Wild, J. P., & McCready, L. L. 1950, Aust. J. Sci. Res. A Phys. Sci., 3, 387 [Google Scholar]
  106. Zaitsev, V. V. 1969, Sov. Astron., 12, 610 [NASA ADS] [Google Scholar]
  107. Zimovets, I., Vilmer, N., Chian, A. C.-L., Sharykin, I., & Struminsky, A. 2012, A&A, 547, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Zlobec, P., Messerotti, M., Karlicky, M., & Urbarz, H. 1993, Sol. Phys., 144, 373 [NASA ADS] [CrossRef] [Google Scholar]
  109. Zlotnik, E. Y., Klassen, A., Klein, K. L., Aurass, H., & Mann, G. 1998, A&A, 331, 1087 [NASA ADS] [Google Scholar]
  110. Zucca, P., Morosan, D. E., Rouillard, A. P., et al. 2018, A&A, 615, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1.

Dynamic radio spectra recorded by the Culgoora Solar Radio Spectrograph during the flare/CME event on September 27, 2012. The fundamental (F) and harmonic (H) bands of the high frequency type II burst are indicated by F and H.
In the text
thumbnail Fig. 2.

Dynamic radio spectra recorded by STEREO A/WAVES (top), STEREO B/WAVES (middle), and Wind/WAVES (bottom) showing the radio event associated with the flare/CME observed on September 27, 2012. The recorded radio flux is in normalized solar flux units (sfu). The black arrows mark the fundamental and harmonic bands of the high frequency type II burst. The white arrows mark the fundamental and harmonic bands of the low frequency type II burst and the red arrows mark examples of type III radio bursts associated with the event.
In the text
thumbnail Fig. 3.

Source regions of the LF-type II radio burst obtained from radio triangulation presented as observed from different viewpoints namely: STEREO B (left panel), Earth/Wind (center panel), and A (right panel), respectively. The different colored spheres correspond to the respective frequency pairs (in kHz), while their diameters are defined by the distance between the two wave vectors (source region). The plot is in sun-centred x, y, z 3D Cartesian coordinates with R⊙ units.
In the text
thumbnail Fig. 4.

Shock wave fitting was done using multi-viewpoint observations from STEREO B/COR2 (top panel) and SOHO/LASCO C2 (bottom panel) at 00:24 UT. This is the time of observation of the highest triangulated frequency pair of the LF-type II burst. The red spherical mesh represents the fit to the white light shock. The regions indicated as under-fitted are the regions that are not accounted for in the shock wave modelling. The red and the fuchsia points are the centroids of the highest frequency LF-type II sources and the dark-shaded region is the full source region obtained from radio triangulation.
In the text
thumbnail Fig. 5.

Snapshots of the modelled shock wave parameters at different times (a–d) and with different parameters estimated at the reconstructed pressure wave front surface (1–3). The yellow sphere represents the Sun and the colour coded ellipse represents the modelled pressure wave. The arrows indicate the propagation direction of the different triangulated radio bursts, while the black arrow indicates the Sun-Earth line. The coloured meridians visible on the surface of the Sun represent the solar central meridian as viewed from STEREO A (red), STEREO B (blue), and Earth (black). The presented times are: the start of the HF-type II (panel a), middle of HF-type II (panel b), start of LF-type II (panel c), and the end of LF-type II (panel d). The different parameters plotted in the rows are, (1) the Alfvén Mach number (MA), (2) the density compression ratio, and (3) the angle between the shock normal and the upstream magnetic field (θBN).
In the text
thumbnail Fig. 6.

Global evolution of the wave parameters computed on the surface of the pressure wave. Panel a: evolution of the Alfvén Mach number (MA), panel b: fast magnetosonic Mach number, panel c: angle between the shock normal and the upstream magnetic field (θBN), and panel d: density compression ratio. The statistical distribution of the values are represented by the black line (median), blue line (mean), pink shade (quartiles), and the gray shade (decile) values.
In the text
thumbnail Fig. 7.

HF-type II source regions on the pressure wave bubble. Panel a: modelled wave with the values of MA plotted on the wave’s surface roughly around the start of HF-type II radio burst. Circles titled L1–L4 represent the regions where the source of HF-type II could be located. Panel b: temporal evolution of the Alfvén mach number (MA) in the selected regions which are represented by the colored median lines. The quartiles and decile values are given only for L2. The temporal evolution of the geometry in these regions is presented in panel c.
In the text
thumbnail Fig. 8.

Shock wave association with the LF-type II radio burst. Panel a: modelled pressure wave with the values of MA plotted on its surface around the start time of LF-type II radio burst. The colour-coded source regions named R1−R4 represent the LF-type II source regions observed in the time interval between 00:25 and 00:50 UT. The varying diameters of the source regions account for the large source sizes obtained from the radio triangulation results. Panel b: temporal evolution of the Alfvén mach number (MA) in the selected regions which are represented by the colored median lines. The quartiles and decile values are shown only for R4. The temporal evolution of the θBN in all regions is presented in panel c.
In the text
thumbnail Fig. 9.

Histogram maps of different shock wave parameters plotted in a form of dynamic spectra. The four rows of 2D-histogram maps were produced in different areas of the wave. The histogram maps were constructed considering: (a) the full shock surface, (b) only L3 region of HF-type II, (c) region L2 of HF-type II (Sect. 5.2.2), and (d) region R4 of LF-type (Sect. 5.2.3). The three columns show different wave parameters: (1) the Alfen Mach number (MA), (2) the Shock wave geometry (θBN), and (3) the Langmuir wave conversion ratio (LWC > 1).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.