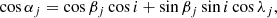| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202141484 | |
| Published online | 01 October 2021 | |
Analysis of apsidal motion in eclipsing binaries using TESS data
II. A test of internal stellar structure⋆
1
Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
e-mail: claret@iaa.es
2
Dept. Física Teórica y del Cosmos, Universidad de Granada, Campus de Fuentenueva s/n, 10871 Granada, Spain
3
Centro de Astrobiologia (CSIC-INTA), 28850 Torrejón de Ardoz, Madrid, Spain
4
International Space Science Institute (ISSI), Hallerstrasse 6, 3012 Bern, Switzerland
5
Institut de Ciències de l’Espai (ICE, CSIC), Campus UAB, c/ Can Magrans s/n, 08193 Bellaterra, Barcelona, Spain
6
Institut d’Estudis Espacials de Catalunya (IEEC), c/ Gran Capità 2-4, 08034 Barcelona, Spain
Received:
7
June
2021
Accepted:
13
July
2021
Context. The measurement of apsidal motion rates in eccentric eclipsing binaries is a unique way to gain insight into the internal structure of stars through the internal density concentration parameter, k2. High-quality physical parameters of the stellar components, together with precise measurements of the advance of the periastron, are needed for the comparison with values derived from models.
Aims. As a product of the Transiting Exoplanet Survey Satellite (TESS) mission, high-precision light curves of a large number of eclipsing binaries are now available. Using a selection of well-studied, double-lined eccentric eclipsing binary systems, we aim to determine their apsidal motion rates and place constraints on the internal density concentration and compare with the predictions from state-of-the-art theoretical models.
Methods. We computed times of minimum light using the TESS light curves of 34 eclipsing binaries with precise absolute parameters. We used the changing difference over time between primary and secondary eclipse timings to determine the apsidal motion rate. To extend the time baseline, we combined the high-precision TESS timings with reliable archival data. On the other hand, for each component of our sample of double-lined eclipsing binaries, we computed grids of evolutionary stellar models for the observed stellar mass exploring ranges of values of the overshooting parameter fov, the mixing-length parameter, and the metallicity. To find the best solution for the two components we adopted a χ2 statistic to infer the optimal values of the overshooting parameter and the mixing-length parameter. The theoretical internal structure constants to be compared with the observed values were calculated by integrating the differential equations of Radau for each stellar model.
Results. We have determined the apsidal motion rate of 27 double-lined eclipsing binaries with precise physical parameters. The obtained values, corrected for their relativistic contribution, yield precise empirical parameters of the internal stellar density concentration. The comparison of these results with the predictions based on new theoretical models shows very good agreement. Small deviations are identified but remain within the observational uncertainties and the path for a refined comparison is indicated.
Key words: binaries: eclipsing / binaries: close / stars: evolution / stars: interiors / stars: rotation
Full Table 2 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/654/A17
© ESO 2021
1. Introduction
Double-lined eclipsing binaries (DLEBs) have demonstrated to be the basic source of information about fundamental stellar properties, such as masses and radii (Andersen 1991). The comparison of observed physical properties with theoretical models has been used to perform critical tests of stellar structure and evolution models (Ribas et al. 2000a; Torres et al. 2010; Claret & Torres 2019). Precise masses and radii are needed for a solid and reliable comparison between observations and theory, essentially better than 3%, and this generally calls for the use of DLEBs. Furthermore, the binary systems have to be well detached, for instance, with the radii of both components being much smaller than their Roche limits, to ensure that the components represent the behavior of single stars with the same physical properties.
Eccentric eclipsing binaries offer further opportunities to characterize the internal structure of stars through the measurement of the precession rate of the line of the apses of the orbit, for instance, the apsidal motion rate. Such secular motion can be understood as the sum of two terms, one classical and one relativistic. The classical, or Newtonian, effect is related to the quadrupole interactions that depend on the internal mass distribution of the stellar components (basically the degree of mass concentration toward the center). The second term is a contribution arising from general relativity (GR), the best known example of which is the advance of the perihelion of Mercury. Of course, if there is a third body gravitationally bound to the close binary, an additional term in the apsidal motion has to be considered.
Precise determinations of apsidal motion require long-term monitoring of the times of eclipse, generally spanning several decades, with high-quality measurements, although apsidal motion rates can also be derived from long time series of radial velocity data (Schmitt et al. 2016). The Transiting Exoplanet Survey Satellite (TESS) mission to study exoplanets through photometric transits (Ricker et al. 2015), with its nearly full sky coverage, provides, as a bonus, precise photometry of a large sample of eclipsing binary systems with a time baseline of at least 27 days and up to two years in some cases. Precise monitoring of binary light curves is thus possible from space, without the disturbing day/night effect, and accurate eclipse timings can be derived thanks to the uniform sampling. Equipped with this new tool, we have established a program to make precise apsidal motion determinations in eccentric eclipsing binaries with accurate absolute dimensions, in some cases for the first time, and compared them with theoretical models.
The first results of our program were presented in Baroch et al. (2021), hereafter referred to as Paper I. This paper addressed eclipsing binary systems with accurate dimensions and with apsidal motion rates dominated by the relativistic contribution, with a limit set to be at least 60% of the total apsidal motion rate. This allowed us to perform a stringent test of the predictions of GR, which revealed excellent agreement between observations and theory. In the present paper, we focus on the systems where the classical term is dominant (for instance, GR contribution being less than 60% of the total). For such cases, we calculate the GR apsidal motion rate analytically (which Paper I shows to be accurate) and we subsequently subtract it from the observed rate to determine the observational classical term. We can then compare with stellar model predictions and provide constraints on interior structure (for instance, Claret & Giménez 1993, 2010, and references therein).
This paper is structured as follows. Section 2 is dedicated to describe the observational sample and the measurements of eclipse timings. Section 3 describes the apsidal motion determinations, the methodology and the results, with further details for each individual system in an appendix. Section 4 is dedicated to describe the stellar evolutionary models, the differential equations used to obtain theoretical values of the apsidal motion constants, and the methodology employed to compare with the physical dimensions of the component stars. Section 5 is devoted to the comparison between observed and theoretical values of log k2 and, finally, in Sect. 6 we present our conclusions.
2. The observational sample
For a useful interpretation of the apsidal motion rate observed in eccentric eclipsing binaries, it is essential to have a precise knowledge of the physical properties of the component stars, essentially masses and radii. Some of the equations, for example, have a strong dependence on the relative radii as they contribute to the fifth power. For this reason, we have limited our dynamical study using eclipse timings to those cases where the masses and radii of the components are known with an accuracy better than 3%. A list of well-detached eccentric eclipsing binaries with good absolute dimensions was published by Torres et al. (2010), and we have further added a number of systems from the DEBCAT catalog of Southworth et al. (2015), which is updated permanently. We have only considered systems with TESS measurements of both primary and secondary eclipses, thus permitting the determination of the timing difference. Due to the expected amplitude of the apsidal motion variations, we also set a lower limit to the orbital eccentricity at 0.01.
Our analysis is restricted to systems with an expected relativistic contribution below 60% of the total apsidal motion. Those with a larger relativistic contribution were discussed in Paper I and are less useful for the study of internal structure due to the larger relative uncertainty of the observed classical term. The systems analyzed in the present paper are listed in Table 1, together with their main physical parameters and the corresponding references, sorted by decreasing mass of the primary component. In addition to orbital period, masses and radii of the component stars, we also provide the effective temperatures and the projected rotational velocities, necessary for the computation of the apsidal motion rates, as described in Sect. 4.
Astrophysical parameters.
The systems V380 Cyg (B1.1 III and B2.5/3 V), V636 Cen (G0 V and G0 V) and CM Dra (M4.5 V and M4.5 V) are not considered due to the difficulties found with standard theoretical stellar models in reproducing their observed physical parameters, namely their masses, radii and effective temperatures, independently of the apsidal motion results. This is a requisite of our methodology to obtain theoretical apsidal motion parameters, as described in Sect. 4. Each of these systems has some characteristics that push it beyond the boundaries of our studied parameter space: the evolved stage and the proximity to the Roche limit of the primary component of V380 Cyg, the strong chromospheric activity of V636 Cen, or the very low masses and magnetic activity of CM Dra. Investigating these systems will require detailed individual studies of the observational data and model input physics, which is left for subsequent publications. On the other hand, we have considered three systems that should have been included in Paper I due to an expected relativistic contribution above 60%, but did not have either sufficient TESS data at the time of publication or a reliable apsidal motion determination. These systems are V1022 Cas, EW Ori, and BF Dra, and they are included in Table 1 and discussed in Sect. 3.
For all systems in Table 1 we have analyzed the available TESS photometric information retrieved from Sectors 1 to 34. To compute the time of minimum light of the eclipses, we first normalized the TESS light curves using the out-of-eclipse phases. We selected well-sampled individual eclipses using the same orbital phase interval for all primary and secondary eclipses, and computed their time of minimum light employing the widely-used Kwee & van Woerden (1956) method. We then computed the corresponding difference between primary and secondary eclipse timings, T2 − T1, expressed in days, and listed the resulting values in Table 2, which is available electronically. The table gives the values of T2 − T1 determined from the individual timings, together with their separation in orbital cycles (dN), that we have limited to ±1.
T2 − T1 computed from TESS lightcurves.
3. Determination of the apsidal motion rates
In Paper I we performed the determination of the apsidal motion rate from the analysis of the time-variation of the difference between primary and secondary eclipses, T2 − T1. This method assumes independent knowledge of the orbital eccentricity and that the variations in the timing differences can be represented by a linear relationship with the slope corresponding to the time derivative of the argument of periastron. This method is only valid when considering a small fraction, typically less than 1%, of the total apsidal motion period, U. Otherwise, the nonlinear component of the T2 − T1 variations becomes relevant and the analysis requires a different approach. When this is the case, one can use the equations given by Giménez & Bastero (1995), which are complete up to 𝒪(e5). Linearizing the variations permits computing the argument of periastron, ω, corresponding to each observed value of T2 − T1 with the adopted orbital eccentricity and inclination, as derived from the light curve analysis. This is based on the relation between the phase of the secondary eclipse and the value of e cos ω. Potential ambiguities in the argument of periastron can be resolved with the value of esinω resulting from the light curve analysis. Using this approach, a linear fit to the variation of ω with time yields the determination of the apsidal motion rate with no restriction in terms of the coverage of the period, U.
In both approaches, the basic observational information is the measurement of T2 − T1. We provide in Table 2 the full list of the T2 − T1 TESS values for all systems in Table 1, and we discuss each individual system in Appendix A. In Table 3 we summarize the results of the apsidal motion determination where the orbital eccentricity, e, and the apsidal motion rate, 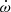 expressed in deg cycle−1, are provided. The anomalistic period, Pa, can be easily computed from the sidereal period in Table 1, using the relation
expressed in deg cycle−1, are provided. The anomalistic period, Pa, can be easily computed from the sidereal period in Table 1, using the relation 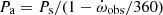 . The letter code in the second column denotes the adopted methodology: A for those based on the linear variation of T2 − T1, and B for those using the argument of periastron, including the comparison of values derived from the light curve analysis. In addition, we use L to denote values adopted from the literature, generally with method B, or using variable ω in the analysis of light curves spanning a long time base. In this case, we checked that the adopted solutions predict values for the relative position of the secondary eclipse in agreement with the new TESS measurements. Obviously, B and L determinations correspond to faster apsidal motion rates and A to slower ones, including those with a higher fractional contribution of the relativistic term. Finally, those systems where the presence of a third body has been proposed, either from the light curve analysis or from the variations of the individual eclipse timings, are marked with an asterisk.
. The letter code in the second column denotes the adopted methodology: A for those based on the linear variation of T2 − T1, and B for those using the argument of periastron, including the comparison of values derived from the light curve analysis. In addition, we use L to denote values adopted from the literature, generally with method B, or using variable ω in the analysis of light curves spanning a long time base. In this case, we checked that the adopted solutions predict values for the relative position of the secondary eclipse in agreement with the new TESS measurements. Obviously, B and L determinations correspond to faster apsidal motion rates and A to slower ones, including those with a higher fractional contribution of the relativistic term. Finally, those systems where the presence of a third body has been proposed, either from the light curve analysis or from the variations of the individual eclipse timings, are marked with an asterisk.
Observed and theoretical apsidal motion rates.
Table 3 does not include all systems in Table 1 because some were discarded due to various reasons. Firstly, let us note that we defined a precision criterion to accept a system for further analysis. We only kept systems with a relative precision better than 25% in the classical term of the apsidal motion determination, for which we derive the internal stellar structure constants. This corresponds to a maximum σ log k2 of 0.11, necessary for a constraining comparison with theoretical models. After our analysis, we found a small fraction of the eclipsing binaries in Table 1 to yield no significant apsidal motion detections. For two systems, BP Vul and AI Phe, we were not able to measure apsidal motion in spite of the precise TESS observations. We encountered a similar situation with MU Cas and V1022 Cas, which resulted in apsidal motion rate determinations having uncertainties above our acceptance threshold because of the narrow time span covered by precise timings. In the case of BF Dra, we found disagreement between the different methodologies to determine the apsidal motion and could thus be affected by large systematic effects. Moreover, the potential presence of a perturbing third body as well as the highly-evolved nature of the component stars, close to the termination-age main-sequence, call for an individual study of this system, including the analysis of a new light curve. Finally, EW Ori does not meet the relative precision limit in the classical term because of the high relative GR contribution (∼80%). This system could have been included in Paper I but we did not have an apsidal motion rate determination at the time. However, we briefly discuss the comparison with GR and the updated post-Newtonian parameters including this eclipsing binary in Appendix A.
4. The theoretical stellar models
We use the Modules for Experiments in Stellar Astrophysics package (MESA; Paxton et al. 2011, 2013, 2015) version r-7385, and adopted the solar-calibrated value of the mixing length parameter to be 1.84 (Torres et al. 2015). The equation relating the temperature gradients was solved using the Henyey option, and for the localization of the boundary of the convection zone we adopted the Schwarzschild criterion. For the opacities we use the mixture of Asplund et al. (2009), for which Z⊙ = 0.0134. These opacities were paired with a linear enrichment law given by Yp = 0.249 (Planck Collaboration XIII 2016) and a slope ΔY/ΔZ = 1.67, where Yp is primordial helium mass fraction. Microscopic diffusion was considered (see details below) for all evolutionary tracks that were computed starting from the pre-main sequence (PMS) stage. For each component of our sample of DLEBs we computed grids for the observed stellar mass exploring ranges of values of the overshooting parameter fov (see below), the mixing-length parameter αMLT, and the metallicity Z. To find the solution providing the best fit to both stellar components we adopted a χ2 statistic and considered fov and αMLT as the optimization parameters. We also adopted the initial metal abundance Z to be the same for the two components.
We calculate evolutionary tracks for the exact component masses and other parameters. Thus, our methodology does not involve computing grids for a wide variety of parameters and avoids interpolation in masses, metallicities, mixing-length, or core overshooting, which could lead to systematic effects. In our calculations we allowed the optimized ages for both components to differ by up to 5%, as long as the radii, effective temperatures and masses were predicted to be within their respective observational error bars. This flexibility is justified by the expected uncertainties in the input physics of the evolutionary tracks, for instance, opacities, equations of state, mass loss, etc., and also in the observational parameters. In some cases this procedure was improved with some additional computations. Starting from previously converged models, we increased the resolution in the input physics (αMLT, fov and Z) to refine the fitting process.
A fraction of the systems in our sample have high-mass components and therefore core overshooting can have a significant effect in the computation of evolutionary model grids. Convective core overshooting is related to the increase of the stellar core beyond the boundary defined by the Schwarzschild criterion. Stellar models computed taking into account this extra-mixing lead to longer main-sequence lifetimes and a higher degree of mass concentration toward the center, with direct impact on the comparison between theoretical and observational rates of apsidal motion. (Claret & Torres 2019, and references therein) selected 50 well-measured detached DLEBs to calibrate the dependency of fov on stellar mass. In such a formulation, the extra-mixture is modeled as a diffusive process (Freytag et al. 1996; Herwig et al. 1997) with a diffusion coefficient at a radial distance r from the boundary given by D(r) = Doexp(−2r/fovHp), where Do is the coefficient inside the boundary and Hp the pressure scale height. As a result of the comparison between theoretical models and observational data from these systems, it has been shown that fov increases sharply up to a mass on the order of 2.0 M⊙ and is practically constant up to 4.43 M⊙, the upper limit in mass of the observational sample adopted by Claret & Torres (2019). There are also some evidences of a dependence of core overshooting on stellar mass from a theoretical point of view (see, for example, the appendices in Claret & Torres 2017; Jermyn et al. 2018). Such kind of calibrations can only be performed with highly evolved stars where the effects of core overshooting are more evident. Unfortunately, this is not the case in our observational sample with only two systems with moderately evolved components (V453 Cyg and V478 Cyg). For all stars more massive than 10 M⊙, we have extended the range of values of fov to be explored with our search methodology.
In all our computations we have included microscopic diffusion (8 elements: H1, He3, He4, C12, N14, O16, Ne20, and Mg24). For those stars showing convective envelopes, we adopted the standard mixing-length formalism (Böhm-Vitense 1958). For the most massive stars in our sample, we have adopted the Vink et al. (2001) formulation for mass loss assuming a multiplicative scale factor η = 0.1 (not to be confused with η of the Radau equation; see below). On the other hand, rotational-mixing was not included in the calculations. For a more complete description of our modeling framework, see Claret & Torres (2019) and references therein.
We also ran a consistency check of our model comparisons with observational data (masses, Teff, log g, Z) between our adopted MESA models and those computed with the GRANADA code (Claret 2004). This was done for a subsample of systems (DI Her, V1143 Cyg, V1647 Sgr, IQ Per, ζ Phe). Convective core overshooting in the GRANADA code is treated as a step-function, characterized by the parameter αov. A similar check-up procedure was already carried out by Claret & Torres (2016, 2017) for a larger sample of DLEBs. From this cross-comparison the relationship αov/fov ≈ 11.36 ± 0.22 was derived. With this procedure we check the consistency between the log k2 computed with MESA and with the GRANADA codes. A very good agreement has been found between the k2 computed with the two codes.
To calculate the theoretical values of log k2 to be compared with the corresponding empirically-determined values, we applied the methodology described above to all systems in Table 1. The theoretical internal structure constants were computed for each component through the integration of the differential equations of Radau of order j, namely
where
and a is the mean radius of the equipotential, ϵj is a measure of the deviation from sphericity (the tesseral harmonics), ρ(a) is the mass density at the distance a from the center, and 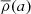 is the mean mass density within an equipotential of radius a. The boundary conditions are: ηj(0) = j − 2, and
is the mean mass density within an equipotential of radius a. The boundary conditions are: ηj(0) = j − 2, and 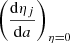 =
= 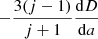 , where
, where 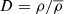 .
.
The theoretical internal structure constant kj, for each component j, is given by
where ηj(R) are the values of ηj at the surface of the star. Finally, the theoretical value of k2 to be compared with observations is given by the weighted average over the model predictions for the two components:
The parameters c2i, for the case of aligned rotation axes, are computed following the equations,
where A is the semi-major axis of the orbit, while f and g are auxiliary functions of the orbital eccentricity given by
and
Additionally, Ωi/ΩK is the ratio between the rotational angular velocity of component i and the average orbital angular velocity, mi are the stellar masses, Ri are the stellar radii and the eccentricity is denoted by the symbol e. As indicated by Claret & Giménez (1993), the contribution of the terms kn (for n > 2) are negligible in the present context.
On the other hand, using the quasi-spherical approximation, Claret (1999) found that the influence of rotation on internal structure depends on the distortion of the configuration following the expression δ log k2 ≈ −0.87Λs + 0.004, where Λs = 2v2/(3gR), with v being the rotational velocity, g the local gravity and R the stellar radius. Such correction was computed at the surface of each star in our sample, using the observed rotational velocities given in Table 1, and applied to the corresponding theoretical models. We note that this correction does not take into account the effects of rotational-mixing on the mass concentration. It is also important to point out some uncertainty in relation to the observed rotational velocities regarding whether or not they are representative of the stellar interior. Most of the systems in our observational sample are not very evolved, from which it follows that the angular velocity gradients in their interiors should not be high. This circumstance reduces the uncertainties although it does not remove them completely.
The effects of stellar compressibility and dynamic tides were also taken into account according to the computations by Claret & Willems (2002). We could verify that in all systems in their Table 2, no significant effect is present except in the most massive and close systems, EM Car and Y Cyg, for which we have applied the calculated correction (2% and 1%, respectively).
As an example of our procedure, we present in Fig. 1 the fitting process in the case of AI Phe. The best input physics for the corresponding models and for each component (subindices 1 and 2) is given by αMLT, 1 = 2.00, αMLT, 2 = 2.10 and fov1 = fov2 = 0. In Fig. 2 we show the resulting models in the log g vs. logage diagram. The observational error bars are very small and were shown in different color for the sake of clarity. This solution, as explained above, is obtained on the basis of the minimum χ2 of the model grid search and imply the log k2i values for the system. In the case of AI Phe, we find log k2, 1 = −1.58 ± 0.30 and log k2, 2 = −2.45 ± 0.03. Although the masses of both components are similar, the large difference between apsidal motion constants is due to the advanced evolutionary stage of the system. While the secondary is still in the main sequence, the primary is much more evolved and is located in the giant branch, where k2 varies very rapidly, and hence the large error bar. As we do not yet have a reliable determination of the apsidal motion rate for AI Phe, we have performed Monte Carlo simulations (see Sect. 5.1 for more details), assuming that the two components are aligned with the orbital spin (see Fig. 3). The asymmetry of the simulations reflect the differences between the uncertainty in log k2 for each of the components. The most probable value of 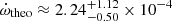 deg cycle−1, should be compared with the observational value when available, but the slow predicted rate is consistent with the lack of a measurable value (see Appendix A). We have selected AI Phe to illustrate our methodology, in spite of not having an observed value of the apsidal motion rate, as a tribute to the late Prof. J. Andersen. This was one of his favorite DLEBs, frequently used as a test case for stellar structure and evolution.
deg cycle−1, should be compared with the observational value when available, but the slow predicted rate is consistent with the lack of a measurable value (see Appendix A). We have selected AI Phe to illustrate our methodology, in spite of not having an observed value of the apsidal motion rate, as a tribute to the late Prof. J. Andersen. This was one of his favorite DLEBs, frequently used as a test case for stellar structure and evolution.
 |
Fig. 1. HR diagram for AI Phe. The models were calculated adopting Z = 0.011. The solid line indicates the primary component while the dashed one represents the secondary. |
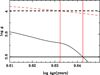 |
Fig. 2. log g and respective error bars as a function of time for AI Phe. The two vertical lines indicate the time interval corresponding to the individual ages for each component. The horizontal lines represent the error bars in log g. Line coding as in Fig. 1. |
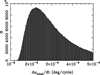 |
Fig. 3. Monte Carlo simulations (106 realizations) for the theoretical apsidal motion of AI Phe. |
5. The apsidal motion test of stellar structure
The weighted values of the model-predicted log k2 given by Eq. (4) are presented in Col. 6 of Table 3, together with the corresponding predicted apsidal motion rates. The adopted methodology ensures that both components have the same age (within the previously mentioned 5% tolerance limit), and that the observed masses, radii and effective temperatures, are reproduced by the respective models within their errors.
The comparison of the theoretical  with the observed values is shown in Fig. 4. As can be seen, the agreement between observed and predicted values is excellent. The only system with marginal agreement, at the limit of the adopted uncertainties, is EM Car, having the highest mass components of our sample. Such good agreement includes the cases where a third body has been identified, as shown in the bottom panel of Fig. 4 (see Sect. 5.2).
with the observed values is shown in Fig. 4. As can be seen, the agreement between observed and predicted values is excellent. The only system with marginal agreement, at the limit of the adopted uncertainties, is EM Car, having the highest mass components of our sample. Such good agreement includes the cases where a third body has been identified, as shown in the bottom panel of Fig. 4 (see Sect. 5.2).
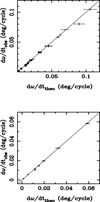 |
Fig. 4. Comparison between |
For the test of stellar models, we have to use the values of k2. Their observational value is a function of 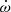 and the c2j coefficients given in Eq. (5):
and the c2j coefficients given in Eq. (5):
This refers only to the classical, or Newtonian, term. The total observed apsidal motion rate in Table 3 contains the contribution of this classical term plus a second additive term corresponding to the relativistic or GR contribution. The GR term is independent of the tidal/rotational distortions and can be computed using the equation given by Levi-Civita (1937) and rewritten by Giménez (1985) as a function of observable parameters. This equation is, in degrees per cycle:
where the apsidal motion rate corresponding to the relativistic term is expressed in degrees per cycle with masses in solar units and the orbital period in days. The classical term in Eq. (8), used to calculate the observed log k2, is then simply calculated as
It should be noted that we have assumed the rotational axes of both components to be aligned with the orbital spin in all cases except DI Her, for which the expression by Shakura (1985) was used together with the observed tilt angles by Albrecht et al. (2009). This is further discussed in Sect. 5.1, together with the suspected, albeit not corrected, cases of V1143 Cyg and EP Cru. Furthermore, all systems for which a third body has been identified through eclipse timing variations or from the measurement of third light are identified by an asterisk and included in Table 3 with no specific correction. They are shown in Fig. 4, at the bottom, and are discussed in Sect. 5.2.
The resulting values of log k2 derived from the observed apsidal motion rates are given in Table 3 and are compared with the theoretical values in Fig. 5. The agreement is very good, with the values of log k2, theoretical and observational, agreeing within their uncertainties for all systems. In spite of the general good agreement, a tendency for slightly more concentrated stars (for instance, lower log k2) than predicted by the models seems to be present around log k2 = −2.2, including EM Car. However, we emphasize that all systems agree within the corresponding uncertainties. This effect is not observed in the comparison of  , shown in Fig. 4, except for the case of EM Car. A detailed inspection of the observed minus computed values shows that it only affects those binaries with large relative radii, above 0.18, and with massive components, the most extreme case being indeed EM Car (Fig. 6). The deviation might therefore be linked to the observational values used for Eq. (5), given in Table 1. This could be explained through multiple factors, and given that the deviation is insignificant, we did not attempt to study it in further detail in the present work.
, shown in Fig. 4, except for the case of EM Car. A detailed inspection of the observed minus computed values shows that it only affects those binaries with large relative radii, above 0.18, and with massive components, the most extreme case being indeed EM Car (Fig. 6). The deviation might therefore be linked to the observational values used for Eq. (5), given in Table 1. This could be explained through multiple factors, and given that the deviation is insignificant, we did not attempt to study it in further detail in the present work.
 |
Fig. 5. Top panel: a comparison between the theoretical predictions and the observed values of the apsidal motion constant log k2 for all systems in Table 3. Bottom panel: the same comparison but without plotting the low mass binary V530 Ori, which has a rather extreme value, so that the bulk of the sample can be better visualized. |
 |
Fig. 6. Differences between |
5.1. Tilted rotational axes
When the rotational axes of the component stars are tilted with respect to the orbital spin, Eq. (5) is no longer valid (Company et al. 1988) and the alternative formulation given by Shakura (1985) is needed. The total Newtonian term of the apsidal motion rate is given by:
where,
The angle i is the inclination of the orbital plane, αj are the angles between the rotation axes and the normal to the orbital plane, and βj are the angles between the rotation axes and the line of sight, while the angles λj are the projection of the spin axes and the orbital axis on the plane of the sky for star j. All other parameters are the same as in Eq. (5). The angles αj and βj cannot be directly measured although they are related by the equation,
where the angles λj can be directly measured using the Rossiter-McLaughlin effect (Rossiter 1924; McLaughlin 1924).
The Monte Carlo simulations of apsidal motion rates were performed from realizations of the masses, radii, k2, orbital parameters and λj angles considering Gaussian distributions for the error bars. Also, we assumed that βj are distributed randomly, for instance, Prob(βj)dβj = sinβjdβj. In other words, cos βj has a uniform distribution. Finally, using Eq. (15), the values of cos αj can be determined. Angles βj implying equatorial rotational velocities exceeding the breakup velocities were discarded.
DI Her was puzzling for long time due to the flagrant disagreement between observed and predicted apsidal motion rates (Guinan & Maloney 1985; Claret 1998), but Albrecht et al. (2009) confirmed, using the Rossiter-McLaughlin effect, that the rotational axes of the components stars are actually tilted. The authors measured the angles λ1 = +72° ±4° and λ2 = −84° ±8° for the primary and the secondary components, respectively. Adopting the values of log k2 derived from the stellar models described in Sect. 4 (log k2, 1 = −2.146 ± 0.050, log k2, 2 = −2.171 ± 0.050), the histogram in Fig. 7 is generated by simulation of the angles not directly measured. The comparison with the observed apsidal motion rate, confirms the solution of the old discrepancy.
 |
Fig. 7. Monte Carlo simulations (106 realizations) for the apsidal motion of DI Her. The two vertical lines indicate the observational error bars. |
Two other eclipsing binaries in our sample, V1143 Cyg and EP Cru, have been suspected of having tilted rotational axes. For V1143 Cyg, Albrecht et al. (2007) observed that the axes of both components are aligned with the orbital spin within uncertainties. To check the effect in the apsidal motion computations we have carried out Monte Carlo simulations for both cases, aligned and misaligned, using their values of λ1 = 0.3° ±1.5° and λ2 = −1.2° ±1.6°. The theoretical internal structure constants derived from our models, namely log k2, 1 = −2.19 ± 0.05 and log k2, 2 = −2.29 ± 0.05, were used to generate the histograms shown in Fig. 8. Both simulations yield very similar results, as expected from the very small angles λ1, 2 and their uncertainties. Although the agreement with the observational value is marginally better in the case of misaligned axes, they both agree within errors and we have adopted the aligned solution in Table 3.
 |
Fig. 8. Monte Carlo simulations (106 realizations) for the total apsidal motion of V1143 Cyg. In the upper panel, we assumed misaligment while in the bottom panel we simulate the case of alignment. The two vertical lines indicate the observational error bars. |
We have also explored the effect of inclined rotation axes in EP Cru, with direct measurement of the angles λ1 = −1.8° ±1.6° and |λ2| < 17° (Albrecht et al. 2013). For the simulation, we adopted the internal structure constants derived from our models as log k2, 1 = −2.351 ± 0.015 and log k2, 2 = −2.348 ± 0.015, corrected for a significant rotation-induced internal density concentration. The corresponding histograms, representing the total predicted apsidal motion, are shown in Fig. 9 (upper panel: not aligned; bottom: aligned). The solutions based on aligned rotation axes show better agreement with the observed 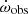 and we have adopted such aligned configuration for Table 3.
and we have adopted such aligned configuration for Table 3.
 |
Fig. 9. Monte Carlo simulations (106 realizations) for the total apsidal motion of EP Cru. In the upper panel, we assumed misalignment while in the bottom panel we simulate the case of alignment. The two vertical lines indicate the observational error bars. |
5.2. Systems with a third body
We have found that some systems with physically bound third bodies actually perform well in the comparison between the observed and predicted internal structure constants. To identify possible dynamical effects in the observed values, we refer to Fig. 4, with the comparison of observed and predicted apsidal motion rates, where systems with a potentially perturbing third body are denoted with a red symbol. The good agreement, within the uncertainties, is evident and no systematic trend is detected. In fact, slightly faster rates should have been observed, compared to those predicted without considering their companions, if an additional term to the total apsidal motion rates is noticeable (see, for instance, Martynov 1973).
For some DLEBs in the sample, the properties of the third body are quite well measured and have determinations of key parameters such as the orbital period and the mass function. This is the case of CW Cep (Wolf et al. 2006), V539 Ara (Wolf & Zejda 2005) and ζ Phe (Zasche & Wolf 2007). For these systems we calculated the additional term in the apsidal motion rate using the approximation of Martynov (1973) for coplanar orbits. The resulting corrections were found to be very small compared with the total apsidal motion rate. In the case of V539 Ara, that shows the largest contribution, it is on the order of 1.5 × 10−6 deg cycle−1, totally undetectable with errors in the observed rate of 0.6 × 10−3 deg cycle−1. Their impact thus should be negligible, as observed.
5.3. Convective core overshooting
As a result of the grid search for the best models fitting the observed properties of the component stars in our sample, we also derive their values for fov. Unfortunately, our sample is dominated by quite unevolved systems that do not provide strong constraints to the core overshooting parameter. We tried, nevertheless, to check the consistency of the results with the semi-empirical calibration obtained by Claret & Torres (2019) for much more evolved binary systems.
We show in Fig. 10 the values of fov resulting from the comparison between the theoretical models and the observed physical parameters, together with the relationship between mass and core overshooting obtained by Claret & Torres (2019). The observed correlation is quite suggestive, especially when considering that most of our systems have components well within the main sequence. We assume a conservative formal error for fov of 0.005. The most massive stars in our sample cannot be included in such a comparison because they are above the upper limit considered by Claret & Torres (2019), ≈5 M⊙.
 |
Fig. 10. Solid line: an approximate representation of the derived fov as a function of stellar mass obtained by Claret & Torres (2019) while symbols: values of fov resulting from the comparison between the theoretical models and the observed absolute dimensions performed in the present study. The error bar displayed represents the typical uncertainties for unevolved or mildly evolved stars. For the more massive stars, beyond the calibration of fov by Claret & Torres (2019), we find an average of the best values from the same methodology to be around 0.025. The only slightly evolved massive system is V453 Cyg, which is discussed in Sect. 5.3, and shows a better fit of the observed parameters with fov = 0.03. |
In order to extend the analysis of the variation of fov to higher masses, we need DLEBs with accurate dimensions like those in our sample but, unfortunately, most are quite unevolved systems. At such early evolutionary stages it becomes difficult to distinguish the impact of different amounts core overshooting both on the physical parameters and also on log k2. The only potential case may be the high-mass system V453 Cyg, whose moderately evolved stage could allow exploring the effect of convective overshooting. Our methodology to model the DLEB observables, described in Sect. 4 and applied to V453 Cyg, favored fov = 0.03, clearly above the highest value given by Claret & Torres (2019) for less massive stars. Comparing the corresponding apsidal motion rate with the observed value, fov = 0.03 is also favored with respect to adopting 0.02. This is illustrated in Fig. 11, which shows log k2 for models with different amounts of core overshooting (fov = 0.02 – dashed line; fov = 0.03 – solid line) for the most massive and evolved component of V453 Cyg. We can see that the effect of core overshooting in log k2 is only noticeable beyond the middle of the main sequence. At less evolved stages (including the PMS phase), the differences in the model predictions when changing the overshooting parameter are well below the observational errors. The differences though become easily observable as we consider evolutionary stages approaching the giant branch phase.
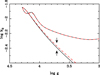 |
Fig. 11. log g − log k2 diagram for the primary of V453 Cyg and adopting Z = 0.0134. The solid line indicates a model with fov = 0.03 while the dashed one represents a model computed with fov = 0.02. The two arrows indicate the observed value of log g. The resulting difference in |
The results for V453 Cyg seem to indicate that apsidal motion can help to put constraints on the convective cover overshooting parameter using suitable DLEBs with eccentric orbits. This was already explored by Guinan et al. (2000) and revisited by Claret (2003) using the evolved high-mass system V380 Cyg. The question of a dependence of core overshooting with mass using DLEB data has been discussed previously without reaching conclusive results (Ribas et al. 2000b; Claret 2007; Tkachenko et al. 2020; Rosu et al. 2020). The tentative increase of fov with stellar mass that we find in the present work would imply a more pronounced dependence than the relationship found by Claret & Torres (2019) for stars more massive than ≈5 M⊙. In the same sense, recent theoretical studies carried out by Martinet et al. (2021) also find a need for larger convective cores at higher masses (see also Scott et al. 2021). However, the indications found are still not sufficiently well established. Further detailed analyses of suitable massive DLEBs should provide the necessary observational evidence to establish a possible overshooting-mass dependence in this interval of masses.
6. Conclusions
We have studied 34 DLEBs with eccentric orbits employing TESS data that we use to determine eclipse timings. This allowed us to determine the apsidal motion rates for 27 DLEBs with sufficient precision to compare their internal structure constants with those predicted by state-of-the-art theoretical models. The precision of the TESS eclipse timings, as well as the expanded span of time covered when compared with archival values, have allowed us to significantly improve previous apsidal motion rate determinations and detect their presence in some cases for the first time.
The sample was selected in such a way that the dominant term in the apsidal motion is the classical, or Newtonian, contribution. In Paper I we used a complementary sample to demonstrate that the relativistic term calculated using GR shows excellent agreement with the observations. Therefore, in the present paper, where we study the internal structure of stars, we subtracted out the relativistic term to the measured apsidal motion rate to ultimately estimate empirical values for the internal concentration parameters of the component stars, namely log k2. A comparison of our theoretical and observational results reveals excellent agreement.
The case of EM Car deserves further attention. In spite of a reasonable agreement between theory and observation, its high mass indicates that some additional effects could be present, including the relative proximity of the components to their Roche limit. For more detailed conclusions, additional observations and improved physical parameters are needed. EM Car could also help to eventually understand the small deviations, in the same sense, observed in our comparison for massive stars with large relative radii.
A rather unexpected result is the good agreement found for systems with an identified third body. The impact of the companion in the dynamical behavior of the close binary should have been observed as systematic differences in the observed vs. computed diagram. This is not the case, and probably indicates that the companions are less massive than the components of the close system, and/or orbit them at a large distance. For those cases with good enough observational constraints on the properties of the third bodies, the negligible contribution of the gravitational effects on the apsidal motion, assuming coplanar orbits, was confirmed.
The systems in our sample are not especially suitable, owing to their relatively unevolved nature, to provide constraints on the best value of the convective core overshooting parameter, fov. Nevertheless, the values resulting from our analysis are clearly compatible with the relation found by Claret & Torres (2019). The particular case of V453 Cyg, a high-mass system with moderately evolved components, albeit still in the main sequence, indicates a larger value of fov than that for lower-mass stars. The analysis of a larger sample of massive DLEBs will be needed to further constrain the increasing value of the overshooting parameter with mass, as suggested in the past in several works.
Acknowledgments
This paper is dedicated to the memory of J. Andersen, a very good friend and colleague, that initiated a systematic approach to the accurate measurement of masses and radii in DLEBs, and motivated us to continue his path. We thank an anonymous referee for the insightful comments and suggestions. The Spanish MEC (ESP2017-87676-C5-2-R, PID2019-107061GB-C64, and PID2019-109522GB-C52) is gratefully acknowledged for its support during the development of this work. A.C. also acknowledges financial support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award for the Instituto de Astrofísica de Andalucía (SEV-2017-0709). D.B., I.R., and J.C.M. acknowledge support from the Spanish Ministry of Science and Innovation and the European Regional Development Fund through grant PGC2018-098153-B-C33, from the Generalitat de Catalunya/CERCA programme, and from the Agància de Gestió d’Ajuts Universitaris i de Recerca of the Generalitat de Catalunya. This paper includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA Explorer Program. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Abstract Service.
References
- Albrecht, S., Reffert, S., Snellen, I., Quirrenbach, A., & Mitchell, D. S. 2007, A&A, 474, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albrecht, S., Reffert, S., Snellen, I. A. G., & Winn, J. N. 2009, Nature, 461, 373 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Albrecht, S., Setiawan, J., Torres, G., Fabrycky, D. C., & Winn, J. N. 2013, ApJ, 767, 32 [CrossRef] [Google Scholar]
- Andersen, J. 1991, A&ARv, 3, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Andersen, J., & Clausen, J. V. 1989, A&A, 213, 183 [NASA ADS] [Google Scholar]
- Andersen, J., & Vaz, L. P. R. 1984, A&A, 130, 102 [NASA ADS] [Google Scholar]
- Andersen, J., Clausen, J. V., Nordstroem, B., & Reipurth, B. 1983, A&A, 121, 271 [Google Scholar]
- Andersen, J., Clausen, J. V., Nordstrom, B., & Popper, D. M. 1985, A&A, 151, 329 [Google Scholar]
- Andersen, J., Clausen, J. V., & Nordstrom, B. 1987, A&A, 175, 60 [Google Scholar]
- Andersen, J., Clausen, J. V., Nordstrom, B., Gustafsson, B., & Vandenberg, D. A. 1988, A&A, 196, 128 [NASA ADS] [Google Scholar]
- Andersen, J., Clausen, J. V., & Giménez, A. 1993, A&A, 277, 439 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bakıs, V., Bakıs, H., Demircan, O., & Eker, Z. 2008, MNRAS, 384, 1657 [Google Scholar]
- Barembaum, M. J., & Etzel, P. B. 1995, AJ, 109, 2680 [NASA ADS] [CrossRef] [Google Scholar]
- Baroch, D., Giménez, A., Ribas, I., et al. 2021, A&A, 649, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Budding, E., Butland, R., & Blackford, M. 2015, MNRAS, 448, 3784 [Google Scholar]
- Bulut, İ. 2013, New Astron., 21, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. F., Guinan, E. F., & Marshall, J. J. 1996, IBVS, 4363, 1 [NASA ADS] [Google Scholar]
- Claret, A. 1998, A&A, 330, 533 [NASA ADS] [Google Scholar]
- Claret, A. 1999, A&A, 350, 56 [NASA ADS] [Google Scholar]
- Claret, A. 2003, A&A, 399, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2007, A&A, 475, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Giménez, A. 1993, A&A, 277, 487 [Google Scholar]
- Claret, A., & Giménez, A. 2010, A&A, 519, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Torres, G. 2016, A&A, 592, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Torres, G. 2017, ApJ, 849, 18 [Google Scholar]
- Claret, A., & Torres, G. 2019, ApJ, 876, 134 [Google Scholar]
- Claret, A., & Willems, B. 2002, A&A, 388, 518 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., Torres, G., & Wolf, M. 2010, A&A, 515, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clausen, J. V. 1996, A&A, 308, 151 [NASA ADS] [Google Scholar]
- Clausen, J. V., & Grønbech, B. 1976, A&A, 48, 49 [NASA ADS] [Google Scholar]
- Clausen, J. V., Helt, B. E., Giménez, A., et al. 2007, A&A, 461, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clausen, J. V., Vaz, L. P. R., García, J. M., et al. 2008, A&A, 487, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clausen, J. V., Bruntt, H., Olsen, E. H., Helt, B. E., & Claret, A. 2010, A&A, 511, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, H. L. 1971, PASP, 83, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Company, R., Portilla, M., & Giménez, A. 1988, ApJ, 335, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Csizmadia, S., Illés-Almár, E., & Borkovits, T. 2009, New Astron., 14, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Dariush, A., Riazi, N., & Afroozeh, A. 2005, Ap&SS, 296, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Değirmenci, Ö. L. 1997, Ap&SS, 253, 237 [Google Scholar]
- Fekel, F. C., Henry, G. W., & Sowell, J. R. 2013, AJ, 146, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Ludwig, H. G., & Steffen, M. 1996, A&A, 313, 497 [NASA ADS] [Google Scholar]
- Garcia, E. V., Stassun, K. G., Hebb, L., Gómez Maqueo Chew, Y., & Heiser, A. 2011, AJ, 142, 27 [CrossRef] [Google Scholar]
- Garcia, E. V., Stassun, K. G., Pavlovski, K., et al. 2014, AJ, 148, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez, A. 1985, ApJ, 297, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez, A., & Bastero, M. 1995, Ap&SS, 226, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez, A., & Margrave, T. 1982, AJ, 87, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez, A., & Margrave, T. E. 1985, AJ, 90, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez, A., Clausen, J. V., & Jensen, K. S. 1986, A&A, 159, 157 [NASA ADS] [Google Scholar]
- Guinan, E. F., & Maloney, F. P. 1985, AJ, 90, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Guinan, E. F., Ribas, I., Fitzpatrick, E. L., et al. 2000, ApJ, 544, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, D. S., Gertken, R. H., & Burke, E. W. 1970, PASP, 82, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Harmanec, P., Holmgren, D. E., Wolf, M., et al. 2014, A&A, 563, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harmanec, P., Brož, M., Mayer, P., et al. 2018, A&A, 609, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hełminiak, K. G., Konacki, M., Ratajczak, M., & Muterspaugh, M. W. 2009, MNRAS, 400, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Bloecker, T., Schoenberner, D., & El Eid, M. 1997, A&A, 324, L81 [NASA ADS] [Google Scholar]
- Hill, G., & Ebbighausen, E. G. 1984, AJ, 89, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Holmgren, D., Hill, G., & Scarfe, C. D. 1995, The Observatory, 115, 188 [Google Scholar]
- Hrivnak, B. J., & Milone, E. F. 1984, ApJ, 282, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Ibanoglu, C. 1974, A&A, 35, 483 [NASA ADS] [Google Scholar]
- Jermyn, A. S., Tout, C. A., & Chitre, S. M. 2018, MNRAS, 480, 5427 [NASA ADS] [CrossRef] [Google Scholar]
- Joergensen, H. E., & Gronbech, B. 1978, A&A, 66, 377 [NASA ADS] [Google Scholar]
- Johnston, C., Pavlovski, K., & Tkachenko, A. 2019, A&A, 628, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kazarovets, E. V., Samus, N. N., Durlevich, O. V., Kireeva, N. N., & Pastukhova, E. N. 2006, Inf. Bull. Variable Stars, 5721, 1 [NASA ADS] [Google Scholar]
- Khaliullin, K. F. 1983, Astronomicheskij Tsirkulyar, 1270, 1 [NASA ADS] [Google Scholar]
- Kim, C. H., Kreiner, J. M., Zakrzewski, B., et al. 2018, ApJS, 235, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkby-Kent, J. A., Maxted, P. F. L., Serenelli, A. M., et al. 2016, A&A, 591, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kozyreva, V. S., & Zakharov, A. I. 2001, Astron. Lett., 27, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Kwee, K. K., & van Woerden, H. 1956, Bull. Astron. Inst. Neth., 12, 327 [NASA ADS] [Google Scholar]
- Lacy, C. H. S. 1997, AJ, 113, 2226 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, C. H., & Frueh, M. L. 1985, ApJ, 295, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, C. H. S., Torres, G., Claret, A., & Sabby, J. A. 2003, AJ, 126, 1905 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, C. H. S., Claret, A., & Sabby, J. A. 2004, AJ, 128, 1340 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, C. H. S., Torres, G., Claret, A., & Vaz, L. P. R. 2005, AJ, 130, 2838 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, C. H. S., Torres, G., Fekel, F. C., Sabby, J. A., & Claret, A. 2012, AJ, 143, 129 [CrossRef] [Google Scholar]
- Lacy, C. H. S., Torres, G., Fekel, F. C., Muterspaugh, M. W., & Southworth, J. 2015, AJ, 149, 34 [CrossRef] [Google Scholar]
- Lee, J. W., Hong, K., & Kristiansen, M. H. 2020, PASJ, 72, 37 [CrossRef] [Google Scholar]
- Lee, J. W., Hong, K., & Kim, H.-Y. 2021, AJ, 161, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Lester, K. V., Gies, D. R., Schaefer, G. H., et al. 2019, AJ, 158, 218 [CrossRef] [Google Scholar]
- Levi-Civita, T. 1937, Am. J. Math., 59, 225 [Google Scholar]
- Martinet, S., Meynet, G., Ekström, S., et al. 2021, A&A, 648, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martynov, D. Y. 1973, Sov. Phys. Usp., 15, 786 [CrossRef] [Google Scholar]
- Maxted, P. F. L., Gaulme, P., Graczyk, D., et al. 2020, MNRAS, 498, 332 [CrossRef] [Google Scholar]
- Mayer, P. 2004, Inf. Bull. Variable Stars, 5498, 1 [NASA ADS] [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60, 22 [Google Scholar]
- Mossakovskaya, L. V., & Khaliullin, K. F. 1996, Astron. Lett., 22, 132 [NASA ADS] [Google Scholar]
- Pavlovski, K., Southworth, J., & Tamajo, E. 2018, MNRAS, 481, 3129 [NASA ADS] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popper, D. M. 1987, ApJ, 313, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Popper, D. M., & Guinan, E. F. 1998, PASP, 110, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Jordi, C., Torra, J., & Giménez, Á. 2000a, MNRAS, 313, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Jordi, C., & Giménez, Á. 2000b, MNRAS, 318, L55 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telescopes Instrum. Syst., 1 [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [Google Scholar]
- Rosu, S., Noels, A., Dupret, M. A., et al. 2020, A&A, 642, A221 [EDP Sciences] [Google Scholar]
- Schmitt, J. H. M. M., Schröder, K. P., Rauw, G., et al. 2016, A&A, 586, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scott, L. J. A., Hirschi, R., Georgy, C., et al. 2021, MNRAS, 503, 4208 [CrossRef] [Google Scholar]
- Sezer, C., Gudur, N., Gulmen, O., & Sengonca, H. 1983, A&AS, 53, 363 [NASA ADS] [Google Scholar]
- Shakura, N. I. 1985, Sov. Astron. Lett., 11, 224 [NASA ADS] [Google Scholar]
- Southworth, J. 2015, in Living Together: Planets, Host Stars and Binaries, eds. S. M. Rucinski, G. Torres, & M. Zejda, ASP Conf. Ser., 496, 164 [Google Scholar]
- Southworth, J. 2020a, The Observatory, 140, 247 [Google Scholar]
- Southworth, J. 2020b, ArXiv e-prints [arXiv:2012.05978] [Google Scholar]
- Southworth, J., Maxted, P. F. L., & Smalley, B. 2004, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Bowman, D. M., Tkachenko, A., & Pavlovski, K. 2020, MNRAS, 497, L19 [Google Scholar]
- Švaříček, P., Wolf, M., Claret, A., et al. 2008, A&A, 477, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tkachenko, A., Pavlovski, K., Johnston, C., et al. 2020, A&A, 637, A60 [CrossRef] [EDP Sciences] [Google Scholar]
- Tomkin, J. 1983, ApJ, 271, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Lacy, C. H. S., Claret, A., et al. 1999, AJ, 118, 1831 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Torres, G., Clausen, J. V., Bruntt, H., et al. 2012, A&A, 537, A117 [EDP Sciences] [Google Scholar]
- Torres, G., Sandberg Lacy, C. H., Pavlovski, K., et al. 2014, ApJ, 797, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Claret, A., Pavlovski, K., & Dotter, A. 2015, ApJ, 807, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Vaz, L. P. R., & Andersen, J. 1984, A&A, 132, 219 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wachmann, A. A. 1973, A&A, 25, 157 [NASA ADS] [Google Scholar]
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, M. 2000, A&A, 356, 134 [NASA ADS] [Google Scholar]
- Wolf, M., & Zejda, M. 2005, A&A, 437, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, M., Sarounova, L., Kozyreva, V. S., & Pogrocheva, T. 1997, Inf. Bull. Variable Stars, 4542, 1 [NASA ADS] [Google Scholar]
- Wolf, M., Diethelm, R., & Zejda, M. 2005, Ap&SS, 296, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, M., Kučáková, H., Kolasa, M., et al. 2006, A&A, 456, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, M., Claret, A., Kotková, L., et al. 2010, A&A, 509, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zasche, P., & Wolf, M. 2007, Astron. Nachr., 328, 928 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Apsidal motion studies
-
EM Car Andersen & Clausen (1989) made a complete study of EM Car obtaining an eccentricity e = 0.0120 ± 0.0005 and an apsidal motion rate
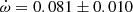 deg/cycle. This value has a relatively large error bar because of the unfavorable configuration with ω ≈ 0 deg, which affects the use of a linear fit to the differential timings. The light curve solution by Andersen & Clausen (1989) yields an argument of periastron of ω = 350 ± 5 deg, and the TESS measurements give a phase for the secondary eclipse of 0.50484 ± 0.00010 which corresponds, adopting also e = 0.0120 ± 0.0005, to a value of ω = 308 ± 2 deg. We used the TESS light curve to exclude the other possible value with positive esinω. By using the two ω determinations at different epochs we obtain an apsidal motion rate
deg/cycle. This value has a relatively large error bar because of the unfavorable configuration with ω ≈ 0 deg, which affects the use of a linear fit to the differential timings. The light curve solution by Andersen & Clausen (1989) yields an argument of periastron of ω = 350 ± 5 deg, and the TESS measurements give a phase for the secondary eclipse of 0.50484 ± 0.00010 which corresponds, adopting also e = 0.0120 ± 0.0005, to a value of ω = 308 ± 2 deg. We used the TESS light curve to exclude the other possible value with positive esinω. By using the two ω determinations at different epochs we obtain an apsidal motion rate 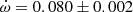 deg/cycle, considering all uncertainties. This value is in excellent agreement, but significantly more precise, than that given by Andersen & Clausen (1989) thanks to the large time-span increase, which is now covering nearly a complete apsidal motion period. Furthermore, Mayer (2004) measured T2 − T1 = 1.683 ± 0.003 days at HJD 2452280, between the two light curve solutions. This is in excellent agreement with the predicted value from our apsidal motion solution T2 − T1 = 1.6828 ± 0.0005 days.
deg/cycle, considering all uncertainties. This value is in excellent agreement, but significantly more precise, than that given by Andersen & Clausen (1989) thanks to the large time-span increase, which is now covering nearly a complete apsidal motion period. Furthermore, Mayer (2004) measured T2 − T1 = 1.683 ± 0.003 days at HJD 2452280, between the two light curve solutions. This is in excellent agreement with the predicted value from our apsidal motion solution T2 − T1 = 1.6828 ± 0.0005 days. -
Y Cyg The physical parameters of Y Cyg were given in the comprehensive study of Harmanec et al. (2014), who analyzed light curve changes with time, using a variable ω, and obtained an orbital eccentricity e = 0.1451 ± 0.0003 together with a precise apsidal motion rate of
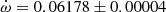 deg/cycle. The authors also studied the changing position of the times of eclipse, obtaining a less precise e = 0.1448 ± 0.0012, using old photographic timings. An earlier study with the same methodology but restricted to the best photoelectric measurements was carried out by Holmgren et al. (1995), determining e = 0.1458 ± 0.0007. Our TESS data, given in Table 2, indicate a clear apsidal motion variation in the observed T2 − T1, with a slope of −0.000138 ± 0.000009 d/cycle and a value of T2 − T1 = 1.74357 ± 0.00003 days at BJD 2458718.9981. The apsidal motion rate cannot be accurately determined using these data alone due to the very narrow time interval, but a value of
deg/cycle. The authors also studied the changing position of the times of eclipse, obtaining a less precise e = 0.1448 ± 0.0012, using old photographic timings. An earlier study with the same methodology but restricted to the best photoelectric measurements was carried out by Holmgren et al. (1995), determining e = 0.1458 ± 0.0007. Our TESS data, given in Table 2, indicate a clear apsidal motion variation in the observed T2 − T1, with a slope of −0.000138 ± 0.000009 d/cycle and a value of T2 − T1 = 1.74357 ± 0.00003 days at BJD 2458718.9981. The apsidal motion rate cannot be accurately determined using these data alone due to the very narrow time interval, but a value of 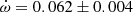 , with ω = 27.8 ± 0.3 deg, is obtained assuming 0.1451 for the eccentricity. Nevertheless, it confirms the solution by (Harmanec et al. 2014), based on the global analysis of all photometric data with variable longitude of the periastron, that we adopt for our discussion.
, with ω = 27.8 ± 0.3 deg, is obtained assuming 0.1451 for the eccentricity. Nevertheless, it confirms the solution by (Harmanec et al. 2014), based on the global analysis of all photometric data with variable longitude of the periastron, that we adopt for our discussion. -
V478 Cyg The absolute dimensions of V478 Cyg were recently measured by Pavlovski et al. (2018) using their own radial velocity curves and a new analysis of the light curve of Sezer et al. (1983). Unfortunately the light curve could not establish a precise value of the orbital eccentricity and e = 0.021 ± 0.005, as derived from the radial velocity curve, was fixed for the analysis. The analysis of the TESS light curve using the Wilson-Devinney code (Wilson & Devinney 1971) resulted in a best fit with e = 0.016. This is in agreement with the apsidal motion variation produced by the eclipse timings presented by Wolf et al. (2006) yielding e = 0.0158 ± 0.0007 and
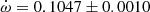 deg/cycle. TESS measurements give an average T2 − T1 value of 1.4120 ± 0.0005 days, in excellent agreement with the expected value, T2 − T1 = 1.4122 ± 0.0005 days, using the solution by Wolf et al. (2006). The comparison of our TESS data with the T2 − T1 extracted from Table 1 of Wolf et al. (2006), with timings within less than 10 orbital cycles, confirms the apsidal motion rate determination by Wolf et al. (2006). However, using the larger and less precise values of the eccentricity e = 0.019 ± 0.002 by Mossakovskaya & Khaliullin (1996) or e = 0.021 ± 0.005 by Pavlovski et al. (2018) produces much poorer fits to the data and predictions that are in contradiction with the TESS light curve. We therefore adopted the solution given by Wolf et al. (2006) for Table 3.
deg/cycle. TESS measurements give an average T2 − T1 value of 1.4120 ± 0.0005 days, in excellent agreement with the expected value, T2 − T1 = 1.4122 ± 0.0005 days, using the solution by Wolf et al. (2006). The comparison of our TESS data with the T2 − T1 extracted from Table 1 of Wolf et al. (2006), with timings within less than 10 orbital cycles, confirms the apsidal motion rate determination by Wolf et al. (2006). However, using the larger and less precise values of the eccentricity e = 0.019 ± 0.002 by Mossakovskaya & Khaliullin (1996) or e = 0.021 ± 0.005 by Pavlovski et al. (2018) produces much poorer fits to the data and predictions that are in contradiction with the TESS light curve. We therefore adopted the solution given by Wolf et al. (2006) for Table 3. -
V578 Mon The most recent and complete determination of the physical parameters of V578 Mon was carried out by Garcia et al. (2014) adopting an earlier apsidal motion determination (Garcia et al. 2011) of
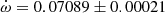 deg/cycle with e = 0.07755 ± 0.00026. Their global analysis of the light curve variations with
deg/cycle with e = 0.07755 ± 0.00026. Their global analysis of the light curve variations with 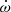 as a free parameter over one complete apsidal motion period allowed such precise results. The TESS measurements of the T2 − T1 differences, obtained in two epochs, yield a less precise determination
as a free parameter over one complete apsidal motion period allowed such precise results. The TESS measurements of the T2 − T1 differences, obtained in two epochs, yield a less precise determination 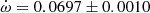 deg/cycle, assuming the eccentricity of Garcia et al. (2011). The individual light curve solutions in table 3 by Garcia et al. (2011) give an apsidal motion rate
deg/cycle, assuming the eccentricity of Garcia et al. (2011). The individual light curve solutions in table 3 by Garcia et al. (2011) give an apsidal motion rate 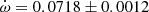 deg/cycle, and including the arguments of periastron derived from the TESS T2 − T1 values, yield a rate of
deg/cycle, and including the arguments of periastron derived from the TESS T2 − T1 values, yield a rate of 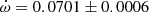 deg/cycle. All values agree within their uncertainties and we adopted for our discussion
deg/cycle. All values agree within their uncertainties and we adopted for our discussion 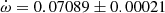 deg/cycle, as derived from the light curve analysis with variable omega.
deg/cycle, as derived from the light curve analysis with variable omega. -
V453 Cyg A detailed analysis of the TESS light curve of V453 Cyg has been recently carried out by Southworth et al. (2020) in their quest to use β Cep pulsations as a tracer of the physical processes that govern the evolution of massive stars. The authors determined the orbital eccentricity to be e = 0.0250 ± 0.0014 with the argument of periastron at ω = 152.5 ± 5.1 deg, but did not analyze the apsidal motion variations. This was done in an earlier paper (Southworth et al. 2004) with less precise data, providing an apsidal motion rate
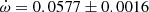 deg/cycle, with an orbital eccentricity e = 0.022 ± 0.003. Nevertheless, this solution predicts an argument of periastron at the time of the TESS observations that is not compatible with the TESS light curve analyzed by Southworth et al. (2020). We have used the TESS measurements in Table 2, giving an average eclipse timing difference T2 − T1 = 1.8896 ± 0.00015 days, and the timings by Wachmann (1973) and Cohen (1971), using only photoelectric measurements separated by less than 10 orbital cycles. We computed the corresponding arguments of periastron, assuming e = 0.0250 ± 0.0014, and a linear fit yielded
deg/cycle, with an orbital eccentricity e = 0.022 ± 0.003. Nevertheless, this solution predicts an argument of periastron at the time of the TESS observations that is not compatible with the TESS light curve analyzed by Southworth et al. (2020). We have used the TESS measurements in Table 2, giving an average eclipse timing difference T2 − T1 = 1.8896 ± 0.00015 days, and the timings by Wachmann (1973) and Cohen (1971), using only photoelectric measurements separated by less than 10 orbital cycles. We computed the corresponding arguments of periastron, assuming e = 0.0250 ± 0.0014, and a linear fit yielded 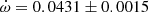 deg/cycle, considering the uncertainty of the eccentricity.
deg/cycle, considering the uncertainty of the eccentricity. -
CW Cep The light curve of this eclipsing binary system has been recently studied by Lee et al. (2021) using TESS measurements. An eccentricity e = 0.0305 ± 0.0009, with an argument of periastron ω = 212.7 ± 3.2 deg were obtained from the analysis. The authors do not discuss the apsidal motion rate, well known from previous studies, but focus on the analysis of the detected β Cep pulsations and confirm the presence of a significant third light. The physical parameters of the components are well determined using the radial velocity amplitudes measured by Johnston et al. (2019). The apsidal motion of CW Cep was studied most recently by Wolf et al. (2006), who clearly observed the effect of the third body through the light-time effect, with a period of P3 = 38.5 ± 1.5 years. After correction for the third-body effect in the eclipse timings, the authors could determine an orbital eccentricity e = 0.0297 ± 0.0005 and an apsidal motion rate
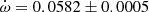 deg/cycle. With the TESS measurements of T2 − T1 in different sectors, apsidal motion is already evident and we determine a slope of (2.8 ± 0.2)×10−5 days/cycle over a time span of 70 orbital cycles. We have added the T2 − T1 values retrieved from the literature to compute the corresponding argument of periastron with the orbital eccentricity given by Lee et al. (2021). We have restricted eclipse timings to those obtained by means of photoelectric measurements and considered pairs within less than 10 orbital cycles. A weighted linear fit yields
deg/cycle. With the TESS measurements of T2 − T1 in different sectors, apsidal motion is already evident and we determine a slope of (2.8 ± 0.2)×10−5 days/cycle over a time span of 70 orbital cycles. We have added the T2 − T1 values retrieved from the literature to compute the corresponding argument of periastron with the orbital eccentricity given by Lee et al. (2021). We have restricted eclipse timings to those obtained by means of photoelectric measurements and considered pairs within less than 10 orbital cycles. A weighted linear fit yields 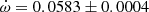 deg/cycle, in excellent agreement with previous determinations.
deg/cycle, in excellent agreement with previous determinations. -
QX Car Precise absolute dimensions of QX Car were obtained by Andersen et al. (1983). The authors also studied apsidal motion, fixing the eccentricity to the result of the light curve analysis, e = 0.278 ± 0.003, and obtained
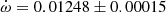 deg/cycle. A revised analysis by Giménez et al. (1986), with the same adopted eccentricity, yielded
deg/cycle. A revised analysis by Giménez et al. (1986), with the same adopted eccentricity, yielded 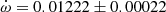 deg/cycle considering more realistic uncertainties. TESS measurements give an average value of T2 − T1 = 1.4853 ± 0.0002 days. Adopting the eccentricity by Andersen et al. (1983), this time difference yields an argument of periastron of ω = 163.1 ± 2.5 deg. The apsidal solution by Giménez et al. (1986) predicts a more precise value of ω = 164.6 ± 0.8 deg at the time of the TESS observations, in good agreement with the value obtained from the T2 − T1 measurements, and we have adopted it for our discussion.
deg/cycle considering more realistic uncertainties. TESS measurements give an average value of T2 − T1 = 1.4853 ± 0.0002 days. Adopting the eccentricity by Andersen et al. (1983), this time difference yields an argument of periastron of ω = 163.1 ± 2.5 deg. The apsidal solution by Giménez et al. (1986) predicts a more precise value of ω = 164.6 ± 0.8 deg at the time of the TESS observations, in good agreement with the value obtained from the T2 − T1 measurements, and we have adopted it for our discussion. -
V539 Ara Accurate physical parameters of this system were obtained by Clausen (1996), who also detected apsidal motion with
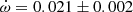 deg/cycle but showing significant variations between different epochs that suggested the presence of a perturbing third body. No third light was reported. The light curve provided a value e = 0.053 ± 0.001. The analysis by Wolf et al. (2005) confirmed the presence of a third body by means of the light-time effect, with a period P3 = 42.3 ± 0.8 years. An apsidal motion rate
deg/cycle but showing significant variations between different epochs that suggested the presence of a perturbing third body. No third light was reported. The light curve provided a value e = 0.053 ± 0.001. The analysis by Wolf et al. (2005) confirmed the presence of a third body by means of the light-time effect, with a period P3 = 42.3 ± 0.8 years. An apsidal motion rate 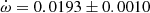 deg/cycle was obtained together with an orbital eccentricity e = 0.0548 ± 0.0015. TESS data provide a value T2 − T1 = 1.4873 ± 0.0005 days and, adopting the eccentricity given by Clausen (1996), the argument of periastron comes out to be ω = 204.9 ± 2.2 deg. When relating it with the result of the light curve analysis in Clausen (1996), ω = 125.1 ± 1.0 deg, an apsidal motion rate
deg/cycle was obtained together with an orbital eccentricity e = 0.0548 ± 0.0015. TESS data provide a value T2 − T1 = 1.4873 ± 0.0005 days and, adopting the eccentricity given by Clausen (1996), the argument of periastron comes out to be ω = 204.9 ± 2.2 deg. When relating it with the result of the light curve analysis in Clausen (1996), ω = 125.1 ± 1.0 deg, an apsidal motion rate 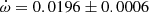 deg/cycle can be derived, in agreement with all previous results.
deg/cycle can be derived, in agreement with all previous results. -
DI Her This system has historically played a key role as a paradigmatic case for relativistic apsidal motion tests. Early apsidal motion rate measurements showed a conspicuous and disturbing disagreement with theoretical predictions. This was resolved by the work of Albrecht et al. (2009), who found a large misalignment of the spin axes of the component stars from measuring the Rossiter-McLaughlin effect. The most recent apsidal motion determination for DI Her, by Claret et al. (2010), yielded a value
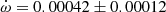 deg/cycle, in good agreement with the predicted value when the observed rotational axes misalignment is considered. Precise values of T2 − T1 can be retrieved from the TESS measurements, as given in Table 2. Using values from the literature, and restricting to photoelectric measurements only, the increase of the observed separation in T2 − T1 gives a slope of (9.3 ± 0.5)×10−6 days/cycle using a weighted least-squares minimization. Assuming an orbital eccentricity e = 0.489 ± 0.003, as given by Torres et al. (2010), the observed apsidal motion rate of DI Her is found to be
deg/cycle, in good agreement with the predicted value when the observed rotational axes misalignment is considered. Precise values of T2 − T1 can be retrieved from the TESS measurements, as given in Table 2. Using values from the literature, and restricting to photoelectric measurements only, the increase of the observed separation in T2 − T1 gives a slope of (9.3 ± 0.5)×10−6 days/cycle using a weighted least-squares minimization. Assuming an orbital eccentricity e = 0.489 ± 0.003, as given by Torres et al. (2010), the observed apsidal motion rate of DI Her is found to be 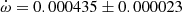 deg/cycle, in good agreement but significantly more precise than previous studies.
deg/cycle, in good agreement but significantly more precise than previous studies. -
EP Cru A first light curve of this eclipsing binary was obtained by Clausen et al. (2007), while Albrecht et al. (2013) determined precise physical parameters with the aim of studying circularization and synchronization timescales as well as a possible misalignment of the rotational axes. With improved absolute dimensions, Albrecht et al. (2013) could predict the presence of apsidal motion but could not measure it. They also pointed out the rotational velocities of the component stars, much larger than their synchronized values. We have used the precise value T2 − T1 = 6.8140 ± 0.0002 days given by Clausen et al. (2007) and compared it with the values obtained from the TESS measurements. A weighted mean of the time differences in Table 2 yields T2 − T1 = 6.8255 ± 0.0005 some 1000 orbital cycles later. This is an increase rate of (1.16 ± 0.05)×10−5 days/cycle. Assuming the orbital eccentricity given by Albrecht et al. (2013), e = 0.1874 ± 0.0005, we obtain
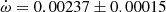 deg/cycle, which becomes the first detection of apsidal motion in EP Cru.
deg/cycle, which becomes the first detection of apsidal motion in EP Cru. -
V760 Sco This system was studied by Andersen et al. (1985), who obtained precise physical parameters and measured an apsidal motion
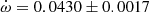 deg/cycle with an orbital eccentricity e = 0.0265 ± 0.0010. Wolf (2000) re-discussed the apsidal motion parameters with new eclipse timings and obtained
deg/cycle with an orbital eccentricity e = 0.0265 ± 0.0010. Wolf (2000) re-discussed the apsidal motion parameters with new eclipse timings and obtained 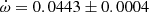 deg/cycle, with e = 0.0270 ± 0.0005. Nevertheless, the new observations were not sufficiently precise for an improved determination of the eccentricity. From the TESS measurements, we obtain a value T2 − T1 = 0.8925 ± 0.0005 days, which is in good agreement with the predicted value by the solution of Andersen et al. (1985) of T2 − T1 = 0.8919 ± 0.0025 days, but not with the value predicted from Wolf (2000) of T2 − T1 = 0.8946 ± 0.0004 days. Considering all the possible T2 − T1 values retrieved from Andersen et al. (1985), computed with individual timings within less than 10 orbital cycles, and adopting their value of the eccentricity, we obtain the corresponding arguments of periastron at different epochs. We adopted for the argument of periastron corresponding to the TESS value of T2 − T1, a negative value of esinω. This conclusion was achieved by fitting the light curve fixing the binary parameters to those reported in Andersen et al. (1985). A weighted linear least-squares fit yields an apsidal motion rate of
deg/cycle, with e = 0.0270 ± 0.0005. Nevertheless, the new observations were not sufficiently precise for an improved determination of the eccentricity. From the TESS measurements, we obtain a value T2 − T1 = 0.8925 ± 0.0005 days, which is in good agreement with the predicted value by the solution of Andersen et al. (1985) of T2 − T1 = 0.8919 ± 0.0025 days, but not with the value predicted from Wolf (2000) of T2 − T1 = 0.8946 ± 0.0004 days. Considering all the possible T2 − T1 values retrieved from Andersen et al. (1985), computed with individual timings within less than 10 orbital cycles, and adopting their value of the eccentricity, we obtain the corresponding arguments of periastron at different epochs. We adopted for the argument of periastron corresponding to the TESS value of T2 − T1, a negative value of esinω. This conclusion was achieved by fitting the light curve fixing the binary parameters to those reported in Andersen et al. (1985). A weighted linear least-squares fit yields an apsidal motion rate of 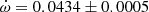 deg/cycle, which includes the uncertainty in the orbital eccentricity.
deg/cycle, which includes the uncertainty in the orbital eccentricity. -
MU Cas A complete photometric and spectroscopic study of MU Cas was carried out by Lacy et al. (2004). The system shows a well-defined orbital eccentricity of e = 0.1930 ± 0.0003, and the phase of the secondary eclipse is observed at 0.61914 ± 0.00015. The argument of periastron obtained from the light curve analysis is ω = 13.4 ± 0.4 deg, but the small time span of eclipses available did not allow the authors to claim the detection of apsidal motion. Moreover, the argument of periastron close to 0 deg, which makes it difficult to observe changes in timing differences, and, also, apsidal motion is expected to be very slow given the observed relative radii. The measurements of T2 − T1 from TESS give a phase of the secondary eclipse of 0.61881 ± 0.00003, yielding an poorly-significant determination of the apsidal motion rate
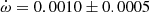 deg/cycle. To obtain this value we adopted the orbital eccentricity from Lacy et al. (2004). The alternative method, that is, using the measured times of eclipse in Table 1 of Lacy et al. (2005) to calculate T2 − T1 differences, provides
deg/cycle. To obtain this value we adopted the orbital eccentricity from Lacy et al. (2004). The alternative method, that is, using the measured times of eclipse in Table 1 of Lacy et al. (2005) to calculate T2 − T1 differences, provides 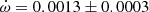 deg/cycle. The alternative method of comparing the argument of periastron in table 4 of Lacy et al. (2004) and that derived from TESS phase of the secondary eclipse (ω = 14.00 ± 0.05 deg) yields
deg/cycle. The alternative method of comparing the argument of periastron in table 4 of Lacy et al. (2004) and that derived from TESS phase of the secondary eclipse (ω = 14.00 ± 0.05 deg) yields  deg/cycle. The low statistical significance of the measurement, although consistent using different techniques, does not allow the use of MU Cas to test internal stellar structure. We derive a log k2 value with a large uncertainty of 0.14 when using the observed apsidal motion rate and after subtracting the relativistic contribution.
deg/cycle. The low statistical significance of the measurement, although consistent using different techniques, does not allow the use of MU Cas to test internal stellar structure. We derive a log k2 value with a large uncertainty of 0.14 when using the observed apsidal motion rate and after subtracting the relativistic contribution. -
GG Lup This system was studied by Andersen et al. (1993), who obtained precise absolute dimensions as well as a good determination of the apsidal motion rate of
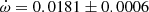 deg/cycles and an orbital eccentricity e = 0.150 ± 0.005. Wolf et al. (2005) revisited the apsidal motion determination and obtained results in good agreement with those of Andersen et al. (1993), with an orbital eccentricity e = 0.1545 ± 0.0010. The most recent study by Budding et al. (2015) confirmed the latter value of the eccentricity with an apsidal motion rate
deg/cycles and an orbital eccentricity e = 0.150 ± 0.005. Wolf et al. (2005) revisited the apsidal motion determination and obtained results in good agreement with those of Andersen et al. (1993), with an orbital eccentricity e = 0.1545 ± 0.0010. The most recent study by Budding et al. (2015) confirmed the latter value of the eccentricity with an apsidal motion rate 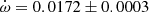 deg/cycle. TESS observations show the expected slow increase of the eclipse timing differences over the short time span covered, and yield an average value T2 − T1 = 0.7561 ± 0.0002 days. This is not compatible with predictions using the eccentricity by Andersen et al. (1993). We have computed the argument of periastron corresponding to the T2 − T1 values available from individual timings separated by less than 10 orbital cycles and adopting an orbital eccentricity e = 0.155 ± 0.005, as indicated by Wolf et al. (2005). A linear least-squares fit of the variation of ω with time yields
deg/cycle. TESS observations show the expected slow increase of the eclipse timing differences over the short time span covered, and yield an average value T2 − T1 = 0.7561 ± 0.0002 days. This is not compatible with predictions using the eccentricity by Andersen et al. (1993). We have computed the argument of periastron corresponding to the T2 − T1 values available from individual timings separated by less than 10 orbital cycles and adopting an orbital eccentricity e = 0.155 ± 0.005, as indicated by Wolf et al. (2005). A linear least-squares fit of the variation of ω with time yields 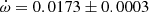 deg/cycle, in excellent agreement with the study by Budding et al. (2015).
deg/cycle, in excellent agreement with the study by Budding et al. (2015). -
ζ Phe This bright eclipsing binary system has been the subject of a recent study using TESS data by Southworth (2020a). The early photometric analyses by Clausen & Grønbech (1976) already showed a significant third light contribution and the spectroscopic analysis by Andersen et al. (1983) allowed accurate absolute parameters to be determined. Apsidal motion was reported by Giménez et al. (1986) using the individual eclipse timings available and obtained
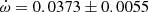 deg/cycle with an eccentricity e = 0.0113 given by the photometric light curve analysis but not taking into account light-time effects. Zasche & Wolf (2007) combined astrometric measurements with light-time modeling to study the orbit of the third body and derived an apsidal motion rate of
deg/cycle with an eccentricity e = 0.0113 given by the photometric light curve analysis but not taking into account light-time effects. Zasche & Wolf (2007) combined astrometric measurements with light-time modeling to study the orbit of the third body and derived an apsidal motion rate of 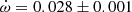 deg/cycle with an eccentricity of e = 0.0107 ± 0.0020 for the close orbit as well as a period of P3 = 221 years and an eccentricity of e = 0.366 for the wide orbit of the outer third companion. The light curve analysis of Southworth (2020a) provides precise absolute dimensions for ζ Phe, and confirms the presence of third light. The orbital eccentricity was found to be e = 0.0116 ± 0.0024, in excellent agreement with previous studies. The argument of periastron is ω = 307 ± 12 deg. The comparison of this value with the light curve of Clausen & Grønbech (1976), almost 10 000 cycles before, indicates an apsidal motion rate of
deg/cycle with an eccentricity of e = 0.0107 ± 0.0020 for the close orbit as well as a period of P3 = 221 years and an eccentricity of e = 0.366 for the wide orbit of the outer third companion. The light curve analysis of Southworth (2020a) provides precise absolute dimensions for ζ Phe, and confirms the presence of third light. The orbital eccentricity was found to be e = 0.0116 ± 0.0024, in excellent agreement with previous studies. The argument of periastron is ω = 307 ± 12 deg. The comparison of this value with the light curve of Clausen & Grønbech (1976), almost 10 000 cycles before, indicates an apsidal motion rate of 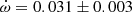 deg/cycle. Using the argument of periastron computed from the T2 − T1 values retrieved from Clausen & Grønbech (1976), and those from all the TESS observations, using e = 0.0116 ± 0.0024, we derive
deg/cycle. Using the argument of periastron computed from the T2 − T1 values retrieved from Clausen & Grønbech (1976), and those from all the TESS observations, using e = 0.0116 ± 0.0024, we derive 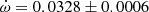 deg/cycle, which is in agreement with but more precise than all the other results.
deg/cycle, which is in agreement with but more precise than all the other results. -
IQ Per This eccentric binary was studied by Lacy & Frueh (1985), who provided absolute dimensions after the preliminary values by Hall et al. (1970) and derived an apsidal motion rate of
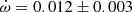 deg/cycle for an orbital eccentricity e = 0.075 ± 0.006, derived from the radial velocity curve. The apsidal motion rate was revised by Değirmenci (1997) to
deg/cycle for an orbital eccentricity e = 0.075 ± 0.006, derived from the radial velocity curve. The apsidal motion rate was revised by Değirmenci (1997) to 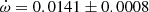 deg/cycle, using an eccentricity e = 0.076 ± 0.004, and by Wolf et al. (2006), obtaining
deg/cycle, using an eccentricity e = 0.076 ± 0.004, and by Wolf et al. (2006), obtaining 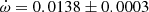 deg/cycle, using e = 0.0763 ± 0.0008. TESS measurements yield a separation between primary and secondary eclipses of T2 − T1 = 0.79827 ± 0.00011 days that does not agree with the previously mentioned apsidal motion solutions. Using the most recent determination, by Wolf et al. (2006), the argument of periastron would be ω = 178 ± 2 deg at the TESS epoch and the predicted time separation is T2 − T1 = 0.78755 ± 0.00007 days, a significant difference of 0.01072 ± 0.00012 days. To solve this, we performed a fit of the high-precision TESS light curve and obtained e = 0.0662 ± 0.0005 and ω = 182 ± 3 deg, with the physical parameters being in agreement with those found by Lacy & Frueh (1985). Precise measurements of the time of the secondary eclipse are difficult to obtain and only a few are available in the literature. Adopting the eccentricity derived from the TESS light curve analysis, we calculated the argument of periastron corresponding to the observed values of T2 − T1 in the literature, restricting to photoelectric data and with primaries and secondaries within 10 orbital cycles. A linear fit yielded an apsidal motion rate
deg/cycle, using e = 0.0763 ± 0.0008. TESS measurements yield a separation between primary and secondary eclipses of T2 − T1 = 0.79827 ± 0.00011 days that does not agree with the previously mentioned apsidal motion solutions. Using the most recent determination, by Wolf et al. (2006), the argument of periastron would be ω = 178 ± 2 deg at the TESS epoch and the predicted time separation is T2 − T1 = 0.78755 ± 0.00007 days, a significant difference of 0.01072 ± 0.00012 days. To solve this, we performed a fit of the high-precision TESS light curve and obtained e = 0.0662 ± 0.0005 and ω = 182 ± 3 deg, with the physical parameters being in agreement with those found by Lacy & Frueh (1985). Precise measurements of the time of the secondary eclipse are difficult to obtain and only a few are available in the literature. Adopting the eccentricity derived from the TESS light curve analysis, we calculated the argument of periastron corresponding to the observed values of T2 − T1 in the literature, restricting to photoelectric data and with primaries and secondaries within 10 orbital cycles. A linear fit yielded an apsidal motion rate 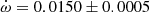 deg/cycle, which we adopted for Table 3.
deg/cycle, which we adopted for Table 3. -
PV Cas Precise absolute dimensions of PV Cas are based on the studies by Popper (1987) and Barembaum & Etzel (1995). An apsidal motion
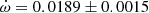 deg/cycle was measured by Giménez & Margrave (1982) assuming an eccentricity value e = 0.0322 ± 0.0005. The most recent subsequent study by Švaříček et al. (2008) gives an apsidal motion rate
deg/cycle was measured by Giménez & Margrave (1982) assuming an eccentricity value e = 0.0322 ± 0.0005. The most recent subsequent study by Švaříček et al. (2008) gives an apsidal motion rate 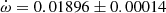 deg/cycle with an orbital eccentricity e = 0.03248 ± 0.00014. The TESS timing data alone indicate the presence of apsidal motion by comparing the measurements of T2 − T1 in the two available sectors, separated by 110 orbital cycles. Adopting an eccentricity e = 0.032, the observed variation yields
deg/cycle with an orbital eccentricity e = 0.03248 ± 0.00014. The TESS timing data alone indicate the presence of apsidal motion by comparing the measurements of T2 − T1 in the two available sectors, separated by 110 orbital cycles. Adopting an eccentricity e = 0.032, the observed variation yields 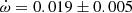 deg/cycle but with poor precision. The more precise apsidal motion solution by Švaříček et al. (2008) predicts an argument of periastron of ω = 21.7 ± 0.6 deg at the time of the TESS observations, equivalent to an eclipse separation T2 − T1 = 0.9090 ± 0.0004 days, which differs from the TESS measurements by 0.0036 ± 0.0005 days. This disagreement prompted us to reanalyze the apsidal motion determination on the basis of the observed T2 − T1 values using all photoelectric data available in the literature, with individual timings separated by no more than 10 orbital cycles. Adopting an orbital eccentricity of e = 0.0325 ± 0.0005 as given by Švaříček et al. (2008) but with a larger, more realistic, uncertainty, the corresponding argument of periastron is calculated for each value of T2 − T1. The value of ω for TESS, close to 360 deg, was checked with an analysis of the full light curve. A linear fit yielded
deg/cycle but with poor precision. The more precise apsidal motion solution by Švaříček et al. (2008) predicts an argument of periastron of ω = 21.7 ± 0.6 deg at the time of the TESS observations, equivalent to an eclipse separation T2 − T1 = 0.9090 ± 0.0004 days, which differs from the TESS measurements by 0.0036 ± 0.0005 days. This disagreement prompted us to reanalyze the apsidal motion determination on the basis of the observed T2 − T1 values using all photoelectric data available in the literature, with individual timings separated by no more than 10 orbital cycles. Adopting an orbital eccentricity of e = 0.0325 ± 0.0005 as given by Švaříček et al. (2008) but with a larger, more realistic, uncertainty, the corresponding argument of periastron is calculated for each value of T2 − T1. The value of ω for TESS, close to 360 deg, was checked with an analysis of the full light curve. A linear fit yielded 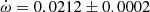 deg/cycle, which we adopt for Table 3. Concerning the argument of periastron at the time of the observations by Ibanoglu (1974), we did not include the value of ω = 180 ± 8 deg from their light curve analysis due to the uncertain determination of esinω. Nevertheless, our solution predicts a value in excellent agreement of ω = 175.8 ± 1.64 deg.
deg/cycle, which we adopt for Table 3. Concerning the argument of periastron at the time of the observations by Ibanoglu (1974), we did not include the value of ω = 180 ± 8 deg from their light curve analysis due to the uncertain determination of esinω. Nevertheless, our solution predicts a value in excellent agreement of ω = 175.8 ± 1.64 deg. -
V364 Lac A detailed spectroscopic and photometric study of this A-type eclipsing binary was performed by Torres et al. (1999). The authors could detect the presence of apsidal motion in V364 Lac at a rate of
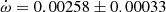 deg/cycle from the combined study of the radial velocity curve and eclipse timings, with an orbital eccentricity e = 0.2873 ± 0.0014. More recently, Bulut (2013) adopted the same value of the eccentricity and obtained
deg/cycle from the combined study of the radial velocity curve and eclipse timings, with an orbital eccentricity e = 0.2873 ± 0.0014. More recently, Bulut (2013) adopted the same value of the eccentricity and obtained 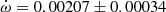 deg/cycle. The TESS data indicate a position of the secondary eclipse with respect to the primary of T2 − T1 = 3.73870 ± 0.00005 days, which yields an argument of periastron ω = 87.43 ± 0.02 deg when adopting the eccentricity of Torres et al. (1999). Comparing with the value in table 3 of Torres et al. (1999), an apsidal motion rate
deg/cycle. The TESS data indicate a position of the secondary eclipse with respect to the primary of T2 − T1 = 3.73870 ± 0.00005 days, which yields an argument of periastron ω = 87.43 ± 0.02 deg when adopting the eccentricity of Torres et al. (1999). Comparing with the value in table 3 of Torres et al. (1999), an apsidal motion rate 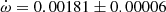 deg/cycle is derived, where the uncertainty in the eccentricity is considered.
deg/cycle is derived, where the uncertainty in the eccentricity is considered. -
SW CMa Lacy (1997) first determined the absolute dimensions of this relatively evolved DLEB and indicated the possible presence of apsidal motion. Clausen et al. (2008) obtained a better-covered light curve and measured a rate
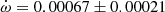 deg/cycle. Finally, Torres et al. (2012) reanalyzed the light curve of Clausen et al. (2008), together with newly obtained radial velocities, and obtained precise physical parameters. SW CMa was observed by TESS in two sectors separated by 60 orbital cycles. The variation in T2 − T1 over this time interval is too small to allow determining a apsidal motion rate value. The average timing difference is T2 − T1 = 3.1141 ± 0.0002 days. The apsidal motion parameters of Clausen et al. (2008) predict an argument of periastron ω = 164.32 ± 0.30 deg while, adopting the eccentricity from the same authors with an uncertainty ±0.0005, the TESS T2 − T1 yields ω = 164.34 ± 0.30 deg. The excellent agreement shows that the apsidal motion rate given by Clausen et al. (2008) is accurate. However, the uncertainty could be reduced thanks to the wider time span. A comparison of the argument of periastron derived from the TESS measurements with the light curve analyses by Lacy (1997) and Clausen et al. (2008) does not allow to improve the determination due to the very slow apsidal motion rate and the proximity of ω to 180 deg. We analyzed the light curve obtained by TESS and obtained a best-fitting e = 0.3180 ± 0.0005. A fit using the observed values of T2 − T1 with TESS, together with those provided by Clausen et al. (2008), yields an apsidal motion rate
deg/cycle. Finally, Torres et al. (2012) reanalyzed the light curve of Clausen et al. (2008), together with newly obtained radial velocities, and obtained precise physical parameters. SW CMa was observed by TESS in two sectors separated by 60 orbital cycles. The variation in T2 − T1 over this time interval is too small to allow determining a apsidal motion rate value. The average timing difference is T2 − T1 = 3.1141 ± 0.0002 days. The apsidal motion parameters of Clausen et al. (2008) predict an argument of periastron ω = 164.32 ± 0.30 deg while, adopting the eccentricity from the same authors with an uncertainty ±0.0005, the TESS T2 − T1 yields ω = 164.34 ± 0.30 deg. The excellent agreement shows that the apsidal motion rate given by Clausen et al. (2008) is accurate. However, the uncertainty could be reduced thanks to the wider time span. A comparison of the argument of periastron derived from the TESS measurements with the light curve analyses by Lacy (1997) and Clausen et al. (2008) does not allow to improve the determination due to the very slow apsidal motion rate and the proximity of ω to 180 deg. We analyzed the light curve obtained by TESS and obtained a best-fitting e = 0.3180 ± 0.0005. A fit using the observed values of T2 − T1 with TESS, together with those provided by Clausen et al. (2008), yields an apsidal motion rate 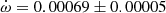 deg/cycle considering all the uncertainties involved, which improves on the precision of the previous determination.
deg/cycle considering all the uncertainties involved, which improves on the precision of the previous determination. -
PT Vel Bakıs et al. (2008) studied this system and derived the physical properties of their components as well as the apsidal motion rate. Together with the orbital eccentricity of e = 0.127 ± 0.006, the authors obtained
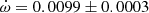 deg/cycle. Nevertheless, these results are based on the light curves obtained by the ground-based All-Sky Automated Survey (ASAS) over a decade, with poor coverage of the secondary eclipse. We have analyzed the TESS light curve and obtained a much better fit with a lower eccentricity e = 0.112 ± 0.003, but with the same relative radii and orbital inclination, thus with no change in the physical parameters. Adopting the eccentricity derived from the TESS light curve, the T2 − T1 measurements already show the presence of apsidal motion. To increase the time span, we have compared the average eclipse time difference of the TESS measurements, T2 − T1 = 1.00687 ± 0.00012 days, with the values obtained from the ASAS survey given by Kim et al. (2018). A linear fit to the corresponding values of ω yields an apsidal motion rate of
deg/cycle. Nevertheless, these results are based on the light curves obtained by the ground-based All-Sky Automated Survey (ASAS) over a decade, with poor coverage of the secondary eclipse. We have analyzed the TESS light curve and obtained a much better fit with a lower eccentricity e = 0.112 ± 0.003, but with the same relative radii and orbital inclination, thus with no change in the physical parameters. Adopting the eccentricity derived from the TESS light curve, the T2 − T1 measurements already show the presence of apsidal motion. To increase the time span, we have compared the average eclipse time difference of the TESS measurements, T2 − T1 = 1.00687 ± 0.00012 days, with the values obtained from the ASAS survey given by Kim et al. (2018). A linear fit to the corresponding values of ω yields an apsidal motion rate of 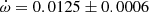 deg/cycle. The significant difference of the eccentricity, determined from the TESS light curve or the ASAS analysis, that we could not reproduce, remains unexplained.
deg/cycle. The significant difference of the eccentricity, determined from the TESS light curve or the ASAS analysis, that we could not reproduce, remains unexplained. -
V1647 Sgr The absolute dimensions of V1647 Sgr were obtained by Andersen et al. (1985), who could also measure an apsidal motion rate of
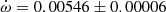 deg/cycle with an orbital eccentricity e = 0.4130 ± 0.0005. The authors also confirmed that the visual companion of V1647 Sgr is physically bound. Wolf (2000) re-analyzed the apsidal motion and obtained a rate
deg/cycle with an orbital eccentricity e = 0.4130 ± 0.0005. The authors also confirmed that the visual companion of V1647 Sgr is physically bound. Wolf (2000) re-analyzed the apsidal motion and obtained a rate 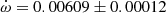 deg/cycle with an eccentricity e = 0.4142 ± 0.0011. The TESS data provide an average position of the secondary eclipse with respect to the primary of T2 − T1 = 1.0880 ± 0.0003 days. The argument of periastron calculated for the TESS measurements and those obtained from the individual timings in table 4 of Andersen et al. (1985) show a well-defined variation of ω. A linear fit yields an apsidal motion rate of
deg/cycle with an eccentricity e = 0.4142 ± 0.0011. The TESS data provide an average position of the secondary eclipse with respect to the primary of T2 − T1 = 1.0880 ± 0.0003 days. The argument of periastron calculated for the TESS measurements and those obtained from the individual timings in table 4 of Andersen et al. (1985) show a well-defined variation of ω. A linear fit yields an apsidal motion rate of 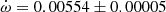 deg/cycle, considering the value and uncertainty in e from Andersen et al. (1985).
deg/cycle, considering the value and uncertainty in e from Andersen et al. (1985). -
AI Hya First absolute dimensions for this system were published by Popper & Guinan (1998) on the basis of their own radial velocity curve and the well-covered light curve by Joergensen & Gronbech (1978). An orbital eccentricity e = 0.230 ± 0.002 was derived from the light curve, and the existence of pulsations in the secondary component was reported but no apsidal motion. AI Hya has recently been studied by Lee et al. (2020), who analyzed the light curve observed by TESS to characterize the δ Scuti-type pulsations. The authors also analyzed the displacement of the argument of periastron and derived a low-significance apsidal motion rate using individual times of minimum of
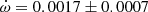 deg/cycle with an orbital eccentricity e = 0.241 ± 0.083. The more precise value derived from their own light curve analysis, e = 0.234 ± 0.002, was not used. We have computed the T2 − T1 values corresponding to individual eclipse timings within less than 10 orbital cycles from table 1 of Lee et al. (2020), including the TESS measurements in our Table 2, and determined the argument of periastron for each of them, adopting e = 0.234 ± 0.002. A linear fit yields
deg/cycle with an orbital eccentricity e = 0.241 ± 0.083. The more precise value derived from their own light curve analysis, e = 0.234 ± 0.002, was not used. We have computed the T2 − T1 values corresponding to individual eclipse timings within less than 10 orbital cycles from table 1 of Lee et al. (2020), including the TESS measurements in our Table 2, and determined the argument of periastron for each of them, adopting e = 0.234 ± 0.002. A linear fit yields 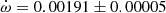 deg/cycle.
deg/cycle. -
VV Pyx This system has kept the name of VV Pyx in spite of its re-naming as V596 Pup in the 78th name-list of variable stars (Kazarovets et al. 2006). A detailed photometric and spectroscopic study of the system by Andersen & Vaz (1984) yielded precise absolute dimensions and an apsidal motion rate
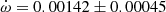 deg/cycle was obtained with the orbital eccentricity derived from the light curve analysis, e = 0.0956 ± 0.0009. A significant contribution from third light was measured and attributed to the close visual companion of the eclipsing binary but no effect in the measured apsidal motion was measured. TESS data alone indicate a small variation of the T2 − T1 values with time, corresponding to an apsidal motion rate of
deg/cycle was obtained with the orbital eccentricity derived from the light curve analysis, e = 0.0956 ± 0.0009. A significant contribution from third light was measured and attributed to the close visual companion of the eclipsing binary but no effect in the measured apsidal motion was measured. TESS data alone indicate a small variation of the T2 − T1 values with time, corresponding to an apsidal motion rate of 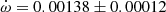 deg/cycle. Using also the two additional T2 − T1 values derived from table 5 in Andersen & Vaz (1984), we obtained a final rate
deg/cycle. Using also the two additional T2 − T1 values derived from table 5 in Andersen & Vaz (1984), we obtained a final rate 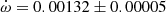 deg/cycle, using e = 0.0956 ± 0.0009.
deg/cycle, using e = 0.0956 ± 0.0009. -
EK Cep Popper (1987) was the first to identify the pre-main sequence nature of the secondary component in EK Cep. Radial velocities were measured by Tomkin (1983) and the light curve was analyzed by Hill & Ebbighausen (1984). An orbital eccentricity e = 0.109 ± 0.003 is derived from the radial velocity curve and adopted for the photometric studies. Giménez & Margrave (1985) obtained an apsidal motion rate
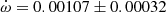 deg/cycle using eclipse timings. TESS measurements provide a value T2 − T1 = 2.3988 ± 0.0002 days, and we have used all available values of T2 − T1 from the literature with precision better than 0.001 days, which are challenging because of the shallow secondary eclipse. With these values, we obtained a slope of ( − 3.61 ± 0.08)×10−6 days/cycle, from which an apsidal motion rate of
deg/cycle using eclipse timings. TESS measurements provide a value T2 − T1 = 2.3988 ± 0.0002 days, and we have used all available values of T2 − T1 from the literature with precision better than 0.001 days, which are challenging because of the shallow secondary eclipse. With these values, we obtained a slope of ( − 3.61 ± 0.08)×10−6 days/cycle, from which an apsidal motion rate of 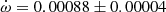 deg/cycle is derived, adopting e = 0.109 ± 0.003.
deg/cycle is derived, adopting e = 0.109 ± 0.003. -
VV Crv Fekel et al. (2013) studied this bright system combining spectroscopic and photometric observations, and obtained the physical parameters given in Table 1. Conspicuous third light was observed, which complicated the light curve analysis. Moreover, the long duration and shallow depth of the eclipses make their timing difficult, and no apsidal motion had been reported. From the TESS measurements we obtain an average eclipse difference T2 − T1 = 1.559 ± 0.004 days. The corresponding argument of periastron, adopting an eccentricity e = 0.0852 ± 0.0010 given by Fekel et al. (2013), is ω = 265.5 ± 1.5 deg with its uncertainty dominated by that of the eclipse timings. Given the observed dispersion in the values of T2 − T1, we performed an analysis of the TESS light curve with the same orbital eccentricity, and obtained an argument of periastron ω = 266.5 ± 0.5 deg, in agreement with the previous value but more precise. The argument of periastron given by Fekel et al. (2013) in their table 7, from the light and velocity curve combined analysis, is ω = 257.7 ± 0.2 deg, thus indicating for the first time the presence of apsidal motion in VV Crv. The change in omega, from the light curve fits, after 807 orbital cycles, gives an apsidal motion rate
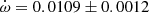 deg/cycle. This result should be nevertheless considered preliminary due to the observed dispersion in the eclipse timings, and difficulties with the photometric analysis, due to the presence of third light.
deg/cycle. This result should be nevertheless considered preliminary due to the observed dispersion in the eclipse timings, and difficulties with the photometric analysis, due to the presence of third light. -
IM Per Absolute properties of IM Per were obtained by Lacy et al. (2015) and revised recently by Lee et al. (2020) using the TESS light curve. A simultaneous radial velocity and timing analysis carried out by Lacy et al. (2015) gave an apsidal motion rate of
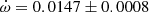 deg/cycle, while a value
deg/cycle, while a value 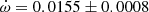 deg/cycle was obtained by the same authors from fitting the light curve with variable ω. In both cases, the orbital eccentricity was fixed to e = 0.047 ± 0.003. The TESS light curve solution by Lee et al. (2020) gives a compatible but slightly larger value at e = 0.0491 ± 0.0010. Using all the T2 − T1 measurements available from table 1 of Lacy et al. (2015) plus the value from TESS T2 − T1 = 1.09484 ± 0.00014 days, we calculated the corresponding argument of periastron adopting this eccentricity. A linear fit to the variation of ω with time then yields
deg/cycle was obtained by the same authors from fitting the light curve with variable ω. In both cases, the orbital eccentricity was fixed to e = 0.047 ± 0.003. The TESS light curve solution by Lee et al. (2020) gives a compatible but slightly larger value at e = 0.0491 ± 0.0010. Using all the T2 − T1 measurements available from table 1 of Lacy et al. (2015) plus the value from TESS T2 − T1 = 1.09484 ± 0.00014 days, we calculated the corresponding argument of periastron adopting this eccentricity. A linear fit to the variation of ω with time then yields 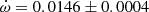 deg/cycle. Considering only the timings used by Lacy et al. (2015), a rate of 0.0149 ± 0.0005 deg/cycle is obtained.
deg/cycle. Considering only the timings used by Lacy et al. (2015), a rate of 0.0149 ± 0.0005 deg/cycle is obtained. -
BP Vul Lacy et al. (2003) obtained precise absolute dimensions for BP Vul, an eccentricity e = 0.0355 ± 0.0027, and the secondary eclipse at phase 0.47968 ± 0.00021. The authors also analyzed the apsidal motion rate but was found to be negative and the potential presence of a perturbing third body was argued to explain this anomaly, but the timespan covered was too narrow for a conclusion. Csizmadia et al. (2009) revised the situation with the analysis of an earlier, unpublished, light curve showing a positive apsidal motion with a rate of 1 deg/year but with only one new secondary eclipse timing. Moreover, their analysis of individual timings requires a light-time effect that is not quantified. On the other hand, TESS measurements give a phase for the secondary eclipse of 0.47989 ± 0.00010 days. Given that this value is not significantly different from the light curve by Lacy et al. (2003) no claim of apsidal motion detection can be made at this time.
-
V1022 Cas A recent analysis of this eclipsing system by Southworth (2020b), using TESS data, provides precise physical parameters in good agreement with those published by Lester et al. (2019) on the basis of a combined astrometric and spectroscopic study. The lack of precise eclipse timings and the small time separation with respect to the TESS measurements makes the detection of apsidal motion very difficult. We have used the spectroscopic solution of Lester et al. (2019), e and ω, in their table 4 to obtain the position of the secondary eclipse at phase 0.66565 ± 0.00009. Comparing this value with the TESS measurements from the light curve solution by Southworth (2020b), 452 orbital cycles later, gives a phase displacement of −0.00026 ± 0.00011, equivalent to an apsidal motion rate
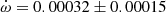 deg/cycle. When subtracting the relativistic term, the classical term comes out to be
deg/cycle. When subtracting the relativistic term, the classical term comes out to be 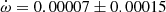 deg/cycle, which cannot be used in the present paper.
deg/cycle, which cannot be used in the present paper. -
PV Pup Despite the presence of intrinsic variability of unknown origin, the light curve obtained by Vaz & Andersen (1984) provides well-defined photometric elements, and their combination with radial velocity measurements yield precise physical properties of the component stars. The orbital eccentricity was found to be e = 0.0503 ± 0.0011 but no apsidal motion was reported. PV Pup belongs to the stellar system ADS 6348 but is most probably an optical pair. TESS measurements of the separation between primary and secondary eclipses present a large dispersion, higher than the individual errors, probably due to the observed intrinsic variability. The average values of T2 − T1 for two sectors, separated by 445 orbital cycles, allowed us to calculate the corresponding argument of periastron with the eccentricity given by Vaz & Andersen (1984), and thus estimate an apsidal motion rate of
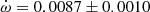 deg/cycle. Given the noise in the eclipse timings, also noticed by Vaz & Andersen (1984), we tried to analyze the light curve of TESS with e = 0.0503. A significant fraction of third light was observed and the intrinsic variability did not allow to achieve a reasonable fit. Leaving only ω as a free parameter, the best fit indicated, when compared with the value of the light curve analysis by Vaz & Andersen (1984), an apsidal motion rate of
deg/cycle. Given the noise in the eclipse timings, also noticed by Vaz & Andersen (1984), we tried to analyze the light curve of TESS with e = 0.0503. A significant fraction of third light was observed and the intrinsic variability did not allow to achieve a reasonable fit. Leaving only ω as a free parameter, the best fit indicated, when compared with the value of the light curve analysis by Vaz & Andersen (1984), an apsidal motion rate of 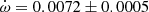 deg/cycle. Therefore, the preliminary result with only the TESS timings cannot be confirmed and we call for further monitoring of PV Pup before establishing its apsidal motion rate.
deg/cycle. Therefore, the preliminary result with only the TESS timings cannot be confirmed and we call for further monitoring of PV Pup before establishing its apsidal motion rate. -
BF Dra Apsidal motion was determined by Wolf et al. (2010) to be
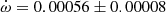 deg/cycle but leaving free the eccentricity to converge to e = 0.3898 despite the poor coverage of the apsidal motion variations. Masses and radii for the components of BF Dra were obtained by Lacy et al. (2012), who also analyzed the apsidal motion by fitting the individual eclipse timings and obtained
deg/cycle but leaving free the eccentricity to converge to e = 0.3898 despite the poor coverage of the apsidal motion variations. Masses and radii for the components of BF Dra were obtained by Lacy et al. (2012), who also analyzed the apsidal motion by fitting the individual eclipse timings and obtained 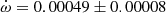 deg/cycle with an eccentricity e = 0.3865 ± 0.0005. BF Dra was observed in 12 TESS sectors, spanning a total of 352 days, and the large number of precise values of T2 − T1 allowed us to determine its apsidal motion rate independently of any previous measurement. A linear fit to the TESS values of T2 − T1 in Table 2 yields a slope of the variation of ( − 2.19 ± 0.14)×10−6 days/cycle. Adopting the eccentricity obtained by Lacy et al. (2012), this gives an apsidal motion of
deg/cycle with an eccentricity e = 0.3865 ± 0.0005. BF Dra was observed in 12 TESS sectors, spanning a total of 352 days, and the large number of precise values of T2 − T1 allowed us to determine its apsidal motion rate independently of any previous measurement. A linear fit to the TESS values of T2 − T1 in Table 2 yields a slope of the variation of ( − 2.19 ± 0.14)×10−6 days/cycle. Adopting the eccentricity obtained by Lacy et al. (2012), this gives an apsidal motion of 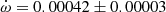 deg/cycle. Because of the difference with previous results, we calculated separately the linear periods for primary and secondary eclipses and obtained a difference ΔP = ( − 2.26 ± 0.04)×10−5 days/cycle, but with systematics present in the residuals of both primary and secondary TESS timings. We interpret these as potentially due to the light travel-time effect induced by a third body orbiting the system. Lacy et al. (2012) did indeed identify the presence of third light in the light curve of BF Dra. The effect of a third body, however, should not hamper the apsidal motion determination using the T2 − T1 values. From the archival times of minimum we could retrieve five precise T2 − T1 measurements, considering only individual eclipse timings within 10 orbital cycles. When adding these to the TESS T2 − T1 measurements the slope becomes ( − 2.35 ± 0.05)×10−5 days/cycle and
deg/cycle. Because of the difference with previous results, we calculated separately the linear periods for primary and secondary eclipses and obtained a difference ΔP = ( − 2.26 ± 0.04)×10−5 days/cycle, but with systematics present in the residuals of both primary and secondary TESS timings. We interpret these as potentially due to the light travel-time effect induced by a third body orbiting the system. Lacy et al. (2012) did indeed identify the presence of third light in the light curve of BF Dra. The effect of a third body, however, should not hamper the apsidal motion determination using the T2 − T1 values. From the archival times of minimum we could retrieve five precise T2 − T1 measurements, considering only individual eclipse timings within 10 orbital cycles. When adding these to the TESS T2 − T1 measurements the slope becomes ( − 2.35 ± 0.05)×10−5 days/cycle and 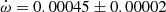 deg/cycle, compatible with the values resulting from the TESS measurements alone and from Lacy et al. (2012). We detected some remaining systematic residuals in the TESS observations that remain unexplained. An alternative determination method is the use of the value of ω from the light curve analysis, rather than the times of eclipse. Comparing the argument of periastron given by Lacy et al. (2012) in their table 7 with that computed from the average TESS T2 − T1 measurements, 430 orbital cycles later, a small but significant increase in ω of 0.16 ± 0.03 deg is observed. This yields an apsidal motion rate of
deg/cycle, compatible with the values resulting from the TESS measurements alone and from Lacy et al. (2012). We detected some remaining systematic residuals in the TESS observations that remain unexplained. An alternative determination method is the use of the value of ω from the light curve analysis, rather than the times of eclipse. Comparing the argument of periastron given by Lacy et al. (2012) in their table 7 with that computed from the average TESS T2 − T1 measurements, 430 orbital cycles later, a small but significant increase in ω of 0.16 ± 0.03 deg is observed. This yields an apsidal motion rate of 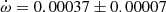 deg/cycle, which is in marginal agreement with the value described before. More observations are needed to obtain a definitive apsidal motion rate as well as analyzing the impact of the third body. In any case, the large fractional relativistic term (68%) of BF Dra implies a classical term with an uncertainty of ∼30% thus rendering this system unsuitable for the comparison with theoretical stellar models.
deg/cycle, which is in marginal agreement with the value described before. More observations are needed to obtain a definitive apsidal motion rate as well as analyzing the impact of the third body. In any case, the large fractional relativistic term (68%) of BF Dra implies a classical term with an uncertainty of ∼30% thus rendering this system unsuitable for the comparison with theoretical stellar models. -
V1143 Cyg Andersen et al. (1987) obtained absolute dimensions for V1143 Cyg, which were more recently revised by Lester et al. (2019) with new observations. Apsidal motion has been studied by Khaliullin (1983), Giménez & Margrave (1985), Burns et al. (1996), Dariush et al. (2005) and, finally, by Wolf et al. (2010). The latter authors gave
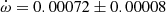 deg/cycle with an eccentricity e = 0.535 ± 0.004. A fit to the TESS timing data alone yields a faster rate at
deg/cycle with an eccentricity e = 0.535 ± 0.004. A fit to the TESS timing data alone yields a faster rate at 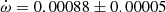 deg/cycle. A wider time span can be obtained by using the individual timings from Wolf et al. (2010), with their original errors when available or otherwise adopting an uncertainty of ±0.005 days, that we judged realistic. The residuals of the fit to all timing differences show a significantly larger dispersion than the uncertainties of the archival measurements, suggesting an underestimation of the errors. However, we assumed that they are globally unbiased and obtained a slope of the T2 − T1 variation of (2.4 ± 0.1)×10−5 days/cycle. Adopting the orbital eccentricity given by Lester et al. (2019), e = 0.5386 ± 0.0004, we obtain an apsidal motion for V1143 Cyg of
deg/cycle. A wider time span can be obtained by using the individual timings from Wolf et al. (2010), with their original errors when available or otherwise adopting an uncertainty of ±0.005 days, that we judged realistic. The residuals of the fit to all timing differences show a significantly larger dispersion than the uncertainties of the archival measurements, suggesting an underestimation of the errors. However, we assumed that they are globally unbiased and obtained a slope of the T2 − T1 variation of (2.4 ± 0.1)×10−5 days/cycle. Adopting the orbital eccentricity given by Lester et al. (2019), e = 0.5386 ± 0.0004, we obtain an apsidal motion for V1143 Cyg of 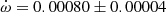 deg/cycle.
deg/cycle. -
IT Cas Precise physical properties of the components of IT Cas were obtained by Lacy (1997). From their light and radial velocity curves the authors obtained an orbital eccentricity e = 0.085 ± 0.004 and a longitude of periastron of ω = 332.6 ± 1.4 deg, but apsidal motion could not be determined due to the short time span covered with photoelectric measurements. Moreover, the same authors obtained different values of the eccentricity from the radial velocity, the light curve and the ephemeris solution. Kozyreva & Zakharov (2001) used their own measurements together with those by Lacy (1997) to obtain e = 0.089 ± 0.002 with an apsidal motion rate
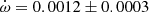 deg/cycle, comparing the values of ω from the different light curve solutions. TESS timings confirm the values of Kozyreva & Zakharov (2001). We have combined the TESS eclipse timing differences with those derived from the most precise individual timings listed in table 1 of Kozyreva & Zakharov (2001), only photoelectric and within 10 orbital cycles. The fit provides a slope of (2.01 ± 0.05)×10−6 days/cycle. Adopting e = 0.089 ± 0.002, yields an apsidal motion rate
deg/cycle, comparing the values of ω from the different light curve solutions. TESS timings confirm the values of Kozyreva & Zakharov (2001). We have combined the TESS eclipse timing differences with those derived from the most precise individual timings listed in table 1 of Kozyreva & Zakharov (2001), only photoelectric and within 10 orbital cycles. The fit provides a slope of (2.01 ± 0.05)×10−6 days/cycle. Adopting e = 0.089 ± 0.002, yields an apsidal motion rate 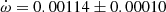 deg/cycle.
deg/cycle. -
AI Phe The light curve obtained by Hrivnak & Milone (1984) was analyzed by Andersen et al. (1988) together with their own radial velocity curve. Maxted et al. (2020) analyzed the light curve provided by TESS and improved the physical parameters using the radial velocity measurements by Hełminiak et al. (2009). TESS measurements indicate a precise position of the secondary eclipse at phase 0.457865 ± 0.000005 and an argument of periastron ω = 110.34 ± 0.11 deg. Unfortunately, accurate eclipse timings are difficult to obtain due to the long orbital period and the duration of the eclipses. Kirkby-Kent et al. (2016) showed significant variations in the sidereal period, probably due to the presence of a third body, and determined the phase of the secondary eclipse at 0.4584 ± 0.0015, which does not differ significantly from the TESS measurement. On the other hand, the light curve solution by Andersen et al. (1988) gives a value of ω = 109.6 ± 1.0 deg, which is again very similar to the value from the TESS light curve. More eclipse timings are certainly needed, as well as a complete dynamical study to evaluate the impact of the potential third body in the measurement of apsidal motion.
-
EW Ori This DLEB was analyzed by Clausen et al. (2010), who obtained the physical parameters of its components and estimated an apsidal motion rate
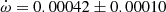 deg/cycle with an orbital eccentricity e = 0.0758 ± 0.0020 derived from the light curve. We obtained precise T2 − T1 values from the TESS light curve. In addition, we retrieved four T2 − T1 values from the literature (Wolf et al. 1997; Clausen et al. 2010) from the evaluation of the secondary phase displacement and using only precise individual timings separated by less than 10 orbital cycles. A linear fit to the T2 − T1 variation with time yields a slope of (1.48 ± 0.11)×10−6 days/cycle. Taking the orbital eccentricity given by Clausen et al. (2010) produces an apsidal motion rate of
deg/cycle with an orbital eccentricity e = 0.0758 ± 0.0020 derived from the light curve. We obtained precise T2 − T1 values from the TESS light curve. In addition, we retrieved four T2 − T1 values from the literature (Wolf et al. 1997; Clausen et al. 2010) from the evaluation of the secondary phase displacement and using only precise individual timings separated by less than 10 orbital cycles. A linear fit to the T2 − T1 variation with time yields a slope of (1.48 ± 0.11)×10−6 days/cycle. Taking the orbital eccentricity given by Clausen et al. (2010) produces an apsidal motion rate of 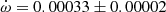 deg/cycle. Unfortunately, this system cannot be used to compare with stellar structure models. EW Orís highly relativistic periastron precession is dominant (79%) and the determination of the classical term carries an uncertainty that is above our threshold. However, this system could be added to our sample in paper I. Following the methodology there, we determine
deg/cycle. Unfortunately, this system cannot be used to compare with stellar structure models. EW Orís highly relativistic periastron precession is dominant (79%) and the determination of the classical term carries an uncertainty that is above our threshold. However, this system could be added to our sample in paper I. Following the methodology there, we determine 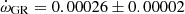 deg/cycle after subtracting the classical term calculated from the models, as described in section 4. It can be shown that the measured relativistic rate is in very good agreement with the other systems plotted in figures 10 and 11 of paper I. A recalculation of the corresponding post-Newtonian parameters, now including EW Ori, yields A = 1.000 ± 0.011 and B = 0.000 ± 0.051.
deg/cycle after subtracting the classical term calculated from the models, as described in section 4. It can be shown that the measured relativistic rate is in very good agreement with the other systems plotted in figures 10 and 11 of paper I. A recalculation of the corresponding post-Newtonian parameters, now including EW Ori, yields A = 1.000 ± 0.011 and B = 0.000 ± 0.051. -
V530 Ori A complete analysis of this G+M system was carried out by Torres et al. (2014), who provided the physical parameters of its components. The shallow total secondary eclipse makes it difficult to study variations in phase. Torres et al. (2014) determined the orbital eccentricity to be e = 0.0862 ± 0.0010 with ω = 130.08 ± 0.14 deg. Apsidal motion was detected by the authors but could not be determined with sufficient significance. From their table 1, only two precise T2 − T1 values could be retrieved with individual timings within 10 orbital cycles. Using those with the new TESS data, we determine an apsidal motion rate
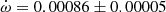 deg/cycle, with the orbital eccentricity of e = 0.0862 ± 0.0010. Nevertheless, additional observations are needed to confirm the apsidal motion rate, given the short span of time available and the difficulty to obtain precise timings.
deg/cycle, with the orbital eccentricity of e = 0.0862 ± 0.0010. Nevertheless, additional observations are needed to confirm the apsidal motion rate, given the short span of time available and the difficulty to obtain precise timings.
All Tables
All Figures
 |
Fig. 1. HR diagram for AI Phe. The models were calculated adopting Z = 0.011. The solid line indicates the primary component while the dashed one represents the secondary. |
| In the text | |
 |
Fig. 2. log g and respective error bars as a function of time for AI Phe. The two vertical lines indicate the time interval corresponding to the individual ages for each component. The horizontal lines represent the error bars in log g. Line coding as in Fig. 1. |
| In the text | |
 |
Fig. 3. Monte Carlo simulations (106 realizations) for the theoretical apsidal motion of AI Phe. |
| In the text | |
 |
Fig. 4. Comparison between |
| In the text | |
 |
Fig. 5. Top panel: a comparison between the theoretical predictions and the observed values of the apsidal motion constant log k2 for all systems in Table 3. Bottom panel: the same comparison but without plotting the low mass binary V530 Ori, which has a rather extreme value, so that the bulk of the sample can be better visualized. |
| In the text | |
 |
Fig. 6. Differences between |
| In the text | |
 |
Fig. 7. Monte Carlo simulations (106 realizations) for the apsidal motion of DI Her. The two vertical lines indicate the observational error bars. |
| In the text | |
 |
Fig. 8. Monte Carlo simulations (106 realizations) for the total apsidal motion of V1143 Cyg. In the upper panel, we assumed misaligment while in the bottom panel we simulate the case of alignment. The two vertical lines indicate the observational error bars. |
| In the text | |
 |
Fig. 9. Monte Carlo simulations (106 realizations) for the total apsidal motion of EP Cru. In the upper panel, we assumed misalignment while in the bottom panel we simulate the case of alignment. The two vertical lines indicate the observational error bars. |
| In the text | |
 |
Fig. 10. Solid line: an approximate representation of the derived fov as a function of stellar mass obtained by Claret & Torres (2019) while symbols: values of fov resulting from the comparison between the theoretical models and the observed absolute dimensions performed in the present study. The error bar displayed represents the typical uncertainties for unevolved or mildly evolved stars. For the more massive stars, beyond the calibration of fov by Claret & Torres (2019), we find an average of the best values from the same methodology to be around 0.025. The only slightly evolved massive system is V453 Cyg, which is discussed in Sect. 5.3, and shows a better fit of the observed parameters with fov = 0.03. |
| In the text | |
 |
Fig. 11. log g − log k2 diagram for the primary of V453 Cyg and adopting Z = 0.0134. The solid line indicates a model with fov = 0.03 while the dashed one represents a model computed with fov = 0.02. The two arrows indicate the observed value of log g. The resulting difference in |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



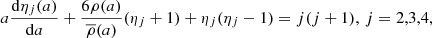
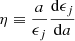
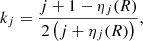
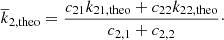
![$$ \begin{aligned} {c_{2 i}} = \left[ \left({\Omega _{i}\over {\Omega _{K}}}\right)^{2} \left(1 + {m_{3-i}\over {m_{i}}}\right) f(e) + {15\, m_{3-i}\over {m_{i}}}\,g(e) \right] {\left({R_{i}\over {A}}\right)^{5}} \end{aligned} $$](/articles/aa/full_html/2021/10/aa41484-21/aa41484-21-eq17.gif)
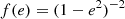
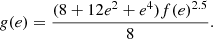
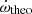
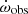
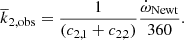
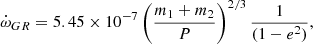
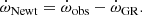
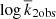
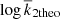
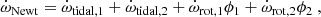
![$$ \begin{aligned} \dot{\omega }_{\mathrm{tidal,} j} = \left[{15 m_{3-j}\over {m_{j}}}k_{2j} g(e)\right]{\left({R_{j}\over {A}}\right)^{5}}~, \end{aligned} $$](/articles/aa/full_html/2021/10/aa41484-21/aa41484-21-eq32.gif)
![$$ \begin{aligned} \dot{\omega }_{\mathrm{rot,} j} = \left[ \left({\Omega _{j}\over {\Omega _K}}\right)^{2} \left(1 + {m_{3-j}\over {m_{j}}}\right)f(e) k_{2j} \right]{\left({R_{j}\over {A}}\right)^{5}}~, \end{aligned} $$](/articles/aa/full_html/2021/10/aa41484-21/aa41484-21-eq33.gif)
![$$ \begin{aligned} \phi _j&= - {1\over {\sin ^2 i}}\left[\cos \alpha _j (\cos \alpha _j - \cos \beta _j \cos i) \right] \nonumber \\&\quad {-{1\over {2}} \left[(1 - 5\cos ^2 \alpha _j)\right].} \end{aligned} $$](/articles/aa/full_html/2021/10/aa41484-21/aa41484-21-eq34.gif)