| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202141248 | |
| Published online | 08 October 2021 | |
Disks in close binary stars
γ-Cephei revisited
1
Institut für Astronomie und Astrophysik, Universität Tübingen,
Auf der Morgenstelle 10,
72076
Tübingen,
Germany
e-mail: lucas.jordan@uni-tuebingen.de
2
Universitäts-Sternwarte, Fakultät für Physik, Ludwig-Maximilians-Universität München,
Scheinerstr 1,
81679
München,
Germany
3
Dipartimento di Fisica, University of Padova,
via Marzolo 8,
35131
Padova,
Italy
Received:
4
May
2021
Accepted:
28
July
2021
Context. Close binaries (abin ≤ 20 au) are known to harbor planets, yet planet formation is unlikely to succeed in such systems. Studying the dynamics of disks in close binaries can help to understand how those planets could have formed.
Aims. We study the impact that numerical and physical parameters have on the dynamics of disks in close binaries. We use the γ-Cephei system as an example and focus on disk quantities such as disk eccentricity and the precession rate as indicators for the dynamical state of the disks.
Methods. We simulate disks in close binaries by performing two-dimensional radiative hydrodynamical simulations using a modified version of the FARGO code. First, we perform a parameter study for different numerical parameters to confirm that our results are robust. In the second part, we study the effects of different masses and different viscosities on the disks’ dynamics.
Results. Previous studies on radiative disks in close binaries used too low resolutions and too small simulation domains, which impacted the disk’s dynamics. We find that radiative disks in close binaries, after an initialization phase, become eccentric with mean eccentricities between 0.06 and 0.27 and display a slow retrograde precession with periods ranging from 4−40Tbin which depends quadratically on the disk’s mean aspect ratio. In general, the disks show a coherent, rigid precession which can be broken, however, by changes in the opacity law reducing the overall eccentricity of the disk.
Key words: hydrodynamics / protoplanetary disks / accretion, accretion disks / planets and satellites: formation / methods: numerical
© ESO 2021
1 Introduction
Up to now, about a dozen known planets have been detected that reside inside a close binary system (abin ≾ 20 au) orbiting one of the stars in the system, in an S-type orbit (Thebault & Haghighipour 2015). One well-studied example is the γ-Cephei system, which is a close binary system with a semi-major axis of 20 au and eccentricity of 0.4 (Endl et al. 2011). It harbors a giant planetary companion (Hatzes et al. 2003) with a mass of m sin i = 1.85 MJup distanced 2 au from the more massive companion (Endl et al. 2011). This minimum planet mass was determined via radial velocity measurements, but recently Benedict et al. (2018) claimed a much larger actual mass of ~9.4 MJup and a non-coplanar system using Hubble Space Telescope astrometry data. The origin of planets in these close binaries incites many questions, as previous studies have shown that the standard planet formation process is highly problematic at the observed positions of the planets due to the presence of a close stellar companion (see Thebault & Haghighipour 2015; Marzari & Thebault 2019 for a full discussion).
The position of the planet in γ-Cephei is not too far from the orbital stability limit of ~4 au (Holman & Wiegert 1999; Pichardo et al. 2005). At this position, the companion plays an important role in the planet formation process. The planetesimal accretion phase was found to be the phase that is most sensitive to gravitational disturbances. The eccentricity of the planetesimals is excited by the companion star and damped by the gas disk. The size dependency of the gas drag causes misalignment in the pericenters for different-sized planetesimals. This leads to orbit-crossings that cause destructive collisions and prevent further growth (Thébault et al. 2006, 2008). The relative velocities between the planetesimals become even larger if the hosting disk is eccentric (Paardekooper et al. 2008). Later, Rafikov (2013) noted that the disk gravity has a dominant effect on the planetesimal’s dynamics and concluded in Rafikov & Silsbee (2015) that planetesimal growth could succeed in close binaries given that the disk is apsidally aligned to the binary and has a very small eccentricity (ed ≤ 0.02). Therefore, precise modeling of disks in close binaries is necessary to understand how planet formation can succeed.
Within the context of superhumps in cataclysmic variables (Pearson 2006), the importance of tidal effects by the secondary star was demonstrated in the simulations by Whitehurst (1988). Later, eccentric disks in circular close binaries were studied by Lubow (1991a) who found, using linear analysis, that the m = 3 eccentric inner Lindblad resonance can drive the growth of disk eccentricity in such systems. This was also confirmed numerically in Lubow (1991b) and Artymowicz & Lubow (1994). Though later it was shown that the m = 3 resonance isnot the only cause for eccentricity growth in disks in close binaries either by removing the resonance from the potential or by using a larger mass ratio of the binary that truncates the disk to sizes such that the m = 3 resonance is not contained in the disk anymore (Kley et al. 2008; Marzari et al. 2009). Generally, hydrodynamical simulations have shown that in close binary star systems, either circular or eccentric, the disks regularly develop large eccentricities ed ≥ 0.2 and start precessing (Paardekooper et al. 2008; Kley et al. 2008; Marzari et al. 2009, 2012; Müller & Kley 2012). In those simulations, it has been seen that the size of the disk is an important indicator for the final disk eccentricity. Disks that are more exposed to the perturbations of the companion tend to develop larger eccentricities. The size of the disk is determined by the viscosity of the gas with higher viscosity leading to larger disks, and by the tidal effect of the secondary star that leads to disk truncation.
Concerning numerical considerations, Paardekooper et al. (2008) noted that the numerical methods used in the simulations can drastically affect the dynamics of the disk. They found that their simulations, which used the RODEO code (Paardekooper & Mellema 2006) with the diffusive minmod limiter, produced disks in a quiet state that have low eccentricity and show no precession. This quiet state was not affected by changes to resolution or boundary conditions. When the less diffusive superbee flux limiter was used, the disks entered an excited state with precession and high eccentricity that strongly depended on the resolution and boundary condition used. Disks in this low eccentric state have also been observed in locally isothermal simulations that include self-gravity (Marzari et al. 2009), or in radiative simulations (Müller & Kley 2012; Marzari et al. 2012), or SPH simulations (Martin et al. 2020).
After all, it is currently not clear how numerical considerations and physical parameters impact the dynamics of circumstellar disks in close binary stars. To better understand the process of planet formation in binary stars and gain more insight into the subgroup of superhump systems in cataclysmic variables, further development in theoretical and numerical models of disk dynamics inbinary star systems is warranted. Additionally, there have been massive advances in computational resources since those studies were performed, and we decided to revisit the problem of disks in close binaries and continue the studies presented in Müller & Kley (2012). The focus of this paper lies again on the system γ-Cephei, being one of the outstanding sample systems, with the first planet discovered in a close binary star (Hatzes et al. 2003). In our study, we treat physically realistic disks by including internal heating and radiative cooling.
This paper is structured as follows. In Sect. 2, we present our model used for the simulations and the methods for analysis. We briefly explain our standard model in Sect. 3. Tests of different grid resolutions, domain-sizes and boundary condition are presented in Sect. 4, and the results from simulations with different disk masses and viscosities are shown in Sect. 5. We discuss global trends of the disks in detail in Sect. 6, highlight difficulties when simulating disks in close binaries in Sect. 7, and finally summarize our results in Sect. 8.
2 Model
In this work, we simulated two-dimensional, radiative disks, using a modified version of the FARGO code including the energy equation. The code solves the vertically integrated hydrodynamical equations on a polar coordinate system (r − ϕ), centered on the primary star. It uses an upwind scheme with a second-order flux limiter (van Leer 1977), linear interpolation to reconstruct variables, and the fast advection in rotating gaseous objects (FARGO) method for the azimuthal advection, for details, see Masset (2000). For shock smoothing, artificial viscosity is used as described in Stone & Norman (1992). The simulated disks are non-self-gravitating and the gravitational back-reaction from the disks onto the binary stars is neglected. The orbit of the binary is integrated with a fifth-order Runge–Kutta method. The source terms for the energy equation include viscous heating and radiative cooling alongside compressive heating. For the Rosseland mean opacity, we used the piece-wise power-laws as put forward in Lin & Papaloizou (1985). The full equations and physical assumptions are specified in detail in Müller & Kley (2012), and we do refer to that work for more information.
Physical and numerical parameters for initializing the standard model.
2.1 Initialization
The physical and numerical parameters of our fiducial model are presented in Table 1. For the initial temperature, we use a power-law with T(r) ∝ r−1, which leads to a disk with constant aspect ratio, h, see Eq. (5). The reference temperature is chosen such that h = 0.05. Since viscous heating and radiative cooling are explicitly included in the models, the actual disk temperature will change quickly during the simulations. For the initial density, we chose the same power-law Σ(r) ∝ r−1. Because the disk around the primary is truncated by the tidal forces of the secondary, the initial disk surface density is smoothly reduced beyond 6 au to start the disk closer to the equilibrium size. The total initial disk mass of our fiducial model (including this tapering) is 10−2 M⊙ which equates to Σ(1 au) = 2570 g cm−2. The initial radial velocity is set to zero, and the initial angular velocity is set to the Keplerian angular velocity.
2.2 Boundary conditions
We use outflow boundaries at the outer edge of the computational domain for all our simulations. At the inner edge of the domain, reflective boundaries are used, unless stated otherwise. The implementation of the boundaries is identical to Müller & Kley (2012) (it is importantto note that the reflective boundary condition in their Sect. 2.2 is missing a minus sign, and it should read v0j = −v2j, for the radial velocity). We added wave damping zones at the inner edge to prevent waves from being reflected into the domain by damping the radial velocity vr to zero and the surface density Σ and internal energy e to the azimuthal average by using the damping mechanism as described by de Val-Borro et al. (2006)
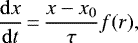 (1)
(1)
where x ∈{vr, Σ, e}, x0 is the desired value, τ is the damping timescale and f(r) is a quadratic ramp-up function that rises from 0 to 1 from the start to the end of the damping zone. The wave damping zone ranges from 1.1 Rmin to Rmin. For the damping timescale we used 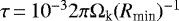 where Ωk is the Keplerian angular velocity around the primary. We also tested slower wave damping and no wave damping and found that it has little effect on the disk’s dynamics.
where Ωk is the Keplerian angular velocity around the primary. We also tested slower wave damping and no wave damping and found that it has little effect on the disk’s dynamics.
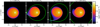 |
Fig. 1 Disk surface density during one binary orbit for the standard parameters, see Table 1, after the equilibrium has been reached. The green line indicates the Roche lobes of the stars. In the leftmost image (t1) the binary is at apastron and the disk is unperturbed. At the binary’s periastron (t2) the diskis maximally distorted and has the highest eccentricity. After the periastron passage (t3) two spiral arms are launched that wind inward and dissipate again (t4). Most of the disk’s mass loss happens in the time frame between t2 and t4 that spans 15% of the binary’s period. |
2.3 Numerical considerations
To avoid numerical instabilities from too low density or energy values at the outer border of the disk, we used a density floor of Σfloor = 10−7 ⋅ Σ0 where Σ0 = Σ(1 au)|t = 0 and a temperature floor of Tfloor = 10 K. We use the α-prescription by Shakura & Sunyaev (1973) to model the viscosity and name simulations for our viscosity study by their α value. Inside plots, we compare the simulations by their kinematic viscosity, as it is the relevant quantity that affects the disk’s dynamics. The coefficient of the kinematic viscosity is defined as
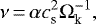 (2)
(2)
where cs is the adiabatic sound speed.
We also tested the disk dynamics of our standard case using additionally the PLUTO code (Mignone et al. 2007). These results, presented in Appendix A, showed similar behavior.
2.4 Analysis
We describe the disk’s dynamics by its global eccentricity ed and longitude of pericenter, ωd. These are calculated from the mass-weighted average over all cells as has been used in previous studies (Kley et al. 2008). The desired quantity is calculated for each cell by assuming that the gas parcel moves on a 2-body Keplerian orbit around the primary star, then the average over the whole disk is calculated as
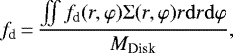 (3)
(3)
where fd ∈{ed, ωd, h, ν}. Similarly, the radial profile of a disk quantity is calculated as
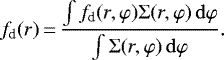 (4)
(4)
In the presentation of our results we refer to the disk temperature mostly through the aspect ratio, h, which is the ratio of the vertical pressure scale height of the disk, H, over the radius. It is given by
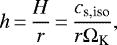 (5)
(5)
where the second equality follows for standard thin accretion disks.
Before engaging in our parameter studies, we first checked if resolution and domain size is sufficient to resolve the disk dynamics. These studies are presented in Sect. 4 below. Afterward, we varied the mass of the disk between 2 × 10−3 M⊙ to 5 × 10−2 M⊙ the α-viscosity parameter from 10−4 to 10−2, and document the effects that these variations have on the disks’ dynamics.
3 Standard model
We present the physical and numerical parameters of our fiducial model in Table 1. In deviation from the standard model used in Müller & Kley (2012), which was also based on the γ-Cephei system, we reduced the viscosityparameter from α = 10−2 to α = 10−3, because thisbetter represents the average viscosity found in recent disk observations (e.g., Rafikov 2017; Sellek et al. 2020; Trapman et al. 2020). Additionally, we increased the numerical resolution of the grid and the extent of the simulation domain.
The general behavior of the disk during a binary revolution is displayed in Fig. 1. During the binary apastron, the disk is eccentric but the overall density is smooth, without any spiral features. Just before periapse, the disk becomes visibly affected by the companion and is extended toward the secondary in a shape that follows the Roche lobe of the primary. Mass loss occurs shortly after the periapse, during the same time, two spiral arms develop that wind toward the disk’s center and dissipate.
The radial disk structure is displayed in Fig. 2 using the time-averaged radial surface density and temperature profiles. The transition between opacity power-laws are visible as bends in the temperature profile, such as the bend at 1 au caused by the sublimation of dust at 1100 K. Inside the dust sublimation region, the temperature gradient becomes shallower due to the lower opacity, and the surface density gradient becomes steeper due to the disk being in a viscous equilibrium. Beyond 4.5 au, surface density drops rapidly because of the tidal truncation of the binary. The kink in temperature close to the inner edge is caused by the wave damping region.
All of our simulations produced retrograde precessing disks with one precession period, lasting between 4− 40 Tbin, depending on their temperature. The effects of the precession on the disk eccentricity are shown for the standard model in Fig. 3. When the disk’s apocenter is aligned with the binary’s periastron, the disk is most affected by the binary’s periastron passage, resulting in the largest perturbations (seen as the largest spikes in Fig. 3). At this point, the disk’s eccentricity is also the largest. When the disk’s longitude of pericenter is moving toward the binary’s periastron, it becomes less affected by the companion, resulting in weaker perturbations during the binary’s periastron passage and a waning disk eccentricity.
 |
Fig. 2 Time-averaged radial profile of the surface density and gas temperature of our fiducial model. Solid lines are averaged over 200 snapshots taken at the binary apastron during the simulation time from 1300 Tbin to 1500 Tbin. The shaded areas show the 1σ variations. |
 |
Fig. 3 Time evolution of the mass-weighted disk eccentricity and the mass weighted longitude of pericenter for the fiducial model. The disk has the lowest eccentricity and has the least variation during one binary orbit when the longitude of pericenter is aligned with the binary periastron (ωd = ± π). From that point the disk’s eccentricity and variation during one binary orbit increases and reaches a maximum when the longitude of pericenter is aligned with the binary apastron (ωd = 0). |
4 Numerical convergence
Before we present our studies on the influence of the physical parameter, we first showcase in this section the impact of the numerical parameters on the disk’s behavior in a close binary star. Starting from our standard model in Table 1, we varied one numerical parameter at a time and studied their effect on the dynamical evolution on the disk. A suitable indicator for the dynamical state of the disk is the mass averaged global disk eccentricity, ed, calculated according to Eq. (3), and we present our finding in terms of ed.
 |
Fig. 4 Time evolution of the mass-weighted disk eccentricity (see Eq. (3)) for different resolutions for a logarithmic grid. Solid lines are time averaged values while the transparent lines are the simulation data. |
4.1 Grid resolution
In Fig. 4 the disk’s eccentricity is shown for different resolutions of the logarithmic grid. For our standard model (green line in Fig. 4) it takes the disk around 400 orbits to reach an equilibrium state (similar values were found in Kley et al. 2008 and Müller & Kley 2012 for locally isothermal simulations). The final eccentricity reached in this equilibrium state depends on the numerical resolution. A too low resolution can damp the disk’s eccentricity significantly, as seen clearly in the lowest resolution case, 376 × 576, in Fig. 4, which ends up in a different, low eccentric state compared to higher resolution cases. In simulations with higher resolutions (with more than six cells per radial pressure scale height) ed grows until a new equilibrium state is reached with ed ≈ 0.17–0.22 for the various resolutions. Our fiducial model has a resolution of eight cells per radial pressure scale height to leave enough headroom to conduct simulations with colder disks (and therefore fewer cells per scale height) on the same grid. Other works, which conducted numerical convergence studies, also found that resolutions of around eight cells per scale height are required to reach convergence, for example, Thun et al. (2017) and Oliva & Kuiper (2020). In the high eccentric state, the disks show a retrograde precession with a period of (9.5–10.2) Tbin, which is always identical to the corresponding oscillation period of ed, as shown in Fig. 3 for the standard case.
We repeated the resolution test with an arithmetic grid and found the same behavior with comparable final disk eccentricity. Although, a significantly higher resolution of 1846 × 1800 on an arithmetic grid was required to match the simulation using a 760 × 1162 resolution on a logarithmic grid. This is caused by the fact that the arithmetic grid has a lower resolution (cells per pressure scale height) in the inner disk region and instead has a higher resolution at the periphery than the logarithmic grid. Reaching convergence between the two grids indicates that our disk is sufficiently resolved throughout the whole domain and that the numerical viscosity should be negligible.
We take these resolution studies as a sign that the excited, eccentric disk state is physical and that the low eccentric state at lower grid resolutions is only numerical. Since increasing the resolution further above our standard model, has little effect on the dynamics, and for computational reasons, we choose the 760 × 1162 resolution as our standard. Considering our new results, it turns out that previous studies of radiative disks (e.g., Müller & Kley 2012) may have suffered from too low grid resolution.
 |
Fig. 5 Time-averaged mass-weighted disk eccentricity plotted against the location of the inner domain boundary. |
4.2 Location of the outer boundary
Previous studies on γ-Cephei used domain-sizes of 0.5–8 au, equivalent to 0.025–0.4 abin, (Kley & Nelson 2008; Müller & Kley 2012; Paardekooper et al. 2008), while Marzari et al. (2009) used 0.5–15 au but with a larger abin = 30 au, instead of our abin = 20. To check the impact of the chosen value of the outer boundary on the disk dynamics, we ran simulations using different values for Rmax. We found that the outer radius Rmax has little effect on the dynamics of the disk, but does change the mass loss rate across the outer boundary. When the companion passes periastron, mass is ejected from the primary disk. If Rmax is too small, mass ejected from the disk is removed from the simulation before it can be re-accreted onto the primary disk. Increasing Rmax further than 12 au (binary distance at periastron) leads to the same mass loss rates once the disk has reached equilibrium. Hence, the simulation domain should therefore at least contain the whole Roche lobe of the primary in apocenter, as in our standard case.
4.3 Location of the inner boundary
The location of the inner domain radius, Rmin, directly influences the dynamics of the disks. The further out the position of the inner boundary, the lower the disk eccentricity with an approximately linear dependency, see Fig. 5. For reflective boundaries, the radial velocity and hence eccentricity is forced to zero at the boundary. If the boundary is closer to the star, it has less influence on the rest of the disk, allowing it to develop higher eccentricity, see Fig. 6. This increase in eccentricity for smaller Rmin could also be explained by additional higher-order resonances still being captured inside the domain (Marzari et al. 2009). Similar to the disk eccentricity, the precession rate increases for decreasing Rmin, from 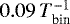 at Rmin = 0.5 au to
at Rmin = 0.5 au to 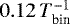 at Rmin = 0.1 au. Therefore, adding an inner disk region influences the eccentricity and precession rate of the whole disk while the radial temperatureand the surface density profile remain unchanged (image not shown).
at Rmin = 0.1 au. Therefore, adding an inner disk region influences the eccentricity and precession rate of the whole disk while the radial temperatureand the surface density profile remain unchanged (image not shown).
For open boundaries, a smaller Rmin reduces the artificial mass loss at the inner boundary. Due to the high computational cost of reducing the inner radius of the domain, we limit Rmin to 0.2 au for the rest of our simulations.
 |
Fig. 6 Azimuthally averaged disk eccentricity (see Eq. (4)) for different locations of the inner radius. Solid lines are averaged over 200 snapshots taken at the binary apastron during the simulation time from 1000 Tbin to 1200 Tbin. The shaded areas show the 1σ variations. The disk has a radius of ≈5 au, eccentricities at radii beyond that do not contribute to the disks eccentricity. |
 |
Fig. 7 Time evolution of the mass-weighted disk eccentricity for different inner boundary conditions. Solid lines are averaged values while the transparent lines are the simulation data. The simulation with an open boundary at the inner domain does not reach an equilibrium state due to the rapid mass loss. The lower temperatures from losing mass slow down the precession rate. |
4.4 Inner boundary condition
We also ran a test using an open inner boundary condition without damping at the inner boundary. The simulation develops a similar eccentricity compared to the standard case with a reflective inner boundary condition (Fig. 7). Since any mass that crosses the inner boundary is removed from the simulation, the disk loses mass very fast and forms an elliptic inner hole (Fig. 8). This behavior is in agreement with the simulations shown in Kley et al. (2008) and Marzari et al. (2012). This rapid mass loss prevents the disk from reaching an equilibrium state as the disk continuously becomes colder, which causes the precession rate to slow down (compare Fig. 17 below). The disk’s eccentricity profile behaves differently. Throughout the whole disk, the eccentricity is constant, whereas in the simulation with reflective boundaries, the eccentricity is forced to zero at the inner boundary and grows outward (Fig. 9). Similarly, the disk precesses as a solid body at all times, while for simulation with reflective boundary, we find deviations from solid body precession, see Sect. 6 for more details. The gas at the edge of the inner eccentric hole develops high radial velocities and variations in the azimuthal velocity that severely limit the timestep, making these simulations computationally too expensive for a full parameter study in this work.
 |
Fig. 8 Snapshot of the disks surface density after 481 orbital periods at the binary apastron. The simulation used an open inner boundary condition. Right: zoom in on the inner 1 au. Mass being removed at the inner boundary (gray area) causes the development of an eccentric hole. |
 |
Fig. 9 Radial profiles of the time averaged mass-weighted disk eccentricity for different inner boundary conditions. Solid lines are averaged over 200 snapshots taken at binary apastron between T = 400 and 600Tbin. The shaded areas show the 1 σ variations. Eccentricity as well as precession are more uniform throughout the disk when open boundaries are used. The radial profiles are cut at a radius where the time averaged surface density drops below 100 times the floor value. |
5 Dependence on physical parameters
Having analyzed the impact of purely numerical parameters, we conclude, that the computational setup of the standard model (see Table 1) seems to be sufficient to capture all relevant physical properties of the disks. We shall use it throughout this section to study the effects of physical parameters on the disk’s dynamics. The α-parameters and initial disk masses tested in this section are listed above in Table 2.
All the simulations for the parameter study.
5.1 Disk mass
The disk’s mass density has a direct influence on its temperature, first by increasing the heating through the viscous stress tensor and secondly by increasing the optical depth thereby reducing the radiative cooling efficiency. Thus, increasing the disk mass should directly increase the disk temperature and subsequently impact the disk dynamics, that is, its eccentricity. We tested this by varying the initial disk masses, ranging from 2 × 10−3 to 5 × 10−2 M⊙, while keeping the other parameters unchanged from the standard model.
5.1.1 Temperature profile
The radial disk temperature (here given as the relative disk thickness) resulting from different disk masses is displayed in Fig. 10, and it clearly shows a monotonic increase in aspect ratio with disk mass within the disk proper, that is, inside of about 6 au. But the individual curves show some substructures. For the lowest mass (2 × 10−3M⊙) case (the blue line in Fig. 10), a drop-off in aspect ratio is visible for radii inside of ~ 2 au. Inside of this radius, the disk temperature surpasses the ice sublimation temperature ~ 160 K. This trend reverses when all the ices are sublimated at ~220 K (at around 1.2au) and the opacity increases with temperature again.
Not considering, for now, the strong increase in h close to the inner boundary, all models show a drop in aspect ratio toward the inner edge, which indicates the sublimation of dust grains at about 1100 K and a lowering of the opacity. With increasing mass, this transition moves further out, as does the maximum of h. The standard model with Md = 10−2 M⊙ reaches the threshold at ~1 au while for the highest disk mass it lies at about 2 au. At the very inner edge, the models with larger disk mass show a strong increase in temperature up to over 3300 K. This is caused by the dissociation of hydrogen, which drastically increases the opacity, leading to high aspect ratios.
We also tested the effect stellar irradiation from the central star would have on our disks using the irradiation model from Menou & Goodman (2004). Following the procedure described in Ziampras et al. (2020), we took a time-averaged radial density profile of our disks and calculated its temperature in thermal equilibrium under the influence of viscous heating, stellar irradiation, and radiative cooling. We found that stellar irradiation does not affect on the optically thick, dense inner half of the disk (r ≲ 2− 4 au depending on model) and only becomes relevant at the outer parts. However, due to the existence of a maximum in the aspect ratio in this region (see Fig. 10), the outer parts would be shadowed by the inner regions (from the star or hot inner disk) if a more realistic irradiation model was used. We conclude that stellar irradiation has no effect on the dynamics of our disks and can be neglected.
 |
Fig. 10 Radial profiles of the time averaged mass-weighted disk scale height, here h = H∕r, for different initial disk masses. Solid lines are averaged over 200 snapshots taken at binary apastron during the simulation time from 1300 Tbin to 1500 Tbin. The shaded areas show the 1 σ variations. The radial profiles are cut at a radius where the time averaged surface density drops below 100 times the floor value. |
5.1.2 Time evolution of the eccentricity
The time evolution of the global disk eccentricity is displayed in Fig. 11 for four different disk masses. After about 600 to 800 Tbin all models settle to a quasi-stationary state. The simulations show that the small eccentricity for the low mass case is accompanied by larger deviations from solid body precession. Deviations from solid body precession appear as varying precession rates at different radii inside the disk. In our simulations, we observe that the disk’s eccentricity is suppressed, when neighboring gas rings precess independently of each other. From Fig. 11 it can also be seen, that the oscillation period of the eccentricity becomes shorter with higher disk mass, which implies a faster retrograde precession rate. We discuss these effects in more detail in Sect. 6.
The low mass case 2 × 10−2 M⊙ (blue line inFig. 11) has a peculiar eccentricity evolution because it is the one farthest away from an equilibrium profile during initialization. It is too cold to precess for the first 20 binary orbits; because the longitude of pericenter ispositive in the beginning, this results in a rapid eccentricity growth (compare the eccentricity growth for ωd > 0 in Fig. 3). The disk becomes more compacted by the tidal forces of the companion and starts precessing, resulting in a hot inner region and cold outer rim with a large temperature gradient across the disk. Due to the strong temperature gradient, the disk precesses at different speeds at different radii, resulting in strong damping of the eccentricity, as mentioned above.
The resulting disk eccentricities in the equilibrium state are shown in Fig. 12, which includes additionally the results for different viscosities. We find that the simulation with a disk mass of 2 × 10−2 M⊙ (resulting in an aspect ratio of h = 0.057) develops thelargest eccentricity. More massive and less massive disks develop a smaller eccentricity (see blue points in Fig. 12). This finding is in agreement with Marzari et al. (2012) who found their eccentricities peaking at h = 0.05 in their locally isothermal runs (compare their Fig. 1). Their explanation states that for cold disks, the perturbations (spiral arms) move inward more slowly and get tightly wound up. They are then more affected by viscous damping and become less efficient at depositing angular momentum in the inner parts of the disk. In hot disks, radiative damping dissipates the perturbations faster, leading to an overall lower disk eccentricity. The drop-off in eccentricity when deviating from the optimal h with the highest ed is much smaller in our simulations, with the time-averaged eccentricity never dropping below ed ~ 0.12.
 |
Fig. 11 Time evolution of the mass-weighted disk eccentricity for different initial disk masses. |
 |
Fig. 12 Time-averaged mass-weighted disk eccentricity plotted against the mass-weighted disk temperature. The arrows indicate the state after 2000 Tbin. At that time the α = 10−2 case has notreached an equilibrium yet. |
 |
Fig. 13 Time evolution of the disk mass for different α values. |
5.1.3 Mass loss
As explained above, the disks lose mass across the outer boundary of the computational domain. Starting from the initial setup, all models typically lose about 2.5% of their mass during the first few orbits. Ignoring this mass loss at the beginning, the disks lose mass on a longer timescale which is mostly ejected during the binary periastron passage when the disk’s longitude of pericenter is aligned to the binary apastron, see Fig. 1 above. Mass outflow only occurs if the disks are large and eccentric enough to overflow the primary’s Roche lobe during the periapse. It regulates itself because at some point, the disks become small enough to fit entirely inside the primary’s Roche lobe and mass loss during pericenter passage becomes negligible. The mass-loss rate increases during the growth of the disk’s eccentricity and then settles to a stationary value. For the standard case, this quasi-equilibrium is reached at around 600Tbin. After that, the disk loses mass at a rate of about 3.6 × 10−9 M⊙ yr−1 for the standard case, and 1.4 × 10−7 M⊙ yr−1 for the more viscous α = 6 × 10−3 case. Disks with a viscosity smaller than our standard case do lose even less mass to outflow, while our most viscous disks lose 80% of their mass within our simulation time of 1500 binary orbits, see Fig. 13.
In the simulation with an open inner boundary, the disk loses 80% of the initial mass within 900 binary orbits. Due to its low viscosity of α = 10−3, very little mass is lost by outflow, and most of the mass is lost through the inner boundary. This mass loss might be enhanced by our artificial large inner boundary. The mass loss through the inner boundary can be described as an exponential decay, as would be expected from the viscous accretion around a single star, and starts at 2.1 × 10−7 M⊙ yr−1 when the disk still has its full mass and drops to 6.5 × 10−8 M⊙ yr−1 at 900 Tbin when the disk mass is at 2.5 × 10−3 M⊙.
5.2 Viscosity
We tested α values ranging from 10−4 to 10−2. The resulting eccentricities as a function of radius are displayed in Fig. 14. For smaller viscosities, from α = 10−4 to 6 × 10−3, we confirm the trend found in Kley et al. (2008) and Müller & Kley (2012) that higher viscosity leads to more eccentric disks.
For even higher α, the disk dynamics evolve differently, and eccentricity drops again, as indicated by the cyan and black curves in Fig. 14. For these two highest α-values (α = 7 × 10−3 and 10−2) the disks first enter a quiet state that is steady, low-eccentric and non-precessing. Only after several hundreds of orbits do the disks start to precess and become more eccentric. At the time of 2000 Tbin the α = 7 × 10−3 simulation reaches the same final eccentricity of ēd ≈ 0.25 as the α = 6 × 10−3 case, while the simulation with α = 10−2 continues to grow its eccentricity at a slow but constant rate.
Higher α values result in stronger viscous torques, causing the disk to spread further outward. A larger disk is more affected by the companion and thus develops a larger eccentricity. The gas at the outer rim of the disk also has the largest eccentricity. Because of that, it is ejected from the disk during periastron passage which prevents further growth of eccentricity and limits the disk radius. The evolution of disk mass for the different disk viscosities is shown in Fig. 13, which shows a clear trend for the lower viscosity cases that the mass loss increases with viscosity, as expected. At first, the two high viscosity cases show relatively small mass loss against the initial expectation. This is due to the disks initially remaining much more circular and only start losing mass after becoming excited, in the same way as described above.
 |
Fig. 14 Radial profiles of the time averaged mass-weighted disk eccentricity for different α values. Solid lines are averaged over 200 snapshots taken at the binary apastron during the simulation time from 1300 Tbin to 1500 Tbin. The shaded areas show the 1 σ variations. The radial profiles are cut at a radius where the time averaged surface density drops below 100 times the floor value. |
6 Global trends
In this section, we look for global trends in the simulations from the previous section. We vary simultaneously, mass and viscosity of the disks and we present the data in different forms to better visualize the connection between the physical state of the disk and its dynamical behavior.
6.1 Eccentricity
Figures 15 and 16 show the averaged disk eccentricity and disk radius plotted against the global averaged disk viscosity. The data is first mass-averaged, see Eq. (3), and then time-averaged over the final ten precession periods, at simulation times between 1200 and 1500 Tbin. We measure the precession periods as the time between two adjacent peaks of the longitude of pericenter (see Fig. 3). The blue dots always represent data from simulations with different disk masses and red dots data from those with different viscosity. Figure 15 shows a positive correlation between viscosity and eccentricity, except for the high viscosity simulations. These start in a quiet state and retain a smaller eccentricity for the whole run time. In the following discussion, we ignore thosetwo simulations because they have not reached an equilibrium state at the end of our standard simulation time of 1500 Tbin. The positive correlation between eccentricity and viscosity is in agreement with earlier studies (Kley et al. 2008; Müller & Kley 2012). It can be explained by larger viscous torques increasing the disk’s size, making it more susceptible to perturbations of the companion and causes a higher eccentricity. The simulations with different disk masses follow the same trend, except for the higher mass simulations, see Fig. 12 above. We attribute the lower eccentricity in high mass simulation to radiative damping of the perturbations.
Similarly, diffusive action of viscosity is reflected in Fig. 16 which shows a positive correlation between disk size and viscosity. The disk expansion due to viscosity stops at an average disk radius of ~ 5.7 au, equivalent to 0.28 abin, see Fig. 16, and a mass-weighted eccentricity of 0.25, Fig. 15. It is important to note that since we keep the number of grid cells constant, simulations with a low aspect ratio are less resolved. This could enhance the drop-off in eccentricity for simulations with low viscosity or low mass.
We find that the disk’s eccentricity increases linearly with its radius, which has been noted by Marzari et al. (2009), who changed the disk size by varying the binary’s eccentricity. We note that the linear correlation between size and eccentricity could also partly be explained by our method of determining the disk’s radius as the distance from the primary that contains 99% of the disk mass.
 |
Fig. 15 Time-averaged mass-weighted eccentricity plotted against the time averaged mass-weighted viscosity. The arrows indicate the state after 2000 Tbin. At that time the α = 10−2 case has notreached an equilibrium yet. |
 |
Fig. 16 Time-averaged disk radius plotted against mass-weighted kinematic viscosity. |
 |
Fig. 17 Precession rate plotted against the mass-weighted disk aspect ratio. Red dots mark the simulations with different α values, blue dots with different disk masses and magenta dots with different cooling factors and lower resolution. The green line is a quadratic fit through the data points. The precession rate depends linearly on the disk Temperature with T ∝ h2. |
6.2 Precession rate
The precession rate was determined as described in the previous section. We find a slow retrograde precession for all disks, with one precession period lasting between 5 to 40 binary orbital periods. The precession rates are shown in Fig. 17 as a function of the global disk aspect ratio. The models for different disk masses and viscosities show a unique quadratic relation, fitted approximately by
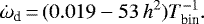 (6)
(6)
In general, the disk’s precession rate depends on the balance of gravitational and pressure forces (Goodchild & Ogilvie 2006). The gravitational forces induce a prograde precession while the pressure forces result in retrograde precession. We find retrograde precession for all our simulations, indicating that the disks are hot enough to be pressure-dominated. Our values for the precession rate and, in particular, the quadratic dependence with the mean scale height h are in excellent agreement with the locally isothermal simulations in Kley et al. (2008), obtained for circular binaries.
Since in our model T ∝ h2, this implies a linear relation between disk temperature and precession rate. We restarted our standard case with a modified heating and cooling rate to test the linear relation between precession rate and temperature. The heating and cooling rate were directly multiplied by factors of either 0.1 or 10. After that, the precession rates adjusted themselves on the thermal timescale, which is only a few (~ 3) binary orbits. The resulting precession rates are shown as purple dots in Fig. 17, and they lie on the same curve. For the simulations with varying α-values, the relation between the precession rate and the temperature is not as pronounced, and simulations that start in the low eccentric disk state do not fit the model anymore (two rightmost big red points in the plot). In Fig. 3, it can be seen that the disks build up eccentricity when the longitude of pericenter is shifting toward the binary’s periastron and reduce their eccentricity when the longitude of pericenter is shifting away from the binary periastron position. This causes disks with lower precession rates to have more time to increase their eccentricity and have therefore a larger variance in eccentricity oscillations.
 |
Fig. 18 Snapshot at T = 662.74 Tbin of the radial profile of the longitude of pericenter, opacity and eccentricity of the fiducial model. The dashed vertical black line indicates the position of the change in the opacity power-law at T = 1100 K. The longitude of pericenter becomes undefined for e = 0 at the inner boundary. |
 |
Fig. 19 Time evolution of the azimuthally mass-weighted average of the longitude of pericenter at two different radii for the fiducial model. The dotted line indicates the time the snapshot used in Fig. 18. |
6.3 Solid body precession
Typically, in our simulations, the disks precess as a solid body, that is, the radial profile of the longitude of pericenter is constant across the whole disk. In some simulations, however, we observe deviations from the solid body precession. These mostly appear as jumps in the longitude of pericenter, at radii at which the opacity changes due to the temperaturegradient in the disk. In our opacity models, the variation with temperature is given by different power-laws. Abrupt changes in these split the disk into regions with different temperature gradients, which affects the propagation of the perturbations in the disk as sound waves are partially reflected at these discontinuities. This can cause the disk to split into two regions at the power-law transition that precess independent of each other.
An example of this effect is displayed in Fig. 18 which shows a snapshot of the disk longitude of pericenter, opacity, andeccentricity of the fiducial model just after the binary periastron passage when the spiral arms had propagated to the inner parts of the disk. The change in wave propagation induced by the opacity law splits the disk’s longitude of pericenter at ~ 1 au where the temperature in the disk surpasses the dust sublimation temperature of T ≈1100 K and the temperature dependence of the opacity changes from κ ~ T1 to κ~ T−9. Figure 19 shows that the precession at the inner region of the disk (blue line) becomes irregular and independent of the outer disk region (red line). By the time the binary reaches apastron, the perturbations have dissipated, and the inner region of the disk starts to realign to the outer region of the disk. While the region’s precession is disconnected, the eccentricity of the disk is reduced at the boundary between the two regions, lowering the eccentricity throughout the whole disk. For our low mass simulation Mdisk = 2 × 10−3M⊙, the longitude of pericenter breaking happens when the temperature surpasses 155 K and the power-law changes from κ ~ T2 to κ ~ T−7. This transition happens further outward at 2 au, causing the eccentricity damping of the differential precession to be more effective (compare the onset of longitude of pericenter breaking for the low mass simulation (blue line) at t = 100 Tbin versus the onset of breaking for the fiducial model (red line) at t = 600 Tbin in Fig. 11).
We calculated the mass-weighted standard deviation of the longitude of pericenter 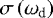 for all cells in the disk and found an anticorrelation between
for all cells in the disk and found an anticorrelation between 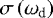 and disk eccentricity, see Fig. 20. This effect acts on top of the other effects that influence the disk eccentricity that we discussed in this work. For the high mass simulations in Fig. 20, the drop in eccentricity without an increase in
and disk eccentricity, see Fig. 20. This effect acts on top of the other effects that influence the disk eccentricity that we discussed in this work. For the high mass simulations in Fig. 20, the drop in eccentricity without an increase in 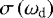 is caused by radiative damping. Simulations with a low α-value develop a lower eccentricity than other simulations with comparable
is caused by radiative damping. Simulations with a low α-value develop a lower eccentricity than other simulations with comparable 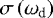 , indicating that the drop is due to their smaller size rather than differential precession.
, indicating that the drop is due to their smaller size rather than differential precession.
Disks that enter a quiet state do not precess and have a highly varying longitude of pericenter; but due to their very low eccentricity, it is not clear whether their high 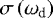 is damping their eccentricity or their low eccentricity makes determining the longitude of pericenter less precise. Additionally, this effect depends on the inner boundary condition. An open inner boundary condition removes mass and reduces the temperature gradient across the disk, reducing the influence of power-law changes in the opacity table. This again highlights the importance the inner boundary has in our simulations.
is damping their eccentricity or their low eccentricity makes determining the longitude of pericenter less precise. Additionally, this effect depends on the inner boundary condition. An open inner boundary condition removes mass and reduces the temperature gradient across the disk, reducing the influence of power-law changes in the opacity table. This again highlights the importance the inner boundary has in our simulations.
 |
Fig. 20 Disk eccentricity plotted against the standard deviation of the longitude of pericenter of all cells. The values mass averaged and time averaged over 200 snapshots at binary periastron from T = 1300 Tbin to T = 1500 Tbin. The old setup is using the standard parameters presented in Müller & Kley (2012). The arrows indicate the state after 2000 Tbin. |
7 Discussion
7.1 Comparison to previous work
Previous studies about radiative disks in the system of γ-Cephei (Müller & Kley 2012; Marzari et al. 2012) found only low disk eccentricities of ed ~ 0.05, which is in contrast to our new simulations presented here. We attribute the differences to a combination of the high viscosity values used for their fiducial models of α ≈ 10−2, a too low resolution, and a too-small simulation domain. For such a high viscosity, the disks stay in a quiet state with low eccentricity and no precession. This quiet state is robust to changes in numerical parameters, giving a false sense that lower resolutions and smaller domains have converged. Figure 21 shows simulations for the standard parameters from Müller & Kley (2012) (green curve) and their convergence test (purple line) and simulations with the domain size of our standard model Table 1 (red and blue lines). After we increased the domain size, the disks started to develop eccentricity and precession after 700 Tbin of simulation time, which is longer than the simulation time of the convergence tests in Müller & Kley (2012). The difference in disk structure for the setups is shown in Fig. 22. The plot compares the radial eccentricity profile of radiative and locally isothermal models for the new and old setup, averaged over 200 snapshots taken at binary apastron. The curves for the old model (red and purple) use the original data from Müller & Kley (2012) with their standard viscosity parameter of α = 10−2. The radiative simulation on the new setup uses a lower viscosity of α = 7 × 10−3 because the α = 1 × 10−2 simulation has not reached an equilibrium state at the end of the simulation time of 2000 Tbin. Figure 22 highlights the drastic difference between a quiet state and an excited state. The eccentricity of the disk in the quiet state is very low (ed ≤ 0.05), and it does not precess. This means that the disk is always in the same state when the binary reaches apastron, as indicated by the vanishing standard deviation of the eccentricity. On the other hand, the dynamics of an excited disk also depend on the disk’s own orientation inside the binary and oscillates with the disk’s precession rate. It can be seen that the dynamics of our radiative simulations are closer to the dynamics of locally isothermal simulations rather than to the radiative simulations performed in previous studies. It is still not clear why radiative simulations perform worse than locally isothermal simulations at low resolutions. Despite locally isothermal and radiative simulations being similar at high resolutions, we recommend performing fully radiative simulations as locally isothermal simulations are overestimating the disk’s eccentricity as they are missing effects like radiative damping and breaking of the solid body precession that can damp perturbations in the disk.
 |
Fig. 21 Time evolution of the mass-weighted disk eccentricity for the parameters of the standard case of Müller & Kley (2012) that is shown in green, and the parameters given in Table 1 but with α = 10−2. |
7.2 Mass loss
The mass-loss rates we found from mass ejection, are negligible compared to the mass accretion rates we found in our simulation with an outflow inner boundary condition. Allowing mass to leave through the inner boundary limits the disk’s lifetime in our simulations to ≾ 105 yr for α = 10−3. This represents a lower estimate for the disk’s lifetime as the mass loss is overestimated by our boundary condition. In realistic systems, the circumprimary disk will be accompanied by a circumsecondary disk and a circumbinary disk that all exchange mass between each other, as shown in numerical simulations (e.g., Günther & Kley 2002; Kaigorodov et al. 2010; Nelson & Marzari 2016; Muñoz & Lai 2016). The circumstellar disks could then be replenished with material from the circumbinary disk, which increases their lifetime (Monin et al. 2007). Observations of GG Tau A, which is a triple star system with a comparable configuration to γ-Cephei that hosts a disk around the primary star and a massive circumbinary disk of ~ 0.15 M⊙, find mass accretion rates from the circumbinary disk onto the circumstellar disks of Ṁ ≈ 6.4 × 10−8 M⊙ yr−1 (Phuong et al. 2020). The infalling mass is expected to be accreted in an approximately equal ratio onto the circumstellar disks (Dittmann & Ryan 2021). Extrapolating the mass loss rate from our open inner boundary condition simulation to the point it would be balanced out by a mass accretion rate of 3.2 × 10−8M⊙ yr−1 results in a disk mass of Md ≈ 8 × 10−4 M⊙. Since our inner outflow boundary condition likely leads to an artificially enhanced mass accretion, circumstellar disks with masses of a few 10−3 M⊙ could have the same lifetime as the circumbinary disk that feeds them. A similar mass has been estimated from observations for the disk around GG Tau Aa (Dutrey et al. 2014). This indicates that the circumstellar disk lifetime inside binaries is not necessarily a constraint for planet formation as they are fed by circumbinary disks that have been observed to have similar lifetimes as disks around single stars (Kuruwita et al. 2018)
 |
Fig. 22 Radial profiles of the time averaged mass-weighted disk eccentricity for our new setup and the standard models from Müller & Kley (2012). Solid lines are averaged over 200 snapshots taken at binary apastron. The shaded areas show the 1 σ variations. |
7.3 Accretion shocks
The mass infalling onto the circumprimary disk is accreted in pulses (Muñoz & Lai 2016), leading to shocks and shock heating in the disk (Nelson & Marzari 2016) and could cause the disk to develop a third spiral arm (Picogna & Marzari 2013). Since those studies did not resolve the circumstellar disks at a high enough resolution or evolved the system long enough to build up eccentricity, the effects of pulsed accretion on the disk dynamics are poorly understood. We conclude from these studies that the perturbations of the infalling material onto the circumprimary disk are minor compared to the gravitational perturbations of the companion. Therefore, we expect the trends we found to hold even if a mass accretion onto the disk is added.
All our simulations are two-dimensional. Running the same setup with three dimensions will affect the disk dynamics. Due to an extra degree of freedom for the gas motion, shock heating is less effective in 3D than in 2D Bate et al. (2003). As the companion excites strong shocks inside the disk that produce significant heat, our 2D approach likely overestimates the disk’s temperatures. Additionally, density wave propagation and their deposition of angular momentum into the disk could be different in three dimensions Lubow & Ogilvie (1998); Lee & Gu (2015) which could affect the disk dynamics. While comparable 3D simulations did find differences to 2D simulations Picogna & Marzari (2013); Zhu et al. (2015), these were located at the disk’s surface. Thus, we expect our 2D simulations to be comparable to the dynamics found in a 3D simulation at the mid-plane, where most of the mass resides.
8 Summary
We revisited the γ-Cephei system by performing grid-based, two-dimensional hydrodynamical simulations to study the dynamics of the disk around the primary star in an eccentric binary star. All of our simulations include viscous heating and radiative cooling. The disk dynamics are analyzed in terms of eccentricity and precession rate. We carefully separated physical from numerical behavior by investigating first the effects of numerical parameters before looking into the impact of physical conditions such as disk mass and viscosity.
We found that previous studies on radiative disks in close binaries used a too low resolution and too small simulation domain to properly resolve the disk dynamics. When using appropriate resolution and domain size, we observe considerablyhigher disk eccentricities. To reach the higher eccentric state, a resolution of at least six grid cells per scale height is required. Also, the simulation domain should contain the whole Roche lobe of the primary at phases of its orbit to avoid artificial mass loss through the outer boundary. The disk eccentricity linearly declines with increasing inner domain radius. This could imply that the disk becomes more circular as the inner region is cleared by photoevaporation.
It was already noted in Paardekooper et al. (2008) that the numerical methods used can change the outcome of the simulations. These effects were not observed in later studies such as Müller & Kley (2012) due to their fiducial model beingcaught in a quiet state that is robust to numerical changes. This quiet state is characterized by a low eccentricity and no disk precession. These occur in the initial phase of the simulations for viscosities larger than α ≥7 × 10−3, and they can last for over ≈700 Tbin. Eventually, the disks do become eccentric and start precessing. We found all of our disks become excited across different numerical and physicalparameters as well as different codes (additionally to our FARGO code, we tested the PLUTO code). We are therefore confident that the excited state is physical and that the very low eccentricities reported for radiative disks in Müller & Kley (2012); Marzari et al. (2012) are inaccurate.
In agreement with Müller & Kley (2012) and Marzari et al. (2012), we find that it is important to perform more realistic simulations that include viscous heating and radiative cooling. Locally isothermal models overestimate the disk’s eccentricity because they are missing effects like radiative damping or breaking of the solid body precession of the disk which can dissipate perturbations and damp the disk’s eccentricity.
We used reflective boundaries at the inner radius for our simulations so that the disks can reach an equilibrium state. This boundary can physically be interpreted as the disk extending to the star’s surface. We also ran a test simulation with an outflow inner boundary condition which coarsely resembles a cavity with perfect accretion, possibly created by a stellar magnetosphere. Despite these being two opposite extremes for the inner boundary condition, they lead to a similar early development of the disks. The disk evolution diverges over time as the open inner boundary simulation rapidly loses mass. We conclude that the trends we find would also apply to a more realistic boundary condition.
For the mass-weighted and time-averaged disk eccentricity, we found values from 0.06 to 0.27 (Fig. 15). The disk’s size is given by a balance of viscous versus gravitational torques. In our simulations, we found values from 4 au for disks with low viscosities, which is identical to the orbital stability limit for massless test particles (Holman & Wiegert 1999; Pichardo et al. 2005), up to a maximum disk size of 5.8 au for higher viscosities (Fig. 16). The disk size, or indirectly the viscosity, is an important factor for the disk eccentricity. Smaller disks are less affected by the perturbations of the secondary and become less eccentric. The disks’ eccentricity can also be reduced by radiative damping. In our simulations, radiative damping becomes effective for hot disks with h ≥ 0.06. The eccentricity of the disk oscillates with the same period as the longitude of pericenter, and we found that the amplitude of the oscillation increases with the precession period. Our simulations did not include the effects of self-gravity, which can change the radial alignment of the longitude of pericenter and can damp the disk’s eccentricity Marzari et al. (2009).
In all our simulations, we observed a slow retrograde precession of the disk. The precession rate depends linearly on the mean disk temperature, or equivalently, quadratically on the aspect ratio, as given by Eq. (6). This relation is in good agreement with the values found in Kley et al. (2008), who performed locally isothermal simulations for disks in circular binaries in the context of the superhump phenomenon in cataclysmic variables. From Eq. (6), we can expect that disks with low temperature will change to a prograde precession which might occur for disks with small disk masses during the dissipation phase.
We noticed in our simulations that the disk needs to precess as a solid body to be able to develop high eccentricities. Changes in the opacity power-law can break the longitude of pericenter alignment inside the disk, splitting the disk into an inner and outer region that precess independently of each other, reducing the overall disk eccentricity (see Fig. 18). We correlate the disk eccentricity to the standard deviation of the longitude of pericenter across all cells and find a downward trend in Fig. 20. We suspect that the low disk eccentricities found in Martin et al. (2020) could be explained similarly. In their isothermal SPH simulations, they observed that particles at different radii have different precession rates (see their Fig. 1). This could have prevented their disks from reaching higher eccentricities.
Concerning the impact on the planet formation process, the temperatures in our models with realistic masses (Md ≤ 10−2M⊙) are cold enough for silicate to be present in a solid-state throughout most of the disk. For our coldest model Md = 2 × 10−3M⊙ the snowline (160 K) is located in the middle of the disk at 2 au and the dust sublimation temperature(1100 K) is reached near the inner boundary at 0.5 au. Due to the low disk mass, the heating of the shocks is also weak. The spiral wave heats the outer parts of the disk to 200 K while the heating strength is reduced in parts where the disk temperature is already higher than 200 K from viscous heating. While the ices are repeatedly sublimated and recondensed by the spiral waves, silicate dust particles are mostly unaffected by the shock heating from the companion. However, we find high eccentricities and a retrograde precession for disks in close binaries over a wide range of parameters. High gas eccentricities have been found to increase the collision velocities between particles inside the disk, which slows down dust coagulation (Zsom et al. 2011)and makes planetesimal accretion less likely to succeed (Paardekooper et al. 2008). Therefore, our results support previous studies that found that the standard planet formation channel is unlikely to succeed in the γ-Cephei system as it is currently observed.
Alternative formation scenarios have been proposed to explain the increasing number of planets detected in close binary stars (see Schwarz et al. 2016 or Fig. 1 in Marzari & Thebault 2019 for a complete list of systems). Instead of in situ formation, the planets could also have formed inside a circumbinary disk and then be scattered and captured on a circumstellar orbit (Gong & Ji 2018). Additionally, they could have formed in a less hostile environment and end up in a close binary through a variety of different star-star scattering scenarios (e.g., Marzari & Barbieri 2007; Malmberg et al. 2007; Fragione 2019). Nevertheless, there are multi-planet systems observed in close binaries, such as the Kepler-444 system (Lillo-Box et al. 2014) which hosts five small, coplanar planets around the primary star. It is unlikely that they formed via scattering events suggesting that planet formation can indeed succeed in close binaries after all (Dupuy et al. 2016).
Acknowledgments
We would like to thank Alexandros Ziampras for helping to utilize the PLUTO code and for helpful discussions about the disk’s thermodynamics. The authors acknowledge support by the High Performance and Cloud Computing Group at the Zentrum für Datenverarbeitung of the University of Tübingen, the state of Baden-Württemberg through bwHPC, and the German Research Foundation (DFG) through grant INST 37/935-1 FUGG. All plots in this paper were made with the Python library matplotlib Hunter (2007).
Appendix A Test of different codes
To corroborate and validate our findings, we performed supplementarily simulations for the standard model using two different codes. Our results are presented in Fig. A.1. All simulations use the physical setup of the standard model. The FARGO run uses 760 × 1160 active cells on a domain ranging from 0.2 − 12 au. The PLUTO run uses the 648 × 1160 cells but has its domain size reduced from 0.3 − 10 au to produce the same cell size as in the FARGO simulation. The inner boundary is larger to reduce computation time, and the outer boundary is smaller for numerical stability. The FARGO simulation utilizes the Fargo method to speed up the simulations while the PLUTO run does not apply the Fargo method and therefore requires approximately ten times more timesteps due to the smaller Δt. The PLUTO code also uses a slightly different definition of the coefficient of the kinematic viscosity of ν = αHcs, which is a factor γ−1∕2 smaller than in our FARGO code, where γ is the adiabatic index.
For both codes, the disks enter an excited state with comparable eccentricity evolution. The differences between the simulations can be explained primarily by the different numerical methods used in the codes. The PLUTO code utilizes a Riemann-solver-based method that conserves total energy, at least in the hydrodynamic part. In contrast, FARGO uses a second-order upwind scheme that is not energy conserving and utilizes artificial viscosity to stabilize discontinuities. This energy-conserving property makes shock heating more effective and causes the PLUTO simulation to develop a higher disk temperature in the outer regions (r > 1 au). Due to the higher temperature, PLUTO produces a faster precessing disk which is in agreement with our predictions. The PLUTO simulation has a steeper eccentricity increase from the inner boundary, which results in an overall higher disk eccentricity. The overall similar dynamical evolution of the disk for the different codes lends strong support to our conclusion that the eccentric disk state is physical.
 |
Fig. A.1 Time evolution of the disk eccentricity using the physical setup of the standard model. Displayed are the results of two different codes that differ slightly in their resolution and domain size, see text for details. |
References
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [Google Scholar]
- Bate, M. R., Lubow, S. H., Ogilvie, G. I., & Miller, K. A. 2003, MNRAS, 341, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., Harrison, T. E., Endl, M., & Torres, G. 2018, RNAAS, 2, 7 [NASA ADS] [Google Scholar]
- de Val-Borro, M., Edgar, R. G., Artymowicz, P., et al. 2006, MNRAS, 370, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Dittmann, A., & Ryan, G. 2021, ApJ, submitted [arXiv:2102.05684] [Google Scholar]
- Dupuy, T. J., Kratter, K. M., Kraus, A. L., et al. 2016, ApJ, 817, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Dutrey, A., di Folco, E., Guilloteau, S., et al. 2014, Nature, 514, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Endl, M., Cochran, W. D., Hatzes, A. P., & Wittenmyer, R. A. 2011, in American Institute of Physics Conference Series, 1331, Planetary Systems Beyond the Main Sequence, eds. S. Schuh, H. Drechsel, & U. Heber, 88 [NASA ADS] [Google Scholar]
- Fragione, G. 2019, MNRAS, 483, 3465 [Google Scholar]
- Gong, Y.-X., & Ji, J. 2018, MNRAS, 478, 4565 [NASA ADS] [CrossRef] [Google Scholar]
- Goodchild, S., & Ogilvie, G. 2006, MNRAS, 368, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Günther, R., & Kley, W. 2002, A&A, 387, 550 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Hatzes, A. P., Cochran, W. D., Endl, M., et al. 2003, ApJ, 599, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kaigorodov, P. V., Bisikalo, D. V., Fateeva, A. M., & Sytov, A. Y. 2010, Astron. Rep., 54, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Nelson, R. P. 2008, A&A, 486, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., Papaloizou, J. C. B., & Ogilvie, G. I. 2008, A&A, 487, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuruwita, R. L., Ireland, M., Rizzuto, A., Bento, J., & Federrath, C. 2018, MNRAS, 480, 5099 [CrossRef] [Google Scholar]
- Lee, W.-K., & Gu, P.-G. 2015, ApJ, 814, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Lillo-Box, J., Barrado, D., & Bouy, H. 2014, A&A, 566, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews, 981 [Google Scholar]
- Lubow, S. H. 1991a, ApJ, 381, 259 [Google Scholar]
- Lubow, S. H. 1991b, ApJ, 381, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., & Ogilvie, G. I. 1998, ApJ, 504, 983 [Google Scholar]
- Malmberg, D., de Angeli, F., Davies, M. B., et al. 2007, MNRAS, 378, 1207 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, R. G., Lissauer, J. J., & Quarles, B. 2020, MNRAS, 496, 2436 [CrossRef] [Google Scholar]
- Marzari, F., & Barbieri, M. 2007, A&A, 467, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marzari, F., & Thebault, P. 2019, Galaxies, 7, 84 [CrossRef] [Google Scholar]
- Marzari, F., Scholl, H., Thébault, P., & Baruteau, C. 2009, A&A, 508, 1493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marzari, F., Baruteau, C., Scholl, H., & Thebault, P. 2012, A&A, 539, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menou, K., & Goodman, J. 2004, ApJ, 606, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Monin, J. L., Clarke, C. J., Prato, L., & McCabe, C. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil, 395 [Google Scholar]
- Muñoz, D. J., & Lai, D. 2016, ApJ, 827, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, T. W. A., & Kley, W. 2012, A&A, 539, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, A. F., & Marzari, F. 2016, ApJ, 827, 93 [Google Scholar]
- Oliva, G. A., & Kuiper, R. 2020, A&A, 644, A41 [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S. J., & Mellema, G. 2006, A&A, 450, 1203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S. J., Thébault, P., & Mellema, G. 2008, MNRAS, 386, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, K. J. 2006, MNRAS, 371, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Phuong, N. T., Dutrey, A., Diep, P. N., et al. 2020, A&A, 635, A12 [CrossRef] [EDP Sciences] [Google Scholar]
- Pichardo, B., Sparke, L. S., & Aguilar, L. A. 2005, MNRAS, 359, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Picogna, G., & Marzari, F. 2013, A&A, 556, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rafikov, R. R. 2013, ApJ, 765, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2017, ApJ, 837, 163 [CrossRef] [Google Scholar]
- Rafikov, R. R., & Silsbee, K. 2015, ApJ, 798, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, R., Bazso, A., Zechner, R., & Funk, B. 2016, in International Conference on the Astrophysics of Planetary Habitability [Google Scholar]
- Sellek, A. D., Booth, R. A., & Clarke, C. J. 2020, MNRAS, 498, 2845 [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
- Thebault, P., & Haghighipour, N. 2015, Planet Formation in Binaries, 309 [Google Scholar]
- Thébault, P., Marzari, F., & Scholl, H. 2006, Icarus, 183, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P., Marzari, F., & Scholl, H. 2008, MNRAS, 388, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Thun, D., Kley, W., & Picogna, G. 2017, A&A, 604, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trapman, L., Rosotti, G., Bosman, A. D., Hogerheijde, M. R., & van Dishoeck, E. F. 2020, A&A, 640, A5 [EDP Sciences] [Google Scholar]
- van Leer, B. 1977, J. Comput. Phys., 23, 276 [Google Scholar]
- Whitehurst, R. 1988, MNRAS, 232, 35 [NASA ADS] [Google Scholar]
- Zhu, Z., Dong,R., Stone, J. M., & Rafikov, R. R. 2015, ApJ, 813, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Ziampras, A., Ataiee, S., Kley, W., Dullemond, C. P., & Baruteau, C. 2020, A&A, 633, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zsom, A., Sándor, Z., & Dullemond, C. P. 2011, A&A, 527, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Disk surface density during one binary orbit for the standard parameters, see Table 1, after the equilibrium has been reached. The green line indicates the Roche lobes of the stars. In the leftmost image (t1) the binary is at apastron and the disk is unperturbed. At the binary’s periastron (t2) the diskis maximally distorted and has the highest eccentricity. After the periastron passage (t3) two spiral arms are launched that wind inward and dissipate again (t4). Most of the disk’s mass loss happens in the time frame between t2 and t4 that spans 15% of the binary’s period. |
| In the text | |
 |
Fig. 2 Time-averaged radial profile of the surface density and gas temperature of our fiducial model. Solid lines are averaged over 200 snapshots taken at the binary apastron during the simulation time from 1300 Tbin to 1500 Tbin. The shaded areas show the 1σ variations. |
| In the text | |
 |
Fig. 3 Time evolution of the mass-weighted disk eccentricity and the mass weighted longitude of pericenter for the fiducial model. The disk has the lowest eccentricity and has the least variation during one binary orbit when the longitude of pericenter is aligned with the binary periastron (ωd = ± π). From that point the disk’s eccentricity and variation during one binary orbit increases and reaches a maximum when the longitude of pericenter is aligned with the binary apastron (ωd = 0). |
| In the text | |
 |
Fig. 4 Time evolution of the mass-weighted disk eccentricity (see Eq. (3)) for different resolutions for a logarithmic grid. Solid lines are time averaged values while the transparent lines are the simulation data. |
| In the text | |
 |
Fig. 5 Time-averaged mass-weighted disk eccentricity plotted against the location of the inner domain boundary. |
| In the text | |
 |
Fig. 6 Azimuthally averaged disk eccentricity (see Eq. (4)) for different locations of the inner radius. Solid lines are averaged over 200 snapshots taken at the binary apastron during the simulation time from 1000 Tbin to 1200 Tbin. The shaded areas show the 1σ variations. The disk has a radius of ≈5 au, eccentricities at radii beyond that do not contribute to the disks eccentricity. |
| In the text | |
 |
Fig. 7 Time evolution of the mass-weighted disk eccentricity for different inner boundary conditions. Solid lines are averaged values while the transparent lines are the simulation data. The simulation with an open boundary at the inner domain does not reach an equilibrium state due to the rapid mass loss. The lower temperatures from losing mass slow down the precession rate. |
| In the text | |
 |
Fig. 8 Snapshot of the disks surface density after 481 orbital periods at the binary apastron. The simulation used an open inner boundary condition. Right: zoom in on the inner 1 au. Mass being removed at the inner boundary (gray area) causes the development of an eccentric hole. |
| In the text | |
 |
Fig. 9 Radial profiles of the time averaged mass-weighted disk eccentricity for different inner boundary conditions. Solid lines are averaged over 200 snapshots taken at binary apastron between T = 400 and 600Tbin. The shaded areas show the 1 σ variations. Eccentricity as well as precession are more uniform throughout the disk when open boundaries are used. The radial profiles are cut at a radius where the time averaged surface density drops below 100 times the floor value. |
| In the text | |
 |
Fig. 10 Radial profiles of the time averaged mass-weighted disk scale height, here h = H∕r, for different initial disk masses. Solid lines are averaged over 200 snapshots taken at binary apastron during the simulation time from 1300 Tbin to 1500 Tbin. The shaded areas show the 1 σ variations. The radial profiles are cut at a radius where the time averaged surface density drops below 100 times the floor value. |
| In the text | |
 |
Fig. 11 Time evolution of the mass-weighted disk eccentricity for different initial disk masses. |
| In the text | |
 |
Fig. 12 Time-averaged mass-weighted disk eccentricity plotted against the mass-weighted disk temperature. The arrows indicate the state after 2000 Tbin. At that time the α = 10−2 case has notreached an equilibrium yet. |
| In the text | |
 |
Fig. 13 Time evolution of the disk mass for different α values. |
| In the text | |
 |
Fig. 14 Radial profiles of the time averaged mass-weighted disk eccentricity for different α values. Solid lines are averaged over 200 snapshots taken at the binary apastron during the simulation time from 1300 Tbin to 1500 Tbin. The shaded areas show the 1 σ variations. The radial profiles are cut at a radius where the time averaged surface density drops below 100 times the floor value. |
| In the text | |
 |
Fig. 15 Time-averaged mass-weighted eccentricity plotted against the time averaged mass-weighted viscosity. The arrows indicate the state after 2000 Tbin. At that time the α = 10−2 case has notreached an equilibrium yet. |
| In the text | |
 |
Fig. 16 Time-averaged disk radius plotted against mass-weighted kinematic viscosity. |
| In the text | |
 |
Fig. 17 Precession rate plotted against the mass-weighted disk aspect ratio. Red dots mark the simulations with different α values, blue dots with different disk masses and magenta dots with different cooling factors and lower resolution. The green line is a quadratic fit through the data points. The precession rate depends linearly on the disk Temperature with T ∝ h2. |
| In the text | |
 |
Fig. 18 Snapshot at T = 662.74 Tbin of the radial profile of the longitude of pericenter, opacity and eccentricity of the fiducial model. The dashed vertical black line indicates the position of the change in the opacity power-law at T = 1100 K. The longitude of pericenter becomes undefined for e = 0 at the inner boundary. |
| In the text | |
 |
Fig. 19 Time evolution of the azimuthally mass-weighted average of the longitude of pericenter at two different radii for the fiducial model. The dotted line indicates the time the snapshot used in Fig. 18. |
| In the text | |
 |
Fig. 20 Disk eccentricity plotted against the standard deviation of the longitude of pericenter of all cells. The values mass averaged and time averaged over 200 snapshots at binary periastron from T = 1300 Tbin to T = 1500 Tbin. The old setup is using the standard parameters presented in Müller & Kley (2012). The arrows indicate the state after 2000 Tbin. |
| In the text | |
 |
Fig. 21 Time evolution of the mass-weighted disk eccentricity for the parameters of the standard case of Müller & Kley (2012) that is shown in green, and the parameters given in Table 1 but with α = 10−2. |
| In the text | |
 |
Fig. 22 Radial profiles of the time averaged mass-weighted disk eccentricity for our new setup and the standard models from Müller & Kley (2012). Solid lines are averaged over 200 snapshots taken at binary apastron. The shaded areas show the 1 σ variations. |
| In the text | |
 |
Fig. A.1 Time evolution of the disk eccentricity using the physical setup of the standard model. Displayed are the results of two different codes that differ slightly in their resolution and domain size, see text for details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


