EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A5 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A5
Number of page(s) 13
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202141071
Published online 01 October 2021

© ESO 2021

1 Introduction

The interstellar medium (ISM) is the mass reservoir for star formation in the Galaxy. It is permeated with matter, radiation, and magnetic fields. The matter consists of a mixture of ionised, atomic, and molecular gas, dust grains, and cosmic-rays (e.g. McKee & Ostriker 1977; Heiles & Haverkorn 2012). The process that converts interstellar matter into stars is highly multi-scale and multi-phase, governed by the interplay of thermal instability, magnetised turbulent motions, gravity, and stellar feedback (e.g. Hennebelle & Falgarone 2012; André et al. 2014; Hennebelle & Inutsuka 2019). In order to unveil this complex cycle of matter that regulates star formation and Galactic evolution, dedicated studies of the diffuse ISM and the dense molecular gas that hosts stellar embryos are needed. Here, we focus on the diffuse component of the ISM in the Milky Way through the unprecedented view of synchrotron emission provided by the LOw Frequency ARray (LOFAR, van Haarlem et al. 2013).

Synchrotron emission is non-thermal radiation produced mostly by relativistic cosmic-ray electrons, and to some extent by positrons, which spiral around magnetic field lines. The emission is highly linearly polarised. The degree of its intrinsic polarisation varies between 69 and 75%, depending on the slope of the cosmic-ray energy spectrum (e.g. Rybicki & Lightman 1986; Padovani et al. 2021).

At low radio frequencies (100–200 MHz), about 70% of the emission is expected to be intrinsically polarised, based on the observed synchrotron spectral index in total intensity (Guzmán et al. 2011; Mozdzen et al. 2017), which reflects the slope of the cosmic-ray energy spectrum. However, only a few percent of the originally polarised emission is observed (Jelić et al. 2014, 2015; Lenc et al. 2016; Van Eck et al. 2017, 2019) because of depolarisation effects associated with Faraday rotation and because of the degree of regularity in the magnetic field along the sight line.

As a linearly polarised wave at a wavelength λ [m] propagates through a magnetised interstellar plasma, its polarisation angle ψ [rad] is Faraday rotated by 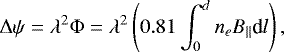(1)

where Φ [rad m−2] is the Faraday depth, ne [cm−3] is the density of the thermal electrons, B|| [μG] is the magnetic field strength of the component parallel to the line of sight l [pc], and the integral is taken from the source (l = 0) to the observer (l = d). The Faraday depth is positive when the magnetic field component parallel to the line of sight points towards the observer, while it is negative when it is in the opposite direction. For more details about the correct sense of Faraday rotation, we refer to Ferriére et al. (2021). In the Milky Way, where the distributions of thermal and cosmic-ray electrons are mixed throughout the entire volume, differential Faraday rotation occurs and depolarises the synchrotron emission (Wieringa et al. 1993; Sokoloff et al. 1998; Shneider et al. 2014). As Faraday rotation is proportional to λ2, depolarisation at low radio frequencies is more prominent than at high frequency. Nevertheless, the small amount of polarised emission that we observe carries valuable information about the physical properties of the intervening magnetised plasma.

A common technique used for analysing radio-polarimetric data is rotation measure (RM) synthesis (Burn 1966; Brentjens & de Bruyn 2005). This technique decomposes the observed polarised synchrotron emission by the amount of Faraday rotation it has experienced, that is, it allows us to perform so-called Faraday tomography. It is commonly used over the whole radio band (e.g. Jelić et al. 2014, 2015; Lenc et al. 2016; Van Eck et al. 2017, 2019; Dickey et al. 2019; Thomson et al. 2019; Wolleben et al. 2019).

Because of the frequency dependence of Faraday rotation and the wide frequency coverage of low-frequency instruments, such as LOFAR and the Murchison Widefield Array (MWA; Tingay et al. 2013), we can perform Faraday tomography at low-radio frequencies at a resolution in Faraday space that is a few orders of magnitude better than at GHz frequencies. At the same time, the maximum width of a structure in Faraday depth that an instrument is sensitive to, the so-called Faraday thickness (Brentjens & de Bruyn 2005), also depends on the frequency. A Faraday-thick structure at low radio frequencies can be Faraday thin at high frequency. This therefore needs to be taken into account when Faraday tomography results are interpreted, and the limitations in different frequency regimes need to be considered (Jelić et al. 2015; Van Eck et al. 2017; Van Eck 2018).

LOFAR observations of the 3C 196 field showed an astonishing variety of structures of Galactic polarised synchrotron emission varying with Faraday depth (hereafter Faraday structures, Jelić et al. 2015). The most striking features, which were seen for the first time, are very straight and long depolarisation canals. Some of them are a few degrees long and seem to extend outside the field of view. They are the result of beam depolarisation in regions of abrupt change in polarisation angle (Haverkorn & Heitsch 2004), while their straightness is likely associated with the projection of the ordered and coherent magnetic field on the scale of the field of view (Jelić et al. 2018). The depolarisation canals as well as some Faraday structures were found to be aligned in the same region with tracers of the neutral ISM. The alignment was observed with the filamentary structure of the 21 cm brightness temperature of atomic hydrogen (HI) and with the plane-of-sky magnetic field component that is probed by interstellar dust polarised emission at 353 GHz (Zaroubi et al. 2015; Kalberla et al. 2017; Van Eck et al. 2017; Jelić et al. 2018; Clark & Hensley 2019; Bracco et al. 2020).

A crucial and pending issue on these correlations observed between LOFAR synchrotron polarisation and tracers of the neutral ISM is understanding their 3D structure and their relative location along the line of sight. Recent studies suggested the possible association of the observed Faraday structures with the edge of the Local Bubble (Jelić et al. 2015, 2018), a 100–200 pc wide cavity around the Sun (e.g. Lallement et al. 2014). Today, powerful diagnostics of the 3D structure of the neutral ISM are represented by accurate and sensitive measures of parallaxes (e.g. Luri et al. 2018) and interstellar dust extinction towards stars across the Galaxy (e.g. Zucker et al. 2019; Green et al. 2019; Lallement et al. 2019; Leike et al. 2020).

In addition to providing a precise probe of the 3D density field in the ISM, stars can also provide information about the morphology of the 3D magnetic field (e.g. Tassis et al. 2018; Panopoulou et al. 2019). This is possible because the visible starlight is polarised by differential extinction of aspherical dust grains that are aligned with the Galactic magnetic field (Hall 1949; Hiltner 1949; Davis & Greenstein 1951).

In this paper, we have two main goals. First, we aim at extending the study of Faraday structures and depolarisation canals in LOFAR observations of three fields located nearby the 3C 196 field (see Fig. 1). Field A is located 10° below the 3C 196 field, towards the Galactic plane; Field B is at a similar Galactic latitude as the 3C 196 field, but 10° towards higher Galactic longitudes; and Field C is in the coldest part of the north Galactic halo. Second, for the first time, we use starlight polarisation data and stellar parallaxes to investigate the spatial distribution of the observed correlation between the depolarisation canals and the neutral ISM as a function of distance. The LOFAR observationsand the Faraday cubes presented in this paper were also used by Bracco et al. (2020) to study the morphological correlation of synchrotron polarisation with the multi-phase and magnetised HI. The authors found that most of the polarised emission seen in LOFAR data is correlated to the filamentary structure of the cold (< 100 K) HI gas (hereafter, cold neutral medium, or CNM).

The paper is organised as follows. LOFAR observations and related data products are described in Sect. 2. Section 3 presents the Faraday tomography of the diffuse polarised emission. The multi-tracer analysis of the depolarisation canals observed in three fields is presented in Sect. 4, while Sect. 5 presents the results based on the starlight polarisation data. The paper concludes with summary and conclusions in Sect. 6.

thumbnail Fig. 1

Stereographic projection of the Haslam 408 MHz map (Remazeilles et al. 2015) of the area nearby the 3C 196 field, given in Galactic coordinates. Positions of the three fields studied in this work (Fields A, B, and C) as well as the position of the 3C 196 field are marked with circles. The size of each circle corresponds to the field of view of each observation (37.6 deg2). For more details, see Sect. 2 and Table 1.
Table 1

Overview of the observational parameters of the three LOFAR-HBA observations.

2 Observations and data processing

The LOFAR High Band Antennas (HBA) observations of the three fields analysed in this paper were taken in January and February 2016 (under project code LC5_008). The array was used in the HBA DUAL INNER configuration (van Haarlem et al. 2013), where the remote stations were tapered to be the same as the core stations. The total observing time of each observation was 7 h and 40 min, with a correlator integration time of 2 s. The observations were symmetric around transit, and they were taken during night time. The observing frequency range was between 115 between 175 MHz, divided into 308 frequency sub-bands of 195.3125 kHz width. The spectral resolution was 3.05 kHz. The phase centres of each observation (see Fig. 1), together with their observational parameters, are given in Table 1.

The initial processing and calibration were performed following the steps described in Jelić et al. (2015). Here we give a brief overview of these steps. First, we applied automatic flagging of the radio-frequency interference (RFI) with AOFlagger (Offringa et al. 2010, 2012), after which we averaged the data in time and frequency. The resulting data have a time resolution of 12 s and a spectral resolution of 183 kHz because the first and last two 3.05 kHz channels of each frequency sub-band were removed. The averaged data were then calibrated in a direction-independent manner using Black Board Selfcal (Pandey et al. 2009). The sky-model used for the calibration was generated by the Global Sky Model1. It includes sources brighter than 1.5 Jy from the VLA Low-Frequency Sky Survey (VLSS) catalogue at 74 MHz (Cohen et al. 2007) and located within 3° from the phase centre of each observation.

We also corrected the data for the Faraday rotation produced by the Earth’s ionosphere using RMextract (Mevius 2018a,b). The ionospheric Faraday rotation was about 0.3 rad m−2 throughout the first two observations (Fields A and B), and it gradually decreased from 0.8 to 0.3 rad m−2 during the third observation (Field C).

The data were imaged in all Stokes parameters (I, Q, U and V) using excon(Yatawatta 2014). We used baselines between 10 and 800 wavelengths weighted with the Briggs scheme, using a robustness parameter equal to 0. This resulted in a frequency-independent angular resolution of 3.9′ × 3.6′, defined by the size of the point spread function (PSF). Finally, to perform Faraday tomography, we applied rmsynthesis2 (Brentjens & de Bruyn 2005) to the Stokes Q and U images of the 170 sub-bands, which had comparable noise levels (≲2.5 mJy PSF−1). These 183 kHz sub-bands covered frequencies between 115 MHz and 150 MHz. The frequencies above 150 MHz were highly affected by broadband RFI. If frequencies above 150 MHz, not affected by the RFI, were included in Faraday tomography, the sparse frequency coverage would give rise to three times higher sidelobes of the rotation measure spread function (RMSF) at |Φ| > 10 rad m−2. On the other hand, limiting our frequency coverage to the frequencies below 150 MHz resulted in a lower resolution inFaraday depth of 1.8 rad m−2, as comparedto 0.9 rad m−2 if all frequencies were taken into account. Observation of Field A was more affected by RFIs than the observations of Fields B and C, resulting in higher sidelobes (see Fig. 2). The final cubes covered a Faraday depth range from − 25 rad m−2 to + 25 rad m−2 in 0.25 rad m−2 steps. Because the resolution was higher than the maximum detectable scale (ΔΦ = 0.8 rad m−2), we were only sensitive to Faraday-thin structures (λ2ΔΦ ≪ 1) or the edges of Faraday-thick structures (λ2ΔΦ ≫ 1, Brentjens & de Bruyn 2005; Van Eck et al. 2017). We did not deconvolve the Faraday cubes for the sidelobe effect of the RMSF.

The noise in the Faraday cubes for the different observations is given in Table 2. It is calculated as the standard deviation of an image at Φ = −25 rad m−2, where we do not observe any polarised emission and the image is dominated by noise. The noise is comparable between Fields A and B, while in the case of FieldC, it is ~1.2 times lower.This difference can be attributed to the lower sky brightness in Field C than in Fields A and B (see Fig. 1). The system noise temperature, which defines the noise in the images at each frequency and consequently in the Faraday cubes, depends on the instrumental noise temperature and on the sky brightness temperature. Hence, the lower the sky brightness contribution, the lower system noise temperature. For all LOFAR frequencies, the sky brightness temperature is dominated by the frequency-dependent Galactic emission (van Haarlem et al. 2013). The noise in the Faraday cube of polarised intensity is consistent with normally distributed noise in Stokes Q, U.

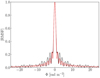thumbnail Fig. 2

Absolute value of the RMSF shown in black for Field A and in red for Fields B and C. The FWHM of the fitted Gaussian to the central peak of the RMSF gives the resolution in Faraday depth, δΦ = 1.8 rad m−2.
Table 2

Noise in the Faraday cubes of the observed fields, defined as a standard deviation of an image at Φ = −25 rad m−2.

3 Observational results

3.1 Faraday tomography of the diffuse polarised emission

Diffuse polarised emission is detected in all three fields, but in each field, the emission shows different characteristics. It has a rich morphology in Fields A and B with the brightness of a few mJy PSF−1RMSF−1. In contrast, the emission in Field C is very faint and patchy and has a diffuse morphology. The emission spans Faraday depths from − 6 to + 8 rad m−2 in Field A, from − 4 to + 8 rad m−2 in Field B, and from + 5 to + 15 rad m−2 in Field C. To emphasise the most prominent features of the observed emission, we constructed images showing the highest peak of the Faraday-depth spectrum at each pixel (hereafter called the maximum polarised intensity image) and the Faraday depth of each peak. We present these images in Fig. 3 for all three fields. Lack of emission at the edges of the fields is due to primary beam attenuation.

The emission in Field A can be divided, based on its distinctive morphology, into three groups of structures that appear at different Faraday depths. This segmentation in Faraday depth is needed because these structures spatially overlap, as can be seen in the greyscale in Fig. 4. The first morphological feature is an extended structure that appears in the centre of the image at a Faraday depth of − 6 rad m−2. As the Faraday depth increases towards − 1 rad m−2, the structure expands and first moves towards the north of the image and then mostly towards the southwest. The brightness temperature of this structure is about 4 mJy PSF−1 RMSF−1. The second morphological feature is large-scale emission that covers almost the whole area of the image within the primary beam. This emission shows many coherent morphological structures and depolarisation canals, with a northwest-southeast orientation. The brightness of this emission is about 2.5 mJy PSF−1 RMSF−1 and spans Faraday depths from − 0.75 to + 3 rad m−2. The third morphological feature is a boomerang-like structure in the southwest part of the image, which builds up from Faraday depths of + 3.25 rad m−2 and then disappears at + 8 rad m−2. The brightness of this structures reaches 2.5 mJy PSF−1 RMSF−1.

The emission in Field B consists of distinctive patches with the brightness of about 1 mJy PSF−1 RMSF−1. These patches first appear in the northwest part of the image at Faraday depth of − 4 rad m−2. As the Faraday depth increases towards + 8 rad m−2, the patches appear and disappear in different parts of the image. The patches at different Faraday depths seem to be organised in a large-scale cross-like structure (see images in the middle of Fig. 3).

The emission in Field C does not have any distinctive morphological features. The emission is very patchy and diffuse, with a brightness of 0.5 mJy PSF−1 RMSF−1. It spans a Faraday-depth range from + 5 to + 15 rad m−2 (see Fig. 3).

Polarised emission in Fields A and B is observed at positive and negative Faraday depths. This implies that the magnetic field component parallel to the line of sight varies across each field in direction and probably in strength as well. In Fig. 3 positive Faraday depths (red regions) are associated with the magnetic field component parallel to the line of sight pointing towards the observer, while negative Faraday depths (blue regions) when it points in the opposite direction. This does not necessarily mean that the magnetic field has the same orientation along the line of sight. It only gives the dominant orientation of the magnetic field as probed by the polarised emission along the line of sight. In case the magnetic field has reversals, structures in Faraday spectra appear at both positive and negative Faraday depths. This is indeed the case for a large portion of Field A, where structures at positive and negative Faraday depths spatially overlap (see Fig. 4). This overlap of structures at positive and negative Faraday depths is seen only in a small fraction of Field B (< 5%). Polarised emission in Field C is observed only at positive Faraday depths, implying the magnetic field component pointing towards the observer across the whole field of view.

The observed range of Faraday depths of polarised emission in the three fields is comparable to the range observed in the 3C 196 field (from − 3 to + 8 rad m−2; Jelić et al. 2015). This suggests possible similar physical conditions contributing to the Faraday rotation in these fields. Furthermore, the large-scale magnetic field component is almost perpendicular to the line of sight in the 3C 196 field, making the plane-of-the-sky magnetic field component the dominant one (Jelić et al. 2015). This was later also supported in multi-tracer analyses of the field (Zaroubi et al. 2015; Jelić et al. 2018). We expect the same to be the case for the three fields studied in this paper, as they are within 20° from the 3C196 field and show polarised emission within a comparable Faraday-depth range as in the 3C 196 field.

3.2 Brightness temperature and polarisation fraction

We integrated the polarised intensity in the Faraday cubes along the Faraday depth axis to estimate the brightness temperature of the observed polarised emission in each field. The integrated brightness for each (RA, Dec) pixel is given by Brentjens (2011), 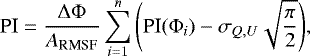(2)

where ΔΦ = |Φi+1 − Φi| is an equidistant step in Faraday depth, 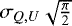is a correction for the non-zero mean of the noise in polarised intensity that is proportional to the noise in Stokes Q, U RM cubes (σQ,U), and ARMSF usually is the area of the restoring beam after deconvolution of the Faraday cubes with the corresponding RMSF (e.g. RM-CLEAN, Heald et al. 2009). Our Faraday cubes are not deconvolved. Thus, instead of the restoring beam, we considered the area of the RMSF function from − 10 to + 10 rad m−2. This is justified in our case as the peak brightness of the observed emission is only a few mJy PSF−1 RMSF−1 and the sidelobes of the RMSF function are of a few percent or smaller at Φ < −10 rad m−2 and Φ > +10 rad m−2. The sidelobe noise is therefore at these lower and higher Faraday depths comparable to or lower than the thermal noise. Finally, for a PSF of 3.9′ × 3.6′, 1 mJy PSF−1 amounts to a brightness temperature of 1.3 K at 130 MHz, a frequency that roughly corresponds to the weighted average of the observed λ2 used in RM synthesis ().

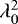The average brightness temperature of the polarised emission in Field A is 5 K, in Field B, it is 1.5 K, and in Field C, it is 0.6 K (see Table 3). To understand this difference, we estimated the total intensity and the polarisation fraction in each field. The polarisation fraction is defined as the ratio of the polarised and the total intensities. Because we have not observed emission in total intensity due to a lack of short baselines in our observations, we used the scaled Haslam 408 MHz All-Sky Map (Haslam et al. 1981, 1982; Remazeilles et al. 2015)3 as a proxy for the brightness temperature at 130 MHz. For the scaling, we use the spectral-index map of Galactic synchrotron emission between 45 and 408 MHz from Guzmán et al. (2011). The corresponding spectral indices, the brightness of the scaled emission at 408 MHz, and the calculated polarisation fractions are given in Table 3. The polarisation fraction in Field A is p = 1.1% ± 0.7%, while Fields B and C show a lower polarisation fraction with values p = 0.5% ± 0.3% and p = 0.2% ± 0.1%, respectively.These values should be taken as lower limits to the polarisation fraction at 130 MHz. LOFAR does not probe scales larger than a few degrees (≳3.5°), and there might be larger-scale polarised emission that we are missing. The lower polarisation fraction in Fields B and C arises because the depolarisation is stronger than in Field A. The same trend is also observed at 1.4 GHz (see also Table 3), where the polarisation fractions are estimated based on the single-dish observationsin total (Stockert 25 m + Villa Elisa 30m; Reich & Steffen 1981; Reich & Reich 1986; Reich et al. 2001)4 and polarised intensity (DRAO 26 m, Wolleben et al. 2006)4. The calculated polarisation fractions cannot be scaled and compared directly at the given frequencies because the data have different angular resolutions (36 arcmin at 1.4 GHz, and 4 arcmin at 130 MHz). The higher-frequency data are more strongly affected by the beam depolarisation than the data at lower frequencies.

thumbnail Fig. 3

Highest peak of the Faraday-depth spectrum in polarised intensity (left) and the map of the Faraday depth of the highest peak (right) for Fields A, B, and C from top to bottom, respectively. The dashed white and black circles have a diameter of 6.92°, corresponding to the full width at tenth maximum of the primary beam at 150 MHz, which is the smallest primary beam in the analysed frequency range.
thumbnail Fig. 4

RHT analysis performed on inverted maximum intensity images of Field A divided into three different Faraday-depth ranges. The upper part of the figure shows the results of the RHT analysis as weighted RHT back-projections (red lines) plotted over the maximum polarised intensity images. The lower part of the figure shows half-polar plots for the corresponding RHT back-projections, scaled according to their maximum. The Galactic plane orientation is at 0°. Red lines mark the averages of distinctive orientations, and light blue areas span the spread of the distributions for the corresponding averaged values.
Table 3

Overview of the brightness temperature and Faraday depth of the detected polarised emission in the observed fields.

4 Depolarisation canals

Striking features that can be seen in the maximum polarised intensity images are the depolarisation canals (see the left side images in Fig. 3). These are linear structures in the images showing no polarised emission, consistent with the noise. We mostly associate them with beam depolarisation at the location of discontinuities in the polarisation angle (Haverkorn & Heitsch 2004; Jelić et al. 2015). The most prominent canals are found in Fields A and B, and they are less abundant in Field C. We computed the orientation of these canals with respect to the Galactic-plane orientation as described in the following subsection.

4.1 Orientation of the depolarisation canals

To estimate the orientation of the depolarisation canals with respect to the Galactic plane, we followed Jelić et al. (2018) and used the rolling Hough transform (RHT5, Clark et al. 2014). The RHT is an algorithm for detecting straight lines in images. The output of the RHT is the quantity R(θ, x, y), where θ is the angle of the parametric straight line and x, y are the pixel coordinates over the coherent linear structure. To visualise the result of the RHT, the back-projection R(x, y) is obtained by integrating R(θ, x, y) over θ. The RHT algorithm uses three input parameters. The first is the smoothing kernel diameter (DK), which controls the suppression of the large-scale structures in the image; the second parameter defines the rolling window diameter (DW); and the last parameter is the probability threshold (Z), which defines a minimum number of pixels (within the rolling window) in a particular direction θ needed for them to be considered as a part of the same linear structure (for more details, see Clark et al. 2014). Jelić et al. (2018) showed that different combinations of the input parameters give very similar results for the orientation of the main linear depolarisation canals identified in the RHT back-projection, as the longest depolarisation canals dominate the overall distribution. The depolarisation canals in our fields have similar lengths as the depolarisation canals in the 3C 196 field. Therefore we used the same RHT input parameters (DK =8′, DW =50′ and Z = 0.8) as in Jelić et al. (2018) and applied the RHT algorithm on inverted images of the maximum polarised intensity (1/image). This highlights the canals over the surrounding emission, as the linear structures that appear in emission are suppressed and the algorithm is only sensitive to the linear depolarisation canals that are enhanced in the inverted images.

In addition to Jelić et al. (2018), we introduced the weighting of the RHT back-projection to analyse only the canals that are surrounded by emission that is at least 7σ above the noise in polarised intensity. For each pixel in the maximum polarised intensity image, we calculated the mean value of emission in its surroundings within a region of 1 × 3 PSF. If this mean brightness was lower than the 7σ threshold, the identified linear structure connected to that pixel was not taken into account. This ensured that we did not analyse linear structures defined by very faint polarised emission, whose morphology is ambiguous and dominated by noise. Different threshold values used for the weighting give similar results for the mean orientation of the depolarisation canals, while the spread of the distribution around the mean is within 20% compared to the results presented in the paper.

As mentioned in Sect. 3.1, the emission in Field A can be divided into three different Faraday-depth ranges according totheir morphologies. Therefore we performed the RHT algorithm separately for each range. The results of the RHT analysis for Field A are given in Fig. 4. The upper part of the figure shows the weighted RHT back-projections plotted overthe maximum polarised intensity images for each Faraday-depth range. The lower part of the same figure presents the half-polar plots for the corresponding weighted RHT back-projections, quantifying the relative orientation of the depolarisation canals with respect to the Galactic plane. To calculate the mean and the spread of the distributions, we made a full-circle projection of the half-polar plot and visualised every point as a vector with length R2 d θ. Integrating over the whole plane gives us a total vector whose direction and value measures the mean and the spread of the distribution (for details, see Jelić et al. 2018). The first Faraday-depth range shows three prominent orientations of the depolarisation canals: θ1 = −23° ± 4°, θ2 = −1° ± 2°, and θ3 = 15° ± 3°. The depolarisation canals have to a large extent negative orientations (θ1 and θ2). Two orientations (θ2 and θ3) are comparable in RHT intensities and have a lower intensity than the third orientation (θ1). Unlike the first, the second and third Faraday-depth ranges have two different orientations with respect to the Galactic plane, a negative and a positive orientation. The second Faraday depth range has orientations with values of θ1 = −11° ± 8° and θ2 = 17° ± 5°. In this case, the depolarisation canals have mostly negative orientations with a large spread. The third Faraday-depth range has orientations with values of θ1 = −59° ± 4° and θ2 = 11° ± 6°. Here the two orientations are represented equally.

Finally, we also applied the RHT on Fields B and C. The results are given in Figs. 5 and 6 and are presented as in Fig. 4. Two main orientations of the depolarisation canals with respect to the Galactic plane are detected in Field B, a negative and a positive orientation, with values of θ1 = −79° ± 5° and θ2 = 19° ± 4°, respectively. In the case of Field C, we find one positive orientation with a value of θ = 20° ± 2°.

4.2 Comparison with the orientation of the HI filaments

We compared the relative orientation of the depolarisation canals with the orientation of the HI filaments using publicly available data from the Galactic Effelsberg–Bonn HI Survey (EBHIS6, Winkel et al. 2016). The EBHIS data have anangular resolution of 10.8′ and a spectral resolution of 1.44 km s−1. We applied the RHT algorithm to the HI brightness temperature at each velocity channel of the EBHIS data, with the RHT input parameters (DK =10′, DW =100′ and Z = 0.8, following Clark et al. 2014; Jelić et al. 2018). We then summed the results over the velocity range in which the filaments are visible (see Fig. 7). The results are robust to the variation in the RHT parameters and to the exact velocity range, as demonstrated and discussed by Clark et al. (2014).

The upper part of Fig. 7 shows the RHT back-projections for the three fields, and the lower part presents the half-polar plots quantifying the relative orientation of the HI filaments with respect to the Galactic plane. We took only the RHT results into account that can be found inside a circle corresponding to the LOFAR primary beam.

The HI filaments in Field A show a broad distribution of orientations (θ = −4° ± 27°), with a mean roughly parallel to the Galactic plane. The distribution encompasses the orientations of the depolarisation canals associated with the structures observed at Faraday depths of [−6, −1] rad m−2 and [−1, +3] rad m−2. Depolarisation canals at Faraday depths of [+3, +8] rad m−2 partially match the orientation of the HI filaments. The RHT results for each velocity channel show that the HI filaments have a dominant orientation of − 21° ± 23° over the velocities of [−26, −15] km s−1, then it becomes 12° ± 19° over the velocities of [−14, −1] km s−1, while at positive velocities of [0, +13] km s−1, their dominant orientation is − 24° ± 25°. The dominant orientation of the depolarisation canals at Faraday depths of [−6, −1] rad m−2 and [−1, +3] rad m−2 seems to be consistent with the orientation of the HI filaments at velocities of [−26, −15] km s−1 and [0, +13] km s−1. One of the two dominant orientations of depolarisation canals at Faraday depths of [+3, +8] rad m−2 (11° ± 6°) seems to be consistent with the orientation of the HI filaments at velocities of [−14, −1] km s−1. However, it is very difficult to make definite conclusions given the broad distribution of the HI filament orientations at different velocities that can overlap. In this field, we might be probing velocity-confused HI gas, which makes the analysis more difficult.

Unlike Field A, Fields B and C show two distinct orientations with respect to the Galactic plane. The HI filaments in Field B have orientations of θ1 = −35° ± 24° and θ2 = 24° ± 14°, while in Field C, they are θ1 = −42° ± 21° and θ2 = 48° ± 21°. The dominant orientation of the HI filaments in Field B, θ2, matches one of the two orientations of the depolarisation canals observed in the same field. The HI filaments coherently show this orientation over a broad velocity range, between − 14 and + 4 km s−1. At high negative velocities, between − 22 and − 15 km s−1, the other orientation of the HI filaments, θ1, dominates. There is no clear correspondence between θ1 orientation of HI filaments and that of the depolarisation canals. In Field C, it is difficult to make a comparison because only a few depolarisation canals are detected. On the one hand, the observed coherence of the HI filament orientations over a wide range of velocities indicates a very uniform and ordered magnetic field. On the other hand, a change in their orientation at different velocities indicates a tangled line-of-sight magnetic field (Clark 2018). To quantify this in our fields, we used publicly available velocity-integrated synthetic HI Stokes parameter maps (IHI, QHI, UHI)7 derived by Clark & Hensley (2019) from the HI4PI all-sky spectroscopic data (HI4PI Collaboration 2016), which combines the EBHIS data (Winkel et al. 2016) in the north and the Parkes Galactic All-Sky Survey data (GASS; McClure-Griffiths et al. 2009) in the south. If the magnetic field is coherent and mostly in the plane of the sky, the synthetic polarisation fraction, defined as 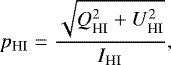(3)

is expected to be high (Clark & Hensley 2019). After averaging HI -based Stokes parameters within the field of view of each field, we find values of p = 10.9% in Field A, p = 7.4% in Field B, and p = 5.6% in Field C. Values for Fields A and B are higher than the all-sky average of p = 6.7%, while for Field C, the value is lower. We therefore conclude that the magnetic field is coherent and mostly in the plane of the sky in Fields A and B.

thumbnail Fig. 5

Same as in Fig. 4, but for Field B.
thumbnail Fig. 6

Same as in Fig. 4, but for Field C.

4.3 Comparison with the plane-of-the-sky magnetic field

We also compared the orientation of the depolarisation canals with the orientation of the plane-of-sky magnetic field component traced by the polarisation angle of dust-polarised emission rotated by 90°. The plane-of-sky magnetic field was obtained from the polarisation maps at 353 GHz of the Planck satellite. The Stokes Q and U maps (Planck Collaboration Int. XIX 2015; Planck Collaboration I 2016) are publicly available at the Planck Legacy Archive8. Due to the low signal-to-noise ratio of the observed polarised dust emission in all three fields, we used the Planck data smoothed to an angular resolution of 30′ via the HEALPix9 package in python, healpy (Górski et al. 2005; Zonca et al. 2019).

The results are shown in Fig. 8. The upper part of the figure shows visualisations of the magnetic field lines in the plane of the sky over the LOFAR polarised intensity as labelled by the different Faraday-depth ranges. The lower part of the figure presents the corresponding half-polar plots showing the relative orientation of the plane-of-the-sky magnetic field with respect to the Galactic plane. As in the case of the HI filaments, we only took magnetic field lines within a central circle of the images into account that corresponded to the LOFAR primary beam.

The mean orientation in Field A is slightly negative with a value of θ = −2° ± 9°, while in Fields B and C, it is positive with a value of θ = 18° ± 6° and θ = 9° ± 18°, respectively.Given the calculated spread around the mean orientation, the plane-of-sky magnetic field is more ordered in Fields A and B than in Field C, as is clearly visible in the images in Fig. 8. Similar results were also obtained when we smoothed the data to 80′, an angular resolution at which most of the intermediate Galactic latitude polarised dust emission has a signal-to-noise ratio higher than 3 (Planck Collaboration XII 2020).

In Fields A and B, most depolarisation canals have the same orientation as the plane-of-the-sky magnetic field component, which seemsto be very ordered on the scale of the fields of view. Field B also includes a distinct group of canals with orientationsthat depart from the plane-of-the-sky magnetic field by ~ 60°. This suggests the presence of two physical regions from which depolarisation canals may originate along the line of sight. Field C also shows acorrespondence between the orientation of the plane-of-the-sky magnetic field component and the depolarisation canals, but the magnetic field is less ordered.

thumbnail Fig. 7

RHT analysis performed on the HI brightness temperature at each velocity channel and integrated over the velocity range where the filaments are evident. The velocity range for each field is given below the images showing the RHT back-projections in the upper part of the figure. The lower part of the figure shows the corresponding distribution of the relative orientation of the HI filaments with respect to the Galactic plane as in Figs. 4–6. The RHT input parameters are DK =10′, DW =100′, and Z = 0.8 (see main text).

5 Starlight polarisation data – tracing distances

In this section, we present an innovative analysis that compares the orientation of the depolarisation canals with that of the polarisation angle detected towards stars in the fields of view. We searched for stars with available starlight polarisation data in the VizieR10 database (Heiles 2000; Berdyugin et al. 2001, 2014; Berdyugin & Teerikorpi 2002; Bailey et al. 2010). We then extracted their distances from the Bailer-Jones catalogue (Bailer-Jones et al. 2018), which is based on Gaia Data Release 2 (Gaia Collaboration 2018).

In the case of Fields A and C, we unfortunately lack a large enough sample of starlight polarisation measurements to make a meaningful analysis. Thus, we only present results for Field B, where we find 25 stars with measured polarisation (see Table A.1). Their locations within the field are given in Fig. 9. Their measured polarisation angles versus their distances are plotted in Fig. 10. Error bars are plotted for both polarisation angles and distances. The error on the distance is larger if the star is farther away, ranging from a few parsecs for the close-by stars to a few dozen parsecs for the more distant stars. The polarisation angles of stars are grouped around two main orientations of the depolarisation canals presented in Fig. 5, that is, at − 80° and + 20°, marked with horizontal lines in Fig. 10. The two stars with polarisation angles close to + 90° are associated with the − 80° orientation of the depolarisation canals due to the modulo π convention in the polarisation angle. The distances are between 100 and 200 pc for stars with polarisation angle of about − 80° and between 200 and 800 pc for stars with a polarisation of about 20°. Distance centroids are 161 ± 1 pc and 302 ± 1 pc for the first and second group of stars, respectively.

The given starlight polarisation measurement directly traces the plane-of-the-sky magnetic orientation, averaged over the dust density-weighted path-length to the star. Due to the complementary role of starlight polarisation produced by differential extinction in the visible and dust-polarised emission at longer wavelengths, the stars grouped at the largest distance likely trace the same average orientation of the magnetic field as is measured by the Planck satellite, namely the orientation of about 20° with respect to the Galactic plane (see Sect. 4.3). The group of stars in the foreground, in contrast, shows a typical magnetic fieldfield orientation of about − 80°, suggesting a tilt in the magnetic field structure between 200 and 300 pc.

We note, however, that the presence of these two separate groups of stars along the sight line with different magnetic field orientations requires a more careful discussion of the comparison between the orientation of the depolarisation canals and that of the starlightpolarisation. As a typical problem of magnetic field tomography based on starlight polarisation data (i.e. Panopoulou et al. 2019), we need to de-rotate the observed polarisation of the stars in the background for the amount of polarisation detected in the foreground. As explained in Appendix A, from the catalogue, we estimate the average Stokes q and u parameters (see Eq. (A.1)) with corresponding errors for the two distinct groups of stars, (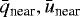)11 and (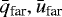). The average true value of the polarisation angle for the background stars can be written as 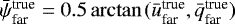, where 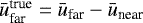and . 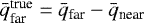Based on the tabulated data, we obtain a value of 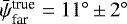, which is still rather consistent with the orientation of the depolarisation canals shown in Fig. 5. The foreground stars do not seem to affect the estimate of the background starlight polarisation much probably because the ratio is low, roughly ~30%, between the degree of polarisation of the nearby stars and that of the far away stars.

thumbnail Fig. 8

Top row: rendering of the magnetic field lines on the plane of the sky from Planck over the LOFAR polarised emission sliced into different Faraday depth ranges as labelled in the figure. Bottom row: corresponding distribution of the relative orientation of the plane-of-sky magnetic field lines with respect to the Galactic plane as in Fig. 4, for instance.
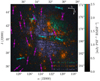thumbnail Fig. 9

Location of the stars in Field B. Colours correspond to two distinct groups of stars that trace different magnetic field orientations (cyan for stars at a distance closer than 200 pc, and magenta for stars at distances larger than 200 pc). The measured starlight polarisation angle is illustrated by two segments, whose aperture represents the error on the polarisation angle.
thumbnail Fig. 10

Angles vs. distance plot for Field B. The angle on the y-axis denotes the polarisation angle of the stars as well as the angle distribution of the depolarisation canals. The x-axis denotes the distance to the stars. Horizontal red lines mark the averages of distinctive orientations of the depolarisation canals, and light blue areas span the spread of the distributions for the corresponding averaged values, the same as in Fig. 5 with two peaks ~ 100° apart. The colours of the stars correspond to the same groups of stars shown in Fig. 9. We can freely shift the polarisation angles of the stars modulo π, meaning that the three stars plotted near 90° could also belong to the area below − 90° around the negative peak of the angle distribution of the depolarisation canals. The horizontal black line marks the average true value of the polarisation angle for the background stars, and the grey area spans the error range.
thumbnail Fig. 11

Summary of the results (see Figs. 4–8) showing the comparison of the orientations of the depolarisation canals (purple distribution), the HI filaments (green distribution), and the plane-of-the-sky magnetic field component (orange distribution) in relative scale. For Field A,we summed RHT results for depolarisation canals identified across the three Faraday-depth ranges given in Fig. 4.

6 Summary and conclusions

We have presented results based on the LOFAR HBA observations of three fields (Fields A, B, and C) in the surroundings of the 3C 196 field. We used Faraday tomography to analyse the observed polarised emission, which appears at Faraday depths between − 10 and + 15 rad m−2. The polarised emission is brightest in Field A (~ 5 K) because it is closest to the Galactic plane of the three fields. While the typical emission brightness in Field B is ~ 1.5 K, in Field C it reaches only ~ 0.6 K as this field is located in the coldest part of the northern Galactic hemisphere.

The observed morphology of emission differs in each field. It is richest in Field A, where we observe three distinct groups of structures at different Faraday depths. The morphology in Field B is dominated by a cross-like structure, while in Field C it is very faint, patchy, and diffuse. While all three fields show a complex system of straight depolarisation canals, they are more prominent in Fields A and B than in Field C. A likely explanation of this is the fact that we observe a lower amount of emission in Field C than in the other two fields. These depolarisation canals are associated with the effect of beam depolarisation in regions of abrupt changes in polarisation angle. The depolarisation canals we observe extend to a few degrees in length and resemble those observed in field 3C 196 (Jelić et al. 2015).

In Fields A, B, and C, Bracco et al. (2020) studied the statistical correlation between the polarised emission detected by LOFAR and the brightness temperature of the HI emission at 21 cm. They found a strong correlation between the two tracers of the multiphase ISM in Field A, in particular, with CNM HI gas, while they observed a lack of statistical correlation in Fields B and C. As explained by the authors, this resulted from limitations of the chosen statistical metrics given the patchy morphological emission in Fields B and C, as described above.

We have focussed on the characteristics of the depolarisation canals. We compared their orientation with that of both HI filaments and the plane-of-the-sky magnetic field component using the RHT. The results of this analysis are summarised in Fig. 11. There is a clear alignment between the three distinct ISM tracers in Fields A and B. The observed orientation in Field A is very similar to the one observed in the 3C 196 field (see Fig. 4 in Jelić et al. 2018). The dominant orientation of the depolarisation canals in Field B is ~ 15° more inclined with respect to the Galactic plane than in Field A and in the 3C 196 field. The alignment found for the HI filaments selected by the RHT is mostly associated with CNM structures (Clark et al. 2014) aligned to the depolarisation canals. This supports the result reported by Bracco et al. (2020) in the same fields of view, but considering polarised intensity.

Furthermore, in Field B, we observed two groups of stars at distances below and above 200 pc, respectively, that probe distinct magnetic field orientations. These are both comparable with the orientations of the depolarisation canals in the same field. The depolarisation canals seem to trace the same change of the magnetic field as probed by the stars. This change occurs at ~ 200 pc, a distance that is compatible with the edge of the Local Bubble, as also supported by 3D maps of the (local) ISM from measurements of starlight extinction by interstellar dust (Lallement et al. 2014, 2019; Capitanio et al. 2017, STILISM12 data), where the extinction seems to increase mostly between 150 and 300 pc.

Because starlight polarisation data are currently limited, however, it is difficult to assess how statistically significant this result is. Future stellar polarisation surveys of the high Galactic latitude sky, such as the Polar-Area Stellar Imaging in Polarisation High-Accuracy Experiment (PASIPHAE; Tassis et al. 2018), will change this and allow us to make a more detailed analysis.

The change in magnetic field traced by the stars and the depolarisation canals is also seen with the orientations of the HI filaments presented in this work.The HI filaments show an alignment over several velocity channels and a coherent change in their orientations towards the highest velocities. As discussed by Clark (2018) and Clark & Hensley (2019), this behaviour is expected if the magnetic field is coherent, mostly in the plane of the sky, but twisted along the line of sight. This is supported by the higher value of the synthetic HI polarisation fraction (pHI) in this field, calculated from the velocity-integrated synthetic HI Stokes parameters maps (Clark & Hensley 2019).

Field A also shows the higher pHI than the all-sky average, as is reported for the 3C 196 field (Clark & Hensley 2019). Therefore the observed alignment between theISM tracers reported in this work (Fields A and B) and in the 3C 196 field (Zaroubi et al. 2015; Jelić et al. 2018; Bracco et al. 2020) indicates a common, very ordered magnetic field with a dominant component in the plane of the sky, which probably shapes the observed morphology in a wide-field area of the sky connecting these three fields.

In contrast, this is not the case in Field C. We do not observe a clear correlation between the ISM tracers there, pHI is smaller than the all-sky average, and the plane of the sky magnetic field component probed by the Planck is less ordered. Hence, the dominant magnetic field component in Field C is probably not so much in the plane of the sky, and it is more random than ordered.

To conclude, multi-tracer analyses of Faraday tomographic data are inevitable if distances to the observed structures are to be constrained and the 3D nature of the magnetic field is to be understood. The magnetic field needs to be ordered with a dominant component in the plane of the sky to observe a correlation between different tracers of the multi-phase ISM. By combining Faraday tomographic data with starlight polarisation data we were able for the first time to directly estimate the distance to the observed depolarisation canals in the LOFAR data. The straight depolarisation canals seem to change orientation at the edge of the Local Bubble.

Acknowledgements

We thank an anonymous referee for their valuable comments which improved the paper. L.T., V.J. and A.E. acknowledge support by the Croatian Science Foundation for a project IP-2018-01-2889 (LowFreqCRO) and additionally L.T. and V.J. for the project DOK-2018-09-9169. M.H. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 772663). A.B. acknowledges the support from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Grant agreement No. 843008 (MUSICA). This paper is based on data obtained with the International LOFAR Telescope (ILT) under project code LC5_008. LOFAR (van Haarlem et al. 2013) is the Low Frequency Array designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, that are owned by various parties (each with their own funding sources), and that are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefited from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d’Orléans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK; Ministry of Science and Higher Education, Poland. The processing of the LOFAR observations were done on a CPU/GPU cluster dedicated to the LOFAR-EoR project, located at the University of Groningen and ASTRON in the Netherlands. Some of the results in this paper have been derived using the healpy and HEALPix package.

Appendix A Starlight polarisation data

This table gives the coordinates, distance, and polarisation angle of the 25 stars we used in the analysis of Field B (Sect. 5). The data are based on a selection of stars from the polarisation catalogues (Heiles 2000; Berdyugin et al. 2001; Berdyugin & Teerikorpi 2002; Bailey et al. 2010; Berdyugin et al. 2014). Their distances are extracted from the Bailer-Jones catalogue (Bailer-Jones et al. 2018), which is based on Gaia Data Release 2 (Gaia Collaboration 2018). The polarisation angles are given with respect to the Galactic plane in the range between − 90° and + 90°, consistently with the analysis of the depolarisation canals, the HI filaments, and the plane-of-the-sky magnetic field. The measurements of starlight polarisation allowed us to retrieve the Stokes parameters (Stokes Q and U) relative to the total intensity (Stokes I) for each star, which we estimated from the degree of polarisation, p, and the polarisation angle, ψ, as follows: 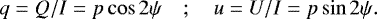(A.1)

Table A.1

List of 25 stars in Field B we used in the analysis, with their positions, distances, and polarisation angles (sorted by distance). A dashed horizontal line separates the two groups of stars discussed in Sect. 5.

References

  1. André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 27 [Google Scholar]
  2. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bailey, J., Lucas, P. W., & Hough, J. H. 2010, MNRAS, 405, 2570 [NASA ADS] [Google Scholar]
  4. Berdyugin, A., & Teerikorpi, P. 2002, A&A, 384, 1050 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Berdyugin, A., Teerikorpi, P., Haikala, L., et al. 2001, A&A, 372, 276 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Berdyugin, A., Piirola, V., & Teerikorpi, P. 2014, A&A, 561, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bracco, A., Jelić, V., Marchal, A., et al. 2020, A&A, 644, L3 [EDP Sciences] [Google Scholar]
  8. Brentjens, M. A. 2011, A&A, 526, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
  11. Capitanio, L., Lallement, R., Vergely, J. L., Elyajouri, M., & Monreal-Ibero, A. 2017, A&A, 606, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Clark, S. E. 2018, ApJ, 857, L10 [NASA ADS] [CrossRef] [Google Scholar]
  13. Clark, S. E., & Hensley, B. S. 2019, ApJ, 887, 136 [CrossRef] [Google Scholar]
  14. Clark, S. E., Peek, J. E. G., & Putman, M. E. 2014, ApJ, 789, 82 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cohen, A. S., Lane, W. M., Cotton, W. D., et al. 2007, AJ, 134, 1245 [NASA ADS] [CrossRef] [Google Scholar]
  16. Davis, Jr. L., & Greenstein, J. L. 1951, ApJ, 114, 206 [Google Scholar]
  17. Dickey, J. M., Landecker, T. L., Thomson, A. J. M., et al. 2019, ApJ, 871, 106 [NASA ADS] [CrossRef] [Google Scholar]
  18. Ferrière, K., West, J. L., & Jaffe, T. R. 2021, MNRAS, 507, 4968 [Google Scholar]
  19. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
  21. Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
  22. Guzmán, A. E., May, J., Alvarez, H., & Maeda, K. 2011, A&A, 525, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Hall, J. S. 1949, Science, 109, 166 [NASA ADS] [CrossRef] [Google Scholar]
  24. Haslam, C. G. T., Klein, U., Salter, C. J., et al. 1981, A&A, 100, 209 [NASA ADS] [Google Scholar]
  25. Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
  26. Haverkorn, M., & Heitsch, F. 2004, A&A, 421, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Heald, G., Braun, R., & Edmonds, R. 2009, A&A, 503, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Heiles, C. 2000, AJ, 119, 923 [NASA ADS] [CrossRef] [Google Scholar]
  29. Heiles, C., & Haverkorn, M. 2012, Space Sci. Rev., 166, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Hennebelle, P., & Falgarone, E. 2012, A&ARv, 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hennebelle, P., & Inutsuka, S.-i. 2019, Fronti. Astron. Space Sci., 6, 5 [NASA ADS] [CrossRef] [Google Scholar]
  32. HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Hiltner, W. A. 1949, Nature, 163, 283 [NASA ADS] [CrossRef] [Google Scholar]
  34. Jelić, V., de Bruyn, A. G., Mevius, M., et al. 2014, A&A, 568, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Jelić, V., de Bruyn, A. G., Pandey, V. N., et al. 2015, A&A, 583, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Jelić, V., Prelogović, D., Haverkorn, M., Remeijn, J., & Klindžić D. 2018, A&A, 615, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Kalberla, P. M. W., Kerp, J., Haud, U., & Haverkorn, M. 2017, A&A, 607, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Lallement, R., Vergely, J.-L., Valette, B., et al. 2014, A&A, 561, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Lallement, R., Babusiaux, C., Vergely, J. L., et al. 2019, A&A, 625, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Leike, R. H., Glatzle, M., & Enßlin, T. A. 2020, A&A, 639, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Lenc, E., Gaensler, B. M., Sun, X. H., et al. 2016, ApJ, 830, 38 [NASA ADS] [CrossRef] [Google Scholar]
  42. Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. McClure-Griffiths, N. M., Pisano, D. J., Calabretta, M. R., et al. 2009, ApJS, 181, 398 [NASA ADS] [CrossRef] [Google Scholar]
  44. McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
  45. Mevius, M. 2018a, Astrophys. Space Sci. Lib., 426, 103 [NASA ADS] [CrossRef] [Google Scholar]
  46. Mevius, M. 2018b, Astrophysics Source Code Library, record [record ascl:1806.024] [Google Scholar]
  47. Mozdzen, T. J., Bowman, J. D., Monsalve, R. A., & Rogers, A. E. E. 2017, MNRAS, 464, 4995 [CrossRef] [Google Scholar]
  48. Offringa, A. R., de Bruyn, A. G., Biehl, M., et al. 2010, MNRAS, 405, 155 [NASA ADS] [Google Scholar]
  49. Offringa, A. R., van de Gronde, J. J., & Roerdink, J. B. T. M. 2012, A&A, 539, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Padovani, M., Bracco, A., Jelić, V., Galli, D., & Bellomi, E. 2021, A&A, 651, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Pandey, V. N., van Zwieten, J. E., de Bruyn, A. G., & Nijboer, R. 2009, ASP Conf. Ser., 407, 384 [NASA ADS] [Google Scholar]
  52. Panopoulou, G. V., Tassis, K., Skalidis, R., et al. 2019, ApJ, 872, 56 [NASA ADS] [CrossRef] [Google Scholar]
  53. Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Planck Collaboration XII. 2020, A&A, 641, A12 [CrossRef] [EDP Sciences] [Google Scholar]
  55. Planck Collaboration Int. XIX. 2015, A&A, 576, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Reich, P., & Reich, W. 1986, A&AS, 63, 205 [NASA ADS] [Google Scholar]
  57. Reich, W., & Steffen, P. 1981, A&A, 93, 27 [NASA ADS] [Google Scholar]
  58. Reich, P., Testori, J. C., & Reich, W. 2001, A&A, 376, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Remazeilles, M., Dickinson, C., Banday, A. J., Bigot-Sazy, M. A., & Ghosh, T. 2015, MNRAS, 451, 4311 [NASA ADS] [CrossRef] [Google Scholar]
  60. Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Hoboken: Wiley) [Google Scholar]
  61. Shneider, C., Haverkorn, M., Fletcher, A., & Shukurov, A. 2014, A&A, 567, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1998, MNRAS, 299, 189 [NASA ADS] [CrossRef] [Google Scholar]
  63. Tassis, K., Ramaprakash, A. N., Readhead, A. C. S., et al. 2018, ArXiv e-prints [arXiv:1810.05652] [Google Scholar]
  64. Thomson, A. J. M., Landecker, T. L., Dickey, J. M., et al. 2019, MNRAS, 487, 4751 [CrossRef] [Google Scholar]
  65. Tingay, S. J., Goeke, R., Bowman, J. D., et al. 2013, PASA, 30, e007 [Google Scholar]
  66. Van Eck, C. 2018, Galaxies, 6, 112 [NASA ADS] [CrossRef] [Google Scholar]
  67. Van Eck, C. L., Haverkorn, M., Alves, M. I. R., et al. 2017, A&A, 597, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Van Eck, C. L., Haverkorn, M., Alves, M. I. R., et al. 2019, A&A, 623, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Wieringa, M. H., de Bruyn, A. G., Jansen, D., Brouw, W. N., & Katgert, P. 1993, A&A, 268, 215 [NASA ADS] [Google Scholar]
  71. Winkel, B., Kerp, J., Flöer, L., et al. 2016, A&A, 585, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Wolleben, M., Landecker, T. L., Reich, W., & Wielebinski, R. 2006, A&A, 448, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Wolleben, M., Landecker, T. L., Carretti, E., et al. 2019, AJ, 158, 44 [NASA ADS] [CrossRef] [Google Scholar]
  74. Yatawatta, S. 2014, MNRAS, 444, 790 [NASA ADS] [CrossRef] [Google Scholar]
  75. Zaroubi, S., Jelić, V., de Bruyn, A. G., et al. 2015, MNRAS, 454, L46 [NASA ADS] [Google Scholar]
  76. Zonca, A., Singer, L., Lenz, D., et al. 2019, J. Open Source Softw., 4, 1298 [NASA ADS] [CrossRef] [Google Scholar]
  77. Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2019, ApJ, 879, 125 [Google Scholar]
11

The bar refers to average quantities.

All Tables

Table 1

Overview of the observational parameters of the three LOFAR-HBA observations.

In the text
Table 2

Noise in the Faraday cubes of the observed fields, defined as a standard deviation of an image at Φ = −25 rad m−2.

In the text
Table 3

Overview of the brightness temperature and Faraday depth of the detected polarised emission in the observed fields.

In the text
Table A.1

List of 25 stars in Field B we used in the analysis, with their positions, distances, and polarisation angles (sorted by distance). A dashed horizontal line separates the two groups of stars discussed in Sect. 5.

In the text

All Figures

thumbnail Fig. 1

Stereographic projection of the Haslam 408 MHz map (Remazeilles et al. 2015) of the area nearby the 3C 196 field, given in Galactic coordinates. Positions of the three fields studied in this work (Fields A, B, and C) as well as the position of the 3C 196 field are marked with circles. The size of each circle corresponds to the field of view of each observation (37.6 deg2). For more details, see Sect. 2 and Table 1.
In the text
thumbnail Fig. 2

Absolute value of the RMSF shown in black for Field A and in red for Fields B and C. The FWHM of the fitted Gaussian to the central peak of the RMSF gives the resolution in Faraday depth, δΦ = 1.8 rad m−2.
In the text
thumbnail Fig. 3

Highest peak of the Faraday-depth spectrum in polarised intensity (left) and the map of the Faraday depth of the highest peak (right) for Fields A, B, and C from top to bottom, respectively. The dashed white and black circles have a diameter of 6.92°, corresponding to the full width at tenth maximum of the primary beam at 150 MHz, which is the smallest primary beam in the analysed frequency range.
In the text
thumbnail Fig. 4

RHT analysis performed on inverted maximum intensity images of Field A divided into three different Faraday-depth ranges. The upper part of the figure shows the results of the RHT analysis as weighted RHT back-projections (red lines) plotted over the maximum polarised intensity images. The lower part of the figure shows half-polar plots for the corresponding RHT back-projections, scaled according to their maximum. The Galactic plane orientation is at 0°. Red lines mark the averages of distinctive orientations, and light blue areas span the spread of the distributions for the corresponding averaged values.
In the text
thumbnail Fig. 5

Same as in Fig. 4, but for Field B.
In the text
thumbnail Fig. 6

Same as in Fig. 4, but for Field C.
In the text
thumbnail Fig. 7

RHT analysis performed on the HI brightness temperature at each velocity channel and integrated over the velocity range where the filaments are evident. The velocity range for each field is given below the images showing the RHT back-projections in the upper part of the figure. The lower part of the figure shows the corresponding distribution of the relative orientation of the HI filaments with respect to the Galactic plane as in Figs. 4–6. The RHT input parameters are DK =10′, DW =100′, and Z = 0.8 (see main text).
In the text
thumbnail Fig. 8

Top row: rendering of the magnetic field lines on the plane of the sky from Planck over the LOFAR polarised emission sliced into different Faraday depth ranges as labelled in the figure. Bottom row: corresponding distribution of the relative orientation of the plane-of-sky magnetic field lines with respect to the Galactic plane as in Fig. 4, for instance.
In the text
thumbnail Fig. 9

Location of the stars in Field B. Colours correspond to two distinct groups of stars that trace different magnetic field orientations (cyan for stars at a distance closer than 200 pc, and magenta for stars at distances larger than 200 pc). The measured starlight polarisation angle is illustrated by two segments, whose aperture represents the error on the polarisation angle.
In the text
thumbnail Fig. 10

Angles vs. distance plot for Field B. The angle on the y-axis denotes the polarisation angle of the stars as well as the angle distribution of the depolarisation canals. The x-axis denotes the distance to the stars. Horizontal red lines mark the averages of distinctive orientations of the depolarisation canals, and light blue areas span the spread of the distributions for the corresponding averaged values, the same as in Fig. 5 with two peaks ~ 100° apart. The colours of the stars correspond to the same groups of stars shown in Fig. 9. We can freely shift the polarisation angles of the stars modulo π, meaning that the three stars plotted near 90° could also belong to the area below − 90° around the negative peak of the angle distribution of the depolarisation canals. The horizontal black line marks the average true value of the polarisation angle for the background stars, and the grey area spans the error range.
In the text
thumbnail Fig. 11

Summary of the results (see Figs. 4–8) showing the comparison of the orientations of the depolarisation canals (purple distribution), the HI filaments (green distribution), and the plane-of-the-sky magnetic field component (orange distribution) in relative scale. For Field A,we summed RHT results for depolarisation canals identified across the three Faraday-depth ranges given in Fig. 4.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.