EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A111 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A111
Number of page(s) 12
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202140600
Published online 19 October 2021

© ESO 2021

1. Introduction

Alfvénicity is a feature of solar wind fluctuations frequently observed in interplanetary data. It is characterized by a strong correlation between velocity and magnetic field vectors, corresponding to large amplitude Alfvén waves propagating mainly away from the Sun (e.g., Belcher et al. 1969; Belcher & Davis 1971; Belcher & Solodyna 1975). In those cases, the fluctuations also show low compressibility, that is to say an almost constant proton number density and magnetic field magnitude. The low magnetic compressibility can be pictured as the tip of the magnetic field vector, with a fixed magnitude, wandering on the surface of a sphere whose radius is the field magnitude (Bruno et al. 2004). Solar wind fluctuations at fluid scales are usually interpreted as a mixture of two different populations, that is to say outward and inward propagating Alfvénic fluctuations. In reality, what we can assess from in situ data is just the level of correlation between magnetic and kinetic fluctuations whose sign corresponds, by definition, to an outward or inward sense of propagation. The Alfvénic nature of outward modes has been widely recognized up to periods on the order of several hours in the s/c rest frame (Bruno et al. 1985). Conversely, the nature of the so-called inward modes is still not completely clear. Tu et al. (1989) proposed a mechanism of generation of inward modes with an Alfvénic nature based on the parametric decay of large amplitude Alfvén waves (Galeev & Oraevskii 1963). Velli et al. (1990) modeled inward modes as that fraction of outward modes back-scattered by the inhomogeneities of the medium due to expansion effects (Velli et al. 1989), taking expansion effects into account. However, there are many indications suggesting that these fluctuations, especially in the hourly frequencies range, have a non-Alfvénic nature (Bruno et al. 1997). Several studies on this topic in the low frequency range have suggested that magnetic structures advected by wind could indeed act as inward propagating modes (Tu & Marsch 1993; Bruno et al. 2001), contributing to the observed excess of magnetic energy over kinetic energy. On the other hand, inward modes may also be associated with quasi-perpendicular propagating slow-mode waves (He et al. 2015), or randomly distributed magnetic structures advected along with the solar wind flows (Yan et al. 2016). Zhu et al. (2020) have shown that in the inner heliosphere (Parker Solar Probe, PSP, measurements), the sunward Alfvén waves are observed more rarely than the sunward slow magnetosonic waves. The origin of Alfvénic ouward and inward fluctuations, as observed in interplanetary space beyond the Alfvénic radius, that is the critical radius where the solar wind becomes super-Alfvénic, must necessarily be different if they correspond to propagating modes. This distance systematically moves from about 15 R⊙ (R⊙ being the solar radius) at solar minimum to about 30 R⊙ at solar maximum (Goelzer et al. 2014). Since the wind becomes super-Alfvénic beyond the Alfvénic radius, it is clear that Alfvénic inward modes observed in space cannot be of solar origin, but they must have been created locally by some generation process (see Bruno & Carbone 2013, and references therein). Obviously, outward modes can have both a solar and local origin.

The Alfvénic content of fluctuations decreases with increasing heliocentric distance. This behavior has been shown by Helios data studying the radial evolution of the same fast wind stream after successive solar rotations (Bruno et al. 2007). On the other hand, although fast streams are typically more Alfvénic than slow wind, the Alfvénic signature of the fluctuations in the slow wind observed close to the Sun by Helios is rapidly lost when reaching 1 AU. The same behavior is found in the slow wind observed by PSP (e.g., Bale et al. 2019). By contrast, observations by Wind at 1 AU during the maximum of solar cycle 23 show that, in some cases, high Alfvénic fluctuations are also observed in slow wind, as highlighted in D’Amicis et al. (2011, 2019), and D’Amicis & Bruno (2015). These studies have shown statistical evidence of a slow solar wind characterized by a high degree of Alfvénicity, even at 1 AU where the v − b correlation is expected to degrade.

In general, solar wind fluctuations show a power-law spectrum (as first observed by Coleman 1968) that closely resembles a typical turbulent spectrum, with a slope in the inertial range between −5/3 (Kolmogorov 1941) and −3/2 (Iroshnikov 1963; Kraichnan 1965). This result has been interpreted as evidence of a nonlinear interaction between inward and outward Alfvén modes present in solar wind in different amounts, which produces a turbulent energy cascade, actively transferring energy from large to small scales (Tu et al. 1984). The predominance of Alfvén modes determines a strong Alfvénic character of solar wind turbulence. Large amplitude Alfvénic fluctuations are especially found within the main portion of fast streams so that Alfvénic turbulence seen during those intervals typically has a larger relative amplitude than the more typical, compressible turbulence seen in slow streams. Ko et al. (2018) show that the transition between high and low amplitude fluctuations changing with wind speed is rather abrupt, with the lowest fluctuation amplitudes which correspond to the lowest speed. Recently, it has been found that power spectra of magnetic (D’Amicis et al. 2019; D’Amicis et al. 2020) and velocity (D’Amicis et al. 2020) field fluctuations in Alfvénic streams (whether fast or slow) are characterized by higher power than that corresponding to the non-Alfvénic wind, which is characterized by a larger amplitude in the fluctuations.

Fast and Alfvénic slow solar wind power spectra show, at low frequencies, a 1/f scaling which might be associated with the saturation of magnetic field fluctuations to amplitudes comparable to those of the average magnitude field in both fast (Matteini et al. 2018) and slow (Bruno et al. 2019; D’Amicis et al. 2020; Perrone et al. 2020) wind. It must be noted that the 1/f scaling is only recovered in the non-Alfvénic slow wind if the interval is long enough to properly capture the low-frequency spectral properties and when perpendicular, directional fluctuations are much larger than the compressive ones (Bruno et al. 2019). The 1/f scaling is separated from the so-called inertial range by a break located around a typical scale that depends on distance and typically lies in between tens of minutes and a few hours. Around the ion characteristic scales, another break, moving to higher frequencies as the wind expands, in the magnetic field power spectra is observed, which separates the inertial range from the kinetic range. The ion-scale spectral break seems to satisfy the cyclotron resonant condition rather than matching the location of the ion inertial length and the Larmor radius (e.g., Bruno & Trenchi 2014; Woodham et al. 2018; Wang et al. 2018; D’Amicis et al. 2019). On the other hand, the ion-scale spectral break may not only be related to the cyclotron-resonance dissipation, but also to the dispersion effect due to ion-electron decoupling. Duan et al. (2018) attribute the observed anisotropy of the spectral break at ion scales to the turbulence diffusion effect, which incorporates both the dissipation and dispersion effects. The radial evolution of the spectral break position and its dependence on plasma beta has been analyzed by Duan et al. (2020) based on PSP measurements in the inner heliosphere. Around the ion scales, spectra become steeper and the slope is closely linked to the power of the fluctuations in the inertial range: the higher the power, the steeper the spectra (Bruno & Trenchi 2014; D’Amicis et al. 2019).

The study of the Alfvénic slow wind represents a topical subject, supported also by the recent observations of PSP. D’Amicis et al. (2021) provide a comprehensive review on the state of the Alfvénic slow wind at different radial distances, both in the inner heliosphere and close to Earth. One of the main open questions remaining pertains to its source region. However, the strong similarities with the fast wind suggest a similar solar source (D’Amicis et al. 2019). Indeed, several pieces of evidence have been given to link the Alfvénic slow wind to open field regions on the solar surface, namely coronal holes (Wang & Sheeley 1990; Wang 1994; Neugebauer et al. 1998; Antonucci et al. 2005; D’Amicis et al. 2019; Bale et al. 2019; Wang & Ko 2019; Wang & Panasenco 2019; Perrone et al. 2020; Stansby et al. 2020; Panasenco et al. 2020) or from small areas with open fields in the quiet-Sun regions (Wang et al. 2019). In particular, the main candidates to be the source of the Alfvénic slow wind are regions of anomalous (larger than the average) expansion rate of magnetic flux tubes near the Sun. The area associated with coronal holes, at both high and low latitudes, varies during a solar cycle. Generally, high-latitude coronal holes dominate during solar minima and their area decreases as the sunspot number increases. In contrast, low-latitude coronal holes are present during the whole solar cycle, but their area shows a minimum at the sunspot minimum (Mazumder et al. 2018). By considering the last two solar cycles, that is cycle 23 and the current cycle 24, it has been observed that low-latitude coronal holes cover a large area during the maxima. Therefore, a significant amount of total open flux on the Sun is expected during these solar maxima. However, during solar cycle 24, the area covered by low-latitude coronal holes is remarkably smaller than in cycle 23 (Lowder et al. 2017).

The common origin of both fast and Alfvénic slow wind was also studied using in situ charge state composition. This approach is used in the present paper. Since the ionization and recombination rates are proportional to the electron density that decreases with distance, they also rapidly decrease with distance within few R⊙. A critical height is reached when the electron density is so low that the two processes are frozen (Owocki et al. 1983). This is the so-called freeze-in process.

Beyond the freeze-in point, the charge states of the heavy ions remain unaltered as the solar wind propagates into the heliosphere and they maintain a record of the thermal properties of the plasma in the inner corona at their freeze-in height. Thus, in situ measurements of the ion charge states can provide critical information on the thermal properties of the inner corona, generally below 10 R⊙, where the solar wind originates (e.g., Zhao et al. 2009, 2014; von Steiger et al. 2010). Generally speaking, composition is observed to be anticorrelated with flow speed. Several studies (e.g., Zurbuchen et al. 1999, and references therein) have shown that a sharp transition is observed when passing from fast to slow streams, with a particular reference to a heavy ion charge state and elemental abundances. In fact, the charge state composition clearly distinguishes a coronal-hole-associated solar wind from a streamer-associated slow solar wind (Geiss et al. 1995; von Steiger et al. 1997, 2000). In addition, variations in the charge state within low-speed solar winds also separate different sources of low-speed solar winds (Zurbuchen et al. 2000). Within this context, the Alfvénic slow wind shows characteristics similar to the fast wind rather than to other typical compressible slow streams (D’Amicis et al. 2019), which is at odds with theoretical predictions.

The purpose of this article is to present an analysis on solar wind Alfvénicity over several years encompassing solar cycle 23 and 24 in order to foresee what should be expected for solar cycle 25. It is worth noting that during the last three solar cycles, a gradual and notable decline in the solar activity has been observed (Basu 2013; Kakad et al. 2019). Several studies suggest that this phase of weakened activity will continue, implying that cycle 25 is still weaker (Hathaway & Wilson 2004; Janardhan et al. 2015, 2018). The paper is organized as follows. Data selection is presented in Sect. 2 along with the introduction of some tools used to characterize solar wind turbulence in Sect. 3. Section 4 is devoted to the presentation of the results. In particular, a first statistical approach is presented in Sect. 4.1 to fully characterize Alfvénicity for different phases of the two solar cycles along with plasma composition (Sects. 4.1.1 and 4.1.2, respectively). A comparison of case studies selected during the maximum of two solar cycles is used to better characterize the Alfvénic solar wind predominant during this phase of solar activity (Sect. 4.2). In particular, Sect. 4.2.1 presents a general description of the case studies and Sect. 4.2.2 focuses on the spectral properties. In Sect. 5, a summary and a discussion of the results are presented.

2. Data selection

The present study is based on several months of data selected at maximum and minimum of both solar cycle 23 and 24, in the following indicated as SC23 and SC24, as shown in Fig. 1 and Table 1. The different phases of the two solar cycles are indicated in Fig. 1, showing the temporal variation in the sunspot number as dashed colored boxes: blue for solar maximum and red for solar minimum. Table 1 displays in detail the start and end of each time interval. In this study, we consider “minimum” to be the time interval, just preceding the real minimum, in which the solar wind is bimodal if observed in the ecliptic plane, that is characterized by an alternation of fast and slow streams. In this case, fast streams are generally recurrent structures (corotating) and they can be observed after successive solar rotations since they come from the same solar source. The same is not observed as clearly during the real minimum of the sunspot number.

thumbnail Fig. 1.

Monthly sunspot number (SN) as a function of time (gray line) and smoothed average (black line) during solar cycles 23 and 24. The dashed colored boxes indicate the selected 30-month intervals: blue for solar maximum and red for solar minimum.

Table 1.

Data selection: maximum and minimum of solar cycle 23 and 24.

This analysis was performed using data from Wind, with a particular focus on solar wind measurements derived from the Three-Dimensional Plasma and Energetic Particle Investigation (3DP) instrument (Lin et al. 1995) at 24 sec resolution. The 3DP database also includes magnetic field measurements from the Magnetic Field Investigation (MFI) instrument (Lepping et al. 1995), linearly interpolated at the plasma resolution. The plasma composition was derived from the Solar Wind Ion Composition Spectrometer (SWICS) instrument (Gloeckler et al. 1998) on board Advanced Composition Explorer (ACE) at 1 h resolution for SC23. Although both Wind and ACE generally occupy a halo orbit about the L1 Earth-Sun libration point L1, Wind was closer to Earth, but still in the solar wind during the interval selected at maximum of SC23. SWICS composition data for SC24 must be used with caution since they involve measurements from the SWICS 2.0 dataset at 2 h resolution released after August 23rd, 2011, when a hardware anomaly altered the instrument’s operational state as widely reported in the release note. The new dataset, however, presents some saturation issues, thus those data are not used for the present analysis. We then perform a comparative study between maximum and minimum of the same solar cycle.

3. Method of analysis

To characterize the state of turbulence, we introduce the Elsässer variables (Elsässer 1950) that are useful to separate the outward from the inward contribution in the solar-wind Alfvénic fluctuations. These variables were used for interplanetary data, for the first time, by Grappin et al. (1991) and Tu et al. (1989). The Elsässer variables are defined in the following way: z± = v ± b, where b is the magnetic field expressed in Alfvén units (b = B/(4πρ)1/2, where ρ is the mass density and B is the magnetic field). The sign in front of b depends on the sign( − k ⋅ B0), where k is the wave vector and B0 is the ambient magnetic field. In fact, for a field directed outward (with respect to the Sun), a negative correlation indicates a mode propagating away from the Sun, while a positive one represents a mode directed toward the Sun. In case the field is directed toward the Sun, the correlation sign reverses with respect to the previous cases. The scientific community has agreed to define Elsässer variables in such a way that z+ always refers to outward modes, while z− refers to inward modes (see also D’Amicis et al. 2007; D’Amicis et al. 2010; D’Amicis et al. 2011; D’Amicis & Bruno 2015 for more details).

Tu & Marsch (1995) introduced the normalized cross-helicity, σC = (e+ − e−)/(e+ + e−), and the normalized residual energy, σR = (ev − eb)/(ev + eb), where e± is the energy (per unit mass) associated to z± modes, while ev and eb are the kinetic and magnetic energy (per unit mass), respectively. They were derived from two of the three invariants for the ideal magnetohydrodynamics (MHD) equations of motion: the total energy and the cross-helicity expressed in terms of Elsässer variables. Being normalized quantities, σC and σR vary from −1 and +1 and they indicate how much a mode (either inward or outward) is dominant with respect to the other and the predominance of magnetic fluctuations on velocity ones or viceversa, respectively. An ideal Alfvén wave satisfies the following conditions: σC = ±1 (where +1 indicates fluctuations that propagate away from the Sun, while −1 modes toward the Sun) and σR = 0 (equipartition between kinetic and magnetic energy). These quantities were computed at a 1 h scale which is a typical characteristic time in the Alfvénic range where solar wind fluctuations show a strong Alfvénic character (Marsch & Tu 1990). We would also like to add that from the definition, 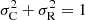. This condition identifies the most correlated measurements, being the correlation coefficient, Cvb, linked to σC and σR by 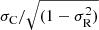, provided that σR ≠ ±1 (Grappin et al. 1982; Roberts et al. 1987). As a consequence, there are cases when σC is lower than expected even if the correlation coefficient is high since σR is not close to equipartition.

4. Results

4.1. Statistical analysis during solar cycles

A comparative study on the Alfvénic content of solar-wind fluctuations between different solar cycles is, to our knowledge, still missing. However, understanding how Alfvénicity could change during different phases of the solar cycle or between different solar cycles is extremely important to predict the solar wind environment where PSP and Solar Orbiter will be embedded in the near future. In particular, since the new solar cycle is approaching, it is now crucial to foresee what should be expected in terms of Alfvénic slow wind in SC25.

4.1.1. Alfvénic content

In Fig. 2 we decided to characterize the state of turbulence in different phases of SC23 and SC24 by using two-dimensional (2D) histograms of σC − σR, as firstly presented by Bavassano et al. (1998). Solar wind observations usually show a predominance of outward fluctuations where a magnetic energy excess is observed since the distribution extends over only one quadrant, that is σC > 0 and σR < 0, as is widely reported in literature (Bruno et al. 1985; Bavassano et al. 1998, 2000; D’Amicis et al. 2007; D’Amicis et al. 2011; D’Amicis & Bruno 2015). These 2D histograms at 1 AU are generally characterized by two populations: one with a pronounced peak corresponding to Alfvénic fluctuations (σC close to 1 and σR close to 0) and a second one around σC ∼ 0 and σR ∼ −1 corresponding to advected magnetic structures (Bavassano et al. 1998). The second population can be present as a tail or as a distinct population if statistically more important. Overall, Fig. 2 confirms these findings. However, the expected predominance of one population with respect to the other is slightly different in the different phases of the solar cycle analyzed. Indeed, at both maxima of SC23 and SC24, a robust predominance of Alfvénic fluctuations is observed (see also D’Amicis & Bruno 2015). Moreover, if the minimum of SC23 is characterized by a predominance of advected magnetic structures, SC24 shows a similar statistical behavior for the two phases of the solar cycle.

thumbnail Fig. 2.

2D histograms of σC and σR at solar maximum (left panels) and minimum (right panels) for SC23 (upper panels) and SC24 (lower panels). The color scale indicates the percentage of occurrences with respect to the maximum value with the lowest value corresponding to 10%.

All of these findings are rather at odds with previous results for SC21 (see e.g., D’Amicis et al. 2007), where advected magnetic structures were found to be more pronounced than the Alfvénic population at the maximum of that solar cycle. Actually, we should expect more Alfvénic solar wind fluctuations during solar minima because of the increased presence in the ecliptic of fast wind coming from the meridional extensions of polar coronal holes. However, while the minimum of SC24 shows a comparable Alfvénic population with respect to that corresponding to advected structures, the same does not occur during the minimum of SC23. This behavior could be explained by the weird structure of the corona during the minimum of SC23. Indeed, the corona did not have a simple configuration of streamers in an equatorial belt, as it was recovered during the previous minimum in 1996, but a considerable latitudinal structure appears in 2009 (Basu 2013).

To really understand which kind of plasma characterizes each phase of these two solar cycles, we studied the dependence of the Alfvénic content (measured by σC) of solar-wind fluctuations on the bulk speed of the wind, Vsw, as shown in Fig. 3. During solar minimum (right-hand side panels), the solar wind is bimodal (clearer at the minimum of SC23), showing two populations that can be discriminated according to the flow speed: fast wind (Vsw > 500 km s−1) and slow wind (Vsw < 500 km s−1). In this case, the fast wind is characterized by a well-defined Alfvénic population (high σC), while the slow wind shows a major non-Alvénic population (σC around zero) together with a wide spread of positive values of σC. During solar maximum (left-hand side panels), a predominance of slow wind is observed, which is as expected but with two different populations. Indeed, one of the two slow-wind peaks is characterized by a dominant Alfvénic population, while the other shows a non-Alfvénic population. The latter is less important during the maximum of SC23, while it is statistically comparable with the Alfvénic peak during the maximum of SC24, further supporting previous statistical studies (D’Amicis et al. 2011; D’Amicis & Bruno 2015). The maximum of SC23 also shows a tail toward an Alfvénic higher-speed solar wind which is instead absent during the same phase of SC24.

thumbnail Fig. 3.

2D histograms of σC and solar wind speed, Vsw, at solar maximum (left panels) and minimum (right panels) for SC23 (upper panels) and SC24 (lower panels). The color scale indicates the percentage of occurrences with respect to the maximum value with the lowest value corresponding to 10%.

4.1.2. Plasma composition variations

The solar wind’s charge state composition is a useful tool to study solar wind origin. Particularly useful to distinguish between a coronal-hole-associated solar wind and a streamer-associated slow solar wind are the abundances of oxygen and carbon. Oxygen is the third most abundant element in the Sun after hydrogen and helium, while the abundance of carbon is approximately half of that of oxygen. Oxygen’s most abundant ions, O5+ to O7+, freeze in very close to the Sun at 1.0−1.9 R⊙ above the surface as well as carbon ions. The low freeze-in height and relatively high abundance of oxygen and carbon make their charge state ratios, such as O7+/O6+ and C6+/C5+, useful diagnostics to indicate the freeze-in temperature of the solar wind coronal sources and to distinguish solar wind types by their different coronal source regions. We note that O7+/O6+ and C6+/C5+ are correlated and are clustered in well-defined regions of the O7+/O6+–C6+/C5+ space, depending on the solar wind regime observed (von Steiger 2008), which is generally anticorrelated with flow speed. However, D’Amicis et al. (2019) show that lower O7+/O6+ and C6+/C5+ characterize the Alfvénic time intervals (both fast and slow) with respect to the streamer-associated slow wind, occupying the same portion of the O7+/O6+–C6+/C5+ space and thus suggesting a similar solar origin of the two plasma regimes.

Figure 4 shows a statistical study related to the dependence on bulk speed of the O and C charge state ratios in different phases of the solar cycle similar to what is shown in Stakhiv et al. (2015, 2016). Their work displays an anticorrelation (e.g., an exponential trend) between the bulk speed and O and C ratios, classifying the solar wind in three groups: slow wind from coronal streamers, fast wind from coronal holes, and boundary wind which exhibits intermediate characteristics between fast and slow. Our analysis shows that both the maximum and minimum of solar cycle 23 are well-described by an anticorrelation between O and C ratios and flow speed, as expected. The distributions corresponding to the solar minimum clearly show the bimodal structure of the solar wind, especially in the C ratio versus Vsw, displaying two distinct peaks: one at V > 500 km s−1 and C < 0.5 and another one at V > 500 km s−1 and C, which is well above 0.5. On the other hand, the solar maximum is characterized by a single peak located at low speed values. This basically confirms the results of Fig. 3 showing the behavior of σC versus the flow speed. The upper panels, showing the O ratio versus Vsw, indicate that the wind with a speed > 500 km s−1, for instance fast wind, comes from the same solar source attributable to polar coronal holes. Moreover, although in general there is an inverse correlation between Vsw and the O ratio (or the C ratio), only the very slow wind (namely Vsw < 450 km s−1) reaches the O ratio above 0.1 and the C ratio above 0.5 in agreement with the results found by Stakhiv et al. (2015, 2016). On the other hand, low O and C ratio values also exist in correspondence of low speed wind, thus identifying the Alfvénic slow wind.

thumbnail Fig. 4.

2D histograms of O (upper panels) and C ratios (lower panels) versus flow speed for maximum (left panels) and minimum (right panels) of SC 23. The color scale indicates the percentage of occurrences with respect to the maximum value with the lowest value corresponding to 10%.

We would also like to add that the Alfvénic slow wind can only be partially identified as the boundary wind classified by Stakhiv et al. (2015, 2016). Indeed, they found that the boundary wind, which has intermediate characteristics between slow and fast streams, is a subset of fast wind, originating from coronal hole boundaries. In our case, instead, the Alfvénic slow wind is not an intermediate speed wind, but it represents a statistically important solar wind regime, resembling the fast wind in many aspects, probably because of similar source regions where magnetic flux tubes from the Sun expand much faster than radially, that is low-latitude coronal holes and/or the boundaries of the polar coronal holes. Moreover, it is worth pointing out that the work by Stakhiv et al. (2015) is related to a different dataset with respect the one used in the present analysis. In fact, they focus on the mid-latitude wind during three fast latitude scans observed by Ulysses: the first and the third ones during solar minimum observing a predominance of fast wind and the second one during maximum, showing both fast and slow wind. In our analysis, instead, Wind observations are in the ecliptic plane with the presence of both fast and slow wind, as discussed in the introduction. Moreover, the second Ulysses pass is taken at maximum of SC23, while the third pass is considered at minimum of SC23. In both cases, the results are slightly different from our analysis since they are observing the solar wind at different latitudes, thus coming from different source regions. Furthermore, even if in the ecliptic plane with ACE Stakhiv et al. (2016) confirmed the results obtained out of the ecliptic in Stakhiv et al. (2015) with Ulysses, these observations only refer to the minimum of SC24. In our case, the Alfvénic slow wind, which is the focus of our study, is more likely to be observed in the ecliptic plane and during solar maximum since it originates from low-latitude small coronal holes.

The larger spread in the O and C ratios observed at solar maximum (see Fig. 4) is likely related to the so-called outliers. Zhao et al. (2016) have shown that although the bulk of O7+/O6+ and C6+/C5+ values are highly correlated, there is a subset of measurements that departs from the linear correlation which could be caused by their relatively low C6+/C5+ or high O7+/O6+ ratio. This is particularly relevant during solar maximum. The same authors found that the majority of these outliers are related, in almost equal measure, to ICMEs and slow speed wind (Vsw < 500 km s−1), while only about 1% of them are related to fast solar wind (Vsw > 500 km s−1). Previous studies (see e.g., D’Amicis et al. 2019) have shown that the Alfvénic slow solar wind is characterized by O and C abundances similar to fast wind, which are therefore lower with respect to the streamer-associated slow wind. This implies that there is not a strong connection between the O and C outliers and the Alfvénic slow solar wind.

It is important to remark that in our comparative analysis, composition data for the maximum of SC24 would have greatly improved the reliability of our prediction for the successive solar maximum (SC25). However, the saturation issues for the composition data make them unreliable for the analysis. In any case, there is statistical evidence showing that the Alfvénic slow wind is characterized by low O and C ratios, which are also similar to the fast wind case implying that the solar sources for the two types of wind could be similar. Moreover, although we do not show O and C ratios versus speed for maximum of SC24, results from Fig. 3, showing σC versus speed, support the fact that the two solar maxima are statistically similar in the sense that both clearly identified a slow wind with a strong Alfvénic character.

4.2. Case studies

To better investigate the behavior of the Alfvénic slow wind, two case studies are analyzed. They were both selected during the maximum of solar activity, where a predominance of the Alfvénic slow wind has been observed on a statistical basis.

4.2.1. General features

The first interval was selected during SC23 and spans from June 1, 2002 (DoY 152) 00:00:00 to June 15, 2002 (DoY 166) 23:59:59. The left panels of Fig. 5 show that the speed values (first panel from the top) do not exceed 500 km s−1 throughout the interval, while the Pearson correlation coefficient between v and b components, ρv − b (second panel), computed at a 1 h scale, indicates portions of Alfvénic wind separated by more variable non-Alfvénic wind. By definition, ρv − b is the ratio between the covariance of the v-b components and their standard deviations. Furthermore, ρv − b can differ from Cvb, but they are both proxy for the correlation of the v − b components. Here, we chose to represent only the z component since it is usually more Alfvénic than the others. Moreover, we decided to represent ρv − b since it shows a clearer and more constant feature than Cvb, thus allowing us to better highlight the Alfvénic intervals. The profile of the first Alfvénic stream (marked as “1”) is similar to that of a typical fast stream, clearly displaying (i) a compression region, (ii) a main portion characterized by large Alfvénic fluctuations and low compressibility (highlighted by the shaded gray box), and (iii) a rarefaction region. This stream is followed by a non-Alfvénic wind and by a slow forward shock at DoY 159.641059, as shown in the Center for Astrophysics (CfA) Interplanetary Shock Database1. The second Alfvénic interval (marked as “2”), which occurred during DoY 162−164, has the same (positive) correlation sign of stream “1”, meaning that the magnetic field is directed inward. Both Alfvénic intervals are characterized by low compressibility and a low oxygen ratio (bottom panel) with respect to the other portions of the interval. The temperature profile (third panel from the bottom) follows the velocity-temperature correlation, as also highlighted in previous studies (see, e.g., Burlaga & Ogilvie 1970; Lopez & Freeman 1986; Matthaeus et al. 2006; Elliott et al. 2012; Perrone et al. 2019).

thumbnail Fig. 5.

Comparison of case studies between the maximum of SC23 (left panels) and SC24 (right panels). From top to bottom: time series of the following: solar wind speed, Vsw in km s−1; v − b correlation coefficient, ρv − b computed at 1 h scale; proton number density, np in cm−3; proton average temperature, Tp in K; magnetic field magnitude, B in nT; and oxygen charge state ratio, O+7/O+6 indicated as O ratio. The shaded gray boxes indicate the following Alfvénic solar wind intervals: slow wind (events “1” and “2”, explanation in the text) and faster wind (marked as “F”).

The second interval was selected during SC24 and spans from March 21, 2014 (DoY 80) 00:00:00 to April 4, 2014 (DoY 94) 23:59:59. The right panels of Fig. 5 show that the beginning of this interval (DoY 82−84) is characterized by an Alfvénic stream with an average speed of 467 km s−1, but with a peak of 597 km s−1. This is an intermediate-speed solar wind that will be identified in the following as a fast stream, named “F”, to distinguish it from the more authentic slow Alfvénic wind. This stream is preceded by a compression region and followed by a fast forward shock at DoY 84.7986982 along with a non-Alfvénic slow wind up to DoY 87.5. The second half of the interval depicts two Alfvénic slow streams with different correlation signs: DoY 87.5−89 correspond to a positive correlation and consequently an inward magnetic field direction; and DoY 91−94 have a negative correlation which indicates an outward magnetic field direction. The two events have been marked as event “2” and “1”, respectively, for a reason we explain in the next subsection. The slow Alfvénic intervals, as also observed for the interval “F”, are characterized by low compressibility and a low oxygen ratio with respect to the other portions of the interval, while the temperature profile follows the well-known velocity-temperature correlation as in the first interval.

The two case studies can be better characterized using some derived quantities. Figure 6 shows a comparison of some quantities for the intervals already shown in Fig. 5, namely for the solar maximum of SC23 (left panels) and SC24 (right panels). We included again the flow speed, Vsw, and the v − b correlation coefficient for an easy identification of the different streams. Here, the shaded gray boxes refer to intervals of one day, within the main portion of the streams chosen in Fig. 5, characterized by the largest fluctuations. All of these intervals are strongly Alfvénic, with ρvb ≳ 0.9. Having characterized the state of turbulence in terms of σC in the statistical section, we decide to analyze here the amount of energy associated with z+ and z− modes, namely e+ (red) and e− (black) at a 1 h scale. In general, there is a clear predominance of e+ with respect to e−, indicating outward propagating Alfvén modes (see the third panels), and the highest e+ values are found in the Alfvénic intervals. For completeness, the averaged values within the one-day intervals for σC and σR are the following: in 2002, σC ≃ 0.77 and 0.85, while σR ≃ −0.31 and −0.23 for events “1” and “2”, respectively. Then, in 2014, σC ≃ 0.88, 0.6, and 0.7, while σR ≃ −0.2, −0.56, and −0.42 for events “F”, “2”, and “1”, respectively. Moreover, the energy content of the fluctuations (per unit mass), indicated as ev (black) and eb (red) for kinetic and magnetic energy computed at a 1 h scale (see the fourth panel), respectively, overall shows an imbalance in favor of magnetic energy (eb > ev), even if the Alfvénic intervals are closer to equipartition (eb ≃ ev).

thumbnail Fig. 6.

Comparison of case studies between the maximum of SC23 (left panels) and SC24 (rights panels). From top to bottom: time series of the following: solar wind speed, Vsw in km s−1; v − b correlation coefficient, ρv − b, computed at a 1 h scale; energy associated to z+ and z− modes, e+ (red) and e− (black) in km2 s−2 (energy per unit mass), respectively, computed at a 1 h scale; kinetic and magnetic energy, ev (black) and eb (red) in km2 s−2 (energy per unit mass), computed at a 1 h scale; magnetic compressibility, Cbi; and plasma beta, β. The shaded gray boxes indicate a one-day interval within the Alfvénic solar wind streams highlighted in Fig. 5.

Following Bruno & Bavassano (1991) and D’Amicis & Bruno (2015), we also analyzed the role of compressible phenomena in determining the Alfvénic character of solar wind fluctuations by means of magnetic compressibility, defined as 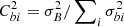, with 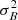and 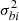being the variance of the B magnitude and of each magnetic field component (with i = x, y, z), respectively, computed over a 1 h scale. In fact, we decided not to show density compressibility since it is less variable when passing from non-Alfvénic to Alfvénic intervals, as is also shown statistically in D’Amicis & Bruno (2015). In this respect, the sixth panels of Fig. 6 shows a lower value of the magnetic field compressibility in the Alfvénic intervals. Indeed, there, Cbi shows values fluctuating around or even less than 0.1, which is well below the values in the rest of the interval. This result is in agreement with previous studies (e.g., D’Amicis & Bruno 2015).

Bottom panels show the behavior of the plasma beta, β, computed as 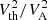. In the previous relation, the thermal speed, Vth, is defined as (2kBTp/mp)1/2, and the Alfvén speed, VA, is defined as B/(4πρ)1/2, with kB being the Bolzmann’s constant, Tp the average proton temperature, and mp the proton mass. In general, the Alfvénic intervals show β less than 1, with VA being larger than Vth (separate characteristic speeds are not shown), even though there is no one-to-one relation between β and the solar wind regime.

4.2.2. Spectral properties

To better highlight similarities between the amplitude of the fluctuations, we computed the normalized power spectral density of the trace of magnetic field fluctuations, similar to D’Amicis et al. (2020) and Bruno et al. (2019) in the following way. We derived the amplitude of the fluctuation δB(f) at a given frequency from the Fourier power spectral density, PB(f), being the two quantities linked by the following relationship: 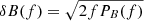. Then, we normalized those values to the corresponding local magnetic field intensity averaged within each interval, ⟨B⟩. For this part of the analysis, we focused on one day of data in each time interval as indicated by the color box in Fig. 6, which corresponds to the part of the stream with larger Alfvénic fluctuations. Figure 7 shows the normalized spectra obtained as explained above. According to this normalization, in the inertial range, the expected Kolmogorov scaling PB(f)∼f−5/3 is characterized by a scaling of δB(f)∼f−1/3, indicated in each panel by dashed lines. Moreover, the low frequency part of each spectrum shows a flattening corresponding to the 1/f scaling, suggesting that the amplitude of the Fourier modes has been saturated, as discussed in Matteini et al. (2018) and Bruno et al. (2019).

thumbnail Fig. 7.

Normalized power spectral density of the trace of magnetic field components, δB/⟨B⟩, as described in the text, of the shaded gray intervals selected in Fig. 6. Upper panels: comparison between different solar wind regimes for years 2002 (left) and 2014 (right), with the red and blue lines identifying the Alfvénic slow wind intervals that are either preceded (events “2”) by a shock or not (events “1”), respectively. The black line refers to the “fast” solar wind. Lower panels: same spectra as in the upper panels, but they are grouped in a different way: Alfvénic winds are characterized by a higher amplitude of the fluctuations on the left (blue and royal blue referring to the events in 2002 and 2014, respectively, and cyan referring to the fast wind interval) and Alfvénic slow wind intervals preceded by a shock are characterized by lower spectra on the right (red and magenta referring to the events in 2002 and 2014, respectively). The dashed line corresponds to the Kolmogorov scaling (PB(f)∼f−5/3) represented by a scaling of δB(f)∼f−1/3, according to the normalization described in the text.

The upper panels display the comparison between different solar wind regimes for years 2002 (left panel – during the maximum of SC23) and 2014 (right panel – during the maximum of SC24). Even if not shown, we found that in both cases the Alfvénic slow wind intervals have a higher power than the typical slow wind. Moreover, we observe that in 2014 the spectra of the Alfvénic slow wind (blue line – event “1” in the right panels of both Figs. 5 and 6) and the fast stream (black line) are overlapped as in D’Amicis et al. (2020). This supports the similarities between fast and Alfvénic slow intervals also from a spectral point of view. However, not all the Alfvénic slow intervals show the same amplitudes for the fluctuations. Indeed, the events marked with a “2” in both cases (red lines in both the left and right upper panels) have a lower amplitude with respect to the events “1” (blue lines). To better understand the recovered behavior, in the lower panels of Fig. 7 we show the same spectra of the above panels, but with a different grouping: on the left we have the spectra with a higher amplitude of fluctuations characterizing the events without a shock ahead (events “1”) and the fast wind observed in 2014, while on the right we show the two intervals of Alfvénic slow wind preceded by a shock (events “2”). With this grouping, the spectra are finally superimposed. This suggests that the lower amplitude of the fluctuations in both events “2” might be connected to the presence of a compression region ahead of them evolved in a shock, thus supporting the idea of an important role was played by magnetic compressibility not only on the Alfvénic content but also in reducing the amplitude of the fluctuations.

5. Discussion

In this study, a statistical comparison between different phases of solar cycles 23 and 24 has been presented with a particular focus on the Alfvénic content of near-Earth solar wind fluctuations. In general, solar wind observations are characterized by a predominance of outward fluctuations with a magnetic energy excess and a presence of two typical populations: one corresponding to Alfvénic fluctuations (σC ∼ 1 and σR ∼ 0) and the other, with σC ∼ 0 and σR ∼ −1, corresponding to advected magnetic structures (Bavassano et al. 1998). Each population can have a different statistical weight with respect to the other, depending on the kind of wind we are analyzing. From a statistical point of view, the solar wind is usually bimodal at solar minimum, showing two populations that can be separated, according to the flow speed, in fast wind and slow wind, the latter showing a major non-Alfvénic population. During solar maximum, instead, a predominance of slow wind is observed, but characterized by a significant Alfvénic population. This atypical slow wind has been identified as a new regime of solar wind, namely Alfvénic slow solar wind, which is the focus of the present study.

Here, through a detailed analysis of both SC23 and SC24, which look very similar, we support the results of previous studies (see, e.g., D’Amicis et al. 2011; D’Amicis & Bruno 2015). Indeed, we have determined that fast wind, which is intrinsically Alfvénic, can be especially found during solar minima, often observed in the form of corotating streams. During solar maxima, instead, only a few isolated fast streams can be observed. On the other hand, the Alfvénic slow wind is more frequent during the maximum of solar activity, in agreement with Wang et al. (2019), while the non-Alfvénic slow wind is present in all phases of the solar activity in both solar cycles. The comparison between the two solar cycles shows that the minima of SC23 and SC24, although bimodal, are dominated by magnetic structures advected by slow wind, mainly attributed to blobs and/or reconnection events in the solar corona (see e.g., Abbo et al. 2016), and by Alfvénic fast wind, respectively. Solar maxima, on the contrary, show a predominance of slow wind, mainly Alfvénic, but they also consist of a second population characterized by magnetic structures advected by the slow wind, especially during SC24. The main difference between the two considered solar cycles can be found at the minima. There, a predominance of Alfvénic fluctuations are generally expected due to the increased presence of fast wind from the meridional extension of polar coronal holes. This is what is observed at the minimum of SC24, while during the minimum of SC23 a predominance of advected magnetic structures is observed, maybe due to a different corona structure with respect to a typical streamer configuration in the equatorial belt (Basu 2013).

The source region of this Alfvénic slow wind is still debated. Useful indications come from the in situ elemental abundance, that is O and C ratios, that are correlated and clustered in well-defined regions of O−C space, depending on the solar wind regime observed. Moreover, both O and C abundances are generally anticorrelated with flow speed. Within this context, lower values of O7+/O6+ and C6+/C5+ characterize the Alfvénic time intervals (both fast and slow) with respect to the streamer-associated slow wind. Furthermore, in the O7+/O6+–C6+/C5+ space, both fast and Alfvénic slow wind occupy the same region, thus suggesting a similar solar origin of the two plasma regimes (D’Amicis et al. 2019), that is open magnetic field regions such as coronal holes, whose difference in speed could be attributed to a larger expansion factor (D’Amicis et al. 2021). Here, we found a well-defined anticorrelation between the O and C abundances and the speed of the wind in all the phases of SC23 and SC24. Moreover, we observed that the anticorrelation is more pronounced for C6+/C5+, especially at the minimum of SC23. Also in this case, our finding could depend on the weird structure of the corona, as already discussed above (Basu 2013).

The second part of the paper focuses on the characterization of the Alfvénic slow wind by presenting two intervals of 15 days (a representative subset of several events) selected during the maximum of solar activity in 2002 and 2014. In these case studies, intervals of slow wind with a strong Alfvénic character (high v − b correlation coefficient and low compressibility) have been identified. Each of the selected streams shows similar features with respect to fast solar wind, apart from the speed, which is lower (Vsw ≃ 400 km s−1). Moreover, we observed that the Alfvénic intervals are characterized by low values for both compressibility and the elemental abundance, clearly indicating a different origin for this kind of wind with respect to the more compressible non-Alfvénic slow wind. Furthermore, we found that, although the Alfvénic streams (fast or slow) have a higher amplitude of fluctuations with respect to the typical non-Alfvénic slow wind, all of them do not have the same power. This difference between Alfvénic slow wind does not seem to depend on different magnetic field topologies at the source regions, but rather on the interaction of these streams with magnetic structures while traveling from Sun to Earth. Indeed, lower amplitudes (comparable between them) are observed for streams preceded by a shock.

6. Conclusion

The Solar Cycle Prediction Panel, co-sponsored by NASA and NOAA, the National Oceanic and Atmospheric Administration, released an official forecast for solar cycle 25 (SC25) on April 5th, 2019. The panel reached a consensus indicating that cycle 25 will most likely peak between 2023 and 2026, basing their prediction on more than 60 forecasts published by various teams using a wide range of methods. The statistical analysis presented in this paper, along with the characterization of case studies, fits in the context of the recent solar missions perfectly, namely PSP and Solar Orbiter, devoted to the study of the inner heliosphere inside Mercury’s orbit. In fact, they were launched during the minimum of SC24 (in August 2018 and February 2020, respectively) and they are supposed to operate at least up to the predicted maximum of SC25. Therefore, the study of solar wind behavior during the solar cycle, with regard to the Alfvénic content of the fluctuations, is extremely important to understand possible future observations of the Alfvénic slow wind during maximum, which is fast approaching. Indeed, the characterization of the Alfvénic slow solar wind observed during the previous solar cycles, which shows persistent features, is then particularly topical in order to foresee the future measurements in the near-Sun solar wind and to finally link this solar wind regime to its source region on the Sun. Indeed, thanks to the Solar Wind Analyzer-Heavy Ion Sensor (SWA-HIS) on board Solar Orbiter, we have the unique opportunity to measure the composition of the solar wind minor ions, their three-dimensional velocity distribution, and temperature anisotropy, for the first time, in the inner heliosphere.

Observations of Alfvénic slow wind in the inner heliosphere have been done by Helios (Marsch et al. 1981; Stansby et al. 2020; Perrone et al. 2020) and PSP (see, e.g., Bale et al. 2019) during solar minima, recovering almost the same characteristics observed at 1 AU during solar maxima by Wind (see D’Amicis et al. 2021, for a review on this topic). Since from our statistical analysis, we found that the Alfvénic slow wind is a predominant feature at the maximum of the solar activity, we would expect that in the near future, PSP and Solar Orbiter will measure several pure intervals of this solar wind regime. In particular, PSP will give information about the Alfvénic slow wind in the unexplored region far closer than ever before, where the plasma has less time to interact with local structures, while Solar Orbiter will finally link solar sources and plasma properties, thus eventually confirming the corona-hole origin of Alfvénic slow wind. We anticipate that the Alfvénic slow wind observed close to the Sun will have stronger fluctuations with respect to the Alfvénic slow wind observed close to Earth. Indeed, the decrease in the fluctuation’s amplitude increasing the radial distance for the fast solar wind, in both the f−1 range (Horbury & Balogh 2001) and the inertial range (Telloni et al. 2015), has already been reported in the literature. In the same way, since there are similarities between the two Alfvénic regimes, the Alfvénic slow wind should show the same behavior. Moreover, for what concerns the spectral slope in the inertial range of the turbulent cascade, we would expect to observe an evolution from a Kolmogorov scaling (Kolmogorov 1941) for the Alfvénic slow wind at 1 AU to a Kraichnan-like scaling (Kraichnan 1965) of the power density for the Alfvénic slow wind close to the Sun (Chen et al. 2020; D’Amicis et al. 2021).

1

See https://www.cfa.harvard.edu/shocks for a complete analysis of the event.

2

See again https://www.cfa.harvard.edu/shocks for a complete analysis of this event.

Acknowledgments

K. A. was partially supported by the COSPAR fellowship program. The authors acknowledge the following people and organizations for data provision: R. Lin (UC Berkeley) and R. P. Lepping (NASA/GSFC) for WIND/3DP and WIND/MFI data, respectively, and G. Gloeckler (University of Maryland) for ACE/SWICS data. Data are available in the NASA-CDAWeb website: https://cdaweb.sci.gsfc.nasa.gov

References

  1. Abbo, L., Ofman, L., Antiochos, S. K., et al. 2016, Space Sci. Rev., 201, 55 [NASA ADS] [CrossRef] [Google Scholar]
  2. Antonucci, E., Abbo, L., & Dodero, M. A. 2005, A&A, 435, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bale, S. D., Badman, S. T., Bonnell, J. W., et al. 2019, Nature, 576, 237 [NASA ADS] [CrossRef] [Google Scholar]
  4. Basu, S. 2013, J. Phys.: Conf. Ser., 440, 012001 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bavassano, B., Pietropaolo, E., & Bruno, R. 1998, J. Geophys. Res., 103, 6521 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bavassano, B., Pietropaolo, E., & Bruno, R. 2000, J. Geophys. Res., 105, 12697 [NASA ADS] [CrossRef] [Google Scholar]
  7. Belcher, J. W., & Davis, L. 1971, J. Geophys. Res., 76, 3534 [Google Scholar]
  8. Belcher, J. W., & Solodyna, C. V. 1975, J. Geophys. Res., 80, 181 [NASA ADS] [CrossRef] [Google Scholar]
  9. Belcher, J. W., Davis, L., Jr., & Smith, E. J. 1969, J. Geophys. Res., 74, 2302 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bruno, R., & Bavassano, B. 1991, J. Geophys. Res., 96, 7841 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bruno, R., & Carbone, V. 2013, Liv. Rev. Sol. Phys., 10, 2 [Google Scholar]
  12. Bruno, R., & Trenchi, L. 2014, ApJ, 787, L24 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bruno, R., Bavassano, B., & Villante, U. 1985, J. Geophys. Res., 90, 4373 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bruno, R., Bavassano, B., & Pietropaolo, E. 1997, J. Geophys. Res., 102, 14687 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E., & Bavassano, B. 2001, Planet. Space Sci., 49, 1201 [Google Scholar]
  16. Bruno, R., Carbone, V., Primavera, L., et al. 2004, Ann. Geophys., 22, 3751 [Google Scholar]
  17. Bruno, R., D’Amicis, R., Bavassano, B., et al. 2007, Ann. Geophys., 25, 1913 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bruno, R., Telloni, D., Sorriso-Valvo, L., et al. 2019, A&A, 627, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Burlaga, L. F., & Ogilvie, K. W. 1970, ApJ, 159, 659 [NASA ADS] [CrossRef] [Google Scholar]
  20. Chen, C. H. K., Bale, S. D., Bonnell, J. W., et al. 2020, ApJS, 246, 53 [Google Scholar]
  21. Coleman, P. J. 1968, ApJ, 153, 371 [Google Scholar]
  22. D’Amicis, R., & Bruno, R. 2015, ApJ, 805, 84 [Google Scholar]
  23. D’Amicis, R., Bruno, R., & Bavassano, B. 2007, Geophys. Res. Lett., 34, 5108 [Google Scholar]
  24. D’Amicis, R., Bruno, R., & Bavassano, B. 2010, Adv. Space Res., 46, 514 [CrossRef] [Google Scholar]
  25. D’Amicis, R., Bruno, R., & Bavassano, B. 2011, J. Atmos. Sol.-Terr. Phys., 3, 653 [CrossRef] [Google Scholar]
  26. D’Amicis, R., Matteini, L., & Bruno, R. 2019, MNRAS, 483, 4665 [NASA ADS] [Google Scholar]
  27. D’Amicis, R., Matteini, L., Bruno, R., & Velli, M. 2020, Sol. Phys., 295, 46 [CrossRef] [Google Scholar]
  28. D’Amicis, R., Perrone, D., Velli, M., & Bruno, R. 2021, J. Geophys. Rev., 126, e28996 [Google Scholar]
  29. Duan, D., He, J., Pei, Z., et al. 2018, ApJ, 865, 89 [NASA ADS] [CrossRef] [Google Scholar]
  30. Duan, D., Bowen, T. A., Chen, C. H., et al. 2020, ApJS, 246, 55 [Google Scholar]
  31. Elliott, H. A., Henney, C. J., McComas, D. J., Smith, C. W., & Vasquez, B. J. 2012, J. Geophys. Res., 117, A09102 [NASA ADS] [Google Scholar]
  32. Elsässer, W. M. 1950, Phys. Rev., 79, 183 [CrossRef] [Google Scholar]
  33. Galeev, A. A., & Oraevskii, V. N. 1963, Sov. Phys. Dokl., 7, 988 [NASA ADS] [Google Scholar]
  34. Geiss, J., Gloeckler, G., & von Steiger, R. 1995, Space Sci. Rev., 72, 49 [NASA ADS] [CrossRef] [Google Scholar]
  35. Gloeckler, G., Cain, J., Ipavich, F. M., et al. 1998, Space Sci. Rev., 86, 497 [NASA ADS] [CrossRef] [Google Scholar]
  36. Goelzer, M. L., Schwadron, N. A., & Smith, C. W. 2014, J. Geophys. Res., 119, 115 [NASA ADS] [CrossRef] [Google Scholar]
  37. Grappin, R., Frisch, U., Léorat, J., & Pouquet, A. 1982, A&A, 105, 6 [NASA ADS] [Google Scholar]
  38. Grappin, R., Velli, M., & Mangeney, A. 1991, Ann. Geophys., 9, 416 [Google Scholar]
  39. Hathaway, D. H., & Wilson, R. M. 2004, Sol. Phys., 224, 5 [NASA ADS] [CrossRef] [Google Scholar]
  40. He, J., Tu, C., Marsch, E., et al. 2015, ApJ, 813, L30 [NASA ADS] [CrossRef] [Google Scholar]
  41. Horbury, T. S., & Balogh, A. 2001, J. Geophys. Res., 106, 15929 [NASA ADS] [CrossRef] [Google Scholar]
  42. Iroshnikov, P. S. 1963, Astronomicheskii Zhurnal, 40, 742 [NASA ADS] [Google Scholar]
  43. Janardhan, P., Bisoi, S. K., Ananthakrishnan, S., et al. 2015, J. Geophys. Res., 120, 5306 [NASA ADS] [CrossRef] [Google Scholar]
  44. Janardhan, P., Fujiki, K., Ingale, M., Biso, S. K., & Rout, D. 2018, A&A, 618, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Kakad, B., Kakad, A., Ramesh, D. S., & Lakhina, G. S. 2019, J. Space Weather Space Clim., 9, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Ko, Y.-K., Roberts, D. A., & Lepri, S. T. 2018, ApJ, 864, 139 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kolmogorov, A. N. 1941, Akademiia Nauk SSSR Doklady, 30, 301 [NASA ADS] [Google Scholar]
  48. Kraichnan, R. H. 1965, Phys. Fluids, 8, 1385 [Google Scholar]
  49. Lepping, R. P., Acũna, M. H., Burlaga, L. F., et al. 1995, Space Sci. Rev., 71, 207 [Google Scholar]
  50. Lin, R. P., Anderson, K. A., Ashford, S., et al. 1995, Space Sci. Rev., 71, 125 [CrossRef] [Google Scholar]
  51. Lopez, R. E., & Freeman, J. W. 1986, J. Geophys. Res., 91, 1701 [Google Scholar]
  52. Lowder, C., Qiu, J., & Leamon, R. 2017, Sol. Phys., 292, 18 [NASA ADS] [CrossRef] [Google Scholar]
  53. Marsch, E., & Tu, C.-Y. 1990, J. Geophys. Res., 95, 8122 [NASA ADS] [Google Scholar]
  54. Marsch, E., Rosenbauer, H., Schwenn, R., Muehlhaeuser, K. H., & Denskat, K. U. 1981, J. Geophys. Res., 86, 9199 [NASA ADS] [CrossRef] [Google Scholar]
  55. Matteini, L., Stansby, D., Horbury, T. S., & Chen, C. H. K. 2018, ApJ, 869, L32 [Google Scholar]
  56. Matthaeus, W. H., Elliott, H. A., & McComas, D. J. 2006, J. Geophys. Res., 111, A10103 [NASA ADS] [CrossRef] [Google Scholar]
  57. Mazumder, R., Bhowmik, P., & Nandy, D. 2018, ApJ, 868, 52 [NASA ADS] [CrossRef] [Google Scholar]
  58. Neugebauer, M., Forsyth, R. J., Galvin, A. B., et al. 1998, J. Geophys. Res., 103, 14587 [NASA ADS] [CrossRef] [Google Scholar]
  59. Owocki, S. P., Holzer, T. E., & Hundhausen, A. J. 1983, ApJ, 275, 354 [CrossRef] [Google Scholar]
  60. Panasenco, O., Velli, M., D’Amicis, R., et al. 2020, ApJS, 246, 54 [Google Scholar]
  61. Perrone, D., Stansby, D., Horbury, T. S., & Matteini, L. 2019, MNRAS, 488, 2380 [Google Scholar]
  62. Perrone, D., D’Amicis, R., De Marco, R., et al. 2020, A&A, 633, A166 [EDP Sciences] [Google Scholar]
  63. Roberts, D. A., Klein, L. W., Goldstein, M. L., & Matthaeus, W. H. 1987, J. Geophys. Res., 92, 11021 [Google Scholar]
  64. Stakhiv, M., Landi, E., Lepri, S. T., et al. 2015, ApJ, 801, 100 [NASA ADS] [CrossRef] [Google Scholar]
  65. Stakhiv, M., Lepri, S. T., Landi, E., et al. 2016, ApJ, 829, 117 [NASA ADS] [CrossRef] [Google Scholar]
  66. Stansby, D., Matteini, L., Horbury, T. S., et al. 2020, MNRAS, 492, 39 [Google Scholar]
  67. Telloni, D., Bruno, R., & Trenchi, L. 2015, ApJ, 805, 46 [NASA ADS] [CrossRef] [Google Scholar]
  68. Tu, C.-Y., & Marsch, E. 1993, J. Geophys. Res., 98, 1257 [NASA ADS] [CrossRef] [Google Scholar]
  69. Tu, C.-Y., & Marsch, E. 1995, Space Sci. Rev., 73, 1 [Google Scholar]
  70. Tu, C.-Y., Pu, Z.-Y., & Wei, F.-S. 1984, J. Geophys. Res., 89, 9695 [NASA ADS] [CrossRef] [Google Scholar]
  71. Tu, C.-Y., Marsch, E., & Thieme, K. M. 1989, J. Geophys. Res., 94, 11739 [NASA ADS] [CrossRef] [Google Scholar]
  72. Velli, M., Grappin, R., & Mangeney, A. 1989, Phys. Rev. Lett., 63, 1807 [Google Scholar]
  73. Velli, M., Grappin, R., & Mangeney, A. 1990, Comput. Phys. Commun., 59, 153 [NASA ADS] [CrossRef] [Google Scholar]
  74. von Steiger, R. 2008, in The Heliosphere Through the Solar Activity Cycle, eds. A. Balogh, L. J. Lanzerotti, & S. T. Suess (Chichester: Praxis Publishing Ltd.), 41 [CrossRef] [Google Scholar]
  75. von Steiger, R., Geiss, J., & Gloeckler, G. 1997, in Cosmic Winds and the Heliosphere, eds. J. R. Jokipii, C. P. Sonett, & M. S. Giampapa, 581 [Google Scholar]
  76. von Steiger, R., Schwadron, N. A., Fisk, L. A., et al. 2000, J. Geophys. Res., 105, 27217 [Google Scholar]
  77. von Steiger, R., Zurbuchen, T. H., & McComas, D. J. 2010, Geophys. Res. Lett., 37, L22101 [Google Scholar]
  78. Wang, Y.-M. 1994, ApJ, 437, L67 [NASA ADS] [CrossRef] [Google Scholar]
  79. Wang, Y.-M., & Ko, Y. K. 2019, ApJ, 880, 146 [NASA ADS] [CrossRef] [Google Scholar]
  80. Wang, Y.-M., & Sheeley, N. R., Jr. 1990, ApJ, 365, 372 [NASA ADS] [CrossRef] [Google Scholar]
  81. Wang, Y.-M., & Panasenco, O. 2019, ApJ, 872, 139 [NASA ADS] [CrossRef] [Google Scholar]
  82. Wang, X., Tu, C., He, J., & Wang, L. 2018, ApJ, 857, 136 [NASA ADS] [CrossRef] [Google Scholar]
  83. Wang, X., Zhao, L., Tu, C., & He, J. 2019, ApJ, 871, 204 [CrossRef] [Google Scholar]
  84. Woodham, L. D., Wicks, R. T., Verscharen, D., & Owen, C. J. 2018, ApJ, 856, 49 [CrossRef] [Google Scholar]
  85. Yan, L., He, J., Zhang, L., et al. 2016, ApJ, 816, L24 [CrossRef] [Google Scholar]
  86. Zhao, L., Zurbuchen, T. H., & Fisk, L. A. 2009, Geophys. Res. Lett., 36, L14104 [NASA ADS] [CrossRef] [Google Scholar]
  87. Zhao, L., Landi, E., Zurbuchen, T. H., Fisk, L. A., & Lepri, S. T. 2014, ApJ, 793, 44 [NASA ADS] [CrossRef] [Google Scholar]
  88. Zhao, L., Landi, E., Kocher, M., et al. 2016, AIP Conf. Proc., 1720, 020006 [NASA ADS] [CrossRef] [Google Scholar]
  89. Zhu, X., He, J., Verscharen, D., Duan, D., & Bale, S. D. 2020, ApJ, 901, L3 [NASA ADS] [CrossRef] [Google Scholar]
  90. Zurbuchen, T. H., Hefti, S., Fisk, L. A., Gloeckler, G., & von Steiger, R. 1999, Space Sci. Rev., 87, 353 [NASA ADS] [CrossRef] [Google Scholar]
  91. Zurbuchen, T. H., Hefti, S., Fisk, L. A., Gloeckler, G., & Schwadron, N. A. 2000, J. Geophys. Res., 105, 18327 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Data selection: maximum and minimum of solar cycle 23 and 24.

In the text

All Figures

thumbnail Fig. 1.

Monthly sunspot number (SN) as a function of time (gray line) and smoothed average (black line) during solar cycles 23 and 24. The dashed colored boxes indicate the selected 30-month intervals: blue for solar maximum and red for solar minimum.
In the text
thumbnail Fig. 2.

2D histograms of σC and σR at solar maximum (left panels) and minimum (right panels) for SC23 (upper panels) and SC24 (lower panels). The color scale indicates the percentage of occurrences with respect to the maximum value with the lowest value corresponding to 10%.
In the text
thumbnail Fig. 3.

2D histograms of σC and solar wind speed, Vsw, at solar maximum (left panels) and minimum (right panels) for SC23 (upper panels) and SC24 (lower panels). The color scale indicates the percentage of occurrences with respect to the maximum value with the lowest value corresponding to 10%.
In the text
thumbnail Fig. 4.

2D histograms of O (upper panels) and C ratios (lower panels) versus flow speed for maximum (left panels) and minimum (right panels) of SC 23. The color scale indicates the percentage of occurrences with respect to the maximum value with the lowest value corresponding to 10%.
In the text
thumbnail Fig. 5.

Comparison of case studies between the maximum of SC23 (left panels) and SC24 (right panels). From top to bottom: time series of the following: solar wind speed, Vsw in km s−1; v − b correlation coefficient, ρv − b computed at 1 h scale; proton number density, np in cm−3; proton average temperature, Tp in K; magnetic field magnitude, B in nT; and oxygen charge state ratio, O+7/O+6 indicated as O ratio. The shaded gray boxes indicate the following Alfvénic solar wind intervals: slow wind (events “1” and “2”, explanation in the text) and faster wind (marked as “F”).
In the text
thumbnail Fig. 6.

Comparison of case studies between the maximum of SC23 (left panels) and SC24 (rights panels). From top to bottom: time series of the following: solar wind speed, Vsw in km s−1; v − b correlation coefficient, ρv − b, computed at a 1 h scale; energy associated to z+ and z− modes, e+ (red) and e− (black) in km2 s−2 (energy per unit mass), respectively, computed at a 1 h scale; kinetic and magnetic energy, ev (black) and eb (red) in km2 s−2 (energy per unit mass), computed at a 1 h scale; magnetic compressibility, Cbi; and plasma beta, β. The shaded gray boxes indicate a one-day interval within the Alfvénic solar wind streams highlighted in Fig. 5.
In the text
thumbnail Fig. 7.

Normalized power spectral density of the trace of magnetic field components, δB/⟨B⟩, as described in the text, of the shaded gray intervals selected in Fig. 6. Upper panels: comparison between different solar wind regimes for years 2002 (left) and 2014 (right), with the red and blue lines identifying the Alfvénic slow wind intervals that are either preceded (events “2”) by a shock or not (events “1”), respectively. The black line refers to the “fast” solar wind. Lower panels: same spectra as in the upper panels, but they are grouped in a different way: Alfvénic winds are characterized by a higher amplitude of the fluctuations on the left (blue and royal blue referring to the events in 2002 and 2014, respectively, and cyan referring to the fast wind interval) and Alfvénic slow wind intervals preceded by a shock are characterized by lower spectra on the right (red and magenta referring to the events in 2002 and 2014, respectively). The dashed line corresponds to the Kolmogorov scaling (PB(f)∼f−5/3) represented by a scaling of δB(f)∼f−1/3, according to the normalization described in the text.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.