EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A132 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A132
Number of page(s) 36
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202140593
Published online 22 October 2021

© ESO 2021

1. Introduction

One of the most controversial topics in galaxy evolution is the so-called co-evolution (e.g., Heckman & Best 2014) between star formation in galaxies and the accretion activity onto their central super-massive black hole (SMBH). We know that the two processes are related on cosmological timescales (Madau & Dickinson 2014). In addition, most cosmological models require ‘feedback’, that is, regulation of the molecular mass reservoir from the central active galactic nucleus (AGN), in order to reproduce observed properties of our Universe such as the cosmic star formation history, the galaxy luminosity function, and the low baryon fraction in massive dark matter halos (Somerville et al. 2008; Vogelsberger et al. 2014; Su et al. 2019), as well as the obscuration statistics of AGN (Hopkins et al. 2016).

The products of both AGN accretion and star-formation are related over many orders of magnitude, as evidenced in the well-known relation between the mass of the SMBH and the velocity dispersion of stars in the bulge (Magorrian et al. 1998; Ferrarese & Merritt 2000; Gebhardt et al. 2000; Kormendy & Ho 2013) and this may be further evidence of a direct link between the two processes (however see for an alternative explanation Jahnke & Macciò 2011).

Observers have struggled for many years, however, to pin down the specific impact that AGN activity might have on star formation or vice versa. This is partly because galaxy mass is the most significant driver of both AGN activity (e.g., Kauffmann et al. 2003) and star formation rate (e.g., Speagle et al. 2014), and also because the apparent relation between AGN and starburst activity may in fact be driven by the presence of large gas reservoirs, which are relevant for both processes (e.g., Heller & Shlosman 1994). This is seen particularly when comparing star formation enhancement in AGNs against mass-matched star-forming non-AGNs. There does not seem to be a significant difference between these systems in terms of star formation rate (Silverman et al. 2009; Rosario et al. 2012; Rovilos et al. 2012; Santini et al. 2012). While AGNs clearly drive outflows (e.g., Fabian 2012), it is unclear if and how these affect the molecular gas reservoirs (Schulze et al. 2019). ‘Positive’ AGN feedback (e.g., radio jets triggering star formation) may also be possible (e.g., Zinn et al. 2013; Zubovas et al. 2013; Maiolino et al. 2017; Gallagher et al. 2019). For a further discussion on this topic, we refer the reader to the recent review by Harrison (2017).

It is also still unclear what triggers nuclear activity in galaxies (e.g., Alexander & Hickox 2012) – and this is not due to a lack of ideas. Mergers may (e.g., Ramos Almeida et al. 2012; Treister et al. 2012; Gao et al. 2020) or may not (e.g., Cisternas et al. 2011; Kocevski et al. 2012; Marian et al. 2019) trigger AGNs, but they in any case represent only part of the answer (Marian et al. 2020). The galactic environment may play a role, too, for AGN fuelling. Davies et al. (2017) found that the group environment is most conducive to X-ray-selected AGNs. Bar instabilities were thought to play a role for AGN feeding in the past (e.g., Knapen et al. 2000), but more recent work does not seem to find this relation (Cisternas et al. 2015; Goulding et al. 2017). Dust lanes correlate with AGN activity, at least in gas-poor galaxies (Martini et al. 2003; Simões Lopes et al. 2007), and may show accretion structures from kiloparsec down to parsec scales (Prieto et al. 2019).

The reason why it remains difficult to identify which, if any, of these processes is the most relevant fuelling mechanism for AGNs is due to their very different timescales compared to AGN activity. AGN activity is likely intermittent on timescales of 105–106 years as predicted by simulations (e.g., Novak et al. 2011) and also evidenced by, for example, the number statistics of ‘starting’ AGNs; so-called X-ray bright, optically normal galaxies (Schawinski et al. 2015); or observations of intermittent outflows (Lutz et al. 2020). The timescale for star formation in the host galaxy, however, is much longer. One typically assumes a galaxy rotation period or dynamical time of ∼108 yr. This mismatch in timescales makes it hard to relate nuclear accretion to global star formation (Hickox et al. 2014; Volonteri et al. 2015).

A much better correlation is expected on smaller scales, however, from simulations (Thompson et al. 2005; Hopkins & Quataert 2010), as well as observationally. Diamond-Stanic & Rieke (2012) found that black hole growth strongly correlates with nuclear (r < 1 kpc) star formation, but only weakly with extended (r > 1 kpc) star formation. Star formation in ‘nuclear rings’ appears on radii of several hundreds of pc up to ∼1.5 kpc in some 20% of disc galaxies (Regan & Teuben 2003; Comerón et al. 2010). It is often said that the processes of star formation and AGN activity take place on scales of many kpc and sub-pc scales, respectively. This is an exaggeration, however, as the gravitational potential of the black hole already becomes dominant at scales of ∼1–10 pc (e.g., Schartmann et al. 2010).

These are the scales where around 80% of both early- and late-type galaxies exhibit nuclear stellar clusters (NSCs), which can also contain young stars (Neumayer et al. 2020). Their relation to AGN feeding is still an active matter of research.

The circum-nuclear environment is also the location of the AGN ‘torus’ as postulated in the original AGN unification model (Antonucci & Miller 1985). Due to its geometrically thick structure, it is supposed to explain the dichotomy in observed AGN types: broad-line (type 1) and narrow-line (type 2) AGNs. It was realised early on, however, that puffing up a thick dusty structure, and keeping it geometrically thick, is quite difficult (Krolik & Begelman 1988). This ‘scale height problem’ is solved in more recent unification models by constructing the torus as a disc-wind puffed up by infrared radiation pressure on only the smallest scales (e.g., Elvis 2000; Hönig 2019), and the disc-wind driven outflow also explains the polar-elongated mid-infrared (mid-IR) morphologies of the AGN heated dust on parsec scales (Burtscher et al. 2013; Hönig et al. 2013; López-Gonzaga et al. 2016).

There is also plenty of material in the torus plane, however, and it can certainly contribute to obscuring the AGN (e.g., Hicks et al. 2009). Sub-millimetre interferometric observations further show that this region is often characterised by counter-rotating gas discs (Combes et al. 2019), which is consistent with simulations that expect various instabilities on these scales (e.g., Hopkins et al. 2012). It is clear that the dusty material surrounding the central engine is not a mere ‘by-stander’ as the torus picture implied, but very likely the reservoir and therefore an active player in fuelling the AGN.

A causal link between AGN activity and nuclear star formation might exist on these scales if infalling gas, stalling at its angular momentum barrier, first forms stars and then fuels the AGN through stellar mass loss (Norman & Scoville 1988; Vollmer et al. 2008; Wada et al. 2009), possibly contributing to AGN obscuration in this phase (Wada & Norman 2002). This fuelling might work best after the violent phase of the starburst (including type II supernovae) has died off and the colliding slow winds of stars in their post-main-sequence evolution can efficiently cancel angular momentum and thus feed the AGN (Schartmann et al. 2009, 2010), but in some models the nuclear starburst and AGN accretion happens at the same time (e.g., Kawakatu & Wada 2008).

Circum-nuclear star formation in AGNs is well established observationally (e.g., Terlevich et al. 1990; Cid Fernandes et al. 2001; Storchi-Bergmann et al. 2000; Riffel et al. 2009; Storchi-Bergmann et al. 2012; Esquej et al. 2014; Lin et al. 2018), but observational efforts to time nuclear starburst versus AGN activity are still scarce and inconclusive. Davies et al. (2007) presented observational evidence that young stars hinder accretion, and that gas can only accrete efficiently to smaller scales after these early turbulent phases of stellar feedback. While other observations are partially consistent with this, young stars may sometimes also be present during the active phase (Cid Fernandes et al. 2004; Sarzi et al. 2007b; Kauffmann & Heckman 2009). To resolve this, one must take into account not only the location of the stellar populations (Riffel et al. 2010, 2011; Diniz et al. 2017), but also the AGN luminosity (i.e., mass accretion rate). The result of Davies et al. (2007) implies that the age of the stellar population is only important for Seyferts with LAGN ≳ 1043 erg s−1, meaning accretion at levels ≳10−3 M⊙ yr−1. Other (less efficient) processes may be sufficient to supply lower accretion rates.

It is, however, difficult to directly characterise the nuclear stellar populations of powerful AGNs in the optical since the glare of the AGN reduces the equivalent width of stellar absorption features below the detectable (or calibratable) accuracy. Past studies of star formation or stellar populations in the nuclei of AGNs have therefore either relied on indirect tracers, such as polycyclic aromatic hydrocarbons (PAHs) (Imanishi et al. 2011; Esquej et al. 2014; Jensen et al. 2017; Esparza-Arredondo et al. 2018) or the far-infrared (Meléndez et al. 2014), or restricted themselves to type 2 AGNs (e.g., Sarzi et al. 2007b). An interesting alternative is to look in the near-infrared (near-IR) where both the glare of the AGN as well as the extinction of the nucleus are significantly reduced compared to the optical. The J, H, and K bands offer a number of useful stellar features, particularly of stars in their post-AGB phase which may be well suited to fuelling the AGN (Riffel et al. 2009, 2015, 2019).

Finally, in order to calibrate the results, it is important to not just look at the nuclear stellar populations of AGNs, but also – and with the same resolution and method – at inactive galaxies that are matched especially in stellar mass. Such a comparison is the main aim of the Local Luminous AGNs and Matched Analogs project (Davies et al. 2015), which has already seen a number of publications, for example, on nuclear obscuration (Burtscher et al. 2015, 2016; Schnorr-Müller et al. 2016), nuclear kinematics and luminosity distributions (Lin et al. 2018), molecular gas content (Rosario et al. 2018), environment (Davies et al. 2017), density of AGN-driven outflows (Davies et al. 2020), and the MBH − σ⋆ relation of LLAMA galaxies (Caglar et al. 2020). In addition, a few ‘special’ sources have also been studied in more detail, such as NGC 5728 (Shimizu et al. 2019) and NGC 2110 (Rosario et al. 2019).

In this article, we analyse the nuclear star formation histories of AGNs and matched inactive galaxies of the LLAMA sample, based on stellar population synthesis of VLT/X-shooter spectra. After describing the sample, the observations, and the data reduction in Sect. 2, we present the stellar population synthesis in Sect. 3. We analyse its results in Sect. 4 and discuss the emission line diagnostics in Sect. 5. In Sect. 6, we interpret our results in terms of the sample statistics and compare them to previous works. We end with conclusions and an outlook in Sect. 7. Appendix A shows all individual galaxy fits.

2. Sample, observations, and data reduction

2.1. The LLAMA sample of type 2 AGNs and control galaxies

The sample (and control sample) selection is one of the most important advances of this work. It is based on the LLAMA sample (Davies et al. 2015), which includes 20 AGNs that have been selected from the Swift/BAT all-sky ultra-hard X-ray (14–195 keV) survey in its 58-month edition. Selecting by ultra-hard X-rays has the advantage of being mostly insensitive to obscuration, except for the most Compton-thick sources. We selected the most luminous (log LX/(erg s−1) > 42.5) sources to limit ourselves to highly accreting, bona fide AGNs and because they are more likely to be fuelled by a single cohesive mechanism. The lower the luminosity, the more options for AGN fuelling there are (Martini et al. 2004). By further selecting only local (z < 0.01, corresponding to distances of ≲40 Mpc) AGNs, we are able to distinguish between the nuclear and circum-nuclear stellar populations. In addition, LLAMA includes 19 control galaxies that have been selected in order to match the AGN sample in distance, Hubble type, stellar mass (H band luminosity), and axis ratio (inclination)1. We consider this matched control sample an integral part of LLAMA as it allows us to calibrate our results against a similar sample of galaxies which only differ from the AGN sample in terms of their nuclear accretion rate. Figure 2 shows the galaxy properties of our AGN and control samples.

For this work, we limited the AGN sub-sample of LLAMA to only the Seyfert 1.8 and more highly obscured AGNs (i.e., Seyfert class ≥1.8), which we collectively refer to as type 2 AGNs. This sub-selection ensures that we can cleanly separate the stellar absorption features from AGN emission (see Fig. 1). Our attempts to do this in the type 1 AGNs of LLAMA were not successful. We also had to remove the type 2 AGN NGC 5128 (Centaurus A) since its nucleus is so highly obscured that the nuclear stellar population cannot be determined in the optical. We further excluded the type 2 AGN NGC 1365, since it showed so many emission lines that no good stellar population fit could be obtained either.

thumbnail Fig. 1.

Comparison of spectra for a Seyfert 1 and a Seyfert 2 galaxy from the LLAMA sample. A number of very broad emission features can be seen in the Seyfert 1 galaxy that outshine any underlying stellar absorption lines. The Balmer emission lines Hα and Hβ at 6562.8 Å and 4861.3 Å, respectively, are indicated with dashed lines.

thumbnail Fig. 2.

Comparison of the most relevant host galaxy properties of our AGN and control sample. From left to right: numerical Hubble type (morphology), log stellar mass M⋆ in units of solar masses M⊙, and distance. The AGN sample is shown in orange, and the control sample is shown in blue.

2.2. Observations

Except for the Seyfert 2 galaxy NGC 4388 and the control galaxy NGC 4260 all galaxies from our volume-complete sample of luminous local type 2 AGNs and control galaxies have been observed at least once with VLT/X-shooter. Together with the explicit exclusions mentioned above, this leaves us with nine type 2 AGNs and 18 control galaxies to be analysed in this work (see Table 1).

Table 1.

Definition of our sample.

For the work presented here, we used UV and optical spectra obtained with X-shooter at the VLT (Vernet et al. 2011). The spectra from the near-IR arm of X-shooter require a different treatment in terms of data reduction (e.g., sky emission line correction is non-trivial in the IFU mode of X-shooter) and analysis (e.g., requiring different stellar population models) and will be analysed in a separate project. X-shooter is a long-slit and integral-field unit (IFU) spectrograph that simultaneously records spectra in a wide wavelength range from the atmospheric UV cut-off at ∼3000 Å to the near-IR K band. It consists of three arms to maximise the sensitivity in the UV, the visible, and the near-infrared wavelength ranges, respectively.

Since we wanted to focus on the nuclear environment of nearby galaxies, we chose to observe in the IFU mode of X-shooter. In this mode, an input field of 40 × 18 is re-imaged onto a pseudo-slit of 120 × 06. The spectral resolving power R ≡ λ/Δλ in this mode is 7900, 12600, and 8100 in the three arms, respectively (Vernet & Mason 2009). We oriented the slit along the parallactic angle to ensure that atmospheric dispersion does not introduce wavelength-dependent flux losses. This means, however, that multiple observing blocks (OBs) will in general have been observed at different position angles on the sky. We therefore quote the parallactic angle at the beginning of each observation in Table 2. We also checked the difference in parallactic angle between the start and end of each observation, and it is ≲3° in all but three cases (MCG523_2: 6°, NGC7172_2: 6°, NGC1315_1: 14°). Since we chose a quadratic extraction aperture (see below), the impact of this slight rotation of PA during the observation did not impact the quality of the spectra, even for the source with the largest rotation of the parallactic angle during the observation, NGC 1315.

Table 2.

All observations.

We integrated, on average, about two hours per target. For most targets, this led to two independent observations (with their own preset and calibration stars), which provided a useful test for systematic errors in the later analysis.

2.3. Data reduction

2.3.1. Raw data reduction

We used the reflex pipeline provided by ESO in version 2.6.8 together with the Kepler GUI interface (Modigliani et al. 2010). Several improvements over previous versions of the pipeline were triggered by our use of X-shooter in the IFU-mode. We essentially then used the pipeline in its default configuration2.

2.3.2. Differential atmospheric refraction and the extraction aperture

The ESO reflex pipeline produces a data cube for each observation and for each of the UVB, VIS, and NIR arms of X-shooter. From these raw-reduced data, we extracted 1D spectra for each of the science, telluric-calibrator, and flux-calibrator stars. The data cubes from our X-shooter IFU observations consist of three spaxels in the x direction of 06 each and several spaxels in y direction. The total extent in the y direction is 60.

For the extraction, we first determined the centroid position in the J and H bands. From there, we propagated the (expected) centroid position to the VIS and UVB arms using the revised Édlen formula from Bönsch & Potulski (1998); specifically, we used Eqs. (6a, 7, 8, and 9a) to compute the refractive index for Paranal reference conditions, with CO2 content adjusted to the current value and a correction for moist air. The derived atmospheric dispersion was converted to detector pixel coordinates to provide a moving extraction window with wavelength. We verified our procedure for standard stars where it resulted in an extraction accuracy better than 1 pixel in the y direction (016) relative to the actual position of the star in each slice.

We then used a rectangular extraction aperture of 18, meaning we used all three slitlets in the x direction and a box with a length of 18 in the along-slit direction y. We also tried to use a smaller square aperture of 06 × 06, but rejected this smaller aperture for two reasons. Firstly, the position of the nucleus is not well defined in the UVB/VIS arms, even for only moderately obscured sources. The brightest region would often be so far away from the expected position of the nucleus in the UVB/VIS arms that it would lie outside this compact aperture. About a third of our sample would be affected by this if we had chosen a smaller extraction aperture. Secondly, our observations are seeing limited, and while the seeing was smaller than 06 in some cases, it has been up to 16 in other observations. By choosing a square aperture of 18 × 18, the extraction aperture is unaffected by seeing variations.

This extraction aperture corresponds to a physical radius of 150 (80) pc at the median distances of our AGN (control) samples, which is sufficient to isolate the nuclear stellar population from the circum-nuclear population (that can be found in nuclear rings)3. An analysis of more than 100 galaxies in our redshift range (Comerón et al. 2010) has shown that ≳90% of nuclear rings have radii larger than 150 pc. Of the five sources we have in common with the sample of Comerón et al. (2010), all have ring radii well outside our extraction aperture. Additionally, we analysed the LLAMA VLT/SINFONI data for 19 out of the 27 objects presented in this paper and only one source (NGC 7582) shows strong evidence for a nuclear ring within the 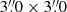field of view of SINFONI (but outside the aperture used for this work). In all other sources, there does not appear to be a circum-nuclear star-forming disc within our field of view, as judged from the (lack of) Br γ emission, the 12CO(2–0) bandhead flux and equivalent width, and the continuum flux. We therefore conclude that the spatial resolution of our observations and data analysis is sufficient to separate the nuclear from the circum-nuclear stellar populations.

2.3.3. Telluric and flux calibration

Telluric calibrator observations have been provided by the observatory. We used the tool molecfit (Smette et al. 2015; Kausch et al. 2015) to model the telluric transmission based on the observation of the closest telluric calibrator. Compared to directly using the telluric calibrator spectrum, this has the advantage of producing a noise-free transmission spectrum. The strongest atmospheric spectral feature in the wavelength range of interest to this work is the atmospheric A band of molecular oxygen starting at 760 nm. Other (weaker) features include the atmospheric B band of molecular oxygen starting at 686 nm as well as two broad bands of water vapour between 715–740 and 810–838 nm. Visually, the correction even in the strongest feature of these (the A band) is very good with the molecfit model spectra, and the main obvious effect is increased noise due to the lower transmission in these features. Quantitatively, we looked at the difference between the molecfit model and the raw spectrum of the science source and found the residuals to be ≲10% of the observed spectrum for the first few strong absorption peaks of the A band, but it was typically less than ±5 % for the whole A band and lower in the other bands.

For the absolute flux calibration, we used the flux calibrated spectra of a small list of spectro-photometric standard stars provided by ESO (Moehler et al. 2014) after applying the telluric absorption correction described above. These flux standards have usually been observed within the same night, and in several cases up to five nights before or after the science observation. Only in one case (OB id NGC5506_2) did we have to use a flux calibrator 13 days later. However, we looked at the count rates of the flux calibrator GD71 in five observations spread over 21 months and found the variations to be smaller than ∼2% in the wavelength range of interest for this work. Since the flux calibrators provided by ESO are cross-calibrated to much better than this (Moehler et al. 2014), we therefore consider our flux calibration (per X-shooter arm) to be accurate at the 2% level.

2.3.4. Further X-shooter calibration steps and tests

Further calibration steps in the X-shooter data processing included an interpolation (in the wavelength direction) for bad pixels and a flux matching between the UVB and VIS arms. We had to multiply the flux-calibrated VIS spectrum by a factor of 1.145 ± 0.140 (median and standard deviation, respectively) to match the UVB spectrum at the connecting point of the two spectra of 560 nm. While we do not know the origin of this flux mismatch, we can determine this ‘inter-calibration’ factor between the UVB and VIS arms with high accuracy for every observation. It does not affect the fidelity of the spectra; the absorption lines in particular, which are the property of most significance to this work, are unaffected by this calibration step.

2.3.5. X-shooter calibration pipeline

While the ESO pipeline for X-shooter provides a complete set of tools for processing the raw data to the final uncalibrated spectra, higher order calibration tasks, such as those described above, need to be performed by the user. We therefore developed a comprehensive high-order calibration pipeline for X-shooter, which is implemented as a Python-class Xspec and freely available at our github project4 containing various tools to reproduce the results presented in this paper.

3. Stellar population synthesis

The goal of stellar population synthesis is to derive a number of properties of a stellar population of which only the integrated spectrum is known. This method essentially determines the best-fitting linear superposition of model spectra of single stellar populations, while simultaneously fitting for extinction and kinematics. The main result of the synthesis is a ‘population vector’ that contains the estimated fractions of light attributable to each of the input single stellar populations (SSP) of different ages (and metallicities and/or other parameters). A number of SSP models exist with different ingredients in terms of empirical or model spectral libraries, different techniques for estimating the impact of the post-main-sequence evolution, various approaches for determining the statistical uncertainties, and a variety of other different assumptions. We refer the reader to Conroy (2013) for a review of both the method of stellar population synthesis itself and its ingredients.

While the plethora of assumptions and models is somewhat perplexing, the situation is less dismal than it seems: Baldwin et al. (2018) and Dahmer-Hahn et al. (2018) showed that population synthesis results in the optical wavelength range do not depend sensitively on the stellar population library that is used, and, with a sufficiently high signal-to-noise ratio, state-of-the-art stellar population synthesis (SPS) codes such as STARLIGHT (Cid Fernandes et al. 2004, 2005) or PPXF (Cappellari & Emsellem 2004) are able to recover reddened input spectra with realistic noise very accurately (Cid Fernandes 2018).

3.1. STARLIGHT fitting

For our stellar population synthesis, we used the publicly available and well-tested tool STARLIGHT version 4 (Cid Fernandes et al. 2004, 2005), in combination with the well-known single stellar population (SSP) library by Bruzual & Charlot (2003, hereafter BC03), and using the Chabrier (2003) initial mass function. More modern stellar population libraries such as MILES (Vazdekis et al. 2016) come with higher spectral resolutions, but they do not cover the youngest stellar populations that are particularly interesting for AGN feeding. Qualitatively, the stellar population synthesis with these models gives similar results to the ones with the BC03 models (Riffel et al. 2021).

In order to decrease the ambiguity in the fitting process, we used a reduced version of this library containing 15 single stellar population spectra of solar metallicity (see discussion about metallicity in Sect. 3.4). Since the BC03 spectra come with a spectral resolution of 3 Å, considerably lower than our X-shooter spectra, we convolved our X-shooter spectra to match this resolution and we further gridded our spectra in bins of constant wavelength range Δλ = 1 Å.

In STARLIGHT we used the default normalisation range for the observed spectra (6810–6870 Å) and the reddening law by Calzetti et al. (1994). We fitted the wavelength range from λ = 3850 Å to λ = 8800 Å. The blue end is given by our self-imposed signal-to-noise ratio (S/N) limit. At 3850 Å, the S/N is typically only a few for the re-binned spectra. The red end was essentially set to include the Ca II triplet for an accurate determination of the redshift and line-of-sight velocity dispersion from these absorption lines. Extending the wavelength coverage further into the infrared did not result in overall good STARLIGHT fits. This may be due to the lack of spectral resolving power in the near-IR in the models of BC03 (Dahmer-Hahn et al. 2018) or the fact that the near-IR light is dominated by different stellar populations (and possibly affected by a different amount of extinction) than the optical light and that a joint fit is therefore not meaningful.

3.2. Masking

Almost all of our galaxies show emission lines that need to be masked in order not to bias the fitting of the stellar absorption lines. While our philosophy for this research is to compare as equally as possible the stellar populations in AGNs and control galaxies, we cannot quite adhere to this approach for the process of masking the emission lines. If we chose a single mask that blocks all emission lines seen in any of our galaxies, essentially no data would be left to fit. We therefore choose a different approach and start the fit for each galaxy with a conservative mask including many of the frequently seen emission lines in AGNs. With this mask, we perform a first SSP fit with STARLIGHT and applied a smoothed version of sigma clipping to the result. Our goal here was not to remove all outliers from the fit – this may easily bias the result – but to exclude strong lines reliably and completely.

To accomplish this, we defined the centre of new masked areas where the observed flux was more than 5σ larger than the flux of the first fit (with the default mask). At this stage, σ is the uncertainty of the observed spectrum as derived by the ESO X-shooter pipeline and propagated through the various subsequent processing steps (telluric calibration, re-binning). We then followed the residual spectrum bluewards and redwards until it reaches a value of < 1σ. The intervals between the defined limits are added to the mask. We note that it does not matter for STARLIGHT if the mask definition contains overlapping regions. In order to further ensure a proper scaling of the uncertainties, we rescaled the residual spectrum such that ∼68% of the residuals actually lie within ±1σ of the distribution. We then repeated the fitting, masking and uncertainty-rescaling three times. Our tests showed that after the third iteration, both the mask and the resulting stellar population vector have converged to a stable solution.

3.3. Uncertainty determination

While stellar population synthesis is a commonly used technique in astronomy, there is no simple way to estimate the uncertainty of its results. The reason is that the final uncertainty depends on a number of parameters. In this section, we discuss and try to estimate the various sources of uncertainties involved in the fitting process.

3.3.1. Statistical uncertainties of the calibration and fitting process

The most straight-forward source of uncertainty is the noise in the spectra, the uncertainties associated with the telluric and flux calibration, and possible degeneracies involved in the fitting process. These uncertainties are taken into account in the fitting process with STARLIGHT internally. However, in order to actually visualise the posterior probability distributions, we obtained a special version of STARLIGHT (R. Cid Fernandes, priv. comm.) that saves the full Markov chain of the Monte Carlo sampling. From these, we computed the actual statistical uncertainties involved for our spectral synthesis as shown in Fig. 3.

thumbnail Fig. 3.

Posterior probability distributions for the fraction of light in the four bins of stellar ages from our STARLIGHT analysis of NGC 1079. We report the fractional value of stellar light associated with the 50% value in the cumulative distribution and take as 1σ uncertainty the range encompassing 68.27% of all values.

The statistical uncertainties involved in the STARLIGHT fitting process were also analysed and discussed in Cid Fernandes et al. (2014), who found the uncertainties in the binned (young, intermediate, and old populations) single stellar populations to be of 3, 9, and 9%, respectively, for random-noise-induced errors at the 1-σ level, and larger errors for shape-changing perturbations (e.g., errors in the spectral flatfield calibration). These values are considerably larger than the values we find from our own re-sampling exercise (see Figs. 3, 4, and 5). The statistical uncertainties that we find are, on average, 0.34% (0.37%), 0.28% (0.62%), 2.07% (2.37%), and 1.99% (2.13%) for the young, young-intermediate, intermediate-old, and old populations and for the AGN (control) populations, respectively. We attribute this to the overall excellent quality and calibration of our X-shooter spectra.

thumbnail Fig. 4.

Individual stellar population fitting results for all observations showing differences between individual observations for the same targets (the individual observations are indexed with underscores, e.g., NGC7582_1 and NGC7582_2). The four age bins marked in blue, green (only visible in one AGN), yellow, and red correspond to log(age/yrs) < 7.5 (young), 7.5 < log(age/yrs) < 8.5 (young-intermediate), 8.5 < log(age/yrs) < 9.5 (intermediate-old), and log(age/yrs) > 9.5 (old), respectively. The statistical uncertainties on the fractions of stellar light for the four age bins are shown as black lines at the right edge of each of these age bins.

thumbnail Fig. 5.

Same as Fig. 4, but for the control sample.

3.3.2. Systematic uncertainties of the observations

Since our original S/N estimate required about two hours of observations per target, we received, on average, two one-hour observations per target. This allows us to assess the systematic uncertainties involved in the observations (e.g., pointing accuracy, slit orientation, and weather conditions). We therefore show the stellar population vector for all individual observations in Figs. 4 and 5 for the AGN and control sample, respectively. The statistical error bars (derived as shown in Fig. 3) are shown on top of these individual results and demonstrate that the systematic uncertainties are of the same order as the statistical uncertainties for most galaxies.

3.3.3. Other uncertainties

Other sources of uncertainty in the derived star formation histories include metallicity (see discussion in Sect. 3.4), the extinction correction (see discussion in Sect. 5.5), and of course the sample size itself, which we assess with a jack-knifing test as described in Sect. 6.2. The specific stellar population models and the SPS fitting code used (STARLIGHT) do not induce further uncertainties in our estimates, as explained above and as shown by Baldwin et al. (2018). We also reiterate that the strength of our analysis lies in the comparison of the stellar populations of the AGN sample with matched analogues.

3.4. Metallicities

Measurements of the gas-phase metallicity in local galaxies using the direct method (i.e., using auroral instead of strong emission lines to derive electron temperature and hence metallicity, since metals are the main coolants in HII regions) show that, while the mass-metallicity relation rises steeply at low mass, it turns over at higher mass, and for galaxy masses > 1010 M⊙ (relevant for the LLAMA galaxies) it is fairly constant at a value consistent with solar metallicity (Andrews & Martini 2013).

Comparing the mass-metallicity relation at different epochs shows that it does evolve with redshift. However, while metallicity increases with cosmic time, the changes from z ∼ 2 to z ∼ 1 and from z ∼ 1 to z = 0 are only about 0.17 dex each (Yuan et al. 2013). Furthermore, Zahid et al. (2011) point out that this change is largely driven by lower mass galaxies, and that for galaxies with typical stellar masses of 1010.6 M⊙ (comparable to the LLAMA galaxies), the difference in average metallicity is much less.

The change in stellar rather than gas-phase metallicity was assessed by Vale Asari et al. (2009) by fitting stellar populations to continuum spectra tracing the stars themselves. Their conclusion is consistent with the results from studies using emission lines showing that, at the present day, galaxies with M > 1010 M⊙ have roughly solar metallicity and that the change with redshift or look-back time is modest for this mass range. Thus, to reduce the number of basis spectra for our fitting in order to avoid complications in our comparative analysis resulting from the age-metallicity degeneracy, we only used solar metallicity (Z = 0.02) spectra rather than including supersolar (Z = 0.05) or sub-solar (Z = 0.008) spectra.

The caveat is that the solar metallicity in the BC03 models is slightly higher than the most recent estimates of solar metallicity: The standard value for Zsun was 0.02 (Anders & Grevesse 1989), and this was adopted by BC03. But Asplund et al. (2009) recommend a solar chemical composition for which Zsun is 0.0134, that is, substantially less. They also indicate that the solar oxygen abundance is 12 + log(O/H) = 8.69. However, in terms of the comparative analysis performed here, this difference in what is adopted as solar metallicity has negligible impact.

3.5. Selection of best OB

Our following interpretation is not limited by the statistical uncertainties from the stellar population fitting (which are small, see above), but rather by the small sample size and, to a lesser extent, by the systematic uncertainties from differences between OBs. We therefore used multiple observations of a source, when available, to estimate the systematic uncertainty rather than to marginally improve the S/N at the cost of more systematic uncertainty.

Usually, the STARLIGHT fits to one of the OBs was noticeably better than the other one(s). We therefore selected only the best-fitting OB for the further analysis. This selection was done on the basis of (1) S/N, (2) masking as little as possible, (3) quality of the spectra5, (4) goodness of residuals (we tried to avoid structure in the residuals and favoured residuals that looked like white noise), (5) if in doubt, we put more weight on the blue part of the spectrum (despite its lower S/N) since this is where more distinctive stellar population features lie. Our selection of OBs can be seen in Table 2.

We illustrate our selection on the basis of three AGNs which show differing results between the multiple OBs. NGC 7172 does not have a young population in NGC7172_1, but it shows one in NGC7172_2. However, the stellar population fit for the latter observation leads to a bad fit and is therefore de-selected. It is also one of the very few galaxies where the mask actually has a noticeable impact on the population vector. Using our starting mask, we find a small fraction of young stellar light even for the observation NGC7172_1. After optimising the mask iteratively based on actually present emission lines (see Sect. 3.2), the young population disappears in this galaxy. NGC 5728 shows a young population in OB 1 and not in OB 2, but OB 2 is a worse fit than OB 1 and has a large masked area, which is why we choose the observation NGC5728_1 for the further analysis. ESO 137-G034 shows a young population in OB 3, which is the best fit. OB 1 results in a fit where a large range between H α and the TiO feature at ∼7500 Å is masked. OB 2 does not see a young population and is also a fairly good fit, but it has a strong ‘emission’ feature at ∼5500 Å that is not real (see discussion above), which is why we deselected it.

4. Stellar population synthesis results

The result of our stellar population synthesis is a so-called stellar population vector that gives the fraction of light (or mass) attributed to each single stellar population spectrum. We show the resulting fit, the (down-sampled and re-binned) data, the masked emission lines, the residuals, and the stellar population vector for one galaxy in Fig. 6 and for all galaxies in Appendix A. We also show a summary plot of all spectral syntheses in Figs. 7 and 8 for the inactive galaxies and AGNs, respectively.

thumbnail Fig. 6.

Example of a stellar population fit, for the AGN MCG-05-23-016. In the main panel, the X-shooter spectrum is displayed, down-sampled to the BC03 spectral resolution (black), the STARLIGHT fit (blue) with masked areas (in red) and the noise in the data in green. Below the spectrum, the residuals are displayed in terms of the local uncertainty in the data (masked areas are not displayed). In the side panel, the light-weighted star formation history (or stellar population vector) is shown.

thumbnail Fig. 7.

Collage of all LLAMA non-AGN X-shooter spectra with best-fitting stellar population synthesis overplotted. To the right of each spectrum, the summarised stellar population vector shows the best-fitting light-weighted fractions of the young (blue), young-intermediate (green), intermediate-old (yellow), and old (red) populations with boundaries of log (age/years) at 7.5, 8.5, and 9.5.

thumbnail Fig. 8.

Same as Fig. 7, but for the active galaxies in this paper.

The resulting fit parameters for both light and mass fractions are displayed for all galaxies in Table 3. In this table (and for the further analysis), we bin the stellar population vector into four age groups: log(age/yrs) < 7.5 (young), 7.5 < log(age/yrs) < 8.5 (young-intermediate), 8.5 < log(age/yrs) < 9.5 (intermediate-old), and log(age/yrs) > 9.5 (old). The choice of these age groups is driven by one of the original aims of this project, namely to discriminate between the youngest stars and young-intermediate stars. The table further contains the S/N in the fiducial wavelength range 605–608 nm, the velocity offset of this galaxy relatively to the assumed redshift (see Table 1)6, measured velocity dispersion, dust extinction, and reduced χ2 of the best-fitting combination of single stellar population spectra. Slightly negative values for AV arise from (small) uncertainties in the spectral flat field and flux calibrations and give an indication of the accuracy of our extinction values (≲0.2 mag). Finally, we quote the total stellar mass within our aperture log M⋆/M⊙ as fitted by STARLIGHT and using the distance quoted in Table 1.

Table 3.

Results from the STARLIGHT fitting.

In this Section, we discuss the accuracy of our fits and the emission line diagnostics, both of which are required in order to reliably analyse and interpret the stellar population results in Sect. 6.

4.1. How robustly can we determine the young stellar population in AGNs?

It has been known for some time that even obscured (Seyfert 2) AGNs show a significant fraction of blue continuum in their nuclei. It is sometimes called featureless continuum, although spectral features of massive stars have been found early on (González Delgado et al. 1998). It also shows relatively low levels of polarisation (Tran 1995). According to AGN unification, it should therefore not originate from the central engine, as any direct light from there would be blocked and only reflected, and thus polarised light should be observable in type 2 AGNs (Cid Fernandes 1995). Nevertheless, its origin has remained contentious. For example, based on HST data Colina et al. (1997) showed that most of the circum-nuclear light originates in young star-forming regions, but could not say whether the nuclear blue light is from nuclear star formation or from an AGN-type power law. Sarzi et al. (2007b), on the other hand, find a good correlation between a tracer of the AGN continuum ([Ne V]) and the blue light in their stellar population synthesis and deduce that the blue light they find originates most likely from the AGN itself rather than from a young stellar population. However, not enough detail is given in Sarzi et al. (2007b) to fully understand these results; for example, we do not know about the strength of the [NeV] line in the Seyfert 2 AGNs for which they do not find a blue continuum.

Both a (very) young stellar population and a partly hidden AGN produce a blue and nearly featureless continuum. We therefore need to carefully monitor whether we can determine the fraction of light in the youngest population robustly in our AGN sub-sample or whether we misinterpret scattered AGN light as young stars.

We test this possible ambiguity in two ways. Firstly, we compare the flux in the blue continuum (at 4000–4200 Å) with the hard X-ray flux from the BAT-105 month survey (Oh et al. 2018). Figure 9 clearly shows that there is no correlation between these two fluxes, meaning there is no direct relation between the hard X-ray flux and the flux in the blue continuum. Pearson’s R coefficient for this relation is −0.0064.

thumbnail Fig. 9.

Relation of the blue continuum and the ultra-hard X-ray flux. The (noise-free) model flux at the blue end of our spectrum is plotted against the BAT 105-month ultra-hard X-ray (14–195 keV) flux. No relation between the two fluxes is seen, providing further evidence that the blue continuum in our spectra is not dominated by AGN light. The uncertainties of the BAT fluxes are within the symbol size.

Secondly, we take a closer look at the type 1.9 AGNs in our sample where we know that direct AGN light is included in our observed spectra since a broad component is observed in the Hα line. Figure 10 shows the Hα/[N II] complex for two regular type 2 AGNs with a significant young population and the two type 1.8 and 1.9 AGNs (NGC 2992 and MCG -05-23-016) in our sample, one with and one without a young population, according to our STARLIGHT fits. This shows both that a young stellar population is found in spectra without broad-line wings, and also conversely that in one spectrum with broad lines no young stellar population is found. The presence of a young population is therefore not obviously related to the presence of broad lines. This is consistent with the results from Cid Fernandes (1995), who found a broad component in Hβ only when the scattered AGN light contributes ≳20% of the optical continuum.

thumbnail Fig. 10.

Presence (or not) of a broad component of the Hα line in four AGNs with different fractions of light in the young population (fy) according to the STARLIGHT fit: NGC 7582 and NGC 3081 do not show broad components of the Hα line, and yet STARLIGHT finds a young stellar population in these two galaxies. And, vice versa, in NGC 2992, there is a very strong broad component to the Hα line, but no young stellar population is found. Only in MCG-05-23-016 do we find both a young population and a broad component. Overall this confirms the robustness of the detection of young stellar light, and that it is likely not confused with the non-stellar continuum from the AGN.

We conclude that the fraction of light in the young stellar population is not polluted by AGN light and that, therefore, we can determine the presence of a young stellar population accurately also in the AGN sub-sample. We therefore do not add a power-law component to account for the AGN featureless continuum in our comparative study in order not to confuse our fits (e.g., Cid Fernandes et al. 2004) and not to bias the AGN fit against that of the inactive galaxies.

4.2. Lower bound on the young stellar populations in AGNs

We can use the equivalent width of Hα (EWHα, see Table 4) to put additional constraints on the recent star formation history of the AGNs. To do so, we first need to estimate the largest fraction of the Hα luminosity that could arise from star formation, and for this we use the group of AGNs with the highest EWHα. There are a number of reasons why AGNs could have lower EWHα, but the maximum values will only be found when both AGN and star formation contribution are maximal. The group of six AGNs with the highest EWHα consists of ESO 137-G034, NGC 3081, NGC 2110, NGC 7582, NGC 2992, and NGC 5728, and their median EWHα is 70 Å. These also tend to have the highest log [OIII]/Hβ, with a median ratio of 1.07. Similarly, their median log [NII]/Hα is 0.01. To assess the star formation contribution to the Hα flux, we consider lines from the most extreme AGN photoionisation models of Groves et al. (2004), to the location of solar metallicity star-forming galaxies (see also Davies et al. 2014b). Since the AGNs are very close to the highest [OIII]/Hβ ratios that the models can produce, we find that at most 10% of their Hα flux could be due to star formation. Applying this correction reduces the EWHα that is associated with star formation to < 7 Å. We also need to make a correction for the old stellar population, since EWHα in models compares the line flux to the continuum due to stars associated with the line emission. We find that 5% of the continuum is associated with young stars. We therefore estimate that the maximum EWHα associated with the most recent star-forming episode is < 7 Å/5%, which is < 140 Å. Comparing this to Starburst99 models (specifically Figs. 83 and 84 in Leitherer et al. 1999) rules out continuous star formation since it would imply a timescale exceeding several Gyr, inconsistent with the stellar population synthesis results. Instead, it means that the recent star formation must have ceased. Based on the rate at which the EWHα falls after star formation stops, we estimate that the end of star formation must have typically happened at least 6 Myr prior.

Table 4.

Results of the emission line fitting.

In addition, we can look into the youngest bin of the individual stellar population fits (Appendix A) and find that six out of the seven AGNs in which we find such a population show this young population in the ∼107 year single stellar population model (and only one in the youngest, 106 year population), further confirming the interpretation that the youngest stellar population in AGNs has ceased forming stars for at least 6 Myr.

4.3. Stellar masses

The stellar masses quoted as the last column of Table 3 are derived from the STARLIGHT fitting itself7, that is, using the decomposition into various stellar populations with its mass/light ratios. The normalisation from measured flux to stellar masses includes the uncertainties of the absolute spectrophotometric flux calibration (better than ∼2%, see Sect. 2.3) and the uncertainty in the distance (see Davies et al. 2015 for a discussion of the distances used in the LLAMA sample).

The median mass that STARLIGHT finds within our aperture is log M⋆/M⊙ = 8.8, while the median total mass that we have previously (Davies et al. 2015) inferred from H band luminosity is log M⋆/M⊙ = 10.35, which is a factor of 35 lower (or ∼3%). This is roughly consistent with the fact that we cover (in the median galaxy) 15 % of the mass of the bulge (see Sect. 6.1). Since our galaxies have a median bulge/total ratio of 0.25 (Lin et al. 2018), this would lead to roughly the ∼3% number found above. The masses obtained by STARLIGHT are therefore consistent with the masses obtained from H band luminosity for the entire galaxy and scaled to the fraction of the galaxy that we include in our aperture for this work.

The total mass in the aperture can be used to convert the fraction of mass in a certain age bin to the star formation rate on this timescale; for example, the star formation rate within the last 107.5 years can be computed by evaluating μy × M⋆/107.5 years, where μy is the mass fraction in the young population, given in Table 3.

5. Emission line diagnostics

5.1. Emission line fitting

In order to allow for a number of diagnostic plots, we determined the flux in the classical BPT and VO07 emission lines (Baldwin et al. 1981; Veilleux & Osterbrock 1987), after subtracting the stellar population fit from our spectra. Our fit strategy is as follows: for the [O III]/Hβ region, we first fit a Gaussian and an offset to the [O III] λ 5007 line and bind both the mean (±0.5 Å) and the standard deviation (σHβ = [0.9…1.1]·σ[OIII]) of the Hβ line to the [O III] fit. For the region encompassing the Hα/[N II] complex, as well as the [O I] λ 6300 and the [S II] λ (6716, 6731) doublet, our fit strategy was similar. In general, we first fitted the [S II] doublet with a constant offset and a Gaussian each, and tied the mean and standard deviation of that fit to the Hα/[N II] complex as described above. Lastly, we fitted [O I] with its mean and standard deviation tied to [S II] as well.

This fitting strategy returned reliable fit results with the LevMarLSQFitter of astropy’s modeling package (Astropy Collaboration 2013, 2018), but for several cases we had to adjust the binding conditions manually and/or fix the continuum level in order to get a good fit of the emission line. The results of the emission line fitting are presented in Table 4.

We also show the extinction AV from the Balmer decrement (see discussion in Sect. 5.5) and the equivalent width of Hα. For the emission lines used in the BPT and VO87 diagnostic diagrams, we give the logarithmic flux ratios rather than the individual fluxes. For the actual fluxes, we refer the reader to Davies et al. (2020) who measured the fluxes of the main emission lines using higher spectral resolution stellar templates compared to the lower spectral resolution, single stellar population models used in this paper. Davies et al. (2020) also show that emission lines in AGNs are generally dominated by outflows, although few have as complex profiles as the LLAMA galaxy NGC 5728 (Shimizu et al. 2019). For the purpose of determining the dominant ionisation mechanism, integrating the entire line flux as we do in this paper is, however, still applicable.

5.2. Emission line diagnostic diagrams

In Figs. 11–13, we show the location of our sample on the classic BPT plots including the extension to [S II] λ (6716, 6731) by Veilleux & Osterbrock (1987). We further show the (empirically derived) boundary between starburst galaxies and AGNs from Kauffmann et al. (2003) on the [N II]/Hα versus [O III]/Hβ plot as well as the (theoretically found) maximum starburst line from Kewley et al. (2001) on all emission line diagrams. For reference, we also show the corresponding line ratios from the MPA-JHU emission line analysis of the SDSS DR 7 galaxies (Brinchmann et al. 2004) in our redshift range where all the six relevant lines (required to produce the four ratios shown here) have been detected at > 5σ.

thumbnail Fig. 11.

BPT plot with [OIII]/Hβ versus [N II]/Hα. Galaxies from the AGN as well as the control sample of star-forming and passive galaxies are shown in blue, deep pink, and red, respectively. The empirical (Kauffmann et al. 2003) and theoretical (Kewley et al. 2001) boundaries between starburst and AGN galaxies are marked with black straight and dashed lines, respectively. The underlying blue cloud of points is from the MPA-JHU emission line analysis of SDSS DR7 galaxies (Brinchmann et al. 2004).

thumbnail Fig. 12.

Same as Fig. 11, but here for [O III]/Hβ versus [S II]/Hα (VO87 plot).

thumbnail Fig. 13.

Same as Fig. 11, but here for [O III]/Hβ versus [O I]/Hα.

It is noteworthy to mention that all nine AGNs and 14 out of 17 control galaxies are shown on these plots, hence our spectra have sufficient S/N to identify all six BPT/VO87 lines in all objects except three non-star-forming (passive/retired) control galaxies. These passive galaxies, where no single BPT line is robustly detected, are NGC 1315, NGC 2775, and NGC 5845. It is furthermore useful to also show our objects on the WHaN (equivalent width of Hα versus log [N II]/Hα) plot, Fig. 14, which allows us to better discriminate between bona fide AGN and retired galaxies with low Hα equivalent widths (Cid Fernandes et al. 2010, 2011). Our AGNs are indeed better separated from the control galaxies in the WHaN plot compared to the BPT/VO87 plots.

thumbnail Fig. 14.

WHaN plot showing the equivalent width of Hα on the y axis versus the BPT flux ratio [N II]/Hα. Galaxies from the AGN as well as the control sample of star-forming and passive galaxies are shown in blue, deep pink, and red, respectively. This plot is useful to show the relative strength of emission line features compared to the continuum. The demarcation lines are from Cid Fernandes et al. (2011). The blue cloud of points in the background is again from Brinchmann et al. (2004), as in Figs. 11–13.

In the BPT/VO87 plots, our AGN population is split into a group of four galaxies that are in the extreme Seyfert regime, another one (NGC 7172) that would also be clearly classified as an AGN, and three AGNs (NGC 2110, ESO 021-G004, and NGC 7582) that would not be classified as such based on their BPT/VO87 optical emission line ratios; NGC 2110 would, however, be classified as an AGN in the WHaN diagram. This is similar to the results for a larger sample of ultra-hard X-ray-selected sources from the BAT AGN Spectroscopic Survey (BASS; Koss et al. 2017) where the authors find that only half of their sources would be selected as AGNs based on optical emission lines.

A similarly split view is seen in our control population. Six of our control galaxies are clearly on the sequence of star-forming galaxies as seen from the [N II]/Hα versus [O III]/Hβ plot, and we refer to them as star-forming control galaxies in the further analysis. What is the nature of the other eight galaxies (and the three that are not detected in Hα)? The clearest separation is seen in the [O I]/Hα plot, Fig. 13, from which one would deduce they are in the LINER regime, which in this case is most likely an indication for an old stellar population since we tested the control sample rigorously for the existence of any nuclear (AGN) activity. The odd one out is NGC 4254, an inactive control galaxy according to our initial classification, which is located in the Seyfert region (see below for a discussion on this). We refer to this latter population as non-star-forming control galaxies.

Since galaxies are more likely identified as AGN using nuclear spectra (such as ours) rather than integrated spectra (e.g., Gavazzi et al. 2018), the fact that none (except perhaps one, see below) of our control galaxies are in the AGN regime can be considered as additional evidence showing the purity of our control sample (we know that our AGNs are bona fide AGNs due to the ultra-hard X-ray selection).

5.3. Metallicities from the BPT diagrams

Kewley et al. (2006) point out that star-forming galaxies form a tight sequence from low metallicities (low [NII]/Hα, high [O III]/Hβ) to high metallicities (high [N II]/Hα, low [OIII]/Hβ). This can be seen in the photoionisation calculations presented in Kewley et al. (2001). While Kewley & Dopita (2002) caution that [NII]/Hα alone is not a good metallicity indicator because of its dependence on the ionisation parameter, they also note that if it can be confirmed that ionisation ratios are due to star formation rather than AGNs or shocks – for example, by their location in diagnostic diagrams – it can be used to provide a zeroth-order estimate of metallicity. Our inactive galaxies form a sequence that extends to the star-forming region of the BPT corresponding to approximately solar metallicity abundances (see e.g., Fig. 9 of Kewley et al. 2001). Furthermore, we take this as confirmation that we can adopt solar abundance for our stellar population fitting as described in Sect. 3.4.

5.4. The misfit in the BPT relation: NGC 4254

The nuclear emission line ratios in NGC 4254 place this object on the Seyfert side of the extreme starburst line in diagnostic plots. If one did an optical emission line selection, this object would be included as an AGN. However, both the available X-ray and mid-infrared observations indicate that there is no significant AGN in NGC 4254. The 0.3–8 keV nuclear luminosity (Grier et al. 2011) is log L/erg s−1 < 38.2, adjusted to our adopted distance of 15 Mpc. This is well below that seen at 2–10 keV for the low-luminosity AGNs in Asmus et al. (2011), and even below the typical range of star-forming galaxies. Similarly, the 3σ limit on the 10 μm luminosity in a 6″ aperture of log L/erg s−1 < 40.6 (Scoville et al. 1983) is well below that typically seen in Seyferts and LINERs.

Can the emission line ratios in NGC 4254 be due to shocks? While Allen et al. (2008) show that models of shocks with speeds of ∼400km s−1 with a precursor (i.e., an H II region in front of the shock caused by ionising photons from the shock front) can produce high [OIII]/Hβ ratios, these are typically associated with lower [NII]/Hα, and higher [SII]/Hα and [OI]/Hα ratios than measured in NGC 4254. However, we can consider whether the addition of shock excitation to stellar photoionisation (by either young stars or post-AGB stars) can move the location of a galaxy from where we find the other inactive galaxies to where we find NGC 4254. This could indeed reproduce [OIII]/Hβ and [NII]/Hα, but not the other ratios. This is because it produces too much [SII] and [OI] to be able to match the ratios involving Hα.

While one can find a particular metallicity and ionisation parameter that roughly matches the location of NGC 4254 (Stasińska et al. 2008), it is hard to understand why this object would be so different from the other inactive galaxies.

We are left speculating that NGC 4254 may be a recently turned off AGN, which would explain its lack of X-ray and mid-IR emission (that are generated on scales of a few pc). The larger narrow-line region could then be the afterglow of such a recently turned off AGN.

Alternatively, it could indeed be a very-low-luminosity AGN. The typical 12 μm luminosity of the AGNs in our sample is log L12 μm/(erg s−1) = 42.8, and the typical observed 2–10 keV luminosity is log L2 − 10 keV/(erg s−1) = 42.2. Comparing these to the luminosities above (and not worrying that the bands are slightly different) suggests that if it is an AGN, NGC 4254 is at least two orders of magnitude lower luminosity than our sample, and that in addition there is likely to be a high X-ray-absorbing column. If all the Hα flux is due to the AGN, one would expect the equivalent width of Hα to be proportionally lower than in the other AGNs. However, it is only a factor 10, rather than 100, less than the majority of the AGNs in our sample. As such, much of the line flux should originate in other processes. However, with regard to the shocks, considerations of mixing do not explain the low [SII]/Hα ratio either.

5.5. Extinction estimates: Comparison between SPS fitting and Balmer decrement analysis

In Fig. 15, we show the comparison of the extinction estimate from our absorption line fitting (STARLIGHT) and from the emission line fitting discussed above. In the latter, we convert the Balmer decrement to an extinction AV using Eqs. (4) and (7) from Domínguez et al. (2013), who in turn used the Calzetti reddening law (Calzetti et al. 1994, 2000). They assumed an intrinsic Hα/Hβ ratio of 2.86, which is applicable for star-forming galaxies, but not strictly for AGNs, where a better value to use would be 3.1 (Wild et al. 2011). However, since we take a logarithm of that number to derive the extinction in magnitudes, the impact on AV is in fact only ∼0.03, meaning it is insignificant. We therefore opted to use just one reddening law for all galaxies.

thumbnail Fig. 15.

Comparison of the extinction estimate from emission line fitting versus absorption-line fitting (STARLIGHT). The dashed line corresponds to a 1:1 ratio, the dash-dotted line represents a ratio of 2:1. Statistical uncertainties in both methods are minute (≲0.2 mag), and the systematic difference between the two estimates is discussed in the main text. Galaxies from the AGN, as well as the control sample of star-forming and passive galaxies, are shown in blue, deep pink, and red, respectively.

Rather than following a 1:1 line (dashed line in Fig. 15), the AV as derived from the emission line fitting is higher than the extinction derived from the absorption line fitting by roughly a factor of two (dash-dotted line in Fig. 15). This is to be expected since the Balmer decrement preferably probes regions of active star formation, typically embedded in dust, while the extinction from STARLIGHT is dominated by light from old stars within an essentially dust-free environment. The reddening law (Calzetti et al. 1994; Calzetti 1997), as stated more simply at the bottom of page 1394 of Förster Schreiber et al. (2009), gives AV(nebular) = 2.27 AV(stars), which is consistent with the relation we find, too. A similar result has recently been shown with the larger sample of MaNGA galaxies by Riffel et al. (2021).

6. Population analysis

6.1. Non-parametric star formation histories

The result of the stellar population synthesis is a so-called stellar population vector that contains the fractional contribution of light that the fitting tool ascribes to the included base spectra. In this so-called non-parametric description of the star formation history (SFH) of a galaxy, stellar ages are described in discrete age bins. It is good to keep in mind how some simple SFHs would look in this description. For example, if the SFH is composed of a number of bursts, we expect to find a depression of the light ascribed to an intermediate-age stellar population. This is a combined effect of mass/light ratio (favouring the very young populations) and logarithmic binning on the age axis (favouring the oldest populations), which results in a bias against an intermediate age population.

We can in addition ask, observationally, how large the fraction of light of the oldest population should be. Photometric decomposition of many of the LLAMA galaxies have shown a large variety of bulge sizes (Lin et al. 2018), with a median effective radius Compared to our fixed aperture of (side of a square extraction region), and using de Vaucouleurs’ law (de Vaucouleurs 1948), this means that we cover ∼15% of the mass of the bulge in our aperture.

Our observations are further designed such that only the light from the nuclear stellar population is seen (apart from the ‘foreground’ bulge light), and the light from the circum-nuclear stellar ring is excluded (see Sec. 2.3.2). The mass in the nuclear stellar population is about ten times larger than the mass of the SMBH (e.g., Davies et al. 2007; Schartmann et al. 2009), and the mass of the bulge is ∼400–700 times the mass of the black hole8. From this, we can infer that the bulge should contribute ∼15%×500/10 ∼ 7.5× more mass than (or about 90% of) that of the nuclear stellar populations. This is consistent with the ∼90% mass fraction we find from the STARLIGHT fitting (see Table 5). This simple calculation is not supposed to lead to an accurate stellar light fraction of the bulge, but it should clarify that we expect to see a significant fraction of light in the oldest stellar population. Additional uncertainties include the large variance of apparent bulge sizes in our sample (Lin et al. 2018), as well as the likely pseudo-bulge nature of many of our galaxies (Caglar et al. 2020).

Table 5.

Summary of stellar populations by galaxy class with uncertainties from jack-knifing as described in the text.

6.2. Summarised star formation histories

Looking at the summarised SFHs it is useful to split our sample not only into AGN and control galaxies, but also to further distinguish between star-forming and non-star-forming control galaxies, as defined in Sect. 5. In Figs. 16 and 17, we show the summarised stellar population vectors for all galaxies with a successful stellar population fit and binned into the four age ranges.

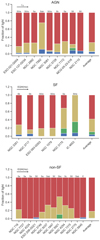thumbnail Fig. 16.

Comparison of stellar populations between the AGN and inactive sample where the inactive sample is split by location on the BPT diagram into a star-forming (SF) sub-population and a non-star-forming (non-SF) sub-population. The stellar populations are split into the same four age bins as in the previous section: young (blue), young-intermediate (green), intermediate-old (yellow), and old (red), with boundaries at log(age/yr) = 7.5, 8.5, and 9.5. The AGN-hosting galaxies are sorted by increasing X-ray luminosity LX, and the inactive control population is sorted by increasing equivalent width of Hα (EQW(Hα)).

thumbnail Fig. 17.

Average SFHs of AGNs, star-forming and non-star-forming control galaxies as in Fig. 16 (left panel), and a zoom into the youngest stellar populations (right panel). The uncertainties are derived through jack-knifing (see text for further discussion).

Apart from the large fraction of light from old stars that is expected (see above), the most obvious observation is that seven out of nine AGNs show a measurable fraction of young stellar light. This is consistent with previous observations that (Seyfert-type) AGN activity is often associated with young nuclear stellar populations (e.g., Cid Fernandes et al. 2004). We further find a similar occurrence rate of young stars in star-forming control galaxies (four out of six galaxies). This may sound trivial, but it is actually a solid cross-check between the absorption and emission line analysis since our SFHs are only derived from the absorption line fitting, while our classification is solely based on emission line diagnostics. The SFH for non-star-forming galaxies, on the other hand, is dominated by old stars.

We evaluate the significance of this difference from a jack-knife re-sampling test9 that indicates the uncertainty due to our relatively small sample size, which is the dominant uncertainty in this analysis. The average and 1σ uncertainties determined in this way are given in Table 5 and are shown in Fig. 17. Both the AGN and the star-forming inactive control galaxies show a significant fraction of light in our youngest age bin. The two sub-samples are indistinguishable within the uncertainties in terms of their nuclear young stellar population but are both very different, at the ∼3σ and ∼2.5σ levels, respectively, to the non-star-forming control population. In terms of the young-intermediate population, however, AGNs appear identical to the non-star-forming control population, and the fraction of light in this age bin for the star-forming galaxies is dominated by a single very young galaxy, IC 4653. Without this galaxy, the fraction of light in the intermediate-young population for the star-forming sub-sample would be 2.27 ± 2.25 %, which is consistent with the AGN and non-star-forming sub-samples.

This finding is consistent with the idea that any galaxy that has a sufficient amount of cold, molecular gas close to its nucleus will turn on as an AGN eventually (e.g., Davies et al. 2012) and that accretion onto black holes is a highly variable process (e.g., Novak et al. 2011) that quickly turns AGNs (hosting nuclear starbursts) into inactive nuclear star-forming galaxies (e.g., Hickox et al. 2014). Regarding their SFHs, the LLAMA star-forming control galaxies could indeed be the parent population of the LLAMA AGNs.

6.3. Number densities of AGNs and star-forming galaxies and an indication of the AGN lifetime

If we identify the LLAMA star-forming control galaxies with the parent population of LLAMA AGNs, we can infer the occurrence rate of AGNs – at the given luminosity threshold and at the stellar masses probed in LLAMA – thanks to the volume-completeness of our sample. For this test, we select all star-forming galaxies from the MPA-JHU catalogue of SDSS DR7 galaxies10 (Brinchmann et al. 2004) within our redshift limits of 0.005 < z < 0.01 and above our lower stellar mass limit of log M⋆/log M⊙ ≳ 9.511.

We apply a correction for the respective areas probed: LLAMA applied a cut for δ < 15°, meaning it covered 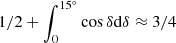of the sky, while SDSS-II DR7 (Legacy survey/spectroscopy) covered about 8000 deg2. Since the whole sky is 4π(180/π)2 ≈ 41000 deg2, the area correction factor is 3.8 (this is the factor by which the LLAMA area is larger than the SDSS area). We tested that in the LLAMA volume, SDSS is complete for star-forming galaxies of the given stellar mass. In this volume, there are 127 star-forming galaxies in SDSS, which, scaled to the LLAMA volume, would give 476 star-forming galaxies. Further assuming that all AGNs of this luminosity show similar SFHs (not just the nine that we were able to probe, but also the other eleven for which we could not perform the stellar population synthesis since they have broad AGN lines or were not observed) and correcting for the (small) number of Compton-thick AGNs that the LLAMA selection missed due to their high absorbing column (5 sources, Ricci et al. 2015), we contrast this number with, in total, 25 AGNs of log L14 − 195 keV/erg s−1 > 42.5 and declination δ < 15°. In other words, in this stellar mass range, we expect to find one AGN (defined by the X-ray luminosity cutoff of our sample) among twenty star-forming galaxies.

We can compare this to an upper bound for this ratio that we derive from the flickering timescale of 105 years that Schawinski et al. (2015) reported for AGNs. Compared to the youngest age bin of our SFH analysis (30 Myr), a total of 300 ‘flickering events’ might have happened within this time if AGN activity and nuclear star formation are totally uncorrelated; that is to say, one might expect to find star-forming galaxies to be up to 300 times more frequent than AGNs (if only one AGN flickering event occurs per nuclear starburst). This upper limit is consistent with the number derived above. We conclude that our analysis supports the notion that an (luminous, 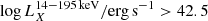) AGN phase occurs in about 5 % of all star-forming galaxies with the given mass limits in the local universe. For comparison, the prevalence of any optically selected AGNs (without luminosity cut) is about 4% of all galaxies as found recently in the CALIFA survey (Lacerda et al. 2020). This is also consistent with larger X-ray-selected AGN samples. For example, Xue et al. (2010) found a median AGN fraction in their most local redshift bin (0 ≤ z ≤ 1) that was between 1.5 and 6 % dependent on luminosity. Our luminosity selection is in between their lower and upper limits, and the numbers are therefore quite consistent.

Goto (2006), on the other hand, identified 840 galaxies in SDSS that show both a post-starburst signature and an AGN; they make up 4.2% of all galaxies in their volume-limited sample. Since these authors were looking for Balmer absorption signatures, indicative of A-type stars, their sample includes starbursts with ages up to 1 Gyr. Our analysis is consistent with this, but we show in addition that the intermediate-young population is insignificant in our nine X-ray-selected AGNs and that post-starburst features are dominated by a population that is between 6 and 30 Myr old (see Sect. 4.2). We conclude from our analysis that the AGN is indeed not ‘on’ during the circum-nuclear starburst, but shortly after it, which is consistent with, for example, Davies et al. (2007).

6.4. Comparison with molecular gas masses

As part of the LLAMA project, we have also obtained molecular gas estimates using APEX observations to search for molecular gas in the central 1–3 kpc (Rosario et al. 2018). Despite the large differences in aperture, we still find some relation between the APEX results and our analysis here. Of the 26 galaxies common to both studies, molecular gas was not detected by APEX in only four. Three of these galaxies, NGC 2775, NGC 5845, and ESO 208-G021, are inactive galaxies characterised by a very old dominant population of stars, and the 0.3–3 Gyr population is invisible in these (however, two of them do show a small fraction of young stellar light). Approaching this from another angle, for three of the non-star-forming control galaxies in our sample, we only have upper limits for gas masses from the APEX observation, while none of the star-forming control galaxies and only one AGN exhibit that behaviour. That AGN is MCG-05-23-016, which shows a substantial fraction of both young and young-intermediate stars in the analysis presented in this article. The APEX limit was not as deep as for the inactive galaxies, and comparable to some of the detections in other galaxies. Interferometric data from ALMA show that there is indeed molecular gas in the central arcsec, from which stars could form and which could feed the AGN, but very little gas in the surrounding 5–10″. This highlights the importance of high-spatial-resolution studies of gas in AGNs to study the relation between gas reservoirs, stellar populations, and AGN activity.

Other recent studies largely corroborate the picture that AGN activity is related to gas mass and star formation, although the observations tend to cover scales of kiloparsecs or more and so are more related galaxy-wide rather than nuclear properties. Jarvis et al. (2020) find high molecular gas masses in z ∼ 0.1 powerful quasars, most of which also had high star formation rates typical of starbursts. Husemann et al. (2017) also found some starbursts in their z < 0.2 sample, but they also highlighted a relation between gas content and AGN accretion rate for the disc-dominated (but not bulge-dominated) QSOs in their sample. Similarly, for a sample of QSOs at z < 0.3, Shangguan et al. (2020) found that AGN luminosity correlates with both CO luminosity and black hole mass, and that the molecular gas content of the AGN was similar to star-forming galaxies of comparable stellar mass. Using the amount of reddening as a proxy for cold molecular gas mass in order to increase the sample size by an order of magnitude, Zhuang et al. (2021) found a similar gas content in AGNs and star-forming galaxies. Yesuf & Ho (2020) also used a proxy for molecular gas content – in this case the dust absorption derived from the Hα/Hβ ratio – in order to study a large sample of galaxies. Based on their analysis, these authors proposed an evolutionary life cycle in which the gas content mediates the star formation rate and AGN activity. Using direct observations of the CO(2–1) line of more than 200 nearby (z < 0.05) hard X-ray selected galaxies, Koss et al. (2021) found that AGN hosts had a higher gas content than inactive galaxies matched by stellar mass but a similar gas content to inactive galaxies matched by star formation rate. They argued this was because the AGN sample is largely missing a population of quenched passive galaxies that are found among the inactive population. This may be because passive galaxies do not have their own large gas supply that can feed a central black hole, and, as suggested by Davies et al. (2014a) and Davies et al. (2017), to become a radiatively efficient AGN they may have to acquire gas from the environment instead. Together, these studies show that when assessing the links between gas content, star formation, and AGN activity, one needs to take into account the global properties of host galaxy (such as the stellar mass, host morphology, etc.) since these can affect the nature of that relation. Our expectation is that, by switching the focus from large to small scales, high-resolution measurements of the nuclear gas content (Rosario et al., in prep.) will lead to a better understanding of those relations.

6.5. Comparison with previous estimates of the nuclear star formation rate and history

When comparing the central star forming properties of AGNs, it is important to bear in mind how the AGNs were selected, the size of the region being considered, and the way the star formation rate or history was derived. These all have an impact on how the various results may fit together. The AGNs presented here were selected solely by their very hard X-ray luminosity (and would not all be classified as AGN based on their optical line ratios and Hα equivalent widths); and their proximity means that our aperture extends to radial scales of typically ∼150 pc. The AGNs from MaNGA presented by Rembold et al. (2017), Mallmann et al. (2018), and Bing et al. (2019) were selected based on BPT ratios and the equivalent width of Hα. As such, Rembold et al. (2017) and Mallmann et al. (2018) contain a large fraction of lower luminosity AGNs. To avoid a possible bias due to this, Bing et al. (2019) also imposed an [O III] luminosity constraint. In addition, the distance to the AGNs in MaNGA means that the 2″ central fibre typically covers radii out to 1 kpc or more. In many cases this is large enough to include a circum-nuclear ring if one is present.

Finally, we note that because Bing et al. (2019) focussed on secular evolution in gaseous discs, they imposed an additional constraint that the host galaxy of the AGN should be star forming. The impact of this selection criterion is not obvious: our Figs. 11, 14, and 16 (and also Fig. 2 in Rembold et al. 2017) show that among the matched inactive galaxies in our sample one finds central regions that are star forming and also those that are not; but there appears to be little relation between large-scale host galaxy classification (spiral versus lenticular) and whether there has been recent nuclear star formation (as defined by emission line ratios or by stellar population fitting). Given all these caveats, it can be difficult to compare published results directly with ours. Nevertheless, here we summarize some of those results and attempt an assessment of whether there is a consistent picture emerging.

The underlying question is whether accretion onto the central black hole is associated with star formation in the nuclear or circum-nuclear region; and if so whether the AGN is synchronous with star formation or whether it occurs after it in a post-starburst phase. Answers to these questions can indicate whether nuclear star formation and AGN activity are only related because both require inflowing gas, whether the young stars themselves help regulate the inflow, or whether the AGN regulates the star formation. Following the early work of Norman & Scoville (1988), a variety of theoretical scenarios have been proposed that support all these options. The analytical model of Kawakatu & Wada (2008) and detailed hydrodynamical simulations of Wada et al. (2009) suggest that inflow and accretion onto the black hole should increase with turbulence in the ISM, and occur simultaneously with star formation. Alternatively, Hobbs et al. (2011) suggested that supernovae may ballistically drive enough of the ISM inwards to fuel an AGN. Schartmann et al. (2009, 2010) used hydrodynamical simulations to model a scenario where, once star formation had ceased, slow stellar winds from AGB stars would flow inwards and fuel the AGN. Vollmer et al. (2008) proposed an analytical model in which inflow to the circum-nuclear region triggers star formation; but soon after, it is quenched by the subsequent supernovae. Vollmer & Davies (2013) argued that turbulence generated by the inflowing gas may also quench the star formation. Hopkins et al. (2012) argued that one might simply expect a delay between star formation and AGN activity due to the time it takes the gas to flow in from 10–100 pc scales.

Observationally, analyses of the nuclear and circum-nuclear region based on stellar population synthesis consistently provide evidence that AGNs are generally characterised by young stellar populations (Storchi-Bergmann et al. 2000; Kauffmann et al. 2003; Cid Fernandes et al. 2004; Sarzi et al. 2007a; Riffel et al. 2009). But these populations do not always seem to be present, and it is not always easy to separate the contribution of a very young stellar population from a featureless continuum associated with the AGN accretion disc. More recent studies have focussed on SDSS-III or SDSS-IV MaNGA data. Using 62 AGNs together with a larger number of matched inactive galaxies, Rembold et al. (2017) found a relation between the contribution from young (∼40 Myr) stars and the [O III] luminosity, supporting the notion that massive starbursts fuel powerful AGNs. Similarly, and using the same active and inactive samples, Mallmann et al. (2018) looked at the spatially resolved stellar properties and found that in the inner 1Re the more luminous AGNs do present larger fractions of young (t ≤ 40 Myr) stars than the control galaxies. In contrast, and perhaps associated to their selection that focuses on galaxies with star-forming discs and their use of Hα to measure star formation rate, Bing et al. (2019) reported that AGNs may have slightly suppressed ongoing nuclear star formation rates compared to matched star-forming inactive galaxies.

For the nuclear regions where one may expect star formation to occur in short bursts rather than continuously, the ionised emission lines are a crucial probe of the current star formation rate. These were a key part of the analysis of Davies et al. (2007) who combined them with mass-to-light ratios and an estimate of the supernova rate from radio continuum imaging, to conclude that there was recent, but no longer on-going, star formation. Hicks et al. (2009, 2013) and Davies et al. (2014a) highlighted the low equivalent widths of the Brγ line in the near-infrared, where extinction has less impact than the optical. After taking into account the contribution to the line from the AGN (e.g., via kinematics) and also the contribution to the continuum from hot dust (e.g., via the slope and CO2-0 bandhead depth), their conclusion was that there could not be on-going star formation. This is consistent with the stellar synthesis analyses in the literature as well as our conclusion from this paper: it means that star formation has occurred recently, but it must also have ceased since. It argues for repeated short-lived bursts of star formation.

A third approach to assessing the central star formation is based on the presence of poly-aromatic hydrocarbons (PAHs), which are known to trace young stars, but over a wider range of ages (∼100 Myr) than the ionised line emission. However, there is a debate about whether the PAHs are excited by stars or by the AGN itself, or whether small PAHs are destroyed by the hard radiation from an AGN (Siebenmorgen et al. 2004; Smith et al. 2007; Sales et al. 2010). This may depend on which PAH feature one considers: Diamond-Stanic & Rieke (2010) found that in AGNs on kpc scales the 6.2, 7.7, and 8.6 μm features were suppressed, while the 11.3 μm feature was not. Partly for this reason, recent studies of PAHs close to AGNs have focussed on the feature at 11.3 μm. Esquej et al. (2014) detected PAHs on subarcsec scales in about half of their sample of 29 nearby Seyfert galaxies. They argued that the high column densities in the torus around the AGN would provide shielding that enables PAHs to survive, and the implied central star formation rate density was much higher than in the circum-nuclear region. A similar conclusion about PAH survival was reached by Esparza-Arredondo et al. (2018) for their sample of 19 AGNs, based on the lack of relation between the X-ray luminosity and a central PAH deficit – while PAHs were detected in most AGNs, the equivalent width was lower in the centre. They attributed this to low star formation rates in that region. On the other hand, while Jensen et al. (2017) also detected PAHs in a sample of 13 AGNs, they argued that the similarity and slope of the radial profiles from tens to hundreds of parsecs point towards an origin in a single compact source of excitation. In order to shed more light on the excitation of PAHs in this context, Alonso-Herrero et al. (2020) compared PAH line ratios in 22 AGNs to models of PAH excitation and analysed this in the context of the measured molecular gas content. They concluded that PAHs can be shielded from the hard AGN radiation.

Of the nine AGNs analysed in this paper, six appear in the PAH papers mentioned above. Four of those have PAH detections in the Spitzer aperture (3.7″ slit width), but only one has a PAH detection from ground-based data in a ≲1″ slit. This detection is NGC 7582, which has the highest young stellar population fraction of our AGN sample. However, three of the AGN with PAH non-detections also have significant young stellar populations (NGC 2110, NGC 3081, and MCG-05-23-016). The other two non-detections are for NGC 2992 and NGC 7172, for which we did not find evidence of a young (or young-intermediate) stellar population. Thus, it seems that while in principle PAHs can be used to trace star formation close to AGNs, the assessment of the implied star formation rates is still open – although it does point in the same direction as the other studies that there is recent star formation close around many, although perhaps not all, AGNs.

7. Conclusions and outlook

Using VLT/X-shooter spectra and Bruzual & Charlot (2003) single stellar population models together with the STARLIGHT fitting code, we fit the integrated light in an aperture corresponding to a physical radius of ≈ 150 pc. We performed the analysis on a sample of nine type 2 AGNs that are part of the volume-complete sample of hard-X-ray-selected, powerful local AGNs presented by Davies et al. (2015). We conducted an identical analysis on a sample of 18 inactive control galaxies that were matched in stellar mass, distance, and Hubble-type. Our main findings can be summarised as follows:

  • We can robustly determine the fraction of young stellar light in type 2 AGNs, and we are not (or only insignificantly) affected by scattered AGN continuum.

  • We find young stellar populations in seven of the nine AGNs and constrain their age to be between 6 and 30 Myr from their location on the diagnostic emission line ratio diagrams from BPT/VO87 and from the stellar population fitting. On average, 4.5 ± 1.2 % of the optical light of our AGNs stems from this population.

  • The analysis of the nuclear stellar populations of a sample of inactive galaxies matched on large scales shows that they fall into two distinct groups: those with and without recent star formation according to their BPT/VO87 emission line ratios.

  • When separated according to their BPT/VO87 emission line ratios, the star-forming inactive control galaxies show very similar fractions (4.2 ± 1.4%) of young stellar light and are clearly different from the non-star-forming control galaxies that only show 0.5 ± 0.3 % of young stellar light.

  • Interpreting the star-forming control galaxies as the parent population of our AGNs, we find that a luminous (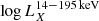/erg s−1 > 42.5) AGN phase occurs in ∼5% of all star-forming galaxies within the mass limits of our sample in the local universe, which is consistent with other estimates.

  • That the matched inactive galaxies form two sub-groups, with the star-forming inactive galaxies identified as the AGN parent population (and for which the timescale to switch between active and inactive is rather short), points also to long timescales of inactivity. This is associated with the inactive galaxies with no recent star formation. Moreover, it is an indication that in those galaxies there is insufficient gas to trigger either nuclear star formation or an AGN. This supports the notion that the relevant criterion for both AGN activity and circum-nuclear star formation is the presence of gas in the central 100 parsecs (e.g., Sabater et al. 2015).

In the future, we plan to enhance our sample size, while keeping the volume-complete nature of the selection. We note that the high spatial resolution afforded by the VLT Unit Telescopes is actually not required in the optical since we are limited by extinction, which confuses the definition of the nucleus on sub-arcsecond scales in the optical. In order to separate the < 100 pc nuclear stellar populations from the nuclear rings at > 100 pc, a resolution of ≈20 is sufficient for galaxies within our redshift limit of z < 0.01, suggesting that a larger sample could be obtained with a significantly smaller telescope. The SOXS instrument (Schipani et al. 2020) seems particularly suited for a follow-up of this kind of research.

In addition to expanding the sample size, we also plan to continue investigating nuclear stellar populations in the (near-)IR, both to further zoom in on the highly obscured nucleus and to obtain the full picture regarding young populations (Riffel et al. 2015).

1

The axis ratio (inclination) match was performed for the dynamical analyses done in other LLAMA projects. For the sample used here, the median axis ratios of AGNs and control galaxies are 0.56 and 0.67, respectively. For the stellar population fitting, the inclination of the host galaxy does not play a major role, except perhaps for obscuration effects, which are discussed separately.

2

We found, however, that we had to set the property GlobalCutUVBSpectrum to False in order to retrieve a correct wavelength calibration in the UVB arm of X-shooter.

3

The median distances of the AGN and control galaxy sub-samples are 35 Mpc and 21.5 Mpc, respectively.

5

In particular, some of our X-shooter spectra show a strong instrumental signature in the region where the UVB/VIS arms are overlapping. This calibration residual is possibly related to variable dichroic transmission due to humidity changes (J. Vernet, priv. comm.) or from flat-fielding residuals when the pipeline chooses different calibration files for the science and flux calibrators, respectively (A. Mehner, priv. comm.).

6

For NGC 5037, we used the redshift reported by Simbad since the redshift from NED (0.009893) is wrong based on our spectral fitting. Also, for IC 4653 the initial recession velocity assumed for the fit had been taken from NED (Corwin et al. 1994, 1890 km/s), which is wrong. We thus used and confirm the updated redshift as previously published by Wegner et al. (2003). We invite the reader to consult Davies et al. (2020) for a further discussion about the systemic velocities of these two galaxies.

7

Using Eq. (2), page 22, of the STARLIGHT manual v0.4, but with the correct number for M⊙.

8

Häring & Rix (2004) give a ratio of ∼700, and McConnell & Ma (2013) look at this ratio for early-type galaxies and give a ratio of about 400 for our typical black holes mass of ∼3 × 107 M⊙ (Caglar et al. 2020). Davis et al. (2019) (Eq. (11), noting that ν = 1 from their Eq. (10)) give a ratio of ∼500 for our typical black hole mass.

9

We use jackknife_stats from astropy.stats with a 1σ confidence level.

10

These galaxies were identified in the SDSS DR7 spectroscopic sample using BPT line ratios. While the SDSS fibre aperture is almost twice as large (30) as our extraction aperture (18), we do not expect this to lead to a significant bias when comparing our sample to the SDSS sample since most of our (powerful) AGNs are clearly detected as AGNs in the emission-line diagnostic diagrams.

11

We note that the stellar mass distribution of so-selected SDSS star forming galaxies is different from the stellar mass distribution of our (LLAMA) AGNs. This is expected since BAT-selected AGNs are known to be found preferentially in the most massive host galaxies (Koss et al. 2011). Our sample is too small to differentiate the AGN incidence per stellar mass bin and the analysis presented here should only be interpreted as an average number for massive galaxies.

Acknowledgments

The authors would like to thank the anonymous referee for comments that improved the paper. Based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme IDs 092.B-0083 and 095.B-0059. L.B. would like to thank Jarle Brinchmann, Anna Feltre, Reynier Peletier, Almudena Prieto, Marc Sarzi, and Scott Trager for helpful discussions and Roberto Cid Fernandes for discussions and for providing a special version of STARLIGHT that allowed us to investigate the posterior probability distribution functions ourselves. L.B. has been partly supported by a DFG grant at the Max-Planck-Institute for Extraterrestrial Physics within the SPP 1573 “Physics of the interstellar medium”. R.R. thanks CNPq, CAPES and FAPERGS for partial financial support. R.A.R. acknowledges financial support from CNPq (302280/2019-7) and FAPERGS (17/2551-0001144-9). D.J.R. acknowledges support from STFC (ST/T000244/1). A.S.M. thanks CNPq for partial financial support.

References

  1. Alexander, D. M., & Hickox, R. C. 2012, New Astron. Rev., 56, 93 [Google Scholar]
  2. Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20 [Google Scholar]
  3. Alonso-Herrero, A., Pereira-Santaella, M., Rigopoulou, D., et al. 2020, A&A, 639, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim., 53, 197 [NASA ADS] [CrossRef] [Google Scholar]
  5. Andrews, B. H., & Martini, P. 2013, ApJ, 765, 140 [NASA ADS] [CrossRef] [Google Scholar]
  6. Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
  7. Asmus, D., Gandhi, P., Smette, A., Hönig, S. F., & Duschl, W. J. 2011, A&A, 536, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  9. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  11. Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
  12. Baldwin, C., McDermid, R. M., Kuntschner, H., Maraston, C., & Conroy, C. 2018, MNRAS, 473, 4698 [Google Scholar]
  13. Baumgartner, W. H., Tueller, J., Markwardt, C. B., et al. 2013, ApJS, 207, 19 [Google Scholar]
  14. Bing, L., Shi, Y., Chen, Y., et al. 2019, MNRAS, 482, 194 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bönsch, G., & Potulski, E. 1998, Metrologia, 35, 133 [CrossRef] [Google Scholar]
  16. Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [Google Scholar]
  17. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  18. Burtscher, L., Meisenheimer, K., Tristram, K. R. W., et al. 2013, A&A, 558, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Burtscher, L., Orban de Xivry, G., Davies, R. I., et al. 2015, A&A, 578, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Burtscher, L., Davies, R. I., Graciá-Carpio, J., et al. 2016, A&A, 586, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Caglar, T., Burtscher, L., Brandl, B., et al. 2020, A&A, 634, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Calzetti, D. 1997, AJ, 113, 162 [NASA ADS] [CrossRef] [Google Scholar]
  23. Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [Google Scholar]
  24. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  25. Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [Google Scholar]
  26. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  27. Cid Fernandes, R. 2018, MNRAS, 480, 4480 [NASA ADS] [CrossRef] [Google Scholar]
  28. Cid Fernandes, R., Jr., & Terlevich, R. 1995, MNRAS, 272, 423 [NASA ADS] [CrossRef] [Google Scholar]
  29. Cid Fernandes, R., Heckman, T., Schmitt, H., González Delgado, R. M., & Storchi-Bergmann, T. 2001, ApJ, 558, 81 [NASA ADS] [CrossRef] [Google Scholar]
  30. Cid Fernandes, R., Gu, Q., Melnick, J., et al. 2004, MNRAS, 355, 273 [Google Scholar]
  31. Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [Google Scholar]
  32. Cid Fernandes, R., Stasińska, G., Schlickmann, M. S., et al. 2010, MNRAS, 403, 1036 [Google Scholar]
  33. Cid Fernandes, R., Stasińska, G., Mateus, A., & Vale Asari, N. 2011, MNRAS, 413, 1687 [Google Scholar]
  34. Cid Fernandes, R., González Delgado, R. M., García Benito, R., et al. 2014, A&A, 561, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Cisternas, M., Jahnke, K., Inskip, K. J., et al. 2011, ApJ, 726, 57 [NASA ADS] [CrossRef] [Google Scholar]
  36. Cisternas, M., Sheth, K., Salvato, M., et al. 2015, ApJ, 802, 137 [NASA ADS] [CrossRef] [Google Scholar]
  37. Colina, L., Vargas, M. L. G., Delgado, R. M. G., et al. 1997, ApJ, 488, L71 [NASA ADS] [CrossRef] [Google Scholar]
  38. Combes, F., García-Burillo, S., Audibert, A., et al. 2019, A&A, 623, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Comerón, S., Knapen, J. H., Beckman, J. E., et al. 2010, MNRAS, 402, 2462 [Google Scholar]
  40. Conroy, C. 2013, ARA&A, 51, 393 [NASA ADS] [CrossRef] [Google Scholar]
  41. Corwin, H. G., Jr, Buta, R. J., & de Vaucouleurs, G. 1994, AJ, 108, 2128 [NASA ADS] [CrossRef] [Google Scholar]
  42. Dahmer-Hahn, L. G., Riffel, R., Rodríguez-Ardila, A., et al. 2018, MNRAS, 476, 4459 [Google Scholar]
  43. Davies, R. I., Mueller Sánchez, F., Genzel, R., et al. 2007, ApJ, 671, 1388 [CrossRef] [Google Scholar]
  44. Davies, R., Burtscher, L., Dodds-Eden, K., & Orban de Xivry, G. 2012, J. Phys. Conf. Ser., 372 [Google Scholar]
  45. Davies, R. I., Maciejewski, W., Hicks, E. K. S., et al. 2014a, ApJ, 792, 101 [Google Scholar]
  46. Davies, R. L., Kewley, L. J., Ho, I. T., & Dopita, M. A. 2014b, MNRAS, 444, 3961 [NASA ADS] [CrossRef] [Google Scholar]
  47. Davies, R. I., Burtscher, L., Rosario, D., et al. 2015, ApJ, 806, 127 [Google Scholar]
  48. Davies, R. I., Hicks, E. K. S., Erwin, P., et al. 2017, MNRAS, 466, 4917 [Google Scholar]
  49. Davis, B. L., Graham, A. W., & Cameron, E. 2019, ApJ, 873, 85 [NASA ADS] [CrossRef] [Google Scholar]
  50. Davies, R., Baron, D., Shimizu, T., et al. 2020, MNRAS, 498, 4150 [Google Scholar]
  51. de Vaucouleurs, G. 1948, Ann. d’Astrophys., 11, 247 [Google Scholar]
  52. Diamond-Stanic, A. M., & Rieke, G. H. 2010, ApJ, 724, 140 [NASA ADS] [CrossRef] [Google Scholar]
  53. Diamond-Stanic, A. M., & Rieke, G. H. 2012, ApJ, 746, 168 [Google Scholar]
  54. Diniz, M. R., Riffel, R. A., Riffel, R., et al. 2017, MNRAS, 469, 3286 [NASA ADS] [CrossRef] [Google Scholar]
  55. Domínguez, A., Siana, B., Henry, A. L., et al. 2013, ApJ, 763, 145 [CrossRef] [Google Scholar]
  56. Elvis, M. 2000, ApJ, 545, 63 [NASA ADS] [CrossRef] [Google Scholar]
  57. Esparza-Arredondo, D., González-Martín, O., Dultzin, D., et al. 2018, ApJ, 859, 124 [NASA ADS] [CrossRef] [Google Scholar]
  58. Esquej, P., Alonso-Herrero, A., González-Martín, O., et al. 2014, ApJ, 780, 86 [Google Scholar]
  59. Fabian, A. C. 2012, ARA&A, 50, 455 [Google Scholar]
  60. Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [Google Scholar]
  61. Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [Google Scholar]
  62. Gallagher, R., Maiolino, R., Belfiore, F., et al. 2019, MNRAS, 485, 3409 [NASA ADS] [CrossRef] [Google Scholar]
  63. Gao, F., Wang, L., Pearson, W. J., et al. 2020, A&A, 637, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Gavazzi, G., Consolandi, G., Belladitta, S., Boselli, A., & Fossati, M. 2018, A&A, 615, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [Google Scholar]
  66. González Delgado, R. M., Heckman, T., Leitherer, C., et al. 1998, ApJ, 505, 174 [CrossRef] [Google Scholar]
  67. Goto, T. 2006, MNRAS, 369, 1765 [NASA ADS] [CrossRef] [Google Scholar]
  68. Goulding, A. D., Matthaey, E., Greene, J. E., et al. 2017, ApJ, 843, 135 [NASA ADS] [CrossRef] [Google Scholar]
  69. Grier, C. J., Mathur, S., Ghosh, H., & Ferrarese, L. 2011, ApJ, 731, 60 [NASA ADS] [CrossRef] [Google Scholar]
  70. Groves, B. A., Dopita, M. A., & Sutherland, R. S. 2004, ApJS, 153, 75 [NASA ADS] [CrossRef] [Google Scholar]
  71. Häring, N., & Rix, H.-W. 2004, ApJ, 604, L89 [Google Scholar]
  72. Harrison, C. M. 2017, Nat. Astron., 1, 0165 [NASA ADS] [CrossRef] [Google Scholar]
  73. Heckman, T. M., & Best, P. N. 2014, ARA&A, 52, 589 [Google Scholar]
  74. Heller, C. H., & Shlosman, I. 1994, ApJ, 424, 84 [NASA ADS] [CrossRef] [Google Scholar]
  75. Hickox, R. C., Mullaney, J. R., Alexander, D. M., et al. 2014, ApJ, 782, 9 [NASA ADS] [CrossRef] [Google Scholar]
  76. Hicks, E. K. S., Davies, R. I., Malkan, M. A., et al. 2009, ApJ, 696, 448 [NASA ADS] [CrossRef] [Google Scholar]
  77. Hicks, E. K. S., Davies, R. I., Maciejewski, W., et al. 2013, ApJ, 768, 107 [NASA ADS] [CrossRef] [Google Scholar]
  78. Hobbs, A., Nayakshin, S., Power, C., & King, A. 2011, MNRAS, 413, 2633 [NASA ADS] [CrossRef] [Google Scholar]
  79. Hönig, S. F. 2019, ApJ, 884, 171 [Google Scholar]
  80. Hönig, S. F., Kishimoto, M., Tristram, K. R. W., et al. 2013, ApJ, 771, 87 [Google Scholar]
  81. Hopkins, P. F., & Quataert, E. 2010, MNRAS, 407, 1529 [Google Scholar]
  82. Hopkins, P. F., Hayward, C. C., Narayanan, D., & Hernquist, L. 2012, MNRAS, 420, 320 [NASA ADS] [CrossRef] [Google Scholar]
  83. Hopkins, P. F., Torrey, P., Faucher-Giguère, C.-A., Quataert, E., & Murray, N. 2016, MNRAS, 458, 816 [NASA ADS] [CrossRef] [Google Scholar]
  84. Husemann, B., Davis, T. A., Jahnke, K., et al. 2017, MNRAS, 470, 1570 [NASA ADS] [CrossRef] [Google Scholar]
  85. Imanishi, M., Ichikawa, K., Takeuchi, T., et al. 2011, PASJ, 63, 447 [NASA ADS] [Google Scholar]
  86. Jahnke, K., & Macciò, A. V. 2011, ApJ, 734, 92 [NASA ADS] [CrossRef] [Google Scholar]
  87. Jarvis, M. E., Harrison, C. M., Mainieri, V., et al. 2020, MNRAS, 498, 1560 [NASA ADS] [CrossRef] [Google Scholar]
  88. Jensen, J. J., Hönig, S. F., Rakshit, S., et al. 2017, MNRAS, 470, 3071 [NASA ADS] [CrossRef] [Google Scholar]
  89. Kauffmann, G., & Heckman, T. M. 2009, MNRAS, 397, 135 [NASA ADS] [CrossRef] [Google Scholar]
  90. Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
  91. Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Kawakatu, N., & Wada, K. 2008, ApJ, 681, 73 [NASA ADS] [CrossRef] [Google Scholar]
  93. Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [Google Scholar]
  94. Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
  95. Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [Google Scholar]
  96. Knapen, J. H., Shlosman, I., & Peletier, R. F. 2000, ApJ, 529, 93 [NASA ADS] [CrossRef] [Google Scholar]
  97. Kocevski, D. D., Faber, S. M., Mozena, M., et al. 2012, ApJ, 744, 148 [NASA ADS] [CrossRef] [Google Scholar]
  98. Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
  99. Koss, M., Mushotzky, R., Veilleux, S., et al. 2011, ApJ, 739, 57 [Google Scholar]
  100. Koss, M., Trakhtenbrot, B., Ricci, C., et al. 2017, ApJ, 850, 74 [Google Scholar]
  101. Koss, M. J., Strittmatter, B., Lamperti, I., et al. 2021, ApJS, 252, 29 [CrossRef] [Google Scholar]
  102. Krolik, J. H., & Begelman, M. C. 1988, ApJ, 329, 702 [Google Scholar]
  103. Lacerda, E. A. D., Sánchez, S. F., Cid Fernandes, R., et al. 2020, MNRAS, 492, 3073 [Google Scholar]
  104. Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [Google Scholar]
  105. Lin, M.-Y., Davies, R. I., Hicks, E. K. S., et al. 2018, MNRAS, 473, 4582 [NASA ADS] [CrossRef] [Google Scholar]
  106. López-Gonzaga, N., Burtscher, L., Tristram, K. R. W., Meisenheimer, K., & Schartmann, M. 2016, A&A, 591, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Lutz, D., Sturm, E., Janssen, A., et al. 2020, A&A, 633, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
  109. Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [Google Scholar]
  110. Maiolino, R., Russell, H. R., Fabian, A. C., et al. 2017, Nature, 544, 202 [Google Scholar]
  111. Mallmann, N. D., Riffel, R., Storchi-Bergmann, T., et al. 2018, MNRAS, 478, 5491 [NASA ADS] [CrossRef] [Google Scholar]
  112. Marian, V., Jahnke, K., Mechtley, M., et al. 2019, ApJ, 882, 141 [CrossRef] [Google Scholar]
  113. Marian, V., Jahnke, K., Andika, I., et al. 2020, ApJ, 904, 79 [NASA ADS] [CrossRef] [Google Scholar]
  114. Martini, P. 2004, in The Interplay Among Black Holes, Stars and ISM in Galactic Nuclei, eds. T. Storchi-Bergmann, L. C. Ho, & H. R. Schmitt, 222 235 [NASA ADS] [Google Scholar]
  115. Martini, P., Regan, M. W., Mulchaey, J. S., & Pogge, R. W. 2003, ApJ, 589, 774 [NASA ADS] [CrossRef] [Google Scholar]
  116. McConnell, N. J., & Ma, C.-P. 2013, ApJ, 764, 184 [Google Scholar]
  117. Meléndez, M., Mushotzky, R. F., Shimizu, T. T., Barger, A. J., & Cowie, L. L. 2014, ApJ, 794, 152 [Google Scholar]
  118. Modigliani, A., Goldoni, P., Royer, F., et al. 2010, in Observatory Operations: Strategies, Processes, and Systems III, eds. D. R. Silva, A. B. Peck, & B. T. Soifer, SPIE Conf. Ser., 7737, 773728 [NASA ADS] [CrossRef] [Google Scholar]
  119. Moehler, S., Modigliani, A., Freudling, W., et al. 2014, A&A, 568, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. Neumayer, N., Seth, A., & Böker, T. 2020, A&ARv, 28, 4 [Google Scholar]
  121. Norman, C., & Scoville, N. 1988, ApJ, 332, 124 [CrossRef] [Google Scholar]
  122. Novak, G. S., Ostriker, J. P., & Ciotti, L. 2011, ApJ, 737, 26 [Google Scholar]
  123. Oh, K., Koss, M., Markwardt, C. B., et al. 2018, ApJS, 235, 4 [Google Scholar]
  124. Prieto, M. A., Fernandez-Ontiveros, J. A., Bruzual, G., et al. 2019, MNRAS, 485, 3264 [NASA ADS] [CrossRef] [Google Scholar]
  125. Ramos Almeida, C., Bessiere, P. S., Tadhunter, C. N., et al. 2012, MNRAS, 419, 687 [NASA ADS] [CrossRef] [Google Scholar]
  126. Regan, M. W., & Teuben, P. 2003, ApJ, 582, 723 [Google Scholar]
  127. Rembold, S. B., Shimoia, J. S., Storchi-Bergmann, T., et al. 2017, MNRAS, 472, 4382 [Google Scholar]
  128. Ricci, C., Ueda, Y., Koss, M. J., et al. 2015, ApJ, 815, L13 [Google Scholar]
  129. Riffel, R., Pastoriza, M. G., Rodríguez-Ardila, A., & Bonatto, C. 2009, MNRAS, 400, 273 [Google Scholar]
  130. Riffel, R. A., Storchi-Bergmann, T., Riffel, R., & Pastoriza, M. G. 2010, ApJ, 713, 469 [NASA ADS] [CrossRef] [Google Scholar]
  131. Riffel, R., Riffel, R. A., Ferrari, F., & Storchi-Bergmann, T. 2011, MNRAS, 416, 493 [NASA ADS] [Google Scholar]
  132. Riffel, R., Mason, R. E., Martins, L. P., et al. 2015, MNRAS, 450, 3069 [NASA ADS] [CrossRef] [Google Scholar]
  133. Riffel, R., Rodríguez-Ardila, A., Brotherton, M. S., et al. 2019, MNRAS, 486, 3228 [Google Scholar]
  134. Riffel, R., Mallmann, N. D., Ilha, G. S., et al. 2021, MNRAS, 501, 4064 [NASA ADS] [CrossRef] [Google Scholar]
  135. Rosario, D. J., Santini, P., Lutz, D., et al. 2012, A&A, 545, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  136. Rosario, D. J., Burtscher, L., Davies, R. I., et al. 2018, MNRAS, 473, 5658 [NASA ADS] [CrossRef] [Google Scholar]
  137. Rosario, D. J., Togi, A., Burtscher, L., et al. 2019, ApJ, 875, L8 [NASA ADS] [CrossRef] [Google Scholar]
  138. Rovilos, E., Comastri, A., Gilli, R., et al. 2012, A&A, 546, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  139. Sabater, J., Best, P. N., & Heckman, T. M. 2015, MNRAS, 447, 110 [NASA ADS] [CrossRef] [Google Scholar]
  140. Sales, D. A., Pastoriza, M. G., & Riffel, R. 2010, ApJ, 725, 605 [NASA ADS] [CrossRef] [Google Scholar]
  141. Santini, P., Rosario, D. J., Shao, L., et al. 2012, A&A, 540, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  142. Sarzi, M., Allard, E. L., Knapen, J. H., & Mazzuca, L. M. 2007a, MNRAS, 380, 949 [NASA ADS] [CrossRef] [Google Scholar]
  143. Sarzi, M., Shields, J. C., Pogge, R. W., & Martini, P. 2007b, in The Central Engine of Active Galactic Nuclei, eds. L. C. Ho, & J. W. Wang, ASP Conf. Ser., 373, 643 [NASA ADS] [Google Scholar]
  144. Schartmann, M., Meisenheimer, K., Klahr, H., et al. 2009, MNRAS, 393, 759 [CrossRef] [Google Scholar]
  145. Schartmann, M., Burkert, A., Krause, M., et al. 2010, MNRAS, 403, 1801 [NASA ADS] [CrossRef] [Google Scholar]
  146. Schawinski, K., Koss, M., Berney, S., & Sartori, L. F. 2015, MNRAS, 451, 2517 [Google Scholar]
  147. Schipani, P., Campana, S., Claudi, R., et al. 2020, SPIE Conf. Ser., 11447, 1144709 [NASA ADS] [Google Scholar]
  148. Schnorr-Müller, A., Davies, R. I., Korista, K. T., et al. 2016, MNRAS, 462, 3570 [Google Scholar]
  149. Schulze, A., Silverman, J. D., Daddi, E., et al. 2019, MNRAS, 488, 1180 [NASA ADS] [CrossRef] [Google Scholar]
  150. Scoville, N. Z., Becklin, E. E., Young, J. S., & Capps, R. W. 1983, ApJ, 271, 512 [NASA ADS] [CrossRef] [Google Scholar]
  151. Shangguan, J., Ho, L. C., Bauer, F. E., Wang, R., & Treister, E. 2020, ApJ, 899, 112 [NASA ADS] [CrossRef] [Google Scholar]
  152. Shimizu, T. T., Davies, R. I., Lutz, D., et al. 2019, MNRAS, 2449, [Google Scholar]
  153. Siebenmorgen, R., Krügel, E., & Spoon, H. W. W. 2004, A&A, 414, 123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  154. Silverman, J. D., Lamareille, F., Maier, C., et al. 2009, ApJ, 696, 396 [NASA ADS] [CrossRef] [Google Scholar]
  155. Simões Lopes, R. D., Storchi-Bergmann, T., de Fátima Saraiva, M., & Martini, P. 2007, ApJ, 655, 718 [Google Scholar]
  156. Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  157. Smith, J. D. T., Draine, B. T., Dale, D. A., et al. 2007, ApJ, 656, 770 [Google Scholar]
  158. Somerville, R. S., Hopkins, P. F., Cox, T. J., Robertson, B. E., & Hernquist, L. 2008, MNRAS, 391, 481 [NASA ADS] [CrossRef] [Google Scholar]
  159. Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]
  160. Stasińska, G., Vale Asari, N., Cid Fernandes, R., et al. 2008, MNRAS, 391, L29 [NASA ADS] [Google Scholar]
  161. Storchi-Bergmann, T., Raimann, D., Bica, E. L. D., & Fraquelli, H. A. 2000, ApJ, 544, 747 [CrossRef] [Google Scholar]
  162. Storchi-Bergmann, T., Riffel, R. A., Riffel, R., et al. 2012, ApJ, 755, 87 [NASA ADS] [CrossRef] [Google Scholar]
  163. Su, K.-Y., Hopkins, P. F., Hayward, C. C., et al. 2019, MNRAS, 487, 4393 [NASA ADS] [CrossRef] [Google Scholar]
  164. Terlevich, E., Diaz, A. I., & Terlevich, R. 1990, MNRAS, 242, 271 [CrossRef] [Google Scholar]
  165. Thompson, T. A., Quataert, E., & Murray, N. 2005, ApJ, 630, 167 [Google Scholar]
  166. Tran, H. D. 1995, ApJ, 440, 597 [NASA ADS] [CrossRef] [Google Scholar]
  167. Treister, E., Schawinski, K., Urry, C. M., & Simmons, B. D. 2012, ApJ, 758, L39 [NASA ADS] [CrossRef] [Google Scholar]
  168. Vale Asari, N., Stasińska, G., Cid Fernandes, R., et al. 2009, MNRAS, 396, L71 [NASA ADS] [Google Scholar]
  169. Vazdekis, A., Koleva, M., Ricciardelli, E., Röck, B., & Falcón-Barroso, J. 2016, MNRAS, 463, 3409 [Google Scholar]
  170. Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [Google Scholar]
  171. Vernet, J., & Mason, E. 2009, X-shooter User Manual, 2nd edn. (Germany: Garching bei München) [Google Scholar]
  172. Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  173. Véron-Cetty, M., & Véron, P. 2010, A&A, 518, A10+ [CrossRef] [EDP Sciences] [Google Scholar]
  174. Vogelsberger, M., Genel, S., Springel, V., et al. 2014, MNRAS, 444, 1518 [Google Scholar]
  175. Vollmer, B., & Davies, R. I. 2013, A&A, 556, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  176. Vollmer, B., Beckert, T., & Davies, R. I. 2008, A&A, 491, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  177. Volonteri, M., Capelo, P. R., Netzer, H., et al. 2015, MNRAS, 449, 1470 [NASA ADS] [CrossRef] [Google Scholar]
  178. Wada, K., & Norman, C. A. 2002, ApJ, 566, L21 [CrossRef] [Google Scholar]
  179. Wada, K., Papadopoulos, P. P., & Spaans, M. 2009, ApJ, 702, 63 [NASA ADS] [CrossRef] [Google Scholar]
  180. Wegner, G., Bernardi, M., Willmer, C. N. A., et al. 2003, AJ, 126, 2268 [NASA ADS] [CrossRef] [Google Scholar]
  181. Wild, V., Groves, B., Heckman, T., et al. 2011, MNRAS, 410, 1593 [NASA ADS] [Google Scholar]
  182. Xue, Y. Q., Brandt, W. N., Luo, B., et al. 2010, ApJ, 720, 368 [Google Scholar]
  183. Yesuf, H. M., & Ho, L. C. 2020, ApJ, 901, 42 [NASA ADS] [CrossRef] [Google Scholar]
  184. Yuan, T. T., Kewley, L. J., & Richard, J. 2013, ApJ, 763, 9 [NASA ADS] [CrossRef] [Google Scholar]
  185. Zahid, H. J., Kewley, L. J., & Bresolin, F. 2011, ApJ, 730, 137 [NASA ADS] [CrossRef] [Google Scholar]
  186. Zhuang, M.-Y., Ho, L. C., & Shangguan, J. 2021, ApJ, 906, 38 [NASA ADS] [CrossRef] [Google Scholar]
  187. Zinn, P. C., Middelberg, E., Norris, R. P., & Dettmar, R. J. 2013, ApJ, 774, 66 [NASA ADS] [CrossRef] [Google Scholar]
  188. Zubovas, K., Nayakshin, S., King, A., & Wilkinson, M. 2013, MNRAS, 433, 3079 [Google Scholar]

Appendix A: Individual stellar population fits

A.1. Control galaxies

thumbnail Fig. A.1.

Same as Fig. 6, but for ESO 093-G003.

thumbnail Fig. A.2.

Same as Fig. 6, but for ESO 208-G021.

thumbnail Fig. A.3.

Same as Fig. 6, but for IC 4653.

thumbnail Fig. A.4.

Same as Fig. 6, but for NGC 1079.

thumbnail Fig. A.5.

Same as Fig. 6, but for NGC 1315.

thumbnail Fig. A.6.

Same as Fig. 6, but for NGC 1947.

thumbnail Fig. A.7.

Same as Fig. 6, but for NGC 2775.

thumbnail Fig. A.8.

Same as Fig. 6, but for NGC 3175.

thumbnail Fig. A.9.

Same as Fig. 6, but for NGC 3351.

thumbnail Fig. A.10.

Same as Fig. 6, but for NGC 3717.

thumbnail Fig. A.11.

Same as Fig. 6, but for NGC 3749.

thumbnail Fig. A.12.

Same as Fig. 6, but for NGC 4224.

thumbnail Fig. A.13.

Same as Fig. 6, but for NGC 4254.

thumbnail Fig. A.14.

Same as Fig. 6, but for NGC 5037.

thumbnail Fig. A.15.

Same as Fig. 6, but for NGC 5845.

thumbnail Fig. A.16.

Same as Fig. 6, but for NGC 5921.

thumbnail Fig. A.17.

Same as Fig. 6, but for NGC 718.

thumbnail Fig. A.18.

Same as Fig. 6, but for NGC 7727.

A.2. AGNs

thumbnail Fig. A.19.

Same as Fig. 6, but for ESO 021-G004.

thumbnail Fig. A.20.

Same as Fig. 6, but for ESO 137-G034.

thumbnail Fig. A.21.

Same as Fig. 6, duplicated here for completeness.

thumbnail Fig. A.22.

Same as Fig. 6, but for NGC 2110.

thumbnail Fig. A.23.

Same as Fig. 6, but for NGC 2992.

thumbnail Fig. A.24.

Same as Fig. 6, but for NGC 3081.

thumbnail Fig. A.25.

Same as Fig. 6, but for NGC 5728.

thumbnail Fig. A.26.

Same as Fig. 6, but for NGC 7172.

thumbnail Fig. A.27.

Same as Fig. 6, but for NGC 7582.

All Tables

Table 1.

Definition of our sample.

In the text
Table 2.

All observations.

In the text
Table 3.

Results from the STARLIGHT fitting.

In the text
Table 4.

Results of the emission line fitting.

In the text
Table 5.

Summary of stellar populations by galaxy class with uncertainties from jack-knifing as described in the text.

In the text

All Figures

thumbnail Fig. 1.

Comparison of spectra for a Seyfert 1 and a Seyfert 2 galaxy from the LLAMA sample. A number of very broad emission features can be seen in the Seyfert 1 galaxy that outshine any underlying stellar absorption lines. The Balmer emission lines Hα and Hβ at 6562.8 Å and 4861.3 Å, respectively, are indicated with dashed lines.
In the text
thumbnail Fig. 2.

Comparison of the most relevant host galaxy properties of our AGN and control sample. From left to right: numerical Hubble type (morphology), log stellar mass M⋆ in units of solar masses M⊙, and distance. The AGN sample is shown in orange, and the control sample is shown in blue.
In the text
thumbnail Fig. 3.

Posterior probability distributions for the fraction of light in the four bins of stellar ages from our STARLIGHT analysis of NGC 1079. We report the fractional value of stellar light associated with the 50% value in the cumulative distribution and take as 1σ uncertainty the range encompassing 68.27% of all values.
In the text
thumbnail Fig. 4.

Individual stellar population fitting results for all observations showing differences between individual observations for the same targets (the individual observations are indexed with underscores, e.g., NGC7582_1 and NGC7582_2). The four age bins marked in blue, green (only visible in one AGN), yellow, and red correspond to log(age/yrs) < 7.5 (young), 7.5 < log(age/yrs) < 8.5 (young-intermediate), 8.5 < log(age/yrs) < 9.5 (intermediate-old), and log(age/yrs) > 9.5 (old), respectively. The statistical uncertainties on the fractions of stellar light for the four age bins are shown as black lines at the right edge of each of these age bins.
In the text
thumbnail Fig. 5.

Same as Fig. 4, but for the control sample.
In the text
thumbnail Fig. 6.

Example of a stellar population fit, for the AGN MCG-05-23-016. In the main panel, the X-shooter spectrum is displayed, down-sampled to the BC03 spectral resolution (black), the STARLIGHT fit (blue) with masked areas (in red) and the noise in the data in green. Below the spectrum, the residuals are displayed in terms of the local uncertainty in the data (masked areas are not displayed). In the side panel, the light-weighted star formation history (or stellar population vector) is shown.
In the text
thumbnail Fig. 7.

Collage of all LLAMA non-AGN X-shooter spectra with best-fitting stellar population synthesis overplotted. To the right of each spectrum, the summarised stellar population vector shows the best-fitting light-weighted fractions of the young (blue), young-intermediate (green), intermediate-old (yellow), and old (red) populations with boundaries of log (age/years) at 7.5, 8.5, and 9.5.
In the text
thumbnail Fig. 8.

Same as Fig. 7, but for the active galaxies in this paper.
In the text
thumbnail Fig. 9.

Relation of the blue continuum and the ultra-hard X-ray flux. The (noise-free) model flux at the blue end of our spectrum is plotted against the BAT 105-month ultra-hard X-ray (14–195 keV) flux. No relation between the two fluxes is seen, providing further evidence that the blue continuum in our spectra is not dominated by AGN light. The uncertainties of the BAT fluxes are within the symbol size.
In the text
thumbnail Fig. 10.

Presence (or not) of a broad component of the Hα line in four AGNs with different fractions of light in the young population (fy) according to the STARLIGHT fit: NGC 7582 and NGC 3081 do not show broad components of the Hα line, and yet STARLIGHT finds a young stellar population in these two galaxies. And, vice versa, in NGC 2992, there is a very strong broad component to the Hα line, but no young stellar population is found. Only in MCG-05-23-016 do we find both a young population and a broad component. Overall this confirms the robustness of the detection of young stellar light, and that it is likely not confused with the non-stellar continuum from the AGN.
In the text
thumbnail Fig. 11.

BPT plot with [OIII]/Hβ versus [N II]/Hα. Galaxies from the AGN as well as the control sample of star-forming and passive galaxies are shown in blue, deep pink, and red, respectively. The empirical (Kauffmann et al. 2003) and theoretical (Kewley et al. 2001) boundaries between starburst and AGN galaxies are marked with black straight and dashed lines, respectively. The underlying blue cloud of points is from the MPA-JHU emission line analysis of SDSS DR7 galaxies (Brinchmann et al. 2004).
In the text
thumbnail Fig. 12.

Same as Fig. 11, but here for [O III]/Hβ versus [S II]/Hα (VO87 plot).
In the text
thumbnail Fig. 13.

Same as Fig. 11, but here for [O III]/Hβ versus [O I]/Hα.
In the text
thumbnail Fig. 14.

WHaN plot showing the equivalent width of Hα on the y axis versus the BPT flux ratio [N II]/Hα. Galaxies from the AGN as well as the control sample of star-forming and passive galaxies are shown in blue, deep pink, and red, respectively. This plot is useful to show the relative strength of emission line features compared to the continuum. The demarcation lines are from Cid Fernandes et al. (2011). The blue cloud of points in the background is again from Brinchmann et al. (2004), as in Figs. 11–13.
In the text
thumbnail Fig. 15.

Comparison of the extinction estimate from emission line fitting versus absorption-line fitting (STARLIGHT). The dashed line corresponds to a 1:1 ratio, the dash-dotted line represents a ratio of 2:1. Statistical uncertainties in both methods are minute (≲0.2 mag), and the systematic difference between the two estimates is discussed in the main text. Galaxies from the AGN, as well as the control sample of star-forming and passive galaxies, are shown in blue, deep pink, and red, respectively.
In the text
thumbnail Fig. 16.

Comparison of stellar populations between the AGN and inactive sample where the inactive sample is split by location on the BPT diagram into a star-forming (SF) sub-population and a non-star-forming (non-SF) sub-population. The stellar populations are split into the same four age bins as in the previous section: young (blue), young-intermediate (green), intermediate-old (yellow), and old (red), with boundaries at log(age/yr) = 7.5, 8.5, and 9.5. The AGN-hosting galaxies are sorted by increasing X-ray luminosity LX, and the inactive control population is sorted by increasing equivalent width of Hα (EQW(Hα)).
In the text
thumbnail Fig. 17.

Average SFHs of AGNs, star-forming and non-star-forming control galaxies as in Fig. 16 (left panel), and a zoom into the youngest stellar populations (right panel). The uncertainties are derived through jack-knifing (see text for further discussion).
In the text
thumbnail Fig. A.1.

Same as Fig. 6, but for ESO 093-G003.
In the text
thumbnail Fig. A.2.

Same as Fig. 6, but for ESO 208-G021.
In the text
thumbnail Fig. A.3.

Same as Fig. 6, but for IC 4653.
In the text
thumbnail Fig. A.4.

Same as Fig. 6, but for NGC 1079.
In the text
thumbnail Fig. A.5.

Same as Fig. 6, but for NGC 1315.
In the text
thumbnail Fig. A.6.

Same as Fig. 6, but for NGC 1947.
In the text
thumbnail Fig. A.7.

Same as Fig. 6, but for NGC 2775.
In the text
thumbnail Fig. A.8.

Same as Fig. 6, but for NGC 3175.
In the text
thumbnail Fig. A.9.

Same as Fig. 6, but for NGC 3351.
In the text
thumbnail Fig. A.10.

Same as Fig. 6, but for NGC 3717.
In the text
thumbnail Fig. A.11.

Same as Fig. 6, but for NGC 3749.
In the text
thumbnail Fig. A.12.

Same as Fig. 6, but for NGC 4224.
In the text
thumbnail Fig. A.13.

Same as Fig. 6, but for NGC 4254.
In the text
thumbnail Fig. A.14.

Same as Fig. 6, but for NGC 5037.
In the text
thumbnail Fig. A.15.

Same as Fig. 6, but for NGC 5845.
In the text
thumbnail Fig. A.16.

Same as Fig. 6, but for NGC 5921.
In the text
thumbnail Fig. A.17.

Same as Fig. 6, but for NGC 718.
In the text
thumbnail Fig. A.18.

Same as Fig. 6, but for NGC 7727.
In the text
thumbnail Fig. A.19.

Same as Fig. 6, but for ESO 021-G004.
In the text
thumbnail Fig. A.20.

Same as Fig. 6, but for ESO 137-G034.
In the text
thumbnail Fig. A.21.

Same as Fig. 6, duplicated here for completeness.
In the text
thumbnail Fig. A.22.

Same as Fig. 6, but for NGC 2110.
In the text
thumbnail Fig. A.23.

Same as Fig. 6, but for NGC 2992.
In the text
thumbnail Fig. A.24.

Same as Fig. 6, but for NGC 3081.
In the text
thumbnail Fig. A.25.

Same as Fig. 6, but for NGC 5728.
In the text
thumbnail Fig. A.26.

Same as Fig. 6, but for NGC 7172.
In the text
thumbnail Fig. A.27.

Same as Fig. 6, but for NGC 7582.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.