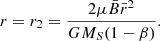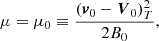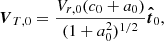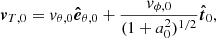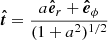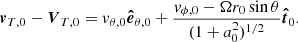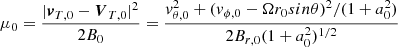| Issue |
A&A
Volume 652, August 2021
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 9 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202141048 | |
| Published online | 24 August 2021 | |
Dynamics of nanodust in the vicinity of a stellar corona: Effect of plasma corotation
1
Space Research Centre, Polish Academy of Sciences, Bartycka 18A, 00-716 Warsaw, Poland
e-mail: ace@cbk.waw.pl
2
Department of Physics and Technology, UiT the Arctic University of Norway, Postboks 6050 Langnes, 9037 Tromso, Norway
e-mail: ingrid.b.mann@uit.no
Received:
11
April
2021
Accepted:
5
June
2021
Context. In the vicinity of the Sun or other stars, the motion of the coronal and stellar wind plasma must include some amount of corotation, which could affect the dynamics of charged dust particles. In the case of the Sun, this region is now investigated in situ by the Parker Solar Probe. Charged dust particles coming from the vicinity of the Sun can also reach, and possibly be detected by, the Solar Orbiter.
Aims. We use numerical simulations and theoretical models to study the effect of plasma corotation on the motion of charged nanodust particles released from the parent bodies moving in Keplerian orbits, with particular attention to the case of trapped particles.
Methods. We used two methods: the motion of nanodust is described either by numerical solutions of full equations of motion, or by a two-dimensional (distance vs. radial velocity) model based on the guiding centre approximation. The models of the plasma and magnetic field in the vicinity of the star are based on analytical solutions that satisfy the freezing-in equations.
Results. Including plasma corotation does not prevent trapping of nanodust in the vicinity of the Sun or other stars. This result can be understood with the help of the model based on the guiding centre approximation. For the amount of corotation expected near the Sun, the outer limit of the trapped region is almost unaffected. If the corotation persists outside the trapping region, the speed of particles ejected from the Sun is moderately increased. A strong effect of plasma corotation on charged particle dynamics occurs for the star with a high rotation rate and/or a low value of the stellar wind speed.
Key words: Sun: heliosphere / solar wind / acceleration of particles / interplanetary medium / circumstellar matter
© A. Czechowski and I. Mann 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The dynamics of charged dust particles with sizes smaller than a few hundred nanometers is strongly affected by the electromagnetic force. In particular, nanodust particles can be picked up and accelerated by the solar wind plasma. In the vicinity of the Sun, these particles can also be trapped by the interplay between the electromagnetic forces and solar gravity. This could happen provided that the ratio of solar radiation to gravity β is lower than 0.5 for small dust grains and that the scatter-free approximation (Luhmann 2003) is applicable.
The process of trapping can be illustrated using the guiding centre approximation, in which the guiding centre moves along the rotating magnetic field line. The force that governs this motion can be described in terms of components corresponding to an effective gravity force, an effective mirror force, and a centrifugal force. At the inner limit of the trapping region, the effective gravity force acting on the particle is balanced by the magnetic mirror force. At the outer limit, the effective gravity force is equal to the centrifugal force term.
The trapping of nanodust particles in the vicinity of the Sun was studied in a number of works (Czechowski & Mann 2010, 2011, 2012, 2018; Czechowski & Kleimann 2017). A similar phenomenon may occur near other stars (cf. Su et al. 2013, 2020; Rieke et al. 2015; Kimura et al. 2020). Calculations of the nanodust trajectories were also made for nanodust around Vega and Fomalhaut (Stamm et al. 2019), two stars with a planetary debris disk.
Our models of nanodust trapping in the vicinity of the Sun were so far restricted to the case of a simple Parker spiral structure of the magnetic field, assuming a radially directed solar wind with no plasma corotation. However, as shown by Weber & Davis (1967), the plasma flow near the Sun is expected to include some amount of corotation. The region affected by corotation extends approximately to the Alfvén radius, the distance at which the velocity of the outflowing plasma equals the Alfvén velocity. The Alfvén radius sets the scale of the region in which the angular momentum of the solar rotation is transmitted to the solar wind plasma, producing a corotating component of the solar wind velocity. For the case of the Sun, the order of magnitude of the Alfvén radius (about 0.1 AU) is comparable to the size of the trapping region (0.16 AU near the solar equator). It follows that the plasma corotation should not be disregarded in a study of charged dust dynamics.
(The value of 0.1 AU was obtained assuming the following values of the slow solar wind parameters: magnetic field radial and azimuthal components Br = Bϕ = 35 μG at 1 AU, number density 5 cm−3 at 1 AU, and a wind speed of 350 km s−1).
The study of dust dynamics near the Sun are at present being compared with observations. The Parker Solar Probe (PSP) is now passing through the regions of high dust fluxes near the Sun. The Electromagnetic Fields Investigation (FIELDS) antenna instrument package (Bale et al. 2016) during the first PSP orbits measured impact events that are consistent with the trajectories of particles under the effect of gravity and radiation pressure force (Page et al. 2020; Szalay et al. 2020; Malaspina et al. 2020). Comparison to a dust collision and dynamics model suggests that the majority of detected particles are 30 nm and larger (Mann & Czechowski 2021). The trajectory of the PSP is evolving, with the orbit perihelion approaching the Sun. In 2020, the perihelion of the PSP orbit came below ∼0.15 AU, the outer limit of the region in which the trapped nanodust particles can be present. At the end of the year, it also approached 0.1 AU, the usual estimate of the Alfvén radius. In 2021, the spacecraft will approach the Sun to within 0.08 AU, the middle point of the trapped region. Although it is not clear whether the impacts of nanodust particles can be detected by the PSP, the observations of the dust distribution may be helpful to understand what is happening in the trapping region.
Another opportunity to study the effects of plasma corotation on trapped dust follows from the discovery of hot dust around early-type stars surrounded by debris disks (Su et al. 2013, 2020; Rieke et al. 2015; Kimura et al. 2020). This case is of particular interest to us because (as we show in this paper) the high rotation rate of a star strengthens the effects of corotation more than for the case of the Sun.
We show that trapping of the nanodust particles in the vicinity of the Sun or other stars is not adversely affected by plasma corotation. Some of our preliminary results were included in Stamm et al. (2019). The argument relies on the model of nanodust motion (Czechowski & Mann 2010, 2011, 2018) based on the guiding centre approximation. The model was used successfully to interpret the results of numerical simulations of charged dust motion. Assuming that the particle motion can be regarded as scatter free, the conditions for the guiding centre approximation were shown to be satisfied for trapped dust particles with radii of 3–10 nm. We also consider effects of plasma corotation on the propagation of nanodust particles that do not become trapped, in particular, those emitted from high-eccentricity orbits.
This paper is structured as follows. In Sect. 2 we describe our adaptation of the Weber & Davis (1967) theory of plasma corotation and present our corotation models. Section 3 presents the equations and assumptions used in our numerical simulations of the nanodust motion. In Sect. 4 we introduce our main tool, the model of nanodust dynamics based on the guiding centre approximation, and show how the trapping of nanodust is described in this model. In Sect. 5 we use this model to explain why the effects of corotation on nanodust dynamics, including the trapping, are small. Section 6 compares results of our simulations of nanodust motion obtained with different assumptions about corotation. In Sect. 7 we consider the case of other stars. The conclusions are given in Sect. 8.
2. Models of the magnetic field and plasma flow including plasma corotation
We considered simple time-stationary models of the magnetic field B and the plasma flow V in the vicinity of the Sun. The models are required to satisfy the freezing-in equations,
We used the heliocentric coordinate system r, θ, ϕ (base vectors 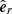 ,
, 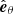 ,
, 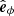 ), where θ is the solar co-latitude, counted from the solar rotation axis. We also made the simplifying assumption that the models are symmetric under rotation around the solar rotation axis. This means that the components of the magnetic field and plasma flow are independent of the azimuthal angle ϕ. Although their components are ϕ independent, the vectors B, V depend on ϕ because so do the base vectors.
), where θ is the solar co-latitude, counted from the solar rotation axis. We also made the simplifying assumption that the models are symmetric under rotation around the solar rotation axis. This means that the components of the magnetic field and plasma flow are independent of the azimuthal angle ϕ. Although their components are ϕ independent, the vectors B, V depend on ϕ because so do the base vectors.
Our treatment of plasma corotation is based on that of Weber & Davis (1967). The main difference is that we did not restrict our model to the solar equator plane, but assumed that the latitudinal (θ) components of B and V are zero. The magnetic field and plasma flow lines lie then on θ = const cones. The simple models such as the radially directed solar wind flow, the Parker spiral magnetic field, as well as their modification by various models of plasma corotation are consistent with our assumptions.
With the assumptions listed above, the magnetic field and the plasma velocity can be written as
where a = a(r, θ)≡ − Bϕ/Br and c = c(r, θ)≡Vϕ/Vr. The form of a(r, θ) and c(r, θ) depends on the model of corotation.
Because of the ∇ ⋅ B = 0 condition, the radial component of the magnetic field must behave as Br = b/r2, where b can depend on θ. In our calculations we specified the r dependence of the radial plasma velocity component Vr = Vr(r). In most calculations referring to the case of the Sun, we used the radial velocity profile (Model 3 in Czechowski & Mann 2018), based on observations by Sheeley et al. (1997). Alternatively, we assumed that the radial component of the solar or stellar wind velocity is a distance- and latitude-independent constant. The value of this constant we took to be 400 km s−1 for the case of the Sun. For other stars, we used the values listed in Table 2 of Kimura et al. (2020).
As in Weber & Davis (1967), we made the additional requirement that the induced electric field −(1/c)V × B = 0 in the frame corotating with the Sun. Transformed into the heliocentric inertial frame, this equation becomes
or, equivalently,
where Ω is the angular speed of the solar rotation. Equations (4) or (5) ensure that the stationary freezing-in Eq. (1) is satisfied.
Weber & Davis (1967) combined the freezing equations with the azimuthal component of the plasma angular momentum equation to derive the “critical point” solution for Vϕ(r). We adapted their derivation to the case of our model.
The azimuthal component of the angular momentum equation at colatitude θ takes the form
where ρ is the plasma density. This equation reduces to
where L = L(θ). Combining with the freezing-in condition Eqs. (4) or (5), we obtain
where
is the square of the Alfvénic Mach number. Weber & Davis (1967) observed that at some distance r = rA, the solution passes through a critical point at which the Alfvénic Mach number crosses 1 (the Alfvén radius). The amount L of angular momentum transferred to the solar wind is determined at this critical point:
Using Eqs. (8)–(10), the azimuthal velocity Vϕ can be written as
where VrA is the value of Vr at r = rA. 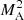 can then be written as
can then be written as
In our simulations we did not attempt to obtain the critical point solution. We assumed a value for rA and used Eqs. (11) and (12) to calculate Vϕ at the required point. The singularity was avoided by interpolating over the region 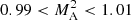 .
.
For comparison, we also considered simpler models that do not rely on the critical point description. In the following we refer to the maximum corotation model. The model is defined by
We also used the moderate corotation model. This is defined as a modification of the maximum corotation azimuthal velocity profile by multiplying the azimuthal velocity by a factor 0.25.
As a test of robustness of trapping against the case of a very strong plasma rotation, we also ran a simulation using the (unrealistic) toy model that we call the “supercorotation model”. This was obtained from the maximum corotation model by multiplying the azimuthal plasma velocity component by a factor of 10. This means that the solar wind plasma rotates at an angular velocity ten times higher than the solar one. The freezing-in condition then produces the magnetic field lines bent backwards, that is, in the direction opposite to the realistic corotation models. The trapping of charged particles is not affected.
The azimuthal velocity profiles for the model based on Weber & Davis (1967) and for the maximum corotation model are shown in Fig. 1. The velocity is plotted along the trajectories of trapped particles created at a heliocentric distance of 0.14 AU and at heliographic latitude 5°. An Alfvén radius of 0.1 AU was assumed. Figure 2 shows the shape of the magnetic field lines (projected onto the solar equator) for our corotation models, also including the toy supercorotation model. In all calculations, the azimuthal component of the magnetic field was obtained from Eq. (4).
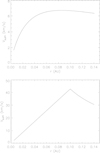 |
Fig. 1. Azimuthal plasma velocity component vs. distance for the model based on Weber & Davis (1967; upper panel) and for the “maximum corotation” model. The value of rA = 0.1 AU was assumed. |
 |
Fig. 2. Magnetic field lines projected to the solar equator plane for different models of plasma corotation: no corotation (solid line), maximum corotation (dotted), model based on Weber and Davis (dashed) and the toy “supercorotation” model (dotted-dashed). |
3. Simulations
The magnetic field and plasma flow described in the previous section was used as a background for numerical simulations of the motion of charged nanodust in the vicinity of the Sun (or other stars). The aim of our simulations is to estimate the effect of plasma corotation on the motion of nanodust. We therefore disregarded the effect of the forces (e.g., the Poynting-Robertson and ion drags) that are potentially strong enough to obscure the effect of corotation. To avoid the drift of charged nanodust along the heliospheric current sheet, we used a single-polarity magnetic field configuration. The radial component of the magnetic field was set equal to 35 μG at 1 AU. The azimuthal component is specified by the choice of the corotation model.
We used the equation of motion of the form
where β is the ratio of radiation pressure to gravity, which we assumed to be low (β = 0.1; see Czechowski & Mann 2010, 2012). The initial condition corresponded to the nanodust particle to be emitted (at zero relative speed) from a parent body moving in a Keplerian orbit. In most calculations, the initial orbits were assumed to be circular. We also considered some examples of nanodust emitted from elongated orbits.
The nanodust charge-to-mass ratio Q/m was assumed to be constant during the motion (we made the implicit assumption that the particles acquired equilibrium charge immediately after release). The only parameters of the solar wind used in the model are the plasma velocity and the magnetic field. In particular, the plasma density (and therefore the Alfvén speed) were not specified, so that we can treat the Alfvén radius as a free parameter. In most calculations presented here, we assumed the value of rA = 0.2 AU, so that strong corotation applies within the whole trapping region. The exceptions are Fig. 1 (rA = 0.1 AU) and Fig. 5 (rA = 0.5 AU).
4. Model of nanodust dynamics in the guiding centre approximation
The results of numerical simulations can be better understood by using the model based on the guiding centre approximation for comparison. The model describes the motion of a charged particle in the (r,vr) phase plane, where r is the heliocentric distance and vr is the radial component of the guiding centre velocity. In previous applications (Czechowski & Mann 2010, 2011, 2018), the model was restricted to the purely radial plasma flow. Here we extend it to include plasma corotation.
The magnetic field and the solar wind velocity are the same as in the previous section. In particular, the freezing-in condition is satisfied.
We used the spherical heliographic coordinates (r, θ, ϕ), where θ and ϕ are the latitudinal and azimuthal angles, respectively. We assumed that the latitudinal (θ) components of the magnetic field B and the plasma velocity V were equal to zero. The remaining components were assumed to be independent of the azimuthal angle ϕ.
We considered the time-stationary case. The equation for the parallel motion of the guiding centre (Northrop 1958) takes the form
where 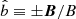 ,
, 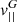 and g|| are the components of the guiding centre velocity and the gravity force parallel to
and g|| are the components of the guiding centre velocity and the gravity force parallel to 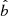 ; VT is the part of the plasma velocity perpendicular to
; VT is the part of the plasma velocity perpendicular to 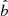 ,
, 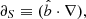 and
and 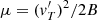 is the adiabatic invariant, with
is the adiabatic invariant, with 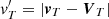 denoting the perpendicular speed of the particle in the plasma frame. The (1 − β) factor accounts for the radiation pressure.
denoting the perpendicular speed of the particle in the plasma frame. The (1 − β) factor accounts for the radiation pressure.
The perpendicular motion of the guiding centre was approximated by
The higher (charge-dependent) terms in the drift equation were neglected (comparison with the full numerical simulations shows that they are small). Because the latitudinal components of V and B were assumed to be zero, the guiding centre motion is (by Eq. (16)) confined to the θ = const cone.
Our model of nanodust dynamics is obtained by expressing 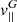 in terms of the radial component of the guiding centre velocity in the inertial frame (including the motion of the field line), which is here denoted by v. In our approximation (Eq. (16)), v is given by
in terms of the radial component of the guiding centre velocity in the inertial frame (including the motion of the field line), which is here denoted by v. In our approximation (Eq. (16)), v is given by
or equivalently,
After evaluating the terms in Eq. (15), we obtain the system of two equations describing the guiding centre motion in the (r, v) phase plane,
where the function W is given by
We have replaced ∂SB by (1 + a2)−1/2∂rB using the assumption that the components of B are independent of ϕ.
If the first adiabatic invariant μ is conserved, W can be expressed as
with the potential function
The last term in Eq. (23) was obtained using the freezing-in condition c + a = (Ω/Vr)r sin θ (Eq. (5)). Equations (19)–(22) then lead to the conservation law
which is a form of energy conservation, related to those considered by Northrop (1958).
The energy E (Eq. (24)) as well as the potential function U (Eq. (23)) are defined per unit mass, so that their dimension is the velocity squared. The unit used in our plots of U is (100 km s−1)2.
The same conservation law was obtained in Czechowski & Mann (2018) for the case of a purely radial solar wind flow. The nanodust particles are trapped when the function U develops the potential well, with the repulsive core at small r and the barrier at the outer limit of the trapping region.
The positions of the minimum of the potential well and of the maximum of the barrier can be approximately estimated as follows (Czechowski & Mann 2010, 2012). At large r, the potential is dominated by the first and third terms: −GMS(1 − β)/r − (1/2)Ω2r2 sin θ2. The maximum of this sum appears at
At small r, the potential U is approximately equal to the sum of first two terms: −GMS(1 − β)/r + μB, where 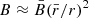 . The approximate position of the minimum is
. The approximate position of the minimum is
The approximation is good when r2 ≪ r1.
5. Why are the corotation effects small? The argument from the model based on the guiding centre approximation
The first and last terms in U are obviously independent of plasma corotation. The corotation affects the value of a in Eq. (24) and the term μB in U.
In the derivation of Eq. (24) we have assumed that the first adiabatic invariant μ is conserved. The value of μ can then be derived from the initial conditions for the particle motion,
where v0, V0, and B0 are the initial values of the particle and plasma velocities and the magnetic field strength, respectively. These values correspond to the moment of release of the nanodust particle from the parent body.
Consider the case when the nanodust particle starts at zero relative velocity with respect to the parent body moving in the circular Keplerian orbit of arbitrary inclination. It is then straightforward to derive the formula for the initial values of the transverse velocity of the plasma flow,
and of the nanodust particle,
where
is the unit vector perpendicular to 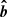 and to
and to 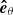 . Using also c + a = (Ω/Vr)r sin θ, we obtain
. Using also c + a = (Ω/Vr)r sin θ, we obtain
This result applies without change to the cases with and without plasma corotation. When the azimuthal plasma velocity component is changed, the freezing-in condition enforces the modification of the magnetic field in such a way that the sum of c0 (the ratio Vϕ, 0/Vr, 0) and a0 (the ratio −Bϕ, 0/Br, 0) is not affected. The plasma velocity component perpendicular to the magnetic field is then changed only by the factor 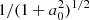 . We note that
. We note that 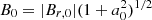 , where Br, 0 in our model is independent of plasma corotation. The initial value of μ
, where Br, 0 in our model is independent of plasma corotation. The initial value of μ
depends on corotation only through the combination 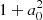 .
.
The freezing-in constraint requires c + a = (Ω/Vr)r sin θ. For corotating plasma, Vϕ ≥ 0 (c ≥ 0), so that there is an upper limit on a: a ≤ (Ω/Vr)r sin θ. The values of a corresponding to our corotation models vary from the maximum value amax = (Ω/Vr)r sin θ (the Parker spiral value) for the case of no corotation to the minimum value a = 0 for the maximum corotation model. In the case of the Sun, a2 ≪ 1 everywhere inside the trapping region r < r1 (Eq. (25)). The value of μ0 is then only weakly dependent on the selected model of corotation.
6. Results
As explained in the previous section, we expect the effects of plasma corotation on nanodust dynamics in the vicinity of the Sun to be small. In this section we present some examples of these effects, obtained by numerical simulations and/or by using the guiding centre model.
Figure 3 (upper panel) illustrates the effect of plasma corotation on the trajectories of charged nanodust emitted at a small heliocentric distance r0 = 0.03 AU. This example contains a systematic difference in the amplitudes of the nanodust motion: increase in the degree of corotation causes a reduction in the amplitude.
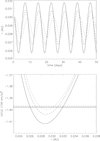 |
Fig. 3. Upper panel: results of the numerical solutions of the full equations of motion (heliocentric distance r plotted against time) for the nanodust particles with Q/m = 10−4 e/mp emitted at 0.03 AU from a parent body moving in a circular Keplerian orbit of 5° inclination at the point of maximum latitude. The solutions correspond to three different models: no corotation (solid line), maximum corotation (dotted), and the critical point model based on Weber & Davis (1967; dashed line). The lower panel shows the potential function U(r) and the conserved quantity E plotted against r for the same assumptions about corotation. |
The lower panel shows the shape of the potential functions U and the energy levels E for the same three models. Particles emitted at 0.03 AU move close to the bottom of the potential well. The depth of the well is sensitive to the model of corotation. The deepest well (and the largest amplitude of a particle motion) occurs for the no-corotation case. The smallest depth and amplitude occur for maximum corotation. The amplitudes of the nanodust motion obtained by numerical simulations agree well with the limits of the E > U region.
Figure 4 (upper panel) shows the trajectories for a particle emitted at 0.14 AU from the solar centre, close to the outer limit of the trapping region. The line styles and the assumptions about corotation are the same as in Fig. 3. In this case, the upper and lower limits of the trajectories are not visibly affected by corotation. Increasing the amount of corotation (i.e., moving from no corotation to the maximum corotation model) produces some reduction in the orbital period.
 |
Fig. 4. As Fig. 3, but for the case of a particle emitted at 0.14 AU, close to the outer limit of the trapping region. The solutions for the different models are lying approximately on top of each other. Lower figure: was restricted in vertical range to show clearly the relative positions of the potential barrier and the energy levels. The minimum value of the potential U occurs at U(r)≈ − 4.3 in our (100 km s−1)2 units. |
The potential function U and the values of conserved energy E are shown in the lower panel. In contrast to the case of particles emitted at 0.03 AU, the potential near the barrier is determined by the c + a term, the value of which is insensitive to the model of corotation. The values of the conserved energy are almost the same for the different models. In consequence, the limits of particle motion are effectively independent of the amount of corotation.
According to our model, the nanodust particles created outside the trapping region are accelerated and escape from the vicinity of the Sun. In Fig. 5 we show the results of the numerical simulation (velocity versus distance plots) for a particle created just outside the trapping region for the three corotation models described above. Because the outer limit of the trapping region occurs at ∼0.16 AU, we made the additional assumption that the corotation region extends to 0.5 AU. We find that plasma corotation can increase the outward velocity of escaping particles, although the effect is strong only in the case of maximum corotation.
 |
Fig. 5. Plots of total speed and the radial velocity component vs heliocentric distance for the nanodust particles (Q/m = 10−4e/mp) released just outside of the trapping region for different assumptions about plasma corotation: no corotation (solid line), maximum corotation (dotted line), and the model of Weber and Davis (dashed line). To extend the corotation region, the Alfvén radius was artificially set at 0.5 AU. |
In Czechowski & Mann (2018) we have discussed the possibility that nanodust emitted from elongated orbits might be trapped. The result was that the trapping becomes impossible for high-eccentricity orbits because the velocity difference between the dust particle and the local plasma is strong. Because this difference can be affected by corotation, we calculated the maximum eccentricity consistent with trapping for the case of particles emitted at perihelium of the parent body orbit. The result is presented in Fig. 6. Increasing the amount of corotation can be seen to facilitate trapping at some heliocentric distances.
 |
Fig. 6. Maximum eccentricity of the parent body orbit consistent with trapping of the emitted nanodust. The nanodust particle is emitted at perihelium. The cases illustrated are no corotation (solid line), maximum corotation (dotted line), and the model of Weber and Davis (dashed line). The curves correspond to particles emitted at the points of maximum heliolatitude from the orbits of 20° inclination (curves on the left) and of 70° inclination (curves on the right). |
In the same work, we have also observed that the nanodust emitted from the inbound part of the high-eccentricity orbit of the parent body can approach very close to the Sun (the “corridors to the Sun”). Figure 7 illustrates the effect of plasma corotation on this phenomenon. For the case shown, the parent body orbit of the dust is assumed to have a perihelion distance and orbital eccentricity corresponding to those of the Aquarids meteor shower.
 |
Fig. 7. Effect of corotation on the propagation of nanodust particles emitted from the orbit of the Aquarids. The distances of the closest approach to the Sun are plotted against the position of the emission point on the orbit, represented by the angle counted from perihelion. The corotation models are the same as in Fig. 6: no corotation (solid line), maximum corotation (dotted line), and the model of Weber and Davis (dashed line). |
To summarize, the effect of corotation on charged nanodust particles in the solar system is weak. A stronger (but moderate) effect is sometimes produced by the maximum corotation model.
7. Can the effects of corotation become important in the case of other stars?
An important limitation on trapping of small dust particles in the vicinity of a star is the requirement that the ratio of radiation pressure to gravity β should be low (β < 0.5). This condition constrains the possibility of dust trapping around hot stars, although it does not prevent it entirely (see e.g., Rieke et al. 2015). In particular, in the case of β-Pictoris, the estimation of the value of β for cristalline olivine gives a value below 0.5 (Kohler & Mann 2002) and an estimate for obsidian particles is even lower (Artymowicz 1988).
In this study we search for examples of stars for which the effect of corotation (measured by the value of a2) is strong. The upper limit for a is (Ω/Vr)r sin θ. Therefore we have to find stars with a high rotation rate Ω and/or low stellar wind speed Vr.
A high rotation rate (more than one order of magnitude above the solar value) is usual for early-type stars. This is of particular interest because of recent observations of dust emissions from their vicinity (Su et al. 2013, 2020; Rieke et al. 2015; Kimura et al. 2020). The question of dust survival in the vicinity of hot stars (Kimura et al. 2020) is beyond the scope of this work. Rotation rates higher than that of the Sun were also observed for some M-type stars (Nielsen et al. 2013).
We first consider the hypothetical case of a star with half the solar mass but a far higher rotation rate (by a factor of 3–4) than the solar value. These parameters may appear for M-type stars.
We assume that the stellar parameters are such that 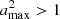 . The value of μ0 can then change significantly between different corotation models. We considered some hypothetical examples of stars with high maximum values of a2. Although we did not find any example for which a choice of the corotation model would preclude trapping, we found that this choice affects the depth of the well in the trapping potential. The deepest potential well of the trapping potential corresponds to the highest value of a, that is, to the case of no corotation.
. The value of μ0 can then change significantly between different corotation models. We considered some hypothetical examples of stars with high maximum values of a2. Although we did not find any example for which a choice of the corotation model would preclude trapping, we found that this choice affects the depth of the well in the trapping potential. The deepest potential well of the trapping potential corresponds to the highest value of a, that is, to the case of no corotation.
To find an example of a star for which the plasma corotation would have a strong effect on the form of U, we require a star with a value of (c + a)2 comparable to or higher than 1. Keeping Ω constant while changing Vr artificially from ∼400 km s−1 to 100 km s−1 would increase c + a by a factor of ∼16. The effect on the potential function U would then be strong, with the depth of the potential well changing by a factor of ∼2. Trapping of low-β particles would be not affected. However, such a low value of the stellar wind speed does not typically occur for Sun-like or hotter stars (Kimura et al. 2020).
Another possibility would be a star with a high rotation rate Ω. If the radiation of the star were to permit low values of β, the trapping region will exist, but its size would contract by a factor proportional to Ω−2/3 so that the value of (c + a) in the trapping region would then only increase proportionally to Ω1/3. Increasing the rotation rate by a factor 10 would then increase the value of (c + a)2 by a factor ∼4.4. Because the value of (c + a)2 in the trapping region is about 0.02 for the Sun, the increase would change it to ∼0.09, which is still far lower than 1.
The trapping potential for two different stars is presented in Fig. 8. The parameters relevant for our purposes are the stellar mass M, the rotation rate Ω, and the value of the ratio of stellar radiation pressure to gravity β for small dust grains. The examples shown represent the hypothetical M- and A-type stars.
 |
Fig. 8. Shape of the trapping potential function U(r) for two hypothetical stars: the M-type star with half the solar mass and 4 times the rotation rate, and the A-type star with twice the solar mass and 23 times the solar rotation rate. The ratio of stellar radiation pressure to gravity β was assumed to be 0.1 for the M star and 0.4 for the A star. The cases of no corotation (solid line), maximum corotation (dotted), and moderate corotation (dashed line) are shown. The horizontal lines show the conserved energy values for each case. |
We consider the case of a particle created at a distance r0 from the star, at the point of maximum stellar latitude of the circular parent body orbit of 5° inclination. The distance r0 we chose to be near to the outer limit r1 of the trapping region. The value of r1 (Eq. (25)) is ∼0.16 AU for the Sun, and depends on M and Ω as r1 ∝ M1/3Ω−2/3. We chose r0 = 0.12 AU × (M/MS)1/3(Ω/ΩS)−2/3, where the subscript S denotes the solar value.
The potential curves are shown for three models of corotation. The horizontal lines show the values of conserved energy E for each case.
The results shown in Fig. 8 illustrate the contraction of the trapping region for each star. The dependence of the potential function on the corotation model is prominent only in the case of the A star because only in this case is the value of a2 of the order 1 within the trapping region. Figure 9 shows the radial velocities of the trapped dust (in the guiding centre approximation) corresponding to the trapping potentials from Fig. 8.
 |
Fig. 9. Radial velocities of trapped particles for the cases illustrated in Fig. 8. The guiding centre radial velocity components calculated from the conservation law (Eq. (24)) are plotted. |
Figure 10 illustrates the effect of corotation on the radial velocity of trapped particles for the hypothetical M-type star. In absence of corotation, the distance – radial velocity plot shows oscillations that do not appear in the maximum corotation case. The oscillation frequency depends on the charge-to-mass ratio Q/m of the trapped particle. We chose a low value of Q/m (low oscillation frequency) to make the plot readable. The oscillations can be understood as due to Larmor rotation of trapped particles around a rotating magnetic field line. In the case of maximum corotation, the field lines are straight, so that the Larmor rotation, with the velocity perpendicular to magnetic field, does not produce any variation in the radial speed.
 |
Fig. 10. Simulated distance – radial velocity plots along the trajectories of trapped particles with Q/m = 10−6e/mp for the star with half the solar mass and three times the solar rotation rate. The solid (dashed) line corresponds to the no corotation (maximum corotation) case. |
Figure 11 shows the outer limits of the trapping region for a hypothetical M-type star compared to the case of the Sun. The ratio of radiation pressure to gravity β for small dust grains is assumed to be 0.1 for both cases. The horizontal axis shows the maximum value of the radius of the parent body orbit consistent with trapping of the emitted nanodust particle, while the vertical axis shows the orbit inclination relative to the stellar equator. Two cases are illustrated, corresponding to different choices of the initial point. Because in our model the magnetic field lines lie on the cones of constant latitude, curve (1) can also be understood as the outer limit of the trapping region in space, applicable to the particles emitted at the point of maximum latitude. On the other hand, the particles corresponding to case (2) remain close to the stellar equator.
 |
Fig. 11. Limits of the dust-trapping region for the hypothetical M-type star (half the solar mass, four times the rotation rate) compared to those for the Sun. The curves show the maximum distance from the star consistent with trapping of the dust particle vs the inclination of the parent body orbit. Two cases are illustrated: (1) The particle starts from the point of maximum latitude along the orbit (curves bending right), and (2) it starts from the point at which the orbit crosses the stellar equator plane (curves bending left). The results assuming no-corotation (solid line), maximum corotation (dotted), and moderate corotation (dashed line) are shown. |
Although Fig. 11 shows the results for three different assumptions about corotation, the results differ very little. The effect of corotation is much stronger for the case of the hypothetical A-type star illustrated in Fig. 12. We assumed β = 0.4 for small grains. The trapping region near the stellar equator is now ∼0.02 AU, compared to 0.16 AU for the Sun and 0.05 AU for the M-type star (see Fig. 11). Increasing the amount of corotation increases the trapping region. Curve (2) has a bimodal structure, with the intermediate region above ∼0.007 AU, passing into the asymptotic branch below this distance. This structure is related to the high value of β (β = 0.4) assumed here for the A star.
 |
Fig. 12. Similar to Fig. 11, but for the hypothetical A star with twice the solar mass, 23 times the solar rotation rate, and β = 0.4. The no-corotation (solid line), maximum corotation (diamonds), and moderate corotation (triangles) cases are shown. Curve 2 has a bimodal structure. The results were obtained using simulated trajectories for the dust grains with Q/m = 10−5e/mp. |
The results shown in Fig. 11 were derived using our guiding centre model (a comparison with trajectory simulations for the case of the Sun can be found in Czechowski & Mann 2012). The results in Fig. 12 were obtained from numerical simulations of particle trajectories, assuming Q/m = 10−5e/mp and the solar value of the radial component of the magnetic field at 1 AU.
8. Conclusions
The aim of this work was to study the effect of plasma corotation on the dynamics of small charged dust particles in the vicinity of the Sun. Our main conclusion, obtained using the model based on the guiding centre approximation and confirmed by numerical simulations, is that this effect is weak for the case of the Sun. In particular, the trapping of charged nanodust particles with β < 0.5 is not prevented by corotation.
The mechanism that is responsible for the weakness of the effect of plasma corotation on the charged dust dynamics is a simple consequence of the freezing of the magnetic field in the plasma flow. The freezing-in condition affects the shape of the magnetic field lines in such a way that the main repulsive force acting on a charged particle in the guiding centre approximation (the centrifugal force associated with the rotation of the magnetic field line) is not affected by any choice of the corotation model. The other repulsive force (the magnetic mirror force) depends on the corotation model through a combination 1 + a2, where a = −Bϕ/Br. For the case of the Sun, we find that a2 ≪ 1 for all realistic models of corotation, implying that the mirror force is also approximately independent of the corotation model. By “realistic” models we understand here all models where plasma rotates in the same direction as the star, with the angular velocity not higher than that of the star.
Our results also have some implications for the dust in the vicinity of other stars, and in particular, for the innermost zone of planetary debris disks. A detailed study of dust trapping around other stars is beyond the scope of the present work. Nevertheless, we include a brief discussion of the case of the stars with a high rotation rate. The value of a2 may then become high. If a2 ∼ 1 or higher, the choice of a corotation model would have a stronger effect on charged particle dynamics. We have considered two (hypothetical) examples of M- and A-type stars. We found that plasma corotation does not prevent trapping, but (for the case of the rapidly rotating, hot A-type star) significantly affects the dust dynamics, in particular, the shape of the outer boundary of the trapping region.
Acknowledgments
This work is supported by the Research Council of Norway (grant number 262941). We thank the anonymous reviewer for constructive comments.
References
- Artymowicz, P. 1988, ApJ, 335, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Bale, S. D., Goetz, K., Harvey, P. R., et al. 2016, Space Sci. Rev., 204, 49 [Google Scholar]
- Czechowski, A., & Kleimann, J. 2017, Ann. Geophys., 35, 1033 [Google Scholar]
- Czechowski, A., & Mann, I. 2010, ApJ, 714, 89 [Google Scholar]
- Czechowski, A., & Mann, I. 2011, ApJ, 732, 127 [Google Scholar]
- Czechowski, A., & Mann, I. 2012, Nanodust Dynamics in the Interplanetary Space, in Nanodust in the Solar System: Discoveries and Interpretations, eds. I. Mann, N. Meyer-Vernet,& A. Czechowski (Springer), 47 [Google Scholar]
- Czechowski, A., & Mann, I. 2018, A&A, 617, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juhasz, A., & Horanyi, M. 2013, Geophys. Res. Lett., 40, 2500 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, H., & Mann, I. 1998, ApJ, 499, 454 [Google Scholar]
- Kimura, H., Kunitomo, M., Suzuki, T. K., et al. 2020, Planet. Space Sci., 183, 104581 [NASA ADS] [CrossRef] [Google Scholar]
- Kohler, M., & Mann, I. 2002, Model Calculations of Dynamical Forces and Effects on Dust in Circumstellar Debris Disks, in Asteroids, Comets, and Meteors: ACM 2002, 500, 771 [NASA ADS] [Google Scholar]
- Krivov, A., Kimura, H., & Mann, I. 1998, Icarus, 134, 311 [Google Scholar]
- Luhmann, J. G. 2003, ApJ, 592, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Malaspina, D. M., Szalay, J. R., Pokorny, P., et al. 2020, ApJ, 892, 115 [Google Scholar]
- Mann, I. 1992, A&A, 261, 329 [NASA ADS] [Google Scholar]
- Mann, I. 2017, Phil. Trans. R. Soc. A, 375, 20160254 [CrossRef] [Google Scholar]
- Mann, I., & Czechowski, A. 2005, ApJ, 624, L125 [Google Scholar]
- Mann, I., & Czechowski, A. 2021, A&A, 650, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mann, I., Kimura, H., Biesecker, D. A., et al. 2004, Space Sci. Rev., 110, 269 [Google Scholar]
- Mann, I., Murad, E., & Czechowski, A. 2007, Planet. Space Sci., 55, 1000 [Google Scholar]
- Mann, I., Meyer-Vernet, N., & Czechowski, A. 2014, Phys. Rep., 536, 1 [Google Scholar]
- Nielsen, M. B., Gizon, L., Schunker, H., & Karoff, C. 2013, A&A, 557, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Northrop, T. G. 1958, Adiabatic Motion of Charged Particles (New York: J. Wiley and Sons) [Google Scholar]
- Page, B., Bale, S. D., & Bonnell, J. W. 2020, ApJS, 246, 51 [Google Scholar]
- Rieke, G. H., Gaspar, A., & Ballering, N. P. 2015, ApJ, 816, 50 [Google Scholar]
- Schatten, K. H., Wilcox, J. M., & Ness, N. F. 1969, Sol. Phys., 6, 442 [Google Scholar]
- Sheeley, N. R., Wang, Y.-M., Hawley, S. H., et al. 1997, ApJ, 484, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Stamm, J., Czechowski, A., Mann, I., Baumann, C., & Myrvang, M. 2019, A&A, 626, A107 [EDP Sciences] [Google Scholar]
- Su, K. Y. L., Rieke, G. H., Malhotra, R., et al. 2013, ApJ, 763, 118 [CrossRef] [Google Scholar]
- Su, K. Y. L., Rieke, G. H., Melis, K., et al. 2020, ApJ, 898, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Szalay, J. R., Pokorny, P., Bale, S. D., et al. 2020, ApJS, 246, 27 [Google Scholar]
- Weber, E. J., & Davis, L. 1967, ApJ, 148, 217 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Azimuthal plasma velocity component vs. distance for the model based on Weber & Davis (1967; upper panel) and for the “maximum corotation” model. The value of rA = 0.1 AU was assumed. |
| In the text | |
 |
Fig. 2. Magnetic field lines projected to the solar equator plane for different models of plasma corotation: no corotation (solid line), maximum corotation (dotted), model based on Weber and Davis (dashed) and the toy “supercorotation” model (dotted-dashed). |
| In the text | |
 |
Fig. 3. Upper panel: results of the numerical solutions of the full equations of motion (heliocentric distance r plotted against time) for the nanodust particles with Q/m = 10−4 e/mp emitted at 0.03 AU from a parent body moving in a circular Keplerian orbit of 5° inclination at the point of maximum latitude. The solutions correspond to three different models: no corotation (solid line), maximum corotation (dotted), and the critical point model based on Weber & Davis (1967; dashed line). The lower panel shows the potential function U(r) and the conserved quantity E plotted against r for the same assumptions about corotation. |
| In the text | |
 |
Fig. 4. As Fig. 3, but for the case of a particle emitted at 0.14 AU, close to the outer limit of the trapping region. The solutions for the different models are lying approximately on top of each other. Lower figure: was restricted in vertical range to show clearly the relative positions of the potential barrier and the energy levels. The minimum value of the potential U occurs at U(r)≈ − 4.3 in our (100 km s−1)2 units. |
| In the text | |
 |
Fig. 5. Plots of total speed and the radial velocity component vs heliocentric distance for the nanodust particles (Q/m = 10−4e/mp) released just outside of the trapping region for different assumptions about plasma corotation: no corotation (solid line), maximum corotation (dotted line), and the model of Weber and Davis (dashed line). To extend the corotation region, the Alfvén radius was artificially set at 0.5 AU. |
| In the text | |
 |
Fig. 6. Maximum eccentricity of the parent body orbit consistent with trapping of the emitted nanodust. The nanodust particle is emitted at perihelium. The cases illustrated are no corotation (solid line), maximum corotation (dotted line), and the model of Weber and Davis (dashed line). The curves correspond to particles emitted at the points of maximum heliolatitude from the orbits of 20° inclination (curves on the left) and of 70° inclination (curves on the right). |
| In the text | |
 |
Fig. 7. Effect of corotation on the propagation of nanodust particles emitted from the orbit of the Aquarids. The distances of the closest approach to the Sun are plotted against the position of the emission point on the orbit, represented by the angle counted from perihelion. The corotation models are the same as in Fig. 6: no corotation (solid line), maximum corotation (dotted line), and the model of Weber and Davis (dashed line). |
| In the text | |
 |
Fig. 8. Shape of the trapping potential function U(r) for two hypothetical stars: the M-type star with half the solar mass and 4 times the rotation rate, and the A-type star with twice the solar mass and 23 times the solar rotation rate. The ratio of stellar radiation pressure to gravity β was assumed to be 0.1 for the M star and 0.4 for the A star. The cases of no corotation (solid line), maximum corotation (dotted), and moderate corotation (dashed line) are shown. The horizontal lines show the conserved energy values for each case. |
| In the text | |
 |
Fig. 9. Radial velocities of trapped particles for the cases illustrated in Fig. 8. The guiding centre radial velocity components calculated from the conservation law (Eq. (24)) are plotted. |
| In the text | |
 |
Fig. 10. Simulated distance – radial velocity plots along the trajectories of trapped particles with Q/m = 10−6e/mp for the star with half the solar mass and three times the solar rotation rate. The solid (dashed) line corresponds to the no corotation (maximum corotation) case. |
| In the text | |
 |
Fig. 11. Limits of the dust-trapping region for the hypothetical M-type star (half the solar mass, four times the rotation rate) compared to those for the Sun. The curves show the maximum distance from the star consistent with trapping of the dust particle vs the inclination of the parent body orbit. Two cases are illustrated: (1) The particle starts from the point of maximum latitude along the orbit (curves bending right), and (2) it starts from the point at which the orbit crosses the stellar equator plane (curves bending left). The results assuming no-corotation (solid line), maximum corotation (dotted), and moderate corotation (dashed line) are shown. |
| In the text | |
 |
Fig. 12. Similar to Fig. 11, but for the hypothetical A star with twice the solar mass, 23 times the solar rotation rate, and β = 0.4. The no-corotation (solid line), maximum corotation (diamonds), and moderate corotation (triangles) cases are shown. Curve 2 has a bimodal structure. The results were obtained using simulated trajectories for the dust grains with Q/m = 10−5e/mp. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



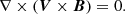
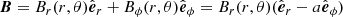
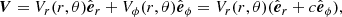
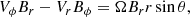
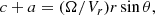
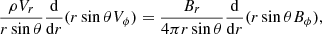
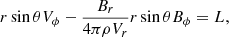
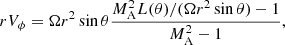
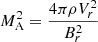
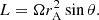
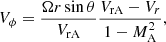
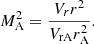
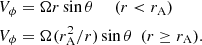
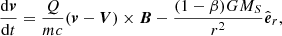
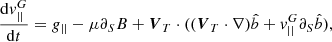
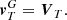
![$$ \begin{aligned} { v}\equiv \hat{\boldsymbol{e}}_{r}\cdot \left[{ v}^G_{||}\hat{\boldsymbol{b}}+\boldsymbol{V}_T\right] ,\end{aligned} $$](/articles/aa/full_html/2021/08/aa41048-21/aa41048-21-eq30.gif)
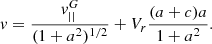
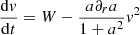
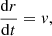
![$$ \begin{aligned} W=-\frac{1}{1+a^2}\left[\frac{GM_S(1-\beta )}{r^2} +\mu \partial _{r} B-\frac{V_{r}^2(c+a)^2}{r}\right] .\end{aligned} $$](/articles/aa/full_html/2021/08/aa41048-21/aa41048-21-eq34.gif)
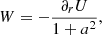
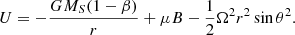
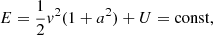
![$$ \begin{aligned} r=r_1 =\left[\frac{GM_S(1-\beta )}{\Omega ^2 \sin \theta ^2}\right]^{1/3} .\end{aligned} $$](/articles/aa/full_html/2021/08/aa41048-21/aa41048-21-eq38.gif)