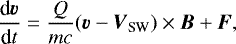| Issue |
A&A
Volume 650, June 2021
Parker Solar Probe: Ushering a new frontier in space exploration
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 9 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202039362 | |
| Published online | 02 June 2021 | |
Dust observations from Parker Solar Probe: dust ejection from the inner Solar System
1
Department of Physics and Technology,
Postboks 6050 Langnes,
9037
Tromso,
Norway
e-mail: ingrid.b.mann@uit.no
2
Space Research Centre, Polish Academy of Sciences,
Bartycka 18A,
00-716
Warsaw,
Poland
e-mail: ace@cbk.waw.pl
Received:
7
September
2020
Accepted:
12
November
2020
Context. The FIELDS instrument onboard Parker Solar Probe (PSP) observes dust impacts on the spacecraft. The derived dust flux rates suggest that the particles originate from the vicinities of the Sun and are ejected by radiation pressure. Radiation pressure typically ejects particles of several 100 nm and smaller, which are also affected by the electromagnetic force.
Aims. We aim to understand the influence of the electromagnetic force on the dust trajectories and to predict the dust fluxes along the orbit of PSP, within 1 AU and near Earth.
Methods. We study the trajectories of dust particles influenced by gravity, radiation pressure, and the electromagnetic force assuming that pitch-angle scattering can be neglected (scatter-free approximation). We estimate the dust fluxes along the second orbit of PSP and in the vicinity of the Earth based on average dust velocities derived from the trajectory calculations and dust production rates derived from a fragmentation model.
Results. The calculated cumulative flux of dust particles larger than 100 nm is of the same order (within a factor of ~2) as implied by PSP observations. In this size interval, the dynamics of most particles is dominated by the radiation pressure force. The Lorentz force becomes more important for smaller particles and fluxes can vary with magnetic field conditions. The calculated flux of the 30 to 75 nm particles at the PSP is negligible for most of the second orbit, except for an isolated peak at the perihelion. The 30–75 nm particles that were created inwards from 0.16 AU from the Sun are in trapped orbits if the radiation pressure force is weaker than gravity, which is the case for dust from asteroids and for cometary dust that was altered in space.
Conclusions. The inner Solar System is the most likely source of dust smaller than 100 nm that enters Earth’s atmosphere and our results suggest the flux is time-variable.
Key words: interplanetary medium / Sun: heliosphere / zodiacal dust / solar wind
© I. Mann and A. Czechowski 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The Solar Systems interplanetary dust cloud is primarily made out of the collision fragments of the comets and asteroids and of their larger meteoroid fragments. Due to the combination of orbital motion and Poynting-Robertson deceleration, the dust number density increases towards the Sun, as can be seen from Zodiacal light observations (cf. Mann et al. 2014, e.g.). The mass (size) distribution of the dust particles is well described near 1 AU (Grün et al. 1985) based on a number of different observations. Detailed simulations showed, however, that destruction by collisions needs to be compensated by an additional dust source to explain the observed fluxes and it is likely that the fragmentation of cometary meteoroids produces parts of the dust that is observed inwards from 1 AU (Ishimoto 2000; Mann et al. 2004).
The collisional fragmentation also produces an outward directed dust flux in the Solar System since the repelling radiation pressure force may be comparable to or larger than the gravitational attraction to the Sun for small fragment particles. A fragment from a parent object that moves in a circular orbit attains a hyperbolic orbit when the radiation pressure to gravity ratio β exceeds 0.5. These particles are known as β-meteoroids in contrast to α-meteoroids that are in bound orbit. Many in situ measurements do not provide the dust impact directions, and the α-meteoroids and β-meteoroids are often not distinguished. Some estimates of β-meteoroid fluxes were inferred from Helios observations (Zook & Berg 1975) and from Ulysses observations (Wehry & Mann 1999).
Parker Solar Probe (PSP) is the first spacecraft which entered the region near the Sun where a high dust production rate by mutual collisions in the circumsolar dust cloud is expected. PSP carries the FIELDS antenna instrument package whose measurements respond to dust impacts (Bale et al. 2016). The dust impacts observed with PSP have recently been discussed in a number of works (Szalay et al. 2019; Page et al. 2019; Malaspina et al. 2020). They show that trajectories of β-meteoroids can better explain the observed dust flux rates than those of α-meteoroids. This suggests that the observed particles have sizes of few 100 nm and smaller.
The smaller dust is also more influenced by an electromagnetic force. Near the Sun, this affects the distribution of the dust with sizes smaller than 0.5 μm (Krivov et al. 1998; Mann et al. 2000, 2004); this limit of 0.5 μm applies to solid particles. The dust particles with a size in the 1–100 nm range are strongly affected by the electromagnetic force. Within ~0.16 AU from the Sun, the nanoparticles with low β may be trapped due to interplay between the electromagnetic forces and the solar gravity; at a larger distance, they are accelerated outwards and picked up by the solar wind plasma. The conditions for trapping and pick-up depend on the distance from the Sun where the small particles form and on their initial velocity (Czechowski & Mann 2010, 2011, 2012, 2018).
In the present work, we study the trajectories of dust particles while taking radiation pressure and electromagnetic forces into account. Wecombine a dust production model by collisional fragmentation with simulations of the trajectories of charged nanodust, and we compare the dust fluxes derived from our model with those derived from PSP observations during the second perihelion passage.
This paper is organised as follows. In Sect. 2 we describe the dust model assumptions. The dust trajectory and flux calculations are presented in Sect. 3 where we restrict the discussion to the case of escaping particles. The calculated fluxes are then compared to PSP measurements (Sect. 4). Section 5 discusses the possibility of trapping dust particles near the Sun by electromagnetic forces. Section 6 is concerned with the dust fluxes that we derived from the calculations and our results are summarised in Sect. 7. The method of calculating the dust flux is further detailed in the appendix.
2 Dust model assumptions
Previous works analysing the PSP dust observations suggest that the observed flux is generated by β meteoroids that are ejected by the radiation pressure force (Szalay et al. 2019; Page et al. 2019; Malaspina et al. 2020). The dust is also influenced by the electromagnetic force. For our calculations, we thus relied on model assumptions about the values of β (the radiation pressure to gravity ratio) and Q∕m (the charge to mass ratio).
Since the impacts of very small dust particles may not be detectable by PSP, we considered the particles near the outer size limit for the nanodust, specifically the radii of about 30 nm and about 100 nm. To compare this with PSP observations, we constructed approximate cumulative flux distributions along the orbit of PSP for the cases of nanodust above the minimum radii equal to 30 and 100 nm, respectively.
We referred to two different models (Wilck & Mann 1996) of the radiation pressure to gravity ratio, corresponding to asteroidal dust and to young cometary dust, respectively. The dust particles that have been freshly ejected from comets were assumed to be very porous and absorbing (young cometary dust). In space, the cometary dust was assumed to change structure and composition, and radiation pressure properties of old cometary dust were assumed to become similar to those of asteroidal dust. Most of the calculations reported here correspond to the case of asteroidal dust. The values of β were derived using Mie calculations and the Maxwell-Garnett mixing rule to simulate the refractive index for dust with different porosity and material compositions (Wilck & Mann 1996). The β-values of dust with radii 10, 30, 100, and 310 nm are 0.768, 0.901, 1.790, and 1.213 for the cometary dust assumption and 0.106, 0.163, 0.751, and 0.772 for the asteroidal dust assumption, respectively.
The dust electric surface charge is caused by interactions with the solar wind and the solar photons (Mukai 1981; Kimura & Mann 1998). The particles reach an equilibrium charge within a short time and the charges can be taken to be approximately constant. We assumed the values of charge-to-mass ratios Q/m of 10−6 e∕mp (102 C kg−1) and 10−7 e∕mp (10 C kg−1) for the 30–40 nm and 100–140 nm dust grains, respectively (see Czechowski & Mann 2010, 2012). For other dust sizes, we assumed that Q/m behaves approximately as a−2 where a is the grain radius. The size ranges used in our calculations of cumulative distributions and the assumed values of Q/m and β are listed in Table 1.
To estimate fluxes, we assumed that the dust particles are collision fragments of larger parent objects and that the parent mass distribution is given by the interplanetary flux model (Grün et al. 1985) at all heliocentric distances considered. We assumed that the dust cloud is concentrated within 12 degrees below and above the ecliptic (Czechowski & Mann 2012). The average relative velocities between dust particles are 20 km s−1 at 1 AU and increase proportionally to r−0.5 with a decreasing distance from the Sun. The mass distribution of fragments depends on the collision velocity and the mass of colliding particles. We made the same model assumptions used in a previous study (Mann & Czechowski 2005) that are based on a semi-empirical collision model that was developed to describe interstellar medium dust (Jones et al. 1996). We note that in previous studies (Czechowski & Mann 2010, 2012), we have included a second component of dust in high inclination orbits. This was found to have only a small effect on the number of produced fragments and it was therefore not included in the fragmentation estimate. The calculated production rates with a distance from the Sun are shown for two size intervals of fragments in Fig. 1. Since the small particles are fragments of the dust cloud near the ecliptic and in bound approximately circular orbit, it is reasonable to assume that the radiation pressure properties are those of asteroidal dust or old cometary dust.
The propagation of charged nanodust is very sensitive to the solar wind and the magnetic field structure. According to Fig. 1 in Lavraud et al. (2020), during the first orbit of PSP, the radial component of the solar magnetic field was positive in the northern hemisphere, suggesting the “defocusing” polarity with the electric field pointing away from the current sheet. The heliospheric current sheet was close to the solar equator. In the following, we use a simplified model of this configuration with a flat current sheet lying in the solar equator plane. In a defocusing field, positively charged particles drift away from the solar equator. Since the orbit of PSP is restricted to low latitudes, we expect that the drift would reduce the impact rate of the charged dust.
Assumed Q∕m and β values.
3 Estimations of the dust flux: escaping particles
In this section we specifically focus on dust particles which are not trapped near the Sun by the electromagnetic forces. These include all dust particles with a high enough radiation pressure to gravity ratio (β ~ 0.5) and those particles with small β which are created outside the limit of the trapping region, which, near the solar equator, occurs at the heliocentric distance of ~0.16 AU (Czechowski & Mann 2010, 2012, see also Stamm et al. 2019). Assuming that these particles are created by collisional fragmentation from the larger dust, their subsequent motion will be ultimately directed outwards due to the radiation pressure or the electromagnetic forces. We can then consider a simple model in which the loss rates of the larger dust can be neglected and the spatial distribution of dust particles inside the region traversed by the PSP is time-stationary. For trapped dust, the loss processes cannot be neglected.
The orbit of PSP lies close (~4° tilt) to the solar equator plane. Therefore, it is embedded inside the circumsolar dust disk. To obtain an approximate estimation of the dust flux, we made additional simplifying assumptions. We neglected the tilt of the dust disk relative to the solar equator, and we assumed that at low ecliptic and heliographic latitudes (to which the orbit of the spacecraft is restricted) the production rate ρ of nanodust particles only depends on the heliocentric distance r. The production rates for nanodust that were used in our calculations for the size ranges 30–40 nm and 100–140 nm are shown in Fig. 1.
To determine the flux of nanodust, we had to refer to numerical simulations. We used a simple time-stationary model of the solar wind and the magnetic field. We considered the solar wind flow to be purely radial, with a constant speed of VSW = 400 km s−1. The magnetic field has the form of the Parker spiral
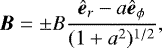 (1)
(1)
where a ≡ a(r, θ) = (ΩS∕VSW)rsinθ, r,ϕ, and θ are the heliocentric distance, longitude, and co-latitude in the HGI system, and ΩS is the solar rotation rate near the equator. The radial component of the magnetic field is positive in the northern hemisphere and equal to 30 μG at 1 AU.
where F includes gravity and the radiation pressure force. The velocity-dependent Poynting-Robertson force and the ion drag force were included in the code, but we only used them for trapped trajectory calculations. We solved Eq. (2) numerically, with the initial conditions corresponding to dust particles released at zero relative velocity from a parent body moving in a circular Keplerian orbit with inclinations within ±12° relative to the solar equator.
The advantage of our simple model is that the distribution of the nanodust is time-independent and has a rotational symmetry relative to the solar axis. We could then estimate the flux of nanodust without needing to carry out full three-dimensional simulations. Since the particle trajectories are symmetric under rotations around the solar axis, it is sufficient to have a trajectory passing through the point with the heliocentric distance r and the heliographic latitude λ equal to those of the spacecraft (rS,λS).
Figures 2 and 3 illustrate the effect of latitudinal drift on trajectories of the nanodust particles with charge-to-mass ratios of 10−7 e∕mp (size ~100–140 nm, radiation pressure to gravity ratio β = 0.751) and 10−6 e∕mp (size ~30–40 nm, β = 0.163), respectively.In Fig. 2 the drift towards the poles dominates the motion at low latitudes and almost all trajectories miss the positions of the spacecraft. In consequence, the 30–40 nm particles can strike the PSP only if they are produced close to the spacecraft position. Moreover, because of a low β value, the 30–40 nm particles created within r < 0.16 AU are trapped inside this region.
For the 100–140 nm particles, the strong radiation pressure (β > 0.5) prevents thetrapping and contributes to outward acceleration. Figure 3 shows that the 100–140 nm particles coming from the vicinity of the Sun, where the production rate by collisional fragmentation is high, should be present along the whole orbit of PSP. On the other hand, most of particles created beyond ~0.25 AU from the Sun drift away from low latitudes.
Figure 4 illustrates the drift pattern of the 30–40 nm dust with a large β = 0.901, corresponding to the hypothetical case of dust made of cometary material. For large β, the trapping is absent, so that the region r < 0.16 AU contributes to the escaping dust.
We estimated the contribution to the flux density at the position of the spacecraft (heliographic distance rS and heliolatitude λS) of the dust particles originating in the volume element ri ≤ r < ri+1 of the dust disk as follows. We calculated a set of nanodust trajectories starting from this volume and found the points where the trajectories cross the sphere of radius rS. We let Λm and Λx be the minimum and maximum latitudes of the points in this set. The contribution to the flux was obtained by dividing the particle production rate in the initial volume by the area of the “belt” contained between the latitudes Λm and Λx, that is by 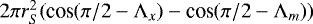 . The flux density arriving at the spacecraft was obtained by integrating over all initial r under the condition that the spacecraft latitude λS lied within the latitude limits of the belt. The symmetry of our model simplifies the calculations: the azimuthal angle does not need to be considered.
. The flux density arriving at the spacecraft was obtained by integrating over all initial r under the condition that the spacecraft latitude λS lied within the latitude limits of the belt. The symmetry of our model simplifies the calculations: the azimuthal angle does not need to be considered.
For a more precise estimation of the flux, we needed to account for the possibility that the trajectory crossing points were not uniformly distributed inside the Λm, Λx interval. We used the following method. We divided the interval Λm, Λx into n equal parts; nS being the number of trajectories passing though the interval that includes the spacecraft latitude λS. The flux estimation was then corrected by multiplying by the factor nS∕ntraj, where ntraj is the number of all trajectories passing between Λm, Λx.
For the case where the latitudinal drift is very strong (30–40 nm, see Fig. 2), we used a different method. Weconsidered the flux passing through the surface of constant latitude, equal to the latitude of PSP: λ = λS. By inspecting the trajectories we found that, except for the region near the perihelion, the particles striking the spacecraft come from the region of the disk between the solar equator and the spacecraft latitude. Since their latitudinal velocity is larger than the radial component (see Figs. 2, 5), the flux reaching the vicinity rx ≥ rS ≥ rm of the spacecraft is approximately given by the production rate integrated over the volume defined by the rx ≥ r ≥ rm, λS ≥ λ ≥ 0 part of the disk and divided over 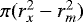 , the area of the ring belonging to the λ = λS surface. We note that the flux obtained by the first method is the radial component of the flux, while the second method gives the latitudinal component.
, the area of the ring belonging to the λ = λS surface. We note that the flux obtained by the first method is the radial component of the flux, while the second method gives the latitudinal component.
To compare with the PSP impact data, which do not include information about the impacting dust size, we had to construct approximate cumulative flux distributions including a wide range of the dust sizes. We directed our attention to the dust made of asteroidal material, with the radii between 30 and 500 nm; we also included the contribution of the dust in the 500 to 1000 nm range moving in Keplerian orbits. We divided this range of sizes into intervals given in Table 1. For particles with Q∕m less than 10−7 e∕mp and β ≥ 0.5, we assumed the Lorentz force to be weak enough to be neglected. The flux was then estimated by combining our dust production rates with the analytically calculated trajectories. For Q/m = 10−7 e∕mp and larger, we assumed that the flux within each interval can be approximated by numerical simulations assuming the values of Q/m and β shown in Table 1.
We used the first method for the case of 75–100 nm and 100–140 nm particles, for which β > 0.5. For 30–40 nm and 40–75 nm particles, we used the first method for the region near the PSP perihelion, where the particles flux is high, and the second method for the remaining, low flux part of the orbit. We approximated the flux of the 500–1000 nm dust moving in Keplerian orbits by the product of the dust number density derived from the interplanetary flux model (Grün et al. 1985) and the relative velocity between the orbital velocities of the dust and the PSP. The details of our calculations of the dust flux and the average dust velocities are presented in the appendix.
For a simple estimation of other quantities, such as the flux relative to the PSP Frel, we used the approximate formula
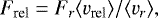 (3)
(3)
where Fr is the radial flux obtained as described above, and ⟨vr⟩ and ⟨vrel⟩ are the averages of the radial component of the dust velocity and of the dust speed relative to PSP, both at the position of the spacecraft. If the second method is used, Fr is replaced by Fθ and ⟨vr⟩ by ⟨vθ⟩. The averages were calculated by weighing the trajectories by the contributions to Fr or Fθ from their initial volumes.
 |
Fig. 1 Production rates of 30–40 nm and 100–140 nm nanodust particles in the circumsolar dust disk assumed in the calculations. |
 |
Fig. 2 Two samples of trajectories of 30–40 nm dust with β = 0.163, projected onto the heliocentric distance-heliographic latitude plane (the r,λ plane). The magnetic field is positive in the northern hemisphere and negative in the southern hemisphere (defocusing configuration). The crosses mark the daily positions of the spacecraft during the second orbit. The diamonds show the upper and lower limits in latitude for each of the two samples. The initial latitudes are between −12° and 12° (Czechowski & Mann 2012). Only a small fraction of trajectories encounter the orbit of the spacecraft. |
 |
Fig. 3 Similar to Fig. 2, but for the 100–140 nm dust with β = 0.751. All trajectories shown start from the southern hemisphere with initial latitudes between −12° and −(4/33)° (the trajectories starting from the northern hemisphere are not shown). The orbit of PSP is now within the region crossed by one of the trajectory groups. |
 |
Fig. 4 Same as Fig. 3, but for the 30–40 nm dust with high β = 0.901 corresponding to the cometary material. A high radiation pressure force reduces the poloidal drift; however, the impacts on more distant parts of the orbit of PSP would be rare. |
 |
Fig. 5 Average speed relative to PSP (solid line, diamonds) and the average velocity components: radial (dotted line, triangles), latitudinal (dashed, squares), and azimuthal (dotted-dashed, x signs) of 30–40 nm particles with β = 0.163 that encounter PSP along the second orbit. The symbols show the averages weighted by the radial flux (first method, the peak region). Lines show the averages obtained by using the latitudinal flux (second method). See Sect. 3and Appendix A for details. |
 |
Fig. 6 Same as Fig. 5, but for the 100–140 nm particles (β = 0.751) that encounter PSP along the second orbit. |
4 Dust fluxes at PSP
To calculate the flux of nanodust at PSP, the initial conditions for particle trajectories must cover the whole region from which the nanodust particles can reach the spacecraft. We assumed all nanodust particles to be collision fragments. For initial conditions, we used a grid of initial heliocentric distances ri (from ~300 to a couple thousand values on a logarithmic grid) and initial heliographic latitudes λk (typically 100 equidistant values). In the case of particles which are subject to trapping (β <0.5), ri must lie outside the trapping region. The latitudes λk are restricted to the region between −12° and 12°. All particle trajectories start from circular Keplerian orbits at maximum or minimum latitude.
From the discussion in the previous section, it is clear that the electromagnetic forces strongly affect the propagation of nanodust in the size ranges from 30 to 40 nm and 100 to 140 nm. We first consider the average velocities of the different dust populations. Figures 5 and 6 show the dust velocity components (radial, azimuthal, and latitudinal in the heliographic inertial frame) along the second orbit of PSP, as well as the absolute value of the dust speed relative to PSP. It is important to note that all the velocities correspond to the dust approximately at the spacecraft position. The velocities are averages over the calculated trajectories of nanodust.
For the case of 30–40 nm particles with β = 0.163 (see Fig. 5), the radial velocity of the dust is small, while their latitudinal and azimuthal components are large and approximately symmetric relative to perihelion. The dust speed relative to PSP has, therefore, only a small asymmetry between the incoming and outgoing parts of the orbit. A small radial component of the dust velocity at low heliographic latitudes can be related to strong latitudinal drift (Fig. 2).
On the other hand, for the 100–140 nm dust with β = 0.751 illustrated in Fig. 6, the velocity relative to PSP is significantly higher for the incoming part than for the outgoing part of the orbit. This is a simple consequence of having the radial dust velocity component that is large and approximately symmetric relative to perihelion. This is related to the 100–140 nm nanodust propagation pattern (Fig. 3) with a latitudinal drift that is much less pronounced than for the 30–40 nm nanodust (Fig. 5).
A comparison of our model to the impact rates observed by PSP is not straightforward, because every impact of the dust grain on the surface of the spacecraft does not need to be accompanied by a voltage burst. To obtain the impact rate from the simulated dust flux, we considered the product of the flux with the conversion factor C with the dimension of the area. The value of C was selectedto make the maximum value of the product approximately equal to the maximum of the observed impact rate. This value could then be compared to the effective area of the PSP (4.5–7 m2 ; cf. Page et al. 2019). If C is larger (smaller) than this area, we conclude that the simulated flux is lower (higher) than implied by observations provided that each dust impact would cause a voltage burst.
In Fig. 7 we compare the calculated flux of 100–140 nm particles with β = 0.751 (asteroidal dust) to dust impact rates observed with PSP along the second orbit. We find that the conversion factor, which is equal to 3 × 104 cm2, makes the flux to agree with the impact rate at the perihelion. The agreement between the flux and observations is good for the part of the peak before the perihelion. We note that our conversion factor is of the same order of magnitude as the effective area of PSP (4.5–7 m2 ; cf. Page et al. 2019).
The calculated flux of 30 to 40 nm particles compared to the PSP dust impact rate is shown in Fig. 8. The conversion factor is 4.5 × 103 cm2. Except for the vicinity of the perihelion, the 30–40 nm dust flux is effectively absent for most of the orbit as a result of high poloidal drift (Figs. 2, 4). Finally, to illustrate the situation where the electromagnetic forces acting on dust particles are absent, we show the calculated fluxes for neutral particles in the 100–140 nm size range compared to PSP impact rates in Fig. 9. We assume two different β values: 0.5 (conversion factors 3.7 × 104 cm2) and 1.5 (conversion factor 4.8 × 104 cm2).
The following two figures show the comparison of the PSP impact data to simulated cumulative distributions of the dust flux. Figure 10 corresponds to dust sizes above 100 nm, with the conversion factor 1.9 × 104 cm2. Figure 11 presents the case of dust with a size above 30 nm. The conversion factor is then 0.65 × 104 cm2. The flux distribution along the orbit of PSP is only similar to observations for the case of the sizes above 100 nm, although some differences still remain. The value of C suggests that the flux above 100 nm is two to three times higher than observations. A possible conclusion is that the impacts observed by PSP come from the dust with the radius above 140 nm, while the smaller dust does not contribute to observations.
Figure 12 compares the behaviour of the PSP impact rates and the calculated dust fluxes as functions of distance. As noted before (Szalay et al. 2019; Page et al. 2019; Malaspina et al. 2020), the PSP impact rates and flux behave approximately as 1/r2 and we also find this for the 100 to 140 nm dust flux that we calculated.
Together with our discussion of Figs. 10 and 11, this comparison suggests that the FIELDS experiments detect dust particles above the 100 nm size. The antenna signals that are generated by dust impacts increase with the mass and impact speed of the particles and in taking the estimated impact speeds into account (Sect. 3), it is likely that the particles in the 30–40 nm size range generate smaller pulses. The formation of the impact signals depends, however, on a number of parameters which are variable near the Sun (Mann et al. 2019) so that the smaller particles are possibly detected during partsof the orbit.
 |
Fig. 7 Comparison of calulated fluxes to PSP observations. The solid line shows the calculated flux of 100 to 140 nm particles assuming Q/m = 10−7 e∕mp and β = 0.751 (asteroidal dust material). The simulated flux values were adjusted to the impact rate observed at the perihelion, assuming a spacecraft cross section of 3 × 104 cm2. |
 |
Fig. 8 Comparison of calculated fluxes to PSP observations. The solid line shows the estimated flux of 30 to 40 nm particles relative to PSP, assuming Q/m = 10−6 e∕mp and β = 0.163. To agree with the observed impact rate at the perihelion, the calculated flux had to be multiplied by a factor of 4.5 × 104 cm2. We note thelow flux intensity away from the peak. |
 |
Fig. 9 Comparison of calculated fluxes of neutral dust to PSP observation. The solid line shows the fluxof 100–140 nm chargeless particles with beta = 1.79, multiplied by a factor of 4.8 × 104 cm2. The dashed line is for beta = 0.751 with the multiplication factor 3.7 × 104 cm2. |
 |
Fig. 10 Cumulative flux relative to PSP of the dust with the radii above 100 nm (solid line) along the second orbit compared to the observed impact rate. The dotted lines (in the order from top to bottom) show the contributions of the dust with sizes above 140, 200, 300, 400, and 500 nm, respectively. The fluxes were rescaled by a common factor equal to 1.9 × 104 cm2. |
 |
Fig. 11 Cumulative flux relative to PSP of the dust with the radii above 30 nm (solid line) along the second orbit compared to the observed impact rate. The dotted lines (in the order from top to bottom) show the contributions of the dust with sizes above 140, 200, 300, 400, and 500 nm, respectively. The fluxes were rescaled by a common factor equal to 0.65 × 104 cm2. |
5 Electromagnetic force and trapped particles
PSP passes a region that is of particular importance for the smallest nanodust with a charge-to-mass ratio that is high enough to make thenanodust dynamics qualitatively different from that of the larger dust grains. In particular, if the scatter-free approximation holds, the nanodust particles can be trapped in non-Keplerian orbits by the interplay between thesolar gravity and the Lorentz force (Czechowski & Mann 2010, 2011, 2012, 2018; Czechowski & Kleimann 2017).
The trapping can occur for particles with a large charge-to-mass ratio and a small radiation pressure to gravity ratio. For particles in the size range between 3 and 30 nm, we expect a low value of β (~0.1) but a high charge-to-mass ratio (between 10−4 and 10−6 in the units e∕mp). If the nanodust dynamics can be considered scatter-free (that is, the pitch-angle scattering can be neglected), these particles can be trapped near the Sun. The nanodust particles released within the trapping limit (~0.16 AU from the Sun near the solar equator) are not accelerated away from the Sun, but they become trapped. On the other hand, if the pitch-angle scattering is important for nanodust, one would expect the nanodust interaction with the solar wind to be similar to that of the heavy pick-up ions.
Under the scatter-free assumption, the nano dust created in this region oscillates between an upper r1 and a lower r2 limit in r. The values r1 and r2 depend on the initial distance at which the nanodust particle was created (Czechowski & Mann 2010, 2012). When the lower limit r2 is close enough to the Sun, the losses of nanodust cannot be neglected. Even if the particle escapes sublimation, the ion drag (Minato et al. 2004) slows it down and reduces the value of r1 for the subsequent cycle (Czechowski & Kleimann 2017).
For particles released near the outer limit of the trapping region, the lower limit r2 occurs well inside the solar corona, so that the probability of destruction by sublimation for these particles is high. The particles created at r1 near the middle of the trapped region have r2 close to r1 and therefore a low probability of destruction by sublimation. A simple model of scatter-free nanodust dynamics, which may be adequate for the escaping particles, is insufficient to estimate the lifetime of trapped nanodust, particularly in the “long-living” middle region. Observations from PSP, which has already entered well inside the trapping region during the year 2020, could resolve the question of existence of the scatter-free nanodust population provided that impacts of nanodust below the ~50 nm size could be detected.
 |
Fig. 12 PSPimpact rates (diamonds) and the normalised cumulative fluxes relative to PSP of charged dust with the radii above 30 nm (dashed line) and above 100 nm (solid line), shown in a logarithmic plot as functions of the heliocentric distance along the orbit of PSP. Both incoming (the upper branch) and outgoing parts of the orbit are shown. The PSP impact rates and the flux of the dust above 100 nm size approximately follow the 1/r2 law as for the case of free expansion, while the flux of the dust between 30 and 100 nm is steeper in the peak region. |
6 Dust flux near earth’s orbit
Bearing in mind the uncertainties of the fragmentation model and assumptions entering trajectory calculations, we now discuss the flux rate at Earth’s orbit. The estimated flux at 1 AU of the 100–140 nm particles ranges from 0.51 × 10−10 cm−2 s−1 for particles passing within 2.4 degree from the solar equator and 0.39 × 10−8 cm−2 s−1 when we assume that particles pass within 4.8 degree from solar equator. There is a large variation and both numbers are for the defocusing magnetic field polarity. The latter flux estimate is of the same order as the 100 nm β-meteoroids flux of 1–6 × 10−5 m−2 s−1 that Zaslavsky et al. (2012) derived from observations of the STEREO S/WAVES radio instruments made from 2007 to 2010. The STEREO observationsdistinguish an additional flux of interstellar dust (with sizes of 100–300 nm). The 100 nm particles have a mass of ~ 10−14 g, assuming an average bulk silicate composition.
This value of dust flux near Earth’s orbit is of a similar order as previous measurements. The measurements with the Ulysses dust instrument provide a more reliable dust identification for each measurement, but they are limited by statistics and by the non-optimum orientation of the instrument which should not be exposed to direct sunlight. From 25 impact events during the first 65 days of the Ulysses mission, Wehry & Mann (1999) could estimate a β-meteoroids flux of 1.5 ± 0.3 × 10−4 m−2 s−1 between 1 and 1.6 AU and for estimated dust radii of 100–200 nm.
The interplanetary dust flux model (Grün et al. 1985) of the dust flux near 1 AU is based on Zodiacal light observations, in situ observations, and impact studies; it lists a cumulative flux of 2.5 × 10−4 m−2 s−1 for particles with a mass of < 10−14 g. We expect that the ongoing PSP observations in combination with observations of the Solar Orbiter spacecraft will help to better estimate the flux of β-meteoroids near 1 AU and onto Earth. We note that our results on the influence of electromagnetic forces on dust fluxes suggest that the flux of dust particles that reach Earth from the inner Solar System varies with time. Time variations of the dust fluxes were also observed inside 50 solar radii during the first three solar encounters of PSP (Malaspina et al. 2020).
The dust particles that reach Earth can enter its atmosphere without deflection at its magnetosphere (cf. Czechowski & Mann 2012). The mass flux onto Earth from the β-meteoroids in the 100 nm size range of roughly g per day is negligible in comparison to the total meteoroid mass accretion given in a recent estimate with 43 tons per day and a factor of 20 uncertainty (Plane et al. 2015). The particle flux is, however, around ~ 1014 per day and because of the small size, those particles are likely to survive entry into the atmosphere because they do not reach melting temperature and pass Earth’s atmosphere with only little alteration. According to Popova (2004), dust particles (meteoroids) smaller than about 1000 nm are not heated enough to ablate. Vondrak et al. (2008) inferred from their ablation model that the lowest mass threshold for complete vaporisation is 10−10 g. This value is for the highest impact velocity of 72.5 km s−1 that they considered, but the mass threshold is a factor of 10 000 above the mass of the β-meteoroids.
We suggest that it is possible that β-meteoroids are part of dust samples that were collected in the stratosphere with balloons (Rietmeijer et al. 2016). The particles were randomly collected in the upper stratosphere in 2008 and 2011. Rietmeijer et al. (2016) find that the particles with sizes from 100 to 8500 nm that they analysed show evidence of mineral alteration that is typical for catastrophic geological processes or meteoroid impact cratering. They conclude, therefore, that the particles formed in bolides or fireballs during fragmentation events. We suggest that the smaller of these particles are possibly β-meteoroids that show signs of alteration because they form by fragmentation in the vicinity of the Sun. As can be seen from Fig. 1, the vast majority of the dust particles are generated within 0.2 AU from the Sun where temperatures are 600 K and higher. The fragmentation at collision velocities of several 10 km s−1 and higher leads to additional alteration.
7 Summary
We consider the possibility that the dust fluxes observed at PSP may be caused by impacts of charged dust. Assuming a simple model of the solar wind and the magnetic field structure as well as the model of the dust production rate, we estimate the fluxes of charged dust relative to PSP along the second orbit and compare to the observed impact rate.
The PSP impact rate and the calculated cumulative flux of the dust above 100 nm size approximately follow the 1/r2 law, as for the case of free expansion. For smaller particles, this slope is steeper in the vicinity of the Sun. For the dust in the size range of 30 to 100 nm, which is strongly affected by the Lorentz force, the flux relative to the spacecraft shows a different distribution along the orbit than the observed impact rate. This behaviour can be understood as the effect of the Lorentz force causing the positively charged particle to drift away from the solar equator plane and, therefore, away from the orbit of PSP. However, this behaviour is only expected for the defocusing magnetic field polarity. If the field polarity changes, even locally,one should expect a high intensity nanodust flux whenever the spacecraft crosses the current sheet. The 30–40 nm particles may, nevertheless, be difficult to detect because of a small amount of charge released on impact.
We note that for the first time, PSP offers a possibility of observing the trapped nanodust population. This topic requires a separate study.
Finally, we use our results to discuss the flux of ejected dust particles that cross Earth’s orbit and the nanodust flux into Earth’satmosphere. A closer investigation, however, needs to consider the influence on the signals’ shape from charge production during the impacts which depends on the speed and mass of the dust (see e.g. Zaslavsky et al. 2012).
Acknowledgements
This work is supported by the Research Council of Norway (grant number 262941).
Appendix A Method
Our method of calculating the dust flux was restricted to the case where the magnetic field, the plasma flow, and the distribution of the dust production rate were time-stationary and rotationally symmetric relative to the solar rotation axis. We considered the trajectories starting from initial heliocentric distances r = ri (i = 1…nr) and initial (equally spaced) heliolatitudes λk (k = 1…nλ). Our aim is to estimate the dust flux at s = 1…ns daily positions of PSP. The dust production region was restricted to the circumsolar dust disk, which was assumed to be limited to (λ−, λ+) = (−12o,12o) in heliolatitude. Within the disk, the production rate ρ of dust of a given material and size only depends on r.
We let Wi be the dust production rate integrated over the ri ≤ r < ri+1 part of the disk (the ith initial volume):
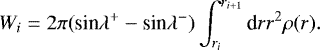 (A.1)
(A.1)
The contribution of the ith initial volume to the (radial) flux of dust at the sth position of PSP (heliocentric distance Rs) is then given by
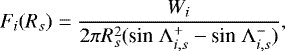 (A.2)
(A.2)
where 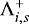 and
and 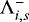 define the limits in latitude of the region where the trajectories starting from ri cross the surface r = Rs. We then denote the contribution of a single trajectory starting from ri, λk to the flux at Rs as fi,k(Rs) = Fi(Rs)∕nλ.
define the limits in latitude of the region where the trajectories starting from ri cross the surface r = Rs. We then denote the contribution of a single trajectory starting from ri, λk to the flux at Rs as fi,k(Rs) = Fi(Rs)∕nλ.
We let λs be the sth heliolatitude of the spacecraft. The radial flux at the position of the spacecraft is then given approximately by the sum ∑iFi(Rs) over those initial r intervals for which the spacecraft latitude λs is within the latitude limits (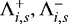 ) at r= Rs.
) at r= Rs.
This estimation of the flux became imprecise when the distribution of the points where trajectories crossed the surface r = Rs was not approximately uniform in latitude. To improve the estimation, instead of a whole 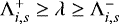 region, we considered a part of it:
region, we considered a part of it: 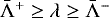 , which must include the spacecraft latitude. We note that the new limits
, which must include the spacecraft latitude. We note that the new limits 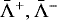 may be chosen to depend on i and s. This is the case in our calculations, where we divided the
may be chosen to depend on i and s. This is the case in our calculations, where we divided the 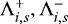 region into N equal parts and selected the subinterval which includes
region into N equal parts and selected the subinterval which includes
λs. The contribution of the ith volume to the flux is then a sum ∑kfi,k(Rs) over the trajectories starting at ri and passing at r = Rs through the (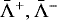 ) region. The total radial flux at Rs is a double sum ∑i,kfi,k(Rs).
) region. The total radial flux at Rs is a double sum ∑i,kfi,k(Rs).
The contributions to the radial flux fi,k(Rs) were used as weights for calculating the averages. We let ![$[A]_s$](/articles/aa/full_html/2021/06/aa39362-20/aa39362-20-eq16.png) denote the weighted sum over the trajectories contributing to the flux at r = Rs, which includes the condition that their crossing points are within the
denote the weighted sum over the trajectories contributing to the flux at r = Rs, which includes the condition that their crossing points are within the 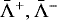 region,
region,
![\begin{equation*} [A]_s=\sum_{i,k} f_{i,k}(R_s) A_{i,k,s},\end{equation*}](/articles/aa/full_html/2021/06/aa39362-20/aa39362-20-eq18.png) (A.3)
(A.3)
where Ai,k,s is the value (e.g. of a velocity component vr) for a trajectory starting at r = ri, λ = λk, taken at the point where it crosses the r = Rs surface. The average ⟨A⟩ at Rs is then given by
![\begin{equation*} \langle A\rangle_s=\frac{[A]_s}{[1]_s},\end{equation*}](/articles/aa/full_html/2021/06/aa39362-20/aa39362-20-eq19.png) (A.4)
(A.4)
where ![$[1]_s$](/articles/aa/full_html/2021/06/aa39362-20/aa39362-20-eq20.png) is our estimation of the radial flux Fr at the sth position of the spacecraft.
is our estimation of the radial flux Fr at the sth position of the spacecraft.
We used Eq. (A.4) to calculate the averages of the dust speed relative to the spacecraft ⟨|vrel|⟩ and of the components of the dust velocity ⟨vr⟩, ⟨vϕ ⟩, and ⟨vθ ⟩. We used Eq. (A.3) to estimate the dust number density nust as ndust = [1∕vr] and the dust flux relative to spacecraft Frel as Frel ≈ [|vrel∕vr]. In the latter case, we found that the result is close to Frel = Fr⟨|vrel|⟩∕⟨vr⟩.
The trajectories used in our calculations were not strictly aimed at the positions of the spacecraft, so that our results are averages over some region in the vicinity of the spacecraft. We estimated the size of this region by listing the limits in latitude of the points at which theflux was calculated during the run of the code. For the case of 30 to 40 nm dust (the peak region), we found the values of 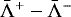 between 2° and 4°. For the 100 to 140 nm particles, the values were between 1° and 8° near the perihelion and 5° and 12° in the distant part of the orbit of PSP.
between 2° and 4°. For the 100 to 140 nm particles, the values were between 1° and 8° near the perihelion and 5° and 12° in the distant part of the orbit of PSP.
We also estimated the weighted average deviation from the spacecraft latitude (Eq. (A.4)) and found it to be of the order of 1° for the 30 to 40 nm dust (where a large number of trajectories were employed) and up to 3° for the 100 to 140 nm case. For a simple calculation with no subdivision of the Λ interval, the deviation was 3°–5.5° (100–140 nm dust).
References
- Bale, S. D., K. Goetz K., Harvey, P. R., et al. 2016, Space Sci. Rev., 204, 49 [Google Scholar]
- Czechowski, A., & Kleimann, J. 2017, Ann. Geophys., 35, 1033 [Google Scholar]
- Czechowski, A., & Mann, I. 2010, ApJ, 714, 89 [Google Scholar]
- Czechowski, A., & Mann, I. 2011, ApJ 732, 127 [Google Scholar]
- Czechowski, A., & Mann, I. 2012, The Solar System: Discoveries and Interpretations, eds., I. Mann, N. Meyer-Vernet, & A. Czechowski (Berlin: Springer), 2012 [Google Scholar]
- Czechowski, A., & Mann, I. 2018, A&A 617, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grün, E., Zook, H. A., Fechtig, H., Giese, R. H. 1985, Icarus, 62, 244 [Google Scholar]
- Ishimoto, H. 2000, A&A, 362, 1158 [NASA ADS] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [Google Scholar]
- Kimura, H., & Mann, I. 1998, ApJ, 499, 454 [Google Scholar]
- Krivov, A., Kimura, H., & Mann, I. 1998, Icarus 134, 311 [Google Scholar]
- Lavraud, B., Fargette, N., Reville, V., et al. 2020, ApJ, 894, L19 [Google Scholar]
- Malaspina, D. M., Szalay, J. R., Pokorny, P., et al. 2020, ApJ 892, 115 [Google Scholar]
- Mann, I. 1992, A&A, 261, 329 [NASA ADS] [Google Scholar]
- Mann, I., & Czechowski, A. 2005, ApJ 624, L125 [Google Scholar]
- Mann, I., Krivov, A., & Kimura, H. 2000, Icarus, 146, 568 [Google Scholar]
- Mann, I., Murad, E., & Czechowski, A. 2007, Planet. Space Sci., 55, 1000 [Google Scholar]
- Mann, I., Meyer-Vernet, N., & Czechowski, A. 2014, Phys. Rep. 536, 1 [Google Scholar]
- Mann, I., Kimura, H., Biesecker, D. A., et al. 2004, Space Sci. Rev., 110, 269 [Google Scholar]
- Mann, I., Nouzak, L., Vaverka, J., et al. 2019, Ann. Geophys. 37, 1121 [Google Scholar]
- Minato, T., Kohler, M., Kimura, H., Mann, I., & Yamamoto, T. 2004, A&A, 424, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mukai, T. 1981, A&A, 99, 1 [NASA ADS] [Google Scholar]
- Page, B., Bale, S. D., Bonnell, J. W., et al. 2019, ApJS, 246, 51 [Google Scholar]
- Plane, J. M., Feng, W., & Dawkins, E. C. 2015, Chem. Rev., 115, 4497 [Google Scholar]
- Popova, O. 2004, Earth Moon Planets, 95, 303 [Google Scholar]
- Rietmeijer, F. J. M., Della Corte, V., Ferrari, M., Rotundi, A., & Brunetto, R. 2016, Icarus, 266, 217 [Google Scholar]
- Stamm, J., Czechowski, A., Mann, I., Baumann, C., & Myrvang, M. 2019, A&A, 626, A107 [EDP Sciences] [Google Scholar]
- Szalay, J. R., Pokorný, P., Bale, S. D., et al. 2020, ApJS, 246, 27 [Google Scholar]
- Vondrak, T., Plane, J. M. C., Broadley, S., & Janches, D. 2008, Atmos. Chem. Phys., 823 [Google Scholar]
- Wehry, A., & Mann, I. 1999, A&A, 341, 296 [NASA ADS] [Google Scholar]
- Wilck, M., & Mann, I. 1996, Planet. Space Sci., 44, 493 [Google Scholar]
- Zaslavsky, A., Meyer-Vernet, N., Mann, I. et al. 2012, J. Geophys. Res. 117, 5102 [Google Scholar]
- Zook, H. A., & Berg, O. E. 1975, Planet. Space Sci., 23, 183 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Production rates of 30–40 nm and 100–140 nm nanodust particles in the circumsolar dust disk assumed in the calculations. |
| In the text | |
 |
Fig. 2 Two samples of trajectories of 30–40 nm dust with β = 0.163, projected onto the heliocentric distance-heliographic latitude plane (the r,λ plane). The magnetic field is positive in the northern hemisphere and negative in the southern hemisphere (defocusing configuration). The crosses mark the daily positions of the spacecraft during the second orbit. The diamonds show the upper and lower limits in latitude for each of the two samples. The initial latitudes are between −12° and 12° (Czechowski & Mann 2012). Only a small fraction of trajectories encounter the orbit of the spacecraft. |
| In the text | |
 |
Fig. 3 Similar to Fig. 2, but for the 100–140 nm dust with β = 0.751. All trajectories shown start from the southern hemisphere with initial latitudes between −12° and −(4/33)° (the trajectories starting from the northern hemisphere are not shown). The orbit of PSP is now within the region crossed by one of the trajectory groups. |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but for the 30–40 nm dust with high β = 0.901 corresponding to the cometary material. A high radiation pressure force reduces the poloidal drift; however, the impacts on more distant parts of the orbit of PSP would be rare. |
| In the text | |
 |
Fig. 5 Average speed relative to PSP (solid line, diamonds) and the average velocity components: radial (dotted line, triangles), latitudinal (dashed, squares), and azimuthal (dotted-dashed, x signs) of 30–40 nm particles with β = 0.163 that encounter PSP along the second orbit. The symbols show the averages weighted by the radial flux (first method, the peak region). Lines show the averages obtained by using the latitudinal flux (second method). See Sect. 3and Appendix A for details. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but for the 100–140 nm particles (β = 0.751) that encounter PSP along the second orbit. |
| In the text | |
 |
Fig. 7 Comparison of calulated fluxes to PSP observations. The solid line shows the calculated flux of 100 to 140 nm particles assuming Q/m = 10−7 e∕mp and β = 0.751 (asteroidal dust material). The simulated flux values were adjusted to the impact rate observed at the perihelion, assuming a spacecraft cross section of 3 × 104 cm2. |
| In the text | |
 |
Fig. 8 Comparison of calculated fluxes to PSP observations. The solid line shows the estimated flux of 30 to 40 nm particles relative to PSP, assuming Q/m = 10−6 e∕mp and β = 0.163. To agree with the observed impact rate at the perihelion, the calculated flux had to be multiplied by a factor of 4.5 × 104 cm2. We note thelow flux intensity away from the peak. |
| In the text | |
 |
Fig. 9 Comparison of calculated fluxes of neutral dust to PSP observation. The solid line shows the fluxof 100–140 nm chargeless particles with beta = 1.79, multiplied by a factor of 4.8 × 104 cm2. The dashed line is for beta = 0.751 with the multiplication factor 3.7 × 104 cm2. |
| In the text | |
 |
Fig. 10 Cumulative flux relative to PSP of the dust with the radii above 100 nm (solid line) along the second orbit compared to the observed impact rate. The dotted lines (in the order from top to bottom) show the contributions of the dust with sizes above 140, 200, 300, 400, and 500 nm, respectively. The fluxes were rescaled by a common factor equal to 1.9 × 104 cm2. |
| In the text | |
 |
Fig. 11 Cumulative flux relative to PSP of the dust with the radii above 30 nm (solid line) along the second orbit compared to the observed impact rate. The dotted lines (in the order from top to bottom) show the contributions of the dust with sizes above 140, 200, 300, 400, and 500 nm, respectively. The fluxes were rescaled by a common factor equal to 0.65 × 104 cm2. |
| In the text | |
 |
Fig. 12 PSPimpact rates (diamonds) and the normalised cumulative fluxes relative to PSP of charged dust with the radii above 30 nm (dashed line) and above 100 nm (solid line), shown in a logarithmic plot as functions of the heliocentric distance along the orbit of PSP. Both incoming (the upper branch) and outgoing parts of the orbit are shown. The PSP impact rates and the flux of the dust above 100 nm size approximately follow the 1/r2 law as for the case of free expansion, while the flux of the dust between 30 and 100 nm is steeper in the peak region. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.