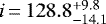| Issue |
A&A
Volume 651, July 2021
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 31 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202039993 | |
| Published online | 02 July 2021 | |
Catalogue of exoplanets accessible in reflected starlight to the Nancy Grace Roman Space Telescope
Population study and prospects for phase-curve measurements
1
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin,
Hardenbergstraße 36,
10623
Berlin,
Germany
e-mail: o.carriongonzalez@astro.physik.tu-berlin.de; oscar.carrion.gonzalez@gmail.com
2
AIM, CEA, CNRS, Université Paris-Saclay, Université de Paris,
91191
Gif-sur-Yvette, France
3
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas,
4150-762
Porto, Portugal
4
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre,
4169-007
Porto, Portugal
5
Deutsches Zentrum für Luft- und Raumfahrt,
Rutherfordstraße 2,
12489
Berlin, Germany
6
Institute of Geological Sciences, Freie Universität Berlin,
Malteserstraße 74-100,
12249
Berlin, Germany
Received:
25
November
2020
Accepted:
8
April
2021
Context. Reflected starlight measurements will open a new path in the characterization of directly imaged exoplanets. However, we still lack a population study of known targets to which this technique can be applied.
Aims. We investigate which of the about 4300 exoplanets confirmed to date are accessible for the Roman Space Telescope coronagraph in reflected starlight at reference wavelengths λ = 575, 730, and 825 nm. We carry out a population study and also address the prospects for phase-curve measurements.
Methods. We used the NASA Exoplanet Archive as a reference for planet and star properties and explored the effect of their uncertainties on the exoplanet detectability by applying statistical arguments. We defined a planet as Roman-accessible on the basis of the inner and outer working angles of the instrument and its minimum planet-to-star contrast (IWA, OWA, and Cmin). We adopted three plausible configurations for these technical specifications, labeled pessimistic, intermediate, and optimistic. Our key outputs for each exoplanet are its probability of being Roman-accessible (Paccess), the range of observable phase angles, the evolution of its equilibrium temperature, the number of days per orbit for which it is accessible, and its transit probability.
Results. In the optimistic scenario, we find 26 Roman-accessible exoplanets with Paccess > 25% and host stars brighter than V = 7 mag. This population is biased towards planets more massive than Jupiter, but also includes the super-Earths tau Cet e and f, which orbit near the habitable zone of their star. Thirteen planets are part of multi-planetary systems. Three of these planets have known transiting companions, which offers opportunities for a contemporaneous atmospheric characterization. The intermediate and pessimistic scenarios yield ten and three Roman-accessible exoplanets, respectively. We find that inclination estimates (e.g. with astrometry) are required to refine the detectability prospects.
Conclusions. A science phase of the coronagraph instrument has a remarkable potential for characterizing the atmospheres of exoplanets that cannot be studied with other techniques.
Key words: catalogs / planets and satellites: detection / planets and satellites: fundamental parameters / planets and satellites: gaseous planets / planets and satellites: terrestrial planets
© ESO 2021
1 Introduction
The population of more than 4000 exoplanets confirmed to date shows a vast diversity of worlds, many of which have no analogue in the Solar System. Yet, a large number of them, in particular those that orbit far from their host stars, are still not accessible to atmospheric characterization with the available techniques. Upcoming direct-imaging space telescopes observing at optical wavelengths will enable the investigation of cold and temperate exoplanets on long-period orbits by measuring the starlight that they reflect. The atmospheres of these planets remain largely unexplored, but they may represent a key piece in the exoplanet diversity puzzle by helping to trace the history and evolution of the planets.
The Nancy Grace Roman Space Telescope1 (Spergel et al. 2013; the Roman Telescope for short) will be the first space-borne facility designed to directly image exoplanets in reflected starlight. Planned for launch in the mid-2020s, it will be equipped with an optical coronagraph and a set of filters for imaging and spectroscopy for technology demonstration (Akeson et al. 2019; Mennesson et al. 2020). This instrument will be able to characterize far-out non-transiting exoplanets, most of them presumably discovered in radial velocity (RV) searches. For long-period planets, reflected starlight measurements will provide insight into atmospheric layers that are lower than those probed during transit, which are masked by refraction (García Muñoz et al. 2012; Misra et al. 2014). Probing deep down in the atmosphere will be particularly relevant in the search for biosignatures (Rauer et al. 2011), which is a main goal of future direct-imaging missions targeting Earth-like exoplanets, such as LUVOIR2 (Bolcar et al. 2016)or HabEx3 (Mennesson et al. 2016).
The question of which exoplanets will be observable by the Roman Telescope and next-generation direct-imaging space telescopes istimely. Answering it will provide technical context for future designs, will motivate new and follow-up RV and astrometric measurements, and will encourage modellers to build tools with which the prospective spectra can be interpreted. Understanding this population of exoplanets will help plan the observations and select the most interesting targets. Several works have addressed the possible science outcome of direct-imaging missions and discussed potential criteria to define observation strategies (e.g. Traub et al. 2014; Brown 2015; Greco & Burrows 2015; Kane et al. 2018; Lacy & Burrows 2020; Stark et al. 2020).
For instance, Traub et al. (2014) studied the detection yield of different coronagraph architectures proposed for the WFIRST-AFTA mission based on a population of over 400 confirmed RV exoplanets, assuming circular orbits and sky-projected orbital inclinations i = 60°. Depending on the specific coronagraph architecture, the predictions of that study resulted in detection yields between 0 and 31 exoplanets. Brown (2015) also analysed over 400 RV exoplanets that lack an inclination determination and tried toinfer this value from simulated direct-imaging measurements to constrain the true masses of the planets. This study concluded that the uncertainties in the orbital parameters may prevent an accurate estimate of i. Kane et al. (2018) computed the maximum angular separation between planet and star (Δθmax) for a subsetof 300 RV exoplanets. They identified the planets with the largest Δθmax and estimated their orbital position and uncertainty as of January 1, 2025. For exoplanets with incomplete orbital information, Kane et al. (2018) assumed an inclination i = 90°, an eccentricity e = 0, or argument of periastron ω = 90° when the corresponding parameter was missing. However, they did not consider other factors affecting the detectability, such as the planet-to-star contrast ratio (Fp ∕F⋆). Greco & Burrows (2015) studied the change in Fp∕F⋆ with the orbital configuration of an exoplanet and its position on the orbit. They found that the contrast is indeed a major limitation for the detectability of direct-imaging exoplanets in reflected starlight.
Focusing on thermal emission rather than reflected starlight, and with the aim of specifying possible targets for the Roman Telescope, Lacy & Burrows (2020) provided a list of 14 known self-luminous planets and brown dwarf companions that might be observable in the optical wavelength range. These objects will have higher contrasts than mature planets at the same orbital distance. Although their study discusses the prospects of observing a reflected-light component in the spectra of such objects, their masses, temperatures, and orbital distances in practice limit the possible observations of these targets to primarily thermal emission.
Our first goal in this work is to determine which of the currently confirmed exoplanets might be observable with the Roman Telescope in reflected starlight. For planets whose orbital solution is not completely known, we compute the likelihood of the exoplanet to be accessible based on a statistical analysis rather than assuming fixed values for the unconstrained parameters. Our second goal is to understand the main properties of the population of known exoplanets that will potentially be detectable with the Roman Telescope. We compare this subset to the whole population of confirmed exoplanets as well as to those that have been observed in transit. In this way we outline how direct-imaging space missions will contribute to completing the larger picture of exoplanet diversity.
In addition, we explore the possibility of measuring the phase curve of these exoplanets. To do this, we compute the planet-star-observer phase angles (α) that would be observable and the corresponding uncertainties for each planet. Optical phase-curve observations have proven valuable to constrain the atmospheric properties of Solar System planets (e.g. Arking & Potter 1968; Mallama et al. 2006; García Muñoz et al. 2014; Dyudina et al. 2016; Mayorga et al. 2016) and their energy budget (e.g. Pollack et al. 1986; Li et al. 2018). Optical phase curves have also been used to investigate the atmospheres of transiting exoplanets and infer their thermal properties and the presence of clouds (e.g. Demory et al. 2013; Angerhausen et al. 2015; Esteves et al. 2015; García Muñoz & Isaak 2015; Hu et al. 2015). According to recent theoretical investigations (Nayak et al. 2017; Damiano et al. 2020), observing at multiple phases will help improve the characterization of directly imaged exoplanets in reflected starlight. Remarkably, no previous work has addressed the feasibility and limitations of such optical phase-curve measurements for the confirmed exoplanets, which is essential for prioritizing the best targets for atmospheric characterization.
Finally, we discuss the benefits of constraining the orbital inclination by means of astrometric measurements or dynamical stability studies. We do so by comparing the detectability prospects if i is assumed constrained or unconstrained for a selection of exoplanets with available estimates of i. Future data releases from the Gaia mission (Perryman et al. 2001; Gaia Collaboration 2016) and ensuing enhanced astrometry will strengthen these synergies.
The paper is structured as follows. In Sect. 2 we describe the general conditions under which an exoplanet would be accessible. Section 3 contains the definition of the orbital geometry and the parameters determining the position andbrightness of an exoplanet. In Sect. 4 we outline the dataset of planet and star properties we used and the assumptions we adopted. We present our results in Sect. 5 and discuss the observational prospects for a selection of particularly interesting targets more thoroughly in Sect. 6, as well as the implications for their atmospheric characterization. Section 7 contains the summary and conclusions.
2 Direct imaging of exoplanets. Technical requirements
The technique of direct imaging applied to exoplanets relies on suppressing the light from their host stars with optical devices such as coronagraphs or starshades. In this way, the faint planetary point source can be distinguished from the stellar glare. As the star is masked, a certain region around it is also masked. This region is defined by the inner working angle (IWA) and prevents thedetection of planets at smaller star-planet angular separations. Coronagraphs also have an outer working angle (OWA) thatsets an outer limit to the observable region.
Another factor that affects the detectability of exoplanets is the minimum contrast (Cmin) of the instrument. The planet needs to be bright enough to be distinguished from background noise. The usual way to quantify the planet brightness is through the contrast ratio between the flux from the planet and that from the star at a certain wavelength λ and observing condition, given by
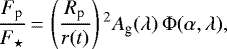 (1)
(1)
where Rp is the planet radius, r is the star-planet distance at the orbital position being considered, and α is the corresponding phase angle. Ag is the geometrical albedo of the exoplanet, and Φ is its normalized scattering phase law. Both Ag and Φ depend on the properties of the planetary atmosphere. These properties are discussed in more detail in Sect. 3.
From this perspective, the limitations set by the IWA, OWA, and Cmin shape the population of exoplanets that can be directly imaged. For instance, hot and ultra-hot short-period planets orbit too close to their host star and thus inside the IWA of any realistic coronagraph, which means that they cannot be detected. In turn, exoplanets on long-period orbits and inclinations close to face-on may fall outside the OWA during their whole orbit, which prevents them from being observed. In addition, the planet-to-star contrast decreases as the planet-star distance increases, and observing planets in reflected starlight will therefore become progressively difficult for the longer-period planets. This is particularly important for small exoplanets as the number of photons reflected by them scales with the planet cross section.
In this work, we consider the mission design of the Roman Telescope as envisioned in Spergel et al. (2015), with a telescope diameter of D = 2.4 m. It will be equipped with a coronagraph instrument (CGI) including an optical hybrid Lyot coronagraph and a shaped pupil coronagraph (Trauger et al. 2016) as a technology demonstrator for future direct-imaging missions targeting Earth-like planets. The original design aimed at a minimum planet-to-star contrast ratio Cmin of about 10−9 after post-processing (Spergel et al. 2015; Douglas et al. 2018). More recent expectations according to the Roman Telescope at IPAC (Roman-IPAC) website4 aim for Cmin of about 2–3 × 10−9 at a moderate signal-to-noise ratio (S∕N) = 5.
At the time of writing, only one spectroscopy filter, centred at 730 nm, and two imaging filters, centred at 575 and 825 nm, are planned for full commissioning. However, other filters that are not officially supported will fly with the coronagraph and might be commissioned for science operations if the three-month technology demonstration phase is successful and a potential science phase is funded (Akeson et al. 2019). The three currently official observing modes according to the Roman-IPAC website are the imaging mode N (IWA = 3 λ∕D, OWA = 9.7 λ∕D, Cmin = 2.94 × 10−9), the spectroscopy mode (IWA = 3 λ∕D, OWA = 9.1 λ∕D, Cmin = 2.2 × 10−9), and the imaging mode W (IWA = 5.9 λ∕D, OWA = 20.1 λ∕D, Cmin = 1.95 × 10−9). The latter will mainly be devoted to observations of debris discs (Akeson et al. 2019).
As these figures and the Cmin requirement will likely evolve as the mission design progresses, we will adopt three possible configurations of IWA, OWA, and Cmin for the exoplanet observing modes (Table 1). We define a pessimistic scenario with an IWA = 4 λ∕D, OWA = 8 λ∕D, and Cmin = 5 × 10−9, an intermediate scenario with an IWA = 3.5 λ∕D, OWA = 8.5 λ∕D, and Cmin = 3 × 10−9, and an optimistic scenario with an IWA = 3 λ∕D, OWA = 9 λ∕D, and Cmin = 1 × 10−9. These are not officially bounded scenarios, and different performances of the instrument (e.g. worse than our pessimistic scenario) cannot be ruled out. However, the cases proposed herein are representative of a plausible range of performances within the CGI capabilities considered realistic at this point. Table 2 summarizes the available CGI filters and corresponding IWA and OWA for the optimistic scenario. Unless noted otherwise, we assume as a reference the imaging filter centred at 575 nm.
We acknowledge that additional factors will limit the detectability of exoplanets by the Roman Telescope. For instance, the most recent update on the Roman-IPAC website (January 14, 2021) states a CGI host star requirement of V ≤ 5 mag but also notes that stars with V = 6−7 could potentially be targeted. The performance of the instrument on such fainter stars is still to be determined after the technology demonstration phase. The solar or anti-solar telescope pointing at the time of the observation may also affect any proposed target list (e.g. Brown 2015), although zodiacal light will not be as determinant as in future instruments with a contrast sensitivity 10–100 times higher. This effect, however, will depend on the final launch date and mission schedule. Exo-zodiacal dust may also prevent the detection of certain targets, but this noise source will have to be analysed individually through follow-up observations of each planetary system and is not considered here.
For the sake of generality, we adopted the IWA, OWA, and Cmin at λ = 575 nm as our main detectability criteria. For exoplanets that meet these criteria, we coined the term Roman-accessible. Our current focus is the geometrical constraints for exoplanet detectability. We therefore leave the computation of the S/N that might be achieved for each Roman-accessible planet or the required integration times for future work.
Plausible configurations of CGI exoplanet observing modes we considered.
3 Theoretical setting: planet detectability throughout the orbit
In this section, we introduce the equations for the trajectory of a planet in the three-dimensional space and the evolution of Δθ, α, and Fp ∕F⋆ with time. We base the description of the planet orbit on Hatzes (2016). Figure 1 sketches the geometry and main elements of the orbit and is based on Fig. 1.36 in Hatzes (2016), with additional information specific to the reference axes.
For a general elliptic orbit, the distance between planet and star at each orbital position is given by
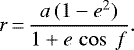 (2)
(2)
Here, e is the eccentricity, a is the semi-major axis, and f is the true anomaly. A more thorough description of the orbital equations and parameters can be found in Appendix A.
The orbit can be given in a three-dimensional space with the host star at the origin, the X and Y axes defining the plane of the sky, and Z oriented away from the observer. The three coordinates of the planet position vector rp are
![\begin{equation*}\begin{array}{r@{\,}c@{\,}l} X&=&r\, \cos\,(\omega_{\textrm{p}}+f) \\[3pt] Y&=&r\, \cos\, i\, \sin\,(\omega_{\textrm{p}}+f) \\[3pt] Z&=&r\, \sin\, i\, \sin\,(\omega_{\textrm{p}}+f), \end{array} \end{equation*}](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq3.png) (3)
(3)
where i is the orbital inclination and ωp is the argument of periastron of the planet. The longitude of ascending node is assumed Ω = 0 here without loss of generality.
3.1 Angular separation
The sky-projected distance between planet and star is given by
 (4)
(4)
When the stellar system is located at a distance d from the observer, the apparent angular separation is
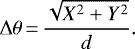 (5)
(5)
3.2 Observed phase angles
The phase angle α is the planetocentric angle between the directions to the star and to the observer (see Fig. 1). It can be computed at each orbital position from the dot product of the reversed planet position vector (− rp) and a unit vector in the direction of the observer (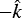 , as d ≫ r). With the components of rp defined in Eq. (3),
, as d ≫ r). With the components of rp defined in Eq. (3),
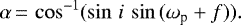 (6)
(6)
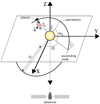 |
Fig. 1 Sketch of the orbital geometry and graphical definition of the planet-star-observer phase angle α for a planet at a certain position on its orbit. |
3.3 Scattering and planet-to-star contrast
To compute the brightness of the planet at each orbital position, we substitute the expressions given above for r and α into Eq. (1). We assume a Lambertian scattering phase law for the planet,
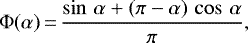 (7)
(7)
and a geometrical albedo Ag = 0.3. Both Ag and Φ(α) are assumedto be wavelength-independent and to represent the reflecting properties of the planet over the operational spectral range of the Roman Telescope.
Our assumed albedo provides a reasonable representation of the outer planets in the Solar System (Karkoschka 1994, 1998). Other worksinvestigating the prospects of measuring reflected starlight of exoplanets have also assumed or predicted values of Ag between 0.3 and 0.5 for Neptune and Jupiter analogues (e.g. Cahoy et al. 2009, 2010; Traub et al. 2014; Greco & Burrows 2015). Higher values of Ag will potentially increase the number of exoplanets exceeding the Cmin of the instrument, and vice versa.
The Lambertian scattering phase law is a pragmatic approximation to the scattering of planetary atmospheres. It has frequently been applied in studies that planned the science outcome of reflected-starlight observations of exoplanets (e.g. Stark et al. 2014; Guimond & Cowan 2018). At small phase angles, the Lambertian function yields brighter values than other models such as isotropic or Rayleigh-like scattering. The results under a Lambertian assumption may differ slightly from those obtained with other phase laws. Nevertheless, the scattering properties of a planet in reality depend on the specifics of its atmosphere, which are unknown a priori.
3.4 Time dependence of the orbital position
The relation of the true anomaly and time (t) can be derived from Kepler’s equation (Appendix A).
For an exoplanet with orbital period P and time of periastron passage tp,
![\begin{equation*}\frac{t-t_{\textrm{p}}}{P}\,{=}\,\frac{1}{2\,\pi} \left[ 2\, \textrm{arctan}\left(\sqrt{\frac{1-e}{1+e}}\, \tan\frac{f}{2} \right) - e\,\frac{\sin\,f\, \sqrt{1-e^2}}{1+e\, \cos\,f} \right] .\end{equation*}](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq9.png) (8)
(8)
This equation combined with Eqs. (2), (5), and (6) yields the planet-star distance, angular separation, and phase angle, respectively, at a given time. Leaving aside Ω and tp, which are not important here (Appendix A), the planet orbit is specified by five parameters, namely a, i, ωp, e, and P.
4 Building a complete set of confirmed exoplanets
We downloaded the complete set of confirmed exoplanets from the NASA Exoplanet Archive5 (Akeson et al. 2013), which we used as our main source of known planets and corresponding planet-star properties. As of September 16, 2020 it contains 4276 confirmed planets. For specific targets, complementary information was obtained from the original references, from correspondence with the authors of those references, or from other resources such as the Extrasolar Planets Encyclopaedia (Schneider et al. 2011). We refer to this compilation that is mainly based on the NASA Exoplanet Archive as our input catalogue (Table D.1).
4.1 Completing missing orbital information
Not all of the Keplerian elements are known or listed in the input catalogue for each of the confirmed exoplanets. When any orbital parameter is missing, we needed to make additional assumptions in order to compute the orbital solution. For 246 exoplanets, a is missing, but P as well as the masses of the star (M⋆) and the planet (Mp) are available. For 124 of these exoplanets, P is missing, but a, M⋆, and Mp are available. In these cases, we computed the missing value by means of Kepler’s third law.
A significant number of exoplanets (2513) still lacks information on Mp or Mp sin i. For these, we approximated M⋆ + Mp ≈M⋆, which results in a negligible underestimation of a for planetary mass objects (Stevens & Gaudi 2013). No information is available on at least two of the three critical parameters in Kepler’s third law (M⋆, P, and a) for 119 exoplanets. This prevented us from including them in our study.
When the values of the orbital inclination or the argument of periastron were not available in the NASA Exoplanet Archive, we assigned them random values assuming that the possible orbital orientations are isotropically distributed with respect to the observer. We therefore assumed cos(i) and ωp to be distributed uniformly over the intervals [ − 1,1] and [0, 2π], respectively.
4.1.1 Note of caution about ωp
There is no homogeneous convention in the literature to report the argument of periastron. This has been noted previously (e.g. Brown 2015; Xuan & Wyatt 2020), but stands out as a particularly relevant issue for our work and for the direct imaging of RV planets. In some cases, the reported ω refers to the argument of periastron of the planet (ωp) as it orbits around the system barycenter, while in others, it refers to the argument of periastron of the star (ω⋆). There is a shift of 180° between ωp and ω⋆ (ωp = ω⋆ + 180°) (Perryman 2011). In addition, the assumed location of the observer with respect to the + Z axis and the definition of the origin for the argument of periastron may also introduce additional 180°−shifts in ω.
The lack of a homogeneous convention and the fact that it is not always stated how the reported ω is defined potentially complicate a systematic analysis as proposed in this work. We verified that both the NASA Exoplanet Archive and the Extrasolar Planets Encyclopaedia quote for each planet the ω given in the original reference without assessing the actual definitions used in them6.
The value of ω has no effect on the range of angular separations over the orbit (see Eq. (5)), but it does affect the position of an exoplanet at a given time (Eq. (3)), its phase angle (Eq. (6)), and therefore the value of Fp ∕F⋆. ω will also affect the probability that a planet will transit its host star (see Sect. 4.3). As the design of direct-imaging missions and the corresponding target selection progress, it would be desirable to have clearly defined conventions for all the reported orbital parameters. We therefore urge efforts towards a standardization of the data available in the exoplanet catalogues and towards the compilation of self-consistent catalogues (e.g. Hollis et al. 2012) that are updated with new discoveries. We discuss in Appendix B the effect that mistakenly using the value of ω⋆ instead of ωp has on the detectability of exoplanets and on the prospects for measuring their optical phase curves.
We generally assumed that the ω reported by the NASA Exoplanet Archive corresponds to the argument of periastron of the star, which is the prevailing convention for RV (Perryman 2011; Hatzes 2016). For all the exoplanets that we find to be Roman-accessible (see Sect. 5), we searched in the corresponding reference papers or contacted the authors to confirm the values of ω as quoted in Table D.1. Extending this case-by-case inspection to the 4276 confirmed exoplanets is beyond the scope of this paper.
4.1.2 Eccentricity distribution
For exoplanets that lack a measured eccentricity, we drew its value from a uniform distribution in e ∈ [0, 1). This is a simplification of the reality, which suggests that short-period exoplanets tend to have low eccentricities while long-period planets show broader e distributions (Winn & Fabrycky 2015). However, empirically derived distributions of e might be affected by observational biases, especially for long-period planets, whose orbits are more challenging to characterize and for which the discovery numbers are relatively low. For reference, uniform distributions of e have been used in previous works that analysed the detection yield of direct-imaging missions (e.g. Stark et al. 2014).
We note, however, that this is not the only approach considered in the literature. For instance, Steffen et al. (2010) used both Rayleigh and exponential probability distributions to describe the eccentricity, and Wang & Ford (2011) used a distribution with both uniform and exponential components. Kipping (2013) described the observed dispersion of e with two beta probability distributions for short- and long-period planets (P < 382.3 and >382.3 days, respectively). In Sect. 5.1 we compare the e distributions of exoplanets with short and long periods as described by Kipping (2013) with that of the Roman-accessible exoplanets. Future studies with access to a larger sample of long-period planets will result in refined representations of the e distribution.
4.2 Planet radius
The value ofRp can only be measured for transiting exoplanets. It may be estimated from thermal emission measurements, for instance with young, self-luminous exoplanets, but these estimates are by definition model dependent (e.g. Mawet et al. 2019; Lacy & Burrows 2020). The population of exoplanets suitable for direct imaging in reflected starlight will therefore generally lack an estimate of Rp.
To assign a value of Rp to the planets in our input catalogue, we use the mass-density relationship from Hatzes & Rauer (2015) for giant planets, defined in term of Jupiter’s mass (MJ) as those with 0.3MJ < Mp < 65 MJ:
![\begin{equation*}\log_{10}(\rho)\, [\textrm{g\,cm}^{-3}]\,{=}\,(1.15\,{\pm}\,0.03)\, \log_{10}(M_{\textrm{p}}/M_J) - (0.11\,{\pm}\,0.03) \end{equation*}](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq10.png) (9)
(9)
Eq. (9) is therefore valid for planets more massive than Saturn, approximately. A priori, we cannot rule out that lower-mass exoplanets will be detectable (Robinson et al. 2016; see also Sect. 5.1). Thus, for planets less massive than 120 Earth masses (M⊕), we use the mass-radius relationships in Otegi et al. (2020). They distinguish between rocky and volatile-rich exoplanets, and obtain two different mass-radius relationships depending on the planet density (ρ):
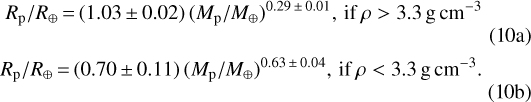
Although Otegi et al. (2020) note that the Mp –Rp statistics suggest a lower limit of 5 M⊕ for volatile-rich planets, we extend the mass-radius relationship to 3.1 M⊕ in order to achieve a continuous coverage in Mp. This causes that some exoplanets with ρ > 3.3 g cm−3 (those with 3.1 M⊕ < Mp < 5 M⊕) are modelled in our case with Eq. (10b).
In summary, for planets with Mp < 3.1 M⊕ we use the rocky Mp –Rp relationshipin Eq. (10a), for 3.1M⊕<Mp < 0.36 MJ we use the volatile-rich relationship in Eq. (10b) and for Mp > 0.36 MJ we use the giant-planet relationship in Eq. (9). In all cases, we account for the quoted uncertainties to estimate Rp (see Sect. 4.5). Figure 2 shows these relationships together with all of the confirmed exoplanets with measurements of both Mp and ρ in the NASA Exoplanet Archive. For reference, we added the Solar System planets to the diagram. We find an overall good fit to the observed population of both Solar System and extrasolar planets.
4.3 Transit requirements
Exoplanets that are suitable for both direct imaging and transit spectroscopy will become prime targets for atmospheric characterization (Carrión-González et al. 2020; Stark et al. 2020). Because they are of special interest, we computed the transit probability (Ptr) of the Roman-accessible exoplanets (Sect. 5).
Based on Eq. (4), the eclipses (transits and occultations) take place when the planet-star distance in the sky plane 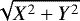 is at a local minimum. Following Winn (2010), we considered that transits occur at inferior conjunctions (i.e. when X = 0 and the planet is in front of the star). With our viewing geometry (Fig. 1), this means
is at a local minimum. Following Winn (2010), we considered that transits occur at inferior conjunctions (i.e. when X = 0 and the planet is in front of the star). With our viewing geometry (Fig. 1), this means
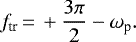 (11)
(11)
The impact parameter is defined as the distance between the centres of the planet and the star, projected onto the plane of the sky and normalized to the stellar radius. Substituting Eqs. (11) into (4), the impact parameter at transit is given by
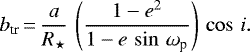 (12)
(12)
The condition for a full transit to be observed is therefore
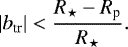 (13)
(13)
We used R⋆ − Rp to exclude grazing transits from the analysis because they only provide a lower limit for Rp. For systems without an R⋆ determination in the input catalogue, we extracted its value from the Planetary Systems database in the NASA Exoplanet Archive. Preferentially, we used the value from the source referencing Gaia DR2 (Gaia Collaboration 2018), or when this was not available, from the source referencing the Revised TESS Input Catalog (Stassun et al. 2019). When R⋆ was not available in any of these sources either, we were unable to compute the transit probability for that system.
The mass of a planet discovered in RV cannot be unlimitedly high, and this sets a limit on the range of physically realistic inclinations for a measured Mp sin i. In this respect, Stevens & Gaudi (2013) noted that the prior distribution of possible Mp affects the prior distribution of i, thereby affecting the calculated transit probabilities. For generality, we did not consider any prior information on the Mp distribution.
 |
Fig. 2 Mass-radius relationships used in this work compared to the confirmed exoplanets that have a known value of both Mp and ρ (grey dots). Planets for which only Mp sin i is known are not included. Solid black line shows the mass-density relationship for giant exoplanets, obtained from Hatzes & Rauer (2015). The dashed blue line and dotted red line show the mass-density relationship for low-mass exoplanets with volatile-rich and with rocky composition, respectively, obtained from the Mp –Rp equations inOtegi et al. (2020). Coloured squares mark the rocky planets of the Solar System (Mercury in black, Venus in orange, Earth in green, and Mars in red). Coloured dots mark the giant planets of the Solar System (Jupiter in orange, Saturn in yellow, Uranus in light blue, and Neptune in dark blue). |
4.4 Planetary equilibrium temperature
The equilibrium temperature of a planet (Teq) provides an indication of its possible atmospheric structure and the potential conditions for habitability. For each orbital position r, we computed Teq by assuming a Bond albedo (AB) of 0.45 and applying
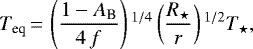 (14)
(14)
where the factor f accounts for the heat redistribution of the planet. We assumed f = 1, which is consistent with rapid rotators (Traub & Oppenheimer 2010).
Teq does not affect the detectability criteria in our method. Because it is important for atmospheric modelling, however, we computed Teq throughout the planetary orbit. In future work, it could be used to investigate the temporal variability of the atmosphere and to estimate the emitted radiation from the planet.
Summary of the parameters used to compute the exoplanet detectability.
4.5 Statistical analysis of detectability
For a given orbit specified by its Keplerian parameters, we assessed whether the detectability criteria for IWA, OWA, and Cmin described in Sect. 2 were met at any orbital position. We repeated this for each of the pessimistic, intermediate, and optimistic scenarios described in Table 1. To describe the orbit, we divided it into 360 points with a step in the true anomaly Δf = 1°, which is related to time through Eq. (8). We checked for a few selected cases a posteriori that the adopted Δf step affects our findings only negligibly. The planetary and orbital parameters we used are summarized in Table 3.
For each parameter from Table 3, we considered the upper and lower uncertainties quoted in the NASA Exoplanet Archive. We also considered the uncertainties in the coefficients of the mass-radius relationships in Eqs. (9) and (10). All these uncertainties were taken into account when we produced random realizations of the planet orbits and corresponding planet-to-star contrasts. For each planet, we accounted for all the uncertainties simultaneously and computed 10 000 independent realizations of the orbital and non-orbital parameters. When the value of a specific parameter was not available in the NASA Archive but instead had to be estimated for example through Kepler’s third law or the Mp -Rp relationships of Eqs. (9) and (10), our treatment ensured that the uncertainties were properly propagated. We used this bootstrap-like method to derive statistical conclusions (Press et al. 2007) for properties of interest such as Δθ, α, and Fp ∕F⋆.
Some of the parameters in Table 3 are indeed correlated through the specific techniques with which they were originally estimated, and hence their uncertainties are not independent. We also note that the uncertainties in the NASA Archive are extracted from references with no homogeneous criteria in the statistical treatment of the data. A re-evaluation of the orbital parameters to obtain their joint confidence intervals is beyond the scope of this paper, and for simplicity, we sampled each of them independently from uniform probability distributions between the quoted uncertainty limits.
We considered an exoplanet to be Roman-accessible if the detectability criteria defined by the IWA, OWA, and Cmin were met over at least one point in the numerically discretized orbit of at least one of the 10 000 independent orbital realizations. The probability of a planet to be Roman-accessible (Paccess) is given by the number of orbital realizations in which the exoplanet is accessible, compared to the total of 10 000 realizations. The transit probability (Ptr) was computed as the fraction of orbital realizations in which the condition in Eq. (13) was met. For a particular orbit, the number of days for which the planet remains observable (tobs) can be computed with Eq. (8) by time-integration along the orbit. We computed this for each accessible orbital realization to derive a statistical distribution of tobs. We inferred the median value of this distribution and upper and lower uncertainties corresponding to the 16th and 84th percentiles, which is equivalent to ±1σ for Gaussian errors. In addition, we computed the interval of observable phase angles (αobs) with Eq. (6) for each accessible orbit. We refer to the minimum and maximum phase angles (αobs(min), αobs(max)), together with the corresponding ± 1σ uncertainties. We emphasize that the distributions of tobs and αobs are based only on the accessible orbital realizations. This results in intrinsically biased statistics because the null detections are not accounted for. However, we opted for these definitions to have metrics that specifically describe the accessible orbits because αobs is not defined in a non-accessible orbit, for instance. The corresponding Paccess quantifies the bias introduced in these metrics.
For each planet in the input catalogue, this statistical method produces posterior distributions for each of the sampled parameters in Table 3. With this, we created an output catalogue (Table D.2) with the resulting median values of each parameter and their corresponding uncertainties.
The above definition of Paccess is flawed, however, because some planets have very low associated values of this metric. It is difficult to justify a future observational effort for these planets. In order to keep our findings useful for target prioritization, in what follows we only consider planets that have Paccess > 25% in the optimistic CGI configuration (Table 1). In addition, we restrict our analysis to targets orbiting stars brighter than V = 7 mag, according to the updated CGI possible performances. These additional vetting criteria determine the population of planets studied in Sects. 5 and 6. For reference, the complete list of Roman-accessible exoplanets including those with Paccess < 25% or V > 7 mag is kept in the input and output catalogues (Tables D.1 and D.2).
5 Results: Roman-accessible exoplanets
We next identify the Roman-accessible exoplanets that meet the additional vetting criteria (Paccess > 25%, V < 7 mag) in the optimistic CGI configuration. We compare their properties to the complete set of confirmed exoplanets, as well as to those that have been observed in transit (Sect. 5.1). Afterwards, we describe their overall detectability conditions (Paccess, αobs, tobs, Ptr) as well as the main limiting factors (Sect. 5.2) in the different CGI scenarios from Table 1. Finally, we report the equilibrium temperatures computed for these planets and the variation in Teq throughout their orbit (Sect. 5.3).
5.1 Population analysis: subset of direct-imaging exoplanets
We analysed all confirmed exoplanets as described in Sect. 4.5 and found that 26 of the total 4276 exoplanets meet the criteria of angular separation and planet-to-star contrast for the optimistic CGI configuration, with the additional vetting criteria Paccess > 25% and V < 7 mag. The numberof planets meeting these criteria in the intermediate and pessimistic scenarios drops to 10 and 3, respectively. Focusing on the optimistic scenario, we study the main properties below as listed in our input catalogue (Table D.1) of thissubset of Roman-accessible exoplanets.
Figure 3 displays for all confirmed exoplanets the semi-major axis and distance to the Earth. This shows how different discovery techniques are sensitive to different ranges of these parameters. The population of Roman-accessible exoplanets is composed of RV-discovered objects, with the exception of HD 100546 b, which was discovered in imaging (Quanz et al. 2015). The existence of this protoplanet with 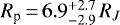 is controversial, however, as indicated in the NASA Archive. Although the transit method is the most fruitful technique so far in terms of thenumber of discovered planets (76% of the total), none of them is Roman-accessible. New transit missions with long baselines that focus on nearby stars such as TESS or PLATO (Ricker et al. 2014; Rauer et al. 2014) are expected to yield additional transiting planets accessible to direct imaging (Stark et al. 2020). Other planets may be accessible in thermal emission to the Roman Telescope (Lacy & Burrows 2020). Computing the contribution of thermal emission for each confirmed exoplanet, which depends on the age of the system and the evolutionary models assumed, is beyond the scope of this work.
is controversial, however, as indicated in the NASA Archive. Although the transit method is the most fruitful technique so far in terms of thenumber of discovered planets (76% of the total), none of them is Roman-accessible. New transit missions with long baselines that focus on nearby stars such as TESS or PLATO (Ricker et al. 2014; Rauer et al. 2014) are expected to yield additional transiting planets accessible to direct imaging (Stark et al. 2020). Other planets may be accessible in thermal emission to the Roman Telescope (Lacy & Burrows 2020). Computing the contribution of thermal emission for each confirmed exoplanet, which depends on the age of the system and the evolutionary models assumed, is beyond the scope of this work.
Long-period planets typically have higher eccentricities than short-period ones, and this affects the median eccentricity of the ensemble of Roman-accessible planets. Figure 4 displays the statistics of orbital period and eccentricity (when reported in the NASA Archive). The top panel shows the total number of planets in different ranges of orbital periods. Correspondingly, the right panel shows the normalized distributions of e, such that the integral below the histogram is equal to one for the selected bin size7. The key informative property of the normalized distributions is their shape, enabling a more evident comparison of populations with different total counts. We find that the Roman Telescope will be able to detect a relatively large proportion of highly eccentric planets. The median value of this distribution is e = 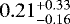 . In comparison, the total population of confirmed exoplanets with a measurement of e has a median eccentricity of e =
. In comparison, the total population of confirmed exoplanets with a measurement of e has a median eccentricity of e = 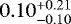 and the subset of those that have been observed in transit (even when discovered by other methods), e =
and the subset of those that have been observed in transit (even when discovered by other methods), e = 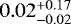 . The observed e distribution for the Roman-accessible exoplanets behaves similarly to that of the long-period planets defined by Kipping (2013). However, this remains a modest sample, and more long-period exoplanets therefore need to be followed up to understand the biases in the observed e distributions.
. The observed e distribution for the Roman-accessible exoplanets behaves similarly to that of the long-period planets defined by Kipping (2013). However, this remains a modest sample, and more long-period exoplanets therefore need to be followed up to understand the biases in the observed e distributions.
Figure 5 shows that the statistics of known exoplanets is dominated by giant planets because they are generally easier to detect. This bias is particularly noticeable in the Roman-accessible population, however. Because most of these exoplanets lack an estimate of i and we only know their minimum mass (Table D.1), some of these objects may actually be at the boundary between giant exoplanets and brown dwarfs. Interestingly, we also find that the Roman Telescope may be able to detect tau Cet e and f, both with minimum masses of 3.9 M⊕ and thus in the super-Earth to mini-Neptune mass regime (see Sect. 5.2). The ongoing efforts to discover low-mass exoplanets around nearby stars (Quirrenbach et al. 2016; Pepe et al. 2021) as well as the future development of direct-imaging missions with lower Cmin and smaller IWA are expected to reduce this observational bias.
Host-star properties such as the spectral type or the mass may be of interest to test hypotheses about the formation and evolution of an exoplanet (Laughlin et al. 2004; Boss 2006). The spectral type also determines the chemistry of the star, which affects the plausible structure and composition of its exoplanets (Santos et al. 2017). Furthermore, the age of the star and its spectral type set constraints on the stellar activity, which affects the possible exoplanetary atmospheres.
We find that the median value of the metallicity of host stars of Roman-accessible exoplanets is 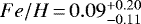 . This shows a mild but not significant bias towards super-solar metallicities (Fig. 6) compared to the total population of confirmed exoplanets, with
. This shows a mild but not significant bias towards super-solar metallicities (Fig. 6) compared to the total population of confirmed exoplanets, with 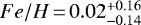 . The bias is consistent with the observed trend of giant planet hosts to be more metal rich than low-mass planet hosts(Santos & Buchhave 2018). The stars hosting Roman-accessible planets are currently dominated by G-type stars, similar to the total population of confirmed planet hosts (Fig. 7). In turn, this figure showsan under-representation of F, K, and M stars for the Roman-accessible exoplanets in comparison to the complete population. This lack of K and M stars in the Roman-accessible targets is mainly caused by the V < 7 mag threshold. Ifthe condition on the stellar magnitude were omitted, we would obtain an overabundance of M-type stars hosting Roman-accessible targets (see Table D.2).
. The bias is consistent with the observed trend of giant planet hosts to be more metal rich than low-mass planet hosts(Santos & Buchhave 2018). The stars hosting Roman-accessible planets are currently dominated by G-type stars, similar to the total population of confirmed planet hosts (Fig. 7). In turn, this figure showsan under-representation of F, K, and M stars for the Roman-accessible exoplanets in comparison to the complete population. This lack of K and M stars in the Roman-accessible targets is mainly caused by the V < 7 mag threshold. Ifthe condition on the stellar magnitude were omitted, we would obtain an overabundance of M-type stars hosting Roman-accessible targets (see Table D.2).
We also find that the stars hosting Roman-accessible planets show no clear bias to a particular stellar age, whereas in the total set of planet-hosting stars the bias favouring ages of 3–4 Gyr is clear. The Roman-accessible planets in the youngest systems are HD 100546 b (0.005 Gyr), discovered in imaging, and eps Eri b (0.5 Gyr) and HD 62509 b (0.980 Gyr), which were discovered by RV. Figure 7c shows similar M⋆ distributions in the direct-imaging subset and in the total population of host stars. The lack of low-mass stars is again due to the V < 7 mag threshold that rules M stars out from the target list. However, we do not find any Roman-accessible exoplanet orbiting a star more massive than 2 M⊙. This may partly be caused by the difficulties of searching for RV planets around early-type stars. In future work, we will compare these trends in stellar properties with those from self-consistently computed stellar catalogues such as the SWEET-Cat (Santos et al. 2013).
These findings show that the population of Roman-accessible exoplanets does indeed differ from the general population of confirmed exoplanets or from those observed in transit. These differences are partly affected by the sensitivity of different discovery techniques to reveal suitable targets. Reflected-starlight measurements will therefore enable the atmospheric characterization of exoplanets that are not accessible with other techniques.
 |
Fig. 3 Confirmed exoplanets that are Roman-accessible in the optimistic CGI configuration, with Paccess > 25% and orbiting stars brighter than V = 7 mag (solid stars). For comparison, we show the confirmed exoplanets for which we know d and can derive a as explainedin Sect. 4.1 (semi-transparent dots). The colour code indicates the corresponding discovery technique (with which the planet was identified first), as detailed in the legend. “Others” refers to all other possible discovery techniques considered in the NASA Exoplanet Archive. HD 100546 b is the only Roman-accessible exoplanet discovered in imaging, although its existence is marked as controversial in the NASA Archive. |
 |
Fig. 4 Eccentricity and orbital period for all confirmed exoplanets (grey dots in the main panel), those that have been observed in transit (regardless of whether they were discovered by that method; orange dots) and those that are Roman-accessible in the optimistic CGI configuration, with Paccess > 25% and V < 7 mag (green dots). We only consider those planets for which e is known and P can be derived as explained in Sect. 4.1. The black line shows the limit between short- and long-period exoplanets (P = 382.3 days) as defined in Kipping (2013) (see Sect. 4.1.2). Top panel: P distribution of all confirmed exoplanets (grey), those observed in transit (orange line), and those that are Roman-accessible (semi-transparent green). Right panel: normalized distribution of e such that it shows the relative frequency instead of the total count of planets. The same colour code applies as for the top panel. The green bars are semi-transparent (so that the grey distribution underneath can also be seen), so that the overall graph becomes either darker or lighter green depending on whether the two histograms overlap. For reference, we include the eccentricity for the subsets of short- and long-period exoplanets in Kipping (2013; red and blue lines, respectively). |
 |
Fig. 5 Distribution of mass and orbital period for all confirmed exoplanets (semi-transparent grey), those observed in transit (semi-transparent orange), and those that are Roman-accessible in the optimistic CGI configuration, with Paccess > 25% and V < 7 mag (green).The plot considers planets for which either Mp or Mp sin i are known without distinction. |
 |
Fig. 6 Distribution of stellar metallicity and semi-major axis of the planet for all confirmed exoplanets (semi-transparent grey), those observed in transit (semi-transparent orange), and those that are Roman-accessible in the optimistic CGI configuration, with Paccess > 25% and V < 7 mag (green). |
 |
Fig. 7 Properties of the stars hosting Roman-accessible planets. Panel a: total count of planet-hosting stars of each spectral type. Panel b: normalized distributions of the stellar age. Panel c: normalized distributions of the stellar mass. Grey bars with diagonal ‘/’ hatching correspond to the total population of confirmed exoplanets. Over-plotted semi-transparent green bars with dotted hatching correspond to exoplanets that are Roman-accessible in the optimistic CGI configuration, with Paccess > 25% and V < 7 mag. We note that these parameters are not available for all of the confirmed exoplanets in the NASA Exoplanet Archive. The spectral type is available for all of the 24 stars hosting Roman-accessible planets, the stellar age is known for 13 of them, and the metallicity for 16 stars. Panel d: count of Roman-accessible-planet host stars of different optical magnitudes in each CGI configuration. Green bars with dotted hatching correspond to the optimistic scenario. Semi-transparent yellow bars with diagonal ‘\’ hatching correspond to the intermediate scenario. Red stars mark the three stars hosting Roman-accessible planets in the pessimistic scenario. |
5.2 General detectability conditions
Some key findings (Paccess, αobs, tobs) for the detectability of the up to 26 Roman-accessible exoplanets with Paccess > 25% and V < 7 mag are listed in Table 4 for all the CGI scenarios. For reference, we also add the corresponding findings at λ = 730 and 825 nm, which are the effective wavelengths of the other two commissioned filters for the coronagraph. At these wavelengths, we assumed an albedo of Ag = 0.3 and accounted for the modified IWA and OWA. The transit probability of these planets is listed in the output catalogue (Table D.2). Figure 8 (left panel of each diagram) shows the tracks of contrast and angular separation of the random orbital realizations in our analysis. It also shows (right panel) the corresponding distributions of αobs for the optimistic CGI scenario, which indicate the observable phase angles that occur more often. As we have discretized the orbits evenly in the true anomaly (rather than in time), these distributions do not translate directly into time spent at any given interval of phase angles.
At our reference wavelength λ = 575 nm, the number of Roman-accessible exoplanets in the optimistic, intermediate, and pessimistic CGI scenarios is 26, 10, and 3, respectively (Table 4). HD 219134 h, 47 UMa c, and eps Eri b are the only planets that would be accessible in all three scenarios with Paccess > 25%. Generally, Paccess decreases at longer wavelengths because the IWA increases with λ, masking a larger region around the host star. Particular cases such as that of eps Eri b or HD 219134 h show an increase in Paccess at longer λ. These are planets that reach large angular separations and at λ = 575 nm, orbit partly outside the OWA of the coronagraph (Fig. 8). Hence, their Paccess increases at longer wavelengths because both the IWA and OWA move outwards.
The transit probability of the Roman-accessible exoplanets is low in all cases (Table D.2), with the maximum being Ptr = 2.29% for HD 62509 b. This super-Jupiter (Mp sin i = 2.3 MJ) orbits the nearby (d = 10.34 pc) K0 III giant Pollux. With an orbital period of 589.6 days, HD 62509 b may require observations spanning multiple years to confirm its possible transits. However, improving the orbital characterization with RV measurements could constrain the time of inferior conjunction and reduce the required baseline. This star was targeted for 27 days in TESS Sector 20, but its high optical magnitude (V = 1.14) poses a problem with photometric saturation. If this planet were found to transit and were also imaged (Paccess = 73.84% in the optimistic CGI scenario), it would be a unique opportunity to characterize its atmosphere by combining the two techniques. An astrometric determination of its inclination, which should be near 90° for the planet to transit, would help refine its transit probability.
In Fig. 8 the exoplanets with larger uncertainties in their orbital parameters (see Table D.1) generally show larger scatter in their Fp ∕F⋆–Δθ tracks. Figure 8 also shows that planets in the sub-giant regime (i.e. those with Mp< 0.36 MJ) experience large increases of Fp∕F⋆ in a small number of realizations (see e.g. tau Cet e, HD 192310 c, and tau Cet f in Fig. 8). This corresponds to orbital configurations with inclinations i ≈ 0 or 180° that result in high values of Mp and in turn Rp (Eq. (10b)). These unlikely configurations produce the outlying tracks in Fig. 8.
Generally, phase angles both before and after quadrature (α < 90° and α > 90°, respectively) can be observed at λ = 575 nm in the optimistic CGI configuration (Table 4 and Fig. 8). This is important to better constrain some of the optical properties of the atmosphere that may be more sensitive to the scattering angles (Nayak et al. 2017; Carrión-González et al. 2020; Damiano et al. 2020). The minimum value of αobs is in most cases not smaller than about 30°. The main limitation to measuring values of α closer to full phase is the IWA. In this sense, eps Eri b is an outlier that can only be detected at small phase angles in the observing mode that we considered (see Sect. 6.3). Correspondingly, the maximum αobs is not larger than 110° for most of these exoplanets. Typically, the planet is not bright enough at large phase angles and its contrast drops below the specified Cmin. In the intermediate and pessimistic CGI scenarios, only phase angles smaller than quadrature are generally observed (Table 4). This means that the IWA and Cmin are key factors that limit the detectability windows. This also explains why tobs and the range of αobs typically both decrease at longer wavelengths (Table 4).
We defined the interval of observable phase angles as Δαobs = αobs(max) − αobs(min) and computed the corresponding upper and lower uncertainties. Table 5 shows the planets with the largest Δαobs at our reference λ = 575 nm, which a priori might become prime targets for phase-curve measurements in each CGI scenario. Figure 9 shows the computed ranges of Δαobs for each exoplanet against the total time they are observable, tobs, for the optimistic CGI configuration. This information is potentially relevant for finding optimal targets for phase-curve measurements. For instance, HD 219134 h shows a large variation of α in the optimistic configuration (Δαobs = 94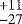 ) taking place in a detectability window of 2.5 yr (tobs = 917
) taking place in a detectability window of 2.5 yr (tobs = 917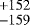 days), the shortest value of tobs of the planets of Table 5. Furthermore, this planet has particularly large intervals of αobs in the intermediate and pessimistic scenarios (Δαobs = 41
days), the shortest value of tobs of the planets of Table 5. Furthermore, this planet has particularly large intervals of αobs in the intermediate and pessimistic scenarios (Δαobs = 41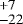 and 33
and 33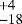 deg, respectively).
deg, respectively).
 |
Fig. 8 Detectability conditions for the Roman-accessible exoplanets. In each left panel, the solid black lines in the Fp ∕F⋆ -Δθ diagram correspond to independent orbital realizations. For the sake of clarity, only 1000 of the total 10 000 realizations are shown. Horizontal dashed lines indicate Cmin and vertical dashed lines show the IWA and OWA of the CGI at λ = 575 nm for the optimistic (green), intermediate (yellow), and pessimistic (red) configurations (Table 1). Regions in green are the detectability windows in the optimistic CGI configuration at this wavelength, and the green histograms in the right panels show the posterior distributions of αobs for this scenario. |
Detectability conditions for the Roman-accessible exoplanets with Paccess > 25% and V < 7 mag for each of the CGI scenarios.
Exoplanets with the widest ranges of αobs at λ = 575 nm for each of the CGI configurations.
Multi-planetary systems
Thirteen of the optimistic 26 Roman-accessible exoplanets are part of stellar systems with other confirmed planetary companions.Table 6 lists these multi-planetary systems, with the number of exoplanets that they host and the number of these that are Roman-accessible in each CGI scenario. Three of these exoplanets also show some of the largest Δαobs in Table 5: HD 219134 h, 47 UMa c, and HD 190360 b.
We find that in the optimistic CGI scenario, the systems 47 UMa and tau Cet have more than one Roman-accessible exoplanet. In the case of 47 UMa, planets b and c are accessible with Paccess = 100%. We note that 47 UMa d also has a marginal Paccess = 9.41% in this scenario (Table D.2). The system tau Cet stands out because planets e and f (Mp sin i ~ 4 M⊕) are Roman-accessible (Paccess = 87.75 and 26.74%,respectively). In Sect. 6.1 we further discuss the prospects of observing tau Cet e and f.
Table 6 also shows three systems for which a transiting inner exoplanet is known to exist. This offers the possibility of studying both the outer planet in direct imaging and the inner planet with transmission spectroscopy. Such scenarios are potentially valuable because we may gain insight into the system as a whole and into the processes that may have led to the final arrangements. In the optimistic scenario, this is the case of 55 Cnc d, with the transiting ultra-short period planet e, pi Men b, with a transiting super-Earth (planet c), and HD 219134 h, with two transiting super-Earths (b and c). These systems are discussed in more detail in Sect. 6.2.
 |
Fig. 9 Range of observable phase angles against the time the planet is accessible per orbit at λ = 575 nm in the optimistic CGI configuration. The colour of the markers indicates the Paccess of the exoplanet. Horizontal and vertical error bars correspond to the upper and lower uncertainties of tobs and Δαobs, respectively. |
5.3 Equilibrium temperatures of the Roman-accessible planets
In order to facilitate future atmospheric modelling of the Roman-accessible exoplanets, we computed their Teq at each orbital position by means of Eq. (14). In our output catalogue (Table D.2) we quote the range of Teq and the corresponding uncertainties, computed for each planet in the 10 000 orbital realizations (regardless of whether it is detectable). In addition, for some planets we report under Teq(obs) the range of equilibrium temperatures that correspond only to the orbital positions that are Roman-accessible (Table 7). This provides a first estimate of the possible variations that the planetary atmosphere might undergo during the time that it remains accessible.
Figure 10 shows the evolution of Teq with time for the accessible orbits of the planets that have an estimate of e in the NASA Archive (all but HD 100546 b). Planets on eccentric orbits experience large changes of Teq(obs) and therefore are prime targets in which to search for atmospheric variability. On the other hand, this would complicate an eventual atmospheric characterization by multiple-phase observations.
The planets with the largest changes in Teq(obs) (ΔTeq(obs)) for each CGI configuration are listed in Table 7. In the optimistic scenario, ups And d and pi Men b experience changes of about 30 K during the time that they remain accessible, which is about a year in both cases. HD 114613 b remains observable for about two years, and we find that it undergoes a 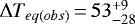 K. Both psi 1 Dra B b and HD 190360 b have a tobs of about four years, and in this time, they show variations in Teq of about 40 K. These variations in Teq during the time that they are observable will likely trigger variability in the cloud coverage of their atmospheres (Sánchez-Lavega et al. 2004). These five planets have Paccess = 100% and therefore appear to be suitable targets in which to search for atmospheric variability with the Roman Telescope. In more conservative CGI scenarios, however, the observable variability of Teq is significantly reduced. In these cases, only HD 190360 b in the intermediate CGI scenario shows a noteworthy ΔTeq(obs) (17
K. Both psi 1 Dra B b and HD 190360 b have a tobs of about four years, and in this time, they show variations in Teq of about 40 K. These variations in Teq during the time that they are observable will likely trigger variability in the cloud coverage of their atmospheres (Sánchez-Lavega et al. 2004). These five planets have Paccess = 100% and therefore appear to be suitable targets in which to search for atmospheric variability with the Roman Telescope. In more conservative CGI scenarios, however, the observable variability of Teq is significantly reduced. In these cases, only HD 190360 b in the intermediate CGI scenario shows a noteworthy ΔTeq(obs) (17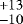 K). The remaining planets in the intermediate or pessimistic scenarios have ΔTeq(obs) smaller than 10 K, which is likely unable to trigger atmospheric variability during the time that they are observable.
K). The remaining planets in the intermediate or pessimistic scenarios have ΔTeq(obs) smaller than 10 K, which is likely unable to trigger atmospheric variability during the time that they are observable.
Figure 11 shows the median value of the computed Teq distributions against the median value of the Mp resulting from our statistical exercise for the optimistic CGI scenario (Table D.2). This shows that the population of exoplanets probed with the Roman Telescope will be remarkably different from the population that has been explored with previous techniques. This population of Roman-accessible planets will include Jupiter and Saturn analogues. On the other hand, analogues of Uranus and Neptune are still beyond reach for the Roman Telescope. We note that although some planets in this range of Teq and Mp can be found in our output catalogue (Table D.2), they orbit stars fainter than V = 7 mag and are thus excluded from our analysis. Interestingly, we find Roman-accessible planets with Teq comparable to that of the Earth such as the super-Earth tau Cet e, the giant planet gam Cep b, or the super-Jupiter bet Pic c. bet Pic c is a young exoplanet in a system of about 18.5 Myr (Miret-Roig et al. 2020), and thus Eq. (14) used here will severely underestimate its effective atmospheric temperatures. On the other hand, both gam Cep b and tau Cet e are mature systems with ages of 6.6 Gyr (Torres 2006) and 5.8 Gyr (Tuomi et al. 2013), respectively.
Multi-planetary systems that are Roman-accessible in each CGI configuration.
Exoplanets with the widest ranges of Teq(obs) at λ = 575 nm for each of the CGI configurations.
6 Discussion of selected targets
We next elaborate on eight targets that show new study cases in exoplanet science. The exercise explores possibilities for their characterization in reflected starlight, but also limitations arising from uncertainties on their orbital solutions or the brightness of their host stars, for example. First, we focus on the two super-Earths tau Cet e and f, which orbit near the habitable zone (HZ) of their star. Then, we study the cases of pi Men b, 55 Cnc d and HD 219134 h, planets in multi-planetary systems whose known innermost companions are accessible to atmospheric characterization through transit spectroscopy. We also analyse the gas giant eps Eri b, whose orbital solution remains somewhat controversial, demonstrating the potential of the Roman Telescope to characterize its orbit. Finally, we discuss the candidate super-Earths Proxima Centauri c (Proxima c) and Barnard’s Star b (Barnard b) as key targets for the next generation of directly imaged exoplanets.
In addition, estimates or reasonable guesses of the orbital inclination are available for most of these exoplanets. This affects their prospects for direct imaging. For these cases, we compare their detectability with the scenario in which i is unconstrained. In this way, we show the relevance of multi-technique strategies for exoplanet characterization, an approach that will become more common with upcoming Gaia data releases.
 |
Fig. 10 Evolution of Teq with time for the accessible orbits of the Roman-accessible exoplanets with a constrained value of e (Table D.1). Green indicates the orbital positions that are accessible in the optimistic CGI scenario. For the sake of clarity, only one of each ten orbital realizations is shown. |
 |
Fig. 11 Median Teq against the median Mp for each Roman-accessible planet in the optimistic CGI configuration as computed in our 10 000 orbital realizations. The colour of the markers indicates the Paccess of the exoplanet. Horizontal and vertical error bars correspond to the upper and lower uncertainties of Mp and Teq, respectively.Magenta letters in the diagram indicate the Solar System planets Venus (V), Earth (E), Jupiter (J), Saturn (S), Uranus (U), and Neptune (N). |
6.1 Two super-Earths near the habitable zone
tau Cet is a nearby G8 V star with an effective temperature T⋆ = 5344 K (Santos et al. 2004). It hosts four super-Earths with minimum masses in the range 1.75−3.93 M⊕ (Tuomi et al. 2013; Feng et al. 2017). Based on HIPPARCOS astrometry, Kervella et al. (2019) reported an anomaly in the tangential velocity of the star that is attributable to a possible outer giant companion. We find that the two outermost confirmed exoplanets, tau Cet e and f, are Roman-accessible in the optimistic CGI scenario with Paccess of about 88 and 27%, respectively. In the intermediate and pessimistic CGI scenarios, the probabilities drop below 13% for both planets (Table D.2).
For a planet with a mass of 5 M⊕, Feng et al. (2017) estimated a conservative HZ between 0.68 and 1.26 AU and an optimistic HZ between 0.55 and 1.32 AU. This mass is consistent with the Mp ≈ 4.84 M⊕ obtained from our statistical method for tau Cet e and f (Table D.2). Together with our obtained Rp ≈ 1.87 R⊕, this places them in the super-Earth regime if defined as Rp < 2 R⊕ and Mp < 10 M⊕8. Accounting for the uncertainties in the values of a (Table D.1), tau Cet e and f orbit within the optimistic HZ and slightly outside the conservative HZ. We note that if additional planets in this mass range were found inside the HZ of the system, as suggested by Dietrich & Apai (2021), they would likely also lie in the accessible region of the Roman Telescope. These planets are quite unique to potentially understand habitability beyond the Earth.
tau Cet hosts a debris disc with a total mass of about 1 M⊕ (Greaves et al. 2004) that might hinder the direct imaging of the planets in the system. Based on Herschel images, Lawler et al. (2014) reported that the disc is inclined by i = 35° ± 10° from face-on. They also found that the disc inner edge is most likely located between 2 and 3 AU (555 and 833 milliarcseconds, respectively), but did not rule out solutions between 1 and 10 AU. The disc outer edge is at about 55 AU. MacGregor et al. (2016) observed this system with the Atacama Large Millimeter/submillimeter Array (ALMA) and estimated an inner edge of the disc at 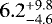 AU. This is consistent with recent findings by Hunziker et al. (2020) based on observations in the 600−900 nm range with the SPHERE/ZIMPOL instrument at the Very Large Telescope (VLT). Based on their non-detection of extended sources around tau Cet, Hunziker et al. (2020) concluded that either the disc is too faint or its inner edge lies at a distance farther than about 6 AU. Overall, the ALMA and SPHERE/ZIMPOL observations suggest that the debris disc will not interfere with the prospective imaging of the exoplanets, but further measurements are needed to confirm it. We find that if the disc inner edge is at 2 AU, it remains outside the optimistic OWA of the Roman Telescope for λ = 575 nm, but it could be detected at λ = 730 nm and 825 nm (see Table 2). The disc is not detectable in any of the exoplanet-devoted CGI filters of any CGI scenario considered here if the inner edge lies farther out than 2.3 AU.
AU. This is consistent with recent findings by Hunziker et al. (2020) based on observations in the 600−900 nm range with the SPHERE/ZIMPOL instrument at the Very Large Telescope (VLT). Based on their non-detection of extended sources around tau Cet, Hunziker et al. (2020) concluded that either the disc is too faint or its inner edge lies at a distance farther than about 6 AU. Overall, the ALMA and SPHERE/ZIMPOL observations suggest that the debris disc will not interfere with the prospective imaging of the exoplanets, but further measurements are needed to confirm it. We find that if the disc inner edge is at 2 AU, it remains outside the optimistic OWA of the Roman Telescope for λ = 575 nm, but it could be detected at λ = 730 nm and 825 nm (see Table 2). The disc is not detectable in any of the exoplanet-devoted CGI filters of any CGI scenario considered here if the inner edge lies farther out than 2.3 AU.
The debris disc may negatively affect the habitability of these planets if they are frequently subject to large impacts. On the other hand, the existence of abundant debris from such impacts may have favoured the formation of exomoons, which could be searched for in direct imaging (Cabrera & Schneider 2007). Furthermore, the disc can be used for a first guess on the inclinations of the planets because systems hosting debris discs and multiple planets are frequently coplanar (Watson et al. 2011; Greaves et al. 2014). Figure 12 shows the orbital realizations for tau Cet e and f, following our general method for planets without a constraint on inclination. We also plot configurations for which i is coincident with the disc orientation. Table 8 compares the detectability results for tau Cet e and f in all CGI scenarios if no prior knowledge of the inclination is assumed and if the orbits of the planets are assumed coplanar with the disc. In the optimistic CGI configuration, an estimate of 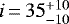 deg results for both planets in statistically higher values of Paccess. This corresponds to an increase in tobs, while the ranges of αobs remain similar in both cases. Similar conclusions are found for tau Cet e in the intermediate CGI configuration, whereas in this configuration, the small Paccess for tau Cet f is reduced to zero when i is constrained (Table 8). tau Cet f remains inaccessible for any CGI configuration out of the best-case optimistic scenario. This reduction of Paccess when
deg results for both planets in statistically higher values of Paccess. This corresponds to an increase in tobs, while the ranges of αobs remain similar in both cases. Similar conclusions are found for tau Cet e in the intermediate CGI configuration, whereas in this configuration, the small Paccess for tau Cet f is reduced to zero when i is constrained (Table 8). tau Cet f remains inaccessible for any CGI configuration out of the best-case optimistic scenario. This reduction of Paccess when 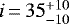 , in comparison to the case of unconstrained i, also happens for both planets in the pessimistic CGI configuration. In the case of tau Cet f, the reason is that if Cmin increases, only the orbital realizations with i close to 0 or 180° (and hence very large Mp and Rp) would be accessible. If i is constrained within 25 and 45°, these orbital realizations will not reach the Cmin threshold. For tau Cet e, the large IWA in the pessimistic CGI scenario is the main limitation for the detectability of the planet.
, in comparison to the case of unconstrained i, also happens for both planets in the pessimistic CGI configuration. In the case of tau Cet f, the reason is that if Cmin increases, only the orbital realizations with i close to 0 or 180° (and hence very large Mp and Rp) would be accessible. If i is constrained within 25 and 45°, these orbital realizations will not reach the Cmin threshold. For tau Cet e, the large IWA in the pessimistic CGI scenario is the main limitation for the detectability of the planet.
In order to determine the orbital parameters that have a stronger effect on the detectability of these planets, we carried out a sensitivity study that is included in Appendix C. There, we fixed all orbital parameters a, e, i, and ωp, leaving one at a time free to vary, and studied how Paccess and αobs changed. For tau Cet e, we find (Fig. C.1) that Paccess does not change significantly; the largest effect is due to variations in ωp. In the case of tau Cet f, i and ωp are the main parameters affecting the detectability (Fig. C.2). This sensitivity study shows the relative effects of each orbital parameter on Paccess and αobs, but the correct values of these parameters are those reported in Table 4, where all uncertainties are accounted for simultaneously.
Contamination from exozodiacal dust (exozodi) might also limit the detectability of tau Cet e and f. Ertel et al. (2020) found that exozodiacal dust levels in the HZ around nearby early- and solar-type stars are generally about three times that of the Solar System. That work concluded that these levels are low and would not impede the spectral characterization of HZ rocky planets with currentdirect-imaging mission concepts such as the WFIRST Starshade Rendezvous (Seager et al. 2019), HabEx, or LUVOIR. Ertel et al. (2020) did not detect exozodi around tau Cet and set an upper limit of 120 exozodis (i.e. 120 times that of the Solar System). Follow-up observations will help determine the actual amount of exozodi, which could also be constrained by the Roman Telescope in its observing mode devoted to disc measurements (Mennesson et al. 2019). Ertel et al. (2020) suggested multi-epoch observations as a path to distinguish between the signal from the exoplanets and that from exozodiacal dust clumps, given their different phase functions. In this respect, we find that even inthe optimistic CGI scenario, only a modest phase coverage could be achieved for tau Cet e and f (α ∈ [61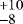 ,100
,100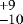 ] and [53
] and [53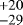 ,74
,74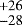 ], respectively).
], respectively).
 |
Fig. 12 Detectability of tau Cet e and f in each CGI configuration, following the same colour code as in Fig. 8. In the left panels, black lines correspond to orbital realizations without an inclination constraint. Solid red lines correspond to orbital configurations with 25° < i < 45°, coplanar with the debris disc of the system (Lawler et al. 2014). For this case, the inclination is sampled from a uniform distributionwithin the quoted limits. The green histograms in the right panels show the posterior distributions of αobs. |
Detectability of tau Cet e and f at λ = 575 nm in each CGI scenario, both without prior knowledge on the orbital inclination and assuming 25° < i <45°.
6.2 Outer companions of transiting exoplanets
The Roman Telescope will be able to characterize several exoplanets in multi-planetary systems, some of them with inner companions accessible to transmission or occultation spectroscopy. This provides unprecedented possibilities for understanding their bulk atmospheric compositions, histories, and the connection between formation, migration, and current-time architecture. Here we discuss the cases of pi Men b, 55 Cnc d and HD 219134 h as representatives of this type of exoplanets.
6.2.1 pi Men b
Planetary systems that contain a far-out Jupiter and a close-in super-Earth appear to be relatively common (Bryan et al. 2019). The mechanisms that result in such architectures remain unclear but are potentially important for understanding the origin and evolution of super-Earths. pi Men (V = 5.67 mag) is one such system. It hosts a far-out Jupiter discovered with RV (Jones et al. 2002) and a close-in transiting super-Earth discovered with photometry and RV (Gandolfi et al. 2018; Huang et al. 2018).
The outer planet, pi Men b, has also been detected in joint HIPPARCOS and Gaia astrometry (Xuan & Wyatt 2020; De Rosa et al. 2020; Damasso et al. 2020b), thereby providing constraints on its sky-projected inclination and the mutual inclination of the two planets in the system. Constraints of this type will become more usual with future releases of Gaia astrometric data. pi Men b is now known to follow an eccentric orbit that is most likely not coplanar with the orbit of the inner planet.
The super-Earth in the system, pi Men c, is accessible to in-transit atmospheric characterization (García Muñoz et al. 2020, 2021). It has been proposed that its atmosphere may not be H2 /He dominated, but rather contains large amounts of heavy gases. Rossiter-McLaughlin measurements during the transit of pi Men c have revealed that its orbital plane is misaligned with the stellar spin axis (Kunovac Hodžić et al. 2021).
Interestingly, the eccentricity and inclination of the outer planet and the orbital misalignment of the inner planet support a formation scenario in which the super-Earth is formed far from the star and migrated into its current orbit following high-eccentricity migration (Kunovac Hodžić et al. 2021). The possibility of obtaining detailed orbital information about the two planets and atmospheric information of the inner one make the pi Men system quite unique. It is of interest here that pi Men b could be directly imaged with the Roman Telescope. This will help to constrain its orbit, especially if multi-phase measurements are made. It will also enable the spectroscopic investigation of its atmosphere, which should set valuable constraints on its chemical composition (e.g. Lupu et al. 2016; Nayak et al. 2017; Carrión-González et al. 2020).
To explore the detectability of pi Men b, we compared the orbital solution given in the NASA Archive (Huang et al. 2018), which has no estimate of i, and the scenario in which i is constrained. We used an inclination of 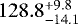 deg that results from translating the inclination angle defined in Xuan & Wyatt (2020) into our own definition in Fig. 1. The inclination is such that the angular momentum vector of the pi Men b orbit points towards the observer (Xuan, priv. comm.).
deg that results from translating the inclination angle defined in Xuan & Wyatt (2020) into our own definition in Fig. 1. The inclination is such that the angular momentum vector of the pi Men b orbit points towards the observer (Xuan, priv. comm.).
Figure 13 compares the Fp ∕F⋆-Δθ diagrams for a constrained and an unconstrained inclination. When i is constrained, 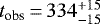 days and αobs = [70
days and αobs = [70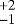 ,95
,95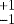 ] in the optimistic CGI scenario. This does not differ substantially from the results for the analysis with unconstrained inclination (Table 4), in which pi Men b is accessible over
] in the optimistic CGI scenario. This does not differ substantially from the results for the analysis with unconstrained inclination (Table 4), in which pi Men b is accessible over 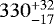 days of its 2093-day orbital period and phase angles α ∈ [69
days of its 2093-day orbital period and phase angles α ∈ [69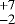 ,95
,95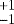 ]. Similarly, when i is constrained, the conclusions for the other CGI scenarios are comparable to those in Table 4, for which we find that the planet is only marginally accessible in the intermediate and not accessible in the pessimistic scenario. The sensitivity study in Fig. C.3 shows that the detectability of the planet does not change much if the orbital parameters vary within the uncertainties reported in the input catalogue (Table D.1). For comparison, we note that a shift of 180° in the value of ωp (as if ω⋆ were mistaken for ωp) would yield a significantly wider range of observable phase angles α ∈ [42
]. Similarly, when i is constrained, the conclusions for the other CGI scenarios are comparable to those in Table 4, for which we find that the planet is only marginally accessible in the intermediate and not accessible in the pessimistic scenario. The sensitivity study in Fig. C.3 shows that the detectability of the planet does not change much if the orbital parameters vary within the uncertainties reported in the input catalogue (Table D.1). For comparison, we note that a shift of 180° in the value of ωp (as if ω⋆ were mistaken for ωp) would yield a significantly wider range of observable phase angles α ∈ [42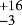 ,111
,111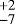 ] (see Appendix B).
] (see Appendix B).
 |
Fig. 13 As Fig. 12, but for the case of pi Men b. Solid red lines correspond to orbital configurations with
|
6.2.2 55 Cnc d
Five planets have been confirmed around 55 Cnc (V = 5.96 mag) to date (Butler et al. 1997; Marcy et al. 2002; Fischer et al. 2008; Winn et al. 2011). Only the super-Earth 55 Cnc e has been found to transit, which allowed constraining the inclination of its orbit.
Nelson et al. (2014) carried out dynamical simulations and determined that the inclination of planets b, c, d, and f, which are assumed to be coplanar in their study, likely coincides with that of planet e. They also found that the system becomes unstable if the mutual inclination between planet e and the others is between 60° and 125°. Baluev (2015) considered this an optimistic estimate and concluded that the inclination of the outer planets could not be below 30°. The NASA Exoplanet Archive quotes i = 90°, with no upper or lower uncertainties, for 55 Cnc b, c, d, and f. We manually set the inclination of these planets to i = 90 ± 60°, which is more in accordance with the conservative scenario in Baluev (2015). Hence, the values of Mp quoted in the NASA Archive for these planets become their minimum masses. In our exploration, we determined the planet masses according to the sampling of i in each realization (see Sect. 4.5).
We find that the only Roman-accessible planet in this system is 55 Cnc d, with Paccess = 100% in the optimistic CGI scenario. This is the outermost and a priori most massive planet (Mp sin i = 3.878 MJ) in the system, which appears to be a frequent architecture in multi-planetary systems (e.g. ups And, pi Men, HD 160691, and HD 219134). The detectability window spans over 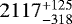 days, with a range of observable phase angles
days, with a range of observable phase angles ![$\alpha \in [30^{+ 20 }_{- 10 },84^{+ 2 }_{- 2 }]$](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq46.png) . One of the limitations in the detectability of 55 Cnc d is the IWA, which mainly affects the smaller phase angles. The value of Cmin prevents the detection of the planet as it orbits from quadrature to inferior conjunction and α increases, reducing Fp∕F⋆. In the intermediate and pessimistic CGI scenarios, the planet is below the Cmin and therefore it is not Roman-accessible.
. One of the limitations in the detectability of 55 Cnc d is the IWA, which mainly affects the smaller phase angles. The value of Cmin prevents the detection of the planet as it orbits from quadrature to inferior conjunction and α increases, reducing Fp∕F⋆. In the intermediate and pessimistic CGI scenarios, the planet is below the Cmin and therefore it is not Roman-accessible.
From the sensitivity study for this planet (Fig. C.4), we conclude that the uncertainties on the orbital parameters have no significant effect on Paccess and that i is the main parameter affecting therange of αobs. Detecting 55 Cnc d in reflected starlight will set constraints on its atmospheric structure and composition. This may help understand the possible evolution of the system and the dynamical processes that have brought 55 Cnc e to its ultra-short-period orbit of P = 0.74 days (Winn et al. 2011).
6.2.3 HD 219134 h
The K3 V star HD 219134 (V = 5.570 mag) hosts a multi-planetary system with up to six exoplanets (Motalebi et al. 2015; Vogt et al. 2015; Gillon et al. 2017). The two innermost, super-Earths b (Mp = 4.74 ± 0.19 M⊕) and c (Mp = 4.36 ± 0.22 M⊕), have been observed in transit (Motalebi et al. 2015; Gillon et al. 2017). The system also includes three mini-Neptunes (planets d, f, and g) and an outer Saturn-mass planet (h), all discovered in RV. Given the different nomenclatures used in the literature, we adopt here the names of the NASA Archive. Johnson et al. (2016) proposed that the signal attributed to planet f may be a false positive due to stellar rotation, and this planet is indeed marked as controversial in the NASA Archive. HD 219134 h, on the other hand, has been suggested to be real despite its reported orbital period of about half the 12-yr stellar activity cycle (Johnson et al. 2016).
We found that HD 219134 h is one of only three exoplanets that are Roman-accessible in all the CGI configurations considered. In all scenarios, this exoplanet also shows the largest interval of αobs, and it is therefore the most favourable target for phase-curve measurements (Table 5). Phase angles near quadrature are less likely to be observed, however, because these orbital positions tend to fall outside the OWA (see Fig. 8). An observing mode reaching larger angular separations, such as the CGI mode devoted to disc measurements (Sect. 2), may complement the observations in this region of Δθ. In the intermediate and even in the pessimistic CGI scenario, HD 219134 h would remain accessible for about 577 and 444 days, respectively. This could facilitate higher S/N observations. We also find that this planet is suitable to be observed with a broad wavelength coverage. Remarkably, its Paccess is about 90% or higher for the three CGI filters (575, 730, and 825 nm) in the optimistic, intermediate, and in the pessimistic CGI scenario (Table 4).
Recently, the evolution and current composition of HD 219134 b and c (Vidotto et al. 2018; Nikolaou et al. 2019) have been investigated. The broad phase and wavelength coverage achievable for HD 219134 h makes it a promising target for atmospheric characterization (Damiano et al. 2020). Furthermore, it can be considered one of the most reliable targets for the Roman Telescope because of its great detectability prospects in all CGI scenarios and wavelengths. The orbital parameters reported in the NASA Archive for this planet correspond to those in the discovery papers, which have not been further updated. Planning for direct-imaging observations will require a refined orbital characterization, for which additional RV campaigns are needed. Such follow-up RV measurements would also help clarify which of the reported signals in the system correspond to actual planets and which are caused by stellar activity.
 |
Fig. 14 Detectability of eps Eri b in the optimistic CGI scenario with the orbital parameters from Mawet et al. (2019; top panel) and Benedict et al. (2006; bottom panel). Left column: Fp ∕F⋆ -Δθ diagram. Yellow lines are specific to the maximum-likelihood orbital configuration providedin the corresponding reference. Middle column: the posterior distributions of αobs. Right column: variation of α with timefor each orbital realization. In this panel, green regions correspond to detectability windows for the maximum-likelihood orbit (yellow line). All orbital realizations are shown for reference in the α-t diagram (black lines), but their corresponding detectability windows are omitted. |
6.3 Prospects for confirming controversial exoplanets: eps Eri b
eps Eri b is a giant planet orbiting a young K2 V nearby star (d = 3.22 pc) with a period of about seven years, discovered in RV data by Hatzes et al. (2000). Benedict et al. (2006) combined RV and astrometry, and found an orbital solution with i = 30.1° ± 3.8° and 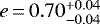 . It has since been a promising target for direct imaging given its predicted large angular separation of up to 1600 mas (Kane et al. 2018) and the interest in the atmospheric processes that could take place on a planet with such an eccentric orbit (Sánchez-Lavega et al. 2003). However, the orbital solution of this planet has remained controversial (e.g. Hollis et al. 2012), and furthermore, the existence of the planet has also been questioned (Anglada-Escudé & Butler 2012). Mawet et al. (2019) combined RV data with high-contrast direct-imaging observations at 4.67 μm, finding a RV signal consistent with a planet on a seven-year orbit but no thermal emission. They inferred a minimum age of 800 Myr, an orbital inclination i = 89° ± 42°, and an eccentricity of
. It has since been a promising target for direct imaging given its predicted large angular separation of up to 1600 mas (Kane et al. 2018) and the interest in the atmospheric processes that could take place on a planet with such an eccentric orbit (Sánchez-Lavega et al. 2003). However, the orbital solution of this planet has remained controversial (e.g. Hollis et al. 2012), and furthermore, the existence of the planet has also been questioned (Anglada-Escudé & Butler 2012). Mawet et al. (2019) combined RV data with high-contrast direct-imaging observations at 4.67 μm, finding a RV signal consistent with a planet on a seven-year orbit but no thermal emission. They inferred a minimum age of 800 Myr, an orbital inclination i = 89° ± 42°, and an eccentricity of 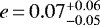 , an order of magnitude lower than the previous reference adopted as default in the NASA Exoplanet Archive. They find this solution marginally compatible with the planet being co-planar with the outer debris disc in the system, which has i = 34 ± 2° (Booth et al. 2017).
, an order of magnitude lower than the previous reference adopted as default in the NASA Exoplanet Archive. They find this solution marginally compatible with the planet being co-planar with the outer debris disc in the system, which has i = 34 ± 2° (Booth et al. 2017).
The NASA Exoplanet Archive updated on September 3, 2020 the information on eps Eri b from that provided by Benedict et al. (2006) to that by Mawet et al. (2019). The scope of our work is not to determine which of the orbital solutions is more reliable. This said, and as shown here, the update dramatically changes the prospects for detecting the planet, and demonstrates the importance of follow-up measurements, preferably with multiple techniques. Focusing on the optimistic CGI scenario, we compare both solutions in Fig. 14 and find that the solution in Benedict et al. (2006) is accessible in all of our realizations (Paccess = 100%) and produces αobs = ![$[60^{+ 3 }_{- 3 }, 107^{+ 4 }_{- 5 }],$](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq49.png) whereas the orbital solution proposed by Mawet et al. (2019) yields Paccess = 57.99% and αobs = [12
whereas the orbital solution proposed by Mawet et al. (2019) yields Paccess = 57.99% and αobs = [12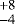 ,24
,24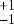 ]. These obvious differences, which are also observable in the intermediate and pessimistic CGI scenarios, have potential implications on the prospects for characterizing the exoplanet atmosphere. As a more positive note and because the ranges of αobs do not overlap, reflected-starlight observations of the planet may help determine the actual orbital solution. In both cases, we find that the OWA of the Roman Telescope is a major limitation to observing the planet. Observing modes with larger OWAs or telescope architectures more flexible in this regard (e.g. Seager et al. 2019; LIFE Collaboration 2021) will facilitate the detection of this planet and increase the interval of αobs. In our sensitivity study for the orbital solution given by Mawet et al. (2019), we find that i is the key factor affecting the detectability of this planet (Fig. C.5). Figure C.5 shows that orbital realizations with i of about 50 or 130° would remain outside the OWA for the whole orbital period, but those close to edge-on reach smaller Δθ that make the planet accessible.
]. These obvious differences, which are also observable in the intermediate and pessimistic CGI scenarios, have potential implications on the prospects for characterizing the exoplanet atmosphere. As a more positive note and because the ranges of αobs do not overlap, reflected-starlight observations of the planet may help determine the actual orbital solution. In both cases, we find that the OWA of the Roman Telescope is a major limitation to observing the planet. Observing modes with larger OWAs or telescope architectures more flexible in this regard (e.g. Seager et al. 2019; LIFE Collaboration 2021) will facilitate the detection of this planet and increase the interval of αobs. In our sensitivity study for the orbital solution given by Mawet et al. (2019), we find that i is the key factor affecting the detectability of this planet (Fig. C.5). Figure C.5 shows that orbital realizations with i of about 50 or 130° would remain outside the OWA for the whole orbital period, but those close to edge-on reach smaller Δθ that make the planet accessible.
The abundant exozodi in the system (Ertel et al. 2020) might create additional difficulties. However, observing the eps Eri system might finally confirm the existence of the planetary companion and constrain its orbital solution, either by directly imaging it or by studying planet-disc interactions. The fact that this planet remains accessible in all three CGI scenarios makes it a potential example of how high-contrast imaging with the Roman Telescope could help resolve conflicting orbital solutions.
Main planetary and stellar properties of the candidate exoplanets Barnard b and Proxima c.
6.4 Potential of direct imaging for confirming RV candidates: Barnard b and Proxima c
A space-based direct-imaging mission will be useful to confirm the existence of a number of targets that are often considered candidate exoplanets. Because of the expected duration of the possible science phase of the Roman Telescope CGI, the use of telescope time in such survey-like observations with uncertain payoff will likely not be favoured. Nevertheless, the next generation of direct-imaging space telescopes will have the search for new exoplanets as one of their goals (Gaudi et al. 2020; The LUVOIR Team 2018). In this context, we analysed the cases of Barnard b (Ribas et al. 2018) and Proxima c (Damasso et al. 2020a), two super-Earth candidates orbiting the closest planet-host stars. The main properties of these targets, which are not included in the NASA Archive of confirmed exoplanets, and the corresponding references are listed in Table 9.
We find (Fig. 15, Table 10) that both planets orbit within the optimistic Roman-accessible region of IWA, OWA, and Cmin if their orbital inclinations are assumed to be unconstrained. Barnard b is accessible in all the orbital realizations (Paccess = 100%), whereas Proxima c, with larger uncertainties on the orbital parameters, has a somewhat lower probability of Paccess = 64.84%. Furthermore, Barnard b remains accessible over about 70% of its orbital period (tobs = 167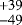 days), but Proxima c is only accessible over less than one-tenth of its orbit (tobs = 116
days), but Proxima c is only accessible over less than one-tenth of its orbit (tobs = 116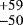 days). The range of αobs is particularly wide for Barnard b (Δαobs ≈ 85°), which may eventually help characterize the composition and structure of its atmosphere (Nayak et al. 2017; Damiano et al. 2020).
days). The range of αobs is particularly wide for Barnard b (Δαobs ≈ 85°), which may eventually help characterize the composition and structure of its atmosphere (Nayak et al. 2017; Damiano et al. 2020).
The brightness of their host stars likely prohibits the observation of these planets with the Roman Telescope. However, both stars will be within the operating range of future direct-imaging missions such as LUVOIR (The LUVOIR Team 2018). Due to its higher brightness, Barnard (V = 9.5 mag) will be a more suitable target star than Proxima (V = 11.13 mag).
In the sensitivity study for these candidates, we find that Barnard b has Paccess = 100% in all cases, and that i and e are the parameters with the largest effect on αobs (Fig. C.6). In the case of Proxima c, the parameter affecting Paccess and αobs most is i. Only the orbits with i ≈ 90° are accessible (Fig. C.6).
Proxima c is indeed accessible to astrometric characterization of its orbit with existing telescopes, which strongly affects the detectability prospects for a direct-imaging mission. Benedict & McArthur (2020) obtained i = 133 ± 1° and e = 0.04 ± 0.01 with astrometric data from Hubble Space Telescope and the SPHERE instrument at the VLT. Correspondingly, assuming a circular orbit and using Gaia data, Kervella et al. (2020) proposed two solutions: a prograde orbit with i = 152 ± 14° and a retrograde orbit with i = 28 ± 14°. We find that in all these cases, Proxima c would not be Roman-accessible because the angular separation is larger than the OWA during the whole orbit (red lines in Fig. 15).
There is a growing population of exoplanet candidates, mostly detected with RV. The examples of Barnard b and Proxima c illustrate the potential of direct-imaging missions to confirm the existence of these canditates when the appropriate orbital conditions are given.
 |
Fig. 15 As Fig. 12, but for Barnard b and Proxima c. Red lines correspond to orbital configurations of Proxima c with e < 0.05 and i ∈ [14°, 42°] or [138°, 166°], consistent with the estimates by Benedict & McArthur (2020) and Kervella et al. (2020). |
Detectability conditions for the exoplanet candidates Barnard b and Proxima c in the optimistic CGI scenario.
7 Conclusions
The Nancy Grace Roman Space Telescope will be the first space mission capable of directly imaging exoplanets in reflected starlight. The first measurements of this type could therefore be available within the decade. Designed as a technology demonstrator, it will pave the way for more ambitious direct-imaging missions such as LUVOIR or HabEx. In this work we showed its potential for several science cases, in particular for phase-curve measurements of exoplanets.
We have analysed the complete set of confirmed exoplanets in the NASA Exoplanet Archive and computed which would be Roman-accessible at 575 nm in three different scenarios of CGI performance. To do this, we compiled the planetary and stellar parameters needed to compute the evolution of the orbital position and brightness of the exoplanet (Table D.1). To account for the uncertainties on the orbital determination and other non-orbital factors, we followed a statistical approach and computed 10 000 random realizations for each exoplanet. In each realization, the values of all parameters were independently drawn from appropriate statistical distributions within their quoted upper and lower uncertainties. For the exoplanets that lack a value of orbital elements, such as e, i, or ωp, we drew their values from uniform distributions assuming an isotropic distribution of possible orbital orientations. In the cases without a value of the planet radius, we derived it by means of published Mp –Rp relationships covering a range of masses from lower than that of Mercury to 60 MJ. From the posterior distribution of Δθ or Fp∕F⋆, we derived the overall probability of the planet to be Roman-accessible, its transit probability, and the values of tobs, αobs and Teq(obs).
As of September 2020, 26 exoplanets orbiting stars brighter than V = 7 mag have Paccess > 25% in the optimistic CGI configuration. This number is reduced to 10 and 3 in the intermediate and pessimistic scenarios, respectively.Only HD 219134 h, 47 UMa c, and eps Eri b are Roman-accessible in all three scenarios. We note that our assumed scenarios do not correspond to officially expected CGI specifications, but rather to a range of plausible coronagraph performances according tocurrent predictions. For instance, the best official estimates of the IWA currently match the value in our optimistic scenario, while the official OWA is slightly less restrictive than the OWA we assume. The best official estimates of Cmin are more restrictive than the value assumed in our optimistic scenario, but are somewhat more favourable than those in our intermediate scenario (see Sect. 2). Additional factors not considered in this work will reduce the number of accessible targets, and therefore a high value of Paccess does not guarantee a detection of the planet, which will be restricted by mission schedule and final instrument performance. For reference, we list in our output catalogue (Table D.2) the up to 76 exoplanets that would be accessible in the optimistic scenario if the host-star magnitude were no limitation.
The catalogue presented here is expected to evolve as follow-up observations are performed, and will be updated in future work as more information about the mission is available. One of the next steps to be performed with our method is to simulate an optimized observing schedule for a direct-imaging telescope, including noise sources and restrictions from the mission timeline. A similar approach was discussed in Brown (2015) under the assumptions of no orbital uncertainties except for i, and Rp = RJ for all considered planets. That work concluded that successful observations of any suitable exoplanet may be restricted to windows of only a few days. Nevertheless, the detectability criteria in that work as well as the resulting target list were shaped by the science requirement of measuring Mp with a fractional uncertainty of 0.10. Relaxing this requirement will broaden the list of observable targets and their detectability windows. On the other hand, accounting for all the parameter uncertainties that we consider in our method will surely increase the uncertainties on the planning. The about 3000 exoplanets discovered between the compilation of the input catalogue in Brown (2015) and ours also increase the options for finding suitable targets as the launch of the Roman Telescope approaches.
A population study was carried out for the set of 26 Roman-accessible exoplanets in the optimistic scenario. We compared their properties with those of the complete population of confirmed exoplanets, and with the exoplanets that have been observed in transit (Sect. 5.1). As expected, we found that the subset of Roman-accessible planets is biased towards massive objects on long-period orbits with high eccentricities. We also noted a lack of F, K, and M stars in the hosts of Roman-accessible planets, caused partially by the threshold specified at V = 7 mag. Overall, this suggests that the Roman Telescope will probe a population of exoplanets that differs in various ways from those accessible to atmospheric characterization with current techniques.
In the optimistic CGI scenario, exoplanets will be accessible mainly near quadrature (α = 90°), and many of them could reach minimum values of αobs of about 30° or 40°. These phases are remarkably brighter than those generally used to estimate planet detectability and S/N, usually α = 90° or up to 60° in optimistic works (e.g. Lacy et al. 2019). This may have a favourable effect on the computation of integration times. We found several exoplanets suitable for phase-curve measurements in reflected starlight with ranges of observable phases Δαobs ≳ 70°. The primarylimitation to accessing smaller phase angles is the IWA of the coronagraph, whereas high phases will mainly be limited by the Cmin of the instrument. This effect also narrowsthe intervals of Δαobs in more conservative CGI scenarios.
Computing the range of αobs is not only useful for computing more accurate levels of S/N, but also for understanding the potential for atmospheric characterization. We have shown that in the optimistic CGI scenario, αobs could range between about 30° and 120° for some targets. The atmosphere-modelling community may use these values to study whether the atmospheric retrievals of an exoplanet would benefit from multiple observations at different phases. Analysing the effect of partial wavelength coverage on the atmospheric characterization is also ongoing theoretical work (e.g. Batalha et al. 2018; Damiano et al. 2020). Such studies will benefit from our findings on the detectability at different CGI filters (Table 4). In addition, our statistical method provides both the Teq of each planet along its orbit and the range of observable temperatures Teq(obs). Respectively, Teq and Teq(obs) are relevant parameters for modelling the structure of (exo)planetary atmospheres (e.g. Hu 2019) and for searching for atmosphericvariability.
Up to 13 of the Roman-accessible exoplanets are part of multi-planetary systems, with the systems 47 UMa and tau Cet hosting two Roman-accessible exoplanets each in the optimistic scenario. In particular, the detectability of tau Cet e and f is severely reduced in more pessimistic CGI configurations (Table D.2). Nevertheless, the possibility of observing two super-Earths inside the optimistic habitable zone of their star motivates follow-up measurements of this system before the Roman Telescope is launched.
55 Cnc d, pi Men b, and HD 219134 h are Roman-accessible planets that have a transiting inner companion. These are especially valuable targets because spectroscopic observations of both planets might be performed. There are constraints on the orbital inclination of the planets in some of these systems. For pi Men b, these constraints are based on astrometry, while for 55 Cnc d, they come from dynamical stability analyses. We showed that an estimate of i reduces the dispersion of possible orbital solutions, thereby improving the accuracy of the computed Paccess. The characterization of these outer planets in reflected starlight will set valuable constraints on the possible structure of the systems and their history.
For pi Men b, we also discussed the effect of a correct value of the argument of periastron of the exoplanet on the prospects for phase-curve measurements. The lack of a homogeneous criterion to report ω in the literature has resulted in multiple definitions that may yield inconsistent results. The main exoplanet catalogues list the ω values as reported in the original references, regardless of the definitions actually used there. Shifts in ω by 180° (the usual outcome of different definitions) do not affect the maximum angular separation. They do affect the computed phase angles, however, and therefore Fp∕F⋆ (Appendix B). The future prioritization of targets for direct-imaging missions will benefit from consistently reported values of ωp, as we do in this work.
Finally, we addressed the potential of direct-imaging measurements of confirming the existence of exoplanets that are controversial or remain candidates. We showed that eps Eri b might be accessible in reflected starlight and confirm in this way the measured RV signal. We also found the candidate super-Earths Barnard b and Proxima c to orbit in the accessible Δθ − Fp∕F⋆ region of the Roman Telescope, but they will be undetectable because their host stars are too faint. However, these examples show the relevance of determining the orbital inclination, such as in the case of Proxima c, and its effect on the detectability prospects. We conclude that in general, direct-imaging missions will strongly rely on preliminary observations with other techniques such as RV or astrometry.
Although planned as a technology demonstrator, our work here has shown some of the possibilities of the Roman Telescope coronagraph during a possible phase of science operations. It would access a population of exoplanets that has not been observed previously, which would widen our understanding of exoplanet diversity. Moreover, it would be able to perform phase-curve measurements of these planets in reflected starlight, which would provide insight into exoplanetary atmospheres that cannot be studied with other techniques.
Acknowledgements
The authors acknowledge the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets (GA 2557/1-1)”. OCG acknowledges the support of COST Action 18104 - Revealing the Milky Way with Gaia. N.C.S. acknowledges the support by FCT - Fundação para a Ciência e a Tecnologia through national funds and by FEDER through COMPETE2020 - Programa Operacional Competitividade e Internacionalização by these grants: UID/FIS/04434/2019; UIDB/04434/2020; UIDP/04434/2020; PTDC/FIS-AST/32113/2017 and POCI-01-0145-FEDER-032113; PTDC/FIS-AST/28953/2017 & POCI-01-0145-FEDER-028953. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. We thank V. Bailey for the useful information about CGI filters. For their help confirming the criteria used to determine the argument of periastron in works that were quoted in the NASA Exoplanet Archive, we thank R. V. Baluev, S. Curiel, F. Feng, D. Fischer, D. Gandolfi, A. Hatzes, D. Mawet, M. Pinamonti, I. Ribas, P. Robertson, S. Vogt, J. Wright and J. W. Xuan.
Appendix A Equations of motion
Assuming an elliptic orbit, we can define a coordinate system with x and y axes co-planar to the orbit. The x -axis is in the direction of the ellipse major axis, positive towards the orbital periastron, the y-axis is perpendicular to x, and z is perpendicular to the orbital plane. Expressed in polar coordinates with respect to an arbitrary reference direction that subtends an angle ωp with the x axis,
![\begin{equation*}\begin{array}{r@{\,}c@{\,}l} x&=&r\, \textrm{cos} f \\[3pt] y&=&r\, \textrm{sin} f \\[3pt] z&=&0. \end{array} \end{equation*}](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq54.png) (A.1)
(A.1)
ωp is referred to as the argument of periastron.
The orbit can be represented in three dimensions with a new coordinate system with an origin in the star, as shown in Fig. 1. The X-, Y -, and Z -axes form a triad such that X lies in the direction of the reference line, Y is in the reference plane, and Z is perpendicular to both. We assume that the direction to the observer is − Z. We note here that our assumption on the observer’s direction is consistent with Hatzes (2016) but differs with respect to Murray & Correia (2010) or Winn (2010), who placed the observer in + Z. A vector (x,y,z) is expressed in the new axes (X,Y,Z) by applying three rotations (Murray & Correia 2010),
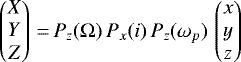
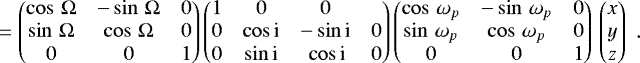 (A.2)
(A.2)
Here theangle i corresponds to the orbital inclination, and Ω is the longitude of the ascending node. The longitude of the ascending node is the angle between the reference direction and the ascending node (the point at which the orbital plane intersects the reference plane moving towards positive values of Z). Ω determines the position of the orbit in the absolute reference frame of the sky. We assume Ω = 0° without loss of generality, which is equivalent to reorienting the XY axes in the plane of the sky.
The orbital position of a planet at a certain time can be computed through Kepler’s equation (Murray & Dermott 1999),
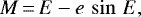 (A.3)
(A.3)
where e is the eccentricity of the orbit, E is called the eccentric anomaly, and M is the mean anomaly. M is defined as
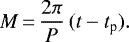 (A.4)
(A.4)
Here, t is the time for which we compute the position, tp is the time of periastron passage, and P is the orbital period of the planet.
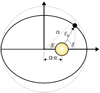 |
Fig. A.1 Sketch of the elliptic orbit and the auxiliary circle that defines the eccentric anomaly E. |
E is defined in terms of the true anomaly f, the orbital semi-major axis a, the eccentricity, and the planet-star distance given in Eq. (2). From the sketch of the orbit in Fig. A.1,
![\begin{equation*}\begin{array}{r@{\,}c@{\,}l} a\, \cos E&=&a\, e + r\, \cos\,f;\\[4pt] \cos\, E&=&\displaystyle\frac{e+\cos\, f}{1+e\, \cos f} \end{array} .\end{equation*}](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq59.png) (A.5)
(A.5)
With this, sin E can be computed as 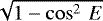 ,
,
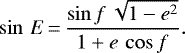 (A.6)
(A.6)
E can be re-expressed in terms of the true anomaly as
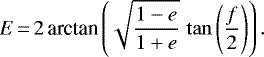 (A.7)
(A.7)
Substituting Eqs. (A.4), (A.6), and (A.7) into Eq. (A.3), we obtain the relation between the true anomaly and time, which is given in Eq. (8). We did not use an absolute reference frame for all of the exoplanets together with the mission timeline, and therefore tp is not relevant for the detectability.
Appendix B ωp versus ω⋆: effect on thedetectability
As discussedin Sect. 4.1.1, the argument of periastron is not consistently reported in the literature. This may change the quoted values of ω in the exoplanet catalogues by 180°.
In Fig. B.1 (upper row) we show the orbital realizations and ranges of αobs for pi Men b and ups And d (optimistic CGI configuration) for the value of ω that was originally reported in the Planet Columns of the NASA Exoplanet Archive. For comparison, we show (lower row) the results for the value of ωp after our standardization process. If the originally reported value of ω is used in our simulations, both pi Men b and ups And d show a wide range of αobs: ![$[42^{+16}_{-3}, 111^{+2}_{-7}]$](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq63.png) and
and ![$[38^{+19}_{-1}, 114^{+1}_{-5}]$](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq64.png) , respectively. With the value of ωp used in this work (Table D.1), the range of αobs decreases in both cases to
, respectively. With the value of ωp used in this work (Table D.1), the range of αobs decreases in both cases to ![$[69^{+7}_{-2}, 95^{+1}_{-1}]$](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq65.png) for pi Men band
for pi Men band ![$[69^{+5}_{-1}, 124^{+1}_{-5}]$](/articles/aa/full_html/2021/07/aa39993-20/aa39993-20-eq66.png) for ups And d.
for ups And d.
 |
Fig. B.1 As Fig. 8, but for pi Men b and ups And d in the optimistic CGI configuration. Upper row: computations using the value of ω quoted in the NASA Archive as if it were ωp. Lower row: computations using the value of ωp after our standardization process, where we add 180° to the ω quoted in the NASA Archive, which is indeed ω⋆. |
This means that if ω⋆ were mistaken for ωp, these two planets would be found among those with better prospects for phase-curve measurements. Because both host stars are bright (V = 5.67 mag for pi Men and 4.10 mag for ups And), these planets could mistakenly be prioritised for atmospheric characterization attempts.
Appendix C Sensitivity study: effect of orbital uncertainties on the detectability
 |
Fig. C.1 Sensitivity study for tau Cet e. Top row: Fp∕F⋆-Δθ diagrams in which all orbital parameters remain fixed (as given in the corresponding title) except for the parameter indicated in the legend, which varies within its upper and lower uncertainties as quoted in the input catalogue (Table D.1). When any of the orbital parameters is unknown, we fix it to i = 90°, e = 0, or ωp = 180° for this sensitivity study. Lines with intermediate colours correspond to orbital realizations with intermediate values of that parameter. A total of 100 orbital realizations are shown. Bottom row: intervals of αobs that would be accessible for each of the orbital realizations in the panel above, using the same colour code. The optimistic CGI configuration is assumed. |
Appendix D Additional tables
Input catalogue with the main planetary and stellar properties for the confirmed exoplanets that are Roman-accessible.
References
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Akeson, R. L., Chen, X., Ciardi, D., et al. 2013, PASP, 125, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Akeson, R. L., Armus, L., Bachelet, E., et al. 2019, ArXiv e-prints [arXiv:1902.05569] [Google Scholar]
- Angerhausen, D., DeLarme, E., & Morse, J. A. 2015, PASP, 127, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Arking, A., & Potter, J. 1968, J. Atmos. Sci., 25, 617 [Google Scholar]
- Baluev, R. V. 2015, MNRAS, 446, 1493 [Google Scholar]
- Batalha, N. E., Smith, A. J. R. W., Lewis, N. K., et al. 2018, AJ, 156, 158 [Google Scholar]
- Benedict, G. F., & McArthur, B. E. 2020, RNAAS, 4, 86 [Google Scholar]
- Benedict, G. F., McArthur, B. E., Gatewood, G., et al. 2006, AJ, 132, 2206 [Google Scholar]
- van den Besselaar, E. J. M., Greimel, R., Morales-Rueda, L., et al. 2007, A&A, 466, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolcar, M. R., Feinberg, L., France, K., et al. 2016, Proc. SPIE, 9904, 99040J [Google Scholar]
- Booth, M., Dent, W. R. F., Jordán, A., et al. 2017, MNRAS, 469, 3200 [Google Scholar]
- Boss, A. P. 2006, ApJ, 643, 501 [Google Scholar]
- Brown, R. A. 2015, ApJ, 805, 188 [Google Scholar]
- Bryan, M. L., Knutson, H. A., Lee, E. J., et al. 2019, AJ, 157, 52 [Google Scholar]
- Butler, R. P., Marcy, G. W., Williams, E., Hauser, H., & Shirts, P. 1997, ApJ, 474, L115 [Google Scholar]
- Cabrera, J., & Schneider, J. 2007, A&A, 464, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cahoy, K., Guyon, O., Schneider, G., et al. 2009, Proc. SPIE, 7440, 74400G [Google Scholar]
- Cahoy, K. L., Marley, M. S., & Fortney, J. J. 2010, ApJ, 724, 189 [Google Scholar]
- Carrión-González, Ó., García Muñoz, A., Cabrera, et al. 2020, A&A, 640, A136 [EDP Sciences] [Google Scholar]
- Damasso, M., Del Sordo, F., Anglada-Escudé, G., et al. 2020a, Sci. Adv., 6, 3 [Google Scholar]
- Damasso, M., Sozzetti, A., Lovis, C., et al. 2020b, A&A, 642, A31 [CrossRef] [EDP Sciences] [Google Scholar]
- Damiano, M., Hu, R., & Hildebrandt, S. R. 2020, AJ, 160, 206 [Google Scholar]
- De Rosa, R. J., Dawson, R., & Nielsen, E. L. 2020, A&A, 640, A73 [EDP Sciences] [Google Scholar]
- Demory, B.-O., de Wit, J., Lewis, N., et al. 2013, ApJ, 776, L25 [Google Scholar]
- Dietrich, J., & Apai, D. 2021, AJ, 161, 17 [Google Scholar]
- Douglas, E. S., Carlton, A. K., Cahoy, K. L. et al. 2018, Proc. SPIE, 10705, 1070526 [Google Scholar]
- Dyudina, U., Zhang, X., Li, L., et al. 2016, ApJ, 822, 76 [Google Scholar]
- Ertel, S., Defrère, D., Hinz, P., et al. 2020, AJ, 159, 177 [Google Scholar]
- Esteves, L. J., De Mooij, E. J. W., & Jayawardhana, R. 2015, ApJ, 804, 150 [Google Scholar]
- Feng, F., Tuomi, M., Jones, H. R. A., et al. 2017, AJ, 154, 135 [Google Scholar]
- Fischer, D. A., Marcy, G. W., Butler, R. P., et al. 2008, ApJ, 675, 790 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandolfi, D., Barragán, O., Livingston, J. H., et al. 2018, A&A, 619, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García Muñoz, A. & Isaak, K. G. 2015, PNAS, 112, 44 [Google Scholar]
- García Muñoz, A., Zapatero Osorio, M. R., Barrena, R., et al. 2012, ApJ, 755, 103 [Google Scholar]
- García Muñoz, A., Pérez-Hoyos, S., & Sánchez-Lavega, A. 2014, A&A, 566, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García Muñoz, A., Youngblood, A., Fossati, L., et al. 2020, ApJ, 888, L21 [Google Scholar]
- García Muñoz, A., Fossati, L., Youngblood, A., et al. 2021, ApJ, 907, L36 [Google Scholar]
- Gaudi, B. S., Seager, S., Mennesson, B., et al 2020, ArXiv e-prints [arXiv:2001.06683] [Google Scholar]
- GRAVITY Collaboration (Lacour, S. et al.) 2019, A&A, 623, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greaves, J. S., Wyatt, M. C., Holland, W. S., & Dent, W. R. F. 2004, MNRAS, 351, L54 [Google Scholar]
- Greaves, J. S., Kennedy, G. M., Thureau, N., et al. 2014, MNRAS, 438, L31 [Google Scholar]
- Greco, J. P., & Burrows, A. 2015, ApJ, 808, 172 [Google Scholar]
- Gillon, M., Demory, B.-O., Van Grootel, V., et al. 2017, Nat. Astron., 1, 0056 [NASA ADS] [CrossRef] [Google Scholar]
- Guimond, C. M., & Cowan, N. B. 2018, AJ, 155, 230 [Google Scholar]
- Han, Z.-T., Qian, S.-B., Zhu, L.-Y., et al. 2018, ApJ, 868, 53 [Google Scholar]
- Hatzes, A. P. 2016, in Methods of Detecting Exoplanets (Cham, Switzerland: Springer) [Google Scholar]
- Hatzes, A., & Rauer, H. 2015, ApJ, 810, L25 [Google Scholar]
- Haztes, A. P., Cochran, W. D., McArthur, B., et al. 2000, ApJ, 544, L145 [Google Scholar]
- Hollis, M. D. J., Balan, S. T., Lever, G., & Lahav, O. 2012, MNRAS, 423, 2800 [Google Scholar]
- Hu, R. 2019, ApJ, 887, 166 [Google Scholar]
- Hu, R., Demory, B.-O., Seager, S., Lewis, N., & Showman, A. P. 2015, ApJ, 802, 51 [Google Scholar]
- Huang, C. X., Burt, J., Vanderburg, A., et al. 2018, ApJ, 868, L39 [Google Scholar]
- Hunziker, S., Schmid, H. M., Mouillet, D., et al. 2020, A&A, 634, A69 [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, M. C., Endl, M., Cochran, W. D., et al. 2016, ApJ, 821, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, H. R. A., Butler, R. P., Tinney, C. G., et al. 2002, MNRAS, 333, 871 [Google Scholar]
- Kane, S. R., Mashkat, T., & Turnbull, M. C. 2018, AJ, 156, 267 [Google Scholar]
- Karkoschka, E. 1994, Icarus, 111, 174 [Google Scholar]
- Karkoschka, E. 1998, Icarus, 133, 134 [Google Scholar]
- Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019, A&A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Arenou, F., & Schneider, J. 2020, A&A, 635, L14 [CrossRef] [EDP Sciences] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Konopacky, Q. M., Marois, C., Macintosh, B. A., et al. 2016, AJ, 152, 28 [Google Scholar]
- Kunovac Hodžić, V., Triaud, A. H. M. J., Cegla, H. M., Chaplin, W. J., & Davies, G. R. 2021, MNRAS, 502, 2893 [Google Scholar]
- Lacy, B., & Burrows, A. 2020, ApJ, 892, 151 [Google Scholar]
- Lacy, B., Shlivko, D., & Burrows, A. 2019, AJ, 157, 132 [Google Scholar]
- Laughlin, G., Bodenheimer, P., & Adams, F. C. 2004, ApJ, 612, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, S. M., Di Francesco, J., Kennedy, G. M., et al. 2014, MNRAS, 444, 2665 [Google Scholar]
- Li, L., Jiang, X., West, R. A., et al. 2018, Nat. Commun., 9, 3709 [Google Scholar]
- LIFE Collaboration (Quanz, S. P., et al.) 2021, A&A, submitted [arXiv:2101.07500] [Google Scholar]
- Lupu, R. E., Marley, M. S., Lewis, N., et al. 2016, AJ, 152, 217 [Google Scholar]
- The LUVOIR Team 2018, ArXiv e-prints [arXiv:1809.09668] [Google Scholar]
- MacGregor, M. A., Lawler, S. M., Wilner, D. J., et al. 2016, ApJ, 828, 113 [Google Scholar]
- Mallama, A., Wang, D., & Howard, R. A. 2006, Icarus, 182, 10 [Google Scholar]
- Marcy, G. W., Butler, R. P., Fischer, D. A., et al. 2002, ApJ, 581, 1375 [Google Scholar]
- Mayorga, L. C., Jackiewicz, J., West, R. A., et al. 2016, AJ, 152, 209 [Google Scholar]
- Mawet, D., Hirsch, L., Lee, E. J., et al. 2019, AJ, 157, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Mennesson, B., Gaudi, S., Seager, S., et al. 2016, Proc. SPIE, 9904, 99040L [Google Scholar]
- Mennesson, B., Bailey, V., Kasdin, J., et al. 2019, ArXiv e-prints [arXiv:1909.02161] [Google Scholar]
- Mennesson, B., Juanola-Parramon, R., Nemati, B., et al. 2020, ArXiv e-prints [arXiv:2008.05624] [Google Scholar]
- Miret-Roig, N., Galli, P. A. B., Brandner, W., et al. 2020, A&A, 642, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misra, A., Meadows, V., & Crisp, D. 2014, ApJ, 792, 61 [Google Scholar]
- Motalebi, F., Udry, S., Gillon, M., et al. 2015, A&A, 584, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, C. D., & Correia, A. C. M. 2010, in Exoplanets (Tucson, USA: University of Arizona Press) [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, in Solar System Dynamics (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Nayak, M., Lupu, R., Marley., Fortney, J. J. et al. 2017, PASP, 129, 973 [Google Scholar]
- Nelson, B. E., Ford, E. B., Wright, J. T., et al. 2014, MNRAS, 441, 442 [Google Scholar]
- Nikolaou, A., Katyal, N., Tosi, N., et al. 2019, ApJ, 875, 11 [Google Scholar]
- Nowak, M., Lacour, S., Lagrange, A.-M., et al. 2020, A&A, 642, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Otegi, J. F., Bouchy, F., & Helled, R. 2020, A&A, 634, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F. A., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C. 2011, The Exoplanet Handbook (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Pollack, J. B., Rages, K., Baines, K., et al. 1986, Icarus, 65, 442 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2003, Numerical Recipes: the art of Scientific Computing, 3rd edn. (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Quanz, S. P., Amara, A., Meyer, M. R., et al. 2015, ApJ, 807, 64 [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2016, Proc. SPIE, 9908, 990812 [Google Scholar]
- Rauer, H., Gebauer, S., von Paris, P., et al. 2011, A&A, 529, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
- Ribas, I., Tuomi, M., Reiners, A., et al. 2018, Nature, 563, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, Proc. SPIE, 9143, 914320 [Google Scholar]
- Robinson, T. D., Stapelfeldt, K. R., & Marley, M. S. 2016, PASP, 128, 025003 [Google Scholar]
- Sánchez-Lavega, A., Hueso, R., & Baeza, S. 2003, in Proceedings of the Conference on Towards Other Earths: DARWIN/TPF and the Search for Extrasolar Terrestrial Planets, ESASP, 539, 569 [Google Scholar]
- Sánchez-Lavega, A., Pérez-Hoyos, S., & Hueso, R. 2004, Am. J. Phys., 72, 767 [Google Scholar]
- Santos, N. C., Israelian, G., García López, R. J., et al. 2004, A&A, 427, 1085 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A&A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Adibekyan, V., Dorn, C., et al. 2017, A&A, 608, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., & Buchhave, L. A. 2018, in Handbook of Exoplanets (Cham, Switzerland: Springer) [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S., Kasdin, N. J., Booth, J., et al. 2019, https://ntrs.nasa.gov/citations/20190028272 [Google Scholar]
- Soummer, R., Hagan, J. B., Pueyo, L., et al. 2011, ApJ, 741, 55 [Google Scholar]
- Spergel, D., Gehrels, N., Breckinridge, J., et al. 2013, ArXiv e-prints [arXiv:1305.5422] [Google Scholar]
- Spergel, D., Gehrels, N., Baltay, C., et al. 2015, ArXiv e-prints [arXiv:1503.03757] [Google Scholar]
- Stark, C. C., Roberge, A., Mandell, A., & Robinson, T. D. 2014, ApJ, 795, 122 [Google Scholar]
- Stark, C. C., Dressing, C., Dulz, S., et al. 2020, AJ, 159, 286 [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
- Steffen, J. H., Batalha, N. M., Borucki, W. J., et al. 2010, ApJ, 725, 1226 [Google Scholar]
- Stevens, D. J., & Gaudi, B. S. 2013, PASP, 125, 933 [Google Scholar]
- Suárez Mascareño, A., Faria, J. P., Figueira, P., et al. 2016 A&A, 639, A77 [Google Scholar]
- Torres, G. 2006, ApJ, 654, 1095 [Google Scholar]
- Traub, W. A., & Oppenheimer, B. R. 2010, in Exoplanets (Tucson, USA: University of Arizona Press) [Google Scholar]
- Traub, W. A., Belikov, R., Guyon, O., et al 2014, Proc. SPIE, 9143, 91430N [Google Scholar]
- Trauger, J., Moody, D., Krist, J. & Gordon, B. 2016, JATIS, 2, 011013 [Google Scholar]
- Tuomi, M., Jones, H. R. A., Jenkins, J. S., et al. 2013, A&A, 551, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidotto, A. A., Lichtenegger, H., Fossati, L., et al. 2018, MNRAS, 481, 5296 [Google Scholar]
- Vogt, S. S., Burt, J., Meschiari, S., et al. 2015, ApJ, 814, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., & Ford, E. B. 2011, MNRAS, 418, 1822 [Google Scholar]
- Wang., J. J., Graham, J. R., Dawson, R., et al. 2018, AJ, 156, 192 [Google Scholar]
- Watson, C. A., Littlefair, S. P., Diamond, C., et al. 2011, MNRAS, 413, L71 [Google Scholar]
- Winn, J. N. 2010, in Exoplanets (Tucson, USA: University of Arizona Press) [Google Scholar]
- Winn, J. N., Matthews, J. M., Dawson, R. I., et al. 2011, ApJ, 737, L18 [Google Scholar]
- Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [Google Scholar]
- Xuan, J. W., & Wyatt, M. C. 2020, MNRAS, 497, 2096 [Google Scholar]
Multiplying the value of the bin size by the value of the normalized distribution in that bin yields the fraction of planets if the total number of planets is normalized to one. This implies that for histogram bin sizes smaller than one, such as in the e histogram of Fig. 4 (with a bin size of 0.05), the value of the normalized distribution may be greater than one (as seen in the figure).
All Tables
Detectability conditions for the Roman-accessible exoplanets with Paccess > 25% and V < 7 mag for each of the CGI scenarios.
Exoplanets with the widest ranges of αobs at λ = 575 nm for each of the CGI configurations.
Exoplanets with the widest ranges of Teq(obs) at λ = 575 nm for each of the CGI configurations.
Detectability of tau Cet e and f at λ = 575 nm in each CGI scenario, both without prior knowledge on the orbital inclination and assuming 25° < i <45°.
Main planetary and stellar properties of the candidate exoplanets Barnard b and Proxima c.
Detectability conditions for the exoplanet candidates Barnard b and Proxima c in the optimistic CGI scenario.
Input catalogue with the main planetary and stellar properties for the confirmed exoplanets that are Roman-accessible.
All Figures
 |
Fig. 1 Sketch of the orbital geometry and graphical definition of the planet-star-observer phase angle α for a planet at a certain position on its orbit. |
| In the text | |
 |
Fig. 2 Mass-radius relationships used in this work compared to the confirmed exoplanets that have a known value of both Mp and ρ (grey dots). Planets for which only Mp sin i is known are not included. Solid black line shows the mass-density relationship for giant exoplanets, obtained from Hatzes & Rauer (2015). The dashed blue line and dotted red line show the mass-density relationship for low-mass exoplanets with volatile-rich and with rocky composition, respectively, obtained from the Mp –Rp equations inOtegi et al. (2020). Coloured squares mark the rocky planets of the Solar System (Mercury in black, Venus in orange, Earth in green, and Mars in red). Coloured dots mark the giant planets of the Solar System (Jupiter in orange, Saturn in yellow, Uranus in light blue, and Neptune in dark blue). |
| In the text | |
 |
Fig. 3 Confirmed exoplanets that are Roman-accessible in the optimistic CGI configuration, with Paccess > 25% and orbiting stars brighter than V = 7 mag (solid stars). For comparison, we show the confirmed exoplanets for which we know d and can derive a as explainedin Sect. 4.1 (semi-transparent dots). The colour code indicates the corresponding discovery technique (with which the planet was identified first), as detailed in the legend. “Others” refers to all other possible discovery techniques considered in the NASA Exoplanet Archive. HD 100546 b is the only Roman-accessible exoplanet discovered in imaging, although its existence is marked as controversial in the NASA Archive. |
| In the text | |
 |
Fig. 4 Eccentricity and orbital period for all confirmed exoplanets (grey dots in the main panel), those that have been observed in transit (regardless of whether they were discovered by that method; orange dots) and those that are Roman-accessible in the optimistic CGI configuration, with Paccess > 25% and V < 7 mag (green dots). We only consider those planets for which e is known and P can be derived as explained in Sect. 4.1. The black line shows the limit between short- and long-period exoplanets (P = 382.3 days) as defined in Kipping (2013) (see Sect. 4.1.2). Top panel: P distribution of all confirmed exoplanets (grey), those observed in transit (orange line), and those that are Roman-accessible (semi-transparent green). Right panel: normalized distribution of e such that it shows the relative frequency instead of the total count of planets. The same colour code applies as for the top panel. The green bars are semi-transparent (so that the grey distribution underneath can also be seen), so that the overall graph becomes either darker or lighter green depending on whether the two histograms overlap. For reference, we include the eccentricity for the subsets of short- and long-period exoplanets in Kipping (2013; red and blue lines, respectively). |
| In the text | |
 |
Fig. 5 Distribution of mass and orbital period for all confirmed exoplanets (semi-transparent grey), those observed in transit (semi-transparent orange), and those that are Roman-accessible in the optimistic CGI configuration, with Paccess > 25% and V < 7 mag (green).The plot considers planets for which either Mp or Mp sin i are known without distinction. |
| In the text | |
 |
Fig. 6 Distribution of stellar metallicity and semi-major axis of the planet for all confirmed exoplanets (semi-transparent grey), those observed in transit (semi-transparent orange), and those that are Roman-accessible in the optimistic CGI configuration, with Paccess > 25% and V < 7 mag (green). |
| In the text | |
 |
Fig. 7 Properties of the stars hosting Roman-accessible planets. Panel a: total count of planet-hosting stars of each spectral type. Panel b: normalized distributions of the stellar age. Panel c: normalized distributions of the stellar mass. Grey bars with diagonal ‘/’ hatching correspond to the total population of confirmed exoplanets. Over-plotted semi-transparent green bars with dotted hatching correspond to exoplanets that are Roman-accessible in the optimistic CGI configuration, with Paccess > 25% and V < 7 mag. We note that these parameters are not available for all of the confirmed exoplanets in the NASA Exoplanet Archive. The spectral type is available for all of the 24 stars hosting Roman-accessible planets, the stellar age is known for 13 of them, and the metallicity for 16 stars. Panel d: count of Roman-accessible-planet host stars of different optical magnitudes in each CGI configuration. Green bars with dotted hatching correspond to the optimistic scenario. Semi-transparent yellow bars with diagonal ‘\’ hatching correspond to the intermediate scenario. Red stars mark the three stars hosting Roman-accessible planets in the pessimistic scenario. |
| In the text | |
 |
Fig. 8 Detectability conditions for the Roman-accessible exoplanets. In each left panel, the solid black lines in the Fp ∕F⋆ -Δθ diagram correspond to independent orbital realizations. For the sake of clarity, only 1000 of the total 10 000 realizations are shown. Horizontal dashed lines indicate Cmin and vertical dashed lines show the IWA and OWA of the CGI at λ = 575 nm for the optimistic (green), intermediate (yellow), and pessimistic (red) configurations (Table 1). Regions in green are the detectability windows in the optimistic CGI configuration at this wavelength, and the green histograms in the right panels show the posterior distributions of αobs for this scenario. |
| In the text | |
 |
Fig. 9 Range of observable phase angles against the time the planet is accessible per orbit at λ = 575 nm in the optimistic CGI configuration. The colour of the markers indicates the Paccess of the exoplanet. Horizontal and vertical error bars correspond to the upper and lower uncertainties of tobs and Δαobs, respectively. |
| In the text | |
 |
Fig. 10 Evolution of Teq with time for the accessible orbits of the Roman-accessible exoplanets with a constrained value of e (Table D.1). Green indicates the orbital positions that are accessible in the optimistic CGI scenario. For the sake of clarity, only one of each ten orbital realizations is shown. |
| In the text | |
 |
Fig. 11 Median Teq against the median Mp for each Roman-accessible planet in the optimistic CGI configuration as computed in our 10 000 orbital realizations. The colour of the markers indicates the Paccess of the exoplanet. Horizontal and vertical error bars correspond to the upper and lower uncertainties of Mp and Teq, respectively.Magenta letters in the diagram indicate the Solar System planets Venus (V), Earth (E), Jupiter (J), Saturn (S), Uranus (U), and Neptune (N). |
| In the text | |
 |
Fig. 12 Detectability of tau Cet e and f in each CGI configuration, following the same colour code as in Fig. 8. In the left panels, black lines correspond to orbital realizations without an inclination constraint. Solid red lines correspond to orbital configurations with 25° < i < 45°, coplanar with the debris disc of the system (Lawler et al. 2014). For this case, the inclination is sampled from a uniform distributionwithin the quoted limits. The green histograms in the right panels show the posterior distributions of αobs. |
| In the text | |
 |
Fig. 13 As Fig. 12, but for the case of pi Men b. Solid red lines correspond to orbital configurations with
|
| In the text | |
 |
Fig. 14 Detectability of eps Eri b in the optimistic CGI scenario with the orbital parameters from Mawet et al. (2019; top panel) and Benedict et al. (2006; bottom panel). Left column: Fp ∕F⋆ -Δθ diagram. Yellow lines are specific to the maximum-likelihood orbital configuration providedin the corresponding reference. Middle column: the posterior distributions of αobs. Right column: variation of α with timefor each orbital realization. In this panel, green regions correspond to detectability windows for the maximum-likelihood orbit (yellow line). All orbital realizations are shown for reference in the α-t diagram (black lines), but their corresponding detectability windows are omitted. |
| In the text | |
 |
Fig. 15 As Fig. 12, but for Barnard b and Proxima c. Red lines correspond to orbital configurations of Proxima c with e < 0.05 and i ∈ [14°, 42°] or [138°, 166°], consistent with the estimates by Benedict & McArthur (2020) and Kervella et al. (2020). |
| In the text | |
 |
Fig. A.1 Sketch of the elliptic orbit and the auxiliary circle that defines the eccentric anomaly E. |
| In the text | |
 |
Fig. B.1 As Fig. 8, but for pi Men b and ups And d in the optimistic CGI configuration. Upper row: computations using the value of ω quoted in the NASA Archive as if it were ωp. Lower row: computations using the value of ωp after our standardization process, where we add 180° to the ω quoted in the NASA Archive, which is indeed ω⋆. |
| In the text | |
 |
Fig. C.1 Sensitivity study for tau Cet e. Top row: Fp∕F⋆-Δθ diagrams in which all orbital parameters remain fixed (as given in the corresponding title) except for the parameter indicated in the legend, which varies within its upper and lower uncertainties as quoted in the input catalogue (Table D.1). When any of the orbital parameters is unknown, we fix it to i = 90°, e = 0, or ωp = 180° for this sensitivity study. Lines with intermediate colours correspond to orbital realizations with intermediate values of that parameter. A total of 100 orbital realizations are shown. Bottom row: intervals of αobs that would be accessible for each of the orbital realizations in the panel above, using the same colour code. The optimistic CGI configuration is assumed. |
| In the text | |
 |
Fig. C.2 Same as Fig. C.1, but for tau Cet f. |
| In the text | |
 |
Fig. C.3 Same as Fig. C.1, but for pi Men b. |
| In the text | |
 |
Fig. C.4 Same as Fig. C.1, but for 55 Cnc d. |
| In the text | |
 |
Fig. C.5 Same as Fig. C.1, but for eps Eri b. |
| In the text | |
 |
Fig. C.6 Same as Fig. C.1, but for Barnard b. |
| In the text | |
 |
Fig. C.7 Same as Fig. C.1, but for Proxima c. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.