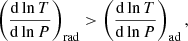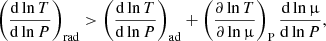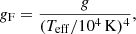| Issue |
A&A
Volume 650, June 2021
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202040105 | |
| Published online | 18 June 2021 | |
Blue supergiants as tests for stellar physics
1
Department of Astronomy, University of Geneva, Chemin Pegasi 51, 1290 Versoix, Switzerland
e-mail: cyril.georgy@unige.ch
2
Astronomical Institute, Graduate School of Science, Tohoku University, 980-8578 Sendai, Japan
Received:
10
December
2020
Accepted:
12
April
2021
Context. Massive star evolution is still poorly understood, and observational tests are required to discriminate between different implementations of physical phenomena in stellar evolution codes.
Aims. By confronting stellar evolution models with observed properties of blue supergiants, such as pulsations, the chemical composition, and position in the Hertzsprung-Russell diagram, we aim to determine which of the criteria used for convection (Schwarzschild or Ledoux) is best able to explain the observations.
Methods. We computed state-of-the-art stellar evolution models with either the Schwarzschild or the Ledoux criterion for convection. Models are for 14 to 35 M⊙ at solar or Large Magellanic Cloud metallicity. For each model, we computed the pulsation properties to know when radial modes are excited. We then compared our results with the position of blue supergiants in the Hertzsprung-Russell diagram, with their surface chemical composition and with their variability.
Results. Our results at Large Magellanic Cloud metallicity shows only a slight preference for the Ledoux criterion over the Schwarzschild one in reproducing, at the same time, the observed properties of blue supergiants, even if the Schwarzschild criterion cannot be excluded at this metallicity. We checked that changing the overshoot parameter at solar metallicity does not improve the situation. We also checked that our models are able to reproduce the position of Galactic blue supergiants in the flux-weighted-gravity–luminosity relation.
Conclusions. We confirm that overall, models computed with the Ledoux criterion are slightly better in matching observations. Our results also support the idea that most Galactic α Cyg variables are blue supergiants from group 2, that is stars that have been through a previous red supergiant phase where they have lost a large amount of mass.
Key words: stars: evolution / stars: interiors / stars: massive / stars: oscillations / supergiants / convection
© ESO 2021
1. Introduction
Although massive stars, progenitors of core-collapse supernovae, play important roles in the chemical evolution of galaxies, their evolution is still poorly understood. Main uncertainties come from our insufficient knowledge of accurate mass-loss rates at various evolutionary stages, the efficiencies of rotational mixing and angular momentum transport, and the range of convective and semi-convective mixing including the extent of overshooting. Constraints to theories for these phenomena should be obtained from the comparison of theoretical models with observations. Surface CNO abundances are very useful for constraining theoretical models of rotational mixing in massive stars. Comparison of the surface CNO elements of B stars with theoretical models has been discussed actively (e.g. Hunter et al. 2009; Przybilla et al. 2010; Brott et al. 2011; Maeder et al. 2014; Martins et al. 2015), but there remain some difficulties reconciling theoretical and numerical results with observations, even for main-sequence (MS) stars.
Convection is one of the main transport processes to be included in stellar evolution calculations. Despite its importance, it is still poorly understood and its treatment in stellar evolution codes is as of yet still based on very simple models, such as the well known ‘mixing-length theory’ (Böhm-Vitense 1958). Moreover, the position of the convective boundaries relies on one of the stability criteria (either the Schwarzschild criterion or the Ledoux one, see e.g. Maeder 2009). It has been known for a long time (e.g. Maeder & Mermilliod 1981) that using either of these criteria produces cores that are too small, making mandatory to arbitrary extend the size of the convective cores (this is called the ‘overshooting’). How this extension has to be done and what the efficiency of the mixing of chemical elements is throughout the convective boundary (so called convective boundary mixing) are so far unknown and largely contribute to our lack of understanding of massive star evolution.
During the last decade, intensive efforts have been started to improve the situation by using three-dimension (3d) hydrodynamics simulations of convection in stellar interior conditions (Meakin & Arnett 2007; Freytag & Höfner 2008; Augustson et al. 2012; Viallet et al. 2013; Müller et al. 2016; Cristini et al. 2017; Mocák et al. 2018, among others). Despite the increasing sophistication and numerical resolution of these simulations as well as the powerful insight they allow on stellar convection, we are still far from having new and more precise algorithms to deal with this phenomenon. Some attempts are currently being made to include lessons learned from 3d hydrodynamics simulations in classical stellar evolution codes (Scott et al. 2021). To validate these approaches, new observational tests are needed (for example see Tkachenko et al. 2020).
We have sought to obtain constraints to theories by using pulsationnal properties of blue supergiant (BSG) stars (Saio et al. 2013; Georgy et al. 2014). Blue supergiants are expected to consist of two groups: one group of stars are evolving towards the red supergiant (RSG) stage (group 1 hereafter), the others are returned back from the RSG stage (group 2 hereafter). We distinguish the two groups using the pulsation properties; BSG stars after a RSG phase show evidence of radial pulsation (α Cyg variables), whereas BSGs evolving from the MS to the RSG branch (first crossing) do not (Saio et al. 2013). We interpreted Deneb (α Cyg) and Rigel (β Ori) as post RSG according to their pulsations which can be reproduced by models which returned to the BSG region after losing significant mass during the RSG phase. The following puzzle emerged, however: Post-RSG models predict surface N/C and N/O ratios much larger than those of Deneb and Rigel for whom N/C and N/O ratios are rather consistent with those of pre-RSG models. The discrepancy indicates that internal mixing was somewhat too strong in our models. Georgy et al. (2014) propose a possible solution for the problem; that is to say the problem of the surface CNO abundance ratios might be remedied by using the Ledoux criterion in determining the convective and radiative boundaries. However, the latter work focused on only one mass, namely 25 M⊙, at solar metallicity. In this paper, we intent to extend our previous research to a broader mass domain and also to the metallicity of the Large Magellanic Cloud (LMC) in order to check if our finding remains valid in other regimes.
Most of the stellar evolution calculations discussed in the literature have been done using Schwarzschild criterion so that discussions of the stellar structure and evolution under the Ledoux criterion are rare even though it is not yet understood which criterion should be used. In this paper, we first discuss the structure and evolution of massive stars calculated with the Ledoux criterion. Then, we compare observed surface compositions of BSGs with those of models obtained by using the Ledoux or the Schwarzschild criterion. Finally, we revisit the Mbol − log gF (luminosity–flux-weighted surface gravity) relation of the BSGs.
2. Massive star models with the Ledoux criterion
As is well known, there are two ways to determine the boundary between convection and radiative regions. If the Schwarzschild criterion is employed, convection is assumed to occur if
where the temperature gradients with subscripts rad and ad indicate the temperature gradient realised if all energy is carried by radiative diffusion (see e.g. Maeder 2009, for the detailed definitions) and an adiabatic temperature gradient, respectively. On the other hand, if we adopt the Ledoux criterion, we assume that the convection occurs if
where dlnμ/dlnP stands for the gradient of mean molecular weight μ caused by an inhomogeneous chemical composition in the stellar interior.
It is known that layers satisfying the Schwarzschild condition (Eq. (1)), but not the Ledoux criterion (Eq. (2)), are thermally unstable (overstable; see Kato 1966). This is one of the reasons why the Schwarzschild criterion is preferred in the evolution calculations. It is not clear, however, how efficiently the vibrational thermal instability should mix layers.
Convection in the Geneva stellar evolution code is treated as follows: The limits of convective regions are defined using either the Ledoux or the Schwarzschild criterion. During the main sequence and core helium-burning phase, the convective core is extended by a fraction of 0.1 HP, where HP is the pressure scale height, evaluated at the strict Ledoux or Schwarzschild limit, respectively. In this extension of the convective core, the thermal gradient is assumed to be the adiabatic one. Chemical mixing inside the convective zone is assumed to be very efficient and fast compared to the nuclear timescale. The chemical composition is thus homogenised inside convective regions, at least during the first stages of nuclear burning (as is the case for all the models computed in this work).
In this paper, we use different sets of models computed with the Schwarzschild or with the Ledoux criterion. In the case that the Ledoux one was used, we assume that there is no semi-convection in the regions where the matter is Schwarzschild unstable, but Ledoux stable. It is important to note, however, that in case we dealt with a model including the effects of rotation, there is a slow mixing of chemical elements inside these regions due to rotational mixing. There are poor constraints on the efficiency of semi-convection in stars, so we made the decision to compute only extreme cases: pure Ledoux models without semi-convection, mimicking models where semi-convection is very inefficient, and pure Schwarzschild models, corresponding to Ledoux models with infinitely efficient semi-convection. Models with intermediate semi-convective efficiency would fall somewhere in between these two cases (a discussion on the effect of varying the efficiency of semi-convection in massive star models can be found in Kaiser et al. 2020, however in the framework of the MESA code). Here, we would also like to emphasise that the post-MS evolution of massive stars is extremely dependent on the detailed mixing scheme adopted in stellar evolution codes, which makes it difficult to draw firm conclusions (e.g. Higgins & Vink 2019; Schootemeijer et al. 2019).
The stability of radial pulsations was computed in the same way as in Saio et al. (2013). Although the effects of rotation were taken into account in the evolution models, no mechanical effects of rotation were included when calculating the stability of radial pulsations. This is justified because, as discussed in the appendix in Saio et al. (2013), the rotation speed is always very slow in the envelopes of supergiant stars, to which the amplitude of radial pulsation is confined.
3. Evolutionary models with Schwarzschild and Ledoux criteria for Z = 0.014
Figure 1 shows evolutions of global parameters until the core-helium exhaustion for 20 and 25 M⊙ models of Z = 0.014 (corresponding to a solar metallicity) computed by using the Ledoux (red lines) and Schwarzschild (black lines) criteria. The Geneva evolution code was used as in Saio et al. (2013) and Georgy et al. (2014). Wind mass loss was considered in the same way as described in our previous works (see also Ekström et al. 2012, for more details). In addition to these standard models, and for comparison purposes, we computed three additional models: a 20 M⊙ computed with the Ledoux criterion and a mass-loss rate multiplied by 2 with respect to our usual mass-loss rates with an initial rotation rate on the zero-age main-sequence (ZAMS) equal to 40% of the critical velocity, and two models of 25 M⊙ computed with the Ledoux criterion and with an overshoot increased to 0.3 HP (non-rotating and with an initial rotation rate on the ZAMS equal to 40% of the critical velocity).
 |
Fig. 1. Evolutionary tracks of 20 (dashed lines) and 25 M⊙ (solid lines) models until central helium exhaustion computed with the Ledoux (red lines) and the Schwarzschild (black lines) criteria for the occurrence of convection for an initial composition of (X, Z)=(0.72, 0.014). The magenta line corresponds to the Ledoux 20 M⊙ model computed with an enhanced mass-loss rate (twice our standard rates). Top panel: HR diagram, middle and bottom panels: changes in mass and in the central helium abundance, Yc, respectively, as a function of Teff. Radial pulsations are excited along the thick-line parts. |
During the main-sequence evolution, the models with either criteria are nearly identical. This is caused by the following: (a) In our models, the chemical composition is initially homogeneous, so that the chemical gradient ∇μ is null everywhere; (b) it implies that in the initial models, both criteria lead to the same convective boundary; and (c) during the MS, the convective core is receding. As the chemical composition inside convective zones is homogeneous, it means that in the convective core, Schwarzschild and Ledoux criteria coincide, making the models computed with either criterion identical.
During the post main-sequence evolution, the models using the Ledoux criterion are slightly less luminous, but overall evolutions of global parameters are similar irrespective of the convection criteria. Is is important to note, however, that the crossing-time of the Hertzsprung-Russell diagram (HRD) can be different due to the activity of the intermediate H-burning convective zone. After the main-sequence, they evolve to the red supergiant region, where they burn a significant fraction of helium in the core and, at the same time, lose a considerable amount of mass. When the helium core occupies about 70% of the total mass, the stars evolve bluewards, crossing the HRD for the second time (Giannone 1967; Farrell et al. 2020). They thus have another BSG stage, where they consume the remaining helium in the core. Here, we would like to mention that the Ledoux 20 M⊙ model at solar metallicity computed with standard mass-loss rates does not lose enough mass during the RSG phase to evolve back to the BSG region of the HRD. As we are interested in stars evolving back to the blue after a RSG phase, we consider in what follows the Ledoux 20 M⊙ with enhanced mass loss: This model is crossing the HRD after its RSG stage and reaches regions in the HRD where the effective temperature corresponds to BSG stars. The Ledoux 20 M⊙ model computed with the standard mass-loss rates instead makes a small blue loop and ends its evolution in cooler regions (see red dashed lines in Fig. 1). All the other models discussed in this work were computed assuming the standard mass-loss rates, as in Ekström et al. (2012).
4. Surface abundances of Galactic blue supergiants
4.1. Models with standard parameters
Figure 2 compares surface N/C and N/O (number) ratios and helium abundances, as well as Ys (mass fraction) of Galactic blue supergiants with theoretical models with rotation (25 M⊙, blue line and 20 M⊙, black line) and without rotation (25 M⊙, red line). The left panels are for models with the Schwarzschild criterion for convection, while the right panels are for the models with the Ledoux criterion. Radial pulsations are excited in the solid-line parts. Physical parameters of observed BSGs shown here can be found in Table A.1 at the end of the paper.
 |
Fig. 2. Surface CNO and helium abundances predicted from 20 M⊙ (with rotation, black lines) and 25 M⊙ (with rotation in blue, without rotation in red line) evolutionary models are compared with observed surface CNO and helium abundances of Galactic blue supergiants, where N/C and N/O are number ratios, and Ys is the mass fraction of helium at the surface. Solid parts of the lines indicate where radial pulsations are excited. Filled circles represent α Cyg variables, while open circles are for non-variable BSGs. Left panels: are for models with the Schwarzschild condition, right panels: are for models with the Ledoux condition. |
The surface helium and CNO abundances in the models after significant mass loss in the red supergiant stage strongly depend on the adopted criterion for convection. As discussed in Georgy et al. (2014), the difference comes from the location of the intermediate convective shell located just above the hydrogen burning shell during the blue supergiant stage evolving towards the red supergiant region (group 1).
Schwarzschild criterion. At the end of the MS, the convective hydrogen-burning core recedes and disappears. Hydrogen burning jumps in a shell located higher inside the star (see the top-left panel of Fig. 3). It creates an associated convective shell which is active enough to sustain the star and prevent a rapid crossing of the HRD. This convective shell is able to transport matter processed by the CNO cycle to a high level inside the star. When the star crosses the HRD for a second time towards the BSG region, it has lost a lot of mass during the RSG phase, uncovering layers highly processed by the CNO cycle, that is with high N/C and N/O ratios.
 |
Fig. 3. Kippenhahn diagrams for four representative models of 25 M⊙: solar metallicity (top row), and Z = 0.006 (bottom row); computed with the Schwarzschild criterion (left column) or Ledoux criterion (right column). Grey zones indicate that this part of the star is convective. The mass coordinate of the surface is shown with a red line. Maxima of the energy generation rate are indicated for H burning (blue solid line) and He burning (green solid line). The dashed lines indicate, for H and He-burning respectively, the level where the energy generation rate reaches 100 [erg s−1 g−1]. The dot-dashed line shows the mass-coordinate of the convective core on the ZAMS. It roughly shows the upper boundary of the region in which H-burning has proceeded and, therefore, has increased the chemical gradient. Due to rotational mixing, the exact extension of the region where a significant chemical gradient is present is slightly larger. |
Ledoux criterion. As in the case of the Schwarzschild criterion, the H-burning convective core disappears at the end of the MS, and the maximum of H-burning migrates at a higher level inside the star. However, it occurs in a region of the star that was previously occupied by the receding H-burning core and, therefore, with a non-zero chemical gradient. Readers are invited to refer to the position of the dot-dashed line, which shows the extension of the convective core on the ZAMS: Due to H-burning, a chemical gradient is progressively built during the MS below this line. This gradient prevents the appearance of a convective zone at the same depth as with the Schwarzschild criterion. Convection is only able to develop in layers closer to the surface (see the top-right panel of Fig. 3), from where it slowly erodes the chemical gradient, making its lower boundary moving towards the centre of the star. It makes the hydrogen-burning shell much less active compared to the Schwarzschild case, as illustrated in Fig. 4. The luminosity of the shell is not sufficient to sustain the star, which crosses the HRD on a very short timescale: The outer layers expand, a convective envelope appears from the surface and develops in depth, while the intermediate convective shell fades away. The matter inside the intermediate convective shell is less processed compared to the Schwarzschild case, making the N/C and N/O ratios remain smaller at the time when these layers are exposed at the surface because of the mass loss (see Fig. 2). This difference is particularly noticeable in the mass range around 20 to 25 M⊙: Higher mass models have a tendency to avoid the red supergiant phase, remaining in the blue part of the HRD during the whole evolution, and lower mass models quickly cross the HRD, but they do not lose enough mass during the RSG phase to evolve back to the blue later on.
 |
Fig. 4. Time evolution of the luminosity associated with the hydrogen-burning shell during the first 3 × 105 years after the end of the MS. Solid lines are for models computed with the Ledoux criterion, and dashed lines are for models computed with the Schwarzschild criterion. Black lines are for 20 M⊙ models at solar metallicity, blue lines are for 25 M⊙ models at solar metallicity, and red lines are for 25 M⊙ models at a metallicity of Z = 0.006. |
For the late B and A type supergiants (4.15 ≳ log Teff ≳ 3.9), the surface helium abundances and N/C and N/O ratios are, irrespective of their variability, close to the values of models from group 1. This is at odds with our explanation of the α Cyg variables as blue supergiants after the red supergiant stages (Saio et al. 2013), in which α Cyg variables should have, in particular for Schwarzschild criterion, higher Ys as well as N/C and N/O ratios. However, for the models with the Ledoux criterion, the discrepancy is considerably reduced since the differences of these quantities for the models before and after the red supergiant stage are much smaller than for the models with the Schwarzschild criterion (Georgy et al. 2014). Due to the much longer time spent on the second crossing compared to the first one (see Table 1), our computations show that there is also a much greater probability of observing a star from the BSG2 group since the duration of the BSG2 phase is at least 30 times longer than the BSG1 one. The comparison between the tracks and the observation should thus focus on the second crossing.
The surface helium abundance (Ys) of Galactic early B supergiants (log T > 4.15) are appreciably higher than later B and A supergiants, although only two cases are available; the surface N/C and N/O ratios of the early B α Cyg variables tend to be higher than those of non-variables, in contrast to the case of the late B and A type supergiants. These values of Ys, N/C, and N/O of the early type α Cyg variables agree with supergiant models returned from the red supergiant stage (group 2) obtained by using the Ledoux criterion, which are much better than those based on the Schwarzschild criterion. Models with the Schwarzschild criterion predict too high Ys and N/C values, in particular. Therefore, we conclude that the available spectroscopic surface abundances of Galactic blue supergiants in the literature indicate that the Ledoux criterion is better in reproducing the surface abundances of α Cyg variables, assuming that these stars are group 2 stars as deduced from their pulsational properties. However, despite our efforts so far, no model seems able to reproduce the surface abundances of pulsating late type BSGs and their pulsational properties simultaneously, even when considering models computed with the Ledoux criterion. Looking at Fig. 2, we could wonder whether Schwarzschild models with a lower initial mass could also fit the observed data. However, Schwarzschild models with masses between about 10 M⊙ to 20 M⊙ do not show bluewards evolution after the RSG phase (Ekström et al. 2012), unless very high mass-loss rates are considered (Georgy 2012; Meynet et al. 2015a).
In summary, our pulsation models for Galactic metallicity indicate that the only way of reproducing the observed pulsational properties of BSGs is to lose a large amount of mass during a previous RSG stage (Saio et al. 2013). These stars should therefore be members of group 2 BSGs. If this result is correct, then models computed with the Ledoux criterion for convection are in better agreement with the observed surface abundances, even if a perfect match is so far not reached. Also, our findings would indicate that stars with an initial mass of about 20 M⊙ need a rather high mass-loss rate during the RSG stage to cross the Hertzsprung gap for a second time. This could be achieved in case the current mass-loss prescriptions for RSGs are underestimated, or by binary interactions.
4.2. Models with an increased overshoot
The fraction of HP over which the convective core is extended is a free parameter of the code. The value of 0.1 HP generally used in this work is our standard value, and it was calibrated by comparing the width of the MS obtained in our calculation with the observed width of the MS around 2 M⊙. It has been suggested that the overshooting as implemented in most stellar evolution codes could be mass-dependent and increase with the stellar mass (e.g. Castro et al. 2014). In this section, we explore the impact of increasing the fraction to 0.3 HP on the properties of BSGs, particularly on their pulsationnal properties and surface abundances.
Evolutionary tracks for models computed with the Ledoux criterion for convection are displayed in Fig. 5 (25 M⊙ without rotation in red, 25 M⊙ with an initial rotation rate of 40% of the critical one in blue, and 20 M⊙ with an initial rotation rate of 40% of the critical one in black). In comparing these to the tracks with a standard overshoot (see Fig. 2), the agreement with the observations is slightly worse: Particularly, the surface abundance of helium is systematically higher in the models, and the N/O and N/C ratios are also too high in the portions of the tracks where radial pulsations are excited (solid part of the tracks to be compared with filled circles). The discussion about the duration of the BSG1 and BSG2 phases still holds in this case (see Table 1).
Part of the explanation for this result resides in the bigger core during the MS produced by the increased overshoot. This reduces the distance between the edge of the convective core (where Y, N/C, and N/O increase as evolution proceeds due to the CNO cycle) and the surface. As a consequence, the chemical elements produced inside the convective core take a shorter time to reach the surface thanks to rotationnal mixing, making these quantities already reach a higher value during the first crossing of the HRD and shift up the overall tracks.
5. Models of massive stars in the LMC
In the previous section, we found that the surface helium and CNO abundances of the Galactic blue supergiants agree with models based on the Ledoux criterion better than those with the Schwarzschild criterion. In this section, we discuss supergiant models with a LMC composition obtained with the Ledoux and the Schwartzschild criteria.
5.1. Evolution
For the LMC star models, we have adopted a chemical composition of (X, Z)=(0.738, 0.006); although, we have also examined a model with Z = 0.008 and no qualitative changes occurred. Figure 6 compares the evolution with the Schwarzschild criterion (left panel) and the Ledoux criterion (right panel) for 20 M⊙, 25 M⊙, 30 M⊙, and 35 M⊙ models. These are rotating models with an initial velocity of 0.4 Vc (where Vc means the critical rotation speed), except for the green track in the right panel, which represents a non-rotating 20 M⊙ model. Again, thick parts of lines indicate where radial pulsations are excited.
 |
Fig. 6. Models with the LMC composition are shown in the same way as in Fig. 1. The initial masses are the following: 20 (magenta), 25 (blue), 30 (red), and 35 M⊙ (black). Left panel: models computed with the Schwarzschild criterion, and the right one shows the models computed with the Ledoux criterion. The green line shows the non-rotating model of 20 M⊙ with the Ledoux criterion, while other cases are rotating models with an initial rotation of 0.4 Vc. |
In contrast to the solar abundance case shown in Figs. 1 and 6 shows that in the case of the LMC composition, core-helium burning tends to occur in a blue region of 4.2 ≳ log Teff ≳ 4, allowing for a significant amount of mass to be lost in this region of the HRD for models with M ≥ 25 M⊙. Evolutions with the Ledoux criterion are similar to those with the Schwarzschild criterion when M ≤ 25 M⊙, while considerable differences occur in more massive cases. In the former case, after a considerable amount of central helium is consumed, the star evolves to the red-supergiant range where core-helium is exhausted.
In the case of the Schwarzschild criterion, 30 and 35 M⊙ models evolve to red or yellow supergiants after the main-sequence, where they start core-helium burning. After some amount of helium is consumed, they go back to the blue region to finish core-helium burning. In the case of the Ledoux criterion, on the other hand, they start core-helium burning at log Teff ∼ 4.2 without becoming a red or yellow supergiant. The 30 M⊙ model loses considerable mass during the helium burning and evolves to a red supergiant after most of the central helium is consumed, while the 35 M⊙ model becomes hotter when it lost more than 10 M⊙.
The non-rotating model of 20 M⊙ (green line) with the Ledoux criterion evolves very differently with a long blue loop reaching as hot as log Teff ≈ 4.6 after the red supergiant stage, which is rather similar to the cases of the solar metallicity shown in Fig. 1. The model ignites helium burning in the core and consumes a significant amount of helium as a red supergiant, during which it loses a mass of about 12 M⊙. Then it becomes a blue supergiant and consumes the remaining helium in the core. This property is, however, sensitive to the rotation rate; if we include a small initial rotation of 0.2 Vc, the loop shrinks significantly, extending only to log Teff ≈ 3.9 (not shown in the figure for clarity purposes).
5.2. Distribution of variable and non-variable supergiants of the LMC
Figure 7 compares the sections of the theoretical tracks where radial pulsations are excited (thick lines) with the observed positions of (semi-) periodic supergiant variables in the LMC (filled symbols). We make the comparison with the HR diagram, rather than the spectroscopic one, because the accurate knowledge of the distance to the LMC probably makes the uncertainties in log L smaller than the uncertainties in log g. Black tracks are for rotating models that started with a rotation velocity of 0.4 Vc. For the case of the Ledoux criterion (right panel), the non-rotating (blue line) 20 M⊙ model and a rotating model with an initial velocity of 0.2 Vc (red line) are also shown for comparison. On the blue loop of the non-rotating model, radial pulsations are excited because the star has lost a significant amount of mass in the previous RSG stage. The excitation of pulsations on the loop seems to contradict the absence of blue variables around the corresponding luminosity. However, due to the sensitivity of the loop to the rotation rate, an initial rotation rate of 20% of the critical rate significantly reduces the loop, removing the discrepancy with the distribution of variable stars in the HR diagram. Since most of the massive stars rotate quite rapidly at this metallicity (most of observed massive stars in the LMC have an equatorial velocity above 100 km s−1, Ramírez-Agudelo et al. 2013), we do not consider the long blue loop of the non-rotating model to be a shortcoming of the Ledoux criterion. We consider models with an initial rotation speed above about 20% the critical one to be representative models to be compared with the properties of stars in the LMC: 20% the critical velocity corresponds to an average equatorial velocity of about 125−150 km s−1 during the MS.
 |
Fig. 7. Evolutionary tracks in the HRD for Z = 0.006 with an initial rotation velocity of 0.4 times the critical value (black lines), of 0.2 times the critical value (red line), and without rotation (blue line). Left and right panels: are for models with the Schwarzschild criterion and the Ledoux criterion, respectively. Thick lines indicate the parts of the tracks where radial pulsations are excited. Blue supergiants (luminosity classes of Ia, Iab) in the LMC are also shown: Blue squares connected with horizontal lines are LBVs (S Dor, R 71, R 110, R 143; from brighter to fainter), for which parameters are obtained from Stahl et al. (1990), Lamers et al. (1998), van Genderen (2001). Red filled circles are known LMC α Cyg variables, whose parameters are given in Table 2. The other circles show the positions of BSGs of which parameters were obtained by Urbaneja et al. (2017). The photometric variability of each of these BSGs has been examined using the Fourier analysis software PERIOD04 (Lenz & Breger 2005) for the G-band lightcurve data from the ASAS-SN database (Shappee et al. 2014; Jayasinghe et al. 2019). Based on the analysis, we show non-variables with open circles, probable α Cyg variables (with clear periodicities shorter than ∼100 days) with filled magenta circles, and marginal variables with filled green circles. |
Selected non-LBV supergiant variables in the LMC.
In Fig. 7, red filled circles are known LMC α Cyg variables whose parameters are given in Table 2, while the other circles are BSGs in the LMC whose parameters were obtained by Urbaneja et al. (2017). We have examined the variabilities of these BSGs using the Fourier analysis software PERIOD04 (Lenz & Breger 2005) for the G-band lightcurve data from the ASAS-SN database (Shappee et al. 2014; Jayasinghe et al. 2019). Open circles are non-variables, filled magenta circles are probable α Cyg variables showing clear periodicities shorter than ∼100 days, and filled green circles are stars which marginally show signs of variability. Squares connected with horizontal line are luminous blue variables (LBV), which are included as α Cyg variables because it is known that the micro-variabilities of LBVs are α Cyg type variations caused by stellar pulsations (e.g. Lamers et al. 1998).
In this figure, we see that most variables are located either at high luminosity or in a cool enough location of the HRD (log Teff < 3.9), roughly agreeing with the theoretical prediction for the excitation of radial pulsations irrespective of the convective criteria employed. For more luminous and hotter stars which have lost considerable mass (see Fig. 6), the pulsations are excited by strange mode instability, while pulsations in less luminous cool stars are excited mainly by the κ-mechanism, as in the classical cepheids.
In contrast to our agreement of the LBV micro-variabilities with the theoretical prediction of pulsational instability, Lamers et al. (1998) claimed that the microvariations of LBVs could not be explained by strange-mode instabilities by comparing models obtained by Kiriakidis et al. (1993) who predicted instability in a region of log L/L⊙ > 6.0 for Z = 0.004. The discrepancy can be attributed to the difference in the evolutionary models; our models include the effect of rotational mixing, which increases the luminosity and loses a considerable amount of mass during the core-helium burning stage around log Teff ∼ 4.2 (Fig. 6). Both effects increase the luminosity-to-mass ratio, which in turn enhances the effect of the strange mode instability. The explanation is consistent with the fact that the result of Lovekin & Guzik (2014) based on the old set of Geneva models (Meynet et al. 1994) without rotation indicates that the luminosity at the stability boundary is located between that of Kiriakidis et al. (1993) and ours. In summary, the distribution in the HRD of the LMC variable and non-variable supergiants does not indicate a preference between the Ledoux and the Schwarzschild criteria.
5.3. Surface compositions
Figure 8 shows the variations of the surface helium abundance and CNO ratios during evolutions of 20, 25, 30, and 35 M⊙ (magenta, blue, red, and black lines, respectively) with the Schwarzschild (left panel) and the Ledoux (right panel) criteria. The initial rotation speed is assumed to be 40% of the critical speed (Vc). Thick solid lines represent evolutionary stages when radial pulsations are excited, while on the thin dashed line parts no radial pulsations are excited. After the main sequence evolution, in which rotational mixing modifies the surface composition, the surface composition starts to change at the beginning of the core-helium burning for models massive enough so that the mass loss is significant (the models of 20 M⊙ hardly change the surface composition after the end of main sequence because they lose only a little amount of mass; see Fig. 6). The increase in the surface N/C and N/O ratios and helium abundances are comparable in both cases of the Ledoux and Schwarzschild criteria, in contrast to the case of solar metallicity shown in Fig. 2.
 |
Fig. 8. Evolution of surface chemical compositions of 20, 25, 30, and 35 M⊙ models (magenta, blue, red, and black lines, respectively) with the Schwarzschild (left panel) and the Ledoux (right panel) criterion being presented as functions of log Teff. In those models, the initial rotation speed was set to be 40% of the critical value (Vc). Observational results available in the literature for massive LMC stars are also plotted; the meanings of the symbols are the same as in Fig. 7. The chemical compositions of the LBVs (filled squares) are adopted from Lennon et al. (1993) and Mehner et al. (2017) for R 71, and from Agliozzo et al. (2019) for R 143. The N/C ratio of the cool α Cyg variable HD 271182 is adopted from Luck & Lambert (1992). Open circles are N/C and N/O ratios of blue supergiants (Ia, Iab) obtained by Hunter et al. (2009); binaries have been removed (Maeder et al. 2014). |
Kippennhahn diagrams are shown in Fig. 3 for the 25 M⊙ model with the Schwarzschild criterion (bottom left panel) and the one with the Ledoux criterion (bottom right panel). There is no drastic difference in the extension of the convective shell between the two cases, in contrast to the solar metallicity models (top panels of Fig. 3). In both cases, the outer boundary of the shell convection zone extends to about Mr ≈ 18 M⊙ at the contraction stage after the main sequence evolution. Due to wind mass loss during the core-helium burning stage, the stellar surface reaches the layers where material was previously processed by H-burning. Then the surface N/C and N/O ratios increase steeply. Since the maximum extent of the convective shell is comparable between the models with the Schwarzschild and the Ledoux criteria, the amounts of changes in the surface compositions are comparable in the two cases for models of the LMC composition.
It is not easy to explain the changes in the behaviours of the intermediate H-burning shell at various metallicities and for different criterion for convection. An important point is whether the model starts core-helium burning in the blue part of the HRD or crosses the HRD and starts core-helium burning as a RSG. This depends on a variety of parameters, which can be interdependent, such as the following: rotation (and its implementation), mass-loss rates, chemical gradients in the radiative zones, activity of the intermediate H-burning shell (Langer & Maeder 1995; Maeder & Meynet 2001). Models at low metallicity tend to remain in the blue region of the HRD longer (e.g. Georgy et al. 2013), and this is also what we observe in the computations used in this work. A similarity between our models at both metallicities is that the luminosity of the hydrogen burning-shell at the onset of shell hydrogen-burning is systematically higher for models computed with the Schwarzschild criterion compared to models computed with the Ledoux one (see Fig. 4). This is due to chemical gradients in the region which was previously occupied by the hydrogen burning-core during the MS (the region below the dot-dashed line in Fig. 3), which prevent a convective zone from appearing at the same location where hydrogen is burnt. Since hydrogen-shell burning starts in a radiative condition with the Ledoux criterion, there is no refueling in fresh hydrogen by convection and then the energy production remains lower. In the Ledoux models, the convective zone appears higher inside the star, where no burning occurs. It then grows at a deeper level by eroding the chemical gradient below the convective zone.
The difference between solar and LMC metallicity is that at solar metallicity, the first crossing of the HRD can be fast: All the Ledoux models and the Schwarzschild 25 M⊙ models ignite central helium burning on the RSG branch after a quick crossing of the HRD. Only the Schwarzschild 20 M⊙ model starts burning its helium as a BSG before slowly crossing the HRD for the first time: The luminosity of the intermediate hydrogen-burning shell is sufficient to maintain the model on the blue side of the HRD, and it remains almost constant; whereas in other cases, it decreases over time. Figure 4 shows the time-evolution of the shell luminosity for 3 × 105 years after the end of the MS. Three different kinds of behaviours can be seen. The first type are models with an abrupt decrease in the shell luminosity shortly after the shell ignites (Ledoux models at solar metallicity). These are the models which cross the Hertzsprung gap very quickly after the end of the MS. The second type are models with a slow decrease in the shell luminosity over time (models at Z = 0.006 and Schwarzschild solar metallicity 20 M⊙ model). These models ignite core-He burning in the blue part of the HRD and cross the gap slowly. The third type is the model with an intermediate behaviour (Schwarzschild solar metallicity 25 M⊙ model). This model crosses the HRD quite quickly, but not as fast as the first type of models. For the models that are quickly crossing the HRD, the intermediate convective zone of the Ledoux models have no time to erode the chemical gradients and to reach the same position as in the Schwarzschild case before the expansion of the external layers switches the intermediate convective zone off. The regions mixed up by convection are thus located at a different depth inside the star at this metallicity, changing the surface chemical composition later on, when mass loss uncovers these regions.
At lower metallicity, the luminosity of the hydrogen-burning shell is still higher in the Schwarzschild than in the Ledoux models (see Fig. 4). However, this difference is no longer sufficient enough to make the Ledoux model cross the HRD quickly. At this metallicity, core helium-burning starts in the blue part of the HRD in both cases. The convective shell of the Ledoux model appears at a higher level inside the star as shown in Fig. 3 (bottom right panel). Then convection erodes the chemical gradient below the convective zone, which progressively reaches the same position as in the Schwarzschild model, preventing a drop in the luminosity of the intermediate burning shell of the Ledoux models, as can be seen in Fig. 4. The external layers of the star does not expand, keeping the star at a rather high effective temperature, and the conditions for keeping an active intermediate convective shell are preserved, contrary to the solar metallicity case. It leads to a very similar evolution of the intermediate convective shell, independent of the criterion used for convection.
Spectroscopic surface helium abundance, Ys, and CNO ratios of LMC supergiants available in the literature are plotted in Fig. 8. For non-variable supergiants (Ia, Iab), results from the VLT-FLAMES survey (Hunter et al. 2009) are shown; in that particular analysis, the He/H number ratio is assumed to be 0.1 (corresponding to Ys = 0.285). These blue supergiants seem to be on the evolution stage just after the main sequence before helium ignition so that the surface N/C and N/O ratios reflect the rotational mixing during the main-sequence stage. We note that if we adopt the Ledoux criterion, two stars with the highest N/C ratios could be in the core-helium burning stage according to the 30 M⊙ model. The N/C ratios of these blue supergiants look comparable (except for one extremely deficient one) with model predictions, while the theoretical predictions of N/O ratios tend to be larger than the observed ratios (see discussion in Maeder et al. 2014).
Very limited spectroscopic results for variable supergiants in the LMC are available. Plotted in Fig. 8 are Ys as well as N/C and N/O ratios for the LBVs R 71 and R 143 (filled squares) obtained by Lennon et al. (1993), Mehner et al. (2017), and Agliozzo et al. (2019), respectively, and the N/C ratio of the cool α-Cyg variable HD 271182 (filled circle) obtained by Luck & Lambert (1992).
In the HR diagram, R 71 and R 143 are located close to the 35 M⊙ and 25 M⊙ tracks (Fig. 7), corresponding to black and blue lines in Fig. 8, respectively. This figure indicates that the helium abundances and CNO abundance ratios of R 71 and R 143 are roughly consistent with models either with the Ledoux or Schwarzschild criterion.
For the cool α-Cyg variable HD 271182, only the N/C ratio obtained by Luck & Lambert (1992) is available. In the HR diagram (Fig. 7), HD 271182, which is shown by a filled circle with horizontal error bars, is located along the 30 M⊙ track in either case of Ledoux or Schwarzschild criterion. The surface N/C and the position on the HRD of HD 271182 are consistent only with the model with the Ledoux criterion, but they are inconsistent with the Schwarzschild criterion. This supports, although only weakly, the Ledoux criterion for the LMC composition. Recently, Neugent et al. (2012) identified many (∼300) yellow supergiants separating from dominant foreground Galactic dwarfs. We hope that spectroscopic abundance analyses as well as time-resolved photometries will be carried out for these yellow supergiants (luminous ones in particular) in the near future.
To summarise, the properties of BSGs in the LMC do not indicate a clear preference between the Schwarzschild and the Ledoux criteria. In the case the evolutionary mass of HD 271182 is correct (about ∼30 M⊙), then the Ledoux criterion is however better at reproducing the observed characteristics of this star in particular.
6. Flux-weighted gravity–luminosity relation
The flux-weighted gravity–luminosity relation (FGLR) was introduced by Kudritzki et al. (2003, 2012) to spectroscopically measure the distances to galaxies. Later, Meynet et al. (2015b) showed that the relation should be a powerful tool to discriminate between BSG1 and BSG2 because the relation depends on the mass-loss that occurred during the stellar evolution. It is thus an important check for our models to compare the predictions of our computations with the observed position of variable BSGs in this diagram. The flux-weighted gravities gF, defined as
of BSGs were found by Kudritzki et al. (2003) to form a tight relation with luminosity (or absolute bolometric magnitude, Mbol), where g is the surface gravity and Teff is the effective temperature. The most recent calibration was obtained from the detailed spectroscopic analysis of blue supergiants in the LMC (Urbaneja et al. 2017). Figure 9 shows the relation with some evolutionary tracks at Z = 0.006. The blue line labelled G2b is the relation corresponding to log L/L⊙ = 3log M/M⊙ + 2.03 obtained by Meynet et al. (2015b) as the lower boundary of the FGLR for BSGs of Local Group galaxies. This figure indicates that the FGLR of the LMC is also bounded by the same relation as that of Local Group galaxies.
 |
Fig. 9. LMC blue supergiants analysed by Urbaneja et al. (2017) are plotted with circles in the log gF − Mbol plane. The colour of the circles have the same meaning as in Fig. 7. The blue straight line labelled as G2b is the lower boundary of the FGLR of BSGs in Local group galaxies (Meynet et al. 2015b). Blue parts (log Teff > 3.9) of some evolutionary tracks with Z = 0.006 are also plotted, where thick line parts indicate where radial pulsations are excited. The labels ‘S0’ and ‘S4’ refer to models with an initial rotation rate of 0 and 0.4 of the critical one, respectively. Some LBVs are plotted with filled squares for comparison, which clearly indicate that LBVs have experienced significant mass losses. |
The positions of the LBVs (filled blue squares) in the gF − Mbol plane are separated from the mean FGLR towards the lower gF side. Since gF ∝ M/L, the LBV positions indicate that they have lost significantly more mass than the ordinary BSGs, which is consistent with our common understanding of the LBVs. In contrast to the fact that the LBV positions in the HRD are intermingled with the ordinary BSGs (Fig. 7), the segregation of LBVs in the gF − Mbol plane is remarkable and could be useful for finding LBV candidates.
Meynet et al. (2015b) wrote about the consistency of the FGLR of Local Group low metallicity galaxies with the theoretical evolution models of Ekström et al. (2012). According to the evolution models, stars whose initial masses are larger than ∼20 M⊙ become BSGs for a second time after a considerable amount of mass is lost in the red supergiant stage. The BSG2 would be located on the right side of the G2b line, and Meynet et al. (2015b) conclude that the tightness of the FGLR indicates that the evolution towards group 2 BSGs should be rare in Local Group galaxies. This conclusion is somewhat inconsistent with our identification of α Cyg variables as BSG2s (Saio et al. 2013).
The conclusion of Meynet et al. (2015b) is based on the FGLR of the BSGs in Local Group galaxies. It is more desirable to examine the theoretical and observational consistency using BSGs in our Galaxy. Thanks to the recent second release of the Gaia parallax data, DR2 (Gaia Collaboration 2016, 2018), it is now possible to accurately plot Galactic blue supergiants on the gF − Mbol plane (Fig. 10). The spectroscopic data of blue supergiants of the Galaxy (see Table A.1) needed to obtain gF are adopted from the literature (Crowther et al. 2006; Searle et al. 2008; Przybilla et al. 2010; Firnstein & Przybilla 2012; Clark et al. 2012). Among the plotted BSG stars, known α Cyg variables are shown with filled circles. For the identifications of the α Cyg type variability, we consulted the literature based on the HIPPARCOS photometry (Koen & Eyer 2002; Lefèvre et al. 2009; Dubath et al. 2011; Rimoldini et al. 2012).
 |
Fig. 10. Left: absolute bolometric magnitudes Mbol versus flux-weighted gravity gF of Galactic blue supergiants are plotted with error bars. For most of the stars, Gaia DR2 parallaxes (Gaia Collaboration 2018) are used. A blue line indicates the mean relation of LMC blue supergiants obtained by Urbaneja et al. (2017). The blue dashed line labelled G2b corresponds to the relation log L/L⊙ = 3log M/M⊙ + 2.03 (Meynet et al. 2015b), which gives the lower bound of the FGLR for the BSGs of Local Group galaxies. Right: blue parts (log Teff > 3.9) of evolutionary tracks with various parameters are compared. The labels ‘S0’ and ‘S4’ refer to models with an initial rotation rate of 0 and 0.4 of the critical one, respectively. Some Galactic LBVs are shown by filled blue squares. The loci on the gF − Mbol diagram clearly indicate that significant mass losses have occurred in LBVs. |
As seen in Fig. 10, the FGLR of the Galactic blue supergiants are similar to that of the LMC, but it is possibly more extended to the lower gF side, which may indicate that the blue supergiants in the Galaxy experienced more mass loss than the blue supergiants in the LMC with a similar luminosity. This is consistent with the evolution tracks of rotating stars presented by Ekström et al. (2012). Also, it is interesting to note that the loci of the Galactic LBVs in the gF − Mbol plane (filled blue squares in Fig. 10) are similar (gF ∼ 10 cm s−2 (K/104)4) to those of the LMC LBVs (Fig. 9) despite the large difference in the metallicity.
In the gF − Mbol plane, the BSG2s should be systematically located on the lower gF side for a given Mbol compared with the location of BSG1s. The parts of the evolution tracks for the BSG2s can be recognised in the right panel of Fig. 10 as the (gently ascending) thick-line parts below the G2b line where pulsations are excited. In addition, this figure indicates that radial pulsations are also excited well above the G2b line if M ≥ 14 M⊙. This is caused by the κ-mechanism in the β-Cep instability strip. As the luminosity increases (i.e. L/M increases), the effect of strange-mode instability gets stronger and the instability range widens to include very luminous α Cyg variables.
In fact, the Galactic α-Cyg variables (red filled circles) are separated into relatively low and very high luminosity groups at Mbol ∼ −9 (or log L/L⊙ ∼ 5.5) in the gF − Mbol plane. The majority of α Cyg variables with Mbol > −9 are below the G2b line in Fig. 10, indicating that the relatively less luminous α Cyg variables are BSG2s, while there are some very luminous α Cyg variables, which belong to BSG1s.
Since gF ∝ M/L, a constant L/M corresponds to a vertical line in the gF − Mbol diagram. The location of L/M = 104 L⊙/M⊙ is shown as a red line in Fig. 10. A star with L/M > 104 L⊙/M⊙ should fall to the right side of the vertical line. This figure shows that the majority of α Cyg variables have L/M ≳ 104 L⊙/M⊙, which indicates that radial pulsations of α Cyg variables are excited by the strange mode instability (e.g. Glatzel 1994; Saio et al. 1998; Saio 2009)1.
There are some less luminous (Mbol ≳ −6) stars located below the G2b line. They cannot be explained by single star evolutions, indicating that transferring a significant envelope mass to a companion in a close binary system would be needed.
7. Conclusion
In this work, we compare models of massive stars computed with both the Schwarzschild and Ledoux criterion with observed pulsating BSGs (α Cyg variables). In particular, we used the position in the HRD, the surface chemical composition, the excitation of radial modes, and the position in the flux-weighted gravity-luminosity diagram to test our models. Confirming our preliminary results (Georgy et al. 2014), our comparisons with observations show the Ledoux criterion is better than the Schwarzschild one at solar metallicity. It particularly improves the fit with the observed surface chemical abundances, while keeping a good agreement with the location where radial pulsations are observed in the HRD. This also supports the idea that relatively less luminous (log L/L⊙ ≲ 5.5) Galactic α Cyg variables are group 2 BSGs, that is stars that have had a previous RSG stage before crossing the HRD for a second time towards higher effective temperatures. In that case, rather high mass-loss rates during the RSG phase are needed to favour a bluewards evolution after the RSG phase.
However, our models still have difficulties in reproducing the surface helium abundance of observed stars, although models computed with the Ledoux criterion are closer to the observations. We also tried to change input physics for convection by changing the efficiency of the overshoot at solar metallicity. We find that this does not help to improve the agreement between the models and the surface chemical abundances observed in α Cyg variables.
At the LMC metallicity, we show that models produce rather similar results independent of the chosen criterion for convection. This is due to the fact that at this metallicity, changing the criterion does not impact the location where helium-core burning starts in the HRD: It begins on the blue side of the HRD in both cases. A comparison with observations does not strongly favour any of the criteria at this metallicity.
We have compared the FGLR of LMC BSGs (Urbaneja et al. 2017) with our evolutionary tracks. We find that variable BSGs are located in the range of log gF ≲ 1.4 (i.e. L/M ≳ 104 L⊙/M⊙). The majority of the LMC BSGs form a relatively tight sequence, which indicates mass losses from them have not been very significant. In contrast, LBVs are located on the significantly lower gF side deviating from the tight relation of the other BSGs, which indicates that they have lost significant mass, in agreement with our common understanding of the LBVs.
We also compare the FGLR of Galactic α Cyg variables with the results of our modelling. We find that the FGLR of Galactic BSGs is broader than that of LMC, indicating that wind mass loss is more active. The FGLR clearly shows that relatively less luminous α Cyg variables are members of group 2 BSGs, while some very luminous α Cyg variables belong to group 1 BSGs.
Our findings suggest that the use of the Ledoux criterion for convection produce slightly better agreements with the observations. More work is needed to confirm this result since it is probably not independent of other choices made in our models (e.g. mass-loss rates, implementation of rotation, implementation of convective boundary mixing). We will continue our efforts to improve the constraints on stellar models that can be deduced from the comparison with observations of BSGs.
This also explains the fact that most of the variable LMC BSGs in Fig. 9 are located in the range log gF < 1.4.
Acknowledgments
The authors thank the anonymous referee for her/his valuable comments that contributed to improve this work. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. CG and GM have received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 833925).
References
- Agliozzo, C., Mehner, A., Phillips, N. M., et al. 2019, A&A, 626, A126 [CrossRef] [EDP Sciences] [Google Scholar]
- Augustson, K. C., Brown, B. P., Brun, A. S., Miesch, M. S., & Toomre, J. 2012, ApJ, 756, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Brott, I., Evans, C. J., Hunter, I., et al. 2011, A&A, 530, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burki, G., Maeder, A., & Rufener, F. 1978, A&A, 65, 363 [Google Scholar]
- Castro, N., Fossati, L., Langer, N., et al. 2014, A&A, 570, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, J. S., Najarro, F., Negueruela, I., et al. 2012, A&A, 541, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cristini, A., Meakin, C., Hirschi, R., et al. 2017, MNRAS, 471, 279 [Google Scholar]
- Crowther, P. A., Lennon, D. J., & Walborn, N. R. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubath, P., Rimoldini, L., Süveges, M., et al. 2011, MNRAS, 414, 2602 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farrell, E. J., Groh, J. H., Meynet, G., et al. 2020, MNRAS, 495, 4659 [CrossRef] [Google Scholar]
- Firnstein, M., & Przybilla, N. 2012, A&A, 543, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [Google Scholar]
- Freytag, B., & Höfner, S. 2008, A&A, 483, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C. 2012, A&A, 538, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Ekström, S., Eggenberger, P., et al. 2013, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Saio, H., & Meynet, G. 2014, MNRAS, 439, L6 [Google Scholar]
- Giannone, P. 1967, Z. Astrophys., 65, 226 [NASA ADS] [Google Scholar]
- Glatzel, W. 1994, MNRAS, 271, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Higgins, E. R., & Vink, J. S. 2019, A&A, 622, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, I., Brott, I., Langer, N., et al. 2009, A&A, 496, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jayasinghe, T., Stanek, K. Z., Kochanek, C. S., et al. 2019, MNRAS, 485, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, E. A., Hirschi, R., Arnett, W. D., et al. 2020, MNRAS, 496, 1967 [Google Scholar]
- Kato, S. 1966, PASJ, 18, 374 [NASA ADS] [Google Scholar]
- Kiriakidis, M., Fricke, K. J., & Glatzel, W. 1993, MNRAS, 264, 50 [NASA ADS] [Google Scholar]
- Koen, C., & Eyer, L. 2002, MNRAS, 331, 45 [Google Scholar]
- Kudritzki, R. P., Bresolin, F., & Przybilla, N. 2003, ApJ, 582, L83 [Google Scholar]
- Kudritzki, R.-P., Urbaneja, M. A., Gazak, Z., et al. 2012, ApJ, 747, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., Bastiaanse, M. V., Aerts, C., & Spoon, H. W. W. 1998, A&A, 335, 605 [NASA ADS] [Google Scholar]
- Langer, N., & Maeder, A. 1995, A&A, 295, 685 [NASA ADS] [Google Scholar]
- Lefèvre, L., Marchenko, S. V., Moffat, A. F. J., & Acker, A. 2009, A&A, 507, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lennon, D. J., Wobig, D., Kudritzki, R.-P., & Stahl, O. 1993, Space Sci. Rev., 66, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Lovekin, C. C., & Guzik, J. A. 2014, MNRAS, 445, 1766 [CrossRef] [Google Scholar]
- Luck, R. E., & Lambert, D. L. 1992, ApJS, 79, 303 [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin, Heidelberg: Springer) [Google Scholar]
- Maeder, A., & Mermilliod, J. C. 1981, A&A, 93, 136 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., Przybilla, N., Nieva, M.-F., et al. 2014, A&A, 565, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Hervé, A., Bouret, J.-C., et al. 2015, A&A, 575, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McDonald, I., Zijlstra, A. A., & Boyer, M. L. 2012, MNRAS, 427, 343 [Google Scholar]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 667, 448 [Google Scholar]
- Mehner, A., Baade, D., Groh, J. H., et al. 2017, A&A, 608, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Maeder, A., Schaller, G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97 [Google Scholar]
- Meynet, G., Chomienne, V., Ekström, S., et al. 2015a, A&A, 575, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Kudritzki, R.-P., & Georgy, C. 2015b, A&A, 581, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mocák, M., Meakin, C., Campbell, S. W., & Arnett, W. D. 2018, MNRAS, 481, 2918 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, B., Viallet, M., Heger, A., & Janka, H.-T. 2016, ApJ, 833, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Neugent, K. F., Massey, P., Skiff, B., & Meynet, G. 2012, ApJ, 749, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Percy, J. R., & Welch, D. L. 1983, PASP, 95, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., Firnstein, M., Nieva, M. F., Meynet, G., & Maeder, A. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez-Agudelo, O. H., Simón-Díaz, S., Sana, H., et al. 2013, A&A, 560, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rimoldini, L., Dubath, P., Süveges, M., et al. 2012, MNRAS, 427, 2917 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H. 2009, Commun. Asteroseismol., 158, 245 [NASA ADS] [Google Scholar]
- Saio, H., Baker, N. H., & Gautschy, A. 1998, MNRAS, 294, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., Georgy, C., & Meynet, G. 2013, MNRAS, 433, 1246 [Google Scholar]
- Schootemeijer, A., Langer, N., Grin, N. J., & Wang, C. 2019, A&A, 625, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scott, L. J. A., Hirschi, R., Georgy, C., et al. 2021, MNRAS, 503, 4208 [CrossRef] [Google Scholar]
- Searle, S. C., Prinja, R. K., Massa, D., & Ryans, R. 2008, A&A, 481, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, ApJ, 788, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Stahl, O., Wolf, B., Klare, G., Juettner, A., & Cassatella, A. 1990, A&A, 228, 379 [NASA ADS] [Google Scholar]
- Stahl, O., Wolf, B., Zickgraf, F.-J., et al. 1983, A&A, 120, 287 [NASA ADS] [Google Scholar]
- Sterken, C., de Groot, M., & van Genderen, A. M. 1997, A&A, 326, 640 [NASA ADS] [Google Scholar]
- Tkachenko, A., Pavlovski, K., Johnston, C., et al. 2020, A&A, 637, A60 [CrossRef] [EDP Sciences] [Google Scholar]
- Urbaneja, M. A., Kudritzki, R.-P., Gieren, W., et al. 2017, AJ, 154, 102 [NASA ADS] [CrossRef] [Google Scholar]
- van Genderen, A. M. 2001, A&A, 366, 508 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Genderen, A. M., & Sterken, C. 2002, A&A, 386, 926 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Genderen, A. M., Sterken, C., & Jones, A. F. 2004, A&A, 419, 667 [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F., van Genderen, A. M., & Zegelaar, I. 1998, A&AS, 128, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viallet, M., Meakin, C., Arnett, D., & Mocák, M. 2013, ApJ, 769, 1 [Google Scholar]
- Zickgraf, F.-J., Wolf, B., Stahl, O., Leitherer, C., & Klare, G. 1985, A&A, 143, 421 [NASA ADS] [Google Scholar]
Appendix A: Additional table
Adopted parameters and variability types for Galactic blue supergiants.
All Tables
All Figures
 |
Fig. 1. Evolutionary tracks of 20 (dashed lines) and 25 M⊙ (solid lines) models until central helium exhaustion computed with the Ledoux (red lines) and the Schwarzschild (black lines) criteria for the occurrence of convection for an initial composition of (X, Z)=(0.72, 0.014). The magenta line corresponds to the Ledoux 20 M⊙ model computed with an enhanced mass-loss rate (twice our standard rates). Top panel: HR diagram, middle and bottom panels: changes in mass and in the central helium abundance, Yc, respectively, as a function of Teff. Radial pulsations are excited along the thick-line parts. |
| In the text | |
 |
Fig. 2. Surface CNO and helium abundances predicted from 20 M⊙ (with rotation, black lines) and 25 M⊙ (with rotation in blue, without rotation in red line) evolutionary models are compared with observed surface CNO and helium abundances of Galactic blue supergiants, where N/C and N/O are number ratios, and Ys is the mass fraction of helium at the surface. Solid parts of the lines indicate where radial pulsations are excited. Filled circles represent α Cyg variables, while open circles are for non-variable BSGs. Left panels: are for models with the Schwarzschild condition, right panels: are for models with the Ledoux condition. |
| In the text | |
 |
Fig. 3. Kippenhahn diagrams for four representative models of 25 M⊙: solar metallicity (top row), and Z = 0.006 (bottom row); computed with the Schwarzschild criterion (left column) or Ledoux criterion (right column). Grey zones indicate that this part of the star is convective. The mass coordinate of the surface is shown with a red line. Maxima of the energy generation rate are indicated for H burning (blue solid line) and He burning (green solid line). The dashed lines indicate, for H and He-burning respectively, the level where the energy generation rate reaches 100 [erg s−1 g−1]. The dot-dashed line shows the mass-coordinate of the convective core on the ZAMS. It roughly shows the upper boundary of the region in which H-burning has proceeded and, therefore, has increased the chemical gradient. Due to rotational mixing, the exact extension of the region where a significant chemical gradient is present is slightly larger. |
| In the text | |
 |
Fig. 4. Time evolution of the luminosity associated with the hydrogen-burning shell during the first 3 × 105 years after the end of the MS. Solid lines are for models computed with the Ledoux criterion, and dashed lines are for models computed with the Schwarzschild criterion. Black lines are for 20 M⊙ models at solar metallicity, blue lines are for 25 M⊙ models at solar metallicity, and red lines are for 25 M⊙ models at a metallicity of Z = 0.006. |
| In the text | |
 |
Fig. 5. Same as the right panel of Fig. 2, but for models with an increased overshoot of 0.3 HP. |
| In the text | |
 |
Fig. 6. Models with the LMC composition are shown in the same way as in Fig. 1. The initial masses are the following: 20 (magenta), 25 (blue), 30 (red), and 35 M⊙ (black). Left panel: models computed with the Schwarzschild criterion, and the right one shows the models computed with the Ledoux criterion. The green line shows the non-rotating model of 20 M⊙ with the Ledoux criterion, while other cases are rotating models with an initial rotation of 0.4 Vc. |
| In the text | |
 |
Fig. 7. Evolutionary tracks in the HRD for Z = 0.006 with an initial rotation velocity of 0.4 times the critical value (black lines), of 0.2 times the critical value (red line), and without rotation (blue line). Left and right panels: are for models with the Schwarzschild criterion and the Ledoux criterion, respectively. Thick lines indicate the parts of the tracks where radial pulsations are excited. Blue supergiants (luminosity classes of Ia, Iab) in the LMC are also shown: Blue squares connected with horizontal lines are LBVs (S Dor, R 71, R 110, R 143; from brighter to fainter), for which parameters are obtained from Stahl et al. (1990), Lamers et al. (1998), van Genderen (2001). Red filled circles are known LMC α Cyg variables, whose parameters are given in Table 2. The other circles show the positions of BSGs of which parameters were obtained by Urbaneja et al. (2017). The photometric variability of each of these BSGs has been examined using the Fourier analysis software PERIOD04 (Lenz & Breger 2005) for the G-band lightcurve data from the ASAS-SN database (Shappee et al. 2014; Jayasinghe et al. 2019). Based on the analysis, we show non-variables with open circles, probable α Cyg variables (with clear periodicities shorter than ∼100 days) with filled magenta circles, and marginal variables with filled green circles. |
| In the text | |
 |
Fig. 8. Evolution of surface chemical compositions of 20, 25, 30, and 35 M⊙ models (magenta, blue, red, and black lines, respectively) with the Schwarzschild (left panel) and the Ledoux (right panel) criterion being presented as functions of log Teff. In those models, the initial rotation speed was set to be 40% of the critical value (Vc). Observational results available in the literature for massive LMC stars are also plotted; the meanings of the symbols are the same as in Fig. 7. The chemical compositions of the LBVs (filled squares) are adopted from Lennon et al. (1993) and Mehner et al. (2017) for R 71, and from Agliozzo et al. (2019) for R 143. The N/C ratio of the cool α Cyg variable HD 271182 is adopted from Luck & Lambert (1992). Open circles are N/C and N/O ratios of blue supergiants (Ia, Iab) obtained by Hunter et al. (2009); binaries have been removed (Maeder et al. 2014). |
| In the text | |
 |
Fig. 9. LMC blue supergiants analysed by Urbaneja et al. (2017) are plotted with circles in the log gF − Mbol plane. The colour of the circles have the same meaning as in Fig. 7. The blue straight line labelled as G2b is the lower boundary of the FGLR of BSGs in Local group galaxies (Meynet et al. 2015b). Blue parts (log Teff > 3.9) of some evolutionary tracks with Z = 0.006 are also plotted, where thick line parts indicate where radial pulsations are excited. The labels ‘S0’ and ‘S4’ refer to models with an initial rotation rate of 0 and 0.4 of the critical one, respectively. Some LBVs are plotted with filled squares for comparison, which clearly indicate that LBVs have experienced significant mass losses. |
| In the text | |
 |
Fig. 10. Left: absolute bolometric magnitudes Mbol versus flux-weighted gravity gF of Galactic blue supergiants are plotted with error bars. For most of the stars, Gaia DR2 parallaxes (Gaia Collaboration 2018) are used. A blue line indicates the mean relation of LMC blue supergiants obtained by Urbaneja et al. (2017). The blue dashed line labelled G2b corresponds to the relation log L/L⊙ = 3log M/M⊙ + 2.03 (Meynet et al. 2015b), which gives the lower bound of the FGLR for the BSGs of Local Group galaxies. Right: blue parts (log Teff > 3.9) of evolutionary tracks with various parameters are compared. The labels ‘S0’ and ‘S4’ refer to models with an initial rotation rate of 0 and 0.4 of the critical one, respectively. Some Galactic LBVs are shown by filled blue squares. The loci on the gF − Mbol diagram clearly indicate that significant mass losses have occurred in LBVs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.