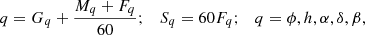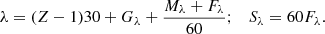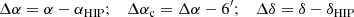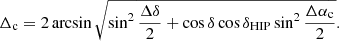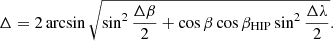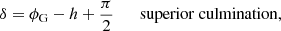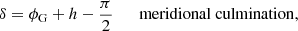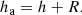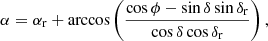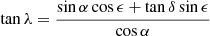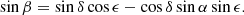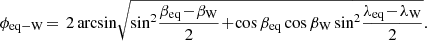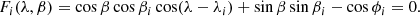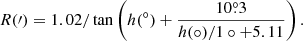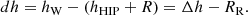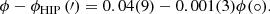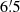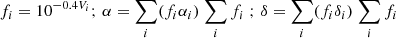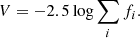| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 12 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202140332 | |
| Published online | 26 May 2021 | |
The star catalogue of Wilhelm IV, Landgraf von Hessen-Kassel
Accuracy of the catalogue and of the measurements⋆
1
Department of Astrophysics/IMAPP, Radboud University, PO Box 9010, 6500 GL Nijmegen, The Netherlands
e-mail: f.verbunt@astro.ru.nl
2
SRON Netherlands Institute for Space Research Utrecht, Utrecht, The Netherlands
3
History of Astronomy and Observational Astronomy, Physics Department, Philipps Universität, Renthof 5, 35032 Marburg, Germany
e-mail: andreas.schrimpf@physik.uni-marburg.de
Received:
13
January
2021
Accepted:
2
March
2021
We analyse a manuscript star catalogue by Wilhem IV, Landgraf von Hessen-Kassel from 1586. From measurements of altitudes and of angles between stars, given in the catalogue, we find that the measurement accuracy averages 26″ for eight fundamental stars, compared to 49″ of the measurements by Brahe. The computation in converting altitudes to declinations and angles between stars to celestial positions is very accurate, with errors that are negligible with respect to the measurement errors. Due to an offset in the position of the vernal equinox, the positional error of the catalogue is slightly worse than that of Brahe’s catalogue; however, when a correction is made for the offset, which was known to 17th century astronomers, the catalogue is more accurate than that of Brahe by a factor of two. We provide machine-readable tables of the catalogue.
Key words: astrometry / history and philosophy of astronomy
Full Tables 5–7 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/649/A112
© ESO 2021
1. Introduction
It is well known that the measurements by Tycho Brahe of the positions of stars and planets in the sky were an order of magnitude more accurate than those of earlier astronomers, such as Ptolemaios (or Hipparchos) and Ulugh Beg. As a result, Brahe’s catalogue of positions of the fixed stars became the new standard, with editions in 1598 (manuscript), 1602 (in Astronomiae Instauratae Progymnasmata), and in 1627 (by Kepler, Tabulae Rudolphinae). Machine-readable versions of these catalogues and an analysis of their accuracy are provided by Verbunt & van Gent (2010, 2012).
It is less well known that Brahe was preceded by Wilhelm IV, Landgraf von Hessen-Kassel, whose measurements were equally accurate. As an aspiring astronomer, Brahe visited the already experienced observer Wilhelm IV in April 1575 and studied his instruments. In the correspondence that followed, Wilhelm IV in turn profited from suggestions for improved measurement accuracy by Brahe (Hamel 2002).
The star catalogue of Wilhelm IV was mostly based on work by Wilhelm IV himself and by two people he employed: the mathematician-astronomer Christoph Rothmann and the brilliant clock-maker, instrument maker, and mathematician Jost Bürgi. All three of them participated in the observations, with instruments made by Bürgi. The computational work was presumably done by Rothmann and Bürgi. We describe the work at the observatory in Kassel and the historical context in a separate paper (Schrimpf & Verbunt 2021). The manuscript of the catalogue was almost ready for print. It is available as a scan via the on-line portal of the library of Kassel University (Wilhelm IV 1587). Rothmann also wrote a handbook for astronomers of his time, describing observational and computational methods that were used to prepare the star catalogue. The Latin manuscript for this handbook is available via the on-line portal of the library of Kassel University (Rothmann Handbook), and it has been printed by Granada et al. (2003), with an introduction in German.
The catalogue only appeared in print, edited by Curtz in 1666, long after the dissemination of Brahe’s catalogue, and as a result it had a rather limited impact, even though the catalogue was reprinted (with adaptations) by Hevelius (1690) and by Flamsteed (1725). Hamel (2002), borrowing extensively from Wolf (1878) and Repsold (1919), has written a monograph on the astronomical research in Kassel under Wilhelm IV, in which he mentions three earlier star catalogues, with 58, 58, and 121 stars, respectively. We intend to compare these different catalogues, which mark the progress to the higher accuracy, in a future paper. In the current paper we study the manuscript version of the final catalogue from 1587, which contains 387 entries.
Rothenberg (in Hamel 2002) compared this final catalogue with the SAO star catalogue (SAO 1966), identified 361 stars securely, found a possible counterpart for seven, and was unable to identify 14 stars. Not included in these numbers are three repeated stars and two clusters of stars (see Table 2). Assuming an offset in right ascensions of 6′, he found systematic + random errors 0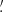 22 + 1
22 + 1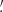 2 in right ascension and 0
2 in right ascension and 0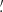 82 + 1
82 + 1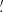 5 in declination, respectively. No details are provided about individual (non-)identifications. We refer to the final catalogue below as Manuscript, identify all of its entries with use of the HIPPARCOS Catalogue (ESA 1997), analyse the results in detail, and provide a machine-readable version of catalogue and analysis in the following three data files: WilhelmIV (see Table 5), WilhelmIV-Dist (Table 6), and WilhelmIV-Alt (Table 7).
5 in declination, respectively. No details are provided about individual (non-)identifications. We refer to the final catalogue below as Manuscript, identify all of its entries with use of the HIPPARCOS Catalogue (ESA 1997), analyse the results in detail, and provide a machine-readable version of catalogue and analysis in the following three data files: WilhelmIV (see Table 5), WilhelmIV-Dist (Table 6), and WilhelmIV-Alt (Table 7).
2. Description of Manuscript and its epoch
Manuscript is organised by constellation and lists all 1028 entries from the star catalogue by Ptolemaios, plus four added stars, of which two are in the Pleiades. For all 1032 entries, column one of Manuscript gives the Latin name or description of the star, column seven provides the position in the catalogue of Ptolemaios, or for the added stars the statement ’in tabulis non extat’ (not present in the table). Column eight gives the magnitude. The longitudes in Manuscript are larger by 21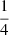 degrees than those in the catalogue of Ptolemaios, to bring them to equinox 1586.
degrees than those in the catalogue of Ptolemaios, to bring them to equinox 1586.
For a limited number of stars, the intermediate columns provide new measurements (angular distances between stars in columns two and three and meridional altitudes in column four) and the equatorial and ecliptic coordinates derived from them (in columns five and six, respectively). Manuscript gives newly determined ecliptic coordinates for 387 out of the 1032 entries. We collected these entries in WilhelmIV, and we numbered the stars in order of occurrence, with a W number (see Table 1). The three stars that are (knowingly) repeated in Ptolemaios also occur twice in the manuscript, so that WilhelmIV contains 384 independent entries. Three of the four added stars have ecliptic coordinates. We list these stars, together with the repeated entries and the entries with non-stellar identifications, in Table 2. For the fourth added star, in Aquila, two angular distances to other stars, but no equatorial or ecliptic position, are given; we did not include this star in WilhelmIV, and we refer to it as W 999. From the angular distances given, we derive that it corresponds to ϵ Aql.
Constellations in Manuscript and numbers of stars in them.
Non-stellar, added, and repeated entries in Manuscript.
For 384 entries (381 independent ones), the manuscript gives the angular distance between the entry and one or more stars named in column two. For all these entries the ecliptic coordinates are given (in Col. 6). We indicate the angular distance with ϕ. No ϕ is given for W 87, W 88, or W 224, but column six does give their ecliptic position. For five stars, the distance to a reference star is repeated, with the roles of star and reference star reversed; we refer to the second occurrence as reverse repeated angle. As we explain below, the position of W 224 (Aldebaran) is the anchor point from which absolute positions for other entries were determined.
For 346 entries (343 independent ones), Manuscript gives the altitude at meridian passage and the equatorial coordinates. For stars that are always above the horizon, both superior and inferior altitudes are listed, which are indicated by ‘superne’ or ‘inferne’. Table 3 details the frequencies of angular distances and altitudes in Manuscript.
Frequency of different combinations of information given in Manuscript, after the removal of three repeated entries and five reverse repeated angles.
All angles in Manuscript are given in degrees and sexagesimal fractions; for latitudes or declinations, S or M was added for Septentrionalis (north) or Meridionalis (south), respectively. For the machine-readable tables, we converted the fraction into seconds:
where ϕ, h, α, δ, and β refer to the angular distance, altitude in the meridian, right ascension, declination, and ecliptic latitude, respectively. The values of Fq in the catalogue are such that Sq is always an integer, one of the following 14: 0, 6, 10, 12, 15, 20, 24, 30, 36, 40, 45, 48, 50, or 54. Remarkably, 18 (=3/10) and 42 (=7/10) were not used. For ecliptic longitude, a zodiacal sign was used, which we converted into a number Z, ranging from 1 for Aries to 12 for Pisces :
In the preamble of the 121-star catalogue from 1586, the equatorial and ecliptic coordinates of Aldebaran are given and said to form the fundament of the coordinates of all other stars in the catalogue. The coordinates of Procyon are also given and said to be very accurate. A translation of this Latin preamble is provided by Schrimpf & Verbunt (2021). The coordinates of Aldebaran and Procyon in this preamble (Table 4) are identical to those given in Manuscript, with the exception of the longitude of Procyon, for which Fλ is larger by 15 in Manuscript.
Equatorial and ecliptic positions of Aldebaran and Procyon.
For geophysical latitude ϕG, the declination of a star follows immediately from its altitude at meridional culmination with Eq. (9). Conversely, from the altitudes in Manuscript (54°17′ for Aldebaran and 44°54′ for Procyon) and their declinations, we can derive the value of ϕG used in constructing the catalogue. For both Aldebaran and Procyon, exactly the same value ϕG = 51° 19′ follows. This agrees with the value given in Chapter 10 of Rothmann’s Handbook.
Ecliptic coordinates were computed from equatorial coordinates with Eqs. (12) and (13), which require a value for the obliquity ϵ. From the equatorial and ecliptic coordinates of Aldebaran and Procyon in the preamble and Manuscript, we can compute the obliquity used in constructing the catalogue. The ecliptic coordinates derived from the equatorial coordinates match those of Aldebaran in the preamble and in the manuscript exactly and, due to rounding, those of Procyon approximately for obliquity ϵ = 23° 31′ (Table 4). Our analysis in Sect. 4.3 of the full catalogue confirms this value for ϵ, somewhat surprisingly since values of ϵ = 23° 31′24″ and ϵ = 23° 31′30″ are given in Chapters 10 and 12 of Rothmann’s Handbook, respectively.
Manuscript does not give the equinox. It is based on observations made in 1586 and 1587, and was presumably written in 1587, which suggests an equinox of 1586 (Wolf 1878). The manuscript of the catalogue for 121 stars gives an equinox of 1586. The stellar positions of the stars in this catalogue are, with few exceptions, identical to those of the manuscript. Therefore, we used 1 January 1586 (old style) = JD 2300345 as the epoch and the equinox of Manuscript.
The positions of the entries in Manuscript are anchored on the position of Aldebaran. Brahe determined the right ascension of this star to be 6 arcmin smaller than the value used in Kassel, and he discussed this discrepancy with Rothmann and Wilhelm IV (see Wolf 1878; Hamel 2002 for more detail). From the way the positions of the other stars were derived from the measurements (see Eqs. (7)–(9) and (11)), this would imply that all right ascensions in the Manuscript are too large by 6 arcmin if Brahe’s value is correct. Comparison with the values computed from HIPPARCOS-2 data (van Leeuwen 2007) show that Brahe’s criticism was justified (Table 4).
3. Identification and machine-readable tables
The method of identification of the stars largely follows the procedure outlined in Verbunt & van Gent (2010), with two modifications. For the computation of the star positions at the epoch of the catalogue, we used data from HIPPARCOS-2, the reanalysis of the HIPPARCOS Catalogue by van Leeuwen (2007). Furthermore, we took the limited spatial resolution of the naked human eye into account by merging stars within 2′ of one another. The visual magnitudes are from the original HIPPARCOS Catalogue (ESA 1997). On the basis of this, we prepared a version of the HIPPARCOS Catalogue converted to epoch 1 January 1586, as detailed in Appendix A. When referring to the HIPPARCOS Catalogue below, this converted version is meant.
In view of the systematic offset of 6′ in right ascension noted by Brahe, which is confirmed in Table 4 and further discussed in Sect. 6, we searched for counterparts with
by looking for the entry with the smallest value of
This equation, the haversine function, is also accurate for very small angles. For stars for which Manuscript gives ecliptic coordinates only, we converted the ecliptic coordinates to equatorial coordinates, using the value for the obliquity that was used in Kassel, ϵ = 23° 31′. In virtually all cases, the nearest star is the counterpart, and in some cases a brighter star at a slightly larger distance is the counterpart. For W 112 and W 247, the counterpart is a star cluster (see Table 2).
The machine-readable version of Manuscript was divided intro three tables to minimise the number of empty slots. WilhelmIV contains the equatorial and ecliptic coordinates and the magnitudes resulting from the observations in Kassel, corresponding to columns one, five, six, and eight of Manuscript (Table 5), and results of our analysis with the HIPPARCOS Catalogue. In addition to the positional errors Δc derived from the corrected right ascensions with Eq. (1), we also list positional errors when no correction for the offset in right ascension is applied. For this, we converted the equatorial coordinates αHIP and δHIP to ecliptic coordinates λHIP and βHIP with the value of the obliquity in 1586 according to modern theory 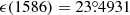 (Seidelman 1992, Eq. 3.222-1). For each HIPPARCOS entry with V ≤ 5.3, we computed the angular distance Δ between the position in the old catalogue and the position computed from HIPPARCOS data with
(Seidelman 1992, Eq. 3.222-1). For each HIPPARCOS entry with V ≤ 5.3, we computed the angular distance Δ between the position in the old catalogue and the position computed from HIPPARCOS data with
First and eigth line of the machine-readable table WilhelmIV.
and
We consider all our identifications to be secure.
WilhelmIV-Dist gives the angles measured between entries and reference stars, corresponding to columns one to three of Manuscript (Table 6). All reference stars listed in the second column of Manuscript also occur in the first column, and thus can be identified with a W number. WilhelmIV-Alt contains the altitude(s) for each star, Col. 4 of Manuscript.
First lines of the machine-readable table WilhelmIV-Dist, with examples of a repeat entry (F = 1) and of a reverse repeat entry (F = 2).
First lines of the machine-readable table WilhelmIV-Alt.
4. Accuracy of the computations
The accuracy of computation can be determined from tabulated numbers in Manuscript that were derived from other tabulated numbers.
4.1. Altitudes and declinations
The relations between the geographical latitude ϕG of the observer, the declination δ of a star, and its altitude h at meridian passage for culminations above (superior) or below (inferior) the celestial north pole in the northern direction as well as culminations in the southern (meridional) direction are
respectively. In these equations h is the true altitude. The observed or apparent altitude ha is affected by atmospheric refraction R:
The values for refraction used by Rothman, RR, are listed in Table 8; according to Rothmann, no refraction occurs for h ≥ 29°. As noted above, all entries in Manuscript for which an altitude is listed have equatorial coordinates. A single altitude is listed for 311 entries, namely 293, ten, and eight entries from meridional, superior, and inferior culmination, respectively; for 32 entries, the altitudes are listed for both superior and inferior culmination. If we enter these altitudes and ϕG = 51° 19′ into Eqs. (7)–(9), we obtain declinations δh equal to the catalogued declinations δW listed in column five of Manuscript for all but three and two values obtained from meridional and superior culmination, respectively, as shown in Fig. 1. For meridional altitudes, h < 29°; this implies that the tabulated altitudes are true altitudes, corrected for refraction – or at least considered as such in the computation of δ. Twenty-four of the inferior altitudes lead to a different declination than given in the catalogue, that is δh ≠ δW. The differences in declinations derived from altitudes of inferior culmination with the catalogued values roughly follow the atmospheric refraction, leading to the assumption that these are apparent altitudes. However, the correspondence is not exact, which we are inclined to ascribe to rounding and/or copying errors.
 |
Fig. 1. Difference between the declination δh computed from the altitude with Eqs. (7)–(9) and the declination δW listed in Manuscript for ϕG = 51° 19′. With few excaptions, the computations are exact for superior and southern culminations. The values δh from inferior culmination are systematically too high for low altitudes. Values for which δh ≠ δW are labelled with W for those entries for which only one altitude is listed, and for W 9. The solid curve gives the refraction RR according to Rothmann. Stars to the right of the vertical dashed line have R = 0, according to Rothmann. |
Refraction as a function of altitude according to Rothmann.
Thus, the 378 altitudes listed in the Manuscript, and collected by us in WilhelmIV-Alt, lead to 343 independent entries with declinations. The other altitudes are three repeated entries and 32 altitudes of inferior culminations, which are not used.
4.2. Angles between stars and right ascensions
The standard equation for the angular distance ϕ between two stars may be rewritten in equatorial coordinates as
showing that the right ascension α of a star can be computed from its declination δ if the angle ϕ is known to a reference star with known equatorial coordinates αr and δr. Manuscript contains 500 values for ϕ between entries, of which 410 are independent and between stars with listed equatorial coordinates. Of these 410 entries, 273 have ϕ with one reference star, 67 with two reference stars (i.e. 134 values of ϕ), and one (W 1) with three reference stars.
To retrace the steps presumably taken in Kassel, we used the tabulated values of ϕ in subsequent iterations. In the first iteration, we have one reference star, Aldebaran, for which angles were given to 21 entries with declination known from an altitude measurement. The first iteration thus allows the computation of the right ascension for these 21 entries. Seven of these, which occur in the second column of WilhelmIV-Dist, can be used as a reference star in the second iteration. After eight iterations, a total of 64 stars have been used as a reference star, and the equatorial coordinates of 342 stars are known. Only one star with equatorial coordinates in Manuscript, W 288, is not found in these iterations; the angle ϕ in WilhelmIV-Dist between this star and W 291 does not help as no altitude h and thus no equatorial coordinates are listed for W 291.
To check the accuracy of the computation of the right ascension αeq from the right-hand side of Eq. (11) with the catalogue value αW, we must take into account that only 14 values for the number of seconds Sα are allowed as tabulated values (as explained with Eq. (1)). Thus, each computed value Sαeq is bracketed by two allowed values. For the 273 entries with ϕ given to a single reference star, the catalogued value Sα corresponds to the nearest bracketing value Sαeq in 181 cases, to the other bracketing value in 54 cases, and to neither in 38 cases.
For the 137 entries with ϕ given to two or, in the case of W 1, three reference stars, the catalogued value of α corresponds to the nearest bracketing value in 74 cases, to the other bracketing value in 28 cases, and to neither in 35 cases. In those cases where both values of α are the same after rounding, no choice is necessary. If the two (or three) computed values for α are different, the catalogue sometimes gives the value derived from the average (for example for W 29); sometimes it gives the value derived from just one computed value of α. We have not been able to determine a criterion on the basis of which this one value is chosen: It can be the one found in the lowest or in the highest iteration, the one found with the largest or smallest angle ϕ to the reference star, or the one found with the reference stars with the lowest or highest absolute value of the declination |δr|.
To see whether in computing the right ascensions the tabulated values of δ or the values computed from altitudes were used, we compared the results for αeq for the reference star W 25 for both options. This indicates that the tabulated values were used.
Figure 2 illustrates the difference distribution between the catalogued value αW and the value αeq computed with Eq. (11). The distributions are shown for the exact values αeq computed with Eq. (11) and for the values αeq rounded to the nearest allowed integers of Sα. For entries with more than one ϕ, we used the first ϕ only to avoid double counting one entry in the catalogue; this leaves 341 values. The difference between the two curves shows the effect of rounding: The rounding masks small computational errors when the catalogued value is the bracketing allowed value closest to the exactly computed one; it increases the error when the catalogued value corresponds to the other bracketing value. As a result, the median value of |αeq − αW| is 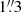 for exact αeq; however, after rounding, 217 entries have |αeq − αW| = 0. The average and rms of αeq − αW are 0
for exact αeq; however, after rounding, 217 entries have |αeq − αW| = 0. The average and rms of αeq − αW are 0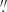 7 and 6
7 and 6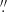 6 for the exact αeq values, and 0
6 for the exact αeq values, and 0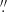 6 and 6
6 and 6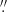 7 for the rounded αeq values. As we see below, these errors are negligible with respect to the measurement errors.
7 for the rounded αeq values. As we see below, these errors are negligible with respect to the measurement errors.
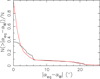 |
Fig. 2. Complement of the normalised empirical cumulative distribution function ECDF, i.e. 1−ECDF for the absolute values of the differences between the right ascension αeq computed with Eq. (11) and the catalogued right ascension αW. Red: vertical axis for the exact values αeq. Black: for the values αeq rounded to the nearest allowed integer of Sα. |
4.3. Conversion of equatorial to ecliptic coordinates
The equations which convert equatorial into ecliptic coordinates are
and
We compare the values for λ and β obtained with these equations from the equatorial coordinates in column five of Manuscript with the values listed in Col. 6. In accordance with our finding in Sect. 2 and Table 4, we set the obliquity to ϵ = 23° 31′.
The angular difference ϕeq − W between the computed and catalogued positions in ecliptic coordinates is found with
Figure 3 shows the complement to the normalised empirical cumulative distribution function ECDF, that is 1−ECDF of the differences ϕeq − W found with Eqs. (12)–(14) for the exact computed values of λeq and βeq and for their values rounded to the nearest allowed values. The average and rms values in our first calculation were very high because of three outliers, W 55, W 214, and W 374. Comparison of the calculated and catalogue positions indicates errors in Manuscript for these entries, and we emended the ecliptic coordinates accordingly (see Appendix B.3). For 113 entries, the rounding leads to ϕeq − W = 0. The median value of ϕeq − W is 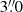 for exact calculation; however, after rounding to allowed values, it becomes
for exact calculation; however, after rounding to allowed values, it becomes 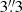 . The average and rms values are 4
. The average and rms values are 4 1 and 4
1 and 4 2 for the exact values, and 3
2 for the exact values, and 3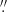 9 and 4
9 and 4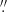 7 for the rounded values.
7 for the rounded values.
 |
Fig. 3. Complement to the normalised empirical cumulative distribution function, i.e. 1-ECDF, of the differences ϕeq − W between the catalogued position and the position computed with Eqs. (12) and (13). Red: vertical axis for the exact computed values λeq and βeq. Black: for the values rounded to the nearest allowed integer of Sλ and Sβ. |
If we adopt a value of the obliquity 1′ higher or lower than 23°31′, the average and rms values of ϕeq − W increase strongly. This confirms that the value actually used is indeed 23°31′.
4.4. Position from angles with two other stars
For 41 catalogue entries, ecliptic coordinates are given, but no altitudes or equatorial coordinates. For 37 of these, angles ϕi are listed to two reference stars with known coordinates λi, βi, i = 1, 2. Each angle ϕi defines a circle around its reference star, and one of the intersections between the circles gives the previously unknown position λ, β for one of the 37 stars. To calculate these, we rewrote the equivalent of Eq. (11) in ecliptic coordinates in the form of two non-linear equations for two unknowns λ and β:
These can be solved iteratively. Whether this is the method by which the ecliptic coordinates of the 37 stars were determined is not clear. The catalogued coordinates of the four stars without altitude and with no or just one angle to another star indicate that not all measured altitudes and/or angles are catalogued.
On the assumption that the coordinates of 37 entries were determined from Eq. (15), presumably by trial and error, we checked its accuracy in two ways. First, we computed |F1(λ, β)| + |F2(λ, β)| from the values λ, β, λi, βi, and ϕi given in the catalogue. Twenty-two values are less than 10−5, and fifteen lie between 10−4 and 10−5, indicating an excellent accuracy of the computations. Second, we used a modern code to solve Eq. (15) by numerically minimising |F1(λ, β)| + |F2(λ, β)| as a function of λ and β, and we computed the angle ϕeq12 − W between the optimal computed position λeq12, βeq12 and the catalogued position λW, βW. As initial guess for the iterative solution of Eq. (15), we used the catalogued position, and we ended the iteration when |F1|+|F2|< 10−6. The results are shown in Fig. 4, ϕeq12 − W for the exactly computed position, and for the computed position rounded to the nearest allowed values of Sλ and Sβ. The median is 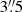 for the exact and
for the exact and 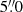 for the rounded solutions.
for the rounded solutions.
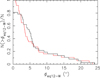 |
Fig. 4. Complement to the normalised empirical cumulative distribution function, i.e. 1-ECDF of the differences ϕeq12 − W between the position computed with Eq. (15) and the catalogued position. Red: vertical axis for the exact computed values λeq12 and βeq12. Black: for the values rounded to the nearest allowed integer of Sλ and Sβ. |
5. Accuracy of the measurements
By comparing the catalogued altitudes at culmination and the angles between stars with values computed from modern HIPPARCOS data and modern refraction values, we can determine the accuracy of the measurements.
5.1. Measured altitudes
As we have seen in Sect. 4.1, the derivation of the declinations of the entries in Manuscript indicates that the catalogued altitudes hW are the true altitudes h. The altitude ha measured in Kassel is found by adding the refraction RR according to Rothmann (see Eq. (10)). From the modern HIPPARCOS data, we determined the declination in 1586, and from this the actual true altitude hHIP with Eqs. (7)–(9) to which the modern value R for refraction was added. Repeated entries were ignored, as were the two entries representing a cluster: W 112 and W 247. Atmospheric refraction, especially at low altitudes, depends on meteorological conditions, and in the absence of detailed information can be given only for average conditions. For this, we used an equation by Sæmundsson (1986, cited in Meeus 1998):
The division by 1° in the denominator is explicitly shown to indicate that the denominator is dimensionless. The difference between the altitudes observed in Kassel and those predicted from HIPPARCOS data is
In the computation of hHIP from the declination, we used the modern value 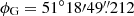 ; this is 10
; this is 10 788 less than the value determined in Kassel – or about 330 m on the ground. If the altitudes tabulated in Manuscript are the apparent altitudes ha (the rationale for this possibility is given below), comparison with modern data gives
788 less than the value determined in Kassel – or about 330 m on the ground. If the altitudes tabulated in Manuscript are the apparent altitudes ha (the rationale for this possibility is given below), comparison with modern data gives
For h > 29°, where RR = 0, dh = Δh. In Fig. 5, we show Δh and dh as a function of the altitude, together with linear fits. To eliminate undue influence of outliers, we iteratively determined the rms of the distances to the best fit and removed points at distances of more than 3 rms. For three entries, the catalogue value is clearly wrong: W 108, W 283, and W 367 with 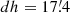 , −49
, −49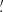 1, and −61
1, and −61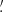 8, respectively. The rms values show that rounding Sh to allowed values has a negligible effect and may be ignored in the analysis.
8, respectively. The rms values show that rounding Sh to allowed values has a negligible effect and may be ignored in the analysis.
 |
Fig. 5. Top: differences Δh (left) and dh (right) between the altitudes measured in Kassel and the altitudes that should have been measured according to modern data (Eqs. (17) and (18)). The solid lines show the best linear fit and its 3-rms range. Points outside this range were ignored in the fit. To the right of the dashed vertical line RR = 0 and thus Δh = dh. Bottom: cumulative distribution of the difference between the measured Δh and dh and their best fit, compared with the distribution expected for a Gaussian with σ equal to the rms of the differences with the best fit. KS indicates the p-value from a two-sided Kolmogorov-Smirnov test for which the observed points are drawn from the Gaussian. |
Figure 5 shows two remarkable features. First, the points from superior culmination on average give a lower difference Δh than the points from meridional culminations at the same altitude. In addition to results for fits to all points, we therefore show in Table 9 the results for fits to data from southern and northern culminations separately. For fits to all h and for fits to h > 29°, the dependence of Δh and dh on altitude h is significantly shallower for the northern culminations than for the southern culminations.
The second striking feature of Fig. 5 is the non-zero slope of the fit to Δh that ill describes the points at h < 29°, which curve upwards towards lower h. The results for the fits of Δh to points at h > 29° are incompatible with the fits to all h, when data combined from northern and southern culminations are considered, and also when data from northern or southern culminations are considered separately. In contrast the fits of dh to data at h > 29° are compatible with the corresponding fits for all h, especially when southern and northern culminations are fitted separately. A striking illustration of this is provided by the three points with the lowest altitude, which are well outside the 3-rms range in the fit for Δh, but well within the 3-rms range in the fits for dh (Fig. 5).
If only points more than 4 rms are iteratively removed in the fitting procedure, all values for the intercept a and slope b of the best fits are the same within the error as those listed in Table 9. Hence our conclusions are independent of the exact criterion for inclusion and rejection of points in the fit.
We are thus faced with the conundrum that the comparison between the altitudes and declinations in the catalogue indicates that the altitudes are the true altitudes, whereas the comparison of the altitudes with those predicted from modern HIPPARCOS data suggests that they are the apparent altitudes. For the fits to all points and to those from southern culminations only Δh and dh are close to zero at altitude 90°. This indicates that the measurement apparatus was aligned to the zenith rather than to the horizon, understandably in hilly country. Most points from northern culminations have Δh < 0 and dh < 0, which may indicate a misalignment with the zenith for these measurements. The dependence of Δh and dh on altitude h could be due to an inaccurate scale division. The problem with this explanation is the near absence of a dependence of Δh on h for the northern culminations.
5.2. Angles between stars
Manuscript lists the angular distances ϕ between stars in column two. From the modern HIPPARCOS data, we computed the angle ϕHIP at the time of the observation and subtracted this from ϕ to obtain the measurement error. The results are shown in Fig. 6. There is no dependence on ϕ and the average difference is compatible with zero. A straight-line fit, iteratively removing outliers at more than 3 rms, gives
 |
Fig. 6. Top: differences between the angles ϕ between two stars as given in Manuscript and the angles ϕHIP derived from modern HIPPARCOS data, as a function of ϕ. For some outliers, W is indicated (Table 6). Bottom: cumulative distribution of the differences compared with a Gaussian centred on zero. |
Assuming that the average value is zero, the rms of ϕ − ϕHIP is 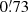 , which is sufficiently large to ensure that rounding Sϕ to allowed values has a negligible effect. The furthest outliers are the angles between W 108-W 105 and between W 339-W 331, for which
, which is sufficiently large to ensure that rounding Sϕ to allowed values has a negligible effect. The furthest outliers are the angles between W 108-W 105 and between W 339-W 331, for which 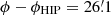 and −20
and −20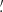 6, respectively.
6, respectively.
6. Accuracy of the catalogue
Figure 7 shows the distributions of the magnitudes of the stars as given in WilhelmIV, and of the modern magnitudes of their counterparts. The magnitudes in the catalogue correlate well with the modern magnitudes. As expected in a catalogue of a limited size, most entries are bright. For the geographical latitude of Kassel, ϕG = 51° 19′, stars with δ < −38° 41′ are always below the geometric horizon, and the practical observation limit is closer to the celestial equator. The southernmost star in WilhelmIV is ϵ Sgr, at δ = −34° 20′, followed by Fomalhout at δ = −31° 41′. WilhelmIV is virtually complete at modern magnitude V < 3.0 and δ > −31°: Only γ2Sgr, γ Hya, γ Eri, and α2CVn are missing. Extending the magnitude limit to V < 3.5 shows that 24 more stars with δ > −31° are missing.
 |
Fig. 7. Left: distribution of the magnitudes given in WilhelmIV (black) and of the magnitudes of their counterparts in the HIPPARCOS catalogue (red) for all securely identified stars. Right: distribution of the magnitudes of the HIPPARCOS counterparts, separately for each magnitude in WilhelmIV. The numbers show the number of stars in each frame. |
The excellent overall accuracy of WilhelmIV is indicated by the fact that all entries can be securely identified with HIPPARCOS counterparts, or in two cases clusters of stars. In Sect. 4.3, we have shown that equatorial coordinates were accurately converted into ecliptic coordinates. We therefore include in our analysis equatorial coordinates which are not in WilhelmIV but were computed by us from the ecliptic coordinates. For small angles Δ between the catalogue and HIPPARCOS positions, we have approximately cos δ ≃ cos δHIP and
A measurement error d in the direction of right ascension leads to an error of Δα ≃ d/cos δ, hence to a large value for Δα at high declinations. This masks the effect of a systematic offset. For this reason, we show in Fig. 8 (top left) the distribution of Δα (Eq. (3)) for angles |δ|< 20° only. The average is 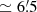 , which is close to the offset of 6′ of the vernal equinox in WilhelmIV found by Brahe (cf. Table 4), and this justifies our correction to the catalogued right ascensions before we identified the entry. Astronomers in the 17th century knew about the offset found by Brahe, and thus they could correct for it. Curtz (1666) approximated the correction by moving the equinox of the catalogue to 1593, seven years later. Figure 8 (top right) shows the distributions of Δαc cos δ, and Δδ, which reflect the measurement errors.
, which is close to the offset of 6′ of the vernal equinox in WilhelmIV found by Brahe (cf. Table 4), and this justifies our correction to the catalogued right ascensions before we identified the entry. Astronomers in the 17th century knew about the offset found by Brahe, and thus they could correct for it. Curtz (1666) approximated the correction by moving the equinox of the catalogue to 1593, seven years later. Figure 8 (top right) shows the distributions of Δαc cos δ, and Δδ, which reflect the measurement errors.
 |
Fig. 8. Distributions of various positional errors. Entries identified with clusters and duplicate entries are not included. The histograms include entries for which equatorial coordinates are not given in WilhelmIV, but computed by us from the ecliptic coordinates. The numbers in the frame indicate the numbers of values to the left of, within, and to the right of the frame limits. Top left: distribution of Δα (Eq. (3)) for entries with |δ|< 20°. The average shift, indicated with a vertical dashed line, is |
The shift of 6′ in the right ascensions leads to an erroneous location of the ecliptic, to the right of the correct location, in the computation of ecliptic coordinates from equatorial coordinates (Eqs. (12) and (13)). This causes an error of 6′ in λ at λ = 90° or 270°, but to an error smaller by a factor of cos ϵ at the equinoxes. It has no effect on β at λ = 90° or 270°, but at the vernal and autumnal equinoxes it leads to errors of about 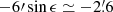 and
and 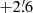 , respectively. Thus the offset in right ascension is reflected in an offset in the longitudes, visible in the distribution of Δλ cos β, and to a double peak in the distribution of Δβ as shown in Fig. 8 (bottom left). The error also increases the angle Δ (Eq. (6)), which peaks slightly above 6′, as shown by the black curve in Fig. 8 (bottom right). The pronounced tails of the distributions of Δλ cos β and of Δ derived from the (uncorrected) ecliptic coordinates arise because the effect of the offset of the vernal equinox decreases with declination with cos δ.
, respectively. Thus the offset in right ascension is reflected in an offset in the longitudes, visible in the distribution of Δλ cos β, and to a double peak in the distribution of Δβ as shown in Fig. 8 (bottom left). The error also increases the angle Δ (Eq. (6)), which peaks slightly above 6′, as shown by the black curve in Fig. 8 (bottom right). The pronounced tails of the distributions of Δλ cos β and of Δ derived from the (uncorrected) ecliptic coordinates arise because the effect of the offset of the vernal equinox decreases with declination with cos δ.
Correcting the right ascensions by subtracting 6′ much improves the accuracy of the catalogue (Table 10), as shown for right ascension and declination in Fig. 8 (top right) and for the total error by the blue curve in Fig. 8 (bottom right). To enable a fair comparison with the positional accuracy of the star catalogue of Brahe – as edited by Kepler (1627) – we show the errors Δ only for those stars that are present in both catalogues.
7. Discussion and comparison with Brahe
The observations of stars made at the castle of Kassel, under the patronage of Wilhelm IV, Landgraf von Hessen-Kassel, with instruments built by Jost Bürgi, reached an accuracy an order of magnitude better than anything achieved before. Meridional altitudes and angles between stars were measured with an accuracy of 44″. The accuracy of instruments and measurements profited from the exchanges on these topics between Wilhelm IV and Tycho Brahe (Hamel 2002). The computations with which the measurements were converted to celestial coordinates were very accurate as well. An error of about 6′ in the position of the vernal equinox, however, corrupted the celestial coordinates, which were tabulated for 382 stars and two open star clusters in ecliptic coordinates and for 342 stars and one open cluster in equatorial coordinates. The offset of the vernal equinox was discovered by Brahe; if a correction is made for this offset, the positional accuracy Δc of WilhelmIV is better by a factor of two than that of the star catalogue of Brahe himself (Table 10).
Wesley (1978) determined the accuracy of the measurements with various instruments by Brahe. He determined the measurement accuracy for eight fundamental stars, used by Brahe as reference stars for measurements on other stars, by comparing the meridian altitudes given by Brahe with modern computation. This is what we did in Sect. 5.1 for WilhelmIV-Alt. Our results are compared with those by Wesley for the mural quadrant of Brahe in Table 11. The measurement errors in WilhelmIV-Alt are on the whole smaller, averaging about half the errors of the mural quadrant of Brahe.
Measurement accuracies determined from meridian altitudes for the mural quadrant of Brahe, determined by Wesley (1978), and for WilhelmIV-Alt, determined in Sect. 5.1, for eight of the fundamental stars of Brahe.
The star catalogue WilhelmIV is corrupted by the offset of the vernal equinox. Thus, the positional errors in WilhelmIV are larger than those for most of the stars in Brahe’s catalogue. The catalogue by Brahe, however, is corrupted for a significant fraction of its entries by errors in converting measurements to celestial positions, for example by confusing measurements of different stars and by scribal errors, as shown by Rawlins (1993). Of the 366 stars that are common to WilhelmIV and the star catalogue of Brahe (Kepler 1627), no less than 36 have a positional error larger than 10′ in Brahe’s catalogue, but only eight in even the uncorrected version of WilhelmIV. It is therefore a moot question as to which of the two catalogues is more accurate. However, when we consider the positional errors in WilhelmIV after correction for the offset in right ascensions, the combination of more accurate measurements and more diligent computing causes WilhelmIV to be more accurate (Fig. 8, bottom right).
The value of the obliquity used in WilhelmIV for the conversion of ecliptic coordinates into equatorial ones, or vice versa, is more accurate than the value ϵ(1601) = 23° 21′30″ used by Brahe. The geographical latitudes used in WilhelmIV and by Brahe are both remarkably accurate, and they have no consequence for the conversion of altitudes into declinations. This conversion is affected, however, by the erroneous values used for atmospheric refraction.
Wilhelm IV and his collaborators did not publish their work, as we mentioned in the Introduction, but it is interesting to know that the accuracy of Brahe was not unique. Of course, Brahe published not only his star catalogue, but many other works on the renovation of astronomy. The accuracy of his planetary positions enabled Kepler to show that Mars moves in an ellipse with the Sun in a focal point, and by extension that all planets do. Thus Brahe and Kepler together revolutionised astronomy.
To our knowledge, Manuscript is the first star catalogue to give both equatorial coordinates and ecliptic coordinates. Earlier star catalogues by Ptolemaios (±150), al-Sufi (±964), and Ulugh Beg (1437), as well as the later star catalogue of Brahe (1627) only provided ecliptic coordinates. Riccioli (1651) and Hevelius (1690) also provided both ecliptic and equatorial coordinates. de Houtman (1603) gave the first printed star catalogue with equatorial coordinates, but no ecliptic coordinates.
Acknowledgments
We thank Erik Høg for instigating this work. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. Computations by FV use Numerical Recipes by Press et al. (1986). Computations by AS use Astropy, a community–developed core Python package for Astronomy (Astropy Collaboration 2013) and The Naval Observatory Vector Astrometry Software (NOVAS) for astrometric quantities and transformations (Bangert et al. 2011).
References
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bangert, J., Puatua, W., Kaplan, G., et al. 2011, User’s Guide to NOVAS Version C3.1 (Washington, DC: USNO) [Google Scholar]
- Bastian, U., & Röser, S. 1993, PPM Star Catalogue, III (Heidelberg: Spektrum Akademischer Verlag) [Google Scholar]
- Curtz, A. 1666, Historia coelestis, Pars Posterior, 553, http://www.e-rara.ch/zut/wihibe/content/titleinfo/2961545 (Augsburg, 1666) [Google Scholar]
- Ducati, J. R. 2002, VizieR On-Line Data Catalog: Catalog of Stellar Photometry in Johnson’s 11-color system. (CDS/ADC Collection of Electronic Catalogues 2237) [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues (Noordwijk: SP-1200, ESA Publications Division) [Google Scholar]
- Flamsteed, J. 1725, Historia Coelestis Brittanicae, Volumen Tertium (London: Meere) [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Granada, M. A., Hamel, J., & von Mackensen, L. 2003, Christoph Rothmanns Handbuch der Astronomie von 1589 (Frankfurt am Main: Harri Deutsch) [Google Scholar]
- Hamel, J. 2002, Die astronomischen Forschungen in Kassel unter Wilhelm IV (Verlag Harri Deutsch: Frankfurt am Main) [Google Scholar]
- Hevelius, J. 1690, Catalogus Stellarum Fixarum (Gdansk: Johann Stolle) [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V., et al. 2010, A&A, 355, L27 [Google Scholar]
- de Houtman, F. 1603, Spraeck ende woord-boeck, inde Maleysch endeMadagaskarsche talen (Amsterdam: Cloppenburch) [Google Scholar]
- Kepler, J. 1627, Tabulae Rudolphinae (Ulm: Jonas Saur) [Google Scholar]
- Knobel, E. B. 1917, Ulugh Beg’s catalogue of stars (Washington: Carnegie) [Google Scholar]
- Meeus, J. 1998, Astronomical Algorithms2 (Willmann-Bell: Richmond) [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1986, Numerical Recipes (Cambridge University Press) [Google Scholar]
- Repsold, J. 1919, Astron. Nachr., 209, 193 [Google Scholar]
- Riccioli, G. B. 1651, Almagestum Novum (Bologna: Benatus) [Google Scholar]
- Röser, S., & Bastian, U. 1988, A&AS, 74, 449 [Google Scholar]
- Rawlins, D. 1993, DIO, 3, 1 [Google Scholar]
- Rothmann, Ch. 1619, Sammlung von Traktaten, Exzerpten und Briefen zu astronomischen Fragen, Aufzeichnungen von Stern- und Planetenbeobachtungen, 2° Ms. astron. 5, https://orka.bibliothek.uni-kassel.de/viewer/image/1350031335734/1/ [Google Scholar]
- Sæmundsson, Th. 1986, Sky Telesc., 72, 70 [Google Scholar]
- Schrimpf, A., & Verbunt, F. 2021, ArXiv e-prints [arXiv:2103.10801] [Google Scholar]
- Seidelman, P. K. 1992, Explanatory Supplement to the Astronomical Almanac (Sausalito, California: University Science Books) [Google Scholar]
- Smithsonian Astrophysical Observatory staff 1966, Star Catalog with positions and proper motions of 258,997 stars for the epoch and equinox 1950.0 (Washington D.C.: Smithsonian Institution) [Google Scholar]
- Ulugh Beg 1437, Manuscript, for edition see Knobel 1917 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verbunt, F., & van Gent, R. H. 2010, A&A, 516, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verbunt, F., & van Gent, R. H. 2012, A&A, 544, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wesley, W. G. 1978, JHA, ix, 42 [Google Scholar]
- Wilhelm IV von Hessen-Kassel, Bürgi, J. 1587, Hessisches Sternenverzeichnis, 2° Ms. astron. 7 https://orka.bibliothek.uni-kassel.de/viewer/image/1336543085355/1/ [Google Scholar]
- Wolf, R. 1878, Astron. Mitt. Eidg. Sternwarte Zürich, 5, 125 [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR On-Line Data Catalog: UCAC4 Catalogue [Google Scholar]
Appendix A: The HIPPARCOS catalogue for epoch 1586.
For a number of stars, the original HIPPARCOS Catalogue did not find a solution for the proper motion. These stars are not present in the revised HIPPARCOS-2 Catalogue by van Leeuwen (2007). We used the position of these stars as given in the HIPPARCOS Catalogue (ESA 1997) and collected their proper motions from various sources, as listed in Table A.1.
Stars added by us to the HIPPARCOS-2 Catalogue.
To take into account that some HIPPARCOS stars cannot be separated by the human eye, we proceeded as follows. We selected all stars in the original HIPPARCOS Catalogue with V < 7.0 and read the positions of these stars in the revised HIPPARCOS-2 Catalogue. We corrected these positions for proper motion over the interval between the HIPPARCOS epoch 1991.25 and the Manuscript epoch 1586 and for precession from HIPPARCOS equinox 2000.0 to the Manuscript equinox 1586, with Eqs. (3.211) and (3.212-2) of Seidelman (1992). For each star, we found all stars within 2′ at that epoch and merged them into one entry. Thus 80 pairs and two triples were merged into 82 entries. To determine the position of the merged entry, the positions of its components were weighted with their fluxes, separately for the right ascension and for the declination. The magnitude of the merged entry was found by adding the fluxes of its components. Thus with fi the flux normalised to the flux of a star with V = 0:
and
Appendix B: Emendations to Manuscript
B.1. Angular distances between stars
For W 36, the name of the reference star is not given. The angular distance indicates W 24, which we entered in WilhelmIV-Dist.
Following W 165, ‘In Cauda’ (in the tail) sc. of Aquila, is an entry ‘Extrema Caudae’ (the end of the tail), which is indicated in Col. 7 as ‘in tabulis non extat’ (not present in the tables sc. of Ptolemaios). Two angles to reference stars are given for this entry, towards Aquila (W 163) and towards Rostrum Cygni (the beak of the Swan), which we identify with W 89. These angles imply that ‘Extrema Caudae’ corresponds to HIP 93244 (ϵ Aql). That star indeed is not in the star catalogue of Ptolemaios.
For W 340 and W 341, Canis maior (W 353) is indicated as the reference star, but it is excluded by the angular distance; we emended this to Canis minor (W 352).
B.2. Altitudes
For W 64, we emended 18°14′to 58°14′.
B.3. Ecliptic coordinates
On the basis of Sect. 4.3, we emended the following.
W 55. β 55°41′10″ to 54°41′10″.
W 214. β 02°49′54″ to 02°47′54″.
W 374. λ 2d42m50s to 2d41m50s.
Appendix C: Notes on individual identifications
Merged with is abbreviated with m.w.
W 26. HIP 85829 (V = 4.84) m.w. HIP 85819 (V = 4.89).
W 32. HIP 86614 (V = 4.57) m.w. HIP 86620 (V = 5.81).
W 53. HIP 110991 (V = 4.07) m.w. HIP 110988 (V = 6.31).
W 59. HIP 75411 (V = 4.31) m.w. HIP 75415 (V = 6.51).
W 73. HIP 79043 (V = 5.00) m.w. HIP 79045 (V = 6.25).
W 83. HIP 91971 (V = 4.34) m.w. HIP 91973 (V = 5.73).
W 89. HIP 95947 (V = 3.05) m.w. HIP 95951 (V = 5.12).
W 99. We chose HIP 99675 (31 Cyg, V = 3.8, 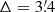 ) as the counterpart above the closer, but fainter HIP 99639 (30 Cyg, V = 4.8,
) as the counterpart above the closer, but fainter HIP 99639 (30 Cyg, V = 4.8, 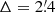 ).
).
W 108. We chose HIP 5542 (θ Cas, V = 4.3, 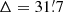 )) as the counterpart above the closer, but fainter HIP 5536 (ρ Cas, V = 5.2,
)) as the counterpart above the closer, but fainter HIP 5536 (ρ Cas, V = 5.2, 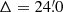 ).
).
W 156. HIP 92946 (V = 4.62) m.w. HIP 92951 (V = 4.98).
W 174. HIP 102532 (V = 4.27) m.w. HIP 102531 (V = 5.15).
W 251. HIP 43103 (V = 4.03) m.w. HIP 43100 (V = 6.58).
W 277. HIP 78820 (V = 2.56) m.w. HIP 78821 (V = 4.90).
W 283. Notwithstanding the large positional error 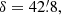 we consider the identification secure.
we consider the identification secure.
W 312. HIP 5737 (V = 5.21) m.w. HIP 5743 (V = 6.44).
W 317. HIP 5131 (V = 5.33) m.w. HIP 5132 (V = 5.55).
W 340. HIP 26220 (V = 4.98) m.w. HIP 26221 (V = 5.13) and HIP 26224 (V = 6.71. The original HIPPARCOS catalogue (ESA 1997) lists V = 4.98 for HIP 26220, but error 0.00 for B − V; this may indicate that the photometry is suspect. Ducati (2002) gave V = 6.73. Since HIP 26220 is a Herbig Ae/Be star, and thus variable, its magnitude is probably variable.
W 367. The positional error 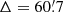 strongly suggests an error of 1° in writing or copying the correct result.
strongly suggests an error of 1° in writing or copying the correct result.
All Tables
Frequency of different combinations of information given in Manuscript, after the removal of three repeated entries and five reverse repeated angles.
First lines of the machine-readable table WilhelmIV-Dist, with examples of a repeat entry (F = 1) and of a reverse repeat entry (F = 2).
Measurement accuracies determined from meridian altitudes for the mural quadrant of Brahe, determined by Wesley (1978), and for WilhelmIV-Alt, determined in Sect. 5.1, for eight of the fundamental stars of Brahe.
All Figures
 |
Fig. 1. Difference between the declination δh computed from the altitude with Eqs. (7)–(9) and the declination δW listed in Manuscript for ϕG = 51° 19′. With few excaptions, the computations are exact for superior and southern culminations. The values δh from inferior culmination are systematically too high for low altitudes. Values for which δh ≠ δW are labelled with W for those entries for which only one altitude is listed, and for W 9. The solid curve gives the refraction RR according to Rothmann. Stars to the right of the vertical dashed line have R = 0, according to Rothmann. |
| In the text | |
 |
Fig. 2. Complement of the normalised empirical cumulative distribution function ECDF, i.e. 1−ECDF for the absolute values of the differences between the right ascension αeq computed with Eq. (11) and the catalogued right ascension αW. Red: vertical axis for the exact values αeq. Black: for the values αeq rounded to the nearest allowed integer of Sα. |
| In the text | |
 |
Fig. 3. Complement to the normalised empirical cumulative distribution function, i.e. 1-ECDF, of the differences ϕeq − W between the catalogued position and the position computed with Eqs. (12) and (13). Red: vertical axis for the exact computed values λeq and βeq. Black: for the values rounded to the nearest allowed integer of Sλ and Sβ. |
| In the text | |
 |
Fig. 4. Complement to the normalised empirical cumulative distribution function, i.e. 1-ECDF of the differences ϕeq12 − W between the position computed with Eq. (15) and the catalogued position. Red: vertical axis for the exact computed values λeq12 and βeq12. Black: for the values rounded to the nearest allowed integer of Sλ and Sβ. |
| In the text | |
 |
Fig. 5. Top: differences Δh (left) and dh (right) between the altitudes measured in Kassel and the altitudes that should have been measured according to modern data (Eqs. (17) and (18)). The solid lines show the best linear fit and its 3-rms range. Points outside this range were ignored in the fit. To the right of the dashed vertical line RR = 0 and thus Δh = dh. Bottom: cumulative distribution of the difference between the measured Δh and dh and their best fit, compared with the distribution expected for a Gaussian with σ equal to the rms of the differences with the best fit. KS indicates the p-value from a two-sided Kolmogorov-Smirnov test for which the observed points are drawn from the Gaussian. |
| In the text | |
 |
Fig. 6. Top: differences between the angles ϕ between two stars as given in Manuscript and the angles ϕHIP derived from modern HIPPARCOS data, as a function of ϕ. For some outliers, W is indicated (Table 6). Bottom: cumulative distribution of the differences compared with a Gaussian centred on zero. |
| In the text | |
 |
Fig. 7. Left: distribution of the magnitudes given in WilhelmIV (black) and of the magnitudes of their counterparts in the HIPPARCOS catalogue (red) for all securely identified stars. Right: distribution of the magnitudes of the HIPPARCOS counterparts, separately for each magnitude in WilhelmIV. The numbers show the number of stars in each frame. |
| In the text | |
 |
Fig. 8. Distributions of various positional errors. Entries identified with clusters and duplicate entries are not included. The histograms include entries for which equatorial coordinates are not given in WilhelmIV, but computed by us from the ecliptic coordinates. The numbers in the frame indicate the numbers of values to the left of, within, and to the right of the frame limits. Top left: distribution of Δα (Eq. (3)) for entries with |δ|< 20°. The average shift, indicated with a vertical dashed line, is |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.