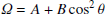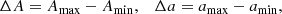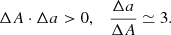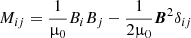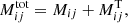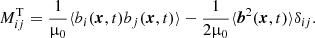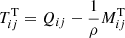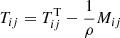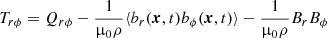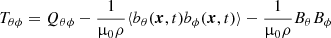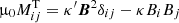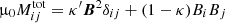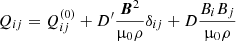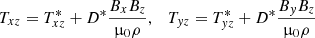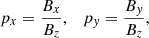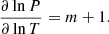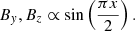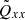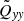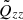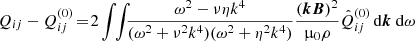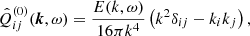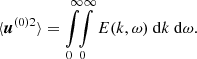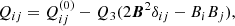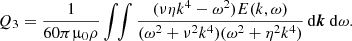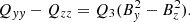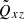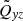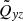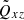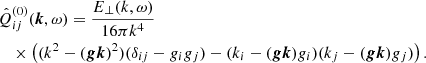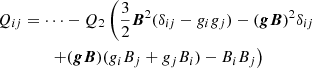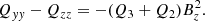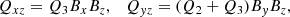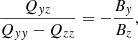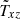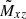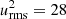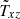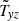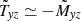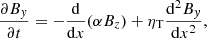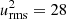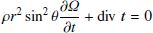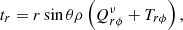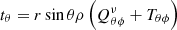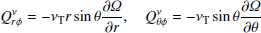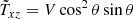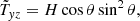| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A173 | |
| Number of page(s) | 10 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202039912 | |
| Published online | 03 June 2021 | |
Angular momentum transport by magnetoconvection and the magnetic modulation of the solar differential rotation
1
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: gruediger@aip.de
2
University of Potsdam, Institute of Physics and Astronomy, 14476 Potsdam, Germany
Received:
14
November
2020
Accepted:
18
March
2021
In order to explain the variance of the solar rotation law during the activity minima and maxima, the angular momentum transport by rotating magnetoconvection is simulated in a convective box penetrated by an inclined azimuthal magnetic field. Turbulence-induced kinetic and magnetic stresses and the Lorentz force of the large-scale magnetic background field are the basic transporters of angular momentum. Without rotation, the sign of the magnetic stresses naturally depends on the signs of the field components as positive (negative) BθBϕ transport the angular momentum poleward (equatorward). For fast enough rotation, however, the turbulence-originated Reynolds stresses start to dominate the transport of the angular momentum flux. The simulations show that positive ratios of the two meridional magnetic field components to the azimuthal field reduce the inward radial as well as the equatorward latitudinal transport, which result from hydrodynamic calculations. Only for BθBϕ > 0 (generated by solar-type rotation laws with an accelerated equator) does the magnetic-influenced rotation at the solar surface prove to be flatter than the nonmagnetic profile together with the observed slight spin-down of the equator. The latter phenomenon does not appear for antisolar rotation with polar vortex as well as for rotation laws with prevailing radial shear.
Key words: magnetic fields / Sun: rotation / convection
© ESO 2021
1. Introduction
The solar surface rotation law exhibits a correlation with solar activity parameters such as sunspot numbers, large-scale magnetic fields, or small bright coronal structures (SBCS). Equatorial rotation is faster during the activity minimum and slower in the activity maximum. The magnetic field seems to decelerate the solar equator (Gilman & Howard 1984; Jurdana-Šepić et al. 2011). This deceleration might be interpreted as a magnetic-originated reduction of the radial shear provided the radial profile Ω = Ω(r) increases outwards (‘superrotation’) while the lower value Ωin is fixed by the tachocline at the bottom of the convection zone.
Simultaneously, the form of the latitudinal rotation law Ω = Ω(θ) at the surface also varies with the phase of the activity cycle. The latitudinal shear is reduced by the magnetic field, that is to say it is larger during the minimum activity and it is smaller during the maximum activity (Ruždjak et al. 2017).
The numbers, however, are small. Expressed with the traditional definition
(with A being the equatorial rotation rate and with θ being the colatitude), the variation of A is about 1% while B varies by about 20% between activity minimum and activity maximum (Xie et al. 2018). The latter value implies that the normalised equator-pole difference of the surface rotation, a = δΩ/Ω > 0, varies in time by about 3%. We write
where the suffixes max and min concern the rotation laws with and without a magnetic field. The observed differences ΔA and Δa are both negative, hence
The magnetic field both reduces the equatorial angular velocity and the latitudinal shear, but the magnetic-induced reduction of the equatorial velocity is weaker than that of the pole-equator difference. We shall explain these observational findings by calculating the angular momentum transport in rotating convective boxes under the influence of a strong azimuthal magnetic field combined with weak meridional components. The Lorentz force of this field as well as the anisotropic Reynolds stresses are the main transporters of angular momentum (Malkus & Proctor 1975; Kitchatinov et al. 1994). We shall see that only one of the possible magnetic configurations provides rotation laws fulfilling the conditions (3). It is just this configuration (BθBϕ > 0) which is a natural outcome of all αΩ dynamos which operate with solar-type rotation laws, that is to say with an accelerated equator. Toroidal fields induced by negative radial shear produce the opposite sign, that is BrBϕ < 0.
With their anelastic spherical harmonic (ASH) code, Brun et al. (2004) demonstrate that the simulated rotation laws at the surface of the convection zone indeed strongly vary for magnetic models and purely hydrodynamic calculation. Both the pole-equator difference of the rotation rate and also its equatorial value are reduced by the dynamo-excited magnetic fields. Also the simulations by Karak et al. (2015), Augustson et al. (2015), Käpylä et al. (2016), and Warnecke et al. (2018) provide reduced equatorial rotation rates during the magnetic maximum. In some of these calculations, the Maxwell stress of the induced large-scale magnetic fields only plays a minor role in the transportation of angular momentum. Because of the complexity of the numerical magnetohydrodynamic simulations (see also Browning et al. 2006), it remains unclear, however, by which mechanism the magnetic field suppresses the non-uniformity of the rotation laws which, in hydrodynamics, is maintained by Reynolds stresses due to the anisotropy of the underlying turbulence.
Brun et al. (2004) prescribe dissipation of the angular momentum by unresolved modes by fixing a magnetically uninfluenced eddy viscosity of 1012 cm2 s−1, which also determines the resulting meridional flow. Consequently, the isolines of the resulting rotation law are more or less cylindrical because of the Taylor-Proudman theorem. Kippenhahn (1963) demonstrated the basic physics: If a turbulence transports angular momentum, for instance, outwards, then the resulting super-rotating rotation law with spherical Ω isolines induces a clockwise meridional circulation (in the northern hemisphere) transporting angular momentum to the equator. The Ω isolines become cylindrical as is also the case in many simulations (see recent papers by Featherstone & Miesch 2015; Warnecke 2018; Warnecke et al. 2018). In mean-field models, anisotropic heat transport due to rotating convection which produces ‘warm’ poles overcomes the Taylor-Proudman theorem (Kitchatinov & Rüdiger 1995), while in numerical simulations the poles must additionally be warmed up (Browning et al. 2006; Miesch et al. 2006).
By a combination of local box simulations (Sect. 5) and global mean-field equations (Sect. 6), we shall demonstrate with the present paper that the observed finding (3) can be explained by the magnetic influence of the dynamo-induced large-scale fields onto the rotation-induced non-diffusive parts of the Reynolds stresses (the ‘Lambda-effect’). The Maxwell stress of the large-scale fields (the ‘Malkus-Proctor effect’), however, appears to play only a minor role. This explanation only succeeds for positive product BθBϕ of the meridional magnetic field component Bθ and the toroidal magnetic field component Bϕ. Just this condition is fulfilled if positive latitudinal shear on the northern hemisphere and negative latitudinal shear on the southern hemisphere is responsible for the induction of the toroidal fields, which indeed complies with the observations.
2. Angular momentum transport
Both turbulence-originated Reynolds stress and Maxwell stress must be formulated for a turbulent fluid under the presence of a uniform background field vector B. The fluctuating flow and field components are denoted by u and by b, respectively. The standard Maxwell tensor
of the large-scale field turns into the generalised stress tensor
with the turbulence-induced Maxwell tensor
The negative coefficients of the Kronecker tensors in Eq. (5) form the total pressure which we can completely ignore in what follows. The difference between the Reynolds tensor and Maxwell tensor is
with the one-point correlation tensor being Qij = ⟨ui(x, t)uj(x, t)⟩ of the flow. The expression
gives the total contribution of turbulence and magnetic background fields to the angular momentum transport. The off-diagonal components
and
represent the fluxes of specific angular momentum in the radial and latitudinal direction by the magnetoconvection under the influence of a magnetic background field. The quantities do not contain pressure terms. Expressions (9) and (10) for purely azimuthal fields have already been calculated for stellar convection under the presence of a purely azimuthal magnetic field where surprisingly a magnetic quenching of the turbulent fluxes of angular momentum did not appear (Käpylä et al. 2004).
It is known that the symmetry of the cross-correlations Trϕ and Tθϕ differs from that of all other components of the tensor Tij. While Trϕ and Tθϕ are antisymmetric with respect to the transformation Ω → −Ω, all other correlations are not. The turbulent angular momentum transport is thus odd in Ω, while the other terms – the cross-correlation Trθ included – are even in Ω. It is easy to show that Trϕ is symmetric with respect to the equator if the averaged flow and the magnetic fields are also symmetric. Then the component Tθϕ is antisymmetric with respect to the equator. These rules can only be violated if, for example, the magnetic field strengths in the two hemispheres are different.
One can easily show that isotropic turbulence even under the influence of rotation does not lead to finite values of Trϕ and Tθϕ. Only with a preferred direction g can a tensor (ϵiklgj + ϵjklgi)gkΩl linear in Ω exist, possessing cross-correlations with the index ϕ as one of the indices (if g is radially directed). Rigidly rotating anisotropic turbulence, therefore, is thus able to transport angular momentum (‘Λ effect’).
As in Rüdiger et al. (1986), we write
(κ > 0 for Ω = 0) so that
for the sum of small-scale and large-scale Maxwell stresses. For the nonrotating fluid, the one-point-correlation tensor may be written as
with 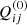 for B = 0. A vertical magnetic field supports the vertical turbulence intensity (Chandrasekhar 1961), which is described by D > 0. It follows that
for B = 0. A vertical magnetic field supports the vertical turbulence intensity (Chandrasekhar 1961), which is described by D > 0. It follows that
with D* = D + κ − 1. In accordance with the geometry of the box simulations presented below, here, we introduced the coordinates (x, y, z) as local Cartesian proxies of the global spherical coordinates (r, θ, ϕ).
We note that the coefficients D and κ of the Reynolds stress and Maxwell stress work in the same direction. The sum D + κ describes the turbulence-induced magnetic angular momentum transport which is accompanied by that of the large-scale Lorentz force, that is to say minus 1 in the coefficient of BxBz or ByBz, respectively. Only the latter terms are odd in the field components Bx and By, but not T* which is even in all single field components by definition. If, therefore, two simulations exist with one and the same Bx, but with opposite Bz, then from Eq. (14) it follows that 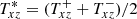 and
and 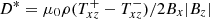 . To introduce physical units for the intensity quantities, a tilde denotes normalisation with the turbulence intensity
. To introduce physical units for the intensity quantities, a tilde denotes normalisation with the turbulence intensity 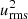 calculated without rotation and without a field. The sum D + κ describes whether the rotating turbulence supports the angular momentum transport by the Lorentz force or not; its sign is not fixed by definition.
calculated without rotation and without a field. The sum D + κ describes whether the rotating turbulence supports the angular momentum transport by the Lorentz force or not; its sign is not fixed by definition.
The magnetic background field may consist of a dominating azimuthal field Bz together with weak meridional components Bx and By forming the inclination (‘pitch’) angles,
(always taken in the northern hemisphere) with |px|≪1 and |py|≪1. We note that for the Sun, py > 0 at the northern hemisphere since, as generally believed, the toroidal large-scale magnetic field Bz is generated from the latitudinal field By by a latitude-dependent rotation law with an accelerated equator. Antisolar rotation leads to py < 0. The negative radial shear in the solar subsurface shear layer would produce negative values of px. Because of the magnetic feedback, the winding-up process is almost independent of the seed field By. One finds 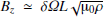 with δΩ as the differential rotation and L as the characteristic length scale so that for the Sun Bz ≲ 104 G. Together with the observed poloidal field strength, py ≳ 10−4. In the spirit of Lenz’s rule, we expect that fields with positive py lead to rotation laws with less latitudinal shear than the nonmagnetic system would produce. We shall indeed show that both the inclinations px and py are able to reduce the nonmagnetic surface shear of the differential rotation, but only a positive py simultaneously reduces the equatorial rotation rate as observed in the cycle maxima.
with δΩ as the differential rotation and L as the characteristic length scale so that for the Sun Bz ≲ 104 G. Together with the observed poloidal field strength, py ≳ 10−4. In the spirit of Lenz’s rule, we expect that fields with positive py lead to rotation laws with less latitudinal shear than the nonmagnetic system would produce. We shall indeed show that both the inclinations px and py are able to reduce the nonmagnetic surface shear of the differential rotation, but only a positive py simultaneously reduces the equatorial rotation rate as observed in the cycle maxima.
3. No rotation
To study the effect of the magnetic field on the angular momentum transport quantitatively, we ran a series of direct numerical simulations to study convection in a rotating rectangular box. The NIRVANA code uses a Godunov scheme as described in Ziegler (2004) to solve the equations of energy conservation and mass conservation, the equation of motion, and the induction equation. The model assumes a fully ionised ideal gas with constant specific heat capacity. The stratification of the gas is piecewise polytropic,
A convectively unstable layer with m = 1 was placed between two stably stratified layers with m = 9. The heat flux is constant throughout the simulation box. The box size is Lx × Ly × Lz = 2 × 6 × 6 in dimensionless units. The unstable layer starts at x = 0.8 and ends at x = 1.8. The boundary conditions in the horizontal y and z directions are periodic. On the lower boundary (x = 0), we imposed a fixed temperature, no penetration, stress-free horizontal flow, and pseudo-vacuum boundary conditions on the magnetic field. On the upper boundary at x = 2, the boundary conditions imply a fixed temperature gradient, while the boundary conditions on the gas flow and the magnetic field are the same as on the lower boundary. The mesh size is Nx × Ny × Nz = 128 × 384 × 384. The simulations start with hydrostatic equilibrium and a small random perturbation and run for about 200 turnover times. The Rayleigh number in the unstable layer is Ra = 107. The ratio of the densities at the bottom and top of the simulation box is (only) 5.8. In code units, the isothermal sound speed is cac = 100 at the top of the unstably stratified layer, and the viscosity is 6.32 × 10−3 while those of the magnetic diffusivity and the heat diffusion coefficient are 6.32 × 10−2. The magnetic field was imposed as an initial condition and periodically reset. It is constant in the vertical (x) direction while the boundary conditions require the horizontal field components to be zero on the upper and lower boundaries. These components therefore vary with depth, that is
The below mentioned field amplitudes By and Bz always refer to the maxima in the centre of the box. If the above introduced Lorentz force factor D is defined for uniform fields, then the D for the simulated nonuniform fields thus slightly depends on the radial profile used in Eq. (17). The background field was introduced as an initial condition and reset after each snapshot. This kept the vertical (x) and toroidal (z) components close to the initial configuration. For the y-component, however, the time between snapshots proved sufficient to develop a significant departure, which limited our ability to apply weak fields in that direction, as discussed below.
Without a magnetic field, the turbulence in the horizontal plane is isotropic hence the Qyy = Qzz. A magnetic field along a coordinate axis forms an anisotropy in the horizontal plane and Qyy ≠ Qzz. For the magnetic fields B = (0, 1, 10), the normalised autocorrelations 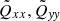 , and
, and 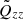 are plotted in Fig. 1. One finds all the intensities to be reduced by the magnetic field where the degree of quenching grows for the stronger field component (red curve). By the magnetic influence, the horizontal intensity excess Qyy − Qzz becomes positive. The normalised numerical value is
are plotted in Fig. 1. One finds all the intensities to be reduced by the magnetic field where the degree of quenching grows for the stronger field component (red curve). By the magnetic influence, the horizontal intensity excess Qyy − Qzz becomes positive. The normalised numerical value is 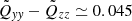 .
.
 |
Fig. 1. Turbulent intensities by nonrotating convection without (left panel) and with a magnetic field (right panel, B = (0, 1, 10)); |
Next the cross-correlations Qxz and Qyz for nonrotating magnetoconvection are discussed. As known within the quasilinear approximation, the correlation tensor of a homogeneous turbulence influenced by a weak large-scale magnetic field B is
with 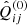 as the spectral tensor of the original nonmagnetic turbulence (Rüdiger 1974). For isotropic and incompressible turbulence, the tensor is simply
as the spectral tensor of the original nonmagnetic turbulence (Rüdiger 1974). For isotropic and incompressible turbulence, the tensor is simply
where the positive-definite spectrum E provides the kinetic energy
The insertion of Eq. (19) into Eq. (18) and some algebra lead to
where the coefficient Q3 evaluates to
One finds Q3 > 0 for all spectra monotonously decreasing with increasing frequency. From Eq. (21) for the magnetic-induced anisotropies in the horizontal plane follows
The turbulence intensity should be increased in the direction of the magnetic field. For dominating Bz, the difference proves to be negative, but it is positive in our simulations (see Fig. 1). For the cross-correlation, one obtains the simple relations
For positive field components, both cross-correlations should be positive, but only the first of these relations is confirmed by the numerical simulations shown in Fig. 2.
 |
Fig. 2. Left: vertical cross-correlation |
The reason for the discrepancies is the anisotropy of the original turbulence field. For anisotropic turbulence fields, the above model is too simple. To the spectral tensor as shown in Eq. (19), an anisotropic turbulence may be added which, for example, has no velocity components in the g direction, that is
A turbulence with a dominating intensity in the g-direction requires E⊥ < 0, while E⊥ > 0 originates a horizontal turbulence. Furthermore, E⊥ < 0 is a necessary condition to describe anisotropic turbulence with dominating vertical intensities.
The total correlation tensor, for example as can be seen in Eq. (21), is completed by
with Q2 similar to (22) but with E⊥ instead of E. Furthermore, Q2 is not positive-definite. We note that the influence of the magnetic field does not provide vertical motions if the turbulence is strictly horizontal. With this turbulence model, Eq. (23) becomes
Here again |Bz| is assumed to be much larger than the other components. Obviously, the magnetic field in the z direction can increase the anisotropy of the turbulence in favour of the z-component of the velocity. The effect vanishes, however, for Q2 + Q3 ≲ 0, that is for turbulence with a dominant vertical intensity. After Eq. (27), the magnetic-induced anisotropy of the turbulence intensity in the horizontal plane changes its sign with the sign of Q2 + Q3.
For the cross-correlations, that is Eq. (24), it now follows that
where the x-direction is parallel to g. The first expression remains uninfluenced by the anisotropy, while the second one no longer has a definite sign. We note that the cross-correlations Qxz and Qyz in anisotropic turbulence differ even for identical field strengths and pitch angles. The vertical cross-correlation Qxz exceeds the horizontal cross correlation Qyz if the vertical turbulence intensity exceeds the horizontal one and vice versa. For turbulence with a dominating intensity in the g-direction, it is Q3 + Q2 ≲ 0 that leads to Qyz ≲ 0, which is confirmed by the simulation results of Fig. 2 with its rather small numerical values of the horizontal cross-correlation Qyz. The correlation Qxz is only due to the isotropic part of the turbulence field and should never vanish if Bx and Bz do not vanish. It only vanishes in a coordinate system with one of the axes parallel to the total magnetic field vector.
The ratio of the cross-correlation to the excess of the autocorrelations results from Eqs. (27) and (28) simply to
which after the numerical results in the right panels of Figs. 1 and 2 is well fulfilled. The numbers may also demonstrate the high accuracy of our numerical code.
As the next step, the total horizontal cross component Tyz may be calculated for the magneto-convective fluid with no rotation but with py = ±0.1. The total stress can be written as Tyz = Qyz − myz − Myz with Q as the Reynolds stress, m as the small-scale Maxwell stress, and M as the large-scale Lorentz force Myz = ByBz/μ0ρ.
As shown by Figs. 3 and 4, the off-diagonal elements Txz and Tyz due to the Reynolds stress and the Maxwell stress exist, but their typical behaviour is different. In contrast to Eq. (24) for isotropic turbulence, the two cross-correlations are not equal by far; Txz is much smaller than Tyz. The reason is that Qxz ≃ Mxz so that Txz ≃ 0, but this is not true for the horizontal correlation (yz). In this case, the Reynolds stress is much smaller than the Maxwell stress hence Tyz ≃ −1.5Myz. The horizontal angular momentum transport is mainly due to the large-scale Lorentz force. The contribution of the Reynolds stress to the total stress is only 25% and that of the turbulent Maxwell stress is only 5%. Because of the averaging procedure, the numerical result 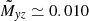 for By = 1 and Bz = 10 is smaller than
for By = 1 and Bz = 10 is smaller than 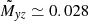 obtained with the amplitudes of By and Bz. For simplicity in the following, we shall use the latter expression so that the applied magnetic fields are slightly overestimated compared with the averaged fields.
obtained with the amplitudes of By and Bz. For simplicity in the following, we shall use the latter expression so that the applied magnetic fields are slightly overestimated compared with the averaged fields.
 |
Fig. 3. Snapshots of the |
 |
Fig. 4. Similar to Fig. 3, but for the horizontal torque |
For toroidal fields Bz with different signs, the two fluxes 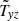 and
and 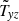 also differ by the sign (Fig. 4). Without rotation, we find
also differ by the sign (Fig. 4). Without rotation, we find 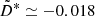 , that is D* ≃ −0.5 and D + κ ≃ 0.5. The density stratification reduces D* by 50%, that is from −1 to −0.5. For rotating boxes, the question remains as to how much the magnetic-influenced Reynolds stress influences these results.
, that is D* ≃ −0.5 and D + κ ≃ 0.5. The density stratification reduces D* by 50%, that is from −1 to −0.5. For rotating boxes, the question remains as to how much the magnetic-influenced Reynolds stress influences these results.
4. Helicity and alpha effect
In rotating boxes also finite values of the α effect should evolve with consequences for the effective large-scale fields. The α effect generates poloidal field components By from the toroidal field component Bz, which is always the largest one in the simulations. If, as in our models, only the radial coordinate x serves for the calculations of gradients, then the only relevant component of the induction equation is
where the α represents the (ϕϕ) component, which is the most important one for the αΩ dynamo mechanism, and the ηT is the eddy diffusivity. We know that intensity stratifications provide finite values of the α effect as in the well-known relation 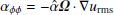 with positive
with positive 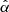 . Because of the radial boundary conditions, the gradient of urms must be negative (positive) at the top (bottom) of the box. In the northern hemisphere, the resulting α effect is thus always positive (negative) at the top (bottom) of the box. The same argument holds for the helicity
. Because of the radial boundary conditions, the gradient of urms must be negative (positive) at the top (bottom) of the box. In the northern hemisphere, the resulting α effect is thus always positive (negative) at the top (bottom) of the box. The same argument holds for the helicity 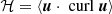 , but with opposite signs: negative at the top and positive at the bottom. We computed the helicity for fast rotation (Ω = 10) of the magnetised fluid. As expected, the quantity ℋ is positive (negative) in the lower (upper) part of the numerical box. It vanishes almost exactly at its centre. We also note, as expected, that the helicity at the poles exceeds the helicity of mid-latitudes (Fig. 5).
, but with opposite signs: negative at the top and positive at the bottom. We computed the helicity for fast rotation (Ω = 10) of the magnetised fluid. As expected, the quantity ℋ is positive (negative) in the lower (upper) part of the numerical box. It vanishes almost exactly at its centre. We also note, as expected, that the helicity at the poles exceeds the helicity of mid-latitudes (Fig. 5).
 |
Fig. 5. Snapshots of the small-scale helicity ℋ at the north pole (θ = 0°, left) and mid-latitudes (θ = 45°, right) for fast rotation. As expected, the helicity vanishes in the middle of the box. The applied magnetic field is B = (0, 0.1, 10), Ω = 10, Pr = 0.1, and Pm = 0.1. |
The rotation rate Ω ≃ 10 represents a Coriolis number of Ω∗ = 2τcorrΩ ≃ 2 if the correlation time τcorr ≲ 0.1 is used, which resulted from an autocorrelation analysis of the same numerical convection model (Küker & Rüdiger 2018). We note that Ω∗ ≃ 2 is close to the solar value. With the same correlation time, the helicity amplitude of 2.5 in Fig. 5 leads to α/urms ≃ 0.05, which is slightly smaller than what Ossendrijver et al. (2001, 2002) found with 10% for rotating magnetoconvection. In their simulations, Käpylä et al. (2009) also found typical values of the order of 10% (see their Fig. 8).
One thus finds unavoidable consequences for the simulations. The α effect automatically generates meridional large-scale fields By from the toroidal field Bz in accordance with the stationary induction Eq. (30), that is ηTd2By/dx2 = Bzdα/dx. For positive Bz and positive dα/dx (α growing with height), the second derivative of By is obviously positive. The small-scale α effect, therefore, generates a minimum of By between the top and bottom of the box. The Maxwell stress ByBz, therefore, is reduced compared to its value without rotation; it may even change its sign. The right panel of Fig. 6 demonstrates how the applied value of By = 0.10 is changed to By = −0.16 by the action of the α effect so that the simulated cross-correlation Tyz is larger than the ‘real’ one without an α effect.
 |
Fig. 6. Snapshots of the large-scale field components Bx (left) and By (right) in the box. We note the transformation of By > 0 to By < 0 by the inbox α effect. The radial field Bx is not concerned; B = (0, 0.1, 10), Ω = 10, Pr = 0.1, Pm = 0.1, and θ = 45°. |
The right panel of Fig. 6 shows negative By in the bulk of the convective box despite the small and positive starting field. Test calculations with Bz = −10 provided the opposite sign of the By. On the other hand, the radial component Bx proves to be completely uninfluenced (left panel of Fig. 6). The stress components Txz are thus not modified by the small-scale α effect resulting from rotating fluids.
To sum up, by the α effect, the latitudinal angular momentum transport is formally increased for the positive inclination angle of the magnetic field (in the northern hemisphere). The ‘real’ stress values without this impact are thus smaller than the simulated values. The Tyz given in Table 1 (and also in Table 3) are thus maximal values. The corrections, however, are only small as for py ≪ 1 and py ≫ 1; the rotation-induced terms are basically larger than the Maxwell stress ByBz for Ω = 0. They are in particular small for models with |py|≫1.
Latitudinal angular momentum transport 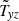 for very large or very small inclination angles, py > 0 in the upper two lines and py < 0 in the lower two lines.
for very large or very small inclination angles, py > 0 in the upper two lines and py < 0 in the lower two lines.
In Table 1 data are given leading to the latitudinal flux Tyz of angular momentum. Different values of Tyz numerically result for the fields B = (0, 0.1, 20) and B = (0, 20, 0.1) if the box rotates with Ω = 10. In all cases, |ByBz| = 2. The magnetic fields of all examples have the same total value of about 20. For the models in the upper two lines, the pitch angle py is positive. Also for negative py, that is for the fields B = (0, 0.1, −20) and B = (0, 20, −0.1) in the lower two lines, the results differ. The fluxes are only equal for zero rotation (the last column of the table). The differences are thus due to the α effect. They also differ for positive and for negative py, as it should; the flux is increased for negative ByBz.
It should be mentioned that the magnetic amplitude Bz = 20 represents a field almost in equipartition with the calculated turbulence rms velocity urms ≃ 5.3. We also conclude from the numbers in Table 1 that for saturated magnetic fields the angular momentum transport by the Lorentz force is by far overcompensated for by the angular momentum transport of the rotating turbulence. The total stress is positive for all the given magnetic field examples, but it is smallest for the field with the positive solar value py = 5 × 10−3. The Lorentz force numbers for Ω = 0 given in the last column of Table 1 only contribute to about 10% of the total stresses. For positive py, the T values with and without rotation even possess opposite signs. It becomes obvious here that the Malkus-Proctor effect does not play a major role in the angular momentum transport in stellar convection zones.
5. Rotating magnetoconvection
In a stratified medium, the (solid-body) rotation alone provides finite cross components of the Reynolds stress without any magnetic fields. The magnetic field, however, modifies these correlations and also enhances or reduces the angular momentum transport by the generation of Maxwell stresses.
Without magnetic fields, a rotation with Ω = 10 produces cross-correlations of the normalised values 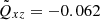 and
and 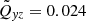 (from Table 3, first line) at a latitude of θ = 45°. With numbers taken from Fig. 1 in both cases, the correlation coefficient
(from Table 3, first line) at a latitude of θ = 45°. With numbers taken from Fig. 1 in both cases, the correlation coefficient 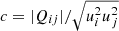 is about 0.5 for the given cross-correlations (see Fig. 1). For fast rotation, the hydrodynamic radial Λ effect is negative (the angular momentum flows inwards), while the latitudinal Λ effect is always positive (the angular momentum flows equatorward). Basically, it is |Qxz|≳Qyz. The numerical values strongly depend on the latitude. By definition, both correlations vanish at the poles and Tyz also vanishes at the equator (Fig. 7). Under the influence of magnetic fields, the values are reduced (‘magnetic quenching’) depending on the inclination of the background fields. We shall assume in Eqs. (35) and (36) that the typical profiles in Fig. 7 are not changed by the magnetic influences.
is about 0.5 for the given cross-correlations (see Fig. 1). For fast rotation, the hydrodynamic radial Λ effect is negative (the angular momentum flows inwards), while the latitudinal Λ effect is always positive (the angular momentum flows equatorward). Basically, it is |Qxz|≳Qyz. The numerical values strongly depend on the latitude. By definition, both correlations vanish at the poles and Tyz also vanishes at the equator (Fig. 7). Under the influence of magnetic fields, the values are reduced (‘magnetic quenching’) depending on the inclination of the background fields. We shall assume in Eqs. (35) and (36) that the typical profiles in Fig. 7 are not changed by the magnetic influences.
 |
Fig. 7. Simulation results for the vertical angular momentum transport Txz (left) and the latitudinal angular momentum transport Tyz (right) without magnetic fields (B = 0) vs. colatitude θ. The red lines give the θ functions used in Eqs. (35) and (36). The crosses at θ = 45° reflect the values of Table 3 (first line); Ω = 10, Pr = 0.1, and Pm = 0.1. |
In order to formulate the magnetic influences on the angular momentum fluxes, we shall restrict our computations to mid-latitudes (θ = 45°).
The influences on the latitudinal angular momentum transport Tyz are represented by Fig. 8, providing the total stresses as well as the Reynolds and both Maxwell stresses for the two inclined fields B = (0, ±1, 10). In both cases, the small-scale Maxwell stresses are only weak and the large-scale Maxwell stresses are of opposite sign. The main result is that for both magnetic configurations, the Tyz are positive in opposition to nonrotating turbulence (see Fig. 4), hence with rotation the Reynolds stresses dominate the Lorentz force.
 |
Fig. 8. Snapshots of the (yz)-correlations (normalised with |
For ByBz > 0, the Reynolds stress grows and for ByBz < 0 it sinks, that is the coefficient D in Eq. (13) is positive in opposition to D* in Eq. (14) which becomes negative. The small numerical value indicates a reduced effectivity of the mean field Lorentz force to transport angular momentum. It is thus very questionable that a theoretical explanation of the solar torsional oscillation with only the action of the dynamo-induced Lorentz force may work.
The code was also probed with the radial flux Txz for an inclined magnetic field Bz = 10 with components Bx varying between ±1 and ±10 (Table 2). Here the nonmagnetic value of 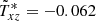 was magnetically reduced to
was magnetically reduced to 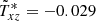 by the field B = ( ± 10, 0, 10). This is a clear but mild magnetic quenching. For Bx = 1 and Bz = 10, the equipartion value of the field is β = 0.50 and for Bx = Bz = 10 it is β = 0.75 with β2 as the ratio of magnetic to kinetic energy. The reported quenching behaviour is similar to that of Käpylä (2019) in a quite different approach. We also find that the coefficient
by the field B = ( ± 10, 0, 10). This is a clear but mild magnetic quenching. For Bx = 1 and Bz = 10, the equipartion value of the field is β = 0.50 and for Bx = Bz = 10 it is β = 0.75 with β2 as the ratio of magnetic to kinetic energy. The reported quenching behaviour is similar to that of Käpylä (2019) in a quite different approach. We also find that the coefficient 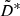 is basically uninfluenced by the magnetic background field. For very strong fields the mean value
is basically uninfluenced by the magnetic background field. For very strong fields the mean value 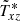 vanishes, while
vanishes, while 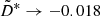 known from Sect. 3 for Ω = 0. The main result is thus that for small fields |Bx|, the flux Txz is always negative but for large |Bx|, when the Lorentz force dominates, both signs appear indicating that the Reynolds stress is smaller than the Maxwell stress.
known from Sect. 3 for Ω = 0. The main result is thus that for small fields |Bx|, the flux Txz is always negative but for large |Bx|, when the Lorentz force dominates, both signs appear indicating that the Reynolds stress is smaller than the Maxwell stress.
Results for the vertical flux 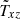 (averaged over radius and time) with Bz = 10, Ω = 10, Pr = Pm = 0.1, and θ = 45°.
(averaged over radius and time) with Bz = 10, Ω = 10, Pr = Pm = 0.1, and θ = 45°.
All correlations are written in units of the reference turbulence intensity 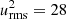 resulting from the nonrotating and unmagnetised turbulent fluid. With Ω = 10, we used a rather fast rotation rate in order to minimise the large-scale shear flows which develop in the turbulent box (Brummell et al. 1998). The faster the rotation is, the weaker the shear of these flows and the smaller their influence onto the calculated correlations. As demonstrated by Rüdiger et al. (2019), both the calculated nondiffusive fluxes V and H are minimum values; they would be slightly larger under suppression of the action of the induced shear flows.
resulting from the nonrotating and unmagnetised turbulent fluid. With Ω = 10, we used a rather fast rotation rate in order to minimise the large-scale shear flows which develop in the turbulent box (Brummell et al. 1998). The faster the rotation is, the weaker the shear of these flows and the smaller their influence onto the calculated correlations. As demonstrated by Rüdiger et al. (2019), both the calculated nondiffusive fluxes V and H are minimum values; they would be slightly larger under suppression of the action of the induced shear flows.
We note that the modified Lorentz force factor D* is always negative and (almost) independent of the magnetic inclination angle. It only grows for very small angles, and it depends on Bx only for |Bx|≪|Bz| when its amount becomes smaller. The dependence on Bx vanishes for larger values. The consequence is that for |Bx|≪|Bz| the magnetic quenching of Qxz cannot be compensated for by the Lorentz force BxBz so that the total sum Txz becomes smaller than the unmagnetised value Qxz(B = 0) as shown in the next to last column of Table 2. This behaviour is the natural counterpart to the phenomenon of negative effective-magnetic-pressure where total pressure is also reduced by the magnetic parts, but only for a weak magnetic field (Brandenburg et al. 2011; Käpylä et al. 2012; Rüdiger et al. 2012). Here, the magnetic-induced reduction of the total angular momentum transport happens for Bx ≲ 0.1Bz (similar for By).
The main results of the simulations for Bz = 20 and various Bx and By are summarised in Table 3. The reference values of the nonmagnetic approximation are given in the first row of the table. The last columns in the table (also in boldface) give the fluxes due to the Lorentz force alone without rotation. The underlined numbers provide the resulting angular momentum fluxes with rotation and the equipartition field Bz = 20 and Bx = ±0.1 or By = ±0.1. For the given rotation rate and the magnetic field geometry, the resulting angular momentum transport is dominated by the turbulence rather than by the Lorentz force of the background field. The magnetic influence on the total stresses is, nevertheless, remarkably strong. The interplay of rotation, magnetic fields, and turbulence mainly leads to a suppression of the turbulence-induced angular momentum transport despite the contribution of the large-scale Lorentz force. The underlined numbers in Table 3 demonstrate how the turbulent transport is suppressed by the inclined field with the given components. The vertical transport Txz for both signs of Bx lies below the hydrodynamic value. The horizontal transport Tyz is also suppressed, but there is a difference for positive and negative By. In the latter case, the magnetic and the nonmagnetic Tyz hardly differ, while for positive By the suppression is very strong. The signs of the total fluxes never differ for different signs of the (small) inclination angles p.
Normalised angular momentum fluxes 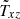 and
and 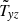 (averaged over radius and time) with Bz = 20 and for various meridional magnetic field components Bx and By.
(averaged over radius and time) with Bz = 20 and for various meridional magnetic field components Bx and By.
6. Rotation laws
To obtain the (axisymmetric) rotation law Ω = Ω(r,θ) in the solar convection zone, the equation for the conservation of angular momentum in spherical coordinates
was solved using a time-dependent finite difference code and the density profile of the solar convection zone with variations of three orders of magnitudes. The relevant components of the angular momentum flux vector t are
with the viscous part of the stress tensor
and constant viscosity coefficient νT. The boundary conditions at the top and bottom of the convection zone are simply tr = 0. They ensure that no angular momentum leaves the convection zone. We note that the angular momentum transport by the meridional flow was neglected here so that only the azimuthal component (31) of the Reynolds equation must have been solved. The complete mean-field theory on the basis of Eq. (33) provides one-cell meridional flows circulating counterclockwise in the northern hemisphere (Rüdiger et al. 2013) close to the recent results of helioseismology (Gizon et al. 2020).
The code started with rigid rotation and was run until a stationary solution was reached. The latitudinal profiles in Fig. 7 are the basis for the formulation
with the minimum at θ = 35° and
with the maximum at θ = 54°. The V and H are dimensionless quantities. They are coupled to the viscosity term in the angular momentum equation by a dimensionless factor 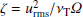 for which solar values provide ζ ≲ 10. The parameter ζ includes all normalisation factors, hence
for which solar values provide ζ ≲ 10. The parameter ζ includes all normalisation factors, hence 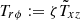 and
and 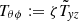 .
.
Equation (35) contains the nontrivial assumption that the radial turbulent transport vanishes at the equator, which is the case for quasilinear analytical calculations without magnetic fields (Rüdiger et al. 2013). We do not expect contradictions by the magnetic fields as the toroidal background field vanishes at the equator. However, without meridional circulation and without turbulence-induced anisotropic heat transport, the immediate consequence of vanishing radial flux along θ = 90° is the uniformity of Ω in the equatorial plane in contrast to the slight superrotation which is observed with methods of helioseismology. This little disadvantage of our model may be accepted by the reader.
The coefficients V and H in Eqs. (35) and (36) were calculated from the numerical results in Table 3 for θ = 45°. For a rotating but nonmagnetic box, one finds from the first line of Table 3 the values V = −0.18 and H = 0.066. The radial flux exceeds the latitudinal one by a factor of three. The resulting isolines of the angular velocity Ω(r,θ) are given by a red colour in the plots of Fig. 9. In the spirit of the Malkus-Proctor approximation, the nonmagnetic rotation law may be modified only by the large-scale Lorentz force of the two fields B = (0, ±0.1, 20) (blue lines). We note again that Bz = 20 represents the equipartition value of the azimuthal field, while By = ±0.1 is still a rather large value for the possible latitudinal field component. The formally resulting momentum fluxes are H = 0.058 for By = 0.1 and H = 0.075 for By = −0.1. Fields with a positive inclination angle transport the angular momentum poleward and fields with a negative inclination angle transport the angular momentum equatorward. In general, the field with the positive inclination angle (as in the solar convection zone) reduces the latitudinal shear, while the field with the negative inclination angle enhances the shear. There is even a tendency of a magnetic deceleration of the equatorial rotation rate but this is only a very small effect which becomes even weaker as By diminishes. To include the magnetic background fields in a consistent way, the underlined coefficients in Table 3 must be used to evaluate the coefficients V and H for px = py = ±5 × 10−3. In Fig. 10 the blue lines again represent the rotation laws under the influence of these magnetic fields, while the red lines are valid for B = 0.
 |
Fig. 9. Rotation laws in radius r and colatitude θ for fast rotation (Ω = 10) under the influence of the large-scale Lorentz force for B = (0, 0.1, 20) (left panel, blue lines) and B = (0, −0.1, 20) (right panel, blue lines). The differential rotation is due to the nonmagnetic Λ effect (red lines). The uppermost Ω-isolines belong to the equator, while the lowest curves belong to the poles. |
In Table 4, the four models with different magnetic geometries are summarised for which the rotation laws have been calculated. All models work with the equipartition value Bz = 20 and with the inclination angles |p| = 5 × 10−3. We focus our attention to the model 1 with positive ByBz, which should be most reliable for the solar convection zone. The combinations of Bx and Bz are much more speculative.
Vertical and the horizontal fluxes of angular momentum for various combinations of the meridional magnetic field components.
The rotation laws for models 1–4 are displayed in Fig. 10. The lines represent the rotation rates within the convection zone for various latitudes. The uppermost profiles belong to the equator, while the lowest lines belong to the poles. All models provide the magnetic-suppression of the equator-pole difference of the surface rotation. The spread of the (non-magnetic) red lines exceeds that of the (magnetic) blue lines for all models except for model 2 where the magnetic influence is basically weak. Only in one case, however, is the equatorial rotation rate also magnetically reduced. This is true for model 1 where the upper blue line clearly lies below the upper red line, hence the equator rotates slower during the magnetic activity maximum. For all other magnetic configurations, the equatorial rotation rate is magnetically uninfluenced. Obviously, the deceleration of the equator is a consequence of the magnetic quenching which reduces the horizontal transport coefficient down to H = 0.045. Model 1 shows the magnetic-originated variation of the equator-pole difference of Ω as 3–4 units of the magnetic-originated variation of the equatorial rotation rate so that not only the first observational condition as shown in Eq. (3) but also the second one will approximately be fulfilled by model 1.
 |
Fig. 10. Similar to Fig. 9, but with the total magnetic stress-tensor from Eq. (8). The applied magnetic fields (at θ = 45°) are B = (0, 0.1, 20) (top left, model 1), B = (0, −0.1, 20) (top right, model 2), B = (0.1, 0, 20) (bottom left, model 3), and B = ( − 0.1, 0, 20) (bottom right, model 4). The red curves are the nonmagnetic rotation laws. |
7. Results and discussion
The explanation of a possible non-regular behaviour in the magnetic activity cycle has been started including the magnetic feedback on the internal solar rotation. Jennings & Weiss (1991), Kitchatinov et al. (1994), and Tobias (1996) added the conservation law of angular momentum in the turbulent convection zone to the dynamo equations including magnetic feedback in order to simulate the interplay of induced magnetic fields and rotation. The form of the rotation law can be influenced by the magnetic field in two ways. If the magnetic field only consists on a (strong) toroidal field, then the Reynolds stress (Λ effect and/or eddy viscosity) is magnetically quenched. If, however, the magnetic field also possess (weak) latitudinal components then small-scale as well as large-scale Maxwell stresses additionally contribute to the angular momentum transport. Yoshimura (1981), Schüssler (1981), Noyes et al. (1984), and Rüdiger et al. (1986) presented the first dynamo models where large-scale Lorentz forces due to induced magnetic fields modified the internal rotation laws.
In the present paper, the total angular momentum transport by rotating magnetoconvection under the influence of prescribed magnetic background fields was calculated by means of 3D MHD box simulations. They are motivated by the observational result that in the solar activity maximum both the equator-pole difference of the surface rotation rate and the equatorial rotation rate is reduced where the latter has only a 1% effect. The question is whether a combination of a (strong) azimuthal field component as well as (weak) radial and latitudinal field components can reproduce these observations.
A natural start of the calculations is given by Fig. 9. The magnetic modifications of the rotation profiles are only due to the large-scale Lorentz force of two prescribed large-scale fields, which is the original configuration used by Malkus & Proctor (1975). The (dominating) azimuthal field with energy in equipartition with the kinetic energy of the turbulence is Bz = 20. If the extra latitudinal field By = 0.1 is added, the resulting Maxwell stress transports the angular momentum poleward and the latitudinal shear is magnetically reduced. It is clear that for By = −0.1, the opposite is true: The shear is increased. These results are almost trivial and for decreasing |By| they disappear.
The calculations have been repeated with the total stresses shown in Eqs. (9) and (10), which are known from box simulations for rotating convection under the influence of magnetic background fields of the same geometry. Then Reynolds stress, small-scale Maxwell stress, and large-scale Maxwell stress are the transporters of the angular momentum. The numerical simulations lead to the two main results that (i) the influence of the large-scale Maxwell stress is only small, that is 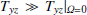 , and (ii) the magnetic influence on the Reynolds stress depends on the sign of By, that is Tyz < Tyz|B = 0 for By = 0.1 and Tyz ≳ Tyz|B = 0 for By = −0.1. Consequently, the equator-pole difference of Ω is almost not influenced if ByBz < 0, but it is strongly reduced if ByBz > 0 (see top panel of Fig. 10). In the latter case, the equator is also decelerated in the activity maximum. Positive ByBz is expected to exist within the solar convection zone and the resulting magnetic behaviour of the rotation law with an accelerated equator fully complies with the observations shown in Eq. (3). The scenario appears to be consistent in the following case: If magnetic fields Bθ exist, the turbulence-originated rotational shear produces positive products of BθBϕ which, in agreement with the observations, simultaneously reduce the equatorial value of the angular velocity and the surface differential rotation. It is also obvious that for the Sun the angular momentum transport by the Maxwell stress does not exceed the transport by the Reynolds stress. With ur ≃ uϕ ≃ 100 m s−1 and with Br ≃ 1 Gauss and Bϕ ≃ 104 Gauss, one finds the ratio BrBϕ/(μ0ρcuruϕ) ≲ O(10−2) where the correlation factor c ≃ 0.1 and the density ρ ≃ 10−2 g cm−3 have approximately been used. Indeed, the solar observations reveal the cycle-dependent velocity variations as never exceeding the 10−2 limit. One would need toroidal fields of the order of 105−6 Gauss in order to find the rotation law as basically modulated by the Lorentz force.
, and (ii) the magnetic influence on the Reynolds stress depends on the sign of By, that is Tyz < Tyz|B = 0 for By = 0.1 and Tyz ≳ Tyz|B = 0 for By = −0.1. Consequently, the equator-pole difference of Ω is almost not influenced if ByBz < 0, but it is strongly reduced if ByBz > 0 (see top panel of Fig. 10). In the latter case, the equator is also decelerated in the activity maximum. Positive ByBz is expected to exist within the solar convection zone and the resulting magnetic behaviour of the rotation law with an accelerated equator fully complies with the observations shown in Eq. (3). The scenario appears to be consistent in the following case: If magnetic fields Bθ exist, the turbulence-originated rotational shear produces positive products of BθBϕ which, in agreement with the observations, simultaneously reduce the equatorial value of the angular velocity and the surface differential rotation. It is also obvious that for the Sun the angular momentum transport by the Maxwell stress does not exceed the transport by the Reynolds stress. With ur ≃ uϕ ≃ 100 m s−1 and with Br ≃ 1 Gauss and Bϕ ≃ 104 Gauss, one finds the ratio BrBϕ/(μ0ρcuruϕ) ≲ O(10−2) where the correlation factor c ≃ 0.1 and the density ρ ≃ 10−2 g cm−3 have approximately been used. Indeed, the solar observations reveal the cycle-dependent velocity variations as never exceeding the 10−2 limit. One would need toroidal fields of the order of 105−6 Gauss in order to find the rotation law as basically modulated by the Lorentz force.
As our model of the solar differential rotation is stationary and the latitude dependence of the Reynolds stress is completely determined through the V and H coefficients, it cannot be directly used for the explanation of the torsional oscillation patterns. Howard & Labonte (1980) determined a global rotation law, which they subtracted from the observed profile of the rotation rate. The residual shows a pattern of alternating bands of fast and slow rotation. Zones of more rapid rotation appear at high latitude and migrate towards the equator similar to the active regions. More recent observations revealed that the zone of faster than average rotation reaches the equator in the solar minimum (Basu & Antia 2003; Howe et al. 2011). This is in line with the findings in the present paper.
References
- Augustson, K., Brun, A. S., Miesch, M., & Toomre, J. 2015, ApJ, 809, 149 [Google Scholar]
- Basu, S., & Antia, H. M. 2003, ApJ, 585, 553 [Google Scholar]
- Brandenburg, A., Kemel, K., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2011, ApJ, 740, L50 [Google Scholar]
- Browning, M. K., Miesch, M. S., Brun, A. S., & Toomre, J. 2006, ApJ, 648, L157 [Google Scholar]
- Brummell, N. H., Hurlburt, N. E., & Toomre, J. 1998, ApJ, 493, 955 [Google Scholar]
- Brun, A. S., Miesch, M. S., & Toomre, J. 2004, ApJ, 614, 1073 [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and Hydromagnetic Stability (Oxford: Clarendon) [Google Scholar]
- Featherstone, N. A., & Miesch, M. S. 2015, ApJ, 804, 67 [Google Scholar]
- Gilman, P. A., & Howard, R. 1984, ApJ, 283, 385 [Google Scholar]
- Gizon, L., Cameron, R. H., Pourabdian, M., et al. 2020, Science, 368, 1469 [Google Scholar]
- Howard, R., & Labonte, B. J. 1980, ApJ, 239, L33 [Google Scholar]
- Howe, R., Hill, F., Komm, R., et al. 2011, in GONG-SoHO 24: A New Era of Seismology of the Sun and Solar-Like Stars, J. Phys. Conf. Ser., 271, 012074 [Google Scholar]
- Jennings, R. L., & Weiss, N. O. 1991, MNRAS, 252, 249 [Google Scholar]
- Jurdana-Šepić, R., Brajša, R., Wöhl, H., et al. 2011, A&A, 534, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J. 2019, A&A, 622, A195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Korpi, M. J., & Tuominen, I. 2004, A&A, 422, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2009, A&A, 500, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Brandenburg, A., Kleeorin, N., Mantere, M. J., & Rogachevskii, I. 2012, MNRAS, 422, 2465 [Google Scholar]
- Käpylä, M. J., Käpylä, P. J., Olspert, N., et al. 2016, A&A, 589, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Käpylä, M. J., Olspert, N., Warnecke, J., & Brandenburg, A. 2017, A&A, 599, A4 [CrossRef] [EDP Sciences] [Google Scholar]
- Karak, B. B., Käpylä, P. J., Käpylä, M. J., et al. 2015, A&A, 576, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kippenhahn, R. 1963, ApJ, 137, 664 [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 1995, A&A, 299, 446 [NASA ADS] [Google Scholar]
- Kitchatinov, L. L., Rüdiger, G., & Küker, M. 1994, A&A, 292, 125 [NASA ADS] [Google Scholar]
- Küker, M., & Rüdiger, G. 2018, Astron. Nachr., 339, 447 [Google Scholar]
- Malkus, W. V. R., & Proctor, M. R. E. 1975, J. Fluid Mech., 67, 417 [Google Scholar]
- Miesch, M. S., Brun, A. S., & Toomre, J. 2006, ApJ, 641, 618 [Google Scholar]
- Noyes, R. W., Weiss, N. O., & Vaughan, A. H. 1984, ApJ, 287, 769 [Google Scholar]
- Ossendrijver, M., Stix, M., & Brandenburg, A. 2001, A&A, 376, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossendrijver, M., Stix, M., Brandenburg, A., & Rüdiger, G. 2002, A&A, 394, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rüdiger, G. 1974, Astron. Nachr., 295, 275 [Google Scholar]
- Rüdiger, G., Tuominen, I., Krause, F., & Virtanen, H. 1986, A&A, 166, 306 [NASA ADS] [Google Scholar]
- Rüdiger, G., Kitchatinov, L. L., & Schultz, M. 2012, Astron. Nachr., 333, 84 [Google Scholar]
- Rüdiger, G., Kitchatinov, L. L., & Hollerbach, R. 2013, Magnetic Processes in Astrophysics: theory, simulations, experiments (Wiley-VCH) [Google Scholar]
- Rüdiger, G., Küker, M., Käpylä, P. J., & Strassmeier, K. G. 2019, A&A, 630, A109 [EDP Sciences] [Google Scholar]
- Ruždjak, D., Brajša, R., Sudar, D., Skokić, I., & Poljančić Beljan, I. 2017, Sol. Phys., 292, 179 [Google Scholar]
- Schüssler, M. 1981, A&A, 94, L17 [NASA ADS] [Google Scholar]
- Tobias, S. M. 1996, A&A, 307, L21 [NASA ADS] [Google Scholar]
- Warnecke, J. 2018, A&A, 616, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warnecke, J., Rheinhardt, M., Tuomisto, S., et al. 2018, A&A, 609, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xie, J., Shi, X., & Qu, Z. 2018, ApJ, 855, 84 [Google Scholar]
- Yoshimura, H. 1981, ApJ, 247, 1102 [Google Scholar]
- Ziegler, U. 2004, J. Comput. Phys., 196, 393 [Google Scholar]
All Tables
Latitudinal angular momentum transport 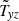 for very large or very small inclination angles, py > 0 in the upper two lines and py < 0 in the lower two lines.
for very large or very small inclination angles, py > 0 in the upper two lines and py < 0 in the lower two lines.
Results for the vertical flux 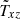 (averaged over radius and time) with Bz = 10, Ω = 10, Pr = Pm = 0.1, and θ = 45°.
(averaged over radius and time) with Bz = 10, Ω = 10, Pr = Pm = 0.1, and θ = 45°.
Normalised angular momentum fluxes 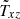 and
and 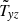 (averaged over radius and time) with Bz = 20 and for various meridional magnetic field components Bx and By.
(averaged over radius and time) with Bz = 20 and for various meridional magnetic field components Bx and By.
Vertical and the horizontal fluxes of angular momentum for various combinations of the meridional magnetic field components.
All Figures
 |
Fig. 1. Turbulent intensities by nonrotating convection without (left panel) and with a magnetic field (right panel, B = (0, 1, 10)); |
| In the text | |
 |
Fig. 2. Left: vertical cross-correlation |
| In the text | |
 |
Fig. 3. Snapshots of the |
| In the text | |
 |
Fig. 4. Similar to Fig. 3, but for the horizontal torque |
| In the text | |
 |
Fig. 5. Snapshots of the small-scale helicity ℋ at the north pole (θ = 0°, left) and mid-latitudes (θ = 45°, right) for fast rotation. As expected, the helicity vanishes in the middle of the box. The applied magnetic field is B = (0, 0.1, 10), Ω = 10, Pr = 0.1, and Pm = 0.1. |
| In the text | |
 |
Fig. 6. Snapshots of the large-scale field components Bx (left) and By (right) in the box. We note the transformation of By > 0 to By < 0 by the inbox α effect. The radial field Bx is not concerned; B = (0, 0.1, 10), Ω = 10, Pr = 0.1, Pm = 0.1, and θ = 45°. |
| In the text | |
 |
Fig. 7. Simulation results for the vertical angular momentum transport Txz (left) and the latitudinal angular momentum transport Tyz (right) without magnetic fields (B = 0) vs. colatitude θ. The red lines give the θ functions used in Eqs. (35) and (36). The crosses at θ = 45° reflect the values of Table 3 (first line); Ω = 10, Pr = 0.1, and Pm = 0.1. |
| In the text | |
 |
Fig. 8. Snapshots of the (yz)-correlations (normalised with |
| In the text | |
 |
Fig. 9. Rotation laws in radius r and colatitude θ for fast rotation (Ω = 10) under the influence of the large-scale Lorentz force for B = (0, 0.1, 20) (left panel, blue lines) and B = (0, −0.1, 20) (right panel, blue lines). The differential rotation is due to the nonmagnetic Λ effect (red lines). The uppermost Ω-isolines belong to the equator, while the lowest curves belong to the poles. |
| In the text | |
 |
Fig. 10. Similar to Fig. 9, but with the total magnetic stress-tensor from Eq. (8). The applied magnetic fields (at θ = 45°) are B = (0, 0.1, 20) (top left, model 1), B = (0, −0.1, 20) (top right, model 2), B = (0.1, 0, 20) (bottom left, model 3), and B = ( − 0.1, 0, 20) (bottom right, model 4). The red curves are the nonmagnetic rotation laws. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.