| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 13 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202039451 | |
| Published online | 20 May 2021 | |
Weak-lensing mass reconstruction using sparsity and a Gaussian random field
1
AIM, CEA, CNRS, Université Paris-Saclay, Université de Paris, 91191 Gif-sur-Yvette, France
e-mail: jstarck@cea.fr
2
Laboratoire de Physique de l’Ecole Normale Supérieure, ENS, Université PSL, CNRS, Sorbonne Université, Université de Paris, Paris, France
3
Department of Physics & Astronomy, University College London, Gower Street, London WC1E 6BT, UK
4
Institute of Physics, Laboratory of Astrophysics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
Received:
16
September
2020
Accepted:
5
February
2021
Aims. We introduce a novel approach to reconstructing dark matter mass maps from weak gravitational lensing measurements. The cornerstone of the proposed method lies in a new modelling of the matter density field in the Universe as a mixture of two components: (1) a sparsity-based component that captures the non-Gaussian structure of the field, such as peaks or halos at different spatial scales, and (2) a Gaussian random field, which is known to represent the linear characteristics of the field well.
Methods. We propose an algorithm called MCALens that jointly estimates these two components. MCALens is based on an alternating minimisation incorporating both sparse recovery and a proximal iterative Wiener filtering.
Results. Experimental results on simulated data show that the proposed method exhibits improved estimation accuracy compared to customised mass-map reconstruction methods.
Key words: cosmology: observations / techniques: image processing / methods: data analysis / gravitational lensing: weak
© J.-L. Starck et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In recent years, interest has increased in exploring the two most dominant components of the universe: dark matter and dark energy. To this end, large-scale imaging and spectroscopic surveys are currently under development, such as the Euclid mission (Laureijs et al. 2011), the Rubin Observatory Legacy Survey of Space and Time (Abell et al. 2009), and the Roman Space Telescope (Spergel et al. 2015), which will map the sky with unprecedented accuracy. A prominent cosmological probe for these surveys is weak gravitational lensing.
Weak gravitational lensing measures correlations in the small distortions of distant galaxies caused by the gravitational potential of massive structures along the line of sight. Its effect on distant source galaxies is twofold: the galaxy shapes are magnified by a convergence field, κ, while the galaxy ellipticities are perturbed from their underlying intrinsic value by a shear field, γ. To contribute constraints on cosmological parameters and models, two-point correlation functions of the shear have been used with considerable success (Kilbinger et al. 2013; Alsing et al. 2016a). This type of correlation is sufficient to statistically describe the Gaussian structures of the lensing field, such as those expected to be present either in the early universe or at large scales that are less affected by gravitational collapse. To capture non-Gaussian structures such as those expected in smaller scales at later time, higher order moments of the shear need to be employed (Munshi & Coles 2017).
On the other hand, the convergence density field is not observed directly as a result of the mass-sheet degeneracy (Bartelmann & Schneider 2001; Kilbinger 2015). Physically, the convergence field reveals the projected total matter density along the line of sight, weighted by a lensing kernel in the mid-distance between the observer and the galaxy sources. The density field is inhomogeneous, encompassing Gaussian-type large-scale structures, as well as non-Gaussian features, such as peaks. To shed light on the way in which the convergence density field constrains cosmology, peak statistics (e.g. Jain & Van Waerbeke 2000; Marian et al. 2011; Lin & Kilbinger 2015; Liu & Haiman 2016; Peel et al. 2017a; Fluri et al. 2018; Li et al. 2019; Ajani et al. 2020) and higher order correlation functions and moments, such as the Minkowksi functionals (e.g. Kratochvil et al. 2012; Shirasaki et al. 2012; Petri et al. 2013), have been applied directly on mass maps. It is therefore essential for mass-mapping methods to preserve both Gaussian and non-Gaussian features during the reconstruction process.
Mass-mapping methods solve an ill-posed problem because the sampling of the lensing field is irregular and the signal-to-noise ratio on small scales is low. A widely used algorithm to perform mass mapping is the Kaiser-Squires method (Kaiser & Squires 1993), which is expressed as a simple linear operator in Fourier space. However, it is inevitable that this estimator returns poor results because it does not take particular care of the noise or missing data. A different approach, motivated also by the Bayesian framework, is that of Wiener filtering (Wiener 1949). In this approach, a Gaussian random field is assumed as a prior for the convergence map, which is responsible for inserting some bias that prevents our estimate from over-fitting (Zaroubi et al. 1995). Moreover, a recently proposed customised method is the algorithm called gravitational lensing inversion and mapping using sparse estimators (GLIMPSE2D; Lanusse et al. 2016). GLIMPSE2D is a highly sophisticated algorithm that takes advantage of the sparse regularisation framework to solve the ill-posed linear inverse problem. GLIMPSE2D is based on sparse representations (i.e. wavelets) and is therefore well designed to recover piece-wise smooth features. An analytical comparison of these three estimators is provided in Jeffrey et al. (2018a).
In this paper we propose to bridge the gap between the sparse regularisation method of GLIMPSE2D and the Wiener-filtering method by modelling the matter density field in the universe using both linear and non-linear characteristics. Specifically, we assume that the density field is modelled as a mixture of two terms: (1) a non-Gaussian term that adopts a sparse representation in a selected wavelet basis (Starck et al. 2015), and (2) a Gaussian term that is modelled using a Gaussian random field (Elsner & Wandelt 2013; Horowitz et al. 2019). The non-Gaussian signal component is able to capture the non-linear characteristics of the convergence field, such as peaks, while the Gaussian component of the signal is responsible for capturing the lower-frequency characteristics of the underlying field, such as smooth variations. To our knowledge, this is the first time that this mixture modelling is proposed for mass-map reconstruction.
This paper is structured as follows. In Sect. 2 we introduce the formalism of weak gravitational lensing and describe the mass-map reconstruction problem. To this end, we provide a brief overview of the current algorithms of Kaiser-Squires, Wiener filtering, and GLIMPSE2D. We then present our proposed mass-mapping method in Sect. 3. The method is novel in the sense that it exploits both sparsity in the wavelet domain and a Gaussian random field model. Section 4 illustrates the enhanced estimation performance of the proposed method by providing experiments conducted on both simulated and real data.
Notation: We use (⋅)* to denote the Hermitian transpose of a matrix or the adjoint operator of a transform. With ∥⋅∥1 and ∥⋅∥2 we denote the ℓ1 and ℓ2 norm, respectively,  . The determinant of a matrix or the absolute value of a scalar is denoted by |⋅|, while diag(x) stands for a diagonal matrix that contains the elements of vector x on its diagonal. Finally, ℛN is the N-dimensional Euclidean space, 0 denotes the zero vector, 1 the all-ones vector, and IK is the K × K identity matrix.
. The determinant of a matrix or the absolute value of a scalar is denoted by |⋅|, while diag(x) stands for a diagonal matrix that contains the elements of vector x on its diagonal. Finally, ℛN is the N-dimensional Euclidean space, 0 denotes the zero vector, 1 the all-ones vector, and IK is the K × K identity matrix.
2. Weak-lensing mass mapping
Gravitational lensing describes the phenomenon where the light emitted from distant galaxies is deflected as it passes through a foreground mass distribution. The lensing effect distorts the images of distant galaxies; the distortion is proportional to the size and shape of the projected matter distribution along the line of sight. Specifically, the mapping between the source coordinates, β, and the lensed image coordinates, θ, is given by the lens equation (e.g. Kilbinger 2015),
where ψ(⋅) defines the lensing potential that conceals the deflection of light rays by the gravitational lens. Under the Born approximation, which assumes that the lensing potential is weak enough, we may linearise the coordinate transformation of Eq. (1) by using the Jacobian 𝔄 = ∂β/∂θ as
where 𝔄ij = ∂βi/∂θj are the coefficients of the amplification matrix 𝔄, and we assume the Einstein summation convention. The symmetrical matrix 𝔄 can also be parametrised in terms of the convergence, κ, and the shear, γ, as
The convergence can then be defined as a dimensionless quantity that relates to the lensing potential through the Poisson equation,
while the shear is mathematically expressed as a complex field whose components also relate to ψ,
Equation (3) shows that the convergence causes an isotropic change in the size of the source image because it appears in the diagonal of 𝔄. In comparison, the shear causes anisotropic changes of the image shapes. The convergence κ can also be interpreted via Eq. (4) as a weighted projection of the mass density field between the observation and the source. Factoring out the term (1 − κ) in Eq. (3) leaves the amplification matrix dependent on the reduced shear,
which is directly measured in lensing surveys, and it is defined as g = γ/(1 − κ). In the weak-lensing limit, where γ, κ ≪ 1, the reduced shear is approximately equal to the true shear, that is, g ≃ γ.
In this paper we are interested in recovering the convergence κ from the reduced shear data. This is an ill-posed inverse problem because of the finite sampling of the reduced shear over a limited area of the survey and the presence of shape noise in the measurements. In the following we review some of the customised weak-lensing mass reconstructing algorithms, namely the Kaiser-Squires, the Wiener filtering, and the GLIMPSE2D methods.
Kaiser-Squires. A theoretical framework for reconstructing convergence maps from the observable weak-lensing shear in the Fourier domain was proposed in Kaiser & Squires (1993). As we showed in Eqs. (4) and (5), the convergence and shear are both expressed as second-order derivatives of the lensing potential. Their interrelation through the lensing potential ψ is expressed by a two-dimensional convolution (Kaiser & Squires 1993),
where 𝔇(θ) = − 1/(θ1 − iθ2)2. This convolution is equivalently expressed in Fourier space as the element-wise multiplication,
where k is the wave vector, and the Fourier transform of the kernel 𝔇(θ) is given by
with k1 and k2 being the two frequency components of k. Discretising Eq. (7) and adopting matrix notation, we may consider that the observed shear γ is generated as a linear combination of the convolution matrix A and the unknown underlying field κ,
where n is the statistical uncertainty vector associated with the data. Based on Eq. (8), A can be decomposed in Fourier space as A = FPF*, where F denotes the discrete Fourier transform, F* is its adjoint, and P is the diagonal operator that defines the convergence field-shear relation in Fourier space,
where  and
and  .
.
Equation (11) corresponds to a discretised version of Eq. (8). As it stands, the Kaiser-Squires inversion of Eq. (11) has several drawbacks. First, it is not defined for k = 0, which stems from the mass-sheet degeneracy (i.e. the mean value of the convergence field cannot be retrieved). Next, it is ill-posed because typically, the shear field is a discrete under-sampling of the underlying convergence field. Neither does it take masked data into account. Nonetheless, the Kaiser-Squires estimate is still used in practice because it is easy to apply.
Wiener filtering. The Wiener filter was introduced in the 1940s (Wiener 1949), and it is the optimal linear filter in the minimum mean-square sense that provides a denoised version of the desired signal. The Wiener-filtered estimate of the convergence map can be expressed using the linear equation
where the matrix W is given by
and Σκ and Σn are the pre-defined covariance matrix of the convergence and the noise, respectively. When the noise is not stationary, the Wiener-filter solution is not straightforward, and an iterative approach is required. This is discussed in the next section.
From a Bayesian perspective, Wiener filtering is equivalent to the maximum a posteriori (MAP) estimator given that the convergence is a zero-mean Gaussian signal with covariance Σκ. When we assume that shear measurements are distorted by uncorrelated Gaussian noise, the likelihood function shares the noise properties, that is,
while the distribution of the Gaussian random field can be written as
Given Eqs. (14) and (15) above, the MAP estimator is expressed as
which leads to the minimisation
It is easy to see that the minimum is attained at κG = Wγ, where W is the Wiener filter given in Eq. (12).
The implementation of the Wiener filter requires the inversion of the matrix W that includes both a signal covariance matrix component and the noise covariance matrix component.
The unknown κG is assumed to be a Gaussian random field with a covariance matrix diagonal in Fourier space, Σκ = F*CκF, where Cκ is a diagonal matrix with diagonal values equal to the theoretical power spectrum Pκ. When the noise is stationary, its covariance matrix is also diagonal with diagonal elements equal to the noise power spectrum Pn. In this case, the filter solution is obtained in Fourier space by  , where the Wiener filter is
, where the Wiener filter is  . In practice, the noise is generally not stationary and depends on the number of shear measurements in the area related to a given pixel of the shear field. Therefore the noise covariance matrix is diagonal in pixel space, not in Fourier space, and the Wiener-filter solution becomes harder to derive, requiring either making an incorrect assumption (i.e. that the noise is stationary) or inverting a very large matrix. This renders its inversion computationally complex and prone to numerical errors. To circumvent this computationally intensive operation, a forward-backward (FB) proximal iterative Wiener filtering was proposed in Bobin et al. (2012) for the denoising of cosmic microwave background spherical maps, exploiting the property that the signal and noise covariance matrices are diagonal in pixel and Fourier space, respectively. Equation (17) comprises two separable terms,
. In practice, the noise is generally not stationary and depends on the number of shear measurements in the area related to a given pixel of the shear field. Therefore the noise covariance matrix is diagonal in pixel space, not in Fourier space, and the Wiener-filter solution becomes harder to derive, requiring either making an incorrect assumption (i.e. that the noise is stationary) or inverting a very large matrix. This renders its inversion computationally complex and prone to numerical errors. To circumvent this computationally intensive operation, a forward-backward (FB) proximal iterative Wiener filtering was proposed in Bobin et al. (2012) for the denoising of cosmic microwave background spherical maps, exploiting the property that the signal and noise covariance matrices are diagonal in pixel and Fourier space, respectively. Equation (17) comprises two separable terms,
Following the FB method (Starck et al. 2015), we can solve Eq. (18) by designing an iterative fixed point algorithm as
which is known to converge when  , Combettes & Wajs (2005).
, Combettes & Wajs (2005).
Computing the proximal operator in Eq. (19), we have the following iterative Wiener-filtering algorithm:
where t is an auxiliary variable, μ = min(Σn), Pη = 2μI and κ0 = 0. This algorithm is free from matrix inversions because both Σn used in Eq. (20) and Pκ used in Eq. (21) are diagonal matrices. A similar algorithm, exploiting transformations between pixel and harmonic space, was proposed by Elsner & Wandelt (2013) using the messenger field framework. These methods can also be adapted to efficiently sample from the posterior distribution of the unknown mass map (Alsing et al. 2017; Jeffrey et al. 2018b). The Wiener approach recovers the Gaussian component of the convergence field well, but it is far from optimal at extracting the non-Gaussian information from the data because peak-like structures are suppressed. This has motivated the development of sparse recovery methods based on wavelets.
Sparse recovery. It has been shown that sparse recovery using wavelets is a very efficient way to reconstruct convergence maps (Starck et al. 2006b; Leonard et al. 2012; Lanusse et al. 2016; Peel et al. 2017b; Price et al. 2020). The mass-mapping problem is addressed as a general ill-posed problem, which is solved through weighted ℓ1-norm regularisation in a wavelet-based analysis sparsity model. Sparsity in the discrete cosine transform (DCT) domain was also proposed to fill the missing data area in the convergence map (Pires et al. 2009).
The GLIMPSE algorithm avoids any binning or smoothing of the input data that could potentially cause loss of information. The primary cost function is
where 𝔗 is the nonuniform discrete Fourier transform (NDFT) matrix, P is defined in Eq. (11), λ is a sparsity regularisation parameter, ω is a weighting vector, Φ* is the adjoint operator of the wavelet transform, and 𝔦ℝ is an identity function that drives the imaginary part of the convergence to zero. This cost function is also generalised in GLIMPSE2D in order to replace the shear by the reduced shear, or to incorporate the flexion information. It has been shown that GLIMPSE2D significantly outperforms Wiener filtering for peaks recovery, while Wiener filtering does better on the Gaussian map content (Jeffrey et al. 2018a).
Deep learning. Deep-learning techniques have recently been proposed and appear to be very promising (Jeffrey et al. 2020). The input of the neural network is not the shear field directly, but rather the Wiener-filter solution. We could imagine that the closer we are to the true solution with standard techniques such as Wiener filter or sparsity, the better deep learning can improve the solution. Open questions related to deep learning remain to be answered, such as its generalisation to cosmologies not present in the training data set, or the potential bias introduced by using a theoretical power spectrum in the Wiener-filter solution serving as input of the neural network.
3. Modelling with sparsity and a Gaussian random field
3.1. New convergence map model
We showed two different models in Sect. 2: the first modelling the convergence map as a Gaussian random field, which recovers the large scales of the convergence map well but suppresses peak structures, and the second assuming the convergence map is compressible in the wavelet domain (i.e. sparse modelling). The sparse recovery is clearly complementary to the Wiener-filter solution because it recovers peaks extremely well, but recovers the Gaussian content poorly.
To address these limitations, it appears to be natural to introduce a novel modelling approach, where the convergence field κ is assumed to comprise two parts, a Gaussian and a non-Gaussian:
The non-Gaussian part of the signal κNG is subject to a sparse decomposition in a wavelet dictionary, while the component κG is assumed to be inherently non-sparse and Gaussian.
The morphological component analysis (MCA) has been proposed (Starck et al. 2004; Elad et al. 2005) to separate two components mixed in a single image when these components have different morphological properties. This appears to be impossible because we have two unknowns and one equation, but it was shown that it is sometimes possible to extract these two components if we can exploit their morphological differences. This requires different penalisation functions CG and CNG on each of these two components, and we need to minimise
The MCA performs an alternating minimisation scheme:
Examples of these decompositions are shown on the MCA web page1. A range of MCA applications in astrophysics can be found in Starck et al. (2003), André et al. (2010), Möller et al. (2015), Bobin et al. (2016), Melchior et al. (2018), Joseph et al. (2019) and Wagner-Carena et al. (2020).
Gaussian component κG. We used the standard Wiener-filter modelling where κG is assumed to be a Gaussian random field,
and the solution of Eq. (25) is obtained using the iterative Wiener filtering presented in the previous section.
Non-Gaussian component. There are different ways to use a sparse model in the MCA framework. The most obvious would be to use standard ℓ1 or ℓ0-norm regularisation in a wavelet-based sparsity model, as is done in the GLIMPSE2D algorithm. This would give
where p = 0 or 1, Φ is the wavelet matrix, and λ is the regularisation parameter (Lagrange multiplier).
After implementing this approach, we found that large wavelet scales and Fourier low frequencies are relatively close, leading to difficulties in separating the information. We therefore investigated another approach that first involves estimating the set Ω of active coefficients, that is, the scales and positions where wavelet coefficients are above a given threshold. These are typically between three and five times the noise standard deviation relative to each wavelet coefficient. Ω can therefore be seen as a mask in the wavelet domain, where Ωj, x = 1 if a wavelet coefficient detected at scale j and position x, that is, when ∣(Φ*A*γ)j, x ∣ > λσj, x, and 0 otherwise. The noise σj, x at scale j and position x can be determined using noise realisations as in the GLIMPSE algorithm. An even faster approach is to detect the significant wavelet coefficients on  instead of Φ*A*γ. The noise is therefore whitened because the noise factor
instead of Φ*A*γ. The noise is therefore whitened because the noise factor  is Gaussian with a standard deviation equal to unity and with a uniform power spectrum. We implemented both approaches and found similar results, although the second approach is easier.
is Gaussian with a standard deviation equal to unity and with a uniform power spectrum. We implemented both approaches and found similar results, although the second approach is easier.
When this wavelet mask Ω is estimated, we can estimate the non-Gaussian component κNG by
with  .
.
This changes the original formalism because the data fidelity term is now different, but it presents a very interesting advantage. When Ω is fixed, the algorithm is almost linear and only the positivity constraint remains. Therefore we can easily derive a good approximation of the error map just by propagating noise and relaxing this positivity constraint. This is further discussed below. Similarly to the GLIMPSE method, a positivity constraint is applied on the non-Gaussian component κNG. Peaks in κ can be on top of voids, and therefore have negative pixel values. As peaks are captured by the non-Gaussian component, they are positive by construction in κNG, but the convergence map κ = κG + κNG can still be negative at peak positions. The larger the non-Gaussianities, the more we can expect MCALens to improve on linear methods such as the Wiener filtering.
The prior signal auto-correlation of the Gaussian component is included within the signal covariance term of the Gaussian component. We encode no explicit prior auto-correlation for the non-Gaussian signal and no explicit prior cross-correlation between the Gaussian and non-Gaussian component. Clearly, these correlations exist, but including their contribution in the prior in this framework would be extremely difficult theoretically and in practice. However, these correlations will still appear in the final reconstruction, driven by the correlation information in the data.
3.2. MCALens algorithm
1: Input: Shear map γ1, γ2, signal and noise covariance Σk, Σn, and detection level γ.
2: Initialise: κNG(0) = κG(0) = Ω = 0, μ = min (Σn) , Pη = 2μI.
3: Calculate wavelet coefficients: 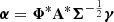 .
.
4: ∀j,x, set Ωj,x = 1 if |(α)j,x| > λ.
5: for n = 0,…,Nmax−1 do
6: ----------------- Find κNG --------------------
7: Calculate the shear residual: 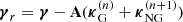 .
.
8: Calculate the sparse residual: 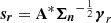 .
.
9: Calculate the sparse residual in the mask: 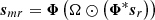 .
.
10: Get the new sparse component: 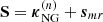 .
.
11: Positivity constraint: ![$ {\boldsymbol{\kappa}_{\rm NG}^{(n+1)}} = [ \mathbf{S} ]_{+} $](/articles/aa/full_html/2021/05/aa39451-20/aa39451-20-eq44.gif) .
.
12: ---------------- Find κG -----------------------
13: Calculate the shear residual: 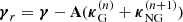 .
.
14: Forward step: 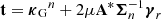 .
.
15: Backward step: κGn+1 =F∗(Pκ(Pη + Pκ)−1)Ft.
16: end for
17: return 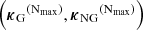 .
.
We solved the recovery problem of Eq. (23) using a two-step optimisation procedure. First, a gradient descent step to minimise Eq. (29) to recover the non-Gaussian component κNG. This was followed by an iteration of the iterative Wiener filtering to minimise Eq. (17). Details of the method are given in Algorithm 1.
The number of scales Ns used to compute the wavelet transform of an Nx × Ny image are automatically derived by Ns = int(log(min(Nx, Ny))). The λ parameter is a detection level, which was fixed for all our experiments with real and simulated data to 5, that is, five times the noise standard deviation. This is a conservative threshold and gave excellent results.
3.3. Errors
Much attention has recently been given to estimate errors or uncertainties with mass-map products. For linear methods such as Wiener filtering or Kaiser-Squires, it is easy to estimate the standard deviation (or root-mean-square, RMS) per pixel, just by propagating noise realisations using the same reconstruction filters. The uncertainty per pixel does not, however, give the probability that a clump in a reconstructed image is true or only due to some noise fluctuations. Another approach, closer to certain science cases with maps, estimates the significance of clumps. Peel et al. (2017b) used Monte Carlo simulations to address the significance of clumps. Repetti et al. (2019) proposed a hypothesis test called BUQO to perform the same task, requiring the user to define manually a mask around the clump. Similarly, Price et al. (2019) performed hypothesis tests of Abell-520 cluster structures using highest posterior density regions. With MCALens, we can include aspects of both approaches.
RMS and signal-to-noise ratio maps. Algorithm 1 includes two steps that involve a non-linear operator, first to estimate Ω in line 4 and then in line 11 to perform the positivity constraint. To propagate noise realisations, Ω has to be set to the one obtained with the data, and this non-linearity step therefore does not occur, so that only the positivity remains. A full linear algorithm could therefore be obtained just by removing this positivity constraint during the noise propagation by replacing ![$ {\boldsymbol{\kappa}_{\rm NG}^{(n+1)}} = [ \mathbf{S} ]_{+} $](/articles/aa/full_html/2021/05/aa39451-20/aa39451-20-eq48.gif) in Algorithm 1, line 11 by
in Algorithm 1, line 11 by  . This causes more noise to enter the solution because few pixel values with negative values in κNG are not thresholded, and the derived RMS map is therefore slightly conservative. We can therefore build noise realisations, run the MCALens algorithm on each realisation, and derive the RMS map by taking pixel per pixel the standard deviation of the obtained reconstructed maps. The signal-to-noise ratio (S/N) map is derived by dividing the absolute value of the reconstructed map by the RMS map.
. This causes more noise to enter the solution because few pixel values with negative values in κNG are not thresholded, and the derived RMS map is therefore slightly conservative. We can therefore build noise realisations, run the MCALens algorithm on each realisation, and derive the RMS map by taking pixel per pixel the standard deviation of the obtained reconstructed maps. The signal-to-noise ratio (S/N) map is derived by dividing the absolute value of the reconstructed map by the RMS map.
Significance map. Algorithm 1 obtains in line 4 the wavelet mask Ω by comparing the wavelet coefficients,  , to the threshold λσ where σ = 1 as the noise is whitened with unit variance. This corresponds to performing a hypothesis test H0 that the wavelet coefficient is due to noise alone, and if a given wavelet coefficient αj, x is such that ∣αj, x ∣ > λ, then the H0 hypothesis is rejected and we assume that the coefficient amplitude cannot be explained by noise fluctuations and is therefore due to signal. λ is therefore directly related to the significance of the wavelet coefficients, and the mask Ω indicates which coefficients are detected with a given significance level. Ωj, x is binary, and we build the significance map s by sx = ∑jΩj, x, that is, a simple co-adding of all binary scales. Such a map could also be used as a way to automatically derive the user mask required in the BUQO method (Repetti et al. 2019). We present in Sect. 4 examples of RMS, S/N, and significance maps.
, to the threshold λσ where σ = 1 as the noise is whitened with unit variance. This corresponds to performing a hypothesis test H0 that the wavelet coefficient is due to noise alone, and if a given wavelet coefficient αj, x is such that ∣αj, x ∣ > λ, then the H0 hypothesis is rejected and we assume that the coefficient amplitude cannot be explained by noise fluctuations and is therefore due to signal. λ is therefore directly related to the significance of the wavelet coefficients, and the mask Ω indicates which coefficients are detected with a given significance level. Ωj, x is binary, and we build the significance map s by sx = ∑jΩj, x, that is, a simple co-adding of all binary scales. Such a map could also be used as a way to automatically derive the user mask required in the BUQO method (Repetti et al. 2019). We present in Sect. 4 examples of RMS, S/N, and significance maps.
3.4. Extension to the sphere
When a wide-field map needs to be reconstructed, the flat approximation can no longer be used, and we have to build a map on the sphere. A traditional approach is to decompose the sphere into overlapping patches, assume a flat approximation on each individual patch, reconstruct each patch independently, and finally, recombine all patches on the sphere. This solution is certainly good enough to recover clumps relative to clusters, that is, the non-Gaussian component, but certainly not good enough for the Gaussian component, which contains information at low frequencies. In the framework of the DES project, a 1500 deg2 map has been reconstructed (Chang et al. 2018) using HEALPIX pixelisation (Górski et al. 2005) and a straightforward spherical Kaiser-Squires algorithm consisting of
1. calculating a spin transform of the HEALPIX shear map to obtein the E and B spherical harmonic coefficients,
2. smoothing by a Gaussian the E and B modes in the spherical harmonic domain,
3. applying an inverse spherical transform independently to each of these two modes to obtain the two convergence maps κE and κB.
Sparsity in a Bayesian framework (Price et al. 2021) and forward-fitting in harmonic space (Mawdsley et al. 2020) have also recently been proposed for spherical mass mapping. Using similarly a HEALPIX shear and convergence pixelisation, we can also easily derive an extension of the iterative-Wiener filtering and the MCALens algorithm by
– replacing the matrix A = FPF* in Eq. (10) by A = 2Y0Y∗, where sY and sY∗ represent the forward and inverse spin-s spherical harmonic transforms, respectively,
– replacing the wavelet decomposition Φ used in Eq. (28) by the spherical wavelet decomposition (Starck et al. 2006a).
Then the same MCAlens algorithm as in Algorithm 1 can be used to derive a spherical convergence map. An example is given in Sect. 4.3.
3.5. B-mode
We focused earlier on the convergence map (i.e. E-mode). The MCAlens algorithm given in Algorithm 1 remains valid when E and B mode are to be estimated by adopting the following notation:
where the matrix Φ consists of applying a sparse decomposition independently on each mode. In practice, we used the same wavelet decomposition for both modes (i.e. ΦE = ΦB). The delicate point is applying the Wiener filter to the B-mode at line 15 of the algorithm. In theory, PκB = 0, and by construction, no Gaussian component can be recovered. Because the B-mode is mainly useful for investigating systematic errors, we are not interested in recovering the B-mode least-squares estimator (which is zero), and we find it more useful to process the B-mode similarly to the E-mode. We therefore advocate use PκB = PκE instead. In this way, the fluctuations in the E-mode can be properly compared to those in the B-mode.
4. Experimental results
4.1. Toy-model experiment
We used a simulation derived from RAMSES N-body cosmological simulations (Teyssier 2002), with a ΛCDM model2, with a pixel size of 0.34′ × 0.34′ and a galaxy redshift of 1. To obtain a realistic mask and noise behaviour, we used the MICE pixel noise covariance derived for the DES project (see Appendix A). As the pixel resolution is different, it leads to an optimistic realisation, but it has the advantage of illustrating the effect of our MCA model well.
We ran MCAlens using 100 iterations, λ = 5 (i.e. detection at 5σ), the MICE covariance matrix, and the theoretical power spectrum was the true map power spectrum. To evaluate the results, we ran 100 different noise realisations, and we applied both Wiener filtering and MCAlens. We calculated the reconstruction error at different resolutions with
where  , κ is the reconstructed convergence map, κt is the true convergence map, Gσ(x) is the convolution of x with a Gaussian with standard deviation σ, and M is the binary mask with Mk = 1 if the covariance matrix is not infinite at location k (i.e. we have data at this location) and 0 otherwise. Figure 1 shows the mean error Err%(σ) for the Wiener filter and MCAlens solutions. The black curve shows the difference between the Wiener-filter error and the MCAlens error. This allows us to better visualise that the improvement is larger at fine scales. It is interesting to note that MCAlens is better than Wiener filter even at large scales. When the MCAlens non-Gaussian component contains a significant number of features as in the case of this experiment, these features also contribute in a a non negligible way on larger scales, which explains why MCAlens remains better than Wiener filtering at large scales. MCAlens leads to a clear improvement in terms of quadratic error. The top panels of Fig. 2 show the simulated convergence map and the MCAlens reconstructed map. The bottom panels show the Gaussian and the non-Gaussian part recovered from the noisy data. The sum of these two components is equal to the MCAlens reconstruction (top right). This shows that the non-linear and linear components can be recovered well. Figure 3 shows the RMS map, the S/N map, and the significance map.
, κ is the reconstructed convergence map, κt is the true convergence map, Gσ(x) is the convolution of x with a Gaussian with standard deviation σ, and M is the binary mask with Mk = 1 if the covariance matrix is not infinite at location k (i.e. we have data at this location) and 0 otherwise. Figure 1 shows the mean error Err%(σ) for the Wiener filter and MCAlens solutions. The black curve shows the difference between the Wiener-filter error and the MCAlens error. This allows us to better visualise that the improvement is larger at fine scales. It is interesting to note that MCAlens is better than Wiener filter even at large scales. When the MCAlens non-Gaussian component contains a significant number of features as in the case of this experiment, these features also contribute in a a non negligible way on larger scales, which explains why MCAlens remains better than Wiener filtering at large scales. MCAlens leads to a clear improvement in terms of quadratic error. The top panels of Fig. 2 show the simulated convergence map and the MCAlens reconstructed map. The bottom panels show the Gaussian and the non-Gaussian part recovered from the noisy data. The sum of these two components is equal to the MCAlens reconstruction (top right). This shows that the non-linear and linear components can be recovered well. Figure 3 shows the RMS map, the S/N map, and the significance map.
 |
Fig. 1. RAMSES simulations: Error vs. scale for Wiener filter (red) and MCAlens (blue). |
 |
Fig. 2. RAMSES simulations. Top panel: true convergence map and MCAlens recovery. Bottom panel: Gaussian components and sparse components. The sum of these two maps is equal to the top right MCAlens map. |
 |
Fig. 3. RAMSES simulations. From left to right: RMS map, S/N map, and significance map. |
4.2. Columbia lensing simulation
We used a convergence map, released by the Columbia lensing group3 (Liu et al. 2018), corresponding to a cosmological model with parameters {Mν,Ωm,109As,Mν,h,w} = {0.1,0.3,2.1,0,0.7,−1}, and with a pixel size of 0.4′ × 0.4′. We rebinned the map to 0.8′ × 0.8′, and similarly to the previous experiment, we simulated noisy data using the same MICE covariance, applying a global rescaling in order to have realistic noise corresponding to a mean number of galaxies equal to 30 per arcmin2, as we expect in future space lensing surveys. To evaluate the results, we ran 100 different noise realisations, and we applied Kaiser-Squires, sparse recovery, Wiener filtering, and MCAlens. For the sparse recovery and MCAlens, we used λ = 5 (i.e. detection at 5σ), and for Wiener filtering and MCAlens, we the used the theoretical power spectrum as the true convergence map power spectrum.
Figure 4 shows the error computed using Eq. (30). In addition to the well-recovered peaks, MCAlens also leads to a clear improvement in terms of quadratic error compared the other methods. In contrast to the RAMSES experiment, we see here a convergence at large scales between MCAlens and Wiener filter because the MCAlens non-Gaussian component contains only a few peaks (see Fig. 5, middle right), which therefore contribute only negligibly to the largest scales.
 |
Fig. 4. Columbia simulations. Error vs. scale for four different methods: Kaiser-Squires (light blue), Wiener (red), sparsity (orange), and MCAlens (blue). |
 |
Fig. 5. Columbia convergence map recovery. Top panel: a true convergence map, a Wiener-filter map, and a Kaiser-Squires map smoothed with a Gaussian with an FWHM of 3.8 arcmin. Middle panel: MCAlens map and its Gaussian and sparse components. The sum of these two last maps is equal to the first map. Bottom panel: RMS, S/N, and significance maps. |
The top row of Fig. 5 shows the simulated convergence map, the Wiener-filter result, and the Kaiser-Squires reconstruction with smoothing applied. The middle row shows the MCAlens map and its Gaussian and non-Gaussian parts recovered from the noisy the data. The sum of these two components is equal to the MCAlens map. Similarly to previous experiments, the non-linear and the linear components are well recovered. The bottom row of Fig. 5 shows the RMS map, the S/N map, and the significance map.
4.3. Spherical data
We created a full shear map from the full-sky MICE simulated map and its covariance matrix, which has about three galaxies per arcmin2. We ran the spherical MCAlens method with 200 iterations, λ = 5 (i.e. detection at 5σ), and we used the power spectrum of the simulation as the theoretical power spectrum. The top row of Fig. 6 shows the simulated noise-free map at 1 and 3 degrees, and the bottom row shows the MCAlens non-Gaussian and Gaussian components.
 |
Fig. 6. MICE simulations. Top panel: true convergence map at 1 and 3 degrees. Bottom: MCAlens sparse and Gaussian components. |
4.4. COSMOS field
In this last section, we apply MCAlens to reconstruct a convergence map of the 1.64 deg2 HST/ACS COSMOS survey (Scoville et al. 2007). We used the bright galaxies shape catalogue produced in Schrabback et al. (2010).
The results after MCAlens was applied on COSMOS data are presented in Fig. 7. The top row shows the galaxy count map, the Wiener-filter map, and the Kaiser-Squires map smoothed with a Gaussian at a full width at half maximum of 2.4 arcmin. The bottom row shows the Glimpse, MCAlens E-mode, and MCAlens B-mode maps. White dots show the locations and redshifts of X-ray selected massive galaxy clusters from the XMM-Newton Wide Field Survey (Finoguenov et al. 2007) with 0.3 < z < 1.0.
 |
Fig. 7. COSMOS data. Top panel: galaxy count map, Wiener-filter map, and Kaiser-Squires map smoothed with a Gaussian with an FWHM of 2.4 arcmin. Bottom panel: Glimpse, MCAlens, and MCAlens B-mode maps. |
5. Conclusion
A novel mass-mapping algorithm has been presented that is able to recover high-resolution convergence maps from weak gravitational lensing measurements. Our proposed process involves a model with two components, a Gaussian and a non-Gaussian, for which we developed an efficient algorithm to derive the solution. We showed that we can also handle a non-diagonal covariance matrix. We extended the method so that it can deal with spherical maps, which is needed for future surveys such as the Euclid space mission. Our experiments clearly show a significant improvement compared to currently used algorithms.
In the spirit of reproducible research, the MCAlens algorithm is publicly available in the CosmoStat’s Github package4, including the material needed to reproduce the simulated experience (folder examples/mcalens_paper and script make_fig.py).
Acknowledgments
We thank Tim Schrabbaack for sending us his COSMOS shear catalog and the Columbia Lensing group (http://columbialensing.org) for making their suite of simulated maps available, and NSF for supporting the creation of those maps through grant AST-1210877 and XSEDE allocation AST-140041.
References
- Abell, P. A., Burke, D. L., Hamuy, M., et al. 2009, Lsst science book, version 2.0, Tech. rep. [Google Scholar]
- Ajani, V., Peel, A., Pettorino, V., et al. 2020, Phys. Rev. D, 102, 103531 [CrossRef] [Google Scholar]
- Alsing, J., Heavens, A., Jaffe, A. H., et al. 2016a, MNRAS, 455, 4452 [NASA ADS] [CrossRef] [Google Scholar]
- Alsing, J., Heavens, A., & Jaffe, A. H. 2016b, MNRAS, 466, 3272 [Google Scholar]
- Alsing, J., Heavens, A., & Jaffe, A. H. 2017, MNRAS, 466, 3272 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bobin, J., Starck, J. L., Sureau, F., & Fadili, J. 2012, Adv. Astron., 2012 [Google Scholar]
- Bobin, J., Sureau, F., & Starck, J. L. 2016, A&A, 591, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretero, J., Castander, F. J., Gaztañaga, E., Crocce, M., & Fosalba, P. 2015, MNRAS, 447, 646 [Google Scholar]
- Chang, C., Pujol, A., Mawdsley, B., et al. 2018, MNRAS, 475, 3165 [CrossRef] [Google Scholar]
- Combettes, P. L., & Wajs, V. R. 2005, Multiscale Modeling & Simulation, 4, 1168 [Google Scholar]
- Crocce, M., Castander, F. J., Gaztanaga, E., Fosalba, P., & Carretero, J. 2015, MNRAS, 453, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Elad, M., Starck, J.-L., Donoho, D., & Querre, P. 2005, Appl. Comput. Harmonic Anal., 19, 340 [CrossRef] [MathSciNet] [Google Scholar]
- Elsner, F., & Wandelt, B. D. 2013, A&A, 549, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finoguenov, A., Guzzo, L., Hasinger, G., et al. 2007, ApJS, 172, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Fluri, J., Kacprzak, T., Sgier, R., Refregier, A., & Amara, A. 2018, J. Cosmol. Astropart Phys., 2018, 051 [Google Scholar]
- Fosalba, P., Crocce, M., Gaztanaga, E., & Castander, F. J. 2015a, MNRAS, 448, 2987 [NASA ADS] [CrossRef] [Google Scholar]
- Fosalba, P., Gaztanaga, E., Castander, F. J., & Crocce, M. 2015b, MNRAS, 447, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffmann, K., Bel, J., Gaztanaga, E., et al. 2015, MNRAS, 447, 1724 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, B., Seljak, U., & Aslanyan, G. 2019, J. Cosmol. Astropart. Phys., 2019, 035 [Google Scholar]
- Jain, B., & Van Waerbeke, L. 2000, ApJ, 530, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., & Lavaux, G. 2014, MNRAS, 447, 1204 [Google Scholar]
- Jeffrey, N., Abdalla, F. B., Lahav, O., et al. 2018a, MNRAS, 479, 2871 [Google Scholar]
- Jeffrey, N., Heavens, A. F., & Fortio, P. D. 2018b, Astron. Comput., 25, 230 [Google Scholar]
- Jeffrey, N., Lanusse, F., Lahav, O., & Starck, J.-L. 2020, MNRAS, 492, 5023 [CrossRef] [Google Scholar]
- Joseph, R., Courbin, F., Starck, J. L., & Birrer, S. 2019, A&A, 623, A14 [EDP Sciences] [Google Scholar]
- Kaiser, N., & Squires, G. 1993, ApJ, 404, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Kilbinger, M. 2015, Rep. Prog. Phys., 78, 086901 [Google Scholar]
- Kilbinger, M., Fu, L., Heymans, C., et al. 2013, MNRAS, 430, 2200 [NASA ADS] [CrossRef] [Google Scholar]
- Kratochvil, J. M., Lim, E. A., Wang, S., et al. 2012, Phys. Rev. D, 85 [CrossRef] [Google Scholar]
- Lanusse, F., Starck, J.-L., Leonard, A., & Pires, S. 2016, A&A, 591, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Leonard, A., Dupé, F.-X., & Starck, J.-L. 2012, A&A, 539, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, Z., Liu, J., Matilla, J. M. Z., & Coulton, W. R. 2019, Phys. Rev. D, 99, 063527 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C.-A., & Kilbinger, M. 2015, A&A, 576, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, J., Bird, S., Matilla, J. M. Z., et al. 2018, J. Cosmol. Astropart. Phys., 2018, 049 [Google Scholar]
- Liu, J., & Haiman, Z. 2016, Phys. Rev. D, 94, 043533 [NASA ADS] [CrossRef] [Google Scholar]
- Marian, L., Hilbert, S., Smith, R. E., Schneider, P., & Desjacques, V. 2011, ApJ, 728, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Mawdsley, B., Bacon, D., Chang, C., et al. 2020, MNRAS, 493, 5662 [Google Scholar]
- Melchior, P., Moolekamp, F., Jerdee, M., et al. 2018, Astron. Comput., 24, 129 [CrossRef] [Google Scholar]
- Möller, A., Ruhlmann-Kleider, V., Lanusse, F., et al. 2015, J. Cosmol. Astropart. Phys., 2015, 041 [Google Scholar]
- Munshi, D., & Coles, P. 2017, J. Cosmol. Astropart. Phys., 2017, 010 [Google Scholar]
- Peel, A., Lin, C.-A., Lanusse, F., et al. 2017a, A&A, 599, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peel, A., Lanusse, F., & Starck, J.-L. 2017b, ApJ, 847, 23 [Google Scholar]
- Petri, A., Haiman, Z., Hui, L., May, M., & Kratochvil, J. M. 2013, Phys. Rev. D, 88, 123002 [NASA ADS] [CrossRef] [Google Scholar]
- Pires, S., Starck, J. L., Amara, A., et al. 2009, MNRAS, 395, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Price, M. A., McEwen, J. D., Cai, X., et al. 2019, MNRAS, 489, 3236 [Google Scholar]
- Price, M. A., Cai, X., McEwen, J. D., et al. 2020, MNRAS, 492, 394 [CrossRef] [Google Scholar]
- Price, M. A., McEwen, J. D., Pratley, L., & Kitching, T. D. 2021, MNRAS, 500, 5436 [Google Scholar]
- Repetti, A., Pereyra, M., & Wiaux, Y. 2019, SIAM J. Imaging Sci., 12, 87 [Google Scholar]
- Schrabback, T., Hartlap, J., Joachimi, B., et al. 2010, A&A, 516, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Abraham, R. G., Aussel, H., et al. 2007, ApJS, 172, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Shirasaki, M., Yoshida, N., Hamana, T., & Nishimichi, T. 2012, ApJ, 760, 45 [Google Scholar]
- Spergel, D., Gehrels, N., Baltay, C., et al. 2015, ArXiv e-prints [arXiv:1503.03757] [Google Scholar]
- Starck, J.-L., Candès, E., & Donoho, D. 2003, A&A, 398, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J.-L., Elad, M., & Donoho, D. 2004, Adv. Imaging Electron Phys., 132 [Google Scholar]
- Starck, J.-L., Moudden, Y., Abrial, P., & Nguyen, M. 2006a, A&A, 446, 1191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J.-L., Pires, S., & Réfrégier, A. 2006b, A&A, 451, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J.-L., Murtagh, F., & Fadili, J. 2015, Sparse Image and Signal Processing: Wavelets and Related Geometric Multiscale Analysis (Cambridge University Press) [Google Scholar]
- Tallada, P., Carretero, J., Casals, J., et al. 2020, Astron. Comput., 32, 100391 [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Upham, R. E., Whittaker, L., & Brown, M. L. 2020, MNRAS, 491, 3165 [Google Scholar]
- Wagner-Carena, S., Hopkins, M., Diaz Rivero, A., & Dvorkin, C. 2020, MNRAS, 494, 1507 [Google Scholar]
- Wandelt, B. D., Larson, D. L., & Lakshminarayanan, A. 2004, Phys. Rev. D, 70, 083511 [NASA ADS] [CrossRef] [Google Scholar]
- Wiener, N. 1949, Extrapolation, Interpolation, and Smoothing of Stationary Time Series: with Engineering Applications (Cambridge: MIT press), 7 [CrossRef] [Google Scholar]
- Zaroubi, S., Hoffman, Y., Fisher, K. B., & Lahav, O. 1995, ApJ, 449, 446 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: MICE simulations
We used the public MICE (v2) simulated galaxy catalogue, which is constructed from a light cone N-body dark matter simulation (Fosalba et al. 2015a,b; Crocce et al. 2015; Carretero et al. 2015; Hoffmann et al. 2015; Tallada et al. 2020). The MICE catalogue provides the calculated weak-lensing (noise-free) observables shear and convergence. In a given patch of simulated sky, we selected galaxies in the redshift5z range [0.6, 1.4]. Each galaxy corresponds to a noisy shear measurement, and we subsampled with a density of ∼8000 galaxies per deg2.
Uncorrelated, complex shape noise values were randomly drawn from a Gaussian distribution and added to the shear value of each selected galaxy. This noise per galaxy is zero mean and has a variance  (as estimated from data (Jeffrey et al. 2018a)). The final pixelised noise (n) has a variance that depends on the number of galaxies per pixel.
(as estimated from data (Jeffrey et al. 2018a)). The final pixelised noise (n) has a variance that depends on the number of galaxies per pixel.
In our simulated data, we mimicked these conditions by choosing to remove all galaxies in given regions. Here no shear measurements are available, and the noise variance is effectively infinite. The top row of Fig. A.1 shows a simulated convergence map with the DES SV footprint and mask, and the bottom row shows two simulated observed shear component maps, γ1 and γ2.
 |
Fig. A.1. Top: true MICE convergence map with DES SV footprint and mask. Bottom: two simulated observed shear components, γ1 and γ2. |
Appendix B: Wiener-filter tour
B.1. Wiener filter and inpainting
Missing data are a common problem for galaxy surveys because foreground objects that obscure the background galaxies have to be masked out. In addition to the non-stationary noise, observed shear fields therefore also present missing data. By noting the mask M as equal to 1 if we have shear measurements at a pixel position and zero otherwise, missing data can be handled in Wiener filtering by forcing the noise covariance matrix to be very high at locations where M = 0. This causes the solution to be different from zero and smoothed in the missing data area, and it remove border-effect artefacts. The Wiener filtering can therefore be seen as an inpainting technique because it fills the missing area in the image. Alternative inpainting techniques were proposed in the past through sparse recovery techniques (Pires et al. 2009; Lanusse et al. 2016) or Gaussian constraint realisations (Zaroubi et al. 1995; Jeffrey et al. 2018a). Because the Wiener model assumed the solution to be a Gaussian random field, it would make sense to have a solution where the inpainted area presents the same statistical properties as in non-inpainted area. This property is by construction verified with constraint realisations, and it was shown that this is also the case with sparse inpainting (Pires et al. 2009). A similar sparse inpainting can be very easily included in the proximal Wiener filtering, minimising the following equation:
where p = 0 or 1, Φ is the discrete cosine eictionary (DCT), and λ is a Lagrangian parameter. We obtain the forward-backward algorithm, called InpWiener:
-
Forward step:
-
Backward step:
where and ΔΦ, λ is the proximal operator defined in Pires et al. (2009), which consists of applying a DCT transform to u, thresholding the DCT coefficients, and reconstructing an image from the thresholded coefficients, and
Areas for which we possess information are processed as in the usual Wiener-filter case, while the inpainting regularisation affects area with missing data (i.e. when M = 0).
Concerning Eq. (B.1), it is interesting to note the following relations between InpWiener and other methods:
– KS: if β = 0, λ = 0 and Σn is diagonal with constant values along the diagonal (i.e. stationary Gaussian noise), InpWiener leads to the non-iterative standard Kaiser-Squires solution.
– GKS: If β = 0 and λ = 0, the least-squares estimator is derived with the iterative algorithm:  , with μ = min(Σn). As it generalises the Kaiser-Squires method, we call this algorithm GKS.
, with μ = min(Σn). As it generalises the Kaiser-Squires method, we call this algorithm GKS.
– FASTLens: If β = 0 and Σn is diagonal with constant values along the diagonal, InpWiener leads to the FASTLens inpainting algorithm (Pires et al. 2009).
– GIKS: If β = 0, InpWiener leads to an inpainted generalised the Kaiser-Squires solution where the InpWiener forward is unchanged, and the backward step becomes
Similarly to Sects. 3.5 and 3.5, these algorithms can handle data on the sphere and jointly reconstruct E and B modes.
Inpainted Wiener-filter experiment. To test InpWiener, we used the public MICE (v2) simulated galaxy catalogue presented in Appendix A.
Figure B.1 shows the Wiener-filter solution (left) and the inpainted Wiener-filter solution (right) derived from the shear components shown in Fig. A.1.
 |
Fig. B.1. Wiener and inpainted Wiener solutions. |
B.2. Agnostic Wiener filtering
The Wiener-filter method needs to know the theoretical power spectrum Pκ, and the solution therefore varies with the assumed cosmological model used to derive Pκ. To avoid this issue, a solution could be to estimate Pκ directly from the shear measurements, for instance using a mask correction as in Upham et al. (2020). Bayesian techniques have also been used to infer the map and power spectrum (Wandelt et al. 2004; Jasche & Lavaux 2014; Alsing et al. 2016b). An alternative approach is to used the GIKS inpainting algorithm to first fill the missing area and then compute the power spectrum of the inpainted map. When GIKS is applied to the data and a set of R noise realisations, the final estimator is
Because the data noise Pκ will still be noisy, a final denoising step or a function fitting can be done.
As an illustration, we fitted the function f(k, a, u, e, c) = exp(∣a * (uk)−e ∣) + c to the estimated noisy Pκ. Figure B.2 shows an example of an estimated power spectrum following this approach.
 |
Fig. B.2. Theoretical power spectrum of one convergence map. In black the true theoretical power spectrum; in red, the spectrum estimated using the GIKS algorithm, corrected from noise power spectrum, and in blue the fit. |
Experiment: Effect of an unknown theoretical power spectrum. In this experiment, we used the same public MICE simulations, and we extracted 18 shear different shear maps with different noise realisations. For each of them, we applied the forward-backward Wiener-filter algorithm using the true theoretical power spectrum, and we applied the inpainted agnostic Wiener-filter method on the same data, re-estimating for each of the 18 shear data sets the theoretical power spectrum. Figure B.3 shows the reconstruction errors at different resolutions for Kaiser-Squires, Wiener filter, and inpainted agnostic Wiener filter. The inpainting clearly has no effect on the reconstruction error, which is expected because only the area where the mask is equal to one is used in the error calculation, and also because the agnostic approach has very little effect on the final solution. We do not claim that we should use an agnostic approach when a Wiener filtering is applied, but it is interesting to have this option available, for example when Wiener filtering is used without any assumption about the cosmology, and to give us the possibility to verify whether cosmological priors affect the results.
 |
Fig. B.3. Reconstruction error at different resolution for Kaiser-Squires, Wiener filter, and inpainted agnostic Wiener filter. |
All Figures
 |
Fig. 1. RAMSES simulations: Error vs. scale for Wiener filter (red) and MCAlens (blue). |
| In the text | |
 |
Fig. 2. RAMSES simulations. Top panel: true convergence map and MCAlens recovery. Bottom panel: Gaussian components and sparse components. The sum of these two maps is equal to the top right MCAlens map. |
| In the text | |
 |
Fig. 3. RAMSES simulations. From left to right: RMS map, S/N map, and significance map. |
| In the text | |
 |
Fig. 4. Columbia simulations. Error vs. scale for four different methods: Kaiser-Squires (light blue), Wiener (red), sparsity (orange), and MCAlens (blue). |
| In the text | |
 |
Fig. 5. Columbia convergence map recovery. Top panel: a true convergence map, a Wiener-filter map, and a Kaiser-Squires map smoothed with a Gaussian with an FWHM of 3.8 arcmin. Middle panel: MCAlens map and its Gaussian and sparse components. The sum of these two last maps is equal to the first map. Bottom panel: RMS, S/N, and significance maps. |
| In the text | |
 |
Fig. 6. MICE simulations. Top panel: true convergence map at 1 and 3 degrees. Bottom: MCAlens sparse and Gaussian components. |
| In the text | |
 |
Fig. 7. COSMOS data. Top panel: galaxy count map, Wiener-filter map, and Kaiser-Squires map smoothed with a Gaussian with an FWHM of 2.4 arcmin. Bottom panel: Glimpse, MCAlens, and MCAlens B-mode maps. |
| In the text | |
 |
Fig. A.1. Top: true MICE convergence map with DES SV footprint and mask. Bottom: two simulated observed shear components, γ1 and γ2. |
| In the text | |
 |
Fig. B.1. Wiener and inpainted Wiener solutions. |
| In the text | |
 |
Fig. B.2. Theoretical power spectrum of one convergence map. In black the true theoretical power spectrum; in red, the spectrum estimated using the GIKS algorithm, corrected from noise power spectrum, and in blue the fit. |
| In the text | |
 |
Fig. B.3. Reconstruction error at different resolution for Kaiser-Squires, Wiener filter, and inpainted agnostic Wiener filter. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





![$$ \begin{aligned} {A} = \left[\begin{array}{cc}1 - \kappa - \gamma _1&-\gamma _2 \\ -\gamma _2&1 - \kappa + \gamma _1 \end{array} \right]. \end{aligned} $$](/articles/aa/full_html/2021/05/aa39451-20/aa39451-20-eq4.gif)


![$$ \begin{aligned} {A} = (1-\kappa ) \left[\begin{array}{cc} 1 - g_1&- g_2 \\ - g_2&1+ g_1 \end{array} \right], \end{aligned} $$](/articles/aa/full_html/2021/05/aa39451-20/aa39451-20-eq7.gif)







![$$ \begin{aligned} p(\boldsymbol{\gamma }| \boldsymbol{\kappa }, \boldsymbol{\Sigma _n}) = |2 \pi \boldsymbol{\Sigma _n}|^{-\frac{1}{2}} \mathrm{exp} \left[ -\frac{1}{2} (\boldsymbol{\gamma }- \mathbf A \boldsymbol{\kappa })^* {\boldsymbol{\Sigma _n}}^{-1} (\boldsymbol{\gamma } - \mathbf A \boldsymbol{\kappa })\right], \end{aligned} $$](/articles/aa/full_html/2021/05/aa39451-20/aa39451-20-eq17.gif)
![$$ \begin{aligned} p(\boldsymbol{\kappa }| \boldsymbol{\Sigma _\kappa }) = |2 \pi \boldsymbol{\Sigma _\kappa }|^{-\frac{1}{2}} \mathrm{exp} \left[ -\frac{1}{2} {\boldsymbol{\kappa }}^* \boldsymbol{\Sigma _\kappa }\boldsymbol{\kappa }\right]. \end{aligned} $$](/articles/aa/full_html/2021/05/aa39451-20/aa39451-20-eq18.gif)
![$$ \begin{aligned} \boldsymbol{\kappa }_{\rm G}&= \mathrm{arg\,max}_{\boldsymbol{\kappa }} \left\{ p(\boldsymbol{\kappa }| \boldsymbol{\gamma }) \right\} \propto \mathrm{arg\,max}_{\boldsymbol{\kappa }} \left\{ p(\boldsymbol{ \gamma } | \boldsymbol{\kappa }, \boldsymbol{\Sigma _n}) p(\boldsymbol{\kappa }| \boldsymbol{\Sigma _\kappa }) \right\} \nonumber \\&\propto \mathrm{arg\,max}_{\boldsymbol{\kappa }} \mathrm{exp} \left[ -\frac{1}{2} {\boldsymbol{\kappa }}^* \boldsymbol{\Sigma _\kappa }\boldsymbol{\kappa }-\frac{1}{2} (\boldsymbol{\gamma }- \mathbf A \boldsymbol{\kappa })^*{ \boldsymbol{\Sigma _n}}^{-1} (\boldsymbol{\gamma }- \mathbf A \boldsymbol{\kappa }) \right] , \end{aligned} $$](/articles/aa/full_html/2021/05/aa39451-20/aa39451-20-eq19.gif)




















