EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 649 (May 2021) A&A, 649 (2021) A86 Full HTML
Free Access
Issue
A&A
Volume 649, May 2021
Article Number A86
Number of page(s) 12
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202039255
Published online 18 May 2021

© ESO 2021

1. Introduction

Globular clusters (GCs) represent the most ancient stellar systems in the Milky Way (MW). For this reason, they are excellent tracers of the formation and chemodynamical evolution of the Galaxy, going from the outer halo to the innermost Galactic regions. In addition, they have survived different dynamical processes, such as dynamical friction, disc and bulge shocking, and evaporation, which nevertheless led some ancient GCs to destruction (Weinberg 1994). Today, we distinguish different kinds of GCs depending on their metallicities, ages, and orbits. The metal-poor GCs could be the oldest population (Barbuy et al. 2006, 2009). More precisely, in the Galactic bulge, they may constitute the first stellar generation whose origin could coincide with the formation of the bulge itself or before the actual configuration of the bulge/bar component; examples are NGC 6522, NGC 6626, and HP 1 (Kerber et al. 2018, 2019). On the other hand, the metal-rich GCs may be the second generation in the MW (Muratov & Gnedin 2010). Furthermore, recent studies have demonstrated that some other luminous GCs may actually be fossil relics of accreted dwarf galaxies, such as Terzan 5 (Ferraro et al. 2009), Liller 1 (Ferraro et al. 2021), Terzan 9 (Ernandes et al. 2019), and Omega Centauri (Lee et al. 1999; Sollima et al. 2008). Further, with the advent of the Gaia mission and deep surveys, it is now possible to associate individual GCs with specific merger events (e.g., Vasiliev 2019; Myeong et al. 2019; Massari et al. 2019).

However, it seems that the frequency of GCs in the MW is lower than it is in Andromeda (van den Bergh 2010) and is also lower than that of open clusters. Indeed, the total number of Galactic GCs (Harris et al. 2013) is about half that of Andromeda (Barmby & Huchra 2001; Huxor et al. 2014), and the number of Galactic open clusters is vastly higher than that of GCs (Bonatto & Bica 2010). There are a number of issues that make their detection a challenging task; certainly we are still missing a number of them because of high stellar extinction and stellar crowding and the very low luminosities of some of them. Nevertheless, in recent decades, the number of star cluster candidates reported in the literature has increased significantly. Indeed, recent near-infrared (IR) surveys, such as the Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006) and the VISTA Variables in the Via Láctea Survey (VVV; Minniti et al. 2010), and mid-IR surveys, such as Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010), have allowed us to search for new GC candidates. In combination with near/mid-IR surveys, optical surveys are fundamental to finding new GCs, such as Gaia Mission DR 2 (Gaia Collaboration 2018), which provides optical photometry and proper motions (PMs). Thus, new GC candidates are being discovered, in particular in the Galactic bulge, using both the optical and near-IR images in order to help complete the census of GCs in the MW. Examples of recently discovered GCs toward to the innermost Galactic regions are VVV-CL001 (Minniti et al. 2011), VVV-CL002 and VVV-CL003 (Moni Bidin et al. 2011), Camargo 1102, 1103, 1104, 1105, and 11061 (Camargo 2018), Camargo 1107, 1108, and 1109 (Camargo & Minniti 2019), and several tens of candidates in Minniti et al. (2017a,b,c) and Palma et al. (2019). Even so, the nature of some new GC candidates has yet to be confirmed and their main parameters have still to be estimated.

In this paper, we focus on two recently discovered and not yet well characterised GC candidates, Patchick 99 and TBJ 3 (or ‘TJ 3’). We are studying GC candidates in order to investigate the GC luminosity function in the Galactic bulge, especially at very faint luminosities. For that purpose, Patchick 99 and TBJ 3 were selected from Bica et al. (2018), who compiled a list of 10 000 good star cluster candidates in the MW, as they had not been studied before. We use a combination of optical and near-IR catalogues, in order to gather a more complete picture for these objects. Our main goals are to confirm their true nature as GCs and to estimate their main parameters for the first time, such as reddening, distance modulus, heliocentric distance, size, total luminosity, mean cluster proper motions, metallicity, and age.

In Sect. 2, we briefly describe the observational data. In Sect. 3 we focus our attention on TBJ 3. Section 4 presents the methods used to estimate the physical parameters and the resulting values for Patchick 99. In Sect. 5, we present a summary and draw conclusions.

2. Observational data

The effects of dust become increasingly prominent towards the centre of our Galaxy. Thus, we have to overcome problems like high differential reddening and extinction (e.g., Alonso-García et al. 2017), which introduce systematic errors in the determination of distances. Additionally, uncertainties in the extinction values affect the estimation of ages when isochrones are used. Also, the stellar density is very high in the inner regions and crowding can prevent the resolution of individual stars. Further uncertainties are due to the foreground and background field contamination that may alter the measurement of the total luminosity. For these reasons, we use combinations of optical and near-IR data in order to substantially reduce uncertainties in the measurements and obtain robust results.

We analyse red clump (RC) and red giant branch (RGB) stars in particular because they are very bright in infrared and they allow us to estimate accurate values of reddening, extinction, distance, and size for our GC candidates. Below we provide a short description of the observational material.

2.1. Infrared Surveys: VVV, VVVX, and 2MASS

We use deep near-IR data from the VVV and VVV eXtended (VVVX) surveys (Minniti et al. 2010; Minniti 2018) acquired with the VISTA InfraRed CAMera (VIRCAM) at the 4.1m wide-field Visible and Infrared Survey Telescope for Astronomy (VISTA; Emerson & Sutherland 2010) at ESO Paranal Observatory. VVV and VVVX data are reduced at the Cambridge Astronomical Survey Unit (CASU; Irwin et al. 2004) and further processing and archiving is performed with the VISTA Data Flow System (VDFS; Cross et al. 2012) by the Wide-Field Astronomy Unit and made available at the VISTA Science Archive1. We use preliminary data from VIRAC (Smith et al. 2018) version 2 described in detail in Smith et al. (in prep.). In summary, VIRAC v2 is based on a point spread function (PSF) fitting reduction of VVV and VVVX images using DoPhot (Schechter et al. 1993; Alonso-García et al. 2012, 2018). Their astrometry is calibrated to the Gaia DR 2 (Gaia Collaboration 2018) astrometric reference system, and their photometry is calibrated against 2MASS using a globally optimised model of frame-by-frame zero points plus an illumination correction. The VVV survey, and in particular the VVVX survey, sample the Galactic bulge and the southern Galactic plane using the J (1.25 μm), H (1.64 μm)), and Ks (2.14 μm)) near-IR passbands, aiming to better disentangle and characterise the stellar populations located at these low-latitude regions. The VISTA Telescope tile field of view is 1.501 deg2, and therefore 196 tiles are needed to map the bulge area and 152 tiles for the disc. Adding some X and Y overlap between tiles for a smooth match, the area of our unit tile covered twice is 1.458 deg2. Specifically, Patchick 99 is located in the VVV tile b251, whereas TBJ 3 is situated in the VVVX tile b462.

In addition, we use 2MASS data (Skrutskie et al. 2006; Cutri et al. 2003). This latter is a near-IR survey of the sky in J (1.25 μm), H (1.65 μm), and Ks (2.17 μm) passbands. We adopt it specifically to extend the RGB VVV colour–magnitude diagrams (CMDs), as these stars are saturated for Ks < 11 mag in VVV images. We downloaded the 2MASS data from the VizieR Online Data Catalogue2, and we merge it with the VVV catalogue, including all stars located within 10′ of the targets centres. However, as the magnitude scale is different in the two photometric systems, we transformed the 2MASS photometry into the VVV magnitude scale3.

2.2. Optical Surveys: Gaia DR 2

The Gaia astrometric mission maps the MW at optical wavelengths, with the aim of revealing motions, composition, formation, and evolution of the Galaxy. Gaia provides very accurate position, PMs, and radial velocity measurements for sources both in our Galaxy and throughout the Local Group. We use Gaia DR 2 data 2018ASPSAMPA...616A...1G for both stellar cluster candidates downloaded from the VizieR Online Data Catalogue. Gaia DR 2 data were prepared by the Gaia Data Processing and Analysis Consortium (DPAC) and contain G-band magnitudes for over 1.6 × 109 sources with G < 21 mag and broadband colours GBP (330–680 nm) and GRP (630–1050 nm) for 1.4 × 109 sources. Proper motion components in equatorial coordinates are available for 1.3 × 109 sources, with an accuracy of 0.06 mas yr−1, 0.2 mas yr−1, and 1.2 mas yr−1, for sources with G < 15 mag, G ∼ 17 mag, and G ∼ 20 mag, respectively. We use the parallax (plx) values to make the first cut in such a way as to exclude clear nearby foreground stars (those with large errors might scatter to plx < 0.5 mas). In our analysis, we did not make any Gaia photometric or colour cuts.

3. TBJ 3: background galaxy

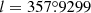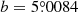TBJ 3 is situated at equatorial coordinates RA = 17h18m14s and Dec = −27d54m15s (J2000) and Galactic coordinates l = 357 . ° 9299 $ l=357{{{\overset{\circ}{.}}}}9299 $ and b = 5 . ° 0084 $ b=5{{{\overset{\circ}{.}}}}0084 $. It was mentioned for the first time as a GC candidate in the list of Terzan & Bernard (1978) and Terzan & Ju (1980) with the name TJ 3. Subsequently, it was spectroscopically studied by Bica et al. (1998), who renamed it as TBJ 3. We believe it to be the same object, although in those works the equatorial coordinates are RA(1950) = 17h15m06s and Dec(1950) = − 27 ° 51′, which correspond to RA(J2000) = 17h17m05.17s and Dec(J2000) = −27d47m49.22s, which are different from those considered in this paper.

From Fig. 1, it is clear that there is an object at these coordinates. Analysing it at different wavelengths and by looking especially at the WISE satellite images, we note that TBJ 3 shows diffuse mid-IR emission, which is not present in GCs. This feature, as well as the oblate and very elliptical shape, lead us to discard TBJ 3 as a possible GC candidate, and consider this to be a background galaxy.

thumbnail Fig. 1.

Finding charts of TBJ 3, adopting different surveys: 2MASS K-band (a), ALLWISE w3 (b), ALLWISE w4 (c), and Spitzer MIPS24 (d).

4. Confirmation of Patchick 99 as a new globular cluster

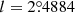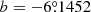Patchick 99 is located in the Galactic bulge at equatorial coordinates RA = 18h15m47s and Dec = −29d48m46s (J2000) and Galactic coordinates l = 2 . ° 4884 $ l=2{{{\overset{\circ}{.}}}}4884 $ and b = − 6 . ° 1452 $ b=-6{{{\overset{\circ}{.}}}}1452 $ (Fig. 2). We found this cluster during our VVV search (Minniti et al. 2017a, 2018; Minniti 2018), but later realised that an object at that position had been reported before as part of the deep sky hunters survey (DHS) of the DSS and 2MASS images (Kronberger et al. 2006, 2012), and so their discovery and nomenclature take precedence. This cluster, which is named after the researcher who discovered it, was then listed in the compilation of Bica et al. (2018), but has not been studied in detail, and we therefore decided to investigate its nature and measure its physical parameters with the VVV data.

thumbnail Fig. 2.

Finding chart of Patchick 99 showing from left to right the central 1.6′×1.1 optical colour images from PanStarrs and near-IR colour images from the VVV and 2MASS surveys.

4.1. Statistical and proper motions decontamination procedures

Contamination by Galactic bulge and disc stars is relevant, so we made some selections in order to decontaminate the CMDs. As mentioned in Sect. 2.2, we only consider stars that have plx < 0.5 mas in order to exclude foreground stars. Moreover, Figure 3 shows the VVV near-IR CMDs of a 3′ radius region centred on Patchick 99 compared with the CMD of a nearby background region, and with the statistically decontaminated CMD. This last CMD was constructed following the procedure described by Piatti & Bica (2012) as applied by Palma et al. (2016, 2019) and Minniti et al. (2017a). We clearly notice the presence of the cluster RGB and RC that remain in the decontaminated diagram, suggesting that a distance of 3′ from the centre is an excellent compromise for our selection. However, there are some blue stars outside of the cluster RGB that probably belong to the foreground MW disc population that persist in this CMD. Therefore, we decided to use the PMs as an independent method to decontaminate the CMD for this cluster, because stars with similar PMs are likely to belong to the same cluster. We compared the vector PM (VPM) diagram for our cluster, including stars in the 3′ radius region and for the field stars located between 4 < r < 5 arcmin away from the cluster centre (Fig. 4). Visually, the main difference between the two PM distributions is that in the case of our cluster selection, this one shows two over-densities, suggesting a bimodal distribution, unlike the field stars that show a shallower homogeneous distribution when we move away from the centre of the cluster, indicating a unimodal distribution. In order to confirm our finding we carried out the Gaussian mixture modelling (GMM) analysis (Muratov & Gnedin 2010), which helps to give us the statistical significance of a unimodal versus a bimodal distribution. We performed the GMM analysis with the heteroscedastic statistic for each sample. In summary, we performed the GMM analysis for our three subsamples: the field stars located between 4 < r < 5 arcmin away from the Patchick 99 centre, the position selection including all stars situated within 3′ from the cluster centre, and our PM selection. Firstly, we did this for field stars and position selection in order to obtain the statistical significance for the two Gaussian distributions shown in Fig. 4. Subsequently, we ran the GMM algorithm to distinguish the two Gaussian peaks shown in Fig. 5. The statistical parameters are shown in Tables 1 and 2. For a mixture of two normal distributions the means and standard deviations along with the mixing parameter (D, separation of the means relative to their widths) are usually used, giving a total of five parameters. Ashman et al. (1994) noted that D > 2 is required for a clean separation between the modes, while if the GMM method detects two modes that are insufficiently separated (D < 2) then such a split is not meaningful.

thumbnail Fig. 3.

Observed VVV near-IR CMDs of a 3′ radius region centred on Patchick 99 (left), of a background region with similar area (middle), and statistically decontaminated CMD (right) following the procedure described by Palma et al. (2016, 2019). We note the clear presence of the cluster RC in the decontaminated diagram.

Table 1.

GMM analysis for each subsample (field stars, position, and PM selection) applied to PM in RA.

Table 2.

GMM analysis for each subsample (field stars, position, and PM selection) applied to PM in Dec.

Applying the GMM analysis to our samples we noted that they may show a bimodal distribution, but with a low significance level. Doing a deep analysis of the GMM resulting parameters, we can confirm that the distribution of field stars located away from the cluster centre is unimodal because the D < 2 and the standard deviation of the second mode is of σ2 ≈ 14, which is not physical. About the 3′ radius region sample, the analysis becomes more complicated. We believe that the two peaks have a very small separation and the method is not able to distinguish both properly; indeed comparing the parameters of the first Gaussian with the second one we see that the first dominates over the second. On the other hand, the GMM method on the PM selection indicates a bimodal distribution, because D > 2. This may be misleading because we should have expected a unimodal distribution for the stars in a cluster. However, we have to highlight that any sample will be contaminated by foreground stars that will have different velocity (and PM) distribution. Thus, having two peaks in the sample of PM selection is not unexpected. In any case, this does not represent a problem because the second mode is very narrow and is not dominant over the first, meaning that our final sample has very little contamination.

Successively, we calculate the mean cluster PMs (adopting the σ-clipping method) measured from Gaia DR2, yielding μα = ( − 2.98 ± 1.74) mas yr−1 and μδ = ( − 5.49 ± 2.02) mas yr−1, which are in good agreement with the PM values found by the GMM method. After that, we selected as cluster members only stars within 3 mas yr−1, following the procedure of Garro et al. (2020), indicated by the black circle drawn in Fig. 4. Also, the size of the circle is set taking into consideration the typical size of GC members in the VPM diagram for other well-studied MW bulge GCs. Additionally, in Fig. 5 we show the PM distributions in a wide range (−20 < μα < 15 mas yr−1 and −20 < μδ < 10 mas yr−1), considering only stars situated within 3′ from the Patchick 99 centre (blue histogram), attempting to minimise field stars. The resulting star sample after the PM cut is shown with the red histogram. Each histogram is constructed considering the sum of all the combined values per unit bin, selecting a fixed bin size of 0.8 mas yr−1 (a value that allowed us to visually distinguish the two peaks of the Gaussian distributions). We see double peaked distributions for both blue histograms, with very little separation (as expected from the GMM method), suggesting that we have at least two overlapping populations: the bulge field stars and the star cluster. Indeed, fitting two Gaussian distributions we assign a narrower and more peaked distribution for Patchick 99 (green curve) and a wider distribution for Bulge field stars (grey curve). The total distribution (black curve) is obtained by coadding the two Gaussians in order to fit the entire sample.

thumbnail Fig. 4.

Top panel: VPM diagram from Gaia DR 2 dataset for star members located within 3′ from the Patchick 99 centre. The black circle indicates the position of the cluster selection within 3 mas yr−1. Bottom panel: VPM diagram for field stars located at 4.8′ from the Patchick 99 centre. In each panel, colour represents density, with magenta being the highest, followed by blue, green, and red.

thumbnail Fig. 5.

Proper motions distributions in RA (top panel) and Dec (bottom panel) for stars located within 3′ of the Patchick 99 centre (blue histogram) and for our cluster PM selection (red histogram). Grey and green curves are the Gaussian distributions for the Bulge field stars and Patchick 99 stars, respectively. The total distribution, obtained by coadding the two Gaussian distributions, is fitted as a black curve.

Figure 6 displays the PM-decontaminated CMDs for VVV and Gaia data. We find that the main GC features remain, such as the RGB and RC, but in comparison with the statistical decontamination (Fig. 3), the foreground disc population is now better removed.

thumbnail Fig. 6.

Observed (left panels) and PM decontaminated (right panels) CMDs for the GC Patchick 99, employing the near-IR VVV (top panels) and optical Gaia DR 2 data (bottom panels).

Following these procedures, we obtained the decontaminated near-IR (Ks vs. J − Ks) and optical (G vs. BP − RP) CMDs for our cluster, as shown in the right panels of Fig. 6 and in Fig. 7. We use those CMDs to derive the main parameters for the cluster. Both diagrams clearly show the RC at Ks = (12.5 ± 0.04) mag and G = (15.5 ± 0.05) mag, suggesting that P99 is a metal-rich GC. It is crucial to use RC stars in this kind of study, because these stars are very good distance indicators.

thumbnail Fig. 7.

VVV near-IR (left panel) and Gaia DR 2 optical (right panel) PM-decontaminated CMD for the GC Patchick 99. The red dotted line is fitted by a PARSEC isochrone with age 10 Gyr and metallicity [Fe/H]= − 0.2 dex. The magenta points represent the position of RR Lyrae star members in the near-IR CMD.

4.2. Estimation of physical parameters for Patchick 99

Nowadays, a wide range of reddening maps exist, such as those by Schlafly & Finkbeiner (2011), Gonzalez et al. (2011, 2018), Minniti et al. (2018), Soto et al. (2019), and Saito et al. (2020). We estimate the reddening and the extinction toward this GC following Ruiz-Dern et al. (2018) and we benefit from the clear position of the RC in the CMDs. We adopt the intrinsic RC magnitude MKs = ( − 1.605 ± 0.009) mag and the intrinsic colour (J − Ks)0 = (0.66 ± 0.02) mag. Using the latter, we calculate a colour excess of E(J − Ks) = (0.12 ± 0.02) mag, in accordance with the adopted reddening map, and the extinction AKs = 0.72 × E(J − Ks) = (0.09 ± 0.01) mag (Cardelli et al. 1989). Consequently, we use these values in order to determine distances: we measure a distance modulus (m − M)0 = (14.02 ± 0.01) mag equivalent to a heliocentric distance D = (6.4 ± 0.2) kpc.

Similarly, for optical wavebands we identify again RC stars and adopt the intrinsic RC magnitude MG = (0.459 ± 0.009) mag (Ruiz-Dern et al. 2018). The near-IR extinction AKs = (0.09 ± 0.01) mag corresponds to the optical extinction AG = 0.86 × AV = (0.68 ± 0.08) mag, deriving also E(BP − RP) = AG/3.12 = (0.21 ± 0.03) mag (Cardelli et al. 1989; O’Donnell 1994). Therefore, the resulting cluster distance modulus from the Gaia optical photometry is (m − M)0 = (14.23 ± 0.1) mag and the distance D = (7.0 ± 0.2) kpc agrees within 3σ with our near-IR distance.

Using our estimates of the reddening and distance we were able to fit PARSEC4 isochrones (Bressan et al. 2012; Marigo et al. 2017) to the CMDs of Patchick 99. This allows us to estimate the metallicity and the age of the GC, finding [Fe/H]=(−0.2 ± 0.2) dex and t = (10 ± 2.0) Gyr, respectively. In order to obtain a more robust result, we also derived the metallicity from the slope of the RGB (α = 0.11 ± 0.01) using the calibration of Cohen et al. (2016), finding [Fe/H]= − 0.3 ± 0.2 dex, in agreement with our original estimate. Figure 7 shows a good fit of the isochrones with the above-mentioned values of metallicity and age in both our optical and near-IR CMDs. We determined the errors in age and in metallicity by changing the isochrones at a fixed metallicity and a fixed age, respectively, until they no longer fit the cluster sequence simultaneously in the near-IR and optical CMDs. Therefore, it is clear that although age is one of the fundamental parameters to characterise GCs, its correct determination is still one of the most complicated tasks to perform, especially in environments with high stellar density and with differential reddening, such as the Galactic bulge. This is mainly due to difficulties in reaching the main sequence turn-off (MS-TO) point. We can see this problem in Fig. 8, which displays the VVV and 2MASS PM-decontaminated CMDs. We include 2MASS cluster members with Ks < 11 mag, as they are more sensitive to the metallicity variations (e.g., McQuinn et al. 2019). We can see that variations in metallicity have an especially strong effect along the RGB and RC; vice versa, we can see evident changes in age in the MS-TO region. For this reason our age should be taken as a crude estimate, because we are unable to measure it precisely.

thumbnail Fig. 8.

Fitting of isochrones in the VVV CMDs at fixed metallicity of [Fe/H]= − 0.2 dex and variation in ages t = 8, 9, 10, 11, 13 Gyr (right panel); while at fixed age of t = 10 Gyr and different metallicities [Fe/H] = 0,   − 0.1,   − 0.2,   − 0.3,   − 0.4 dex (left panel). Black points represent the VVV cluster members, whereas blue points are those from the 2MASS catalogue.

All of the previously derived parameters, including position, metallicity, and kinematics, confirm that Patchick 99 is a bulge GC, but if we consider its age, it could be even younger than typical metal-rich GCs present in the Galactic bulge, which have ages of between 12 and 13 Gyr (e.g., Carretta et al. 2000. However, many studies have demonstrated that GCs show a relatively wide range of ages in the bulge (Zoccali et al. 2003; Clarkson et al. 2011; Valenti et al. 2013; Bernard et al. 2018).

Figure 9 shows the Gaia+VVV optical–near-IR colour–colour diagram (CCD) for the whole catalogue without selection cuts, and for only cluster members of Patchick 99 with Ks < 15 mag. We clearly see that the colour distribution reveals a tighter sequence for star members (circles, right panel) than for the field stars (squares, left panel). In particular, we see that there is little differential extinction in the right panel of Fig. 9. Based on the high-resolution reddening map by Surot et al. 2020, the mean reddening is E(J − Ks) = 0.05 mag in this field, which differs from our reddening value by Δ(E(J − Ks)) = 0.07 mag at most. Hence, we believe that our estimation is in good agreement with the adopted map, discarding this as a significant problem.

thumbnail Fig. 9.

Gaia+VVV optical–near-IR CCDs for Patchick 99 as a density plot. On the left: squares are the observed stars, using the entire catalogue without selection cuts; on the right: circles represent star members of Patchick 99, considering previously selected bright stars. The red arrow in the top left corner of the panel represents the reddening vector.

Finally, we derive the total luminosity of our cluster using the catalogue with only cluster members. Once the flux for each star is measured, we derive the absolute magnitude from the total flux, obtaining MKs = ( − 7.0 ± 0.6) mag, equivalent to MV = ( − 4.5 ± 0.8) (for a typical GC colour of (V − Ks) = (2.5 ± 0.5) mag), indicating that it is a very faint GC. This value is an underestimate of the total luminosity, because the faintest stars are missing. Regarding this, we compared Patchick 99 luminosity with other known GCs with similar metallicity: NGC 6553 ([Fe/H]= − 0.18 dex; D = 6.01 kpc; MV = −7.77 mag), NGC 6528 ([Fe/H]= − 0.11 dex; D = 7.9 kpc; MV = −6.57 mag), and Terzan 5 ([Fe/H]= − 0.23 dex; D = 5.9 kpc; MV = −7.42 mag). Using the same method, and also spanning the same magnitude range (10.7 < Ks < 17.2), we derive the integrated near-IR absolute magnitude for each GC, finding MKs (NGC 6553) = − 9.5 mag, MKs (NGC 6528) = − 8.0 mag, and MKs (Ter5) = − 9.6 mag. We converted them into V−band and scaled to the MV values from the 2010 version of the Harris (1996) catalogue. Estimating the MV differences and assuming the similarities between the GCs, we derive a total luminosity for Patchick 99 of MV = −5.2 mag, which is ∼2.2 mag less luminous than the MW GC luminosity function peak (MV = ( − 7.4 ± 0.2) mag from Harris 1991; Ashman & Zepf 1998). All these parameters are summarised in Table 3.

Table 3.

Main physical parameters for Patchick 99 determined using near-IR and optical datasets.

4.3. The derivation of the surface density profile

A detailed description of the structural parameters of Patchick 99 would require careful treatment of completeness as well as relatively large numbers of member stars from which a radial profile can be derived. Traditionally, King profiles (King 1962) have been fitted to a significant fraction of MW old clusters, but evidence is building that other profiles might provide better fits, especially when extragalactic or massive GCs are included (e.g., Mackey & Gilmore 2003; de Boer et al. 2019). Although rich clusters allow for model-dependent sizes and structural properties, our sample of member stars is not enough to adequately address a comparison among the different models available. Instead, a King function is assumed to be a good approximation for the radial distribution of the stellar density.

Correct determination of the cluster centre is of fundamental importance, because an error in its position can lead to altered results regarding the density profile. For this reason, we used the K-Means algorithm in Python to determine the centre in a robust way from our catalogue of cluster member stars. In summary, this is a machine-learning algorithm that searches for subgroups (or literally ‘clusters’) in a given parameter space among a sample of data points. We checked visually that the resulting centres were close to the expected density peaks and we found that the initial position (RA = 18h15m47s and Dec = −29d48m46s (J2000)) coincides almost perfectly with the resulting values of the centre, with a small separation of ΔRA ≈ 2″ and ΔDec ≈ 5″.

Starting from these new coordinates, we divided our sample of member stars into ten circular annuli, out to a radius of 1.5′ in steps of 0.15′. We do not need to apply geometric corrections as the resulting circular annuli are within the FOV of our catalogue. We analysed the radial density profile of Patchick 99 (see Fig. 10), dividing the total number of stars in each radial bin by the area of that ring in order to derive the density in each bin. Poisson errors are also shown. We note that the error bars are relatively large, mainly because of the low-number statistics in each radial bin, especially in the innermost point (see Fig. 10). No background has been subtracted because we are dealing with a list that is expected to be free from foreground stars and other contaminants.

thumbnail Fig. 10.

Radial surface density of Patchick 99 (black points), taking into consideration only PM- selected member stars. The coloured lines are King model profiles that best reproduce observational data, with a fixed value of the tidal radius of 10′ and different values of core radius, in cyan rc = 1.8′, in red rc = 1.5′, and in blue rc = 1.2′ Poisson errors are shown as error bars.

We overplotted a family of King profiles adopting different values of core radius (rc = 1.8′, 1.5′, 1.2′), but keeping the tidal radius fixed at 10′. The choice to use that value of tidal radius is justified following de Boer et al. (2019; see their Figs. 13 and 14), where a clear correlation between the tidal radius and galactocentric radius of a given GC is illustrated. As shown in Fig. 10, the observational points are best represented by rc = 1.2′, which is equivalent to rc ∼ 1.1 pc. Also, we consider the tidal radius rt = 10′ as the size of the cluster, which corresponds to a physical size of 9.3 pc.

4.4. The RR Lyrae stars in Patchick 99

RR Lyrae variable stars, found in the Galactic halo and bulge, represent a very old population in our Galaxy. In particular, according to Pietrukowicz et al. (2015), their spatial density ranges between 80 and 440 RRL deg−2 in the bulge. They are also considered powerful tools for revealing the nature of a GC candidate because if detected in a stellar cluster, RR Lyrae stars guarantee old age. Although these variables are used as excellent tracers of old and metal-poor populations, there is observational evidence that suggests the presence of RR Lyrae also in metal-rich GCs, such as NGC 6388 ([Fe/H]= − 0.44 dex), NGC 6441 ([Fe/H]= − 0.46 dex) (Pritzl et al. 2002; Clementini et al. 2005), and NGC 6440 [Fe/H]= − 0.36 dex), all of which are somewhat more metal-rich than Patchick 99. Additionally, RR Lyrae variable stars are good reddening and distance indicators.

For these reasons, we searched for these variable stars and detected 21 RR Lyrae stars within 12 arcmin of the Patchick 99 centre, matching the OGLE (Soszyński et al. 2014), the VVV (Majaess et al. 2018), and the Gaia (Clementini et al. 2019) catalogues. They are listed in Table 4, where we summarise their identification, location, period, photometry in different filters, heliocentric distance, distance from the centre of the GC, type, and PM.

Table 4.

Detected RR Lyrae stars within 12′ from the Patchick 99 centre.

Initially we constructed their phased light curves in order to discriminate their pulsation mode. We identify 13 fundamental mode pulsators (ab-type RR Lyrae stars) with long periods (P ≳ 0.4 days) and large amplitudes, and 8 first-overtone pulsators (c-type RR Lyrae stars) with short period (P ≲ 0.4 days) and small amplitudes. The RRc and RRab pulsators also differ in the morphology of their light curves, because the RRabs have typically asymmetrical light curves, unlike RRcs. Figure 11 displays the amplitude–period diagram (so-called Bailey diagram; Bailey et al. 1919) in such a way as to highlight their differences. Indeed, we consider the Bailey diagram a solid tool for verifying our estimations.

thumbnail Fig. 11.

Bailey diagram for detected 21 RR Lyrae stars (black points), situated within 12 arcmin of the Patchick 99 centre, while we highlight the RR Lyrae member stars with magenta points.

Our main goal is to identify which RR Lyrae stars are real members of Patchick 99. Firstly, we measured their projected distance from the centre using the centroid of each variable stars. Based on these distances and considering the size of the cluster, we believe that seven RR Lyrae stars are members of Patchick 99, as shown in Fig. 12 and marked by a star symbol in Table 4. In addition, we compare their projected distance with the resulting heliocentric distance (Fig. 12), confirming again the membership. In detail, we used the period–luminosity (PL) relation in Ks-band following Muraveva et al. (2015) (with RRc stars ‘fundamentalized’ by adding 0.127 to the logarithm of the period) in order to derive their heliocentric distance. For these selected RR Lyrae members, we estimate the mean distance, finding a value of D = 7.06 ± 0.48 kpc, consistent with the heliocentric distances obtained from the VVV and Gaia photometries (see Sect. 4) because these values differ by less than 2σ. On the other hand, we discard the others as members because they have heliocentric distances larger than those found using VVV near-IR photometry, or they are located outside our assumed tidal radius. However, we can restrict the RR Lyrae sample to the ones that have PMs matching the mean GC PM within the errors, and find that only three of them fulfil this requirement, namely OGLE-BLG-RRLYR-35312, 35476, and 35459, favouring a short distance of 6.3 ± 0.5 kpc in the mean. Additionally, Fig. 12 does not show OGLE-BLG-RRLYR-35364 and OGLE-BLG-RRLYR-35381, as their distance values are very large and they are probably located in the Galactic halo or in the Sagittarius dwarf galaxy. We also tested two other PL relations from Gaia Collaboration (2017) and Navarrete et al. (2017), yielding slightly larger distance values. However, we use the comparison between the three PL relations in order to assign a mean distance error of 0.5 kpc. Once absolute magnitudes were obtained, we also built up the PL relation diagram (Fig. 13). This allowed us to confirm the membership again, as we find a stronger relation when the least-square fit is used on the star cluster members (red line), rather than on the whole sample (blue line). We also show the VVV phased light curves for each RR Lyrae member (Fig. 14). We note that the light curve profile for OGLE-BLG-RRLYR-35459 is slightly worse than the others, as this variable appears slightly blended.

thumbnail Fig. 12.

Spatial distribution of RR Lyrae variable stars detected within 12′ of the centre of Patchick 99. The magenta points represent the seven RR Lyrae stars considered cluster members, whereas we highlight the PM members with magenta squares. The distance error bars are of 0.5 kpc for each point. The dotted line depicts the heliocentric distance at D = (6.4 ± 0.2) kpc derived from the VVV near-IR photometry.

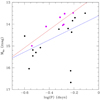thumbnail Fig. 13.

MKs − log(P) diagram for the whole RR Lyrae sample (black points) and all RR Lyrae star members (magenta points, while the squares represent the PM variable members). Blue and red lines represent the least-squares fit for the whole RR Lyrae sample and all cluster members, respectively.

thumbnail Fig. 14.

Phased light curves for the RR Lyrae star members of the GC Patchick 99, classified as ab-type with P > 0.4 days and c-type with P < 0.4 days.

Moreover, we derive the expected spatial density from Pietrukowicz et al. (2015) and Navarro et al. (2021). Specifically, following Navarro et al. (2021), we are able to predict a mean density of four field RR Lyrae type-ab stars in the same field as Patchick 99. We find 21 variables in total, including 13 RRab. Hence, this value represents a clear excess over the background (∼4.5σ detection).

Finally, the magenta points in Fig. 7 define the position of the seven RR Lyrae stars in the VVV CMD. Their near-IR magnitudes are on average much fainter than the RC (∼1 − 1.5 mag). However, both theory and observations suggest that the RR Lyrae should indeed be fainter than the RC in the near-IR CMDs and also indicate that more metal-rich RR Lyrae are fainter than their metal-poor counterparts. Cassisi et al. (2004) for example explored the predicted behaviour of the pulsators as a function of the horizontal branch morphology and over the metallicity range Z = 0.0001–0.006, finding that the RR Lyrae luminosity decreases with increasing metallicity. Further, Marconi et al. (2018) constructed new sets of helium-enhanced (Y = 0.30, Y = 0.40) non-linear, time-dependent convective hydrodynamical models of RR Lyrae stars covering a broad range in metal abundances (Z = 0.0001–0.02), finding that an increase in helium content from the canonical value (Y = 0.245) to Y = 0.30–0.40 causes a simultaneous increase in stellar luminosity and in pulsation period (see their Figs. 1 and 2).

Also, from an observational point of view, we compared the location of our RR Lyrae with those confirmed PM members of the cluster NGC 6441 from Alonso-García et al. (in prep.). The RR Lyrae stars in Patchick 99 fall in the expected region of the near-IR CMD for this metal-rich cluster. In any case, spectroscopic metallicities are needed to confirm if this is the most metal-rich GC known with RR Lyrae.

5. Summary and conclusions

We investigated the GC candidates Patchick 99 and TBJ 3 in order to understand their true nature.

We analysed them in optical and near-IR wavelengths to determine their physical parameters. Visual examination of TBJ 3 at various wavelengths confirms that it is not a GC but from its mid-IR emission we conclude that TBJ 3 is a background galaxy. We therefore focused our work on Patchick 99. We measured its reddening, extinction, distance modulus and heliocentric distance, size, proper motion, total luminosity, metallicity, and age. We summarise all these values in Table 3.

Even though the field contamination is severe, we used two different methods (statistical and PM decontamination) recovering the same results with the GC RGB and RC clearly present. We conclude that Patchick 99 is a metal-rich GC located in the Galactic bulge at a heliocentric distance of D = 6.6 ± 0.6 kpc obtained as an average distance from three-independent methods (Gaia DR 2 and VVV photometries, and three RR Lyrae star members). We define it as a genuine GC because both CCD and CMDs yield a population with an age of 10 Gyr. These results are confirmed by the presence of seven RR Lyrae stars located at d < 12′ from the cluster centre and at the same distance as the cluster from the Sun. However, analysing their PM we can confirm that three of these RR Lyrae are surely members of our cluster, namely OGLE-BLG-RRLYR-35312, 35476, and 35459, because their PMs match the mean cluster PM within the errors. Patchick 99 may be the most metal-rich GC with RR Lyrae, but this is to be confirmed by spectroscopic observations. As mentioned previously, even if position, metallicity, and kinematics confirm that it is a bulge GC, the age of Patchick 99 is a few gigayears younger than the typical age of metal-rich GCs (∼12 − 13 Gyr) in the same regions. In any case, it is important to underline that our estimation of age is quite rough and deeper observations are required for improved accuracy.

Another important conclusion is that Patchick 99 is a low-luminosity GC (MKs = −7.0 mag), suggesting that many other faint GCs are still to be revealed in the bulge of the Milky Way.

Acknowledgments

We gratefully acknowledge the use of data from the ESO Public Survey program IDs 179.B-2002 and 198.B-2004 taken with the VISTA telescope and data products from the Cambridge Astronomical Survey Unit. ERG acknowledges support from an UNAB PhD scholarship. D.M. acknowledges support by the BASAL Center for Astrophysics and Associated Technologies (CATA) through grant AFB 170002. D.M. and M.G. are supported by Proyecto FONDECYT No. 1170121. J.A.-G. acknowledges support from Fondecyt Regular 1201490 and from the ANID’s Millennium Science Initiative ICN12_009, awarded to the Millennium Institute of Astrophysics (MAS). This work has made use of the University of Hertfordshire’s high-performance computing facility.

References

  1. Alonso-García, J., Mateo, M., Sen, B., et al. 2012, AJ, 143, 70 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alonso-García, J., Minniti, D., Catelan, M., et al. 2017, ApJ, 849, L13 [Google Scholar]
  3. Alonso-García, J., Saito, R. K., Hempel, M., et al. 2018, A&A, 619, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Ashman, K. M., & Zepf, S. E. 1998, Cambridge Astrophysics Series (Cambridge: Cambridge Univ. Press), 30 [Google Scholar]
  5. Ashman, K. M., Bird, C. M., & Zepf, S. E. 1994, AJ, 108, 2348 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bailey, S. I., Leland, E. F., Woods, I. E., & Pickering, E. C. 1919, Ann. Harvard College Obs., 78, 195 [Google Scholar]
  7. Barmby, P., & Huchra, J. P. 2001, ApJ, 122, 2458 [Google Scholar]
  8. Barbuy, B., Bica, E., Ortolani, S., & Bonatto, C. 2006, A&A, 449, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Barbuy, B., Zoccali, M., Ortolani, S., et al. 2009, A&A, 507, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bernard, E. J., Schultheis, M., Di Matteo, P., et al. 2018, MNRAS, 477, 3507 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bica, E., Claria, J. J., Piatti, A. E., & Bonatto, C. 1998, A&AS, 131, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bica, E., Pavani, D. B., Bonatto, C. J., & Lima, E. F. 2018, AJ, 157, 12 [Google Scholar]
  13. Bonatto, C., & Bica, E. 2010, A&A, 521, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
  15. Camargo, D. 2018, ApJ, 860, L27 [Google Scholar]
  16. Camargo, D., & Minniti, D. 2019, MNRAS: Lett., 484, L90 [Google Scholar]
  17. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
  18. Carretta, E., Gratton, R. G., Clementini, G., & Pecci, F. F. 2000, ApJ, 533, 215 [NASA ADS] [CrossRef] [Google Scholar]
  19. Cassisi, S., Castellani, M., Caputo, F., & Castellani, V. 2004, A&A, 426, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Clarkson, W. I., Sahu, K. C., Anderson, J., et al. 2011, ApJ, 735, 37 [NASA ADS] [CrossRef] [Google Scholar]
  21. Clementini, G., Gratton, R. G., Bragaglia, A., et al. 2005, ApJ, 630, L145 [NASA ADS] [CrossRef] [Google Scholar]
  22. Clementini, G., Ripepi, V., Molinaro, R., et al. 2019, A&A, 622, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Cohen, R. E., Moni Bidin, C., Mauro, F., Bonatto, C., & Geisler, D. 2016, MNRAS, 464, 1874 [Google Scholar]
  24. Cross, N. J. G., Collins, R. S., Mann, R. G., et al. 2012, A&A, 548, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, II/246 [Google Scholar]
  26. de Boer, T. J. L., Gieles, M., Balbinot, E., et al. 2019, MNRAS, 485, 4906 [NASA ADS] [CrossRef] [Google Scholar]
  27. Emerson, J., & Sutherland, W. 2010, Messenger, 139, 2 [Google Scholar]
  28. Ernandes, H., Dias, B., Barbuy, B., et al. 2019, A&A, 632, A103 [EDP Sciences] [Google Scholar]
  29. Ferraro, F. R., Dalessandro, E., Mucciarelli, A., et al. 2009, Nature, 462, 483 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  30. Ferraro, F. R., Pallanca, C., Lanzoni, B., et al. 2021, Nat. Astron., 5, 311 [Google Scholar]
  31. Gaia Collaboration (Clementini, G., et al.) 2017, A&A, 605, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Garro, E. R., Minniti, D., Gómez, M., et al. 2020, A&A, 642, L19 [EDP Sciences] [Google Scholar]
  34. Gonzalez, O. A., Rejkuba, M., Zoccali, M., Valenti, E., & Minniti, D. 2011, A&A, 534, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Gonzalez, O. A., Minniti, D., Valenti, E., et al. 2018, MNRAS, 481, L130 [NASA ADS] [CrossRef] [Google Scholar]
  36. Harris, W. E. 1991, ARA&A, 29, 543 [NASA ADS] [CrossRef] [Google Scholar]
  37. Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  38. Harris, W. E., Harris, G. L. H., & Alessi, M. 2013, ApJ, 772, 82 [NASA ADS] [CrossRef] [Google Scholar]
  39. Huxor, A. P., Mackey, A. D., Ferguson, A. M. N., et al. 2014, MNRAS, 442, 2165 [NASA ADS] [CrossRef] [Google Scholar]
  40. Irwin, M. J., Lewis, J., Hodgkin, S., et al. 2004, in Optimizing Scientific Return for Astronomy through Information Technologies, eds. P. J. Quinn, A. Bridger, et al., Int. Soc. Opt. Photonics (SPIE), 5493, 411 [Google Scholar]
  41. Kerber, L. O., Nardiello, D., Ortolani, S., et al. 2018, ApJ, 853, 15 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kerber, L. O., Libralato, M., Souza, S. O., et al. 2019, MNRAS, 484, 5530 [NASA ADS] [CrossRef] [Google Scholar]
  43. King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kronberger, M., Teutsch, P., Alessi, B., et al. 2006, A&A, 447, 921 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Kronberger, M., Reegen, P., Alessi, B. S., Patchick, D., & Teutsch, P. 2012, Astrophys. Space Sci. Proc., 29, 105 [Google Scholar]
  46. Lee, Y. W., Joo, J. M., Sohn, Y. J., et al. 1999, Nature, 402, 55 [Google Scholar]
  47. Mackey, A. D., & Gilmore, G. F. 2003, MNRAS, 338, 85 [NASA ADS] [CrossRef] [Google Scholar]
  48. Majaess, D., Dékány, I., Hajdu, G., et al. 2018, Astrophys. Space Sci., 363, 127 [Google Scholar]
  49. Marconi, M., Bono, G., Pietrinferni, A., et al. 2018, ApJ, 864, L13 [Google Scholar]
  50. Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [NASA ADS] [CrossRef] [Google Scholar]
  51. Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. McQuinn, K. B. W., Boyer, M., Skillman, E. D., & Dolphin, A. E. 2019, ApJ, 880, 63 [CrossRef] [Google Scholar]
  53. Minniti, D. 2018, in The Vatican Observatory, Castel Gandolfo: 80th Anniversary Celebration, eds. G. Gionti, & J. B. Kikwaya Eluo, 51, 63 [Google Scholar]
  54. Minniti, D., Lucas, P. W., Emerson, J. P., et al. 2010, New Astron., 15, 433 [Google Scholar]
  55. Minniti, D., Hempel, M., Toledo, I., et al. 2011, A&A, 527, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Minniti, D., Palma, T., Dékány, I., et al. 2017a, ApJ, 838, L14 [NASA ADS] [CrossRef] [Google Scholar]
  57. Minniti, D., Alonso-García, J., Braga, V., et al. 2017b, Res. Notes Am. Astron. Soc., 1, 16 [CrossRef] [Google Scholar]
  58. Minniti, D., Dékány, I., Majaess, D., et al. 2017c, AJ, 153, 179 [NASA ADS] [CrossRef] [Google Scholar]
  59. Minniti, D., Saito, R. K., Gonzalez, O. A., et al. 2018, A&A, 616, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Moni Bidin, C., Mauro, F., Geisler, D., et al. 2011, A&A, 535, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Muratov, A. L., & Gnedin, O. Y. 2010, ApJ, 718, 1266 [NASA ADS] [CrossRef] [Google Scholar]
  62. Muraveva, T., Palmer, M., Clementini, G., et al. 2015, ApJ, 807, 127 [NASA ADS] [CrossRef] [Google Scholar]
  63. Myeong, G. C., Vasiliev, E., Iorio, G., Evans, N. W., & Belokurov, V. 2019, MNRAS, 488, 1235 [Google Scholar]
  64. Navarrete, C., Catelan, M., Contreras Ramos, R., et al. 2017, A&A, 604, A120 [CrossRef] [EDP Sciences] [Google Scholar]
  65. Navarro, M. G., Minniti, D., Capuzzo-Dolcetta, R., et al. 2021, A&A, 646, A45 [EDP Sciences] [Google Scholar]
  66. O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
  67. Palma, T., Minniti, D., Dékány, I., et al. 2016, New Ast., 49, 50 [Google Scholar]
  68. Palma, T., Minniti, D., Alonso-García, J., et al. 2019, MNRAS, 487, 3140 [Google Scholar]
  69. Piatti, A. E., & Bica, E. 2012, MNRAS, 425, 3085 [NASA ADS] [CrossRef] [Google Scholar]
  70. Pietrukowicz, P., Kozłowski, S., Skowron, J., et al. 2015, ApJ, 811, 113 [NASA ADS] [CrossRef] [Google Scholar]
  71. Pritzl, B. J., Smith, H. A., Catelan, M., & Sweigart, A. V. 2002, AJ, 124, 949 [NASA ADS] [CrossRef] [Google Scholar]
  72. Ruiz-Dern, L., Babusiaux, C., Arenou, F., Turon, C., & Lallement, R. 2018, A&A, 609, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Saito, R. K., Minniti, D., Benjamin, R. A., et al. 2020, MNRAS, 494, L32 [CrossRef] [Google Scholar]
  74. Schechter, P. L., Mateo, M., & Saha, A. 1993, PASP, 105, 1342 [NASA ADS] [CrossRef] [Google Scholar]
  75. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
  76. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  77. Smith, L. C., Lucas, P. W., Kurtev, R., et al. 2018, MNRAS, 474, 1826 [NASA ADS] [CrossRef] [Google Scholar]
  78. Sollima, A., Ferraro, F. R., Pancino, E., & Bellazzini, M. 2008, Mem. Soc. Astron. It., 79, 342 [Google Scholar]
  79. Soszyński, I., Udalski, A., Szymański, M. K., et al. 2014, Acta Astron., 64, 177 [NASA ADS] [Google Scholar]
  80. Soto, M., Barbá, R., Minniti, D., et al. 2019, MNRAS, 488, 2650 [Google Scholar]
  81. Surot, F., Valenti, E., Gonzalez, O. A., et al. 2020, A&A, 644, A140 [CrossRef] [EDP Sciences] [Google Scholar]
  82. Terzan, A., & Bernard, A. 1978, Messenger, 15, 14 [Google Scholar]
  83. Terzan, A., & Ju, K. H. 1980, Messenger, 20, 6 [Google Scholar]
  84. Valenti, E., Zoccali, M., Renzini, A., et al. 2013, A&A, 559, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. van den Bergh, S. 2010, AJ, 140, 1043 [Google Scholar]
  86. Vasiliev, E. 2019, MNRAS, 484, 2832 [NASA ADS] [CrossRef] [Google Scholar]
  87. Weinberg, M. D. 1994, AJ, 108, 1414 [NASA ADS] [CrossRef] [Google Scholar]
  88. Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
  89. Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1.

GMM analysis for each subsample (field stars, position, and PM selection) applied to PM in RA.

In the text
Table 2.

GMM analysis for each subsample (field stars, position, and PM selection) applied to PM in Dec.

In the text
Table 3.

Main physical parameters for Patchick 99 determined using near-IR and optical datasets.

In the text
Table 4.

Detected RR Lyrae stars within 12′ from the Patchick 99 centre.

In the text

All Figures

thumbnail Fig. 1.

Finding charts of TBJ 3, adopting different surveys: 2MASS K-band (a), ALLWISE w3 (b), ALLWISE w4 (c), and Spitzer MIPS24 (d).
In the text
thumbnail Fig. 2.

Finding chart of Patchick 99 showing from left to right the central 1.6′×1.1 optical colour images from PanStarrs and near-IR colour images from the VVV and 2MASS surveys.
In the text
thumbnail Fig. 3.

Observed VVV near-IR CMDs of a 3′ radius region centred on Patchick 99 (left), of a background region with similar area (middle), and statistically decontaminated CMD (right) following the procedure described by Palma et al. (2016, 2019). We note the clear presence of the cluster RC in the decontaminated diagram.
In the text
thumbnail Fig. 4.

Top panel: VPM diagram from Gaia DR 2 dataset for star members located within 3′ from the Patchick 99 centre. The black circle indicates the position of the cluster selection within 3 mas yr−1. Bottom panel: VPM diagram for field stars located at 4.8′ from the Patchick 99 centre. In each panel, colour represents density, with magenta being the highest, followed by blue, green, and red.
In the text
thumbnail Fig. 5.

Proper motions distributions in RA (top panel) and Dec (bottom panel) for stars located within 3′ of the Patchick 99 centre (blue histogram) and for our cluster PM selection (red histogram). Grey and green curves are the Gaussian distributions for the Bulge field stars and Patchick 99 stars, respectively. The total distribution, obtained by coadding the two Gaussian distributions, is fitted as a black curve.
In the text
thumbnail Fig. 6.

Observed (left panels) and PM decontaminated (right panels) CMDs for the GC Patchick 99, employing the near-IR VVV (top panels) and optical Gaia DR 2 data (bottom panels).
In the text
thumbnail Fig. 7.

VVV near-IR (left panel) and Gaia DR 2 optical (right panel) PM-decontaminated CMD for the GC Patchick 99. The red dotted line is fitted by a PARSEC isochrone with age 10 Gyr and metallicity [Fe/H]= − 0.2 dex. The magenta points represent the position of RR Lyrae star members in the near-IR CMD.
In the text
thumbnail Fig. 8.

Fitting of isochrones in the VVV CMDs at fixed metallicity of [Fe/H]= − 0.2 dex and variation in ages t = 8, 9, 10, 11, 13 Gyr (right panel); while at fixed age of t = 10 Gyr and different metallicities [Fe/H] = 0,   − 0.1,   − 0.2,   − 0.3,   − 0.4 dex (left panel). Black points represent the VVV cluster members, whereas blue points are those from the 2MASS catalogue.
In the text
thumbnail Fig. 9.

Gaia+VVV optical–near-IR CCDs for Patchick 99 as a density plot. On the left: squares are the observed stars, using the entire catalogue without selection cuts; on the right: circles represent star members of Patchick 99, considering previously selected bright stars. The red arrow in the top left corner of the panel represents the reddening vector.
In the text
thumbnail Fig. 10.

Radial surface density of Patchick 99 (black points), taking into consideration only PM- selected member stars. The coloured lines are King model profiles that best reproduce observational data, with a fixed value of the tidal radius of 10′ and different values of core radius, in cyan rc = 1.8′, in red rc = 1.5′, and in blue rc = 1.2′ Poisson errors are shown as error bars.
In the text
thumbnail Fig. 11.

Bailey diagram for detected 21 RR Lyrae stars (black points), situated within 12 arcmin of the Patchick 99 centre, while we highlight the RR Lyrae member stars with magenta points.
In the text
thumbnail Fig. 12.

Spatial distribution of RR Lyrae variable stars detected within 12′ of the centre of Patchick 99. The magenta points represent the seven RR Lyrae stars considered cluster members, whereas we highlight the PM members with magenta squares. The distance error bars are of 0.5 kpc for each point. The dotted line depicts the heliocentric distance at D = (6.4 ± 0.2) kpc derived from the VVV near-IR photometry.
In the text
thumbnail Fig. 13.

MKs − log(P) diagram for the whole RR Lyrae sample (black points) and all RR Lyrae star members (magenta points, while the squares represent the PM variable members). Blue and red lines represent the least-squares fit for the whole RR Lyrae sample and all cluster members, respectively.
In the text
thumbnail Fig. 14.

Phased light curves for the RR Lyrae star members of the GC Patchick 99, classified as ab-type with P > 0.4 days and c-type with P < 0.4 days.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.