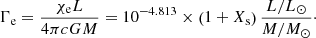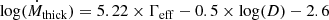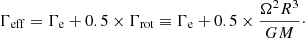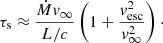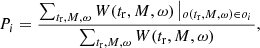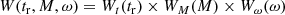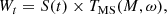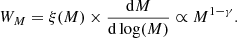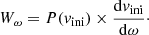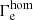| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202040037 | |
| Published online | 26 February 2021 | |
Physics and evolution of the most massive stars in 30 Doradus
Mass loss, envelope inflation, and a variable upper stellar mass limit⋆
Argelander-Institut für Astronomie der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: goetz@astro.uni-bonn.de
Received:
1
December
2020
Accepted:
8
January
2021
Context. The identification of stellar-mass black-hole mergers with up to 80 M⊙ as powerful sources of gravitational wave radiation led to increased interest in the physics of the most massive stars. The largest sample of possible progenitors of such objects, very massive stars (VMS) with masses up to 300 M⊙, have been identified in the 30 Dor star-forming region in the Large Magellanic Cloud (LMC). In this young starburst analogue, VMS were found to dominate stellar feedback. Despite their importance, the physics and evolution of VMS is highly uncertain, mainly due to their proximity to the Eddington limit.
Aims. In this work, we investigate the two most important effects that are thought to occur near the Eddington limit: enhanced mass loss through optically thick winds and the formation of radially inflated stellar envelopes.
Methods. We compute evolutionary models for VMS at LMC metallicity and perform a population synthesis of the young stellar population in 30 Dor. We adjust the input physics of our models to match the empirical properties of the single-star population in 30 Dor as derived in the framework of the VLT-Flames Tarantula Survey.
Results. Enhanced mass loss and envelope inflation near the Eddington limit have a dominant effect on the evolution of the most massive stars. While the observed mass-loss properties and the associated surface He-enrichment are well described by our new models, the observed O-star mass-loss rates are found to cover a much larger range than theoretically predicted, with particularly low mass-loss rates for the youngest objects. Also, the (rotational) surface enrichment in the O-star regime appears to not be well understood. The positions of the most massive stars in the Hertzsprung-Russell diagram (HRD) are affected by mass loss and envelope inflation. For instance, the majority of luminous B supergiants in 30 Dor, and the lack thereof at the highest luminosities, can be explained through the combination of envelope inflation and mass loss. Finally, we find that the upper limit for the inferred initial stellar masses in the greater 30 Dor region is significantly lower than in its central cluster, R 136, implying a variable upper limit for the masses of stars.
Conclusions. The implementation of mass-loss and envelope physics in stellar evolution models turns out to be essential for the modelling of the observable properties of young stellar populations. While the properties of the most massive stars (≳100 M⊙) are well described by our new models, the slightly less massive O stars investigated in this work show a much more diverse behaviour than previously thought, which has potential implications for rotational mixing and angular momentum transport. While the present models are a big step forward in the understanding of stellar evolution in the upper HRD, more work is needed to understand the mechanisms that regulate the mass-loss rates of OB stars and the physics of fast-rotating stars.
Key words: stars: evolution / stars: early-type / stars: winds, outflows / stars: massive / stars: mass-loss / stars: Wolf-Rayet
Model data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/647/A13
© ESO 2021
1. Introduction
The recent identification of massive black-hole binaries with masses up to 80 M⊙ as powerful sources of gravitational waves (Abbott et al. 2016a,b) opened the first direct view onto the end products of the evolution of the most massive stars. To be able to exploit this new information, it is necessary to model stellar populations that are young enough to contain very massive stars (VMS) with masses ≳100 M⊙. Because of the steep increase in stellar luminosities with increasing mass, VMS in this regime have luminosities well in excess of 106 L⊙. The resulting high L/M ratios ≳104 L⊙/M⊙ bring such VMS close to the Eddington limit, where the radiative acceleration arad equals the gravitational acceleration g.
Due to the resulting low effective surface gravities, VMS are subject to physical effects that impact their outer envelope structure and stellar winds. The envelopes of VMS are predicted to be subject to the envelope inflation effect, which leads to the formation of radially extended low-density envelopes (Ishii et al. 1999; Petrovic et al. 2006). In the limit of low convective efficiency, inflated envelopes become unstable above a specific L/M ratio because of a lack of hydrostatic envelope solutions (Gräfener et al. 2012). This leads to numerical problems in stellar evolution models, which are often tackled by an artificial increase in the convective efficiency (cf. Paxton et al. 2013). As a result, the inflation effect is suppressed in most evolutionary models. Relaxing this assumption leads to the formation of relatively cool stars with inflated envelopes at the top of the main sequence (Gräfener et al. 2012; Köhler et al. 2015; Sanyal et al. 2015).
One key question addressed in this work is whether the existence of the inflation effect can be corroborated by observations. This is particularly interesting because the inflation effect may be related to the still enigmatic group of luminous blue variables (LBVs) and their S-Dor type (radius) variability on timescales of months to years (cf. Gräfener et al. 2012; Grassitelli et al. 2020).
The enhanced mass loss of VMS and its transition from optically thin O-star winds to optically thick Wolf-Rayet (WR) winds have been investigated by numerical wind models (Gräfener & Hamann 2008; Vink et al. 2011) that are supported by systematic empirical studies of samples of VMS (Gräfener et al. 2011; Bestenlehner et al. 2014). Gräfener et al. (2011) pointed out that the underlying reason for the enhanced mass loss of WR stars is their proximity to the Eddington limit, and not their surface chemistry as is usually assumed in stellar evolution models. The enhanced mass loss is the reason why VMS often appear as emission-line stars, namely as hydrogen-rich Wolf-Rayet (WNh) stars, even during their main-sequence evolution (Hamann et al. 2006; Schnurr et al. 2008, 2009; Crowther et al. 2010). Due to the extreme luminosities of such very massive WNh stars, their spectral signatures are detectable in young starbursts even at cosmological distances (Wofford et al. 2014; Gräfener & Vink 2015).
The winds of WNh stars are often confused with those of classical WR stars. Classical WR stars are massive stars near the end of their evolution, predominantly in the phase of core He-burning. These stars lost their hydrogen-rich envelopes during their previous evolution and have much lower masses. They reach high Eddington factors due to the high luminosity of their He-burning cores. Classical WR stars have different physical and wind properties than the more massive core hydrogen-burning WNh stars, but they are usually treated with the same mass-loss prescriptions in evolutionary models.
In this work, we construct evolutionary models that take the enhanced mass-loss rates and the envelope inflation of VMS into account. We compute model grids for massive main-sequence stars up to 500 M⊙ and compare the results with the most massive stars in the VLT-Flames Tarantula Survey (VFTS), the largest and best studied sample of VMS obtained to date (Evans et al. 2011). The VFTS is a near-complete spectroscopic survey of ≈1000 hot luminous stars in 30 Dor in the Large Magellanic Cloud (LMC), the closest analogue of a young starburst in our neighbourhood, with a well-controlled brightness cut-off. All single stars in the VFTS sample have been analysed individually, and their star-formation histories (SFHs) and rotational-velocity distributions have been investigated in detail (Schneider et al. 2018a,b; Ramírez-Agudelo et al. 2013; Dufton et al. 2013). This makes the sample an ideal target for detailed population synthesis modelling, enabling quantitative predictions of the expected numbers of stars in specific evolutionary phases.
We describe our evolutionary models in Sect. 2 and the population synthesis in Sect. 3. In Sect. 4 we compare our models with the observed population of VMS in 30 Dor, and in Sect. 5 we discuss the results. The most important conclusions are summarised in Sect. 6.
2. Stellar evolution models
We use the Modules for Experiments in Stellar Astrophysics (MESA) version 11701 (Paxton et al. 2011, 2013, 2015, 2018, 2019) to compute single-star evolutionary models covering the main-sequence phase from zero to 99% hydrogen exhaustion in the stellar core. The same input physics as in Schootemeijer & Langer (2018), Schootemeijer et al. (2019) are used, except for the treatment of convection in the outer stellar envelope and stellar-wind mass loss (see below). In particular, we adopt a wind-scaling as a function of XFe/XFe, ⊙, as described by Schootemeijer et al. (2019) We use the MESA default chemical composition from Grevesse & Sauval (1998) scaled to an initial metallicity of Z = 0.008 (compared to the corresponding solar metallicity of Z⊙ = 0.0169) to match the metallicity, and in particular XFe, in the LMC.
Because of our interest in the envelope inflation effect we employ standard mixing-length theory (MLT) instead of the modified treatment of superadiabatic convection in radiation-dominated regions (MLT++, Paxton et al. 2013) that is used by default in MESA models. Furthermore, we introduce a new treatment of stellar-wind mass loss to meet the requirements for VMS near the Eddington limit. In the following sections these new mass-loss relations are described.
2.1. The winds of OB stars
The most widely used mass-loss prescription for OB stars is the relation by Vink et al. (2000, 2001). These theoretical mass-loss estimates are based on a Monte-Carlo approach that makes use of the first-order Sobolev approximation. In the Sobolev approximation spectral lines are assumed to be infinitely narrow, but their flux-mean opacity is high due to the effective line broadening through Doppler shifts in the wind. Consequently, the radiative acceleration depends predominantly on the velocity gradient ∂v/∂r, leading to the same wind physics as in Castor et al. (1975, CAK) who described the first closed theory for the formation of optically thin OB-star winds.
Notably, the Sobolev approximation does not apply in the limit of large wind optical depths where the photon mean-free path becomes small, and Doppler shifts become inefficient (cf. the discussion in Gräfener et al. 2017). In this work we therefore only apply the Vink et al. (2001) relation in the optically thin regime. Furthermore, we change the absolute value and the slope of Ṁ as a function of luminosity L, to match the average observed mass-loss rates of O stars in 30 Dor as in Bestenlehner et al. (2014).
For the absolute calibration of our mass-loss relations with empirical results in Sect. 4.2 we adopt a wind clumping factor of D = 10. This means that we assume that the wind consists of dense clumps with a density that is a factor D higher than the mean density, while the inter-clump medium is void. Clumping constitutes the main uncertainty in the empirical mass-loss rates of OB and WR stars. It increases the line strengths of recombination lines, and therefore reduces the empirical mass-loss rates derived from this type of lines by a factor 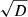 (Hillier 1991; Hamann & Koesterke 1998).
(Hillier 1991; Hamann & Koesterke 1998).
For the most massive O and WNh stars in 30 Dor Bestenlehner et al. (2014) found clumping factors of the order of D = 10, based on the relative strengths of the electron-scattering wings of strong recombination lines (cf. also Vink & Gräfener 2012). For O stars with weaker winds even higher clumping factors up to D ≈ 100 have been discussed, based on the strength of non-saturated UV resonance lines (Fullerton et al. 2006). However, considering the influence of optically thick clumps on the UV line profiles Oskinova et al. (2007), Sundqvist et al. (2014) derived more moderate values of the order of 10. Here we adopt D = 10 for all stars in our sample, resulting in a reduction of the empirical mass-loss rates by a factor of 3.3 compared to un-clumped winds.
Our comparison with observations in Sect. 4.2 leads to a considerable reduction of O-star mass-loss rates, and a shallower slope as a function of L. For the slope we adopt the value of 1.45 derived by Bestenlehner et al. (2014) and replace it in Eq. (24) of Vink et al. (2001) instead of the original value of 2.194. This substitution already lowers the mass-loss rates in the VFTS O-star range considerably. To match the observations, we further apply a constant factor of 0.8 to the altered mass-loss relation. For the dependence of Ṁ on the rotational velocity, we use the standard relation implemented in MESA (Eq. (26) in Paxton et al. 2013).
2.2. The winds of WNh stars
The most massive and luminous main-sequence stars are thought to appear spectroscopically as WNh stars (Gräfener & Hamann 2008; Crowther et al. 2010). WNh stars are therefore the extension of the O-star regime towards higher masses and luminosities. Previous implementations of wind mass loss in stellar evolution models do not take the transition from the optically thin winds of OB stars to the optically thick winds of WNh stars into account. Instead, they extrapolate the Vink et al. (2000) relations to higher luminosities. Only when the surface composition becomes substantially deficient in hydrogen, the mass-loss relations switch to WR type mass loss, where no distinction between the mass loss of very massive WNh stars, and the mass loss of classical core He-burning WR stars is made. For instance, in the default ‘DUTCH’ MESA wind-scheme the empirical mass-loss relation from Nugis & Lamers (2000) is used for hot stars (Teff > 10 kK) with hydrogen surface mass fractions Xs < 0.4, otherwise the Vink et al. (2000) relations are used.
In this work we follow previous theoretical (Gräfener & Hamann 2008; Vink et al. 2011) and empirical (Gräfener et al. 2011; Bestenlehner et al. 2014) studies of the mass-loss properties of VMS that suggest that the proximity to the Eddington limit determines the formation of optically thick WR-type winds. According to these studies WR-type winds show a distinct, strong dependence on the proximity to the Eddington limit, which is most easily expressed via a dependence on the classical Eddington factor
Here we define Γe as the ratio between the radiative acceleration on free electrons (with the electron-scattering opacity χe for a fully ionised plasma) and the gravitational acceleration of the star. Because χe depends only on the number of free electrons per gram, Γe depends only on fundamental stellar parameters, namely the hydrogen surface abundance Xs and the L/M ratio. In this picture the mass loss of VMS, which are still in the core hydrogen-burning phase, differs from the mass loss of classical core He-burning WR stars because of their different L/M ratios, effective temperatures, and chemical compositions.
In the following we concentrate on VMS at LMC metallicity. We employ the empirical mass-loss relation for VMS in 30 Dor from Bestenlehner et al. (2014) who derived a relation of the form
for the optically thick winds of WNh stars. Here D denotes the wind clumping factor (cf. Sect. 4.2), and Γeff the effective Eddington factor including centrifugal acceleration (cf. the discussions in Gräfener & Hamann 2008; Gräfener & Vink 2015). As Γeff varies over the stellar surface, we use an intermediate value that lies between the value at the poles, where the centrifugal acceleration is zero, and the equator, where grot = Ω2R:
As a result, our mass-loss prescription is sensitive to a combination of the proximity to the Eddington limit and the critical rotation rate similar to the ΓΩ-limit discussed by Maeder & Meynet (2000), Langer (1997).
As a criterion to switch between the regimes of WR-type winds and optically thin OB-star winds, we evaluate their sonic-point optical depth τs. This approach is motivated by the theory of optically thick winds, where the properties of winds with large τs are largely constrained by the conditions at the sonic point and τs itself (Nugis & Lamers 2002; Gräfener et al. 2017). As described in Sect. 2.1, the different wind physics for the optically thin winds of OB stars (with small values of τs) leads to lower mass-loss rates.
To decide whether a stellar model with given surface values of M, L, R, Ω, and Xs can develop a WR-type wind, we estimate the value of τs that its wind would have if it had an optically thick wind. To this purpose we compute Ṁthick from Eq. (2) and estimate the terminal wind velocity v∞ using the empirical relation from Lamers et al. (1995) with 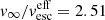 (cf. also Bestenlehner et al. 2014). For given Ṁ and v∞ we estimate τs using a relation between τs and the wind efficiency factor η ≡ Ṁv∞/(L/c) from Gräfener et al. (2017). η denotes the ratio between the mechanical wind momentum and the momentum of the radiation field driving the wind. It is related to τs via the number of absorption and re-emission processes needed to drive the wind. Gräfener et al. (2017) derived an approximate relation of the form
(cf. also Bestenlehner et al. 2014). For given Ṁ and v∞ we estimate τs using a relation between τs and the wind efficiency factor η ≡ Ṁv∞/(L/c) from Gräfener et al. (2017). η denotes the ratio between the mechanical wind momentum and the momentum of the radiation field driving the wind. It is related to τs via the number of absorption and re-emission processes needed to drive the wind. Gräfener et al. (2017) derived an approximate relation of the form
In our models we use τs from Eq. (4) as a criterion for the onset of WR-type mass loss. For cases where τs < τ1 we use the mass-loss prescriptions for optically thin winds from Sect. 2.1, and for τs > τ2 we use the Γ-dependent mass-loss relation Eq. (2). For τ1 < τs < τ2 we interpolate between both cases. As demonstrated in Sect. 3 we can reproduce the observed mass-loss rates for VMS in 30 Dor from Bestenlehner et al. (2014) very well with values of τ1 = 2/3 and τ2 = 1.
3. Population synthesis models
In this section we describe the population synthesis models that we use to compare the models from Sect. 2 with observations.
3.1. Stellar evolution models
Each of our population synthesis models is based on a set of stellar evolution models for massive stars with initial masses in the range of 9−500 M⊙ and initial rotational velocities between 0 and 90% of the critical rotation rate. Typically, each model grid consists of models with 18 different masses and 11 different rotational velocities, that is, a total of 198 models. As start models we use rotating, chemically homogeneous models in thermal equilibrium, with a default initial composition with Z = 0.008 (cf. Sect. 2). The models cover the main-sequence phase up to 99% hydrogen exhaustion.
3.2. Population synthesis
The goal of our population synthesis models is to compute the fraction of stars in a specific stellar population that show one or more observables o in a given parameter range oi. The population is defined through a given initial mass function 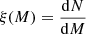 , initial rotational velocity distribution
, initial rotational velocity distribution 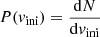 , the SFH
, the SFH 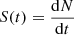 , and the total number of stars N.
, and the total number of stars N.
Our models provide stellar parameters p as a function of time t for each evolutionary track with a given initial mass M and initial fraction of the critical rotation rate ω ≡ Ω/Ωcrit. We further determine the main-sequence lifetime TMS for each evolutionary track and define the relative age tr ≡ t/TMS, so that the p are given as a function of the form p(tr, M, ω) on the model grid. To compute the oi we transform the p(tr, M, ω) onto a homogeneous grid that is logarithmic in M and linear in ω and tr, through linear interpolation between evolutionary tracks. In this step we typically use 100 grid points in M and tr, and 64 grid points in ω, where tr lies between 0 and 1, M between 9 and 500 M⊙, and ω between 0 and 0.9. Based on the p(tr, M, ω) we then compute any observable o(tr, M, ω) of interest on the same grid.
To compute the probability distribution of the different oi for the adopted stellar population we need to compute a weight function W(tr, M, ω) that takes S(t) and the initial distributions of M and ω into account. The probability Pi to find an observable o in a given parameter range oi is then
where the summation is a sum over all grid points, and the weight W(tr, M, ω) takes the initial distribution of M and ω and the sampling of tr, M and ω into account. We write W(tr, M, ω) in the form
and compute Wt, WM and Wω in the following way.
As we use linear time steps Δtr, Wt is given by the product of S(t) and the derivative dt/dtr = TMS
with t = tr × TMS(M, ω).
For M we use a logarithmic grid with dM/dlog(M) = M, and adopt an initial mass function ξ(M) ∝ M−γ, so that
For ω we use a linear grid, but the initial rotational distribution P(vini) is given as a function of the rotational velocity, so that
Here we compute dvini/dω numerically, where we define vini(M, ω) ≡ vrot(tr = 0.01, M, ω) to avoid problems due to the rapid adjustment phase of the internal rotation profile at the start of each evolutionary sequence.
4. Very massive stars in 30 Dor
In this section we compare the results of our population synthesis with the empirically derived properties of the stellar population in 30 Dor. The empirical data consist of the sub-sample of single main-sequence stars from the VFTS as compiled by Schneider et al. (2018a). In particular, the empirical data are based on detailed spectroscopic analyses of the most massive stars in 30 Dor from Bestenlehner et al. (2014), O-type giants and supergiants from Ramírez-Agudelo et al. (2017), O-type dwarfs from Sabín-Sanjulián et al. (2017), B-type supergiants from McEvoy et al. (2015) and B dwarfs from Schneider et al. (2018a).
For the population synthesis we used the SFH S(t) and initial mass function (IMF) ξ(M) for 30 Dor from Schneider et al. (2018a), together with the rotational velocity distribution P(v) for single O stars from Ramírez-Agudelo et al. (2013). Analogous to the work of Schneider et al. (2018a) the present work thus focuses on single stars with a luminosity ≳104.5 L⊙, well above the VFTS brightness cut-off. This means that only stars with masses ≳15 M⊙ and ages ≲12 Myr are considered in the present analysis.
We further employed evolutionary models for single stars as described in Sect. 2, tailored to match the empirical properties of the massive single-star population in 30 Dor. Because of our focus on the physics of VMS these models are designated as VMS models. We compare these models with empirical data from VFTS and models based on alternative input physics and/or common standard assumptions.
4.1. Mass distribution
An important input parameter for our population synthesis models is the exponent γ of the IMF with ξ(M) ∝ M−γ. In Fig. 1 we compare the present-day luminosity distribution resulting from our population synthesis with the observed distribution in the VFTS sample. In this plot we normalised the synthetic distribution to match the total number of 288 observed, putatively single stars above log(L/L⊙) = 4.5. We further adjusted γ to match the number of 20 observed VMS in the range 6.0 < log(L/L⊙) < 6.6 (roughly corresponding to a mass range of 70−200 M⊙). For our VMS models this was achieved using a value of γ = 1.977, slightly higher than the value of 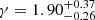 derived by Schneider et al. (2018a). Using alternative models employing the DUTCH MESA wind scheme (cf. Sect. 2.2) we obtain γ = 1.935, in agreement with Schneider et al. (2018a). Altogether our models confirm a top-heavy IMF in comparison to the standard Salpeter (1955) IMF with γ = 2.35, but with a moderate impact of the adopted mass-loss prescription on the present stellar masses and therefore on γ. In the remainder of this work, we use γ = 1.977 to achieve consistency between our models and observations.
derived by Schneider et al. (2018a). Using alternative models employing the DUTCH MESA wind scheme (cf. Sect. 2.2) we obtain γ = 1.935, in agreement with Schneider et al. (2018a). Altogether our models confirm a top-heavy IMF in comparison to the standard Salpeter (1955) IMF with γ = 2.35, but with a moderate impact of the adopted mass-loss prescription on the present stellar masses and therefore on γ. In the remainder of this work, we use γ = 1.977 to achieve consistency between our models and observations.
 |
Fig. 1. Observed luminosity distribution of single stars in 30 Dor compared to theoretical predictions. The histogram shows the observed numbers of single stars in the VFTS sample as function of luminosity (blue) compared to the theoretical distribution resulting from our VMS population synthesis models described in Sect. 4 (green). Both distributions are plotted transparent so that overlaps appear in dark green. |
Notably, there are no stars with luminosities higher than log(L/L⊙) = 6.6 in the VFTS sample while our VMS models predict 4.7 stars above this luminosity. This upper luminosity limit corresponds to an upper initial-mass limit of Mini ≈ 200 M⊙. We will discuss the relevance of this upper mass limit in Sect. 5.2. For the investigation of the physical properties of VMS in the remainder of this work, we consider the consistency between observed and predicted stellar numbers below 200 M⊙ as satisfactory.
4.2. Mass-loss rates
To test the validity of the mass-loss prescriptions employed in our models we compare the mass-loss relations resulting from our population synthesis models directly with empirical data. In Figs. 2 and 3 the resulting modified wind momenta 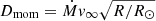 are shown as a function of luminosity L. According to the CAK theory for optically thin winds, OB stars are expected to follow a tight wind-momentum luminosity relation (WLR; Kudritzki et al. 1999), largely independent of secondary parameters, such as mass or radius.
are shown as a function of luminosity L. According to the CAK theory for optically thin winds, OB stars are expected to follow a tight wind-momentum luminosity relation (WLR; Kudritzki et al. 1999), largely independent of secondary parameters, such as mass or radius.
 |
Fig. 2. Wind-momentum – luminosity relation for O and WNh stars in 30 Dor. Different symbols indicate empirical results for the most massive stars in 30 Dor from Bestenlehner et al. (2014) in blue, O-type giants and supergiants from Ramírez-Agudelo et al. (2017) Tables C.4 (dark green) and C.5 (light green), and O-type dwarfs from Sabín-Sanjulián et al. (2017) Tables A.1 (red) and A.2 (pink). Upper limits are indicated in grey. Evolutionary tracks are indicated by coloured lines analogous to Fig. 5 but restricted to the O star range. Predicted absolute numbers of stars according to our population synthesis models are mapped and colour coded as indicated by the colour bar on the right. |
 |
Fig. 3. Wind-momentum – luminosity relation as in Fig. 2 compared with population synthesis models based on standard MESA models using the DUTCH wind scheme. |
In Figs. 2 and 3, we indicate the expected numbers of stars in this diagram according to our population synthesis models by colour maps. The synthetic Dmom were computed based on mass-loss rates Ṁ, radii R and stellar masses M from the underlying stellar evolution models. The v∞ were computed from the resulting effective escape velocities using a ratio of 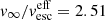 as described in Sect. 2.2. The empirical wind momenta were compiled from Ramírez-Agudelo et al. (2017), Sabín-Sanjulián et al. (2017), Bestenlehner et al. (2014) and cover the complete sample of single O and WNh stars in the VFTS, meaning that they include all apparently single main-sequence stars with effective temperatures > 29 kK. The same temperature cut-off has been applied to the theoretical results.
as described in Sect. 2.2. The empirical wind momenta were compiled from Ramírez-Agudelo et al. (2017), Sabín-Sanjulián et al. (2017), Bestenlehner et al. (2014) and cover the complete sample of single O and WNh stars in the VFTS, meaning that they include all apparently single main-sequence stars with effective temperatures > 29 kK. The same temperature cut-off has been applied to the theoretical results.
Our VMS models in Fig. 2 show a good agreement with observations. In particular, the location of the transition from O-star winds to the enhanced mass loss in the WNh phase is reproduced well. On the other hand, the WLR resulting from the oft-used DUTCH wind scheme in Fig. 3 matches the WNh stars well, but over-estimates the mass-loss rates of the O stars in the VFTS sample. Also, the slope of the WLR appears to be too steep in the O-star range. For both wind schemes it is noticeable that the synthetic WLRs are much narrower than the observed one. In particular for O stars the observed WLR shows a large spread in Dmom, where dwarfs tend to have lower wind momenta than giants and supergiants by up to a factor of ten. As we will show later, this may hint on substantially reduced mass-loss rates for younger O stars.
A novelty in our VMS models is the treatment of the transition between the regimes of optically thin O-star winds and optically thick WNh winds. This transition occurs qualitatively differently in the VMS and DUTCH approaches. In the VMS wind scheme in Fig. 2 stars with luminosities above log(L/L⊙) ≈ 5.5 reach high enough Eddington factors at some point during their main-sequence evolution to perform a quick transition to enhanced WR-type mass-loss rates. In the WNh regime the evolution then proceeds at nearly constant luminosity (cf. Fig. 5). On the other hand, the DUTCH models in Fig. 3 show no marked transition between the two regimes but change their behaviour at some point during the WNh stage, when they reach a helium surface mass fraction of Ys = 0.4. Before this point they evolve continuously with increasing luminosity from the O-star regime into the WNh stage. After they reached Ys = 0.4 their mass-loss rates increase, and their evolution continues with decreasing luminosity.
As noted earlier, the absolute mass-loss rates in the WNh range are reproduced well by both mass-loss prescriptions. One notable outlier in Figs. 2 and 3 is VFTS 108, which has a WR-type mass-loss rate despite of its low luminosity of log(L/L⊙) = 5.7. This star is highly enriched in helium (Ys ≈ 0.8) and most likely already in the core helium-burning phase. Bestenlehner et al. (2014) demonstrated that this star matches the adopted Ṁ(Γeff) relation (Eq. (2)) precisely, if a lower mass, corresponding to the core helium-burning case, is adopted.
In Fig. 4 we put the Γe-dependent mass-loss prescription (Eq. (2)) in our VMS models to a direct test. As Γe is not directly observable, we estimate the Eddington factor 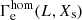 for the chemically homogeneous case instead, where we compute
for the chemically homogeneous case instead, where we compute 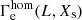 from Eq. (1) using the mass estimate Mhom(L, Xs) for a chemically homogeneous star from Gräfener et al. (2011). Notably,
from Eq. (1) using the mass estimate Mhom(L, Xs) for a chemically homogeneous star from Gräfener et al. (2011). Notably, 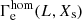 depends only on observable quantities. In reality, most stars are of course not chemically homogeneous, but have a chemical profile with an increasing mean molecular weight towards their centre. For fixed values of M and Xs this results in a higher luminosity than for a chemically homogeneous star. The other way round, for given L and Xs, Mhom(L, Xs) constitutes a strict upper limit to the real mass of a star, and
depends only on observable quantities. In reality, most stars are of course not chemically homogeneous, but have a chemical profile with an increasing mean molecular weight towards their centre. For fixed values of M and Xs this results in a higher luminosity than for a chemically homogeneous star. The other way round, for given L and Xs, Mhom(L, Xs) constitutes a strict upper limit to the real mass of a star, and 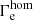 a lower limit to Γe.
a lower limit to Γe.
 |
Fig. 4. Mass loss as a function of Eddington factor. Mass-loss rates Ṁ as a function of the estimated classical Eddington factor for chemically homogeneous stars |
In Fig. 4 we plot the synthetic and observed mass-loss rates Ṁ for our O/WNh sample as a function of 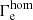 . To allow for a direct comparison between theory and observations, the
. To allow for a direct comparison between theory and observations, the 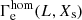 are computed in an identical manner for models and observations. Analogous to the WLR in Fig. 2 the theoretical mass-loss rates increase rapidly as soon as the formation of optically thick winds becomes possible. The transition between O and WR-type winds happens at
are computed in an identical manner for models and observations. Analogous to the WLR in Fig. 2 the theoretical mass-loss rates increase rapidly as soon as the formation of optically thick winds becomes possible. The transition between O and WR-type winds happens at 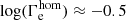 and continues with a steeper slope for high
and continues with a steeper slope for high 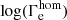 , in good agreement with the observations. As our Γe-dependent mass-loss prescription (Eq. (2)) was initially derived from the same data under the assumption that
, in good agreement with the observations. As our Γe-dependent mass-loss prescription (Eq. (2)) was initially derived from the same data under the assumption that 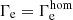 (cf. Bestenlehner et al. 2014) this can be seen as a confirmation that most WNh stars in our sample are in fact evolving chemically homogeneously.
(cf. Bestenlehner et al. 2014) this can be seen as a confirmation that most WNh stars in our sample are in fact evolving chemically homogeneously.
Again, the overall agreement between models and observations in the WNh stage (with log(Ṁ/M⊙ yr−1) ≳ − 5.2) is very good, except for a short phase directly after the transition. In this short phase the surface is still more hydrogen-enriched than the stellar core, and thus 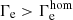 . However, as soon as the enhanced mass loss in the WNh phase sets in, the H-rich surface layers are quickly removed, and the stars become nearly chemically homogeneous.
. However, as soon as the enhanced mass loss in the WNh phase sets in, the H-rich surface layers are quickly removed, and the stars become nearly chemically homogeneous.
While the O-star mass-loss rates in Fig. 4 (with log(Ṁ/M⊙ yr−1) ≲ − 5.2) show a good agreement with observations for 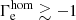 , the agreement gets worse for lower values of
, the agreement gets worse for lower values of 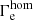 . For the O dwarfs in this regime Sabín-Sanjulián et al. (2017) derived upper limits for Ṁ which are indicated in grey. For O (super)giants Ramírez-Agudelo et al. (2017) provided explicit values for Ṁ that tend to be higher than those in our models. Notably, Ramírez-Agudelo et al. (2017) did not provide absolute values for Dmom for the same objects (cf. Figs. 2 and 3) because they considered the results as uncertain (H. Sana and A. de Koter, priv. comm.). Depending on whether the mass-loss rates in this parameter range can be believed or not the differences between O dwarfs and (super)giants, which were already apparent in Fig. 2, may be even more pronounced for these objects. This is further supported by recent results of Bestenlehner (2020, 2020) who investigated the mass-loss properties of the most massive stars in the R 136 cluster in the centre of 30 Dor. These authors determined a very young age of 1−2 Myr for R 136 and derived an Ṁ(Γe) relation that lies up to two orders of magnitude below the values derived for O stars the VFTS sample as indicated by the dashed curve in Fig. 4.
. For the O dwarfs in this regime Sabín-Sanjulián et al. (2017) derived upper limits for Ṁ which are indicated in grey. For O (super)giants Ramírez-Agudelo et al. (2017) provided explicit values for Ṁ that tend to be higher than those in our models. Notably, Ramírez-Agudelo et al. (2017) did not provide absolute values for Dmom for the same objects (cf. Figs. 2 and 3) because they considered the results as uncertain (H. Sana and A. de Koter, priv. comm.). Depending on whether the mass-loss rates in this parameter range can be believed or not the differences between O dwarfs and (super)giants, which were already apparent in Fig. 2, may be even more pronounced for these objects. This is further supported by recent results of Bestenlehner (2020, 2020) who investigated the mass-loss properties of the most massive stars in the R 136 cluster in the centre of 30 Dor. These authors determined a very young age of 1−2 Myr for R 136 and derived an Ṁ(Γe) relation that lies up to two orders of magnitude below the values derived for O stars the VFTS sample as indicated by the dashed curve in Fig. 4.
4.3. Location in the Hertzsprung-Russell diagram
In Fig. 5 we show the theoretical HRD for 30 Dor including a colour-coded map of the expected numbers of stars according to our population synthesis models. For comparison, we show the observed HRD in Fig. 6 with the observed number of stars colour-coded in the same way. Generally, the observed HRD positions of stars above log(L/L⊙) ≈ 5 are well reproduced by our VMS models. The lack of evolved stars below this luminosity in Fig. 5 is caused by the maximum age of 12 Myr adopted in our population synthesis models. Beyond this, our VMS models reproduce the observed bending of the zero-age main sequence (ZAMS) for the highest masses as well as the lack of stars with cooler temperatures than log(Teff/K) ≈ 4.5 above log(L/L⊙) ≈ 6 very well.
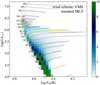 |
Fig. 5. Theoretical HRD for VMS models with standard MLT. Coloured areas indicate the expected number of stars according to our population synthesis models for 30 Dor (cf. Sect. 4). Evolutionary tracks for Ω/Ωcrit = 0.3 are indicated, labelled with ZAMS masses in M⊙. |
 |
Fig. 6. Observed HRD for 30 Dor. Coloured areas indicate the observed number of stars, evolutionary tracks are the same as in Fig. 5. |
The bending of the ZAMS towards cooler temperatures at the top of the main sequence is a consequence of the envelope inflation effect. This is demonstrated in Fig. 7, where the inflation effect has been suppressed by artificially increasing the convective efficiency in radiation-dominated stellar envelopes (MESA option okay_to_reduce_gradT_excess = .true.). As a consequence, the most massive stars above ≈80 M⊙ become much hotter and evolve towards even hotter temperatures during their main-sequence evolution. The reason is that stars in this regime become chemically homogeneous and therefore more and more compact throughout their evolution. Only when standard MLT is used (Fig. 5) does the inflation effect compensates this effect and brings the effective temperatures of stars in this mass range into agreement with observations.
 |
Fig. 7. Influence of envelope inflation. The theoretical HRD for models with reduced envelope inflation effect through an artificially enhanced convective efficiency (MLT++; MESA option okay_to_reduce_gradT_excess = .true.) is indicated analogous to Fig. 5. |
In Figs. 8 and 9 we focus on the distribution of stars in the upper HRD, relative to the ZAMS. To demonstrate how the predicted HRD positions depend on mass loss, we show models with alternative mass-loss prescriptions in Figs. 10 and 11. In Fig. 10 the onset of the enhanced mass loss of WNh stars has been completely omitted while otherwise the same wind scheme as in our VMS models was used. Consequently, the mass loss of the most massive stars is reduced, and the outer H-rich layers are removed much more slowly, leading to higher hydrogen surface mass fractions Xs and therefore higher values of Γe (cf. Eq. (1)). Due to the strong dependence of the inflation effect on Γe (cf. Gräfener et al. 2012, Eqs. (20), (28), and (29)), this leads to an enhanced envelope inflation and correspondingly cooler stellar temperatures.
 |
Fig. 8. Effective temperature distribution. The theoretical HRD for the upper main sequence is indicated analogous to Fig. 5 but as a function of the effective temperature relative to the ZAMS temperature. |
 |
Fig. 10. Influence of mass loss. The theoretical HRD is indicated analogous to Fig. 8 but adopting a pure OB-type mass-loss prescription without enhanced Γ-dependent mass loss. |
The models in Fig. 11 are computed using the standard DUTCH wind scheme with much higher mass-loss rates than our VMS models. Because of the higher mass loss the most massive stars become more compact and less massive, and therefore hotter and less luminous. The qualitatively correct reproduction of the observed HRD positions of the most massive stars with log(L/L⊙) ≳ 6 by our VMS models can therefore be seen as an indirect confirmation of our new mass-loss prescription, and in particular of the adopted clumping factor D in Eq. (2).
 |
Fig. 11. Influence of mass loss. The theoretical HRD is indicated analogous to Fig. 8 but adopting the DUTCH MESA wind scheme. |
For stars with log(L/L⊙) ≲ 6, our models predict very extended envelopes and correspondingly cool stellar temperatures towards the end of the main-sequence evolution, irrespective of the mixing approach (cf. Figs. 5 and 7). In the observed HRD (Fig. 9) this region is populated by B supergiants whose evolutionary origin is still unclear (e.g., Vink et al. 2010; McEvoy et al. 2015). In Fig. 9 there are only a few objects of this type that are clearly located in the Hertzsprung-gap, that is, outside the expected parameter range for main-sequence stars.
To quantify the contribution of the envelope inflation effect, we compare in Fig. 12 the distribution of stars between 5 < log(L/L⊙) < 6 as a function of their distance from the ZAMS (log(Teff/TZAMS)) with observations. Our models predict 22.4 stars with log(Teff/TZAMS) < − 0.2 compared to 30 stars that are observed. This means that we expect the majority of stars in this regime to be evolved main-sequence stars with inflated envelopes. Setting the maximum effective temperature for stars to be classified as B-type stars to 29 kK, we predict 22.4 stars in this phase to appear as B supergiants, while 34 stars are observed. Again, according to our models the majority of B supergiants between 5 < log(L/L⊙) < 6 are evolved main-sequence stars.
 |
Fig. 12. Effective temperature distribution. Histogram of the observed numbers of single stars in the VFTS sample with 5 < log(L/L⊙) < 6 as a function of their distance from the ZAMS (log(Teff/TZAMS)) (transparent blue) compared with the theoretical distribution from our VMS population synthesis models (transparent green). |
While the overall agreement between theory and observation in Fig. 12 appears satisfactory, it is notable that there is a small systematic shift in Teff/TZAMS between the observed and predicted median locations of the main sequence, by 0.025 dex. In principle, this could be an indication that the predicted core masses in our models are too small, similar to what has been claimed, for instance, by Tkachenko et al. (2020). For this reason, we varied the overshooting parameter analogous to Tkachenko et al. (2020) as well as the parameters for rotational mixing in our models but did not achieve a satisfactory agreement between theory and observations. Also, the relatively high oxygen abundance in our models (based on the solar composition from Grevesse & Sauval 1998) does already bring our models towards slightly lower effective temperatures than what would result from more recent estimates (such as Asplund et al. 2009). Therefore, it remains unclear whether the observed shift between theory and observations is due to deficiencies in our models or systematic errors in the spectroscopic analyses of the VFTS sample.
4.4. Helium surface enrichment
In Fig. 13, we show a comparison between the observed and predicted helium surface mass fractions Ys for stars with Teff > 29 kK, that is, for O stars and WNh stars in the VFTS, as a function of their estimated inverse mass-loss timescale Ṁ/Mhom. Again, for a meaningful comparison between models and observations, the mass estimate Mhom(L, X) from Gräfener et al. (2011) has been computed in an identical manner for models and observations.
 |
Fig. 13. Helium surface enrichment through mass loss. The predicted helium surface mass fraction Ys, as a function of the estimated inverse mass-loss timescale Ṁ/Mhom for stars with Teff > 30 kK and log(L/L⊙) > 5, is compared with VFTS O and WNh stars labelled as in Fig. 2. The colour scale indicates the number of objects predicted by our population synthesis. Evolutionary tracks from Fig. 5 are indicated by coloured lines. |
Our population synthesis models show two regions with substantially enhanced values of Ys in Fig. 13. The WNh stars with log Ṁ/Mhom ≳ − 7.5 follow a clear trend of increasing Ys with increasing Ṁ/Mhom (cf. also Bestenlehner et al. 2014, 2020). The reason is that the enhanced mass loss in the WNh regime efficiently removes the hydrogen-rich outer layers, leading to quasi chemically homogeneous evolution with a strong dependence of Ṁ on Γe, and therefore on Ys.
In the O-star range, with lower values of Ṁ/Mhom, our models predict substantial He enrichment for initially fast-rotating stars. This is demonstrated in Fig. 14 where we show the He enrichment for O stars with 5 < log(L/L⊙) < 5.9 (that is, excluding WNh stars) as a function of rotational velocity. According to our models, fast-rotating stars in this regime develop strong winds due to their proximity to the ΓΩ-limit. This leads to a phase of enhanced mass loss that removes angular momentum until the rotational velocity falls below a value of typically 300 km s−1. As a consequence, there is a peak in the rotational velocity distribution for O stars at vrot ≈ 300 km s−1 (cf. the orange step function in Fig. 14). Notably, Ramírez-Agudelo et al. (2013) found a similar feature in the observed rotational velocity distribution of the VFTS O star sample, however, at a higher velocity of ≈400 km s−1.
 |
Fig. 14. Helium surface enrichment through rotation. The predicted helium surface mass fraction Ys, as a function of rotational velocity for O stars with Teff > 29 kK and 5.0 < log(L/L⊙) < 5.9, is compared with observed Ys and v sin i of He-enriched VFTS O stars (with Ys > 0.35) labelled as in Fig. 2; stars with log(L/L⊙) < 5.0 are plotted in grey. The colour scale indicates the number of objects predicted by our population synthesis models. Evolutionary tracks for an initial mass of 30 M⊙ are indicated by coloured lines. Step functions indicate the initial (blue) and present (orange) total number distributions in arbitrary units, as well as the present distribution of He-enriched stars with Ys > 0.35 (red). |
According to our models, the rotational braking associated with this process induces substantial mixing of helium-rich material to the surface, with a maximum in the number distribution of He-enriched stars at ≈300 km s−1 (cf. the red step function in Fig. 14). The same objects constitute the group of helium-enriched stars with log Ṁ/Mhom ≲ − 7.5 in Fig. 13. According to our models, we expect 14.6 O stars with Ys > 0.35 in the luminosity range 5.0 < log(L/L⊙) < 5.9 in the VFTS sample that have been enriched by rotational mixing. This compares to seven observed objects in the same regime, which are indicated by coloured symbols in Fig. 14. For lower luminosities, we expect 0.7 objects, compared to five observed objects, which are indicated by grey symbols in Fig. 14.
Notably, VFTS 285, the star with the highest value of v sin i = 600 km s−1 in our sample and Ys = 0.36 belongs to the group of low-luminosity stars for which no He-enhancement is predicted (VFTS 285 is not visible in Fig. 14). In both, the high- and low-luminosity regime, we expect the vast majority of He-enriched objects near a rotational velocity of ≈300 km s−1. Due to the effect of random inclination angles the expected average value of v sin i is π/4 (cf. Brott et al. 2011), with a decreasing distribution function for small values of sin i. We therefore expect the distribution of He-enriched stars to peak near 235 km s−1, while the observed v sin i distribution appears evenly distributed, with a potential peak near 100 km s−1. This means that neither the predicted numbers of rotationally enriched stars, nor their distribution agrees with observations. The implementation of rotational mixing and/or rotationally induced mass loss in our models therefore seems to leave space for improvements (cf. the discussion in Sect. 5.4).
5. Discussion
In the following we discuss the implications of our results for the physics and evolution of the most massive stars (Sect. 5.1), their upper mass limit (Sect. 5.2), the evolution of OB stars (Sect. 5.3), and the mechanisms for surface He-enrichment in the upper HRD (Sect. 5.4).
5.1. WNh stars: The most massive stars
According to our analysis, at LMC metallicity, stars in excess of ≈80 M⊙ enter the WNh stage at some point during their main-sequence evolution. This means that they reach high enough Eddington factors to initiate optically thick winds, so that they appear as WR-type emission-line stars. Because they still have hydrogen on their surface, they are traditionally classified as H-rich WN stars, or WNh stars. As shown in Sect. 4.2, the absolute mass-loss rates, as well as the onset of WR-type mass loss in this regime, are well described by our VMS models employing a Γe-dependent mass-loss relation.
Because of their enhanced mass loss, the outer radiative layers of WNh stars are quickly removed so that they develop a quasi chemically homogeneous structure, with hydrogen surface abundances starting at near-solar values and almost reaching hydrogen depletion at the end of their main-sequence evolution. This is in stark contrast to the traditional treatment of WR-type mass loss in stellar evolution models, where enhanced mass loss only sets in beyond a limit of Ys > 0.4. In Sect. 4.4, we showed that our VMS models describe the resulting He-enrichment through the enhanced mass loss in the WNh stage well, in good agreement with observations.
Because of their proximity to the Eddington limit, WNh stars are subject to the envelope inflation effect. Therefore, their HRD positions are shifted towards cooler temperatures. For masses ≳80 M⊙ the ZAMS is bent towards cooler temperatures due to this effect. As we showed in Sect. 4.3, our VMS models with standard MLT reproduce this effect very well, in agreement with the observed HRD positions. In particular, there appears to be no need to invoke a clumped envelope structure to explain their radii as it has been proposed for the inflated envelopes of classical WR stars (Gräfener et al. 2012; Gräfener & Vink 2013).
A further consequence of the inflation effect is that WNh stars evolve towards cooler temperatures, that is, towards the right side in the HRD, although they are close to chemical homogeneity. Again, the HRD positions following from our VMS models agree with observations. Models that employ the oft-used modified treatment of super-adiabatic convection in radiation-dominated regions (MLT++, Paxton et al. 2013) clearly fail to reproduce the observed HRD positions of WNh stars. They show much hotter temperatures than observed and evolve towards the left side in the HRD (cf., Figs. 6 and 7).
The general agreement of our models with the observed population of WNh stars in 30 Dor in terms of numbers, HRD positions, mass loss, and surface enrichment strongly support their evolutionary status as VMS in the phase of core H-burning.
5.2. A variable upper stellar mass limit
The first estimate of an upper limit for the masses of stars of ≈150 M⊙ was determined by Figer (2005), based on photometric data of the Arches cluster in the Galactic Centre, one of the youngest and densest clusters in the Galaxy. Later Crowther et al. (2010) analysed the brightest WNh stars in R 136, the central cluster of 30 Dor, and found luminosities up to log(L/L⊙) = 6.94 ± 0.1, corresponding to initial masses up to 300 M⊙. Because of its high stellar density R136 has not been included in the VFTS sample but Bestenlehner et al. (2020) analysed the 55 brightest stars in R 136 based on new HST spectroscopy of Crowther et al. (2016) and revised the upper luminosity limit to log(L/L⊙) = 6.8 ± 0.1, corresponding to an upper mass limit of ≈250 M⊙.
According to our present models the brightest WNh stars evolve with near-constant luminosity, implying slightly higher initial masses than the ones derived by Bestenlehner et al. (2020). As a consequence, a value of log(L/L⊙) = 6.8 corresponds almost precisely to Mini = 300 M⊙. As we showed in Sect. 4.1, the VFTS sample displays an upper luminosity cut-off at a slightly lower value of log(L/L⊙) ≈ 6.6 (cf. Fig. 1), corresponding to an initial mass of ≈200 M⊙. According to our population synthesis models we would expect 4.7 stars above log(L/L⊙) = 6.6 and 1.8 stars above log(L/L⊙) = 6.8 without assuming an upper mass limit. If the R 136 upper mass limit would be universal, we would therefore miss 3.1 stars with 6.6 < log(L/L⊙) < 6.8 in the VFTS sample. Given that there are 20 stars with log(L/L⊙) > 6.0, the probability to miss 3 stars with 6.6 < log(L/L⊙) < 6.8 by chance would be (17/20)20 = 0.039. If there were no uncertainties in the individual luminosity measurements this would indicate a significant difference of the upper mass limits in R 136 and the remainder of 30 Dor.
Now the relevant most massive stars in both samples are spectroscopically remarkably similar objects of subtype WN5h, which have been analysed by Bestenlehner et al. (2014) for the VFTS sample and Bestenlehner et al. (2020) for R 136. In both works individual uncertainties of ±0.1 dex in log(L) were estimated which are of course significant compared to the difference in the maximum luminosities of 0.2 dex. However, we think that the relative uncertainties in the derived log(L) may be smaller than the individual errors because of the similarity of the objects, and because they have been analysed by the same person using the same method of analysis. Moreover, the brightest star in the VFTS sample, VFTS 1025 alias R 136c is in fact a member of R 136 with a luminosity of log(L/L⊙) = 6.58. The second brightest star, VFTS 682 has a much lower luminosity of log(L/L⊙) = 6.51, and has been discussed as a slow runaway from R 136 (Renzo et al. 2019). In any case the VFTS population excluding R 136c clearly displays lower luminosities than log(L/L⊙) = 6.6 compared to R 136 with its brightest member R 136a1 with log(L/L⊙) = 6.78.
As Bestenlehner et al. (2020) report 3 stars with 6.6 < log(L/L⊙) < 6.8 in R 136, in agreement with expectations for a top-heavy IMF, dynamical mass segregation cannot account for the lack of the same number of stars in the VFTS sample. Instead, the higher mass limit for R 136 could imply that R 136 initially formed stars with higher masses, depending on the local conditions in the star-forming region. This could mean that the stars in 30 Dor and R 136 already formed in a mass-segregated way (cf. Pavlík et al. 2019). Alternatively, the most massive stars in R 136 could be the result of successive stellar mergers due to the high stellar density in the cluster (e.g., Portegies Zwart et al. 2004).
5.3. OB stars
5.3.1. Mass-loss rates
For the mass-loss rates of OB stars we employed a modified form of the Vink et al. (2001) recipe adjusted to match the empirical mass-loss rates in the VFTS sample with an adopted clumping factor of D = 10. To this purpose we adopted a shallower dependence on L from Bestenlehner et al. (2014) and used overall reduced mass-loss rates. In Sect. 4.2, we showed that this mass-loss relation does indeed match the average O star mass-loss rates in the VFTS sample, however, it fails to reproduce their observed wide spread. In particular, the O dwarfs analysed by Sabín-Sanjulián et al. (2017) show systematically lower wind momenta and mass-loss rates than the O (super)giants analysed by Ramírez-Agudelo et al. (2017). This trend of reduced mass-loss rates for younger objects becomes even more prominent when the VFTS results are compared with the mass-loss relation from Bestenlehner (2020) for O and WNh stars in R 136. The stars in R 136 are only about 2 Myr old, and therefore even younger than most of the stars in the VFTS sample. Notably, the mass-loss rates for O stars in R 136 are up to two orders of magnitudes lower than those found in the VFTS sample (cf. Fig. 4), possibly indicating a very strong trend of reduced mass-loss rates for young O dwarfs.
A reduction in O-star mass-loss rates is also reported in recent theoretical works that employ more elaborate techniques to compute the radiative force than the oft-used first-order Sobolev approximation as in Vink et al. (2001) Employing higher-order Sobolev models, Owocki & Puls (1999) reported a drop in the line source function near the sonic point due to rapid changes in the velocity gradient. Gräfener (2003) reported a similar effect in non-LTE models employing a co-moving frame (CMF) radiative transfer causing a local drop in the radiative force near the sonic point. More recent mass-loss predictions for OB stars employing higher-order Sobolev or CMF techniques by Lucy (2007), Krtička & Kubát (2017), Sundqvist et al. (2019) report similar effects and predict much lower mass-loss rates than those of Vink et al. (2000). One could speculate that young stars with high log g are more susceptible to this effect because a high log g implies stronger changes in the velocity gradient. Physical effects occurring in more evolved stars that are not included in current wind models, such as turbulence caused by sub-surface convection (Cantiello et al. 2009), could help to overcome the associated local drop in the radiative force for these objects, and help to bring their mass-loss rates closer to the values of Vink et al. (2000) as it is observed for the O supergiants in the VFTS sample (cf. Ramírez-Agudelo et al. 2017).
5.3.2. HRD positions
In agreement with previous studies by Köhler et al. (2015), Sanyal et al. (2015) we find that luminous OB stars are subject to the inflation effect, albeit less dependent on the detailed treatment of convection than for the more luminous WNh stars. As a consequence, such objects appear as B supergiants during their main-sequence evolution, in regions of the HRD that previously may have been attributed to the Hertzsprung-gap. In Sect. 4.3, we showed that, according to our population synthesis models, 22 out of the 34 bright B supergiants in the VFTS sample are expected to be inflated main-sequence stars. However, there are some (at least four) objects in the VFTS sample whose HRD positions cannot be explained by our models, so that alternative explanations, such as blue loops or binary interaction, may still be needed to explain the complete B supergiant population.
Notably, our population synthesis models are also able to reproduce the lack of B supergiants with high luminosities (log(L/L⊙) ≳ 6) in the VFTS sample. In Sect. 4.3 we identified the removal of H-rich layers due to the onset of enhanced WR-type mass loss as the reason for this effect. The successful reproduction of the VFTS population in the HRD is therefore also an indirect confirmation of the absolute mass-loss rates and clumping factors adopted in our models.
Previous works, such as Gräfener et al. (2012) and Grassitelli et al. (2018), associated stars with inflated envelopes with the S Doradus type variability of LBVs. The fact that we expect about 20 objects in the VFTS sample to be in this phase, but none of the observed stars shows LBV-type behaviour, implies that envelope inflation is not generally associated with the LBV phenomenon, in particular not in the H-burning phase. This could still mean that the inflation effect is associated with LBVs, but under rarer conditions, such as fast rotation, or in very late (pre-SN) evolutionary stages (cf. Groh et al. 2006, 2013; Gräfener et al. 2012).
Finally, a clumped density structure inside inflated stellar envelopes has been proposed by Gräfener et al. (2012), Gräfener & Vink (2013) to explain the observed radii of classical core He-burning WR stars. Our present analysis shows that there is no need to invoke similar clumped sub-surface regions to explain the radii of B supergiants through the inflation effect.
5.4. Surface helium enrichment through mass loss and rotation
As outlined in Sect. 5.1 the surface He-enrichment through the strong mass loss of WNh stars is well reproduced by our models. On the other hand, the He-enrichment through rotational mixing appears to be over-predicted by our models. According to our models we expect to find 15 O stars with Ys > 0.35 in the VFTS sample that are He-enriched through rotational mixing. These objects are expected to have high rotational velocities (≈300 km s−1) and high luminosities 5.0 < log(L/L⊙) < 5.9. In reality, we find 12 He-enriched objects that are concentrated at low values of v sin i of ≈100 km s−1, five of which are located at luminosities of log(L/L⊙) < 5.0. Therefore, the observed sample appears to be largely incompatible with our model predictions, implying a much lower number of truly rotationally enriched O stars.
This result implies that either the internal rotational mixing is over-predicted in our models, or that the rotationally enhanced mass loss, which induces mixing, is too high. A large part of the 15 He-enriched stars in the VFTS sample could therefore be false detections (such as unidentified multiple systems) or products of alternative processes, such as binary interaction or mergers (cf. de Mink et al. 2014). Whether the observed discrepancy can be explained through changes in internal mixing parameters, or the previously discussed lower mass-loss rates for young O stars, remains to be shown in future works.
6. Conclusions
The implementation of new mass-loss relations in combination with standard-MLT envelope physics in our present evolutionary models leads to a successful reproduction of the properties of the most massive stars (≳80−100 M⊙) in 30 Dor, including their HRD positions, mass-loss rates, and surface He-enrichment. In particular the transition between optically thin O-star winds and the optically thick winds of WNh stars is well reproduced.
For the less massive O stars (with ≈25−100 M⊙) we find much more diverse mass-loss properties than previously thought, with indications for substantially reduced mass-loss rates for young O dwarfs. Also, the surface helium enrichment in the O-star range does not appear to be well understood as we find no clear indications for rotational mixing of helium in contrast to our model predictions. Both phenomena may be related as reduced mass-loss rates for young fast-rotating stars could lead to less rotational braking and mixing.
According to our models the distribution of stellar luminosities in 30 Dor is in good agreement with the top-heavy IMF from Schneider et al. (2018a), with a very modest dependence on the adopted mass-loss prescription. However, the upper luminosity cut-off in the greater 30 Dor region is lower than for its central cluster R 136, implying an upper initial mass limit of ≈200 M⊙ compared to ≈300 M⊙ in R 136. This could be an indication of a general dependence of the upper stellar mass limit on the conditions in the star-forming environment.
Finally, the observed number distribution of stars as a function of effective temperature supports the existence of inflated stellar envelopes that are theoretically predicted to form when main-sequence stars reach high L/M ratios. This puts the majority of bright B supergiants in the end phase of core hydrogen-burning, where they display cool temperatures due to their large, inflated radii.
Acknowledgments
GG thanks the Deutsche Forschunsgemeinschaft (DFG) for financial support under grant No. GR 1717/5-1, the Stellar Evolution group at the Argelander Institute for Astronomy in Bonn for sharing their expertise in stellar modelling and providing computational resources, and the anonymous referee for reviewing this work.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016a, ApJ, 818, L22 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016b, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bestenlehner, J. M. 2020, MNRAS, 493, 3938 [Google Scholar]
- Bestenlehner, J. M., Gräfener, G., Vink, J. S., et al. 2014, A&A, 570, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bestenlehner, J. M., Crowther, P. A., Caballero-Nieves, S. M., et al. 2020, MNRAS, 499, 1918 [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Langer, N., Brott, I., et al. 2009, A&A, 499, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Schnurr, O., Hirschi, R., et al. 2010, MNRAS, 408, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Caballero-Nieves, S. M., Bostroem, K. A., et al. 2016, MNRAS, 458, 624 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Sana, H., Langer, N., Izzard, R. G., & Schneider, F. R. N. 2014, ApJ, 782, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Dufton, P. L., Langer, N., Dunstall, P. R., et al. 2013, A&A, 550, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. J., Taylor, W. D., Hénault-Brunet, V., et al. 2011, A&A, 530, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Figer, D. F. 2005, Nature, 434, 192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fullerton, A. W., Massa, D. L., & Prinja, R. K. 2006, ApJ, 637, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfener, G. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 533 [Google Scholar]
- Gräfener, G., & Hamann, W.-R. 2008, A&A, 482, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., & Vink, J. S. 2013, A&A, 560, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., & Vink, J. S. 2015, A&A, 578, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., Vink, J. S., de Koter, A., & Langer, N. 2011, A&A, 535, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., Owocki, S. P., & Vink, J. S. 2012, A&A, 538, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., Owocki, S. P., Grassitelli, L., & Langer, N. 2017, A&A, 608, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grassitelli, L., Langer, N., Grin, N. J., et al. 2018, A&A, 614, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grassitelli, L., Langer, N., Mackey, J., et al. 2020, A&A, accepted, https://doi.org/10.1051/0004-6361/202038298 [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
- Groh, J. H., Hillier, D. J., & Damineli, A. 2006, ApJ, 638, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Groh, J. H., Meynet, G., & Ekström, S. 2013, A&A, 550, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W.-R., & Koesterke, L. 1998, A&A, 335, 1003 [NASA ADS] [Google Scholar]
- Hamann, W.-R., Gräfener, G., & Liermann, A. 2006, A&A, 457, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillier, D. J. 1991, A&A, 247, 455 [NASA ADS] [Google Scholar]
- Ishii, M., Ueno, M., & Kato, M. 1999, PASJ, 51, 417 [NASA ADS] [Google Scholar]
- Köhler, K., Langer, N., de Koter, A., et al. 2015, A&A, 573, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krtička, J., & Kubát, J. 2017, A&A, 606, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R. P., Puls, J., Lennon, D. J., et al. 1999, A&A, 350, 970 [Google Scholar]
- Lamers, H. J. G. L. M., Snow, T. P., & Lindholm, D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 1997, in Luminous Blue Variables: Massive Stars in Transition, eds. A. Nota, & H. Lamers, ASP Conf. Ser., 120, 83 [Google Scholar]
- Lucy, L. B. 2007, A&A, 468, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- McEvoy, C. M., Dufton, P. L., Evans, C. J., et al. 2015, A&A, 575, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
- Nugis, T., & Lamers, H. J. G. L. M. 2002, A&A, 389, 162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oskinova, L. M., Hamann, W.-R., & Feldmeier, A. 2007, A&A, 476, 1331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owocki, S. P., & Puls, J. 1999, ApJ, 510, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlík, V., Kroupa, P., & Šubr, L. 2019, A&A, 626, A79 [CrossRef] [EDP Sciences] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Petrovic, J., Pols, O., & Langer, N. 2006, A&A, 450, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., & McMillan, S. L. W. 2004, Nature, 428, 724 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ramírez-Agudelo, O. H., Simón-Díaz, S., Sana, H., et al. 2013, A&A, 560, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez-Agudelo, O. H., Sana, H., de Koter, A., et al. 2017, A&A, 600, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzo, M., de Mink, S. E., Lennon, D. J., et al. 2019, MNRAS, 482, L102 [NASA ADS] [CrossRef] [Google Scholar]
- Sabín-Sanjulián, C., Simón-Díaz, S., Herrero, A., et al. 2017, A&A, 601, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sanyal, D., Grassitelli, L., Langer, N., & Bestenlehner, J. M. 2015, A&A, 580, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, F. R. N., Sana, H., Evans, C. J., et al. 2018a, Science, 359, 69 [Google Scholar]
- Schneider, F. R. N., Ramírez-Agudelo, O. H., Tramper, F., et al. 2018b, A&A, 618, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schnurr, O., Casoli, J., Chené, A., Moffat, A. F. J., & St-Louis, N. 2008, MNRAS, 389, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Schnurr, O., Moffat, A. F. J., Villar-Sbaffi, A., St-Louis, N., & Morrell, N. I. 2009, MNRAS, 395, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Schootemeijer, A., & Langer, N. 2018, A&A, 611, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schootemeijer, A., Langer, N., Grin, N. J., & Wang, C. 2019, A&A, 625, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sundqvist, J. O., Puls, J., & Owocki, S. P. 2014, A&A, 568, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sundqvist, J. O., Björklund, R., Puls, J., & Najarro, F. 2019, A&A, 632, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tkachenko, A., Pavlovski, K., Johnston, C., et al. 2020, A&A, 637, A60 [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., & Gräfener, G. 2012, ApJ, 751, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Brott, I., Gräfener, G., et al. 2010, A&A, 512, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Muijres, L. E., Anthonisse, B., et al. 2011, A&A, 531, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wofford, A., Leitherer, C., Chandar, R., & Bouret, J.-C. 2014, ApJ, 781, 122 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Observed luminosity distribution of single stars in 30 Dor compared to theoretical predictions. The histogram shows the observed numbers of single stars in the VFTS sample as function of luminosity (blue) compared to the theoretical distribution resulting from our VMS population synthesis models described in Sect. 4 (green). Both distributions are plotted transparent so that overlaps appear in dark green. |
| In the text | |
 |
Fig. 2. Wind-momentum – luminosity relation for O and WNh stars in 30 Dor. Different symbols indicate empirical results for the most massive stars in 30 Dor from Bestenlehner et al. (2014) in blue, O-type giants and supergiants from Ramírez-Agudelo et al. (2017) Tables C.4 (dark green) and C.5 (light green), and O-type dwarfs from Sabín-Sanjulián et al. (2017) Tables A.1 (red) and A.2 (pink). Upper limits are indicated in grey. Evolutionary tracks are indicated by coloured lines analogous to Fig. 5 but restricted to the O star range. Predicted absolute numbers of stars according to our population synthesis models are mapped and colour coded as indicated by the colour bar on the right. |
| In the text | |
 |
Fig. 3. Wind-momentum – luminosity relation as in Fig. 2 compared with population synthesis models based on standard MESA models using the DUTCH wind scheme. |
| In the text | |
 |
Fig. 4. Mass loss as a function of Eddington factor. Mass-loss rates Ṁ as a function of the estimated classical Eddington factor for chemically homogeneous stars |
| In the text | |
 |
Fig. 5. Theoretical HRD for VMS models with standard MLT. Coloured areas indicate the expected number of stars according to our population synthesis models for 30 Dor (cf. Sect. 4). Evolutionary tracks for Ω/Ωcrit = 0.3 are indicated, labelled with ZAMS masses in M⊙. |
| In the text | |
 |
Fig. 6. Observed HRD for 30 Dor. Coloured areas indicate the observed number of stars, evolutionary tracks are the same as in Fig. 5. |
| In the text | |
 |
Fig. 7. Influence of envelope inflation. The theoretical HRD for models with reduced envelope inflation effect through an artificially enhanced convective efficiency (MLT++; MESA option okay_to_reduce_gradT_excess = .true.) is indicated analogous to Fig. 5. |
| In the text | |
 |
Fig. 8. Effective temperature distribution. The theoretical HRD for the upper main sequence is indicated analogous to Fig. 5 but as a function of the effective temperature relative to the ZAMS temperature. |
| In the text | |
 |
Fig. 9. Observed HRD analogous to Fig. 8. |
| In the text | |
 |
Fig. 10. Influence of mass loss. The theoretical HRD is indicated analogous to Fig. 8 but adopting a pure OB-type mass-loss prescription without enhanced Γ-dependent mass loss. |
| In the text | |
 |
Fig. 11. Influence of mass loss. The theoretical HRD is indicated analogous to Fig. 8 but adopting the DUTCH MESA wind scheme. |
| In the text | |
 |
Fig. 12. Effective temperature distribution. Histogram of the observed numbers of single stars in the VFTS sample with 5 < log(L/L⊙) < 6 as a function of their distance from the ZAMS (log(Teff/TZAMS)) (transparent blue) compared with the theoretical distribution from our VMS population synthesis models (transparent green). |
| In the text | |
 |
Fig. 13. Helium surface enrichment through mass loss. The predicted helium surface mass fraction Ys, as a function of the estimated inverse mass-loss timescale Ṁ/Mhom for stars with Teff > 30 kK and log(L/L⊙) > 5, is compared with VFTS O and WNh stars labelled as in Fig. 2. The colour scale indicates the number of objects predicted by our population synthesis. Evolutionary tracks from Fig. 5 are indicated by coloured lines. |
| In the text | |
 |
Fig. 14. Helium surface enrichment through rotation. The predicted helium surface mass fraction Ys, as a function of rotational velocity for O stars with Teff > 29 kK and 5.0 < log(L/L⊙) < 5.9, is compared with observed Ys and v sin i of He-enriched VFTS O stars (with Ys > 0.35) labelled as in Fig. 2; stars with log(L/L⊙) < 5.0 are plotted in grey. The colour scale indicates the number of objects predicted by our population synthesis models. Evolutionary tracks for an initial mass of 30 M⊙ are indicated by coloured lines. Step functions indicate the initial (blue) and present (orange) total number distributions in arbitrary units, as well as the present distribution of He-enriched stars with Ys > 0.35 (red). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.