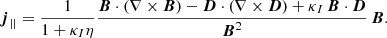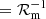| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 14 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202038908 | |
| Published online | 08 March 2021 | |
Computational general relativistic force-free electrodynamics
II. Characterization of numerical diffusivity
1
Departament d’Astronomia i Astrofísica, Universitat de Valéncia, 46100 Burjassot, Valencia, Spain
e-mail: jens.mahlmann@uv.es
2
National Center for Computational Sciences, Oak Ridge National Laboratory, PO Box 2008, Oak Ridge, TN 37831-6164, USA
3
Physics Division, Oak Ridge National Laboratory, PO Box 2008, Oak Ridge, TN 37831-6354, USA
Received:
13
July
2020
Accepted:
27
December
2020
Scientific codes are an indispensable link between theory and experiment; in (astro-)plasma physics, such numerical tools are one window into the universe’s most extreme flows of energy. The discretization of Maxwell’s equations – needed to make highly magnetized (astro)physical plasma amenable to its numerical modeling – introduces numerical diffusion. It acts as a source of dissipation independent of the system’s physical constituents. Understanding the numerical diffusion of scientific codes is the key to classifying their reliability. It gives specific limits in which the results of numerical experiments are physical. We aim at quantifying and characterizing the numerical diffusion properties of our recently developed numerical tool for the simulation of general relativistic force-free electrodynamics by calibrating and comparing it with other strategies found in the literature. Our code correctly models smooth waves of highly magnetized plasma. We evaluate the limits of general relativistic force-free electrodynamics in the context of current sheets and tearing mode instabilities. We identify that the current parallel to the magnetic field (j∥), in combination with the breakdown of general relativistic force-free electrodynamics across current sheets, impairs the physical modeling of resistive instabilities. We find that at least eight numerical cells per characteristic size of interest (e.g., the wavelength in plasma waves or the transverse width of a current sheet) are needed to find consistency between resistivity of numerical and of physical origins. High-order discretization of the force-free current allows us to provide almost ideal orders of convergence for (smooth) plasma wave dynamics. The physical modeling of resistive layers requires suitable current prescriptions or a sub-grid modeling for the evolution of j∥.
Key words: magnetic fields / methods: numerical / plasmas
© ESO 2021
1. Introduction
The numerical modeling of the dissipation, transport, and emission of high-energy particles by strongly magnetized plasma is a necessary ingredient in the theoretical interpretation of the highly energetic astronomical phenomena associated with compact objects such as neutron stars (NSs) and black holes (BHs). Current sheets seem to be one important location where such processes take place. In these, reconnection of the magnetic field results in the acceleration of relativistic particles (see, e.g., Ball et al. 2019; Petropoulou et al. 2019; Kilian et al. 2020, for some recent examples), as well as the locations of Fermi-type processes (Guo et al. 2019).
When the magnetic diffusivity (or resistivity, η) is sufficiently large, plasma dynamics change due to nonideal processes and the plasma can no longer be modeled as ideal, that is, as a perfectly conducting plasma. Astrophysical plasma is typically an environment of extremely low magnetic diffusivity. Thus, resorting to ideal (relativistic) magnetohydrodynamics (MHD) or force-free electrodynamics (FFE) is a reliable assumption when magnetic fields dominate all plasma dynamics. However, a numerical treatment of the challenges at hand requires introducing a controlled (often implicit) amount of numerical diffusivity. Such a diffusivity of numerical origin stems from two main sources: first, from the discretization of a set of physical (balance) laws, often partial differential equations; and second, from the need to stabilize numerical solutions across the various types of discontinuities that exist in ideal MHD or FFE.
The design of numerical codes commonly focuses on minimizing the amount of numerical diffusivity across discontinuities. Howewer, much less weight is placed on minimizing or (at least) characterizing the numerical diffusivity resulting from the discretization of the governing equations (with considerable exceptions, e.g., Rembiasz et al. 2017, in Eulerian MHD, or Obergaulinger & Aloy 2020, in Newtonian hydrodynamics). We find that a thorough account of the numerical diffusivity of algorithms designed to solve the equations of FFE or general relativistic FFE (GRFFE) is of the utmost importance. We therefore assess whether numerical diffusivity behaves as a physical diffusivity and if it introduces pathological biases in the modeling of (astrophysical) plasma. This is a necessary step in grading the quality of numerical results when the FFE approximation reaches its limit. Such limits are specifically expected at the location of current sheets, (smooth) Alfvén waves, and Alfvén discontinuities.
The linear phase of the dynamics in pinched force-free current sheets has been modeled in FFE (Komissarov et al. 2007) and compared to particle-in-cell simulations (Lyutikov et al. 2018). Still, conventional FFE codes are insufficient to account for the nonideal electric fields that drive complex dynamics. In contrast to the limits of nonvanishing particle inertia (MHD), energy is dissipated by violations of the algebraic constraints under which the FFE approximation is valid. In this second part of our two-series publication describing our new GRFFE code, we aim to quantify the impact of such nonideal dissipation in both smooth plasma waves and current sheets as thin current-carrying layers across which the magnetic field either changes direction or changes in magnitude (Harra & Mason 2004). Aiming from a comprehensive numerical modeling of (astrophysical) plasma across magnetization regimes, we ask the questions of why FFE methods fail to resolve the dynamics in current-dominated domains, and what the physical consequences of these failures are.
This second manuscript in our series of publications is dedicated to answering these questions, evaluating previous results obtained by our code, and providing leverage points at which kinetic plasma modeling may bridge the limits of FFE. In the context of instabilities in magnetar magnetospheres, Parfrey et al. (2013), Carrasco et al. (2019), and Mahlmann et al. (2019) have encountered current sheets at the stellar surface, and sensitivity to a (conservative) transport of charges throughout the domain. The longest variability timescales in the observed TeV emission, for example, in M87, have recently been linked to recurring periods of efficient Blandford/Znajek (Blandford & Znajek 1977) type outflows induced by the accretion of magnetic flux tubes (Parfrey et al. 2015; Mahlmann et al. 2020). Reconnection and plasmoid formation in BH accretion processes are likely to act on much shorter timescales (studied in the ideal limit by, e.g., Nathanail et al. 2020) and involve relevant physical nonideal electric fields (analyzed in the resistive limit by, e.g., Ripperda et al. 2020). A large array of work makes use of numerical laboratories set up in (GR)FFE in order to simulate the most extreme environments of the universe while constantly breaking their own limits. Understanding the pathology of such breaches, and providing valid test cases for their evaluation, has motivated this additional technical exploration of our recent code development effort.
This work is organized as a series of papers. This manuscript (Paper II) characterizes the numerical resistivity of our GRFFE code (as introduced in Mahlmann et al. 2021, Paper I) in depth by studying the 1D diffusion of plasma waves (Sect. 2.1) and the growth of 2D tearing modes (TMs; Sect. 2.2) under force-free conditions. In Sect. 3, we explore a phenomenological current, effectively allowing for modeling beyond ideal FFE, namely, driving the evolution with a physical resistivity η. We discuss the implications of our results on GRFFE methods in Sect. 4 and present our conclusions in Sect. 5. We use units with G = c = M⊙ = 1, as in Paper 1.
2. Assessment of numerical resistivity
In this section, we quantify the numerical resistivity of the GRFFE code presented in Paper I. This analysis is analogous to the one in Rembiasz et al. (2017) for Eulerian MHD codes, but applied to the case of FFE. For our analysis, we employ two key techniques: (i) measuring damping rates of plasma waves that are captured in a 1D periodic domain for a large number of dynamical timescales (Sect. 2.1); and (ii) Measuring growth rates of TM perturbations in a 2D force-free current sheet (Sect. 2.2). A similar strategy was followed in Miranda-Aranguren et al. (2018) in resistive relativistic MHD. Since the development of TMs requires, at the minimum, a longitudinal current sheet in 2D (though, obviously, they can also develop in 3D), the study of the growth rate of resistive TMs allows us to quantify the numerical resistivity of our code in more than one dimension.
2.1. Diffusion of 1D plasma waves
One of the simplest 1D assessments of numerical resistivity is checking the capacity of the code for maintaining standing or propagating waves over significant numbers of light-crossing times (Rembiasz et al. 2017). Hereafter, quantities without any subscript refer to the total electromagnetic field, which we assume to be composed of a background field (annotated with subscript 0) and a perturbation (annotated with subscript 1), namely,
which correspond to the magnetic field, the electric field, and the charge density, respectively. These are the main evolved variables in our code, apart from the two potentials that we used to preserve the value of the divergence of the fields (which we always initialize to zero, see Paper I). We performed three series of 1D simulations for different kinds of waves with the goal of measuring the damping rate induced by the existence of a finite numerical diffusivity.
Series A corresponds to a standing wave in FFE, which is excited by initializing the variables to
where k is the wavenumber. ρ1 is initialized numerically to ensure ∇ ⋅ D1 = ρ1 (here and in all the tests hereafter). B0 is the scale-free amplitude of the standing wave, which we set to B0 = 1 for the sake of simplicity.
Series B corresponds to fast magnetosonic waves traveling in the direction of a guide field B0 along the y-direction, which are excited by the following initial perturbation (Punsly 2003):
Here, the amplitude of the perturbations is controlled by the dimensionless parameter ϵ. We chose the perturbation amplitude to be sufficiently small, ϵ = 10−5, to guarantee that the perturbation can be regarded as linear with respect the FFE equations. This will allow us to measure the numerical resistivity from the damping rate of the waves (see below).
Series C corresponds to Alfvén waves traveling along the x-direction at an angle θ = π/4 to the guide field. The initial perturbations in this case are (Punsly 2003):
where ϵ is of the same value as in series B. In all series, the 1D domain is discretized in the y-direction with an extent L = 16 in the domain [−L/2,L/2]. The initial data for the different cases is evolved for 125 light crossing times (τ = L) of the domain. We impose periodic boundary conditions, so we chose a wavenumber k = 2πm/L, with m ∈ ℕ. Simulations of the cases m = 1, 2 and 3 (and linear combinations) are performed using different numerical resolutions to study the convergence of the method. We use the monotonicity preserving (MP, Suresh & Huynh 1997) reconstruction with three different orders: MP5, MP7 and MP9. In all cases we use a CFL factor of fCFL = 0.2.
For incompressible, viscous-resistive MHD, Campos (1999) found that the damping rate, 𝔇, of Alfvén and fast magnetosonic waves is proportional to the square of the wavenumber and to the diffusivity, ξ, namely
Here, the diffusivity is a linear combination of the shear and bulk viscosity as well as the resistivity, η. Expression (5) strictly holds in the so-called weak damping approximation, namely,  (where vA is the Alfvén velocity).
(where vA is the Alfvén velocity).
Komissarov et al. (2007) has shown that the equations of FFE in the so-called incompressible limit can be cast into a form nearly identical to that of incompressible MHD. In the incompressible limit, the drift speed V = D × B/B2 fulfills ∇ ⋅ V = 0. For models of the series A, V = 0 and ∇ ⋅ V = 0 strictly hold, while for the series B and C, V = 𝒪(ϵ2)≈0 and ∇ ⋅ V = 𝒪(ϵ2)≈0 to first order in ϵ. Hence, for our choice of ϵ, we can safely make the assumption that the damping of Alfvén and fast modes in incompressible FFE proceeds analogously to their incompressible MHD counterparts.
Since FFE neglects the thermal and inertial contributions of the plasma, its equations are not affected by either bulk or shear viscosity (neither of physical nor of numerical origin). Thus, the diffusivity may only come from resistive effects. Provided that in FFE there is no physical resistivity, the diffusivity in our numerical results comes exclusively from the numerical resistivity, η*. Following Campos (1999) with the notation of Rembiasz et al. (2017), we find ξ = η for all three series of initial data,
Hence, the diffusion of 1D plasma waves proceeds according to
where B1i denotes the magnetic field of the ideal solution of wave dynamics in the absence of any numerical dissipation. The diffusion of the electric field D1 can be modeled analogously.
In order to evaluate the diffusive properties of our code, we define the electromagnetic energy contained in the wave components (B1 and D1)
Since the energy U1 is associated with the perturbations of the background electromagnetic field, we may refer to it also as free energy. In our analysis, we evaluate the right-hand side of Eq. (8), for which we obtain the linear relation
where U1i is the initial energy in the respective waves. Eq. (9) allows us to obtain 𝔇 (and hence, η*) from the slope of linear fits of the form lnU1 versus t. The values of η* computed from the fits depend on the grid spacing with which the model is run or, equivalently, on the number of points per wavelength, p = N/m (N is the number of points in the domain and m is the number of full modes), with which a target mode is resolved in a given setup. Fixing the remaining parts of the numerical method, the value of η* also depends on the cell interface reconstruction employed. Following Rembiasz et al. (2017, Sect. 4.3.3), we assume that the numerical resistivity can be written in the form
where 𝔑 is a (resolution-independent) numerical coefficient, r the measured order of convergence of the employed scheme, Δx = L/N the grid spacing, and ℒ and 𝒱 are the characteristic length and speed of the problem. In the case of FFE, differently from incompressible MHD, the characteristic velocity is the speed of light, thus 𝒱 = 1 in our units. The characteristic length is equal to the wavelength of the induced modes (Rembiasz et al. 2017), namely, ℒ = λ = 2π/k = L/m = pΔx. Thus, we can rewrite expression (10) as
In view of the previous relation, we define subsets of tests where the cell interface reconstruction is fixed and different number of points per wavelength are considered. For every subset of tests (i.e., reconstruction method), we fit the function
where the fit parameter d (from which we may compute 𝔑) corresponds to
In Fig. 1 we combine Eqs. (12) and (13) in order to visualize the quantity
 |
Fig. 1. Assessment of numerical resistivity (normalized, see Eq. (14)) as a function of grid points per wavelength for a 1D static diffusion test (series A) as well as propagating 1D plasma waves (series B and C, i.e., fast and Alfvén). Numerical fit parameters (Table 1) are obtained for the data points of the m = 1 mode (dashed lines). For series C, the discretization order of the numerical derivatives in the calculation of the current j∥ has significant impact on the order of convergence. Thick lines in the background employ standard fourth-order finite differences in the calculation of reconstruction of j∥, while solid thin lines display the improved high-order finite differences (Sect. 3.4, Paper I). |
We therefore combine measurements of different wave modes m in the same numerical domain as a measure of numerical resistivity. For the entire set of considered cases (series A/B/C) we find that at least eight grid points per wave mode are required in order to resolve the respective plasma wave with an order of convergence which approaches the theoretical order of the employed reconstruction scheme. Table 1 shows the coefficients 𝔑 and r obtained by a linear fit to Eq. (14). For MP5 their values are similar (as expected from Eq. (11)) independent of the series. The numerical diffusivity in series B is somewhat larger compared to series A and C (the last of which uses the eighth-order accurate discretization of j||) for the set of models using the MP9 reconstruction. We have not been able to identify a single, dominant source for the slight reduction of the order (and the slightly increased diffusivity) of MP9 when applied to fast waves. However, the ≲5% reduction of r does not seem to be a great drawback for applying MP9 in combination with either 4th or eighth-order accurate discretization of j|| to numerical models involving fast waves.
In the right panel of Fig. 1, we also show the effects of the order of discretization of the derivatives appearing in the parallel current (Sect. 3.4, Paper I). The thick (opaque) lines show the results when a fourth-order accurate discretization is employed in combination with MP7 (blue thick line) or MP9 (black thick line) reconstruction. For comparison, the blue (black) thin lines show the fits to the resolution dependence of the numerical resistivity using a sixth(eighth)-order accurate parallel current discretization in combination with MP7 (MP9). In order to obtain an empirical order of convergence close to the theoreticaly expected values (r = 7 and 9 for MP7 and MP9, respectively), increasing the order of the discretization of j|| is crucial. We note that for resolutions of fewer than eight points per wavelength, the values of the numerical resistivity are not too different. This justifies our choice of a fourth-order accurate discretization of j|| (Mahlmann et al. 2019, 2020) in combination with MP7. The resolution employed in these global 3D models is smaller than p ∼ 8 zones per wavelength. However, future models with higher resolution will have to incorporate, at least, a sixth(eighth)-order accurate discretization of the current when used in combination with MP7 (MP9).
We therefore conclude that modeling force-free plasma wave interactions requires resolving the shortest wavelength mode with more than p = 8 (p = 20) grid zones in order to reduce the numerical resistivity below ∼10−4 (∼10−7). In this way, we avoid significant wave damping over sufficiently long timescales. The typical timescale for energy damping in FFE waves is τ ≈ 1/(2𝔇)≈1/(η*k2). In a domain of size L ∼ 1, where we fit m ∼ 10 full waves, τ ∼ 2.5 × 10−4/η*. Hence, we need a numerical resistivity smaller than 2.5 × 10−4 in order to evolve the set of waves for more than a single domain light crossing time (tlc = L) without significant numerical dissipation. That requires p > 10. Applying these requirements to 3D numerical experiments (by taking cubical meshes with the aforementioned number of points per wavelength in each dimension) reveals the huge computational effort needed to resolve the dynamics of the interaction of FFE modes with sufficiently small numerical resistivity. This happens because, usually, in global 3D simulations (e.g., of magnetospheres around magnetars), the wavelength of Alfvén waves, λ, is much smaller than the typical domain size L. If, say, L/λ ∼ 100, one may require at least ∼1000 cells per dimension to prevent numerical damping of the waves before they interact for a time on the order of a single light crossing time of the computational domain. If longer evolutionary times are considered, even more stringent numerical resolutions are required.
Figure 2 gives an illustrative example of mode damping for different resolutions per wavelength, including the superposition of two selected modes of fast waves with the same initial amplitude (adding the initial data in Eq. (3) for m = 1 and m = 2). The damping for all cases proceeds exponentially according to the assumption we stated in Eq. (7) with numerical resistivities inferred from Fig. 1. This holds also for the case of mode superposition, where the damping of the m = 2 mode is dominant due to its capture by fewer points per wavelength as compared to the m = 1 mode. The results for propagating FFE waves highlight the ability of our code to properly resolve their linear superposition with decreasingly small numerical resistivity as the numerical resolution is increased.
 |
Fig. 2. Exemplary amplitude evolution of selected modes of the fast wave model (showing m = 1, m = 2, as well as the superposition m = 1, 2). The time is normalized to the light crossing time of the computational domain (τ). Left: field amplitude at the point y = 0 for a superposition of modes m = 1, 2 (top panel), m = 2 (middle), and m = 1 (bottom). The analytic solution is indicated in the background (thick magenta lines). Different resolutions are visualized by solid (Ny = 12) and dotted (Ny = 24) lines. Right: evolution of the energy contained in the perturbations, given by Eq. (8), scaled to |
2.2. Tearing modes
TM instabilities are resistive instabilities, which can develop in current sheets, and dissipate magnetic energy into kinetic energy if a plasma fluid is considered. We note, however, that in a pure force-free approximation, the only existing energy is that of the electromagnetic field, and, thus, the dissipation of magnetic energy may simply result in an actual energy sink. In GRFFE, besides the standard sources of numerical diffusivity, there is yet another one, namely the numerical resistivity induced by the algorithms used to control the violations of the force-free conditions. As we shall see, both the standard sources of numerical resistivity as well as the resistivity produced by the violation of the force-free constraints are especially sensitive to the resolution of the numerical mesh and provide a source of (numerical) resistivity from which TMs may develop.
In this test, we adapt the relativistic resistive MHD current sheet setup of Del Zanna et al. (2016) to FFE, employing a 2D domain of (x, z)∈[−L/2,L/2] × [−25a,25a]. Here, a = 0.1 is the width of the current sheet, and L = 2π/k is its length. In FFE, the theoretical growth rate of TMs is analogous to that in incompressible MHD (e.g., Komissarov et al. 2007). For the wavenumber of the perturbation we employ k = π. This value allows us to fulfill approximately L ≫ a and ka ≪ 1, required for the development of TMs. We use periodic boundary conditions in the x direction (i.e., along the current sheet) and copy boundary conditions in the z direction (i.e., in the direction perpendicular to the current sheet). The numerical grid is uniform and consists of Nx × Nz zones, where Nx = 32 in all cases. In order to trigger TM instabilities, the initial magnetic field
is perturbed by
We set B0 = 1 and the perturbation amplitude parameter ϵ = 10−4. We assume that the initial electric field and the charge density are zero. The growth rate of the TMs, γTM, may be traced, for example, by examining the growth of the magnetic field component Bz (cf. Rembiasz et al. 2017), which grows exponentially,  . To obtain a globally and positively defined quantity for the growth rate, we study the integral of
. To obtain a globally and positively defined quantity for the growth rate, we study the integral of  over a suitably chosen patch of the computational domain (covering the entire length and width of the current sheet):
over a suitably chosen patch of the computational domain (covering the entire length and width of the current sheet):
The slope 2γTM of the linear relation in Eq. (17) may be obtained by fitting  versus t. In the fits we disregard the initial (numerically dominated) adjustment phase. We measure the growth rate for series of simulations with different numerical resolutions and numerical schemes. Apart from the MP reconstruction schemes used in the previous sections we also test slope limited TVD reconstruction with a monotonized central (MC) limiter (van Leer 1977).
versus t. In the fits we disregard the initial (numerically dominated) adjustment phase. We measure the growth rate for series of simulations with different numerical resolutions and numerical schemes. Apart from the MP reconstruction schemes used in the previous sections we also test slope limited TVD reconstruction with a monotonized central (MC) limiter (van Leer 1977).
We aim to provide an estimate of the numerical resistivity as a function of the numerical resolution based on two different approximations. The first one (model A) assumes that the plasma is inviscid. In this case, the growth rate of the TM mode (for a given mode k) depends on the physical resistivity as (Rembiasz et al. 2017, Eq. (147))
In our system of units, the Alfvén speed is vA = 1. For the specific choice of k and a employed in our setup, we can write Eq. (18) as
Alternatively, in the so-called long-wavelength approximation (model B, characterized by ka ≪ 1), the maximum growth rate (i.e., the growth rate of the fastest-growing mode) can be evaluated from Fig. 3 of Furth et al. (1963), resulting in
or, equivalently,
The force-free models we run do not include any physical resistivity. Hence, the growth of TM modes is induced by the action of the resolution-dependent numerical resistivity η*. Thus, we may replace η in Eqs. (19) and (21) by η*.
Once the TM growth rate is obtained for each resolution and reconstruction method, we can compute the corresponding numerical resistivity (as we did in Eq. (10), cf. Rembiasz et al. 2017, Sect. 4.3.3). Like in the previous section, the light speed (𝒱 = 1) is the only possible choice for the characteristic velocity of the problem in the force-free regime. The selection of ℒ is much more involved (see Rembiasz et al. 2017, for a detailed discussion) and prone to accuracy restrictions since typically ℒ ≪ a, which can result in a prohibitive numerical resolution needed to reliably measure the growth rate. To obtain an order of magnitude estimate, we may assume that
but cautiously note that assuming that ℒ is constant, in other words resolution-independent, is not fully accurate (Rembiasz et al. 2017). A partial justification for this choice (but see discussion in Sect. 4) is the shape of the drift velocity, V = D × B/B2, displayed in Fig. 4, which shows that 0.1a (region with gray lines) covers a significant part of the width of the current sheet (estimated as the distance between the two extrema).
We express the numerical resistivity in terms of the number of grid zones within the transition layer, namely, p = a/Δz (Δz being the grid spacing in the z direction). We note that p here has a different meaning as in Sect. 2.1, and the numerical resistivity (Eq. (10)) in these tests can be written as (compare with Eq. (11))
where 𝔑 is, again, a (resolution-independent) numerical coefficient. Plugging Eq. (23) into either Eq. (19) or Eq. (21) one obtains a linear relation between lnγTM and lnp that allows us to compute 𝔑 and r from the coefficients of the linear fit
where the specific definition of m and d depends on the employed growth model.
Figure 3 visualizes the growth rates γTM for different resolutions and reconstruction methods. We summarize the numerical fit parameters, namely, the coefficient 𝔑 and the estimated order of the scheme r in Table 2. The order of convergence estimated from the fits is roughly correct for models using the MC reconstruction, but is significantly smaller than the formal order of convergence estimated for MP methods, where values of r = 5, 7 and 9 are expected. In fact, we expect that the methodology employed in this test may only allow us to infer order of magnitude estimates of the numerical resistivity and rough values of the empirical order of convergence of the algorithm, r.
 |
Fig. 3. Growth rate of the (2D) TM instability (Sect. 2.2) for different resolutions and reconstruction schemes. We depict the measurements of γTM from numerical experiments (squares) and the corresponding best fit parameters (solid lines, Eq. (24)). The scale on the right shows the numerical resistivity computed from the measurements of the growth rate employing model A (Eq. (19)). |
 |
Fig. 4. Evolution of the drift velocity Vz along the mid-point of the current sheet (x = 0.5) in the direction transverse to the current sheet (z-direction) during the linear phase (time-interval [t0,t1] for which the growth rate is derived in Fig. 3). The different panels correspond to different reconstruction schemes (see legends) and a resolution of p = 25.6 numerical zones per transverse size of the current sheet. The assumed width of the resistive layer LR employed for the analysis in Sect. 2.2 is indicated by the vertical gray lines in the background; each of these lines denotes the limits of the computational zones in the z-direction. The growth of the velocity component Vz is strongly suppressed for higher-order (MP) reconstruction methods and is significantly larger when using the MC reconstruction (we note the different scale for the lower panel). |
The reason for the discrepancy is related to the nature of the TM itself, which involves dissipation in a current sheet. Dissipative effects do not exist in FFE (except numerically) and the presence of these current sheets breaks the force-free condition itself (see the discussion in Sect. 4). In this regime, it is not surprising that our numerical methods do not behave as expected and, hence, the theoretical order of convergence is not recovered. These circumstances are not present in the tests in Sect. 2.1 where no current sheets are on hand and no reduction of the expected order of convergence is observed. A possible solution to this problem is to include a physically consistent model for the dissipation in FFE, such that TMs can develop in a physically realistic way forming resistive layers resolvable by numerical simulations. Its application to different astrophysical scenarios (where the resistivity is likely too small to be handled) would be done by studying the limit of decreasing resistivity. The next section explores this possibility.
The influence of the exact boundary conditions on the growth rate in the direction transverse to the current layer is probably significant and deserves further study, something that is beyond the scope of this publication. We have considered different values of a, finding that a = 0.1 is a compromise to fulfill all the physical requirements to develop TMs and the (unfortunately unsuccessful) attempt to resolve the resistive layer width. However, we stress the fact that our results are numerically robust in several ways. For instance, we have checked the influence of the computational box size in the direction perpendicular to the current sheet. We find that boxes extending in the z-direction by less than ±20a induce significant modifications in the growth rate of TMs. Our choice of a box size extending up to z = ±25a was validated by cross-checking against even larger computational boxes and finding no appreciable changes in the growth rate. We have also considered higher-order discretizations of the derivatives used to compute j|| (Sect. 3.4, Paper I), finding no significant influence in this test, likely because of the non-smoothness of the parallel current at z = 0. The discontinuity of the field derivatives makes a high-order discretization of j|| less effective (i.e., noisier). This result is consistent with our finding that higher-order discretization of j|| does not significantly change the results of the 1D Riemann problems presented in Sect. 4.1 of Paper I.
3. Beyond ideal force-free electrodynamics
FFE is inherently formulated in the limit of infinite conductivity, effectively resulting in the magnetic dominance and ideal fields condition (see Paper I and also Lyutikov 2003)
Under these conditions the 4-vector electric current density takes the form of the force-free current (Eq. (47) in Paper I):
where ρ = −nμIμ = αIt is the charge density, nμ = α−1(1, βi) is the vector normal to the hypersurfaces in the 3+1 decomposition of the spacetime, α is the lapse function and βi is the shift vector, respectively. Equation (27) is a direct consequence of
where ℒn is the Lie derivative with respect to nμ. The current density three-vector appearing in the 3+1 decomposition of Maxwell’s equations can be computed as Ji = αIi. Additionally, one can define the current density 3-vector for the normal observer (nμ) as the projection of Iμ onto the hypersurface, namely j i = Ii − βiIt, which is related to Ji by Ji = αj i − βiρ.
Any occurring resistivity measured in such ideal schemes must, hence, be of numerical origin; we quantify this numerical resistivity for our method in Sect. 2. The absence of any physical resistivity makes resolving genuinely resistive layers a true limit of FFE. Thus, it is desirable to extend the theory to include a small phenomenological resistivity η and reduce to FFE in the limit η → 0. Several attempts to undertake this task have been presented in the literature (e.g., Lyutikov 2003; Gruzinov 2007; Li et al. 2012; Parfrey et al. 2017). In spite of the oxymoron, it is common to refer to these prescriptions as resistive FFE. All of them have in common that they integrate the full set of Maxwell’s equations together with a suitable choice of Ohm’s law. In practice, this replaces the force-free electric current density  by a more general form explicitly including the resistivity. For this section, we have tested the generalization of a current density recently introduced by Parfrey et al. (2017). Its covariant form (cf. Eq. (27)) is
by a more general form explicitly including the resistivity. For this section, we have tested the generalization of a current density recently introduced by Parfrey et al. (2017). Its covariant form (cf. Eq. (27)) is
where κI is a constant and η is the resistivity. With this new 4-current the evolution of B ⋅ D fulfills (cf. Parfrey et al. 2017)
where || indicates the component of a vector parallel to B. Therefore, 1/κI is the timescale over which the parallel electric field D|| is driven toward α−1η J|| (or in for the case of flat spacetime, toward η j||). Therefore, the form of this current effectively is enforcing a form of Ohm’s law for the parallel current. In the limit η → 0 one recovers B ⋅ D → 0 and hence  .
.
The current density observed by the normal observer naturally splits into components parallel and perpendicular to the magnetic field three-vector (j = j⊥ + j||, cf. Eq. (70) in Komissarov 2011):
In the following subsections, we will investigate the ability of the current given by Eq. (29) to model resistivity in FFE. We specifically address its ability to a) resolve current carrying discontinuities in 1D plasma wave tests (extending Sect. 4.1 of Paper I) as well as b) its capacity to resolve the resistive layer in 2D TMs (cf. previous Sect. 2.2). Along the way, we cross-validate our procedure to evaluate the numerical resistivity of our algorithm by comparing this prescription for resistive FFE with its ideal limit.
From the numerical point of view, the introduction of resistive effects needs to be done with extra care. The choice of the driving rate κI is guided by numerical convenience. Its value shall be large enough to drive D|| toward α−1η J|| as quickly as possible., however, it shall not be so large as making the driving timescale become much smaller than the time step of the numerical model (1/κI ≪ Δt). In this case, Maxwell’s equations become numerically stiff and suitable time evolution algorithms such as implicit Runge-Kutta methods (Palenzuela et al. 2009; Miranda-Aranguren et al. 2014, 2018) would need to be employed. Numerical experimentation leads us to resort to κIΔt ∼ 1 − 10. We note that if the modified current is employed, the perpendicularity condition D ⋅ B = 0 must not be enforced anymore. We note that Eq. (30) is actually similar to the evolution equation used by Alic et al. (2012) to drive B ⋅ D toward zero in FFE simulations (with η = 0), an alternative to our approach described in Paper I.
3.1. Charge-carrying 1D discontinuities
The three-wave test in Sect. 4.1.2 of Paper I is a well-suited testbed for the analysis of resistivity introduced by Ohm’s law. This test consists of an initial discontinuity that splits into two fast discontinuities and one stationary central standing Alfvén wave. The Alfvén wave is a charge carrying discontinuity, which is effectively stabilized by strong currents. In this section, we compare the results of the three-wave test using three different Ohm’s laws. In all tests we use the highest resolution employed in Paper I, namely, Δx = 0.0125. First, we consider the force-free current given by Eq. (27) and enforce the force-free conditions algebraically (corresponding theoretically to η = 0), as described in Paper I. Second, we set j∥ = 0 (Yu 2011), again enforcing the force-free conditions algebraically. Third, we employ the current density given by Eq. (29) (with κI = 512) and refrain from algebraically enforcing the perpendicularity condition. In other words, the magnetic dominance condition is always validated algebraically; the different Ohm’s laws deviate in their action on D∥.
Figure 5 combines test results with the following observations. The force-free current  preserves the central charge carrying discontinuity well. Setting j∥ = 0 triggers the splitting of the central discontinuity into two waves: One charge-carrying discontinuity moving to the right, and a shallow layer to the left of the mid-point (x = 0). The resistive Ohm’s law implementing Iμ approaches the force-free solution for decreasing values of η. For η = 10−1, the largest considered value, the charge-carrying discontinuity shifts to the right of the central point. Decreasing the resistivity to smaller values η = 10−3 almost reproduces the ideal FFE results: Both charge and stabilizing currents around the central point gradually increase.
preserves the central charge carrying discontinuity well. Setting j∥ = 0 triggers the splitting of the central discontinuity into two waves: One charge-carrying discontinuity moving to the right, and a shallow layer to the left of the mid-point (x = 0). The resistive Ohm’s law implementing Iμ approaches the force-free solution for decreasing values of η. For η = 10−1, the largest considered value, the charge-carrying discontinuity shifts to the right of the central point. Decreasing the resistivity to smaller values η = 10−3 almost reproduces the ideal FFE results: Both charge and stabilizing currents around the central point gradually increase.
 |
Fig. 5. Three-wave test (Δx = 0.0125) employing different Ohm’s laws. We display the magnetic field component By, the electric charge ρ, as well as the magnitudes of the parallel (j∥) and perpendicular (j⊥) projections of the current. Top panels: conventional force-free current IFF (black color, Eq. (27)) and j∥ = 0 (blue color) with an algebraic enforcement of the force-free conditions. Bottom panels: FFE current (Eq. (29)) for different values of η. |
The fact that decreasing values of the phenomenological resistivity η approach the results from ideal FFE is showing (reassuringly) that the numerical resistivity in our ideal formulation of FFE is below 10−3 even in charge-carrying discontinuities. This physical resistivity corresponds to a magnetic Reynolds number of ℛm = 𝒱ℒ/η = 12.5, when one considers 𝒱 = 1 and ℒ = Δx (the natural lengthscale ℒ for this test is the width of the discontinuity, which is numerically of order Δx). We note that the typical length scale is purely numerical, while the resistivity is physical. Since the Riemann problem we are dealing with is self-similar (at least in the ideal limit η → 0), strictly speaking, there is no physical characteristic length scale. Thus, interpretation of the estimated value of the Reynolds number has to be taken with caution. It simply compares the light-crossing time of a numerical cell, Δt = Δx, with the resistivity (which has dimensions of time in our units), and states that the resistivity is ∼10 times smaller than Δt in this test. The results presented in Fig. 5 also include somewhat counter-intuitive observations: Setting j∥ = 0 and enforcing the force-free conditions algebraically (hence, η → 0, Yu 2011) shows a similar behavior as the case of η = 10−1 (hence, η ≫ 0) in the resistive modeling. We attribute this contradictory behavior to the feature of enhanced charge conservation, which we ensure in our code (see Paper I). Abandoning part of the current (j∥) and only enforcing D ⋅ B = 0 algebraically leads to an inconsistency between the charge ρ and the electric field D. As we evolve the continuity equation of the charge density (and do not reconstruct ρ = divD in every timestep, as most other FFE codes do) the algebraic reset of the electric fields to enforce D ⋅ B = 0 without a consistent modeling of the respective Ohm’s law in the source terms is no longer adequate. The possible mismatches between charge densities and electric fields become obvious in this test and justifies the additional evolution equation we include into our scheme to ensure the long-term validity of charge-densities and electromagnetic fields in global astrophysical simulations (as we found especially useful in Mahlmann et al. 2019, 2020).
3.2. Tearing modes driven by physical resistivity
In this section, we repeat the TM tests from Sect. 2.2 for the resistive current Iμ from Eq. (29). In all cases we use κI = 512. We aim at probing if such phenomenological currents can be used to model resistive layers in FFE more accurately, in the limit of decreasing resistivity. The principal idea behind this test is that in resistive FFE simulations we have two sources of resistivity. Namely, the physical resistivity η, set in the expression for the current, and the numerical resistivity η*, depending on the numerical scheme and resolution (as seen in Sect. 2.2). For sufficiently high resolution, one should obtain convergent results depending only on η. If the resolution is decreased, the point at which the growth rate γTM starts differing from the converged result should correspond to η* ∼ η, and marks the limit at which effects of numerical resistivity become dominant. This allows for an independent estimation of the numerical resistivity of the code, to be compared with those in Sect. 2.2.
Figure 6 assembles growth rates for different values of the resistivity parameter η. If the imposed physical resistivity is well above the numerical resistivity quantified in Sect. 2.2, namely, η* < η, the measured growth rates γTM converge to a single value almost independently of the employed resolution and reconstruction method. As η is reduced approaching the limit set by the numerical resistivity, the growth rates become more scattered around the corresponding converged value. In cases where numerical and imposed resistivity are comparable, η* ≈ η, (e.g., for MC reconstruction with the lowest η) the growth rate can be explained by the combined effect of numerical and physical resistivity. Finally, we expect that in case of η* > η, the evolution is fully dominated by numerical resistivity.
 |
Fig. 6. Measured growth rates for simulations using different resistivity parameters η in the resistive current density, Eq. (29), and for different reconstruction schemes (MC: magenta, MP5: red, MP7: blue, MP9: black) as a function of the numerical resolution. Thick lines in the background show the fits obtained in Sect. 2.2 for numerical simulations without any added resistivity (see Fig. 3). As η is lowered, the effect of numerical resistivity emerges (especially in the bottom left corner of the panel). Dashed gray lines mark the values of the growth rates corresponding to the values of η used in the different series of simulations, computed using Eq. (19). |
The solution in the regime with finite resistivity differs in qualitative ways with respect to the ideal FFE case. According to (Low 1973) the velocity component Vz is driven to a finite value η/a asymptotically by the employed isotropic resistivity model. We observe this feature in Fig. 7, where the drift velocity approaches asymptotically the dashed gray line representing η/a. This behavior differs from the ideal case studied in Sect. 2.2, where V = 0 asymptotically (for sufficiently high numerical resolution, as seen in Fig. 4). The key difference between both cases is that the numerical resistivity measured in Sect. 2.2 acts mainly in the region of the current sheet, while in the resistive simulations in this section η is the same over the whole domain. Therefore, the (physical) boundary conditions of both sets of simulations differ slightly (although in the limit η → 0 they do converge).
 |
Fig. 7. As Fig. 4 but showing one specific reconstruction method (MP7) for different resistivity parameters η. The asymptotic velocity is driven to a magnitude η/a (dashed gray lines), different from zero, by the isotropic phenomenological resistivity employed in Iμ. |
The widths of the resistive layers also differ from the FFE results. In Sect. 2.2 (see Fig. 4) we found that the size of the resistive layer was effectively of the size of a few numerical cells. However, in the resistive simulations (see Fig. 7) the widths of the resistive layers (estimated as the extent between the extrema of the drift velocity profile) extends well beyond a few grid zones off the central current sheet, especially for η > η*. In this case, the layer is well resolved. The difference between the two classes of simulations is that in resistive FFE the width of the resistive layer is set by the value of η while in the ideal FFE case its width is set by the numerical resistivity and shrinks with increasing resolution. In other words, the velocity should vanish as the numerical resistivity decreases and indeed this is what is seen in Fig. 4: for higher reconstruction order there is smaller resistivity and, hence, smaller drift velocity. Similar behavior is observed for the case with physical resistivity (Fig. 7) in which, as long as the physical resistivity dominates over the numerical one, the drift velocity decreases with decreasing resistivity. We note however, that close to the current sheet, numerical resistivity starts to dominate toward the lower panels. In conclusion, the width of the shear layer in FFE is a moving target as we increase resolution and, depending on the numerical scheme used, it may not be possible to resolve it with increasing resolution. For cases with η ≈ η*, additional (local) maxima emerge corresponding to a thinner resistive layer associated with numerical resistivity (see bottom panels of Fig. 7).
The fact that the region of convergent results of η > η* roughly coincides with the limits established in our previous tests further supports our findings from Sect. 2.2: For intermediate resolutions of p ≈ 10, our GRFFE tool has a numerical resistivity below η* ≈ 10−4, corresponding to a magnetic Reynolds number of ℛm ≈ 100 (estimated by taking the characteristic length scale given by Eq. (22)). We stress that other physical length scales could be used to define a magnetic Reynolds number, for example, L or a, for which one would find ℛm, L ≈ 20 000 and ℛm, L ≈ 2 × 1000, respectively. Hence, a magnetic Reynolds number classifies the diffusive regime in which our results are obtained ambiguously at best.
Phenomenological Ohm’s laws as the one introduced in Eq. (29) are apt to model resistive effects in FFE. Although we cannot expect, for the time being, to be able to work with the values of resistivity expected in most astrophysical scenarios, at least we can aim at performing simulations with controlled values of the resistivity and study its behavior in the limit of vanishing η. Notwithstanding these encouraging results, using resistive FFE brings its own problems, such as the appearance of a non zero asymptotic drift velocity moving away from the resistive layer in TMs. This indicates the need for further fine-tuning when employing resistive Ohm’s laws in FFE. Non-isotropic resistivities (as employed, e.g., in Komissarov 2004) or current-sheet-capturing models (as used in Parfrey et al. 2017) are candidates for driving the asymptotic dynamics of current sheet instabilities further toward the physical solution. Such fine tuning is very likely to depend on the employed method and the problem at hand, namely, the correct determination of the threshold η ≈ η*. A full implementation of different resistive FFE models with nonconstant or non-isotropic resistivities will be further explored in the future. Correctly modeling phenomenological Ohm’s laws could be a valuable asset when bridging codes of different plasma regimes as they allow for physical transition layers (and consistent signal propagation).
4. Discussion
The discretization of any system of partial differential equations (PDEs) on a finite mesh of cells to make them amenable for their numerical integration unavoidably introduces numerical diffusion and dispersion. The equations of GRFFE are no exception to this rule. Furthermore, the necessity of enforcing the conditions specific to GRFFE (D ⋅ B = 0 and B2 − D2 > 0) is an additional source of numerical diffusion. The use of monotonic and consistent numerical methods guarantees the convergence to the physical non-dissipative solution of a problem in the limit of vanishing cell size. In this limit (which is unreachable in practice), the effects of numerical diffusivity are unimportant. However, for any finite cell size of practical use (especially in 3D models), numerical diffusion does not necessarily mimic the effects of physical dissipation, particularly when the numerical discretization of the PDEs is performed employing high-order methods. It is therefore sound to assess the effects of numerical diffusion as a source of dissipation specifically in (GR)FFE, which should, in theory, not incorporate any physical dissipation.
We have performed a number of tests to quantify the amount of numerical dissipation as a function of resolution in our numerical algorithm. For that purpose, we have employed tests in 1D and 2D, but not 3D tests. This is, firstly, due to the lack of straightforward genuinely 3D analytic solutions including resistivity in the literature. Secondly, 3D tests are computationally much more expensive than 1D or 2D numerical experiments. Nevertheless, we assume that the multidimensional nature of 2D tests presented should also shed light on the numerical dissipation in 3D. Numerical experience tells us that the dissipation introduced by algorithms based upon a directional (split) integration of the equations is only (very) weakly dependent on dimensionality. Backing up these assumption, we have shown here in this work that the level of numerical resistivity depends on the number of zones per characteristic size to be resolved in every dimension (compare the values of η* in Sect. 2.1 for 1D, Sect. 2.2 for 2D), and not on the dimensionality of the problem.
In the following sections, we address the similarities and differences between numerical and physical resistivity in FFE. The aim of this discussion is to provide support for the interpretation of the numerical dissipation found in astrophysical applications of our code (Mahlmann et al. 2019, 2020) as a consistent model of physical dissipation. Along the way, we may also contribute to asses whether suitably extended FFE models (including physical dissipation, albeit not at the astrophysically expected levels) may be used to study a number of dissipative processes in relativistic astrophysics, for example, resistive solutions for pulsar magnetospheres (Li et al. 2012), the dissipation induced by the kink instability in relativistic jets (Bromberg et al. 2019), or the conversion between fast and Alfvén modes (Li et al. 2019).
4.1. Tearing modes in ideal FFE
In physically driven TMs, the resistive effects are restricted to the so-called resistive layer, with width LR ≪ a for inviscid, incompressible MHD plasma (e.g., Furth et al. 1963). Resolving the resistive layer numerically is challenging, due to the hierarchy of scales LR ≪ a ≪ L that must be spanned in these experiments (Rembiasz et al. 2017). LR depends on resistivity and TM growth rate (Rembiasz et al. 2017):
where we have replaced the physical resistivity by the numerical one in account of the fact that the TMs in our models employing the force-free current  are induced by numerical resistivity. Also, we used vA = 1 (in the limit of FFE) and highlighted the dependence of LR on the product (γTMη∗)1/4.
are induced by numerical resistivity. Also, we used vA = 1 (in the limit of FFE) and highlighted the dependence of LR on the product (γTMη∗)1/4.
The growth rate, γTM, and the physical resistivity, η, depend on each other (Eqs. (19) and (21)). However, the relation between γTM and the numerical resistivity η* is, a priori, unknown. This is the reason to test more than a single possible limit in Sect. 2.2 (i.e. to consider models A and B). In both, γTM → 0 and η* → 0 as the grid spacing decreases; the rate at which they approach zero depends on the order of the method. Hence, there is no guarantee that the product γTMη∗ in Eq. (33) tends toward a finite (nonzero) value as the grid spacing is decreased (independently of the order of spatial convergence of the method).
The width of the resistive layer in our numerical experiments can be approximately obtained by the half-distance between the two extrema of the component of the drift velocity associated with the growth of the TMs (Vz in our setup, see Fig. 4; cf. Rembiasz et al. 2017, Fig. 10). We locate the position of these velocity extrema (measured at x = 0.5) within |z| ≲ 2Δz, and typically, at z = ±Δz. In practice, these results imply that for every resolution we use, the numerical value LR ≲ Δz and, hence, there is no possibility of finding a convergent behavior. The finer the grid spacing, the smaller LR. A finer grid spacing yields smaller η*, which translates into a shorter timescale of energy-momentum loss (see below). This prevents the resistive layer to fully reach the conditions under which the growth of TMs would develop theoretically.
In order to cross-validate these findings, we assume that the numerical TMs develop in regimes where the approximations that hold for model A or model B are correct. Plugging Eq. (19) or Eq. (21) into Eq. (33), one obtains two expressions for LR(γTM), which implicitly depend on the grid spacing. For the two models A and B, the right panel of Fig. 8 shows the ratio LR(γTM)/Δz for different resolutions, and different methods of cell interface reconstruction. The obtained values LR(γTM)/Δz < 1 demonstrate that the resistive layer width is unresolved: Less than one grid zone covers the central region of the current layer, confirming our direct measurement of LR (see above). Interestingly, the estimated value of LR(γTM)/Δz depends on the spatial order of accuracy of the method. The highest-order reconstruction (MP9) yields the smallest γTMη∗, while the second-order accurate MC method allows us to resolve the resistive layer width very marginally as LR(γTM)/Δz ≳ 1.5 if more than p = 20 grid zones span the current width a.
 |
Fig. 8. TM growth rates and resistive layer size for different numerical schemes. Left: growth of the (2D) TM instability for different treatments of the parallel current and a fixed number of points per current sheet width p = 6. We display our standard method for treating J|| (i.e., with a fourth-order accurate discretization of the derivatives, solid lines), extreme cases in which J|| = 0 (dotted lines, following Yu 2011), and the case in which the algebraic condition D ⋅ B = 0 is not enforced (dashed lines). Different colors correspond to distinct reconstructions (see legends). In the case of no enforcement of the D ⋅ B = 0, the results are indistinguishable for the three MP reconstructions. Right: size of the resistive layer LR normalized to the grid spacing Δz in the direction perpendicular to the current sheet for all the reconstruction methods (see legends) and models (A, circles and B, squares). |
In the light of the previous considerations, we can now discuss our assumption of a fixed characteristic length, independent of resolution (22). For that, we have also analyzed the results following more closely the procedure of Rembiasz et al. (2017): We use ℒ = LR, substitute expression (33) into Eq. (10), and isolate η* as a function of γTM, Δz, and the remaining parameters of the problem. This expression η∗(γTM,Δz) is then provided to Eq. (18), which yields a power-law dependence γTM ∝ Δz3r/(3 + 2r) for model A. Analogously, for model B one obtains γTM ∝ Δz4r/(5 + 3r). Thus, the slope of the relation in Eq. (24) is related with the order of convergence r through
Evaluating r using Eqs. (34) or (35) yields inaccurate results, since the assumption that LR is given by Eq. (33) is only approximated (as shown above). The degree of inaccuracy is roughly quantified in the last column of Table 2, where we show the deviation of the fit parameter m with respect to its analytical value, ma, assuming that r is equal to the formal order of convergence of the respective method (i.e., we calculate Δm/m := 1 − ma/m). The empirical order of convergence is very sensitive to the exact value of m. This sensitivity is rooted on the dependence of LR on Δz. We evaluate this dependence in our results in the right panel of Fig. 8. Repeating the exercise of the previous paragraph but isolating LR, one finds a dependence with resolution LR/Δz ∝ ΔzmL, where
Therefore, mL ≲ 0 for positive values of r. A direct comparison with the data in the right panel of Fig. 8 suggests a small positive value of the exponent mL, namely, mL ≳ 0. We also highlight the fact that a value mL ≈ 0 would not allow one to reliably obtain r from the slope of the linear fit in Eq. (24). Therefore, assuming that the physical relation of Eq. (33) holds is not appropriate in our models.
Admittedly, the assumption made in Eq. (22) is simplistic, but it serves for a double purpose. First, it states that ℒ ≪ a. Second, it provides an order of magnitude estimate of the numerical resistivity. A direct inspection of Fig. 3 shows that η* is below 10−4 (2 × 10−6) even using p = 6 points across the current layer width and employing MC (MP9) reconstruction. A direct comparison with the results obtained by the diffusion of 1D plasma waves (Sect. 2.1) is not straightforward due to the different meaning of p. For 1D plasma waves p expresses the number of numerical zones per characteristic length of the problem (i.e., the wavelength of the waves). Here it is the number of zones per current sheet width, a scale that is (significantly) larger than the characteristic scale of the problem at hand (i.e., LR). Thus, the estimate of η* via TMs is less accurate than it is in the 1D case. It is a lower bound to the true numerical resistivity of our method as verified with the results of Sect. 3.2.
4.2. Contrasting Numerical Resistivity in MHD and FFE
The described situation is specific to the numerical modeling of FFE: The dissipation of energy in current sheets proceeds nearly instantaneously when the force-free conditions are algebraically enforced (Sect. 3.3 of Paper I). Energy-momentum may leak out of the system. Contrasting this, the electromagnetic energy in resistive MHD may be stored in other forms of energy (kinetic or thermal) as resistive processes develop within the system. Indeed, even when employing an ideal MHD numerical modeling, the numerical resistivity may find channels to convert magnetic energy-momentum into other dynamical components of the system (e.g., Rembiasz et al. 2017). In Fig. 9 we directly compare the estimates of numerical resistivity determined in Sects. 2.1 and 2.2, for our FFE code, with the characterization of the 3D Eulerian MHD code AENUS (Obergaulinger 2008; Rembiasz et al. 2017). The contrasting results for plasma waves and TMs lucidly illustrate a key feature of FFE methods: While smooth plasma waves are resolved with very competitive accuracy, comparable to the reference MHD code, the limits of ideal FFE are reached in resistive layers and discontinuities (e.g., current sheets). The presented comparison of TMs (right panel of Fig. 9) is merely an approximation due to the physical differences between the FFE and MHD regime. The fact that our FFE method shows less numerical diffusion than the MHD reference at small resolutions must be taken with care. Rather than an improvement of the method, this signature highlights the fact that, in the presence of current sheets, numerical resistivity in FFE does not necessarily behave as the physical one.
 |
Fig. 9. Comparison of normalized numerical resistivity η*/(ℒ𝒱) ( |
The physical conditions under which FFE is valid may mimic, to some extend, plasma regimes The enforcement of the constraints of FFE is an intrinsically nonconservative process, acting almost instantaneously (see Sect. 3.3 of Paper I). As a direct consequence, energy-momentum may leak out of the numerical domain over timescales as small as the simulation time step. Differently from (relativistic) MHD, the numerical resistivity of an FFE code not only depends on the discretization of the partial differential equations, but also on the degree by which the FFE constraints are violated during the time evolution. The amount by which FFE conditions are not preserved does not necessarily decrease with increasing resolution. Thus, the numerical resistivity effectively acts as a timescale for the numerical dissipation of the electromagnetic energy-momentum, where smaller values of η* yield shorter cooling timescales in the sense that ideal (perfectly conducting) FFE most efficiently dissipates nonideal electric fields. However, the effects of cooling are not specifically accounted for in the derivation of the dispersion relation of TMs (in our case Eqs. (18) and (19)). We may interpret that the standard TM dispersion relation (which strictly holds in adiabatic, incompressible MHD) is adequate for conditions of extremely slow cooling rather than in the limit of effective cooling that the FFE conditions impose. As η* is predominantly dictated by the order of the method, only FFE methods of relatively low-order may yield numerical dissipation timescales long enough that conditions of (sufficiently) slow cooling hold. However, this feature significantly differentiates FFE from (relativistic) MHD, where η* cannot be interpreted as a cooling timescale at all.
4.3. The role of j|| in FFE codes
The part of the force-free current which is along the magnetic field (j||) is closely related to the force free conditions: The current  conserves the perpendicularity of the electromagnetic fields. This can be done either by combining
conserves the perpendicularity of the electromagnetic fields. This can be done either by combining  , namely, the condition ℒn(B ⋅ D) = 0 or its flat space equivalent ∂t(D⋅B) = 0, with an algebraic enforcement of perpendicularity. Alternatively, the algebraic enforcement can be replaced by suitable Ohm’s laws in the limit of low resistivity, as the one employed by Parfrey et al. (2017), which we probed in Sect. 3.
, namely, the condition ℒn(B ⋅ D) = 0 or its flat space equivalent ∂t(D⋅B) = 0, with an algebraic enforcement of perpendicularity. Alternatively, the algebraic enforcement can be replaced by suitable Ohm’s laws in the limit of low resistivity, as the one employed by Parfrey et al. (2017), which we probed in Sect. 3.
As commented above, not enforcing an instantaneous fulfilment of the FFE conditions is equivalent to introducing a finite timescale for (resistive) dissipation of energy-momentum in the system of equations. If this finite timescale is long enough, the effective cooling may be relatively small during a sizable fraction of the linear phase of TM development. Hence, conditions of relatively slow (inefficient) cooling can be phenomenologically mimicked in this way. However, beyond the timescale mentioned above, energy-momentum yet continues to leak out of the system. This energy is not converted to other dynamical forms, again, differing from the physical mechanisms of energy-momentum transformation operating in resistive MHD.
The left panel of Fig. 8 shows the effect of different methods for the discretization of j|| on the measured TM growth rates. The solid lines correspond to our default fourth-order accurate discretization of j|| in combination with different methods of cell interface reconstruction and a fixed number of points per current sheet width p = 6. The dashed lines correspond to taking j|| = 0 (following Yu 2011). Clearly, employing j|| = 0 yields a significantly smaller growth rate and, hence a significantly smaller numerical resistivity. However, employing this procedure, the three-wave Riemann problem renders nonphysical results as the reduced numerical diffusivity of the method allows for the breakup of the fast waves into a pair of discontinuities (one of which should not exist; see top left panel of Fig. 5). We further probed this specific pathology in the context of nonideal FFE in Sect. 3.1. We attribute the inaccurate modeling of charge carrying current-layers in this particular case (j|| = 0, but enforcing the force-free conditions algebraically) to the continuity equation of charge which we evolve in our method (Mahlmann et al. 2021). Not supplying a current which is consistent with the plasma dynamics, namely, altering the electric field algebraically without feedback to the currents and charges they support, introduces errors into the numerical solution that will eventually lead to nonphysical behavior. For reference, we also display our default fourth-order discretization of j|| (dash-dotted lines). However, in this case, we do not enforce the algebraic fulfillment of the D ⋅ B = 0 condition. This is an extreme case (or upper bound) in terms of numerical resistivity since it yields the largest growth rate of all the models displayed in Fig. 8. The growth is so fast, that results with different cell interface reconstructions are indistinguishable and all the lines are located on top of each other. From these results, we conclude that without resorting to phenomenological approaches to introduce resistive dissipation in the current parallel to the magnetic field, the limits of FFE as a zeroth-order approximation of relativistic MHD are reached (and breached) in current sheets.
At this point, it is important to highlight that alternative expressions of the force-free current  (Eq. (27)) may help to increase the timescale over which electromagnetic dissipation in FFE is generated. These alternative expressions of the spatial current encode different forms of Ohm’s law in order to derive the functional form of j|| (see, e.g., Sect. 2.3 of Alic et al. 2012, for a comprehensive overview and also Lyutikov 2003; Li et al. 2012; Parfrey et al. 2017). Such alternative Ohm’s laws relax the strict fulfillment of the FFE conditions temporarily. Instead, the FFE constraints are asymptotically enforced with suitable driving terms (see Sect. 3.3 of Paper I) or by adopting some phenomenological form of anisotropic electric conductivity, similar to the approach we have introduced in Sect. 3. There, we employ and test the isotropic resistivity model suggested in Parfrey et al. (2017), which induces a simple Ohm’s law of the form
(Eq. (27)) may help to increase the timescale over which electromagnetic dissipation in FFE is generated. These alternative expressions of the spatial current encode different forms of Ohm’s law in order to derive the functional form of j|| (see, e.g., Sect. 2.3 of Alic et al. 2012, for a comprehensive overview and also Lyutikov 2003; Li et al. 2012; Parfrey et al. 2017). Such alternative Ohm’s laws relax the strict fulfillment of the FFE conditions temporarily. Instead, the FFE constraints are asymptotically enforced with suitable driving terms (see Sect. 3.3 of Paper I) or by adopting some phenomenological form of anisotropic electric conductivity, similar to the approach we have introduced in Sect. 3. There, we employ and test the isotropic resistivity model suggested in Parfrey et al. (2017), which induces a simple Ohm’s law of the form  . Several other choices of suitable Ohm’s laws are imaginable and found at least to some extend throughout the literature, for example, with different values along and across the magnetic field lines (Komissarov 2004). By employing such techniques, Komissarov et al. (2007) reproduce the theoretical dispersion relation for TMs roughly, employing a second-order accurate method in combination with a (phenomenological) anisotropic conductivity. As such, it corresponds to a plasma with seemingly large resistivity (η = 10−4 − 10−3), and even qualitatively reproduces the linear phase of collapse of stressed current sheets as compared with PIC simulations (Lyutikov et al. 2017). Future upgrades of our methodology will explore the impact of different forms of the Ohm’s law in the numerical diffusivity of the algorithm more quantitatively; in Sect. 3 we have characterized one specific prescription of resistive FFE in this context.
. Several other choices of suitable Ohm’s laws are imaginable and found at least to some extend throughout the literature, for example, with different values along and across the magnetic field lines (Komissarov 2004). By employing such techniques, Komissarov et al. (2007) reproduce the theoretical dispersion relation for TMs roughly, employing a second-order accurate method in combination with a (phenomenological) anisotropic conductivity. As such, it corresponds to a plasma with seemingly large resistivity (η = 10−4 − 10−3), and even qualitatively reproduces the linear phase of collapse of stressed current sheets as compared with PIC simulations (Lyutikov et al. 2017). Future upgrades of our methodology will explore the impact of different forms of the Ohm’s law in the numerical diffusivity of the algorithm more quantitatively; in Sect. 3 we have characterized one specific prescription of resistive FFE in this context.
5. Conclusions
We have very carefully assessed the numerical resistivity of our new GRFFE code. This topic is of the utmost importance to interpret the dissipation of magnetic flux and energy in magnetically dominated astrophysical scenarios. The intrinsic numerical resistivity of our code depends on the number of numerical cells per characteristic size of the structure we aim to resolve. We have considered two types of tests. (1) The damping of 1D plasma waves. Such ideal (smooth) waves allow for a direct comparison of the damping rates with existing analytic results in the literature. (2) The growth of TMs, induced by the action of the numerical resistivity, in a simple 2D setup. The growth rate of the TMs depends (nonlinearly) on the numerical resistivity. We have performed an extensive suite of tests with different resolutions, spatial reconstruction methods and different forms of Ohm’s law (i.e., different closure relations for the current as a source of the electromagnetic field and flux of charge conservation). With this strategy, we have assessed the signatures of numerical resistivity in our specific method, and FFE codes in general. We have related these findings to the employed numerical techniques as well as to the grid spacing employed for the discretization of the plasma continuum.
Resolving a characteristic length ℒ with at least ∼5 (10) numerical zones is required to reduce the numerical resistivity to values below η* ∼ 10−2 (η* ∼ 10−4). In practical applications of our code to, for example, global 3D models of magnetar magnetospheres (Mahlmann et al. 2019) we employ a typical resolution of 32 zones per radius of the magnetar, R*. Hence, at scales of 1R* our magnetosphere models incorporate a numerical resistivity of ∼10−5 − 10−8 (MP5 vs. MP9 reconstruction). In the same models, we observe that there exists dissipation of magnetic energy on structures with sizes as small as ∼0.1R* (Mahlmann et al. 2019). At these scales, the numerical resistivity can be as large as η* ∼ 10−2. Similar comments are in place for global 3D models of BH magnetospheres, where we have also used 32 cells per gravitational radius in the finest grid surrounding the BH (but 16 zones in the extended region surrounding the BH; Mahlmann et al. 2020). Finding dissipation on scales on the order of one gravitational radius in the vicinity of the BH (induced by the generation of local current sheets) means that the numerical resistivity of our code was ≲10−5 in these (small) regions of the whole computational domain. We highlight the non-uniform character of numerical resistivity in practical applications. For sufficiently small scales, a GRFFE code may become extremely resistive. This justifies the implementation of very high-order spatial reconstruction methods in GRFFE, even at the cost of some parallel performance loss due to the increased number of (internal) boundary zones that need to be synchronized. As we have shown, for resolutions at reach in global 3D numerical simulations (say of 5 − 10 cells per length scale to be resolved) using a seventh-order accurate method as MP7 reduces the numerical resistivity by more than two orders of magnitude compared to, for example, employing a second-order accurate method such as MC reconstruction.
The tested resistive FFE using a simple Ohm’s law (Eq. (29), and Parfrey et al. 2017) is able to induce the expected phenomenological behavior in a current-carrying discontinuity (Sect. 3.1): With increasing (physical) resistivity η, the current (and associated charge density) sustaining a standing Alfvén wave becomes weaker and the layer diffuses (Fig. 6). Eventually, the solution becomes nonphysical and sharp transition layers emerge. On the other hand, the force-free solution is recovered for low values of η. In the case of TMs, the considered Ohm’s law converges toward growth rates comparable to the ones expected by the dynamics driven by a physical resistivity when endowed with η above the threshold of numerical resistivity.
We are, in conclusion, able to give three answers to the initially posed questions: (a) With an accurate modeling of the current j∥ (including a sufficiently high-order discretization of it), our finite volume ideal FFE code resolves smooth current-carrying plasma waves with close-to-exact accuracy. (b) In force-free current sheets a true limit of ideal FFE is reached; resistive layers cannot be resolved on distances on the order of the grid-scale. (c) When reducing the numerical resistivity by increasing resolution or the numerical accuracy (increasing the order of the spatial reconstruction), growth rates of the considered dynamical instability (TMs) in FFE are not fully comparable with their counterpart in numerical experiments, for example, in resistive MHD. The estimated order of accuracy of the FFE method is reduced in such regions. The action of numerical resistivity in the limit of validity of FFE does not exactly match the action of physical resistivity. In other words, numerical resistivity does not necessarily mimic physical resistivity in tearing-unstable current sheets. Alternative Ohm’s laws that incorporate a physical resistivity are promising candidates for a correct physical modeling of genuinely resistive effects in FFE. Thus, they may be used as an algorithmic strategy to bridge between plasma regimes in hybrid simulation tools combining, for example, FFE with particle in cell simulations (Parfrey et al. 2019). The numerical techniques presented in this series of publications are able to resolve the global dynamics of force-free plasma with a great consistency of its physical constituents and achieves competitive accuracy.
Acknowledgments
We appreciate the helpful comments and perspectives contributed by the anonymous referee. We thank B. Ripperda and A. Philippov for their perspectives on plasma (codes). We acknowledge the fruitful discussions with T. Rembiasz, as well as his critical revision of the results related to the characterization of the numerical diffusivity of our code. JM acknowledges a Ph.D. grant of the Studienstiftung des Deutschen Volkes. We acknowledge the support from the grants AYA2015-66899-C2-1-P, PGC2018-095984-B-I00, PROMETEO-II-2014-069, and PROMETEU/2019/071. We acknowledge the partial support of the PHAROS COST Action CA16214 and GWverse COST Action CA16104. PCD acknowledges the Ramon y Cajal funding (RYC-2015-19074) supporting his research. VM is supported by the Exascale Computing Project (17-SC-20-SC), a collaborative effort of the US Department of Energy (DOE) Office of Science and the National Nuclear Security Administration. Work at Oak Ridge National Laboratory is supported under contract DE-AC05-00OR22725 with the US Department of Energy. VM also acknowledges partial support from the National Science Foundation (NSF) from Grant Nos. OAC-1550436, AST-1516150, PHY-1607520, PHY-1305730, PHY-1707946, and PHY-1726215 to Rochester Institute of Technology (RIT). The shown numerical simulations have been conducted on infrastructure of the Red Española de Supercomputación (AECT-2020-1-0014) as well as of the University of Valencia Tirant and LluisVives supercomputers. This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the US Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a nonexclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
References
- Alic, D., Moesta, P., Rezzolla, L., Zanotti, O., & Jaramillo, J. L. 2012, ApJ, 754, 36 [Google Scholar]
- Ball, D., Sironi, L., & Özel, F. 2019, ApJ, 884, 57 [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [Google Scholar]
- Bromberg, O., Singh, C. B., Davelaar, J., & Philippov, A. A. 2019, ApJ, 884, 39 [Google Scholar]
- Campos, L. M. B. C. 1999, Phys. Plasmas, 6, 57 [Google Scholar]
- Carrasco, F., Viganò, D., Palenzuela, C., & Pons, J. A. 2019, MNRAS, 484, L124 [Google Scholar]
- Del Zanna, L., Papini, E., Landi, S., Bugli, M., & Bucciantini, N. 2016, MNRAS, 460, 3753 [Google Scholar]
- Furth, H. P., Killeen, J., & Rosenbluth, M. N. 1963, Phys. Fluids, 6, 459 [Google Scholar]
- Gruzinov, A. 2007, ArXiv e-prints [arXiv:0710.1875] [Google Scholar]
- Guo, F., Li, X., Daughton, W., et al. 2019, ApJ, 879, L23 [Google Scholar]
- Harra, L., & Mason, K. 2004, Space Science (Imperial College Press) [Google Scholar]
- Kilian, P., Li, X., Guo, F., & Li, H. 2020, ApJ, 899, 151 [Google Scholar]
- Komissarov, S. S. 2004, MNRAS, 350, 427 [Google Scholar]
- Komissarov, S. S. 2011, MNRAS, 418, L94 [Google Scholar]
- Komissarov, S. S., Barkov, M., & Lyutikov, M. 2007, MNRAS, 374, 415 [Google Scholar]
- Li, J., Spitkovsky, A., & Tchekhovskoy, A. 2012, ApJ, 746, 60 [Google Scholar]
- Li, X., Zrake, J., & Beloborodov, A. M. 2019, ApJ, 881, 13 [Google Scholar]
- Low, B. C. 1973, ApJ, 181, 209 [Google Scholar]
- Lyutikov, M. 2003, MNRAS, 346, 540 [Google Scholar]
- Lyutikov, M., Sironi, L., Komissarov, S. S., & Porth, O. 2017, J. Plasma Phys., 83 [Google Scholar]
- Lyutikov, M., Komissarov, S., Sironi, L., & Porth, O. 2018, J. Plasma Phys., 84, 635840201 [Google Scholar]
- Mahlmann, J. F., Akgün, T., Pons, J. A., Aloy, M. A., & Cerdá-Durán, P. 2019, MNRAS, 490, 4858 [Google Scholar]
- Mahlmann, J. F., Levinson, A., & Aloy, M. A. 2020, MNRAS, 494, 4203 [Google Scholar]
- Mahlmann, J. F., Aloy, M. A., Mewes, V., & Cerdá-Durán, P. 2021, A&A, 647, A57 (Paper I) [EDP Sciences] [Google Scholar]
- Miranda-Aranguren, S. M., Aloy, M. A., & Aloy, C. 2014, in Magnetic Fields throughout Stellar Evolution, eds. P. Petit, M. Jardine, & H. C. Spruit, IAU Symp., 302, 64 [Google Scholar]
- Miranda-Aranguren, S., Aloy, M. A., & Rembiasz, T. 2018, MNRAS, 476, 3837 [Google Scholar]
- Nathanail, A., Fromm, C. M., Porth, O., et al. 2020, MNRAS, 495, 1549 [Google Scholar]
- Obergaulinger, M. 2008, Ph.D. Thesis, Max-Planck-Institut für Astrophysik, Garching bei München [Google Scholar]
- Obergaulinger, M., & Aloy, M.-Á. 2020, J. Phys. Conf. Ser., 1623, 012018 [Google Scholar]
- Palenzuela, C., Lehner, L., Reula, O., & Rezzolla, L. 2009, MNRAS, 394, 1727 [Google Scholar]
- Parfrey, K., Beloborodov, A. M., & Hui, L. 2013, ApJ, 774, 92 [Google Scholar]
- Parfrey, K., Giannios, D., & Beloborodov, A. M. 2015, MNRAS, 446, L61 [Google Scholar]
- Parfrey, K., Spitkovsky, A., & Beloborodov, A. M. 2017, MNRAS, 469, 3656 [Google Scholar]
- Parfrey, K., Philippov, A., & Cerutti, B. 2019, Phys. Rev. Lett., 122, 035101 [Google Scholar]
- Petropoulou, M., Sironi, L., Spitkovsky, A., & Giannios, D. 2019, ApJ, 880, 37 [Google Scholar]
- Punsly, B. 2003, ApJ, 583, 842 [Google Scholar]
- Rembiasz, T., Obergaulinger, M., Cerdá-Durán, P., Aloy, M.-Á., & Müller, E. 2017, ApJS, 230, 18 [Google Scholar]
- Ripperda, B., Bacchini, F., & Philippov, A. 2020, ApJ, 900, 2 [Google Scholar]
- Suresh, A., & Huynh, H. T. 1997, J. Comput. Phys., 136, 83 [Google Scholar]
- van Leer, B. 1977, J. Comput. Phys., 23, 276 [Google Scholar]
- Yu, C. 2011, MNRAS, 411, 2461 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Assessment of numerical resistivity (normalized, see Eq. (14)) as a function of grid points per wavelength for a 1D static diffusion test (series A) as well as propagating 1D plasma waves (series B and C, i.e., fast and Alfvén). Numerical fit parameters (Table 1) are obtained for the data points of the m = 1 mode (dashed lines). For series C, the discretization order of the numerical derivatives in the calculation of the current j∥ has significant impact on the order of convergence. Thick lines in the background employ standard fourth-order finite differences in the calculation of reconstruction of j∥, while solid thin lines display the improved high-order finite differences (Sect. 3.4, Paper I). |
| In the text | |
 |
Fig. 2. Exemplary amplitude evolution of selected modes of the fast wave model (showing m = 1, m = 2, as well as the superposition m = 1, 2). The time is normalized to the light crossing time of the computational domain (τ). Left: field amplitude at the point y = 0 for a superposition of modes m = 1, 2 (top panel), m = 2 (middle), and m = 1 (bottom). The analytic solution is indicated in the background (thick magenta lines). Different resolutions are visualized by solid (Ny = 12) and dotted (Ny = 24) lines. Right: evolution of the energy contained in the perturbations, given by Eq. (8), scaled to |
| In the text | |
 |
Fig. 3. Growth rate of the (2D) TM instability (Sect. 2.2) for different resolutions and reconstruction schemes. We depict the measurements of γTM from numerical experiments (squares) and the corresponding best fit parameters (solid lines, Eq. (24)). The scale on the right shows the numerical resistivity computed from the measurements of the growth rate employing model A (Eq. (19)). |
| In the text | |
 |
Fig. 4. Evolution of the drift velocity Vz along the mid-point of the current sheet (x = 0.5) in the direction transverse to the current sheet (z-direction) during the linear phase (time-interval [t0,t1] for which the growth rate is derived in Fig. 3). The different panels correspond to different reconstruction schemes (see legends) and a resolution of p = 25.6 numerical zones per transverse size of the current sheet. The assumed width of the resistive layer LR employed for the analysis in Sect. 2.2 is indicated by the vertical gray lines in the background; each of these lines denotes the limits of the computational zones in the z-direction. The growth of the velocity component Vz is strongly suppressed for higher-order (MP) reconstruction methods and is significantly larger when using the MC reconstruction (we note the different scale for the lower panel). |
| In the text | |
 |
Fig. 5. Three-wave test (Δx = 0.0125) employing different Ohm’s laws. We display the magnetic field component By, the electric charge ρ, as well as the magnitudes of the parallel (j∥) and perpendicular (j⊥) projections of the current. Top panels: conventional force-free current IFF (black color, Eq. (27)) and j∥ = 0 (blue color) with an algebraic enforcement of the force-free conditions. Bottom panels: FFE current (Eq. (29)) for different values of η. |
| In the text | |
 |
Fig. 6. Measured growth rates for simulations using different resistivity parameters η in the resistive current density, Eq. (29), and for different reconstruction schemes (MC: magenta, MP5: red, MP7: blue, MP9: black) as a function of the numerical resolution. Thick lines in the background show the fits obtained in Sect. 2.2 for numerical simulations without any added resistivity (see Fig. 3). As η is lowered, the effect of numerical resistivity emerges (especially in the bottom left corner of the panel). Dashed gray lines mark the values of the growth rates corresponding to the values of η used in the different series of simulations, computed using Eq. (19). |
| In the text | |
 |
Fig. 7. As Fig. 4 but showing one specific reconstruction method (MP7) for different resistivity parameters η. The asymptotic velocity is driven to a magnitude η/a (dashed gray lines), different from zero, by the isotropic phenomenological resistivity employed in Iμ. |
| In the text | |
 |
Fig. 8. TM growth rates and resistive layer size for different numerical schemes. Left: growth of the (2D) TM instability for different treatments of the parallel current and a fixed number of points per current sheet width p = 6. We display our standard method for treating J|| (i.e., with a fourth-order accurate discretization of the derivatives, solid lines), extreme cases in which J|| = 0 (dotted lines, following Yu 2011), and the case in which the algebraic condition D ⋅ B = 0 is not enforced (dashed lines). Different colors correspond to distinct reconstructions (see legends). In the case of no enforcement of the D ⋅ B = 0, the results are indistinguishable for the three MP reconstructions. Right: size of the resistive layer LR normalized to the grid spacing Δz in the direction perpendicular to the current sheet for all the reconstruction methods (see legends) and models (A, circles and B, squares). |
| In the text | |
 |
Fig. 9. Comparison of normalized numerical resistivity η*/(ℒ𝒱) ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.










![$$ \begin{aligned} U_1=\frac{1}{2}\int \mathrm{d}V \left[\boldsymbol{B}_1^2+\boldsymbol{D}_1^2\right]\equiv U_{\rm 1i}\,e^{-2\mathfrak{D} t}. \end{aligned} $$](/articles/aa/full_html/2021/03/aa38908-20/aa38908-20-eq9.gif)




![$$ \begin{aligned} d=\ln \left[\mathfrak{N} \times \lambda \right]=\ln \left[\mathfrak{N} \times L\right]-\ln m. \end{aligned} $$](/articles/aa/full_html/2021/03/aa38908-20/aa38908-20-eq14.gif)
![$$ \begin{aligned} \ln \left[m\times \eta _{*}\right]=-r \ln p+ \ln \left[\mathfrak{N} \mathcal{V} L\right]. \end{aligned} $$](/articles/aa/full_html/2021/03/aa38908-20/aa38908-20-eq15.gif)















![$$ \begin{aligned} I^\mu&=\rho n^\mu +\frac{\rho }{{\boldsymbol{B}}^2}\eta ^{\nu \mu \alpha \beta }n_\nu D_\alpha B_\beta \nonumber \\&\quad +\frac{1}{1+\kappa _I\eta }\frac{B^\mu }{{\boldsymbol{B}}^2} \left[\,\eta ^{\sigma \alpha \beta \lambda }n_\sigma \left(B_{\lambda ; \,\beta }B_\alpha -D_{\lambda ; \,\beta }D_\alpha \right)+\kappa _I B^\sigma D_\sigma \right], \end{aligned} $$](/articles/aa/full_html/2021/03/aa38908-20/aa38908-20-eq35.gif)