| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202039515 | |
| Published online | 04 February 2021 | |
Lithium depletion and angular momentum transport in solar-type stars
1
Department of Astronomy, University of Geneva, Chemin des Maillettes 51, 1290 Versoix, Switzerland
e-mail: thibaut.dumont@unige.ch
2
LUPM, Université de Montpellier, CNRS, Place Eugène Bataillon, 34095 Montpellier, France
3
IRAP, UMR 5277 & Université de Toulouse, 14 avenue Edouard Belin, 31400 Toulouse, France
4
University of Exeter, Department of Physics and Astronomy, Stocker Road, Devon, Exeter EX4 4QL, UK
5
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris-Diderot, Sorbonne Paris Cité, 91191 Gif-sur-Yvette Cedex, France
Received:
24
September
2020
Accepted:
24
November
2020
Context. Transport processes occurring in the radiative interior of solar-type stars are evidenced by the surface variation of light elements, in particular 7Li, and the evolution of their rotation rates. For the Sun, inversions of helioseismic data indicate that the radial profile of angular velocity in its radiative zone is nearly uniform, which implies the existence of angular momentum transport mechanisms that are efficient over evolutionary timescales. While there are many independent transport models for angular momentum and chemical species, there is a lack of self-consistent theories that permit stellar evolution models to simultaneously match the present-day observations of solar lithium abundances and radial rotation profiles.
Aims. We explore how additional transport processes can improve the agreement between evolutionary models of rotating stars and observations for 7Li depletion, the rotation evolution of solar-type stars, and the solar rotation profile.
Methods. Models of solar-type stars are computed including atomic diffusion and rotation-induced mixing with the code STAREVOL. We explore different additional transport processes for chemicals and for angular momentum such as penetrative convection, tachocline mixing, and additional turbulence. We constrain the resulting models by simultaneously using the evolution of the surface rotation rate and 7Li abundance in the solar-type stars of open clusters with different ages, and the solar surface and internal rotation profile as inverted from helioseismology when our models reach the age of the Sun.
Results. We show the relevance of penetrative convection for the depletion of 7Li in pre-main sequence and early main sequence stars. The rotational dependence of the depth of penetrative convection yields an anti-correlation between the initial rotation rate and 7Li depletion in our models of solar-type stars that is in agreement with the observed trend. Simultaneously, the addition of an ad hoc vertical viscosity νadd leads to efficient transport of angular momentum between the core and the envelope during the main sequence evolution and to solar-type models that match the observed profile of the Sun. We also self-consistently compute for the first time the thickness of the tachocline and find that it is compatible with helioseismic estimations at the age of the Sun, but we highlight that the associated turbulence does not allow the observed 7Li depletion to be reproduced. The main sequence depletion of 7Li in solar-type stars is only reproduced when adding a parametric turbulent mixing below the convective envelope.
Conclusions. The need for additional transport processes in stellar evolution models for both chemicals and angular momentum in addition to atomic diffusion, meridional circulation, and turbulent shear is confirmed. We identify the rotational dependence of the penetrative convection as a key process. Two additional and distinct parametric turbulent mixing processes (one for angular momentum and one for chemicals) are required to simultaneously explain the observed surface 7Li depletion and the solar internal rotation profile. We highlight the need of additional constraints for the internal rotation of young solar-type stars and also for the beryllium abundances of open clusters in order to test our predictions.
Key words: stars: abundances / stars: rotation / stars: interiors / stars: evolution / stars: solar-type
© ESO 2021
1. Introduction
Solar-type stars (e.g., stars with an initial mass of 1 ± 0.1 M⊙ and a value of [Fe/H] = 0 ± 0.2 dex, but possibly not the same age as the Sun) have been extensively used to constrain and study transport processes of chemicals and angular momentum in stellar interiors (e.g., Pinsonneault et al. 1989; Zahn 1992; Richard et al. 1996; Talon et al. 2002; Talon & Charbonnel 2003, 2005; Eggenberger et al. 2005, 2019a; Charbonnel & Talon 2008; Castro et al. 2009; Amard et al. 2016; Baraffe et al. 2017). Currently the main challenge is to simultaneously explain the time evolution of their photospheric 7Li (hereafter Li) abundances, and of the rotation of their surface and interior. Several hints point to rotation-induced transport and mixing processes as the cause for Li depletion in the Sun and in main sequence (MS) solar-type stars (e.g., Lebreton & Maeder 1987; Pinsonneault et al. 1990; Charbonnel et al. 1992; Richard et al. 1996; Do Nascimento et al. 2009), although other mechanisms have been invoked, such as penetrative convection (Böhm 1963; Schlattl & Weiss 1999; Baraffe et al. 2017; Jørgensen & Weiss 2018); tachocline mixing (Brun et al. 1999); mass loss (Guzik & Mussack 2010); planet accretion (Montalbán & Rebolo 2002); and mixing by internal gravity waves (Montalban 1994). On the other hand, the currently available prescriptions for anisotropic turbulence and meridional circulation that are induced by rotation and that transport both chemicals and angular momentum fail to reproduce the internal rotation rates evidenced by helio- and asteroseismology (e.g., Mosser et al. 2012; Deheuvels et al. 2012, 2014, 2015, 2020; Ceillier et al. 2013; Marques et al. 2013; Benomar et al. 2015; Eggenberger et al. 2017, 2019a; Gehan et al. 2018; García & Ballot 2019; Mathis et al. 2018; Amard et al. 2019; Aerts et al. 2019). More efficient mechanisms are required for the transport of angular momentum, which could be driven by internal gravity waves or magnetic processes and instabilities (e.g., Schatzman 1993; Spruit 2002; Charbonnel & Talon 2005; Mathis & Zahn 2005; Eggenberger et al. 2005, 2010, 2019b,c; Denissenkov et al. 2010; Charbonnel et al. 2013; Belkacem et al. 2015; Pinçon et al. 2017; Fuller et al. 2019). These mechanisms also impact the transport of chemicals induced by rotation and influence the way Li is depleted with time in solar-type stars (e.g., Charbonnel & Talon 2005; Talon & Charbonnel 2005).
In this work we explore the possibilities to reproduce simultaneously the chemical and rotational constraints for solar-type stars along their evolution up to the end of the MS. In Sect. 2 we present the observational data that we aim to account for with our stellar evolution models. In Sect. 3 we describe the input physics of the models and recall the state-of-the-art expressions from the literature for the different transport processes implemented in the stellar evolution code STAREVOL, and tested in this work. In Sect. 4 we compare the predictions of the so-called Type I models for rotating stars (which only include meridional circulation, shear induced turbulence, and atomic diffusion) to the observational constraints for solar-type stars over a broad age range. In Sect. 5 we probe for effects of penetrative convection and tachocline turbulence using for the first time some rotation-dependent prescriptions. This allows us to quantify the efficiency of still missing processes that we simulate in the form of a vertical diffusivity for the transport of angular momentum, and of an ad hoc turbulence for the transport of chemicals. We summarise our results and conclude in Sect. 6.
2. Observational constraints
To best constrain the physics at play in the interior of solar-type stars along their evolution up to the MS turnoff, we use both chemical and rotational data.
2.1. Lithium abundances
Lithium has long been claimed to be a useful and constraining element that can be used to understand the transport of chemicals and of angular momentum in stellar interiors (e.g., Wallerstein & Conti 1969; Boesgaard 1976; Vauclair et al. 1978; Spite & Spite 1982; Baglin et al. 1985; Vauclair 1988; Lebreton & Maeder 1987; Baglin & Lebreton 1990; Boesgaard 1991; Charbonnel et al. 1992, 1994; Deliyannis et al. 2000; Montalban & Schatzman 1996; Montalbán & Schatzman 2000; Piau & Turck-Chièze 2002; Charbonnel & Talon 2005; Talon & Charbonnel 2010). Because of its relatively low burning temperature (∼2.5 MK, close to the temperature at the base of the convective zone in solar-type stars), Li is indeed easily destroyed by proton capture in stellar interiors. According to classical stellar evolution theory, this destruction is expected to manifest itself at the surface of solar-type stars during the pre-main sequence (PMS) in the form of a decrease in the surface Li abundance. Classical models that include no transport processes beyond convection predict no further surface Li variation until the first dredge-up episode when the stars evolve towards the red giant branch.
Spectroscopic observations, however, show that the abundance of lithium at the surface of field and open cluster solar-type stars decreases along the main sequence (e.g., King et al. 1997; Sestito & Randich 2005; Chen & Zhao 2006; Takeda et al. 2010; Smiljanic et al. 2011; Xing & Xing 2012; Delgado Mena et al. 2014; Waite et al. 2017; Cummings et al. 2017; Beck et al. 2017; Harutyunyan et al. 2018; Carlos et al. 2020). In the case of the Sun, Li has decreased from its original (i.e. meteoritic) value of A(7Li) = 3.311 down to A(7Li) = 1.05 (Greenstein & Richardson 1951; Schwarzschild et al. 1957; Asplund et al. 2009). Solar twins (solar-type stars with ages close to that of the Sun, i.e. 4.6 ± 0.5 Gyr) all present significant Li depletion, with non-negligible dispersion, and with the Sun being among the most Li-depleted (e.g., Takeda et al. 2007; Meléndez & Ramírez 2007; Carlos et al. 2019).
In this work we use a consistent set of lithium abundances provided by Sestito & Randich (2005) for a group of open clusters with [Fe/H] between −0.21 and +0.14 dex: NGC 2264, IC 2391, IC 2602, IC 4665, α Per, Pleiades, Blanco I, NGC 2516, M 34, NGC 6475, M 35, Praesepe, NGC 6633, and NGC 752. We identify the solar-type stars as those that have an effective temperature as derived by Sestito & Randich (2005), corresponding to the effective temperature ±100 K of our model including atomic diffusion and rotation at the age of the corresponding cluster. We assume the cluster ages given by Bossini et al. (2019). Given the relatively large uncertainty on actual age determination, this slight inconsistency with the ages that would be derived with our models should not affect our conclusions. In Fig. 1 (also appearing in Figs. 2, 3, 6, and 8) we show the corresponding Li range for the solar-type stars with the observational boxes, and indicate the age uncertainty for each cluster. We also consider and show the Li data for M 67 and field solar twins by Carlos et al. (2019, 2020).
 |
Fig. 1. Top: lithium surface abundance evolution with time for the R1 models including different overshoot prescriptions (colour-coded). Individual points are data for solar twins (Carlos et al. 2019). Boxes are for Li observations of solar-type stars in different open clusters (Sestito & Randich 2005; Carlos et al. 2020 for M 67) with ages from Bossini et al. (2019). The numbers 1–10 identify the clusters: (1) NGC 2264, (2) IC 2391, IC 2602 and IC 4665, (3) α Per, Pleiades, Blanco I, (4) NGC 2516, (5) M 34, (6) NGC 6475, (7) M 35, (8) Praesepe, NGC 6633, (9) NGC 752, and (10) M 67. The colour of the boxes indicates the [Fe/H] value: Netopil et al. (2016): pink: −0.17 to −0.05; grey: −0.05 to 0.05; light blue: 0.05–0.16. Bottom: evolution of the angular velocity of the convective envelope and of the radiative core (in solar units Ω⊙ = 2.86 × 10−6 s−1; solid and dotted lines, respectively) vs age. The observational data is from Gallet & Bouvier (2015), except the four stars of M 67 from Barnes et al. (2016). Crosses are for individual stars; open diamonds show the 50th percentiles of the observed rotational distributions in each cluster. |
 |
Fig. 3. Same as Fig. 1, but for the models with a fixed viscosity νadd (νR1A, |
2.2. Surface and internal rotation
2.2.1. Surface rotation
Many observations exist of the rotation rates of solar-type stars of different ages (e.g., Stauffer & Hartmann 1986; McQuillan et al. 2014; García et al. 2014; Gallet & Bouvier 2015; dos Santos et al. 2016; Lorenzo-Oliveira et al. 2020). They clearly establish that the surface rotation of these stars evolves with time under the effect of multiple processes. Magnetic interactions between the star and its accretion disc early on the PMS and later with its wind are successfully invoked to explain the evolution and the dispersion of the rotation periods provided by photometric surveys (e.g., Matt et al. 2015; Amard et al. 2016; Gallet et al. 2019, and references therein).
To constrain the surface rotation of the models we use the observational data set gathered by Gallet & Bouvier (2015) for a large number of solar-type stars in open clusters of various ages. We also use the data from Barnes et al. (2016) for a subsample of four stars of M67, selected because their magnitudes are close to the solar value, with a magnitude B − V ∈ [0.6; 0.7].
2.2.2. Internal rotation
The internal rotation of the Sun is constrained by helioseismology. It is assumed to be similar for other solar-type stars, and asteroseismology constrains it for stars in more advanced evolutionary stages beyond the MS (i.e. subgiant and red giant stars; e.g., Mosser et al. 2012; Deheuvels et al. 2012, 2014, 2015; Benomar et al. 2015; Gehan et al. 2018; García & Ballot 2019). The analysis of p-modes gives access to the rotation profile of the Sun between about R = 0.2 R⊙ and the surface (Kosovichev 1988; Elsworth et al. 1995; Thompson et al. 2003; Mathur et al. 2008; Eff-Darwich et al. 2008). The inverted rotation profile is compatible with solid-body rotation in the radiative zone. Moreover, the analysis of mixed modes in solar-mass subgiant and red giant stars (hereafter SGB and RGB) presenting solar-like oscillations also points to a low degree of radial differential rotation in the core indicating that the strong coupling found at the solar age is essentially maintained during further evolution (Eggenberger et al. 2017, 2019a; Mathis et al. 2018; Aerts et al. 2019). No observational clue exists yet regarding the structure of the internal rotation during the PMS and the early MS evolution, although there are hints that the quasi solid-body rotation of the solar interior may not be an exception from the analysis of asteroseismic data for solar-type stars (Nielsen et al. 2014) and for F to late G main sequence stars (Benomar et al. 2015).
We thus require that our best models reach an internal rotation profile similar to the solar profile at the age of the Sun as this is basically the only proper constraint for the phases investigated in this paper. For this profile we use the results of the inversion of MDI-GOLF-GONG2 data by Eff-Darwich et al. (2008).
3. Stellar evolution models
We use an updated version of the stellar evolution code STAREVOL (for general information and previous versions, see Siess et al. 2000; Palacios et al. 2006; Decressin et al. 2009; Lagarde et al. 2012; Amard et al. 2019). All our models are evolved without accretion starting prior to the deuterium birthline on the PMS from initial structures corresponding to homogeneous polytropes. This sets the time zero of our computations.
3.1. Input physics
We adopt the solar reference abundances from Asplund et al. (2009) including the enhancement of neon recommended by Young (2018) as reported in Table 1. The opacities are interpolated within the OPAL opacity tables (Iglesias & Rogers 1996) when T > 8000 K and the low-temperature opacity tables from the Wichita opacity database when T < 8000 K (Ferguson, priv. comm.) that are fully consistent with the adopted solar reference abundances.
Initial chemical mixture adopted for the different solar calibrated models.
The equation of state is analytical and follows Eggleton et al. (1973) and Pols et al. (1995), as described in Siess et al. (2000). We use the nuclear reactions rates from the NACRE2 database generated using the NetGen web interface (Xu et al. 2013a,b).
In the current version of STAREVOL the full set of stellar structure equations is solved for the whole star; there is no decoupling between the interior and the envelope (where the diffusion approximation becomes valid). The surface boundary conditions are treated using the Hopf function q(τ), which provides a correction to the grey approximation (see Hopf 1930; Morel et al. 1994)
at a given optical depth τ, Teff being the temperature of the equivalent black body and T(τ) the temperature profile. We use the analytical expression from Krishna Swamy (1966) for q(τ), as is also done in Pietrinferni et al. (2013) and Zhang et al. (2019), for instance. The numerical surface is set at τ0 = 0.005, as in Amard et al. (2019), and the connection to the atmosphere is made at τph = 2.
The models without rotation take into account mass loss starting at the ZAMS3 following the empirical relation by Reimers (1975), with ηR = 0.5, as advocated by McDonald & Zijlstra (2015) and Guo et al. (2017) for solar-type stars from observational constraints on the red giant branch. When the effects of rotation are taken into account, we use the mass loss prescription by Cranmer & Saar (2011), as in Amard et al. (2019).
Heat transport by convection follows the Mixing Length Theory (MLT; Böhm-Vitense 1958; Cox & Giuli 1968). The convective boundaries are determined with the Schwarzschild criterion. When included, the effect of penetrative convection is treated as overshoot (without changing the temperature gradient in the concerned region; see Zahn 1991) below the convective envelope.
3.2. Model calibration
The abundances of helium and metals vary according to the input physics of the models; in other words, they depend on the mixing processes considered. Consequently, for each case the initial chemical composition needs to be evaluated so that the ratio Zsurf/Xsurf from Asplund et al. (2009) is reproduced at the age of the Sun. In this calibration procedure the mixing length parameter αMLT and the initial chemical composition are calibrated so as to reproduce the solar radius and solar luminosity at the age of the Sun (4.57 Gyr) with a relative accuracy of the order of 10−4–10−6. We make two different calibrations depending on the physics of the models (see Table 2). The classical model (C) is without any transport processes in the radiative region and the rotating model (R) includes atomic diffusion and rotational mixing with the assumptions made for model R1 (Table 3) and the median rotation rate (see Sect. 3.4), but it does not include overshoot. The calibration corresponding to model R1 is then used for all the models produced including rotation, in particular for models 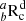 which include additional transport processes for angular momentum and chemicals (see Sect. 4 and the Appendix for further details). Details on the models resulting from these calibrations are given in Table 2 and the initial chemical mixtures for each calibration are reported in Table 1.
which include additional transport processes for angular momentum and chemicals (see Sect. 4 and the Appendix for further details). Details on the models resulting from these calibrations are given in Table 2 and the initial chemical mixtures for each calibration are reported in Table 1.
Solar calibration results for the STAREVOL classical model (C: no transport other than convection) and rotating model (R: atomic diffusion and type I rotation-induced transport).
3.3. Evolution of chemical abundances: General equation and atomic diffusion
Chemical abundances within the star evolve under the effect of nuclear reactions and transport processes. This is described by the general diffusion equation (e.g., Maeder 2009), which involves the different physical processes operating in the star
where ρ is the density; Xi refers to the mass fraction of element i; r is the radius; D = ∑jDj is the total coefficient for turbulent diffusion, written as the sum of the j different diffusion coefficients describing turbulent processes such as shear, penetrative convection, or any other unidentified process (see Sects. 3.4.1, 3.5, and 3.6); vi is the diffusion velocity of element i; mi is the mass of nuclei i; and rij the reaction rate producing nuclei j from nuclei i.
Atomic diffusion is implemented in STAREVOL with the formalism of Thoul et al. (1994) to solve the Burgers equations and compute the individual atomic diffusion velocities of each element taken into account in STAREVOL (see Table 1). The computation of the collision integrals is done according to Paquette et al. (1986). We take into account the partial ionisation of chemical elements for temperatures lower than 5 × 106 K (Schlattl 2002). Radiative accelerations are not taken into account in our models. According to Turcotte et al. (1998) their impact on abundances for light elements in the solar case is only about 2%. Radiative accelerations mainly impact the heavy elements such as iron, and become important for stars more massive than solar-type stars (Richer et al. 1998; Richard et al. 2002; Deal et al. 2018).
3.4. Angular momentum evolution and rotation-induced mixing
Stellar rotation, and in particular differential rotation, is a potent trigger of transport for both angular momentum and chemicals in stellar radiation zones. It generates the large-scale currents of the meridional circulation and several large-scale hydrodynamical instabilities that induce turbulence such as the vertical and horizontal shear instabilities, which are the ones included in our models (Zahn 1992; Maeder & Zahn 1998; Mathis & Zahn 2004; Mathis et al. 2004). This ensemble is referred to as Type I rotational mixing as it does not include the transport by magnetohydrodynamic (MHD) instabilities and magnetic fields or transport by internal gravity waves (see e.g., Mathis 2013; Aerts et al. 2019 for a description of these processes).
3.4.1. Prescriptions for shear induced turbulent transport
Stellar rotation is implemented in STAREVOL as described by Amard et al. (2016, 2019). We use the formalism of the shellular rotation hypothesis developed by Zahn (1992), Maeder & Zahn (1998), and Mathis & Zahn (2004) to describe the transport of angular momentum and chemicals by meridional circulation and turbulent shear (vertical and horizontal). The transport of angular momentum obeys the advection-diffusion equation
where ρ, r, Ω, U2, and νv are the density, radius, angular velocity, meridional circulation velocity, and vertical shellular component of the turbulent viscosity, respectively. Meridional circulation appears through its velocity U2 in Eq. (3), and can be described as a diffusion coefficient Deff in Eq. (2) for the transport of chemicals, as shown by Chaboyer & Zahn (1992) when assuming a strong turbulent transport in the horizontal direction. The turbulent shear in the vertical and horizontal directions appears as a viscosity νv (νh) in Eq. (3) and as a diffusivity Dv (Dh) in Eq. (2), that is assumed to be proportional to the corresponding viscosity, with a proportionality factor of 1 as usually assumed in stellar evolution models (Zahn 1992; Mathis et al. 2018; Eggenberger et al. 2008; Ekström et al. 2012). Several prescriptions exist for both (Dv, νv) and (Dh, νh), and stellar evolution models computed with different combinations of these prescriptions can be found in the literature. As demonstrated by Meynet et al. (2013) and Amard et al. (2016), this choice strongly affects the outcome of the models. To explore this aspect we compute models with three different combinations listed in Table 3 and referred to as R1, R2, and R3. We used these combinations in our previous works (e.g., Talon & Charbonnel 2005; Amard et al. 2016; Mathis et al. 2018), motivated by the outcomes of numerical simulations (e.g., Prat & Lignières 2013, 2014; Prat et al. 2016; Garaud et al. 2017; Gagnier & Garaud 2018). The nomenclature of the models and the detailed expressions of the different turbulent diffusion coefficients are given in Appendices A and B, respectively.
Parameters of the rotating models.
3.4.2. Magnetic braking and initial rotation velocities
The extraction of angular momentum at the stellar surface due to magnetised winds is accounted for following the formalism by Matt et al. (2015). We use the prescription as written in Eqs. (7)–(9) in Amard et al. (2019) with the following values for the parameters m = 0.22 and p = 2.1, which refer respectively to an exponent related to the magnetic field geometry and the exponent relating rotation and activity. We take 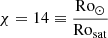 , the ratio of the solar Rossby number to the saturation value of the Rossby number4, at which the magnetic activity indicators saturate. They are fitted on the clusters of different ages to reproduce the rotation velocity dispersion according to Amard et al. (2019). Finally, a last complement parameter linked to magnetised wind braking, K, is calibrated so as to reproduce the solar surface rotation at the age of the Sun. We use a value of K = 7.5 × 1030 erg for our models unless otherwise indicated (see also Appendix A).
, the ratio of the solar Rossby number to the saturation value of the Rossby number4, at which the magnetic activity indicators saturate. They are fitted on the clusters of different ages to reproduce the rotation velocity dispersion according to Amard et al. (2019). Finally, a last complement parameter linked to magnetised wind braking, K, is calibrated so as to reproduce the solar surface rotation at the age of the Sun. We use a value of K = 7.5 × 1030 erg for our models unless otherwise indicated (see also Appendix A).
The models with rotation are computed as in Amard et al. (2019) for three values of the initial rotation period on the PMS: 1.6, 4.5, and 9.0 days, which will be referred to as the fast (FR), median (R), and slow (SR) rotating models, respectively. The disc coupling timescale is set at τdisc = 2.5 Myr for the fast rotators and at τdisc = 5 Myr for the median and the slow rotators. These values are chosen in agreement with Gallet & Bouvier (2015) in order to reproduce the observed rotation spread of open clusters stars.
3.5. Overshooting and penetrative convection
Using the MLT formalism associated with the Schwarzschild criterion for the instability to describe the extent of the convective regions, which is a classical approach in stellar evolution codes, is known to be flawed as the convective edges are defined according to null acceleration instead of null velocity of convective eddies. Convection actually penetrates in the sub-adiabatic layers below (for the convective envelopes) the superadiabatic unstable region, which generates mixing beyond the convective region down to where convective eddies are braked or eroded (e.g., Zahn 1991). Several formalisms for penetrative convection exist; we test three recent ones with an associated turbulent diffusion coefficient that scales with depth. We assume that the transport of angular momentum is not impacted by this process. The diffusion coefficients given below enter the expression of D in Eq. (2).
3.5.1. Baraffe et al. (2017)
The formalism proposed by Baraffe et al. (2017) is based on 2D and 3D hydrodynamic simulations of a young Sun on the PMS at 1 Myr and at solar metallicity (Pratt et al. 2017). These simulations allow them to characterise the depth of the penetrative convection below the convection zone; they show the existence of extreme events (deep penetrating plumes), which can have an outsized impact on transport mechanisms, especially ones that are meant to be inviscid. The diffusion coefficient obtained by Pratt et al. (2017) and reproduced here in Eq. (4), describes the mixing in the penetration layers and is characterised by the cumulative distribution function of the maximum penetration depth obtained in the simulations:
Here D0 = (υconv × Hp × αMLT)/3 is the convective turbulent diffusivity (with υconv the mean velocity of the convective elements obtained from MLT and αMLT the mixing length parameter), r is the local radius, rbcz is the radius at the base of the convective zone, and R is the total radius of the star. The coefficients λ = 6 × 10−3 and μ = 5 × 10−3 are as prescribed by Baraffe et al. (2017) and obtained from the simulations of Pratt et al. (2017). They are assumed to be independent of the stellar structure and age. All physical quantities are in cgs units (here and throughout the paper). The penetration depth of the overshooting is limited by the free parameter dov linked to the pressure scale-height and adjusted to take into account the limiting effect of stellar rotation. Baraffe et al. (2017) determined that this parameter should be dov ≈ 0.30Hp − 0.35Hp to reproduce the solar lithium abundance.
3.5.2. Augustson & Mathis (2019)
We tested for the first time in a stellar evolution code including rotation the description of penetrative convection by Augustson & Mathis (2019), which is based on a new model of rotating convection in stellar interiors. Contrary to Eq. (4), the penetration depth is now based on the one obtained by Zahn (1991). In his work Zahn (1991) linearised the equations of motion in the region of penetration, and the depth of penetration is then solved for given the velocity at the upper boundary of that region, which is assumed to reside in the convection zone. In Augustson & Mathis (2019) the impact of rotation on the convection is accounted for by using a modal convection model for rotating Rayleigh-Benard convection (Barker et al. 2014) where it is assumed to be locally valid in the region of penetration. This model has the asymptotic property that the velocity scales as (v/v0)∝Ro1/5, with Ro the Rossby number, which is inversely proportional to the angular velocity in the convective region. The depth of the overshooting zone then depends on the pressure scale-height, the convective Rossby number (hence angular velocity), and the thermal diffusivity, and is dynamically estimated. Using this model for penetrative convection and the functional form proposed by Pratt et al. (2017), Augustson & Mathis (2019) derive a new expression for the diffusion coefficient (their Eq. (70)), an approximation of which we use in this paper:
Here D0, μ, and λ are the same as in Eq. (4); dov is the free parameter for controlling the depth of the overshoot; and (v/v0) is the ratio of the velocity of the convective elements when taking rotation into account to the non-rotating inviscid value. The scaling between the velocity scales and the angular velocity implies that the diffusion coefficient in Eq. (5) is smaller when the star rotates faster, mimicking the fact that fast rotation inhibits convective motions to penetrate deep into the stably stratified region below. Thus, this model is a combination of the Baraffe et al. (2017) fit to their numerical stellar convective penetration simulations and those theoretical results of Augustson & Mathis (2019).
3.5.3. Korre et al. (2019)
Korre et al. (2019) propose a diffusive prescription suitable for 1D stellar evolution codes based on hydrodynamical simulations of penetrative convection and overshooting in a non-rotating Boussinesq spherical shell. In comparison to the simulations of Pratt et al. (2017), these simulations include an explicit diffusion, being the Navier-Stokes equations rather than an approximation of the Euler equations. The prescription is given by their Eq. (45),
where D0 (denoted Dcz in the original paper) is the same as in Eq. (4) and δG controls the depth of the penetration and writes
where E0 is the energy in the non-rotating convection zone, Pr = ν/κ is the Prandtl number defined as the ratio of the viscosity ν to the thermal diffusivity κ, S is the stiffness that measures the stability of the interface between the radiative zone and the convective zone, and Ra0 is the Rayleigh number defined by Eq. (11) in Korre et al. (2019) as
with αth the thermal expansion coefficient, g the gravity, 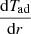 the adiabatic temperature gradient,
the adiabatic temperature gradient, 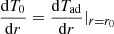 , r0 the outer radius of the convection zone, κ the thermal diffusivity, and ν the viscosity.
, r0 the outer radius of the convection zone, κ the thermal diffusivity, and ν the viscosity.
In this work we used Eq. (9) (instead of Eq. (6)), which is a result of fits to the numerical penetrative convection simulations carried out in Korre et al. (2019) where the overshooting length is adapted to contain information about the local rotation rate through the convective model of Augustson & Mathis (2019) and its implications for a linearised convective penetration model
where δG is approximated using the same principle as for DA(r) and adding the velocity dependence (v/v0) (Augustson & Mathis 2020)
Due to this inverse dependence on rotation, DK(r) is also smaller when the star rotates faster. Regarding the initial numerical simulation of Korre et al. (2019), the way that we adapted the rotational dependence with the help of the Augustson & Mathis (2019) should be taken with precautions. However, in the framework of slow-rotators, it is a relevant assumption.
3.6. Additional transports of chemicals
3.6.1. Tachocline turbulence
The tachocline is a shear layer located at the base of the solar convection zone where the radial rotation profile goes from differential in the convective envelope to flat in the radiative interior (Christensen-Dalsgaard & Schou 1988). First modelled by Spiegel & Zahn (1992) in a hydrodynamical framework, it is considered to be the seat of strong turbulence, with an associated diffusion coefficient that can be parametrised with respect to the Brunt-Väisälä frequency, the thickness of the tachocline, and the horizontal turbulent viscosity within it. Here we present models including the time-dependent expression given by Eqs. (15) and (16) in Brun et al. (1999),
where νH is the horizontal turbulent viscosity; rbcz is the radius at the base of the convective envelope; ζ = μ4(rbcz − r)/d is a non-dimensional depth; μ4 = 4.933; 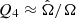 , with
, with 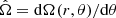 the latitudinal differential rotation at the base of the convective envelope; and d is a measure of the tachocline thickness h ≈ d/2:
the latitudinal differential rotation at the base of the convective envelope; and d is a measure of the tachocline thickness h ≈ d/2:
The depth of the convective envelope rbcz, the angular velocity Ω, the horizontal viscosity νH, the thermal diffusivity KT, and the Brunt-Väisälä frequency N all vary in time, as predicted by the structure and rotation equations. Defining
we can compute the fully time-dependent equation of DTach as
The treatment of the meridional circulation in the framework of Zahn’s theory is based on the expansion of all the physical quantities, including meridional circulation, in Legendre polynomials. The meridional circulation velocity is expanded to the second-order Legendre polynomials in the original works by Zahn (1992) and Maeder & Zahn (1998), which is the formalism adopted in STAREVOL. In that case, as shown by Mathis & Zahn (2004), the differential rotation in latitude is not explicitly accounted for. An expansion to the fourth-order of the departures from spherical symmetry is required to simultaneously treat the bulk of a radiative region and its tachocline, which is beyond the scope of this study. Hence, we need a prescription to evaluate 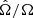 , and we adopt the same proportionality as in Brun et al. (1999), namely
, and we adopt the same proportionality as in Brun et al. (1999), namely 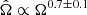 , which in turn comes from the paper from Donahue et al. (1996), and has been confirmed since then (e.g., Saar 2009; Brun et al. 2017), even if some uncertainties subsist (e.g., Augustson et al. 2012, who found that it would scale inversely with Ω in the case of F-type stars).
, which in turn comes from the paper from Donahue et al. (1996), and has been confirmed since then (e.g., Saar 2009; Brun et al. 2017), even if some uncertainties subsist (e.g., Augustson et al. 2012, who found that it would scale inversely with Ω in the case of F-type stars).
Equation (14) can thus be recast as
where we make explicit the proportionality coefficient adopted and the actual expression used in our computations for 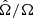 .
.
3.6.2. Parametric turbulent transport coefficients
The physical turbulent processes generating chemical mixing in radiative interiors, and more specifically in the radiative regions bordering convective ones, cannot all be accounted for given our current state of knowledge. Instead, these processes are parametrised to simulate diffusive turbulent mixing. Specifically, we follow Richer et al. (2000) and Richard et al. (2005) who discussed the use of additional turbulence competing with atomic diffusion to account respectively for observed abundance anomalies in Am and Fm stars and for the lithium abundances of Population II halo low-mass stars. In both classes of objects, atomic diffusion can be very efficient, and comparing models with observations calls for additional transport processes to be able to counteract its effects, as already anticipated in different kinds of stars by a vast amount of literature (e.g., Eddington 1929; Vauclair 2013; Michaud et al. 2015). Richer et al. (2000) and Richard et al. (2005) propose a purely parametric approach to model turbulence, with no assumptions on the underlying physical mechanism (see also Talon et al. 2006 for a comparison with rotation-induced mixing). Their diffusion coefficient is proportional to ρ−3 (see Proffitt & Michaud 1991) and attached to a specific temperature or to the density at the base of the convective envelope. These fixed points control where the turbulence is generated and thus the mixing depth. The parametric diffusivities DT0 and DPMa0 correspond to Eqs. (2) and (3) of Richard et al. (2005), respectively,
where T0 is a free parameter corresponding to the temperature at which the diffusivity is set to be 400 times larger than the atomic diffusion coefficient for He (e.g., DHe(T0)), which is computed with the analytical approximation, as advised by Richer et al. (2000), and ρ(T0) is the density at the location where T ≡ T0:
Here a0 is a free factor and ρbcz is the density at the base of the convective zone. To avoid numerical issues a minimum value of 1 is imposed on DT0 and DPMa0.
4. Type I rotating models with atomic diffusion and penetrative convection
As discussed in the introduction, classical models do not account for the evolution of Li with time observed in solar-type stars. However, we computed such a model for comparison purposes (C models, see Table 2), but we focus our discussion on models including rotation (R models), which all include atomic diffusion. In this section we present Type I rotating models, where the transport of angular momentum is driven only by meridional circulation and shear turbulence (Sect. 3.4); we focus on median rotators (see Sect. 3.4.2). We discuss the impact of the initial rotation rate in Sect. 5.
4.1. General behaviour
We start with model R15 for which we adopt the same prescriptions for the horizontal and vertical shear induced turbulent viscosities (Mathis et al. 2018 and Zahn 1992, respectively; see Table 3), the same initial rotation period (4.5 days), and the same disc lifetime (5 Myr) as for the 1 M⊙, Z⊙ median rotator model of Amard et al. (2019). The predicted evolution of the Li surface abundance and of the mean core and envelope angular velocities is shown in Fig. 1. As the envelope is convective and is assumed to rotate as a solid body, we have 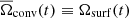 . The averaged core angular velocity represents the angular velocity of a solid body of equal angular momentum to that of the entire radiation zone, and is defined as in Amard et al. (2019),
. The averaged core angular velocity represents the angular velocity of a solid body of equal angular momentum to that of the entire radiation zone, and is defined as in Amard et al. (2019),
with MBCE the mass coordinate at the base of the convective envelope.
As discussed in Amard et al. (2019), such a model reproduces well the 50th percentiles of the period distributions of most of the clusters for solar-type stars in open clusters from the early PMS to the age of the Sun and beyond. This behaviour is mainly driven by the extraction of angular momentum at the surface via magnetised winds modelled following Matt et al. (2015). As seen in Fig. 1, we confirm that the meridional circulation and shear turbulence are too weak to enforce the coupling between the core and the surface, leading to a core spinning too fast at the age of the Sun compared to the internal rotation profile inferred through helioseismology (see Sect. 4.3). On the other hand, the associated transport of chemicals is dominated by vertical shear-induced turbulence, which remains weak during the entire evolution (see Sect. 5.3, and Mathis et al. 2018) and only partially counteracts atomic diffusion. Consequently, at the age of the Sun the predicted lithium abundance is ∼1.5 dex higher than observed.
4.2. Penetrative convection
As extensively discussed in the literature, model predictions for PMS Li depletion strongly depend on the treatment of convection and of penetrative convection (see e.g., D’Antona & Mazzitelli 1994; Piau & Turck-Chièze 2002; Baraffe et al. 2017; Thévenin et al. 2017). Here we test three different prescriptions for penetrative convection beyond the convective envelope that depend on the evolution of the internal angular velocity profile (Baraffe et al. 2017, Augustson & Mathis 2019, and Korre et al. 2019; see Sect. 3.5 and Table 3). Penetrative convection is assumed to only transport chemicals. It does not affect the surface and internal angular velocity evolution, which behave as in R1 (Fig. 1).
Concerning the impact on Li, and as already shown by Baraffe et al. (2017), its evolution when assuming a constant value for the extent of the overshoot region dov does not match the observed Li behaviour with time. As shown in Fig. 1, the models R1B.S and R1B.E implementing Eq. (4) with dov = 0.34Hp and 0.1Hp, respectively, fit either the solar Li abundance or the Li abundances in the youngest open clusters (between 10 Myr and 100 Myr). Baraffe et al. (2017) thus proposed to vary the depth of the overshooting zone depending on rotation, as supported by numerical studies (Ziegler & Rüdiger 2003; Brummell 2007; Brun et al. 2017). They reproduce the Li temporal evolution fairly well when adopting dov = 0.1Hp when the star is rapidly rotating (Ω > 5Ω⊙, i.e. typically on the late PMS and around the ZAMS, and similarly to what we find) and a much deeper overshooting zone (dov = 1Hp) for slower, more evolved rotating stars.
We decided not to fine-tune the depth of the overshooting zone for the slow rotators (after ∼1 Gyr), however, considering that other slow mixing processes may be responsible for Li depletion during this phase (see Sect. 5.2). We found the same behaviour as above with the prescription by Augustson & Mathis (2019) that accounts for the impact of the rotation on penetrative convection efficiency, and with the prescription by Korre et al. (2019). In both cases (models R1A and R1K, Fig. 1, Table 3) we adjusted the free parameter dov to reproduce the Li behaviour observed in the youngest open clusters around 30 Myr as in model R1B.E..
The Li evolution in all these models is characterised by a mild decrease from A(7Li) = 3.3 dex to A(7Li) = 2.8 dex at ∼15 Myr, followed by a plateau and a further slow decrease later on the MS. The convective envelope slowly recedes along the MS, which increases the term (r − rbcz) in the exponential of Eqs. (4), (5), and (9), leading to an increased efficiency of the slow mixing in the overshooting region that slowly depletes Li at the surface. In models R1A and R1K the transport in the overshoot region also depends on the rotation rate, which affects the depth of convective penetration via the ratio (v/v0). This results in a multiplying factor to the convective turbulent diffusivity D0 in Eq. (5) larger than that in Eq. (9), hence a more efficient mixing and a greater Li depletion in model R1A than in model R1K.
4.3. Impact of turbulent diffusion modelling
From now on we consider models for median rotators including atomic diffusion, penetrative convection according to Augustson & Mathis (2019) with the calibration described above, and rotation-induced transport of chemicals and angular momentum associated with meridional circulation and shear turbulence. We explore the impact of different sets of prescriptions for the horizontal and vertical shear diffusivities (Dv and Dh, respectively) reported in Table 3. Figure 2 shows the evolution of A(7Li) and core and envelope angular velocities as a function of age for the corresponding models R1A (Sect. 4.2), R2A, 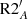 , and R3A. Figure 5 presents the internal rotation profiles predicted by these models at the age of the Sun.
, and R3A. Figure 5 presents the internal rotation profiles predicted by these models at the age of the Sun.
Models R2A and 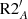 include the same prescriptions for Dv and Dh (Talon & Zahn 1997 and Zahn 1992, respectively) as in Charbonnel & Talon (2005), and they differ from each other by the adjustment of the torque parameters to better fit the surface rotation rate (Table 3). In both cases we confirm that these prescriptions fail to reproduce the Li evolution with time and the internal rotation rate of the Sun. In particular, the (too) strong Li depletion is driven by the vertical shear coefficient prescribed by Talon & Zahn (1997), which is much greater than that of Zahn (1992), and which is fed by the very strong differential rotation inside the star during most of its evolution beyond 20 Myr. A similar behaviour for Li was found by Amard et al. (2016) using the same prescription for Dv but that of Dh from Mathis et al. (2004), although this combination provides a stronger coupling between the core and the surface (which is still irreconcilable with the solar rotation profile). We thus discard the vertical shear diffusivity as prescribed by Talon & Zahn (1997) based on these results on lithium; however, this remains an open question considering that additional transport mechanisms for angular momentum may lead to different conclusions (see e.g., Charbonnel & Talon 2005, who invoke the effects of internal gravity waves).
include the same prescriptions for Dv and Dh (Talon & Zahn 1997 and Zahn 1992, respectively) as in Charbonnel & Talon (2005), and they differ from each other by the adjustment of the torque parameters to better fit the surface rotation rate (Table 3). In both cases we confirm that these prescriptions fail to reproduce the Li evolution with time and the internal rotation rate of the Sun. In particular, the (too) strong Li depletion is driven by the vertical shear coefficient prescribed by Talon & Zahn (1997), which is much greater than that of Zahn (1992), and which is fed by the very strong differential rotation inside the star during most of its evolution beyond 20 Myr. A similar behaviour for Li was found by Amard et al. (2016) using the same prescription for Dv but that of Dh from Mathis et al. (2004), although this combination provides a stronger coupling between the core and the surface (which is still irreconcilable with the solar rotation profile). We thus discard the vertical shear diffusivity as prescribed by Talon & Zahn (1997) based on these results on lithium; however, this remains an open question considering that additional transport mechanisms for angular momentum may lead to different conclusions (see e.g., Charbonnel & Talon 2005, who invoke the effects of internal gravity waves).
Model R3A provides a very good fit of the observed evolution of both the surface rotation period and the Li abundance. The rotational evolution of this model is very similar to that of model R1A, as it is dominated by vertical shear in the early phases and by the surface extraction of the angular momentum by the magnetised winds beyond the ZAMS. Stronger Li depletion is achieved, however, thanks to a steeper angular velocity profile below the convective envelope (see Fig. 5 for a snapshot at the age of the Sun), which translates into an enhanced turbulent diffusive transport between the base of the convective envelope and the region where Li is destroyed by proton capture. This behaviour is directly related to the modelling of the horizontal shear turbulent viscosity. Accounting for an additional source of horizontal shear turbulence when using the Mathis et al. (2018) prescription, as in model R1A, was shown in this previous paper to lead to a lower vertical shear turbulent viscosity than when using the prescription from Mathis et al. (2004), as in model R3A. In the absence of astero- and helioseismic constraints R3A would be the best model. However, it also predicts a strong internal differential rotation at the age of the Sun.
4.4. Conclusions on Type I models
We confirm that all current prescriptions for shear-induced turbulence fail to reproduce simultaneously the internal rotation profile of the Sun and the surface constraints (see e.g., Amard et al. 2016, 2019 and references therein for similar Type I rotating models without atomic diffusion and penetrative convection; see also Ceillier et al. 2013; Marques et al. 2013; Eggenberger et al. 2017, 2019a; Mathis et al. 2018; Aerts et al. 2019; Deheuvels et al. 2020). We favour, however, the prescriptions for Dv and Dh from Mathis et al. (2018) and Zahn (1992), respectively. For the modelling of horizontal turbulence, we recall that the treatment of Mathis et al. (2018) is the first one that accounts for the action of stratification and rotation on horizontal turbulent motions. We couple it with the prescription for the vertical turbulent transport, which is the only one that has been validated by direct numerical simulations (Prat & Lignières 2013; Garaud et al. 2017). Their coupling with angular momentum wind extraction is done with the help of Matt et al. (2015); they reproduce well the evolution of the surface rotation rate with time as observed in solar-type stars in open clusters. Additionally, the three prescriptions that we tested for rotationally dependent penetrative convection help the models more closely fit the Li abundances observed in the youngest clusters (after calibration). Given our choice for the treatment of shear turbulence, accounting for Li in the more advanced stages requires either a very strong dependence between convective penetration depth and rotation, or an additional mixing process that may depend, or not, on the missing transport of angular momentum.
5. Improving the models
In this section we explore the possibilities to fit all the observational constraints by including additional transport processes for both angular momentum and chemical species. All the models discussed in this section include rotation-induced mixing, atomic diffusion, and penetrative convection.
5.1. Transport of angular momentum by additional viscosity
Several processes have been proposed to explain the strong coupling between the core and the surface of low-mass stars, and to flatten the angular velocity profile at the solar age and beyond (in particular, internal gravity waves and processes related to magnetism; Schatzman 1993; Spruit 2002; Charbonnel & Talon 2005; Mathis & Zahn 2005; Eggenberger et al. 2005, 2010, 2019b,c; Denissenkov et al. 2010; Charbonnel et al. 2013; Fuller et al. 2014, 2019; Cantiello et al. 2014; Rüdiger et al. 2015; Belkacem et al. 2015; Pinçon et al. 2017). However, no complete solution has been found yet. Parametric studies thus remain necessary to estimate the efficiency of the missing transport processes, and to potentially determine their nature. This is the approach we chose here.
We follow Eggenberger et al. (2012b, 2019b, see also Lagarde et al. 2014 and Spada et al. 2016) who proposed introducing a parametric vertical viscosity νadd in the equation describing the transport of angular momentum to reproduce the core rotation rates of SGB and RGB stars. In this context, Eq. (3) becomes
There νadd was assumed to be either constant in time or dependant on the stellar rotation. Possible variations of νadd within stellar interiors were not considered. We tested both options and in the second case, we followed Spada et al. (2016, their Eq. (3)) and assumed that the angular momentum transport efficiency depends on the radial rotational shear, i.e.
where ν0 and α are free parameters, and 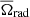 and
and 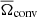 are the mean angular velocity in the radiative interior and convective envelope, respectively, as defined in Sect. 4.1. We computed models with the three different combinations of turbulent shear prescriptions discussed in Sect. 4.3 for different values of νadd and of α and ν0 (Table 3).
are the mean angular velocity in the radiative interior and convective envelope, respectively, as defined in Sect. 4.1. We computed models with the three different combinations of turbulent shear prescriptions discussed in Sect. 4.3 for different values of νadd and of α and ν0 (Table 3).
The impact of the additional viscosity on the internal rotation profile and on the Li depletion and surface rotation rate can be seen in Figs. 3–5. In Fig. 4 we show the level of internal differential rotation
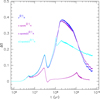 |
Fig. 4. Differential rotation evolution with time for the νR1A, ν.spadaR1A, ν.spada(t)R1A, and ν2.spada(t)R1A models (details in Table 3). |
 |
Fig. 5. Angular velocity profiles vs the radius at solar age for models presented in Fig. 3 compared to the rotation profile of the Sun (in dark grey) obtained from helioseismology from Eff-Darwich et al. (2008). The solid line, the dotted line, the dashed line, and the dot-dashed line refer to the differential, solid, νadd, and νadd(t) rotation cases, respectively. |
with Ωsurf and 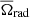 defined in Sect. 4.1.
defined in Sect. 4.1.
Clearly, the higher the value of νadd, or the higher the value of α for a given ν0, the earlier and the stronger the coupling between the core and the surface. In our models, the values for νadd required to obtain a flat internal rotation profile at the age of the Sun while accounting for the surface rotation constraints vary between 2.5 × 104 and 4 × 104 cm2 s−1 depending on the adopted prescriptions for Dv and Dh. This is in agreement with the values required for the models to fit the asteroseismic data in subgiants and red giant stars (≈104 to 3 × 104; Eggenberger et al. 2012b; Spada et al. 2016). In addition, in this case the evolution of the modelled surface rotation rate matches the observed values fairly well all along the evolution of the stars. When we adopt the value of 2.5 × 105 cm2 s−1 (model ν.spadaR1A) advocated by Spada et al. (2016) for their solar benchmark, the internal rotation profile flattens very early in the evolution. In that case, a lower value for the magnetic braking parameter K is needed to fit the solar surface rotation rate6, but this destroys the agreement between the model predictions and the observed evolution of the surface rotation rate on the MS (between 100 Myr and 2 Gyr). When assuming a dependency of the transport of angular momentum with the radial rotational shear (Eq. (20)), we obtain a reasonable rotation profile at the age of the Sun with ν0 = 2.5 × 104 cm2 s−1 and α = 0.5 (model ν.spada(t)R1A), where we keep ν0 of the same order as the constant νadd calibrated above. We also obtain reasonable rotation profiles at solar age with other combinations (e.g., ν0 = 100 cm2 s−1, α = 12, model ν2.spada(t)R1A, and ν0 = 1000 cm2 s−1, α = 9, not shown); in these cases, because of the high value of α, the differential rotation is reduced earlier on the MS and slowly continues receding after 100 Myr. It results in a lower surface rotation velocity than for model ν.spada(t)R1A when K is not re-adjusted.
In summary, in the absence of asteroseismic data that could reveal the actual internal rotation profile in MS stars younger than the Sun, we cannot better constrain the efficiency of the transport of angular momentum or the nature of the underlying mechanism. We show, however, that the mean evolution of the surface rotation rate can be fairly well reproduced by the models with moderate values for the additional viscocity and with magnetic braking efficiency in agreement with the calibration value from Matt et al. (2019). However, with the stronger viscosity adopted in model ν.spadaR1A, no value for the magnetic braking parameter K can reconcile the observed periods along the entire evolution. The same problem occurs for the model where we assume solid-body rotation all along the evolution (models solidRA). This provides a hint that rigid rotation may not be achieved very early on the MS in solar-type stars. This partially agrees with previous works by Gallet & Bouvier (2013, 2015), and by Lanzafame & Spada (2015) and Spada & Lanzafame (2020) for solar-type stars, who find, using two-zone models for the angular momentum transport, that quasi solid-body rotation should be achieved around 1 Gyr in order to fit the same observations. Our models, where the transport of angular momentum is self-consistently treated, resulting in fully resolved angular velocity radial profiles, seem to indicate that quasi rigid rotation may be reached even later in the evolution (see Fig. 4, where ΔΩ = 0 corresponds to a solid-body rotation and where increasing values of ΔΩ correspond to higher differential rotation).
Finally, Li depletion is slightly less efficient in the models with parametric diffusivity than in the corresponding Type I models, due to the weaker turbulent shear. In particular, model νR3A does not reproduce the Li depletion on the MS contrary to what was obtained for model R3A. However, Li depletion remains too strong in model 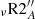 as it is dominated by the vertical shear associated with the Dv from Talon & Zahn (1997). In Sect. 4.3 we favoured the prescriptions for Dv and Dh included in models R1 and νR1. We see that model νR1 reproduces the evolution of surface rotation along time, and predicts an almost flat rotation profile at the age of the Sun. However, this model does not reproduce the Li depletion observed in open clusters beyond 500 Myr, in solar twins, and in the Sun. An additional transport of chemicals is consequently needed to increase the mixing and the depletion of the lithium during the MS.
as it is dominated by the vertical shear associated with the Dv from Talon & Zahn (1997). In Sect. 4.3 we favoured the prescriptions for Dv and Dh included in models R1 and νR1. We see that model νR1 reproduces the evolution of surface rotation along time, and predicts an almost flat rotation profile at the age of the Sun. However, this model does not reproduce the Li depletion observed in open clusters beyond 500 Myr, in solar twins, and in the Sun. An additional transport of chemicals is consequently needed to increase the mixing and the depletion of the lithium during the MS.
5.2. Additional transport for chemicals
5.2.1. Tachocline mixing
As explained in Sect. 3.6.1 the tachocline is the transition layer from the latitudinally differentially rotating convective envelope and the uniformly rotating radiative core. It can be the seat of strong anisotropic turbulent transport when assuming that the dynamics of this layer is driven by hydrodynamical mechanisms (Spiegel & Zahn 1992). We compute a model 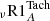 using Eqs. (12) and (15). Model
using Eqs. (12) and (15). Model 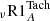 is shown as a medium orange dashed line in Fig. 6. This model implements for the first time the self-consistent computation of the tachocline thickness according to Spiegel & Zahn (1992). It appears to become thinner as the star evolves from the PMS to the age of the Sun7 at which time it extends over 0.035 R⊙. This value is larger, yet compatible with the estimate of ≈0.02 R⊙ given by Elliott & Gough (1999) from helioseismology. The efficiency of the transport is also driven by a value of DTach(t) that varies between ≈109 − 1010 cm2 s−1. At young ages, the transport is very efficient and prevails over the penetrative convection to transport Li because of the deep location of the base of the convective envelope. It leads to an early and strong Li depletion (≈1 dex), which is too large to reproduce the Li evolution in young open clusters before 1 Gyr. The same result was obtained by Piau & Turck-Chièze (2002) with a parametric treatment of the tachocline depth and turbulent diffusivity as in Brun et al. (1999). As the star evolves and the convective envelope becomes shallower, the thickness of the tachocline does not increase enough, and even decreases, so that the tachocline becomes inefficient to transport the Li after 20 Myr whatever the value of DTach. This prediction differs from that of Piau & Turck-Chièze (2002), who achieved a solar Li abundance by the age of the Sun. Such a difference is most probably due to the parametrisation they adopted for the thickness of tachocline.
is shown as a medium orange dashed line in Fig. 6. This model implements for the first time the self-consistent computation of the tachocline thickness according to Spiegel & Zahn (1992). It appears to become thinner as the star evolves from the PMS to the age of the Sun7 at which time it extends over 0.035 R⊙. This value is larger, yet compatible with the estimate of ≈0.02 R⊙ given by Elliott & Gough (1999) from helioseismology. The efficiency of the transport is also driven by a value of DTach(t) that varies between ≈109 − 1010 cm2 s−1. At young ages, the transport is very efficient and prevails over the penetrative convection to transport Li because of the deep location of the base of the convective envelope. It leads to an early and strong Li depletion (≈1 dex), which is too large to reproduce the Li evolution in young open clusters before 1 Gyr. The same result was obtained by Piau & Turck-Chièze (2002) with a parametric treatment of the tachocline depth and turbulent diffusivity as in Brun et al. (1999). As the star evolves and the convective envelope becomes shallower, the thickness of the tachocline does not increase enough, and even decreases, so that the tachocline becomes inefficient to transport the Li after 20 Myr whatever the value of DTach. This prediction differs from that of Piau & Turck-Chièze (2002), who achieved a solar Li abundance by the age of the Sun. Such a difference is most probably due to the parametrisation they adopted for the thickness of tachocline.
In its current form and with the adopted description of rotation-induced turbulence in our models, mixing in the tachocline prevents the models from fitting the observed Li evolution in solar-type stars. The efficiency of the turbulent transport in the tachocline as expressed by Eq. (11) remains difficult to model correctly as we lack good estimates of the evolution of the ratio 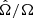 . A fully consistent model should solve the equations for the structure of the turbulent tachocline as derived by Spiegel & Zahn (1992) with taking into account boundary conditions that describe the variations of the latitudinal differential rotation at the base of the convective envelope as a function of time. This differential rotation is a function of the global rotation of the star (Brun et al. 2017), and will thus evolve all along its evolution.
. A fully consistent model should solve the equations for the structure of the turbulent tachocline as derived by Spiegel & Zahn (1992) with taking into account boundary conditions that describe the variations of the latitudinal differential rotation at the base of the convective envelope as a function of time. This differential rotation is a function of the global rotation of the star (Brun et al. 2017), and will thus evolve all along its evolution.
5.2.2. Parametric turbulence
Following Richard et al. (2005), we use the parametric prescriptions for an additional transport of matter as described by Eqs. (16) and (17). We compute two models, 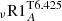 and
and 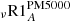 , for which we adjust the two free parameters of Eqs. (16) and (17) as respectively log(T0) = 6.425 and a0 = 5000 to best fit the evolution of Li abundance observed at the surface of solar-type stars and the Sun. We consider this to be in rather good agreement with the values obtained by Richard et al. (2005, log(T0) = 6.4 and a0 = 2000) for their solar model, considering that it did not include rotation and that it was computed with different basic input physics (in particular nuclear reaction rates, eos, opacities).
, for which we adjust the two free parameters of Eqs. (16) and (17) as respectively log(T0) = 6.425 and a0 = 5000 to best fit the evolution of Li abundance observed at the surface of solar-type stars and the Sun. We consider this to be in rather good agreement with the values obtained by Richard et al. (2005, log(T0) = 6.4 and a0 = 2000) for their solar model, considering that it did not include rotation and that it was computed with different basic input physics (in particular nuclear reaction rates, eos, opacities).
The parametric turbulent mixing becomes efficient beyond 200–300 Myr, as can be seen from Fig. 6. The form of Eqs. (16) and (17) leads to an increase in the diffusion coefficient between the base of the convective envelope and the Li burning region as the star evolves on the MS. The evolution of the coefficient DT6.425 is illustrated alongside that of the other diffusivities at four different ages in Fig. 7. We adopt Eq. (16) included in model 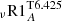 because it is independent of the depth of the convective envelope and is scaled by the atomic diffusion coefficient for 4He in the Li burning region. While the transport by penetrative convection is the main process responsible for surface Li depletion during the PMS (upper left panel of Fig. 7), the coefficient DT6.425 dominates the transport within the Li burning region on the MS, as shown in the lower panels of Fig. 7 (at 1 Gyr and 4.57 Gyr). The addition of this mixing process does not affect the predicted evolution of the surface rotation rate (lower panel Fig. 6) because it is independent of rotation. We also tested a solid-body rotating counterpart to model
because it is independent of the depth of the convective envelope and is scaled by the atomic diffusion coefficient for 4He in the Li burning region. While the transport by penetrative convection is the main process responsible for surface Li depletion during the PMS (upper left panel of Fig. 7), the coefficient DT6.425 dominates the transport within the Li burning region on the MS, as shown in the lower panels of Fig. 7 (at 1 Gyr and 4.57 Gyr). The addition of this mixing process does not affect the predicted evolution of the surface rotation rate (lower panel Fig. 6) because it is independent of rotation. We also tested a solid-body rotating counterpart to model 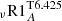 , called model
, called model 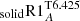 , which is also presented in Fig. 6. It predicts slightly less depletion of Li due to a lower efficiency of the transport in that case.
, which is also presented in Fig. 6. It predicts slightly less depletion of Li due to a lower efficiency of the transport in that case.
 |
Fig. 7. Profiles of the logarithm of the diffusion coefficients (left axis) of the meridional circulation (Deff), the vertical shear (Dshear = Dv), the overshoot (DA), the parametric turbulence (DT6.425), and the total transport coefficient (Dtot = Deff + Dshear + DA + DT6.425) as a function of the radius normalised to solar radius at four different ages (107 years, 5 × 107 years, 109 years, and solar age) for model |
Model 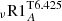 meets the goal of reproducing the surface evolution of the Li abundance and the angular velocity together with an angular velocity profile compatible with that of the Sun at the solar age.
meets the goal of reproducing the surface evolution of the Li abundance and the angular velocity together with an angular velocity profile compatible with that of the Sun at the solar age.
5.3. Models with optimal prescriptions
We explore the impact of the initial angular velocity on our optimal model 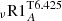 and discuss its predictions for other chemical constraints. We compute
and discuss its predictions for other chemical constraints. We compute 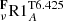 ,
, 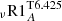 , and
, and 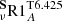 for fast, median, and slow rotators, respectively, and present the associated evolution of Li and surface angular velocity in Fig. 8, together with the non-rotating model C (Table 2).
for fast, median, and slow rotators, respectively, and present the associated evolution of Li and surface angular velocity in Fig. 8, together with the non-rotating model C (Table 2).
 |
Fig. 8. Same as Fig. 1, but for the different R1 models, the selected |
The relation between surface rotation rate and Li abundance in solar-type stars was first observed by Soderblom et al. (1993) in the Pleiades and has been confirmed by more recent studies in several clusters (Bouvier et al. 2018; Arancibia-Silva et al. 2020). The observations indicate that rapidly rotating stars possess higher Li abundances than slowly rotating stars, which is related to the PMS rotational evolution (Bouvier 2008). In particular, it is related to the difference in the disc lifetime between the fast and slow rotators (e.g., Eggenberger et al. 2012a) and/or alternately to the correlation between rotation and penetrative convection efficiency (e.g., Baraffe et al. 2017). Contrary to the models of Amard et al. (2016, 2019) our models comply with the expected behaviour and the PMS Li depletion is larger for slower rotators, as shown in upper panel of Fig. 8. As we use the same treatment for rotational transport and the same disc lifetimes as in Amard et al. (2019), the inclusion of penetrative convection according to Eq. (5) is clearly shaping the Li evolution prior to the ZAMS.
On the MS, when the parametric turbulence takes over the Li transport, all models converge to the solar Li value since we have adjusted the parametric turbulence to fit the Sun. The tracks follow the lower envelope of the data from solar twins (Carlos et al. 2019, 2020). The slightly shallower turbulent mixing used in model 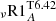 permits us to fit these points. The parameters we adopted for turbulence and magnetic braking lead to a good general agreement between the theoretical and the observed Li behaviour for both field and open cluster solar-type stars.
permits us to fit these points. The parameters we adopted for turbulence and magnetic braking lead to a good general agreement between the theoretical and the observed Li behaviour for both field and open cluster solar-type stars.
Regarding surface and internal rotation, the fast, median, and slow models are also in good agreement with the observed velocity distribution (solid lines, bottom panel Fig. 8) in solar-type stars, similar to the models of Amard et al. (2019), which did not include additional viscosity for the transport of angular momentum. Moreover, all the models predict a flat rotation profile in the radiative interior at the age of the Sun due to the extra transport of angular momentum by the adopted ad hoc viscosity νadd, regardless of the initial angular velocity. The evolution of the rotation rate slightly differs, however, depending on the assumed initial rotational rate. The model 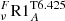 rotates almost as a solid body on the PMS and the early MS. The strong torque exerted by the magnetised winds leads to a sharp deceleration of the surface of this model between 300 Myr and 500 Myr, and differential rotation develops in the interior during that period. When the surface torque becomes inefficient, around 500 Myr, the surface angular velocity evolution settles on a Skumanich-like path (Skumanich 1972) while angular momentum is continuously extracted from the core by the additional transport, modelled here with νadd, so that at the age of the Sun the internal rotation profile agrees with the helioseismic constraint. On the MS the coupling between the core and the surface is larger for larger initial angular velocity (compare
rotates almost as a solid body on the PMS and the early MS. The strong torque exerted by the magnetised winds leads to a sharp deceleration of the surface of this model between 300 Myr and 500 Myr, and differential rotation develops in the interior during that period. When the surface torque becomes inefficient, around 500 Myr, the surface angular velocity evolution settles on a Skumanich-like path (Skumanich 1972) while angular momentum is continuously extracted from the core by the additional transport, modelled here with νadd, so that at the age of the Sun the internal rotation profile agrees with the helioseismic constraint. On the MS the coupling between the core and the surface is larger for larger initial angular velocity (compare 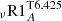 and
and 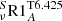 in Fig. 8). This behaviour differs from what was obtained from bi-zone models (Gallet & Bouvier 2013; Lanzafame & Spada 2015). In slow rotators, the large angular velocity gradient and the small surface angular velocity at the ZAMS and during the early MS evolution lead to the stronger Li depletion discussed above.
in Fig. 8). This behaviour differs from what was obtained from bi-zone models (Gallet & Bouvier 2013; Lanzafame & Spada 2015). In slow rotators, the large angular velocity gradient and the small surface angular velocity at the ZAMS and during the early MS evolution lead to the stronger Li depletion discussed above.
Beryllium (hereafter Be) is also easily destroyed in stellar interiors, but at higher temperatures (≈3.5 MK) than Li and can thus also be used to further constrain the mixing. Spectroscopic determination of Be in open cluster solar-type stars (e.g., Boesgaard et al. 2003a,b, 2004) indicate that it should be only slightly depleted during the PMS and the MS of solar-like stars. In Fig. 9, we present the evolution of the surface Be abundance as a function of the age for the models shown in Fig. 8. The evolution of Be at the stellar surface is only affected by the parametric turbulent mixing introduced to reproduce the MS depletion of Li in our models. It does not depend on the initial velocity. The parametric turbulent mixing leads to a 0.3 dex depletion of Be by the age of the Sun, which is slightly too large compared to observations. Model 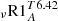 which better reproduces the Li abundances of solar twins (see previous section), is compatible within the error bars with the Be abundance at the solar surface. However, the limited number of Be abundance determinations currently prevents us from using this nuclide as a good constraint for internal transport processes.
which better reproduces the Li abundances of solar twins (see previous section), is compatible within the error bars with the Be abundance at the solar surface. However, the limited number of Be abundance determinations currently prevents us from using this nuclide as a good constraint for internal transport processes.
 |
Fig. 9. Same as Fig. 8, but for Be. Boxes are for Be observations of solar-mass stars in different open clusters and are colour-coded according to their metallicity, as in Fig. 1. The numbers I–V identify the clusters: (I) IC 2602 and IC 2391 (Smiljanic et al. 2011), (II) Pleiades (Boesgaard et al. 2003a), (III) Ursa Major (Boesgaard et al. 2003b), (IV) Coma Ber (Boesgaard et al. 2003b), and (V) Hyades (Boesgaard et al. 2004). The solar beryllium with uncertainties comes from Asplund et al. (2009, photospheric value). The orange dots refer to the four profiles extracted from the star evolution shown in Fig. 7. |
6. Summary and discussion
We computed models of solar-like stars including atomic diffusion and rotation and we analysed the impact of different internal transport processes on the chemical and rotational evolution of these stars. Our models confirm the need for additional transport processes beyond atomic diffusion and Type I rotation-induced processes (meridional circulation and turbulent shear) for both angular momentum and chemicals in order to reproduce observations of Li and internal rotation for MS solar-type stars. In the framework of our study, we chose to parametrise the action of complex processes and adopt the simpler approach of an additional turbulent viscosity νadd to the angular momentum transport equation, either constant or time-dependent. We follow the propositions by Eggenberger et al. (2012b) and Spada et al. (2016) to account for the low degree of (radial) differential rotation in evolved stars (subgiants and red giant stars). We show that such a parametrisation of a yet-to-be-identified physical process can indeed lead to a strong coupling between the interior and the envelope in solar-type stars at the age of the Sun without significantly modifying the predicted evolution of their surface rotation. Our models also indicate that all the current observational constraints can be satisfied without reaching a full rotational coupling between the core and the envelope until 2–3 Gyr. Moreover, a higher degree of differential rotation is predicted for the slow rotators before this age. Asteroseismic constraints on the internal rotation of young solar-type MS stars would be of great value to test this prediction.
Concerning the transport of chemicals, we confirm that the Li depletion observed in MS solar-type stars of open clusters cannot be reproduced by rotational mixing alone when the solar internal rotation constraint is also taken into account. We implemented for the first time the prescription for penetrative convection dependent on rotation, according to Augustson & Mathis (2019). We show that this process is key to reproducing the surface Li abundance evolution of solar-type stars during the PMS and the very early MS. The dependence of the convective penetration depth on the rotation rate in the convective envelope is the main factor explaining the anti-correlation between the surface rotation rate and Li abundance observed in open clusters. It dominates over the effect of the disc lifetime first pointed out by Eggenberger et al. (2012a).
For the first time since its publication we were able to self-consistently compute the tachocline thickness according to the model by Spiegel & Zahn (1992, their Eq. (12)). Using the parametrisation for the horizontal turbulent viscosity from Mathis et al. (2018), our model predicts a tachocline thickness at the solar age, which is compatible with the helioseismic estimate by Elliott & Gough (1999). On the other hand, the associated turbulent transport as described in Brun et al. (1999) depends on the degree of latitudinal differential rotation, whose evolution remains poorly constrained. Using estimates based on activity indicators from Donahue et al. (1996) leads to very efficient tachocline mixing and an over-depletion of Li surface abundance during the PMS evolution. In addition, the shallow thickness of the tachocline during the MS evolution prevents our models from reproducing the expected Li depletion during this evolutionary phase. Furthermore, the models that account self-consistently for the tachocline mixing according to the formalisms of Spiegel & Zahn (1992) and Brun et al. (1999) fail to reproduce the observed evolution of Li abundance in solar-type stars. However, this specific formalism calls for observational constraints on the degree of latitudinal differential rotation. The development of the meridional circulation to the fourth order, as proposed by Mathis & Zahn (2004), was designed to self-consistently include the tachocline region and associated transport in stellar evolution models and could help to sort out the actual impact of tachocline mixing along the evolution of solar-type stars. In this context new developments on the horizontal turbulent transport induced by the instability of the horizontal shear of the differential rotation would be of great importance (Park et al. 2020; Garaud 2020; Cope et al. 2020).
Our optimal models (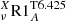 ) are obtained when including a parametric turbulence according to Richer et al. (2000), which was first proposed as a way to counteract the impact of atomic diffusion with radiative accelerations in F-, A-, and B-type stars for several evolutionary stages. The depth of the turbulence appears to be slightly greater for the Sun than for solar twins based on the comparison of our models (
) are obtained when including a parametric turbulence according to Richer et al. (2000), which was first proposed as a way to counteract the impact of atomic diffusion with radiative accelerations in F-, A-, and B-type stars for several evolutionary stages. The depth of the turbulence appears to be slightly greater for the Sun than for solar twins based on the comparison of our models (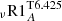 and
and 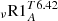 ) to the Li and Be data in open clusters, confirming that the Sun might not be the best benchmark for testing transport processes in solar-type stars (e.g., see also Carlos et al. 2020).
) to the Li and Be data in open clusters, confirming that the Sun might not be the best benchmark for testing transport processes in solar-type stars (e.g., see also Carlos et al. 2020).
MDI: Michelson Doppler Imager (Scherrer et al. 1995), GOLF: Global Oscillations at Low Frequencies (Gabriel et al. 1995). These instruments are on board the SOlar and Heliospheric Observatory (SOHO) spacecraft of ESA/NASA (Domingo et al. 1995). GONG: Global Oscillation Network Group (e.g., Howe et al. 2020, and references therein).
The Rossby number is defined here according to Matt et al. (2015) as Ro = (Ω τcz)−1, where τcz is the convective turnover timescale, characterised by the size of the studied convective region divided by the convective velocity.
See Appendix A for model notation.
K = 1.2 × 1030 erg (see Table 3) to be compared with K = 6.3 × 1030 erg advised by Matt et al. (2019).
Acknowledgments
We thank J. W. Ferguson for providing us with low-temperature opacity tables adapted to the solar mixture we adopt in this work, P. Eggenberger for fruitful discussions, and the anonymous referee for constructive comments on the manuscript. This work was supported by the Swiss National Science Foundation (Projects 200021-169125 and 200020-192039 PI C.C.). We thank the Programme National de Physique Stellaire (PNPS) of CNRS/INSU co-funded by CEA and CNES. This research has made use of NASA’s Astrophysics Data System Bibliographic Services. L.A. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant agreement No. 682393 AWESoMe-Stars). K.C.A. and S.M. acknowledge support from the ERC SPIRE 647383 grant and PLATO & GOLF CNES Grants at CEA/DAp-AIM. A.P. acknowledge support from the PLATO CNES grant at LUPM.
References
- Aerts, C., Mathis, S., & Rogers, T. M. 2019, ARA&A, 57, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Allen, C. W. 1976, Astrophys. Quantities, [Google Scholar]
- Amard, L., Palacios, A., Charbonnel, C., Gallet, F., & Bouvier, J. 2016, A&A, 587, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amard, L., Palacios, A., Charbonnel, C., et al. 2019, A&A, 631, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arancibia-Silva, J., Bouvier, J., Bayo, A., et al. 2020, A&A, 635, L13 [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Augustson, K. C., & Mathis, S. 2019, ApJ, 874, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Augustson, K. C., Mathis, S. 2020, in Stars and their Variability Observed from Space, eds. C. Neiner, W. W. Weiss, D. Baade, et al., 311 [Google Scholar]
- Augustson, K. C., Brown, B. P., Brun, A. S., Miesch, M. S., & Toomre, J. 2012, ApJ, 756, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., & Lebreton, Y. 1990, in Surface Abundances of Light Elements as Diagnostic of Transport Processes in the Sun and Solar-Type Stars, eds. G. Berthomieu, & M. Cribier, Astrophys. Space Sci. Lib., 159, 437 [Google Scholar]
- Baglin, A., Morel, P. J., & Schatzman, E. 1985, A&A, 149, 309 [NASA ADS] [Google Scholar]
- Bahcall, J. N., Pinsonneault, M. H., & Wasserburg, G. J. 1995, Rev. Mod. Phys., 67, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Pratt, J., Goffrey, T., et al. 2017, ApJ, 845, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, A. J., Dempsey, A. M., & Lithwick, Y. 2014, ApJ, 791, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A., Weingrill, J., Fritzewski, D., Strassmeier, K. G., & Platais, I. 2016, ApJ, 823, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., & Antia, H. M. 1995, MNRAS, 276, 1402 [NASA ADS] [Google Scholar]
- Beck, P. G., do Nascimento, J. D., Duarte, T., et al. 2017, A&A, 602, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Marques, J. P., Goupil, M. J., et al. 2015, A&A, 579, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benomar, O., Takata, M., Shibahashi, H., Ceillier, T., & García, R. A. 2015, MNRAS, 452, 2654 [NASA ADS] [CrossRef] [Google Scholar]
- Boesgaard, A. M. 1976, PASP, 88, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Boesgaard, A. M. 1991, ApJ, 370, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Boesgaard, A. M., Armengaud, E., & King, J. R. 2003a, ApJ, 583, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Boesgaard, A. M., Armengaud, E., & King, J. R. 2003b, ApJ, 582, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Boesgaard, A. M., Armengaud, E., & King, J. R. 2004, ApJ, 605, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm, K.-H. 1963, ApJ, 138, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Bossini, D., Vallenari, A., Bragaglia, A., et al. 2019, A&A, 623, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J. 2008, A&A, 489, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Barrado, D., Moraux, E., et al. 2018, A&A, 613, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brummell, N. H. 2007, in Convection in Astrophysics, eds. F. Kupka, I. Roxburgh, & K. L. Chan, IAU Symp., 239, 417 [Google Scholar]
- Brun, A. S., Turck-Chièze, S., & Zahn, J. P. 1999, ApJ, 525, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., Strugarek, A., Varela, J., et al. 2017, ApJ, 836, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., Mankovich, C., Bildsten, L., Christensen-Dalsgaard, J., & Paxton, B. 2014, ApJ, 788, 93 [Google Scholar]
- Carlos, M., Meléndez, J., Spina, L., et al. 2019, MNRAS, 485, 4052 [Google Scholar]
- Carlos, M., Meléndez, J., do Nascimento, J. D., & Castro, M. 2020, MNRAS, 492, 245 [Google Scholar]
- Castro, M., Vauclair, S., Richard, O., & Santos, N. C. 2009, A&A, 494, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceillier, T., Eggenberger, P., García, R. A., & Mathis, S. 2013, A&A, 555, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaboyer, B., & Zahn, J. P. 1992, A&A, 253, 173 [NASA ADS] [Google Scholar]
- Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [Google Scholar]
- Charbonnel, C., & Talon, S. 2008, in The Art of Modeling Stars in the 21st Century, eds. L. Deng, & K. L. Chan, IAU Symp., 252, 163 [Google Scholar]
- Charbonnel, C., Vauclair, S., & Zahn, J. P. 1992, A&A, 255, 191 [Google Scholar]
- Charbonnel, C., Vauclair, S., Maeder, A., Meynet, G., & Schaller, G. 1994, A&A, 283, 155 [NASA ADS] [Google Scholar]
- Charbonnel, C., Decressin, T., Amard, L., Palacios, A., & Talon, S. 2013, A&A, 554, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y. Q., & Zhao, G. 2006, AJ, 131, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., & Schou, J. 1988, in Seismology of the Sun and Sun-Like Stars, ed. E. J. Rolfe, ESA SP, 286, 149 [Google Scholar]
- Cope, L., Garaud, P., & Caulfield, C. P. 2020, J. Fluid Mech., 903, A1 [Google Scholar]
- Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure (New York: Gordon and Breach) [Google Scholar]
- Cranmer, S. R., & Saar, S. H. 2011, ApJ, 741, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Cummings, J. D., Deliyannis, C. P., Maderak, R. M., & Steinhauer, A. 2017, AJ, 153, 128 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., & Mazzitelli, I. 1994, ApJS, 90, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Deal, M., Alecian, G., Lebreton, Y., et al. 2018, A&A, 618, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Mathis, S., Palacios, A., et al. 2009, A&A, 495, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Ballot, J., Beck, P. G., et al. 2015, A&A, 580, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Ballot, J., Eggenberger, P., et al. 2020, A&A, 641, A117 [EDP Sciences] [Google Scholar]
- Delgado Mena, E., Israelian, G., González Hernández, J. I., et al. 2014, A&A, 562, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deliyannis, C. P., Pinsonneault, M. H., & Charbonnel, C. 2000, in The Light Elements and their Evolution, eds. L. da Silva, R. de Medeiros, & M. Spite, IAU Symp., 198, 61 [Google Scholar]
- Denissenkov, P. A., Pinsonneault, M., Terndrup, D. M., & Newsham, G. 2010, ApJ, 716, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Do Nascimento, J. D., Castro, M., Meléndez, J., et al. 2009, A&A, 501, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domingo, V., Fleck, B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Donahue, R. A., Saar, S. H., & Baliunas, S. L. 1996, ApJ, 466, 384 [NASA ADS] [CrossRef] [Google Scholar]
- dos Santos, L. A., Meléndez, J., do Nascimento, J. D., et al. 2016, A&A, 592, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eddington, A. S. 1929, MNRAS, 90, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Eff-Darwich, A., Korzennik, S. G., Jiménez-Reyes, S. J., & García, R. A. 2008, ApJ, 679, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Maeder, A., & Meynet, G. 2005, A&A, 440, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2010, A&A, 519, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012a, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Haemmerlé, L., Meynet, G., & Maeder, A. 2012b, A&A, 539, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Lagarde, N., Miglio, A., et al. 2017, A&A, 599, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Buldgen, G., & Salmon, S. J. A. J. 2019a, A&A, 626, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Deheuvels, S., Miglio, A., et al. 2019b, A&A, 621, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., den Hartogh, J. W., Buldgen, G., et al. 2019c, A&A, 631, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggleton, P. P., Faulkner, J., & Flannery, B. P. 1973, A&A, 23, 325 [NASA ADS] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elliott, J. R., & Gough, D. O. 1999, ApJ, 516, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Elsworth, Y., Howe, R., Isaak, G. R., et al. 1995, Nature, 376, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, J., Lecoanet, D., Cantiello, M., & Brown, B. 2014, ApJ, 796, 17 [Google Scholar]
- Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
- Gabriel, A. H., Grec, G., Charra, J., et al. 1995, Sol. Phys., 162, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Gagnier, D., & Garaud, P. 2018, ApJ, 862, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., & Bouvier, J. 2015, A&A, 577, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., Zanni, C., & Amard, L. 2019, A&A, 632, A6 [CrossRef] [EDP Sciences] [Google Scholar]
- Garaud, P. 2020, ApJ, 901, 146 [Google Scholar]
- Garaud, P., Gagnier, D., & Verhoeven, J. 2017, ApJ, 837, 133 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., & Ballot, J. 2019, Liv. Rev. Sol. Phys., 16, 4 [Google Scholar]
- García, R. A., Ceillier, T., Salabert, D., et al. 2014, A&A, 572, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehan, C., Mosser, B., Michel, E., Samadi, R., & Kallinger, T. 2018, A&A, 616, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greenstein, J. L., & Richardson, R. S. 1951, ApJ, 113, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, J., Lin, L., Bai, C., & Liu, J. 2017, Ap&SS, 362, 15 [Google Scholar]
- Guzik, J. A., & Mussack, K. 2010, ApJ, 713, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Harutyunyan, G., Steffen, M., Mott, A., et al. 2018, A&A, 618, A16 [CrossRef] [EDP Sciences] [Google Scholar]
- Hopf, E. 1930, MNRAS, 90, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, R., Chaplin, W. J., Basu, S., et al. 2020, MNRAS, 493, L49 [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, A. C. S., & Weiss, A. 2018, MNRAS, 481, 4389 [NASA ADS] [CrossRef] [Google Scholar]
- King, J. R., Deliyannis, C. P., Hiltgen, D. D., et al. 1997, AJ, 113, 1871 [NASA ADS] [CrossRef] [Google Scholar]
- Korre, L., Garaud, P., & Brummell, N. H. 2019, MNRAS, 484, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Kosovichev, A. G. 1988, Sov. Astron. Lett., 14, 145 [NASA ADS] [Google Scholar]
- Krishna Swamy, K. S. 1966, ApJ, 145, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Lagarde, N., Decressin, T., Charbonnel, C., et al. 2012, A&A, 543, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagarde, N., Eggenberger, P., Miglio, A., & Montalbàn, J. 2014, in SF2A-2014: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. J. Ballet, F. Martins, F. Bournaud, R. Monier, & C. Reylé, 483 [Google Scholar]
- Lanzafame, A. C., & Spada, F. 2015, A&A, 584, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebreton, Y., & Maeder, A. 1987, A&A, 175, 99 [Google Scholar]
- Lorenzo-Oliveira, D., Meléndez, J., Ponte, G., & Galarza, J. Y. 2020, MNRAS, 495, L61 [CrossRef] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin Heidelberg: Springer) [Google Scholar]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S. 2013, in Transport Processes in Stellar Interiors, eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green, 865, 23 [Google Scholar]
- Mathis, S., & Zahn, J. P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Zahn, J. P. 2005, A&A, 440, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Palacios, A., & Zahn, J. P. 2004, A&A, 425, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Prat, V., Amard, L., et al. 2018, A&A, 620, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Eff-Darwich, A., García, R. A., & Turck-Chièze, S. 2008, A&A, 484, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matt, S. P., Brun, A. S., Baraffe, I., Bouvier, J., & Chabrier, G. 2015, ApJ, 799, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S. P., Brun, A. S., Baraffe, I., Bouvier, J., & Chabrier, G. 2019, ApJ, 870, L27 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, I., & Zijlstra, A. A. 2015, MNRAS, 448, 502 [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Meléndez, J., & Ramírez, I. 2007, ApJ, 669, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., Ekstrom, S., Maeder, A., et al. 2013, in Models of Rotating Massive Stars: Impacts of Various Prescriptions, eds. M. Goupil, K. Belkacem, C. Neiner, et al., 865, 3 [Google Scholar]
- Michaud, G., Alecian, G., & Richer, J. 2015, Atomic Diffusion in Stars (Switzerland: Springer International Publishing) [CrossRef] [Google Scholar]
- Montalban, J. 1994, A&A, 281, 421 [NASA ADS] [Google Scholar]
- Montalban, J., & Schatzman, E. 1996, A&A, 305, 513 [NASA ADS] [Google Scholar]
- Montalbán, J., & Schatzman, E. 2000, A&A, 354, 943 [Google Scholar]
- Montalbán, J., & Rebolo, R. 2002, A&A, 386, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, P., van’t Veer, C., Provost, J., et al. 1994, A&A, 286, 91 [NASA ADS] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Netopil, M., Paunzen, E., Heiter, U., & Soubiran, C. 2016, A&A, 585, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nielsen, M. B., Gizon, L., Schunker, H., & Schou, J. 2014, A&A, 568, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palacios, A., Charbonnel, C., Talon, S., & Siess, L. 2006, A&A, 453, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paquette, C., Pelletier, C., Fontaine, G., & Michaud, G. 1986, ApJS, 61, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Park, J., Prat, V., & Mathis, S. 2020, A&A, 635, A133 [EDP Sciences] [Google Scholar]
- Piau, L., & Turck-Chièze, S. 2002, ApJ, 566, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Hidalgo, S. 2013, A&A, 558, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinçon, C., Belkacem, K., Goupil, M. J., & Marques, J. P. 2017, A&A, 605, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., & Demarque, P. 1990, ApJS, 74, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Prat, V., & Lignières, F. 2013, A&A, 551, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prat, V., & Lignières, F. 2014, A&A, 566, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prat, V., Guilet, J., Viallet, M., & Müller, E. 2016, A&A, 592, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, J., Baraffe, I., Goffrey, T., et al. 2017, A&A, 604, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Proffitt, C. R., & Michaud, G. 1991, ApJ, 380, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D. 1975, Mem. Soc. R. Sci. Liege, 8, 369 [NASA ADS] [Google Scholar]
- Richard, O., Vauclair, S., Charbonnel, C., & Dziembowski, W. A. 1996, A&A, 312, 1000 [NASA ADS] [Google Scholar]
- Richer, J., Michaud, G., Rogers, F., et al. 1998, ApJ, 492, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Richer, J., Michaud, G., & Turcotte, S. 2000, ApJ, 529, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, O., Michaud, G., Richer, J., et al. 2002, ApJ, 568, 979 [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2005, ApJ, 619, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G., Gellert, M., Spada, F., & Tereshin, I. 2015, A&A, 573, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saar, S. H. 2009, in Solar-Stellar Dynamos as Revealed by Helio- and Asteroseismology: GONG 2008/SOHO 21, eds. M. Dikpati, T. Arentoft, I. González Hernández, C. Lindsey, & F. Hill, ASP Conf. Ser., 416, 375 [Google Scholar]
- Schatzman, E. 1993, A&A, 279, 431 [NASA ADS] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Schlattl, H. 2002, A&A, 395, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlattl, H., & Weiss, A. 1999, A&A, 347, 272 [NASA ADS] [Google Scholar]
- Schwarzschild, M., Howard, R., & Härm, R. 1957, ApJ, 125, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Sestito, P., & Randich, S. 2005, A&A, 442, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Smiljanic, R., Randich, S., & Pasquini, L. 2011, A&A, 535, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soderblom, D. R., Jones, B. F., Balachandran, S., et al. 1993, AJ, 106, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, F., & Lanzafame, A. C. 2020, A&A, 636, A76 [CrossRef] [EDP Sciences] [Google Scholar]
- Spada, F., Gellert, M., Arlt, R., & Deheuvels, S. 2016, A&A, 589, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spiegel, E. A., & Zahn, J. P. 1992, A&A, 265, 106 [NASA ADS] [Google Scholar]
- Spite, F., & Spite, M. 1982, A&A, 115, 357 [NASA ADS] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stauffer, J. B., & Hartmann, L. W. 1986, PASP, 98, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., Kawanomoto, S., Honda, S., Ando, H., & Sakurai, T. 2007, A&A, 468, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, Y., Honda, S., Kawanomoto, S., Ando, H., & Sakurai, T. 2010, A&A, 515, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., & Zahn, J. P. 1997, A&A, 317, 749 [NASA ADS] [Google Scholar]
- Talon, S., & Charbonnel, C. 2003, A&A, 405, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., & Charbonnel, C. 2005, A&A, 440, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., & Charbonnel, C. 2010, in Light Elements in the Universe, eds. C. Charbonnel, M. Tosi, F. Primas, & C. Chiappini, IAU Symp., 268, 365 [Google Scholar]
- Talon, S., Kumar, P., & Zahn, J.-P. 2002, ApJ, 574, L175 [Google Scholar]
- Talon, S., Richard, O., & Michaud, G. 2006, ApJ, 645, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Thévenin, F., Oreshina, A. V., Baturin, V. A., et al. 2017, A&A, 598, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, M. J., Christensen-Dalsgaard, J., Miesch, M. S., & Toomre, J. 2003, ARA&A, 41, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Thoul, A. A., Bahcall, J. N., & Loeb, A. 1994, ApJ, 421, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Turcotte, S., Richer, J., Michaud, G., Iglesias, C. A., & Rogers, F. J. 1998, ApJ, 504, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Vauclair, S. 1988, ApJ, 335, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Vauclair, S. 2013, in EAS Pub. Ser., eds. G. Alecian, Y. Lebreton, O. Richard, & G. Vauclair, 63, 233 [Google Scholar]
- Vauclair, S., Vauclair, G., Schatzman, E., & Michaud, G. 1978, ApJ, 223, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Waite, I. A., Marsden, S. C., Carter, B. D., et al. 2017, MNRAS, 465, 2076 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G., & Conti, P. S. 1969, ARA&A, 7, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Xing, L. F., & Xing, Q. F. 2012, A&A, 537, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, Y., Goriely, S., Jorissen, A., Chen, G. L., & Arnould, M. 2013a, A&A, 549, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, Y., Takahashi, K., Goriely, S., et al. 2013b, Nucl. Phys. A, 918, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R. 2018, ApJ, 855, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahn, J. P. 1991, A&A, 252, 179 [Google Scholar]
- Zahn, J. P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zhang, Q.-S., Li, Y., & Christensen-Dalsgaard, J. 2019, ApJ, 881, 103 [CrossRef] [Google Scholar]
- Ziegler, U., & Rüdiger, G. 2003, A&A, 401, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Model convention
In order to simplify the notations, we used the following convention to identify the models:
where we defined
-
Model type (Mtype)
-
Classical model (C)
-
Rotational model (R)
-
-
Dh/Dv prescription/adjusted K parameter (X)
-
Dh = Mathis et al. (2018)/Dv = Zahn (1992)/ K = 7.5 × 1030 erg (1)
-
Dh = Zahn (1992)/Dv = Talon & Zahn (1997)/ K = 7.5 × 1030 erg (2)
-
Dh = Zahn (1992)/Dv = Talon & Zahn (1997)/ K = 3 × 1030 erg (2′)
-
Dh = Zahn (1992)/Dv = Talon & Zahn (1997)/ K = 4.5 × 1030 erg (2″)
-
Dh = Mathis et al. (2004)/Dv = Zahn (1992)/ K = 7.5 × 1030 erg (3)
-
-
Initial rotation velocity (Rotini)
-
Slow (S)
-
Median (none = default)
-
Fast (F)
-
-
Rotation type (Rtype) – All rotation models include meridional circulation and shear turbulence
-
Impose solid rotation (solid)
-
Addition of a viscosity νadd (ν)
-
Addition of the viscosity νadd advised by Spada et al. (2016) for the Sun (ν.spada)
-
Addition of the time-dependent viscosity νadd(t) according to Spada et al. (2016) (ν.spada(t) and ν2.spada(t))
-
-
Turbulence mixing (Turb)
-
Turbulence fixed at temperature T0 (T6.425)
-
Turbulence fixed at the base of the convection zone (PM5000)
-
Tachocline turbulence (Tach)
-
-
Overshoot (Oversh)
-
Overshoot from Baraffe et al. (2017) (B)
-
Overshoot from Augustson & Mathis (2019) (A)
-
Overshoot from Korre et al. (2019) (K).
-
Appendix B: Prescriptions for tubulent viscosities
B.1. Vertical turbulent viscosities
In the framework of the shellular rotation hypothesis and assuming strong anisotropic turbulence, Zahn (1992) proposed defining Dv as
with Ric the critical Richardson number (= 1/4) beyond which the initial instability exists, κT the thermal diffusivity, θ a spherical coordinate, and NT the thermal term of the Brunt-Väisälä frequency.
Talon & Zahn (1997) developed another version of Dv that considers the effect of thermal and chemical stratifications. The Richardson criterion was then modified; it now involves Nμ, the chemical term of the Brunt-Väisälä frequency. The coefficient Dv is defined as
where 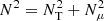 is the Brunt-Väisälä frequency.
is the Brunt-Väisälä frequency.
B.2. Horizontal turbulent viscosities
Zahn (1992) defined Dh as
with 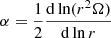 the shear rate (α = 1 means uniform rotation), V2 the latitudinal component, and U2 the radial component of the meridional circulation developed to the second order:
the shear rate (α = 1 means uniform rotation), V2 the latitudinal component, and U2 the radial component of the meridional circulation developed to the second order:
Here Γ(m) refers to the gain or loss of angular momentum in the isobar enclosing m(r).
Mathis et al. (2004) defined Dh as
where β is a parameter close to 1.5 × 10−5.
Mathis et al. (2018) accounted for the fact that horizontal turbulence is generated from both horizontal and vertical shears. The coefficient Dh then writes as Dh = Dh, h + Dh, v. The first index means the direction of the transport and the second index refers to the shear that generates the transport. This additional transport (Dh, v) is active only if the vertical shear does not fulfil the Reynolds criterion (Re > Re; c with Re; c = 7νm with νm the molecular viscosity):
Here Dv, v ≡ Dv from Eq. (B.1), and τ is a characteristic timescale for the turbulence, taken to be equal to the time characterising the radial shear, τ = 1/S, where S = r sin θ∂rΩ, as in Amard et al. (2019).
All Tables
Solar calibration results for the STAREVOL classical model (C: no transport other than convection) and rotating model (R: atomic diffusion and type I rotation-induced transport).
All Figures
 |
Fig. 1. Top: lithium surface abundance evolution with time for the R1 models including different overshoot prescriptions (colour-coded). Individual points are data for solar twins (Carlos et al. 2019). Boxes are for Li observations of solar-type stars in different open clusters (Sestito & Randich 2005; Carlos et al. 2020 for M 67) with ages from Bossini et al. (2019). The numbers 1–10 identify the clusters: (1) NGC 2264, (2) IC 2391, IC 2602 and IC 4665, (3) α Per, Pleiades, Blanco I, (4) NGC 2516, (5) M 34, (6) NGC 6475, (7) M 35, (8) Praesepe, NGC 6633, (9) NGC 752, and (10) M 67. The colour of the boxes indicates the [Fe/H] value: Netopil et al. (2016): pink: −0.17 to −0.05; grey: −0.05 to 0.05; light blue: 0.05–0.16. Bottom: evolution of the angular velocity of the convective envelope and of the radiative core (in solar units Ω⊙ = 2.86 × 10−6 s−1; solid and dotted lines, respectively) vs age. The observational data is from Gallet & Bouvier (2015), except the four stars of M 67 from Barnes et al. (2016). Crosses are for individual stars; open diamonds show the 50th percentiles of the observed rotational distributions in each cluster. |
| In the text | |
 |
Fig. 2. Same as Fig. 1, but for the R1A, R2A, |
| In the text | |
 |
Fig. 3. Same as Fig. 1, but for the models with a fixed viscosity νadd (νR1A, |
| In the text | |
 |
Fig. 4. Differential rotation evolution with time for the νR1A, ν.spadaR1A, ν.spada(t)R1A, and ν2.spada(t)R1A models (details in Table 3). |
| In the text | |
 |
Fig. 5. Angular velocity profiles vs the radius at solar age for models presented in Fig. 3 compared to the rotation profile of the Sun (in dark grey) obtained from helioseismology from Eff-Darwich et al. (2008). The solid line, the dotted line, the dashed line, and the dot-dashed line refer to the differential, solid, νadd, and νadd(t) rotation cases, respectively. |
| In the text | |
 |
Fig. 6. Same as Fig. 1, but for models |
| In the text | |
 |
Fig. 7. Profiles of the logarithm of the diffusion coefficients (left axis) of the meridional circulation (Deff), the vertical shear (Dshear = Dv), the overshoot (DA), the parametric turbulence (DT6.425), and the total transport coefficient (Dtot = Deff + Dshear + DA + DT6.425) as a function of the radius normalised to solar radius at four different ages (107 years, 5 × 107 years, 109 years, and solar age) for model |
| In the text | |
 |
Fig. 8. Same as Fig. 1, but for the different R1 models, the selected |
| In the text | |
 |
Fig. 9. Same as Fig. 8, but for Be. Boxes are for Be observations of solar-mass stars in different open clusters and are colour-coded according to their metallicity, as in Fig. 1. The numbers I–V identify the clusters: (I) IC 2602 and IC 2391 (Smiljanic et al. 2011), (II) Pleiades (Boesgaard et al. 2003a), (III) Ursa Major (Boesgaard et al. 2003b), (IV) Coma Ber (Boesgaard et al. 2003b), and (V) Hyades (Boesgaard et al. 2004). The solar beryllium with uncertainties comes from Asplund et al. (2009, photospheric value). The orange dots refer to the four profiles extracted from the star evolution shown in Fig. 7. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



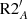
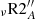
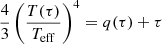
![$$ \begin{aligned}&\rho \frac{\partial X_i}{\partial t}\!=\! \frac{1}{r^2}\frac{\partial }{\partial r}\! \left(r^2 \rho D \frac{\partial X_i}{\partial r}\right)-\frac{1}{r^2}\frac{\partial }{\partial r} \left(r^2 \rho X_i {{ v}_i}\right)\nonumber \\ &\qquad \qquad \qquad \qquad + m_i \left[ \sum _j r_{ji} - \sum _k r_{ik} \right], \end{aligned} $$](/articles/aa/full_html/2021/02/aa39515-20/aa39515-20-eq7.gif)
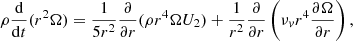
![$$ \begin{aligned} D_{B}(r) = D_{0} \left[1-\mathrm{exp}\left(-\mathrm{exp}\left(-\frac{\frac{r_{bcz}-r}{R}-\mu }{\lambda }\right)\right)\right]. \end{aligned} $$](/articles/aa/full_html/2021/02/aa39515-20/aa39515-20-eq16.gif)
![$$ \begin{aligned} D_{\rm A}(r) \approx D_0 \left[1-\exp \left(-\exp \left(\frac{r-r_{bcz}}{d_{\rm ov} \times \left({\frac{v}{{v}_{0}}}\right)^{3/2}} + \frac{\mu }{\lambda } \right)\right)\right]. \end{aligned} $$](/articles/aa/full_html/2021/02/aa39515-20/aa39515-20-eq17.gif)
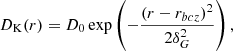
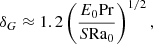
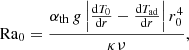
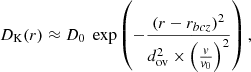
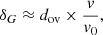
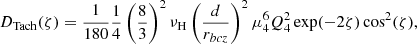
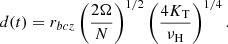
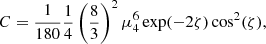
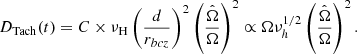
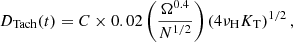
![$$ \begin{aligned} D_{{T_0}} = 400 D_{\rm {He}}(T_0)\left[\frac{\rho (T_0)}{\rho }\right]^3, \end{aligned} $$](/articles/aa/full_html/2021/02/aa39515-20/aa39515-20-eq35.gif)
![$$ \begin{aligned} D_{\rm {PMa_0}} = a_0 \left[\frac{\rho _{{bcz}}}{\rho }\right]^3 \end{aligned} $$](/articles/aa/full_html/2021/02/aa39515-20/aa39515-20-eq36.gif)
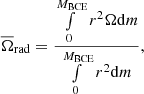
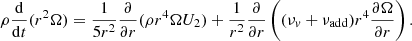
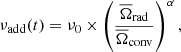
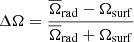
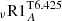
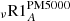
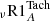
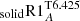
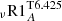
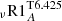
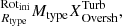
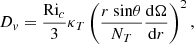
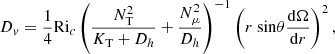
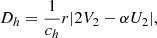
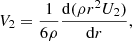
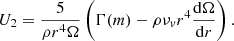
![$$ \begin{aligned} D_h = \left(\frac{\beta }{10}\right)^{1/2} (r^2 \Omega )^{1/2} [r | 2V_2 - \alpha U_2 |]^{1/2}, \end{aligned} $$](/articles/aa/full_html/2021/02/aa39515-20/aa39515-20-eq83.gif)
![$$ \begin{aligned} D_{h,h} = \left(\frac{\beta }{10}\right)^{1/2} (r^2 \Omega )^{1/2} [r | 2V_2 - \alpha U_2 |]^{1/2}, \end{aligned} $$](/articles/aa/full_html/2021/02/aa39515-20/aa39515-20-eq84.gif)