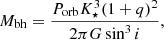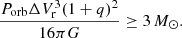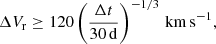EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 645 (January 2021) A&A, 645 (2021) A72 Full HTML
Open Access
Issue
A&A
Volume 645, January 2021
Article Number A72
Number of page(s) 6
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202039317
Published online 14 January 2021

© M. Clavel et al. 2021

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

Known compact binaries with neutron stars (NSs) or black holes (BHs) as compact objects are currently identified thanks to their bright X-ray outbursts (McClintock & Remillard 2006; Corral-Santana et al. 2016) or from follow-up observations of X-ray surveys (e.g., Walter et al. 2015). However, these bright X-ray sources most likely represent only a small fraction of the overall population of compact binaries, with a larger number of X-ray faint objects missed by the current approach because of long quiescent periods in between outbursts (Dubus et al. 2001; Yungelson et al. 2006; Yan & Yu 2015) or because they are persistently very faint (Menou et al. 1999; King & Wijnands 2006).

Radial velocity variations in optical spectra could be a means to uncover the population of quiescent compact objects that have a stellar companion (Casares et al. 2014; Giesers et al. 2018; Thompson et al. 2019; Makarov & Tokovinin 2019). Recently, Gu et al. (2019) selected spectra of bright late-type giants obtained at different times by the LAMOST spectral survey and identified seven candidates with large radial velocity variations that are compatible with the presence of an unseen solar mass companion of > 3 M⊙. One of them (UCAC4 721-037069, which corresponds to their source #4, hereafter GS4) has a possible X-ray counterpart and is presented by Gu et al. (2019) as their best BH candidate.

In this paper, we investigate the available data, including two dedicated observation programs, to identify the nature of this intriguing source. The optical spectra, the orbital parameters, and the properties of the X-ray counterpart of GS4 are described in Sect. 2. The identification of this source as an RS CVn is then discussed in Sect. 3, along with considerations on how constraints on the orbital period could further help discriminate between this type of source and quiescent BHs that have a stellar companion.

2. Optical and X-ray constraints

GS4 corresponds to Gaia DR2 273187064220377600. Located at RA (J2000) = 04h56m12.7739s and Dec (J2000) = 54°00′21.2768″, this source has a parallax of 1.07 ± 0.03 mas, which corresponds to a distance of 0.91 ± 0.03 kpc (Bailer-Jones et al. 2018).

The All-Sky Automated Survey for Supernovae (ASAS-SN, Shappee et al. 2014; Kochanek et al. 2017; Jayasinghe et al. 2019) and Gaia DR2 (Gaia Collaboration 2016, 2018) provide aperture photometry light curves for GS4. As previously reported by Zheng et al. (2019), these light curves have a strong modulation with a period p ≈ 5.2 days, and the morphology of GS4’s folded light curve is typical of eclipsing binaries (see Fig. 1, top, and Sect. 2.2).

thumbnail Fig. 1.

Aperture photometry and radial velocity. Top: ASAS-SN light curve of GS4, folded using the period p = 5.20906 ± 0.0005 d and t0 = 2457384.6 HJD. Bottom: corresponding radial velocity of the system as observed by the LT. We do see a 0.04 phase shift between the radial velocity curve and the ASAS-SN light curve, but we have no clear explanation for it (see Sect. 2.1). The blue curves correspond to the best fit model obtained with PHOEBE on the ASAS-SN light curve when fixing the semi-amplitude radial velocity of the system to the one measured from the LT curve (see Sect. 2.2).

The extinction toward GS4 can be estimated from the 3D map of interstellar dust reddening derived from the Pan-STARRS 1 and 2MASS surveys (Green et al. 2018). At 910 pc, the reddening is E(g − r) = 0.35 ± 0.02, which corresponds to an extinction AV = 1.06 ± 0.061. This value converts into a column density NH ≈ 2.3 × 1021 cm−2 (see Güver & Özel 2009).

2.1. Time-resolved spectroscopy and radial velocity

In agreement with the star’s position in the Gaia Hertzsprung-Russell diagram, the LAMOST spectra of GS4 reveal a late-type giant that has radial velocity variations as large as ΔVr = 127.2 ± 7.8 km s−1 (Gu et al. 2019; Zheng et al. 2019). We obtained refined radial velocity measurements using the medium resolution spectrograph FRODOSpec at the robotic Liverpool Telescope (LT, Steele et al. 2004; Barnsley et al. 2012) to establish the orbital parameters of this source.

The spectrograph is fed by a fiber bundle array consisting of 12 × 12 lenslets of 0.82″ each, which is reformatted as a slit. FRODOSpec was operated in high resolution mode, providing a spectral resolving power of R ∼ 5500 in the blue arm and R ∼ 5300 in the red arm. The spectral coverage was 3900−5215 Å and 5900−8000 Å, respectively. A total of 26 spectra of 1200 s were obtained in each arm, with a cadence of 1−3 spectra per night between 2019 August 28 and 2019 December 1. For the sake of radial velocity analysis, we also obtained a 300 s spectrum of the K0III standard HD 210185 on the night of 2019 September 17, using the same spectral configuration. The FRODOSpec pipeline produces fully extracted and wavelength-calibrated spectra with rms ≤ 0.1 Å above 4400 Å. The analysis presented in this paper was performed with the FRODOSpec pipeline products.

Radial velocities were extracted through the cross-correlation of every GS4 red-arm spectrum with the K0III template in the spectral range 6300−7900 Å, after masking the main telluric and interstellar absorption bands. The Hα line was also excluded as some spectra show evidence of variable narrow-emission, reminiscent of chromospheric activity.

The spectrum obtained for GS4 is compatible with a K0III star that has a temperature on the order of 4800 K (consistent with the effective temperature derived from LAMOST DR6, see e.g., Gu et al. 2019), and a periodogram analysis of the radial velocity points shows a clear peak at 5.2081(34) d, in excellent agreement with the ASAS-SN photometric period (see below). The radial velocity curve is shown in Fig. 1 (bottom). Modeling the light curve with a simple sinusoid gives the systemic velocity γ = −7.8 ± 1.1 km s−1 and the semi-amplitude radial velocity K1 = 69.0 ± 1.7 km s−1. Together with the orbital period of the system determined by phase dispersion minimization on the ASAS-SN V-band light curve, Porb = 5.20906 ± 0.0005 d, this corresponds to a binary mass function f = 0.18 ± 0.01 M⊙.

We observe a shift of 0.04 in phase between the ASAS-SN light curve and the LT radial velocity curve (see Fig. 1, bottom). This corresponds to five hours, so we can rule out any instrumental effect2. A persistent asymmetry in the stellar radiation field (due to, e.g., star spots, see also Sect. 3.1) could be a possible physical origin, but we have no evidence for this. We note that an asymmetric flux distribution combined with eclipses has also been discussed as the possible origin of a similar phase lag detected in the BH X-ray binary XTE J1118+480 during its decay to quiescence (McClintock et al. 2001).

In order to constrain the rotational broadening of the K0III star, we broadened the red-arm spectrum of the template star (HD 210185) from 0 to 120 km s−1 in steps of 2 km s−1 using a Gray profile (Gray 1992) with a linear limb-darkening law with coefficient ϵ = 0.75, which is appropriate for the wavelength range and spectral type of our star (see Al-Naimiy 1978). The broadened versions of the template star were multiplied by fractions f <  1 to account for the fractional contribution to the total light and, subsequently, subtracted from the Doppler-corrected average of the 26 red spectra of GS4 using our orbital solution. A χ2 test on the residuals yields V sin i = 80 ± 1 km s−1. The comparison of the GS4 spectrum with the best broadened version of the template star is shown in Fig. 2 (top).

thumbnail Fig. 2.

Sample of LT spectra. Top: from bottom to top: red-arm LT spectrum of HD 210185 (the K0III template), the same spectrum broadened by 80 km s−1, and the Doppler-corrected average spectrum of GS4. Bottom: from bottom to top: blue-arm LT spectrum of the K0III template in comparison with the Doppler-corrected averages of GS4 obtained during the primary eclipse (photometric phase 0.00 ± 0.05) and outside the eclipse (remaining phases). The top spectrum shows the Hβ line (at 4861 Å) to be slightly stronger (relative to the nearby metallic lines), possibly because of the contribution from the A-type secondary. The secondary is eclipsed in the middle spectrum, which seems to show a better match to the K0III spectrum. Scaling factors have been applied to the three spectra so that the equivalent widths of the metallic lines in the 4900−5000 Å range are the same.

2.2. System parameters derived from the light curve

We modeled the ASAS-SN light curve using the eclipsing binary modeling software PHOEBE3 with PHOENIX model atmosphere (Jones et al. 2020), in combination with the Markov chain Monte Carlo (MCMC) sampler emcee (Foreman-Mackey et al. 2013). We fixed the orbital period to the value derived from phase dispersion minimization (see Sect. 2.1). We set the reddening to AV = 1.06, derived from the map of Green et al. (2018, see above). The free parameters of the fit were the system inclination cos i, the primary (K0III) star mass M1, the effective temperatures of the binary components T1, 2, the ratio of the primary star radius R1 to the Roche lobe radius RL, the radius of the secondary (unseen) star R2, and the parallax π. The mass of the secondary star M2 was set from M1, i, and K1 = 69 km s−1. We used flat priors except for the parallax π, where we used a Gaussian prior (1.0981 ± 0.0421 mas). The parallax takes into account the parallax zero point of 0.03 mas and the error increase suggested by Lindegren et al.4. The sampler ran for 30 000 steps, after which we found that the chain had converged, based on the sampled parameters and the autocorrelation time. We discarded the initial 5000 steps (burn-in phase). The errors quoted in Table 1 are based on the tenth and 90th percentiles. A major source of uncertainty is the adopted reddening. We did not attempt to model light curves in different bands. Taking AV = 0 significantly lowers the effective temperatures (T1 ≈ 5060 K and T2 ≈ 7860 K), significantly lowers R2 to 1.3 R⊙, and slightly lowers M1 to 1.6 M⊙, but it has no impact on i or R1/RL since they are constrained by the light curve shape. In all cases, the primary nearly fills its Roche lobe, with R1 = 7.5 ± 0.5 R⊙.

Table 1.

Parameters of the binary system GS4 obtained from a fit of the ASAS-SN V-band light curve using PHOEBE.

2.3. X-ray counterpart

As pointed out by Gu et al. (2019), GS4 is compatible with the position of the ROSAT source 2RXS J045612.8+540024 (4″ away from GS4, with a 12″ X-ray position uncertainty, Voges et al. 2000), with an association likelihood of 55% (Flesch 2016). In the 0.1−2.4 keV range, this X-ray source is rather hard, with an X-ray flux of F0.1 − 2.4 keV = 4.4 × 10−13 erg cm−2 s−1. To test this association, we obtained a 5 ks Chandra/ACIS-I observation (Obs. ID 22399) that targets the Gaia position of GS4. This X-ray observation spanned from MJD 58728.017 to 58728.075, which corresponds to phase ≈0.02 in Fig. 1: It was performed during the primary eclipse.

The data was reduced using CIAO software v.4.12 along with the calibration database CALDB v.4.9.0. Chandra_repro was used to produce the clean event file, and then wavdetect (default parameters) was run to detect all sources in the field of view. Sixteen sources were detected, including one source consistent with the Gaia position of GS4, detected with a significance of 18σ. The X-ray source coordinates are RA = 04h56m12.76s, Dec = 54° 00′21.2″. The source was therefore named CXO J045612.8+540021. Its position accuracy is limited by the Chandra absolute astrometric accuracy and is therefore ∼1″.

We then extracted the source spectrum using specextract and a circular region of radius r = 2″ centered on the position of CXO J045612.8+540021, while the background spectrum was extracted from an annulus region between 5″ and 20″ and centered on the same coordinates. A total of 36 counts were detected from the source in the 0.5−8 keV energy range (there are ten counts in the background region in the same energy range, so we only expect a 0.1 background count in the source region). The source spectrum was binned to have at least five counts per bin and then background subtracted. We note that the last bin from 5 to 8 keV only contains one count. We therefore used Gehrels weights (Gehrels 1986) to better account for the errorbar in each bin. Spectral fits were performed with Xspec v.12.10.1, and the errorbars correspond to the 90% confidence interval. The absorption is modeled with tbabs, using Wilms abundances (Wilms et al. 2000), and fixed to NH = 2.3 × 1021 cm−2 (see beginning of Sect. 2).

We first tested a power-law model to fit the source spectrum. The best fit gives a reduced 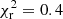(six degrees of freedom, d.o.f.) and a photon index 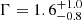. The source spectrum is somewhat better fitted by a black body model (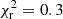, six d.o.f.) with a temperature 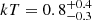keV; the 0.5−10 keV flux of the source is then 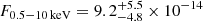erg cm−2 s−1, which, at a distance of 0.91 kpc, translates into a luminosity L0.5 − 10 keV = (9 ± 5)×1030 erg s−1.

Extrapolating the best fit model to the ROSAT energy range, we find a flux that is F0.1 − 2.4 keV = 3.4 × 10−14 erg cm−2 s−1. This is more than one order of magnitude below the ROSAT detection in 1990. While we cannot exclude that the ROSAT source could be a transient that is unrelated to GS4 and that is now under the detection limit of our 2019 Chandra observation, it is also likely that the source has varied, either due to the eclipsing pattern and/or a longer-term variability.

3. Discussion

3.1. Nature of the unseen companion

The orbital model fitting the orbital light curve of GS4, presented in Sect. 2.2, describes a stellar binary composed of a giant star nearly filling its Roche lobe and a hotter but smaller companion. At phase 0, the giant star is totally eclipsing its companion, while at phase 0.5 the companion is in front of the giant star and only partly eclipsing it. The deformed shape of the giant star produces the ellipsoidal modulation in addition to the eclipse at phase 0. Therefore, the fit to the orbital modulation constrains the inclination and the Roche lobe filling factor of the primary very well. The rotational broadening (≈80 km s−1) is compatible with the primary star being tidally locked and synchronized with R1 ≈ 8 R⊙, as expected since it nearly fills its Roche lobe.

Under the assumption that the K0III star fully fills its Roche lobe and is tidally locked in its orbit, the binary mass ratio q can be derived through the expression V sin i ≃ 0.462K1q1/3(1 + q)2/3 (Wade & Horne 1988). In our case, q = M1/M2, where M1 is the mass of the K0III star and K1 = 69.0 ± 1.7 km s−1, so we find q = 1.89 ± 0.07. This is slightly larger than, but consistent with, the mass ratio derived through the PHOEBE modeling (Table 1).

From the orbital evolution of the veiling factor (i.e., the fractional contribution of the K0III template spectrum to the total light), we find that the K0III spectrum contributes 60% outside the primary eclipse and 91% at phase 0. This means that the secondary accounts for ≈30% of the total flux and suggests the presence of additional light in the system that is not accounted for in the orbital modulation fit. Such additional light could also explain why the temperature T1 ≈ 5800 K derived from the fit is incompatible with the K0III spectral classification (≈4800 K). Since the primary star nearly fills its Roche lobe, a mass transfer creating an accretion disk around the secondary star is the most likely explanation for this additional source of light.

The mass, temperature, and radius of the secondary derived from the orbital fit suggest an A- or F-type main sequence companion. This identification of the unseen companion is fully consistent with the fact that it is not detected spectroscopically. It is worth noting that at phase ∼0.5 the spectrum of the secondary is hinted at by the large depth of the Balmer lines (especially Hβ and Hγ in the blue-arm LT spectra) relative to the nearby metallic lines, as compared to a typical K0 spectrum (see Fig. 2, bottom).

These optical constraints and the X-ray emission described in Sect. 2.3 are fully consistent with a chromospherically active giant star in a semidetached binary, and we therefore classify GS4 as an RS CVn (see e.g., Pandey & Singh 2012, for the X-ray properties of such systems). These systems do display variability in their X-ray and orbital modulation light curves due to the activity of the giant star. We note that the binary mass ratio is relatively large (∼1.6−1.9). This value approaches (but does not exceed) the critical mass ratio for unstable mass transfer from intermediate-mass donor stars with convective envelopes, as computed in recent simulations (Misra et al. 2020). In addition, the asymmetry of the light curve seen at phase 0.8−0.9 (Fig. 1, top) is fairly typical for an RS CVn and is explained by the presence of starspots at the surface of the giant star.

3.2. Radial velocities as a probe for quiescent black holes

Population studies indicate that there may be from 103 to 105 BHs with solar mass companions (e.g., Shao & Li 2019; Olejak et al. 2020). The ≈60 BH X-ray binaries sample only a fraction of this binary population (Corral-Santana et al. 2016). With a duty cycle ≤0.02 (Yan & Yu 2015), many are hiding in quiescence, with the accretion disk building up mass before the next outburst. Many more systems may be non-accreting if they were unable to evolve to shorter periods during the common envelope phase or through angular momentum losses (de Kool et al. 1987; Iben et al. 1995; Podsiadlowski et al. 2003; Yungelson et al. 2006; Shao & Li 2019). These binaries can therefore provide important insights into BH evolution even though they harbor only a small fraction of the ∼108 BHs estimated to reside in our Galaxy.

Radial velocity surveys of field or globular cluster stars can provide dynamical evidence for invisible companions (Giesers et al. 2018; Zheng et al. 2019; Gu et al. 2019; Yi et al. 2019; Wiktorowicz et al. 2020). For a circular binary,

(1)

where K⋆ is the semi-amplitude of the radial velocity modulation of the stellar companion and q = M⋆/Mbh. If a radial velocity difference ΔVr is measured between two epochs, a sufficient condition to have a > 3 M⊙ unseen companion is

(2)

We plot this limit in Fig. 3 for Mbh = 3, 10, and 30 M⊙, assuming M⋆ = 1 (dashed lines) or 3 (solid lines) M⊙. It is important to highlight that these lines would be shifted toward the left for systems that are known to have a low inclination. The limit below which the star will overfill its Roche lobe is also highlighted. Overlaid on this plot, we show BH candidates based on radial velocity measurements: the BH low-mass X-ray binaries listed in Table A.4 of Corral-Santana et al. (2016), the BH candidate found in the APOGEE survey (Thompson et al. 2019), the candidate LB-1 found in the LAMOST survey (we note the companion is a B star, Liu et al. 2019, and follow-up discussions by e.g., Irrgang et al. 2020; Shenar et al. 2020), the BH candidates found in MUSE observations of the NGC 3201 globular cluster (some have nonzero eccentricity, Giesers et al. 2019), and the non-accreting BH candidate in the triple system HR 6819 (Rivinius et al. 2020, but see also follow-up discussions in: Bodensteiner et al. 2020; Safarzadeh et al. 2020; El-Badry & Quataert 2020). X-ray binaries are nearly all located within the mass transfer region and above the limit defined by Eq. (2), except 4U 1543−475, which is known to have a low inclination i ≈ 20°.

thumbnail Fig. 3.

Black hole candidates with solar mass companions in the orbital period – radial velocity amplitude plane. Solid (dashed) lines show the lower limit on Porb that, according to Eq. (2), is sufficient to have a 3, 10, or 30 M⊙ BH in circular orbit with a 3 M⊙ stellar companion (1 M⊙ companion). Colored areas indicate where a 3, 10, or 30 R⊙ stellar companion would overfill its Roche lobe. Candidate BHs from radial velocity measurements: low-mass X-ray binaries (black dots); APOGEE candidate (open circle); LAMOST LB-1 candidate (open diamond); MUSE candidates in NGC 3201 (open squares); HR 6819 candidate (open triangle) and the latest LAMOST selection of giant stars having large ΔVr and optically invisible companions (crosses), including GS4 (star). More details are given in the text.

For comparison, the latest selection of giant stars that have large ΔVr and optically invisible companions from the LAMOST survey (Zheng et al. 2019) are also shown. All, including GS4, lie in the gray area, indicating that the constraint on the radial velocity is not sufficient to reveal quiescent BHs given their relatively short orbital periods. To match the Mbh ≥ 3 M⊙ criterion, these systems would need to have an upper limit on their inclination of i ≲ 65° for the source closest to the line (source #8 in Zheng et al. 2019) and between i ≲ 40° and i ≲ 20° for all the other candidates, if we assume the conservative M⋆ = 3 M⊙. However, at such a low inclination, we do not expect to detect the strong ellipsoidal modulations that are seen in the ASAS-SN light curves (see e.g., Zheng et al. 2019). Therefore, it is likely that most of these systems are also stellar binaries.

Non-interacting systems clearly lie at longer orbital periods, as supported by the recent detection of one such system using the APOGEE radial velocity survey (Thompson et al. 2019, and follow-up discussions: van den Heuvel & Tauris 2020; Thompson et al. 2020). A simple, conservative criterion to select candidate BH systems for follow-up is, using Eq. (2),

(3)

with Δt the elapsed time between the maximum and minimum velocity. This is similar to how Thompson et al. (2019) prioritized their candidate list for follow-up, leading to the detection of a strong candidate. GS4, with an initial ΔVr = 100 km s−1 measured from the survey (Gu et al. 2019), is at the limit of the criterion, although this is possibly lowered by a long Δt (the six LAMOST observations are probably spread in time over several years). Surveys with long time bases such as LAMOST are well suited to probe the region of the diagram with detached giant stellar companions. However, as GS4 highlights, the long Δt induced by the sampling may also lead to the incorrect identification of stellar binaries with short orbital periods as BH candidates. A work-around to avoid these false positives could be to sample spectra on various timescales.

4. Conclusion

The large radial velocity variations detected in LAMOST spectra have been used to highlight potential BH candidates (Gu et al. 2019; Zheng et al. 2019). We tested this selection by further investigating the parameters of the one system, GS4, that has a known X-ray counterpart and which was presented by Gu et al. (2019) as a likely BH or NS system with mass transfer from the giant to the compact object. The time-resolved spectra that we obtained from the LT along with the ASAS-SN V-band light curve of GS4 allowed us to fully constrain the orbital parameters of this eclipsing binary, thereby excluding the possibility of a massive and compact companion. Our Chandra observation did confirm the existence of an X-ray counterpart for this system: its X-ray spectrum and luminosity are fully consistent with a chromospherically active giant star, allowing us to classify GS4 as an RS CVn.

Given the radial velocity variations sampled by LAMOST ΔVr ∼ 100 km s−1 and the very high inclination of GS4 constrained from its eclipsing behavior, we argue that its short orbital period Porb ≈ 5.2 d is sufficient to exclude the BH companion hypothesis for this system. The same reasoning likely also applies to all other LAMOST candidates, except for one (source #8 in Zheng et al. 2019), since they all have similar radial velocity variations, relatively short orbital periods, and rather high inclinations inferred from the orbital modulations seen in their ASAS-SN light curve (Zheng et al. 2019). Therefore, the orbital period or the timescale of the radial velocity variations appear as the keys to verify the viability of these radial-velocity selected BH candidates.

1

Using the Gaia and 2MASS surveys, Lallement et al. (2019) derived an extinction of 1.4 mag in this direction and at this distance. Using this value would require a higher luminosity from the binary components to account for the observed flux: It would increase the tension between spectral type and luminosity, furthering the need for additional light (see Sects. 2.2 and 3.1).

2

Both the LT and ASAS-SN curves are provided in Heliocentric Julian Day (HJD), and the ASAS-SN photometry aligns well with publicly available data from other observatories (e.g., Gaia).

Acknowledgments

The scientific results reported in this article are based on observations made with the Liverpool Telescope operated on the island of La Palma by Liverpool John Moores University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias with financial support from the UK Science and Technology Facilities Council, and on observations made by the Chandra X-ray Observatory. MC and GD acknowledge financial support from the Centre National d’Etudes Spatiales (CNES). JC acknowledges support by the Spanish MINECO under grant AYA2017-83216-P.

References

  1. Al-Naimiy, H. M. 1978, Ap&SS, 53, 181 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barnsley, R. M., Smith, R. J., & Steele, I. A. 2012, Astron. Nachr., 333, 101 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bodensteiner, J., Shenar, T., Mahy, L., et al. 2020, A&A, 641, A43 [CrossRef] [EDP Sciences] [Google Scholar]
  5. Casares, J., Negueruela, I., Ribó, M., et al. 2014, Nature, 505, 378 [Google Scholar]
  6. Corral-Santana, J. M., Casares, J., Muñoz-Darias, T., et al. 2016, A&A, 587, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. de Kool, M., van den Heuvel, E. P. J., & Pylyser, E. 1987, A&A, 183, 47 [NASA ADS] [Google Scholar]
  8. Dubus, G., Hameury, J. M., & Lasota, J. P. 2001, A&A, 373, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. El-Badry, K., & Quataert, E. 2020, MNRAS, submitted [arXiv:2006.11974] [Google Scholar]
  10. Flesch, E. W. 2016, PASA, 33, e052 [NASA ADS] [CrossRef] [Google Scholar]
  11. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  12. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
  15. Giesers, B., Dreizler, S., Husser, T.-O., et al. 2018, MNRAS, 475, L15 [NASA ADS] [CrossRef] [Google Scholar]
  16. Giesers, B., Kamann, S., Dreizler, S., et al. 2019, A&A, 632, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Gray, D. F. 1992, The Observation and Analysis of Stellar Photospheres (Cambridge: Cambridge University Press), 20 [Google Scholar]
  18. Green, G. M., Schlafly, E. F., Finkbeiner, D., et al. 2018, MNRAS, 478, 651 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gu, W.-M., Mu, H.-J., Fu, J.-B., et al. 2019, ApJ, 872, L20 [CrossRef] [Google Scholar]
  20. Güver, T., & Özel, F. 2009, MNRAS, 400, 2050 [NASA ADS] [CrossRef] [Google Scholar]
  21. Iben, I., Jr., Tutukov, A. V., & Yungelson, L. R. 1995, ApJS, 100, 233 [NASA ADS] [CrossRef] [Google Scholar]
  22. Irrgang, A., Geier, S., Kreuzer, S., Pelisoli, I., & Heber, U. 2020, A&A, 633, L5 [CrossRef] [EDP Sciences] [Google Scholar]
  23. Jayasinghe, T., Stanek, K. Z., Kochanek, C. S., et al. 2019, MNRAS, 486, 1907 [NASA ADS] [Google Scholar]
  24. Jones, D., Conroy, K. E., Horvat, M., et al. 2020, ApJS, 247, 63 [CrossRef] [Google Scholar]
  25. King, A. R., & Wijnands, R. 2006, MNRAS, 366, L31 [NASA ADS] [Google Scholar]
  26. Kochanek, C. S., Shappee, B. J., Stanek, K. Z., et al. 2017, PASP, 129, 104502 [Google Scholar]
  27. Lallement, R., Babusiaux, C., Vergely, J. L., et al. 2019, A&A, 625, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Liu, J., Zhang, H., Howard, A. W., et al. 2019, Nature, 575, 618 [NASA ADS] [CrossRef] [Google Scholar]
  29. Makarov, V. V., & Tokovinin, A. 2019, AJ, 157, 136 [CrossRef] [Google Scholar]
  30. McClintock, J. E., Haswell, C. A., Garcia, M. R., et al. 2001, ApJ, 555, 477 [NASA ADS] [CrossRef] [Google Scholar]
  31. McClintock, J. E., & Remillard, R. A. 2006, Black Hole Binaries (Cambridge: Cambridge University Press), 39, 157 [Google Scholar]
  32. Menou, K., Narayan, R., & Lasota, J.-P. 1999, ApJ, 513, 811 [NASA ADS] [CrossRef] [Google Scholar]
  33. Misra, D., Fragos, T., Tauris, T., Zapartas, E., & Aguilera-Dena, D. R. 2020, A&A, 642, A174 [CrossRef] [EDP Sciences] [Google Scholar]
  34. Olejak, A., Belczynski, K., Bulik, T., & Sobolewska, M. 2020, A&A, 638, A94 [CrossRef] [EDP Sciences] [Google Scholar]
  35. Pandey, J. C., & Singh, K. P. 2012, MNRAS, 419, 1219 [NASA ADS] [CrossRef] [Google Scholar]
  36. Podsiadlowski, P., Rappaport, S., & Han, Z. 2003, MNRAS, 341, 385 [NASA ADS] [CrossRef] [Google Scholar]
  37. Rivinius, T., Baade, D., Hadrava, P., Heida, M., & Klement, R. 2020, A&A, 637, L3 [CrossRef] [EDP Sciences] [Google Scholar]
  38. Safarzadeh, M., Toonen, S., & Loeb, A. 2020, ApJ, 897, L29 [CrossRef] [Google Scholar]
  39. Shao, Y., & Li, X.-D. 2019, ApJ, 885, 151 [CrossRef] [Google Scholar]
  40. Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, ApJ, 788, 48 [NASA ADS] [CrossRef] [Google Scholar]
  41. Shenar, T., Bodensteiner, J., Abdul-Masih, M., et al. 2020, A&A, 639, L6 [Google Scholar]
  42. Steele, I. A., Smith, R. J., Rees, P. C., et al. 2004, in Ground-based Telescopes, eds. J. Oschmann, & M. Jacobus, SPIE Conf. Ser., 5489, 679 [CrossRef] [Google Scholar]
  43. Thompson, T. A., Kochanek, C. S., Stanek, K. Z., et al. 2019, Science, 366, 637 [NASA ADS] [CrossRef] [Google Scholar]
  44. Thompson, T. A., Kochanek, C. S., Stanek, K. Z., et al. 2020, Science, 368, eaba4356 [CrossRef] [Google Scholar]
  45. van den Heuvel, E. P. J., & Tauris, T. M. 2020, Science, 368, eaba3282 [CrossRef] [Google Scholar]
  46. Voges, W., Aschenbach, B., Boller, T., et al. 2000, IAU Circ., 7432, 3 [NASA ADS] [Google Scholar]
  47. Wade, R. A., & Horne, K. 1988, ApJ, 324, 411 [NASA ADS] [CrossRef] [Google Scholar]
  48. Walter, R., Lutovinov, A. A., Bozzo, E., & Tsygankov, S. S. 2015, A&ARv, 23, 2 [NASA ADS] [CrossRef] [Google Scholar]
  49. Wiktorowicz, G., Lu, Y., Wyrzykowski, Ł., et al. 2020, ApJ, 905, 134 [CrossRef] [Google Scholar]
  50. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
  51. Yan, Z., & Yu, W. 2015, ApJ, 805, 87 [NASA ADS] [CrossRef] [Google Scholar]
  52. Yi, T., Sun, M., & Gu, W.-M. 2019, ApJ, 886, 97 [CrossRef] [Google Scholar]
  53. Yungelson, L. R., Lasota, J. P., Nelemans, G., et al. 2006, A&A, 454, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Zheng, L.-L., Gu, W.-M., Yi, T., et al. 2019, AJ, 158, 179 [CrossRef] [Google Scholar]

All Tables

Table 1.

Parameters of the binary system GS4 obtained from a fit of the ASAS-SN V-band light curve using PHOEBE.

In the text

All Figures

thumbnail Fig. 1.

Aperture photometry and radial velocity. Top: ASAS-SN light curve of GS4, folded using the period p = 5.20906 ± 0.0005 d and t0 = 2457384.6 HJD. Bottom: corresponding radial velocity of the system as observed by the LT. We do see a 0.04 phase shift between the radial velocity curve and the ASAS-SN light curve, but we have no clear explanation for it (see Sect. 2.1). The blue curves correspond to the best fit model obtained with PHOEBE on the ASAS-SN light curve when fixing the semi-amplitude radial velocity of the system to the one measured from the LT curve (see Sect. 2.2).
In the text
thumbnail Fig. 2.

Sample of LT spectra. Top: from bottom to top: red-arm LT spectrum of HD 210185 (the K0III template), the same spectrum broadened by 80 km s−1, and the Doppler-corrected average spectrum of GS4. Bottom: from bottom to top: blue-arm LT spectrum of the K0III template in comparison with the Doppler-corrected averages of GS4 obtained during the primary eclipse (photometric phase 0.00 ± 0.05) and outside the eclipse (remaining phases). The top spectrum shows the Hβ line (at 4861 Å) to be slightly stronger (relative to the nearby metallic lines), possibly because of the contribution from the A-type secondary. The secondary is eclipsed in the middle spectrum, which seems to show a better match to the K0III spectrum. Scaling factors have been applied to the three spectra so that the equivalent widths of the metallic lines in the 4900−5000 Å range are the same.
In the text
thumbnail Fig. 3.

Black hole candidates with solar mass companions in the orbital period – radial velocity amplitude plane. Solid (dashed) lines show the lower limit on Porb that, according to Eq. (2), is sufficient to have a 3, 10, or 30 M⊙ BH in circular orbit with a 3 M⊙ stellar companion (1 M⊙ companion). Colored areas indicate where a 3, 10, or 30 R⊙ stellar companion would overfill its Roche lobe. Candidate BHs from radial velocity measurements: low-mass X-ray binaries (black dots); APOGEE candidate (open circle); LAMOST LB-1 candidate (open diamond); MUSE candidates in NGC 3201 (open squares); HR 6819 candidate (open triangle) and the latest LAMOST selection of giant stars having large ΔVr and optically invisible companions (crosses), including GS4 (star). More details are given in the text.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.