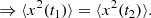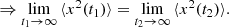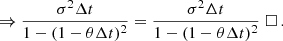| Issue |
A&A
Volume 645, January 2021
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 13 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202039097 | |
| Published online | 13 January 2021 | |
Ornstein-Uhlenbeck parameter extraction from light curves of Fermi-LAT observed blazars
1
Institute for Theoretical Physics and Astrophysics, Julius-Maximilians-Universität Würzburg, Emil-Fischer-Straße 31, Campus Hubland Nord, 97074 Würzburg, Germany
e-mail: paul.r.burd@astro.uni-wuerzburg.de
2
Astrobiology and Space Science Division, NASA Ames Research Center, Moffett Field, CA 94035-1000, USA
Received:
3
August
2020
Accepted:
22
October
2020
Context. Monthly binned γ-ray light curves of 236 bright γ-ray sources, particularly blazars, selected from a sample of 2278 high-galactic latitude objects observed with Fermi-LAT show flux variability characterized by power spectral densities consisting of a single power-law component, ranging from Brownian to white noise.
Aims. The main goal here is to assess the Ornstein-Uhlenbeck (OU) model by studying the range of its three parameters that reproduces these statistical properties.
Methods. We develop procedures for extracting values of the three OU model parameters (mean flux, correlation length, and random amplitude) from time series data and apply them to compare numerical integrations of the OU process with the Fermi-LAT data.
Results. The OU process fully describes the statistical properties of the flux variations of the 236 blazars. The distributions of the extracted OU parameters are narrowly peaked around well-defined values (σ, μ, θ) = (0.2, −8.4, 0.5) with variances (0.004, 0.07, 0.13). The distributions of rise and the decay time scales of flares in the numerical simulations, meaning major flux variations fulfilling pre-defined criteria, are in agreement with the observed ones. The power spectral densities of the synthetic light curves are statistically indistinguishable from those of the measured light curves.
Conclusions. The long-term γ-ray flux variability of blazars on monthly time scales is well described by a stochastic model that involves only three parameters. The methods described here are powerful tools for studying randomness in light curves and thereby for constraining the physical mechanisms responsible for the observed flux variations.
Key words: galaxies: active / gamma rays: general / time / methods: statistical / methods: numerical
© ESO 2021
1. Introduction
The stochastic differential equation (SDE) of the Ornstein-Uhlenbeck (OU) process was originally proposed to describe the Brownian motion of particles with individual velocity u(t) and average velocity μ in an ambient medium (Uhlenbeck & Ornstein 1930). It is given by
where θ denotes the friction parameter of the medium. It can also be interpreted as a mean reversion rate responsible for the stationarity of the process by driving the process back to the mean reversion level μ. The term denoted with W(t) represents a white noise term. Drawing identically and independently distributed (IID) values from the noise for every time step, the OU process generates a time series. The IID values represent causally disconnected realizations of an observable describing the physical state of the time-variable system. Since its first use in physics, the OU process has also been employed to describe a plethora of dynamical processes in diverse fields such as economics, biology, geophysics, and in particular in astronomy. In each case, the three OU parameters describe similar effects for the time evolution of the processes, but must be interpreted in different ways. In economics, the Vasicek (1977) model utilizes the OU process to describe the evolution of interest rates driven by a random process, the market risk. In the context of the Vasicek model, the variable u(t) in Eq. (1) is interpreted as the interest rate at a given time, μ as the long-term interest rate, θ as the speed of reversion, measuring how quickly a volatile value of u(t) is drawn back to the long-term interest rate, and σ as the instant volatility, measuring the volatility of the system at each time step. Szarek et al. (2020) used a modification of the Vasicek model to predict the long-term price evolution of metals. In a medical study of the mechanical acceleration of humans during physical exercises, Billat et al. (2018) used the OU process to describe how runners accelerate along a certain distance in an optimum time, showing that humans are able to precisely regulate their acceleration. The variable u(t) in this context is interpreted as the acceleration of the runner, μ as the mean acceleration, θ as the runner’s ability to vary the acceleration u(t) around μ, and σ as the range of the human-induced variations of the acceleration. A combination of OU process and higher-order stochastic processes can be used to predict the breaking of an oil drill by modeling the vibrations along the drill caused by the bit-rock interaction (Lobo et al. 2020).
In the context of astrophysics, studies of sources with time-variable brightness are common, typically using a multitude of discrete methods for the time-binned data. The continuous OU process offers a promising pathway toward constraining physical models of the variability described by integro-differential equations.
Here, we consider the OU process to describe the flux variations of blazars, most prominently observed at the wavelengths of γ-rays. Blazars are a special class of highly variable astronomical sources considered to represent active galactic nuclei containing supermassive black holes that expell relativistic plasma jets producing γ-ray emission by unknown mechanisms. So far, most physical models have been constrained only by the sparse information from the spectral domain. Including the information from the time-domain offers the chance for an improvement of our understanding of these enigmatic objects. To facilitate the OU description of the variability, u(t) is interpreted as a (it turns out: logarithmic) flux density value at a given time step in a time series of flux measurements, the so-called light curve; μ as the long-term value around which the (logarithmic) flux variations evolve1; θ as the reversion rate that describes how quickly a flux value at a given time is drawn back toward μ; and σ as the so-called innovation, the amplitude of the random flux variation initiated at a given time t.
The OU process has been employed to study the optical LCs of active galactic nuclei (Kelly et al. 2009, 2011; Takata et al. 2018). Based on a small sample of 13 blazars, Sobolewska et al. (2014) showed that satisfactory fits to individual Fermi-LAT γ-ray LCs can be obtained by simulating LCs with single or linear combinations of several OU processes. Abdo et al. (2010) found indications for a correlated noise behavior in Fermi-LCs. The effects of the sampling time on the power spectral densities (PSDs) obtained from the LCs by a Fourier transformation were studied in Timmer & König (1995). Motivated by the success of simple stochastic descriptions of blazar γ-ray variability and following Ockham’s principle, we question whether our sample of 236 extragalactic Fermi-LAT LC, in particular blazars, can be reproduced employing a single (Gaussian) OU process. Rather than fitting individual LCs, we seek to encompass the distribution of statistical properties of the observed LCs by choosing proper parameters that characterize the OU process.
In Sect. 2, the sample of Fermi-LAT LCs (thereafter called the observed LCs), and the data from which they were obtained, are described. The recursion formula generating a stationary OU process needed to obtain synthetic LCs is derived in Sect. 3. In Sect. 4, we introduce our new method to extract OU parameters from time series. The procedure is first tested with a set of generic time series with known OU parameters. We then extract the OU parameters of the observed LCs and generate synthetic LCs from them. Section 5 addresses to what extent the synthetic OU LCs resemble the properties of the observed Fermi-LCs, comparing their distributions of PSD slope, flux, rise and decay time, and the sparsity of large amplitude surges.
2. The sample of Fermi-LAT light curves
In order to develop and test the methods discussed in this paper, we make use of a sample of γ-ray LCs from Fermi-LAT, which is a pair-conversion telescope sensitive to γ rays with energies from 20 MeV to greater than 300 GeV (Atwood et al. 2009). It has a large field of view (> 2sr) and scans the entire sky every three hours during standard operation. Thanks to its almost uninterrupted all-sky monitoring since 2008, continuous observations over more than a decade are available for a large number of γ-ray sources. In this work, we utilize 28-day binned γ-ray light curves, computed at energies above 1 GeV, for 2278 extragalactic Fermi-LAT sources. In the following, we briefly report the basic procedure followed for the LAT analysis, while for more details we refer the reader to another paper where this sample was already employed (see e.g., IceCube Collaboration 2018). The data analysis was performed according to the Fermi-LAT collaboration recommendations for point-source analysis2.
LAT data of the Pass 8 source class spanning the time interval from August 2008 to October 2017 were selected and analyzed using the Fermi-LAT ScienceTools package version v11r05p3 available from the Fermi Science Support Center3 (FSSC) and the P8R2_SOURCE_V6 instrument response functions, along with the fermipy software package (Wood et al. 2018). To minimize the contamination from γ-rays produced in the Earth’s upper atmosphere, a zenith angle cut of θ < 90° was applied. We also applied the standard data quality cuts (DATA_QUAL > 0)& & (LAT_CONFIG = = 1) and removed time periods coinciding with solar flares and γ-ray bursts detected by the LAT. For each source, we selected a 10° ×10° region of interest centered at its catalog position. Then, the γ-ray flux in each time bin was derived following a binned likelihood analysis (binned in space and energy), by a simultaneous fit of the source of interest and the other Fermi-LAT sources included in a 15° ×15° region, along with the Galactic and isotropic diffuse backgrounds (gll_iem_ext_v06.fits and iso_P8R2_SOURCE_V6_v06.txt). For all following calculations and extractions from Fermi-LAT LCs, only flux bins with TS ≥ 9 corresponding to a detection significance of ∼3σ are considered. If more than 62% of the data points in an LC are excluded, the entire LC is discarded. The threshold of 38% of the remaining data points has proven to yield a good balance between having enough data to perform the OU parameter extraction while excluding less significantly measured data points. This leaves 253 of the original 2278 LCs. Cross-checking the associations reported in the latest released Fermi-LAT catalogs for these 253 sources, we find that there are 144 BL Lac objects, 88 FSRQs, four blazars (class unknown), four Pulsars, four radio galaxies, seven unclassified sources, one active galactic nucleus of unknown class, and one narrow-line Seyfert 1 Galaxy (Abdollahi et al. 2020; Ajello et al. 2020). In this paper we, are specifically interested in blazar LCs. Therefore, the OU-parameter extraction and parameter analysis is performed only for blazar type sources. This leaves 236 LCs, which will be referred to as the observed LCs within this work. It has been shown that in order to interpret the observed LCs in a physical way, specifically in order to find the nature of the mechanism driving flux variations, time-binning on scales of minutes or possible even shorter is needed, see Shukla & Mannheim (2020). Such time resolution is only possible for extremely bright sources due to the necessary signal-to-noise ratio. In this paper, to ensure a trade-off between the study of a sufficiently large set of LCs and computational limitations for the analysis a large amount of Fermi-LAT data, we chose to deploy the methods discussed in the following sections on monthly binned LCs. This LC sample has also been used to study the long-term variability and possible periodic behavior of the Fermi-LAT sources, see Peñil et al. (2020).
3. Ornstein-Uhlenbeck process and stationarity
Equation (1) describes the OU process. The parameters and variables can be interpreted in different ways depending on the implementation of the process as a model description of a random dynamical evolution, as discussed in the introduction. In the following, we discuss the conditions for the IID variables required to generate an OU process:
Equation (2a) requires the expectation value of W to be zero, moreover Eq. (2b) requires the product of W at two different time steps to average to zero, which means that W is uncorrelated at any given two time steps. Equation (2c) defines W as a martingale, meaning that the conditional expectation value of a given time step (given all prior time steps) is exactly the expectation value at said time step. Equation (2d) describes statistical independence: The joint probability distribution of W at different time steps is required to be the product of the individual probability distributions of those. Independent draws from a normal distribution of the form 𝒩(m = 0, σ2) (Gillespie 1996), for instance, fulfill Eqs. (2a)–(2d). The following properties of 𝒩 are needed later on
The time differential of the white noise term can be written as
with 𝒩(t) = 𝒩(m = 0, σ2 = 1, t) (Gillespie 1996).
3.1. Discrete updating formula
The time derivative in Eq. (1) can be rewritten as
Solving for u(t + dt) and inserting Eq. (1) yields
In the following, we chose the white noise term to be described with a Gaussian (Eq. (4)), hence the SDE reads
The discretization needs to be executed such that the process equals or approximates a sampled continuous process
where T is a positive integer describing a time step. If the sampling of time steps is denser than the relevant time scales of the considered processes, the continuous SDE can be approximated by a discrete function (dt→Δt≪1)
3.2. Stationarity
As already mentioned in the introduction, formulae resulting from the proof of stationarity of the OU process are needed to extract parameters, (μ,σ,θ) from a given LC. Proofs concerning statements that are not explicitly needed for the parameter extraction, are listed in the appendix. A process X is stationary if its elements x(t) fulfill
Equation (6a) states that the mean value is a constant function and thus independent of time, Eq. (6b) ensures a finite variance for all time steps, and Eq. (6c) states that the covariance only depends on the difference between two time steps.
3.3. Recursion formula
The discrete SDE Eq. (5e) is rewritten in terms of computational steps usΔt = x(s) reads
An x(0) dependent explicit formula can be written as
as shown in Appendix A. Substituting according to n = s − k → k = s − n, and swapping the start and end points yields
Equation (3c) can now be applied. All normally distributed independent variables from 0 to ((s − n) ⋅ Δt)−1 are summed. For each new time step a new IID variable is added. The sum equals a normal distribution at a given time step.
Using Eq. (3a) the factors can be absorbed into the normal distribution yielding
We note that Eqs. (6a) and (6b) are fulfilled for this expression, while Eq. (6c) is not. The dependence of a certain time step on any other time step vanishes when absorbing all factors into the normal distribution. The proof of the third criterion can be found in Appendix A.1.
3.4. The OU process in light of different commonly used models
The physically motivated discrete OU model is mathematically equivalent to the autoregressive (AR), particularly the AR(1) time series model, which in turn is equivalent to the moving average (MA) model, guaranteed by the Wold Decomposition theorem to describe any stationary process (Scargle 1981, 2020). As Scargle (2020) depicts the AR(1) model is typically written as
where R(n) is uncorrelated white (not necessarily Gaussian) noise, referred to as the innovation. Comparing Eq. (7f) with Eq. (7a) the connection between the discrete OU process and the AR(1) model becomes clear. The revision level in the AR(1) model is typically set to μ = 0. Furthermore, the AR coefficient A translates in the OU terminology to the terms with the mean reversion rate (1 − θΔt) and the innovation translates to the Gaussian white noise term 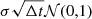 .
.
Goyal (2019) used the zero mean Continuous-Time Auto-Regressive Moving Average (CARMA(p,q)) process
(Kelly et al. 2014) to characterize long- and short-term variability of the blazar PKS 2155-304. They found that the intra-night variability of this particular blazar is well described by a CARMA(1,0) process. The CARMA(1,0) process is equivalent to the Continuous-time Auto-Regressive (CAR(1)) process which in turn is also called damped random walk (Ivezić et al. 2014). CARMA(1,0)4 is equivalent to the OU process with μ = 0. The reversion rate θ in the OU translates in the CARMA(1,0) model to −2α0 and the innovation is represented by the ϵ(t) term in Eq. (7g). Single light curves might very well be modeled by higher order CARMA(p,q) terms, see Goyal (2019) or any amount of OU superpositions, see Takata et al. (2018). In this context we aim employing the simplest model to find out whether a large amount of LCs can be adequately described by a simple stochastic process and whether we are able to find a systematic clustering of the OU parameters that we wish to extract from the observed LCs.
4. Extraction of OU parameters from given LCs
We refer to an OU process characterized by the parameters (μ, θ, σ) from the SDE (Eq. (5e)) as time series, which represents the logarithm (base 10) of the flux in an LC5. Based on the properties of the logarithm (base 10) of the flux, we present a mathematical description of the method to extract the parameters μ, σ, and θ from any given LC. The procedure is realized in python code6. The parameter μ is extracted straight forward by calculating the expectation value (mean) of a given time series. We assume that the time series can be decomposed into a white noise and a correlated colored noise part7. σ (nondeterministic part) is obtained by finding the white noise part and the extraction of θ (deterministic part) follows from that. We test our extraction method with a set of 105 generic LCs with known input OU parameters (μ, θ, σ) drawn from normal distributions of the form (𝒩(0, 1),𝒩(0, 1),𝒩(5, 5)) and Δt = 0.1. Unstable solutions are filtered to ensure stationarity of these generic LCs, see Eq. (A.3c). The same procedure is applied to the observed Fermi-LCs. The resulting parameters (μ, θ, σ) are then used to generate synthetic OU-LCs that mimic the observed ones.
4.1. Extraction of μ
Extracting μ via the expectation value in the measured Fermi time series, implies that there is a state of flux which can be interpreted as stable on long time scales (with respect to the time sampling). This requires that within the detector sensitivity the source emits constantly with an underlying constant energy flux. So-called flares can then be seen as occasionally occurring (scarcity) outbreaks in the flux regime overlaying the ground state. This in turn implies that a given source for which the parameters are extracted resembles a stationary process in terms of Eqs. (6a)–(6c).
4.2. Extraction of σ
To extract σ, data points where uT is close to the mean (in an ϵ environment) are considered. Let uT be the sum of μ and a small deviation from μ, ϵ.
the SDE Eq. (5e), then reads
Solving for the difference between two sequential time steps, yields
If we chose 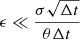 , the terms containing the mean reversion rate θ become negligible.
, the terms containing the mean reversion rate θ become negligible.
Under the condition that a given set of uT lie within the ϵ environment of μ, the variance is calculated on both sides:
Therefore,
4.3. Extraction of θ
If the expression 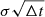 is known, θ can be extracted from the variance of the complete time series. With the proof of the second criterion of stationarity (see Appendix A.2), the variance of stationary processes reads (see Eq. (A.3c))
is known, θ can be extracted from the variance of the complete time series. With the proof of the second criterion of stationarity (see Appendix A.2), the variance of stationary processes reads (see Eq. (A.3c))
Solving for α = 1 − θΔt yields
The variance is insensitive to the sign of the deviation from the mean. Therefore, Eq. (8h) yields only the absolute value for α reliably
To extract the sign of α, a similar method as in the extraction of σ is used, however now the interest lies on data points sufficiently far from μ. Due to the scarcity of relatively high values in the amplitude of LCs this method is by its very nature more imprecise than the method yielding |α|. Nevertheless it suffices for extracting the sign. For the following consideration Eq. (5e) is analyzed for large deviations of uT from μ and a small impact of σ. In this case, the white noise term is small compared to the terms that are dependent on the mean reversion rate θ:
with α = 1 − θΔt, and solved for α, Eq. (8j), becomes
Equations (8i) and (8k) can now be combined to obtain α:
Therefore, the mean reversion rate is
4.4. Constraining the ϵ parameter
To constrain ϵσ and ϵα, which define the region close to and far from μ, respectively, the relation of
to the standard deviation 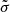 of the time series is studied. This is studied with a set of 105 generic OU time series with parameters
of the time series is studied. This is studied with a set of 105 generic OU time series with parameters 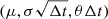 drawn from normal distributions of the form (𝒩(0, 1),𝒩(0, 1),𝒩(5, 5)). The input and extracted output parameters are compared with different statistical rank correlation methods like Kendall-τ, the Spearman and Pearson correlation coefficient and Pearson R for varying ϵσ and ϵα environments, as shown in Fig. 1. All rank correlation methods yield consistent results for the ϵσ and ϵα environments also showing that the results are robust for the method depending on the standard deviation of the given time series. Utilizing the standard deviation makes the method independent of μ which, if not given, would cause problems for μ ∼ 0. The dependence of ϵ on the standard deviation of a time series also scales with
drawn from normal distributions of the form (𝒩(0, 1),𝒩(0, 1),𝒩(5, 5)). The input and extracted output parameters are compared with different statistical rank correlation methods like Kendall-τ, the Spearman and Pearson correlation coefficient and Pearson R for varying ϵσ and ϵα environments, as shown in Fig. 1. All rank correlation methods yield consistent results for the ϵσ and ϵα environments also showing that the results are robust for the method depending on the standard deviation of the given time series. Utilizing the standard deviation makes the method independent of μ which, if not given, would cause problems for μ ∼ 0. The dependence of ϵ on the standard deviation of a time series also scales with 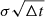 and α which ensures that for each time series enough data points can be found within the set ϵ environments. To determine the optimum ϵ values, the gradient along the σ axis is calculated, yielding a value for each combination of mσ and mα. The absolute values of all gradients is calculated for all mσ and summed over all mα. The optimum is defined for mσ that minimizes the sum. To decouple mσ and mα the gradients along the mα direction are calculated for the optimum of mσ, determined before. The minimum of the absolute gradient defines the optimum for mα. Analyzing the extreme values in the 2D-histograms where the values of the rank correlation coefficients find their respective maximum, yields optimum values for the parameters in Eqs. (8n)–(8o) of ϵσ = 0.343 ± 0.0036, resulting in ϵα = 1.48 ± 0.36.
and α which ensures that for each time series enough data points can be found within the set ϵ environments. To determine the optimum ϵ values, the gradient along the σ axis is calculated, yielding a value for each combination of mσ and mα. The absolute values of all gradients is calculated for all mσ and summed over all mα. The optimum is defined for mσ that minimizes the sum. To decouple mσ and mα the gradients along the mα direction are calculated for the optimum of mσ, determined before. The minimum of the absolute gradient defines the optimum for mα. Analyzing the extreme values in the 2D-histograms where the values of the rank correlation coefficients find their respective maximum, yields optimum values for the parameters in Eqs. (8n)–(8o) of ϵσ = 0.343 ± 0.0036, resulting in ϵα = 1.48 ± 0.36.
 |
Fig. 1. Color code shows rank correlation coefficients τKendall (top), RPearson (mid) and RSpearman (bottom) between known input and extracted output OU parameters σ and θ of the generic OU time series for different values of mσ vs. mα, that is basically ϵσ vs. ϵα. The blue regions define values of ϵσ and ϵα that yield robust results for the extraction method. An analysis of the maximum valued for each rank correlation index yields environments of ϵσ = 0.343 ± 0.0036 and ϵθ = 1.48 ± 0.36. |
4.5. Error estimates
To estimate the errors for the extracted θΔt and σ values, a cone is applied to the 2D histograms which includes 68% of the data in Figs. 2 and 3. The opening angle in the σ case gives an estimate for the relative error of Δrelσ ∼ 4.5%. The θ values yield
 |
Fig. 2. 2D density histogram of the input |σ| vs. the extracted σ shows a clear correlation. The contour lines are separated by a factor of 2 and cover a range of |
 |
Fig. 3. Inserted and extracted θ show a correlation for θ values far from one. This can be understood in the following way. If θ = 1 then the reversion rate in Eq. (5e) cancels leaving only the white noise term. In the case of white noise the approximation in Sect. 4.3 does not hold and the method breaks. The contour lines cover a range of [2500]/[σΔt] and are separated by 48.9. |
since two different cases have to be considered due to the widening of the cone up to a value of θΔt = 1 and its contracting between 1 < θΔt ≤ 2. The two cases arise from the fact that the reversion rate term in Eq. (5e) cancels if θΔt = 1. In that case only the white noise term drives the time series, the approximation in Sect. 4.3 does not fulfill our requirements. With this procedure the OU parameters and their uncertainty can be extracted from any stationary time series. We apply this to the observed Fermi-LCs and obtain 236 μ, θ, and σ values that are shown in Fig. 4.
 |
Fig. 4. Extracted parameters from the Fermi time series with the fit PDFs (singlea Gaussian for μ and σ, two Gaussians for θ). Top: extracted expectation values μ of the Fermi time series. Mid: extracted white noise prominence of the Fermi time series |
4.6. Number generators for μ, θ and σ
In order to analyze how well the OU process can mimic the observed LCs, we generate a large sample of synthetic LCs based on the parameters extracted from the observed LCs. To obtain number generators returning values for μ, σ, and θ, the probability density functions of the extracted parameters from the LCs are fit. The distributions for μ and θ are fit with an exponentially modified Normal distribution of the form
see Kalambet et al. (2011), where 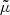 is the mean of the distribution,
is the mean of the distribution, 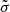 the variance and λ = 1/τ is connected to the exponential relaxation parameter τ. The complementary error function is given by
the variance and λ = 1/τ is connected to the exponential relaxation parameter τ. The complementary error function is given by
The fit parameters for the μ-distribution are 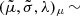 (−8.6, 0.005, 3.0). The θ-distribution the fit parameters are
(−8.6, 0.005, 3.0). The θ-distribution the fit parameters are 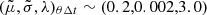 . The
. The 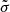 distribution is fit with a single Gaussian of the form
distribution is fit with a single Gaussian of the form
The fit parameters for the σ distribution are 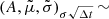 (0.95, 0.20, 0.06). The distribution and the corresponding fits are shown in Fig. 4. With this, the cumulative distribution functions (CDF) can be calculated. The number generator returns a number between zero and one based on a uniform probability for each of the three parameters. To then obtain the respective parameter, the intersection of the CDF and the respective x-axis at the rolled value is determined. In this way, a set of OU parameters μ, θ, and σ is obtained, given by the properties of the observed Fermi-LCs. For each data point calculated by the OU generator the maximum error can then be estimated to ΔrelOUi ∼ 18.1% based on the error cones discussed above.
(0.95, 0.20, 0.06). The distribution and the corresponding fits are shown in Fig. 4. With this, the cumulative distribution functions (CDF) can be calculated. The number generator returns a number between zero and one based on a uniform probability for each of the three parameters. To then obtain the respective parameter, the intersection of the CDF and the respective x-axis at the rolled value is determined. In this way, a set of OU parameters μ, θ, and σ is obtained, given by the properties of the observed Fermi-LCs. For each data point calculated by the OU generator the maximum error can then be estimated to ΔrelOUi ∼ 18.1% based on the error cones discussed above.
5. Results and discussion
We simulated 105 OU time series with parameters (μ, σ, θ) drawn from the number generators described in Sect. 4.6. To discuss their implications for the interpretation of the observed LCs, we obtained the innovation as the product of the drawn σ value and the standard normal distribution with a variance of 1 and centered around 0, [𝒩(0,1)] and transformed the simulated time series to synthetic flux LCs retaining their scarcity of large flux variations and nonnegative flux values.
5.1. Scarcity, non-negativity, and flux distributions
For the discussion the terms time series and light curve are connected in the following way. The OU process itself yields a time series XOU, the corresponding OU LC YOU is then given by
The same logic is applied to Fermi-LAT LCs. The Fermi-LAT LC YF is connected to its time series XF by
A time series obtained with the OU generator yields a synthetic data stream scattered around an expectation value. One instance of such a synthetic time series is shown in Fig. 5 on the top right with the corresponding generated OU parameters. The relatively low mean reversion rate allows the process to evolve to greater deviations from the expectation value before being forced back toward the mean. This has implications on the final flux distribution of the OU LCs.
 |
Fig. 5. OU time series and the OU light curves (left) are shown with the respective flux distributions (right). Top: generated OU time series. Bottom: OU light curve. |
To generate the OU LC, it is important to transform the time series in a way that the values are nonnegative and a certain scarcity is given, reflecting the fact that most sources show strong outbursts only relatively seldom with respect to a mean flux. If the source driving the white noise part of the OU process is to be a physical source of radiation it has to yield nonnegative flux densities. In addition, a Gaussian process in itself does not produce a sufficient scarcity of large outliers and can therefore not be a good model for a flare process. Scargle (2020) shows that it is possible to achieve non-negativity and scarcity by defining the white noise term in a way where the auto-regressive process itself results in a time series with these attributes. In this paper, however, rather than tweaking the white noise term in a special way, we obtain the OU light curve by taking the time series to a power of ten. If the OU process is considered as a model of the flux variability, the exponentiation is motivated by the idea that random fluctuations of plasma properties have to first grow exponentially to give rise to the observed γ-ray variability, as we are dealing with nonthermal processes far from equilibrium. Another, more specific motivation, is to consider differential Doppler boosting to be responsible for the flux variations. In this case, the exponentiation results from the relativistic beaming of particles radiating primarily into the direction of motion, as the direction of this motion sweeps across the line of sight to the observer (Cohen et al. 2007).
5.2. Power spectral density
To calculate the PSDs of the observed Fermi-LCs and the synthetic OU LCs, the Lomb-Scargle algorithm (Lomb 1976; Scargle 1982; Townsend 2010) implemented in SciPy (Virtanen et al. 2020) is used. Each of the acquired periodograms is fit with a single power law to obtain the PSD slope ξ. We note that this method is insensitive for possible breaks in the PSD slope. The priority here is to establish the method of OU-parameter extraction for the sample of monthly binned blazar light curves which can be fit well with single PSD slopes. It is straightforward to extend the method to more complex PSD shapes produced by mechanisms operating on different spatial scales in the jets. The ξ distributions of the calibrated OU LCs and the Fermi-LAT LCs show similar mean values, peaking at ∼ − 1, meaning that most LCs account for power spectra of pink noise while the test LCs peak at −0.6. Additionally the variance, the skew and kurtosis cannot be distinguished. The distributions span a range between −2 ≲ ξ ≲ 0, see Fig. 6. A pink noise LC typically features fluctuations on short time scales (on the order of several units of time sampling), (see e.g. Timmer & König 1995; Milotti 2002, 2005). The ξ-distribution of the test OU LCs show a peak around 0, while also spanning to −2. This results in a variance and skew which are larger by a factor of ∼2 − 3 compared to the others. This shows that the range of OU parameters must be narrowed down to the range determined with the extraction method to obtain valid synthetic LCs that resemble the observed ones. The first four statistical moments for the different Ξ distributions are listen in Table 1.
 |
Fig. 6. PSD slope distribution for different data sets. The green histogram represents the ξ distribution for the test OU light curves (parameters are drawn from Gaussian distributions) used to test of the extraction method. The red histogram represents the ξ distribution of the observed Fermi-LAT data. The blue ξ distribution represents the OU LCs where the OU parameters are calibrated with the observed data. The bins are determined with the Bayesian block algorithm (Scargle et al. 2013). |
Statistical moments of the ξ distributions derived from the observed Fermi-LCs, the generic test OU LCs as well as the synthetically generated OU LCs based on the extraction of the observed data.
For the synthetic OU LCs, the impact of the OU parameters on the PSD slope is studied by investigating the density plots of the set OU parameters, obtained for each OU LC as described in Sect. 4.6 and the PSD slopes. Figure 7 illustrates the impact of the parameters σ and θ on the PSD slopes. The top left plot shows the relation between σ and ξ. The larger the impact of the white noise (given larger values of σ) in Eq. (5e), the flatter the slope. The yellow contour lines in the area of the densest data population indicates this trend, however if σ is large and θ is small, the white noise part and the reversion rate parts counteract each other in Eq. (5e) which can be seen in the distribution becoming bulky at −2.5 ≲ ξ ≲ −0.5. The plot in the top right shows the impact of θ on ξ. The contour lines might indicate a relation between the reversion rate and PSD slope. The smaller the reversion rate, the steeper the slope. However, this breaks when θ → 1. If θ = 1, the reversion rate terms in Eq. (5e) cancel and only the white noise terms remain. The plot in the bottom of Fig. 7 suggests that σ and θ are uncorrelated. However, the distribution has a skewness where θ → 1. This skewness can explain the crowding in certain areas of the distributions in the plots above.
 |
Fig. 7. 2D histograms illustrating the impact of the OU parameters σ and θ on the PSD slopes. The parameters are set in the simulation for each LC and are obtained from the number generators, as discussed in Sect. 4.6. The density plots are over plotted with contours, spanning the domain of the color scales and are all separated by a factor of |
5.3. Time asymmetry of flux variations
The flux variability of the observed LCs as well as of the synthetic ich OU LCs is further studied by applying the Bayesian block algorithm (Scargle et al. 2013). It determines the best step-wise constant function to describe the data. Based on this, the HOP algorithm (Eisenstein & Hut 1998) can be used to determine flares with so-called HOP groups, as introduced in Meyer et al. (2019). It identifies the local maxima of the blocks (peaks) and proceeds downward as long as the adjacent blocks are subsequently lower analogous to the watershed method of topological data analysis. The onset and offset of a flare is given by the flux exceeding and going under a certain limit. This is motivated by the fact that blazar variability often appears superimposed on a constant (or relatively slowly varying) flux level. For studying intrinsic source variability this background should be removed – especially if the two components arise from different mechanisms. Noting that the background contributes randomness only through observational errors, for example photon counting statistics, assumed to be symmetrically distributed about the true level, Meyer et al. (2019) introduced a robust procedure to determine this “quiescent background”. The mean flux, since it includes contributions from both, always overestimates the true background. For the sake of this work, we neglect this difference and consider the mean flux of the LC to be the limit for the onset and offset of flares, leaving a more principled approach to future work. Each HOP group defines a flare with starting, end, and peak time where the latter is assumed at the center of the highest block in the HOP group. This results in a well defined rise time tr and decay time td for each flare. Based on these, the time asymmetry measure A of the flux variation is given by
Three main cases can be distinguished. If A = 0 there is no difference between rise and decay time as seen for example in a purely Gaussian shot. In the case where A < 0 the decay time is larger than the rise time. Such “fast rise – exponential decay” flare shapes can be seen in gamma-ray bursts (e.g., Peng et al. 2010). In the case where A > 0, the rise time is larger than the decay time. This asymmetry measure is derived for each HOP group within the observed 236 LCs. As mentioned above, the mean represents a rather conservative estimate for the limit of a flare. Since the quiescent background’ by Meyer et al. (2019) is consistently lower than the mean, additional information about lower flux variations could be obtained by using this as a limit in the HOP algorithm. In future work, this will be elaborated on in more detail. In order to test whether the synthetic LCs generated with the OU based on the parameters extracted from the observed LCs can mimic the latter, we conduct the same procedure 1000 times for 236 synthetic LCs randomly drawn form the entire sample.
HOP groups containing only one Bayesian block are filtered because they yield A = 0 by definition. Two block HOP groups are conservatively filtered because individual blocks in the observed LCs often contain just few data points. Successively, HOP groups containing, four or fewer Bayesian blocks are omitted to study the systematic behind the method and compare synthetic and observed asymmetry measures via a KS test. For each three and four block HOP groups omitted an example is shown in Fig. 8. For each set the fraction of p-values indicating the 5% (2σ) and the 0.3% (3σ) threshold, possibly inferring difference between the synthetic and observed asymmetry measures, is determined. The results are listed in Table 2. The fractions of LCs where the asymmetry measures differ at a 2σ level is (∼37%, ∼12%) for three and four block HOP omitted. At the 2σ level the fractions are (∼4%, ∼0.6%). Overall the asymmetry measure for the synthetic OU and the observed Fermi-LCs match well.
 |
Fig. 8. Asymmetry measures for the observed LAT LCs compared to a subset of synthetic OU LCs. The bins are set by the Bayesian block algorithm. The dashed and transparent bins are set to 0.25 and are plotted for convenience to show a “classical” histogram. The Bayesian binning shows that the asymmetry measures for both data sets basically are present in a range between (−1,1) with the same probability. Top: three- block HOP group omitted; bottom: four-block HOP groups omitted. |
Fraction of the data sets where a statistical difference is hinted in the asymmetry measure listed for flares containing more than one, two, or three blocks.
5.4. Examples
To show that the OU process is capable of reproducing the full range of properties in the observed LCs, Fig. 9 illustrates sources with different PSD slopes. The OU LCs with pink-ish noise feature flickering noise on short time scales, while the LCs with steeper PSD slopes tend to show variability on large time scales (compared to the binning time scale). As the PSD slope becomes steeper, the variability changes from shorter (flickering) time scales (pink) noise to variability on larger time scales (red) noise. The LC in the bottom left is a peculiar case of a white noise LC featuring one major outbreak within the simulation (observed) time span.
 |
Fig. 9. Representative examples of LCs generated with the extracted OU parameters are shown. Each block illustrates a time series and its histogram (red) and the corresponding LC with its histogram (blue). The OU parameters used to simulate the corresponding data sets are shown in the top right. The comparison of these plots show that the OU process allows us to recreate LCs, that show various kinds of colored noise (−2 ≤ (ξ) ≤ 0, red-pink-white). Top left: ξ ∼ −0.2; top right: ξ ∼ −0.5; mid left: ξ ∼ −1; mid right: ξ ∼ −1.5; bottom left: ξ ∼ −2; bottom right: ξ ∼ −0.2. |
6. Conclusion and outlook
We have shown that the statistical properties featured in Fermi-LAT LCs can be reproduced with a stationary (exponential) OU process. The key step to achieving this result was to develop a method for the extraction of the best-fit OU parameters from the comparison of simulated and observed LCs. In detail our findings are:
-
Fitting the observed monthly binned Fermi-LAT LCs with a stationary (exponential) OU process yields the parameters of equivalent synthetic LCs.
-
The best-fit set of OU parameters is given by (σ, μ, θ) = (0.2, −8.4, 0.5).
-
The flares extracted from the observed Fermi-LAT LCs do not show any preference for shorter or longer rise time scales compared to their decay time scales which is also reproduced by the OU LCs. This is unexpected if the rise times are determined by an acceleration process and the decay times by cooling which in general are very different unless not exactly balanced at the observed energy.
-
The OU process can reproduce the range of colored noise (PSD slopes) of Fermi-LAT LCs, including the LCs of sources showing flickering variability, variability on larger time scales, and even sources that show only one large outbreak within the simulation (observation) time span.
-
We note that the OU process describes the random fluctuations of a logarithmic energy flux which indicates that the underlying physical mechanism amplifies random fluctuations exponentially. Such processes have been discussed in models of the nonlinear evolution of fluid-dynamical instabilities leading to particle acceleration by magnetic reconnection (Yuan et al. 2016; Blandford et al. 2017; Christie et al. 2019) or the runaway acceleration of particles confined between random sequences of colliding shock waves triggered by fluctuations of the jet velocity (Böttcher & Baring 2019).
Our results have been obtained using monthly binned Fermi-LAT LCs E > 1 GeV of 236 blazars, which cover a time interval of approximately ten years. The binning time scale exceeds the minimum variability time scales of blazars, which can be as short as minutes, by a large margin. The LCs apparently track secular changes of the energy dissipation on the dynamical scale of sub-parsec jets associated with fluid-dynamical instabilities and nonthermal flux amplification due to particle acceleration events. Further diagnosis, using shorter time-scale binning and multifrequency monitoring data will be needed to identify the physical origin of the observed randomness and its limitations by searching for short-range correlations in the time- and frequency domains. The methods described in this paper and their implementation are versatile tools to carry out such studies.
The nature of the value will be discussed later in Sect. 4.
This ensures nonnegative flux densities and sparse large outbreaks as discussed in Sect. 5.1.
See https://github.com/PRBurd/astro-wue/tree/master/OU for the code.
The Wold theorem guarantees that any stationary process (for example an LC) can be decomposed into a deterministic and a non-deterministic part (Wold 1939).
Acknowledgments
We thank Greg Madejski for extensive discussions on blazar variability. We also thank the referee Dr. Norris for conscientious comments and constructive criticism. SMW acknowledges support by Stiftung der deutschen Wirtschaft and hospitality of the KIPAC at SLAC. The DATEV Stiftung Zukunft is acknowledged for funding the interdisciplinary data lab DataSphere@JMUW where most of this collaborative research was borne out.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 722, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Angioni, R., Axelsson, M., et al. 2020, ApJ, 892, 105 [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Billat, V., Brunel, N. J. B., Carbillet, T., et al. 2018, Phys. A Stat. Mech. Appl., 506, 290 [CrossRef] [Google Scholar]
- Blandford, R., Yuan, Y., Hoshino, M., & Sironi, L. 2017, Space Sci. Rev., 207, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M., & Baring, M. G. 2019, ApJ, 887, 133 [CrossRef] [Google Scholar]
- Christie, I. M., Petropoulou, M., Sironi, L., & Giannios, D. 2019, MNRAS, 482, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M. H., Lister, M. L., Homan, D. C., et al. 2007, ApJ, 658, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., & Hut, P. 1998, ApJ, 498, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Gillespie, D. T. 1996, Phys. Rev. E, 54, 2084 [NASA ADS] [CrossRef] [Google Scholar]
- Goyal, A. 2019, Galaxies, 7, 73 [CrossRef] [Google Scholar]
- IceCube Collaboration (Aartsen, M. G., et al.) 2018, Science, 361, eaat1378 [NASA ADS] [Google Scholar]
- Ivezić, Ž, & MacLeod, C. 2014, in Multiwavelength AGN Surveys and Studies, eds. A. M. Mickaelian, & D. B. Sanders, IAU Symp., 304, 395 [Google Scholar]
- Kalambet, Y., Kozmin, Y., Mikhailova, K., et al. 2011, J. Chemom., 25, 352 [CrossRef] [Google Scholar]
- Kelly, B. C., Bechtold, J., & Siemiginowska, A. 2009, ApJ, 698, 895 [Google Scholar]
- Kelly, B. C., Sobolewska, M., & Siemiginowska, A. 2011, ApJ, 730, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C., Becker, A. C., Sobolewska, M., et al. 2014, ApJ, 788, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lobo, D. M., Ritto, T. G., & Castello, D. A. 2020, Mech. Syst. Signal Proc., 141, 106451 [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
- Meyer, M., Scargle, J. D., & Blandford, R. D. 2019, ApJ, 877, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Milotti, E. 2002, ArXiv e-prints [arXiv:physics/0204033] [Google Scholar]
- Milotti, E. 2005, Phys. Rev. E, 72, 056701 [CrossRef] [Google Scholar]
- Peñil, P., Domínguez, A., Buson, S., et al. 2020, ApJ, 896, 134 [CrossRef] [Google Scholar]
- Peng, Z., Yin, Y., Bi, X., et al. 2010, ApJ, 718, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1981, ApJS, 45, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
- Scargle, J. D. 2020, ApJ, 895, 90 [CrossRef] [Google Scholar]
- Scargle, J. D., Norris, J. P., Jackson, B., & Chiang, J. 2013, ApJ, 764, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Shukla, A., & Mannheim, K. 2020, Nat. Commun., 11, 4176 [CrossRef] [Google Scholar]
- Sobolewska, M. A., Siemiginowska, A., Kelly, B. C., & Nalewajko, K. 2014, ApJ, 786, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Szarek, D., Bielak, Ł., & Wyłomańska, A. 2020, Phys. A Stat. Mech. Appl., 555, 124659 [CrossRef] [Google Scholar]
- Takata, T., Mukuta, Y., & Mizumoto, Y. 2018, ApJ, 869, 178 [CrossRef] [Google Scholar]
- Timmer, J., & König, M. 1995, A&A, 300, 707 [Google Scholar]
- Townsend, R. H. D. 2010, ApJS, 191, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Uhlenbeck, G. E., & Ornstein, L. S. 1930, Phys. Rev., 36, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Vasicek, O. 1977, J. Financial Econ., 5, 177 [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wold, H. 1939, J. R. Stat. Soc., 102, 295 [CrossRef] [Google Scholar]
- Wood, M., Caputo, R., Charles, E., et al. 2018, PoS ICRC2017, 35, 824 [Google Scholar]
- Yuan, Y., Nalewajko, K., Zrake, J., et al. 2016, ApJ, 828, 92 [CrossRef] [Google Scholar]
Appendix A: Proof of validity of explicit formula for the discrete SDE
By definition the initial case is fulfilled with:
Thus the induction can be initialized
A.1. Proof of the 1st criterion for stationarity
To prove the first criterion (Eqs. (6a)), (A.2a) is shown to hold for all s, where s is an positve integer:
Hence x(s) can be written as normal distributions (Eq. (7e)), the mean is the first argument of N. Therefore, Eq. (A.2a) simplifies to:
We will let
If a system runs sufficiently long, the criterion of A.2e loses importance because, after a sufficient amount of time, a steady-state is reached. Therefore, the system is insensitive to the initial conditions. Hence
A.2. Proof of the 2nd criterion for stationarity
For the proof of (6b) the normal distributed nature of x(s) is used and that ⟨d2⟩=Var(d) for a given distribution distribution d,
This expression is required to be finite for all times. Therefore, a lower limit of s = 0 is given and the analysis of the limit s → ∞ suffices
Thus a stationary process fulfills this requirement for |1 − θΔt|< 1. Additionally, the parameter space θΔt can be constrained with this expression.
A.3. Proof of the third criterion for stationarity
For the following proof it is necessary to express x(t + τ), dependent on x(t) and independent form x(0).
Separating the sums, from index 1 to s and from s + 1 to s + τ yields
Factorizing (1 − θΔt)τ from the first two terms yields
where x(s) substitutes the under braced part. The indices of the remaining sum are shifted by s:
With the explicit expression for x(s + τ), the thrid criterion (Eq. (6c)) can be given.
Multiplying x(s) in the sum and the linearity of the expectation value yields
utilizing the linearity of the expectation value
Auxiliary to simplify the last summand:
Replace x(s) in Eq. (A.5da) with the explicit form:
Expending the product inside the sum into the inner sum yields
Using linearity, the expectation value of each of the inner summands can be calculated separately.
Using linearity of the expectation value yields
By definition the expectation value of the normal distribution ⟨N(0, 1, t)⟩ = ⟨Γ(t)⟩ = 0⟩ (Eq. (2a)) and the auto-correlation ⟨N(0, 1, t)N(0, 1, t + τ) = ⟨Γ(t)Γ(t + τ)⟩ = δ(τ) (Eq. (2b)). Thus the first summand vanishes and the equation reads
(k + s − 1)−(i − 1) = k + s − i with k > 1 and i < s. Thus k + s − i > 0 ∀k, i. →δ((k + s − i)Δt) = 0 ∀k, i.
Inserting Eq. (A.5dg) into Eq. (A.5c) and applying Eq. (A.2f)
Considering the relative auto-covariance, between two time steps, following statement must hold
If t1 and t2 is sufficiently large, while the difference t1 − t2 is constant, Eq. (A.5h) reads
Using Eq. (A.3a) and (A.3c), Eq. (A.5i) becomes
All Tables
Statistical moments of the ξ distributions derived from the observed Fermi-LCs, the generic test OU LCs as well as the synthetically generated OU LCs based on the extraction of the observed data.
Fraction of the data sets where a statistical difference is hinted in the asymmetry measure listed for flares containing more than one, two, or three blocks.
All Figures
 |
Fig. 1. Color code shows rank correlation coefficients τKendall (top), RPearson (mid) and RSpearman (bottom) between known input and extracted output OU parameters σ and θ of the generic OU time series for different values of mσ vs. mα, that is basically ϵσ vs. ϵα. The blue regions define values of ϵσ and ϵα that yield robust results for the extraction method. An analysis of the maximum valued for each rank correlation index yields environments of ϵσ = 0.343 ± 0.0036 and ϵθ = 1.48 ± 0.36. |
| In the text | |
 |
Fig. 2. 2D density histogram of the input |σ| vs. the extracted σ shows a clear correlation. The contour lines are separated by a factor of 2 and cover a range of |
| In the text | |
 |
Fig. 3. Inserted and extracted θ show a correlation for θ values far from one. This can be understood in the following way. If θ = 1 then the reversion rate in Eq. (5e) cancels leaving only the white noise term. In the case of white noise the approximation in Sect. 4.3 does not hold and the method breaks. The contour lines cover a range of [2500]/[σΔt] and are separated by 48.9. |
| In the text | |
 |
Fig. 4. Extracted parameters from the Fermi time series with the fit PDFs (singlea Gaussian for μ and σ, two Gaussians for θ). Top: extracted expectation values μ of the Fermi time series. Mid: extracted white noise prominence of the Fermi time series |
| In the text | |
 |
Fig. 5. OU time series and the OU light curves (left) are shown with the respective flux distributions (right). Top: generated OU time series. Bottom: OU light curve. |
| In the text | |
 |
Fig. 6. PSD slope distribution for different data sets. The green histogram represents the ξ distribution for the test OU light curves (parameters are drawn from Gaussian distributions) used to test of the extraction method. The red histogram represents the ξ distribution of the observed Fermi-LAT data. The blue ξ distribution represents the OU LCs where the OU parameters are calibrated with the observed data. The bins are determined with the Bayesian block algorithm (Scargle et al. 2013). |
| In the text | |
 |
Fig. 7. 2D histograms illustrating the impact of the OU parameters σ and θ on the PSD slopes. The parameters are set in the simulation for each LC and are obtained from the number generators, as discussed in Sect. 4.6. The density plots are over plotted with contours, spanning the domain of the color scales and are all separated by a factor of |
| In the text | |
 |
Fig. 8. Asymmetry measures for the observed LAT LCs compared to a subset of synthetic OU LCs. The bins are set by the Bayesian block algorithm. The dashed and transparent bins are set to 0.25 and are plotted for convenience to show a “classical” histogram. The Bayesian binning shows that the asymmetry measures for both data sets basically are present in a range between (−1,1) with the same probability. Top: three- block HOP group omitted; bottom: four-block HOP groups omitted. |
| In the text | |
 |
Fig. 9. Representative examples of LCs generated with the extracted OU parameters are shown. Each block illustrates a time series and its histogram (red) and the corresponding LC with its histogram (blue). The OU parameters used to simulate the corresponding data sets are shown in the top right. The comparison of these plots show that the OU process allows us to recreate LCs, that show various kinds of colored noise (−2 ≤ (ξ) ≤ 0, red-pink-white). Top left: ξ ∼ −0.2; top right: ξ ∼ −0.5; mid left: ξ ∼ −1; mid right: ξ ∼ −1.5; bottom left: ξ ∼ −2; bottom right: ξ ∼ −0.2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



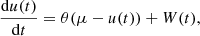
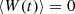
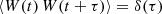
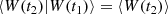
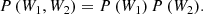
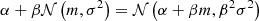
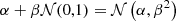
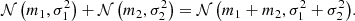
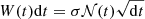
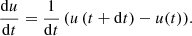
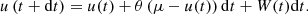
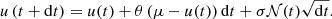
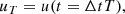
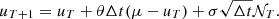
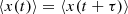
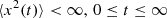
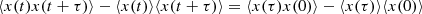
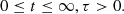
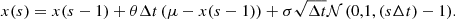
![$$ \begin{aligned} x(s)&= (1-\theta \Delta t)^s x(0)\\&\quad + \sum _{k=1} ^s \left[(1-\theta \Delta t)^{s-k}(\theta \Delta t \mu +\sigma \sqrt{\Delta t} \mathcal{N} (0,1,(k-1)\Delta t))\right]\!, \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq20.gif)
![$$ \begin{aligned} { \begin{aligned} x(s)&= (1-\theta \Delta t)^{s} x(0)\\&\quad + \sum _{n=0}^{s-1}{[(1-\theta \Delta t)^{n} \cdot (\theta \Delta t \mu + \sigma \sqrt{\Delta t} \mathcal{N} (0, 1, ((s-n)\cdot \Delta t)-1))]}. \end{aligned}} \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq21.gif)
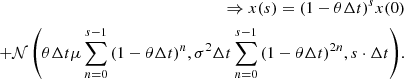
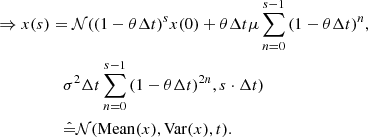
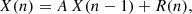
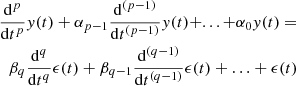
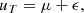
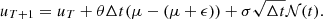
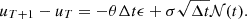
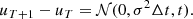
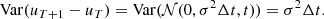
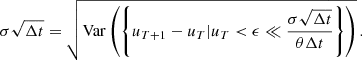
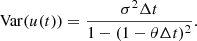
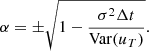
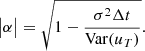
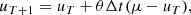
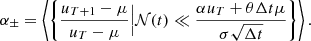
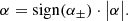
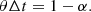
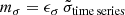
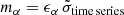
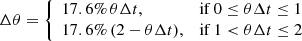
![$ [2300]/[\sigma \sqrt{\Delta t}] $](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq48.gif)
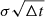
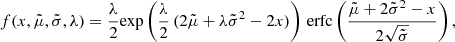
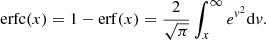
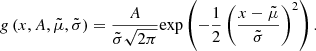
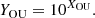
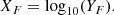
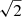
![$ [1,800]/[\theta \Delta t * \sigma \sqrt{\Delta t}] $](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq62.gif)
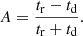
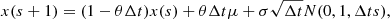
![$$ \begin{aligned} x(s+1)&= (1-\theta \Delta t) \Bigg [ (1-\theta \Delta t)^{s}x(0) + \\&\quad \sum _{k=1}^{s}\Big ((1-\theta \Delta t)^{s-k}(\theta \Delta t \mu + \sigma \sqrt{\Delta t} N(0, 1, (k-1)\Delta t)\Big ) \Bigg ]\\&\quad + \theta \Delta t \mu + \sigma \sqrt{\Delta t} N(0, 1, \Delta t s), \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq66.gif)
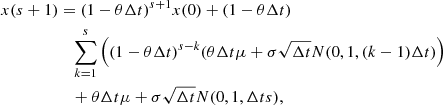
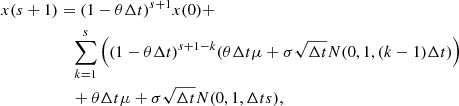
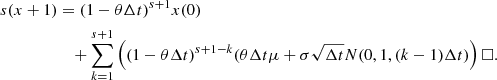
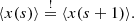
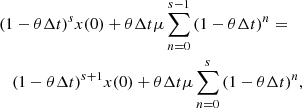
![$$ \begin{aligned} 0 = [(1-\theta \Delta t)^{s+1}-(1-\theta \Delta t)^{s}] x(0) + \theta \Delta t \mu (1-\theta \Delta t)^{s}, \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq72.gif)
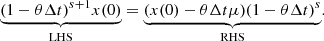
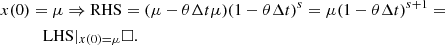
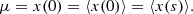
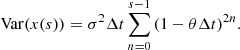
![$$ \begin{aligned} \mathrm{Var}(x(s))&=\lim \limits _{s \rightarrow \infty }{\sigma ^{2}\Delta t \sum _{n=0}^{s-1}{(1-\theta \Delta t)^{2n}}} =\lim \limits _{s \rightarrow \infty }{\sigma ^{2}}\Delta t \\&\quad \sum _{n=0} ^{s-1} {[(1-\theta \Delta t)^{2}]^{n}}, \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq77.gif)
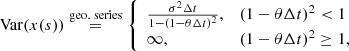
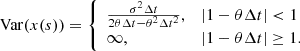
![$$ \begin{aligned} x(s+\tau )&=(1-\theta \Delta t)^{s+\tau }x(0)\\&\quad + \sum _{k=1}^{s+\tau }{\left[(1-\theta \Delta t)^{s+\tau -k}\cdot (\theta \Delta t \mu +\sigma \sqrt{\Delta t} N(0, 1, (k-1)\Delta t))\right]}\, . \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq80.gif)
![$$ \begin{aligned} x(s+\tau ) =& (1-\theta \Delta t)^{s}(1-\theta \Delta t)^{\tau }x(0)+ \\ &\sum _{k=1}^{s}\left[(1-\theta \Delta t)^{s-k}(1-\theta \Delta t)^{\tau }\right.\\ &\left. \cdot (\theta \Delta t \mu +\sigma \sqrt{\Delta t} N(0, 1, (k-1)\Delta t))\right]+ \\ &\sum _{k=s+1}^{s+\tau }{\left[(1-\theta \Delta t)^{s+\tau -k}\cdot (\theta \Delta t \mu +\sigma \sqrt{\Delta t} N(0, 1, (k-1)\Delta t))\right]}. \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq81.gif)
![$$ \begin{aligned} {\begin{aligned} x(s+\tau ) =&(1-\theta \Delta t)^{\tau }\\ &\underbrace{\left((1-\theta \Delta t)^{s}x(0)+\sum _{k=1}^{s}{\left[(1-\theta \Delta t)^{s-k}(\theta \Delta t \mu +\sigma \sqrt{\Delta t} N(0, 1, (k-1)\Delta t)\right]}\right)}_{x(s)} \\ &+\sum _{k=s+1}^{s+\tau }{\left[(1-\theta \Delta t)^{s+\tau -k}\cdot (\theta \Delta t \mu +\sigma \sqrt{\Delta t} N(0, 1, (k-1)\Delta t))\right]}, \end{aligned}} \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq82.gif)
![$$ \begin{aligned} { \begin{aligned} x(s+\tau )&= (1-\theta \Delta t)^{\tau }\cdot x(s) \\&\quad +\sum _{k=1}^{\tau }{\left[(1-\theta \Delta t)^{\tau -k}\cdot (\theta \Delta t \mu +\sigma \sqrt{\Delta t} N(0, 1, (k+s-1)\Delta t))\right]}. \end{aligned}} \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq83.gif)
![$$ \begin{aligned} \langle x(s) x(s+\tau ) \rangle&= \bigg \langle x(s) \bigg ( (1-\theta \Delta t)^{\tau } x(s) +\sum _{k=1}^{\tau }\left[(1-\theta \Delta t)^{\tau -k}\right.\\&\left.\quad \times (\theta \Delta t \mu +\sigma \sqrt{\Delta t} N(0, 1, (k+s-1)\Delta t))\right] \bigg ) \bigg \rangle . \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq84.gif)
![$$ \begin{aligned} \langle x(s) x(s+\tau ) \rangle&= \left\langle (1-\theta \Delta t)^{\tau } x^{2}(s) \right\rangle \nonumber \\&\quad + \left\langle \sum _{k=1}^{\tau }{\left[ x(s) (1-\theta \Delta t)^{\tau -k} \theta \Delta t \mu x(s) \right]} \right\rangle \nonumber \\&\quad + \left\langle \sum _{k=1}^{\tau }{(1-\theta \Delta t)^{\tau -k} \sigma \sqrt{\Delta t} N(0, 1, (k+s-1)\Delta t)} \right\rangle , \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq85.gif)
![$$ \begin{aligned} \langle x(s) x(s+\tau ) \rangle &= (1-\theta \Delta t)^{\tau }\left\langle x^{2}(s) \right\rangle \\ &+ \sum _{k=1}^{\tau }{\left[ (1-\theta \Delta t)^{\tau -k} \theta \Delta t \mu \left\langle x(s) \right\rangle \right]} \\ &+\left\langle \sum _{k=1}^{\tau }{x(s) (1-\theta \Delta t)^{\tau -k} \sigma \sqrt{\Delta t} N(0, 1, (k+s-1)\Delta t)} \right\rangle . \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq86.gif)
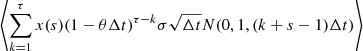
![$$ \begin{aligned}&\Bigg \langle \sum _{k=1}^{\tau }{\Bigg [\sum _{i=1}^{s}{\left[ (1-\theta \Delta t)^{s}(\theta \Delta t \mu + \sigma \sqrt{\Delta t}N(0, 1, (i-1)\Delta t)) \right]}}, \nonumber \\&\quad (1-\theta \Delta t)^{\tau -k} \sigma \sqrt{\Delta t} N(0, 1, (k+s-1)\Delta t)\Bigg ] \Bigg \rangle . \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq88.gif)
![$$ \begin{aligned}&\Bigg \langle \sum _{k=1}^{\tau }{\sum _{i=1}^{s}{\Big [(1-\theta \Delta t)^{s+\tau -k}\theta \Delta t \sigma \sqrt{\Delta t} N(0, 1, (k+s-1)+ }}\\&\quad (1-\theta \Delta t)^{s+\tau -k} \sigma ^{2} \Delta t N(0, 1, (i-1)\Delta t) N(0, 1, (k+s-1)\Delta t\Big ] \Bigg \rangle . \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq89.gif)
![$$ \begin{aligned}&\left\langle \sum _{k=1}^{\tau } \sum _{i=1}^{s} \Big [(1-\theta \Delta t)^{s+\tau -k}\theta \Delta t \sigma \sqrt{\Delta t} N(0, 1, (k+s-1)\Big ] \right\rangle \\&+\quad \qquad \Bigg \langle \sum _{k=1}^{\tau }\sum _{i=1}^{s}\Big [(1-\theta \Delta t)^{s+\tau -k} \sigma ^{2} \Delta t \\&\qquad N(0, 1, (i-1)\Delta t) N(0, 1, (k+s-1)\Delta t \Big ] \Bigg \rangle . \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq90.gif)
![$$ \begin{aligned}&\sum _{k=1}^{\tau }\sum _{i=1}^{s}[(1-\theta \Delta t)^{s+\tau -k}\theta \Delta t \sigma \sqrt{\Delta t} \langle N(0, 1, (k+s-1)\rangle ] + \\&\quad \sum _{k=1}^{\tau }\sum _{i=1}^{s}\Big [(1-\theta \Delta t)^{s+\tau -k} \sigma ^{2} \Delta t \\&\quad \left\langle N(0, 1, (i-1)\Delta t) N(0, 1, (k+s-1)\Delta t \right\rangle \Big ] . \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq91.gif)
![$$ \begin{aligned} \sum _{k=1}^{\tau }{\sum _{i=1}^{s}{[(1-\theta \Delta t)^{s+\tau -k} \sigma ^{2} \Delta t \delta ((k+s-1)\Delta t-(i-1)\Delta t)] }} \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq92.gif)
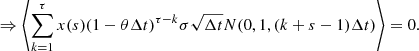
![$$ \begin{aligned} (1-\theta \Delta t)^{\tau }\left\langle x^{2}(s) \right\rangle + \sum _{k=1}^{\tau }{\left[ (1-\theta \Delta t)^{\tau -k} \theta \Delta t \mu ^{2} \right]}. \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq94.gif)
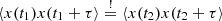
![$$ \begin{aligned}&\overset{\text{24e} \text{ in} \text{ 24f}}{\Leftrightarrow } (1 - \theta \Delta t)^{\tau } \langle x^{2}(t_{1}) + \rangle \sum _{k=1}^{\tau }{\left[ (1-\theta \Delta t)^{\tau -k} \theta \Delta t \mu ^{2} \right]} = \\&\quad (1 - \theta \Delta t)^{\tau } \langle x^{2}(t_{2}) + \rangle \sum _{k=1}^{\tau }{\left[ (1-\theta \Delta t)^{\tau -k} \theta \Delta t \mu ^{2} \right]} \end{aligned} $$](/articles/aa/full_html/2021/01/aa39097-20/aa39097-20-eq96.gif)