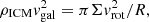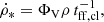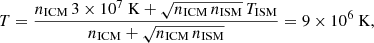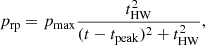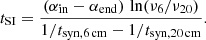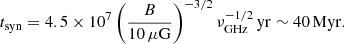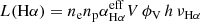| Issue |
A&A
Volume 645, January 2021
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 29 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202038507 | |
| Published online | 22 January 2021 | |
A Virgo Environmental Survey Tracing Ionised Gas Emission (VESTIGE)
VIII. Modeling ram pressure stripping of diffuse gas in the Virgo cluster spiral galaxy NGC 4330⋆
1
Université de Strasbourg, CNRS, Observatoire astronomique de Strasbourg, UMR 7550, 67000 Strasbourg, France
e-mail: Bernd.Vollmer@astro.unistra.fr
2
Dipartimento di Fisica G. Occhialini, Università degli Studi di Milano Bicocca, Piazza della Scienza 3, 20126 Milano, Italy
3
Institute for Computational Cosmology and Center for Extragalactic Astronomy, Durham University, South Road, Durham DH1 3LE, UK
4
Aix Marseille Université, CNRS, CNES, LAM, Marseille, France
5
Astronomical Observatory, Jagiellonian University, Kraków, Poland
6
NRC Herzberg Astronomy and Astrophysics, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
7
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris Diderot, Sorbonne Paris Cité, Observatoire de Paris, PSL University, 91191 Gif-sur-Yvette Cedex, France
8
Centro de Astronomía (CITEVA), Universidad de Antofagasta, Avenida Angamos 601, Antofagasta 1270300, Chile
9
Department for Astrophysics, University of Vienna, Türkenschanzstrasse 17, 1180 Vienna, Austria
Received:
27
May
2020
Accepted:
3
November
2020
NGC 4330 is one of the Virgo galaxies whose UV emission distributions show a tail structure. An associated tail structure is also observed in the HI and Hα emission distributions. Previous dynamical modeling has shown that the galaxy is approaching the cluster center and is therefore undergoing increasing ram pressure stripping. Recent stellar population fitting of deep optical spectra together with multiband photometry led to the determination of the time when star formation was quenched in the galactic disk. We introduce a new version of the dynamical model that includes not only the dense neutral gas, but also the diffuse ionized gas, and we aim to reproduce the HI, Hα, and UV distributions together with the star formation histories of the outer gas-free parts of the galactic disk. We present the results of 50 simulations with five different Lorentzian temporal ram pressure profiles and five different delays between the simulation onset and peak ram pressure. The delays were introduced to study the influence of galactic structure on the outcome of the simulations. The inclusion of diffuse gas stripping significantly changes the HI, UV, and Hα emission distributions. The simulations with diffuse gas stripping naturally led to vertical low surface density filaments in the downwind region of the galactic disk. These filaments occur less frequently in the simulations without diffuse gas stripping. The simulations with diffuse gas stripping led to better joint fits to the spectral energy distributions (SEDs) and optical spectra. The HI, near-UV, and Hα morphologies of the model snapshots that best reproduce the SEDs and optical spectra are sufficiently different to permit a selection of best-fit models. We conclude that the inclusion of diffuse gas stripping significantly improves the resemb+lance between the model and observations. Our preferred model yields a time to peak ram pressure of 140 Myr in the future. The spatial coincidence of the radio continuum and diffuse Hα tails suggests that both gas phases are stripped together. We suggest that the star formation in the outer tail is sporadic and low level, and this explains the absence of a significant amount of cosmic ray electrons there. Furthermore, we suggest that the mixed interstellar medium is ionized by collisions with the thermal electrons of the ambient intracluster medium, which confines the filaments.
Key words: galaxies: evolution / galaxies: individual: NGC 4330 / galaxies: interactions / galaxies: kinematics and dynamics / galaxies: ISM
Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-French-Hawaii Telescope (CFHT), which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii.
© B. Vollmer et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Once a galaxy has entered a galaxy cluster, its evolution will change, sometimes drastically. Multiple gravitational interactions together with the influence of the cluster potential can remove the stellar and gaseous content of its outer disk (galaxy harassment; Moore et al. 1996). The rapid motion of the galaxy within the cluster atmosphere, the hot (temperature T ∼ 107 K) and tenuous (density n ∼ 10−4 cm−3) intracluster medium (ICM), causes the removal of the outer gas disk via ram pressure. In contrast to galaxy harassment, ram pressure stripping does not affect the stellar content of the galaxy. Spiral galaxies that underwent or are undergoing ram pressure stripping show a truncated gas disk together with a symmetric stellar disk (e.g., VLA Imaging of Virgo in Atomic gas, VIVA, Chung et al. 2009). If the interaction is ongoing, a gas tail mainly detected in HI is present (e.g., Chung et al. 2007). The gas truncation radius is set by the galaxy’s closest passage to the cluster center via the criterion introduced by Gunn & Gott (1972):
where ρICM is the ICM density, vgal the galaxy velocity, Σ the surface density of the interstellar medium (ISM), vrot the rotation velocity of the galaxy, and R the stripping radius. If peak ram pressure occurred more than 400–500 Myr ago, the gas tails have disappeared and the truncated gas disk has become symmetric again (Vollmer et al. 2009).
Under extreme conditions, ram-pressure stripped galaxies often show extraplanar, one-sided optical and UV emission as well as important tails of ionized gas (e.g., Yagi et al. 2010, 2017; Poggianti et al. 2017). Because of their optical appearance, these objects are called jellyfish galaxies. Most of the Hα emission in these tails is due to photoionization by massive stars born in situ in the tails (Poggianti et al. 2019). Extraplanar molecular gas is often found in jellyfish galaxies (Jáchym et al. 2014, 2019; Moretti et al. 2018), from which the ionizing stars are formed.
Once the gas has been removed from the outer galactic disk under the action of ram pressure, the corresponding stellar content remains gas- and dust-free and gradually stops star formation. Optical spectroscopy together with multiwavelength photometry can be used to determine the stellar populations and thus the star formation history (SFH) of the ram-pressure stripped parts of the galactic disk (Boselli et al. 2006; Crowl & Kenney 2008). These SFHs can then be compared to those of dynamical models. For the Virgo cluster galaxy NGC 4388, an observed quenching timescale of ∼200 Myr was determined by Pappalardo et al. (2010) based on a Very Large Telescope (VLT) spectrum and optical and UV photometry. An updated dynamical model including ram pressure stripping was able to reproduce the observed quenching timescale together with additional observational characteristics (Vollmer et al. 2018): HI distribution and velocity field as well as far-UV (FUV), Hα, and polarized radio continuum emission distribution. A realistic model has to fulfill all these observational constraints. From the model, the ram pressure temporal profile, time to peak ram pressure, and the angle between the galaxy velocity within the cluster and its disk plane can be determined. A model-based time series of ram-pressure stripped galaxies was established by Vollmer et al. (2009). The Virgo spiral galaxy NGC 4330 is part of this time series.
The ISM of a spiral galaxy consists of different phases: (i) cool dense molecular gas (T ∼ 10–30 K, n ≳ 100 cm−1), (ii) cold neutral hydrogen (T ∼ 100 K, n ∼ 100 cm−1), (iii) warm neutral hydrogen (T ∼ 8000 K, n ∼ 1 cm−1), and (iv) warm diffuse ionized hydrogen (T ∼ 8000 K, n ∼ 0.4 cm−1). Since the acceleration of a gas cloud by ram pressure is inversely proportional to the gas surface density (Eq. (1)), the different phases are expected to be stripped with different efficiencies. Indeed, the stripped diffuse ionized gas is accelerated to higher velocities and is therefore observed at larger distances from the host galaxy than the dense gas (Vollmer et al. 2009; Moretti et al. 2018). On the other hand, the stripped dense CO-emitting gas seems to be well mixed with the warm HI (Vollmer et al. 2008, 2012a,b; Jáchym et al. 2014; Nehlig et al. 2016), which is consistent with a scenario where the neutral turbulent ISM is stripped as an entity. We therefore expect that the distribution of the stripped diffuse ionized gas is more extended than that of the neutral gas. The detection of this gas in deep Hα observations represents an important additional constraint on simulations of ram-pressure stripped galaxies. An additional constraint on the simulations comes from the SFH of stripped gas-free regions of the stellar disk. Detailed simulations of a ram-pressure stripped galaxy can thus not only give access to the interaction parameters (see Vollmer et al. 2009), but can also provide insight into the reaction of the different gas phases to ram pressure.
In this article, we (i) test a new version of the dynamical model that includes not only the dense neutral gas, but also the diffuse ionized gas and apply it to NGC 4330 and (ii) aim to reproduce the observed HI, Hα, and near-UV (NUV) distributions of NGC 4330 together with the SFHs of the outer gas-free parts of the galactic disk. This article represents a continuation and update of the work of Vollmer et al. (2012a,b).
2. NGC 4330
NGC 4330 is one of the Virgo spiral galaxies with a long HI tail that was observed by Chung et al. (2007). It has a maximum rotation velocity of vrot ∼ 180 km s−1 and a total HI mass of MHI = 4.5 × 108 M⊙ (Chung et al. 2009). NGC 4330 is located at a projected distance of ∼2° (600 kpc) from the cluster center (i.e., it is relatively close to M 87) and has a radial velocity of 400 km s−1 with respect to the Virgo cluster mean. The H I deficiency of NGC 4330 – which is defined as the logarithm of the ratio of the HI content of a field galaxy of the same morphological type and diameter as the observed HI mass – is 0.8 (Chung et al. 2007), that is to say, the galaxy has lost about 80% of its atomic hydrogen. The HI distribution in the galactic disk (upper-left panel of Fig. 1) is truncated at about half the optical radius. In addition, NGC 4330 is one of the rare Virgo galaxies that show extended UV tails (Abramson et al. 2011). The HI and UV tails show a significant offset, with the HI tail being downwind of the UV tail. At the leading edge of the interaction, the Hα emission and dust extinction distribution bend sharply out of the galactic disk. These features are signs of active ram pressure stripping. Roediger & Hensler (2005) elaborated on the subsequent stripping phases for face-on ram pressure stripping. NGC 4330 undergoes the instantaneous stripping phase where the outer part of the gas disk is displaced but only partially unbound. This leads to a straightly bent but coherent outer gas disk.
 |
Fig. 1. NGC 4330. Upper-left panel: VIVA survey H I emission distribution (contours) on the GALEX NUV image. Upper-right panel: GALEX FUV emission distribution (contours) on the VESTIGE continuum-subtracted Hα+[NII] image. Lower-left panel: model HI emission distribution (contours) on the model extinction-free NUV image. Lower-right panel: model FUV emission distribution (contours) on the model extinction-free Hα image. |
Vollmer et al. (2012a,b) presented a detailed dynamical model for NGC 4330. Their best-fit model qualitatively reproduced the observed projected position, the radial velocity of the galaxy, the molecular and atomic gas distribution and velocity field, and the UV distribution in the region where a gas tail is present. In contrast to other Virgo spiral galaxies affected by ram pressure stripping, NGC 4330 does not show an asymmetric ridge of polarized radio continuum emission. This is due to the particular projection of NGC 4330, where the compressed large-scale magnetic fields are oriented along the light-of-sight. Vollmer et al. (2012a,b) concluded that the ISM is stripped as a whole entity and that only a tiny fraction of dense clouds can be left behind. Extraplanar star formation proceeds in dense gas arms pushed by ram pressure. The collapsing clouds decouple rapidly from the ram pressure wind, and the young, UV-emitting stars stay behind the gas.
On the basis of dynamical models, the galaxy moves toward the north and continues to approach the cluster center, with the closest approach occurring in ∼100 Myr. Despite the success of their model, Vollmer et al. (2012a,b) noted that the observed red UV color on the windward side was not reproduced by the model. Moreover, their simulations could only produce the model distribution of HII regions, that is, compact regions of high ionized gas density and high Hα surface brightness (Fig. 9 of Vollmer et al. 2012a,b). Since the diffuse ionized gas is much less dense than the gas in the HII regions, it has a much lower surface brightness and can only be detected through deep narrowband observations. Such observations for NGC 4330 have only now become available. Therefore, the Vollmer et al. (2012a,b) model was upgraded to enable the simulation of diffuse ionized gas stripping.
Within the Virgo Environmental Survey Tracing Ionised Gas Emission (VESTIGE; Boselli et al. 2018), Fossati et al. (2018) detected a low surface brightness 10 kpc Hα tail exhibiting a peculiar filamentary structure. In addition, these authors collected literature photometry in 15 bands from the FUV to the far-infrared (FIR) and VLT FORS2 deep optical long-slit spectroscopy. Using a Monte Carlo code that jointly fits spectroscopy and photometry, they reconstructed the SFHs in apertures along the major axis of NGC 4330. In this way, they found a clear outside-in gradient of the time when the ram-pressure induced star formation quenching started: the outermost radii were stripped about 500 Myr ago, while the stripping reached the inner 5 kpc from the center within the last 100 Myr. In addition, Fossati et al. (2018) discovered a low surface brightness 10 kpc tail of ionized gas exhibiting a peculiar filamentary structure (upper-right panel of Fig. 1). The ionized gas tail is associated with the HI tail but extends further to the south.
3. The dynamical model
We used the N-body code described in Vollmer et al. (2001), which consists of two components: (i) a non-collisional component that simulates the stellar bulge, stellar disk, and the dark halo and (ii) a collisional component that simulates the ISM as an ensemble of gas clouds. A scheme for star formation was implemented, where stars were formed during cloud collisions and then evolved as non-collisional particles.
3.1. Halo, stars, and gas
The non–collisional component consists of 81 920 particles, which simulate the galactic halo, bulge, and disk. The characteristics of the different galactic components are shown in Table 1.
Total mass, number of collisionless particles N, particle mass M, and smoothing length l for the different galactic components.
The resulting rotation velocity is ∼180 km s−1, and the rotation curve becomes flat at a radius of about 5 kpc.
We adopted a model where the ISM is simulated as a collisional component, that is, as discrete particles that each possess a mass and a radius and can have inelastic collisions (sticky particles). The advantage of our approach is that ram pressure can be easily included as an additional acceleration on particles that are not protected by other particles (see Vollmer et al. 2001).
The 20 000 particles of the collisional component represent gas cloud complexes that evolve in the gravitational potential of the galaxy. The total assumed gas mass is 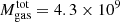 M⊙, which corresponds to the total neutral gas mass before stripping (i.e., to an HI deficiency of 0). A radius is attributed to each particle, which depends on its mass assuming a constant surface density. The normalization of the mass-size relation was taken from Vollmer et al. (2012a). During each cloud-cloud collision, the overlapping parts of the clouds are calculated. Let b be the impact parameter and r1 and r2 the radii of the larger and smaller clouds. If r1 + r2 > b > r1 − r2, the collision can result in fragmentation (high-speed encounter) or mass exchange. If b < r1 − r2, mass exchange or coalescence (low-speed encounter) can occur. The outcome of the collision is simplified following Wiegel (1994). If the maximum number of gas particles or clouds (20 000) is reached, only coalescent or mass-exchanging collisions are allowed. In this way, a cloud mass distribution is naturally produced. The cloud-cloud collisions result in an effective gas viscosity in the disk.
M⊙, which corresponds to the total neutral gas mass before stripping (i.e., to an HI deficiency of 0). A radius is attributed to each particle, which depends on its mass assuming a constant surface density. The normalization of the mass-size relation was taken from Vollmer et al. (2012a). During each cloud-cloud collision, the overlapping parts of the clouds are calculated. Let b be the impact parameter and r1 and r2 the radii of the larger and smaller clouds. If r1 + r2 > b > r1 − r2, the collision can result in fragmentation (high-speed encounter) or mass exchange. If b < r1 − r2, mass exchange or coalescence (low-speed encounter) can occur. The outcome of the collision is simplified following Wiegel (1994). If the maximum number of gas particles or clouds (20 000) is reached, only coalescent or mass-exchanging collisions are allowed. In this way, a cloud mass distribution is naturally produced. The cloud-cloud collisions result in an effective gas viscosity in the disk.
As the galaxy moves through the ICM, its clouds are accelerated by ram pressure 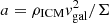 . In addition, the gas clouds are accelerated by the gradients of the gravitational potential a = −∇ϕ. The ISM surface density is assumed to be Σ(r) = (1 + exp(−r/2 kpc)) × 10 M⊙ pc−2. The constant surface density at the outer disk is motivated by the observed saturation of the HI surface density (e.g., Leroy et al. 2008). The radial dependence takes into account the increased surface density that is due to the presence of molecular gas. Within the galaxy’s inertial system, the galaxy’s clouds are exposed to a wind coming from a direction opposite to that of the galaxy’s motion through the ICM. The temporal ram pressure profile has the form of a Lorentzian, which is realistic for galaxies on highly eccentric orbits within the Virgo cluster (Vollmer et al. 2001). The effect of ram pressure on the clouds is simulated by an additional force on the clouds in the wind direction. Only clouds that are not protected from the wind by other clouds are affected. This results in a finite penetration length of the ICM into the ISM (see Appendix B). Since the gas cannot develop instabilities, the influence of turbulence on the stripped gas is not included in the model. The mixing of the ICM into the ISM is very crudely approximated by the finite penetration length of the ICM into the ISM; in other words, up to this penetration length, the clouds undergo an additional acceleration caused by ram pressure.
. In addition, the gas clouds are accelerated by the gradients of the gravitational potential a = −∇ϕ. The ISM surface density is assumed to be Σ(r) = (1 + exp(−r/2 kpc)) × 10 M⊙ pc−2. The constant surface density at the outer disk is motivated by the observed saturation of the HI surface density (e.g., Leroy et al. 2008). The radial dependence takes into account the increased surface density that is due to the presence of molecular gas. Within the galaxy’s inertial system, the galaxy’s clouds are exposed to a wind coming from a direction opposite to that of the galaxy’s motion through the ICM. The temporal ram pressure profile has the form of a Lorentzian, which is realistic for galaxies on highly eccentric orbits within the Virgo cluster (Vollmer et al. 2001). The effect of ram pressure on the clouds is simulated by an additional force on the clouds in the wind direction. Only clouds that are not protected from the wind by other clouds are affected. This results in a finite penetration length of the ICM into the ISM (see Appendix B). Since the gas cannot develop instabilities, the influence of turbulence on the stripped gas is not included in the model. The mixing of the ICM into the ISM is very crudely approximated by the finite penetration length of the ICM into the ISM; in other words, up to this penetration length, the clouds undergo an additional acceleration caused by ram pressure.
3.2. Star formation
We assume that the star formation rate (SFR) is proportional to the cloud collision rate. A mass-size relation based on a constant gas surface density is assumed for the collisional particles. The collisions are explicitly calculated for each timestep (∼104 yr) via the simplified geometrical recipes of Wiegel (1994). We verified that the SFR of an unperturbed galaxy is constant within 1 Gyr.
Vollmer & Beckert (2003) expanded on an analytical model for a galactic gas disk that considers the warm, cold, and molecular phases of the ISM as a single, turbulent gas. This gas is assumed to be in vertical hydrostatic equilibrium, with the midplane pressure balancing the weight of the gas and the stellar disk. The gas is taken to be clumpy, so that the local density is enhanced relative to the average density of the disk. Using this local density, the free-fall time of an individual gas clump (i.e., the governing timescale for star formation) can be determined. The SFR is used to calculate the rate of energy injection by supernovae. This rate is related to the turbulent velocity dispersion and the driving scale of turbulence. These quantities in turn provide estimates of the clumpiness of gas in the disk (i.e., the contrast between the local and average density) and the rate at which viscosity moves matter inward. Vollmer & Leroy (2011) applied the model successfully to a sample of local spiral galaxies. Within the framework of the model, the SFR per unit volume is given by
where ΦV and 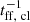 are the volume filling factor and free-fall time of self-gravitating gas clouds, respectively, and ρ is the overall gas density. The volume filling factor is
are the volume filling factor and free-fall time of self-gravitating gas clouds, respectively, and ρ is the overall gas density. The volume filling factor is 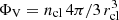 , where ncl is the internal number density of clouds and rcl is the cloud radius. For a self-gravitating cloud, the free-fall time equals the turbulent crossing time tff, cl = 2 rcl/vturb, cl. With the collision time given by
, where ncl is the internal number density of clouds and rcl is the cloud radius. For a self-gravitating cloud, the free-fall time equals the turbulent crossing time tff, cl = 2 rcl/vturb, cl. With the collision time given by 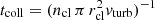 , this leads to
, this leads to 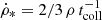 . Thus, the SFRs of the two recipes are formally equivalent.
. Thus, the SFRs of the two recipes are formally equivalent.
In numerical simulations, the star formation recipe usually involves the gas density ρ and the free-fall time  :
: 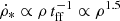 . We verified that our star formation recipe based on cloud-cloud collisions leads to the same exponent of the gas density in a simulation of an isolated spiral galaxy. As a consequence, our code reproduces the observed SFR-total gas surface density, SFR-molecular gas surface density, and SFR-stellar surface density relations (Vollmer et al. 2012a,b).
. We verified that our star formation recipe based on cloud-cloud collisions leads to the same exponent of the gas density in a simulation of an isolated spiral galaxy. As a consequence, our code reproduces the observed SFR-total gas surface density, SFR-molecular gas surface density, and SFR-stellar surface density relations (Vollmer et al. 2012a,b).
During the simulations, stars are formed in cloud-cloud collisions. In each collision, a collisionless particle is created, which is added to the ensemble of collisional and collisionless particles. The newly created collisionless particles have zero mass (they are test particles) and the positions and velocities of the colliding clouds after the collision. These particles are then evolved passively with the whole system. Since in our sticky-particle scheme there is mass exchange, coalescence, or fragmentation at the end of a collision, the same clouds do not collide infinitely. The local collision rate traces the cloud density and the velocity dispersion of the collisional component.
The information about the time of creation is attached to each newly created star particle. In this way, the Hα emission distribution caused by HII regions can be modeled by the distribution of star particles with ages younger than 20 Myr. The UV emission of a star particle in the two GALEX bands is modeled by the UV flux of single stellar population models produced from the STARBURST99 software (Leitherer et al. 1999). The age of the stellar population equals the time since the creation of the star particle. The total UV distribution is then the extinction-free distribution of the UV emission of the newly created star particles.
3.3. Diffuse gas stripping
Our numerical code is not able to treat diffuse gas in a consistent way. For a realistic treatment, 3D hydrodynamical simulations should be adopted. Nevertheless, we can mimic the action of ram pressure on diffuse gas by applying very simple recipes based on the fact that the acceleration by ram pressure is inversely proportional to the gas surface density, which in turn depends on the gas density for a gas cloud of constant mass. For the sake of simplicity, we do not modify the radii of the diffuse gas clouds for the calculation of the cloud-cloud collisions. The diffuse clouds are thus mostly ballistic particles under the influence of a ram-pressure induced acceleration. The recipes only take the gas cooling of the hot phase into account.
We assume that the warm (∼104–105 K) gas clouds become diffuse (i.e., their sizes and volume filling factor increase and their densities and column densities decrease) if they are stripped out of the galactic plane and if their densities fall below the critical density of 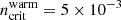 cm−3. We further assume that the first condition is fulfilled if the stellar density at the location of the gas particle is lower than
cm−3. We further assume that the first condition is fulfilled if the stellar density at the location of the gas particle is lower than 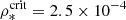 M⊙ pc−3. For our model galaxy, this density is reached at a disk height of ∼3.5–4 kpc.
M⊙ pc−3. For our model galaxy, this density is reached at a disk height of ∼3.5–4 kpc.
Once the ionized gas has a high volume filling factor (i.e., it becomes diffuse), its volume and surface densities decrease. The decrease in the surface density is taken into account by considering a gas cloud of a constant mass: for 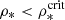 , the cloud size is proportional to n−1/3, the cloud surface density is proportional to n2/3, and the acceleration caused by ram pressure
, the cloud size is proportional to n−1/3, the cloud surface density is proportional to n2/3, and the acceleration caused by ram pressure 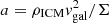 is increased by a factor of (0.044 cm−3/nISM)2/3. This last normalization and the critical densities were chosen such that they led to acceptable results for several observed galaxies undergoing ram pressure stripping. The critical stellar density is motivated by the fact that a significant change in the ISM properties only occurs once the ISM has entirely left the galactic disk. It turns out that this condition is necessary to avoid excessive gas stripping. The gas and stellar densities are calculated via the 50 nearest neighboring particles.
is increased by a factor of (0.044 cm−3/nISM)2/3. This last normalization and the critical densities were chosen such that they led to acceptable results for several observed galaxies undergoing ram pressure stripping. The critical stellar density is motivated by the fact that a significant change in the ISM properties only occurs once the ISM has entirely left the galactic disk. It turns out that this condition is necessary to avoid excessive gas stripping. The gas and stellar densities are calculated via the 50 nearest neighboring particles.
The hot (> 106 K) diffuse gas is taken into account in the following way: We assume that once the stripped gas has left the galactic disk, it mixes with the ambient ICM. The initial temperature of the ISM is TISM = 104 K. If (i) the gas density falls below the critical value of 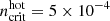 cm−3, (ii) the stellar density is below
cm−3, (ii) the stellar density is below 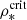 , and (iii) the ISM temperature is below 9 × 106 K, ICM-ISM mixing begins to take place. On the other hand, if the stellar density exceeds its critical value (i.e., the gas is located within or close to the galactic disk), then the gas is assumed to cool rapidly and its temperature is set to TISM = 105 K1. We assume that mixing occurs instantaneously and raises the temperature of the mixed gas clouds to
, and (iii) the ISM temperature is below 9 × 106 K, ICM-ISM mixing begins to take place. On the other hand, if the stellar density exceeds its critical value (i.e., the gas is located within or close to the galactic disk), then the gas is assumed to cool rapidly and its temperature is set to TISM = 105 K1. We assume that mixing occurs instantaneously and raises the temperature of the mixed gas clouds to
where nICM is the density of the mixed ICM, which is calculated for each particle. If an exceedingly high mixed ICM density (nICM > 2 × 10−3 cm−3) is needed to heat the gas cloud to 9 × 106 K, ICM-ISM heating is not allowed. The temperature of the mixed hot gas clouds TISM, if not heated, decreases with a cooling timescale of 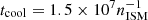 yr, where the ISM density nISM is given in cm−3. Once mixed, the gas cloud is not allowed to cool below a temperature of 106 K2. This algorithm ensures that stripped gas below the critical density ncrit is kept at a temperature of 9 × 106 K, whereas denser gas can cool to a temperature of 106 K.
yr, where the ISM density nISM is given in cm−3. Once mixed, the gas cloud is not allowed to cool below a temperature of 106 K2. This algorithm ensures that stripped gas below the critical density ncrit is kept at a temperature of 9 × 106 K, whereas denser gas can cool to a temperature of 106 K.
For the stripped hot gas clouds (> 106 K), we modified the equation of motion by adding the acceleration caused by the gas pressure gradient a = −∇pISM/ρISM using a Smoothed-particle hydrodynamics (SPH) formalism. For the sake of simplicity, an isothermal stripped ISM with a sound speed of cs = 235 km s−1 is assumed for this purpose. We thus do not solve an explicit energy equation and the calculation of hydrodynamic effects is approximate. Its main purpose is to keep the hot diffuse ISM from clumping.
For the calculation of the acceleration caused by ram pressure 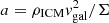 , the acceleration is further increased by a heuristic factor of ten if the ISM temperature exceeds 105 K and the stellar density is below ρ* = 2.5 × 10−4 M⊙ pc−3. We note that without the inclusion of hydrodynamical effects, thin gas filaments cannot be produced by our simple model. The diffuse gas is assumed to emit in the Hα line if its temperature is below 106 K.
, the acceleration is further increased by a heuristic factor of ten if the ISM temperature exceeds 105 K and the stellar density is below ρ* = 2.5 × 10−4 M⊙ pc−3. We note that without the inclusion of hydrodynamical effects, thin gas filaments cannot be produced by our simple model. The diffuse gas is assumed to emit in the Hα line if its temperature is below 106 K.
3.4. Parameters of the ram pressure stripping event
Following Vollmer et al. (2001), we used a Lorentzian profile for the time evolution of ram pressure stripping:
where pmax is the maximum ram pressure occurring at the galaxy’s closest passage to the cluster center, tHW is the width of the profile, and tpeak is the time of peak ram pressure. The simulations were calculated from t = 0 to t = 800 Myr. We set pmax = 5000, 6000, 10 000 cm−3(km s−1)2 and tHW = 100, 200, 300 Myr. Following Nehlig et al. (2016) and Vollmer et al. (2018), we investigated the influence of galactic structure (i.e., the position of spiral arms) on the results of ram pressure stripping by varying the time of peak ram pressure between tpeak = 570 Myr and 690 Myr. The ram pressure profiles are specified in Table 2 and shown in Fig. 2. The parameters of the Vollmer et al. (2012a,b) model were pmax = 5000 cm−3(km s−1)2 and tHW = 100 Myr.
 |
Fig. 2. Model ram pressure profiles. The thick red line shows the best-fit model, and the vertical red line shows the timestep of the best-fit model. |
Model ram pressure stripping profiles.
We adopted the Vollmer et al. (2012a,b) values for the angle between the ram pressure wind and the disk plane (75°). The inclination of the model galaxy is i = 90° to the line-of-sight.
4. Observations and model fitting
The deep optical spectrum was obtained with the FOcal Reducer and low dispersion Spectrograph (FORS2; Appenzeller et al. 1998) mounted on Unit Telescope 1 of the ESO VLT. With a length of 6.8′, the FORS2 slit covered the full extent of the galaxy. A slit aperture of 1.3″ was used to optimize the covered area without compromising the spectral resolution of R ∼ 1000. We obtained six exposures of 900 s each using the 600B+22 grism, which covers the wavelength range 3300–6210 Å, and three exposures of 900 s each using the 600RI+19 grism, which covers the wavelength range 5120–8450 Å. The deep continuum-subtracted Hα+[NII] observations were obtained within the VESTIGE survey (Boselli et al. 2018) using MegaCam at the Canada-French-Hawaii Telescope (CFHT) with the narrowband filter (MP9603) and the broadband r filter (MP9602). The ancillary GALEX, CFHT, Calar Alto 2.2m telescope, Spitzer, and Herschel photometric data are described in Fossati et al. (2018). In addition, for the comparison with our models, we used VIVA survey HI and 20 cm continuum data (Chung et al. 2009) and 6 cm radio continuum data from Vollmer et al. (2013).
Fossati et al. (2018) reconstructed the quenching histories of NGC 4330 in various regions along the major axis by means of stellar population fitting. They performed a joint fitting of spectra and photometry using Monte Carlo techniques to optimally explore the parameter space. The emission of the galactic disk was divided into 13 apertures along the major axis of NGC 4330, as shown in Fig. 3.
 |
Fig. 3. NGC 4330. Left panel: VLT slit position on the GALEX NUV image. Right panel: VLT slit position on the CFHT r band image adapted from Fossati et al. (2018). The downturn region includes slit regions 11 to 13, and the tail region includes slit regions 1–3. The downturn plus tail region includes slit regions 1–3 and 11–13. |
Aperture photometry was obtained by summing the calibrated flux values in each pixel that contributes to a given aperture minus the background value in the same aperture. To estimate the background, each aperture was randomly placed in empty regions of the images and the sum of the counts was taken. This procedure was repeated 1000 times and the median value was adopted as the best estimator for the background value. For the UV, optical, and near-infrared (NIR) bands, the measured fluxes were corrected for the Galactic attenuation. The spectra from the FORS2 reduced 2D spectral images were extracted by summing the flux in the spatial pixels contributing to each region along the slit direction.
For the reconstruction of the quenching history of each radial bin, a model of its unperturbed radial SFH is needed. For this purpose, Fossati et al. (2018) adopted the multizone models for the chemical and spectrophotometric unperturbed disk evolution originally presented in Boissier & Prantzos (2000) and later updated by Muñoz-Mateos et al. (2011). The model was projected to fit the high inclination of the disk of NGC 4330, and the SFHs were derived in each of the apertures. Fossati et al. (2018) further modified the unperturbed SFHs by introducing an exponential decline of the SFR to parametrize the quenching event.
Parametric models to the spectrophotometric data were produced using MULTINEST (Feroz & Hobson 2008; Feroz et al. 2009; Feroz & Skilling 2013). A grid of stellar spectra was constructed using the quenched SFHs coupled to Bruzual & Charlot (2003) high-resolution models. Nebular emission lines were added to the stellar template. To do so, Fossati et al. (2018) first computed the number of Lyman continuum (λ < 912 Å) photons QH0 for a given stellar spectrum. They then assumed that all the ionizing radiation is absorbed by the gas and that the ionizing photons do not contribute to the heating of dust. However, they modeled the uncertainty in the conversion of QH0 into emission line flux by adding a nuisance parameter (Lyscale) in their Monte Carlo Spectro-Photometric Fitter (MC-SPF) code. This parameter also takes into account differential aperture effects between the 1.3″ spectral slit and the larger photometric apertures. A double (Calzetti et al. 2000) attenuation law was assumed to include the effects of dust attenuation on the stellar and nebular emission line spectrum. Fossati et al. (2018) coupled the stellar spectrum with dust emission models from the mid-infrared to the FIR by means of an energy balance between the stellar flux absorbed by the dust and reemitted in the infrared. They jointly fit the photometric data points and the FORS2 spectra at their native resolution. The multidimensional likelihood space was sampled by using PYMULTINEST (Buchner et al. 2014), a python wrapper for the MULTINEST code. For direct comparison with the results obtained from our model SFHs, we reproduce the results of Fossati et al. (2018) in Figs. A.4–A.9.
For our purposes, we used the modeling of Fossati et al. (2018) to obtain the synthetic photometry and the optical spectra for our model SFHs. The model photometry and spectrum is then compared to observations using MULTINEST and the total evidence is calculated. The goodness is evaluated using the Bayesian evidence. This value is formally defined as the integral of the likelihood of a given model over the entire parameter space. When two models are compared, their goodness in describing the data can be summarized in the ratio of their evidence (or the difference in log space). The Bayesian evidence automatically penalizes models with more free parameters, thus optimally highlighting the best model even in the event that the models under considerations have a different number of free parameters. In our case, these free parameters are the temporal ram pressure profile, the chosen timestep, and the inclusion of diffuse gas stripping. The variation of the parameters that are used to compare the model to the data (stellar libraries, the attenuation model, and the Lyscale parameter) can change the goodnesses and thus the order of the preferred models. A better model yields a higher goodness.
5. Results
We calculated the model photometry and spectrum for all timesteps (Δt = 10 Myr) of the 50 simulations presented in Table 2 with (format Nanew) and without (format Na) a diffuse gas component. In addition, we decided to handle the Lyscale nuisance parameter in two different ways: (i) We set it to the fixed values found by Fossati et al. (2018), and (ii) we treated it as a free parameter and kept the value that led to the best fit to observations. The distributions of the total goodnesses for all model timesteps are shown in Fig. C.1. The distributions show a tail to high values containing about 10–20 timesteps. The resulting total goodnesses are presented in Table 3. The last number of the model names is the simulation timestep N. The time to peak ram pressure is ((N − 1) × 10)−tpeak Myr, where tpeak is given in Table 2.
Model fitting results.
We then searched for the 12 timesteps with the highest goodnesses for the downturn, tail, and total (downturn plus tail) regions. These different regions are generally not best fit by a single timestep (Table 4). Figure C.2, compared to Fig. A.6, gives an impression of the meaning of the total goodness g: The model as well as the observed spectra and spectral energy distributions (SEDs) of region 3 for two timesteps (models 4new_47 and 1cnew_46), with a goodness difference of Δg ∼ 200, show that the FUV and NUV fluxes are significantly better reproduced by model 4new_47. We therefore presume that goodness differences in excess of Δg ≳ 200 are significant.
Model fitting results.
All of our total model goodnesses are smaller than that of the parametric (Fossati et al. 2018) model. This is expected because the parametric model had a higher degree of freedom. The models with a diffuse stripped ISM lead to somewhat higher goodnesses than those without a diffuse stripped ISM. Moreover, models with a variable Lyscale parameter systematically yield higher goodnesses thanks to the physical relevance of this parameter in reproducing the observed emission lines in the spectra. This is true for the downturn, tail, and total regions.
Model 4new_47 with diffuse gas stripping has the highest total goodness of all the tested models (Table 3). Given that a goodness difference of Δg ≳ 200 is significant, models 1cnew_47 (diffuse gas stripping), 4b_67, and 2b_80 are also acceptable amongst the models with a variable Lyscale parameter. For a constant Lyscale parameter, only model 2b_80 is acceptable.
If we look at the goodnesses of the downturn and tail regions separately (Table 4), the results change: In the case of a variable Lyscale parameter, all 12 best-fit models of the downturn region are acceptable whether or not diffuse gas stripping is included. For the tail region, all models without diffuse gas stripping are acceptable. If the stripping of diffuse gas is included in the simulations, only the first three models are acceptable. In the case of a constant Lyscale parameter, the four and two best-fit models are acceptable whether or not diffuse gas stripping is included. In the tail region, only the eight best-fit models without diffuse gas stripping are acceptable.
We conclude that the best-fit models based on the total goodness are pre-peak ram pressure models if diffuse gas stripping is included, otherwise the preferred timesteps are post-peak ram pressure (see Table 2).
5.1. The NUV and HI morphologies
The observed HI emission stems from warm (∼8000 K) gas with densities ≳1 cm−3. The NUV is emitted by the photospheres of massive hot stars. It traces the star formation on timescales < 300 Myr.
The 48 simulation snapshots of Table 3 yield the highest total goodnesses for each kind of simulation (with or without diffuse gas stripping, with a variable or constant Lyscale parameter). Models with total goodnesses that exceed g = 32 000 for a variable Lyscale parameter (4new_47, 1cnew_47, 4b_67, and 2b_80) and g = 31650 for a constant Lyscale parameter (2b_80) are acceptable fits to the spectrophotometric observations. However, the observed HI, NUV, and Hα morphologies also have to be reproduced by the model snapshots. To assess the quality of the fits, we compared the model and observed morphologies of the downturn and tail regions by eye. The results are presented in Table 3. The key features used for the quality assessment are: HI: truncated disk, extraplanar gas south of the galactic disk, and southwestern tail; NUV: disk emission extending farther than the HI emission and southwestern tail offset from the HI tail; Hα: truncated disk, southwestern tail offset from the NUV tail, and low surface brightness north-south filaments. The “+” sign indicates it is reproduced, the “∼” indicates it is approximately reproduced, and “−” indicates it is not reproduced.
The model NUV and HI distributions of the six model snapshots with the highest goodnesses from the simulations with a diffuse ISM component and a variable Lyscale scale parameter are presented in Fig. 4. They can be directly compared to the upper-left panel of Fig. 1.
 |
Fig. 4. Models with a diffuse ISM component. The grayscale represents NUV images, solid contours represent HI images, and dotted contours represent stellar images. For the spectral fitting, a variable nuisance parameter Lyscale was used. |
The observed truncation radius of the HI disk of 7.5 kpc as well as its symmetry along the major axis are well reproduced by all model snapshots. The observed strong asymmetry of the HI distribution along the minor axis with a significant amount of gas pushed by ram pressure downwind of the major axis is also reproduced by all model snapshots. The observed southwestern tail is present in all model snapshots. However, the gas tails of models 4new_47, 1cnew_47, 3dnew_47, and 4anew_47 are somewhat more extended than the observed gas tail. Moreover, the gas distribution of the eastern downturn region of all model snapshots are more extended in the downwind direction than is observed. The observed gas distribution of the downturn region is best reproduced by model 4new_47.
In the downturn region, the observed NUV distribution is more extended along the disk than the HI distribution. This feature is reproduced by all model snapshots. However, the extent of all six model NUV disks are smaller than the observed one. In addition, the NUV emission of all model snapshots is extended in the downwind direction. While the model NUV downturn filaments are perpendicular to the galactic disk in models 1cnew_47, 4anew_47, 2anew_64, and 2anew_65, they are further bent toward the galactic disk in models 4new_47 and 3dnew_47. In this respect, the latter two model snapshots are most similar to observations.
We observe an interesting feature in the NUV distribution of models 2anew_64 and 2anew_65: an extension in the upwind direction on the northwestern side of the galactic disk. This extent is caused by star created in the UV tail that has the time to rotate into the downturn region. Since their angular momentum is that of the tail gas, these stars rotate in a plane that is tilted with respect to the galactic plane, leading to a position angle opposite to that of the tail in the downturn region. Because these stars need to have the time to fulfill about half of a galactic rotation, this effect occurs in simulation snapshots more than several 10 Myr after peak ram pressure. These model snapshots can thus be excluded. The observed bending of the southwestern NUV tail is reproduced by all model snapshots. Its observed offset with respect to the HI tail is only present in model 1cnew_47. We conclude that the observed HI and NUV morphologies are best reproduced by model 4new_47, followed by model 1cnew_47.
To demonstrate the effect of diffuse gas stripping on the model HI and NUV distribution, we show the same model snapshots as in Fig. 4 for the simulation without diffuse gas stripping in Fig. 5. The resulting HI and NUV distributions of all model snapshots are more extended than those of the snapshots of the corresponding models with diffuse gas stripping and observations. Indeed, the snapshots with the highest goodnesses for the models without diffuse gas stripping are not the same as those presented in Figs. 4 and 5 (see Table 3).
The snapshots with the highest goodnesses for the models without diffuse gas are presented in Fig. 6. All model with high snapshot numbers (4b_67, 2b_80, 4b_68, and 2d_70) show extensions in the upwind direction on the northwestern side of the galactic disk and are therefore excluded. The HI and NUV tails of the two other models, 3c_47 and 3_47, are less bent than the best-fit models with diffuse gas stripping (4new_47 and 1cnew_47). In addition, extended HI tails in the downturn regions of 3c_47 and 3_47 are not observed. We thus conclude that the models with diffuse gas stripping reproduce the observed HI and NUV morphologies significantly better than the models without diffuse gas stripping.
 |
Fig. 6. NUV (grayscale), HI (solid contours), and stellar (dotted contours) images. Models without a diffuse ISM component are shown. For the spectral fitting, a variable nuisance parameter Lyscale was used. |
5.2. The Hα morphology
The model Hα images consist of two components: (i) the H II regions ionized by young massive stars and (ii) diffuse ionized gas that is ionized by the stellar UV radiation or possibly by strong shocks induced by ram pressure stripping. The first component is modeled by the distribution of stellar particles with ages less than 20 Myr. This is the only component used for the images of the models without diffuse gas stripping. For the second component, the emission measure for all gas particles with temperatures lower than 106 K was calculated: EM = ρ2 d, where ρ is the gas density calculated with the SPH algorithm and the cloud diameter is given by d = 2 (3 Mcl/(4 πρ))1/3 with the cloud mass Mcl. In the absence of a model for the ISM ionization fraction, we assume a constant ionization for the diffuse and dense gas. We then added the HII region component with a heuristic normalization, which worked best to insure that extraplanar HII regions are well visible within the emission of the diffuse ionized component. In these images, the surface brightness of the disk emission with respect to the extraplanar emission is realistic in a qualitative, but not quantitative, sense.
Fossati et al. (2018) observed an Hα tail whose high surface brightness part is clumpy and follows the NUV tail (upper-right panel of Fig. 1). A diffuse component of low surface brightness extends downwind to the south. In addition, low surface brightness filaments extend further from the tail to the south. Another low surface brightness Hα filament is detected close to the downturn in the northeast. As noted by Fossati et al. (2018), all filaments indicate the direction of the motion of the galaxy.
The resulting model Hα emission maps for the snapshots of the highest goodness of the diffuse gas stripping model are presented in Fig. A.1. All model snapshots show an Hα tail that has the same extent as the observed NUV tail. Most of the models show extraplanar linear filaments in the downwind region of the galactic disk. These filaments are thicker than the observed Hα filaments (see Sect. 3.3). They are labeled for model 4new_47 in the upper-left panel of Fig. A.1. Their lengths are comparable to those of the observed Hα filaments. All models show an extraplanar linear filament originating from the downturn region, which extends out of the disk toward the south. This filament has a north-south direction in models 4new_47, 1cnew_47, and 3dnew_47. It has a position angle of ∼135° (i.e., it extends toward the southeast) in the other models. A second linear filament originating close to the galaxy center and extending into the downwind region is observed in models 4new_47, 1cnew_47, and 4anew_47. A third north-south filament is observed in the middle of the tail of model 4new_47. A fourth north-south filament starting from the outer edge of the Hα or NUV tail is present in models 4new_47, 1cnew_47, and 4anew_47. The direct comparison between model 4new_47 and the VESTIGE observations (Fig. 1) shows that this last filament might be interpreted as an extension of the gas tail. Because of the vertical orientation of its outermost part (compare to model 1cnew_47), we instead interpreted this feature as a filament.
Fossati et al. (2018) identified five extraplanar filaments in the downwind region: one originating close to the downturn region and four filaments in the tail region. Model 4new_47 with its four Hα filaments most closely resembles the observed Hα morphology. We therefore conclude that model 4new_47 best reproduces the deep VESTIGE Hα observations (lower-right panel of Fig. 1).
To demonstrate the effect of diffuse gas stripping on the model Hα emission distribution, we show the same model snapshots as in Fig. A.1 for the simulation without diffuse gas stripping in Fig. A.2. All model snapshots show an Hα tail comparable to that of the simulations with diffuse gas stripping. As expected, the number of extraplanar linear filaments is significantly decreased compared to the simulations with diffuse gas stripping. Only models 4_47, 1c_47, and 3d_47 show such a filament starting from the downturn region. However, its position angle differs significantly from zero (north-south direction). Vertical filaments along the projected direction of ram pressure stripping are only present in the diffuse gas because of its increased stripping efficiency. The ratio between tidal and ram pressure acceleration is higher for the dense gas, which is thus less accelerated along the wind direction. Based on the absence of north-south filaments, we conclude that the presence of diffuse gas stripping increases the number of extraplanar Hα filaments in the downwind region and leads to a north-south alignment of these filaments. The simulations with diffuse gas stripping thus reproduce observations best.
The snapshots with the highest goodnesses for the models without diffuse gas are presented in Fig. A.3. The Hα tail is comparable to that of the previously discussed models. The extraplanar filaments starting from the downturn region are still present in all model snapshots. However, their position angle is not zero, contrary to the observations. Only model 2d_70 shows north-south filaments starting from the galactic disk and the tail region. Only the filament originating at the end of the tail deviates from the north-south alignment of the other filaments, in contrast to the corresponding filament 4 in model 4new_47 (upper-left panel of Fig. A.1). We think that this difference is significant.
We conclude that the existence of north-south Hα filaments is a natural consequence of the presence of diffuse gas stripping. However, in rare cases, such filaments can also be created in models without diffuse gas stripping. Models 4new_47 and 2d_70 reproduce the deep VESTIGE Hα observations best.
5.3. The best-fit model
The results of the comparison between the model and observed H I, NUV, and deep Hα emission distributions are presented in Table 3. Model 4new_47 reproduces the HI and Hα emission distribution in the downturn and tail region in a satisfactory way. Moreover, the overall morphology of the observed NUV emission is qualitatively reproduced by the model. However, the NUV disk in the tail region is less extended than observed. This is mainly an effect of NUV surface brightness, which is lower in the model NUV tail compared to observations (see also the UV photometry in Figs. A.4–A.6). As a result, the offset between the Hα and NUV tails is much less pronounced relative to the observations. Moreover, the model NUV emission of the downturn region shows too much extraplanar emission on the downwind side compared to the GALEX observations. The observed offset between the NUV and the HI tail is absent in this model. This offset is only present in model 1cnew_47, and the observed NUV emission distribution is reproduced best by this model snapshot. However, model 1cnew_47 shows too much extraplanar HI emission in the downturn region. Based on the comparison of all observed characteristics with our model snapshots (Table 3), we conclude that model 4new_47 fits the available observations, including the optical spectra, best.
5.4. The optical spectra
The model optical spectra and the model SED for the best-fit model 4new_47 (including diffuse gas stripping and a variable nuisance parameter Lyscale) are presented in Figs. A.4–A.9 together with the SFH for the regions labeled in Fig. 3. The optical-to-NIR SED depends only on the SFH prior to the onset of the simulations and is always well reproduced by the models. The FUV and NUV flux densities are well reproduced by the model in regions 2, 3, and 11. They are somewhat underestimated by the model in downturn regions 12 and 13 and overestimated in the outer tail region 1. The optical spectra of all positions are well reproduced by the model. For a seamless comparison, we added the results from Fossati et al. (2018) for each position to Figs. A.4–A.93. It becomes clear that the good resemblance between the model and observations for all regions is thanks to the good resemblance between the observed and modeled SFHs. Whereas the SFHs of Fossati et al. (2018) are analytical with exponentially declining SFR after gas stripping, the model SFHs show more variations. If the model SFHs show a late peak of the SFR after the general decline of the SFR (regions 2 and 12), the onset of the decline occurs earlier than that derived with a simple analytical function, as in Fossati et al. (2018), because this additional young stellar population has to be compensated for via a removal of the stellar populations that were created just prior to the onset of SFR quenching. We conclude that our best-fit model 4new_47 reproduces the observed optical spectra and SED in a satisfactory way.
5.5. A constant nuisance parameter Lyscale
For the calculation of the model goodness, the nuisance parameter Lyscale was varied systematically between 1/3 and 3 to search for the value that led to the highest goodness. The parameter Lyscale takes into account that either some UV flux from the massive stars located in a given aperture escapes the region without ionizing the gas or that massive star outside the aperture ionize gas located inside the aperture. In addition, ram pressure induced shock can in principle lead to the ionization of the ambient gas. In the first case, Lyscale is less than one, while in the last two cases it exceeds unity. The resulting Lyscale parameters for the Fossati et al. (2018) model SFH along with the SFHs derived from the dynamical models with the highest goodnesses are presented in Table 5.
Nuisance parameter Lyscale.
The analytical SFHs of Fossati et al. (2018) lead to Lyscale values of less than one for all regions. Its values range from 0.33 to 0.75. The Lyscale parameter found for the dynamical models can exceed unity, ranging from 0.33 to 1.83. Our best-fit model in particular, 4new_47, leads to Lyscale > 1 in five out of six regions. Since these values are not exceedingly high, we think that this model is very much acceptable. Values exceeding unity could imply that ram-pressure induced shock probably plays a role in ionizing the ambient ISM. However, the high flexibility of the fitting model and the point spread function mismatch between the spectrum and the photometry prevent such a conclusion.
All spectra and SEDs were recalculated using the values of the Lyscale parameter found by Fossati et al. (2018). The resulting model snapshots with the highest goodnesses are presented in Table 3 for the simulations with and without a diffuse gas stripping. As stated previously, all goodnesses of the models without diffuse gas stripping are smaller than those of the model with diffuse gas stripping. In addition, a fixed Lyscale parameter for each region leads to the highest goodnesses for snapshots at later times compared to models with a variable Lyscale parameter.
The resulting model HI, NUV, and Hα images are presented in Figs. D.1–D.4. Whereas the model HI distributions are similar to the models with a variable Lyscale parameter, the snapshots from the models that include a fixed Lyscale parameter all show extraplanar NUV emission in the upturn region on the upwind side (Figs. D.1 and D.3). This NUV emission, which is not observed, is due to massive stars created in the tail region that had the time to rotate into the upturn region (see Sect. 5.1). In addition, none of the models with a fixed Lyscale parameter show the vertical low surface brightness Hα filaments on the downwind side of the NUV or Hα tail. We therefore conclude that the models with a fixed Lyscale parameter should be discarded and that this parameter primarily plays a nuisance role in the fit rather than having a physical meaning.
6. Discussion
The inclusion of diffuse gas stripping significantly changed the results of our simulations. Since a variable Lyscale parameter leads to the highest goodnesses, we do not consider the models with a constant Lyscale parameter in the following analysis. When the tail region is considered separately, the timesteps of interest are ∼50 Myr before peak ram pressure when diffuse gas stripping is included in the simulations (Table 4).
This is expected because the gas that is pushed into the tail becomes diffuse and is stripped with a higher efficiency than the denser gas. Unexpectedly, the opposite trend is found for the downturn region: The timesteps of interest are ∼70 Myr before peak ram pressure when diffuse gas stripping is not included. The reason for this behavior is the following: As expected, the diffuse gas is stripped rapidly out of the galactic disk on the windward side when diffuse gas stripping is included. At the same time, the gas that remains within the disk is compressed to higher densities compared to the simulations without diffuse gas stripping. This results in a more compact gas distribution at t ≳ 200 Myr after the onset of the simulations, that is to say, the surface density contrast of the gas located within the galactic disk is enhanced. Since more time is needed to push the outer dense arms to smaller galactic radii, the timesteps of interest for the downturn (windward) side are delayed when diffuse gas stripping is included. The bulk of the star formation occurs in the dense gas arms.
The situation changes when both, the downturn and tail regions, are fitted together (Table 3). Generally, the Hα and NUV emission distributions of the downturn region are more often reproduced when diffuse gas stripping is not included in the simulation. Overall, the HI distribution of the downturn region is hard to reproduce (4new_47 and 4_d70). The best reproductions of the observed HI distribution of the tail are only found in models with diffuse gas stripping. The Hα emission distribution of the tail region is often reproduced when diffuse gas stripping is not included, but only for peak and post-peak models. Most frequently, post-peak models are not allowed, because they show an NUV horn feature on the leeward side of the downturn region (see Sect. 5.1).
While the two acceptable models with diffuse gas stripping according to the total goodness (4new_47 and 1cnew_47) have Δtpeak = t − tpeak ∼ −170 Myr (i.e., they are pre-peak models), the two acceptable models without diffuse gas stripping (4b_67 and 2b_80) are post-peak models (Δtpeak > 0 Myr). Based on the comparison between the model and observed HI, NUV, and Hα distributions, the pre-peak models 4new_47 and 1cnew_47 are clearly preferred (Sect. 5.3).
6.1. The best-fit model
The best-fit model is 4new_47, with a maximum ram pressure of pmax = 6000 cm−3(km s−1)2, a width of the Lorentzian temporal profile of tHW = 200 Myr, and a time to peak ram pressure of Δt = t − tpeak = −140 Myr. The face-on projection of the distribution of the total gas surface density at the beginning of the simulation and at Δt = −140 Myr is presented in Fig. 7. The initial gas distribution of the galaxy has multiple spiral arms with surface densities between 10 and 20 M⊙ pc−2. During the ram pressure stripping event, we observe a highly nonlinear interaction between these arms and the induced gas compression. The gas distribution at Δt = −140 Myr has a compressed windward side and a gas tail with a multi-arm structure on the opposite side.
 |
Fig. 7. Face-on projection of the distribution of the total gas surface density at the beginning of the simulation (upper panel) and at Δt = −140 Myr (lower panel). The contours correspond to 1, 3, 5, 10, 20, 30, 40, and 50 M⊙ pc−2. The resolution is 820 pc. |
The model includes the stripping of diffuse gas and a variable Lyscale parameter for the calculation of the model optical spectra and thus the model goodness. The interaction parameters are close to those found by Vollmer et al. (2012a,b): pmax = 5000 cm−3(km s−1)2, tHW = 100 Myr, and Δt = −100 Myr. The Vollmer et al. (2012a,b) model was not able to reproduce the UV color in the stripped gas-free regions because the width of the Lorentzian profile was too small. A larger width permits an earlier gas stripping, which is consistent with the available UV observations and the optical spectra. In addition, the inclusion of diffuse gas stripping is essential. Only when this ingredient is added to the simulations does the gas leave the galactic disk early enough to lead to FUV and NUV flux densities and optical spectra consistent with observations. The diffuse gas stripping leads to the formation of linear filaments of the diffuse ionized gas that is present in deep VESTIGE Hα observations. The model filaments are thicker than the observed filaments because of the coarse spatial resolution of the diffuse gas particles. It should be noted that pronounced filamentary structures are naturally produced in simulations whenever magnetic fields are taken into account (Ruszkowski et al. 2014; Tonnesen & Stone 2014). To determine whether or not this effect is ubiquitous, it has to be shown for other galaxies undergoing ram pressure stripping.
6.2. Ram pressure stripping of cosmic ray electrons
NGC 4330 does not show an asymmetric ridge of polarized emission, in contrast to other ram-pressure stripped galaxies (Vollmer et al. 2012a,b). This is due to the NGC 4330 projection that places the region of compressed gas along the line-of-sight. On the other hand, Vollmer et al. (2012a,b) discovered a tail structure bending southward in their 6 cm radio continuum data (upper panel of Fig. 8). This tail structure is also visible in the VIVA 20 cm data (lower panel of Fig. 8). In addition, an outer tail of low surface brightness extending toward the southwest is detected at 20 cm.
 |
Fig. 8. Radio continuum emission (contours) on the VESTIGE Hα map. Upper panel: emission at 6 cm. The contour levels are (1, 2, 3, 5, 7, 10, 15, 20, 30, 50, 100) × 50 μJy beam−1. The resolution is (22″ × 22″). Lower panel: emission at 20cm from VIVA (Chung et al. 2009). The contour levels are (1, 2, 3, 5, 7, 10, 15, 20, 30, 50, 100) × 75 μJy beam−1. The resolution is (19.4″ × 15.4″). |
The tail, which is detected at 6 and 20 cm, bends to the south at the southwestern edge of the star-forming disk. It coincides with the northern part of the low surface brightness diffuse Hα emission. The cosmic ray electrons produced in the luminous H II regions of the galactic disk are most probably pushed to the south by ram pressure. This hypothesis is corroborated by the vertical magnetic field lines detected within the radio continuum tail (Vollmer et al. 2013). The spatial coincidence of the radio continuum and diffuse Hα tails suggests that both gas phases are stripped together.
We do not observe a steepening of the spectral index in the 6 and 20 cm tail, as expected for an aging cosmic electron population. The spectral index is given by α = ln(f6/f20)/ln(ν6/ν20), where f is the surface brightness or flux density. For a purely aging population of cosmic ray electrons, the evolution of the flux density is given by f = f0 × exp(−t/tsyn). The time that is needed for a steepening of the spectral index from an initial value αin to a final value αend can be calculated in the following way:
Based on equipartition between the energy densities of the cosmic ray electrons and the magnetic field, we estimate the magnetic field strength to be B ∼ 6–7 μG in the tail region, assuming an extent along the line-of-sight of l ∼ 4 kpc. The associated synchrotron timescale at 6 cm is then
If we assume that αin − αend ≲ 0.2 in the 6 and 20 cm tail, the timescale for the steepening of the spectral index is tSI ≲ 24 Myr. With a north-south extent of 3.5 kpc, the southward bulk velocity is ≳140 km s−1 within the sky plane.
Assuming that the outer radio continuum tail is barely detected at a 2σ level at 6 cm, we estimate a spectral index between 6 and 20 cm of ∼ − 1.5. With an initial spectral index of αin = −0.7 to −0.5, a final spectral index αin = −1.5, and a magnetic field strength of B = 6 μG, we obtain tSI ∼ 90–120 Myr. If the cosmic ray electrons were produced in the normally star-forming disk before gas stripping, tSI should be comparable to the star formation quenching time derived for that region, which corresponds to region 2 in Fossati et al. (2018). Whereas Fossati et al. (2018) determined a quenching time of 175 Myr based on their simple analytical SFHs, our preferred model shows that a more recent star formation episode (about 50 Myr ago; Fig. A.5) is also consistent with the data. It is not clear if such an episode can create enough cosmic ray electrons to make the synchrotron emission detectable. On the other hand, a somewhat lower magnetic field strength of B = 4–5 μG would lead to tSI ∼ 175 Myr. We thus conclude that a scenario in which the cosmic ray electrons were produced in the healthy disk before gas stripping, and were then pushed southward together with the diffuse ionized gas, is consistent with the available data.
It is surprising that there is no 20 cm emission associated with the upper part of the outer Hα tail where we see compact emission, which is most probably produced by HII regions. Either these HII regions are too young and have not yet produced cosmic ray electrons, or the production of cosmic ray electrons by these regions is low. We suggest that the present star formation in the outer tail is sporadic and low level and that this explains the absence of a significant amount of cosmic ray electrons there.
6.3. How to ionize the stripped diffuse gas
It is surprising that the surface brightness of the Hα filaments does not systematically decrease southward. These filaments therefore need to be confined by the ambient ICM for ∼60 Myr without recombining, that is to say, there must be a continuous ionization mechanism. In the following, we argue that the stripped diffuse gas is ionized by thermal conduction. With a recombination timescale trec = 0.1 (ne/1 cm−3)−1 Myr = 60 Myr, this yields an electron density of ne ∼ 2 × 10−3 cm−3. The mean electron density of the Hα filaments can be estimated by the relation
(Osterbrock & Ferland 2006), where np = ne is the proton density, 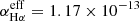 cm3 s−1 is the Hα effective recombination coefficient, V is the volume of the emitting region, ϕV is its volume filling factor, h is the Planck constant, and νHα is the frequency of the Hα transition. The volume V is the product of the emitting surface and the extent along the line-of-sight l ∼ 4 kpc. Following Boselli et al. (2016), we assume ϕV = 0.1 and [N II]/Hα = 0.5. With a mean Hα+[NII] surface brightness of 4 × 10−18 erg cm−2 s−1 arcsec−2 (Fossati et al. 2018), we obtain a mean electron density of ne = 0.05 cm−3. With an emitting surface of 25 kpc2, the mass of ionized gas in the filaments is about 107 M⊙.
cm3 s−1 is the Hα effective recombination coefficient, V is the volume of the emitting region, ϕV is its volume filling factor, h is the Planck constant, and νHα is the frequency of the Hα transition. The volume V is the product of the emitting surface and the extent along the line-of-sight l ∼ 4 kpc. Following Boselli et al. (2016), we assume ϕV = 0.1 and [N II]/Hα = 0.5. With a mean Hα+[NII] surface brightness of 4 × 10−18 erg cm−2 s−1 arcsec−2 (Fossati et al. 2018), we obtain a mean electron density of ne = 0.05 cm−3. With an emitting surface of 25 kpc2, the mass of ionized gas in the filaments is about 107 M⊙.
Since the derived mean electron density of the filaments exceeds that derived from the recombination timescale, the hydrogen atoms in the filaments have to be continuously ionized. Boselli et al. (2016) reached the same conclusion for the long, low surface brightness Hα tails of NGC 4569, another ram-pressure stripped galaxy in the Virgo cluster. The source of ionization might be (i) collisional ionization through shocks, (ii) collisional ionization through the thermal electrons of the ambient ICM that confines the filaments, or (iii) radiative ionization by embedded massive stars. We discard the third hypothesis because the gas density in the filaments is not high enough to permit continuous star formation. Hypothesis (i) is improbable because the direction of filaments is aligned with the ram pressure wind and it is difficult to perceive how ram-pressure induced shocks can pervade the entirety of the filaments.
We are thus left with hypothesis (ii): If we assume that the timescale for evaporation by the ICM equals the collisional ionization timescale by ICM-ISM collisions tICM − ISM = tevap = 10(NH/1020cm−2) Myr (Vollmer et al. 2001), and if the recombination timescale is trec = 0.1(0.3 cm−3/1 cm−3)−1 Myr = 0.3 Myr, we obtain a hydrogen column density of NH ∼ 3 × 1018 cm−2. This is well below the VIVA detection limit (∼2 × 1019 cm−2; Abramson et al. 2011). We thus suggest that the most probable mechanism for the ionization of the Hα filaments is collisions between the ICM thermal electrons and the hydrogen atoms of the filaments (as in ionized gas filaments in cooling flow clusters; see e.g., McDonald et al. 2010).
7. Summary and conclusions
The edge-on Virgo spiral galaxy NGC 4330 shows signs of ongoing ram pressure stripping: a truncated HI disk together with a one-sided tail (Chung et al. 2007, 2009), a UV tail associated with the HI tail (Abramson et al. 2011), a truncated Hα disk (Abramson et al. 2011), and an Hα tail with vertical low surface density filaments (Fossati et al. 2018; upper panels of Fig. 1). There is no asymmetric ridge of polarized radio continuum emission as observed in other ram-pressure stripped Virgo galaxies because the compression is occurring in the sky plane (Vollmer et al. 2012a,b). A previous dynamical model could reproduce all observed characteristics except the UV color of the stripped gas-free regions of the outer galactic disk (Vollmer et al. 2012a,b). Since the UV color depends on the SFH of the observed region, the stripping timescale of the dynamical model was not consistent with observations.
Fossati et al. (2018) obtained VLT FORS2 deep optical spectra along the major axis of NGC 4330. In addition, they collected literature photometry in 15 bands from the FUV to the FIR. Star formation histories in apertures along the major axis of the galaxy were constructed by means of stellar population fitting to the joint observational data: the SED and the optical spectrum. Based on an analytical model of quenched SFHs, they found that the outermost radii of the galactic disk were stripped ∼500 Myr ago, while the stripping reached the inner 5 kpc in the last 100 Myr.
We present new dynamical simulations to reproduce all observed characteristics of NGC 4330: the HI, UV, and Hα morphologies together with the SEDs and the optical spectra. The dense gas is modeled by a sticky particle scheme (Sect. 3). The influence of galactic structure (i.e., spiral arms) on the gas stripping process was studied by delaying the ram pressure peak with respect to the beginning of the simulations. Most importantly, we introduce a new recipe for the stripping of diffuse gas with a low density and a high volume filling factor (Sect. 3.3):
Warm diffuse gas: Once a gas particle has left the galactic disk and its density falls below a critical density 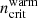 , ram pressure is increased by (0.044 cm−3/nISM)2/3.
, ram pressure is increased by (0.044 cm−3/nISM)2/3.
Hot (T > 106 K) diffuse gas: temperatures are assigned to the gas particles. Once a gas particle has left the galactic disk and its density falls below a critical density, 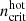 , ICM-ISM mixing sets in and immediately increases the temperature to 9 × 106 K. If the density of the mixed gas increases through compression, it can cool through X-ray emission according to its density and temperature. The acceleration due to ram pressure is increased by a factor of ten once the temperature of a particle exceeds T = 105 K. Moreover, the equation of motion for the hot gas particles was modified by adding the acceleration caused by the gas pressure gradient. We do not solve an explicit energy equation, and the calculation of hydrodynamic effects is approximate.
, ICM-ISM mixing sets in and immediately increases the temperature to 9 × 106 K. If the density of the mixed gas increases through compression, it can cool through X-ray emission according to its density and temperature. The acceleration due to ram pressure is increased by a factor of ten once the temperature of a particle exceeds T = 105 K. Moreover, the equation of motion for the hot gas particles was modified by adding the acceleration caused by the gas pressure gradient. We do not solve an explicit energy equation, and the calculation of hydrodynamic effects is approximate.
We ran 50 simulations with five different Lorentzian temporal ram pressure profiles, with five different delays between the simulation onset and peak ram pressure, and with (newprof) and without (prof) diffuse gas stripping (Table 2). Model photometry and spectra were calculated for every timestep (Δt = 10 Myr) of the 50 simulations. In addition, we decided to handle the Lyscale nuisance parameter (Sect. 4) in two different ways: (i) We set it to the fixed values found by Fossati et al. (2018), and (ii) we treated it as a free parameter and kept the value that led to the best fit to observations. We then searched for the 12 timesteps with the highest goodnesses for the downturn, tail, and both (downturn plus tail) regions (Table 3). The individual regions (downturn and tail) were generally not best fitted by the same model nor by the same timestep. This is due to the limitations of our model, where the gas stripping is treated with relatively simple recipes (see Sect. 3.3), and the limited number of temporal ram pressure profiles. Our analysis is based on the combined goodness of both regions.
Based on the direct comparison between our model snapshots and the available observations (Table 3), we conclude that the inclusion of diffuse gas stripping:
-
Significantly changes the gas, NUV (Figs. 4 and 5), and Hα morphologies (Figs. A.1 and A.2) of the simulations.
-
Naturally leads to vertical low surface density filaments in the downwind region of the galactic disk (Fig. A.1). These filaments occur less frequently in the simulations without diffuse gas stripping (Figs. A.2 and A.3).
-
Leads to better joint fits to the SEDs and optical spectra (Table 3). In general, the SEDs and optical spectra of the downturn and tails regions fitted separately are best reproduced by different model snapshots (Table 3). We based our selection of the best-fit model on the goodness of the joint fit of the downturn and tail regions.
-
Significantly improves the resemblance between the model and observations.
The HI, NUV, and Hα morphologies of the model snapshots that best reproduce the SEDs and optical spectra are sufficiently different to permit a selection of best-fit models. Model 4new_47 is our preferred model (Table 3, lower panels of Fig. 1), with a maximum ram pressure of pmax = 6000 cm−3(km s−1)2, a width of the Lorentzian temporal profile of tHW = 200 Myr, and a time to peak ram pressure of Δt = −140 Myr. The model includes the stripping of diffuse gas and a variable Lyscale parameter for the calculation of the model optical spectra. A variable Lyscale nuisance parameter leads not only to higher goodnesses (i.e., better joint fits to the SEDs and optical spectra), as expected, but also to a much better reproduction of the observed Hα and NUV images. The interaction parameters are close to those found by Vollmer et al. (2012a,b), who found a time to peak ram pressure of ∼100 Myr.
The radio continuum morphology of the Hα tail is twofold: (i) a tail of relatively high surface brightness detected at 6 cm and 20 cm and originating from the southwestern part of the galactic disk, which still actively forms stars; and (ii) a low surface brightness tail associated with the outer Hα tail, with a steep spectral index only detected at 20 cm (Fig. 8). The magnetic field strength of both radio continuum tails is estimated to be B ∼ 6–7 μG. The spatial coincidence of the radio continuum and diffuse Hα tail suggests that both gas phases are stripped together. The southward bulk motion of the 6 cm and 20 cm is about 150 km s−1, with a timescale of ∼25 Myr. For the outer part of the Hα tail, a scenario in which the cosmic ray electrons were produced in the healthy disk before gas stripping and were then pushed southward together with the diffuse ionized gas is consistent with the available data. We suggest that the star formation in the outer tail is sporadic and low level and that this explains the absence of a significant amount of cosmic ray electrons there.
Since the surface brightness of the Hα filaments does not systematically decrease southward (upper-right panel of Fig. 1), they need to be confined by the ambient ICM for ∼60 Myr without recombining. We suggest that the mixed ISM is ionized via collisions with the thermal electrons of the ambient ICM that confines the filaments.
The modeling of diffuse gas stripping represents an important step toward understanding the reaction of the multiphase ISM to ram pressure. The inclusion of diffuse gas stripping improves the resemblance between the model and observations (SEDs and optical spectra) and naturally gives rise to extended low surface density filaments oriented along the wind direction (diffuse Hα emission). More detailed simulations of cluster galaxies affected by ram pressure are needed to confirm our findings.
The spectra of regions 1, 3, 11, 12, and 13 are not shown in Fossati et al. (2018).
Acknowledgments
BV would like to thank R. Beck for useful discussions. We are grateful to the CFHT team who assisted us in the observations: T. Burdullis, D. Devost, B. Mahoney, N. Manset, A. Petric, S. Prunet, K. Withington. The VESTIGE project is financially supported by the “Programme National de Cosmologie and Galaxies” (PNCG). M. F. has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 757535). We would like to thank the anonymous referee for her/his comments which helped to improve the article.
References
- Abramson, A., Kenney, J. D. P., Crowl, H. H., et al. 2011, AJ, 141, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, Messenger, 94, 1 [Google Scholar]
- Boissier, S., & Prantzos, N. 2000, MNRAS, 312, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., et al. 2006, ApJ, 651, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Cuillandre, J. C., Fossati, M., et al. 2016, A&A, 587, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Fossati, M., Ferrarese, L., et al. 2018, A&A, 614, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, A., van Gorkom, J. H., Kenney, J. D. P., et al. 2007, ApJ, 659, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, A., van Gorkom, J. H., Kenney, J. D. P., et al. 2009, ApJ, 138, 1741 [CrossRef] [Google Scholar]
- Crowl, H. H., & Kenney, J. D. P. 2008, AJ, 136, 1623 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., & Hobson, M. P. 2008, MNRAS, 384, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., & Skilling, J. 2013, Am. Inst. Phys. Conf. Ser., 106, [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, M., Mendel, J. T., Boselli, A., et al. 2018, A&A, 614, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., & Gott, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jáchym, P., Combes, F., Cortese, L., et al. 2014, ApJ, 792, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Jáchym, P., Kenney, J. D. P., Sun, M., et al. 2019, ApJ, 883, 145 [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [Google Scholar]
- McDonald, M., Veilleux, S., Rupke, D. S. N., et al. 2010, ApJ, 721, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Katz, N., Lake, G., et al. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, A., Paladino, R., Poggianti, B. M., et al. 2018, MNRAS, 480, 2508 [Google Scholar]
- Muñoz-Mateos, J. C., Boissier, S., Gil de Paz, A., et al. 2011, ApJ, 731, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Nehlig, F., Vollmer, B., & Braine, J. 2016, A&A, 587, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (CA: University Science Books) [Google Scholar]
- Pappalardo, C., Lançon, A., Vollmer, B., et al. 2010, A&A, 514, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poggianti, B. M., Moretti, A., Gullieuszik, M., et al. 2017, ApJ, 844, 48 [Google Scholar]
- Poggianti, B. M., Gullieuszik, M., Tonnesen, S., et al. 2019, MNRAS, 482, 4466 [Google Scholar]
- Roediger, E., & Hensler, G. 2005, A&A, 433, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruszkowski, M., Brüggen, M., Lee, D., et al. 2014, ApJ, 784, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Tonnesen, S., & Stone, J. 2014, ApJ, 795, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., & Beckert, T. 2003, A&A, 404, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., & Leroy, A. K. 2011, AJ, 141, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., Cayatte, V., Balkowski, C., et al. 2001, ApJ, 561, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., Braine, J., Pappalardo, C., et al. 2008, A&A, 491, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Chung, A., et al. 2009, A&A, 496, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Braine, J., et al. 2012a, A&A, 537, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Braine, J., & Soida, M. 2012b, A&A, 547, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Beck, R., et al. 2013, A&A, 553, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Pappalardo, C., Soida, M., et al. 2018, A&A, 620, A108 [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Beck, R., et al. 2020, A&A, 633, A144 [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegel, W. 1994, Diploma Thesis, Univ. Heidelberg, Germany [Google Scholar]
- Wiener, J., Pfrommer, C., & Oh, S. P. 2017, MNRAS, 467, 906 [NASA ADS] [Google Scholar]
- Yagi, M., Yoshida, M., Komiyama, Y., et al. 2010, AJ, 140, 1814 [Google Scholar]
- Yagi, M., Yoshida, M., Gavazzi, G., et al. 2017, ApJ, 839, 65 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional figures
 |
Fig. A.1. Hα (grayscale) and NUV (contours) images. Models with a diffuse ISM component are shown. For the spectral fitting, a variable nuisance parameter Lyscale was used. |
 |
Fig. A.3. Hα (grayscale) and NUV (contours) images. Models without a diffuse ISM component are shown. For the spectral fitting, a variable nuisance parameter Lyscale was used. |
 |
Fig. A.4. Region 1. Upper panel: FORS2 spectrum (black), Fossati et al. model (blue), model 4new_47 with a diffuse ISM component and a variable Lyscale scale parameter (red). Middle panel: fit residuals. Lower-left panel: observed SED (black), Fossati et al. model (blue), model 4new_47 (red). Lower-right panel: SFH, Fossati et al. model (blue), model 4new_47 (red). |
Appendix B: ICM-ISM penetration length
To estimate the model ICM penetration length into the ISM, we considered a slice (−2 pc < y < 2 pc) of model 1 at a time to peak ram pressure of Δtpeak = −100 Myr, when the gas tail is in place. In the chosen projection, the wind direction has no component perpendicular to the image plane. It is therefore possible to estimate the penetration length, which, by definition, depends on the density of the gas clouds. From Fig. B.1, we estimate the penetration lengths to be about 100 pc, 200–300 pc, and about 1 kpc for regions of highest, medium, and lowest densities, respectively. The penetration length, which is the mean free path between clouds, depends on the number of particles and the mass-size relation of the gas clouds. We used the relation found by Vollmer et al. (2001), which leads to realistic gas stripping radii.
 |
Fig. B.1. Edge-on projection of a slice (−2 pc < y < 2 pc) of model 1 at a time to peak ram pressure of Δtpeak = −100 Myr. The black dots represent gas clouds that are protected from the ram pressure wind by other clouds. The gray dots represent gas clouds that are not protected from the ram pressure wind by other clouds. The arrows indicate the wind direction that is opposite to the direction of the galaxy’s motion within the ICM. |
Appendix C: Total goodness
The distributions of the total goodnesses of the simulations with a variable and a constant Lyscale parameter and with and without diffuse gas stripping are presented in Fig. C.1. All distributions show a tail to high goodnesses, which comprise ∼20 models.
 |
Fig. C.1. Goodness distributions of the different simulations. The vertical lines delimit the 12 models with the highest goodnesses (see Table 3). |
To give an impression of the quality of the fits with respect to the total goodness g, Fig. C.2 shows two models with Δg = 178. The model with the higher goodnesses reproduces the observed UV and, as a consequence, FIR fluxes significantly better.
 |
Fig. C.2. Model 1cnew_46, region 3. The total goodness is g = 6004, Δg = 178 less than the total goodness of model 4new_47 (Fig. A.6). Upper panel: FORS2 spectrum (black), Fossati et al. model (blue), and model 1cnew_46 (red). Middle panel: fit residuals. Lower-left panel: observed SED (black), Fossati et al. model (blue), and model 1cnew_46 (red). Lower-right panel: SFH, Fossati et al. model (blue), and model 1cnew_46 (red). |
Appendix D: Model fitting with a constant Lyscale scale parameter
The model results obtained with a constant nuisance parameter Lyscale are presented for the HI and NUV emission distributions and the Hα emission distribution. For the models with the highest total goodnesses (Table 3), the corresponding observed emission distributions are less well reproduced by these models compared to the models with a variable nuisance parameter.
 |
Fig. D.1. Models with a diffuse ISM component. The grayscale represents NUV images, the solid contours represent HI images, and the dotted contours represent stellar images. For the spectral fitting, a constant nuisance parameter Lyscale was used. |
 |
Fig. D.2. Models without a diffuse ISM component. The grayscale represents NUV images, the solid contours represent H I images, and the dotted contours represent stellar images. For the spectral fitting, a constant nuisance parameter Lyscale was used. |
 |
Fig. D.3. Models with a diffuse ISM component. The grayscale represents Hα images and the contours represent NUV images. For the spectral fitting, a constant nuisance parameter Lyscale was used. |
 |
Fig. D.4. Models without a diffuse ISM component. The grascale represents the Hα images and the contours represent the NUV images. For the spectral fitting, a constant nuisance parameter Lyscale was used. |
All Tables
Total mass, number of collisionless particles N, particle mass M, and smoothing length l for the different galactic components.
All Figures
 |
Fig. 1. NGC 4330. Upper-left panel: VIVA survey H I emission distribution (contours) on the GALEX NUV image. Upper-right panel: GALEX FUV emission distribution (contours) on the VESTIGE continuum-subtracted Hα+[NII] image. Lower-left panel: model HI emission distribution (contours) on the model extinction-free NUV image. Lower-right panel: model FUV emission distribution (contours) on the model extinction-free Hα image. |
| In the text | |
 |
Fig. 2. Model ram pressure profiles. The thick red line shows the best-fit model, and the vertical red line shows the timestep of the best-fit model. |
| In the text | |
 |
Fig. 3. NGC 4330. Left panel: VLT slit position on the GALEX NUV image. Right panel: VLT slit position on the CFHT r band image adapted from Fossati et al. (2018). The downturn region includes slit regions 11 to 13, and the tail region includes slit regions 1–3. The downturn plus tail region includes slit regions 1–3 and 11–13. |
| In the text | |
 |
Fig. 4. Models with a diffuse ISM component. The grayscale represents NUV images, solid contours represent HI images, and dotted contours represent stellar images. For the spectral fitting, a variable nuisance parameter Lyscale was used. |
| In the text | |
 |
Fig. 5. Same as Fig. 4 but without a diffuse ISM component. |
| In the text | |
 |
Fig. 6. NUV (grayscale), HI (solid contours), and stellar (dotted contours) images. Models without a diffuse ISM component are shown. For the spectral fitting, a variable nuisance parameter Lyscale was used. |
| In the text | |
 |
Fig. 7. Face-on projection of the distribution of the total gas surface density at the beginning of the simulation (upper panel) and at Δt = −140 Myr (lower panel). The contours correspond to 1, 3, 5, 10, 20, 30, 40, and 50 M⊙ pc−2. The resolution is 820 pc. |
| In the text | |
 |
Fig. 8. Radio continuum emission (contours) on the VESTIGE Hα map. Upper panel: emission at 6 cm. The contour levels are (1, 2, 3, 5, 7, 10, 15, 20, 30, 50, 100) × 50 μJy beam−1. The resolution is (22″ × 22″). Lower panel: emission at 20cm from VIVA (Chung et al. 2009). The contour levels are (1, 2, 3, 5, 7, 10, 15, 20, 30, 50, 100) × 75 μJy beam−1. The resolution is (19.4″ × 15.4″). |
| In the text | |
 |
Fig. A.1. Hα (grayscale) and NUV (contours) images. Models with a diffuse ISM component are shown. For the spectral fitting, a variable nuisance parameter Lyscale was used. |
| In the text | |
 |
Fig. A.2. Same as Fig. A.1 but without a diffuse ISM component. |
| In the text | |
 |
Fig. A.3. Hα (grayscale) and NUV (contours) images. Models without a diffuse ISM component are shown. For the spectral fitting, a variable nuisance parameter Lyscale was used. |
| In the text | |
 |
Fig. A.4. Region 1. Upper panel: FORS2 spectrum (black), Fossati et al. model (blue), model 4new_47 with a diffuse ISM component and a variable Lyscale scale parameter (red). Middle panel: fit residuals. Lower-left panel: observed SED (black), Fossati et al. model (blue), model 4new_47 (red). Lower-right panel: SFH, Fossati et al. model (blue), model 4new_47 (red). |
| In the text | |
 |
Fig. A.5. Same as Fig. A.4 but for region 2. |
| In the text | |
 |
Fig. A.6. Same as Fig. A.4 but for region 3. |
| In the text | |
 |
Fig. A.7. Same as Fig. A.4 but for region 11. |
| In the text | |
 |
Fig. A.8. Same as Fig. A.4 but for region 12. |
| In the text | |
 |
Fig. A.9. Same as Fig. A.4 but for region 13. |
| In the text | |
 |
Fig. B.1. Edge-on projection of a slice (−2 pc < y < 2 pc) of model 1 at a time to peak ram pressure of Δtpeak = −100 Myr. The black dots represent gas clouds that are protected from the ram pressure wind by other clouds. The gray dots represent gas clouds that are not protected from the ram pressure wind by other clouds. The arrows indicate the wind direction that is opposite to the direction of the galaxy’s motion within the ICM. |
| In the text | |
 |
Fig. C.1. Goodness distributions of the different simulations. The vertical lines delimit the 12 models with the highest goodnesses (see Table 3). |
| In the text | |
 |
Fig. C.2. Model 1cnew_46, region 3. The total goodness is g = 6004, Δg = 178 less than the total goodness of model 4new_47 (Fig. A.6). Upper panel: FORS2 spectrum (black), Fossati et al. model (blue), and model 1cnew_46 (red). Middle panel: fit residuals. Lower-left panel: observed SED (black), Fossati et al. model (blue), and model 1cnew_46 (red). Lower-right panel: SFH, Fossati et al. model (blue), and model 1cnew_46 (red). |
| In the text | |
 |
Fig. D.1. Models with a diffuse ISM component. The grayscale represents NUV images, the solid contours represent HI images, and the dotted contours represent stellar images. For the spectral fitting, a constant nuisance parameter Lyscale was used. |
| In the text | |
 |
Fig. D.2. Models without a diffuse ISM component. The grayscale represents NUV images, the solid contours represent H I images, and the dotted contours represent stellar images. For the spectral fitting, a constant nuisance parameter Lyscale was used. |
| In the text | |
 |
Fig. D.3. Models with a diffuse ISM component. The grayscale represents Hα images and the contours represent NUV images. For the spectral fitting, a constant nuisance parameter Lyscale was used. |
| In the text | |
 |
Fig. D.4. Models without a diffuse ISM component. The grascale represents the Hα images and the contours represent the NUV images. For the spectral fitting, a constant nuisance parameter Lyscale was used. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.