EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 645 (January 2021) A&A, 645 (2021) A108 Full HTML
Free Access
Issue
A&A
Volume 645, January 2021
Article Number A108
Number of page(s) 16
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202037872
Published online 26 January 2021

© ESO 2021

1. Introduction

The presence of short-lived, early-type main sequence (MS) stars at high Galactic latitudes has long been a puzzle that, now more than ever, demonstrates the existence of violent astrophysical phenomena, which lead to the ejection of these stars from their birthplaces, such as open clusters and OB associations. In the classical picture, Galactic runaway stars are accelerated through variations of the “binary supernova mechanism” (Blaauw 1961) and “dynamical ejection” from open clusters (Poveda et al. 1967). In the first case, the runaway star is subsequently ejected to the core-collapse supernova of a more massive companion; in the second case, binary interactions in massive clusters provide the ejection mechanism. Both phenomena are seen to take place early in the stellar lifetime, within the same regions of high-mass star formation (Hoogerwerf et al. 2001). The predicted ejection velocity distribution of these mechanisms ranges from a few tens of km s−1 up to 400–500 km s−1, strongly depending both on the mass of the runaway star and on the kind of interactions (Portegies Zwart 2000; Gvaramadze et al. 2009; Tauris 2015; Renzo et al. 2019; Evans et al. 2020). The binary ejection mechanism is highly efficient at forming runaway stars if a “birth kick” is imparted as a consequence of asymmetric supernova explosions (see discussions by Renzo et al. 2019; Evans et al. 2020). For the dynamical ejection scenario, the birth rate of runaway stars is seen to strongly correlate with increasing cluster density and stellar mass (Perets & Šubr 2012; Oh & Kroupa 2016). The fastest runaway stars are expected to form mostly via the binary supernova mechanism and to reach no further away than a few tens of kilo-parsecs above the Galactic plane, implying that just a negligible fraction of them might escape from the Milky Way.

The literature is rich with works focusing on the identification and classification of runaway stars. Notably, Silva & Napiwotzki (2011) produced a large systematic study of previously known runaway blue stars, arguing that their ejection velocity distribution is compatible with the binary supernova ejection scenario. Although, they suggest that a small contribution could also arise from the dynamical ejection from open clusters. The assortment of runaway early-type MS stars is not just populated by former Galactic disk members. In fact, there are extra-galactic visitors such as HE 0437−5439 (also known as HVS 3), which seems to have been ejected from the Large Magellanic Cloud (Edelmann et al. 2005; Irrgang et al. 2018a; Erkal et al. 2019a). In addition, other more energetic phenomena have also been suggested to operate in the Milky Way. One of them is the “Hills mechanism” (Hills 1988), which could be responsible for the formation of the “hyper-velocity” stars through the interaction of binaries with the supermassive black hole at the center of our Galaxy. With ejection velocities in the range of 1000 km s−1, these stars could also escape the Milky Way (see Brown 2015, for a review).

Wider samples of runaway stars have recently become more accessible thanks to the ESA Gaia astrometric mission (Gaia Collaboration 2016). Following the promising search for runaway stars in the first data release of Gaia (Maíz Apellániz et al. 2018), the second data release (DR2; Gaia Collaboration 2018a) has been the real game changer, due to the high precision of its space-based proper motions, parallaxes, broad-band photometry, and radial velocities (e.g., Boubert et al. 2018; Brown et al. 2018; Irrgang et al. 2018a; Shen et al. 2018; Hattori et al. 2018; Raddi et al. 2018, 2019; Koposov et al. 2020; Kreuzer et al. 2020).

In this paper, we present a selection of blue stars at high Galactic latitudes, guided by the Gaia Hertzsprung-Russell diagram (Sect. 2), with the goal of testing the prospects for the identification of blue MS runaway candidates in our Galaxy. We obtained low-resolution optical spectra for 48 stars (Sect. 3), which enable us to determine effective temperatures, surface gravities, and radial velocities. We classify 12 likely MS stars, 27 blue horizontal branch (BHB) stars, and two very hot evolved stars via the agreement between spectrophotometric and parallax-based distances (Sect. 4). We determine the Galactic orbits of the MS candidates (Sect. 5), and discuss their key properties in the context of runaway MS stars (Sect. 6). The results of this work suggest future improvements for the identification of runaway stars could be made by exploiting the synergy between Gaia and optical spectroscopy.

2. Target selection

We queried the Gaia DR2 in order to identify candidate MS runaway stars with masses above 2 M⊙ at high Galactic latitudes (|b|≥15°). We required that parallaxes are measured with a precision of better than 30%, and we applied color and absolute magnitude cuts of GBP − GRP ≤ 0.05 mag and MG = G + 5 − 5log(1000/ϖ) ≤ 3.7 mag, respectively, where G, GBP, and GRP are the Gaia magnitudes, and ϖ is the parallax given in mas yr−1. We filtered the Gaia photometry and astrometry, requiring high quality data as prescribed by Lindegren et al. (2018) and the Gaia Collaboration (2018b). In addition, we requested that our selection had a renormalized unit weight error (ruwe) smaller than 1.4 (Lindegren 2018). This procedure delivered 10 342 objects. The ADQL code that was used to perform our query is given in Appendix A.

We note that the G magnitude distribution of the selected candidates is double peaked at ≈8.5 and 14.5 mag, and that apparently brighter objects present relatively small tangential velocities in a heliocentric reference frame. In order to reduce contamination from objects that are less-likely runaway stars, we applied an additional cut defined via the tangential velocity as

v tan = 4.74 × μ α ∗ 2 + μ δ 2 ϖ ≥ 150 km s − 1 , $$ \begin{aligned} { v}_{\rm tan} = 4.74 \times \frac{\sqrt{{\mu ^{*}_{\alpha }}^{2} + \mu _{\delta }^{2}}}{\varpi } \ge 150\,\mathrm{km} \,\mathrm{s} ^{-1}, \end{aligned} $$(1)

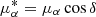where μ α ∗ = μ α cos δ $ \mu^{*}_{\alpha} = \mu_{\alpha} \cos{\delta} $ and μδ are the proper motion components along the right ascension and declination directions, respectively. This velocity cut delivers 2392 objects that are displayed in Fig. 1, along with the 48 stars for which we have collected follow-up spectroscopy.

thumbnail Fig. 1.

Gaia Hertzsprung-Russell diagram of candidate blue stars at high Galactic latitudes (gray cross symbols). The observed targets are shown as large circles. Solid curves represent the zero-age and terminal-age MS, while the evolutionary tracks for representative initial masses are plotted as dashed curves (Choi et al. 2016). The light-blue strip represents the horizontal branch (Dorman 1992). The reddening vector and typical error bars of the observed targets are displayed at the top edge of the figure.

Since we focus on blue stars, our selection does not overlap with previous work (e.g., Hattori et al. 2018), which targeted cool stars for which six-dimensional data were delivered by Gaia DR2. Those studies included radial velocities that are not available for stars that are bluer than an early-F spectral type, because they also have their pitfalls (Boubert et al. 2019). Instead, we note that towards the lower edge of Fig. 1, that is to say the faint absolute magnitude cut, our candidates overlap with the hot subluminous star candidates identified by Geier et al. (2019), which we avoided as much as possible in our spectroscopic follow-up. In addition, we note that our target selection of blue stars at high Galactic latitudes would contain a large fraction of BHB stars and field blue stragglers (Brown et al. 2010) out of which we aim to disentangle MS runaway candidates.

3. Observations

The time allocation for our follow-up observations consisted of five nights at the New Technology Telescope (NTT) on 2019 August 15–20, with the ESO Faint Object Spectrograph and Camera (EFOSC2; Buzzoni et al. 1984). Based on the on-sky visibility of suitable targets, we defined our priority list according to two empirical criteria. First, we favored objects having colors and absolute magnitudes that place them in the proximity of the unreddened MS (Fig. 1). Second, we covered a wide range of tangential velocities so as to not solely favor stars with the highest apparent motion, as this quantity is negatively affected by larger parallax uncertainties (Fig. 2). Due to the time allocation in August, we observed 48 stars with right ascension between 16.5 h and 3 h. Figure 3 shows the spatial distribution of all of the identified candidates and observed targets, which are compared to known runaway stars (Silva & Napiwotzki 2011). The relevant Gaia data for the observed targets are listed in Table 1.

thumbnail Fig. 2.

Relative parallax uncertainties and tangential velocities plotted against parallax-based distances in the top and bottom panels, respectively. The early-type star candidates are marked by cross symbols, while the observed targets are represented by circles with error bars.

thumbnail Fig. 3.

On-sky distribution of Gaia-selected candidate blue stars at high Galactic latitude (gray “+” symbols). The 48 observed targets (circles) and known MS runaway stars (red “x” symbols; Silva & Napiwotzki 2011) are also shown.

Table 1.

Gaia DR2 data for the observed 48 targets.

All the stars were observed with grism #7 and 2 × 2 CCD binning, taking two exposures that ranged between 5–30 min, followed by one He-Ar arc exposure at the same position of the observed star. We typically observed three white dwarf flux standards per night (GD 50, LAWD 74, and LTT 7987). Our observations were undertaken near the full moon and the weather conditions were generally stable, frequently reaching sub-arcsec seeing; the sole exception was the first night, when thick clouds disrupted the second half of the night.

We used standard IRAF (Tody 1986, 1993) procedures for the reduction of long-slit spectra (Massey et al. 1992; Massey 1997), which we bias subtracted, flat-field corrected, and wavelength and flux calibrated. The observing setup delivered a useful spectral coverage between 3650−5050 Å, with a dispersion of 1.9 Å pixel−1 (that translates to ≈120 km s−1 at Hβ). Because the point-spread-function of the spectral trace was smeared due to tracking limitations, the resolving power is strictly determined by the slit width. We measured a spectral resolution of Δλ = 6.5 Å from the full width at half maximum of the He-Ar lines of the calibration lamp. The residuals of the wavelength solution have a root-mean-square of 0.2 Å. Given that no strong emission line from the night sky is detectable within the wavelength range of our spectra, we assessed the accuracy of the wavelength calibration by measuring the radial velocities of the white dwarf standards GD 50 and LTT 7987. Following the line-fitting technique adopted by Napiwotzki et al. (2020), we used their analysis software, FITSB2, to measure the radial velocity, vrad, of the white dwarf standards by iteratively combining synthetic spectra (Koester 2010) with Gaussian and/or Lorentzian functions. From this procedure, we estimated an average systematic uncertainty of ±25 km s−1 with respect to the values published by Napiwotzki et al. (2020), which we will add in quadrature to that obtained for the radial measurements of our science targets.

4. Data analysis

For the atmospheric characterization of the observed targets, we followed a three-step approach. First, we performed model fitting of their entire spectral energy distributions (SED) that consist of the available ground-based and space-borne broad-band photometry from which we estimated the atmospheric parameters of each star, that is to say the effective temperature and surface gravity, as well as the interstellar reddening and angular diameter (Teff, log g, E(44 − 55), and Θ). Here, E(44 − 55) is the monochromatic reddening measured at 4400 and 5500 Å, which is closely related to the more traditional band-integrated color excess E(B − V), following the definition of Fitzpatrick et al. (2019). Second, we used the photometric estimates as initial guesses for the spectral analysis of flux calibrated spectra. Third, we redetermined E(44 − 55) and Θ by employing the spectroscopic best-fit model in the SED-fitting procedure.

4.1. Grids of synthetic spectra

Due to the low resolution of the spectra in hand, only stellar parameters such as Teff and log g can be reliably measured, while rotation, metallicity, and a helium abundance are very poorly constrained, especially in the late-B and early-A spectral type transition, where many candidates are found. In this region of the Hertzsprung–Russell diagram, MS and BHB stars cannot be distinguished on the basis of their atmospheric parameters alone (see Fig. 1), but additional information on the chemical composition and rotation of the stars is needed (see e.g., Heber et al. 2008a). Because the lack of spectral resolving power did not allow us to accurately obtain this auxiliary information, we performed the analysis of the SEDs and spectra for all targets twice by using two different grids of synthetic models, one being appropriate for MS stars and one being tailored to BHB stars (see below). The distinction between the MS and BHB nature is then made based on the agreement of their spectrophotometric and parallax-based distances (see Sect. 4.4).

For MS stars, it is self-evident to adopt a solar chemical composition. In contrast, the abundance patterns of BHB stars are diverse. Because the targets were selected to have high tangential velocities, BHB candidates are likely halo stars and thus metal poor. However, the stars’ chemical composition also varies along the horizontal branch. The morphology of BHBs of globular clusters reveals a universal discontinuity at Teff ∼ 11 500 K (Grundahl et al. 1999; Brown et al. 2016), which coincides with a drastic change in the chemical composition. While BHB stars that are cooler than 11 500K have the same metal content as the bulk of the stars of the host cluster, the abundance pattern of the hotter stars is peculiar, with helium depletion and iron enrichment (Behr 2003). These chemical pecularities have been attributed to atomic diffusion, that is to say to an interplay of gravitational settling and radiative levitation. The former leads to helium depletion and the latter causes the iron enrichment. The onset of atomic diffusion coincided with the disappearance of surface convection (Sweigart 2002; Michaud et al. 2011). Because we could not determine the abundance pattern of the individual BHB stars, we calculated model atmospheres and synthetic spectra assuming a metallicity of one-tenth solar for all BHB stars, but different helium abundances, that is, solar helium content for stars cooler than 11 500 K and one-tenth solar for the hotter ones.

Both grids span Teff = 7200–33 000 K and log g = 3.0–4.6. For Teff ≥ 9000 K, we adopted the hybrid approach “ADS” (Przybilla et al. 2011; Irrgang et al. 2014), which combines ATLAS12 (Kurucz 1996) to compute hydrostatic model atmospheres in local thermodynamic equilibrium (LTE) with DETAIL (Giddings 1981) to account for non-LTE effects; the SURFACE software (Giddings 1981) was used to produce the synthetic spectrum. Another set of models, which extends below 10 000 K, was generated by only accounting for LTE by means of the ATLAS12 and SYNTHE software (Kurucz 1993). All models include the recent improvements introduced by Irrgang et al. (2018b) for the computation of level dissolution in proximity of the Balmer jump. The synthetic photometry is based on SEDs computed with ATLAS12 using a ten times finer frequency grid, which were convolved with the appropriate transmission profile of each band-pass and subsequently shifted to the respective zero point.

4.2. SED fitting

We used the STILTS software (Taylor 2006) to query all the major photometric surveys that are available through the Table Access Protocol (TAP) of the VizieR online service (Ochsenbein 2019), which is hosted by the Strasbourg Astronomical Data Center. For most of the stars, in addition to Gaia photometry, there is reliable coverage from the ultraviolet (GALEX; Bianchi et al. 2017) through the optical (APASS and SkyMapper; Henden et al. 2015; Wolf et al. 2018, as well as SDSS and PanSTARRS, for targets with δ ≳ −30 deg; Alam et al. 2015; Chambers et al. 2016) and infrared (VHS, 2MASS, and WISE; McMahon et al. 2013; Skrutskie et al. 2006; Cutri 2014; Schlafly et al. 2019)

We adopted the most recent calibration of GALEX (Wall et al. 2019), well-validated zero points and uncertainties for the other photometric surveys1, as well as suggested corrections of Gaia DR2 photometry and the corresponding filter transmission profiles (Evans et al. 2018; Maíz Apellániz & Weiler 2018).

The SED fitting procedure follows the methods outlined by Heber et al. (2018), allowing us to directly estimate the four parameters: Θ, Teff, log g, and E(44 − 55). We adopted the monochromatic extinction law by Fitzpatrick et al. (2019) with the total-to-selective extinction coefficient R(55) = 3.02, which is typical for the interstellar medium. The best-fit was found by matching observed and synthetic photometry via χ2 minimization. Each stellar SED was fitted with both model grids described in the previous section. Six examples are displayed in Fig. 4.

thumbnail Fig. 4.

Examples for SED fits, from top left to bottom right: the MS candidates 0259−1705, 1900−7033, 2207−4329, and 2259−4931; the BHB candidate 1851−5036; and the binary 1944−4628. In each plot, the top panels show the measurements (color-coded by photometric system) as well as the best-fitting model spectra (gray), while the bottom panels show the error-normalized best-fit residuals, χ = (Oi − Mi)/σi, for each band-pass. The object 1944−4628 requires a composite SED fit, which is the combination of a Teff ≈ 24 400 K and a Teff ≈ 5900 K component (blue and red curve, respectively).

The preliminary SED fitting does not only provide an initial guess for the spectroscopic analysis, but it is also crucial for identifying problematic objects such as binary stars that exhibit composite SEDs. Indeed, we find that a single stellar component is not sufficient to model the SED of 1944−4628, which is likely an evolved low-mass star with an infrared excess due to a cooler binary companion (Fig. 4). Last but not least, photometric temperature estimates provide an important consistency check for our spectroscopic analysis (see the following section).

4.3. Spectroscopic fitting

The analysis of flux-calibrated spectra follows the methods outlined by Irrgang et al. (2014), where the best-fits are determined via χ2 statistics through comparison with our model grids. We preferentially use ADS models, but we switched to the ATLAS12/SYNTHE grid in order to avoid extrapolation at the edge of the ADS grids. We ignored macroturbulence and assumed a microturbulence of 2 km s−1. As stated in Sect. 4.1, the low resolution of our spectra makes it difficult to measure detailed metal abundances and stellar rotation, hence, our approach is to fit the spectra with both the solar composition and the metal-deficient grids, respectively.

The only elements for which the individual abundances are allowed to independently vary when using the ADS grids are Mg and Si. However, we note that most measurements are poorly constrained and do not deliver reliable abundances, which is why we refrain from giving those numbers. Although we kept the projected rotational velocity, v sin i, as a free parameter, it can hardly be resolved from our low-resolution spectra (Δv ≈ 400 km s−1). The spectra were corrected for the barycentric velocity and the radial velocities, vrad, were independently determined from each exposure. Statistical uncertainties affecting Teff and log g are numerically inconspicuous. The systematic uncertainties dominating the error budget of Teff and log g were estimated to the level of 4% and 0.1 dex, respectively. The error budget of vrad is also dominated by systematic uncertainties, which were estimated from the difference between the measured values of the two available exposures for each star (≲10 km s−1) and the 25 km s−1 error, which were determined by comparing the vrad of the white dwarf standards to values from the literature (Sect. 3).

The main results of our analysis are presented in Fig. 5, which displays the comparison between photometric and spectroscopic Teff for the MS and BHB model analyses. The good agreement seen in Fig. 5 confirms the robustness of the SED and spectroscopic analyses, but also suggests that an additional method (such as the distance comparison discussed in the following section) is necessary to distinguish between MS and BHB candidates.

thumbnail Fig. 5.

Comparisons between photometric Teff, measured via SED fitting, and spectroscopic Teff. The result for MS (top left panel) and BHB models (top right panel) are shown. The dashed lines represent the equality curves. The residuals are displayed as a function of photometric Teff in the lower panels. The gray-shaded area represents the 4% systematic uncertainty assumed for the spectroscopic results.

Two stars, 1621−8350 and 1944−4628, are considerably hotter than the bulk of the sample, and are not included in Fig. 5; 1621−8350 is the only star that shows a He II line (at 4685.8 Å) in its spectrum (Fig. 6). This leads to the classification of an O-type star that is consistent with a high Teff ≈ 30 000 K. Furthermore, 1944−4628 is an early B-type star in a binary system (Fig. 4) at Teff ≈ 24 400 K. Both stars are discussed separately in Sect. 4.4.

thumbnail Fig. 6.

Observed spectra, sorted by decreasing Teff.

A spectral atlas of our program stars is presented in Fig. 6, while examples of spectroscopic best-fits are shown in Fig. 7 for four stars (0259−1705, 1900−7033, 2207−4329, and 2259−4931), which are later classified as MS candidates based on their spectrophotometric distances (Sect. 4.4). In this figure, we exhibit three typical temperature regimes of our sample. We note that for hot stars such as 1900−7033, shown in Fig. 7, and 1939−1640 and 2054−2526, it would indeed be possible to have more reliable He abundance measurements rather than assuming solar composition, but this exercise is beyond the scope of this paper. For cool objects such as 2207−4329 and 2259−4931, we can see just a few weak metal lines. In these specific cases, both MS and BHB models seem to overestimate the intensity of the Ca II H line, hinting at a subsolar abundance that could be better investigated with higher-resolution spectra. The intensity of the Mg II 4481 line of 2207−4329 is also overestimated. This issue, although to a lesser extent, also characterizes the best-fit obtained with subsolar metallicity models. The star with an intermediate temperature, 0259−1705, shows an excellent agreement with the model.

thumbnail Fig. 7.

Examples of spectroscopic best-fits for four MS candidates (Sect. 4.4) with error-normalized residuals; from top left to bottom right: 1900−7033, 0259−1705, 2207−4329, and 2259−4931. The normalized spectra and the best-fit solar-metallicity models are shown in black and red, respectively. Two top panels: ADS models, while the bottom ones are obtained from the ATLAS12/SYNTHE grid. The H and He lines are labeled at the corresponding wavelengths. The Ca II lines were masked out during the fitting procedure due to possible interstellar contamination, which is recognizable in the spectrum of 1900−7033; masked regions are plotted using lighter colors.

Finally, we report that three stars were previously studied by other authors:

1900–7033. Kilkenny (1989) determined Teff = 18 000 K and log g = 4.0 with 10% errors from 3 Å-resolution spectra, which is in agreement with our results. This author proposed the star to be mildly He-rich (nHe/nH ∼0.3). This finding is supported by our observations because the He lines appear slightly deeper than those of the best-fit model with solar log(He/H) = −1.01 (see Fig. 7). Kilkenny (1989) also measured v sin i = 175 km s−1 from the He lines, while the Hγ and Hδ fits delivered smaller v sin i ≈ 75 and 100 km s−1, respectively. If we keep He as a free parameter, the best-fit result favors slightly super-solar He, but the line cores of the observed spectrum are still deeper than the model. Given that we could not disentangle the effect of stellar rotation due to the low resolution of our spectra, we adopted the atmospheric parameters obtained for a solar He abundance. Finally, Kilkenny (1989) reported a previous measurement of vrad ≈ −95 km s−1, which is at 2 σ from our result.

2239–2455. Kilkenny (1987) used Strömgren photometry to classify this star as B7V, which is compatible with our spectral analysis. Ortiz et al. (2007) obtained 1.2 Å-resolution spectra over the Hβ–Hϵ spectral range, from which they suggest Teff >  17 000 K and log g = 4.5 ± 0.5 via measurements of equivalent widths and depths of the Balmer lines.

2307–3157. Ortiz et al. (2007) determined Teff = 8500–10 000 K and log g = 3–3.5 with errors of 500 K and 0.5 dex, respectively, which roughly agree with our results.

4.4. Distance-driven classification and physical parameters

Figure 8 displays the Teff and log g distribution of the observed stars in the Kiel diagram, as derived from the spectral analysis with synthetic spectra representing MS and BHB stars. For reference purposes, we plotted the theoretical evolutionary tracks for MS rotating stars (Ekström et al. 2012), and the horizontal branch and post-horizontal branch tracks (Dorman 1992; Dorman et al. 1993). Given the degeneracy between MS stars of 3–4 M⊙ and BHB stars, whose evolutionary tracks overlap in the Kiel diagram, and the lack of additional information, such as v sin i and metal abundances, it is a priori impossible to classify the majority of stars in our sample by just using Teff and log g.

thumbnail Fig. 8.

Kiel diagrams showing the atmospheric parameters of the observed stars as determined via the spectroscopic best-fit with model spectra representing MS and BHB stars (top and bottom panels, respectively). Top panel: evolutionary tracks for rotating MS stars are plotted in black (Ekström et al. 2012). The initial masses of each model are noted below the zero-age MS (thick solid curve), while the stellar ages for selected evolutionary points along the tracks are given in mega years. Bottom panel: the horizontal branch is represented by the gray-shaded area, and the evolutionary tracks for post-horizontal branch stars of different masses are drawn as solid curves (Dorman 1992).

Hence, to assess the nature of our program stars, we proceeded in a different fashion by comparing the Gaia parallaxes to the spectrophotometric distances, D(SpT), which were determined under the assumption that the observed stars are either MS or BHB stars. In order to estimate D(SpT) under the MS-star assumption, we first determined the stellar masses, radii, and luminosities via interpolation of the tracks from Ekström et al. (2012) with the spectroscopic Teff and log g, which were obtained from the solar-metallicity grid fitting. The spectrophotometric distance was then computed from the resulting stellar radius and the angular diameter was determined via SED-fitting: D(SpT) = 2R/Θ. In the BHB-star assumption, we assumed a canonical BHB-star mass of M = 0.5 ± 0.1 M⊙ from which we inferred the stellar radius as 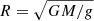R = G M / g $ R = \sqrt{G M/g} $, where G is the gravitational constant and g is the surface gravity measured with the representative metal-poor model grid. Then, the D(SpT) was calculated as above using the appropriate Θ.

Figure 9 displays the comparison between parallax-based distance estimators, D(ϖ), and spectrophotometric distances for the MS and BHB results. The simplest estimator that we considered is D(ϖ) = 1/ϖ, where D(ϖ) is the median of the 1/ϖ distribution. We also considered the effect of a global zero-point shift of +0.03 mas, identified by Lindegren et al. (2018) from the analysis of an all-sky sample of extra-galactic sources; however, these authors also note that such an offset has relatively large variations over degree-wide scales. Finally, as advised by Bailer-Jones et al. (2018) and Luri et al. (2018), we also compared their prior-based distance estimate, D (Bailer-Jones), against D(SpT).

thumbnail Fig. 9.

Comparisons between spectrophotometric distances and three different parallax-based distance estimates. Upper panels: MS candidates (blue-colored symbols) are identified via the 1σ agreement, which is represented by the dashed equality line and the gray-shaded area. Lower panels: same as the upper panels, but BHB candidates are represented by orange filled symbols. We note that three stars are classified both as MS and BHB candidates, hence they are color-coded in both the upper and lower panels.

MS and BHB stars are expected to lie on the identity lines depicted in Fig. 9, when the D(SpT) that is computed from the corresponding models agrees with the parallax-based distance estimates. From this comparison, we identify 15 MS candidates that have D(SpT) in agreement within 1σ with one of the three D(ϖ) estimators (top panels of Fig. 9). The same comparisons for BHB estimates deliver 29 candidates (lower panels in Fig. 9). We note that three stars (0035−5900, 2127−6300, and 2304−4021) are both identified as MS and BHB candidates, while all the others are uniquely classified either as MS or BHB candidates. Among the 29 BHB candidates, there are 1621−8350 and 1944−4628 too, which we discuss in more detail below as evolved extreme horizontal branch stars (post-EHB). Seven stars from our sample do not fit in any of the two proposed classification schemes.

In general, we note that all MS candidates agree with the 1/ϖ estimator and that the other two estimators tend to bring the parallax-based distances closer to the Sun. This effect is more extreme for the D (Bailer-Jones) estimator of stars that have larger spectrophotometric distances, and it is also noticeable for the BHB candidates. The overlap between the MS and BHB candidates is limited to three stars, reinforcing the validity of this method. Nevertheless, this ambiguity and the presence of seven unclassified stars suggests that the use of higher-resolution spectroscopy would be beneficial for a future analysis in addition to improved parallaxes from future Gaia releases. Finally, we note that unclassified objects may point towards the presence of either unresolved binaries or other kinds of stars, such as field blue stragglers (Brown et al. 2010) that we do not account for. We note that Brown et al. (2010) estimate that 74% of their blue halo star sample are BHBs and 26% are blue stragglers, which comes close to the 27 BHB stars versus seven unclassified objects in our sample.

Table 2 lists the atmospheric parameters corresponding to the spectroscopic best-fit models implied by the unique distance-driven classification as MS and BHB candidates, along with the signal-to-noise ratio (S/N) of the stacked spectra and the E(44 − 55). In passing, we note that the seven unclassified stars cluster around Teff ≈ 10 000 K and log g = 3.6. For the remainder of the paper, we take a conservative approach by considering the 12 stars that uniquely agree within 1σ of the identity line in either of the top panels of Fig. 9 as runaway MS candidates at high Galactic latitudes, while also assuming that the three stars with an ambiguous classification are BHB candidates.

Table 2.

Spectroscopic parameters of the sample derived from model spectra, as appropriate for their classification (MS or BHB candidate, respectively).

The spectra of the two hottest stars previously mentioned (1621−8350 and 1944−4628) resemble those of MS objects of late O- and early B-type (see Fig. 6). However, the respective spectroscopic distances would be about 30 and 10 kpc, which is at variance with their Gaia parallaxes (top panels of Fig. 9). Therefore, they must be evolved low-mass stars that mimic hot massive stars. Such stars are rare but do exist; examples include the B-type star HZ 22 of Teff = 29 200 K and log g = 4.04 (Saffer et al. 1997) and the O-type star PG2 120+062 (Moehler et al. 1994). HZ 22, in fact, is a binary orbited by an unseen white dwarf, which allowed for its mass to be estimated at 0.39 M⊙ (Schönberner 1978). Hence, those stars are likely post-RGB or post-AGB stars. For a brief account of such so-called ultraviolet (UV)-bright stars, see also Heber (2016).

While the SED of 1621−8350 can be matched by a single hot star model, this is not the case for 1944−4628, which shows an infrared excess indicative of a cool companion (Fig. 4). By adding a grid of SEDs from Husser et al. (2013), the infrared excess can be well matched by a composite model SED that includes a companion of Teff = 5900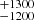 − 1200 + 1300 $ ^{+1300}_{-1200} $ K with a radius of 1.34 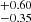− 0.35 + 0.60 $ ^{+0.60}_{-0.35} $ R⊙. Although uncertainties are large, the derived radius and luminosity of the companion are consistent with those of a G-type MS star.

We list the physical parameters of the 12 MS candidates in Table 3. The physical parameters of the 27 BHB candidates as well as those of the two post-EHB candidates and the late-type companion of 1944−4628 are given in Table 4.

Table 3.

Physical parameters of the MS candidates.

Table 4.

Physical parameters of BHB and post-EHB candidates computed adopting the atmospheric parameters derived from metal deficient atmospheric models and a mass of M = 0.5 ± 0.1 M⊙.

To conclude this section, we present the results of our classification in the two theoretical Hertzsprung-Russell diagrams of Fig. 10, displaying the MS and BHB candidates with their appropriate evolutionary tracks. A few MS candidates appear to be fairly evolved, with evolutionary timescales, τevo, in the range of 300–400 Myr. The BHB candidates are mostly distributed along their main locus. From Figs. 8–10, we conclude that the positions of 1621−8350 and 1944−4628 are well matched by the evolution of EHB stars (subluminous B stars) after core helium exhaustion (Dorman et al. 1993).

thumbnail Fig. 10.

Theoretical Hertzsprung-Russell diagrams. Top panel: our candidate MS stars over-plotted on the evolutionary tracks of Ekström et al. (2012) for rotating stars. The masses of each model are plotted in correspondence of the zero-age MS. The luminosities were derived by adopting the spectrophotometric distances. Bottom panel: our candidate BHB stars over-plotted on the horizontal branch that is represented by a gray-shaded area and the evolutionary tracks for post-horizontal branch stars of given masses (Dorman 1992; Dorman et al. 1993). We note that three stars are classified both as MS and BHB candidates, hence they are featured in both panels with the appropriate parameters.

5. Galactic orbit simulation

To model the trajectories of our MS candidates in the Milky Way’s gravitational potential, we used the PYTHON package GALPY for galactic dynamics (Bovy 2015). We adopted the Model I potential of Irrgang et al. (2013), which is implemented in GALPY in a simplified fashion that serves our purposes. This potential is a revised version of that described by Allen & Santillan (1991). The Sun is located at R⊙ = 8.4 kpc from the Galactic center, around which it orbits with v0 = 242 km s−1. The local escape velocity is v⊙,  esc = 614.4 km s−1. We note that the GALPY reference potential, MWPotential2014, accounts for a lower-mass Galactic halo model which, however, has a relatively small impact on determining the past trajectories of the youngest and nearest runaway candidates in our sample. The mass of the Milky Way’s halo can be relevant for the study of unbound stars, as we discuss in the following section.

The past and future trajectories of the runaway candidates were determined in a statistical fashion, as we randomly sampled the observed quantities (α, δ, 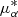μ α ∗ $ \mu^{*}_{\alpha} $, μδ, D(SpT), vrad) by adopting their uncertainties and relevant correlations. We drew 10 000 initial conditions, which were evolved for 10 Gyr in the future and traced back in the past for a sufficiently long time (i.e., up to τevo). For each star, we note the rest-frame velocity, vrf, the past and future Galactic Cartesian coordinates, and the corresponding velocity components. We estimated the escape probability from the Milky Way, Pesc, for each star as the fraction of initial conditions where (vrf − vesc) > 0. We determined the vertical component of the angular momentum, LZ, which indicates the direction towards which the star has been ejected. We also numerically estimated the eccentricity, e, the median orbital apocenter and pericenter, Rapo and Rperi, and the maximum vertical displacement, Zmax. The most recent Galactic plane crossings, R(Z = 0), were recorded and used to determine the flight time from such locations, τflight. The ejection velocity, vej, was determined as the velocity possessed by the star at R(Z = 0), which was corrected for the solar motion and the Galactic rotation. Table 5 lists the relevant orbital quantities for the 12 MS runaway candidates in a Galactocentric reference system that is left-handed, that is, with the x- and y-axis pointing, respectively, from the Milky Way’s center towards the Sun and along the direction of the Galactic rotation.

Table 5.

Orbital parameters of our MS candidates.

6. Properties of the runaway candidates

6.1. Orbit analysis

As expected for nearby runaway MS stars, all but one candidate are bound to the Milky Way’s potential, since they have vrf that is on average two times smaller than vesc at their Galactic coordinates. The only exception is 2207−4329 that has an escape probability of Pesc = 0.4, which is defined as the fraction of simulated trajectories with vrest >  vesc.

Due to our selection cut of vtan >  150 km s−1 (Eq. (1)), all stars in our sample (both the MS and BHB candidates) ended up having |vrad|≲vtan within the error bars. Three stars, 2034−5307, 2207−4329, and 2259−4931, have the largest vtan ≳ 450 km s−1 of all MS candidates. This unusual feature can also be noted in the Toomre diagram of Fig. 11, where the three stars have large negative Galactic Cartesian V components (i.e., they lag behind the Milky Way’s rotation), as it is more typically seen for the majority of BHB candidates in our sample. The remaining MS candidates, instead, have moderate tangential velocities of vtan ≃ 200 km s−1. The mostly retrograde motions of the BHB stars implies that they belong to the halo population. In the future, additional runaway candidates could be selected on the basis of their location in the Galactic Cartesian velocity space, as depicted by the Toomre diagram (Fig. 11).

thumbnail Fig. 11.

Positions of the program stars in the Toomre diagram. The quantity V is the velocity component in the direction of Galactic rotation, U is towards the Galactic center, and W is perpendicular to the Galactic plane. The local standard of rest (LSR) is marked by a yellow asterisk. The dashed circles centered around the LSR represent boundaries for three restframe velocities. The observed stars are plotted with error bars. Blue symbols correspond to MS candidates, while orange symbols are used for the BHB stars. All the targets identified in Sect. 2 are plotted as gray crosses, adopting vrad = 0 km s−1.

Following the general direction of the Galactic rotation, most MS candidates have LZ >  0 kpc km s−1, with the exception of the three more extreme stars that have large negative, Cartesian velocity V components. While our distance-based method entirely classifies them as MS stars, these three stars appear to possess kinematics that are more typical of BHB stars. We note that 2034−5307 and 2207−4329 have Teff and log g in the overlapping region of MS tracks and the horizontal branch (Fig. 8). Instead, 2259−4931 has a larger log g, which excludes a BHB nature. As already mentioned in Sect. 4, our distance-based method identifies MS candidates for which we envisage higher-resolution spectroscopy for a more detailed assessment of their nature.

All the MS candidates are found below the Galactic plane and are currently moving away from it, with the exception of three stars, 2034−1108, 2034−5307, and 2054−2526, which are approaching the plane. The orbits of the observed runaway candidates cover a wide range of eccentricities, e = 0.2–0.9, that is to say larger than the typical values for thin disk stars. All the runaway candidates have their orbital apocenters roughly between the solar circle and Rapo = 20 kpc, with a few exceptions potentially reaching out to very far Galactic radii. Their orbits are typically enclosed within Zmax = 4–40 kpc from the Galactic plane.

The trajectories of 2307−3157 have their orbital pericenters relatively close to the Galactic center (Rperi <  1 kpc); hence, its motion could be affected by the shape and orientation of the Galactic bar, which is not accounted for in our Galactic potential model. The trajectories of stars reaching beyond Rapo ≳ 20 kpc, instead, might experience gravitational perturbations due to the Large Magellanic Cloud (Kenyon et al. 2018; Erkal et al. 2019b), which our Galactic model also does not account for.

Finally, we do not list the orbital parameters (e, Rperi, Rapo, and Zmax) of 2207−4329 in Table 5, since they are unconstrained due to its nonzero probability of escaping the Milky Way. For this star, a significant fraction of simulated trajectories reaches extremely large Galatocentric radii without returning back, within the 10 Gyr time-frame of our simulation. As for the other stars, the parallax uncertainty has a major role in determining the agreement with the spectrophotometric distance and its classification as an MS candidate. For the time being, we note that the adopted potential (Model I of Irrgang et al. 2013) delivers a v⊙,  esc that is already a few tens of km s−1 larger than more recent Gaia-based estimates (Monari et al. 2018; Deason et al. 2019), suggesting a real chance for this star to escape the Milky Way if it is confirmed as an MS candidate.

6.2. Birthplace and flight times

The birthplaces of B-type MS stars are open clusters and associations within the thin disk of the Milky Way. The MS life of late-B and early-A-type stars can span from several 10 Myr up to ∼1 Gyr, thus making the identification of their birthplaces a relatively complex issue.

In Sect. 5, we have determined the most recent crossings of the Galactic plane for the MS candidates from which we estimated the flight times. To confirm the runaway hypothesis, the flight times need to be shorter than the ages estimated from evolutionary tracks (τflight ≤ τevo). In the case of ejection via the binary supernova mechanism, a runaway star could be rejuvenated due to mass-transfer prior to the core-collapse explosion of the primary (Schneider et al. 2015); hence, it could even appear slightly younger than the flight time.

In Fig. 12, we show the comparison between these two quantities, and we specifically note that – within the error bars – all the candidates are below or overlap with the solid curve representing the identity line. Two-thirds of our runaway candidates have ages that are more than two times longer than the flight times. This result poses the question of whether the reported crossing locations of the Galactic plane, R(Z = 0), identify the real birthplaces and flight times. In fact, we note that all candidates with τevo >  100 Myr, with the exclusion of 2207−4329, could have crossed the Galactic plane two or more times in the past. If the mechanisms that caused their runaway status occurred early in their lifetime, as it is generally accepted for the binary supernova and dynamical ejection scenarios, the most recent R(Z = 0) do not constrain their τflight.

thumbnail Fig. 12.

Comparison of flight times and stellar ages for the runaway MS candidates. The solid line represents the identity curve. The dashed lines mark the ranges where τevo = 2,  5, and 10 times τflight.

The various ejection mechanisms have intrinsic timescales. For example, the canonical binary ejection mechanism necessarily occurs on very short timescales of a few million years, which are driven by the core-collapse supernova (Portegies Zwart 2000), and the dynamical ejection from clusters can produce runaway stars for several hundred million years (Moyano Loyola & Hurley 2013). Therefore, future intermediate- and high-resolution spectroscopy would enable an improved understanding, for example, via the detection of polluting elements from supernova ejecta (Pan et al. 2012) as found for the hyper-runaway giant HD 271971 (Przybilla et al. 2008) or via the comparison of measured abundances with the average elemental abundances of specific locations in the Galactic disk (Irrgang et al. 2010).

Of all MS candidates, the possibly unbound runaway, 2207−4329, also has the Galactic plane crossing radius that is the furthest from the Galactic center at 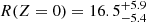R ( Z = 0 ) = 16 . 5 − 5.4 + 5.9 $ R(Z=0) = 16.5^{+5.9}_{-5.4} $. Such a large distance is similar to the case of HD 271791, which also originates from the outer Galactic disk (Heber et al. 2008b; Przybilla et al. 2008); the ejection velocity of which, however, is much lower (390 ± 4 km s−1; Irrgang et al. 2019). If the MS classification of 2207−4329 is confirmed by future Gaia data releases and higher-resolution spectroscopy, alternative birthplaces above the Galactic plane (e.g., the tidal stream of a satellite galaxy colliding with the Milky Way; Abadi et al. 2009) or other exotic scenarios involving intermediate-mass black holes (Fragione & Gualandris 2019) should also be investigated.

6.3. Ejection velocity distribution

Analyzing a sample of blue runaway stars, Silva & Napiwotzki (2011) interpret the relation between stellar mass and ejection velocity as it is mostly caused by the binary supernova mechanism. They also note that the dynamical ejection from clusters could contribute to the low-ejection velocity population. On the contrary, the fastest runaway stars could have an overlap with the slowest hyper-velocity stars.

In Fig. 13, our runaway candidates occupy a lower mass range with respect to the samples of Silva & Napiwotzki (2011) and Irrgang et al. (2019). The increase in ejection velocities towards lower masses that characterize our sample appears to be in agreement with the predictions for binary supernova ejections in the most extreme scenarios (Tauris 2015; Evans et al. 2020). However, Renzo et al. (2019) suggest that the dominant fraction of runaway stars with large ejection velocities could be mostly formed via dynamical interactions in open clusters, or more exotic scenarios. Interestingly, the ejection velocities of three runaway candidates, 2207−4329, 2259−4931, and 2307−3157, could largely exceed 400–500 km s−1, which would challenge the classical runaway scenarios (Irrgang et al. 2018a, 2019). Of the three stars, 2207−4329 is by far the fastest (802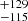 − 115 + 129 $ ^{+129}_{-115} $ km s−1); 2259−4931, which is the least massive star of our sample, is the second fastest one, ejected at 541 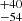− 54 + 40 $ ^{+40}_{-54} $ km s−1 from near the solar circle. If confirmed as an MS star, 2207−4329 would be the fastest known hyper-runaway star (cf. Table 5 of Irrgang et al. 2019). Its ejection velocity would exceed that of HVS 5 (640 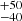− 40 + 50 $ ^{+50}_{-40} $ km s−1; Irrgang et al. 2019), even when we allow for the rather large uncertainty of the former. 2259−4931 would also gain a prominent position in the list of Galactic disk runaways with the largest ejection velocities, next to the well studied PG 1610+062 (550 ± 20 km s−1).

thumbnail Fig. 13.

Ejection velocities of runaway stars are plotted against their masses. Our 12 MS runaway candidates are represented by blue circles with error bars; it is important to note that two stars have very similar masses and, thus, overlapping symbols. The runaway stars studied by Silva & Napiwotzki (2011) are plotted as squares. More recently discovered high-velocity runaway stars as listed by Irrgang et al. (2019) are plotted as triangles, with masses updated from Kreuzer et al. (2020) when available.

7. Conclusions

We have presented the selection of bright early-type MS candidates at high Galactic latitudes, relying on the Gaia DR2 astrometry and photometry, with the goal of identifying new runaway stars. To test our selection, we have followed 48 stars obtaining low-resolution optical spectroscopy. By comparing spectrophotometric distances and parallax-based distance estimators, we propose 12 stars as MS candidates. Of the remaining stars, 27 are likely BHB stars, two are rare, highly evolved hot stars, and seven stars that have yet to be classified could be binaries or blue stragglers.

The newly identified runaway candidates are mostly found within the 2–4 M⊙ range. We numerically traced the past trajectories of these stars, identifying their nearest Galactic disk crossings locations, flight times, and ejection velocities. Most stars have ejection velocities between 200–450 km s−1. Three stars exceed the 450 km s−1 upper limit of classical ejection scenarios (see Irrgang et al. 2019) such as the binary supernova mechanism and dynamical ejection from open clusters and, thus, call for an ejection process that is still unknown (see also Evans et al. 2020). One of the three stars has a non-negligible escape probability, but more precise and accurate astrometry is required to check whether they are bound to the Galaxy. According to their kinematics, the BHB stars belong to the halo population.

We remark that high-resolution spectroscopy is crucial to asses precise rotational velocities and abundances, which are necessary to confirm the MS nature of these candidates and shed light on their ejection mechanisms and birthplaces. We also envisage an improved kinematic analysis and stellar classification of the wider target lists, arising from the future Gaia data releases. More accurate and precise parallaxes will make it possible to extend the current volume beyond ∼10 kpc, which is currently limited by the parallax precision and accuracy.

Acknowledgments

RR, AI, and UH acknowledge funding by the German Science foundation (DFG) through grants HE1356/71-1 and IR190/1-1. DS was supported by the Deutsche Forschungsgemeinschaft (DFG) under grants HE1356/70-1 and IR190/1-1. RR has received funding from the postdoctoral fellowship programme Beatriu de Pinós, funded by the Secretary of Universities and Research (Government of Catalonia) and by the Horizon 2020 programme of research and innovation of the European Union under the Maria Skłodowska-Curie grant agreement No 801370. We thank I. Condor for his support during the NTT observing run. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programme 0103.D-0530. This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France (DOI : https://doi.org/10.26093/cds/vizier). The original description of the VizieR service was published in Ochsenbein et al. (2000). This work made use of the IPython package (Pérez & Granger 2007) This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. Based on observations made with the NASA Galaxy Evolution Explorer. GALEX is operated for NASA by the California Institute of Technology under NASA contract NAS5-98034. This publication makes use of data products from the Wide-field Infrared Survey Explorer (Wright et al. 2010), which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration.

References

  1. Abadi, M. G., Navarro, J. F., & Steinmetz, M. 2009, ApJ, 691, L63 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
  3. Allen, C., & Santillan, A. 1991, Rev. Mex. Astron. Astrofis., 22, 255 [NASA ADS] [Google Scholar]
  4. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
  5. Behr, B. B. 2003, ApJS, 149, 67 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bianchi, L., Shiao, B., & Thilker, D. 2017, ApJS, 230, 24 [NASA ADS] [CrossRef] [Google Scholar]
  7. Blaauw, A. 1961, Bull. Astron. Inst. Neth., 15, 265 [NASA ADS] [Google Scholar]
  8. Boubert, D., Guillochon, J., Hawkins, K., et al. 2018, MNRAS, 479, 2789 [NASA ADS] [CrossRef] [Google Scholar]
  9. Boubert, D., Strader, J., Aguado, D., et al. 2019, MNRAS, 486, 2618 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
  11. Brown, W. R. 2015, ARA&A, 53, 15 [Google Scholar]
  12. Brown, W. R., Geller, M. J., Kenyon, S. J., & Diaferio, A. 2010, AJ, 139, 59 [NASA ADS] [CrossRef] [Google Scholar]
  13. Brown, T. M., Cassisi, S., D’Antona, F., et al. 2016, ApJ, 822, 44 [NASA ADS] [CrossRef] [Google Scholar]
  14. Brown, W. R., Lattanzi, M. G., Kenyon, S. J., & Geller, M. J. 2018, ApJ, 866, 39 [NASA ADS] [CrossRef] [Google Scholar]
  15. Buzzoni, B., Delabre, B., Dekker, H., et al. 1984, The Messenger, 38, 9 [NASA ADS] [Google Scholar]
  16. Casagrande, L., Wolf, C., Mackey, A. D., et al. 2019, MNRAS, 482, 2770 [NASA ADS] [Google Scholar]
  17. Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
  18. Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
  19. Cutri, R. M. 2014, VizieR Online Data Catalog: II/328 [Google Scholar]
  20. Deason, A. J., Fattahi, A., Belokurov, V., et al. 2019, MNRAS, 485, 3514 [Google Scholar]
  21. Dorman, B. 1992, ApJS, 80, 701 [NASA ADS] [CrossRef] [Google Scholar]
  22. Dorman, B., Rood, R. T., & O’Connell, R. W. 1993, ApJ, 419, 596 [CrossRef] [Google Scholar]
  23. Edelmann, H., Napiwotzki, R., Heber, U., Christlieb, N., & Reimers, D. 2005, ApJ, 634, L181 [NASA ADS] [CrossRef] [Google Scholar]
  24. Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Erkal, D., Boubert, D., Gualandris, A., Evans, N. W., & Antonini, F. 2019a, MNRAS, 483, 2007 [CrossRef] [Google Scholar]
  26. Erkal, D., Belokurov, V., Laporte, C. F. P., et al. 2019b, MNRAS, 487, 2685 [NASA ADS] [CrossRef] [Google Scholar]
  27. Evans, D. W., Riello, M., De Angeli, F., et al. 2018, A&A, 616, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Evans, F. A., Renzo, M., & Rossi, E. M. 2020, MNRAS, 497, 5344 [Google Scholar]
  29. Fitzpatrick, E. L., Massa, D., Gordon, K. D., Bohlin, R., & Clayton, G. C. 2019, ApJ, 886, 108 [NASA ADS] [CrossRef] [Google Scholar]
  30. Fragione, G., & Gualandris, A. 2019, MNRAS, 489, 4543 [Google Scholar]
  31. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Gaia Collaboration (Brown, A. G. A., et al.) 2018a, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Gaia Collaboration (Babusiaux, C., et al.) 2018b, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Geier, S., Raddi, R., Gentile Fusillo, N. P., & Marsh, T. R. 2019, A&A, 621, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Giddings, J. R. 1981, Ph.D. Thesis, University of London, UK [Google Scholar]
  36. González-Fernández, C., Hodgkin, S. T., Irwin, M. J., et al. 2018, MNRAS, 474, 5459 [Google Scholar]
  37. Grundahl, F., Catelan, M., Landsman, W. B., Stetson, P. B., & Andersen, M. I. 1999, ApJ, 524, 242 [NASA ADS] [CrossRef] [Google Scholar]
  38. Gvaramadze, V. V., Gualandris, A., & Portegies Zwart, S. 2009, MNRAS, 396, 570 [NASA ADS] [CrossRef] [Google Scholar]
  39. Hattori, K., Valluri, M., Bell, E. F., & Roederer, I. U. 2018, ApJ, 866, 121 [CrossRef] [Google Scholar]
  40. Heber, U. 2016, PASP, 128, 082001 [NASA ADS] [CrossRef] [Google Scholar]
  41. Heber, U., Hirsch, H. A., Edelmann, H., et al. 2008a, in Hot Subdwarf Stars and Related Objects, eds. U. Heber, C. S. Jeffery, R. Napiwotzki, ASP Conf. Ser., 392, 167 [NASA ADS] [Google Scholar]
  42. Heber, U., Edelmann, H., Napiwotzki, R., Altmann, M., & Scholz, R. D. 2008b, A&A, 483, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Heber, U., Irrgang, A., & Schaffenroth, J. 2018, Open Astron., 27, 35 [Google Scholar]
  44. Henden, A. A., Levine, S., Terrell, D., & Welch, D. L. 2015, Am. Astron. Soc. Meeting Abstracts, 225, 336.16 [NASA ADS] [Google Scholar]
  45. Hewett, P. C., Warren, S. J., Leggett, S. K., & Hodgkin, S. T. 2006, MNRAS, 367, 454 [NASA ADS] [CrossRef] [Google Scholar]
  46. Hills, J. G. 1988, Nature, 331, 687 [Google Scholar]
  47. Holberg, J. B., & Bergeron, P. 2006, AJ, 132, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Hoogerwerf, R., de Bruijne, J. H. J., & de Zeeuw, P. T. 2001, A&A, 365, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Irrgang, A., Przybilla, N., Heber, U., Nieva, M. F., & Schuh, S. 2010, ApJ, 711, 138 [NASA ADS] [CrossRef] [Google Scholar]
  51. Irrgang, A., Wilcox, B., Tucker, E., & Schiefelbein, L. 2013, A&A, 549, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Irrgang, A., Przybilla, N., Heber, U., et al. 2014, A&A, 565, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Irrgang, A., Kreuzer, S., & Heber, U. 2018a, A&A, 620, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Irrgang, A., Kreuzer, S., Heber, U., & Brown, W. 2018b, A&A, 615, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Irrgang, A., Geier, S., Heber, U., Kupfer, T., & Fürst, F. 2019, A&A, 628, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Jarrett, T. H., Cohen, M., Masci, F., et al. 2011, ApJ, 735, 112 [Google Scholar]
  57. Kenyon, S. J., Bromley, B. C., Brown, W. R., & Geller, M. J. 2018, ApJ, 864, 130 [CrossRef] [Google Scholar]
  58. Kilkenny, D. 1987, MNRAS, 228, 713 [NASA ADS] [CrossRef] [Google Scholar]
  59. Kilkenny, D. 1989, MNRAS, 238, 955 [NASA ADS] [CrossRef] [Google Scholar]
  60. Koester, D. 2010, Mem. Soc. Astron. It., 81, 921 [NASA ADS] [Google Scholar]
  61. Koposov, S. E., Boubert, D., Li, T. S., et al. 2020, MNRAS, 491, 2465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Kreuzer, S., Irrgang, A., & Heber, U. 2020, A&A, 637, A53 [CrossRef] [EDP Sciences] [Google Scholar]
  63. Kurucz, R. L. 1993, SYNTHE Spectrum Synthesis Programs and Line Data [Google Scholar]
  64. Kurucz, R. L. 1996, in Status of the ATLAS 12 Opacity Sampling Program and of New Programs for Rosseland and for Distribution Function Opacity, eds. S. J. Adelman, F. Kupka, & W. W. Weiss, ASP Conf. Ser., 108, 160 [NASA ADS] [Google Scholar]
  65. Lindegren, L. 2018, Re-normalising the astrometric chi-square in Gaia DR2, Tech. Rep. GAIA-C3-TN-LU-LL-124-01 (Lund, Sweden: Lund Observatory) [Google Scholar]
  66. Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Maíz Apellániz, J., & Weiler, M. 2018, A&A, 619, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Maíz Apellániz, J., Pantaleoni González, M., Barbá, R. H., et al. 2018, A&A, 616, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Massey, P. 1997, A User’s Guide to CCD Reductions with IRAF [Google Scholar]
  71. Massey, P., Valdes, F., & Barnes, J. 1992, A User’s Guide to Reducing Slit Spectra with IRAF [Google Scholar]
  72. McMahon, R. G., Banerji, M., Gonzalez, E., et al. 2013, Messenger, 154, 35 [Google Scholar]
  73. Michaud, G., Richer, J., & Richard, O. 2011, A&A, 529, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Moehler, S., Heber, U., & Dreizler, S. 1994, A&A, 282, L29 [Google Scholar]
  75. Monari, G., Famaey, B., Carrillo, I., et al. 2018, A&A, 616, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Moyano Loyola, G. R. I., & Hurley, J. R. 2013, MNRAS, 434, 2509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Napiwotzki, R., Karl, C. A., Lisker, T., et al. 2020, A&A, 638, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Ochsenbein, F. 2019, The VizieR Database of Astronomical Catalogues [Google Scholar]
  79. Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Oh, S., & Kroupa, P. 2016, A&A, 590, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Ortiz, R., Malacarne, M., Wilhelm, R., et al. 2007, AJ, 134, 1183 [NASA ADS] [CrossRef] [Google Scholar]
  82. Pan, K.-C., Ricker, P. M., & Taam, R. E. 2012, ApJ, 750, 151 [NASA ADS] [CrossRef] [Google Scholar]
  83. Perets, H. B., & Šubr, L. 2012, ApJ, 751, 133 [NASA ADS] [CrossRef] [Google Scholar]
  84. Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
  85. Portegies Zwart, S. F. 2000, ApJ, 544, 437 [NASA ADS] [CrossRef] [Google Scholar]
  86. Poveda, A., Ruiz, J., & Allen, C. 1967, Boletin de los Observatorios Tonantzintla y Tacubaya, 4, 86 [Google Scholar]
  87. Przybilla, N., Fernanda Nieva, M., Heber, U., & Butler, K. 2008, ApJ, 684, L103 [Google Scholar]
  88. Przybilla, N., Nieva, M.-F., & Butler, K. 2011, J. Phys. Conf. Ser., 328, 012015 [NASA ADS] [CrossRef] [Google Scholar]
  89. Raddi, R., Hollands, M. A., Gänsicke, B. T., et al. 2018, MNRAS, 479, L96 [NASA ADS] [CrossRef] [Google Scholar]
  90. Raddi, R., Hollands, M. A., Koester, D., et al. 2019, MNRAS, 489, 1489 [Google Scholar]
  91. Renzo, M., Zapartas, E., de Mink, S. E., et al. 2019, A&A, 624, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Saffer, R. A., Keenan, F. P., Hambly, N. C., Dufton, P. L., & Liebert, J. 1997, ApJ, 491, 172 [NASA ADS] [CrossRef] [Google Scholar]
  93. Schlafly, E. F., Meisner, A. M., & Green, G. M. 2019, ApJS, 240, 30 [Google Scholar]
  94. Schneider, F. R. N., Izzard, R. G., Langer, N., & de Mink, S. E. 2015, ApJ, 805, 20 [Google Scholar]
  95. Schönberner, D. 1978, A&A, 70, 451 [NASA ADS] [Google Scholar]
  96. Shen, K. J., Boubert, D., Gänsicke, B. T., et al. 2018, ApJ, 865, 15 [Google Scholar]
  97. Silva, M. D. V., & Napiwotzki, R. 2011, MNRAS, 411, 2596 [NASA ADS] [CrossRef] [Google Scholar]
  98. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  99. Sweigart, A. V. 2002, Highlights Astron., 12, 292 [NASA ADS] [CrossRef] [Google Scholar]
  100. Tauris, T. M. 2015, MNRAS, 448, L6 [Google Scholar]
  101. Taylor, M. B. 2006, in STILTS - A Package for Command-Line Processing of Tabular Data, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 666 [NASA ADS] [Google Scholar]
  102. Tody, D. 1986, in The IRAF Data Reduction and Analysis System, ed. D. L. Crawford, SPIE Conf. Ser., 627, 733 [NASA ADS] [Google Scholar]
  103. Tody, D. 1993, in IRAF in the Nineties, eds. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 173 [NASA ADS] [Google Scholar]
  104. Tonry, J. L., Stubbs, C. W., Lykke, K. R., et al. 2012, ApJ, 750, 99 [Google Scholar]
  105. Wall, R. E., Kilic, M., Bergeron, P., et al. 2019, MNRAS, 489, 5046 [NASA ADS] [CrossRef] [Google Scholar]
  106. Wolf, C., Onken, C. A., Luvaul, L. C., et al. 2018, PASA, 35, e010 [Google Scholar]
  107. Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]

Appendix A: Gaia archive query

We performed the following query via the online service offered by the Astronomisches Rechen-Institut of the Heidelberg University2:

SELECT *
FROM gaiadr2.gaia_source
WHERE parallax_error/parallax<=0.3
AND parallax > 0
AND phot_g_mean_mag + 5 -
5*log10(1000/parallax)<= 3.7
AND ABS(b)>=15 AND bp_rp<=0.05
AND phot_bp_rp_excess_factor
<= 1.3 + 0.06*power(bp_rp,2)
AND phot_bp_rp_excess_factor
>= 1.0 + 0.015*power(bp_rp,2)
AND visibility_periods_used >= 8
AND phot_g_mean_flux_over_error >= 50
AND phot_bp_mean_flux_over_error >= 20
AND phot_rp_mean_flux_over_error >= 20
AND ruwe <= 1.4

In addition, we filtered the data with the prescription of Eq. (1).

All Tables

Table 1.

Gaia DR2 data for the observed 48 targets.

In the text
Table 2.

Spectroscopic parameters of the sample derived from model spectra, as appropriate for their classification (MS or BHB candidate, respectively).

In the text
Table 3.

Physical parameters of the MS candidates.

In the text
Table 4.

Physical parameters of BHB and post-EHB candidates computed adopting the atmospheric parameters derived from metal deficient atmospheric models and a mass of M = 0.5 ± 0.1 M⊙.

In the text
Table 5.

Orbital parameters of our MS candidates.

In the text

All Figures

thumbnail Fig. 1.

Gaia Hertzsprung-Russell diagram of candidate blue stars at high Galactic latitudes (gray cross symbols). The observed targets are shown as large circles. Solid curves represent the zero-age and terminal-age MS, while the evolutionary tracks for representative initial masses are plotted as dashed curves (Choi et al. 2016). The light-blue strip represents the horizontal branch (Dorman 1992). The reddening vector and typical error bars of the observed targets are displayed at the top edge of the figure.
In the text
thumbnail Fig. 2.

Relative parallax uncertainties and tangential velocities plotted against parallax-based distances in the top and bottom panels, respectively. The early-type star candidates are marked by cross symbols, while the observed targets are represented by circles with error bars.
In the text
thumbnail Fig. 3.

On-sky distribution of Gaia-selected candidate blue stars at high Galactic latitude (gray “+” symbols). The 48 observed targets (circles) and known MS runaway stars (red “x” symbols; Silva & Napiwotzki 2011) are also shown.
In the text
thumbnail Fig. 4.

Examples for SED fits, from top left to bottom right: the MS candidates 0259−1705, 1900−7033, 2207−4329, and 2259−4931; the BHB candidate 1851−5036; and the binary 1944−4628. In each plot, the top panels show the measurements (color-coded by photometric system) as well as the best-fitting model spectra (gray), while the bottom panels show the error-normalized best-fit residuals, χ = (Oi − Mi)/σi, for each band-pass. The object 1944−4628 requires a composite SED fit, which is the combination of a Teff ≈ 24 400 K and a Teff ≈ 5900 K component (blue and red curve, respectively).
In the text
thumbnail Fig. 5.

Comparisons between photometric Teff, measured via SED fitting, and spectroscopic Teff. The result for MS (top left panel) and BHB models (top right panel) are shown. The dashed lines represent the equality curves. The residuals are displayed as a function of photometric Teff in the lower panels. The gray-shaded area represents the 4% systematic uncertainty assumed for the spectroscopic results.
In the text
thumbnail Fig. 6.

Observed spectra, sorted by decreasing Teff.
In the text
thumbnail Fig. 7.

Examples of spectroscopic best-fits for four MS candidates (Sect. 4.4) with error-normalized residuals; from top left to bottom right: 1900−7033, 0259−1705, 2207−4329, and 2259−4931. The normalized spectra and the best-fit solar-metallicity models are shown in black and red, respectively. Two top panels: ADS models, while the bottom ones are obtained from the ATLAS12/SYNTHE grid. The H and He lines are labeled at the corresponding wavelengths. The Ca II lines were masked out during the fitting procedure due to possible interstellar contamination, which is recognizable in the spectrum of 1900−7033; masked regions are plotted using lighter colors.
In the text
thumbnail Fig. 8.

Kiel diagrams showing the atmospheric parameters of the observed stars as determined via the spectroscopic best-fit with model spectra representing MS and BHB stars (top and bottom panels, respectively). Top panel: evolutionary tracks for rotating MS stars are plotted in black (Ekström et al. 2012). The initial masses of each model are noted below the zero-age MS (thick solid curve), while the stellar ages for selected evolutionary points along the tracks are given in mega years. Bottom panel: the horizontal branch is represented by the gray-shaded area, and the evolutionary tracks for post-horizontal branch stars of different masses are drawn as solid curves (Dorman 1992).
In the text
thumbnail Fig. 9.

Comparisons between spectrophotometric distances and three different parallax-based distance estimates. Upper panels: MS candidates (blue-colored symbols) are identified via the 1σ agreement, which is represented by the dashed equality line and the gray-shaded area. Lower panels: same as the upper panels, but BHB candidates are represented by orange filled symbols. We note that three stars are classified both as MS and BHB candidates, hence they are color-coded in both the upper and lower panels.
In the text
thumbnail Fig. 10.

Theoretical Hertzsprung-Russell diagrams. Top panel: our candidate MS stars over-plotted on the evolutionary tracks of Ekström et al. (2012) for rotating stars. The masses of each model are plotted in correspondence of the zero-age MS. The luminosities were derived by adopting the spectrophotometric distances. Bottom panel: our candidate BHB stars over-plotted on the horizontal branch that is represented by a gray-shaded area and the evolutionary tracks for post-horizontal branch stars of given masses (Dorman 1992; Dorman et al. 1993). We note that three stars are classified both as MS and BHB candidates, hence they are featured in both panels with the appropriate parameters.
In the text
thumbnail Fig. 11.

Positions of the program stars in the Toomre diagram. The quantity V is the velocity component in the direction of Galactic rotation, U is towards the Galactic center, and W is perpendicular to the Galactic plane. The local standard of rest (LSR) is marked by a yellow asterisk. The dashed circles centered around the LSR represent boundaries for three restframe velocities. The observed stars are plotted with error bars. Blue symbols correspond to MS candidates, while orange symbols are used for the BHB stars. All the targets identified in Sect. 2 are plotted as gray crosses, adopting vrad = 0 km s−1.
In the text
thumbnail Fig. 12.

Comparison of flight times and stellar ages for the runaway MS candidates. The solid line represents the identity curve. The dashed lines mark the ranges where τevo = 2,  5, and 10 times τflight.
In the text
thumbnail Fig. 13.

Ejection velocities of runaway stars are plotted against their masses. Our 12 MS runaway candidates are represented by blue circles with error bars; it is important to note that two stars have very similar masses and, thus, overlapping symbols. The runaway stars studied by Silva & Napiwotzki (2011) are plotted as squares. More recently discovered high-velocity runaway stars as listed by Irrgang et al. (2019) are plotted as triangles, with masses updated from Kreuzer et al. (2020) when available.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.