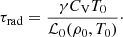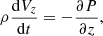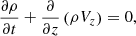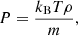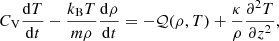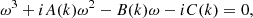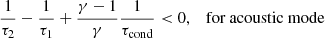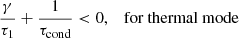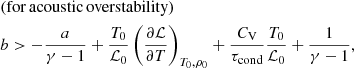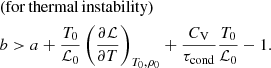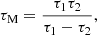EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 644 (December 2020) A&A, 644 (2020) A33 Full HTML
Free Access
Issue
A&A
Volume 644, December 2020
Article Number A33
Number of page(s) 6
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202039095
Published online 25 November 2020

© ESO 2020

1. Introduction

The existence of the one million Kelvin solar corona requires a continuous supply of energy to compensate for energy losses by optically thin radiation and field-aligned thermal conduction down to the chromosphere (De Moortel & Browning 2015). Otherwise, without a re-supply of energy by some heating mechanism, radiative losses acting alone would cause the corona to cool down on the timescale

τ rad = γ C V T 0 L 0 ( ρ 0 , T 0 ) · $$ \begin{aligned} \tau _{\rm rad} = \frac{\gamma C_{\rm V}T_0}{\mathcal{L} _0(\rho _0, T_0)}\cdot \end{aligned} $$(1)

In this equation, γ is the adiabatic index, CV is the specific heat capacity (see Table 1), and ℒ0 is the radiative loss function depending on temperature, T0 and density, ρ0 and measured in W kg−1 in this work. Estimations show that for typical coronal conditions the radiative cooling timescale τrad (1) ranges approximately from 103 s to 104 s (De Moortel & Hood 2004; Aschwanden & Terradas 2008; Provornikova et al. 2018), that is substantially shorter than the observed lifetime of typical coronal structures. Revealing the nature of such a mechanism for retaining the hot coronal temperature constitutes the long-standing coronal heating problem. In this work, we determine empirical constraints on the coronal heating function by the observed behaviour of slow magnetoacoustic waves.

Table 1.

Typical parameters of the coronal plasma and slow waves used for the analysis.

There is abundant evidence of the existence of slow magnetoacoustic waves in the corona (De Moortel 2009; Banerjee et al. 2011; Wang 2011; De Moortel & Nakariakov 2012), which almost always show rapid damping. In particular, rapidly damped slow waves are observed in hot and warm coronal loops (Wang 2011, 2016; Nakariakov et al. 2019), and in coronal holes (Banerjee et al. 2011; Banerjee & Krishna Prasad 2016). Thus, thermodynamical properties of those plasma structures, including heating, must lead to wave behaviour that is consistent with observations. Coronal slow waves are sensitive to effects of thermal conduction, optically thin radiation, and compressive viscosity (De Moortel & Hood 2003, 2004; Selwa et al. 2005; Krishna Prasad et al. 2014; Mandal et al. 2016a; Bahari & Shahhosaini 2018). Historically, thermal conduction is invoked as the dominant mechanism for the rapid damping of coronal slow waves (Ofman & Wang 2002; De Moortel & Hood 2003). Yet observations measuring a change in the effective polytropic index with temperature show that in some cases thermal conduction alone is insufficient to describe the damping (Owen et al. 2009; Wang et al. 2015; Krishna Prasad et al. 2018). The measured phase shifts between density and temperature perturbations in a slow wave are different to the phase shift predicted to arise from thermal conduction in Owen et al. (2009). This discrepancy is supported by the apparent lack of the decrease in damping length with temperature, as would be expected for thermal conduction (Krishna Prasad et al. 2019). Combined with different dependences of the damping time upon wave period, observed in warm coronal loops and cooler plumes (Krishna Prasad et al. 2014), and at different heights (Gupta 2014), this demonstrates the need to account for an additional damping mechanism.

For compressive waves, the coronal plasma that appears to be in thermal equilibrium formed by the balance of energy losses and gains acts as an active medium. That is to say, the wave can gain energy from the medium. In other words, the wave is subject to a back-reaction of the modification of the cooling and heating rates by the density and temperature perturbations in the wave, that is, a wave-induced heating/cooling misbalance. This effect can cause enhanced damping or amplification of slow waves (Nakariakov et al. 2000, 2017; Carbonell et al. 2006; Kumar et al. 2016; Perelomova 2018; Claes & Keppens 2019; Kolotkov et al. 2019). Characteristic timescales of the thermal misbalance lead to wave dispersion (Ibanez et al. 1993; Zavershinskii et al. 2019). The specific behaviour depends on the equilibrium parameters and derivatives of the combined heating/cooling function with respect to density and temperature (in the linear regime). In addition to a slow wave, there exists also a non-propagating entropy mode. This mode causes thermal misbalance and is affected by the back-reaction too, in particular leading to radiative instability (Field 1965). When physical conditions for such a thermal instability are fulfilled, rapid condensations of the coronal plasma and the phenomenon of coronal rain may occur (Dahlburg & Mariska 1988; Antolin et al. 2010).

The importance of the plasma activity depends on the ratio of the characteristic times of thermal misbalance and wave oscillation periods. This question has so far received only limited attention (cf. the previous works by Kumar et al. 2016; Nakariakov et al. 2017; Kolotkov et al. 2019; Zavershinskii et al. 2019, on thermal misbalance). In this work, we demonstrate that characteristic timescales of thermal misbalance are about typical periods of slow magnetoacoustic waves observed in various coronal plasma structures, such as polar plumes and quiescent and flaring loops. As such, the dynamics of slow waves is proved to be highly sensitive to the discussed thermodynamic activity of the corona, including thermodynamic properties of the enigmatic heating mechanisms. We perform quantitative assessment of the acoustic and thermal instability criteria in a broad range of coronal conditions and for various heating models. We identify heating models in which the plasma is either stable to thermal instability and slow magnetoacoustic over-stability or the growth rate is relatively low, thereby allowing for the existence of long-lived plasma structures in the corona and causing the rapid damping of slow magnetoacoustic waves observed in the corona.

2. Governing equations and dispersion relation

In the infinite magnetic field approximation with plasma β → 0, slow magnetoacoustic waves propagate strictly along the field and their dynamics in a heated plasma is governed by the set of one-dimensional equations,

ρ d V z d t = − ∂ P ∂ z , $$ \begin{aligned}&\rho \frac{\mathrm{d} V_{z}}{\mathrm{d} t} = -\frac{\partial P}{\partial z},\end{aligned} $$(2)

∂ ρ ∂ t + ∂ ∂ z ( ρ V z ) = 0 , $$ \begin{aligned}&\frac{\partial \rho }{\partial t} + \frac{\partial }{\partial z} \left(\rho V_{z} \right) = 0,\end{aligned} $$(3)

P = k B T ρ m , $$ \begin{aligned}&P=\frac{k_{\rm B} T \rho }{m},\end{aligned} $$(4)

C V d T d t − k B T m ρ d ρ d t = − Q ( ρ , T ) + κ ρ ∂ 2 T ∂ z 2 , $$ \begin{aligned}&C_{\rm V}\frac{\mathrm{d}T}{\mathrm{d}t} - \frac{k_{\rm B}T}{m\rho }\frac{\mathrm{d}\rho }{\mathrm{d}t}=-\mathcal{Q} (\rho ,T)+\frac{\kappa }{\rho }\frac{\partial ^2T}{\partial z^2}, \end{aligned} $$(5)

where ρ, T, and P are the density, temperature, and pressure, respectively; Vz is the velocity along the z-axis directed along the magnetic field. Equilibrium parameters and constant quantities are given in Table 1, and d/dt stands for the total derivative. Below, we apply this model to both standing and propagating slow waves in coronal loops. For standing slow-mode oscillations observed by Solar Ultraviolet Measurements of Emitted Radiation onboard Solar and Heliospheric Observatory (SOHO/SUMER) in hot flaring loops, the stratification scale height is large enough to allow us to neglect gravitational stratification (e.g. Wang et al. 2018; Wang & Ofman 2019). In the quiescent one million Kelvin loops, however, the loop height is comparable to the gravitational scale height, but the propagating slow waves damp near to the very bottom of the loop (e.g. McEwan & de Moortel 2006), where the effects of stratification are not yet fully developed. We also neglect the effect of viscosity because in terms of regulating the coronal thermal equilibrium, thermal conduction is of greater importance than viscosity (see e.g. De Moortel & Hood 2003); thus, we choose to include thermal conduction with the expectation that viscosity plays a less influential role. Also, to keep the application of this seismological approach as simple and generic as possible, the effects of anomalous plasma transport coefficients (e.g. Wang et al. 2015) and plasma flows are not considered in this work.

Terms on the right-hand side of energy Eq. (5) represent non-adiabatic processes, which are some unspecified heating ℋ(ρ, T) and optically thin radiative cooling ℒ(ρ, T), combined in the net heat/loss function 𝒬(ρ, T) = ℒ − ℋ; and the field-aligned thermal conduction with the coefficient κ. In the equilibrium, 𝒬0 = 0 and the plasma temperature is uniform. The assumption of the isothermal equilibrium along the coronal part of the loop is, on one hand, motivated by observations (e.g. Gupta et al. 2015, 2019; Mandal et al. 2016b; Nisticò et al. 2017); on the other hand, this assumption is consistent with a common approach in theoretical modelling of coronal loop oscillations (e.g. Selwa et al. 2005; Owen et al. 2009; Mandal et al. 2016a; Wang et al. 2018; Wang & Ofman 2019). Hence, in the equilibrium, the second term on the right-hand side of Eq. (5) is zero. Thus, in addition to the perturbation of the mechanical equilibrium provided by the force balance, we consider a perturbation of the thermal equilibrium: that is allow both heating and cooling processes to be perturbed by the wave. The latter causes an additional mechanism for the energy exchange between the plasma and the wave, that is the heating/cooling misbalance.

In the linear regime and assuming the harmonic dependence of the wave-perturbed plasma parameters upon time and spatial coordinate in Eqs. (2)–(5), the relation between the cyclic frequency ω and wavenumber k, written in terms of the characteristic timescales of the considered non-adiabatic processes, is

ω 3 + i A ( k ) ω 2 − B ( k ) ω − i C ( k ) = 0 , $$ \begin{aligned} \omega ^3 + iA(k)\omega ^2 - B(k)\omega - iC(k) = 0, \end{aligned} $$(6)

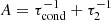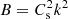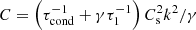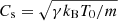with A = τ cond − 1 + τ 2 − 1 $ A={\tau_{\mathrm{cond}}^{-1}}+{\tau_2^{-1}} $, B= C s 2 k 2 $ B=C_{\rm s}^2k^2 $, C = ( τ cond − 1 + γ τ 1 − 1 ) C s 2 k 2 / γ $ C = \left(\tau_{\mathrm{cond}}^{-1}+{\gamma}{\tau_1^{-1}}\right) C_{\mathrm{s}}^2k^2/\gamma $, where C s = γ k B T 0 / m $ C_{\mathrm{s}}=\sqrt{\gamma k_{\mathrm{B}}T_0/m} $ is the sound speed and τcond = ρ0CVk−2/κ is the characteristic time of the wavelength-dependent thermal conduction. Likewise, τ1 = γCV/[𝒬T−(ρ0/T0)𝒬ρ] and τ2 = CV/𝒬T in Eq. (6) are the timescales describing the rates of change of the perturbed heat/loss function 𝒬 with plasma density 𝒬ρ ≡ (∂𝒬/∂ρ)T and temperature 𝒬T ≡ (∂𝒬/∂T)ρ, respectively. This dispersion relation was derived in Kolotkov et al. (2019) and Zavershinskii et al. (2019). Because it is the third-order polynomial in ω, dispersion relation (6) describes two slow waves coupled with a thermal (entropy-related) mode.

3. Stability of acoustic and thermal modes for varying heating models

In the infinite magnetic field approximation, slow and thermal modes become unstable and gain energy from the plasma if (Field 1965; Zavershinskii et al. 2019; Kolotkov et al. 2019)

1 τ 2 − 1 τ 1 + γ − 1 γ 1 τ cond < 0 , for acoustic mode $$ \begin{aligned}&\frac{1}{\tau _2}-\frac{1}{\tau _1}+\frac{\gamma -1}{\gamma }\frac{1}{\tau _{\rm cond}} < 0,&\text {for}\text { acoustic}\text { mode} \end{aligned} $$(7)

γ τ 1 + 1 τ cond < 0 , for thermal mode $$ \begin{aligned}&\frac{\gamma }{\tau _1}+\frac{1}{\tau _{\rm cond}} < 0,&\text {for thermal mode} \end{aligned} $$(8)

where τcond, τ1, and τ2 are the characteristic wavelength-dependent time of the field-aligned thermal conduction, and wavelength-independent timescales of the heating/cooling misbalance, determined in Eq. (6). The thermal conduction time τcond is essentially positive and therefore always contributes to damping. In contrast, the values of τ1, 2, as well as their difference, can be either positive or negative depending on the equilibrium plasma parameters and properties of the heating and cooling functions. In general, negative characteristic times correspond to the perturbation growing in time. We discriminated between the overstable regime, which refers to an oscillation with a growing amplitude, and the unstable regime, in which the perturbation grows aperiodically. Table 2 summarises qualitative behaviours of the thermal and acoustic modes for all six possible combinations of positive and negative τ1, 2 and τ1 − τ2.

Table 2.

Possible regimes of the thermal and acoustic modes in the corona, determined by Eqs. (7) and (8).

We synthesised the coronal optically thin radiation function ℒ(ρ, T) from CHIANTI atomic database v. 9.0.1 (Dere et al. 1997, 2019) for the ranges of densities and temperatures shown in Table 1. The coronal heating function is parametrised as ℋ(ρ, T) = hρaTb, where the coefficient h is determined from the initial thermal equilibrium condition, 𝒬0 = 0, as 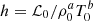h= L 0 / ρ 0 a T 0 b $ h=\mathcal{L}_0/\rho_0^aT_0^b $; and the power indices a and b are treated as free parameters. In this parametrisation, the dependence of the heating function on the magnetic field strength is omitted, as it was shown to have no effect on the slow wave dynamics in the zero-β limit considered in our work (see Eqs. (27) and (28) in Nakariakov et al. 2017). Similar forms of the heating model were considered in, for example Dahlburg & Mariska (1988), Ibanez et al. (1993), Mandrini et al. (2000), and Carbonell et al. (2006). We note the difference in the units of the heating function used in this work [W kg−1] (see also Field 1965) and in Ibanez et al. (1993) [W m−3], leading to the difference in the density index a by 1. This allowed us to rewrite conditions (7) and (8) in terms of the heating power indices a and b as

( for acoustic overstability ) b > − a γ − 1 + T 0 L 0 ( ∂ L ∂ T ) T 0 , ρ 0 + C V τ cond T 0 L 0 + 1 γ − 1 , $$ \begin{aligned}&\mathrm{ (for\,acoustic\,overstability)}\\&b > -\frac{a}{\gamma -1} + \frac{T_0}{\mathcal{L} _0}\left(\frac{\partial \mathcal{L} }{\partial T}\right)_{T_0,\rho _0} + \frac{C_{\rm V}}{\tau _{\rm cond}}\frac{T_0}{\mathcal{L} _0} +\frac{1}{\gamma -1}, \end{aligned} $$(9)

( for thermal instability ) b > a + T 0 L 0 ( ∂ L ∂ T ) T 0 , ρ 0 + C V τ cond T 0 L 0 − 1 . $$ \begin{aligned} &\mathrm {(for\,thermal\,instability)} \\&b > a + \frac{T_0}{\mathcal{L} _0}\left(\frac{\partial \mathcal{L} }{\partial T}\right)_{T_0,\rho _0} + \frac{C_{\rm V}}{\tau _{\rm cond}}\frac{T_0}{\mathcal{L} _0} - 1.\nonumber \end{aligned} $$(10)

These conditions allowed us to delineate different coronal heating models (i.e. values of a and b), for which slow magnetoacoustic and thermal modes either damp or grow, which could be directly verified in observations.

First, we analysed Eqs. (9) and (10) in the regime of suppressed thermal conduction, taking τcond → ∞ (see e.g. Wang et al. 2015, 2018). We obtained instability thresholds for a broad range of coronal plasma densities and temperatures (Table 1) typical for hot jets, plumes, and interplume regions in coronal holes (Cranmer 2009; Wilhelm et al. 2011), warm quiescent coronal loops, and hot and dense flaring loops (Reale 2014). The thresholds are manifested as two intersecting families of parallel straight lines with the slopes of −(γ − 1)−1 and 1 in the parametric plane (a, b). From both sets, we picked the outermost boundaries that allowed us to identify intervals of a and b for which thermal and acoustic modes appear in different regimes (Fig. 1, left panel).

thumbnail Fig. 1.

Power indices a and b in the parametrisation of the coronal heating function as ℋ(ρ, T) ∝ ρaTb, determining stability of acoustic and thermal modes with (right panel) and without (left panel) thermal conduction. The red triangles show the values of a and b for the heating models from Ibanez et al. (1993). The green triangle shows the heating model used as an example in Fig. 2.

In the case with a finite Spitzer thermal conductivity, for a characteristic wavelength of the perturbation λ ≃ 360 Mm (typical of standing slow waves; Wang 2011), those critical intervals get softened (Fig. 1, right panel), and the regions of omnipresent thermal and acoustic instabilities disappear. The increase in λ weakens the effect of thermal conductivity. However, for all plausible values of λ extending up to 2000 Mm, no change to the behaviour of the acoustic and thermal modes shown in the right-hand panel in Fig. 1 was detected. Likewise, the effect of the thermal conductivity strengthens for shorter λ (typical of propagating slow waves in quiescent loops, for example), pushing the regions of omnipresent instabilities further away from the considered intervals of a and b. Thus, both modes are found to damp through the whole considered intervals of plasma densities and temperatures for the values of a and b in the region outlined by a triangle with approximate vertices ( − 2.5, −5), (1, −1.5), and (3.5, −5). In other words, for all heating models with a and b in this region, the slow mode is seen in observations as a damped wave in a thermally stable plasma. For example, for the heating models suggested by Rosner et al. (1978), Ibanez et al. (1993) – including Ohmic heating (a = 0, b = 1), constant heating per unit volume (a = −1, b = 0) and mass (a = 0, b = 0), and heating by Alfvén waves via mode conversion (a = 1/6, b = 7/6) and anomalous conduction damping (a = −0.5, b = −0.5) – the thermal mode is always unstable in the case of suppressed conduction; there are combinations of coronal densities and temperatures for which the thermal mode can be either stable or unstable in the case of finite conduction (see Fig. 1). Likewise, the models a = −1, b = 0; a = −0.5, b = −0.5; and a = 0, b = 0 always cause damping of the acoustic mode in the regime of finite conductivity, while the other two models lead to acoustic over-stability for certain densities and temperatures.

4. Comparison of the thermal misbalance timescales to observed wave periods

We can combine the timescales τ1 and τ2 in Eq. (7) into a single misbalance time

τ M = τ 1 τ 2 τ 1 − τ 2 , $$ \begin{aligned} \tau _{\rm M}=\frac{\tau _1\tau _2}{\tau _1-\tau _2}, \end{aligned} $$(11)

and estimate it for various combinations of plasma density and temperature (Fig. 2) and for varying parameters of the heating function (Fig. 3).

thumbnail Fig. 2.

Characteristic thermal misbalance time τM (11) for typical coronal densities and temperatures and a fixed heating model a = 0.5 and b = −3.5, for which both acoustic and thermal modes are stable over the entire intervals of plasma densities and temperatures considered (see Fig. 1). The colour scheme is adjusted so that the values of τM from about 10 min to 100 min are shown in green. The blue symbols illustrate typical combinations of coronal plasma density and temperature in hot and dense loops in active regions (star), warm and less dense quiescent loops (circle), and polar plumes (box).

thumbnail Fig. 3.

Estimations of τM (the black contours, in minutes) for varying heating models (power indices a and b) in warm and less dense quiescent loops (left), polar plumes (middle), and hot and dense loops (right). For specific combinations of the plasma density and temperature for these cases see Sect. 4. The colour schemes in all panels show the ratio of τM to typical periods τ of slow waves observed in those structures. The red solid lines show the values of a and b, above which the thermal mode becomes unstable. The red dashed lines indicate the intervals for which the thermal mode instability growth time is up to 5 times longer than the corresponding acoustic period τ.

Figure 2 shows variation of the misbalance time τM (11) with plasma density and temperature for a fixed heating model a = 0.5 and b = −3.5. In this illustrative example both the acoustic and thermal modes are found to damp for all considered plasma densities and temperatures (see Fig. 1). As shown by Fig. 2, the time τM varies from a few minutes to several tens of minutes for typical combinations of the plasma density and temperature. In particular, the value of τM is similar, approximately several minutes, both in hot and dense plasmas (e.g. with T0 ≃ 10 MK and n0 ≃ 1010 cm−3) and in a cooler and less dense plasma (e.g. with T0 ≃ 1 MK and n0 ≃ 109 cm−3). These values of τM are similar to the slow wave periods detected in typical coronal plasma structures (see Table 1). In contrast, in very dense and cool or very hot and rarified plasmas, τM is either very short (< 0.5 min) or long (> 500 min).

For the analysis of the dependence of τM on the heating function power indices a and b, we chose three typical combinations of the plasma density and temperature, corresponding to typical long-lived (i.e. apparently stable to instabilities), plasma structures supporting slow waves: hot and dense loops in active regions (T0 = 6 MK, n0 = 1010 cm−3), warm and less dense quiescent loops (T0 = 1 MK, n0 = 1.5 × 109 cm−3), and plumes (T0 = 1 MK, n0 = 0.5 × 109 cm−3). Slow waves observed in those structures have typical periods of several minutes and damping times comparable to the oscillation periods (see also Table 1).

Values of the misbalance time τM and its ratio to the typical wave periods τ detected in corresponding plasma structures are shown in Fig. 3. According to Eqs. (7) and (9), the acoustic mode damps for τM >  0 and grows for τM <  0, which corresponds to two distinct regions in the parametric plane (a, b). We also used Eq. (10) to obtain the values of a and b for which the heating/cooling misbalance leads to thermal mode instability. Moreover, we solved the full dispersion relation (6) numerically to obtain the intervals of a and b for which the growth time of the thermal-mode instability is long enough (e.g. five times longer than the acoustic period τ) to have just a mild effect on the dynamics of the acoustic mode. The latter could be referred to as a soft stability of thermal mode. Accounting for all these conditions in Fig. 3, we obtain that for a reasonable choice of the heating model, that is for −1 ≲ a ≲ 0.5 and −1.5 ≲ b ≲ −0.5 (for propagating slow waves in loops and plumes), and for −2 ≲ a ≲ 0 and −1.5 ≲ b ≲ −0.5 (for standing SUMER-type oscillations) the thermal mode is in the stable or soft-stable regime. Also in these parametric regions of a and b, the values of the misbalance time τM are either equal to or up to a factor of two longer than the acoustic wave period τ, indicating a strong effect of the heating/cooling misbalance on the wave dynamics in these regimes. For example as shown by Fig. 3, the heating model by Alfvén waves via anomalous conduction damping (a = −0.5 and b = −0.5) from Ibanez et al. (1993) appears to cause strong damping, with the damping time ≈τM is about the wave oscillation period, of standing SUMER-type oscillations in flaring loops, while the oscillating loop itself remains soft-stable to the thermal instability. We also note that these estimations of a and b are fully based on the effect of the heating/cooling misbalance and can be softened by finite thermal conductivity and other dissipative processes.

5. Discussion and conclusions

The coronal heating function can be constrained seismologically using observations of damped slow magnetoacoustic waves in long-lived coronal plasma structures. The developed approach is based on the effect of the heating/cooling misbalance, which occurs owing to the violation of the coronal thermal equilibrium between heating and cooling processes by compressive (e.g. slow) magnetoacoustic waves, causing a back-reaction on the waves, which can either attenuate or amplify the wave. The latter leads to acoustic over-stability or thermal instability, which are incompatible with the observed lifetimes of typical thermodynamically stable coronal structures (cf. the phenomenon of catastrophic cooling due to thermal instability; e.g. Dahlburg & Mariska 1988; Antolin et al. 2010).

Parametrising the coronal heating function as ℋ(ρ, T) ∝ ρaTb, we derived and evaluated conditions for the slow magnetoacoustic (acoustic) overstability and thermal instability in the infinite magnetic field approximation, in terms of the power indices a and b (Eqs. (9) and (10)). The heating models outlined by a triangle with approximate vertices ( − 2.5, −5), (1, −1.5), and (3.5, −5) in the parametric plane (a, b) allow for a stable corona (see Fig. 1). In particular, the five heating models from Ibanez et al. (1993) are all shown to be potentially unstable to the thermal mode in the regime of suppressed thermal conduction, and there are certain combinations of coronal plasma densities and temperatures for which some of those heating models can lead to acoustic and thermal stability of coronal structures with finite thermal conduction.

We showed that characteristic times of the thermal misbalance, τ1, 2 (6), and their specific combination τM (11), determined by the dependences of the cooling and heating rates on the plasma parameters perturbed by the wave, are comparable to the slow wave oscillation periods and damping times (about several minutes) typical for the corona, in a broad range of typical coronal plasma temperatures and densities (see Fig. 2). This demonstrates the broad importance and applicability of this effect for probing heating functions in various specific coronal structures. We also note that those misbalance timescales are independent of the amplitudes of the heating ℋ0 and cooling ℒ0 processes in the linear regime and describe how quickly the plasma perturbed by a compressive wave returns to the thermal equilibrium or becomes thermodynamically unstable (cf. the radiative cooling time τrad (1), which depends on ℒ0 and shows how quickly the hot plasma cools down by radiation if for some reason the heating process switches off).

We compared the thermal misbalance timescale τM (11) with observed oscillation periods and damping times of slow waves in quiescent and flaring loops, and plumes in coronal holes. We requested the thermal mode to be either stable or at least to grow at a relatively low rate (soft-stable). We thus obtained that the heating models with −1 ≲ a ≲ 0.5 and −1.5 ≲ b ≲ −0.5 (for propagating slow waves in quiescent loops and polar plumes) and −2 ≲ a ≲ 0 and −1.5 ≲ b ≲ −0.5 (for standing SUMER-type oscillations in flaring loops) can cause a strong damping consistent with observations, where the thermal misbalance timescale τM is about observed slow wave periods (see Fig. 3). The empirically revealed negative values of the parameter b imply that coronal plasma with colder temperatures (at constant density) would require a greater heating rate to be thermally and acoustically stable. The observation of slow magnetoacoustic oscillations in coronal plasma structures with other combinations of the density and temperature would help to improve the estimation of the heating function.

Thus, we demonstrated that the effect of the thermodynamic activity of the corona is strong and crucial for modelling and interpreting observed slow magnetoacoustic waves and has promising seismological implications. It opens up a new perspective for the use of observations of slow waves for inferring thermodynamic parameters of unknown coronal heating mechanisms. Our study is based on a linear analysis in a plasma uniform along the magnetic field. In this regime, the effect of the density non-uniformities generated by the wave itself is neglected as a higher-order effect. Also, the effects of the nonlinear stabilisation of linearly unstable structures, nonlinear instabilities of linearly stable structures, and plasma non-uniformity could be considered as the next step.

Acknowledgments

The work was supported by the STFC consolidated grants ST/P000320/1 and ST/T000252/1. V.M.N. was supported by the Russian Foundation for Basic Research Grant No. 18-29-21016. D.Y.K. was supported by the budgetary funding of Basic Research program No. II.16. CHIANTI is a collaborative project involving George Mason University, the University of Michigan (USA) and the University of Cambridge (UK).

References

  1. Antolin, P., Shibata, K., & Vissers, G. 2010, ApJ, 716, 154 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aschwanden, M. J., & Terradas, J. 2008, ApJ, 686, L127 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bahari, K., & Shahhosaini, N. 2018, MNRAS, 478, 342 [CrossRef] [Google Scholar]
  4. Banerjee, D., & Krishna Prasad, S. 2016, Washington DC American Geophysical Union Geophysical Monograph Series, 216, 419 [NASA ADS] [CrossRef] [Google Scholar]
  5. Banerjee, D., Gupta, G. R., & Teriaca, L. 2011, Space Sci. Rev., 158, 267 [NASA ADS] [CrossRef] [Google Scholar]
  6. Carbonell, M., Terradas, J., Oliver, R., & Ballester, J. L. 2006, A&A, 460, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Claes, N., & Keppens, R. 2019, A&A, 624, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cranmer, S. R. 2009, Liv. Rev. Sol. Phys., 6, 3 [Google Scholar]
  9. Dahlburg, R. B., & Mariska, J. T. 1988, Sol. Phys., 117, 51 [NASA ADS] [CrossRef] [Google Scholar]
  10. De Moortel, I. 2009, Space Sci. Rev., 149, 65 [NASA ADS] [CrossRef] [Google Scholar]
  11. De Moortel, I., & Browning, P. 2015, Phil. Trans. R. Soc. London Ser. A, 373, 20140269 [Google Scholar]
  12. De Moortel, I., & Hood, A. W. 2003, A&A, 408, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. De Moortel, I., & Hood, A. W. 2004, A&A, 415, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. De Moortel, I., & Nakariakov, V. M. 2012, Phil. Trans. R. Soc. London Ser. A, 370, 3193 [Google Scholar]
  15. Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Dere, K. P., Del Zanna, G., Young, P. R., Landi, E., & Sutherland, R. S. 2019, ApJS, 241, 22 [NASA ADS] [CrossRef] [Google Scholar]
  17. Field, G. B. 1965, ApJ, 142, 531 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gupta, G. R. 2014, A&A, 568, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Gupta, G. R., Tripathi, D., & Mason, H. E. 2015, ApJ, 800, 140 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gupta, G. R., Del Zanna, G., & Mason, H. E. 2019, A&A, 627, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Ibanez, S., Miguel, H., Escalona, T., & Orlando, B. 1993, ApJ, 415, 335 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kolotkov, D. Y., Nakariakov, V. M., & Zavershinskii, D. I. 2019, A&A, 628, A133 [CrossRef] [EDP Sciences] [Google Scholar]
  23. Krishna Prasad, S., Banerjee, D., & Van Doorsselaere, T. 2014, ApJ, 789, 118 [NASA ADS] [CrossRef] [Google Scholar]
  24. Krishna Prasad, S., Raes, J. O., Van Doorsselaere, T., Magyar, N., & Jess, D. B. 2018, ApJ, 868, 149 [NASA ADS] [CrossRef] [Google Scholar]
  25. Krishna Prasad, S., Jess, D. B., & Van Doorsselaere, T. 2019, Front. Astron. Space Sci., 6, 57 [CrossRef] [Google Scholar]
  26. Kumar, S., Nakariakov, V. M., & Moon, Y. J. 2016, ApJ, 824, 8 [NASA ADS] [CrossRef] [Google Scholar]
  27. Mandal, S., Magyar, N., Yuan, D., Van Doorsselaere, T., & Banerjee, D. 2016a, ApJ, 820, 13 [NASA ADS] [CrossRef] [Google Scholar]
  28. Mandal, S., Yuan, D., Fang, X., et al. 2016b, ApJ, 828, 72 [NASA ADS] [CrossRef] [Google Scholar]
  29. Mandrini, C. H., Démoulin, P., & Klimchuk, J. A. 2000, ApJ, 530, 999 [NASA ADS] [CrossRef] [Google Scholar]
  30. McEwan, M. P., & de Moortel, I. 2006, A&A, 448, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Nakariakov, V. M., Mendoza-Briceño, C. A., & Ibáñez, S. M. H. 2000, ApJ, 528, 767 [NASA ADS] [CrossRef] [Google Scholar]
  32. Nakariakov, V. M., Afanasyev, A. N., Kumar, S., & Moon, Y. J. 2017, ApJ, 849, 62 [NASA ADS] [CrossRef] [Google Scholar]
  33. Nakariakov, V. M., Kosak, M. K., Kolotkov, D. Y., et al. 2019, ApJ, 874, L1 [Google Scholar]
  34. Nisticò, G., Polito, V., Nakariakov, V. M., & Del Zanna, G. 2017, A&A, 600, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Ofman, L., & Wang, T. 2002, ApJ, 580, L85 [NASA ADS] [CrossRef] [Google Scholar]
  36. Owen, N. R., De Moortel, I., & Hood, A. W. 2009, A&A, 494, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Perelomova, A. 2018, Phys. Plasmas, 25, 042116 [CrossRef] [Google Scholar]
  38. Provornikova, E., Ofman, L., & Wang, T. 2018, Adv. Space Res., 61, 645 [NASA ADS] [CrossRef] [Google Scholar]
  39. Reale, F. 2014, Liv. Rev. Sol. Phys., 11, 4 [Google Scholar]
  40. Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] [Google Scholar]
  41. Selwa, M., Murawski, K., & Solanki, S. K. 2005, A&A, 436, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Wang, T. 2011, Space Sci. Rev., 158, 397 [Google Scholar]
  43. Wang, T. J. 2016, Washington DC American Geophysical Union Geophysical Monograph Series, 216, 395 [NASA ADS] [CrossRef] [Google Scholar]
  44. Wang, T., & Ofman, L. 2019, ApJ, 886, 2 [CrossRef] [Google Scholar]
  45. Wang, T., Ofman, L., Sun, X., Provornikova, E., & Davila, J. M. 2015, ApJ, 811, L13 [NASA ADS] [CrossRef] [Google Scholar]
  46. Wang, T., Ofman, L., Sun, X., Solanki, S. K., & Davila, J. M. 2018, ApJ, 860, 107 [NASA ADS] [CrossRef] [Google Scholar]
  47. Wilhelm, K., Abbo, L., Auchère, F., et al. 2011, A&ARv, 19, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  48. Zavershinskii, D. I., Kolotkov, D. Y., Nakariakov, V. M., Molevich, N. E., & Ryashchikov, D. S. 2019, Phys. Plasmas, 26, 082113 [CrossRef] [Google Scholar]

All Tables

Table 1.

Typical parameters of the coronal plasma and slow waves used for the analysis.

In the text
Table 2.

Possible regimes of the thermal and acoustic modes in the corona, determined by Eqs. (7) and (8).

In the text

All Figures

thumbnail Fig. 1.

Power indices a and b in the parametrisation of the coronal heating function as ℋ(ρ, T) ∝ ρaTb, determining stability of acoustic and thermal modes with (right panel) and without (left panel) thermal conduction. The red triangles show the values of a and b for the heating models from Ibanez et al. (1993). The green triangle shows the heating model used as an example in Fig. 2.
In the text
thumbnail Fig. 2.

Characteristic thermal misbalance time τM (11) for typical coronal densities and temperatures and a fixed heating model a = 0.5 and b = −3.5, for which both acoustic and thermal modes are stable over the entire intervals of plasma densities and temperatures considered (see Fig. 1). The colour scheme is adjusted so that the values of τM from about 10 min to 100 min are shown in green. The blue symbols illustrate typical combinations of coronal plasma density and temperature in hot and dense loops in active regions (star), warm and less dense quiescent loops (circle), and polar plumes (box).
In the text
thumbnail Fig. 3.

Estimations of τM (the black contours, in minutes) for varying heating models (power indices a and b) in warm and less dense quiescent loops (left), polar plumes (middle), and hot and dense loops (right). For specific combinations of the plasma density and temperature for these cases see Sect. 4. The colour schemes in all panels show the ratio of τM to typical periods τ of slow waves observed in those structures. The red solid lines show the values of a and b, above which the thermal mode becomes unstable. The red dashed lines indicate the intervals for which the thermal mode instability growth time is up to 5 times longer than the corresponding acoustic period τ.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.