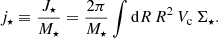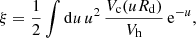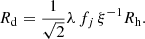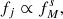| Issue |
A&A
Volume 644, December 2020
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202038474 | |
| Published online | 02 December 2020 | |
The impact of the halo spin-concentration relation on disc scaling laws
1
Université de Strasbourg, CNRS UMR 7550, Observatoire Astronomique de Strasbourg, 11 Rue de l’Université, 67000 Strasbourg, France
e-mail: lorenzo.posti@astro.unistra.fr
2
Department of Physics, ETH Zurich, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
3
Kapteyn Astronomical Institute, University of Groningen, 9700 AV Groningen, The Netherlands
4
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50127 Firenze, Italy
Received:
22
May
2020
Accepted:
16
October
2020
Galaxy scaling laws, such as the Tully–Fisher, mass-size, and Fall relations, can provide extremely useful clues on our understanding of galaxy formation in a cosmological context. Some of these relations are extremely tight and well described by one single parameter (mass), despite the theoretical existence of secondary parameters such as spin and concentration, which are believed to impact these relations. In fact, the residuals of these scaling laws appear to be almost uncorrelated with each other, posing significant constraints on models where secondary parameters play an important role. Here, we show that a possible solution is that such secondary parameters are correlated amongst themselves, in a way that removes correlations in observable space. In particular, we focus on how the existence of an anti-correlation between the dark matter halo spin and its concentration, which is still debated in simulations, can weaken the correlation of the residuals of the Tully–Fisher and mass-size relations. Interestingly, in using simple analytic galaxy formation models, we find that this happens only for a relatively small portion of the parameter space that we explored, which suggests that this idea could be used to derive constraints on galaxy formation models that have yet to be explored.
Key words: galaxies: kinematics and dynamics / galaxies: spiral / galaxies: structure / galaxies: formation
© L. Posti et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The fact that some of the most basic and fundamental dynamical properties of disc galaxies, such as mass, velocity, and angular momentum, are very simply correlated to one another is a crucial testimony of how galaxies assembled in our Universe. The relationships between such structural and dynamical properties, often called scaling laws, are invaluable probes of how galaxies have formed and evolved (McGaugh et al. 2000; Dutton et al. 2007; Lelli et al. 2016a; Posti et al. 2019a).
The simple power-law shapes of many observed scaling relations are commonly used as a test-bed for theoretical galaxy formation models. The observed slopes and normalisations of, for example, the mass-velocity relation (Tully & Fisher 1977; McGaugh et al. 2000, hereafter TF relation), the mass-size relation (Kormendy 1977, hereafter MS relation), and the mass-angular momentum relation (Fall 1983, hereafter Fall relation) can in principle directly constrain the galaxy-halo connection, which is the backbone of any galaxy formation model in the Λ cold dark matter (ΛCDM) cosmogony (Mo et al. 1998; Lapi et al. 2018; Posti et al. 2019a). The assembly and the structure of CDM halos is well understood and we know that they are fully rescalable, that is, there exist simple power-law scalings between mass, velocity, angular momentum, size, etc. (e.g. Mo et al. 2010). These relations for halos immediately translate into those for galaxies through some fundamental parameters of the galaxy-halo connection, such as the efficiency at turning baryons into stars or the efficiency at retaining the angular momentum initially acquired from the gravitational torques exerted by nearby structures (e.g. Posti et al. 2019a).
In ΛCDM, the TF relation is set to first order by the stellar-to-halo mass relation (e.g. Navarro & Steinmetz 2000). Halos acquire angular momentum through tidal torques at turnaround (e.g. Peebles 1969) and when the galaxy disc settles in the centre, incorporating a given fraction of that angular momentum; its size then depends on the amount of angular momentum of the halo (e.g. Fall & Efstathiou 1980). The fact that the baryonic TF relation (McGaugh et al. 2000; Lelli et al. 2016a), relating the total mass in stars and cold gas to the flat circular velocity, appears tighter than the stellar TF relation makes the picture more complicated, as it indicates that the scatter in the stellar-to-halo mass relation might be related to the scatter in cold gas mass. As such, the small scatter of the baryonic TF is still challenging for our current understanding of galaxy formation (Di Cintio & Lelli 2016; Desmond 2017).
The residuals of the TF around the mean also carry important information that is sensitive to the details of the galaxy formation process (e.g. Courteau & Rix 1999; Pizagno et al. 2007; van der Kruit & Freeman 2011). In particular, considering for example stellar mass and rotational velocity as two fundamental properties of a galaxy, if the residuals of the TF were found to correlate with a third property (e.g. galaxy size), it would then mean that the TF is not a fundamental law, but just a projection of a more general M − V − R relation. Thus, many have looked for additional quantities that correlate with the TF residuals, only to find no significant correlations (e.g. Barton et al. 2001; Kannappan et al. 2002; McGaugh 2005; Courteau et al. 2007). In particular, the fact that the TF residuals do not appear to correlate with the disc size (Lelli et al. 2016a; Ponomareva et al. 2018, but see also Mancera Piña et al. 2020a who instead find a correlation in the dwarf galaxy regime) nor with the residuals of the MS relation (McGaugh 2005; Desmond 2017) poses several challenges to our understanding of disc galaxies. For instance, Dutton et al. (2007, see also Dutton & van den Bosch 2012) generated rather sophisticated semi-empirical models, based on the assumption that the angular momentum of the galaxy is proportional to that of the halo, and found that it was complicated to find a model that matched the observed scaling laws while having a negligible correlation in the TF residuals versus MS residuals (when calculated at a fixed mass, not luminosity, see e.g. Fig. 10 in Dutton et al. 2007). In fact, this issue has later been used to argue that the observed absence of correlations in the TF and MS residuals provides evidence against the hypothesis that the galaxy’s and halo’s specific angular momenta are directly proportional, leaning towards an empirical, but less physically motivated, anti-correlation between galaxy size and halo concentration (Desmond et al. 2019; Lelli et al. 2019).
However, these simple inferences often neglect the existence of correlations between the parameters of the theory themselves. For instance, it has been proposed that the halo spin and concentration are in fact correlated with each other (Macciò et al. 2007; Johnson et al. 2019) and, furthermore, there are reasons to expect that the stellar-to-halo mass fraction and angular momentum fraction are also correlated (e.g. Dutton & van den Bosch 2012). In this paper, we examine the question of how these correlations impact our expectations on the residuals of galaxy scaling relations. We focus, in particular, on the impact of two physical effects on the residuals of the TF, MS, and Fall relation: We allow (i) the halo spin to be anti-correlated with the halo concentration (as it is observed in N-body simulations, e.g. Macciò et al. 2007) and (ii) the stellar-to-halo mass fraction to be correlated with the stellar-to-halo specific angular momentum fraction (as it is expected if the formation of disc galaxies proceeds inside-out, e.g. Romanowsky & Fall 2012; Pezzulli et al. 2015; Posti et al. 2018a). Our goal here is then to understand the effect of these two ingredients in a rather isolated and simplified context. Thus, we generated semi-empirical models based on the assumption that the galaxy’s and halo’s angular momenta are related, but we keep this deliberately simple in order to answer the question of whether the addition of the two new ingredients mentioned above can help in reproducing the observed disc scaling laws.
We note, however, that the correlation of the residuals of scaling laws are intrinsically noisy observables that typically provide a very poor statistical inference compared to, for instance, the global shape (slope, normalisation) of the scaling laws themselves. In fact, (i) just by definition, they rely on a fit of the observed scaling law, which is itself subject to systematic uncertainties; (ii) estimating a correlation coefficient from a discrete distribution of points is sensitive to Poisson noise for the sample sizes typically considered here (hundreds and thousands); (iii) covariance and correlation estimators are sensitive to outliers and biases in the population samples. To mitigate these limitations, we used the Spitzer Photometry and Accurate Rotation Curves catalogue of nearby spirals (SPARC, see Lelli et al. 2016b), which is of the highest quality for dynamical studies and which has already been used to study this topic (Desmond et al. 2019; Lelli et al. 2019). However, even though this is currently the best available data-set, it does not remove all of the issues mentioned above.
Throughout the paper, we use a fixed critical overdensity parameter Δ = 200 to define virial masses, radii, etc. of dark matter haloes and the standard ΛCDM model, with parameters estimated by the Planck Collaboration VI (2020). This includes the baryon fraction, which is fb ≡ Ωb/Ωm ≃ 0.157, and the Hubble constant, which is H0 = 67.4 km s−1 Mpc−1.
2. Models
Here, we describe the ingredients and the procedure that we used to build our analytic models. These rely heavily on the seminal paper of Mo et al. (1998, hereafter MMW98). These simple models neglect the contribution of the gas to the dynamics, hence we restrict the comparison to stellar-dominated galaxies in the SPARC sample of Lelli et al. (2016b).
2.1. Dark matter halo population
We generated a population of dark matter halos as follows.
Mass function. We started by sampling an analytic halo mass function, which is a well-known property of the cosmological model we adopted. In particular, we used the halo mass function from Tinker et al. (2008, evaluated and sampled using the code hmf, Murray et al. 2013).
Spin. Each halo was assigned a spin parameter of 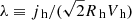 (see Bullock et al. 2001), where Rh, Vh, and jh are the virial radius, velocity, and specific angular momentum, respectively. The spin parameter λ was drawn from a log-normal distribution with a mean of
(see Bullock et al. 2001), where Rh, Vh, and jh are the virial radius, velocity, and specific angular momentum, respectively. The spin parameter λ was drawn from a log-normal distribution with a mean of 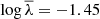 and a scatter of σλ = 0.22 dex (e.g. Macciò et al. 2007).
and a scatter of σλ = 0.22 dex (e.g. Macciò et al. 2007).
Halo density profiles. We assumed that each DM halo follows a Navarro et al. (1996, hereafter NFW) profile, which is characterised by the following two parameters: the virial mass Mh and concentration c. These two parameters follow a well-established anti-correlation, known as the c − Mh relation, such that more massive halos are less concentrated. We assigned the halo concentration following the parametrisation of the c − Mh relation from Dutton & Macciò (2014), with an intrinsic scatter of σc = 0.11 dex (but this could be as high as 0.16 dex, see e.g. Diemer & Kravtsov 2015).
Spin-concentration anti-correlation. We allowed the spin λ and the concentration c of DM halos to be negatively correlated, as is found in numerical N-body simulations (e.g. Macciò et al. 2007). The existence of this negative correlation might be a result of the assembly history of haloes, that is, haloes that have assembled later spin faster and have shallower density profiles due to the material deposited in the outskirts by recent mergers (e.g. Johnson et al. 2019). However, it is still debated whether this correlation is a robust prediction of ΛCDM and how much it is sensitive to the sample selection, since including or excluding halos that are defined to be unrelaxed seems to have an effect on the measured strength of this correlation (e.g. Macciò et al. 2007; Neto et al. 2007). As this issue does not appear to be fully settled, it is worthwhile asking what happens to the predictions of a semi-empirical galaxy formation model that includes this correlation. Since we could not find any analytic description of this correlation, we parametrised the λ − c correlation with a correlated 2D normal distribution in log λ and log c, with a correlation coefficient rλ − c that is a free parameter of the model. Hereafter, it is shown how one of our main results is that only a tight range of values of this parameter allowed us to reproduce the absence of correlation of the residuals of observed scaling relations. In Appendix A, we perform a simple exploration of the public halo catalogues of the dark-matter-only Bolshoi simulation (Klypin et al. 2016; Rodríguez-Puebla et al. 2016), where we estimate that the correlation coefficient is of the order of rλ − c ≃ − 0.3.
2.2. Galaxies
We assigned a single galaxy to each dark matter halo, thus assuming that each galaxy is central to its halo.
Stellar mass. Each halo hosts a galaxy whose stellar mass M⋆ follows a given stellar-to-halo mass relation, in this case not from abundance matching but from Posti et al. (2019a). This is an unbroken power-law relation which is valid for spiral galaxies, and it was in fact derived using data from the SPARC galaxy catalogue. We assumed a scatter of σM⋆ − Mh = 0.15 dex, similar to what is typically expected for the M⋆ − Mh relation (e.g. Moster et al. 2013) and measured using a variety of techniques (More et al. 2011; Yang et al. 2009; Zu & Mandelbaum 2015, see also Wechsler & Tinker 2018, and references therein, for a recent review).
Stellar density profiles. We assumed that galaxies are thin exponential discs, with a stellar surface density of Σ⋆ = Σ0 exp(−R/Rd), where Rd is the disc scale length and 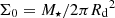 is the central surface density. As we neglected the presence of a gas disc, we restrict the comparison to stellar-dominated galaxies in the SPARC sample, that is MHI/M⋆ < 1.
is the central surface density. As we neglected the presence of a gas disc, we restrict the comparison to stellar-dominated galaxies in the SPARC sample, that is MHI/M⋆ < 1.
Circular velocity. The circular velocity of our model galaxies is made up of the contribution of dark matter (VDM) and stars (V⋆) as 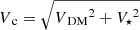 , where both V⋆ and VDM are analytic functions for an exponential disc and an NFW profile, respectively (Freeman 1970; Navarro et al. 1996).
, where both V⋆ and VDM are analytic functions for an exponential disc and an NFW profile, respectively (Freeman 1970; Navarro et al. 1996).
Disc scale length. We calculated the disc scale lengths using the iterative procedure proposed by MMW98. The specific angular momentum of a disc galaxy, assuming that stars are on circular orbits, is as follows:
If the rotation curve had been perfectly constant and equal to Vh, for example, in the case of a dominant singular isothermal halo (MMW98), then the disc specific angular momentum would have been equal to 2RdVh; thus, for convenience, we introduce the ratio of j⋆ to 2RdVh, that is1
where u = R/Rd, such that j⋆ = 2RdVhξ. In our model, galaxies acquire angular momentum from the same tidal torques that set the dark halo spinning, thus we can relate the stellar angular momentum j⋆ to the halo spin parameter λ by introducing the retained fraction of angular momentum fj ≡ j⋆/jh, from which it follows that 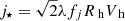 . By rearranging this, together with Eqs. (1) and (2), we can write the relation between the disc size and halo size as
. By rearranging this, together with Eqs. (1) and (2), we can write the relation between the disc size and halo size as
In practice, to solve for Rd for each model galaxy, we have to proceed iteratively (as in MMW98). We started with a first guess for Rd by setting ξ = 1, which is the case of an isothermal halo that gives j⋆ = 2RdVh, and an expression for fj that is discussed below. With this guess for Rd, we proceeded to compute ξ as in Eq. (2) and subsequently Rd again as in Eq. (3). We iterated this procedure five times for each galaxy, which is enough to guarantee convergence on the value of the disc scale length.
Retained fraction of angular momentum. We finally allowed the ratio of stellar-to-halo specific angular momentum fj ≡ j⋆/jh to be a function of the stellar mass fraction fM ≡ M⋆/Mh. These kinds of models are commonly known as biased collapse models, where stars are formed from the inside-out cooling of gas, from the poorest angular momentum material to the richest angular momentum material (Dutton & van den Bosch 2012; Kassin et al. 2012; Romanowsky & Fall 2012; Posti et al. 2018a). Thus we have
where s is a free parameter of the model. We assumed an intrinsic scatter of σfj = 0.07 dex on this relation, which is consistent with the analysis of Posti et al. (2019a) on the local disc scaling laws. We note that the case of specific angular momentum equality between stars and the halo, fj = 1, for example, used by MMW98, is obtained if s = 0.
3. Results
In this section, we present the results of our modelling technique and comparisons to observations. In particular, we used a Monte-Carlo method to sample the distributions of dark matter halo parameters (mass, concentration, spin), we generated a catalogue of model galaxies, and then we fitted their scaling relations with power-laws. We start by comparing the predicted scaling laws with the observations, then we investigate how their scatter is affected by the model parameters, and finally we compare the predicted correlation of the TF and MS residuals with what is observed in SPARC.
Our aim here is not to find the best fitting parameters of the model and then discuss their physical implications; instead, we merely provide a proof-of-concept of the fact that introducing a λ − c correlation and an fj − fM correlation has a significant impact on the correlation of the TF versus MS residuals, which can fully erase them for a narrow range of parameters. Thus, in what follows, we first fix the two free parameters of the model (rλ − c = −0.4 and s = 0.4) and explore its predictions, and later we show what is the effect of varying these two parameters. A full fitting of the observations is left for a future work, with more parameters including a bulge component and a gas disc.
3.1. The Tully–Fisher, mass-size, and Fall relations
We now explore the predictions of the model, with fixed rλ − c = −0.4 and s = 0.4, on the TF, MS, and Fall relations. For the TF, we adopted two different radii to define the velocity plotted in the TF diagram in comparison with the SPARC observations: RTF = 2.2Rd and RTF = 5Rd. While the former is a very typical choice, commonly used for TF studies (e.g. Courteau & Rix 1999; Pizagno et al. 2007), we compare the latter with observations of Vflat, the velocity in the flat part of the rotation curves (e.g. Lelli et al. 2016a) since at 5Rd, the circular velocities of our model galaxies are approximately constant.
Figure 1 shows the TF, MS, and Fall relations for the SPARC sample (grey circles) with gas fractions of MHI/M⋆ ≤ 1 compared to the predictions of the model (red lines). The agreement of this simple analytic model is remarkable and even the intrinsic vertical scatter of the (stellar) TF of ∼0.05 dex in Vflat is almost consistent with that estimated on the dataset (∼0.04 dex, using the procedure outlined in Lelli et al. 2019).
 |
Fig. 1. Comparison of the predictions of the model with rλ − c = −0.4 and s = 0.4 (red lines) against the observations from the SPARC catalogue (grey circles). We adopt two different velocity definitions for the TF relation: V2.2, the circular velocity at 2.2Rd, and Vflat, which we compare with Vc(5Rd) where our model rotation curves are approximately flat. The light red band shows the 1σ intrinsic scatter of the model. |
It is interesting to notice that the agreement of the model with the TF relation is quite good for both velocity definitions (V2.2 and Vflat), meaning that the shape of the model’s rotation curves are, to first order, representative of those of real spirals. Also the observed sizes and angular momenta of spirals are in relatively good agreement with those expected by our analytic model of an exponential disc in an NFW halo. The predicted MS and Fall relations of the model are, however, possibly slightly shallower than what is observed. This might be related to the fact that we do not have bulges in our model: at fixed M⋆, the presence of a bulge would make a galaxy more compact and have a lower specific angular momentum (e.g. Romanowsky & Fall 2012).
The model predictions for the scaling laws are basically straight lines and this is mostly due to two facts. The TF is straight because we employed a power-law stellar-to-halo mass relation (thus monotonic in fM), which is suggested by the rotation curve analysis of Posti et al. (2019b) and it provides a good description of the disc galaxy distribution2 (Posti et al. 2019a). Nonetheless, the MS and Fall relations could still be non-linear since they strongly depend on the luminous and dark matter distribution within galaxies. In fact, to also obtain straight MS and Fall relations, it is also important to have log fj ∝ log fM as well (Posti et al. 2018a).
3.2. The Tully–Fisher and mass-size scatters and their correlation
While it is not completely new that a simple analytic model of the type presented in Sect. 2 is able to predict the general structure of disc galaxies relatively well, we now move to a more detailed analysis of the residuals of the disc scaling laws, on which models of this kind have had less successful comparisons with data (Courteau & Rix 1999; Dutton et al. 2007; Desmond et al. 2019). We show that when allowing the halo concentration and spin to be anti-correlated (rλ − c < 0) and the stellar angular momentum fraction to the stellar mass fraction to be correlated (s > 0), the models can actually predict residuals on the scaling laws in good agreement with what is observed.
In Fig. 2 we show the residuals on the TF as a function of the residuals on the MS and on the Fall relations. Here, we define residuals as ΔX = log X − log Xfit(M⋆) for X = Vflat, Rd, j⋆, where the fits to the scaling relations were computed with the procedure described in Lelli et al. (2019). The SPARC galaxies are shown as (grey) points, while the distribution of model galaxies is represented by the two (red) contours encompassing 68% and 95% of the total population, respectively. The figure also shows the histograms of the marginalised distributions of the residuals of the three scaling laws for the observed (grey) and model galaxies (red). From these histograms, it is clear that the scatter predicted by the model agrees very well with that of the SPARC sample, which perhaps only has a slightly tighter Fall relation than expected (0.20 dex as opposed to 0.23 dex of the model).
 |
Fig. 2. Residuals of the Tully–Fisher vs. mass-size (left) and of the Tully–Fisher vs. Fall relation (right). Data from SPARC are shown as grey circles, while the red curves are the 1- and 2-σ contours of the predicted galaxy distribution of the same model as in Fig. 1. The dashed line shows the slope of the correlation of the model. The histograms on top and on the right show the marginalised distributions of the respective residuals for the data (grey filled) and the model (red empty), respectively. |
More importantly, the model presented here has residuals on the TF and MS that are not correlated, as is shown by the dashed red line in the bottom left panel of Fig. 2. For this model, the Spearman’s rank correlation coefficient of the TF and MS residuals is negligible (−0.03 ± 0.02, where the uncertainty was estimated with a bootstrap technique). This proves that simple, semi-empirical models where the sizes of discs are physically linked to their angular momentum can be made compatible with current observational data on the sizes and rotational velocities of discs. Similarly, the model is also compatible with the shallow correlation that is observed between the residuals of the TF and Fall relations. This is also present in the observed scaling laws simply because the specific angular momentum of the discs is not independent of their rotation velocity.
3.3. The effect of the model’s intrinsic scatter on the TF versus MS residuals
Here, we explore what the effect is of the scatters of the various ingredients of the model on the relation between the residuals of the TF and MS. In particular, we show what happens if we vary the scatter of one particular ingredient of the model, while the others are fixed, amongst: (i) the stellar-to-halo mass relation (σM⋆ − Mh), the halo mass-concentration relation (σc − M), the retained fraction of angular momentum (σfj), and the halo spin parameter (σλ). These scatters are, in fact, an important property of the model which directly determine both the scatters of the observed scaling laws and their residuals; for example, a model with no scatter would predict scaling laws with null scatter and thus no residuals.
However, even in a simple framework such as ours, the model scatters combine in a rather non-trivial way, which makes it complicated to predict analytically what the relation is between (σM⋆ − Mh, σc − M, σfj, σλ) and the resultant residuals of the TF, MS, and Fall relations. Thus we have numerically explored how the predictions of the model vary as a function of the four scatters above while rλ − c and s are fixed in order to build some intuition of their effect on the correlation between the residuals on the TF and MS. We show this in Fig. 3. It is clear that while adopting a smaller or larger scatter on the distribution of fj does not significantly alter the prediction of the model, varying σc − M and σλ, on the other hand, has a significant effect on the correlation of the TF versus MS residuals. We also find that the resulting Spearman correlation coefficient does not significantly depend on the scatter of the M⋆ − Mh relation either: This is perhaps surprising since the M⋆ − Mh relation is the centrepiece of the galaxy–halo connection, but it is somewhat reassuring since the value of its scatter is still rather uncertain (e.g. Wechsler & Tinker 2018).
 |
Fig. 3. Effect of varying the four intrinsic scatters of our model, σM⋆ − Mh, σc − M, σfj, σλ, on the Spearman correlation coefficient of the residuals of the TF versus MS. Each curve was computed by varying only one scatter at a time, while leaving the others fixed to their fiducial values. The grey band shows the 1-σ uncertainty (estimated with a bootstrap) of the correlation of the observed residuals of the TF vs. MS in SPARC. |
Let us now analyse in more detail some limiting cases. In what follows, we discuss what happens for model galaxies at a fixed M⋆ and we probed their rotation curves at RTF = 5Rd to define Vflat.
-
(i)
For σc − M ≃ 0, the range of concentrations of halos of different Mh is very small as it is given only by the shallow slope of the c − Mh relation. At a fixed M⋆, both high-λ and high-Mh halos host galaxies with large Rd (because of Eq. (3)), thus they tend to have positive MS residuals. For a given M⋆, large Rd also implies a larger circular velocity, since the radius at which we probed the rotation curve, RTF, is closer to the peak of the curve (the peak is also higher for high-Mh halos). These effects combine to produce a positive correlation of the TF versus MS residuals.
-
(ii)
For a large σc − M (≃0.3 dex), the range of concentrations spanned by halos in a given M⋆ bin is instead large, such that variations in Vc are mainly caused by halos having different c. The larger σc − M, the more this effect is important over (i), so that high-c halos tend to have positive TF residuals. Since λ and c are anti-correlated and since Rd scales with λ and inversely with c (via the factor ξ in Eq. (3)), the TF versus MS residuals become significantly anti-correlated.
-
(iii)
For σλ ≃ 0, the variation of the disc sizes is proportional to fj and inversely proportional to c (via the factor ξ in Eq. (3)). Thus high-c halos tend to have negative MS residuals. This, together with the fact that high-c halos have larger Vc and thus positive TF residuals, induces an anti-correlation between the TF versus MS residuals.
-
(iv)
For a large σλ (≃0.3 dex), the variations of Rd at a fixed M⋆ are dominated by the variations in λ, such that high-λ halos have positive MS residuals. In this case, Vc is significantly influenced by two factors: (a) high-c halos have larger Vc and (b) high-λ implies high-Rd and therefore high-Vc, since the circular velocity in the TF is probed at a radius closer to its peak. While (a) tends to induce an anti-correlation of the TF versus MS residuals because of the λ − c anti-correlation, if σλ is large enough (b) becomes increasingly more important and tends to positively correlate the TF versus MS residuals.
In any case, while the correlation of the TF and MS residuals significantly depends on the scatter of the halo concentration-mass relation, most numerical studies are in agreement that the plausible range for σc − M is between 0.1 and 0.15 dex (e.g. Dutton & Macciò 2014; Diemer & Kravtsov 2015). We emphasise that the values of rλ − c and s that give the best match to the observations also slightly depend on the adopted value for σc − M.
3.4. The effect of varying the model parameters on the residuals across the rotation curves
We now explore what the effect is of the two key parameters of the model, the spin-concentration correlation rλ − c, and the stellar fraction-angular momentum fraction correlation s. Since we have full rotation curves both in the data and in the model, for completeness we show what the effect is of varying rλ − c or s, while fixing the other on the correlation of the TF and MS residuals across the rotation curve (similarly to Desmond et al. 2019). In particular, we consider the rotation curve as a function of radius R; we fitted the Vc(R)−M⋆ relation at that radius and we define the TF residuals as a function of radius as ΔVc(R) = log Vc(R)−log Vc, fit(R|M⋆), where log Vc, fit(R|M⋆) is the velocity from the fit at a given radius and stellar mass. We did this for both the SPARC data and our models.
First, we show in Fig. 4 the behaviour of the Spearman correlation coefficient of the TF and MS residuals as a function of rλ − c and s, when the TF is evaluated at RTF = 5Rd. While the correlation coefficient monotonically increases for increasing rλ − c; it appears to be always negative for all values of s, with a clear maximum in the range of 0.2 ≲ s ≲ 0.6. In this range of s, the values of the Spearman correlation coefficient are compatible with what is observed in SPARC.
 |
Fig. 4. Effect of varying the halo spin-concentration correlation (rλ − c) and the power-law index of the relation between fj and fM (s) on the Spearman correlation coefficient of the residuals of the TF versus MS. The grey band is the same as in Fig. 3. |
Figure 5 shows the comparison of the correlation coefficient of the TF and MS residuals as a function of the radius where the TF is evaluated for the data (grey dashed) and for our fiducial model (thick red). The model is in very good agreement with what is observed across the wide range probed by rotation curves in the outskirts of spirals: Both the model and the data have a negligible correlation of the TF and MS residuals for R ≳ Rd. On the other hand, the model is not reliable in the innermost regions (R ≲ Rd) since we do not include a bulge component. In fact, in this simple model, the Vc in the inner regions is typically still dominated by dark matter; thus, at a fixed mass, the Vc of a galaxy with a larger Rd is larger because it is evaluated at a larger physical radius and VDM rises close to the centre.
 |
Fig. 5. Effect of changing the correlation coefficient between halo spin and concentration rλ − c (left) and the slope of the relation between the stellar angular momentum fraction and the stellar mass fraction s (right) on the correlation of the TF and MS residuals as a function of the radius where the TF velocity was measured. The grey dashed curve shows the data from the SPARC sample, while the different red curves are models with different values of such parameters. In both panels, the thick red curve is our fiducial model (shown also in Figs. 1 and 2) with rλ − c = −0.4 and s = 0.4; while we fixed s = 0.4 in the left panel and rλ − c = −0.4 in the right panel. The grey area marks the region where the predictions of our model are not reliable, since we do not include a bulge component in our galaxies. |
Desmond et al. (2019) already noted the fact that having basically uncorrelated residuals across the rotation curve corresponds, in this framework, to an anti-correlation between the residuals on the halo concentration Δ c and the disc scale length Δ Rd at a fixed stellar mass (Δc ≃ −0.5 ΔRd in the case of our model). However, while Desmond et al. (2019) impose this correlation a posteriori to explain the observed residuals, here it follows naturally from the correlations of parameters of the theory, which may have well-defined physical origins: λ and c are correlated since halos that have assembled later, and are therefore less concentrated, spin faster (e.g. Johnson et al. 2019, see also Bett et al. 2007); and fj and fM are correlated since star formation in discs proceeds inside-out, collapsing material at progressively larger j (so-called biased collapse, e.g. Dutton & van den Bosch 2012; Romanowsky & Fall 2012; Kassin et al. 2012).
The different thin red curves in Fig. 5 show the effect of varying rλ − c (left panel) and s (right panel) on the correlation of the TF versus MS residuals as a function of the radius. At fixed M⋆, high-λ halos tend to have positive MS residuals since they host high-Rd galaxies. At the same time, high-Rd also implies positive TF residuals, since the TF is probed in the rising part of the rotation curve, which leads to positive Spearman coefficients. This can be significantly counteracted with a λ − c anti-correlation: In fact, if at fixed M⋆, high-λ halos have low-c, then their circular velocity has a lower peak and this can lead to negative TF residuals if the anti-correlation strength rλ − c is strong enough. Both models with too high or too low rλ − c (≳ − 0.2 or ≲ − 0.6 respectively) seem to be ruled out by the current data. The value of the optimal spot, rλ − c ≈ −0.4, is instead compatible with state-of-the-art N-body simulations (see Appendix A and Macciò et al. 2007).
A similar behaviour, but slightly more complicated in the details, is observed if we vary the power-law index (s) of the relation between fj and fM. A model in which fj is constant, that is s = 0, has a significant correlation of the TF and MS residuals that strongly varies with the radius, from a positive to negative correlation. This effect is, again, mitigated by an increasing value of s that tends to make the correlation less prominent and more constant as a function of the radius, which is in better agreement with the SPARC data. We note that some of the effects mentioned in Sect. 3.3 do depend, in a rather non-trivial way, on the radius (i.e. those related to Vc affecting the TF residuals) and it is thus not surprising that their interplay also depends, non-trivially, on the radius, leading to the behaviours presented in Fig. 5. However, of particular interest is the value of s ∼ 0.4 at which we have the optimal spot, since that is precisely the value that is required to match the observations of the Fall relation3 (see Posti et al. 2018b).
3.5. Limitations of our model
Our results are useful to get a first order understanding of the importance of the λ − c and fj − fM correlations in reproducing the observed disc scaling laws. In this work, we showcase the effect of these two ingredients in a deliberately simple galaxy formation model, with the purpose of isolating – as much as possible – the effect that these new ingredients have. Naturally, for this reason, our model is far from being complete and has a number of limitations that one should keep in mind.
For instance, Dutton et al. (2007) developed sophisticated semi-empirical models, which are very similar to ours in spirit, in order to predict the TF and MS relations and the correlation of their residuals. With respect to what we have presented here, their models neglect the possibility of a λ − c or of a fj − fM correlation; however, they do include a bulge component, halo contraction, and a prescription for the formation of stars out of a gaseous disc. In their work, they show what the effect is of all the ingredients that they include in determining the shape of the TF and MS relations, as well as on the correlation of their residuals, and they find that they all play a role in principle. Our work should in fact be considered complementary to theirs, as we have shown what the effect is of two previously unexplored parameters (rλ − c and s) on the correlation of the TF versus MS residuals. Their effects should be dominant over those of the additional ingredients that Dutton et al. (2007) included, at least for the galaxies we considered here: All SPARC galaxies have relatively small bulges and we have focussed on a radial range where the bulge should be sub-dominant anyway (R > Rd); in our analysis, we have excluded gas-dominated discs and Desmond et al. (2019) already pointed out that halo contraction seems to have a minor effect on the correlation of TF versus MS residuals. To make sure that the last point also applies to our models, we ran our model again, also including a prescription for halo contraction parametrised in the same way as in Dutton et al. (2007): We find that the effect it has on the correlation coefficient of the TF versus MS residuals is marginal with respect to the effect of rλ − c and s in Fig. 4.
Our models can, and will in the future, be made much more predictive by adding some of the additional ingredients mentioned above. For example, the absence of a bulge component limits our predictive power in the inner regions of massive spirals and the absence of a cold gas component limits our inference at dwarf mass scales, where galaxies are increasingly more gas-dominated (e.g. SPARC). In particular, the fact that the baryonic TF relation appears tighter than the stellar TF relation might indicate that the cold gas mass should, for reasons that have yet to be understood, tightly correlate with the halo mass at a given stellar mass (e.g. Desmond 2017). Also, in our model, stars are assumed to be on circular orbits, while in reality some asymmetric drift is present in real galaxies and can, in principle, modify the stellar specific angular momentum from that in Eq. (1), especially for low-mass discs (e.g. Posti et al. 2018b; Mancera Piña et al. 2020b).
Dutton et al. (2007, see also Firmani & Avila-Reese 2000; van den Bosch 2000) noticed that if star formation and surface density are related, this impacts the scaling laws, since a halo with a larger spin forms a larger disc, with a lower surface density, thus forming fewer stars. This effect, which is not considered in our model, induces at a fixed Mh an anti-correlation of M⋆ with λ which, when combined with a λ − c anti-correlation, makes galaxies residing in halos with different λ to scatter approximately along the TF. While this is potentially important for understanding the residuals of the TF, this effect is based on the idea that the disc total mass (gas+stars) to halo mass relation is more fundamental than the stellar-to-halo mass relation and on a star formation law with a fixed density threshold. This might however not be the case if, for instance, the link of disc mass to halo mass is actually determined by the self-regulatory action of star formation, which primarily sets the stellar-to-halo mass relation regardless of the specific form of the star formation law (e.g. Lilly et al. 2013). Therefore, the importance of the star formation law in setting the scatter of scaling relations appears to be an interesting possibility, which however needs further scrutiny including a complete treatment of feedback.
Recently, Jiang et al. (2019) used cosmological hydrodynamical simulations to study the relation between the specific angular momentum of galaxies and dark matter halos and found evidence for a weak correlation, due to a combination of complex phenomena that lead to the formation of galaxies (see also Danovich et al. 2015). These results are potentially very interesting since they revisit the physical basis of the MMW98 study; however, it has yet to be demonstrated whether they can reproduce the observed Fall relation since from their main result j⋆/jh ∝ λ−1, it would follow that 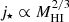 – because
– because 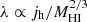 – which is not compatible with observations of the Fall relation, unless in the case of a quasi-linear stellar-to-halo mass relation (M⋆ ∝ Mh) which is excluded by the data (Posti et al. 2019a). In any case, their results highlight that while the classical framework of MMW98 is capable of representing the overall shape of the scaling laws, the physics it describes is inevitably limited and its results should be taken into account with caution. The advantage of the MMW98 framework is that it encapsulates all the complexity of galaxy formation into a couple of simple parameters, fj and fM, and it is successful since the observed galaxy–halo connection is indeed overall simple (Posti et al. 2019a).
– which is not compatible with observations of the Fall relation, unless in the case of a quasi-linear stellar-to-halo mass relation (M⋆ ∝ Mh) which is excluded by the data (Posti et al. 2019a). In any case, their results highlight that while the classical framework of MMW98 is capable of representing the overall shape of the scaling laws, the physics it describes is inevitably limited and its results should be taken into account with caution. The advantage of the MMW98 framework is that it encapsulates all the complexity of galaxy formation into a couple of simple parameters, fj and fM, and it is successful since the observed galaxy–halo connection is indeed overall simple (Posti et al. 2019a).
4. Summary and conclusions
Galaxy disc scaling laws can be used extensively to provide powerful constraints for galaxy formation models. For instance, the observed absence of correlations between the residuals of the TF and MS relations has been claimed to pose a challenge to traditional analytic models based on the assumption that disc sizes are regulated by halo angular momentum. In this contribution, we revisit this issue and we show that including correlations amongst some parameters of the galaxy formation model, which have some physical grounds, can help in reproducing what is observed. Our aim here is to provide a proof-of-concept of the fact that the inclusion of previously unexplored correlations of the theory’s parameters has a significant effect on the prediction of the disc scaling laws. In summary, we find the following.
-
If we allow the halo concentration to be anti-correlated to halo spin (as suggested by N-body simulations, e.g. Macciò et al. 2007) and the stellar-to-halo specific angular momentum fraction to be correlated to the stellar-to-halo mass fraction (as it is needed to reproduce the observed angular momenta of galaxies, e.g. Posti et al. 2018b), a simple semi-empirical model where disc sizes follow from the disc angular momentum can have correlations of TF-MS residuals and TF-Fall residuals, as observed.
-
The introduction of an anti-correlation between halo spin and concentration induces an anti-correlation between disc size and concentration, which in turn is needed to wash out the correlation between the residuals of the TF and MS relations. Thus, contrary to some recent claims, we were able to find a semi-empirical model based on the assumption that the halo angular momentum is related to that of the disc, which correctly reproduces the scaling relations.
-
The range of parameters rλ − c and s (controlling the λ − c and fj − fM correlations) allowed by the observations is relatively tight. In particular, we find that the values of these parameters that provide the best representation of the observed galaxy distribution are interestingly compatible with the values expected by N-body simulations (Appendix A and Macciò et al. 2007) and by previous works (e.g. Posti et al. 2018b).
Despite the fact that the residuals of the galaxy scaling laws are an intrinsically noisy observable, it is worthwhile modelling them since they carry unique constraints to galaxy formation models. In order to surpass the current limitations given by the paucity of high-quality data for dynamical studies of disc galaxies, it is, thus, imperative to observationally measure the scaling laws on a much larger and, hopefully, complete sample of spirals in the local Universe, albeit with a similar quality in order to be able to model all of the facets of galaxy formation properly, which remains a difficult long-term challenge.
It is important to note that the parameter ξ is just the inverse of what MMW98 call fR. We use a different notation here so as to not confuse the reader with the ratio of disc size to halo virial radius, which we refer to as fR in a previous paper (Posti et al. 2019a).
It is important to specify that this is valid only for discs, as it is well known that the stellar-to-halo mass relation has a different shape for different galaxy types (e.g. Dutton et al. 2010; Rodríguez-Puebla et al. 2015).
In fact, from 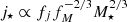 (Eq. (5) in Posti et al. 2018b), if
(Eq. (5) in Posti et al. 2018b), if 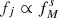 , it follows that
, it follows that 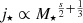 , since roughly
, since roughly 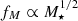 (Moster et al. 2013; Posti et al. 2019b). The slope of the observed Fall relation of spirals is therefore matched for about s ≈ 0.45.
(Moster et al. 2013; Posti et al. 2019b). The slope of the observed Fall relation of spirals is therefore matched for about s ≈ 0.45.
Acknowledgments
We thank the referee for a report that helped improving the quality and clarity of this paper. We are grateful to Aaron Dutton for useful discussions. LP acknowledges support from the Centre National d’Etudes Spatiales (CNES). BF and RI acknowledge funding from the Agence Nationale de la Recherche (ANR project ANR-18-CE31-0006 and ANR-19-CE31-0017) and from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 834148). GP acknowledges support by the Swiss National Science Foundation, grant PP00P2_163824.
References
- Barton, E. J., Geller, M. J., Bromley, B. C., van Zee, L., & Kenyon, S. J. 2001, AJ, 121, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Wu, H.-Y. 2013, ApJ, 762, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Bett, P., Eke, V., Frenk, C. S., et al. 2007, MNRAS, 376, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Dekel, A., Kolatt, T. S., et al. 2001, ApJ, 555, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S., & Rix, H.-W. 1999, ApJ, 513, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S., Dutton, A. A., van den Bosch, F. C., et al. 2007, ApJ, 671, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Danovich, M., Dekel, A., Hahn, O., Ceverino, D., & Primack, J. 2015, MNRAS, 449, 2087 [NASA ADS] [CrossRef] [Google Scholar]
- Desmond, H. 2017, MNRAS, 472, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Desmond, H., Katz, H., Lelli, F., & McGaugh, S. 2019, MNRAS, 484, 239 [Google Scholar]
- Di Cintio, A., & Lelli, F. 2016, MNRAS, 456, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Diemer, B., & Kravtsov, A. V. 2015, ApJ, 799, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., & Macciò, A. V. 2014, MNRAS, 441, 3359 [Google Scholar]
- Dutton, A. A., & van den Bosch, F. C. 2012, MNRAS, 421, 608 [NASA ADS] [Google Scholar]
- Dutton, A. A., van den Bosch, F. C., Dekel, A., & Courteau, S. 2007, ApJ, 654, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., Conroy, C., van den Bosch, F. C., Prada, F., & More, S. 2010, MNRAS, 407, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M. 1983, in Internal Kinematics and Dynamics of Galaxies, ed. E. Athanassoula, IAU Symp., 100, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M., & Efstathiou, G. 1980, MNRAS, 193, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Firmani, C., & Avila-Reese, V. 2000, MNRAS, 315, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [Google Scholar]
- Jiang, F., Dekel, A., Kneller, O., et al. 2019, MNRAS, 488, 4801 [CrossRef] [Google Scholar]
- Johnson, J. W., Maller, A. H., Berlind, A. A., Sinha, M., & Holley-Bockelmann, J. K. 2019, MNRAS, 486, 1156 [CrossRef] [Google Scholar]
- Kannappan, S. J., Fabricant, D. G., & Franx, M. 2002, AJ, 123, 2358 [NASA ADS] [CrossRef] [Google Scholar]
- Kassin, S. A., Devriendt, J., Fall, S. M., et al. 2012, MNRAS, 424, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Yepes, G., Gottlöber, S., Prada, F., & Heß, S. 2016, MNRAS, 457, 4340 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J. 1977, ApJ, 218, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., Salucci, P., & Danese, L. 2018, ApJ, 859, 2 [Google Scholar]
- Lilly, S. J., Carollo, C. M., Pipino, A., Renzini, A., & Peng, Y. 2013, ApJ, 772, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016a, ApJ, 816, L14 [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016b, AJ, 152, 157 [Google Scholar]
- Lelli, F., McGaugh, S. S., Schombert, J. M., Desmond, H., & Katz, H. 2019, MNRAS, 484, 3267 [NASA ADS] [CrossRef] [Google Scholar]
- Macciò, A. V., Dutton, A. A., van den Bosch, F. C., et al. 2007, MNRAS, 378, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Mancera Piña, P. E., Fraternali, F., Oman, K. A., et al. 2020a, MNRAS, 495, 3636 [CrossRef] [Google Scholar]
- Mancera Piña, P. E., Posti, L., Fraternali, F., Adams, E. A. K., & Oosterloo, T. 2020b, A&A, submitted [arXiv:2009.06645] [Google Scholar]
- McGaugh, S. S. 2005, Phys. Rev. Lett., 95, 171302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McGaugh, S. S., Schombert, J. M., Bothun, G. D., & de Blok, W. J. G. 2000, ApJ, 533, L99 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [Google Scholar]
- Mo, H., van den Bosch, F. C., & White, S. 2010, Galaxy Formation and Evolution (Cambridge: Cambridge University Press) [Google Scholar]
- More, S., van den Bosch, F. C., Cacciato, M., et al. 2011, MNRAS, 410, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [Google Scholar]
- Murray, S. G., Power, C., & Robotham, A. S. G. 2013, Astron. Comput., 3, 23 [CrossRef] [Google Scholar]
- Navarro, J. F., & Steinmetz, M. 2000, ApJ, 538, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
- Neto, A. F., Gao, L., Bett, P., et al. 2007, MNRAS, 381, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1969, ApJ, 155, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzulli, G., Fraternali, F., Boissier, S., & Muñoz-Mateos, J. C. 2015, MNRAS, 451, 2324 [NASA ADS] [CrossRef] [Google Scholar]
- Pizagno, J., Prada, F., Weinberg, D. H., et al. 2007, AJ, 134, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponomareva, A. A., Verheijen, M. A. W., Papastergis, E., Bosma, A., & Peletier, R. F. 2018, MNRAS, 474, 4366 [NASA ADS] [CrossRef] [Google Scholar]
- Posti, L., Pezzulli, G., Fraternali, F., & Di Teodoro, E. M. 2018a, MNRAS, 475, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Posti, L., Fraternali, F., Di Teodoro, E. M., & Pezzulli, G. 2018b, A&A, 612, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Posti, L., Marasco, A., Fraternali, F., & Famaey, B. 2019a, A&A, 629, A59 [CrossRef] [EDP Sciences] [Google Scholar]
- Posti, L., Fraternali, F., & Marasco, A. 2019b, A&A, 626, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-Puebla, A., Avila-Reese, V., Yang, X., et al. 2015, ApJ, 799, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Puebla, A., Behroozi, P., Primack, J., et al. 2016, MNRAS, 462, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., & Fall, S. M. 2012, ApJS, 203, 17 [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- van den Bosch, F. C. 2000, ApJ, 530, 177 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C., & Freeman, K. C. 2011, ARA&A, 49, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Wechsler, R. H., & Tinker, J. L. 2018, ARA&A, 56, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., & van den Bosch, F. C. 2009, ApJ, 695, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Zu, Y., & Mandelbaum, R. 2015, MNRAS, 454, 1161 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: λ–c correlation in the Bolshoi-Planck simulation
We used the publicly available catalogues of the Bolshoi-Planck simulation provided by Rodríguez-Puebla et al. (2016) to have a simple estimate of the strength of the λ − c correlation for halos in a dark matter only simulation with the standard Planck cosmology. We considered the z = 0 snapshot of the simulation where the halos were identified and characterised with the ROCKSTAR software (Behroozi et al. 2013).
We calculated the residuals at a fixed halo virial mass Mh of the λ − Mh and c − Mh relations, where λ is defined as in Bullock et al. (2001). We show, in Fig. A.1, the correlation of the Δ λ and Δ c residuals for the halos in the simulation with the black solid contours containing 68%−95% of the halo population, respectively. We then calculated the covariance matrix of the distribution of points in this diagram and we used this matrix to define the 2D normal distribution shown with the red dashed contours in Fig. A.1. This Gaussian has standard deviations of σlog c ≃ 0.18 dex and σlog λ ≃ 0.25 dex (consistent with previous estimates, e.g. Macciò et al. 2007) and a correlation coefficient of rλ − c ≃ −0.29. Since our analysis is very simple, this number should just be used to have a rough idea of what the correlation coefficient that is expected for the halo population in ΛCDM is.
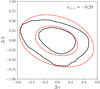 |
Fig. A.1. Correlation between the λ and c residuals at a fixed halo virial mass, for the z = 0 halo population in the Bolshoi-Planck simulation, represented with the black solid contours (containing 68%−95% of the halo population). The red dashed contours are the 1- and 2-σ contours of the 2D normal distribution defined with the covariance matrix calculated from the distribution of points in this plane. |
All Figures
 |
Fig. 1. Comparison of the predictions of the model with rλ − c = −0.4 and s = 0.4 (red lines) against the observations from the SPARC catalogue (grey circles). We adopt two different velocity definitions for the TF relation: V2.2, the circular velocity at 2.2Rd, and Vflat, which we compare with Vc(5Rd) where our model rotation curves are approximately flat. The light red band shows the 1σ intrinsic scatter of the model. |
| In the text | |
 |
Fig. 2. Residuals of the Tully–Fisher vs. mass-size (left) and of the Tully–Fisher vs. Fall relation (right). Data from SPARC are shown as grey circles, while the red curves are the 1- and 2-σ contours of the predicted galaxy distribution of the same model as in Fig. 1. The dashed line shows the slope of the correlation of the model. The histograms on top and on the right show the marginalised distributions of the respective residuals for the data (grey filled) and the model (red empty), respectively. |
| In the text | |
 |
Fig. 3. Effect of varying the four intrinsic scatters of our model, σM⋆ − Mh, σc − M, σfj, σλ, on the Spearman correlation coefficient of the residuals of the TF versus MS. Each curve was computed by varying only one scatter at a time, while leaving the others fixed to their fiducial values. The grey band shows the 1-σ uncertainty (estimated with a bootstrap) of the correlation of the observed residuals of the TF vs. MS in SPARC. |
| In the text | |
 |
Fig. 4. Effect of varying the halo spin-concentration correlation (rλ − c) and the power-law index of the relation between fj and fM (s) on the Spearman correlation coefficient of the residuals of the TF versus MS. The grey band is the same as in Fig. 3. |
| In the text | |
 |
Fig. 5. Effect of changing the correlation coefficient between halo spin and concentration rλ − c (left) and the slope of the relation between the stellar angular momentum fraction and the stellar mass fraction s (right) on the correlation of the TF and MS residuals as a function of the radius where the TF velocity was measured. The grey dashed curve shows the data from the SPARC sample, while the different red curves are models with different values of such parameters. In both panels, the thick red curve is our fiducial model (shown also in Figs. 1 and 2) with rλ − c = −0.4 and s = 0.4; while we fixed s = 0.4 in the left panel and rλ − c = −0.4 in the right panel. The grey area marks the region where the predictions of our model are not reliable, since we do not include a bulge component in our galaxies. |
| In the text | |
 |
Fig. A.1. Correlation between the λ and c residuals at a fixed halo virial mass, for the z = 0 halo population in the Bolshoi-Planck simulation, represented with the black solid contours (containing 68%−95% of the halo population). The red dashed contours are the 1- and 2-σ contours of the 2D normal distribution defined with the covariance matrix calculated from the distribution of points in this plane. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.