| Issue |
A&A
Volume 643, November 2020
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202039143 | |
| Published online | 16 November 2020 | |
A physical model for the magnetosphere of Uranus at solstice time
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris,
5 place Jules Janssen,
92195
Meudon,
France
e-mail: filippo.pantellini@observatoiredeparis.psl.eu
Received:
10
August
2020
Accepted:
2
October
2020
Context. Uranus is the only planet in the Solar System whose rotation axis and orbital plane are nearly parallel to each other. Uranus is also the planet with the largest angle between the rotation axis and the direction of its magnetic dipole (roughly 59°). Consequently, the shape and structure of its magnetospheric tail is very different to those of all other planets in whichever season one may consider. The only in situ measurements were obtained in January 1986 during a flyby of the Voyager II spacecraft. At that date, Uranus was near solstice time, but unfortunately the data collected by the spacecraft were much too sparse to allow for a clear view of the structure and dynamics of its extended magnetospheric tail. Later numerical simulations revealed that the magnetic tail of Uranus at solstice time is helically shaped with a characteristic pitch of the order of 1000 planetary radii.
Aims. We aim to propose a magnetohydrodynamic model for the magnetic tail of Uranus at solstice time.
Methods. We constructed our model based on a symmetrised version of the Uranian system by assuming an exact alignment of the solar wind and the planetary rotation axis and an angle of 90° between the planetary magnetic dipole and the rotation axis. We do also postulate that the impinging solar wind is steady and unmagnetised, which implies that the magnetosphere is quasi-steady in the rotating planetary frame and that there is no magnetic reconnection at the magnetopause.
Results. One of the main conclusions is that all magnetic field lines forming the extended magnetic tail follow the same qualitative evolution from the time of their emergence through the planet’s surface and the time of their late evolution after having been stretched and twisted several times downstream of the planet. In the planetary frame, these field lines move on magnetic surfaces that wind up to form a tornado-shaped vortex with two foot points on the planet (one in each magnetic hemisphere). The centre of the vortex (the eye of the tornado) is a simple double helix with a helical pitch (along the symmetry axis z) λ = τ[vz+Bz/(μ0ρ)1/2], where τ is the rotation period of the planet, μ0 the permeability of vacuum, ρ the mass density, vz the fluid velocity, and Bz the magnetic field where all quantities have to be evaluated locally at the centre of the vortex. In summary, in the planetary frame, the motion of a typical magnetic field of the extended Uranian magnetic tail is a vortical motion, which asymptotically converges towards the single double helix, regardless of the line’s emergence point on the planetary surface.
Key words: planets and satellites: magnetic fields / planet–star interactions / plasmas / magnetohydrodynamics (MHD) / methods: analytical
© F. Pantellini 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The magnetosphere of Uranus was traversed by the Voyager II spacecraft on January 1986. Most of the planet’s parameters such as the rotation period, the internal magnetic dipole strength, and the orientation of the associated axis were discovered or refined on that occasion (Ness et al. 1986; Desch et al. 1986; Bagenal 1992, 2013; Richardson & Smith 2003). Since then, we have also learned that the solar wind impacting the magnetosphere has a high Mach number and low β (the thermal pressure to magnetic pressure ratio), with a typical sonic Mach number in the range of 20–30 and β in the range of 0.1–0.2. These values imply wind velocities largely in excess of the fast magnetosonic speed with typical fast Mach numbers in the 6 to 12 range. Voyager’s measurements also showed that the planet’s internal magnetic dipole intensity is high enough to counter the solar wind’s dynamic pressure. Uranus is thus surrounded by a magnetopause (the boundary between the solar wind flow and the regions dominated by the planetary magnetic field) and by a bow shock located upstream of the magnetopause. In the sub-solar direction, the magnetopause and the bow shock are located at a distance of ~25RU and ~30RU upstream of the planet’s centre (RU is the radius of Uranus). Numerical simulations show that the extended nightside Uranian magnetosphere is a particularly complex one compared to the other planetary magnetospheres in the Solar System. Such a complexity is due to both the large angle of 59° between the planet’s rotation axis and a rotation period fast enough (sidereal period: 17.24 h) to be comparable to the magnetosphere’s relaxation time. The magnetosphere of Uranus is thus highly variable on a daily timescale. In addition, the planet’s rotation axis being nearly parallel with respect to the orbital plane also makes the magnetosphere highly variable on a seasonal timescale (with an orbital period of 84 yr). For comparison, Saturn’s rotation and magnetic axis are aligned (see e.g. Cowley 2013, Fig. 2), so under constant wind conditions its magnetosphere is stationary, which is an enormous difference with respectto Uranus. Unfortunately, in situ measurements of the Uranian magnetosphere are very sparse. Voyager II, the only spacecraft having approached Uranus, only explored a small portion of the planet’s magnetic tail of the order of ~ 60 RU, which is a scale much shorter than the characteristic spatial oscillations of 103 RU observed in the pioneering simulations by Tóth et al. (2004). Since that time, only a relatively small number of simulations have been published. The reasons are likely the lack of new observational data for the simulations to be confronted with and the exceptionally large simulation domain required to capture the oscillations of the magnetic tail. As for Tóth et al. (2004), all subsequent simulations are also based on single or multi-fluid equations for equinox configuration (Cao & Paty 2017; Griton et al. 2018) and solstice configuration (Cao & Paty 2017; Griton & Pantellini 2020; Lai & Kiang 2020). It is however worth mentioning that only in Tóth et al. (2004) is the simulation domain large enough to allow for a fully developed magnetic tail. This is also the case in the simulations by Griton et al. (2018) and Griton & Pantellini (2020), where the authors opted to accelerate the planet’s rotation in order to reduce the spatial scale of the tail oscillation and thus the size of the simulation domain. Cao & Paty (2017) and Lai & Kiang (2020) focused on the dayside structure of the magnetosphere, which allows for a small simulation domain but excludes the possibility to observe the oscillations in the tail of the simulation, which is a central aspect of the physical model we present in this study.
The physical model presented here is restricted to the case of Uranus at solstice. In order to reduce complexity, while keeping all the fundamental ingredients that make the specificity of Uranus, we symmetrised the solstice configuration. First, we increased the angle between the magnetic dipole and the rotation axis from 59 to 90°. Second, we aligned the planet’s rotation axis and the solar wind direction, which are in reality separated by 7°. Finally, we postulate that the solar wind is not magnetised (as in the Tóth et al. 2004 simulations) so that no magnetic reconnection is allowed in the model. Reconnection is be briefly discussed at the end of this paper. A more in-depth discussion of the subject can be found in the work by Masters (2014).
The paper is organised as follows. In Sects. 2 and 3, we comment on the symmetries and the physical assumptions of the model. In Sects. 4 and 5, we discuss the time evolution and the twisting of a typical magnetic field line in the magnetospheric tail. In Sect. 6, we give a crude estimate of the pole-to-pole electric current induced by the planet’s rotation. In Sects. 7 and 8, we briefly comment on the model’s limits and speculate on the generic case (with no symmetries). Conclusions are given in Sect. 9.
2 A simplified configuration of the problem
In order to reduce the complexity of the real system and facilitate insight, we assume that the planet’s rotation axis points in the direction opposite to the solar wind direction. We also postulate that the magnetic dipole of the planet is centred on the planet and oriented perpendicularly to the rotation axis, as illustrated in Fig. 1.
In addition to assuming a stationary solar wind, we also assume that it does not carry any magnetic field. The wind is therefore rotationally invariant with respectto the z-axis. Also, in agreement with Voyager’s measurement, the wind is assumed to be supersonic and the planetary’s internal field strong enough to support an anti-sunward-oriented magnetopause as shown in Fig. 1. We add that, during its flyby, Voyager II saw the magnetic field intensity rise by one order of magnitude at the magnetopause, providing an observational justification for neglecting the magnetic field carried by the solar wind (see Ness et al. 1986). As there are no field lines in the wind, the magnetopause can also be identified as the magnetic surface traced by the outermost magnetic field lines connected to the planet.
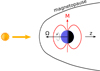 |
Fig. 1 Symmetrised configuration of Uranus at solstice used in our physical model. The rotation axis and solar wind flow are both aligned on the z-axis. Ω is the planet’s angular velocity. The planetary field is a dipole of strength M located at the centre of the planet and oriented perpendicularly to the z-axis. |
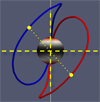 |
Fig. 2 Example of symmetries of system in Fig. 1. System is viewed looking to the planet along the z-axis. Two mutually conjugate magnetic field lines are shown, as well as two conjugate points (represented by the two large yellow dots). |
2.1 Symmetries of the simplified configuration
The system depicted in Fig. 1 has many interesting symmetries. First, since the wind direction and the planet’s rotation axis are aligned and since the former is rotationally invariant, the system can be assumed to be time stationary in the rotating frame, at least on timescales of the order of the rotation period. Second, the system is invariant under successive application of the following actions: (1) a specular reflection with respect to a plane containing the z-axis followed by (2) a specular reflection with respect to another plane perpendicular to the first one and also sharing the z-axis, followed by (3) a reversal of all charges in the system. We note that action (3) corresponds to a symmetry of the magnetohydrodynamic (MHD) system of equation, which does not hold at small (kinetic) scales. In practice, the action of reversing the charges in an MHD system corresponds to the action of reversing the sign of all currents and magnetic fields in the system.
2.2 Specificities of the simplified configuration
Figure 2, extracted from a 3D MHD simulation respecting the symmetries of the configuration of Fig. 1, shows two field lines that are mutually symmetric with respect to application of the three mentioned symmetry actions. For the remainder of the paper, we call such pairs of field lines “conjugate field lines”, and the points with reversed x and y coordinates are referred to as “conjugate points” (large yellow points in the figure). We do not list all consequences of the system’s symmetries. We do however note that one important consequence is that only the z component of the fluid velocity can be non-zero on the z-axis, which also implies that magnetic field lines are not allowed to cross the z-axis. Another consequence is that on conjugate points, the z components of both the current and the magnetic field are reversed, while the perpendicular components (with respect to the z-axis) are equal. The exact contrary holds for the fluid velocity.
3 Model assumptions
Besides the symmetries mentioned in the previous section, we have to make some assumptions about the boundaries. These are the magnetopause and the planetary surface. Concerning the magnetopause, we assume it to be an impermeable surface. No plasma fromthe wind can penetrate through the surface, which is coherent with the assumption of no magnetic field in the wind. On the other hand, the planetary surface is the only source or sink of magnetic flux. As already mentioned, we assumed a dipolar intrinsic planetary field, which we placed at the planet’s centre, implying that field lines emerge at the planet’s magnetic equator. The plasma is governed by the equations of ideal MHD everywhere except at the planet’s surface, where a finite conductivity is assumed such that the foot points of the magnetic field lines are allowed to move across the surface. Even though the detailed structure of the magnetosphere may depend on the boundary conditions, we assume that the latter are not critical in shaping the distant tail structure and choose not to specify these boundaries further. As for most plasmas in the solar system, the interaction of the solar wind with a planetary magnetosphere can be treated in the weakly relativistic limit. We therefore assume that the plasma in our model is governed by the equations of magnetohydrodynamic limited to first order in v∕c, where v is a characteristic velocity (fluid velocity or phase velocity), and c the speed of light. Under such circumstances when changing from one frame of reference to another (e.g., from the planetary rotating frame to the inertial frame), velocities transform according to the Galilean transformation rules. All other quantities (density, pressure, and magnetic field) are invariant. Finally, on Uranus, the escape velocity from the planet’s surface is small compared to the Alfvén speed. We therefore ignored gravity.
4 Trajectory of a magnetic field line
In a three-dimensional system, magnetic field lines can form complex and interlaced structures. The difficulty of apprehending a complex three dimensional magnetic structure is even greater in a case where the structure is a time-dependent one. As already mentioned, the model, based on the symmetries of Fig. 1, can be considered to be time stationary in the rotating frame. Thus, in the following, unless specified otherwise, we place ourself in the rotating frame. The downside of choosing the rotating frame instead of the inertial frame is that in addition to the standard forces, which are the pressure gradient and the Lorentz force, we have to take into account the Coriolis and the centrifugal forces in the momentum equations (see e.g. Tóth et al. 2004). In order to further facilitate the investigation of a complex three-dimensional structure, it is sometimes instructive to trace the motion of the intersection of the magnetic field lines with a given plane. Figure 3 illustrates the case of the intersection of two conjugate field lines with the magnetic equatorial plane. We note that due to the system’s symmetries, the intersection points of the conjugate field lines are always equidistant from the z-axis, for any arbitrary plane that contains the z-axis. The description of the time evolution of the intersecting points of the magnetic field lines with the equatorial plane is one of the main objectives of the present study (see Sect. 4.1). However, before proceeding to the formulation of a physical model of the simplified version of the magnetosphere of Uranus at solstice, it isworth mentioning another of its properties by noting that field lines successively emerging at a given position on the planet’s surface do all follow the exact same path. Obviously, all these field lines together define a magnetic surface. An example of a portion of such a magnetic surface described by the time evolution of two conjugate field lines is shown in Fig. 4. Figure 4 illustrates a central aspect of the system: field lines move towards an asymptotic position (the grey tubes located inside the magnetic surfaces). From the figure, one may already deduce that the trajectory of the intersecting point of the field line with an arbitrary plane is a spiral with the asymptotic position at its centre.
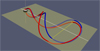 |
Fig. 3 Twisted field lines on Uranus at solstice. Points corresponding to the intersection of two conjugate magnetic field lines with any plane containing the z-axis are disposedsymmetrically on each side of the axis. |
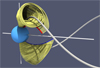 |
Fig. 4 Planetary (rotating) frame. Magnetic surfaces described by the time evolution of two conjugate magnetic field lines (red and blue). Only a portion of the surface described by the future evolution of the two field lines is shown. We anticipate that the thick grey tubes show the end positions of the field lines. |
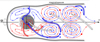 |
Fig. 5 Polar view in the rotating frame. Shown are the trajectory of the foot points of selected field lines in the ionosphere (one hemisphere only), as well as the trajectory of the field lines’ intersection points with the equatorial plane. Blue and red correspond to mutually conjugate lines. The grey tubes represent the asymptotic position of all field lines. |
4.1 Trajectory on the planetary surface and in the (magnetic) equatorial plane
Having assembled all the basic ingredients, and based on results from numerical simulations, we are now in a position to propose a coherent physical model of a Uranus-at-solstice-type magnetosphere. We start, in Fig. 5, with the presentation of a qualitative sketch of the path of the field line crossing point in the equatorial plane and the path of their foot points on the planetary surface. We note that, as a consequence of the difference between the velocity of a fluid parcel and the velocity of a virtual point, such as the point corresponding to the intersection of a field line with a plane, the pattern described by the projected fluid velocity can be very different from the pattern described by the motion of a virtual point, as in Fig. 5. This is namely the case for the multiple spiralling trajectories in the equatorial plane that are not seenwhen tracing the projection of the fluid velocity. The reason is that in some parts of the equatorial plane, for example near position 2 in the figure, field lines are oriented nearly parallel with respect to the plane, in which case the velocity of the intersection point and the fluid velocity differ substantially. On the other hand, the projected fluid velocity and the velocity of the intersection point coincide when the field line is perpendicular to the plane. Of course, the path described by a field line depends on the basic parameters of the problem (rotation period of the planet, solar-wind dynamic pressure, planetary field strength, etc.), but also on the position of its point of emergence on the planetary surface. However, from the topological point of view, all field lines behave as described in Fig. 5 as long as they do not go back to the planet, an eventuality not shown on the figure.
We now comment more thoroughly in Fig. 5, where three successive positions of a typical magnetic field line (inthis case the blue line) are labelled with numbers. At position 1, the foot point of the line on the planetary surface and the crossing point of the field line on the equatorial plane have already moved away from their emerging point at the magnetic equator. Simply as a consequence of its shape, which makes the emerging field line parallel to the planetary surface, the foot point of an emerging dipolar field line moves towards the pole. Obviously, the poleward motion of the foot point does not simply follow a meridian line as its motion is guided by various forces (pressure gradient, Lorentz, Coriolis, and centrifugal) and by the properties of the boundary. We note that a similar, but not symmetric poleward motion affects the second foot point located below the equatorial plane. However, recalling the symmetries of the system (see Fig. 2), we know that the shape of a given field line in the hidden hemisphere is equal to the shape of the conjugate field line in the visible hemisphere. Thus, in Fig. 5, the hidden part of the blue line can be obtained by applying the transformations x → −x and y → −y to the red line.
In order to keep things as simple as possible, even though emerged field lines may disappear again through the planetary surface, we only considered the case of field lines not disappearing through the planet’s surface. The foot point of these lines must then converge towards some asymptotic position near the nominal magnetic pole. As all foot points move along spirals that also represent the trace of the corresponding magnetic surfaces (which do not cross by definition), it follows that the field lines must converge towards a common position represented by the black square in Fig. 5. Because of the tailward bending of the field lines, the asymptotic position is expected to be located tailward of the nominal magnetic pole. Figure 5 suggests that an asymmetric polar vortex in the ionospheric plasma circulation has to be expected on Uranus. Distant observations of auroras using the Hubble Space Telescope are become possible and may be used as a tool to get access to the magnetic structure near the magnetic poles Lamy et al. (2012, 2017). Unfortunately, besides the fact that observed signals are quite faint and not sufficiently sharp to offer further help, no distant observations have ever been made at solstice. The next opportunity is in 2028, 42 yr after the last occurrence in 1986.
We now take inspiration from past MHD simulations (see e.g. Tóth et al. 2004; Griton et al. 2018) to understand the more profound reason for the formation of the vortices in Fig. 5. Indeed, one of the basic outcomes of these simulations is that the tailward extending magnetic field lines wind helically around the z-axis. This apparently trivial and intuitive result is an important constraint for our physical model. Looking at Fig. 5, we note that the only possible way to make the blue line in position 1 wind around the z-axis is to stretch the visible part of the line over both the pole and the z-axis until, guided by the magnetopause, it crosses the equatorial plane near the point labelled 2. Once the return point of the field line has disappeared below the equatorial plane, the line continues to be stretched and twisted by 180° before emerging at position 3, and so on. One should note that all these movements are constrained by the prohibition of the field line to intersect the z-axis. For completeness, the path of the conjugate line (in red) is also shown in Fig. 5.
As pointed out earlier (see discussion in Fig. 4), the intersecting points of a field line with the equatorial plane are seen to move on a spiral converging towards a final position given by the intersecting points of the light grey tubes in Fig. 5. Thus, the two (red and blue) field lines labelled 2 will gradually move towards the leftmost grey tube in the figure, the upper strand of the blue line labelled 2 will move towards the central grey tube, and the blue line labelled 3 will move towards the rightmost grey tube. We note that the polarity of the field lines converging towards the position of the central tube (which is connected to the magnetic pole below the equatorial plane) is opposite with respect to the polarity of the field lines converging towards the other visible portions of the grey tube (this portion being connected to the visible pole).
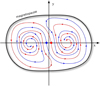 |
Fig. 6 Planetary rotating frame. Trajectories of the intersection point of two conjugate magnetic field lines with a plane perpendicular to the z-axis located downstream of the planet. Colours distinguish the trajectory of two mutually conjugate lines. The large blue and red dots indicate the position where the two conjugate lines cross the plane in the first place. |
4.2 Trajectory in a plane perpendicular to the z-axis
Figure 6 shows the trajectory of two conjugate field lines in a plane perpendicular to the z-axis approximately positioned at the z location and corresponding to the centre of a couple of vortices in Fig. 5. The two points near the origin indicate the position where the two field lines appear first, that is, at the time when the field lines’ loop-return points reach the plane. As in the equatorial plane, after emergence, the two intersecting points of each of the two conjugate field lines (the red and the blue line) move on spiral shaped trajectories towards the asymptotic position at the centre of the two vortices. Again, it may be worth pointing out that the polarity (i.e. the z component of the magnetic field) is opposite in the two vortices. We now make a few more comments on Fig. 6. First, we note that at the position where the field lines appear, the magnetic field is necessarily oriented perpendicularly to the z-axis, so the field line velocity and the plasma velocity in the z direction must be equal at this particular position. One of the macroscopic consequences of this is that the whole magnetic tail structure as seen froman inertial frame is seen to propagate downstream of the planet at exactly the plasma speed at these locations. Second, except in the region of acceleration near the planet, the structure of Fig. 6 is representative for all positions along the z-axis modulo a rotation about the z-axis.
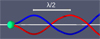 |
Fig. 7 A double helix in the magnetic tail of Uranus. Time asymptotic position of a generic magnetic field line is a double helix with helical pitch λ. Colour-code refers to the sign of Bz. |
5 Wavelength of the magnetic tail
As already mentioned, numerical simulations show that the magnetic tail of Uranus at solstice is spatially twisted downstream of the planet (along the z-axis in our model). As distance from the planet grows, the twist along the z-axis rapidly converges towards a sharply defined spatial oscillation scale λ = 2π∕k. In simulations, the spatial oscillation may be best made evident by plotting an “old” field line, meaning a field line that had time to become twisted several times with respect to the position of its foot points on the planet. Such a field line is located close to the centre of the tornado (showing up as vortices in the cuts of Figs. 5 and 6) over most of its length. An example of such a field line (the same as the grey line in Fig. 4) is shown in Fig. 7. It is probably illusory to search for an expression of the wavelength λ as a function of the global parameters of the problem. On one side, even while keeping within the strict limits of MHD theory and for the simple configuration of Fig. 1, the number of parameters required to fully specify the problem is pretty large as it includes the wind parameters (at least velocity, density, and pressure) as well as the planetary parameters (at least the dipole field strength, the rotation speed, and most likely the planetary radius). In addition, λ may also depend on the conditions at the planetary surface such as the ionospheric resistivity and the allowed mass flux from or towards the planet. Expressing λ as a function of the global parameters of the problem may be difficult or impossible, but expressing λ as a function of the plasma parameters in the tail or in some specific parts of is clearly conceivable. In this respect, we already mentioned in Sect. 4.2 that the z component of the plasma velocity near the field line turning point is equal to the phase speed of the whole magnetic structure. Thus, a measure of the velocity vz of the turning point of a field line allows us to write λ = τvz where τ = 2π∕Ω is the planet’s rotation period. In the next section, we show that λ can also be expressed as a function of the Alfvén speed measured near the centres of the vortices described earlier.
5.1 Equilibrium of forces near the vortices’ centres
We now know that in the frame of our simplified configuration of the Uranus-at-solstice magnetosphere, all field lines migrate towards the same asymptotic position reminiscent of the eye of an atmospheric tornado. In Fig. 8, a portion of the tornado’s eye is represented as a tube.
Since in the rotating frame the system can be assumed to be in a quasi-steady state, we may write the momentum equation as follows:
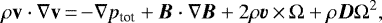 (1)
(1)
where ρ is the plasma mass density, ptot ≡ p + B2∕2 the total (plasma+magnetic) pressure, and D the vector pointing from the z-axis to the point under consideration. To avoid confusion, we name all terms in Eq. (1). On the left-hand side, we have the inertial term, while on the right-hand side, we have, successively, the pressure gradient term, the magnetic tension term, the Coriolis term, and the centrifugal term. Also, in order to ease readability, we set the vacuum permeability to μ0 = 1 in Eq. (1). Unless specified otherwise, we adhere to this convention for the remainder of the paper. Equation (1) can be simplified further near the vortex centre where the total pressure is expected to have an extremum (as for the gas pressure in the centre of a cyclone), so one may neglect the pressure gradient term in Eq. (1). In addition, as illustrated in Figs. 5 and 6, field lines become static when approaching the asymptotic positions implying that the fluid velocity must become more and more aligned on the magnetic field. The asymptotic position being characterised by a wavelength λ = 2π∕k in the z direction and an excursion D with respect to the z-axis we can then write
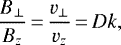 (2)
(2)
where the direction ⊥ has to be considered with respect to the z-axis. Accordingly, Eq. (1) can be simplified and rewritten as
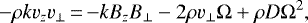 (3)
(3)
an equilibrium graphically illustrated in Fig. 8. Equation (3) has a surprisingly simple general solution:
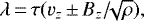 (4)
(4)
where 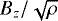 is the Alfvén speed in the z direction (not along the field direction).
is the Alfvén speed in the z direction (not along the field direction).
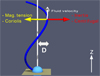 |
Fig. 8 Magnetic field line in tail of Uranus at solstice. In the planetary (rotating) frame, field lines converge towards an asymptotic position where they become motionless and where the fluid velocity and field lines are aligned. It turns out that only the four mentioned terms of the momentum equation (see Eq. (3)) ensure the equilibrium. |
5.2 An aside on numerical simulations
Expression (4) with the + sign was tested by Tóth et al. (2004), who found a significant discrepancy between estimate of the right hand side of Expression (4), giving λ ≈ 1300 RU and the wavelength observed in their simulation λobs ≈ 900 RU. The authorsascribe the discrepancy to a frictional interaction between the solar wind plasma and the helical tail. Such an effect cannot be excluded. However, besides the fact that the tailward extension of their simulation domain was too small (= 704 RU) to contain one full wavelength λ, the other important point we raise here is that, strictly speaking, Eq. (4) is only valid at two particular positions in the (x, y) plane, that is, at the centre of the vortices in Fig. 6. Instead, Tóth et al. (2004) evaluated the right-hand side of Eq. (4) by taking averages of vz, Bz, and ρ across the magnetic tail. Now, all simulations, including the ones by Tóth et al. (2004) show that the plasma parameters vary considerably in the (x, y) plane, even at large distances from the planet.
6 Order of magnitude estimate of the currents induced by the rotation
The twisting and stretching of the magnetic field lines in the tail do generate currents flowing to or from the polar regions in order to close by flowing over the ionosphere. Taking 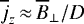 as an estimate of the average z component of the current at a position, z, down the tail, where the torsion of the field lines by the rotation is effective (e.g. at the position of the first vortex in Fig. 5), we find (using (2) as an estimate for the average
as an estimate of the average z component of the current at a position, z, down the tail, where the torsion of the field lines by the rotation is effective (e.g. at the position of the first vortex in Fig. 5), we find (using (2) as an estimate for the average 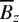 field) that
field) that 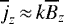 . Since all the magnetic field lines crossing half of the surface delimited by the magnetopause in the (x, y) plane of Fig. 6 (of order ~πD2) stem from an area S surrounding one of the magnetic poles, it follows that
. Since all the magnetic field lines crossing half of the surface delimited by the magnetopause in the (x, y) plane of Fig. 6 (of order ~πD2) stem from an area S surrounding one of the magnetic poles, it follows that 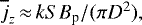 where Bp is the surface field strength given by
where Bp is the surface field strength given by 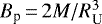 and M being the planetary dipole strength (units T m3). The total current flowing through a polar region is then
and M being the planetary dipole strength (units T m3). The total current flowing through a polar region is then 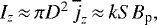 where SBp should be interpreted as the magnetic flux through the planetary surface due to all field lines from one hemisphere being sufficiently twisted to contribute to the current. For Uranus, M = 3.9 × 1017 Tm3, and simulations indicate that λ = 2π∕k ≈ 103RU. The total current at one pole can thus be estimated to be of the order
where SBp should be interpreted as the magnetic flux through the planetary surface due to all field lines from one hemisphere being sufficiently twisted to contribute to the current. For Uranus, M = 3.9 × 1017 Tm3, and simulations indicate that λ = 2π∕k ≈ 103RU. The total current at one pole can thus be estimated to be of the order 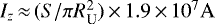 with a surface ratio
with a surface ratio 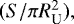 which we may arbitrarily guess to fall within the range of 10−1 to 10−3.
which we may arbitrarily guess to fall within the range of 10−1 to 10−3.
7 Limits of the model
The (inevitable) formation of magnetic vortices anchored on the planet is a challenging aspect of the model. Indeed, a continuous injection of magnetic field lines at the equator and a continuous concentration of field lines at the centre of the vortices is incompatible with the assumption of time steadiness given that the field intensity in the vortices increases with time. One may safely argue that the incoherence of the model is more conceptual than practical, atleast if the characteristic timescale for the flux concentration is long compared to the rotation period of the planet. A steady-state Dungey-type cycle (Dungey 1961), where magnetic flux emerges from the dayside planetary surface and disappears through the nightside surface of the planet, could be invoked. The problem is that the Dungey mechanism requires reconnection through the magnetopause and may only be a solution if reconnection impedes the twisting of the magnetic field lines. Such an eventuality (not allowed in our model, where the interplanetary plasma does not carry any magnetic field) cannot definitely be excluded for Uranus, as the duration of the Dungey cycle is comparable to the rotation period of the planet (e.g. Bagenal 2013). If, however, as simulations seem to suggest, the twisting of the magnetic field lines is real, even for the relatively slowly rotating Uranus, another mechanism must impede the vortical concentration of magnetic flux. The difficulty stems from the fact that there is no evident way to limit the vortical concentration of the magnetic flux other than by stopping the emergence of magnetic flux, in which case the only theoretically possible system would be a static one. On the other hand, if one assumes (1) a rigorous steady state; (2) that magnetic flux emerges through the planetary surface; and (3) the formation of a twisted magnetic tail, then, a mechanism of evacuation of the magnetic flux from the vortex centres must necessarily operate. Such a mechanism implies the topological reconfiguration of the stretched magnetic field lines approaching the vortex centre to detach them from the planet. However, a topological reconfiguration of a field line such as the one in Fig. 7 is not easily imaginable in a globally steady state system. Even a hypothetical reconfiguration through reconnection with an outer magnetic field through the magnetopause seems unrealistic given that the asymptotic field lines are located deep inside the volume delimited by the magnetopause (see Figs. 5 and 6). A reconfiguration through self-reconnection appears unrealistic for the same reasons, portions of a field line approaching the asymptotic position with opposite Bz polarity being always separated by a large distance (in comparison to an ion’s Larmor radius) either of order 2D in the tail (see Fig. 8) or of order RU, near the magnetic foot points. Finally, despite appearances, and the high degree of symmetry, the system is a complex one, plagued with ill-defined boundaries, for which no stability analysis has ever been made, even within the restrictive frame of ideal MHD. In addition, since the magnetic structure is neither axisymmetric nor periodic, we expect its global stability properties to differ substantially from the well-documented stability properties of tokamak plasmas. One may consider that the system is approximately axisymmetric in the vicinity of the vortex centre (where magnetic flux slowly concentrates) with a component of the flow velocity perpendicular to the axis of the vortex. Under such circumstances, Goedbloed et al. (2004) showed that the axisymmetric structure turns unstable as soon as the flow velocity exceeds the slow mode velocity. Whether or not this “trans-slow” instability plays a role in the reconfiguration process of a complex double helix magnetic tail cannot be established without a more in-depth numerical or theoretical stability analysis. It should be considered merely as one out of many other possible ideal (and non-ideal) fluid instabilities that may affect the system on the long timescale associated with the concentration of magnetic flux near the asymptotic position.
The conclusion we draw at this point is that the model is not compatible with a rigorous steady state. Catastrophic reconfigurations on a yet undetermined timescale must be invoked. Successive reconfigurations likely occur on a timescale of the order of the time necessary to substantially increase the vortical magnetic flux, but other external factors such as variations of the solar wind dynamic pressure or of the interplanetary magnetic field orientation (not considered in the model) may also play a role in triggeringthe reconfiguration.
8 Speculative extrapolation to the general case
Our model is admittedly an oversimplification for Uranus. With regard to what we learned about the planet after Voyager’s flyby in January 1986 (see Ness et al. 1986), the most drastic simplification is the assumption of a 90° angle between the planetary rotation axis and its magnetic dipole. While the consequences of having reduced the angle between the rotation axis and the solar wind direction from 7° to 0° are certainly minor, the consequences of having increased the angle between the rotation axis and the planetary magnetic field axis from 59° to 90° must be considered. Clearly, the principal difference of the real configuration with respect to the one in Fig. 1 is that with a 59° the two magnetic poles are not equivalent in the real case, where one magnetic pole is always on the dayside, while the other is always on the nightside. The system is still time stationary in the rotating frame, at least on not-too-long timescales, as discussed in Sect. 7, and as long as no interplanetary field is assumed, but many of the other symmetries exposed in Sect. 2.1 are lost. The simulations by Tóth et al. (2004) who used the effective orientations (see their Fig. 17) do indeed show that the symmetry between the polarities of the stretched and twisted field lines is broken, especially in the vicinity of the planet. The main reason is that the field lines emanating from the nightside pole have direct access to the volume enclosed by the magnetopause downstream of the planet, while the field lines emanating from the dayside pole have tocircumvent the planet first and therefore tend to run along the magnetopause. Interestingly, their simulation also shows that the asymmetry fades away rapidly downstream (over a distance much shorter than λ), suggesting that the spiralling movement of the magnetic field lines observed in our model may not apply to the field lines emanating from the nightside pole but also (to some extent) to the field lines emanating from the dayside pole. Whether the spiralling motion drives the magnetic field lines towards a curve as in our symmetric model (cf. Fig. 8), or much more likely towards a surface, is a question that may be investigated in new dedicated simulations.
The other important simplification of our model is the unmagnetised wind assumption, which excludes the possibility of magnetic reconnection at the magnetopause. Magnetic reconnection has been observed in simulations of a fast-rotating Uranus-type magnetosphere in the same configuration as the one of Fig. 1 except for the presence of a magnetised wind (see Griton et al. 2018, Fig. 1). The consequence of reconnection in the sketches of Figs. 5 and 6 would be an “erosion” of the outermost magnetic surfaces located near the magnetopause. However, a complete reconnection-driven disruption of all magnetic surfaces surrounding the asymptotic position is much too slow a process to be effective over distances of order λ downstream of the planet. For example, no significant erosion was observed in Griton et al. (2018).
9 Conclusions
We present an MHD-based physical model for the magnetic tail of a Uranus-type planet at solstice time. In order to limit complexity and facilitate understanding, we based our model on a symmetrised version of the Uranian system at solstice plunged in a unmagnetised solar wind. Consequently, in our model, the planet’s rotation axis is parallel with respect to the solar wind direction, the (centred) planetary magnetic dipole is perpendicular to the rotation axis, and no magnetic reconnection is possible at the magnetopause. Given these assumptions, a quasi-steady state can be reached in the rotating planetary frame. The main consequences we draw from the model are as follows: (1) magnetic field lines emerge near the magnetic equator, and their foot points move on a spiralling path (see Fig. 5) towards a final point located nightside of the nominal magnetic poles; (2) in the planetary (rotating) frame, each spiralling field line describes tornado-shaped magnetic surfaces (see Fig. 4); (3) the tornados’ eyes are thus surrounded by a “millefeuille” of magnetic surfaces, one for each emergence point on the planetary surface; (4) the two eyes are interlaced curves extending downstream of the planet with a characteristic wavelength λ given by Eq. (4). We note that the model implies a continuous accumulation of magnetic flux in the eyes and is thus incompatible with a rigorous steady state. Therefore, in the long-term, the system is expected to turn unstable and possibly subject to catastrophic reconfiguration of its magnetic structure, even under constant wind conditions.
Acknowledgements
Fruitful discussions with the newly founded Laboratoire Cogitamus, must be warmly acknowledged in this place. Thank you to the referee for his/her highly pertinent and constructive comments and suggestions.
References
- Bagenal, F. 1992, Annu. Rev. Earth Planet. Sci., 20, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bagenal, F. 2013, Planet. Magnetospheres (Dordrecht: Springer Science+ Business Media) [Google Scholar]
- Cao, X., & Paty, C. 2017, J. Geophys. Res. (Space Phys.), 122, 6318 [Google Scholar]
- Cowley, S. W. H. 2013, J. Geophys. Res. (Space Phys.), 118, 2897 [NASA ADS] [CrossRef] [Google Scholar]
- Desch, M. D., Connerney, J. E. P., & Kaiser, M. L. 1986, Nature, 322, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Dungey, J. W. 1961, Phys. Rev. Lett., 6, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Goedbloed, J., Beliën, A., van der Holst, B., & Keppens, R. 2004, Phys. Plasmas, 11, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Griton, L., & Pantellini, F. 2020, A&A, 633, A87 [CrossRef] [EDP Sciences] [Google Scholar]
- Griton, L., Pantellini, F., & Meliani, Z. 2018, J. Geophys. Res. (Space Phys.), 123, 5394 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, C.-M., & Kiang, J.-F. 2020, Sensors, 20, 1673 [CrossRef] [Google Scholar]
- Lamy, L., Prangé, R., Hansen, K. C., et al. 2012, Geophys. Res. Lett., 39 [Google Scholar]
- Lamy, L., Prangé, R., Hansen, K. C., et al. 2017, J. Geophys. Res. (Space Phys.), 122, 3997 [CrossRef] [Google Scholar]
- Masters, A. 2014, J. Geophys. Res. (Space Phys.), 119, 5520 [Google Scholar]
- Ness, N. F., Acuna, M. H., Behannon, K. W., et al. 1986, Science, 233, 85 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Richardson, J. D., & Smith, C. W. 2003, Geophys. Res. Lett., 30, 1206 [NASA ADS] [Google Scholar]
- Tóth, G., Kovács, D., Hansen, K. C., & Gombosi, T. I. 2004, J. Geophys. Res. (Space Phys.), 109, A11210 [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Symmetrised configuration of Uranus at solstice used in our physical model. The rotation axis and solar wind flow are both aligned on the z-axis. Ω is the planet’s angular velocity. The planetary field is a dipole of strength M located at the centre of the planet and oriented perpendicularly to the z-axis. |
| In the text | |
 |
Fig. 2 Example of symmetries of system in Fig. 1. System is viewed looking to the planet along the z-axis. Two mutually conjugate magnetic field lines are shown, as well as two conjugate points (represented by the two large yellow dots). |
| In the text | |
 |
Fig. 3 Twisted field lines on Uranus at solstice. Points corresponding to the intersection of two conjugate magnetic field lines with any plane containing the z-axis are disposedsymmetrically on each side of the axis. |
| In the text | |
 |
Fig. 4 Planetary (rotating) frame. Magnetic surfaces described by the time evolution of two conjugate magnetic field lines (red and blue). Only a portion of the surface described by the future evolution of the two field lines is shown. We anticipate that the thick grey tubes show the end positions of the field lines. |
| In the text | |
 |
Fig. 5 Polar view in the rotating frame. Shown are the trajectory of the foot points of selected field lines in the ionosphere (one hemisphere only), as well as the trajectory of the field lines’ intersection points with the equatorial plane. Blue and red correspond to mutually conjugate lines. The grey tubes represent the asymptotic position of all field lines. |
| In the text | |
 |
Fig. 6 Planetary rotating frame. Trajectories of the intersection point of two conjugate magnetic field lines with a plane perpendicular to the z-axis located downstream of the planet. Colours distinguish the trajectory of two mutually conjugate lines. The large blue and red dots indicate the position where the two conjugate lines cross the plane in the first place. |
| In the text | |
 |
Fig. 7 A double helix in the magnetic tail of Uranus. Time asymptotic position of a generic magnetic field line is a double helix with helical pitch λ. Colour-code refers to the sign of Bz. |
| In the text | |
 |
Fig. 8 Magnetic field line in tail of Uranus at solstice. In the planetary (rotating) frame, field lines converge towards an asymptotic position where they become motionless and where the fluid velocity and field lines are aligned. It turns out that only the four mentioned terms of the momentum equation (see Eq. (3)) ensure the equilibrium. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


